A 31-channel integrated “AC/DC” B₀ shim and RF receive array coil for improved 7 Tesla MRI

Abstract

PURPOSE:

To test an integrated “AC/DC” array approach at 7 Tesla, where B₀ inhomogeneity poses an obstacle for functional imaging, diffusion-weighted MRI, MR spectroscopy, and other applications.

METHODS:

A close-fitting 7T 31-channel brain array was constructed and tested using combined Rx and ΔB₀ shim channels driven by a set of rapidly-switchable current amplifiers. The coil was compared to a shape-matched 31-channel reference receive-only array for RF safety, signal-to-noise ratio (SNR), and inter-element noise correlation. We characterize the coil array’s ability to provide global and dynamic (slice-optimized) shimming using ΔB₀ field maps and echo planar imaging (EPI) acquisitions.

RESULTS:

The SNR and average noise correlation were equivalent to the 31ch reference array. Global and slice-optimized shimming provide 11% and 40% improvements respectively compared to baseline 2^nd-order spherical harmonic shimming. Birdcage transmit coil efficiency was similar for the reference and AC/DC array setups.

CONCLUSION:

Adding ΔB₀ shim capability to a 31ch 7T receive array can significantly boost 7T brain B₀ homogeneity without sacrificing the array’s RF performance, potentially improving ultra-high field neuroimaging applications that are vulnerable to off-resonance effects.

INTRODUCTION

Ultra-high field (UHF) brain imaging at 7 Tesla provides improved signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) compared to conventional field strengths of 1.5 and 3 Tesla MRI. The SNR gain enables high resolution imaging useful for depicting small brain structures, while the improved CNR derives from increased contrast such as T₂* for blood oxygenation level-dependent functional MRI (BOLD fMRI) and improved T₁ contrast for MR angiography. However, it has been difficult to achieve the full potential of UHF MRI in practice due to both static and time-varying perturbations of the static magnetic field (ΔB₀) introduced by the human body. These field inhomogeneities lead to a variety of image artifacts (1). Static ΔB₀ inhomogeneities arise primarily at the air-tissue interfaces (near the sinus, ear canal, and oral cavities). They cause a variety of problems including: (i) disruption of the RF pulse excitation in limited bandwidth pulses (such as shaped excitation pulses) as well as frequency selective pulses such as fat saturation pulses; (ii) spectroscopic line broadening; and (iii) signal voids, geometric distortion and blurring along the phase-encode direction in echo planar imaging (EPI) data. In standard gradient-echo BOLD fMRI, this leads to a loss in BOLD sensitivity (2), region-dependent resolution loss, difficulty in registering distorted EPI to a reference anatomical image (3), and in some cases singularities in the distortion that cause unrecoverable losses of information (3). The B₀ inhomogeneity is also problematic for measurements of fine-scale microscopic and mesoscopic anatomy based on T₂* since the overlaying macroscopic ΔB₀ patterns can mask subtle microstructural details. Time-varying ΔB₀ shifts arise from motion and motion-related physiological processes such as respiration. These lead to ghosting and ringing artifacts in multi-shot structural images as well as phase instability (time-varying distortion) in single-shot EPI time series. Unfortunately, the 1^st- and 2^nd-order spherical harmonic (SH) based shim coils available on most 7T scanners offer limited capacity for nulling the high-spatial order ΔB₀ profiles. Moreover, commercial 2^nd-order SH shim coils are typically not set up for rapid switching to compensate time-varying ΔB₀.

Both post-processing (4) and acquisition acceleration methods (5) have been used to reduce ΔB₀ induced geometric distortion in single-shot EPI at the expense of sacrificed spatial resolution and SNR. While now standard practice, significant geometric distortion remains, especially as measured in units of pixel displacement in high-resolution single-shot EPI (6). In contrast, improved B₀ shimming addresses geometric distortion at its source. Higher-order SH coils built into the gradient coil or operated as shim insert coils have the longest track record for B₀ shimming at 7T. Global 1^st-to-4^th order SH shimming of the whole brain at 7T has been used to improve B₀ homogeneity by 25% (σ^WB: standard deviation of ΔB₀ over the whole brain) and reduce geometric distortion in EPI (typically using up to 10A per SH channel) (7). SH shim currents can also be dynamically switched to optimally shim each slice in 2D acquisitions, however the size of these structures requires attention to eddy current effects through the use of pre-emphasis (8,9), probe monitoring (10), and/or constraints on current switching (11).

A second approach uses close-fitting multi-coil (MC) shim arrays with small loop coils patterned around the anatomical region-of-interest to generate non-orthogonal B₀ shim fields at high spatial orders (12),(13). These small, low-inductance coils can be driven by low-voltage, low-cost amplifiers (14). Because they are mounted nearer to the head, away from conductive structures in the magnet, they can be switched rapidly without inducing eddy currents (15)(14) and experience less induced voltage from gradient coil slewing. It has been shown that B₀-shim capability of small loops can share the structure (loop) of the Rx-coil element itself. In this approach, inductive chokes provide a DC bridge across the RF tuning capacitors (16–18). This approach has been employed for Rx/Tx loops as Integrated Parallel Receive, Excitation, and Shimming (iPRES) and for Rx-only arrays as the “AC/DC” coil array. Either enables a single array of loops on a close-fitting helmet to be used for both B₀ shimming and RF purposes. Despite the single-turn nature of most RF loop array, their close proximity to the body allows sufficient shim performance with modest current amplitudes (1–2A). While originally proposed as a tool for static or slice-by-slice optimized shimming with a given setting applied for the whole TR period, MC arrays have recently been used as a tool for dynamic local field control by exploiting the ability to rapidly switch to different B₀ states within the TR period. For example, a B₀ pattern can be created during RF excitation which facilitates zoomed imaging (19,20), improves lipid suppression for spectroscopy (21)(22), or reduces flip-angle inhomogeneity (23) and then returns to a “uniform B₀” setting during readout. MC arrays with greater numbers of turns have also been explored for image encoding as a supplement or replacement for conventional linear gradient coils (24,25)(26).

While beneficial at 3T (17),(27) and for primate imaging at 7T (28), the AC/DC or iPRES approach has not been shown for human imaging at 7T, where the need for shimming is greater. Additionally, technical barriers increase at ultrahigh field due to higher current needs, increased number of distributed RF capacitors, and exacerbated RF tuning and coupling challenges. In this work, we designed a 7T AC/DC coil array – with 31 RF receive channels and 31 B₀ shim channels – that addresses these technical barriers, constructed the array, and assessed its RF and dynamic B₀-shimming performance. We validated the shimming capabilities through B₀ field mapping and EPI-based brain imaging on healthy volunteers.

We previously explored the feasibility of adding B₀ shim capability to individual 7T receive elements (29); the AC/DC modifications for shimming produced similar SNR maps before/after the modification. Preliminary results from for the full AC/DC array were reported in a recent review paper (1) and abstract (30).

METHODS

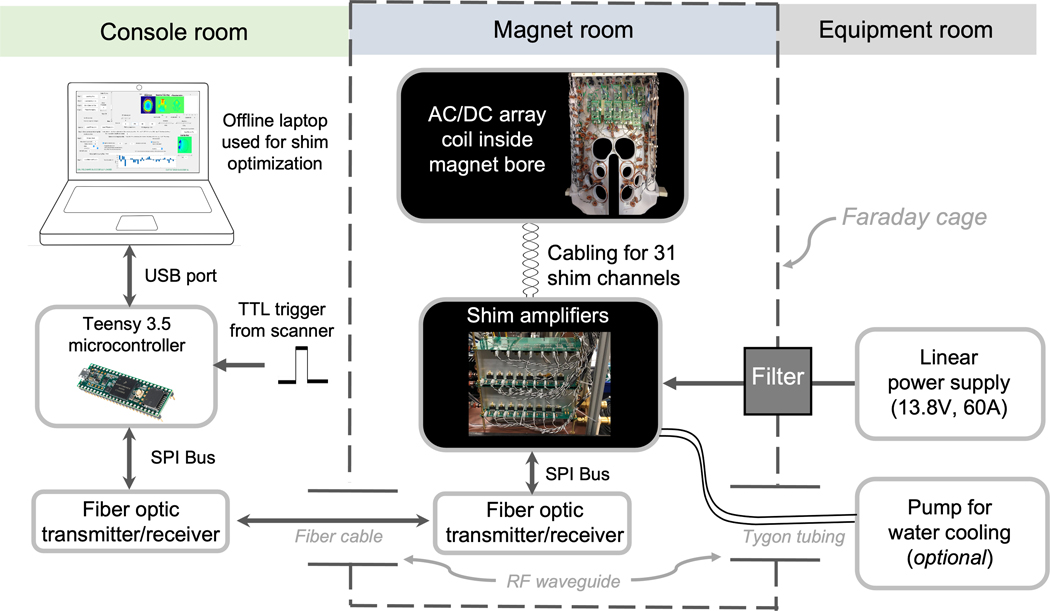
The complete hardware setup for B₀ shimming experiments is outlined in Figure 1. The equipment components can be divided into three categories by their position either in the magnet room, the console room, or the equipment room.

Figure 1.

Experimental setup of dynamic B₀ shimming hardware. ΔB₀ field maps are processed off-line on a laptop computer and optimal shim currents for each slice are computed. The shim settings are sent to a Teensy 3.5 microcontroller which then sends SPI bus commands to the digital-to-analog converters on the amplifier boards via fiber optic cable. The amplifiers are placed inside the magnet room to minimize the number of feedthrough filters required. Only the 13.8V power rail and ground for the amplifiers required filtering. The amplifier outputs are supplied via twisted pair cables to the AC/DC array coil inside the magnet bore. For slice-optimized, dynamic shimming, TTL pulses supplied by the scanner trigger the microcontroller to update the shim currents 1ms before the beginning of each TR. Amplifier output currents are monitored and sent back to the microcontroller via an analog-to-digital converter.

Magnet Room subsystems

Coil element design

To inform the coil element design, we first assessed RF transmit and receive performance losses associated with the extra circuitry for the DC current path in the AC/DC coil. The loaded-to-unloaded quality factor (Q) ratio of a single RF test loop was measured before and after adding the shim components to the loop. The coil impedance match, PIN diode detuning, and preamp decoupling characteristics were also measured.

We first compare coil performance metrics to an industry-standard, vendor-provided 32-ch array with birdcage transmit (Nova Medical, Wilmington, MA). We then compared coil performance metrics to an existing, in-house-built 31-channel (31-ch) RF Rx-only array with the same helmet geometry but lacking the shimming capacities. The basic RF circuit design was the same for the Rx-only and AC/DC arrays except for the number of distributed tuning capacitors. Fewer distributed capacitors were used on the AC/DC coil elements (4 instead of 6) to reduce the number of bridging chokes needed. Wire gauge choices were made after simulating the tradeoff between B₀ shim performance and maximum current-per-channel (see “B₀ shimming simulations”).

Details of the Rx and Tx designs are provided as Supporting Information. In summary, both in-house arrays used 31 RF receive elements rather than 32 to allow one of the system receive channels to be available for volume coil reception (useful for testing). Of the Rx elements, 25 were set up as AC/DC elements. -The two RF loops above the eyes, which share a conductor where the two loops meet, were set up as a single DC shim loop. The five most inferior and posterior neck loops were not set up for shimming based on (i) the difficulty of running wires all the way through the coil to these loops, and (ii) preliminary B₀ shimming simulations suggesting that they provide only minor gains for B₀-shim performance. To bring the number of shim channels up to 31, six multi-turn shim-only loops were added over the face area to target prefrontal cortex, an idea previously explored experimentally by Juchem et al. (31) and Zhou et al. (32), as well as in simulations (1). These 4–6cm dia. “shim-only” coils consisted of 3–4 turns of 22 AWG wire with 3 chokes in series to ensure that any self-resonances were shifted at least 50 MHz above or below the Larmor-frequency (297.2 MHz).

B₀ shim capability was added to RF loops by using 325nH toroidal (self-shielded) inductive chokes to bridge the loop’s tuning capacitors (Figure S1). Additional chokes placed at intervals of roughly 𝜆/10 apart were used to block RF on the twisted-pair DC feed wires.

Helmet design and layout

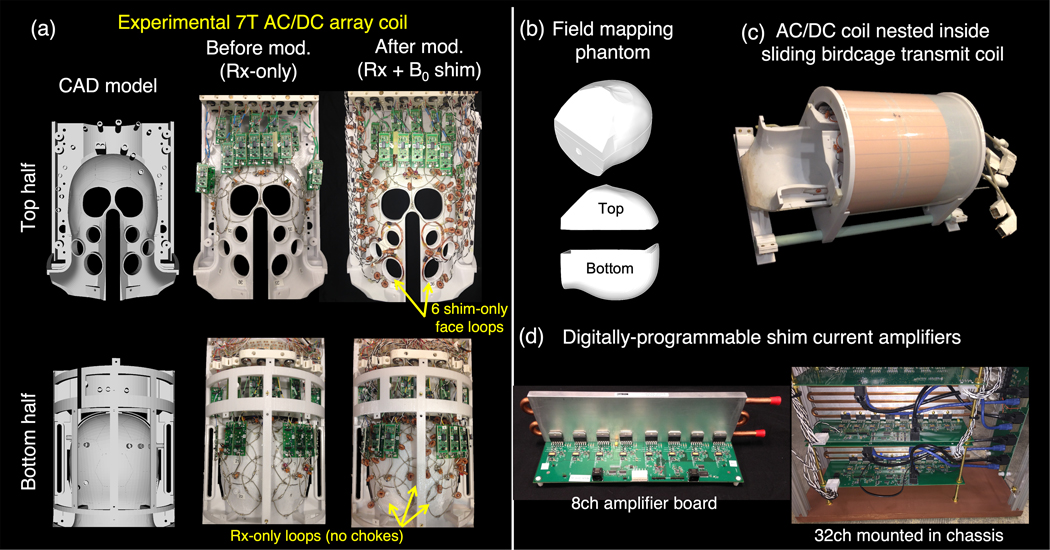
Figure 2 shows the CAD model for the close-fitting helmet alongside photos of the two halves of the RF array before and after the addition of shim chokes and feed wires. Figure 2c shows the receive array mounted inside the birdcage transmit coil. The birdcage and top half of the receive array slide back to make it easier for subjects to position their head inside the housing.

Figure 2.

Hardware used for 7T imaging and B₀ shimming experiments. (a) 32-ch RF receive array shown before and after conversion to a combined AC/DC coil through the addition of toroidal choke inductors, DC feed wires, and six additional shim-only loops over the face. CAD model of the helmet is also shown. (b) Phantom 3D printed in two halves that fills the entire space within the helmet for ΔB₀ field mapping each shim coil. A low permittivity liquid was chosen (silicone oil) to avoid B₁⁺ dielectric wavelength effects and provide good B0 field map image quality over the whole FOV. (c) The array coil is paired with a 16-rung detunable birdcage coil. (d) Low-cost, digitally-programmable current driver boards are used to supply stable shim currents to each coil in the array. A single 8-ch board is shown along with the bank of 32ch amplifiers installed in a non-magnetic enclosure.

Shim amplifiers

Figure 2d shows the open-source 8-channel amplifier boards used to provide digitallyprogrammable shim currents that can be switched rapidly (as fast as 30μs) (14),(33). Schematics and layout files along with Matlab circuit simulation software are available in the support material and online (http://rflab.martinos.org). The shim amplifiers are placed at the back of the magnet room and are connected to the coil with a cable along the scanner’s energy chain (see Supporting Information for further details).

Control components

The amplifiers are controlled via fiber optic lines entering the scanner room through a waveguide. A custom graphical user interface written in MATLAB (Mathworks, Natick, MA, USA) is used to process in vivo brain ΔB₀ field maps and calculate optimal shim currents using the shim coil basis set of 31 ΔB₀ maps. A laptop computer sends the current amplitudes via USB cable to a Teensy 3.5 microcontroller (PJRC, Sherwood, OR, U.S.) which in turn relays commands to the 8-channel LTC2656 digital-to-analog-converter on each amplifier board.

Human subjects

Eight healthy volunteers (4 female, 4 male) provided informed consent and were enrolled for system performance evaluations. All experiments were approved by the Institutional Review Board of Massachusetts General Hospital. Four of the volunteers were used for RF performance assessment and the remaining four were used for B₀ shimming experiments.

RF performance assessment

All experiments used a Siemens Magnetom whole-body 7 Tesla scanner with an SC72 gradient coil (G_max = 70 mT/m, slew rate = 200 T/m/s) equipped with 2^nd-order static shim coils. Standardized phantom tests were performed to identify any RF focusing or component heating from interactions between the Tx and Rx coil or between the gradient and RF components (34). RF performance evaluations were run on the vendor array, the Rx-only 31-ch reference array, and the AC/DC array, including transmit B₁⁺ mapping, receive SNR, noise correlation, and geometry factor (g-factor) of each Rx array. B₁⁺ maps were acquired using the Actual Flip-angle Imaging (AFI) method (35) to assess the impact of shim chokes and wiring on birdcage coil transmit efficiency (3D gradient-echo, TR=5.8/28 ms, TE=2.73 ms, 3 mm isotropic, 64×64×56 matrix, nominal FA=60°, readout BW=260 Hz/pixel, TA=2:07). The maps were then normalized by the transmit voltage to obtain B₁⁺ efficiency in units of nT/V. The receive SNR measurement followed the method of Kellman et al. using a noise-covariance-weighted optimal coil combination (equation 5 in (36)). A proton-density-weighted gradient-echo image was acquired using a nominal flip-angle of 90° to limit the impact of B₁⁺ inhomogeneity on signal intensity over the FOV (axial, TR=10s, TE=3.82ms, matrix=[256×176], FOV=[256×176] mm, 2mm slice, readout BW=340 Hz/pixel, TA=14:42). Following the approach in Ref. (37), the impact of B₁⁺ variability was further reduced by dividing the SNR maps by the sine of the flip-angle from the AFI maps. The noise correlation matrix was computed using raw complex-valued noise data acquired on each receive channel with the transmit voltage set to zero.

A 3D multi-echo magnetization-prepared rapidly-acquired gradient-echo (ME-MPRAGE) acquisition was used to qualitatively compare assess the impact of B₁⁺ inhomogeneity and efficiency on image quality for AC/DC and Rx-only 31-ch arrays (38) (3D gradient-echo, TR=2550ms, TI=1100ms, TE=[1.62, 3.44, 5.26, 7.08] ms, 0.88×0.88×1 mm, GRAPPA R=3, matrix=[226×226×176], FA=9°,TA=3:37). Anatomical imaging was also assessed in high-resolution structural gradient-echo images (axial, TR=1000ms, TE=21ms, 300μm or 400μm in-plane, matrix = [512×512], FOV=208×208 mm, 10 slices with 600% gap, 1-mm slice thickness, a phase stabilization navigator was used to track B₀ drifts, TA=4:34). Full-detail protocol summaries are included as Supporting Information.

B₀ shimming simulations

To assess the benefits provided by the 6 face-shim elements, we simulated B₀ shim performance of three array geometries: a 30-ch design where all RF coil elements were used as AC/DC elements (with eye-loops tied together); the hybrid 31-ch design with 25 AC/DC elements and 6 face-shim elements which we planned to build for this study; and a 36ch design with 30 AC/DC elements and 6 face-shim elements. Wire patterns for all three geometries are included in PUMCIN format as Supporting Information (39). Bio-Savart simulations (40) were used to compute the static magnetic field generated by each loop. Using the field basis set for each array we attempted to shim the measured field distributions from all 8 volunteers. The ΔB₀ field maps for these 8 individuals were acquired using a vendor-provided gradient-echo two-echo field mapping sequence with relatively thin slices (1.3mm) to limit through-plane dephasing. The scan parameters included TE=[2.0 3.02] ms, TR=465ms, FA=40°, matrix=112×112, FOV=212×212mm (2mm in-plane resolution), readout BW=1207 Hz/pixel, 100 slices, 1.3mm slice thickness, TA=1:47. The magnitude image obtained from the field mapping sequence was masked using the FSL-Brain Extraction Tool (BET) (41) using a threshold of 0.2 and residual phase wrap was removed using FSL PRELUDE (42). The “whole-brain” shimming simulations used the entire brain mask over the full cerebrum and cerebellum (typically spanning 14–15cm in the superior-inferior direction). Stray voxels were removed by applying the MATLAB ‘imerode’ function and by thresholding to remove voxels with intensities less than 0.3 times the average of the magnitude image. The maps were smoothed using the Matlab ‘wiener2’ pixel-wise adaptive low-pass filter with a 3×3 kernel.

MATLAB’s ‘quadprog’ solver was used to calculate optimal shim currents within the mask using a least-squares penalty on the residual ΔB₀ subject to current constraints for each loop and for the entire array. The optimization problem is framed as a quadratic program with a Tikhonov-regularization term added to prevent noise in ΔB₀ field maps from causing large changes in the optimal computed solution. Regularization also reduces the size of current steps between adjacent slices. The first step in the simulations was to globally shim using 1st- and 2nd-order SH terms to ensure that the starting maps were corrected to this order using the same algorithm, optimization region, and metrics applied to the higher-order shim terms. The final shim was characterized by the standard deviation over the brain region mask (σ_WB), the standard deviation within each slice (σ_SL), as well as the 80%, 90%, and 95% whole-brain ΔB₀ residuals (ΔB_80%, ΔB_90%, and ΔB_95%). Multi-coil B₀ shimming was examined (a) globally over the whole brain and (b) dynamically on a slice-by-slice basis. Slice-optimal shims were computed using three adjacent slices to limit through-slice field variation of the applied shim fields.

We compared conventional static shimming using up to 2^nd-order spherical harmonics (“2SH”) for both global shimming and slice-optimized dynamic MC shimming. For all MC shim simulations and experiments, we included the 1^st- and 2^nd-order SH shims applied as global (whole brain) shims prior to adding the MC shim terms. For dynamic shimming simulations, we allow the first order SH components (gradient offset currents) to be dynamically updated on a slice-by-slice basis since this is, in principle, achievable on most scanners through offset currents to the gradients. The benefit of doing this in conjunction with MC shimming has been previously demonstrated (13). Additionally, we simulated shimming with SH basis fields up to 5^th order. The SH shim results were checked for consistency by computing the solution both with an unconstrained pseudoinverse and a constrained ‘quadprog’ solver with very high current limits.

Simulations were also used to evaluate the shim performance of 31-ch AC/DC coil as a function of current limits varying from 1A to 15A per element and total current constraints from 10A to 400A; the results were used to guide the choice of wire gauge for the DC shim components (see “Coil element design” above). To provide some basis for comparison, we also simulated the SH basis up to 5^th as well as a reference 48-ch 7T MC shim array from the literature consisting of 100-turn loops patterned on a cylinder around the head (12).

Electric field (E-field) simulations in a realistic head model (Sim4Life, Zürich, Switzerland) (43,44) were computed for a 1 KHz sinusoidal current to assess whether rapid switching of the shim fields could potentially induce peripheral nerve stimulation (PNS). Specifically, we examined whether the maximum current applied at 1 KHz generates E-fields in excess of 5 V/m (45) or dB/dt fields in excess of the IEC guideline of 20 T/s (46).

B₀ shimming experiments

The shimming basis functions needed to compute the in vivo shim currents were obtained once in a phantom measurement. The phantom was designed in CAD software to closely match the helmet to maximally extend the field measurement region. The 3D printed phantom (Figure 2b) was filled with silicone oil (Super Lube, P/N-56101, Bohemia, NY) rather than water to provide a more homogeneous B₁⁺ profile. The B_z-field component generated by each shim element was obtained using the two-echo B₀ field mapping sequence after applying +750mA and –750mA to each coil loop. The difference between these two field maps was computed to remove the background field. The maps were then normalized to provide ΔB₀ in Hz/A. We also applied a similar method to create basis maps for the scanner’s 1^st-and-2^nd-order SH shims.

For B₀ shimming experiments, we adjusted the 1^st- and 2^nd-order SH global shims using two methods: (i) the vendor-provided online field-mapping and shim optimization tool and (ii) our own offline mapping and optimization tools which use a more detailed masking procedure.

After setting the SH shims, we acquired a field map of the remaining ΔB₀ field and attempted to remove these variations with the shim array. Shim array currents were computed using the optimization described in the shim simulation section above. After applying the MC shims, a final field map was acquired to assess performance. All calculations were run on a laptop equipped with 16GB RAM and a 4-core 2.7GHz i7-processor (Apple, Cupertino, CA, USA).

Validation using EPI acquisitions.

Single-shot gradient-echo 1mm EPI scans were acquired with phase-encoding (PE) set to the anterior-posterior (AP) as well as posterior-anterior (PA) directions to observe the geometric distortion arising from residual ΔB_0. (1mm axial slices, 300% slice gap, TR/TE/flip=2560ms/25ms/80°, matrix=174×174, FOV=192×192mm, GRAPPA R=4, readout BW=1596 Hz/pixel, echo spacing=0.83ms yielding an effective echo spacing of 207μs after considering the R=4 acceleration. Trigger output pulses were added to both the field mapping and EPI sequences (including during GRAPPA autocalibration prescans) to signal the microcontroller to update the shim currents.

The EPI slices before and after shimming were compared to a contrast-matched T₂*-weighted gradient-echo volume, providing a distortion-free (in PE direction) reference. Temporal SNR maps (47) were computed from EPI time-series data for the baseline, global MC, and slice-optimal MC shims using 60 consecutively-acquired volumes that were motion-corrected using FSL.

Acoustic noise levels during current switching from 0 to 1.5 amps on every channel were recorded inside the coil helmet using a Bruël-and-Kjaer sound level meter (Naerum, Denmark) and compared to sound levels generated by the scanner gradient coil running localizer and EPI sequences.

Results

RF performance

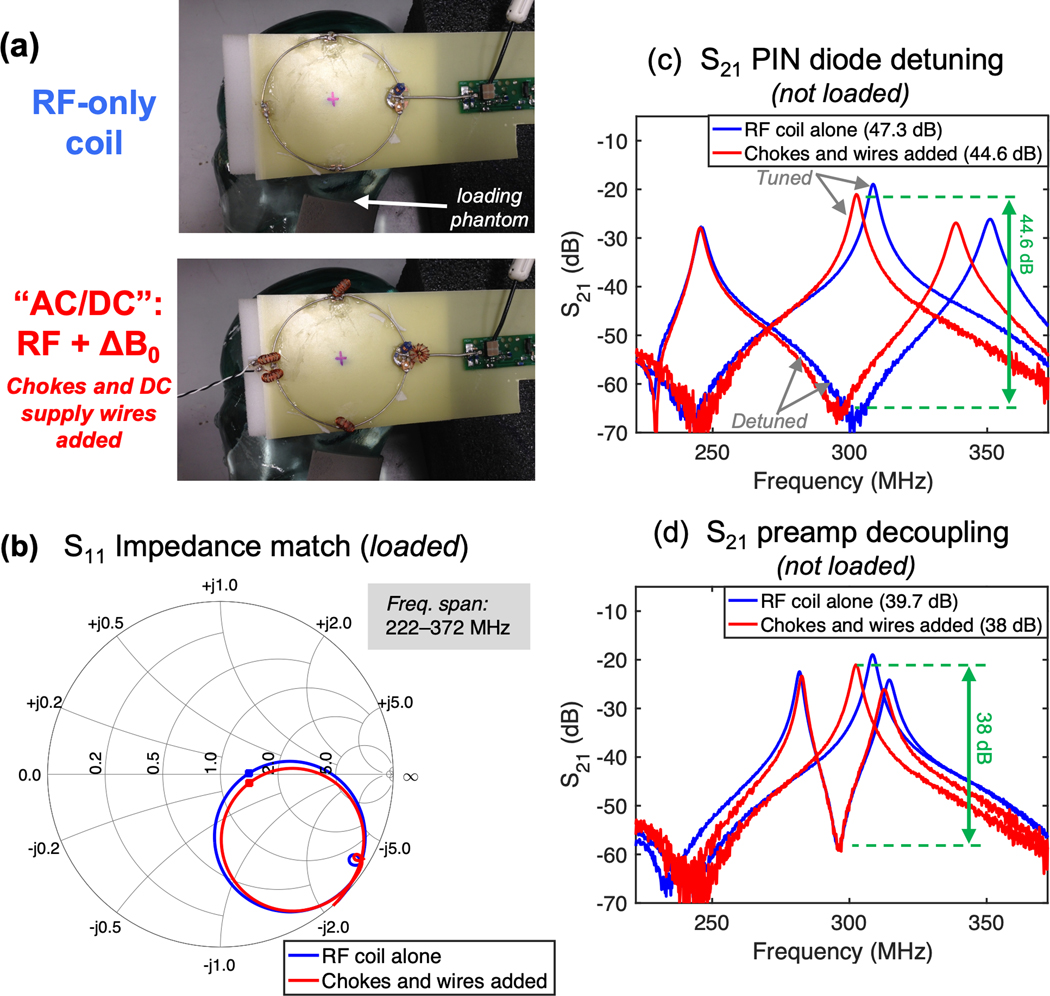
Figure 3 shows RF bench performance metrics measured on a single RF test coil element before and after the addition of DC shim chokes and twisted-pair feed wires. The coil element input-impedance changes only slightly when the DC shim components are added. Supporting Information Figure S2 shows that properly tuned chokes approximate an open circuit and thus cause a negligible shift in the RF resonant frequency. The shim hardware caused a small shift of roughly 3 MHz, which was easily corrected using a trimmer capacitor. Figures 3c–d show double-probe |S₂₁| measurements for assessing preamp decoupling and PIN-diode detuning. Although the |S₂₁| curves shift slightly, a large peak-to-trough distance is preserved in both cases (more than 35dB), showing that the DC shim components do not adversely impact PIN-diode detuning or preamp decoupling.

Figure 3.

RF receive coil performance metrics using a single test loop before and after B₀ shim hardware is added. (a) Photographs of the test loops on an anthropomorphic loading phantom. (b) Smith chart plot of S₁₁ impedance match for a loaded loop. The center of chart is normalized to 50 ohms; the optimal noise match for the preamp used in experiments is 75 ohms. (c) S₂₁ measured by a double probe during PIN diode-actuated detuning of unloaded test loop showing a difference between tuned and detuned states of 47.3 dB and 44.6 dB without and with shim hardware, respectively (loop input was open-circuited). (d) S₂₁ measured with the loop connected to a powered preamp showing preamp decoupling of 39.7 dB and 38 dB without and with shim hardware, respectively. In all three measurements, the addition of shim hardware caused only a negligible shift in the plots and did not significantly degrade RF performance.

The change in coil-element quality factor (Q) before and after adding DC shim components was as follows. Without shim components the Rx-only element had Q_unloaded=207 and Q_loaded=22 giving an unloaded to loaded Q ratio of R_ul/l = 9.4. With the components needed for the AC/DC array: Q_unloaded=183, Q_loaded=22, R_ul/l = 8.3.

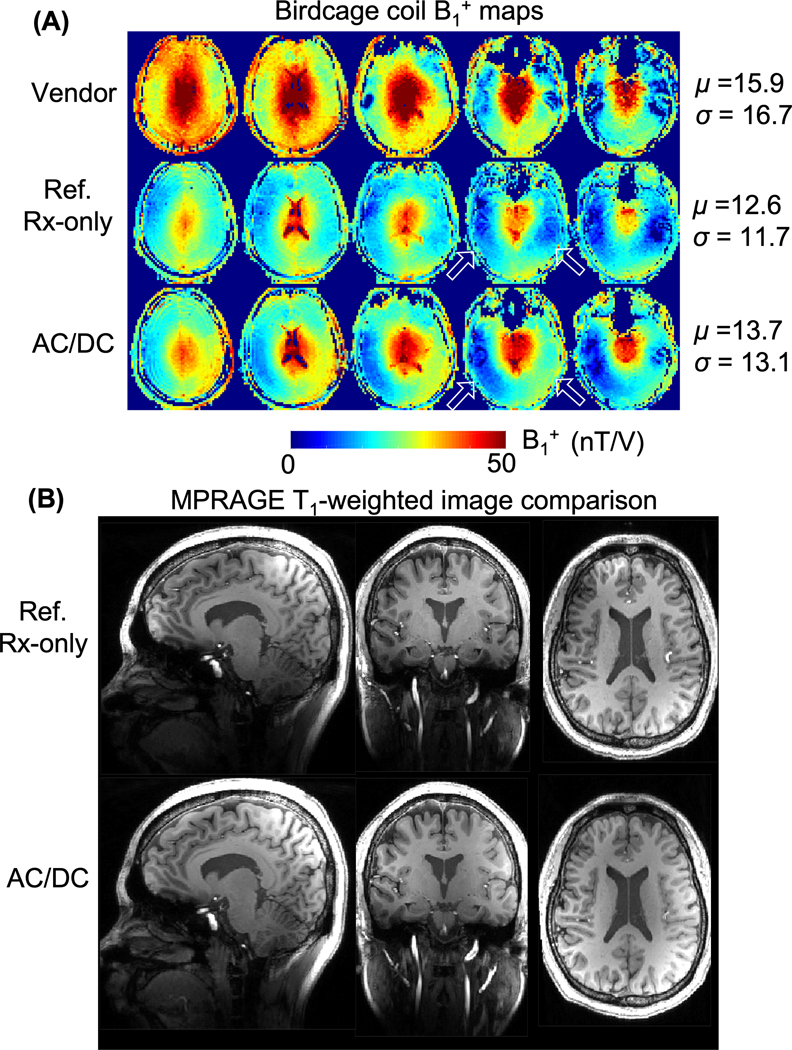
The RF transmit-receive coil system passed all RF and gradient eddy-current heating safety tests in the 7T scanner with less than 4°C temperature rise on the coil surface. B₁⁺ maps in Figure 4 quantitatively compare the transmit efficiency of the birdcage coils used with the vendor array, “Reference” (non-shimming) array, and the AC/DC array. For the reference and AC/DC arrays, the mean and standard deviation of B₁⁺ values over the brain volume agree to within 10%. A few differences are noted, such as greater left-right asymmetry in the temporal lobes for the AC/DC array setup. The vendor birdcage shows modestly higher efficiency, which may be partially attributable to its smaller size (e.g., rung diameter of 29.5 cm vs. 33.8 cm for the in-house birdcages). Figure 4b shows co-registered T₁-weighted MPRAGE images acquired using the in-house coils. Some loss of contrast occurs due to B₁⁺ dropout, particularly in the inferior temporal lobes and cerebellum, but these flip-angle patterns are typical for single-channel 7T birdcage transmit coils and overall image quality is comparable for the two arrays.

Figure 4.

Assessment of quadrature birdcage transmit coil performance for different coil setups. (A) Normalized B₁⁺ maps in units of nTesla/Volt for a vendor coil, Reference Rx-only coil, and AC/DC coil. The mean and standard deviation of the normalized B₁⁺ over the head are listed. Comparable transmit efficiency is observed for the Reference and AC/DC coils. Some differences are noted, such as greater left-right asymmetry in the temporal lobes for the AC/DC coil (arrow). The vendor birdcage coil shows higher efficiency likely due to its small physical size. (B) Co-registered T₁-weighted MPRAGE images show broadly similar image quality for the Ref. and AC/DC coils (sagittal, 0.88mm in-plane with 1mm partition, R=3 acceleration). Some loss of contrast occurs due to B₁⁺ dropout, particularly in the inferior temporal lobes and cerebellum, but these patterns of flip angle inhomogeneity are typical for single-channel 7T birdcage transmit coils and are comparable across the two cases shown.

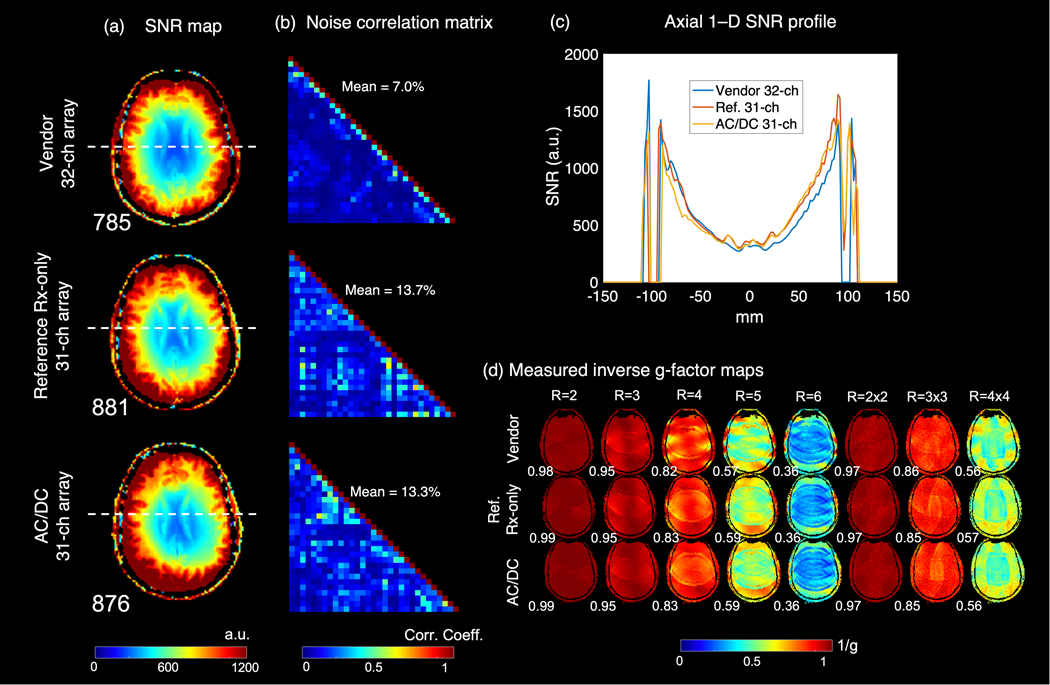
Figure 5 shows SNR maps, noise correlation coefficient matrices, and inverse g-factor maps. The SNR maps show roughly equivalent performance for the three arrays. The average off-diagonal noise correlation coefficient is also comparable for the two in-house arrays (13.3% and 13.7%) and inverse g-factor maps show similar retained SNR for accelerated imaging. Figure S3 shows 300 μm and 400 μm in-plane T₂*-weighted gradient-echo images acquired with the AC/DC array demonstrating that the coil has adequate sensitivity and stability to perform high-resolution 7T structural imaging.

Figure 5.

In vivo RF performance comparison between vendor 32-ch array, 7T AC/DC array, and size-matched 7T receive-only service coil. (a) Axial receive SNR maps after normalization by flip angle maps. (b) Noise correlation matrices. (c) Overlaid 1–D SNR profiles. (d) Measured inverse g-factor maps for an axial slice (retained SNR) for a variety of acceleration factors along with the mean 1/g value for each factor.

B₀ shim simulations

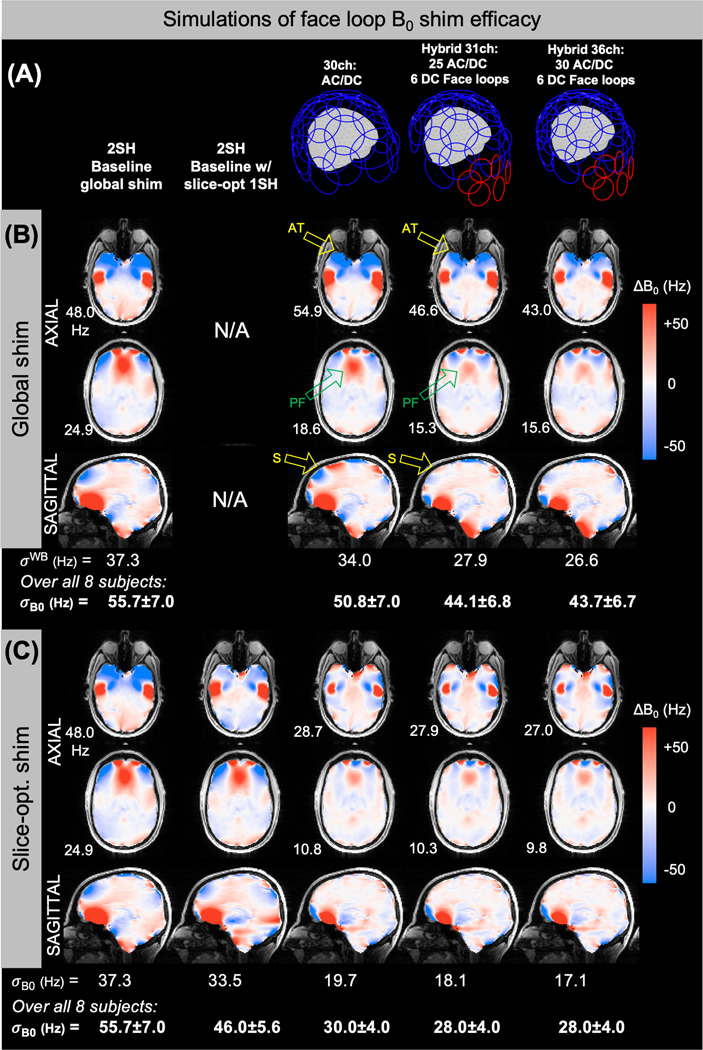
Figure 6 summarizes simulated B₀ shim performance over eight ΔB₀ brain field maps (current was limited to 3.5A/ch or 40A total). Further shim performance metrics including residuals are summarized in Supporting Information Table S1. Figure 6a shows the three simulated array geometries. Global shimming (Figure 6b) with the 31ch “hybrid” AC/DC array including face elements improves σ^WB by 21% compared to 2SH shimming, versus a 9% improvement for a 30ch AC/DC-only array. For slice-optimized shimming (Figure 6c), the hybrid 31ch array achieved a 50% improvement over the 2SH baseline compared to 44% for the 30ch array. As shown by the 36ch hybrid design results, adding shim capability to the remaining 5 RF-only coils omitted from the 31ch design brings only modest additional gains.

Figure 6.

B₀ shim simulations assessing the benefit of adding 6 shim-only four-turn coils over the face area. (A) Three array designs are compared to two cases: baseline static 2^nd-order shimming (2SH) and slice-optimized 0^th-to-1^st-order shimming applied on top of the 2SH shim. The three designs are: A 30ch shim array with all RF coils converted to DC shim coils; a hybrid coil with 25 AC/DC shim coils and 6 DC-only shim coils added over the face area; and a hybrid coil with all 30 AC/DC coils plus the 6 face coils. (B) ΔB₀ maps for global shimming of one representative subject are shown along with slice-wise (𝜎^SL) and whole-brain (𝜎^WB) st. dev. and residuals. The face loops improve the shim in anterior temporal cortex (“AT”) and prefrontal cortex (“PF”). The 30ch AC/DC coil generates unwanted field offsets in the most superior part of the head (“S”) when these coils attempt to shim the frontal area; the 31ch array largely mitigates this problem. Relative to 2SH global shimming, the 𝜎^WB is reduced by 9% and 21% without and with the face coils, respectively. (C) In slice-optimized shimming, the face coils provide a more modest benefit, achieving a 50% reduction in 𝜎_B0 versus 46% for the 30ch array. For both global and slice-opt. shimming, the addition of 5 more AC/DC coils on the inferior-posterior area in the 36ch array brings only modest gains compared to the 31ch array. For (B) and (C), metric are also reported for the whole set of 8 field maps used in the simulations.

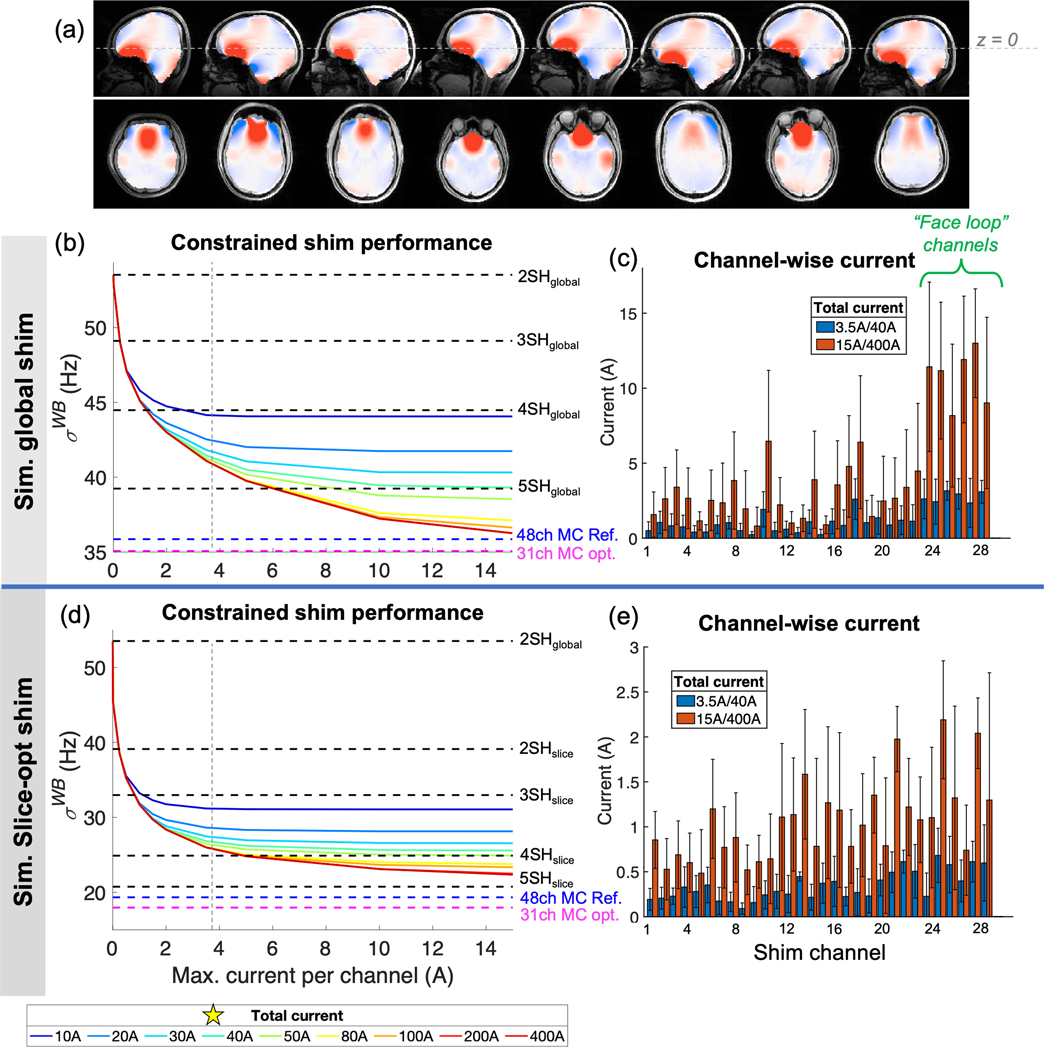
Figure 7 plots simulated shim performance (σ^WB) on 8 brain B₀ maps for the 31ch hybrid design (which we chose to construct) as a function of maximum shim current. The “L-curves” show steep performance gains up until the knee of the curve is reached, beyond which the performance slowly converges to the theoretical limit (pseudoinverse solution). We chose the wire gauges to allow 3.5A per channel and 40A total for the fabricated array (without excessive heating), lying near the knee of the L-curves for both global and slice-optimized shimming. At this operating point, the gains in σ^WB compared to 2SH shimming are 17% and 49% for global and slice-optimized cases (similar to the 4SH basis), respectively, compared to 29% and 65% in the unconstrained cases (similar to 5SH basis). Figures 7c and 7e show the simulated channel-wise current used for the 8 field maps for global and slice-optimized shimming. Above the 3.5A/40A operating point, the remaining performance gains come largely from improved shimming of the frontal lobes, with an outsized role played by the face-elements. For slice-optimized shimming, by contrast, increasing the current limits results in a more even spread of the added current across the array.

Figure 7.

Simulated ΔB₀ MC shimming performance of 31ch AC/DC coil as a function of maximum channel-wise and total current for the 8 in vivo ΔB₀ brain field maps. (a) The field maps are shown as acquired (no registration) relative to the nominal coil center line (z=0). (b,d) 𝝈^WB is shown as a function of current limits for global and slice-optimized shimming, respectively. The unconstrained optimal solution (pseudoinverse) is shown by a red dotted line. Simulations of spherical harmonics up to 5^th order (with no constraints) as well as a reference 48-ch MC shim array are shown for reference. For both global and slice-optimal shimming, diminishing performance gains are achieved for each incremental increase in current used. For the constructed AC/DC array, 3.5A per loop and 40A total were deemed sufficient and chosen as the operating limits (shown by vertical gray dotted line and star). The gains in 𝝈^WB for global and slice-opt. shimming using the current constraints are 17% and 49%, respectively, compared to 29% and 65% in the unconstrained case. (c,e) Channel-wise current used for global and slice-opt. shimming (mean and st. dev.). For global shimming, much of the benefit from higher current limits comes from the face loops, suggesting that increasing the number of wire turns or current limit in these loops may be beneficial, while for slice-opt. shimming, the benefits of increased current limits are spread more evenly across the array.

B₀ shimming experiments

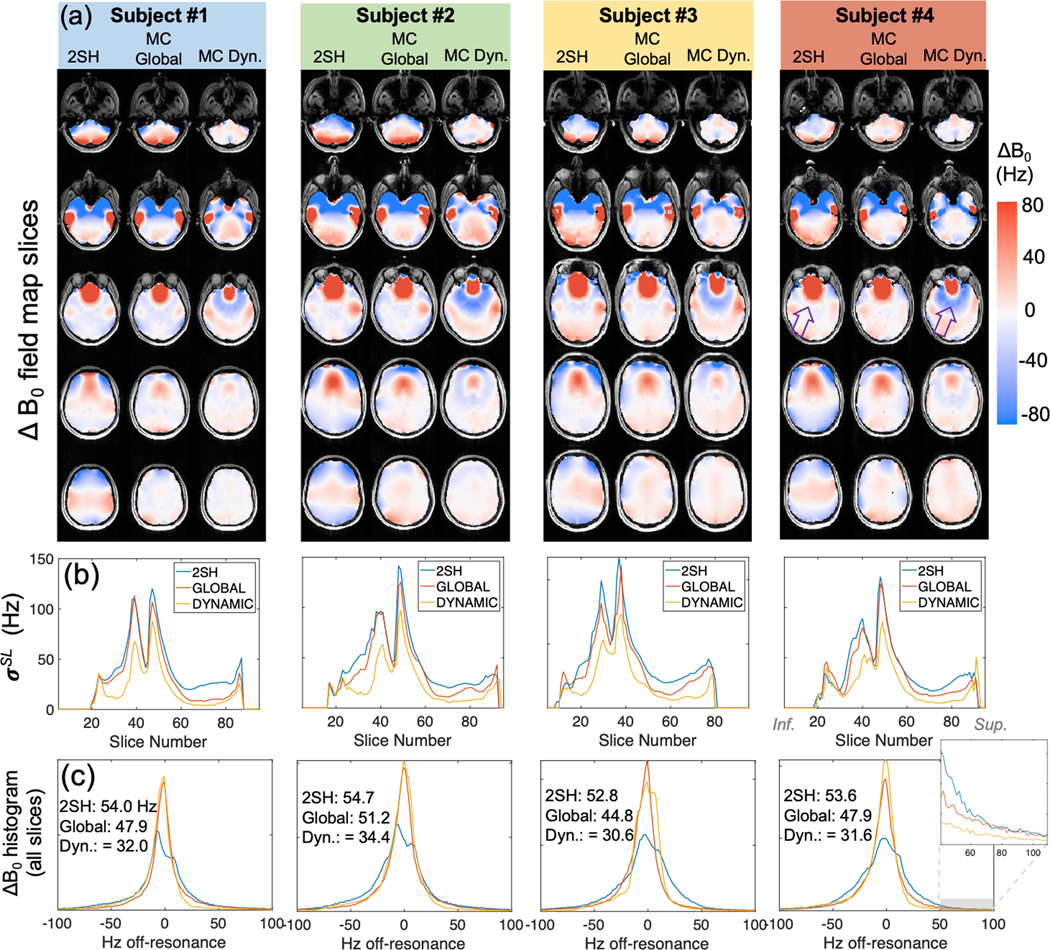
Table 1 lists σ^WB and residuals for both the predicted and acquired ΔB₀ field maps with global 2SH, global MC, and slice-optimized MC shims applied. Across all four subjects, σ^WB improved by 11% and 40% for global and slice-optimized MC shimming, respectively (or 14% and 44% for the 95% residual). The table also summarizes EPI voxel-shift metrics (computed for each voxel using the ΔB₀ maps and effective echo-spacing) as well as the fraction of voxels that improve or worsen. Figure 8 provides a more detailed look at shim performance for each case, showing representative slices for each volunteer, plots of the st. dev. within each slice (σ^SL), and ΔB₀ histograms over the whole brain. MC shimming narrows the ΔB₀ histogram and reduces the number of outlier voxels that correspond to the largest geometric distortions in EPI slices.

Table 1.

Metrics of B₀ shim performance and EPI voxel shifts for experimental data shown in Figs. 8, 9, and S3–S5. The mean, st. dev., and residual metrics are computed over the 4 subjects scanned in the B₀ shimming experiments.

Case	ΔB0 Residuals (Hz)				EPI voxel shift (#)		Percentage of voxels with less vs. more voxel shift relative to 2SH shim
	St. dev. (σWB)	80%	90%	95%	Mean	St. dev.	Less (%)	More (%)
2nd order shim baseline	53.8	85.7	126.4	208.5	1.1	1.8	N/A	N/A
Global MC (predicted)	47.9 (46.2)	62.0 (58.0)	107.0 (114.8)	187.3 (181.6)	0.8	1.6	69.8%	30.2%
Slice-optimal MC (predicted)	32.2 (30.8)	47.0 (39.9)	78.8 (72.3)	120.4 (111.5)	0.6	1.1	67.4%	32.5%

Figure 8.

Summary of global and dynamic MC shimming experiments on four volunteers. (a) Representative slices of acquired ΔB₀ maps from each volunteer for the 2SH baseline, global MC shim, and dynamic MC shim cases. (Axial, sagittal, and coronal slices of the ΔB₀ maps for Subject 3 are shown in Supporting Information Figure S4). While MC shimming reduces the size of the ΔB₀ “hotspot” in the frontal lobes, the coil basis set does not have sufficiently high spatial order to match the shape of the hotspot exactly. The compensating shim fields thus extend past the hotspot and reduce B₀ homogeneity toward the middle of the head (purple arrow). (b) The standard deviation in each slice (𝜎^SL) is plotted for each shimming case. (c) The overall histogram of ΔB₀ over the whole brain for each subject along with summary of 𝜎^WB in Hz for each subject. A zoomed inset shows the improvements in outlier voxels achieved using MC shimming.

For 2SH shimming, σ^WB improves from 61.2Hz to 53.8 Hz (12%) when the offline shim optimization and brain mask are used instead of the vendor-provided online shim adjustment.

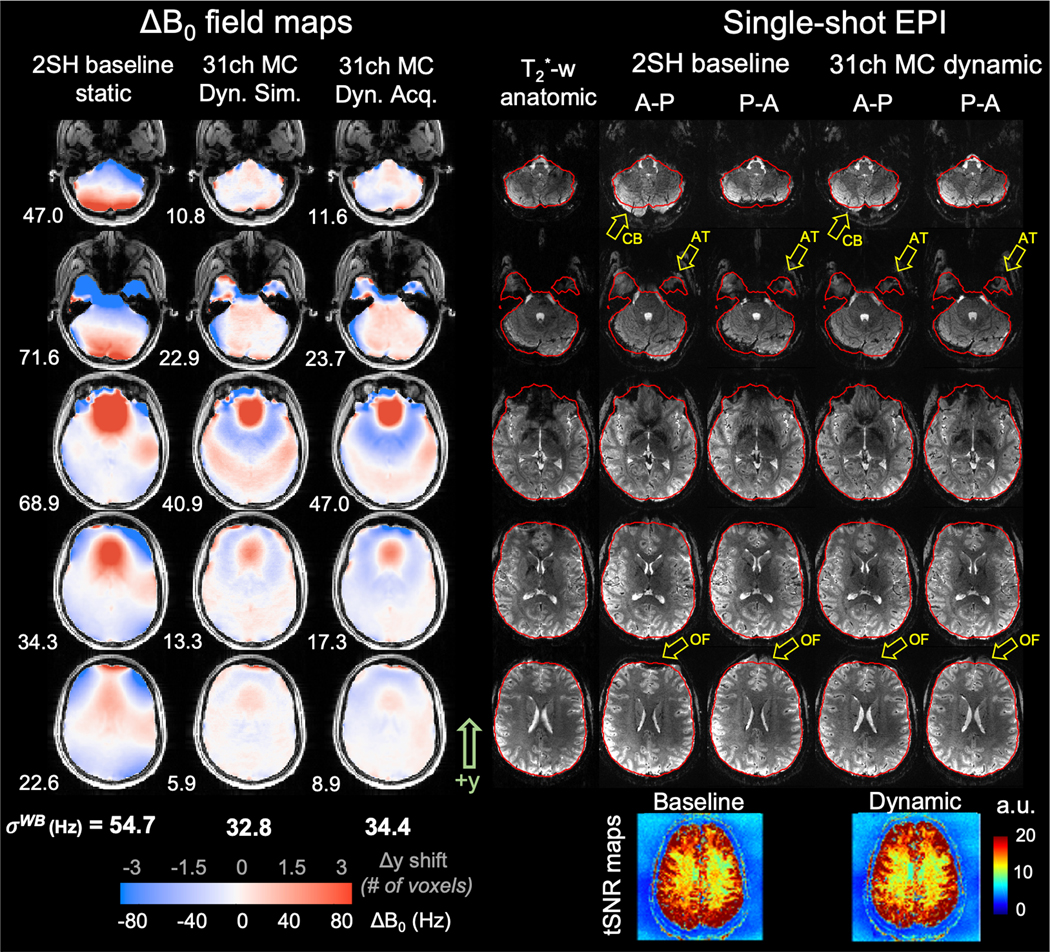
Figure 9 shows representative EPI slices and ΔB₀ field maps for a dynamic shimming experiment on one volunteer (results for the other 3 volunteers are shown in Figures S5, S7, and S8). MC shimming reduces geometric distortion by an average of 41.3% over the brain, bringing many features back into closer alignment with the T₂*-weighted anatomic image. The change in distortion is more apparent in Supporting Information Video S2, which toggles between EPI slices acquired with the two phase-encode directions (see also Videos S1, S3 and S4 for the other 3 subjects).

Figure 9.

Images from Subject #2 showing improvements in ΔB₀ and in echo planar imaging (EPI) geometric distortion achieved using dynamic shimming with AC/DC coil (7 representative slices shown for subject 3). Column 1: ΔB₀ field map after global 2^nd-order shimming (2SH). Columns 2–3: Simulated and acquired ΔB₀ field maps after dynamic, slice-optimized multi-coil (MC) shims are applied within brain mask (red outline). Dynamic MC shimming improves ΔB₀ by 45% compared to the baseline. Column 4: Gradient echo T₂*-weighted image that is contrast-matched to the EPI slices (TE=25ms) showing an undistorted anatomic baseline. Columns 5–6: Single-shot EPI acquired with 2SH shim using anterior-posterior (A-P) and posterior-anterior (P-A) phase encode k-space ordering to emphasize geometric distortion (phase encode direction is along y-axis). Columns 7–8: EPI slices acquired with dynamic, slice-optimized multi-coil shims applied. Dynamic shimming improves geometric distortion, bringing features in the A-P and P-A slices into closer alignment with one another and with the anatomic slices (see also Supporting Information Video S2). Yellow arrows show example areas demonstrating reduced distortion including orbitofrontal cortex (OF), anterior temporal horns (AT) and cerebellum (CB). Red lines show the brain mask outline for the undistorted anatomic slices. Temporal SNR maps (bottom row) show similar array stability for the baseline and dynamic shim cases. EPI parameters: TE=25ms, TR=2560, 1.1mm in-plane, 2mm slice, GRAPPA R=4, echo spacing=0.83ms, NA=1.

The EPI slices do not show ghosting, spiking, or other effects that typically result from coil instability. Temporal SNR maps derived from EPI time series data are similar for the static 2SH and dynamic MC shim cases, showing that shim current settling times and mechanical torque transients during shim updating are too small and/or too short-lived to measurably impact coil stability. A fuller presentation of the tSNR maps is shown in Figure S9.

Figure S10 shows measured ΔB₀ maps in the three cardinal planes for all 31 shim channels. The maps have been made available as Supporting Information along with the eight co-registered in vivo ΔB₀ field maps.

In dynamic shimming EPI acquisitions, reduced signal intensity was observed in some brain regions when slice-optimized shim currents were updated prior to the fat saturation pulse at the beginning of each TR. Figure S11 shows that this effect is caused by applied B₀ offsets outside the acquired slice that frequency-shift water into the bandwidth of the fat saturation pulse, resulting in incomplete T₁ recovery in those areas. The problem was solved by adding an additional trigger to disable the MC shim fields during fat saturation.

Maximum sound pressure levels measured inside the coil helmet during current switching were 90 dBA. This is two orders of magnitude lower than the 110 dBA recorded from the scanner gradient coil during a localizer scan. Volunteers reported hearing a sound on the coil helmet during dynamic shim updating (qualitatively described as “tapping” or “buzzing”), but no subjects reported discomfort.

Figure S12 shows maximal-intensity projections of the E-field distribution in the face area for a four-turn shim-only coil driven by 1A of 1KHz sinusoidal current. The E-field in this case reaches a peak amplitude of approximately 0.015 V/m inside the body. Since this amplitude scales with rise time and the current, for switching from −3.5A to +3.5A in 250μs, the E field is expected to be 0.45 V/m, which is still safely below the 5 V/m PNS threshold seen for head-gradient systems (45). The maximum B-field change is 0.6mT and dB/dt is 2.4T/s. This is below the IEC guidance of 20T/s (46).

DISCUSSION

We extend the integrated “AC/DC” brain array approach to 7T, building upon our previous realization at 3T (17). RF performance tests show broadly similar SNR, average noise correlation coefficient, g-factor maps, coil stability, and transmit efficiency for the AC/DC and a size-matched reference array. By providing a large number of channels for both RF receive and B₀ shimming, the AC/DC coil gives access to multiplicative reductions in geometric distortion: a factor provided by parallel imaging acceleration and a further factor of nearly 2 provided by dynamic slice-optimized B₀ shimming. This gives the user the option of either (i) using conventional acceleration-factors and reducing the image distortion via the improved shim, or alternatively (ii) reducing the accelerationfactor, thereby increasing SNR and image quality, and achieving conventional levels of distortion.

A key challenge of the AC/DC approach is making efficient use of the space inside the birdcage transmit coil while minimizing coupling between the transmit fields and the DC shim components. Spatial nonuniformity of 7T birdcage coil B₁⁺ profiles resulting from dielectric wavelength effects is a well-known issue, which has been shown in simulations of ideal birdcage coils (48). However, the increased right-left asymmetry in the AC/DC case suggests that the chokes used in the DC wiring have not entirely eliminated coupling between the birdcage coil and the DC components. A possible remedy may be to route shim feed wire paths more carefully so as to avoid areas of high electric-field and/or add more chokes to the wires. Further investigation of this topic is needed.

The DC shim components cause an 11% drop in unloaded quality factor in single-element bench testing. The cause of this Q loss is not well understood by us, but factors could include (a) the AC resistance of the chokes and/or (b) “copper shading” of the loop fields due to RF eddy-currents induced in the chokes.

A discussion of practical issues related to the dynamic shimming experiments has been included as Supporting Information.

Slice-optimized shimming reduced σ^WB to 32.2 Hz across four volunteers at 7T. For comparison, the 2SH shim routine of the manufacturer at 3T typically achieves σ^WB values in the low-to-mid-20s of Hz. Thus, the shim array does not quite bring the 7T homogeneity down to what users are accustomed to at 3T. As shown in Fig. 8c, the gains provided by slice-optimized shimming vary considerably from slice to slice. The superior half of the brain shows large improvements, with low residual ΔB₀ after AC/DC shimming (σ^WB=5–15 Hz). By contrast, the inferior slices show less consistent gains, since focal B₀ “hotspots” in the frontal and temporal lobes are impossible to fully null with the available AC/DC coil basis set, which cannot generate field profiles of sufficiently high spatial order.

Global MC shimming provided only 11% improvement over 2SH shims, suggesting that there is room for improvement in future iterations of the coil design. However, we note that the global shim performance of any MC shim array will converge toward an asymptote as more and more shim sources are added. For B₀ offset fields caused by sources outside the ROI, LaPlace’s equation implies that the field can be shimmed to any desired level of homogeneity if a sufficiently large number of shim coil basis functions are used (e.g., shimming an empty magnet bore). But when there are tissue susceptibility interfaces located inside the body, LaPlace’s equation is no longer valid (49),(50). The resulting fields can be represented as a combination of regular and irregular solid harmonic functions (51,52), but only the regular solid harmonic field terms can be fully compensated using shim sources placed outside the body. Thus, using successively greater numbers of terms of shim terms, even for an orthogonal basis set such as the spherical harmonics, does not provide smooth convergence toward a completely uniform shim.

Simulations in Figure 7 show that for the 3.5A/40A current limits chosen, the AC/DC coil provides global shim performance comparable to the 4SH shim basis and slice-optimized shim performance in between 3SH and 4SH. The same simulations show that with higher current limits, the AC/DC performance could in principle be further improved, reaching or surpassing the 5SH basis. With unconstrained current, the AC/DC array performance is comparable to the reference 48-ch MC array, but with the 3.5A/40A constraint, the 48-ch array achieves a further 13–15% reduction in σ^WB relative to the AC/DC array. While increasing the current limit above 3.5A could be challenging in practice, performance of the face loops could potentially be boosted by using target-field approaches for designing the wire patterns (53,54) or by increasing the number of wire-turns.

Other groups have investigated joint optimization of the linear and MC shims in slice-optimized shimming (13). MC shimming for simultaneous multi-slice (SMS) acquisitions has also been explored in simulations (1) and EPI acquisitions at 3T (55). Finally, MC shim arrays have also been used for emerging local field control applications like volume-tailored lipid suppression (21) and zoomed-imaging (19,20).

An alternative MC shimming approach for UHF MRI is to place dedicated multi-turn shim coils just outside the transmit coil shield, as recently demonstrated at 9.4T (13,56). Compared to AC/DC arrays, this approach provides (i) reduced interaction of DC shim components with the transmit coil(s) and (ii) less complexity for the receive-array design, and (iii) greater flexibility to use target field-based shim coil designs optimized for the human head anatomy (51,54,57). However, shim coil placement outside the shield could be geometrically constrained, for example if a head-gradient insert coil is used. Also, the higher inductance may be an obstacle for some emerging local field control applications (58),(59) where waveforms with KHz-range frequencies (1–100 KHz) are played out on MC arrays to provide supplementary spatial encoding. Larger inductances will require higher amplifiers voltages to slew at these frequencies. An additional complication is the potential for coupling to the gradient coils, which increases the amount of amplifier voltage compliance required to reject gradient slew-induced disturbances. Finally, since these coils typically use >20 turns of wire, they experience stronger mechanical torques, which can create problematic noise and vibrations inside the coil if they are not addressed with suitable mechanical constraints. Nevertheless, in existing realizations, many of these concerns have already been addressed (13,56).

CONCLUSION

The feasibility of an integrated 32ch AC/DC B₀ shim array was explored for 7T brain imaging. RF performance was found to have comparable SNR, noise correlation, g-factor, and Tx efficiency to a size-matched 32ch reference array. Dynamic, slice-optimized B₀ shimming experiments showed that shim currents can be rapidly switched between TRs without introducing artifacts or compromising temporal SNR. Geometric distortion in 7T EPI slices was significantly reduced, especially in superior slices.