Abstract
The exploitation of underground space is accompanied by complex geotechnical problems. The development of electromagnetic exploration technology provides a new perspective for preventing and avoiding these problems. In this work, electrochemical impedance spectroscopy (EIS) was used to test the single-phase and mixed-phase medium. Based on the unsaturated soil theory and the dual-water conductivity theory, an equivalent circuit model to describe the electrochemical characteristics and microstructure of silty soil with temperature changes through comparative research. The results indicate that the resistance of near-water layer is not affected by temperature, the resistance of silty soil increases mainly results from the influence of the far-water layer until which increases significantly after freezing. The capacitance change of silty soil is mainly affected by the slowing down of the orientation movement of polar molecules in the far-water layer. Based on the fitting data, a mathematical model for calculating the unfrozen water content of frozen soil was proposed, which reasonably verified the relationship between the unfrozen water content and electrical resistance. By improving the testing conditions of electrochemical impedance spectroscopy, this method may provide new insights for future research of soil electromagnetic testing technology.
Keywords: Silty soil, Electrochemical impedance spectroscopy (EIS), Equivalent circuit model, Physical property indices, Unfrozen water
1. Introduction
Silty soil is a kind of soil with special engineering properties between sandy soil and clay, which is widespread on the earth because of complex origin. But regardless of the type of origin of silty soil, its structure and stability performance are always poor, which leads to the soil sample easily disturbed by conventional physical experiments and results in the final experimental data to high variability [1]. As the public's recognition of electromagnetic technology gradually deepens, electromagnetic technology can be effectively applied as a test method with less disturbance to the soil. Therefore, fast, reliable, and conventional electromagnetic technology is needed to test the physical and chemical properties of soil in all aspects of hydrology, agriculture, and civil engineering [2].
For nearly a century, modern electronic technology has provided strong support for the research of electromagnetic testing. Resistivity method [3], [4], conductivity method [5], [6], permittivity [7], [8], time domain reflection (TDR) method [9], etc. are widely used to obtain underground information, such as soil properties (soil type, porosity, pore fluid, metal structures, transfer and diffusion of pollutants). At the same time of outdoor exploration, laboratory electrical measurements are carried out to describe soil characteristics, to enhance the understanding of the internal structure of geotechnical materials. Due to the physical property, microstructure, composition, especially electrical property of the soil sharply changes affected by the surrounding environment, and the inhomogeneous charge distribution (polarization) reduces the conductivity of the overall system. When the system is subjected to an external potential, the electrode polarization is influenced by soil in a unique way, and conventional electrical measurements turn to difficult results from this phenomenon [10]. Thus, the measurement method not disturbed by polarization effects at MHz frequencies and higher frequencies becomes important, the focus of electrochemical research has shifted from time concentration dependence to frequency-related phenomenon, and tends to study small-signal alternating current.
Electrochemical impedance spectroscopy (EIS) is proven to be a powerful nondestructive tool for characterization of batteries, hardened cement slurry, concrete, and metal corrosion [11], [12]. As shown in Fig. 1, the change of impedance Z with frequency is used to characterize the kinetics of the bound or moving charge in the various material within a wide range of frequency.
| (1) |
where t is the time, ΔV and ΔI are the maximum values for voltage and current signals respectively, ω=2πf is the angular frequency, with f being the frequency (Hz), φ is the phase difference between the voltage and current, =-1, is the real component equal to |Z|cosφ, is the imaginary component equal to |Z|sinφ, and |Z| is the magnitude of the impedance equal to .
Figure 1.

Scheme of impedance Z.
As shown in Eq. (1), the impedance Z is a complex curve characterized by the real part quantity (X axis) and the imaginary part quantity (Y axis) in the coordinate system. The phase angle φ=arctan(-/) reflects the change of the chemical reaction process with frequency in the system [13]. The dynamic and frequency related processes of electrochemical system in the frequency region of electrochemical impedance spectroscopy are summarized in Fig. 2 [14]. The impedance spectroscopy data in the 10103 Hz can be used to characterize electrochemical process of conductive medium. Subsequent experiments also confirmed this result.
Figure 2.
Dynamic response process corresponding to frequency in EIS [14].
Electrochemical impedance spectroscopy is the measure of the charge transfer law with frequency at an applied electric field. However, electrochemical impedance spectroscopy data obtained through experiments usually requires to develop an accurate equivalent circuit model to decipher [15]. The establishment of equivalent circuit model is based on the charge transfer process inside the materials. Charge conduction in the soil is mainly derived from ion migration in the pore fluid [16]. At present, some scholars have studied the AC characteristics of soil, Han [17] proposed an integrated equivalent circuit model and impedance formula for sandy soils, based on three different kinds of conductive paths in microstructure of soil and theory of electrochemical impedance spectroscopy. Hui Dong [18] illustrated the structural characteristics of soil-rock mixtures, aiming at deducing the relationship between physical property indices based on the three-level equivalent circuit. However, the electrical conductivity mechanism of the soil and the specific physical meaning contained in the circuit component parameters have not been explained in detail. Furthermore, different from the sandy soil or the rock, since the silty soil contains a considerable amount of clay particles (grain size<0.005 mm), moisture-distribution and ion transfer in the pore of silty soil are greatly influenced by the unique physicochemical properties of the clay mineral, and the overall conductivity is further affected, especially under the influence of the temperature field of soil, the phase change of pore solution complicates the pore structure and affects the electroconductibility of soil.
In this study, a new equivalent circuit model about charge conduction in silty soil is established. EIS is applied to obtain complex impedance curves of single-phase medium (dry soil particles, different concentrations of NaCl electrolyte) and mixed-phase medium (silty soil with pore solution containing different concentrations of NaCl) at different temperatures. The electrochemical characteristics of silty soil that affect the charge transfer are studied by comparing the fitting electrical parameters of different medium at various temperatures, the mathematical relationship between the physical indexes and the electrical parameters of silty soil is established, to demonstrate that electrochemical impedance spectroscopy is a reasonable detection method for soil. Furtherly, long-term practicality of electrochemical impedance spectroscopy to test soil is discussed by improving test conditions.
2. Equivalent circuit model and impedance of three-phase conductive medium
2.1. Integrated conductive paths of silty soils
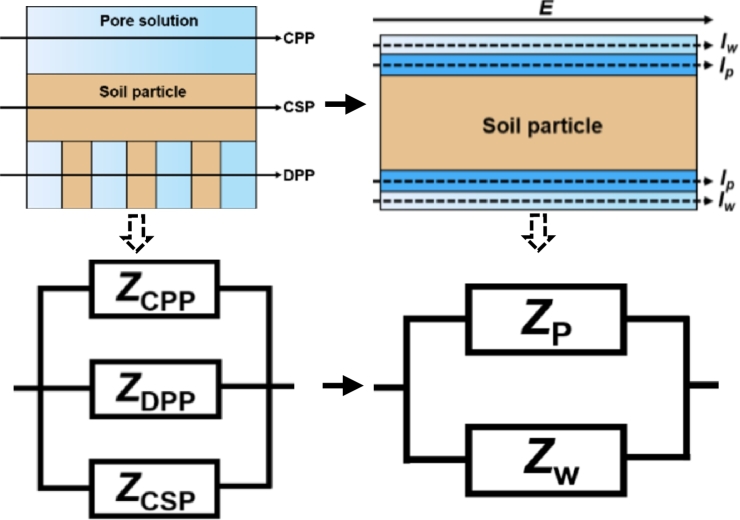
Soil is a porous and multiphase medium, consisting of solid skeleton composed of soil particles, pores filled with liquid and gas phases. The conductivity of soil is not only related to the conductivity of pore solution, but also depends on the degree of interaction of pore solution with the solid-phase skeleton [19]. In particular, the clay particles occupied in the silty soil have a strong adsorption to pore solution. Clay minerals are usually flaky particles because of the isomorphic replacement and uncompensated bond at the edge of particle, excessive negative charges are attached to edges of particles. The surface charge of the clay particles is maintained in balance from the presence of cations. When the soil is dried, cations are tightly adsorbed on the surface of particles, and salt precipitation is derived from excess ions. When the soil is wet, the polar water molecules contact with the cations to form the electrolyte fills pores, namely free water molecules and hydrated ions. The cations leave the clay surface and move relatively freely in the water, which improves the conductivity of soil. Although the hydrated cations on the surface of the clay particles are fluid, their distribution in the water is not uniform. These cations are still attracted near the surface of the clay, and their distribution is determined by thermal motion and coulomb force, presenting a characteristic concentration distribution of high cation concentration near the particle, that is, the electric double layer structure on the surface of particle, until the position away from the surface of particle reaches the overall concentration of pore solution.
According to the study by Clavier et al., the fluid in the electric double layer is different from the conductive properties outside the electric double layer due to the adsorption of clay particles. Therefore, they proposed the dual-water model for conductivity of geotechnical medium [20] The conductive fluid in the soil pores is divided into two parts by the model, that is, the conductive path of the pore water is divided into two parts. As shown in Fig. 3, the water outside the electric double layer is called “far-water” or free water, is the current of the far-water conductive path. The water on the surface of the clay (in the electric double layer) is called “near-water” or clay water, including strongly bound water and weakly bound water, is the current of the near-water conductive path. In order to facilitate the description of the following article, the “near-water” and “far-water” conduction paths are only mentioned. The theoretical basis of dual-water model is consistent with the charge transfer mechanism and adhesion characteristics of silty soil. Therefore, it can be used as an important reference for studying the conductivity of geotechnical medium.
Figure 3.
Microscopic schematic diagram of soil conductivity based on the Dual-water model. I1-free water conductivity path, I2-clay water conductivity path [20].
Based on the conductive mechanism of dual-water model, an equivalent circuit model of electrochemical impedance spectroscopy of silty soil is established. According to the 300 times magnified microstructure photo of silty soil compacted in the laboratory, following the approach of predecessor [21], [22], the conductive path of soil containing pore solution is divided into three parallel elements:
(1) continuous pore conductive paths (CPPs, path 1 in Fig. 4), conductive paths through the continuous interstitial soil pore solution (a liquid element).
Figure 4.

Microstructure of silty soil in lab (X300 amplification): 1-continuous pore conductive paths (CPPs), 2-discontinuous soil particle-pore conductive paths (DPPs), 3-continuous soil particle conductive paths (CSPs), SPs-soil particles blocked in continuous pore paths.
(2) discontinuous soil particle-pore conductive paths (DPPs, path 2 in Fig. 4), conductive paths through alternating layers of soil particles and interstitial soil solution (a solid-liquid series element), continuous pores in the soil are blocked by soil particles (SPs), so they are designated as discontinuous points in the conductive path, and the charge will be conducted along the near-water layer on the surface of soil particles.
(3) continuous soil particle conductive paths (CSPs, path 3 in Fig. 4), conductive paths through or along the surfaces of continuous soil particles (primarily associated with near-water layer) in direct contact with one another (a solid element).
The impedance of silty soil depends on three different conductive paths on consideration of the above content. Most of clay minerals in the silty soil that constitutes the solid skeleton component are classified as the electronic semiconductor type. The impedance of the soil particle skeleton can be regarded as infinite relative, and its influence is usually ignored. As Sauer's study shows that the soil particles are filled by the liquid or air in the pores and the water film surrounding surface. Obviously, there is not enough direct contact between the particle aggregate units in the soil structure [23].
The microstructure of silty soil can be simplified as shown in Fig. 5, the dark blue area is the near-water conductive path, the light blue area is the far-water conductive path, and the yellow area is silty soil particles. The electrical conductance of the gas phase in the soil is zero, so the influence of air can be ignored. Correspondingly, the impedance of two parallel conductive paths combined into the total impedance of silty soil is expressed as Eq. (2)
| (2) |
where Z is the total impedance of silty soil; ZCPP is the impedance of continuous pore conductive paths, ZDPP is the impedance of discontinuous soil particle-pore conductive paths, ZCSP is the impedance of continuous soil particle conductive paths, is the impedance of far-water layer, is the impedance of near-water layer. Therefore, the conduction mechanism of most silty soil can be simplified to a dual-path model according to the dual-water model (Fig. 5). That is, the total resistance is contributed by the near-water resistance and the far-water resistance .
Figure 5.
The simplified equivalent model and circuit for silty soils. Iw-far-water conductivity path, Ip-near-water conductivity path.
In fact, when alternating voltage is applied at both ends of conductive medium, the positive and negative carriers or dipoles in the medium will be polarized by the action of the electric field, the bound charge opposite to the free charge of the plate appears on the surface of the medium [24]. The stronger the polarization of the conductive medium, the greater the surface density of bound charges. Generally, the change in capacitance after being charged with a medium is used to describe the polarization performance of conductive medium. This phenomenon is set as the bulk capacitance of the conductive medium in this study. In wet soil and fine-textured soil, the near-water layer or electric double layer structure on the surface of clay particles is affected by the content of clay particles and the differentiation of soil particles [25]. The dielectric properties of the mixed-phase are quite complex result from the interaction between pore water and soil particles [26]. Therefore, the electric double layer capacitance on the surface of the soil particles is also a factor cannot be ignored. In a matrix with obvious soil-water interaction such as silty soil, the influence from the adsorption of the soil matrix on the electrochemistry of the medium system is worthy for further study, not be elaborated here.
The near-water path and the far-water path are set as two parallel conductive paths, a new equivalent circuit model of soil conductivity is proposed by combining the two groups of , and , in parallel. Finally, the circuit model shown in Fig. 6 is transformed through further integration. The total impedance of silty soil is expressed as Eqs. (3)–(5)
| (3) |
| (4) |
| (5) |
Figure 6.

A new equivalent model and circuit for silty soils.
is the bulk capacitance of the soil sample because of the phenomenon of ion polarization, is the resistance of the free water or the far-water layer, is the electric double layer capacitance produced by the adsorption of cations on the surface of the soil particle, and is the resistance of the near-water layer.
The complex impedance curve of the soil mass transfer process is correspondingly generated in the coordinate system through the derivation of Eqs (3) ∼ (5), and a simple method to evaluate the microstructure of the soil and the electrical parameters and from the electrochemical impedance spectroscopy obtained from the experiment is provided. The complex impedance spectrum curve corresponding to the and parallel circuit (RC) in the coordinate system is obtained by using computer software to simulate (Fig. 7).
Figure 7.
Theoretical Nyquist EIS spectrum based on the equivalent circuit model as shown in Eq. (3). (the spectrum displayed in this figure is computer-generated using the following parameters: Rs=1000 Ω•cm2, and Cs=5E-5 F).
3. Experimental
3.1. EIS test
The electrochemical test was carried out by CS 350 electrochemical workstation with three-electrode system (WE, working electrode, copper bar; RE, reference electrode, calomel electrode; CE, counter electrode, platinum electrode), as shown in Fig. 8. The experimental condition of EIS was scanning frequency for 100 kHz ∼ 0.01 Hz. And the soil temperature was 20°C, 10°C, 5°C, 0°C, -5°C, -10°C, and -20°C respectively.
Figure 8.

Electrochemical testing apparatus under the thermostatic equipment.
3.2. Test sample
The silty soil used in the experiment was taken from Dongshan, Taiyuan City, Shanxi Province, China, as shown in Fig. 9. It can be seen from particle grading curve in Fig. 10, soil color is brown-yellow. The mass of silty particles accounted for nearly 80%. The physical parameters of silty soil are shown in Table 1.
Figure 9.

Location map of silty soil.
Figure 10.
Photography and grain size accumulation curve of silty soil.
Table 1.
Physical and mechanical properties of silty soil.
| Liquid limit (%) | Plastic limit (%) | Plasticity index | Maximum dry density (g•cm−3) | optimum moisture content (%) | Specific gravity | pH |
|---|---|---|---|---|---|---|
| 25.25 | 15.61 | 9.64 | 1.82 | 15.3 | 2.70 | 7.94 |
This electrochemical experiment is directed at single-phase and mixed-phase medium, including dry silty soil (after drying at 105°C for 8 hours) [27], different concentrations of NaCl electrolyte (mixed with distilled water and NaCl), and silty soil mixed with different concentrations of NaCl electrolyte.
3.3. Microstructure and material characterization
Before the EIS test, part of the compacted sample was taken to SEM scanning for surface characterization. The microstructure of the compacted soil samples with 300 times magnification was observed through the Japanese TM 3000 scanning electron microscope. Moreover, part of the dry soil sample was subjected to XRD diffraction analysis, X-ray diffraction data was completed by Ultima IV automatic diffractometer, the excitation conditions in the experiment are 40 kV, 40 mA, the diffraction angle 2θ varies from 5° to 85° in the continuous scanning mode, the scanning step angle is 0.01°, and the scanning speed is 2θ20°/min. The data obtained in the experiment was analyzed by the software Jade 6.0.
3.4. Equivalent circuit model fitting
Equivalent circuit models of different conductive medium at different temperatures are fitted and analyzed by Zsimdemo software, to study the changes of different charge conduction paths on these parameters, and to find out the relationship between these parameters and the state of the conductive medium, temperature, and salt content. These are discussed in the follow-up content.
4. Experimental results
4.1. The independent discussion for conductivity law of solid phase
Aimed to distinguish the influence of solid phase and liquid phase on the overall electrical properties of the conductive medium, this study starts with the impedance characteristics of the single-phase system. Firstly, this study focuses on the conductive path of continuous soil particles (near-water layer), so the electrochemical impedance spectroscopy of dry silty soil is tested. The Nyquist complex plane impedance plot and the Bode plot of dry silty soil are shown Fig. 11. When the frequency is higher than 1 Hz, the phase angle stabilizes at approximately 90°, which indicates that the system is an ideal capacitor [28] With the frequency lower than 1 Hz, the system is restricted by the high impedance properties of the porous structure of silty soil, and the curve appears obvious fluctuation and randomness [29].
Figure 11.
(a) Nyquist complex plane impedance plot of dry silty soil at different temperatures. (b) Bode plots of dry silty soil at different temperatures.
The (RC) circuit was fitted in the test data, ideal fitting curves can be observed from Nyquist diagram (Fig. 11a). The electrochemical parameters of equivalent circuit model (RC) of the dry silty soil at different temperatures are shown in Fig. 12. Bulk capacitance value almost stabilizes around 2.35E-9 F as the temperature decreases. According to the statement in 2.1, this part of the electrical property mainly derives from the electric double layer capacitance on the surface of the soil particles. It can be concluded that the temperature has little effect on the charge activity distribution constrained by the coulomb force for rotational freedom on the surface of the soil particles, which is also consistent with the research of Pepin [25]. Although high impedance properties of dry silty soil results from the complex porous structure, the value of remain stable at 5E8 Ω•cm2 with the temperature decrease, which also confirms that the effect of temperature on the charge conduction of dry soil matrix or near-water layer is little that can be ignored.
Figure 12.
Fitting parameters at different temperatures. (a) Bulk resistance of dry silty soil Cs. (b) Bulk capacitance of dry silty soil Rs.
Based on the above test results, it is confirmed that the conductive mechanism of continuous soil particles or near-water layer can be represented by an equivalent circuit (RC). In fact, alternating current can penetrate the almost “insulating” silty matrix through the charge and discharge effect of electrode plate. In this case, the two electrode end planes in contact with silty matrix act as a parallel plate capacitor, and the silty matrix is the capacitor's medium. Strictly speaking, dry silty soil is not a real “insulator”, silicate minerals in silty soil have limited conductivity and can be regarded as bulk resistance [30]. Studies have shown that the long-term effect on the surface of clay minerals at 105°C mainly changes the bound water between the layers or the surface of the clay minerals and the part of the ionized hydrated water between the layers, except for the lost free water [31]. Although the soil samples were dried according to the experimental standards, there was still a certain amount of strongly and weakly bound water attached to the surface, which contributes to the “near-water” conductive path.
The XRD test results (Fig. 13) confirms the existence of clay minerals in the soil sample. Because of the surface absorbability of soil particles, there is always a certain amount of unfrozen liquid water in the soil during the freezing process [32]. This case means that a small amount of unfrozen liquid water is still attached to the surface of soil particles, and this volume of water is almost equal to the volume of near-water layer, and plays the important role on the resistance of the near-water layer, when the soil sample is in a low temperature environment. Simultaneously, the hydrated ions and adsorbed water molecules in the near-water layer turn to polarized under the action of the electric field, the two elements contribute to the bulk capacitance . The above analysis and fitting results show that temperature has little effect on the electrochemical properties of the near-water layer.
Figure 13.
XRD spectrum of dry silty soil.
4.2. The independent discussion for conductivity law of liquid phase
This study focused on the conductive path of the continuous pore solution (far-water layer) furtherly, and tested the electrochemical impedance spectroscopy of the single liquid phase (different concentrations of NaCl electrolyte). The Nyquist complex plane impedance plots of NaCl electrolyte with concentration of 0.3%, 1.0%, 2.0% at different temperatures are shown in Fig. 14. The characterization of the charge transfer law of the metal interface at different temperature environments on the impedance spectrum curves includes two capacitive reactance arcs (dissolution and passivation reaction of the electrode interface) in the middle and low frequency region and a diagonal line close to 45°, indicating that the ion diffusion resistance near the metal interface. Normally, the NaCl electrolyte exhibits a single intersection with the real axis in the high frequency region of the impedance spectrum because of excellent conductivity. The conductive medium is represented by a solution resistance by the Ohm's law [33]. In fact, the phenomena observed from the experimental results show that the crystalline phase change occurs after the NaCl electrolyte of different concentration decreased to the freezing temperature (Fig. 14 (d)), the conductive property of the medium affected by the temperature gradually evolves from conductors to semiconductors to insulators. Macroscopically, the conductive medium's ability to constrain charges becomes stronger [34], which occurs polarization phenomenon and gradually turns to an accumulation of charges at both ends of the electrode plate. The high-frequency region of the impedance curve gradually extends from the point intersects with the real axis to a semi-circular arc formed by (RC).
Figure 14.
Nyquist complex plane impedance plots of NaCl electrolyte. (a) 0.3% NaCl. (b) 1.0% NaCl. (c) 2.0% NaCl. (d) The cooling curve of NaCl electrolyte.
The changes of bulk resistance and bulk capacitance of NaCl electrolyte are obtained after fitting in Fig. 15. Without considering the electrode interface reaction, temperature and salt content are two main factors that affect the conduction mechanism of NaCl electrolyte. Although the increase of NaCl content weakens the constraint of the medium to the charge, causing the high-frequency region circuit to change from (RC) to R. Once the solution reaches the freezing temperature, the crystalline phase change of the medium will greatly increase the resistance of the medium. But the resistance value of NaCl electrolyte is much smaller than that of pure water, Na+ and Cl− do not enter the crystal lattice after the solution is crystallized, and still exist in the gaps of the crystals [35], and better conductivity than pure water. At the same time, anions and cations are adsorbed on the surface of their respective electrode plates to form electric double layer capacitors, contributing to a higher dielectric constant (ε=/, is the capacitance of the empty measuring bulk) [36]. represents the bulk resistance of the NaCl solution, which is still equivalent to the far-water path in the soil on the principle of conduction. represents the bulk capacitance of the NaCl solution, the content of Na+ is higher, the capacitance of the electric double layer adsorbed on the electrode plate is greater, the decrease in temperature inhibits the oriented movement of hydrated ions and polar water molecules, which also correspond the rule of Fig. 15.
Figure 15.
Fitting parameters of NaCl electrolyte.
The resistance is proportional to the length of the conductive path and inversely proportional to the cross-sectional area of the current.
| (6) |
Where ρ is the specific resistance of NaCl solution, the length l is 3 cm, the cross-sectional area A is 1 cm2. The value of ρ is got by substituting l and A into Eq. (6). The liquid resistivity ρ and the liquid concentration c can be expressed as ρ=K/c (K is the constant when the liquid temperature is constant). Therefore, it can be assumed that the resistivity of the NaCl electrolyte at the same temperature is equal to the resistivity of the far-water path according to the ratio shown in Table 2.
Table 2.
Resistance of NaCl solution at different temperatures.
| T (°C) |
ρ (Ω•cm) |
||
|---|---|---|---|
| 0.3% | 1.0% | 2.0% | |
| 20 | 3.12 | 1.16 | 0.81 |
| 10 | 4.68 | 1.51 | 0.90 |
| 5 | 5.49 | 1.74 | 1.06 |
| 0 | 6.64 | 2.03 | 1.17 |
| -5 | 19.01 | 2.15 | 1.40 |
| -10 | 31.70 | 4.37 | 1.55 |
| -20 | 130.27 | 19.09 | 8.95 |
4.3. The integrated discussion for conductivity law of solid-liquid phase
After analyzing the charge transfer laws of two single-phase medium, the electrical properties of the near-water layer conduction path and the far-water layer conduction path. The Nyquist complex plane impedance plots of silty soil (solid-liquid phase) with NaCl electrolyte at different temperatures are presented in Fig. 16. Different from the single-phase medium, although the soil contains a high salt content pore solution with excellent conductivity, the electrode interface reaction can occur smoothly, that is, the whole can be expressed as R under certain conditions. In fact, compared with the same concentration of NaCl solution, electrochemical impedance spectroscopy of silty soil containing different concentrations of NaCl solution still shows (RC) arcs with different radius in the high frequency region. Because silty soil contains a considerable amount of clay minerals, according to the electrical model established in this section 2.1, it is reasonable to believe that the value includes the electric double layer capacitance .
Figure 16.
Nyquist complex plane impedance plots of silty soil with NaCl electrolyte. (a) 0% NaCl. (b) 0.3% NaCl. (c) 1.0% NaCl. (d) 2.0% NaCl. (e) The cooling curve of silty soil with NaCl electrolyte.
Fig. 16 shows that the mass transfer process in the high frequency region and the interface reactions of metal in the middle and low frequency region at different temperatures include dissolution and passivation reactions and the diffusion of ions near the metal interface. Further, the fitting results for the value and value of the soil system in Fig. 17. Obviously, as the temperature decreases, the free water crystalline phase change and increases viscosity restrains the conductivity path so that the value rises. Therein, the bulk resistance of silty soil < the bulk resistance of NaCl electrolyte , which also conforms to the Eq. (5), which also verifies the rationality of the equivalent circuit model. The capacitance of the two systems in the same temperature environment: the bulk capacitance of silty soil < the bulk capacitance of NaCl electrolyte . Normally, the dielectric constant of a solid-liquid system is mainly controlled by the dielectric constant of the pore fluid [37], the fluid capacity of a solid-liquid system is lower compared with the same volume of a single-phase fluid medium, so the bound charge density on the surface of the medium is also lower than that of a single-phase fluid medium, resulting in the capacitance value is somewhat lower than that of a pure solution, the decrease in temperature also inhibits the molecular of displacement polarization and turning polarization in the medium. In the future, it is worthy of further study for the polarization phenomenon of composite medium, especially the change law and quantitative mechanism of the bound water of soil particles (electric double layer structure) affected by temperature with the help of electrochemical impedance spectroscopy.
Figure 17.
Schematic diagram of parameters obtained from fitting the impedance spectra of silty soil with NaCl electrolyte at different temperatures. (a) Bulk resistance of silty soil Rs. (b) Bulk capacitance of silty soil Cs.
5. Discussion
5.1. Identification of model parameters
Silty soil containing different concentrations of NaCl solution becomes ice-containing soil when the temperature is lower than 0°C. After the soil is partially or completely frozen, not all liquid water can be transformed into solid ice. A certain amount of liquid water (unfrozen water) is always maintained in the soil because of the action of capillary and particle surface energy. After the soil is frozen, except for a small amount of unfrozen free water, the main volume results from the near-water layer adsorbed on the surface of the clay particles, namely, the diffusing electric double layer cation solution [38]. The volume of clay water (near-water layer) per unit volume of silty soil is equal to the product of the thickness of unit volume near-water layer and the surface area of clay particles per unit volume [39]. In the research process of diffusing electric double layer, Bolt [40] proposed a formula for calculating the thickness of the electric double layer according to the characteristics of the electric double layer in the soil,
| (7) |
where ε is the dielectric constant of the water, k is the Boltzmann constant, T is the Kelvin absolute temperature, c is the concentration of the bulk solution, v is the valence of the cation, e is the basic charge unit. The value of each parameter is shown in Table 3.
Table 3.
Several parameters involved in the Eq. (7).
| ε | k (J/K) | T (K) | c (num/cm3) | v | e (C) |
|---|---|---|---|---|---|
| 80 | 1.38×10−23 | 293.15, 283.15, 278.15, 273.15, 268.15, 263.15, 253.15 | 1.93×1020, 6.44×1020, 1.29×1021 | 1 | 1.6×10−19 |
In practical applications, most soil measured data do not include specific surface area, but the measurement of soil grain size distribution is very common, the calculation methods of soil specific surface are mostly based on soil grain size distribution or average grain size, and combined with other mathematical methods. The calculation of in this paper is based on the Sun Meiling [41] method to calculate the specific surface area of silty soil. First, the distribution information of soil grain size is substituted into Eq. (9) and Eq. (8) to obtain its average grain size . Furthermore, the average grain size is substituted into Eq. (10), the specific surface area of the silty soil is obtained based on the exponential function. This calculation result is an approximate value.
| (8) |
| (9) |
| (10) |
, , are the mass percentages of clay particles, silty particles, and sandy particles respectively in Eq. (9). As shown in Fig. 10, =1.8%,=78.9%,=19.3%, so =15.95 m2/g. Inserting the proportion of clay of the silty soil into Eq. (10) gives the surface area of the clay particles in 1 g of soil as [39]
| (11) |
Therefore, the volume of the near-water layer in 1 g of silty soil is acquired
| (12) |
According to Eq. (7) ∼ (12), the change law of the volume of the near-water layer in the silty soil containing different salinity with temperatures is calculated. As shown in Table 4, when the temperature is between -20°C and 20°C, the volume change of the near-water layer does not exceed 2%, and the thickness of the near-water layer is not greatly affected by the temperature [42]. So, the volume of the near-water layer is approximately set to a constant value (average value).
Table 4.
Water content of near-water layer in different temperature environment.
| T (°C) |
(cm3/g) |
||
|---|---|---|---|
| 0.3% | 1.0% | 2.0% | |
| 20 | 0.008 | 0.002 | 0.001 |
| 10 | 0.008 | 0.002 | 0.001 |
| 5 | 0.008 | 0.002 | 0.001 |
| 0 | 0.007 | 0.002 | 0.001 |
| -5 | 0.007 | 0.002 | 0.001 |
| -10 | 0.007 | 0.002 | 0.001 |
| -20 | 0.007 | 0.002 | 0.001 |
| average value | 0.007 | 0.002 | 0.001 |
As mentioned in 2.1, according to the conduction mechanism of the dual-water model, the conductive part of the pore solution in the silty soil is divided into the water inside the electric double layer and the water outside the electric double layer. The structure of water in the soil is shown in Fig. 18. Soil minerals, including the mineral part of clay particles, are non-conductive, and air is not conductive. Only the liquid phase can make the current pass through the soil. The two current paths are assumed to have the same parallel length in the soil [43]. Therefore, the volume of silty soil with length and cross-sectional area A is designed according to the experimental device. A is divided into each component phase. In the model (Fig. 18), the cross-sectional areas of the soil solid, the volume of the far-water layer, the volume of the near-water layer, the volume of ice and the air are , , , , , respectively. , , and are the resistance of the silty soil system, the far-water layer, and the near-water layer, respectively.
Figure 18.
Configuration of water in bulk soil and schematic representation of bulk soil as conducting elements acting in parallel.
For the overall system of silty soil
| (13) |
Where the specific resistivity of the silty soil system. Similarly, the resistance of the far-water layer and the near-water layer is expressed as
| (14) |
| (15) |
Where and are the specific resistivity of the far-water layer and the near-water layer respectively. In Eq. (14) and Eq. (15), is the length of the tortuous path of the current passing through the far-water layer and the near-water layer. Two conductive paths are parallel,
| (16) |
Substituting the values of , and from Eq. (14) ∼ (16) into Eq. (17),
| (17) |
Fig. 18 shows that the volume of the near-water layer is =, the volume of the far-water layer is = , and A = 1 cm2, so the formula can be further transformed into Eq. (18)
| (18) |
Where the ratio / = F is the tortuosity of the pores of the conductive path in the silty soil, represents the tortuous path, and always longer than the experimental length of the soil sample. The F value depends on the soil water content and tissue structure, = 3 cm, so /3 = F. The volume of the far-water layer is the difference between the total liquid water volume V and the volume of the near-water layer ( = V-).
| (19) |
After the phase change of the pore solution, the total volume V of the pore solution decreases as the temperature falls, and the freezing temperature of the pore solution falls as the salt content increases [44]. The pore solution in the soil at positive temperature cannot freeze, V is a steady-state value. As shown in Fig. 16, the freezing temperature of 0.3% and 1.0% of salinity is 0 ∼ -5°C, and the freezing temperature of 2.0% is -5 ∼ -10°C, so can be divided into two formulas by freezing temperature. The resistance expressions of the silty soil system are listed in Table 5 before and after the freezing temperature. The specific resistivity value of the far-water layer path is approximately equivalent to the same concentration of NaCl electrolyte (Table 2).
Table 5.
Segmentation formula involved Eq. (19).
| 0.3% | ≥0°C | |
| <0°C | ||
| 1.0% | ≥0°C | |
| <0°C | ||
| 2.0% | ≥-5°C | |
| <-5°C | ||
| V=1 cm0.16/1 g•cm−3=0.787 cm3=0.007 cm3/g×4.92 g=0.034 cm3=0.002 cm3/g×4.92 g=0.010 cm3=0.001 cm3/g×4.92 g=0.005 cm3 | ||
The specific resistivity value in Table 5 is based on the derivation of Clavier [20] as Eq. (20)
| (20) |
Where is the volume of clay water in the counter ion , T is the temperature, °C, α is the expansion factor of the diffusion layer , salw is the degree of mineralization of NaCl solution, meq/cm3, β is the equivalent conductivity of the compensation ion (Na+) in the near-water layer . The calculation results of the specific resistivity of the near-water layer are shown in the Table 6.
Table 6.
Specific resistivity ρp of near-water layer of silty soil at different temperatures.
| T (°C) |
(Ω•cm) |
||
|---|---|---|---|
| 0.3% | 1.0% | 2.0% | |
| 20 | 0.18 | 0.15 | 0.13 |
| 10 | 0.18 | 0.15 | 0.13 |
| 5 | 0.18 | 0.15 | 0.14 |
| 0 | 0.18 | 0.15 | 0.14 |
| -5 | 0.21 | 0.15 | 0.14 |
| -10 | 0.23 | 0.15 | 0.14 |
| -20 | 0.27 | 0.17 | 0.14 |
Tortuosity F can be given by the Eq. (21) [45]
| (21) |
Where n is the porosity of the frozen soil, the porosity refers to the ratio of the volume of unfrozen water flowing in the soil to the volume of soil particles [46]. The difference between the near-water layer and the far-water layer is that it is distributed on the surface of the clay particles by strong adsorption. Its physical and chemical properties are different from those of the bulk solution in the pores, and basically have no fluidity. The volume of soil particles = 1 cm×3 cm1.64 g•cm−3/2.70=1.82 cm3. Therefore, when the silty soil reaches the freezing temperature, the unfrozen water flowing in the soil designed in this study mainly derives from the volume of the far-water layer. So, tortuosity F is expressed as Eq. (22)
| (22) |
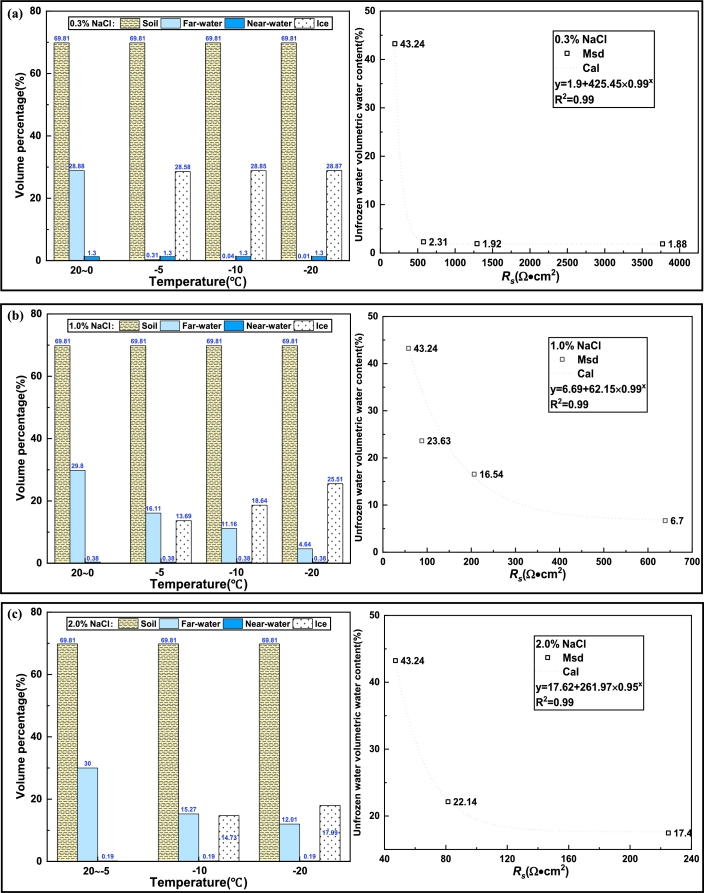
Substituting the above F value expression and value into Table 6, the change of unfrozen water content in the silty soil during the freezing process can be calculated. The calculation result is shown in Fig. 19, the decrease of freezing temperature results from the increase of salinity of the pore solution. Simultaneously, the higher the Na+ content of the bulk solution, the more cations adsorbed on the surface of the clay particles, the thinner the electric double layer, that is, the lower the volume content of the near-water layer, the higher the volume content of the far-water layer at the same temperature environment.
Figure 19.
Scheme of changes in the content of several elements in silty soil at different temperatures. (a) 0.3% NaCl mixed with silty soil, (b) 1.0% NaCl mixed with silty soil, (c) 2.0% NaCl mixed with silty soil.
By fitting the relationship between the value and the volumetric water content of unfrozen water, the mathematical relationship can be described by Eq. (23)
| (23) |
The expression shows that the electrical resistance of silty soil is inversely proportional to the unfrozen water content, and the unfrozen water content is related to temperature. This relationship is consistent with the experimental results, which verify the relationship between the unfrozen water content and the resistivity in the proposed frozen soil resistance model reasonably, the parameters inside need further study.
As shown in Fig. 20, the above changes can be explained that the water in the outer layer of the soil is uniform and the current is stable before the soil is frozen, so the total resistance value of the soil is relatively stable. After freezing occurs, the unfrozen water content of the outer layer of the soil first decreases, and the ice crystals produced by freezing will hinder the channel for the directional movement of conductive ions, and the total resistance of the soil will increase slightly. The continuous decrease in the water content of the outer soil in the middle period of freezing causes the change of soil water potential, and the difference of soil water potential provides the driving force for water migration in the freezing state. The suction force near the freezing front in the outer layer of soil increases, prompting the moisture in the inner layer of the soil to quickly migrate to the outer layer. The unfrozen water that migrated to the outer layer continued to freeze, and the content of unfrozen water inside the soil continued to decrease, causing a significant increase in the electrical resistance of the soil sample. In the post stage of freezing, the unfrozen water in the soil has basically frozen, and the remaining water in the soil is mainly contributed by the near-water layer, the free water in the capillary and the water in the closed cavity. The current path is blocked by ice crystals, so the resistance values increase sharply.
Figure 20.
Scheme of unfrozen water and resistance Rs changes in silty soil freezing process.
5.2. Improved applicability of electrochemical spectroscopic impedance system
The soil is influenced by the environment such as temperature, humidity, salinity, and so on that the electrical double layer structure on the surface of the soil particles and pore fluid occurs physical or chemical changes. According to the above research, an electrochemical mass transfer model of silty soil is established based on the dual-water model proposed by Clavier, and the factors affecting various electrical parameters in the equivalent circuit model are discussed through theoretical analysis and experiments. Electrochemical impedance spectroscopy can be applied to test various information about soil in complex environment. In addition, electrochemical impedance spectroscopy has the advantages of no damage to the test object, less time and workload. Fig. 21 shows the concept of field applicability of the electrochemical impedance spectroscopy system for testing soil electrical parameters and moisture distribution. At the field, in order to reduce the amount of labor, the working electrode, the reference electrode and the auxiliary electrode are combined as an integrated electrode, meantime, a soil salinity sensor and moisture sensor are integrated inside. Then the electrode is inserted into the soil, and the test is started after the electrode surface is stable-state. The impedance spectrum curve obtained by the test is fitted to the curve of the high-frequency region with the built-in computer program to obtain the value. At the same time, by extracting the model expression of different soil samples accumulated in previous laboratory experiments, the corresponding distribution law of soil water with temperature changes can be generated by computer.
Figure 21.

Concept of field applicability of electrochemical impedance spectroscopy system for testing soil information.
Therefore, the equivalent circuit model and test method proposed in this study can be used to study the water distribution and charge transfer laws of soil. However, the actual experiment results show that the high frequency region of the complex impedance curve is not completely relying on electrochemical workstations (maximum frequency is 105 Hz) currently on the market. The higher the content of cations in the soil, the greater the number of charges adsorbed on the surface of the soil particles and electrode plates, the stronger the capacity of the matrix to hold charges, and the system can respond to higher frequency alternating currents confirmed by the characteristic frequency ω⁎ (>105 Hz) corresponding to each medium shown in Table 7.
Table 7.
The characteristic frequency value ω⁎ of each conductive medium.
| T (°C) |
ω⁎ (Hz) |
||
|---|---|---|---|
| 0.3% | 1.0% | 2.0% | |
| 20 | 4.3×106 | 8.3×106 | - |
| 10 | 4.6×106 | 6.9×106 | - |
| 5 | 4.1×106 | 6.5×106 | - |
| 0 | 3.4×106 | 6.1×106 | 7.6×106 |
| -5 | 1.2×106 | 4.8×106 | 7.5×106 |
| -10 | 5.5×105 | 2.0×106 | 5.2×106 |
| -20 | 1.9×105 | 7.1×105 | 3.1×106 |
The fitting data is simulated by Zsimdemo with the example of 1.0% NaCl silty soil (Fig. 22). The ideal curve of (RC) circuit result can only be satisfied when initial frequency in the high frequency region is 10 108 Hz. The current test frequency is 105 Hz, which results in errors in the subsequent fitting accuracy. If the mass transfer process of soil or other substrates is studied in detail, higher frequency testing equipment must be used to ensure that a complete high-frequency arc appears in the complex impedance curve and improves fitting accuracy.
Figure 22.
Schematic diagram of measured and simulated complex impedance curves of silty soil mixed with 1.0% NaCl. (a) 20°C, (b) 10°C, (c) 5°C, (d) 0°C, (e) -5°C, (f) -10°C, (g) -20.
Detection of underground soil is a technical problem faced by engineering construction. In this study, the theoretical and applied study about charge transfer mechanism and electrochemical characteristics of silty soil was conducted by EIS, contributing to deepen the electrochemical theory of soil microstructure, guiding the geological survey, site construction and other engineering applications further. It is significant to promote regional economic development and economic transformation.
6. Conclusion
Based on the unsaturated soil theory and the dual-water conductivity model, this study establishes an equivalent circuit model of silty soil, and discusses the factors affecting the electrical parameters of conductive medium through theoretical analysis and related experiments. According to the fitting results, the model expression of resistance of frozen soil and the volume of unfrozen water is established. The main conclusions are as follows:
(1) This model considers the influence of absorption from clay particles in the soil sample, effectively reflecting the electrical characteristics of silty soil. The adaptability of the circuit is closely related to the physical indexes of silty soil. The experimental results and the model results in a wide frequency range fit better.
(2) The mass transfer process of the conductive medium (single-phase, mixed-phase) corresponds to the first semicircular arc in the high frequency region of the impedance spectrum so that is described as a parallel (RC) circuit. The decrease of temperature effectively affects the ion transfer rate of the conductive medium, and the resistance of the soil increases with the decrease of temperature. The influence of temperature on soil resistance decreases with the increase of salinity.
(3) The decrease in temperature limits the orientation movement (polarization) of the molecules in the conductive medium. The capacitance value of conductive medium (containing electrolyte) decreases with the decrease of temperature, and the opposite is true for pure water medium.
(4) Based on the fitting results, the mathematical relationship between the unfrozen water content V in frozen soil and the bulk resistance is proposed through further derivation. This relationship is consistent with the experimental results, which reasonably verifies the relationship between the unfrozen water content and electrical resistance in the mathematical model.
(5) After improving the test conditions, this method can be used to evaluate the underground structure of rock or soil, such as pore structure and unfrozen water distribution.
Declarations
Author contribution statement
Funan Sun: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper. Zhiwei Chen, Xinyu Liu: Analyzed and interpreted the data. Xiangling Bai, Yuting Wang: Performed the experiments. Bin He: Contributed reagents, materials, analysis tools or data. Pengju Han: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.
Funding statement
Pengju Han was supported by The Applied Basic Research Program in Shanxi Province [20210302123139].
Data availability statement
Data included in article/supp. material/referenced in article.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Warner James. John Wiley & Sons; Hoboken, N.J.: 2004. Practical Handbook of Grouting: Soil, Rock, and Structures. [Google Scholar]
- 2.Larisa G., Anatoly I.P. Electrical geophysical methods in agriculture. In: Zhao C.J., editor. Proceedings of the 4th International Symposium on Intelligent Information Technology in Agriculture (ISIITA); Beijing; 2007. [Google Scholar]
- 3.Shan W., Liu Y., Hu Z.G., Xiao J.T. A model for the electrical resistivity of frozen soils and an experimental verification of the model. Cold Reg. Sci. Technol. 2015;119:75–83. [Google Scholar]
- 4.Tang L.Y., Wang K., Jin L., Yang G.S., Jia H.L., Taoum A. A resistivity model for testing unfrozen water content of frozen soil. Cold Reg. Sci. Technol. 2018;153:55–63. [Google Scholar]
- 5.Klein K.A., Santamarina J. Carlos. Electrical conductivity in soils: underlying phenomena. J. Environ. Eng. Geophys. 2003;8 [Google Scholar]
- 6.Mccarter W.J., Desmazesa P. Soil characterization using electrical measurements. Geotechnique. 1997;47:179–183. [Google Scholar]
- 7.Świergiel J., Jadz̀yn J. Electric relaxational effects induced by ionic conductivity in dielectric materials. Ind. Eng. Chem. Res. 2011;50:11935–11941. [Google Scholar]
- 8.Dobson M.C., Ulaby F.T., Hallikainen M.T., El-Rayes M.A. 1985. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. [Google Scholar]
- 9.Malicki M.A., Plagge R., Roth C.H. Improving the calibration of dielectric TDR soil moisture determination taking into account the solid soil. Eur. J. Soil Sci. 1996;47:357–366. [Google Scholar]
- 10.Klein K.A., Santamarina J.C. Methods for broad-band dielectric permittivity measurements (soil-water mixtures, 5 Hz to 1.3 GHz) J. Environ. Eng. Geophys. 1997;20:168–178. [Google Scholar]
- 11.Svensson A.M., Valøen L.O., Tunold R. Modeling of the impedance response of porous metal hydride electrodes. Electrochim. Acta. 2005;50:2647–2653. [Google Scholar]
- 12.Jain J., Neithalath N. Electrical impedance analysis based quantification of microstructural changes in concretes due to non-steady state chloride migration. Mater. Chem. Phys. 2011;129:569–579. [Google Scholar]
- 13.Zhang J.Q. first. Chemical Industry Press; Beijing: 2010. Electrochemical Measurement Technology. [Google Scholar]
- 14.Danzer M.A. Generalized distribution of relaxation times analysis for the characterization of impedance spectra. Batteries. 2019;5:1–16. [Google Scholar]
- 15.Barsoukov E., Macdonald J.R. Third. John Wiley & Sons; Hoboken: 2018. Impedance Spectroscopy Theory, Experiment, and Applications. [Google Scholar]
- 16.Zhou M., Wang J._G, Cai L., Fan Y.D., Zheng Z.N. Laboratory investigations on factors affecting soil electrical resistivity and the measurement. IEEE Trans. Ind. Appl. 2015;51:5358–5365. [Google Scholar]
- 17.Han P.J., Zhang Y.F., Chen F.Y., Bai X.H. Interpretation of electrochemical impedance spectroscopy (EIS) circuit model for soils. J. Cent. South Univ. 2015;22:4318–4328. [Google Scholar]
- 18.Dong H., Zhu X.M., Jiang X.Z., Chen L., Gao Q.F. Structural characteristics of soil-rock mixtures based on electrochemical impedance spectroscopy. Catena. 2021;207 [Google Scholar]
- 19.Brovelli A., Cassiani G. Combined estimation of effective electrical conductivity and permittivity for soil monitoring. Water Resour. Res. 2011;47:1–14. [Google Scholar]
- 20.Clavier C., Coates G., Dumanoir J. Theoretical and experimental bases for the dual-water model for interpretation of 'Shaly sands. Soc. Pet. Eng. J. 1984;24:153–168. [Google Scholar]
- 21.Wyllie Member M.R.J., Southwick A.P.F. An experimental investigation of the S.P. and resistivity phenomena in dirty sands. J. Pet. Technol. 1953:44–57. http://onepetro.org/JPT/article-pdf/6/02/44/2238037/spe-302-g.pdf/1 [Google Scholar]
- 22.Mitchell J.K., Soga K. 3rd ed. John Wiley & Sons; Hoboken, N.J.: 2005. Fundamentals of Soil Behavior. [Google Scholar]
- 23.Sauer J.M.C., Southwick P.F., Spiegler K.S., Wyllie M.R.J. Electrical conductance of porous plugs ion exchange resin-solution systems. Ind. Eng. Chem. 1955;47:2187–2193. [Google Scholar]
- 24.Zhang P. 2013. Analysis to Effects of Main Factors on Dielectric Properties of Soils. Yangling. [Google Scholar]
- 25.Pepin S., Livingston N.J., Hook W.R. Temperature-dependent measurement errors in time domain reflectometry determinations of soil water. Soil Sci. Soc. Am. J. 1995;59:38–43. [Google Scholar]
- 26.Kurt R., Rainer S., Hannes F., Werner A. Calibration of time domain reflectometry for water content measurement using a composite dielectric approach. Water Resour. Res. 1990;26:2267–2273. [Google Scholar]
- 27.China Planning Press; Beijing: 2019. Standard for geotechnical testing method. GB/T 50123-2019. [Google Scholar]
- 28.Cao C.N., Zhang J.Q. first. Science Press; Beijing: 2002. An Introduction to Electrochemical Impedance Spectroscopy. [Google Scholar]
- 29.Xie R.Z., Chen Z.G., Feng C., He B., Ma F.L., Han P.J., Chen Y.F. Electrochemical impedance spectroscopy of sand of varied particle size and water. Mater. Test. 2018;60:841–847. [Google Scholar]
- 30.Song G.L. Equivalent circuit model for AC electrochemical impedance spectroscopy of concrete. Cem. Concr. Res. 2000;30:1723–1730. [Google Scholar]
- 31.Zeng Z.T., Shao J.S., Mo H.Y., Xu Y.S., Liang Z. Effect of heating time on physical properties of bentonite under high-temperature condition. J. Disaster Prev. Mitig. Eng. 2021;41:463–469. [Google Scholar]
- 32.Daikhin L., Tsionsky V. Hydration forces and liquid-like layer on the ice/metal interface. J. Phys. Condens. Matter. 2007;19 [Google Scholar]
- 33.Wang C.T., Li W., Wang Y.Q., Yang X.F., Xu S.Y. Study of electrochemical corrosion on Q235A steel under stray current excitation using combined analysis by electrochemical impedance spectroscopy and artificial neural network. Constr. Build. Mater. 2020;247 [Google Scholar]
- 34.Jin W.F. first. China Machine Press; Beijing: 1997. Dielectric Physics. [Google Scholar]
- 35.Grimm R.E., Stillman D.E., Dec S.F., Bullock M.A. Low-frequency electrical properties of polycrystalline saline ice and salt hydrates. J. Phys. Chem. B. 2008;112:15382–15390. doi: 10.1021/jp8055366. [DOI] [PubMed] [Google Scholar]
- 36.Shah N.S., Shah P.S., Rana V.A. Dielectric and electrical properties of coconut water and distilled water in the frequency range 20 Hz to 2 MHz at different temperatures. Ionics (Kiel) 2015;21:3217–3222. [Google Scholar]
- 37.A. Kaya, H.Y. Fang, Identification of Contaminated Soils by Dielectric Constant and Electrical Conductivity, n.d.
- 38.Tsytovich N.A. Science Press; Beijing: 1985. The Mechanics of Frozen Soil. [Google Scholar]
- 39.Mojid M.A., Rose D.A., Wyseure G.C.L. A model incorporating the diffuse double layer to predict the electrical conductivity of bulk soil. Eur. J. Soil Sci. 2007;58:560–572. [Google Scholar]
- 40.Bolt G.H. Analysis of the validity of the gouy-chapman theory of the electric double layer. J. Colloid Sci. 1955;10:206–218. [Google Scholar]
- 41.Sun M. 2014. Analysis of the specific surface area of loess in Lanzhou. [Google Scholar]
- 42.Du Y., Cui S., Wang X. Effect of temperature on the properties of bentonite and its mixtures. J. Shaanxi Univ. Technol. (Nat. Sci. Ed.) 2017;33:50–54. [Google Scholar]
- 43.Rhoades J.D., Manteghi N.A., Shouse P.J., Alves W.J. Soil electrical conductivity and soil salinity: new formulations and calibrations. Soil Sci. Soc. Am. J. 1989;53:433–439. [Google Scholar]
- 44.Jin X., Yang W., Meng X.H., Lei L.L. Deduction and application of unfrozen water content in soil based on electrical double-layer theory. Yantu Lixue. 2019;40:1449–1456. [Google Scholar]
- 45.Xiao B.Q., Tu X., Ren W., Wang Z.C. Modeling for hydraulic permeability and Kozeny-Carman constant of porous nanofibers using a fractal approach. Fractals. 2015;23 [Google Scholar]
- 46.Ming F., Chen L., Li D.Q., Wei X.B. Estimation of hydraulic conductivity of saturated frozen soil from the soil freezing characteristic curve. Sci. Total Environ. 2020;698:1–9. doi: 10.1016/j.scitotenv.2019.134132. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. material/referenced in article.