Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 20;127(4):838–845. doi: 10.1021/acs.jpcb.2c05335

Isotope Substitution Effects on the Magnetic Compass Properties of Cryptochrome-Based Radical Pairs: A Computational Study

Gediminas Jurgis Pažėra †, Philip Benjamin †, Henrik Mouritsen ‡,§, P J Hore †,*
PMCID: PMC9900586  PMID: 36669149

Abstract

graphic file with name jp2c05335_0008.jpg

The biophysical mechanism of the magnetic compass sense of migratory songbirds is thought to rely on the photochemical reactions of flavin-containing radical pairs in cryptochrome proteins located in the birds’ eyes. A consequence of this hypothesis is that the effect of the Earth’s magnetic field on the quantum yields of reaction products should be sensitive to isotopic substitutions that modify the hyperfine interactions in the radicals. In this report, we use spin dynamics simulations to explore the effects of 1H → 2H, 12C → 13C, and 14N → 15N isotopic substitutions on the functioning of cryptochrome 4a as a magnetic direction sensor. Two main conclusions emerge. (1) Uniform deuteration of the flavin chromophore appears to be the best way to boost the anisotropy of the magnetic field effect and to change its symmetry. (2) 13C substitution of three of the 12 flavin carbons, in particular C4, C4a, and C8α, seems to be the best recipe for attenuating the anisotropy. These predictions should give insight into the factors that control the magnetic sensitivity once spectroscopic techniques are available for measuring magnetic field effects on oriented protein samples.

Introduction

Migratory songbirds have a remarkable ability to use the direction of the Earth’s magnetic field to help them navigate between their breeding and wintering grounds.1,2 The biophysical mechanism of this light-dependent magnetic compass is uncertain but seems to involve magnetically sensitive photochemical reactions within photoreceptor cells in the retina.3−7 The most likely magnetoreceptor is Cry4a, one of the six known avian cryptochrome (Cry) proteins, in which short-lived radical pairs can be formed by the passage of an electron along a chain of four tryptophan (TrpH) residues to the photoexcited flavin adenine dinucleotide (FAD) chromophore in the center of the protein.3,8−13 In support of this proposal, flavin-tryptophan radical pairs, [FAD•–TrpH•+], in purified Cry4a from the migratory European robin (Erithacus rubecula, Er) have recently been shown to be sensitive to weak applied magnetic fields.14,15 However, it has yet to be demonstrated that Cry4a has the same photochemistry in vivo or that it satisfies other requirements for a viable magnetic direction sensor. Another possibility, for which there is currently less evidence, is that the magnetic sensitivity in vivo originates in a different radical pair, formed during the dark recovery of a photochemically reduced state of the protein.16−18 There has also been some discussion of Cry1a as an alternative to Cry4a, even though it does not bind FAD strongly in vitro.19−21

It is well established that radical pair reactions can be influenced by weak magnetic fields when certain chemical and physical conditions are satisfied.3,22−25 One of the most important in the context of magnetoreception is that, in at least one of the radicals, the unpaired electron must have magnetic hyperfine interactions with one or more atomic nuclei such as 1H and 14N.3 These interactions, which drive coherent interconversion of the singlet and triplet electronic states of the radical pair, determine to a large degree the effect of a weak applied magnetic field on the yields of the reaction products. If, as is usually the case for organic radicals, the hyperfine interactions are anisotropic, the radical pair can form the basis of a magnetic direction sensor. Both FAD•– and TrpH•+ radicals satisfy these conditions, and indeed, the 1H and 14N hyperfine interactions in FAD•– seem to be near optimum for magnetic compass sensing.26

A consequence of the fundamental role of hyperfine interactions in the spin dynamics of radical pairs is that isotopic substitution can in principle be used to provide insight into the factors that control the magnetic sensitivity.27,28 Replacing one isotope of an element by another either changes the nuclear magnetic moment and therefore the hyperfine interaction (e.g., 1H → 2H, 14N → 15N) or introduces a hyperfine interaction where none existed before (e.g., 12C → 13C). In this report, we use spin dynamics simulations to explore the effects of H, C, and N isotopic substitution on the operation of Cry4a as a compass magnetosensor. Results for both [FAD•–TrpH•+] and [FAD•–Z•] radical pairs, hereinafter abbreviated to FAD-Trp and FAD-Z, are presented (Z• is a hypothetical radical with no hyperfine interactions). The aim is to determine patterns of isotopic substitution that could be interesting for future in vitro measurements of anisotropic magnetic field effects on oriented proteins using optical spectroscopic methods.14,29−32

Methods

The spin dynamics of FAD-Trp and FAD-Z radical pairs were simulated as described in ref (33), using a density matrix master equation to account for the relevant magnetic interactions and recombination kinetics. Singlet and triplet radical pairs were assumed to react spin-selectively with equal rate constants, k = 105 s–1, to give distinct products.34 Reaction product fields were calculated as a function of the direction of an external Earth-strength (49 μT) magnetic yield. The dipolar (D) and exchange (J) interactions in FAD-Trp were taken from a preliminary analysis of electron paramagnetic resonance data obtained from an ErCry4 mutant in which the fourth (terminal) tryptophan of the Trp-tetrad had been replaced by phenylalanine to block the final electron transfer step: D = −11.2 MHz, J = −0.65 MHz. Within the point–dipole approximation, this value of D corresponds to a center-to-center separation of 1.91 nm. A subsequent, more refined analysis14 of the same data gave slightly different values of the two parameters; however we do not expect these differences to affect the conclusions of the present study. The orientation of TrpH•+ relative to FAD•– is that of Trp318 (the third component of the Trp-tetrad) relative to FAD in the crystal structure of pigeon (Columba livia) Cry4a,35 which has been predicted to closely resemble the structures of other bird Cry4s including Cry4a from the European robin.36 The third tryptophan was chosen, rather than the fourth (Trp369), because it seems to make a much larger contribution to the magnetic field effects on wild-type Cry4a.14,15 The same values of D and J were used for the FAD-Z radical pair. The g-values of both radicals were taken to be equal to the free-electron value, ge.

1H → 2H, 12C → 13C, and 14N → 15N isotopic substitutions were considered. The natural abundance of 1H, 12C, and 14N in the unsubstituted radicals was taken to be 100% for all three isotopes. The hyperfine tensors for 1H, 13C, and 14N nuclei in FAD•– were calculated using density functional theory (Supporting Information Tables S1–S3).26 The corresponding tensors for 2H and 15N were obtained using the proportionality between the strength of the coupling and the nuclear magnetogyric ratio (γ): γ(15N)/γ(14N) = −1.402 and γ(2H)/γ(1H) = 0.154. The flavin component of FAD•– has 11 hydrogens and 4 nitrogens, and TrpH•+ has 10 hydrogens and 2 nitrogens. Exact simulations of the spin dynamics of multiple isotopologues of such a large spin system would be prohibitive. Therefore, unless otherwise stated, we chose the seven nuclei in FAD•– with the largest hyperfine interactions: N5, N10, H6, 3 × H8α, and one of the H1′ protons.26 The spin system of the TrpH•+ radical comprised the electron spin coupled to the indole nitrogen via its strongly anisotropic hyperfine interaction.26 See Figure 1 for atom labeling and representations of the FAD•–1H, 13C, and 14N hyperfine tensors.

Figure 1.

Figure 1

Open in a new tab

Representations of the hyperfine tensors of (a) 13C (green) and (b) 1H (yellow) and 14N (blue) in FAD•–. Nuclei with strongly anisotropic hyperfine interactions have large, nonspherical surfaces, e.g., N5 and C8. Atom labels follow IUPAC nomenclature. The molecular axis system is shown in (a).

To assess the directional information available from each radical pair, we calculated ΦS(θ, ϕ), the fractional yield of the singlet recombination reaction. θ (colatitude) and ϕ (azimuth) define the direction of the magnetic field vector, B = |B|(sin θ cos ϕ, sin θ sin ϕ, cos θ), relative to the flavin axis system (shown in Figure 1a). B is parallel to the z-axis when θ = 0 and the x-axis when θ = 90°, ϕ = 0. The hyperfine tensor representations in Figure 1 were calculated as follows. The distance from the nucleus in question to the plotted three-dimensional surface in the direction (θ, ϕ) is proportional to bT·A·b where A is the hyperfine tensor and bT = (sin θ cos ϕ, sin θ sin ϕ, cos θ).

In some calculations, a two-site hopping model was used to assess the impact of electron spin relaxation induced by small-amplitude librational motions of the FAD•– within its binding site in the protein. The FAD•– radical was allowed to jump back and forth (with rate constant km) between two equally probable orientations, rotated by ±5° around the flavin x-axis. The reaction yield was calculated by solving two coupled stochastic Liouville equations, one for each site. Reference (37) gives full details of this calculation.

Results

Hydrogen and Nitrogen Isotopologues: Coherent Spin Dynamics

We start by investigating the effects of hydrogen and nitrogen isotopic substitution in the FAD•– component of the FAD-Trp and FAD-Z radical pairs. The results are summarized in Figures 2 and 3. Figure 2a,b shows the anisotropy of the singlet reaction yield, defined as

graphic file with name jp2c05335_m001.jpg 1

for several isotopologues. ΔΦS is regarded as the “signal” that provides the information a bird would need to orient itself in the geomagnetic field: we assume that the bigger the signal, the better the compass sensor. For the same radical pairs, Figure 3a–d plots the dependence of ΦS(θ,0) on θ, the direction of the magnetic field vector in the xz-plane of FAD•–.

Figure 2.

Figure 2

Open in a new tab

Values of ΔΦS for nitrogen and hydrogen isotopologues of FAD•– in (a) FAD-Trp and (b) FAD-Z radical pairs. U denotes the unsubstituted radical pair. N5 and N10 denote 15N substitution. −H and D indicate that all five hydrogens in FAD•– were omitted or replaced by deuterium, respectively. See Supporting Information Tables S4 and S5 for a summary of the nuclei included in these calculations and a key to the notation.

Figure 3.

Figure 3

Open in a new tab

(a–d) Plots of ΦS(θ,0) – ΦS(0, 0) as a function of magnetic field direction, θ, for nitrogen and hydrogen isotopologues of (a, c) FAD-Trp and (b, d) FAD-Z radical pairs. (e, f) Anisotropy of ΦS(θ, ϕ), i.e., Φ̅S(θ, ϕ) = ΦS(θ, ϕ) – ⟨ΦS⟩ where ⟨ΦS⟩ is the isotropic component of ΦS(θ, ϕ). In (e) and (f), red and blue indicate reaction yields that are, respectively, larger and smaller than the isotropic (i.e., average) reaction yield. (e) FAD-Trp radical pair with two 14N and no 1H in FAD•– and one 14N in TrpH•+. Axis lengths = 0.008. (f) FAD-Trp radical pair with two 14N and five 1H in FAD•– and one 14N in TrpH•+. Axis lengths = 0.003. The plot labels are the same as in Figure 2. The small dips at θ ≈ 120° in the N5, N10, −H traces in (c) and (d) arise from avoided level crossings. See Supporting Information Tables S4 and S5 for a summary of the nuclei included in these calculations and a key to the notation.

The signals for the FAD-Z isotopologues (Figures 2b and 3b,d) are about twice the size of those of FAD-Trp (Figures 2a and 3a,c). Otherwise, FAD-Trp and FAD-Z show broadly similar magnetic isotope effects; we concentrate here on FAD-Trp (Figures 2a and 3a,c). All the ΔΦS values shown in Figures 2 and 3 are small (∼10–3) because of the inclusion of a realistic dipolar interaction (−400 μT) which inhibits the singlet–triplet interconversion caused by the somewhat smaller Zeeman interaction (49 μT).

The first bar in Figure 2a, labeled U, is the FAD-Trp pair without isotopic substitution, i.e., two 14N nuclei and five 1H in FAD•– and a single 14N in TrpH•+. The next three bars in Figure 2a show the effects of 14N → 15N substitution of either N5 alone, N10 alone or N5 and N10 together. The change in ΔΦS is small. One might have expected a modest increase in ΔΦS on the basis that the 14N hyperfine interactions of the nitrogens at positions 5 and 10 in FAD•– are strongly anisotropic (Figure 1) and increase by 40% on 15N substitution. Presumably, any such increase is offset by the smaller spin quantum number of 15N (I = 1/2) compared to 14N (I = 1): the magnetic moments 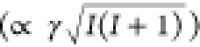Inline graphic of 15N and 14N are in the ratio 0.86 to 1 which would be consistent with the small magnetic isotope effects in Figure 2.

The fifth bar in Figure 2a, labeled N5, N10, D, is for a radical pair in which N5 and N10 are 15N, and all five hydrogens have been replaced by deuterium. The result is a modest increase in ΔΦS, compared to the unsubstituted case (U). This can be understood in terms of the ∼6.5-fold reduction in the hyperfine interactions on deuteration. Most of the 1H interactions in FAD•– are either nearly isotropic (e.g., H8α), small (e.g., H7α), or both (see Figure 1). Deuteration reduces these couplings so that, overall, the flavin radical is magnetically more anisotropic; i.e., the effect of the two anisotropic nitrogens is less diluted by the approximately isotropic hydrogens. This is confirmed by the sixth and seventh bars in Figure 2a: complete removal of the five hydrogens, whether the nitrogens are substituted (N5, N10, −H) or not (−H), results in a further increase in ΔΦS. Deuteration of all five hydrogens in FAD•–, without substituting the nitrogens (eighth bar in Figure 2) gave ΔΦS values comparable to the unsubstituted case.

As well as increasing ΔΦS, deuteration also changes the form of ΦS(θ, 0) in a way that 15N substitution does not. The four traces in Figure 3a (which show the effects of 14N → 15N replacement and correspond to the first four bars of Figure 2a) have essentially the same shape, with maxima near θ = 90° and minima around θ = 0°, 180°. The four colored traces in Figure 3c (corresponding to bars 5–8 in Figure 2a), however, have maxima and minima around θ = 110°–125° and θ = 30°–45°, respectively, suggesting that deuterated radical pairs could signal a different compass bearing. This effect is confirmed by Figure 3e,f which shows the anisotropic part of ΦS(θ, ϕ) for (e) −H (where both nitrogens are 14N and all five hydrogens were omitted) and (f) U (where both nitrogens are 14N and all 5 1H are present). Removal of the 1H hyperfine interactions rotates the anisotropy by about 30° around the y-axis. We anticipate that deuteration would have a similar effect.

Carbon Isotopologues: Coherent Spin Dynamics

We now turn to carbon isotopologues with the expectation that replacement of a nonmagnetic nucleus (12C) with one that has a magnetic moment (13C) might lead to larger changes in ΔΦS than found for 1H → 2H or 14N → 15N substitutions. The 10 ring carbons (C2, C4, C4a, C5a, C6, C7, C8, C9, C9a, C10a) and the two methyl carbons (C7α, C8α) in the isoalloxazine portion of FAD•–(Figure 1) were considered. All 220 combinations of three 12C → 13C substitutions were simulated for both FAD-Trp and FAD-Z. Some of the results are summarized in bar-chart form in Figure 4a,b and as a function of θ in Figure 4c,d. In both cases, the hyperfine interaction of the H1′ proton in FAD•– in FAD-Trp was omitted to reduce the size of the calculation.

Figure 4.

Figure 4

Open in a new tab

(a, b) Values of ΔΦS for carbon isotopologues of FAD-Trp and FAD-Z radical pairs, respectively. (c, d) Plots of ΦS(θ, 0) – ΦS(0, 0) as a function of magnetic field direction, θ, for carbon isotopologues of FAD-Trp and FAD-Z radical pairs, respectively. (e, f) Values of ΔΦS for carbon isotopologues of FAD-Trp and FAD-Z radical pairs, respectively. (g, h) Plots of ΦS(θ, 0) – ΦS(0, 0) as a function of magnetic field direction, θ, for carbon isotopologues of FAD-Trp and FAD-Z radical pairs, respectively. The plot and bar chart labels are explained in the text. See Supporting Information Table S4 for a summary of the nuclei included in these calculations.

Once again, the results for FAD-Z (Figure 4b,d,f,h) were larger by a factor of ∼2 but otherwise similar to those for FAD-Trp (Figure 4a,c,e,g). Focusing now on the bar chart for FAD-Trp (Figure 4a), none of the 220 carbon isotopologues gave a value of ΔΦS larger than the unsubstituted case (U, the first bar in Figure 4a). The combination that came closest to the unsubstituted radical pair was C6, C8, C9a (second bar). Even though these carbons have strongly anisotropic hyperfine tensors, with the same symmetry as N5 and N10 (large z-component, small x- and y-components, Figure 1), they do not enhance the anisotropy of the magnetic field effect, which appears to be largely “saturated” by the effects of N5 and to a lesser extent N10.

The combination of three carbons that produced the smallest ΔΦS (3.1 times smaller than the unsubstituted case, U) was C4, C4a, C8α (third bar in Figure 4a). ΔΦS is smaller still (4.2 times smaller than U) if, in addition, N5 and N10 are replaced by 15N (fourth bar). C4, C4a, and C8α are among the carbons with the largest hyperfine components in the xy-plane of the flavin (Figure 1). The large xy-components of these nuclei could reduce ΔΦS by offsetting the effect of the large z-components of N5 and N10, i.e., by making FAD•– less anisotropic overall.

A smaller reduction in ΔΦS (compared to the unsubstituted case) is seen when any two of C4, C4a, and C8α are substituted (bars 5–7 in Figure 4a). Replacing a fourth 12C by 13C, in addition to C4, C4a, and C8α, gave neither a further reduction in ΔΦS (Figure 4e) nor much of a change in the θ-dependence (Figure 4g).

Smaller reductions in ΔΦS were found for other combinations of three carbons. Table 1 shows the ten “best” sets (best at reducing ΔΦS), starting with C4, C4a, C8α and working down. All but one of the ten sets contain two of C4, C4a, and C8α. C8α was present in all ten, C4a in six, and C4 in four. The reductions in ΔΦS, relative to the unsubstituted case, varied between 2.9-fold (set 2) and 2.6-fold (set 10) compared to 3.1 for C4, C4a, C8α (set 1).

Table 1. Ten Sets of Three 12C → 13C Substitutions That Give the Biggest Reductions in ΔΦSa.

  C2 C4 C4a C7 C7α C8α C9a C10a 103 ΔΦS
1   • •     •     1.70
2 •   •     •     1.81
3   •       •   • 1.85
4     •     • •   1.91
5     •     •   • 1.94
6     • •   •     1.96
7     •   • •     1.97
8   •       • •   1.98
9           • • • 1.99
10   •   •   •     2.00
Open in a new tab
a

The largest reduction was found for C4, C4a, C8α. The final column gives values of the reaction yield anisotropy.

Nitrogen Isotopologues: Spin Relaxation

None of the calculations reported above included spin relaxation, a process that is unlikely to be negligible in vivo and is expected to attenuate the magnetic field effects that arise from the coherent spin dynamics.38−41 To explore the magnetic isotope effect on the loss of spin coherence, we modeled the librational motion of the FAD radical in its binding site in a protein by allowing it to wobble back and forth between two equally probable orientations, rotated by ±5° around the flavin x-axis.37 Very similar results were found when this rocking motion was around the y-axis. Little relaxation is expected either in the motional narrowing limit, when the rate constant km for the wobbling motion is much larger than the hyperfine interactions, or in the static limit in which km is much smaller than the hyperfine interactions. It is when km is comparable to the hyperfine interactions, i.e., 107 s–1 < km < 108 s–1, that the spin relaxation should be most effective at destroying the coherence on which the magnetic sensitivity relies.

Figure 5a shows the dependence of ΔΦS on km for unsubstituted (black) and 14N → 15N substituted (color) FAD-Z radical pairs. Similar results are expected for FAD-Trp. ΔΦS for the unsubstituted radical pair (U) is reduced 11-fold from 0.0160 when km = 104 s–1 to 0.0015 when km = 108 s–1. Replacing either N5 or N10 or both by 15N reduced ΔΦS for all but the km values (107–108 s–1) that induce the fastest relaxation. Given that the difference between the unsubstituted radical pair and the 15N isotopologues in Figure 5a is only present for very slow and very fast motions, where spin relaxation is ineffective, it seems that the majority of the 14N → 15N effect arises from the coherent spin dynamics (shown in Figure 2) rather than this form of spin relaxation.

Figure 5.

Figure 5

Open in a new tab

(a) Plots of ΔΦS for nitrogen isotopologues as a function of the rate constant for the wobbling motion of FAD•– in a FAD-Z radical pair. (b, c) Values of ΔΦS for carbon isotopologues of FAD-Z radical pairs with and without spin relaxation, respectively. The plot and bar chart labels are explained in the text. See Supporting Information Table S4 for a summary of the nuclei included in these calculations.

Carbon Isotopologues: Spin Relaxation

We anticipate that replacement of nonmagnetic 12C nuclei by 13C nuclei that have strongly anisotropic hyperfine interactions (Figure 1) could enhance spin relaxation effects and lead to bigger differences between substituted and unsubstituted radical pairs. To keep the computational demands within reasonable bounds, FAD-Z was modeled for a single value of km (= 108 s–1, chosen to give a large change in ΔΦS) with just four hyperfine interactions in FAD•– (N5, N10, H6 and one of the H8α protons). As above, all 220 three-carbon substitutions were considered.

Data for the five sets of three carbons that produce the largest reductions in ΔΦS compared to the unsubstituted case (bar 1) are shown as bars 2–7 in Figure 5b. All six attenuate the signal by ∼75%. Similar reductions were found when spin relaxation was not included (Figure 5c). The similarity of Figure 5b,c suggests that the spin relaxation induced by the librational motion of FAD•– is dominated by the modulation of the 14N hyperfine tensors.

Magnitude of ΔΦS

Finally in this section, we comment briefly on the strength of the signal (ΔΦS) assumed to allow a bird to orient in the geomagnetic field. In all of the simulations presented here, ΔΦS is of the order of 10–3, corresponding to a ∼0.1% change in the reaction yield for a ∼90° change in orientation with respect to the ∼50 μT magnetic field. One might reasonably ask whether such a small magnetic field effect is sufficient to form the basis of a viable compass magnetoreceptor. An answer to this important question will have to wait until more is known about the structure, binding partners, and signaling of cryptochromes in vivo. We have so little knowledge of factors such as spin relaxation, amplification mechanisms, spatial and temporal integration of information from receptors distributed around the retina, and so on that it is impossible to say how big ΔΦS would need to be. Magnetic field effects at the level of 0.1% are undeniably small but if cryptochromes really are the magnetoreceptors, Nature must have found a way to cope with weak signals.

Discussion and Conclusions

The dominant effect of isotopic substitution on the spin dynamics of radical pairs is to scale the strength of the hyperfine interactions and thereby alter the sensitivity to external magnetic fields. In the context of magnetoreception, the relevant quantities are the variation of the reaction yield, ΦS(θ, ϕ), with the direction of a ∼50 μT magnetic field and the magnitude of this anisotropy, ΔΦS (eq 1). In the calculations reported here, we explored the effects of replacing 1H by 2H, 12C by 13C, and 14N by 15N, for both of the candidate radical pairs in cryptochrome: FAD-Trp and FAD-Z.

Broadly similar magnetic isotope effects were found for FAD-Trp and FAD-Z, with FAD-Z having ΔΦS values about twice those of FAD-Trp, other things being equal (Figures 2–4). The difference between the two radical pairs is less pronounced than reported by Lee et al.26 because of the inclusion of a realistic dipolar coupling.42

Nitrogen substitution does not produce large changes in either ΦS(θ, ϕ) or ΔΦS whether spin relaxation arising from librational modulation of the hyperfine interactions is included or not (Figures 2 and 5a). This is consistent with the similarity of the magnetic moments of the two isotopes (15N:14N = 0.86:1.00).

Replacement of hydrogen by deuterium, which scales hyperfine couplings by a factor of 0.154 and the nuclear magnetic moment by 0.251, has the effect of increasing ΔΦS and changing the shape of ΦS(θ, ϕ) (Figure 3). This seems to occur because the approximately isotropic 1H hypefine interactions dilute the contributions of N5 and N10 to ΔΦS, an effect that is diminished by deuteration.26 Spin relaxation of the deuterated FAD•– radical was not investigated. Recalling the quadratic dependence on the hyperfine coupling strength,43 spin relaxation arising from modulation of 2H hyperfine couplings should be [γ(2H)/γ(1H)]2 = 42 times slower than that from the corresponding 1H hyperfine couplings.

The set of three 12C → 13C substitutions that produces the largest reduction in ΔΦS is C4, C4a, and C8α (Figure 4). This reduction is smaller when only two of C4, C4a, and C8α are replaced or when another carbon is added to this set of three. These three carbons feature strongly in the 10 best sets (Table 1).

It is not clear why C4, C4a, C8α have the largest effect on ΔΦS; a clue comes from the scatter plot in Figure 6 in which the principal components (Axx, Ayy, Azz) of the 13C hyperfine interactions are shown in red for C4, C4a, and C8α, in green for the carbons that feature in the top 10 sets in Table 1, and in orange for the rest. Broadly speaking, it is the carbons with small |Azz| and large |Axx + Ayy|/2 that have the greatest effect on ΔΦS. Inclusion of these 13C atoms seems to offset the anisotropic effects of N5 and N10, which both have large |Azz| ≫ |Axx + Ayy|/2, and so reduce the overall magnetic anisotropy.

Figure 6.

Figure 6

Open in a new tab

Principal hyperfine tensor components for the 12 carbons in the flavin portion of FAD•–. The color code is explained in the text. The blue line is Azz = (Axx + Ayy)/2.

Two main conclusions emerge from this work. (1) Perdeuteration of FAD appears to be the best way to boost the reaction yield anisotropy and to change its symmetry. (2) 13C substitution of C4, C4a, and C8α, or one of the other nine combinations in Table 1 seems to be the best way of reducing the reaction yield anisotropy. Both predictions will be tested by measuring magnetic field effects on cryptochromes with the appropriate FAD isotopologues incorporated.

Acknowledgments

We thank Adelbert Bacher and Stefan Weber for helpful discussions. We are grateful to the following for generous financial support: the European Research Council (under the European Union’s Horizon 2020 research and innovation program, Grant Agreement 810002, Synergy Grant QuantumBirds, awarded to P.J.H. and H.M.), the Office of Naval Research Global, Award N62909-19-1-2045, awarded to P.J.H., and the Deutsche Forschungsgemeinschaft (Projektnummer 395940726-SFB 1372 Magnetoreception and Navigation in Vertebrates awarded to H.M. and P.J.H.), and GRK 1885 Molecular Basis of Sensory Biology, awarded to H.M.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c05335.

  • Hyperfine coupling tensors, lists of nuclei included in calculations shown in Figures 2–5, and notation used in Figures 2 and 3 (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry B virtual special issue “Honoring Michael R. Berman”.

Supplementary Material

jp2c05335_si_001.pdf (195.3KB, pdf)

References

  1. Wiltschko R.; Wiltschko W.. Magnetic Orientation in Animals; Springer Verlag, 1995. [Google Scholar]
  2. Mouritsen H. Long-Distance Navigation and Magnetoreception in Migratory Animals. Nature 2018, 558, 50–59. 10.1038/s41586-018-0176-1. [DOI] [PubMed] [Google Scholar]
  3. Hore P. J.; Mouritsen H. The Radical Pair Mechanism of Magnetoreception. Annu. Rev. Biophys. 2016, 45, 299–344. 10.1146/annurev-biophys-032116-094545. [DOI] [PubMed] [Google Scholar]
  4. Karki N.; Vergish S.; Zoltowski B. D. Cryptochromes: Photochemical and Structural Insight into Magnetoreception. Protein Sci. 2021, 30, 1521–1534. 10.1002/pro.4124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Kavet R.; Brain J. Cryptochromes in Mammals and Birds: Clock or Magnetic Compass?. Physiology 2021, 36, 183–194. 10.1152/physiol.00040.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Wiltschko R.; Niessner C.; Wiltschko W. The Magnetic Compass of Birds: The Role of Cryptochrome. Front. Physiol. 2021, 12, 667000. 10.3389/fphys.2021.667000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Wong S. Y.; Frederiksen A.; Hanic M.; Schuhmann F.; Grüning G.; Hore P. J.; Solov’yov I. A. Navigation of Migratory Songbirds: A Quantum Magnetic Compass Sensor. Neuroforum 2021, 27, 141–150. 10.1515/nf-2021-0005. [DOI] [Google Scholar]
  8. Liedvogel M.; Mouritsen H. Cryptochromes—A Potential Magnetoreceptor: What Do We Know and What Do We Want to Know?. J. R. Soc. Interface 2010, 7, S147–S162. 10.1098/rsif.2009.0411.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Günther A.; Einwich A.; Sjulstok E.; Feederle R.; Bolte P.; Koch K. W.; Solov’yov I. A.; Mouritsen H. Double-Cone Localization and Seasonal Expression Pattern Suggest a Role in Magnetoreception for European Robin Cryptochrome 4. Curr. Biol. 2018, 28, 211–223. 10.1016/j.cub.2017.12.003. [DOI] [PubMed] [Google Scholar]
  10. Wu H.; Scholten A.; Einwich A.; Mouritsen H.; Koch K. W. Protein-Protein Interaction of the Putative Magnetoreceptor Cryptochrome 4 Expressed in the Avian Retina. Sci. Rep. 2020, 10, 7364. 10.1038/s41598-020-64429-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hochstoeger T.; Al Said T.; Maestre D.; Walter F.; Vilceanu A.; Pedron M.; Cushion T. D.; Snider W.; Nimpf S.; Nordmann G. C.; et al. The Biophysical, Molecular, and Anatomical Landscape of Pigeon Cry4: A Candidate Light-Based Quantal Magnetosensor. Sci. Adv. 2020, 6, eabb9110. 10.1126/sciadv.abb9110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chetverikova R.; Dautaj G.; Schwigon L.; Dedek K.; Mouritsen H. Double Cones in the Avian Retina Form an Oriented Mosaic Which Might Facilitate Magnetoreception and/or Polarized Light Sensing. J. R. Soc. Interface 2022, 19, 20210877. 10.1098/rsif.2021.0877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Görtemaker K.; Yee C.; Bartölke R.; Behrmann H.; Voss J. O.; Schmidt J.; Xu J. J.; Solovyeva V.; Leberecht B.; Behrmann E.; et al. Direct Interaction of Avian Cryptochrome 4 with a Cone Specific G-Protein. Cells 2022, 11, 2043. 10.3390/cells11132043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Xu J.; Jarocha L. E.; Zollitsch T.; Konowalczyk M.; Henbest K. B.; Richert S.; Golesworthy M. J.; Schmidt J.; Déjean V.; Sowood D. J. C.; et al. Magnetic Sensitivity of Cryptochrome 4 from a Migratory Songbird. Nature 2021, 594, 535–540. 10.1038/s41586-021-03618-9. [DOI] [PubMed] [Google Scholar]
  15. Wong S. Y.; Wei Y.; Mouritsen H.; Solov’yov I. A.; Hore P. J. Cryptochrome Magnetoreception: Four Tryptophans Could Be Better Than Three. J. R. Soc. Interface 2021, 18, 20210601. 10.1098/rsif.2021.0601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pooam M.; Arthaut L. D.; Burdick D.; Link J.; Martino C. F.; Ahmad M. Magnetic Sensitivity Mediated by the Arabidopsis Blue-Light Receptor Cryptochrome Occurs During Flavin Reoxidation in the Dark. Planta 2019, 249, 319–332. 10.1007/s00425-018-3002-y. [DOI] [PubMed] [Google Scholar]
  17. Wiltschko R.; Ahmad M.; Niessner C.; Gehring D.; Wiltschko W. Light-Dependent Magnetoreception in Birds: The Crucial Step Occurs in the Dark. J. R. Soc. Interface 2016, 13, 20151010. 10.1098/rsif.2015.1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Player T. C.; Hore P. J. Viability of Superoxide-Containing Radical Pairs as Magnetoreceptors. J. Chem. Phys. 2019, 151, 225101. 10.1063/1.5129608. [DOI] [PubMed] [Google Scholar]
  19. Niessner C.; Denzau S.; Peichl L.; Wiltschko W.; Wiltschko R. Magnetoreception in Birds: I. Immunohistochemical Studies Concerning the Cryptochrome Cycle. J. Exp. Biol. 2014, 217, 4221–4224. 10.1242/jeb.110965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Niessner C.; Denzau S.; Peichl L.; Wiltschko W.; Wiltschko R. Magnetoreception: Activation of Avian Cryptochrome 1a in Various Light Conditions. J. Comp. Physiol. A 2018, 204, 977–984. 10.1007/s00359-018-1296-7. [DOI] [PubMed] [Google Scholar]
  21. Bolte P.; Einwich A.; Seth P. K.; Chetverikova R.; Heyers D.; Wojahn I.; Janssen-Bienhold U.; Feederle R.; Hore P. J.; Dedek K.; et al. Cryptochrome 1a Localisation in Light- and Dark-Adapted Retinae of Several Migratory and Non-Migratory Bird Species: No Signs of Light-Dependent Activation. Ethol. Ecol. Evol. 2021, 33, 248–272. 10.1080/03949370.2020.1870571. [DOI] [Google Scholar]
  22. Steiner U. E.; Ulrich T. Magnetic Field Effects in Chemical Kinetics and Related Phenomena. Chem. Rev. 1989, 89, 51–147. 10.1021/cr00091a003. [DOI] [Google Scholar]
  23. Rodgers C. T.Magnetic Field Effects in Chemical Systems. D.Phil. Thesis, University of Oxford, 2007. [Google Scholar]
  24. Jones A. R. Magnetic Field Effects in Proteins. Mol. Phys. 2016, 114, 1691–1702. 10.1080/00268976.2016.1149631. [DOI] [Google Scholar]
  25. Miura T. Studies on Coherent and Incoherent Spin Dynamics That Control the Magnetic Field Effect on Photogenerated Radical Pairs. Mol. Phys. 2020, 118, e1643510. 10.1080/00268976.2019.1643510. [DOI] [Google Scholar]
  26. Lee A. A.; Lau J. C. S.; Hogben H. J.; Biskup T.; Kattnig D. R.; Hore P. J. Alternative Radical Pairs for Cryptochrome-Based Magnetoreception. J. R. Soc. Interface 2014, 11, 20131063. 10.1098/rsif.2013.1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Woodward J. R.; Timmel C. R.; McLauchlan K. A.; Hore P. J. Radio Frequency Magnetic Field Effects on Electron-Hole Recombination. Phys. Rev. Lett. 2001, 87, 077602. 10.1103/PhysRevLett.87.077602. [DOI] [PubMed] [Google Scholar]
  28. Rodgers C. T.; Norman S. A.; Henbest K. B.; Timmel C. R.; Hore P. J. Determination of Radical Re-Encounter Probability Distributions from Magnetic Field Effects on Reaction Yields. J. Am. Chem. Soc. 2007, 129, 6746–6755. 10.1021/ja068209l. [DOI] [PubMed] [Google Scholar]
  29. Maeda K.; Neil S. R. T.; Henbest K. B.; Weber S.; Schleicher E.; Hore P. J.; Mackenzie S. R.; Timmel C. R. Following Radical Pair Reactions in Solution: A Step Change in Sensitivity Using Cavity Ring-Down Detection. J. Am. Chem. Soc. 2011, 133, 17807–17815. 10.1021/ja206783t. [DOI] [PubMed] [Google Scholar]
  30. Neil S. R. T.; Li J.; Sheppard D. M. W.; Storey J.; Maeda K.; Henbest K. B.; Hore P. J.; Timmel C. R.; Mackenzie S. R. Broadband Cavity-Enhanced Detection of Magnetic Field Effects in Chemical Models of a Cryptochrome Magnetoreceptor. J. Phys. Chem. B 2014, 118, 4177–4184. 10.1021/jp500732u. [DOI] [PubMed] [Google Scholar]
  31. Maeda K.; Robinson A. J.; Henbest K. B.; Hogben H. J.; Biskup T.; Ahmad M.; Schleicher E.; Weber S.; Timmel C. R.; Hore P. J. Magnetically Sensitive Light-Induced Reactions in Cryptochrome Are Consistent with Its Proposed Role as a Magnetoreceptor. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 4774–4779. 10.1073/pnas.1118959109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sheppard D. M. W.; Li J.; Henbest K. B.; Neil S. R. T.; Maeda K.; Storey J.; Schleicher E.; Biskup T.; Rodriguez R.; Weber S.; et al. Millitesla Magnetic Field Effects on the Photocycle of Drosophila Melanogaster Cryptochrome. Sci. Rep. 2017, 7, 42228. 10.1038/srep42228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Efimova O.; Hore P. J. Role of Exchange and Dipolar Interactions in the Radical Pair Model of the Avian Magnetic Compass. Biophys. J. 2008, 94, 1565–1574. 10.1529/biophysj.107.119362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Timmel C. R.; Till U.; Brocklehurst B.; McLauchlan K. A.; Hore P. J. Effects of Weak Magnetic Fields on Free Radical Recombination Reactions. Mol. Phys. 1998, 95, 71–89. 10.1080/00268979809483134. [DOI] [PubMed] [Google Scholar]
  35. Zoltowski B. D.; Chelliah Y.; Wickramaratne A.; Jarocha L.; Karki N.; Xu W.; Mouritsen H.; Hore P. J.; Hibbs R. E.; Green C. B.; et al. Chemical and Structural Analysis of a Photoactive Vertebrate Cryptochrome from Pigeon. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 19449–19457. 10.1073/pnas.1907875116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hanic M.; Schuhmann F.; Frederiksen A.; Langebrake C.; Manthey G.; Liedvogel M.; Xu J. J.; Mouritsen H.; Solov’yov I. A. Computational Reconstruction and Analysis of Structural Models of Avian Cryptochrome 4. J. Phys. Chem. B 2022, 126, 4623–4635. 10.1021/acs.jpcb.2c00878. [DOI] [PubMed] [Google Scholar]
  37. Hiscock H. G.; Worster S.; Kattnig D. R.; Steers C.; Jin Y.; Manolopoulos D. E.; Mouritsen H.; Hore P. J. The Quantum Needle of the Avian Magnetic Compass. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 4634–4639. 10.1073/pnas.1600341113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Lau J. C. S.; Wagner-Rundell N.; Rodgers C. T.; Green N. J. B.; Hore P. J. Effects of Disorder and Motion in a Radical Pair Magnetoreceptor. J. R. Soc. Interface 2010, 7, S257–S264. 10.1098/rsif.2009.0399.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kattnig D. R.; Solov’yov I. A.; Hore P. J. Electron Spin Relaxation in Cryptochrome-Based Magnetoreception. Phys. Chem. Chem. Phys. 2016, 18, 12443–12456. 10.1039/C5CP06731F. [DOI] [PubMed] [Google Scholar]
  40. Kattnig D. R.; Sowa J. K.; Solov’yov I. A.; Hore P. J. Electron Spin Relaxation Can Enhance the Performance of a Cryptochrome-Based Magnetic Compass Sensor. New J. Phys. 2016, 18, 063007. 10.1088/1367-2630/18/6/063007. [DOI] [PubMed] [Google Scholar]
  41. Worster S.; Kattnig D. R.; Hore P. J. Spin Relaxation of Radicals in Cryptochrome and Its Role in Avian Magnetoreception. J. Chem. Phys. 2016, 145, 035104. 10.1063/1.4958624. [DOI] [PubMed] [Google Scholar]
  42. Babcock N. S.; Kattnig D. R. Electron-Electron Dipolar Interaction Poses a Challenge to the Radical Pair Mechanism of Magnetoreception. J. Phys. Chem. Lett. 2020, 11, 2414–2421. 10.1021/acs.jpclett.0c00370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Atherton N. M.Principles of Electron Spin Resonance; Ellis Horwood, 1993. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp2c05335_si_001.pdf (195.3KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES