Skip to main content
NCBI home page
RSC Advances logoLink to RSC Advances
. 2023 Feb 3;13(7):4565–4577. doi: 10.1039/d2ra08180f

Machine learning based implicit solvent model for aqueous-solution alanine dipeptide molecular dynamics simulations†

Songyuan Yao a, Richard Van a, Xiaoliang Pan a, Ji Hwan Park b, Yuezhi Mao c,✉, Jingzhi Pu d,✉, Ye Mei e,f,g,✉, Yihan Shao a,✉
PMCID: PMC9900604  PMID: 36760282

Abstract

Inspired by the recent work from Noé and coworkers on the development of machine learning based implicit solvent model for the simulation of solvated peptides [Chen et al., J. Chem. Phys., 2021, 155, 084101], here we report another investigation of the possibility of using machine learning (ML) techniques to “derive” an implicit solvent model directly from explicit solvent molecular dynamics (MD) simulations. For alanine dipeptide, a machine learning potential (MLP) based on the DeepPot-SE representation of the molecule was trained to capture its interactions with its average solvent environment configuration (ASEC). The predicted forces on the solute deviated only by an RMSD of 0.4 kcal mol−1 Å−1 from the reference values, and the MLP-based free energy surface differed from that obtained from explicit solvent MD simulations by an RMSD of less than 0.9 kcal mol−1. Our MLP training protocol could also accurately reproduce combined quantum mechanical molecular mechanical (QM/MM) forces on the quantum mechanical (QM) solute in ASEC environment, thus enabling the development of accurate ML-based implicit solvent models for ab initio-QM MD simulations. Such ML-based implicit solvent models for QM calculations are cost-effective in both the training stage, where the use of ASEC reduces the number of data points to be labelled, and the inference stage, where the MLP can be evaluated at a relatively small additional cost on top of the QM calculation of the solute.

Here we investigated the use of machine learning (ML) techniques to “derive” an implicit solvent model based on the average solvent environment configurations from explicit solvent molecular dynamics (MD) simulations.graphic file with name d2ra08180f-ga.jpg

1. Introduction

One of the central tasks in the field of Computational Chemistry is to simulate various chemical processes and conformational changes of molecules and macromolecules in aqueous solutions.1–5 In general, molecular mechanics (MM), quantum mechanics (QM),6 or combined quantum mechanics molecular mechanics (QM/MM)7 molecular dynamics (MD) simulations incorporate the aqueous environment through explicit or implicit solvent models.8–10 In the explicit solvent models, the solvent molecules are accounted for explicitly, where solvent–solute interactions can be calculated with atomistic resolution. Popular models for explicit solvents include TIPnP,11–13 SPC,14 and AMOEBA.15,16 On the other hand, the implicit solvent models (also known as the continuum solvent models)17–20 treat the solvent implicitly as a dielectric continuum, thus reducing the number of explicit particle–particle interactions. Popular methods include the Poisson–Boltzmann (PB),21 COSMO/polarized continuum model (PCM),22–33 or Generalized Born (GB) models.34–37

With fewer atoms involved in the calculation, the implicit solvent models offer an advantage in terms of its lower computational cost.38 However, the accuracy of implicit solvent models can be limited by its inadequacy to capture specific solute–solvent interactions and solvent structure fluctuations.39 In MM-based modeling, implicit solvent model based simulations do not always accurately reproduce folded40–42 and unfolded structural distributions.8,38,43,44 For QM-based modeling, pKa predictions of the solute can sometimes be off by a couple of pH units, if the hydrogen bonding between solute and the nearby solvent molecules is completely ignored in implicit solvent calculations.45 In principle, such deficiencies in implicit solvent based MM and QM modelings can be mitigated by including one or multiple solvent molecules or the entire first solvation shell into the solute region of implicit solvent calculations.46–48 However, such a treatment might inadvertently reduce the mobility of those solvent molecules and thus over-stabilize the short-range solute–solvent interactions.

To guide the development of more accurate implicit solvent models, it would be highly desirable if one can “derive” an implicit solvent model directly from explicit solvent MD simulations of the system. A breakthrough along this line was made recently by Noé and coworkers.49,50 Specifically, after collecting configurations from an explicit-solvent MD simulation of alanine dipeptide and chignolin, they successfully trained the first machine learning (ML) based implicit solvent model for peptides. The ML model reproduced the forces on solute atoms from the explicit-solvent calculation and could thus be employed to drive solution-phase MD simulations. Their pioneering work follows the recent, rapidly growing use of ML techniques51 in the development of computational chemistry models.52–54 As far as the solvent effect is concerned, ML models have been developed to capture the effect on chemical reactions,55,56 spectral properties,57–60 identify solvation characteristics in general molecular environment,50,61,62 and explore the solvent effect on mixture solvent system.63–65

Inspired by the work of Noé and coworkers,42,49,50,66 in this paper we will also use the solvated alanine dipeptide67–69 as an example and further explore the possibility of “deriving” an implicit solvent model directly from explicit solvent MD simulations. As Noé and coworkers pointed out, for a system with solute atoms at positions r, solvent atoms at positions w = {w1, w2, …}, and a total potential expressed as V(r, w), an implicit solvent model should correspond to the solute potential-of-mean-force (PMF),70,71

1. 1

Clearly, this opens the possibility of acquiring the corresponding forces on the solute atoms (at geometry r) by extensively sampling solvent configurations, w(m) (m = 1, 2, …, M), around the solute,

1. 2

where M is the number of solvent configurations. Furthermore, if both solute and solvent molecules are described by fixed-charge force fields, the solute is essentially interacting in this expression with the average solvent environment configuration (ASEC) potential,72–80

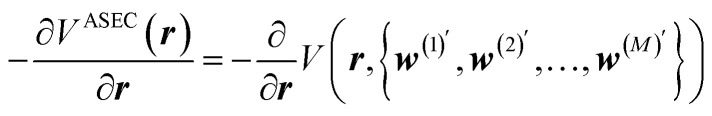1. 3

where the solvent environment is represented by M frames of solvent configuration. For each solvent configuration, w(m)′, the solvent atomic charges are scaled by Inline graphic and van der Waals epsilon values by Inline graphic (due to the geometric combination rule). For a solute that is described by a QM method or a polarizable force field, the ASEC description (with scaled charge and epsilon values) still holds approximately despite the fact the polarization effect from solvent molecules has nonlinear components. Formally, for a single solvent configuration, w(m) with K solvent molecules, the many-body expansion81–83 of the force on the solute is

1. 4

where VVAC is the potential energy of an isolated molecular solute, and the two-body term (second term on the right-hand side) involve the permanent electrostatic, polarization, and higher-order (non-linear) polarization interaction between solute and one solvent molecule, while the third term on the right-hand side corresponds to the non-linear, three-body interactions of the solute with two solvent molecules. As shown in Table S14 of ref. 84, the two-body permanent electrostatic interaction contributes roughly 90% of the QM/MM solute–solvent interaction energy. The remaining 10% is expected to be dominated by the two-body polarization, thus justifying the ASEC formula in eqn (3).

In this work, we will thus seek to build a Δ machine learning potential (MLP) to capture the solute–solvent interactions within the ASEC environment, which is acquired from explicit solvent MD simulations. In the spirit of widely-used force-matching techniques,85,86 the MLP will be trained to minimize a loss function,

1. 5

where VML is the solute–solvent interaction energy predicted by the Δ machine learning potential model. The two-body term (second term on the right-hand side) it is the mean square difference in the solute–solvent interaction forces over N solute configurations, each within its ASEC embedding potential. Note that this loss function closely resembles that of Noé and coworkers (eqn (18) in ref. 49). In comparison to their pioneering work, our effort differs in a couple of ways: (a) for the training/validation configurations, the conformations of alanine (the solute) with different combinations of torsional angles (ϕ, ψ; shown later in Fig. 2) will be used instead of those from a single MD simulation; (b) the labelling data—forces on solute atoms due to solute–solvent interactions—will be evaluated from independent ASEC calculations for each solute configuration; (c) the features of the solute structure will be defined using the widely used Deep Potential-Smooth Edition (DeepPot-SE) representation from E and coworkers;87–90 and (d) MLP implicit solvent model will be constructed not only for MM modeling of solvated alanine dipeptide, but also for the ab initio QM modeling of the solvated molecule.

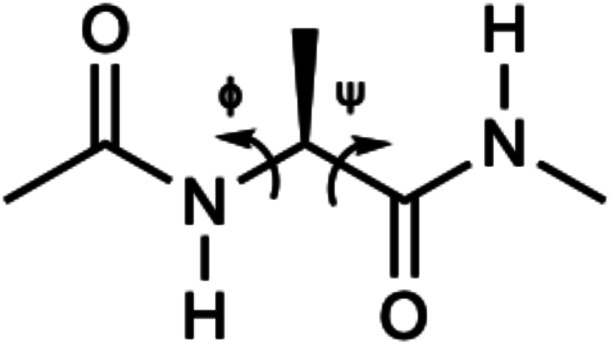
Fig. 2. Structure of alanine dipeptide.

Fig. 2

Open in a new tab

It should be noted that, as far as the solvent effect is concerned, there exists a separate line of efforts towards an accurate ML-based prediction of solvation free energies.48,91–93 While progress along that line has been rather encouraging (with the average error often falling below 0.5 kcal mol−1), those ML models are usually based on SMILES and other descriptors that do not explicitly depend on the coordinates of solute atoms. So, even with neural network automatic differentiation, most of those ML models do not readily provide the forces on solute atoms to drive their dynamical motions, which is the main objective of our work.

This paper is structured as follows. Section 2 summarizes the procedure for training our MLP model, with the corresponding simulation details provided in Section 3. Results and discussion on the MLP implicit solvent models for MM and QM simulations of alanine dipeptide in an aqueous solution will be presented in Section 4. Concluding remarks are made in Section 5.

2. Machine learning based implicit solvent model for MM and QM modeling of solute molecules

For the construction of our machine-learning based implicit solvent model, we will adopt the Deep Potential-Smooth Edition (DeepPot-SE).87,89,90 The overall workflow for our training of the MLP implicit solvent model is shown in Fig. 1, which closely resembles our previous use of DeepPot-SE for the simulation of enzyme reactions.94

Fig. 1. Workflow for the training of the MLP for implicit solvation of alanine dipeptide. The neural networks are optimized to predict the solute–solvent interaction energy V and the corresponding forces on each solute atom.

Fig. 1

Open in a new tab

2.1. Descriptor for the solute molecule

The first step of feature abstraction within this presentation is to build an environment matrix, Ri, for each atom (labelled i),

2.1. 6

where s(Rji) = 1/Rji = 1/|Rj − Ri| represents the reciprocal of the distance between the i-th atoms and one of its neighbors, the j-th atom. If the i-th atom has n neighbors, then the corresponding environment matrix, Ri, is a n-by-4 array. Unlike most other uses of the DeepPot-SE representation, we do not apply any spatial cutoff in the determination of the neighbors list in this work due to the small size of our solute molecule. Therefore, for our alanine dipeptide molecule, which has a total of 22 atoms, each atom would have 21 neighbors (i.e., n = 21).

In the next step of feature abstraction, an embedding neural network (ENN), G, is used to map each s(Rji) value through multiple hidden layers into m1 outputs, which form the j-th row of the embedding matrix gi.

2.1. 7

To ensure the permutational symmetry of the MLP, all s(RHC) values for a carbon atom connecting to a hydrogen atom neighbor are fed into the same embedding neural network, GHC. The same goes with RCC, RNC, ROC, RHH, RCH, RNH, ROH and other distances. For a system with Nelements different elements, there would be Nelements2 distinct embedding neural networks, each fully-connected with one input, three hidden layers of neurons, and an output layer with m1 neurons.

In the next step, an encoded feature matrix Di of size m1 by m2 is computed

Di = (g1i)TRiRTig2i, 8

where g1i is the same as gi (in eqn (7)) and a submatrix g2i contains the first m2 columns of gi (i.e., m2 ≤ m1). Both m1 and m2 are additional hyperparameters of the DeepPot-SE representation of our MLP model, besides the number of hidden layers and the number of neurons in each layer.

2.2. The fitting neural networks (FNN) and loss function

As shown in Fig. 1, the next key component of our machine learning architecture are fitting neural networks (FNN). Specifically, a fitting neural network will be used for each element (C, H, O, N for the alanine dipeptide test system in our work). For each FNN, its input is the feature matrix defined in eqn (8). As the output, FNN predicts the solute–solvent interaction energy for each solute atom,

VMLi = FNN( Created by potrace 1.16, written by Peter Selinger 2001-2019 i) 9

which can be summed up to yield the total solute–solvent interaction energy,

2.2. 10

Through automatic differentiation, it also produces the corresponding force on each atom, Inline graphic. The loss function in eqn (5) measures the mean square difference (MSD) between the predicted forces and reference values,

2.2. 11

over the N training (or validation) configurations, where the reference solute–solvent interaction force is

2.2. 12

Our detailed procedure for the collection of the training/validation configurations and the computation of the corresponding reference forces will be provided in the next Section.

3. Computational details

Alanine dipeptide was used in this work as a test molecule for exploring the possibility of building machine learning based implicit solvent models for MD simulations. This molecule, which is shown in Fig. 2, consists of 22 atoms and has two key torsion angles ϕ(C–N–Cα–C) and ψ(N–Cα–C–N). This system has been widely used in the development of simulation methodologies, such as free energy analyses,95,96 conformational analysis,49,67,97,98 reaction coordinates,99–101 and free energy surface computation.68

3.1. Training/validation configurations

Instead of employing a single MD trajectory for explicitly solvated alanine dipeptide like Noé and coworkers,49,102 we collected the training/validation configurations at various combinations of (ϕ, ψ) dihedral angles of the alanine dipeptide solute molecule. Furthermore, we utilized two slightly different ways to generate these configurations, depending on whether the solute molecule adopted a minimized energy structure (with the two dihedral angles restrained to their respective values). This would lead to two sets of machine learning potentials, which were termed “MLP” and “MLP-O”.

For the training of MLP, short MD simulations using the Inline graphic program in AmberTools21 (ref. 103) were performed at 362 = 1296 combinations of dihedral angles, with a 10-degree increment for each angle. Specifically, for each of these combinations, the solute molecule (as described with the ff14SB force field104) was solvated in TIP3P water molecules11 in a simulation box of ∼33 Å × 33 Å × 33 Å. Then each system was equilibrated with 50 ps NPT simulations, where the two dihedral angles were restrained to their target values using the restraint potential (shown later in eqn (13)) with a force constant of 1000 kcal mol−1 rad−2. The NPT simulations were performed at 1.0 atm (with Berendsen barostat) and 300 K (with Langevin thermostat) using a leapfrog integration (at 1.0 fs time step) under periodic boundary conditions. Once equilibrated, the solute molecule was frozen at its final geometry, and the entire system underwent another NVT simulation for 500 ps at 300 K. During this simulation, the configurations were saved every 0.1 ps, which resulted in 5000 solvent configurations for each solute structure for subsequent ASEC calculations.

For the training of MLP-O, restrained geometry optimizations of the gas-phase solute molecule was carried out using the Inline graphic program in AmberTools21, again with the force constant for each dihedral angle set to be 1000 kcal mol−1 rad−2. The optimization continued for 500 steepest descent and 1500 conjugated gradient steps. The relative energy of these configurations was shown in Fig. S1,† which closely resembled the vacuum Ramachandran plot in ref. 49. Subsequently, with the solute retaining a fixed geometry, each system was first solvated in the water box, equilibrated with NPT simulations at 300 K and 1.0 atm and then subjected to a solvent configuration simulation, which also involved a 500 ps NVT simulation at 300 K. With the configurations saved every 0.1 ps, 5000 configurations were also obtained for each solute structure.

3.2. Labelling data

3.2.1. Data for training implicit solvent models for MM simulations

For MM simulations, the reference force in eqn (12) for each solute structure can be computed equivalently from the PMF formula (eqn (2)) or the ASEC formula (eqn (3)). In this work, the PMF formula was adopted for MM simulations. Namely, for each of the 1296 solute structure, the Inline graphic program was used to compute the force on solute atoms for each of the 5000 solvent configurations. Then the total force was averaged over the 5000 solvent configurations, and the reference force was obtained by subtracting the corresponding vacuum force.

3.2.2. Data for training implicit solvent models for QM simulations

On the other hand, the ASEC formula in eqn (3) was used to generate the labelling data for the MLP implicit solvent model for the potential QM simulations of solvated alanine dipeptide. For each solute structure, one tenth of the previous 5000 solvent configurations (one configuration per ps along the 500 ps trajectory) were used to generate the ASEC environment. Thereby, all 22 atoms of alanine dipeptide were treated as QM atoms and described by density functional theory (DFT) using the B3LYP functional and 6-31G* basis set.105–108 The QM region was electrostatically embedded in 500 solvent configurations with all partial charges scaled by 1/500 (i.e., −0.001668 for water oxygen atoms and 0.000834 for water hydrogen atoms). To enable an efficient QM/MM-PBC calculation, the QM/MM-AC scheme109 was utilized with inner water molecules (within 10 Å from the solute) carrying augmentary charges projected from outer MM water molecules and image cells. The Lennard-Jones interactions between the QM atoms and MM atoms were described using the classical 6–12 formula within the ff14SB/TIP3P force fields, where the epsilon values for water oxygen were scaled by 1/5002. For each solute configuration, the net QM/MM force on the solute atoms were computed using Q-Chem.110 After removing the vacuum DFT forces, the reference force was obtained.

3.3. Training of the machine-learning models

In the training of our ENN and FNN, the labelling dataset was composed of 1296 solute configurations, each containing the coordinate data as input for the ENN and the reference force from ASEC calculations as label. This dataset was randomly split into a training set of 1245 configuration and a validation set of 51 configurations. An additional 500 configurations were collected from an explicit-solvent simulation trajectory of alanine dipeptide and used as the testing set to assess the accuracy our new models. The distribution of the testing set were shown in Fig. S2.† For these configurations, the ASEC forces were obtained with the same procedure as in Section 3.1.

The ENN/FNN were optimized using the training set and then tested on the validation set to determine the accuracy of the prediction. The neural networks for learning the reference ASEC forces from MM and QM/MM simulations were trained for 200 epochs. Other hyperparameters used for the training are listed in Table 1.

Hyperparameters for the training of MLP models.

Hyperparameter Value
ENN layer size [5, 10, 20]
FNN layer size [240, 240]
Activation function tanh
Optimizer Adam
Initial learning rate 5 × 10−4
Decay rate (per epoch) 0.95
Batch size 32
(m1, m2) (20, 4)
Open in a new tab

3.4. Umbrella sampling

The umbrella sampling technique was used to produce the 2-dimensional free energy surface of alanine dipeptide.111 Specifically, a sequence of sampling windows with a harmonic biasing potential,

3.4. 13

where ϕ0i and ψ0i are the restraint torsional angle values for the i-th window, and ki the corresponding force constant. To ensure an adequate coverage of the configurations, a total of 1296 windows were arranged at a 10-degree interval for the ϕ and ψ angles. For each window, a 500 ps NVT simulation trajectory was generated using a force constant of 100 kcal mol−1 rad−2 for each angle. NVT simulation is more compatible with a frozen solute molecule because the volume update in an isobaric simulation would change the geometry of the solute. After 100 ps of equilibration, a frame was saved every 100 fs, resulting in 4000 frames per window. Together, a total over 5 million frames were accumulated.

Three sets of umbrella sampling simulations (vacuum, implicit solvation with the trained ML potential, and explicit solvations) were performed with same setting. For vacuum and explicit solvations, the Inline graphic and Inline graphic programs were used, respectively, while the implicit solvent simulation with the ML potential were performed using the Inline graphic plug-in for the OpenMM package.112 To construct the 2-dimensional free energy surface profile, the 2-d Weighted Histogram Analysis method (WHAM) was employed.113 The free energy surface was calculated with a convergence tolerance of 1.0 × 10−6 kcal mol−1, where the results in the next section (shown later in Fig. 4) are nearly indistinguishable from those obtained using the 100–300 ps segments of the trajectories (Fig. S3,† left column) and the 300–500 ps segments (Fig. S3,† right column).

Fig. 4. Two-dimensional free energy surfaces of alanine dipeptide: (a) implicit solvation with MLP trained by non-minimized solute configurations; (b) explicit solvation; and (c) solute in vacuum. The color bar is in kcal mol−1.

Fig. 4

Open in a new tab

4. Results and discussion

4.1. MLP implicit solvent model for MM modeling

For the training of our MLP models, the optimization learning curves were shown in Fig. S5a and b.† To examine the accuracy of the optimized MLP model for handling the implicit solvation of alanine dipeptide, the predicted solvation forces were plotted against the reference ASEC values for the training and validation configurations (whose ϕ and ψ values were constrained to the grid values) in the top row of Fig. 3. Clearly, our MLP reproduced the ASEC solvation forces on the molecule within the chemical accuracy: the RMSE value of the force difference was 0.342 kcal mol−1 Å−1 for the training set and 0.327 kcal mol−1 Å−1 for the validation set. This can be alternatively seen from the narrow distributions in the force differences in the bottom row of Fig. 3. As shown in Fig. S4,† the MLP-O model, which was trained with an energy-optimized geometry for the solute at each given (ϕ, ψ) combination (the same set of torsional angle values were used as for the training of the MLP model), the RMSE value for the predicted force was 0.268 kcal mol−1 Å−1 and 0.259 kcal mol−1 Å−1 for the training and validation sets, respectively.

Fig. 3. ML predicted solvation forces acquired from ASEC simulation using trajectory configurations. Top: ML-predicted solvation forces versus reference values (in kcal mol−1 Å−1) for the training, validation, and testing sets, which consist of 1245, 51, and 500 configurations, respectively. Bottom: the distribution of errors in the ML-predicted forces.

Fig. 3

Open in a new tab

For the 500 testing set configurations (Section 3.3.), our MLP and MLP-O models predicted the solvation forces with an RMSE of 0.393 kcal mol−1 Å−1 and 0.415 kcal mol−1 Å−1, respectively. With these force differences comparable to those of the training and validation sets, it indicated that our MLP and MLP-O models could accurately predict the interaction of alanine dipeptide with the aqueous environment and can be readily employed to model the solvation dynamics of alanine peptides.

Henceforth, umbrella sampling trajectories were generated using the MLP and MLP-O models and then subject to WHAM analysis to produce the free energy surface (i.e., Ramachandran plots) for solvated alanine dipeptide. A comparison of the free energy landscapes between the MLP and explicit solvent models in Fig. 4 indicated that the MLP model replicated the critical free energy minima (such as C5, PII, αR, αD, and αL). Our MLP Ramachandran plot (or the MLP-O one in Fig. S6b†) was also similar to the explicit-solvent free energy landscape using the same ff14SB force field reported in Fig. S1B of ref. 104. Specifically, our MLP model as shown in Fig. 4a accurately captured the PII, αR, αL and αD regions, with slightly larger errors for the C5 and α′ regions. The surfaces revealing the free energy differences between predictions of the (a) MLP, (b) MLP-O, and (c) vacuum models and the explicit solvent result were shown in Fig. S7.† Panels a and b indicated that the MLP and MLP-O models can yield a free energy surface with the maximum deviation from the explicit solvent result smaller than 0.9 kcal mol−1. This was substantially lower than the difference between gas-phase and explicit solvent simulations (panel c, Fig. S7†).

There results clearly demonstrated that our MLP models can reliably predict the solute–solvent interaction forces for alanine dipeptide. Most importantly, by including solute configurations with all possible combinations of torsional angles in the training set, we could reproduce the high-energy regions, which are essential for studying the transition between different peptide conformations.

4.2. MLP implicit solvent model for QM modeling

So far, our MLP models have been used to predict the solute–solvent interaction forces with the solute described at the MM level. However, with the large number of neuron in our current PyTorch implementation (see Table 1 for details), the anticipated cost to compute MLP (i.e. the force for driving the dynamics) at each time step is higher than to that of an explicit solvent calculation (with a MM description for both the solute and solvent). This could be clearly seen from Table 2, which collected the timings for 10 ns MD trajectories for alanine dipeptide with vacuum, explicit solvent, and MLP models. This suggests that a substantial optimization of the neural network model would be needed before such MLP-based implicit solvent models can be routinely adopted in MM MD simulations.

MD simulation timings for different solvent models with a 1 fs time step. Note that for OpenMM simulations, the time was based on a 10 ns cumulative trajectory. All calculations were carried using an Intel(R) Xeon(R) CPU (E5-2650 v3 2.30 GHz).

Solvent model (package) Time (ns per day)
MM vacuum (SANDER) 450
Explicit solvent (PMEMD) 90
MM + MLP (OpenMM-Torch) 11
QM vacuum (Q-Chem) ∼0.03
Open in a new tab

However, as is well known, QM calculations of the solute molecule have a much higher cost, which can be seen from the timing in Table 2 for gas-phase ab initio QM MD simulation using the Q-Chem software110 at the B3LYP/6-31G* level of theory. Therefore, it would be more attractive to employ our MLP training protocol to learn the QM/MM solute–solvent forces and thus to build ML-based implicit solvent models for the QM modeling.

Our preliminary results for training MLPs to produce QM/MM-quality interaction forces between alanine dipeptide (QM region) and water molecules (MM region) were summarized in Fig. 5. The RMSE values of the predicted QM/MM forces were 0.559, 0.567, and 0.795 kcal mol−1 Å−1, respectively, for the training, validation, and testing sets. To this extent, it also reached the target accuracy level of 1 kcal mol−1 Å−1 for ML force predictions.94,114

Fig. 5. Scatter plots (top row) and histograms (bottom row) displaying the differences between predicted and reference forces for the QM/MM MLP model. The training set, validation set, and testing set all remain the same as for the MM MLP model. The RMSE values in kcal mol−1 Å−1 are also shown.

Fig. 5

Open in a new tab

Recently, there has been a great success in the construction of QM-quality MLPs for small to medium size molecules.115–124 Our work constitutes a natural extensions of these MLP models to offer an implicit description for the interaction of a QM molecule with their solvent environments. Cost-wise, the results above showed that the QM/MM-quality MLP interaction forces could be predicted using the same ML architecture for the prediction of the MM-quality solute–solvent interaction MLP forces, which was far less expensive than the QM calculation of the solute molecule (see Table 2). Therefore, it pointed to the feasibility of utilizing ML to construct QM/MM-quality implicit solvent models.

5. Conclusions

In this work, we employed the DeepPotential descriptors to learn the solute–solvent interaction forces on the alanine dipeptide molecule within an average solvent environment configuration (ASEC). Here are the highlights:

• Compared to the inspiring work by Chen et al.,49 our training/validation sets consisted of 1296 ASEC configurations, in each of which a fixed-geometry solute of varying (ϕ, ψ) angles was embedded in thermally-fluctuating water molecules (as described by the TIP3P model). This contrasted with the employment of long MM trajectories with a flexible-geometry solute by Chen et al. From our point of view, our ML training against the ASEC forces more closely aligned with the goal of the implicit solvent models, which was to integrate over the solvent degrees of freedom.

• Our MLP predicted the ASEC solute–solvent interaction forces on alanine dipeptide with RMSEs below 0.5 kcal mol−1 Å−1 for MM-level simulations and below 1.0 kcal mol−1 Å−1 for QM/MM-level simulations. It opened the possibility of developing accurate ML based “implicit” solvation models for simulating biomolecules in solvent environments. This is especially encouraging for implicit-solvent QM simulations, where the MLP adds little extra computational cost to the simulation.

On the other hand, there are a couple of issues that need to be further addressed:

• Our MLP training protocol, which is based on restrained MD simulations at grid points of the Ramanchandran plot, was not necessarily transferable to other biomolecules. We imagine that, for other molecules, a 2-D or higher-dimensional scan of the most relevant dihedral angles (like ours) can produce an initial training set. However, the dataset will need to be augmented on-the-fly using active learning techniques to detect (and account for) solute configurations out of the trust region.

• Unlike commonly-used implicit solvent models in QM calculations, our MLP implicit solvent model for QM simulations in Section 4.2 did not affect the electronic structure of the QM solute. This can be overcome by developing a different MLP, which is trained to reproduce the external electrostatic potential and field at QM solute atom positions arising from the ASEC environment. The machine-learning potential/field can then be used to polarized the QM solute wavefunction.

These issues will be explored in our future work.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-013-D2RA08180F-s001

Acknowledgments

YS and JP were supported by the National Institutes of Health through Grant R01GM135392. YS is also supported by Grant P30GM145423. YM acknowledges the support from San Diego State University Startup Fund. The authors thank the OU Supercomputing Center for Education & Research (OSCER) for the computational resources.

†

Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra08180f

References

  1. Jorgensen W. L. Tirado-Rives J. Potential Energy Functions for Atomic-level Simulations of Water and Organic and Biomolecular Systems. Proc. Natl. Acad. Sci. U. S. A. 2005;102:6665–6670. doi: 10.1073/pnas.0408037102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Liu X. Zhou G. Huo F. Wang J. Zhang S. Unilamellar Vesicle Formation and Microscopic Structure of Ionic Liquids in Aqueous Solutions. J. Phys. Chem. C. 2016;120:659–667. doi: 10.1021/acs.jpcc.5b08977. [DOI] [Google Scholar]
  3. Smith D. E. Dang L. X. Computer Simulations of NaCl Association in Polarizable Water. J. Chem. Phys. 1994;100:3757–3766. doi: 10.1063/1.466363. [DOI] [Google Scholar]
  4. Liu X. Zhou G. He H. Zhang X. Wang J. Zhang S. Rodlike Micelle Structure and Formation of Ionic liquid in Aqueous Solution by Molecular Simulation. Ind. Eng. Chem. Res. 2015;54:1681–1688. doi: 10.1021/ie503109z. [DOI] [Google Scholar]
  5. Walker T. W. Chew A. K. Li H. Demir B. Zhang Z. C. Huber G. W. Lehn R. C. V. Dumesic J. A. Universal Kinetic Solvent Effects in Acid-catalyzed Reactions of Biomass-derived Oxygenates. Energy Environ. Sci. 2018;11:617–628. doi: 10.1039/C7EE03432F. [DOI] [Google Scholar]
  6. Cieplak P. Bash P. Singh U. C. Kollman P. A. A Theoretical Study of Tautomerism in the Gas Phase and Aqueous Solution: A Combined Use of State-of-the-art ab initio Quantum Mechanics and Free Energy-perturbation Methods. J. Am. Chem. Soc. 1987;109:6283–6289. doi: 10.1021/ja00255a010. [DOI] [Google Scholar]
  7. Gao J. Xia X. A Priori Evaluation of Aqueous Polarization Effects through Monte Carlo QM-MM Simulations. Science. 1992;258:631–635. doi: 10.1126/science.1411573. [DOI] [PubMed] [Google Scholar]
  8. Nymeyer H. Garcia A. E. Simulation of the Folding Equilibrium of α-Helical Peptides: A Comparison of the Generalized Born Approximation with Explicit Solvent. Proc. Natl. Acad. Sci. U.S.A. 2003;100:13934–13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Anandakrishnan R. Drozdetski A. Walker R. C. Onufriev A. V. Speed of Conformational Change: Comparing Explicit and Implicit Solvent Molecular Dynamics Simulations. Biophys. J. 2015;108:1153–1164. doi: 10.1016/j.bpj.2014.12.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cumberworth A. Bui J. M. Gsponer J. Free Energies of Solvation in the Context of Protein Folding: Implications for Implicit and Explicit Solvent Models. J. Comput. Chem. 2016;37:629–640. doi: 10.1002/jcc.24235. [DOI] [PubMed] [Google Scholar]
  11. Jorgensen W. L. Chandrasekhar J. Madura J. D. Impey R. W. Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
  12. Vega C. Abascal J. L. F. Nezbeda I. Vapor-liquid Equilibria from the Triple Point up to the Critical Point for the New Generation of TIP4P-like Models: TIP4P/Ew, TIP4P/2005, and TIP4P/Ice. J. Chem. Phys. 2006;125:034503. doi: 10.1063/1.2215612. [DOI] [PubMed] [Google Scholar]
  13. Mahoney M. W. Jorgensen W. L. Diffusion Constant of the TIP5P Model of Liquid Water. J. Chem. Phys. 2001;114:363–366. doi: 10.1063/1.1329346. [DOI] [Google Scholar]
  14. Berendsen H. J. C. Grigera J. R. Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987;91:6269–6271. doi: 10.1021/j100308a038. [DOI] [Google Scholar]
  15. Ren P. Ponder J. W. Temperature and Pressure Dependence of the AMOEBA Water Model. J. Phys. Chem. B. 2004;108:13427–13437. doi: 10.1021/jp0484332. [DOI] [Google Scholar]
  16. Ponder J. W. Wu C. Ren P. Pande V. S. Chodera J. D. Schnieders M. J. Haque I. Mobley D. L. Lambrecht D. S. DiStasio R. A. Head-Gordon M. Clark G. N. I. Johnson M. E. Head-Gordon T. Current Status of the AMOEBA Polarizable Force Field. J. Phys. Chem. B. 2010;114:2549–2564. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Roux B. Simonson T. Implicit Solvent Models. Biophys. Chem. 1999;78:1–20. doi: 10.1016/S0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
  18. Cramer C. J. Truhlar D. G. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
  19. Tomasi J. Mennucci B. Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  20. Ho J. Klamt A. Coote M. L. Comment on the Correct Use of Continuum Solvent Models. J. Phys. Chem. A. 2010;114:13442–13444. doi: 10.1021/jp107136j. [DOI] [PubMed] [Google Scholar]
  21. Yang X. Lei H. Gao P. Thomas D. G. Mobley D. L. Baker N. A. Atomic Radius and Charge Parameter Uncertainty in Biomolecular Solvation Energy Calculations. J. Chem. Theory Comput. 2018;14:759–767. doi: 10.1021/acs.jctc.7b00905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Miertuš S. Scrocco E. Tomasi J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of AB initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981;55:117–129. doi: 10.1016/0301-0104(81)85090-2. [DOI] [Google Scholar]
  23. Klamt A. Schüürmann G. COSMO: A New Approach to Dielectric Dcreening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc., Perkin Trans. 2. 1993;2:799–805. doi: 10.1039/P29930000799. [DOI] [Google Scholar]
  24. Truong T. N. Stefanovich E. V. A New Method for Incorporating Solvent Effect into the Classical, ab initio Molecular Orbital and Density Functional Theory Frameworks for Arbitrary Shape Cavity. Chem. Phys. Lett. 1995;240:253–260. doi: 10.1016/0009-2614(95)00541-B. [DOI] [Google Scholar]
  25. Cancès E. Mennucci B. Tomasi J. A New Integral Equation Formalism for the Polarizable Continuum Model: Theoretical Background and Applications to Isotropic and Anisotropic Dielectrics. J. Chem. Phys. 1997;107:3032–3041. doi: 10.1063/1.474659. [DOI] [Google Scholar]
  26. Mennucci B. Cancès E. Tomasi J. Evaluation of Solvent Effects in Isotropic and Anisotropic Dielectrics and in Ionic Solutions with a Unified Integral Equation Method: Theoretical Bases, Computational Implementation, and Numerical Applications. J. Phys. Chem. B. 1997;101:10506–10517. doi: 10.1021/jp971959k. [DOI] [Google Scholar]
  27. York D. M. Karplus M. A Smooth Solvation Potential Based on the Conductor-Like Screening Model. J. Phys. Chem. A. 1999;103:11060–11079. doi: 10.1021/jp992097l. [DOI] [Google Scholar]
  28. Chipman D. M. Reaction Field Treatment of Charge Penetration. J. Chem. Phys. 2000;112:5558–5565. doi: 10.1063/1.481133. [DOI] [Google Scholar]
  29. Marenich A. V. Cramer C. J. Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B. 2009;113:6378–6396. doi: 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  30. Lange A. W. Herbert J. M. A Smooth, Nonsingular, and Faithful Discretization Scheme for Polarizable Continuum Models: The Switching/Gaussian Approach. J. Chem. Phys. 2010;133:244111. doi: 10.1063/1.3511297. [DOI] [PubMed] [Google Scholar]
  31. Mennucci B. Polarizable Continuum Model. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012;2:386–404. [Google Scholar]
  32. Klamt A. Moya C. Palomar J. A Comprehensive Comparison of the IEFPCM and SS(V)PE Continuum Solvation Methods with the COSMO Approach. J. Chem. Theory Comput. 2015;11:4220–4225. doi: 10.1021/acs.jctc.5b00601. [DOI] [PubMed] [Google Scholar]
  33. Ho J. Ertem M. Z. Calculating Free Energy Changes in Continuum Solvation Models. J. Phys. Chem. B. 2016;120:1319–1329. doi: 10.1021/acs.jpcb.6b00164. [DOI] [PubMed] [Google Scholar]
  34. Marenich A. V. Olson R. M. Kelly C. P. Cramer C. J. Truhlar D. G. Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges. J. Chem. Theory Comput. 2007;3:2011–2033. doi: 10.1021/ct7001418. [DOI] [PubMed] [Google Scholar]
  35. Lange A. W. Herbert J. M. Improving Generalized Born Models by Exploiting Connections to Polarizable Continuum Models. I. An Improved Effective Coulomb Operator. J. Chem. Theory Comput. 2012;8:1999–2011. doi: 10.1021/ct300111m. [DOI] [PubMed] [Google Scholar]
  36. Marenich A. V. Cramer C. J. Truhlar D. G. Generalized Born Solvation Model SM12. J. Chem. Theory Comput. 2013;9:609–620. doi: 10.1021/ct300900e. [DOI] [PubMed] [Google Scholar]
  37. Lee M. S. Olson M. A. Comparison of Volume and Surface Area Nonpolar Solvation Free Energy Terms for Implicit Solvent Simulations. J. Chem. Phys. 2013;139:044119. doi: 10.1063/1.4816641. [DOI] [PubMed] [Google Scholar]
  38. Onufriev A. Bashford D. Case D. Exploring Protein Native States and Large-scale Conformational Changes with a Modified Generalized Born Model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
  39. Lipparini F. Barone V. Polarizable Force Fields and Polarizable Continuum Model: A Fluctuating Charges/PCM Approach. 1. Theory and Implementation. J. Chem. Theory Comput. 2011;7:3711–3724. doi: 10.1021/ct200376z. [DOI] [PubMed] [Google Scholar]
  40. Zhou R. Berne B. J. Can a Continuum Solvent Model Reproduce the Free Energy Landscape of a β-Hairpin Folding in Water? Proc. Natl. Acad. Sci. U.S.A. 2002;99:12777–12782. doi: 10.1073/pnas.142430099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Noé F. Schütte C. Vanden-Eijnden E. Reich L. Weikl T. R. Constructing the Equilibrium Ensemble of Folding Pathways from Short Off-equilibrium Simulations. Proc. Natl. Acad. Sci. U. S. A. 2009;106:19011–19016. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Noé F. De Fabritiis G. Clementi C. Machine Learning for Protein Folding and Dynamics. Curr. Opin. Struct. Biol. 2020;60:77–84. doi: 10.1016/j.sbi.2019.12.005. [DOI] [PubMed] [Google Scholar]
  43. Lang E. J. M. Baker E. G. Woolfson D. N. Mulholland A. J. Generalized Born Implicit Solvent Models Do Not Reproduce Secondary Structures of De Novo Designed Glu/Lys Peptides. J. Chem. Theory Comput. 2022;18:4070–4076. doi: 10.1021/acs.jctc.1c01172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Shao Q. Zhu W. Assessing AMBER Force Fields for Protein Folding in an Implicit Solvent. Phys. Chem. Chem. Phys. 2018;20:7206–7216. doi: 10.1039/C7CP08010G. [DOI] [PubMed] [Google Scholar]
  45. Chen J. Shao Y. Ho J. Are Explicit Solvent Models More Accurate than Implicit Solvent Models? A Case Study on the Menschutkin Reaction. J. Phys. Chem. A. 2019;123:5580–5589. doi: 10.1021/acs.jpca.9b03995. [DOI] [PubMed] [Google Scholar]
  46. Thapa B. Schlegel H. B. Improved pKa Prediction of Substituted Alcohols, Phenols, and Hydroperoxides in Aqueous Medium Using Density Functional Theory and a Cluster-Continuum Solvation Model. J. Phys. Chem. A. 2017;121:4698–4706. doi: 10.1021/acs.jpca.7b03907. [DOI] [PubMed] [Google Scholar]
  47. Ho J. Are Thermodynamic Cycles Necessary for Continuum Solvent Calculation of pKas and Reduction Potentials? Phys. Chem. Chem. Phys. 2015;17:2859–2868. doi: 10.1039/C4CP04538F. [DOI] [PubMed] [Google Scholar]
  48. Hutchinson S. T. Kobayashi R. Solvent-Specific Featurization for Predicting Free Energies of Solvation through Machine Learning. J. Chem. Inf. Model. 2019;59:1338–1346. doi: 10.1021/acs.jcim.8b00901. [DOI] [PubMed] [Google Scholar]
  49. Chen Y. Krämer A. Charron N. E. Husic B. E. Clementi C. Noé F. Machine Learning Implicit Solvation for Molecular Dynamics. J. Chem. Phys. 2021;155:084101. doi: 10.1063/5.0059915. [DOI] [PubMed] [Google Scholar]
  50. Noé F. Tkatchenko A. Müller K.-R. Clementi C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020;71:361–390. doi: 10.1146/annurev-physchem-042018-052331. [DOI] [PubMed] [Google Scholar]
  51. Sarker I. H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021;2:160. doi: 10.1007/s42979-021-00592-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Unke O. T. Meuwly M. PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges. J. Chem. Theory Comput. 2019;15:3678–3693. doi: 10.1021/acs.jctc.9b00181. [DOI] [PubMed] [Google Scholar]
  53. Gastegger M. Schwiedrzik L. Bittermann M. Berzsenyi F. Marquetand P. wACSF-Weighted Atom-centered Symmetry Functions as Descriptors in Machine Learning Potentials. J. Chem. Phys. 2018;148:241709. doi: 10.1063/1.5019667. [DOI] [PubMed] [Google Scholar]
  54. Grimme S. Schreiner P. R. Computational Chemistry: The Fate of Current Methods and Future Challenges. Angew. Chem., Int. Ed. Engl. 2018;57:4170–4176. doi: 10.1002/anie.201709943. [DOI] [PubMed] [Google Scholar]
  55. Meuwly M. Machine Learning for Chemical Reactions. Chem. Rev. 2021;121:10218–10239. doi: 10.1021/acs.chemrev.1c00033. [DOI] [PubMed] [Google Scholar]
  56. Khorshidi A. Peterson A. Amp: A Modular Approach to Machine Learning in Atomistic Simulations. Comput. Phys. Commun. 2016;207:310–324. doi: 10.1016/j.cpc.2016.05.010. [DOI] [Google Scholar]
  57. Gastegger M. Schütt K. T. Müller K.-R. Machine Learning of Solvent Effects on Molecular Spectra and Reactions. Chem. Sci. 2021;12:11473–11483. doi: 10.1039/D1SC02742E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. He Q. Yang W. Luo W. Wilhelm S. Weng B. Label-Free Differentiation of Cancer and Non-Cancer Cells Based on Machine-Learning-Algorithm-Assisted Fast Raman Imaging. Biosensors. 2022;12:250. doi: 10.3390/bios12040250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Gastegger M. Behler J. Marquetand P. Machine Learning Molecular Dynamics for the Simulation of Infrared Spectra. Chem. Sci. 2017;8:6924–6935. doi: 10.1039/C7SC02267K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Chandra A. Ichiye T. Dynamical Properties of the Soft Sticky Dipole Model of Water: Molecular Dynamics Simulations. J. Chem. Phys. 1999;111:2701–2709. doi: 10.1063/1.479546. [DOI] [Google Scholar]
  61. Magdău I.-B. Miller T. F. Machine Learning Solvation Environments in Conductive Polymers: Application to ProDOT-2Hex with Solvent Swelling. Macromolecules. 2021;54:3377–3387. doi: 10.1021/acs.macromol.0c02132. [DOI] [Google Scholar]
  62. Basdogan Y. Groenenboom M. C. Henderson E. De S. Rempe S. B. Keith J. A. Machine Learning-Guided Approach for Studying Solvation Environments. J. Chem. Theory Comput. 2020;16:633–642. doi: 10.1021/acs.jctc.9b00605. [DOI] [PubMed] [Google Scholar]
  63. Walker T. W. Chew A. K. Van Lehn R. C. Dumesic J. A. Huber G. W. Rational Design of Mixed Solvent Systems for Acid-Catalyzed Biomass Conversion Processes Using a Combined Experimental, Molecular Dynamics and Machine Learning Approach. Top. Catal. 2020;63:649–663. doi: 10.1007/s11244-020-01260-9. [DOI] [Google Scholar]
  64. Chew A. K. Walker T. W. Shen Z. Demir B. Witteman L. Euclide J. Huber G. W. Dumesic J. A. Van Lehn R. C. Effect of Mixed-Solvent Environments on the Selectivity of Acid-Catalyzed Dehydration Reactions. ACS Catal. 2020;10:1679–1691. doi: 10.1021/acscatal.9b03460. [DOI] [Google Scholar]
  65. Maldonado A. M. Basdogan Y. Berryman J. Rempe S. Keith J. First-principles Modeling of Chemistry in Mixed Solvents: Where to Go from Here? J. Chem. Phys. 2020;152:130902. doi: 10.1063/1.5143207. [DOI] [PubMed] [Google Scholar]
  66. Wang J. Charron N. Husic B. Olsson S. Noé F. Clementi C. Multi-body Effects in a Coarse-grained Protein Force Field. J. Chem. Phys. 2021;154:164113. doi: 10.1063/5.0041022. [DOI] [PubMed] [Google Scholar]
  67. Tobias D. J. Brooks C. L. Conformational Equilibrium in the Alanine Dipeptide in the Gas Phase and Aqueous Solution: a Comparison of Theoretical Results. J. Phys. Chem. 1992;96:3864–3870. doi: 10.1021/j100188a054. [DOI] [Google Scholar]
  68. Apostolakis J. Ferrara P. Caflisch A. Calculation of Conformational Transitions and Barriers in Solvated Systems: Application to the Alanine Dipeptide in Water. J. Chem. Phys. 1999;110:2099–2108. doi: 10.1063/1.477819. [DOI] [Google Scholar]
  69. Mironov V. Alexeev Y. Mulligan V. K. Fedorov D. G. A Systematic Study of Minima in Alanine Dipeptide. J. Comput. Chem. 2019;40:297–309. doi: 10.1002/jcc.25589. [DOI] [PubMed] [Google Scholar]
  70. Guàrdia E. Rey R. Padró J. Potential of Mean Force by Constrained Molecular Dynamics: A Sodium Chloride Ion-pair in Water. Chem. Phys. 1991;155:187–195. doi: 10.1016/0301-0104(91)87019-R. [DOI] [Google Scholar]
  71. Guàrdia E. Rey R. Padró J. Na+–Na+ and Cl−–Cl− Ion Pairs in Water: Mean Force Potentials by Constrained Molecular Dynamics. J. Chem. Phys. 1991;95:2823. doi: 10.1063/1.460934. [DOI] [Google Scholar]
  72. Orozco-Gonzalez Y. Manathunga M. Marín M. d. C. Agathangelou D. Jung K.-H. Melaccio F. Ferré N. Haacke S. Coutinho K. Canuto S. Olivucci M. An Average Solvent Electrostatic Configuration Protocol for QM/MM Free Energy Optimization: Implementation and Application to Rhodopsin Systems. J. Chem. Theory Comput. 2017;13:6391–6404. doi: 10.1021/acs.jctc.7b00860. [DOI] [PubMed] [Google Scholar]
  73. Nikolaev D. M. Manathunga M. Orozco-Gonzalez Y. Shtyrov A. A. Guerrero Martínez Y. O. Gozem S. Ryazantsev M. N. Coutinho K. Canuto S. Olivucci M. Free Energy Computation for an Isomerizing Chromophore in a Molecular Cavity via the Average Solvent Electrostatic Configuration Model: Applications in Rhodopsin and Rhodopsin-Mimicking Systems. J. Chem. Theory Comput. 2021;17:5885–5895. doi: 10.1021/acs.jctc.1c00221. [DOI] [PubMed] [Google Scholar]
  74. Sanchez M. L. Aguilar M. A. del Valle F. J. O. Study of Solvent Effects by Means of Averaged Solvent Electrostatic Potentials Obtained from Molecular Dynamics Data. J. Comput. Chem. 1997;18:313–322. doi: 10.1002/(SICI)1096-987X(199702)18:3<313::AID-JCC2>3.0.CO;2-X. [DOI] [Google Scholar]
  75. Mendoza M. Aguilar M. del Valle F. A Mean Field Approach that Combines Quantum Mechanics and Molecular Dynamics Simulation: The Water Molecule in Liquid Water. J. Mol. Struct. 1998;426:181–190. doi: 10.1016/S0166-1280(97)00319-9. [DOI] [Google Scholar]
  76. Coutinho K. Georg H. Fonseca T. Ludwig V. Canuto S. An Efficient Statistically Converged Average Configuration for Solvent Effects. Chem. Phys. Lett. 2007;437:148–152. doi: 10.1016/j.cplett.2007.02.012. [DOI] [Google Scholar]
  77. Zhou X. Kaminski J. W. Wesolowski T. A. Multi-scale Modelling of Solvatochromic Shifts from Frozen-density Embedding Theory with Non-uniform Continuum Model of the Solvent: The Coumarin 153 Case. Phys. Chem. Chem. Phys. 2011;13:10565. doi: 10.1039/C0CP02874F. [DOI] [PubMed] [Google Scholar]
  78. Laktionov A. Chemineau-Chalaye E. Wesolowski T. A. Frozen-density Embedding Theory with Average Solvent Charge Densities from Explicit Atomistic Simulations. Phys. Chem. Chem. Phys. 2016;18:21069–21078. doi: 10.1039/C6CP00497K. [DOI] [PubMed] [Google Scholar]
  79. Brandão I. Fonseca T. L. Georg H. C. Castro M. A. Pontes R. B. Assessing the Structure and First Hyperpolarizability of Li@B10H14 in Solution: A Sequential QM/MM Study Using the ASEC–FEG Method. Phys. Chem. 2020;22:17314–17324. doi: 10.1039/D0CP01268H. [DOI] [PubMed] [Google Scholar]
  80. González-Espinoza C. E. Rumble C. A. Borgis D. Wesolowski T. A. Quantifying Fluctuations of Average Solvent Environments for Embedding Calculations. J. Chem. Theory Comput. 2022;18:1072–1088. doi: 10.1021/acs.jctc.1c01108. [DOI] [PubMed] [Google Scholar]
  81. Gordon M. S. Fedorov D. G. Pruitt S. R. Slipchenko L. V. Fragmentation Methods: A Route to Accurate Calculations on Large Systems. Chem. Rev. 2012;112:632–672. doi: 10.1021/cr200093j. [DOI] [PubMed] [Google Scholar]
  82. Richard R. M. Lao K. U. Herbert J. M. Understanding the Many-body Expansion for Large Systems. I. Precision Considerations. J. Chem. Phys. 2014;141:014108. doi: 10.1063/1.4885846. [DOI] [PubMed] [Google Scholar]
  83. Collins M. A. Bettens R. P. A. Energy-Based Molecular Fragmentation Methods. Chem. Rev. 2015;115:5607–5642. doi: 10.1021/cr500455b. [DOI] [PubMed] [Google Scholar]
  84. Koenig G. Mei Y. Pickard F. C. Simmonett A. C. Miller B. T. Herbert J. M. Woodcock H. L. Brooks B. R. Shao Y. Computation of Hydration Free Energies Using the Multiple Environment Single System Quantum Mechanical/Molecular Mechanical Method. J. Chem. Theory Comput. 2016;12:332–344. doi: 10.1021/acs.jctc.5b00874. [DOI] [PMC free article] [PubMed] [Google Scholar]
  85. Zhou Y. Pu J. Reaction Path Force Matching: A New Strategy of Fitting Specific Reaction Parameters for Semiempirical Methods in Combined QM/MM Simulations. J. Chem. Theory Comput. 2014;10:3038–3054. doi: 10.1021/ct4009624. [DOI] [PubMed] [Google Scholar]
  86. Kim B. Snyder R. Nagaraju M. Zhou Y. Ojeda-May P. Keeton S. Hege M. Shao Y. Pu J. Reaction Path-Force Matching in Collective Variables: Determining Ab Initio QM/MM Free Energy Profiles by Fitting Mean Force. J. Chem. Theory Comput. 2021;17:4961–4980. doi: 10.1021/acs.jctc.1c00245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Zhang L., Han J., Wang H., Saidi W., Car R., E W., End-to-end Symmetry Preserving Inter-atomic Potential Energy Model for Finite and Extended Systems, Advances in Neural Information Processing Systems, 2018, vol. 31, pp. 4436–4446 [Google Scholar]
  88. Zhang L. Han J. Wang H. Car R. E W. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018;120:143001. doi: 10.1103/PhysRevLett.120.143001. [DOI] [PubMed] [Google Scholar]
  89. Wang H. Zhang L. Han J. H. E W. DeePMD-kit: A Deep Learning Package for Many-body Potential Energy Representation and Molecular Dynamics. Comput. Phys. Commun. 2018;228:178–184. doi: 10.1016/j.cpc.2018.03.016. [DOI] [Google Scholar]
  90. Han J. Zhang L. Car R. E W. Deep Potential: A General Representation of a Many-body Potential Energy Surface. Commun. Comput. Phys. 2017;23:629–639. [Google Scholar]
  91. Vermeire F. H. Green W. H. Transfer Learning for Solvation Free Energies: From Quantum Chemistry to Experiments. Chem. Eng. J. 2021;418:129307. doi: 10.1016/j.cej.2021.129307. [DOI] [Google Scholar]
  92. Lim H. Jung Y. Delfos: Deep Learning Model for Prediction of Solvation Free Energies in Generic Organic Solvents. Chem. Sci. 2019;10:8306–8315. doi: 10.1039/C9SC02452B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  93. Zhang D. Xia S. Zhang Y. Accurate Prediction of Aqueous Free Solvation Energies Using 3D Atomic Feature-Based Graph Neural Network with Transfer Learning. J. Chem. Inf. Model. 2022;62:1840–1848. doi: 10.1021/acs.jcim.2c00260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  94. Pan X. Yang J. Van R. Epifanovsky E. Ho J. Huang J. Pu J. Mei Y. Nam K. Shao Y. Machine-Learning-Assisted Free Energy Simulation of Solution-Phase and Enzyme Reactions. J. Chem. Theory Comput. 2021;17:5745–5758. doi: 10.1021/acs.jctc.1c00565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  95. Feig M. Kinetics from Implicit Solvent Simulations of Biomolecules as a Function of Viscosity. J. Chem. Theory Comput. 2007;3:1734–1748. doi: 10.1021/ct7000705. [DOI] [PubMed] [Google Scholar]
  96. Behler J. Representing Potential Energy Surfaces by High-Dimensional Neural Network Potentials. J. Condens. Matter Phys. 2014;26:183001. doi: 10.1088/0953-8984/26/18/183001. [DOI] [PubMed] [Google Scholar]
  97. Nüske F. Boninsegna L. Clementi C. Coarse-graining Molecular Systems by Spectral Matching. J. Chem. Phys. 2019;151:044116. doi: 10.1063/1.5100131. [DOI] [PubMed] [Google Scholar]
  98. Wang W. Gómez-Bombarelli R. Coarse-graining Auto-encoders for Molecular Dynamics. Npj Comput. Mater. 2019;5:125. doi: 10.1038/s41524-019-0261-5. [DOI] [Google Scholar]
  99. Bolhuis P. G. Dellago C. Chandler D. Reaction Coordinates of Biomolecular Isomerization. Proc. Natl. Acad. Sci. U.S.A. 2000;97:5877–5882. doi: 10.1073/pnas.100127697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  100. Wu S. Ma A. Mechanism for the Rare Fluctuation that Powers Protein Conformational Change. J. Chem. Phys. 2022;156:054119. doi: 10.1063/5.0077444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  101. Wu S. Li H. Ma A. A Rigorous Method for Identifying a One-Dimensional Reaction Coordinate in Complex Molecules. J. Chem. Theory Comput. 2022;18:2836–2844. doi: 10.1021/acs.jctc.2c00132. [DOI] [PubMed] [Google Scholar]
  102. Wang J. Olsson S. Wehmeyer C. Pérez A. Charron N. E. de Fabritiis G. Noé F. Clementi C. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019;5:755–767. doi: 10.1021/acscentsci.8b00913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  103. Case D. A., Aktulga H. M., Belfon K., Ben-Shalom I., Brozell S. R., Cerutti D. S., Cheatham III T. E., Cruzeiro V. W. D., Darden T. A., Duke R. E., Giambasu G., Gilson M. K., Gohlke H., Goetz A. W., Harris R., Izadi S., Izmailov S. A., Jin C., Kasavajhala K., Kaymak M. C., King E., Kovalenko A., Kurtzman T., Lee T., LeGrand S., Li P., Lin C., Liu J., Luchko T., Luo R., Machado M., Man V., Manathunga M., Merz K. M., Miao Y., Mikhailovskii O., Monard G., Nguyen H., O'Hearn K. A., Onufriev A., Pan F., Pantano S., Qi R., Rahnamoun A., Roe D. R., Roitberg A., Sagui C., Schott-Verdugo S., Shen J., Simmerling C. L., Skrynnikov N. R., Smith J., Swails J., Walker R. C., Wang J., Wei H., Wolf R. M., Wu X., Xue Y., York D. M., Zhao S., and Kollman P. A., Amber 2021, University of California, San Francisco, p. 2021 [Google Scholar]
  104. Maier J. A. Martinez C. Kasavajhala K. Wickstrom L. Hauser K. E. Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015;11:3696–3713. doi: 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  105. Becke A. D. Density-functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  106. Becke A. D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993;98:1372–1377. doi: 10.1063/1.464304. [DOI] [Google Scholar]
  107. Lee C. Yang W. Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  108. Hariharan P. C. Pople J. A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chim. Acta. 1973;28:213–222. doi: 10.1007/BF00533485. [DOI] [Google Scholar]
  109. Pan X. Nam K. Epifanovsky E. Simmonett A. C. Rosta E. Shao Y. A Simplified Charge Projection Scheme for Long-range Electrostatics in ab initio QM/MM Calculations. J. Chem. Phys. 2021;154:024115. doi: 10.1063/5.0038120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  110. Epifanovsky E. Gilbert A. T. B. Feng X. Lee J. Mao Y. Mardirossian N. Pokhilko P. White A. F. Coons M. P. Dempwolff A. L. Gan Z. Hait D. Horn P. R. Jacobson L. D. Kaliman I. Kussmann J. Lange A. W. Lao K. U. Levine D. S. Liu J. McKenzie S. C. Morrison A. F. Nanda K. D. Plasser F. Rehn D. R. Vidal M. L. You Z.-Q. Zhu Y. Alam B. Albrecht B. J. Aldossary A. Alguire E. Andersen J. H. Athavale V. Barton D. Begam K. Behn A. Bellonzi N. Bernard Y. A. Berquist E. J. Burton H. G. A. Carreras A. Carter-Fenk K. Chakraborty R. Chien A. D. Closser K. D. Cofer-Shabica V. Dasgupta S. de Wergifosse M. Deng J. Diedenhofen M. Do H. Ehlert S. Fang P.-T. Fatehi S. Feng Q. Friedhoff T. Gayvert J. Ge Q. Gidofalvi G. Goldey M. Gomes J. González-Espinoza C. E. Gulania S. Gunina A. O. Hanson-Heine M. W. D. Harbach P. H. P. Hauser A. Herbst M. F. Hernández Vera M. Hodecker M. Holden Z. C. Houck S. Huang X. Hui K. Huynh B. C. Ivanov M. Jász A. Ji H. Jiang H. Kaduk B. Kähler S. Khistyaev K. Kim J. Kis G. Klunzinger P. Koczor-Benda Z. Koh J. H. Kosenkov D. Koulias L. Kowalczyk T. Krauter C. M. Kue K. Kunitsa A. Kus T. Ladjánszki I. Landau A. Lawler K. V. Lefrancois D. Lehtola S. Li R. R. Li Y.-P. Liang J. Liebenthal M. Lin H.-H. Lin Y.-S. Liu F. Liu K.-Y. Loipersberger M. Luenser A. Manjanath A. Manohar P. Mansoor E. Manzer S. F. Mao S.-P. Marenich A. V. Markovich T. Mason S. Maurer S. A. McLaughlin P. F. Menger M. F. S. J. Mewes J.-M. Mewes S. A. Morgante P. Mullinax J. W. Oosterbaan K. J. Paran G. Paul A. C. Paul S. K. Pavošević F. Pei Z. Prager S. Proynov E. I. Rák A. Ramos-Cordoba E. Rana B. Rask A. E. Rettig A. Richard R. M. Rob F. Rossomme E. Scheele T. Scheurer M. Schneider M. Sergueev N. Sharada S. M. Skomorowski W. Small D. W. Stein C. J. Su Y.-C. Sundstrom E. J. Tao Z. Thirman J. Tornai G. J. Tsuchimochi T. Tubman N. M. Veccham S. P. Vydrov O. Wenzel J. Witte J. Yamada A. Yao K. Yeganeh S. Yost S. R. Zech A. Zhang I. Y. Zhang X. Zhang Y. Zuev D. Aspuru-Guzik A. Bell A. T. Besley N. A. Bravaya K. B. Brooks B. R. Casanova D. Chai J.-D. Coriani S. Cramer C. J. Cserey G. DePrince A. E. DiStasio R. A. Dreuw A. Dunietz B. D. Furlani T. R. Goddard W. A. Hammes-Schiffer S. Head-Gordon T. Hehre W. J. Hsu C.-P. Jagau T.-C. Jung Y. Klamt A. Kong J. Lambrecht D. S. Liang W. Mayhall N. J. McCurdy C. W. Neaton J. B. Ochsenfeld C. Parkhill J. A. Peverati R. Rassolov V. A. Shao Y. Slipchenko L. V. Stauch T. Steele R. P. Subotnik J. E. Thom A. J. W. Tkatchenko A. Truhlar D. G. Van Voorhis T. Wesolowski T. A. Whaley K. B. Woodcock H. L. Zimmerman P. M. Faraji S. Gill P. M. W. Head-Gordon M. Herbert J. M. Krylov A. I. Software for the Frontiers of Quantum Chemistry: An Overview of Developments in the Q-Chem 5 Package. J. Chem. Phys. 2021;155:084801. doi: 10.1063/5.0055522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  111. Virnau P. Müller M. Calculation of Free Energy through Successive Umbrella Sampling. J. Chem. Phys. 2004;120:10925–10930. doi: 10.1063/1.1739216. [DOI] [PubMed] [Google Scholar]
  112. Eastman P. Swails J. Chodera J. D. McGibbon R. T. Zhao Y. Beauchamp K. A. Wang L.-P. Simmonett A. C. Harrigan M. P. Stern C. D. Wiewiora R. P. Brooks B. R. Pande V. S. OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLoS Comput. Biol. 2017;13:e1005659. doi: 10.1371/journal.pcbi.1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
  113. Kumar S. Rosenberg J. M. Bouzida D. Swendsen R. H. Kollman P. A. The Weighted Histogram Analysis Method for Free-energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992;13:1011–1021. doi: 10.1002/jcc.540130812. [DOI] [Google Scholar]
  114. Ramakrishnan R. Dral P. O. Rupp M. von Lilienfeld O. A. Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput. 2015;11:2087–2096. doi: 10.1021/acs.jctc.5b00099. [DOI] [PubMed] [Google Scholar]
  115. Behler J. Perspective: Machine Learning Potentials for Atomistic Simulations. J. Chem. Phys. 2016;145:170901. doi: 10.1063/1.4966192. [DOI] [PubMed] [Google Scholar]
  116. Butler K. T. Davies D. W. Cartwright H. Isayev O. Walsh A. Machine Learning for Molecular and Materials Science. Nature. 2018;559:547–555. doi: 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
  117. Dral P. O. Quantum Chemistry in the Age of Machine Learning. J. Phys. Chem. Lett. 2020;11:2336–2347. doi: 10.1021/acs.jpclett.9b03664. [DOI] [PubMed] [Google Scholar]
  118. Zhang J. Lei Y.-K. Zhang Z. Chang J. Li M. Han X. Yang L. Yang Y. I. Gao Y. Q. A Perspective on Deep Learning for Molecular Modeling and Simulations. J. Phys. Chem. A. 2020;124:6745–6763. doi: 10.1021/acs.jpca.0c04473. [DOI] [PubMed] [Google Scholar]
  119. Deringer V. L. Bartók A. P. Bernstein N. Wilkins D. M. Ceriotti M. Csányi G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021;121:10073–10141. doi: 10.1021/acs.chemrev.1c00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  120. Westermayr J. Gastegger M. Schütt K. T. Maurer R. J. Perspective on Integrating Machine Learning into Computational Chemistry and Materials Science. J. Chem. Phys. 2021;154:230903. doi: 10.1063/5.0047760. [DOI] [PubMed] [Google Scholar]
  121. Zubatiuk T. Isayev O. Development of Multimodal Machine Learning Potentials: Toward a Physics-Aware Artificial Intelligence. Acc. Chem. Res. 2021;54:1575–1585. doi: 10.1021/acs.accounts.0c00868. [DOI] [PubMed] [Google Scholar]
  122. Fedik N. Zubatyuk R. Kulichenko M. Lubbers N. Smith J. S. Nebgen B. Messerly R. Li Y. W. Boldyrev A. I. Barros K. Isayev O. Tretiak S. Extending Machine Learning beyond Interatomic Potentials for Predicting Molecular Properties. Nat. Rev. Chem. 2022;6:653–672. doi: 10.1038/s41570-022-00416-3. [DOI] [PubMed] [Google Scholar]
  123. Gokcan H. Isayev O. Learning Molecular Potentials with Neural Networks. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2022;12:e1564. [Google Scholar]
  124. Kulik H. J. Hammerschmidt T. Schmidt J. Botti S. Marques M. A. L. Boley M. Scheffler M. Todorović M. Rinke P. Oses C. Smolyanyuk A. Curtarolo S. Tkatchenko A. Bartók A. P. Manzhos S. Ihara M. Carrington T. Behler J. Isayev O. Veit M. Grisafi A. Nigam J. Ceriotti M. Schütt K. T. Westermayr J. Gastegger M. Maurer R. J. Kalita B. Burke K. Nagai R. Akashi R. Sugino O. Hermann J. Noé F. Pilati S. Draxl C. Kuban M. Rigamonti S. Scheidgen M. Esters M. Hicks D. Toher C. Balachandran P. V. Tamblyn I. Whitelam S. Bellinger C. Ghiringhelli L. M. Roadmap on Machine Learning in Electronic Structure. Electron. Struct. 2022;4:023004. doi: 10.1088/2516-1075/ac572f. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-013-D2RA08180F-s001
RA-013-D2RA08180F-s001.pdf (11.9MB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES