Static and dynamic functional connectomes represent largely similar information

Abstract

Functional connectivity (FC) in blood oxygen level-dependent (BOLD) fMRI time series can be estimated using methods that differ in sensitivity to the temporal order of time points (static vs. dynamic) and the number of regions considered in estimating a single edge (bivariate vs. multivariate). Previous research suggests that dynamic FC explains variability in FC fluctuations and behavior beyond static FC. Our aim was to systematically compare methods on both dimensions. We compared five FC methods: Pearson’s/full correlation (static, bivariate), lagged correlation (dynamic, bivariate), partial correlation (static, multivariate) and multivariate AR model with and without self-connections (dynamic, multivariate). We compared these methods (i) directly, by assessing the similarities between the FC matrices, and (ii) indirectly, by comparing the patterns of brain-behavior associations. Although FC estimates did not differ as a function of sensitivity to temporal order, we observed differences between the multivariate and bivariate FC methods. The dynamic FC estimates were highly correlated with the static FC estimates, especially when comparing group-level FC matrices. Similarly, there were high correlations between the patterns of brain-behavior associations obtained using the dynamic and static FC methods. We conclude that the dynamic FC estimates represent information largely similar to that of the static FC.

1. Introduction

Brain functional connectivity (FC) is estimated by calculating statistical associations between time series of brain signal [1], which reflect functional relationships between brain regions [2]. The investigation of FC has improved our understanding of brain function in health and disease and has been shown to be useful as a tool to predict interindividual differences, such as cognition, personality, or the presence of mental or neurological disorders [3, 4]. In functional magnetic resonance imaging (fMRI) studies, FC is most commonly estimated using the Pearson’s correlation coefficient between time series of pairs of regions. Although correlation is simple to understand and compute, it is insensitive to the temporal order of time points. Measures or models that are sensitive to the temporal order of time points are called dynamic, while measures that are insensitive to temporal order are measures of static FC. Given that the information flow in the brain is causally organized in time [5, 6], dynamic connectivity models could be more informative in terms of understanding brain function and investigating brain-behavior associations.

Dynamic FC can be estimated using measures of lag-based connectivity, such as lagged correlation or multivariate autoregressive (AR) model. In contrast to static FC, dynamic FC methods can be used to estimate the directionality of information flow based on temporal precedence [7]. Although these methods have been commonly used, some studies [7, 8, 9, 10, 11] have warned that the ability of these methods to accurately estimate the presence and directionality of connections is compromised due to the convolution of the neural signal with the hemodynamic response function (HRF) and the resulting blurring of the signal, due to interregional variability of HRF, noise [7, 8, 9, 10], and/or downsampling of the neural signal in fMRI [11]. Other studies [12, 13, 14] have shown that the measures of dynamic FC complement the measures of static FC. For example, lagged FC measures can improve discrimination between individuals and between tasks [12, 13] and can be used to improve effective connectivity estimates [14]. Furthermore, Liégeois et al. [15] have shown that the multivariate AR model explains temporal FC fluctuations better than Pearson’s correlations.

In subsequent research Liégeois et al. [16] showed that static FC and dynamic FC exhibit different patterns of brain-behavior associations. They concluded that dynamic FC explains additional variance in behavior beyond variance that can be explained by static FC. However, this comparison confounds two orthogonal properties of FC methods. Although Pearson’s correlation and multivariate AR models differ in their sensitivity to temporal reordering (i.e., static vs. dynamic), they also differ in terms of how many variables (brain regions) are taken into account during the estimation of a single edge (bivariate vs. multivariate). Hence, a more valid comparison between static and dynamic FC methods should consider both dimensions: the number of variables and the sensitivity to temporal reordering. Combining these two factors enables us to differentiate between four basic classes of FC methods (see Figure 1).

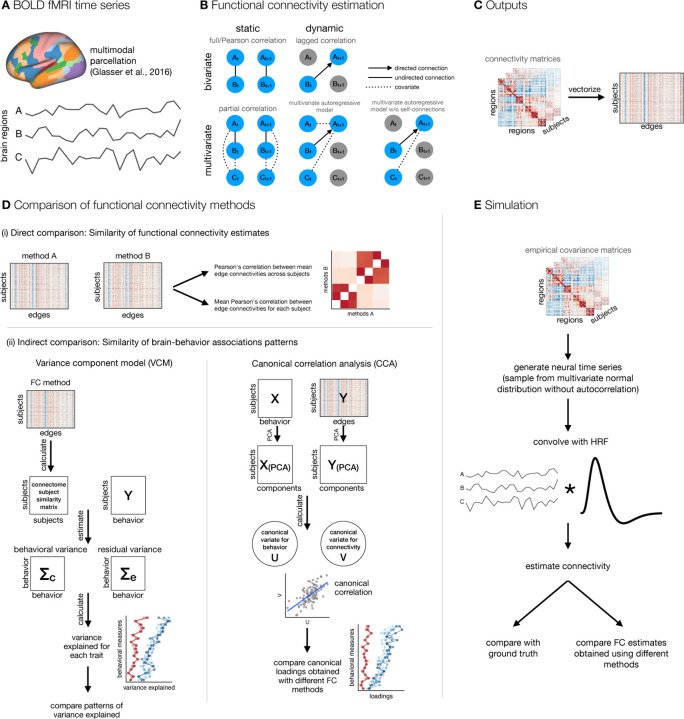
Figure 1: A schematic of analysis steps.

A. BOLD fMRI data was preprocessed, parcellated, and individual parcel timeseries were extracted. B. Functional connectivity (FC) was estimated with five methods that differed along two dimensions: static vs. dynamic and bivariate vs. multivariate. Static FC refers to measures that are insensitive to temporal order and can be estimated using full/Pearson’s correlation or partial correlation, whereas measures of dynamic FC are sensitive to temporal order of time points. Dynamic FC can be estimated using measures of lag-based connectivity, such as lagged correlation, or using the linear multivariate autoregressive (AR) model. The lagged correlation between two time series is calculated by shifting one time series by p time points. Similarly, a p-th order multivariate (or vector) autoregressive model predicts the activity of a particular brain region at time point t based on the activity of all regions at time point(s) from t − p to t − 1. Bivariate and multivariate FC methods differ in terms of number of variables (regions) taken into account when estimating connectivity at a single edge: bivariate connectivity between two regions depends only on the two regions, whereas multivariate connectivity between two regions includes all other regions as covariates. C. FC matrices were vectorized. D. FC estimates were compared both (i) directly by calculating correlations between FC estimates and (ii) indirectly by comparing estimates of brain-behavior associations across FC methods. E. Additionally, we performed simulation to assess the influence of random noise and signal length on the similarity between FC estimates obtained using different methods.

Our aim was to systematically compare the FC estimated by both dimensions, that is, the sensitivity to temporal reordering (static vs. dynamic) and the number of independent variables (bivariate vs. multivariate). We focused on five mathematically related methods: full/Pearson’s correlation, partial correlation, lagged correlation, and multivariate AR model with and without self-connections, where self-connections refer to autocorrelation of the region with itself [17, 18]. We were interested in similarities of the FC estimates and patterns of brain-behavior associations. We compared FC methods (i) directly by assessing similarities between FC matrices and (ii) indirectly by comparing brain-behavior associations. In addition, to better understand the results obtained using different methods and the relationship between them, we generated and analyzed synthetic data in which we systematically varied the length of time series and the amount of noise.

We used empirical and simulated data to test two hypotheses. First, we predicted that dynamic and static FC methods will provide similar FC estimates due to autocorrelation of the fMRI time series. Autocorrelation is inherent to the fMRI signal and originates from two main sources: physiological noise and convolution of neural activity with HRF [19]. We expected that the degree of similarity between static and dynamic FC estimates would be similar to or larger than the average autocorrelation of the fMRI time series. Furthermore, we expected the similarity between dynamic and static FC to be smaller when the fMRI time series is pre-whitened (i.e., when autocorrelation is removed before computation of FC).

Second, we predicted that multivariate methods can improve inferences about causal relationships between regions, as they estimate direct connections by removing the confounding influence of indirect associations [2] as opposed to bivariate methods, which cannot separate indirect and direct connections [18]. By providing more direct information on causal relationships between brain regions [20], multivariate methods could improve brain-behavior associations in terms of explained variance and/or brain-behavior correlation estimates. Existing research has shown inconsistent differences in behavior predictive accuracy between partial and full/Pearson’s correlations, favoring either partial [21, 22] or full correlation [23] or showing negligible differences between them [24].

2. Method

2.1. Participants

To address the research questions, the analyzes were performed on publicly available deidentified data from 1096 participants (M_age = 28.8, S D_age = 3.7, 596 women) included in the Human Connectome Project, 1200 Subjects Release [25]. Each participant took part in two imaging sessions over two consecutive days that included the acquisition of structural, functional (rest and task), and diffusion-weighted MR images. The study was approved by the Washington University institutional review board and informed consent was signed by each participant.

2.2. fMRI data acquisition and preprocessing

Data were acquired in two sessions using the Siemens 3T Connectome Skyra tomograph. Structural MPRAGE T1w image (TR = 2400 ms, TE = 2.14 ms, TI = 1000 ms, voxel size = 0.7 mm isotropic, SENSE factor = 2, flip angle = 8°) and T2w image (TR = 3200 ms, TE = 565 ms, voxel size = 0.7 mm isotropic) were acquired in the first session. The participants underwent four resting state fMRI runs, two in each session (gradient echo EPI sequence, multiband factor: 8, acquisition time: 14 min 24 s, TR = 720 ms, TE = 33.1 ms, flip angle = 52°).

Initial preprocessing was performed by the HCP team and included minimal preprocessing [26], ICA-FIX denoising [27] and MSMAll registration [28]. The data was then further processed using QuNex [29] to prepare them for functional connectivity analyzes. First, we identified frames with excessive movement and/or frame-to-frame signal changes. We marked any frame that was characterized by frame displacement greater than 0.3 mm or for which the frame-to-frame change in signal, computed as intensity normalized root mean squared difference (DVARS) across all voxels, exceeded 1.2 times the DVARS median across the time series, as well as one frame before and two frames after them. Marked frames were used for motion censoring, which is described in detail in the Appendix. Next, we used linear regression to remove multiple nuisance signals, including six movement correction parameters and their squared values, signals from the ventricles, white matter and the whole brain, as well as the first derivatives of the listed signals. The previously marked frames were excluded from the regression and all subsequent analysis steps were performed on the residual signal. No temporal filtering was applied to the data, except a very gentle high-pass filter at the cutoff of 2000 s applied by the HCP team [26], since temporal filtering could introduce additional autocorrelation [30] and inflate correlation estimates [19, 31].

Only sessions with at least 50% useful frames after motion censoring were used in the further analysis, except where noted otherwise. This resulted in 1003 participants with at least one session. Before FC analyzes, all resting-state BOLD runs from available sessions were concatenated and parcellated using a multimodal cortical parcellation (MMP1.0) containing 360 regions [28]. Each parcel was represented by a mean signal across all the parcel grayordinates.

2.3. Functional connectivity estimation

Functional connectivity was estimated using five methods: full (Pearson’s) correlation, partial correlation, lagged correlation, multivariate AR model (also called vector AR model), and multivariate AR model without self-connections. The listed methods differ in terms of the number of regions used to estimate the connectivity of a single edge (bivariate vs. multivariate) and in terms of sensitivity to temporal reordering of time points (static vs. dynamic) (see Figure 1). A multivariate AR model without self-connections was included to test how much similarity between the multivariate AR model and partial correlation depends on self-connections (the diagonal terms in the autocovariance matrix).

The bivariate static FC was estimated using full correlation. Let x_i be a demeaned T × 1 vector of region i time series (T is the number of time points) and let X = [x₁, … , x_N]′ be a N × T matrix of the demeaned region time series (N is the number of regions). Then the sample covariance matrix C can be estimated with

$$C=\frac{X{X}^{\prime }}{T-1}$$ (1)

A correlation matrix can be obtained by standardizing the time series to zero mean and unit standard deviation (i.e., z-scores) beforehand.

Multivariate static FC was estimated using partial correlation. Partial correlations were computed by taking an inverse of a covariance matrix (i.e., the precision matrix) and then standardizing and sign-flipping according to the equation:

$${\rho }_{ij}=-\frac{w_{\text{ij}}}{\sqrt{w_{\text{ij}}{w}_{\text{ij}}}}$$ (2)

where ρ is an element of a partial correlation matrix, w is an element of a precision matrix, and i and j are the indices of rows and columns, respectively [32].

Dynamic bivariate connectivity was estimated using lagged correlation (also known as autocovariance matrix). Autocovariance is defined as the covariance of time series with lagged time series. Let X_t be an N × (T − p) matrix of shortened time series with time points from 1 to T − p (p is the lag/model order) and X_t+p be a similar matrix with time points from p + 1 to T. Then,

$$C_p=\frac{X_{t+p}{X}_t^{\text{'}}}{T-p}$$ (3)

is p-th order autocovariance or lagged covariance matrix. Diagonal entries are called autocovariances or, sometimes, self-connections or self-loops [18, 17]. Off-diagonal entries of autocovariance matrix are also called cross-covariances. Note that the autocovariance matrix of lag 0 is equal to the ordinary covariance matrix. The autocorrelation matrix was obtained by standardizing time series before computing autocovariance.

Correlations, autocorrelations, and partial correlations were Fisher z-transformed for subsequent analyzes.

Multivariate dynamic connectivity was estimated using the Gaussian multivariate AR model. Let Z be an Np × (T − p) matrix of stacked matrices of shortened time series, $Z={\left[X_{t+p-1}^{\text{'}},\dots ,X_{t+1}^{\text{'}},X_t^{\text{'}}\right]}^{\prime }$. The multivariate AR model can be written in matrix notation as:

$$X_{t+p}=AZ+E$$ (4)

where A is an N × Np matrix of AR coefficients of the p-th order model and E is an N × (T − p) matrix of zero-mean, independent, normally distributed residuals. The matrix A can be estimated using the ordinary least squares (OLS) estimator:

$$\widehat{A}=X_{t+p}{Z}^{\prime }{\left(Z{Z}^{\prime }\right)}^{-1}$$ (5)

For $p=1\widehat{A}$ equals:

$$\widehat{A}=X_{t+p}{X}_t^{\text{'}}{\left(X_t{X}_t^{\text{'}}\right)}^{-1}$$ (6)

The equation shows that the coefficients of the multivariate AR model are a product of the lagged covariance and (non-lagged) precision matrix. Therefore, the multivariate AR model encodes both static and dynamic FC. The same can be inferred from the Yule-Walker equations (see Liégeois et al. [15], Chatfield and Xing [33]). Moreover, for lag 0, the multivariate coefficients of the AR model are equal to the covariance matrix (see [15]).

To estimate the coefficients of the multivariate AR model without self-connections, we fitted the model

$$x_{i,t+p}=X_t^{\text{'}}{a}_i+e_i$$ (7)

for each region i separately, such that we set i-th row of matrix X_t to zero (the equation above applies for p = 1 only, but the model could be extended to include higher lags as in Equation 4). Vectors x_i,t+p were taken from rows of the matrix X_t+p and included time points from p + 1 to T. Vectors e_i represent normally distributed, zero-mean, independent residuals. FC matrix was constructed by organizing N × 1 vectors a_i into the N × N matrix A₁ = [a_i, … , a_N]′. This matrix is asymmetric with zeros on the diagonal. The coefficients of both multivariate AR models were estimated using the coordinate descent algorithm implemented in the GLMnet package for MATLAB [34].

All AR models were estimated for lag 1 only. This order was shown to be optimal for the multivariate AR model for resting state fMRI data with a high number of regions [35, 36], and also in a study using HCP data [37]. There were no differences between the variance of order 1 and the higher-order models explained by the first principal component of the null data generated from the multivariate AR model in a previous study [15]; therefore, we did not consider higher-order autoregressive models.

2.4. Prewhitening

We expected that FC estimates based on AR models would be similar to static FC estimates due to autocorrelation present in the fMRI time series. To test the similarity between static and dynamic FC in the absence of autocorrelation, we computed connectivity both from non-prewhitened time series and on prewhitened time series. The exception was multivariate AR model, where the diagonal term (self-connections) effectively acts as a prewhitening. The difference between the multivariate AR model with and without prewhitening is essentially the difference between the multivariate AR model with and without self-connections. We performed prewhitening by taking the residuals of the regression of the ”raw” time series on lagged time series.

To retain frame sequence after prewhitening, frames that were marked as bad in any of the original or lagged time series were set to zero before computing residuals. For this reason, frames that were preceded by a bad frame in any of the 1 to l previous frames were not prewhitened. At higher orders, this resulted in fewer total prewhitened frames.

Prewhitening was performed on orders 1 to 3 (abbreviated AR1/2/3 prewhitened). Autocorrelations were already significantly reduced at order 1 and were additionally reduced at lags 2 and 3 (Figure S1). Since the results were similar regardless of the prewhitening order, only the results for the prewhitening on order 1 are shown in the main text, and the results for higher orders are shown in the supplement.

2.5. Similarities between FC estimates obtained using different methods

We estimated similarities between the FC estimates by computing the correlation between vectorized FC matrices. We adjusted the vectorization for each pair of methods so that only unique elements were taken into account. For example, correlation and partial correlation matrices are symmetric; therefore, only the upper or lower triangular part of the matrix (without the diagonal) should be considered. On the other hand, the FC matrices derived from the AR models are not symmetric; therefore, the whole matrix must be vectorized. The exception is the multivariate AR model without self-connections, which does not contain any information on the diagonal, so in this case matrix without the diagonal needs to be vectorized. When comparing asymmetric and symmetric matrices, we computed and used the average of the upper and lower triangular parts of the matrix (using equation (X + X′)/2).

We estimated similarities in two ways: first, by computing correlations between connectivity estimates for each subject separately and then averaging the resulting correlations (mean correlations between individual-level FC matrices), and second, by averaging FC matrices over participants and then computing correlation between methods on group FC matrices (correlations between group-level FC matrices).

To test how similarity between FC estimates depends on data quality, we repeated analyses on a subset of 200 participants with the largest number of retained frames.

2.5.1. Correlation between edge similarity and test-retest reliability

To better understand the origin of the similarities between the FC methods, we examined the relationship between the edge similarity of the FC estimates obtained using different methods and test-retest reliability at the edge level. If similarities between FC estimates depend on the signal-to-noise ratio (SNR), more reliable edges will be more similar across methods.

We computed the edge similarity as correlation at every edge for each pair of FC methods. We estimated the test-retest reliability using the intraclass coefficient (ICC) for each method separately. We estimated the variance components within the linear mixed model framework using the restricted maximum likelihood (REML) procedure [38, 39]. We defined variance components as follows:

$$\mathrm{var}\left(y_{pdr}\right)={\sigma }_p^2+{\sigma }_d^2+{\sigma }_r^2+{\sigma }_{p\times r}^2+{\sigma }_{p\times d}^2+{\sigma }_{d\times r}^2+{\sigma }_e^2$$ (8)

where y is an estimate of an edge, p indicates participant, d day, r run and e residual.

We computed the ICC as a ratio between between-subject variance (which included interaction terms pertaining to participants) and the total variance [40]. For this analysis, the runs were not concatenated.

Finally, we applied Fisher’s z-transformation to both edge similarity and ICC and computed the correlation between them. To reduce the number of comparisons, we only investigated the most relevant comparisons: full correlation vs. lagged correlation, partial correlation vs. multivariate AR1, and partial correlation vs. multivariate AR1 without self-connections. Since we estimated test-retest reliability separately for each method in a pair, there were two correlations for each pair of methods. We averaged both correlations for each comparison.

2.6. Brain-behavior associations

To compare the brain-behavior associations obtained by different FC measures, we used 58 behavioral measures (see Table S1) that included cognitive, emotion and personality measures and were previously used in other studies [16, 41, 42].

2.6.1. Variance component model

We computed brain-behavior associations using the multivariate variance component model (VCM), developed by Ge et al. [43] to estimate heritability. The use of the variance component model to estimate associations between the brain and behavior was introduced by Liégeois et al. [16]. We adopted the same approach to allow direct comparison with the results reported by Liégeois et al. [16]. Furthermore, the use of VCM allows an easy calculation of the explained variance for single traits. The model has the form

$$Y=C+E$$ (9)

where Y represents the N × P matrix (number of subjects × number of traits) of behavioral measures, C represents shared effects and E represents unique effects. The model has the following assumptions:

$$\begin{array}{l}\text{Vec}(C)\sim 𝓝\left({\text{Σ}}_c\otimes F\right)\\ \text{Vec}(E)\sim 𝓝\left({\text{Σ}}_e\otimes I\right)\end{array}$$ (10)

where Vec(·) is the matrix vectorization operator, ⊗ is the Kronecker product operator, and I is the identity matrix. F represents N × N matrix of similarities between participants, which were estimated with the Pearson’s correlation coefficient. Σ_c and Σ_e are P × P matrices, which are being estimated. The total variance explained is computed as:

$$M=\frac{\text{Tr}\left({\text{Σ}}_c\right)}{\text{Tr}\left({\text{Σ}}_c\right)+Tr\left({\text{Σ}}_e\right)}$$ (11)

where Tr(·) represents the trace operator, and:

$$M_i=\frac{{\text{Σ}}_c(i,i)}{{\text{Σ}}_c(i,i)+{\text{Σ}}_e(i,i)}$$ (12)

for single traits. M is analogous to the concept of heritability and can be interpreted as the amount of variance in behavior that can be explained with the variance in the connectome.

Before computing VCM, we imputed missing behavioral data using the R package missForest [44]. There were 0.59% missing data points overall. Following the procedure of Liégeois et al. [16], we applied quantile normalization to behavioral data. To remove potential confounding factors, we regressed age, gender, race, education, and movement (mean FD) using the procedure described in Ge et al. [45, 43].

We estimated M for each connectivity method separately. We compared patterns of explained variances by correlating the variance explained at the trait level between all methods.

Since the results of VCM are based on similarities between participants (matrix F), we tested the extent to which the similarities between participants, and thus the results of VCM, depend on the levels of noise in the data. To this end, we performed a simulation in which we added random Gaussian noise (mean 0, standard deviation 0–1 in steps of 0.1) to the standardized time series. To reduce complexity, we performed this analysis only for static FC methods.

2.6.2. Canonical correlation analysis

Since VCM is rarely used to study brain-behavior associations, we repeated the analysis using canonical correlation (CCA). CCA is used to reveal the low-dimensional structure of the shared variability between two sets of variables (in our case, connectivity and behavior).

Let X and Y be N × P and N × Q matrices (N is the number of observations, P and Q are the number of variables), respectively. CCA aims to find a solution to the following set of equations:

$$\begin{gathered} U=XA \\ V=YB \end{gathered}$$ (13)

where U_N×K and V_N×K are matrices of canonical scores (or variables) and A_P×K and B_Q×K are matrices of canonical weights. The solution to the above set of equations is found under the constraint U′U = V′V = I. The columns of the U and V matrices tell us the relative position of each observation in the canonical variables. In contrast, columns of the A and B matrices contain information on the relative contribution of each variable to each of the canonical variables. Canonical correlations are correlations between columns of U and V. Additionally, one can calculate canonical loadings - the correlations between original data matrices and canonical scores. Canonical variables are ordered in descending order according to the size of canonical correlations. Usually, only the first or first few canonical components are of interest, as these explain most of the shared variance. Mathematical details on CCA can be found elsewhere [e.g. ^{46, 47, 48, 49, 50}].

We performed the CCA using the GEMMR package [47]. To prepare the data for CCA, we followed the procedure by Smith et al. [51], including deconfouding using the same variables as for VCM. Prior to CCA, we reduced the dimensionality of both sets of variables to 20 components using principal component analysis (PCA). This number was chosen to optimize the number of samples per feature based on the recommendation by Helmer et al. [47] under the assumption of a real first canonical correlation r = .30. We performed a 5-fold cross-validation to assess the generalizability of the model. We only examined the first canonical correlation since it was shown that the first canonical variable explains the most shared variance, and it was the only statistically significant canonical variable in a previous study [51].

We repeated the CCA for all FC methods. The similarities between the methods were assessed by comparing the first canonical correlation obtained in the training and the test set. Next, we correlated the canonical weights and loadings related to behavior.

2.6.3. Control analyses

Participants in the HCP dataset are genetically and environmentally related, which can inflate between-subject similarities and influence the results related to interindividual differences. Therefore, we repeated all analyses related to brain-behavior associations on two subsamples of genetically unrelated participants (sample sizes 384 and 339).

2.7. Simulation

We hypothesized that dynamic and static FC estimates would be similar due to autocorrelation of fMRI time series, which is partly the result of convolution of neural time series with HRF. In addition, an important source of similarities (or differences) between FC results obtained by different methods could be due to similar (or different) effects of the amount of noise and the amount of available data on the resulting FC matrices. To evaluate the impact of convolution with HRF, signal quality, and the amount of data on estimated similarities between results using different FC measures, we used numerical simulations of data with known covariance structure. We generated multivariate time series of events for 1000 ”participants.” Events were sampled from a multivariate normal distribution with a mean of zero. The covariances differed for each participant and were taken from experimental data parcellated using Schaefer’s local-global parcellation with 100 regions [52]. We used this parcellation instead of MMP to reduce the computational burden and the size of the generated data. Events were not autocorrelated. The generated events were then convolved with HRF using the SimTB toolbox [53]. TR was set to 0.72 s (the same as in HCP data), and HRF parameters were set equal for all participants and regions (delay of response: 6, delay of the undershoot: 15, dispersion of the response: 1, dispersion of the undershoot: 1, the ratio of response to the undershoot: 3, onset in seconds: 0, length of the kernel in seconds: 32). The resulting time series were standardized.

To estimate the effects of signal quality on FC estimates and on similarities between FC methods, we added Gaussian noise with zero mean and standard deviation ranging from 0 to 1 standard deviation in steps of 0.1. This translates to SNR from 10 to 1 (excluding time series without noise, which has infinite SNR). We varied the time-series durations from 500 to 10000 data points in steps of 500.

The first step in the analysis was to establish the ground truth for each method, that is, the results that would be obtained in an ideal situation. We defined the ground truth as FC at maximum length and without noise in the event time series. Note that because events were not autocorrelated, the ground truth for all autoregressive FC methods was a matrix with all zero entries.

Next, we compared results using different FC methods in the same manner as for experimental data for all noise level and signal length combinations on prewhitened and non-prewhitened data. We computed (1) correlations between ground truth FC matrices and simulated FC matrices for all FC methods and (2) correlations between FC estimates obtained using different methods. To reduce the number of comparisons, we only investigated the most relevant comparisons: full correlation vs. lagged correlation, partial correlation vs. multivariate AR, and partial correlation vs. multivariate AR without self-connections.

3. Results

3.1. Experimental data

3.1.1. Similarities between FC estimates obtained using different methods

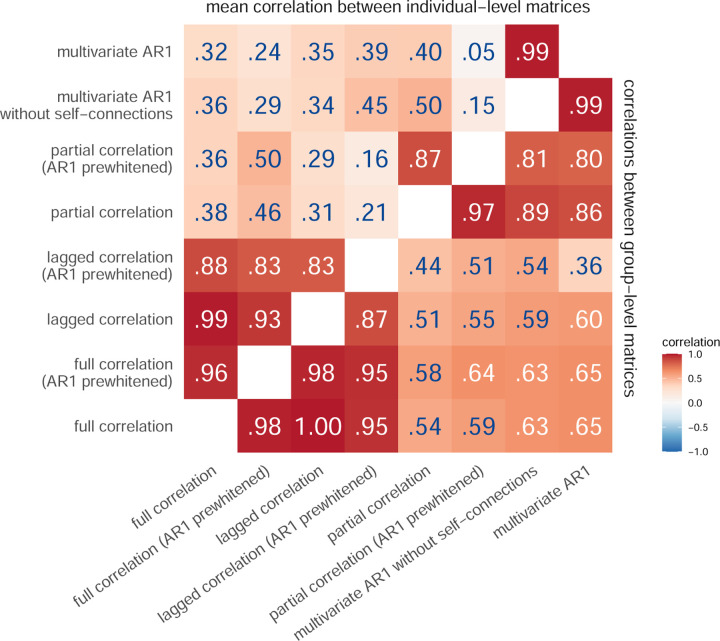
To address our research questions, we first focused on estimating similarities between the results obtained with different FC methods using empirical data. Comparison of group-level FC matrices showed very high correlations between FC results obtained using bivariate methods (r ⩾ .87, Figure 2), as well as between results obtained using multivariate methods (correlation between partial correlation [AR1 prewhitened] and multivariate AR model: r = .80). In contrast, the correlations between the bivariate and multivariate FC estimates were lower and ranged from .36 to .65.

Figure 2: Correlations between FC estimates obtained using different FC methods.

We calculated the similarities between FC estimates obtained using different FC methods (i) by averaging connectivity matrices across participants and then computing correlations between them (correlation between group-level FC, bottom right triangle), and (ii) by computing correlations between the FC estimates for each participant separately and then averaging across participants (correlation between individual-level FC, top left triangle).

When comparing and pooling results based on individual-level FC matrices, the mean correlation between FC matrices obtained using different methods was lower. The correlations between the bivariate methods were still very high (correlation between lagged and full correlation: r = .99, correlation between prewhitened lagged and prewhitened full correlation: r = .83), while the correlations between the multivariate methods were lower on average. In particular, the correlation between the partial correlation (AR1 prewhitened) and the multivariate AR model was .05, compared to .80 between the group-level FC matrices.

The correlations between the results obtained using static and dynamic FC methods were smaller after prewhitening, with the greatest differences when comparing individual-level FC matrices obtained using multivariate methods. Specifically, the correlation between the coefficients of the multivariate AR model and the partial correlation decreased from .40 to .05 in the individual-level FC and from .86 to .80 in the group-level FC. The order of prewhitening had minimal effect on the correlations between the methods (Figure S3), except for the comparison of the results obtained using the multivariate AR model and the partial correlation at the individual-level FC, where the correlations increased from .05 to .12 (r = .15–.22 for the multivariate AR model without self-connections).

The correlations between the FC results obtained using different methods were slightly higher when the analysis was repeated on 200 participants with the highest data quality (Figure S4).

3.1.2. Correlation between edge similarity and test-retest reliability

We computed edge similarity between FC methods as a correlation over subjects at every edge for selected pairs of FC methods. We estimated test-retest reliability at every edge for each method separately. Next, we computed the correlation between edge similarity and test-retest reliability for each of selected pairs of FC methods. The correlation was moderate to high for pairs of multivariate methods (r = .47–.66) and high for pairs of bivariate methods (r = .55–.79, Figure 3)). Prewhitening lowered the correlations..

Figure 3:

Correlations between edge similarity and test-retest reliability for selected pair of FC methods.

3.1.3. Brain-behavior associations estimated using variance component model

Next, we compared patterns of brain-behavior associations derived from different FC methods. The results of the VCM show that bivariate methods explain about 30 percentage points less variance in behavior than multivariate methods (Figure 4A,B). Furthermore, the similarity of patterns of variance explained over behavioral measures was high between static and dynamic FC methods using the same number of variables, i.e., between full correlation and lagged correlation (r = 1.00), and between partial correlation and multivariate AR models (r = .83–.86, Figure 4A,C). The pattern of similarities in behavioral variance explained between the FC methods was comparable to the direct comparison of the FC matrices (Figure 4C, cf. Figure 2). Patterns of similarities between the FC methods were similar when the analysis was performed on subsamples of unrelated participants (Figure S5); however, the differences in total variance explained between the bivariate and multivariate methods were smaller.

Figure 4: Results of variance component model for brain-behavior associations.

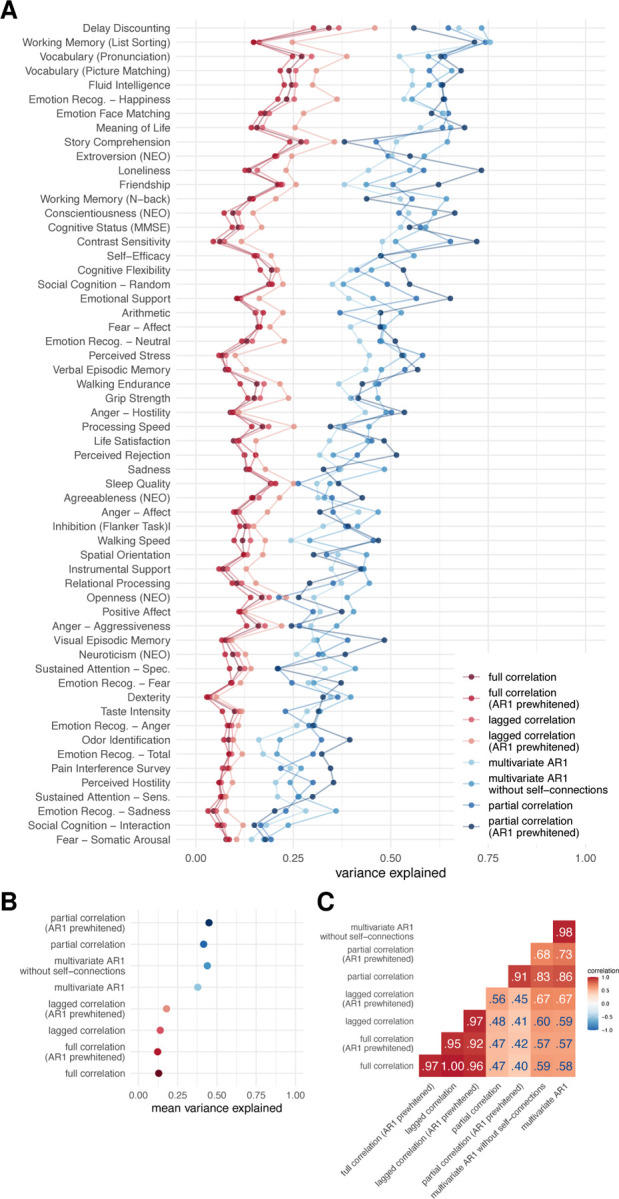
A. Variance explained for individual traits estimated with different connectivity methods – traits are ordered according to the mean variance explained across connectivity methods. B. Mean variance explained. C. Similarities of explained variance patterns between connectivity methods.

Simulation of the effects of noise in which we added various levels of noise to the fMRI time series showed that noise affects estimates of the behavioral variance explained by the connectome. In particular, the mean of the variance explained increased with increasing noise for both the full correlation and the partial correlation, but the increase was more pronounced in the case of partial correlations (Figure 5B). This pattern was not equal for all behavioral variables – for some, the variance explained decreased and for others, it increased (Figure 5A). On the other hand, the similarity between the participants decreased with increasing noise (Figure 5C). This effect was more pronounced for partial correlation compared to full correlation.

Figure 5: Results of variance component model for brain-behavior associations on data with added noise.

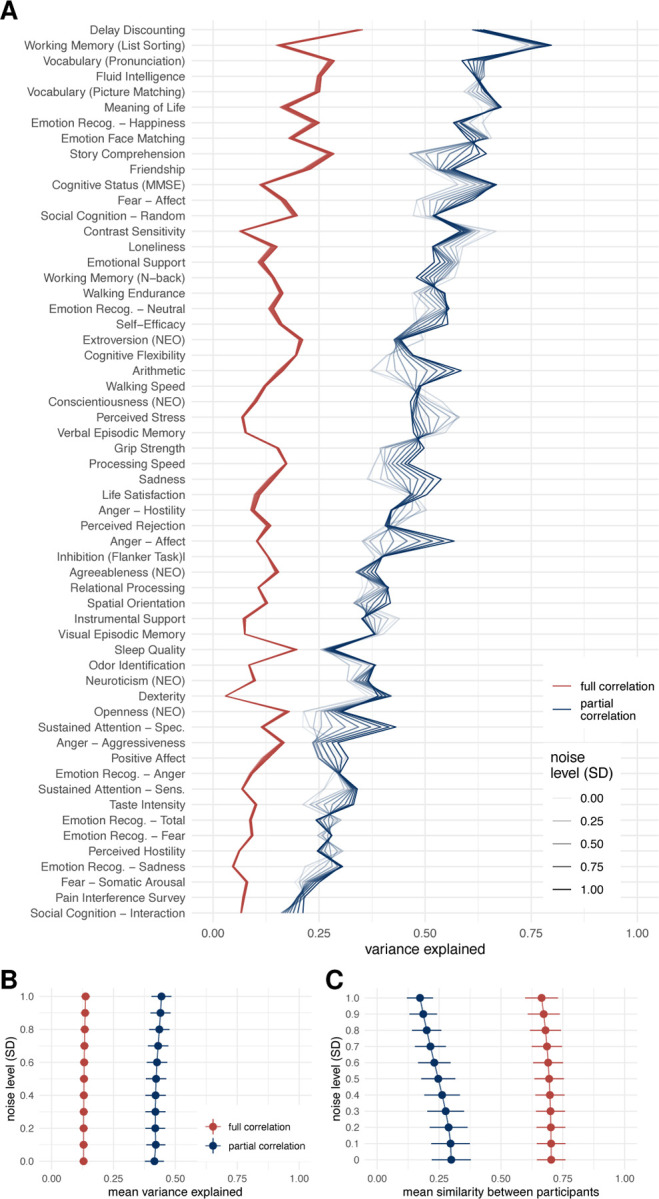
FC was estimated using Pearsons’/full correlation and partial correlation after adding various levels of random Gaussian noise to experimental time series. A. Variance explained for individual traits estimated with different connectivity methods. Traits are ordered according to the mean variance explained across connectivity methods. B. Mean variance explained. Error bars represent jackknife standard deviation. C. Mean similarity between participants. Error bars represent standard deviation.

3.1.4. Brain-behavior associations estimated using canonical correlation analysis

The results of the similarity between the FC methods when investigating brain-behavior associations using CCA were comparable to those obtained using VCM. In particular, the correlations between the weights or loadings on behavioral measures between the FC methods were high when comparing the methods that use the same number of variables for the estimation of a single edge (r > .80) (Figure 6C). On the other hand, there was no discernible difference between dynamic and static FC estimates.

Figure 6: Results of canonical correlation analysis for brain-behavior associations.

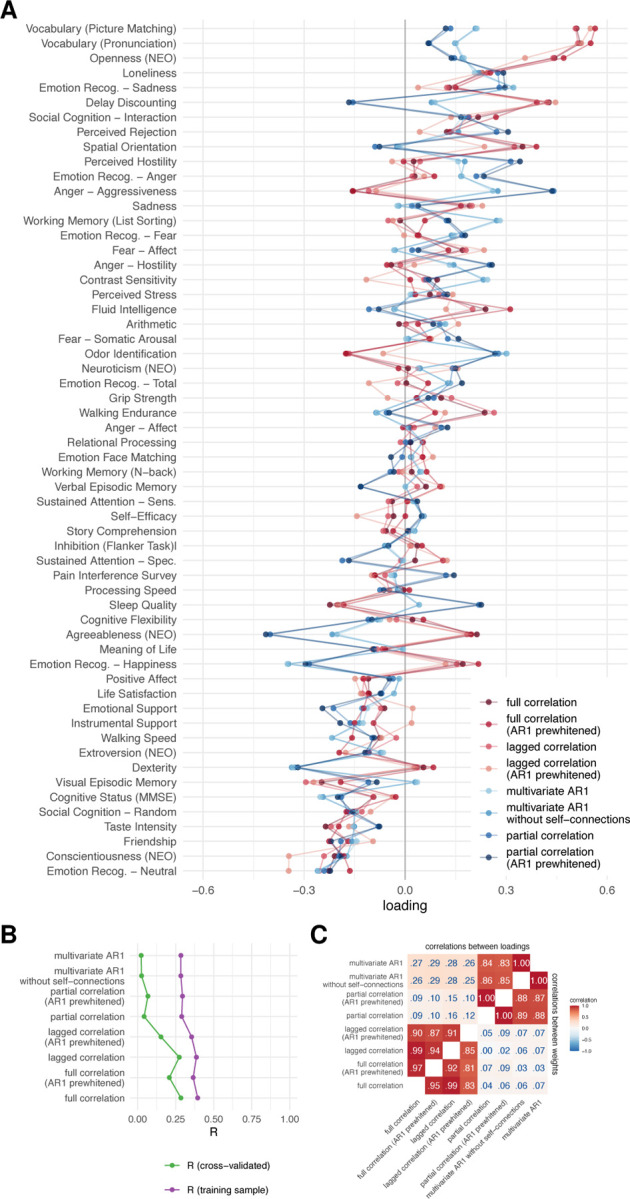
A. CCA loadings. B. First canonical correlation on test and training set, C. Correlations between canonical loadings and weights across functional connectivity methods for first canonical components.

The first canonical correlation was around .70 in the training sample for the bivariate methods and around .50 for the multivariate methods (Figure 6B). Cross-validated R was much lower, around .40 for bivariate methods and around 0.05 for multivariate methods. Although these results differ from VCM (where multivariate methods explained more variance), the pattern of similarity between FC methods is the same.

The pattern of results was similar for the subsamples of unrelated participants, but the differences between the training and test sets were larger (Figure S6). The large difference between the performance of the model in training and test sets is indicative of overfitting, which is characteristic of CCA with a small number of samples per feature [47].

3.2. Evaluation of similarities between methods on simulated data

3.2.1. Relationship between FC estimates and ground truth

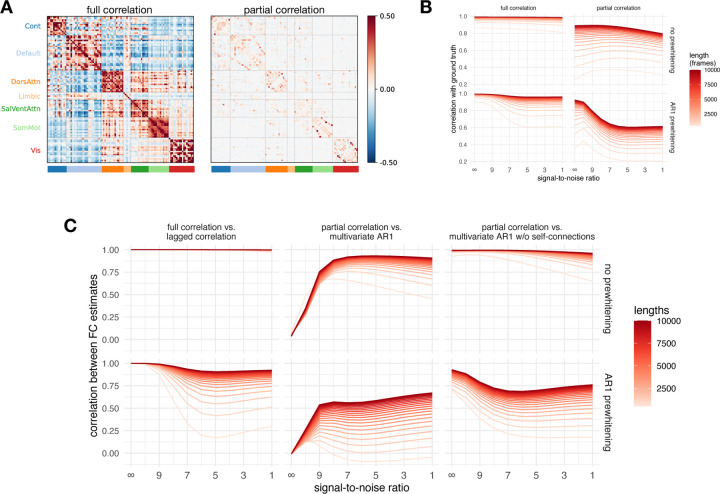
Correlations of FC estimates with ground truth were greater than 0.8 for full correlation and between 0.25 and 0.9 for partial correlation (Figure 7). Prewhitening decreased the correlation with ground truth. This effect was more pronounced for partial correlations. Longer time series also had higher correlations with ground truth (the difference was up to .5 for partial correlation and up to .3 for full correlation). The correlation with ground truth generally decreased with decreasing SNR (increasing noise), but in the case of partial correlation, these effects were not monotonic. In particular, for short time series, correlation with ground truth increased with low to moderate noise. Also in the case of partial correlation, prewhitening increased the correlation with ground truth at low noise. In contrast, prewhitening decreased the correlation with ground truth in the presence of high noise compared to the case without prewhitening.

Figure 7: Results of simulation.

A. Ground truth matrices (mean over participants). Note that all ground truth autoregressive model coefficients equal zero, since the simulated events were not autocorrelated. B. Correlation between the ground truth and the simulated data for all FC methods and their relationship to the noise level and signal length. C. Correlations between selected pairs of FC methods as a function of noise and signal length for simulated data. Note that the data in the second row related to multivariate AR models were not prewhitened before computation because the self-connections act as prewhitening.

3.2.2. Similarity between FC estimates

The connectivity matrices computed on the simulated data were compared in the same manner as for the experimental data. For brevity, we focus only on the three most relevant comparisons (lagged correlation vs. full correlation, multivariate AR model vs. partial correlation, multivariate AR model without self-connections vs. partial correlation).

Estimates based on lagged and full correlation were highly similar (r ≈ 1 in the case without prewhitening) for all levels of noise and signal length (Figure 7). The correlation between FC estimates was reduced for prewhitened data, especially for low signal lengths (< 1000 frames).

The FC estimates of the multivariate AR model did not correlate with the FC estimates based on partial correlation when the noise was low (r = 0 for zero noise). However, with increasing noise and increasing signal length, FC estimates became very similar (up to r = .95), especially in the case without prewhitening and for long signal lengths.

Conversely, FC estimates based on a multivariate AR model without self-connections showed a high similarity to the FC estimates based on partial correlation at a low noise level (r > .95). For prewhitened data, there was a nonmonotonic relationship between FC estimates with increasing noise, but overall correlations remained high in conditions with high signal length.

4. Discussion

In this study, we addressed the question of whether the temporal order of the BOLD fMRI time series contains information important for the study of the fMRI brain functional connectivity. To this end, we compared FC estimates between methods that differed in their sensitivity to temporal order, i.e., static and dynamic measures of FC. We also compared methods that differed in the number of variables considered in estimating the connectivity of individual edges, i.e., bivariate and multivariate. Our results suggest that dynamic FC connectivity methods provide similar connectivity estimates as static FC methods of the same type (bivariate or multivariate), whereas bivariate and multivariate methods differ in terms of the explanation of individual differences in behavior.

4.1. Dynamic functional connectomes represent information similar to static functional connectomes

By directly comparing the FC matrices, we have shown that the estimates of the dynamic FC represent information similar to the estimates of the static FC. The similarity between estimates of FC, obtained by different methods, depended on several factors. First, there were high correlations between the FC estimates when the same number of variables was considered.

Second, similarities between connectomes were greater when averages were compared at the group level than when correlations were aggregated across individual-level FC matrices. We believe that the differences between the group- and individual-level cases are mainly due to better SNR in the case of the group-level data. Two observations support this conclusion: first, similarities in FC estimates between methods were greater for participants with the highest data quality, and this effect was more pronounced when comparing individual-level matrices than at the group level. Second, edges with higher test-retest reliability (an indicator of SNR) were more similar between FC estimates obtained by different methods. Thus, we can conclude that SNR influences the similarity between FC estimates.

Using simulation, we tested the similarities between FC as a function of noise and signal length. We have shown that the dynamic FC estimates resemble static FC estimates even in the absence of true lagged correlation. The similarity between the multivariate AR1 model and partial correlations can be partially explained by the fact that the multivariate AR1 coefficients are a product of inverse covariance and lagged covariance matrix.

We also found a high similarity between the full and the lagged correlation. Therefore, the similarity between the multivariate AR1 model and the partial correlation cannot be explained solely by the inclusion of the precision matrix in the estimation of the coefficients of the multivariate AR model. Rather, the lagged covariance matrix also contributes to this effect.

We hypothesized that the similarities between the dynamic and static FC estimates originate from autocorrelation of the fMRI time series. We predicted that the similarities between the dynamic and static FC estimates would be at least as large as the average autocorrelation of the fMRI time series and that this similarity would be reduced after prewhitening. Both predictions were confirmed in experimental and simulated data. However, even when autocorrelation was reduced to virtually zero at all lags (this occurred at prewhitening order 3), similarities between estimates based on dynamic and static FC models remained high for group-level matrices and simulated data. This suggests that prewhitening (or even the presence of noise that reduces autocorrelation) does not completely eliminate the influence of convolution with HRF on the estimation of dynamic FC.

We conclude that even if AR models represent information that goes beyond the static FC, this cannot be claimed on the basis of a direct comparison of dynamic and static FC estimates. One of the main differences between static and dynamic FC methods is the ability of dynamic FC methods to estimate the directionality of connections [7]. FC matrices based on dynamic FC methods are therefore asymmetric. To allow comparisons between static and dynamic FC matrices, the former were symmetrized and the information about the directionality of the connections was lost. To test the possibility that there is specific information in the dynamic FC estimates that could not be detected in a direct comparison of the FC matrices, we additionally compared the patterns of brain-behavior associations between FC methods.

4.2. Dynamic FC models do not explain additional variance in behavior over static FC models

We used the variance component model (VCM) and canonical correlation analysis (CCA) to estimate brain-behavior associations. The results of both methods showed that there were no large differences between the dynamic and static FC estimates in the patterns of associations with behavior. However, we found large differences between the bivariate and multivariate methods. These differences were specific to the method used to estimate brain-behavior associations.

In the case of CCA, the canonical correlations were higher for bivariate methods than for multivariate methods. The cross-validated canonical correlations were around 0 for multivariate methods, indicating that the results were not generalizable. In contrast, the difference between the canonical correlations in the training and test sets was relatively small for the bivariate methods.

In the case of VCM, the multivariate methods explained on average about 30 percentage points more variance in behavior than the bivariate methods. To better understand this observation, we examined the impact of inter-subject similarities on VCM results. To this end, we added random noise to the data, reducing the similarities between subjects. Interestingly, full correlation and partial correlation explained more variance in behavior on average when we added random noise to the data. This may sound counterintuitive, but keep in mind that VCM was developed to estimate heritability [43], that is, the proportion of variance in phenotype that can be explained by variance in genotype. Holding the environment constant, higher genetic similarity would reduce the estimate of heritability. If all individuals within a sample had the same genotype, heritability would be zero because no variance in phenotype could be explained by variance in genotype. The input to VCM is a between-subject similarity matrix (usually a genetic similarity matrix or, in our case, a connectome similarity matrix). Participants were more similar when we used full correlation as an estimate of FC compared to partial correlation. This explains the observation that the partial correlation explained more variance in behavior.

Our second simulation showed that the partial correlation estimates are less stable and more affected by noise and signal length. This explains the apparent discrepancy between VCM and CCA. Our results show that when we add noise to the experimental data, participants become more dissimilar and, in the case of VCM, the proportion of behavioral variance explained by the variance in the connectome becomes larger. In the case of CCA, lower SNR leads to lower and less generalizable canonical correlations for multivariate FC methods. For this reason, we recommend that great care be taken when estimating brain-behavior associations with measures that are sensitive to noise.

Liégeois et al. [16] have used VCM to compare brain-behavior associations between correlation and the multi-variate AR model. They concluded that the dynamic FC explained variance in behavior beyond that explained by static FC. We have shown that these results are confounded by the mixing of two orthogonal properties of the FC methods: sensitivity to the temporal order of time points and the number of regions used to estimate a single edge. The difference between the explanatory value of the multivariate AR model and the full correlation is better explained by the difference between the multivariate and bivariate nature of the method than by the sensitivity to the temporal order of the time points.

4.3. Limitations and future directions

A number of limitations should be considered in drawing conclusions from our study. First, in our simulation, we generated noise using a multivariate normal distribution. We could have used more advanced noise modeling that incorporated specific noise components such as drift, moving average, physiological noise, and system noise [54]. Unlike white noise, these noise sources are autocorrelated and therefore could affect the (dynamic) FC estimates. We wanted to keep the model simple and interpretable. Even with the simplest noise model without autocorrelation in neural time series, we showed that AR models can be affected by convolution of the neural signal with HRF and that consequently the dynamic FC estimates resemble the static FC. However, more advanced noise modeling could be used for a more realistic assessment of the sources of similarities between different FC methods.

Similarly, we used a very simple procedure, prewhitening, to reduce autocorrelation. Other methods could also be used to reduce autocorrelation, such as advanced physiological modeling [55, 56] or deconvolution [57]. Deconvolution can improve dynamic [10] and static FC estimates [57]. However, Seth et al. [11] have shown that sufficient sampling rate is more important for valid dynamic FC estimates. Unlike fMRI, electrophysiological measurements such as EEG and MEG have sufficient sampling rates and do not require deconvolution, so they could be used to study the relationship between static and dynamic FC [58].

4.4. Conclusions

Our results show that the dynamic FC estimates represent information about connectivity that is broadly similar to the static FC. Moreover, we have shown that the similarity between dynamic and static FC is due, at least in part, to the convolution of neural time series with HRF. In contrast, we observed lower similarities in the patterns of FC estimates between multivariate and bivariate methods. Multivariate methods were more sensitive to noise and CCA models based on multivariate methods were less generalizable.

Although dynamic FC models are useful as a model for directed FC or for modeling the evolution of neural time series over time [15], our results suggest that estimates of the functional connectome do not change when temporal information is taken into account. Dynamic FC estimates also show no advantage or difference from static FC in terms of brain-behavior associations.

5. Data and code availability

Raw data are available as part of the Human Connectome Project (https://www.humanconnectome.org/). The function to compute the variance component model is available in the repository: https://github.com/RaphaelLiegeois/FC-Behavior. For CCA, we used the GEMMR package: https://github.com/murraylab/gemmr. All other relevant functions are available on Open Science Framework: https://dx.doi.org/10.17605/OSF.IO/XFTDH.

10. Appendix

10.1. Motion scrubbing

Motion scrubbing is usually performed by removing bad frames before calculating the correlation or related measure of static FC. This is not appropriate in the case of dynamic FC or autocorrelation, since removing time points disrupts the autocorrelation structure of time series.

To overcome this limitation, a frame was considered bad if it was bad in either original or lagged time series. Frames at transition between concatenated time series (last frame in the first time series and first frame in the next time series) were also marked as bad in this case.

In the case of autoregressive models, transitions between runs (last frame of the previous run, first frame of the next run) were excluded in the same manner as bad frames.