Abstract
Stature estimation is one of the most basic and important methods of personal identification. The long bones of the limbs provide the most accurate stature estimation, with the femur being one of the most useful. In all the previously reported methods of stature estimation using computed tomography (CT) images of the femur, laborious manual measurement was necessary. A semi-automatic bone measuring method can simplify this process, so we firstly reported a stature estimation process using semi-automatic bone measurement software equipped with artificial intelligence. Multiple measurements of femurs of adult Japanese cadavers were performed using automatic three-dimensional reconstructed CT images of femurs. After manually setting four points on the femur, an automatic measurement was acquired. The relationships between stature and five femoral measurements, with acceptable intraobserver and interobserver errors, were analyzed with single regression analysis using the standard error of the estimate (SEE) and the coefficient of determination (R2). The maximum length of the femur (MLF) provided the lowest SEE and the highest R2; the SEE and R2 in all cadavers, males and females, respectively, were 3.913 cm (R2 = 0.842), 3.664 cm (R2 = 0.705), and 3.456 cm (R2 = 0.686) for MLF on the right femur, and 3.837 cm (R2 = 0.848), 3.667 cm (R2 = 0.705), and 3.384 cm (R2 = 0.699) for MLF on the left femur. These results were non-inferior to those of previous reports regarding stature estimation using the MLF. Stature estimation with this simple and time-saving method would be useful in forensic medical practice.
Supplementary Information
The online version contains supplementary material available at 10.1007/s00414-022-02921-y.
Keywords: Stature estimation, Femur, Computed tomography, Artificial intelligence, Semi-automatic measurement
Introduction
Stature estimation is one of the most important and basic methods for individual identification as well as for sex and age estimation [1–10]. Recent forensic anthropology reports have described sex, weight, and age estimation using computed tomographic (CT) images of bones [11–22]. Regarding stature estimation, the long bones of the limbs provide the most accurate stature estimation over a wide age range in studies conducted on different races. Among them, the femur is reported as one of the most useful for stature estimation [4, 10, 23–30].
Conventionally, the femur is measured using an osteometric board, which is placed on a horizontal plane [31–35]. In recent reports, the femur was measured using X-ray photography [36–38]. Some reports have provided stature estimation using CT images of the femur [39–44], and researchers in these studies manually measured the femur on CT images for estimation. However, manual measurement requires a certain level of technical proficiency and can be affected by the performance of the measurer. Thus, using a simpler measurement method than the manual method may provide benefits such as reduction of time and effort required for measurement and prevention of unintentional measurement errors. Herein, we created three-dimensional (3D) reconstructed images from postmortem CT images and measured the femur using a semi-automatic measurement software, with the aim of providing new stature estimation formulae based on these semi-automatic measurements.
Materials and methods
This study included 300 cadavers of known sex and age over 18 that underwent whole-body postmortem CT imaging and subsequent forensic autopsy at the forensic medicine departments at Chiba University and the University of Tokyo in Japan between October 2016 and October 2020. Cadavers with severe decomposition, burn injuries, congenital malformations, postoperative changes, missing parts, femoral fractures, severe deformation of the vertebral bodies, and severe trauma to the head, neck, trunk, or lower limbs were excluded because such conditions have possible effects on the condition of the femur or stature. We included the cadavers of 150 males (10–20 years, n = 1; 21–30 years, n = 21; 31–40 years, n = 19; 41–50 years, n = 37; 51–60 years, n = 38; 61–70 years, n = 20; 71–80 years, n = 12; 81–90 years, n = 2) and 150 females (10–20 years, n = 13; 21–30 years, n = 12; 31–40 years, n = 28; 41–50 years, n = 24; 51–60 years, n = 21; 61–70 years, n = 18; 71–80 years, n = 20; 81–90 years, n = 14). Cadaver stature was measured in the supine position before autopsy using a measuring tape or a ruler. The adjusted stature (AS) was calculated by subtracting 2.0 cm from the measured stature to obtain an estimate of the living stature according to previous studies [45–48].
At Chiba University, postmortem CT was performed using a 64-row detector CT system (Supria Grande; Fujifilm Healthcare Corporation, Tokyo, Japan), and the scanning protocol was as follows: tube voltage, 120 kV; tube current, 250 mA; scan time, 0.75 s; collimation, 0.625 mm. The slice thickness, reconstruction interval, and field of view during image reconstruction were 1.0, 0.725, and 500 mm, respectively. At the University of Tokyo, postmortem CT was performed using a 16-row detector CT system (ECLOS; Fujifilm Healthcare Corporation), and the scanning protocol was as follows: tube voltage, 120 kV; tube current, 200 mA; scan time, 1 s; collimation, 1.25 mm. The slice thickness, reconstruction interval, and field of view during image reconstruction were 1.25, 1.25, and 500 mm, respectively.
Image data were processed on a workstation (Synapse Vincent; Fujifilm Medical), and a semi-automatic application was used to measure the femur. Just after launching, this application automatically recognizes the femur and displays it as a reconstructed 3D image. If it contains other structures, such as calcified blood vessels or cartilage, manual adjustments are necessary. After confirmation that the reconstruction is appropriate, the bone surface information is automatically extracted with a single click. By manually marking the four points—the center of the femoral head, intercondylar notch (ICN), medial epicondyle, and lateral epicondyle—on the model (Fig. 1), 41 measurements are automatically calculated and displayed (Table 1). The time required from manual marking to displaying the results was approximately 40 s. Using the results of each cadaver, the average values of the right and left femurs were also calculated (Fig. 2).
Fig. 1.
Four points where manual marking are necessary (each picture shows one point in the horizontal, coronal, and sagittal planes and the three-dimensional reconstruction of the computed tomography images). a Center of the femoral head: the central point of the femoral head. b Intercondylar notch: posterior 1/4 point on the midline of the recess located between the medial and lateral condyles on the bottom surface of the lower end of the femur. c Medial epicondyle: the most medial point of the medial condyle. d Lateral epicondyle: the most lateral point of the lateral condyle
Table 1.
Definition of measurements
| Measurement | Abbreviation | Definition |
|---|---|---|
| Maximum length of the femur | MLF | Distance between the plane tangent to the lowest points of the medial and lateral condyles of the femur (referred to as plane α) and the plane parallel to plane α that is tangent to the upper end of the femur |
| Valuation angle | VA | Angle formed by the MA and the line segment connecting the center of the femoral diaphysis and the ICN when the femur is observed from the ventral side |
| Lordosis angle | LA | Angle formed by the MA and the line segment connecting the center of femoral diaphysis and the ICN when the femur is observed from the lateral side |
| Lateral anterior–posterior length | LAP | Distance between the two lines when lines parallel to the SEA are drawn to pass through the anterior and posterior ends of the lateral epicondyle when the femur is observed from the bottom side |
| Medial anterior–posterior length | MAP | Distance between the two lines when lines parallel to the SEA are drawn to pass through the anterior and posterior ends of the medial epicondyle when the femur is observed from the bottom side |
| Partial lateral anterior–posterior length | P-LAP | Distance between the two lines when lines parallel to the SEA is drawn to pass through the rearmost end of the lateral condyle and the posterior end of the intercondylar fossa when the femur is observed from the bottom side |
| Partial medial anterior–posterior length | P-MAP | Distance between the two lines when lines parallel to the SEA is drawn to pass through the rearmost end of the medial condyle and the posterior end of the intercondylar fossa when the femur is observed from the bottom side |
| Lateral distal resection amount | LRA | Distance between two lines when straight lines parallel to SEA are drawn through the lower end of the lateral condyle and the ICN when observed facing the plane created by SEA and MA (referred to as plane β) |
| Medial distal resection amount | MRA | Distance between two lines when straight lines parallel to SEA are drawn through the lower end of the medial condyle and the ICN when observed facing plane β |
| Cross-section partial lateral anterior–posterior length | C-P-LAP | Distance on CS A′ (which is a cross section that is orthogonal to plane β and approximates a horizontal section at a height that passes through the ICN) between the SEA and the straight line parallel to the SEA drawn so as to pass through the posterior end of the lateral condyle |
| Cross-section partial medial anterior–posterior length | C-P-MAP | Distance on CS A′ between the SEA and the straight line parallel to the SEA drawn so as to pass through the posterior end of the medial condyle |
| Posterior condyle axis angle | PCA-angle | Angle formed by the SEA and a straight line passing through the posterior ends of the medial and lateral condyles when the femur is observed from the bottom |
| Cross-section lateral-middle length | C-LML | Distance between the two lines when straight lines perpendicular to the SEA are drawn so as to pass through the lateral end of CS A′ and the ICN |
| Cross-section medial-middle length | C-MML | Distance between the two lines when straight lines perpendicular to the SEA are drawn so as to pass through the medial end of CS A′ and the ICN |
| Cross-section medial–lateral width | C-ML | Distance between the two lines when straight lines perpendicular to the SEA are drawn so as to pass through the medial end of CS A′ and the lateral end of CS A′ |
| Lateral distal anterior angle | LDA-angle | Angle formed on CS A′ by the straight line orthogonal to the SEA and line passing through points A and B, which are the intersections of a straight line parallel to the SEA through ICN and the SEA with the outermost side of CS A′ |
| Medial distal anterior angle | MDA-angle | Angle formed on CS A′ by the straight line orthogonal to the SEA and the line passing through points C and D, which are the intersections of a straight line parallel to the SEA through the ICN and the SEA with the innermost side of CS A′ |
| Medial distal radius of the curvature | MDAC | Radiation of the curvature of point C on CS A′ |
| Joint line angle | JL-angle | Angle formed by the line parallel to the SEA passing through the ICN and the straight line passing through the lower end of the lateral condyle and that of the medial condyle when the femur is observed from the ventral side |
| Medial superior-inferior length | MSI | Length from the top to the bottom of CS B′, which is a cross section formed on the medial condyle that is perpendicular to CS A′ and passes through the lateral and medial posterior ends of CS A′ |
| Lateral superior-inferior length | LSI | Length from top to bottom of CS C′, which is a cross section formed on the lateral condyle so as to be perpendicular to CS A′ and passes through the lateral and medial posterior ends of CS A′ |
| Medial condyle width | MCW | Length from the medial end to the lateral end of CS B′ |
| Lateral condyle width | LCW | Length from the medial end to the lateral end of CS C′ |
| Medial condyle to middle width | MCMW | Distance between two lines when the lines perpendicular to CS A′ are drawn so as to pass through the ICN and the medial end of CS B′ when observed so as to face CS B′ |
| Lateral condyle to middle width | LCMW | Distance between two lines when lines perpendicular to CS A′ are drawn so as to pass through the ICN and the lateral end of CS C′ when observed so as to face CS C′ |
| Middle-lateral outer angle | MLO-angle | Angle between the straight line that passes through the lateral end of CS C′ at the height of CS A′ and the lateral end of CS C′ at the height of the lateral epicondyle and the straight line perpendicular to CS A′ when observed so as to face CS C′ |
| Front protrusion length | FPL | Distance between two lines when two straight lines parallel to the MA are drawn so as to pass through the point perpendicular to CS D′, which is formed with a cross section that is parallel to SEA and perpendicular to CS A′, which passes through the anterior end of the intercondylar fossa surface of CS A′, from the ICN and the upper end of CS D |
| Coronal-section outer angle | CSO-angle | Angle formed by the straight line parallel to the MA and the straight-line EF, where point E is the lateral end of CS D′ and point F is the point where the curvature of the outer edge of CS D′ changes from convex to concave |
| Radiation of the curvature of the lateral anterior excision contour | RLAC | Radius of curvature at the midpoint between point F and the upper end of CS D′ |
| Lateral anterior excision contour width | LAEC | Distance between two lines when straight lines parallel to the MA are drawn on CS D′ so as to pass through point E and the ICN |
| Medial anterior excision contour width | MAEC | Distance between two lines when straight lines parallel to the MA are drawn on CS D′ so as to pass through the medial end of CS D′ and the ICN |
| Anterior excision middle-lateral length | AEML | Length of the line segment perpendicular to CS D′ from the front end of the lateral condyle |
| Anterior excision middle-medial length | AEMM | Length of the line segment perpendicular to CS D′ from the front end of the medial condyle |
| Patella coronal-section length | PCS | Length of the line segment connecting the point perpendicular to CS D′ from the point at the rear end of the margin connecting the front end of the medial condyle and that of the lateral condyle |
| Radiation of curvature of the lateral distal condyle | RLDC | Radius of curvature at the point where the straight line connecting the center of the femoral head and the lateral epicondyle intersects the base of the lateral epicondyle when the femur is observed from the lateral side |
| Radiation of curvature of the lateral posterior condyle | RLPC | Radius of curvature at the midpoint of side GH, where point G, which is orthogonal to CS A′, is the intersection of the edge of the shadow of the lateral condyle projected so as to be perpendicular to plane γ (which is the plane in contact with the lateral epicondyle and orthogonal to CS A′) and CS A′; point H is the intersection of a straight line from point G that is orthogonal to CS A′ and the upper edge of the shadow |
| Radiation of curvature of the medial distal condyle | RMDC | Radius of curvature at the point where the straight line connecting the center of the femoral head and the medial epicondyle intersects the base of the medial epicondyle when the femur is observed from the medial side |
| Radiation of curvature of the medial posterior condyle | RMPC | Radius of curvature at the midpoint of side IJ, where point I, which is orthogonal to CS A′, is the intersection of the edge of the shadow of the lateral condyle projected so as to be perpendicular to plane δ (which is the plane in contact with the lateral epicondyle and orthogonal to CS A′) and CS A′; point J is the upper edge of the shadow |
| Epicondyle axis angle | CEA-angle | Angle formed by a straight line connecting the lateral and medial epicondyles and a straight line passing through the posterior ends of the medial and lateral epicondyles |
| C-lateral anterior–posterior length | C-LAP | Distance between two lines when lines parallel to the SEA are drawn on the anterior and posterior ends of the lateral condyle on CS A′ |
| C-medial anterior–posterior length | C-MAP | Distance between two lines when lines parallel to SEA are drawn on the anterior and posterior ends of the medial condyle on CS A′ |
ICN intercondylar notch, which is located at the posterior 1/4 point on the midline of the recess between the medial and lateral condyles on the bottom surface of the lower end of the femur, MA mechanical axis, which is the axis passing through the center of the femoral head and ICN [29], SEA surgical epicondyle axis, which is the axis passing through the medial epicondyle process groove and the lateral epicondyle process [29, 70, 71]
Fig. 2.
Five measurements with acceptable intraobserver and interobserver errors. a Maximum length of the femur (MLF). b Lateral anterior–posterior length (LAP). c Cross-section medial–lateral width (C-ML). d C-lateral anterior–posterior length (C-LAP). e C-medial anterior–posterior length (C-MAP)
First, to select measurements with acceptable intraobserver and interobserver errors, 20 cadavers were randomly selected. To evaluate the intraobserver error, a single researcher measured the femurs twice with an interval of ≥ 1 day for each cadaver. To evaluate the interobserver error, another researcher measured the femurs, and the result was then compared with the first result from the first researcher. The intraobserver and interobserver errors were assessed with the technical error of measurement (TEM), relative technical error of measurement (rTEM), and coefficient of reliability (R) [49, 50]. The acceptance range for rTEM was set at < 1.5% for intraobserver error and < 2.0% for interobserver error [51].
Second, the sexual differences in age, AS, and acceptable measurement were evaluated. If these values followed a normal distribution, Student’s t-test was used. If the values did not follow a normal distribution, the Wilcoxon rank sum test was used instead [52, 53]. The absolute z values of skewness and kurtosis were used to assess normal distribution [54].
Lastly, the relationship between AS and each measurement for all 300 cadavers was assessed using single regression analysis with the statistical values of the coefficient of determination (R2) and the standard error of the estimate (SEE). In this analysis, all manual markings were performed by a single researcher. A residual plot was created with the predicted stature calculated with the obtained regression equation, and the difference between the predicted stature and AS and the existence of heteroscedasticity was examined [55].
Statistical significance was set at P < 0.05 to reject the null hypothesis that there was no significant difference in statistical values between males and females and that the regression coefficient was 0. Statistical analysis was performed using Excel 2010 (Microsoft Corporation, Redmond, WA, USA).
Results
The 41 measurements were classified into groups 1 and 2 based on the results of intraobserver and interobserver errors (Table 2), and the TEM, rTEM, and R values for each measurement of both the right and left femurs are shown in Table 3. Group 1 included measurements with rTEM values < 1.5% for intraobserver error and < 2.0% for interobserver error on both the right and left sides. Group 2 included the other measurements whose rTEM values for intraobserver or interobserver errors were larger than the acceptable range. Group 1 comprised five measurements: maximum length of the femur (MLF), lateral anterior–posterior length (LAP), cross-section medial–lateral width (C-ML), C-lateral anterior–posterior length (C-LAP), and C-medial anterior–posterior length (C-MAP), for which R values were > 0.9. Group 2 was classified into groups 2–1 and 2–2 according to measurement type. Group 2–1 included measurements for angles and curvature radii, and group 2–2 included measurements for length.
Table 2.
Semi-automatic measurement classification
| Group | Measurements | |
|---|---|---|
| 1 | MLF, LAP, C-ML, C-LAP, C-MAP | |
| 2 | 2–1 | VA, LA, PCA-angle, LDA-angle, MDA-angle, JL-angle, MLO-angle, CSO-angle, CEA-angle, MDAC, RLAC, RLDC, RLPC, RMDC, RMPC |
| 2–2 | LRA, MRA, C-P-LAP, C-P-MAP, C-LML, C-MML, P-LAP, P-MAP, MSI, LSI, MCW, LCW, MCMW, LCMW, FPL, LAEC, MAEC, AEML, AEMM, PCS, MAP | |
Group 1: measurements with rTEM values < 1.5% intraobserver error and < 2.0% interobserver error; group 2: measurements with rTEM values ≥ 1.5% intraobserver error or ≥ 2.0% interobserver error; group 2–1: measurements for angles and radius of curvature; group 2–2: measurements for length.
MLF maximum length of the femur, LAP lateral anterior–posterior length, C-ML cross-section medial–lateral width, C-LAP C-lateral anterior–posterior length, C-MAP C-medial anterior–posterior length, MLF maximum length of the femur, AEML anterior excision middle-lateral length, AEMM anterior excision middle-medial length, PCS patella coronal-section length, MAEC medial anterior excision contour width, RLAC radiation of the curvature of the lateral anterior excision contour, LAEC lateral anterior excision contour width, RLPC radiation of curvature of the lateral posterior condyle, RMPC radiation of curvature of the medial posterior condyle, CEA epicondyle axis angle, LAP lateral anterior–posterior length, C-ML cross-section medial–lateral width, C-LAP C-lateral anterior–posterior length, C-MAP C-medial anterior–posterior length.
Table 3.
TEM, rTEM, and R values for each measurement of both the right and 1 left femurs (n = 20)
| Intraobserver error | Interobserver error | |||||
|---|---|---|---|---|---|---|
| TEM (mm) | rTEM (%) | R | TEM (mm) | rTEM (%) | R | |
| Right MLF | 0.14832 | 0.03506 | 0.99997 | 0.07746 | 0.01831 | 0.99999 |
| Left MLF | 0.14318 | 0.03374 | 0.99997 | 0.08062 | 0.01900 | 0.99999 |
| Right VA | 0.15572 | 3.19926 | 0.98174 | 0.38923 | 7.63945 | 0.89849 |
| Left VA | 0.15083 | 3.13741 | 0.98725 | 0.24135 | 4.90799 | 0.97020 |
| Right LA | 0.31024 | 10.89524 | 0.93475 | 0.56613 | 23.78686 | 0.77883 |
| Left LA | 0.29917 | 10.78074 | 0.92963 | 0.60704 | 26.27887 | 0.77118 |
| Right LAP | 0.26173 | 0.41746 | 0.99475 | 0.37550 | 0.59669 | 0.98901 |
| Left LAP | 0.17103 | 0.27458 | 0.99775 | 0.54658 | 0.87352 | 0.97751 |
| Right MAP | 0.70054 | 1.14443 | 0.96109 | 1.26323 | 2.08738 | 0.86675 |
| Left MAP | 0.55159 | 0.90008 | 0.97916 | 1.22913 | 2.03052 | 0.89877 |
| Right P-LAP | 0.91228 | 3.84562 | 0.76938 | 2.20777 | 9.97975 | 0.08897 |
| Left P-LAP | 0.96099 | 4.09629 | 0.76210 | 1.99744 | 9.02898 | 0.21163 |
| Right P-MAP | 1.95371 | 6.67366 | 0.45896 | 5.32863 | 21.07217 | − 0.45641 |
| Left P-MAP | 2.09249 | 7.14159 | 0.47266 | 5.63392 | 22.18077 | − 0.51700 |
| Right LRA | 0.14832 | 1.94651 | 0.98780 | 0.24495 | 3.25514 | 0.96701 |
| Left LRA | 0.17321 | 2.41738 | 0.97740 | 0.15572 | 2.17416 | 0.98023 |
| Right MRA | 0.18841 | 1.77498 | 0.97952 | 0.25348 | 2.42851 | 0.96217 |
| Left MRA | 0.22694 | 2.13086 | 0.97150 | 0.20797 | 1.97828 | 0.97478 |
| Right C-P-LAP | 0.98729 | 5.29168 | 0.77641 | 2.29042 | 13.51676 | 0.19975 |
| Left C-P-LAP | 0.97545 | 5.34785 | 0.73812 | 2.03384 | 12.06310 | 0.09859 |
| Right C-P-MAP | 2.01041 | 7.85700 | 0.38403 | 5.61095 | 26.22858 | − 0.55040 |
| Left C-P-MAP | 2.20528 | 8.53518 | 0.49377 | 5.79055 | 26.61711 | − 0.51468 |
| Right PCA-angle | 2.51501 | 31.90618 | 0.45966 | 5.05962 | 112.74920 | − 0.28593 |
| Left PCA-angle | 2.35372 | 28.03717 | 0.10174 | 5.40562 | 114.22340 | − 0.48830 |
| Right C-LML | 0.79152 | 2.31743 | 0.92812 | 0.98944 | 2.90373 | 0.88707 |
| Left C-LML | 0.80265 | 2.31696 | 0.93975 | 1.45301 | 4.29536 | 0.79284 |
| Right C-MML | 0.84202 | 2.40922 | 0.90767 | 1.60008 | 4.47543 | 0.69924 |
| Left C-MML | 1.18269 | 3.48080 | 0.80431 | 2.49875 | 7.01748 | 0.46790 |
| Right C-ML | 0.82886 | 1.14514 | 0.97573 | 0.40988 | 0.56833 | 0.99405 |
| Left C-ML | 0.51745 | 0.71815 | 0.99089 | 0.37683 | 0.52359 | 0.99540 |
| Right LDA-angle | 2.38065 | 13.67012 | 0.78414 | 4.90607 | 34.90621 | 0.26475 |
| Left LDA-angle | 2.13395 | 12.09209 | 0.81491 | 5.74861 | 41.77768 | 0.16193 |
| Right MDA-angle | 2.28561 | 13.92389 | 0.79549 | 4.06789 | 29.08234 | 0.33301 |
| Left MDA-angle | 2.23523 | 13.09257 | 0.76538 | 5.22705 | 35.32981 | 0.10575 |
| Right MDAC | 217.05863 | 202.73064 | 0.27902 | 48.28600 | 73.31891 | 0.01449 |
| Left MDAC | 11.21474 | 17.03851 | 0.84829 | 17.25977 | 27.19572 | 0.46401 |
| Right JL-angle | 0.20125 | 4.66928 | 0.99325 | 0.24850 | 5.92714 | 0.99014 |
| Left JL-angle | 0.20797 | 4.14482 | 0.98977 | 0.35249 | 7.31689 | 0.96952 |
| Right MSI | 1.06243 | 4.03389 | 0.83388 | 2.08273 | 8.26233 | 0.55417 |
| Left MSI | 0.62510 | 2.38702 | 0.93223 | 2.16038 | 8.67362 | 0.53598 |
| Right LSI | 0.27839 | 1.09666 | 0.99384 | 0.51210 | 2.00884 | 0.98147 |
| Left LSI | 0.38633 | 1.48745 | 0.98837 | 0.37081 | 1.43198 | 0.98978 |
| Right MCW | 1.27112 | 4.73196 | 0.75036 | 2.45260 | 9.67782 | 0.44488 |
| Left MCW | 0.88204 | 3.28936 | 0.86778 | 2.25832 | 8.88577 | 0.61669 |
| Right LCW | 0.27523 | 1.19030 | 0.99234 | 0.49975 | 2.16788 | 0.97684 |
| Left LCW | 0.31024 | 1.32313 | 0.99175 | 0.54521 | 2.33718 | 0.97519 |
| Right MCMW | 1.02445 | 2.81211 | 0.89913 | 0.82234 | 2.25748 | 0.93518 |
| Left MCMW | 0.87878 | 2.44836 | 0.90267 | 1.64628 | 4.49405 | 0.74669 |
| Right LCMW | 0.98362 | 2.84529 | 0.88269 | 1.42241 | 4.19621 | 0.79991 |
| Left LCMW | 1.00735 | 2.85833 | 0.90238 | 2.16991 | 6.39525 | 0.59094 |
| Right MLO-angle | 0.78962 | 3.44737 | 0.99635 | 26.35689 | 143.08842 | − 0.72276 |
| Left MLO-angle | 1.05345 | 4.85515 | 0.99383 | 26.45265 | 149.36559 | − 0.72506 |
| Right FPL | 1.63110 | 18.80235 | 0.58494 | 2.33276 | 24.43316 | 0.39590 |
| Left FPL | 0.98881 | 10.58969 | 0.89538 | 1.72699 | 17.73092 | 0.76812 |
| Right CSO-angle | 2.09165 | 16.92958 | 0.78946 | 1.73458 | 14.6780 | 0.86539 |
| Left CSO-angle | 3.02977 | 22.55131 | 0.47633 | 4.29302 | 30.80745 | 0.38151 |
| Right RLAC | 1993.09811 | 133.54248 | 0.018494 | 2084.36477 | 169.53636 | − 0.17639 |
| Left RLAC | 6665.89030 | 261.041493 | − 0.01652 | 7335.77418 | 270.10845 | − 0.09082 |
| Right LAEC | 0.58758 | 1.97191 | 0.94179 | 0.83830 | 2.80533 | 0.89137 |
| Left LAEC | 0.84720 | 2.75894 | 0.86310 | 1.10182 | 3.67456 | 0.79487 |
| Right MAEC | 1.33154 | 4.95089 | 0.85018 | 1.73465 | 6.69102 | 0.76575 |
| Left MAEC | 1.11018 | 4.15098 | 0.78477 | 1.82941 | 7.02472 | 0.56696 |
| Right AEML | 2.03568 | 12.33373 | 0.67508 | 3.34066 | 23.30421 | 0.27640 |
| Left AEML | 1.93035 | 11.07328 | 0.54821 | 3.75955 | 25.41527 | 0.11808 |
| Right AEMM | 1.11086 | 11.38172 | 0.84995 | 1.40214 | 15.29053 | 0.76770 |
| Left AEMM | 1.23420 | 11.35158 | 0.72772 | 1.74900 | 17.74733 | 0.60414 |
| Right PCS | 0.93635 | 12.43905 | 0.90597 | 5.38E + 37 | 632.45553 | − 0.02564 |
| Left PCS | 5.38E + 37 | 632.45553 | − 0.02564 | 5.38E + 37 | 210.87690 | 0.63944 |
| Right RLDC | 1.00983 | 3.33194 | 0.89579 | 2.17595 | 7.48971 | 0.56117 |
| Left RLDC | 2.31663 | 7.59362 | 0.57532 | 2.03918 | 6.99127 | 0.50181 |
| Right RLPC | 0.42574 | 2.21881 | 0.97252 | 0.71028 | 3.73439 | 0.93883 |
| Left RLPC | 0.46368 | 2.43722 | 0.94439 | 0.95289 | 4.98765 | 0.76205 |
| Right RMDC | 0.87350 | 2.44403 | 0.94240 | 3.55356 | 10.64815 | 0.18188 |
| Left RMDC | 1.81859 | 4.94281 | 0.87463 | 4.86654 | 14.28920 | 0.08782 |
| Right RMPC | 0.33317 | 1.87172 | 0.95407 | 0.51137 | 2.89646 | 0.90400 |
| Left RMPC | 0.38406 | 2.18401 | 0.92483 | 0.50818 | 2.90681 | 0.89752 |
| Right CEA-angle | 1.70147 | 23.45238 | 0.76024 | 4.82237 | 106.63062 | − 0.16380 |
| Left CEA-angle | 2.46232 | 31.85402 | 0.58446 | 5.92326 | 139.37081 | − 0.16024 |
| Right C-LAP | 0.46098 | 0.97304 | 0.98342 | 0.55790 | 1.17335 | 0.97425 |
| Left C-LAP | 0.41201 | 0.88819 | 0.98150 | 0.74967 | 1.60048 | 0.93765 |
| Right C-MAP | 0.39686 | 0.76926 | 0.98435 | 0.96203 | 1.88707 | 0.90044 |
| Left C-MAP | 0.46530 | 0.90139 | 0.98600 | 0.84897 | 1.66440 | 0.95143 |
TEM technical error of measurement, rTEM relative technical error of measurement, R coefficient of reliability, MLF maximum length of the femur, AEML anterior excision middle-lateral length, AEMM anterior excision middle-medial length, PCS patella coronal-section length, MAEC medial anterior excision contour width, RLAC radiation of the curvature of the lateral anterior excision contour, LAEC lateral anterior excision contour width, RLPC radiation of curvature of the lateral posterior condyle, RMPC radiation of curvature of the medial posterior condyle, CEA epicondyle axis angle, LAP lateral anterior–posterior length, C-ML cross-section medial–lateral width, C-LAP C-lateral anterior–posterior length, C-MAP C-medial anterior–posterior length.
The descriptive statistics for age, AS, and five group 1 measurements are presented in Table 4. Age, AS, MLF, LAP, C-LAP and C-MAP followed a normal distribution, while only C-ML did not follow a normal distribution. There was no significant difference in mean age between the sexes (P = 0.482). The mean values of AS and of each measurement were significantly greater in men than in women (C-ML, P < 0.01; AS, MLF, LAP, C-LAP, and C-MAP, P < 0.001).
Table 4.
Descriptive statistics for age, AS, and group 1 measurements
| All cadavers (n = 300) | Male (n = 150) | Female (n = 150) | F value | P value | ||||
|---|---|---|---|---|---|---|---|---|
| Range | Mean ± SD | Range | Mean ± SD | Range | Mean ± SD | |||
| Age (years) | 18–88 | 50.35 ± 17.84 | 19–84 | 49.62 ± 15.15 | 18–88 | 51.07 ± 20.21 | 0.4967 | 0.482 |
| AS (cm) | 141–184 | 162.2 ± 9.84 | 152–184 | 169.6 ± 6.73 | 141–177 | 154.8 ± 6.15 | 398.5 | < 0.001 |
| MLF (cm) | ||||||||
| Right | 36.14 –50.95 | 42.69 ± 2.920 | 39.07–50.95 | 44.71 ± 2.118 | 36.14–48.65 | 40.66 ± 2.092 | 27.72 | < 0.001 |
| Left | 35.83–51.27 | 42.79 ± 2.960 | 38.95–51.27 | 44.86 ± 2.106 | 35.83–48.95 | 40.71 ± 2.116 | 28.98 | < 0.001 |
| Average | 36.06–51.11 | 42.74 ± 2.937 | 39.01–51.11 | 44.79 ± 2.108 | 36.06–48.80 | 40.69 ± 2.099 | 28.47 | < 0.001 |
| LAP (cm) | ||||||||
| Right | 5.16–7.47 | 6.30 ± 0.470 | 5.86–7.47 | 6.638 ± 0.353 | 5.16–6.89 | 5.962 ± 0.298 | 32.12 | < 0.001 |
| Left | 5.26–7.46 | 6.289 ± 0.463 | 5.84–7.46 | 6.627 ± 0.338 | 5.26–6.78 | 5.951 ± 0.292 | 34.30 | < 0.001 |
| Average | 5.235–7.43 | 6.295 ± 0.464 | 5.88–7.43 | 6.633 ± 0.342 | 5.24–6.84 | 5.957 ± 0.292 | 33.98 | < 0.001 |
| C-ML (cm) | ||||||||
| Right | 5.92–8.66 | 7.278 ± 0.628 | 6.97–8.66 | 7.808 ± 0.366 | 5.92–7.72 | 6.748 ± 0.303 | - | < 0.01 |
| Left | 5.95–8.71 | 7.243 ± 0.629 | 6.81–8.71 | 7.776 ± 0.365 | 5.95–7.59 | 6.710 ± 0.297 | - | < 0.01 |
| Average | 5.94–8.58 | 7.261 ± 0.629 | 6.90–8.58 | 7.792 ± 0.361 | 5.94–7.62 | 6.729 ± 0.292 | - | < 0.01 |
| C-LAP (cm) | ||||||||
| Right | 3.47–5.84 | 4.686 ± 0.426 | 4.25–5.84 | 4.941 ± 0.357 | 3.47–5.09 | 4.431 ± 0.325 | 16.75 | < 0.001 |
| Left | 3.75–5.72 | 4.667 ± 0.398 | 4.00–5.72 | 4.889 ± 0.351 | 3.75–5.14 | 4.446 ± 0.308 | 13.51 | < 0.001 |
| Average | 3.63–5.68 | 4.677 ± 0.401 | 4.23–5.68 | 4.915 ± 0.343 | 3.63–5.10 | 4.438 ± 0.301 | 16.42 | < 0.001 |
| C-MAP (cm) | ||||||||
| Right | 4.33–6.27 | 5.258 ± 0.371 | 4.58–6.27 | 5.483 ± 0.307 | 4.33–5.76 | 5.033 ± 0.283 | 17.43 | < 0.001 |
| Left | 4.27–6.41 | 5.240 ± 0.377 | 4.69–6.41 | 5.484 ± 0.302 | 4.27–5.71 | 4.997 ± 0.272 | 21.56 | < 0.001 |
| Average | 4.30–6.34 | 5.249 ± 0.367 | 4.71–6.34 | 5.435 ± 0.296 | 4.30–5.74 | 5.019 ± 0.270 | 20.56 | < 0.001 |
Wilcoxon rank sum test was used to estimate the P value in the C-ML values, and Student’s t-test was used to estimate the P value in the other measurements. AS adjusted stature, which was calculated by subtracting 2.0 cm from the measured stature; SD standard deviation; AZS absolute Z value of skewness; AZK absolute Z value of kurtosis; MLF, maximum length of the femur; LAP lateral anterior–posterior length; C-ML cross-section medial–lateral width; C-LAP C-lateral anterior–posterior length; C-MAP C-medial anterior–posterior length.
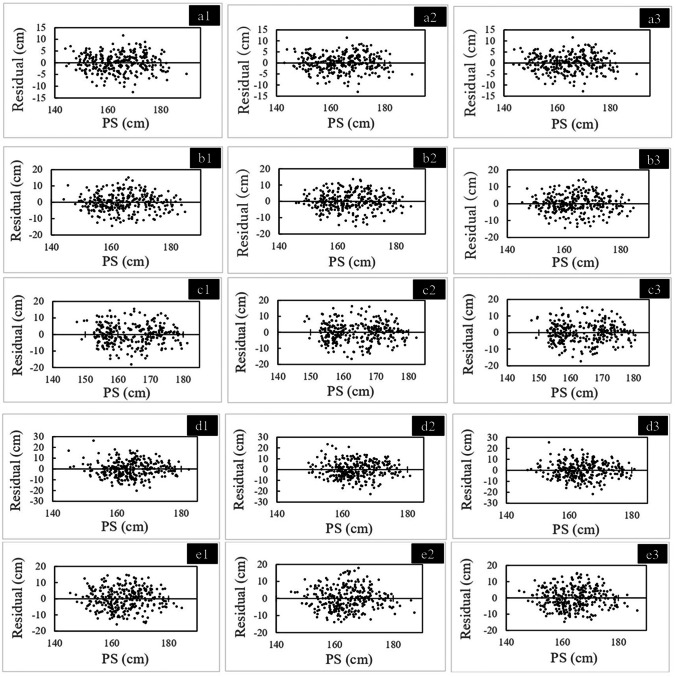
Table 5 describes the result of the single linear regression analysis for estimating AS using five group 1 measurements for all cadavers, regardless of sex. Tables 6 and 7 show the results for males and females, respectively. Significant positive correlations were observed between the AS and each measurement. MLF had the strongest correlation and the lowest SEE for all cadavers, while LAP had the second strongest correlation and lowest SEE. Figures 3, 4, and 5 show the residual plots for the five measurements.
Table 5.
Simple linear regression analyses for stature estimation for all samples regardless of sex
| Side | Regulation formula (cm) | SEE (cm) | R2 | P value | |
|---|---|---|---|---|---|
| MLF (cm) | Right | y = 3.091x + 32.230 | 3.913 | 0.842 | < 0.001 |
| Left | y = 3.060 x + 33.261 | 3.837 | 0.848 | < 0.001 | |
| Average | y = 3.083 x + 32.442 | 3.850 | 0.847 | < 0.001 | |
| LAP (cm) | Right | y = 17.582 x + 53.413 | 5.340 | 0.706 | < 0.001 |
| Left | y = 17.813 x + 52.159 | 5.340 | 0.702 | < 0.001 | |
| Average | y = 17.896 x + 51.533 | 5.287 | 0.712 | < 0.001 | |
| C-ML (cm) | Right | y = 12.358 x + 74.240 | 6.047 | 0.623 | < 0.001 |
| Left | y = 12.380 x + 74.518 | 6.019 | 0.627 | < 0.001 | |
| Average | y = 12.488 x + 73.514 | 5.985 | 0.631 | < 0.001 | |
| C-LAP (cm) | Right | y = 15.768 x + 90.296 | 7.199 | 0.466 | < 0.001 |
| Left | y = 15.786 x + 90.507 | 7.583 | 0.408 | < 0.001 | |
| Average | y = 16.685 x + 86.153 | 7.226 | 0.462 | < 0.001 | |
| C-MAP (cm) | Right | y = 20.192 x + 58.015 | 6.384 | 0.580 | < 0.001 |
| Left | y = 19.710 x + 60.897 | 6.461 | 0.570 | < 0.001 | |
| Average | y = 20.656 x + 55.757 | 6.267 | 0.595 | < 0.001 |
SEE standard error of the estimate, MLF maximum length of the femur, LAP lateral anterior–posterior length, C-ML cross-section medial–lateral width, C-LAP C-lateral anterior–posterior length, C-MAP C-medial anterior–posterior length.
Table 6.
Simple linear regression analyses for stature estimation in males
| Side | Regulation formula (cm) | SEE (cm) | R2 | P value | |
|---|---|---|---|---|---|
| MLF (cm) | Right | y = 2.667x + 52.355 | 3.664 | 0.705 | < 0.001 |
| Left | y = 2.682x + 51.321 | 3.667 | 0.705 | < 0.001 | |
| Average | y = 2.686x + 51.298 | 3.646 | 0.708 | < 0.001 | |
| LAP (cm) | Right | y = 13.391x + 82.717 | 4.807 | 0.493 | < 0.001 |
| Left | y = 13.688x + 80.906 | 4.897 | 0.474 | < 0.001 | |
| Average | y = 13.860x + 79.686 | 4.797 | 0.495 | < 0.001 | |
| C-ML (cm) | Right | y = 10.467x + 89.882 | 5.547 | 0.325 | < 0.001 |
| Left | y = 10.266x + 91.779 | 5.608 | 0.310 | < 0.001 | |
| Average | y = 10.609x + 88.945 | 5.547 | 0.325 | < 0.001 | |
| C-LAP (cm) | Right | y = 9.921x + 122.590 | 5.739 | 0.277 | < 0.001 |
| Left | y = 9.348x + 125.910 | 5.891 | 0.238 | < 0.001 | |
| Average | y = 10.305x + 120.960 | 5.747 | 0.275 | < 0.001 | |
| C-MAP (cm) | Right | y = 14.347x + 92.950 | 5.106 | 0.428 | < 0.001 |
| Left | y = 12.911x + 100.810 | 5.504 | 0.335 | < 0.001 | |
| Average | y = 14.418x + 92.554 | 5.220 | 0.402 | < 0.001 |
SEE standard error of the estimate, MLF maximum length of the femur, LAP lateral anterior–posterior length, C-ML cross-section medial–lateral width, C-LAP C-lateral anterior–posterior length, C-MAP C-medial anterior–posterior length.
Table 7.
Simple linear regression analyses for stature estimation in females
| Side | Regulation formula (cm) | SEE (cm) | R2 | P value | |
|---|---|---|---|---|---|
| MLF (cm) | Right | y = 2.434 x + 57.802 | 3.456 | 0.686 | < 0.001 |
| Left | y = 2.428 x + 57.895 | 3.384 | 0.699 | < 0.001 | |
| Average | y = 2.442 x + 57.409 | 3.403 | 0.696 | < 0.001 | |
| LAP (cm) | Right | y = 12.007 x + 85.171 | 5.012 | 0.340 | < 0.001 |
| Left | y = 12.044 x + 85.083 | 5.060 | 0.327 | < 0.001 | |
| Average | y = 12.319 x + 83.375 | 5.005 | 0.341 | < 0.001 | |
| C-ML (cm) | Right | y = 4.877 x + 123.850 | 5.986 | 0.058 | 0.003 |
| Left | y = 5.440 x + 120.260 | 5.951 | 0.069 | 0.001 | |
| Average | y = 5.424 x + 120.260 | 5.959 | 0.067 | 0.001 | |
| C-LAP (cm) | Right | y = 6.287 x + 128.900 | 5.817 | 0.110 | < 0.001 |
| Left | y = 5.662 x + 131.590 | 5.914 | 0.081 | < 0.001 | |
| Average | y = 6.647 x + 127.260 | 5.833 | 0.106 | < 0.001 | |
| C-MAP (cm) | Right | y = 10.698 x + 102.920 | 5.367 | 0.243 | < 0.001 |
| Left | y = 10.626 x + 103.670 | 5.441 | 0.222 | < 0.001 | |
| Average | y = 11.317 x + 100.000 | 5.354 | 0.247 | < 0.001 |
SEE standard error of the estimate, MLF maximum length of the femur, LAP lateral anterior–posterior length, C-ML cross-section medial–lateral width, C-LAP C-lateral anterior–posterior length, C-MAP C-medial anterior–posterior length.
Fig. 3.
Residual distribution for all samples regardless of sex with the five measurements. a1: Right MLF (maximum length of the femur): a2: left MLF, a3: average MLF; b1: right LAP (lateral anterior–posterior length): b2: left LAP, b3: average LAP; c1: right C-ML (cross-section medial–lateral width): c2: left C-ML, c3: average C-ML; d1: right C-LAP (C-lateral anterior–posterior length): d2: left C-LAP, d3: average C-LAP; e1: right C-MAP (C-medial anterior–posterior length), e2: Left C-MAP, e3: average C-MAP. AS, adjusted stature, PS, predicted stature calculated with the obtained regression equation
Fig. 4.
Residual distribution for male samples with the five measurements. a1: right MLF (maximum length of the femur): a2: left MLF, a3: average MLF; b1: right LAP (lateral anterior–posterior length): b2: left LAP, b3: average LAP; c1: right C-ML (cross-section medial–lateral width): c2: left C-ML, c3: Average C-ML; d1: right C-LAP (C-lateral anterior–posterior length): d2: left C-LAP, d3: average C-LAP; e1: right C-MAP (C-medial anterior–posterior length): e2: left C-MAP, e3: average C-MAP. AS, adjusted stature, PS: predicted stature calculated with the obtained regression equation
Fig. 5.
Residual distribution for female samples with the five measurements. a1: right MLF (maximum length of the femur): a2: left MLF, a3: average MLF; b1: right LAP (lateral anterior–posterior length): b2: left LAP, b3: average LAP; c1: right C-ML (cross-section medial–lateral width): c2: left C-ML, c3: average C-ML; d1: right C-LAP (C-lateral anterior–posterior length): d2: left C-LAP, d3: average C-LAP; e1: right C-MAP (C-medial anterior–posterior length): e2: left C-MAP, e3: average C-MAP. AS, adjusted stature; PS, predicted stature calculated with the obtained regression equation
Discussion
In this study, we obtained stature estimation formulae based on a 3D model reconstructed from CT images using semi-automatic measurement software. This is the first report that obtained stature estimation formulae from measurements in 3D CT-reconstructed images using semi-automatic measurement software. In the present study, artificial intelligence (AI) was used for recognition of the femur, extraction of bone surface information, and semi-automatic measurement. AI has been applied in multiple fields of medical research. In the field of diagnostic imaging, it has been shown to reduce not only time for analysis but also interreader variability or false-positive markings [56–59]. Furthermore, AI has been shown to improve adenoma detection rates and reduce examination time in colonoscopy [60], thus reducing waiting time for outpatients [61] and the time interval between CT angiography at a primary stroke center to door-in at a comprehensive stroke center [62]. In the present study, the advantages of using a semi-automatic measurement software were the following: it is a simple measurement method; the time required for measurement is short (approximately 1 min); multiple measurements can be obtained with a single method.
Previously, some stature estimation methods with a single linear regression analysis from MLF measured using radiographic images were reported (Table 8). In two previous reports that presented intraobserver and interobserver errors [40, 44], the rTEM values for intraobserver errors were 0.108–0.277 and those for interobserver errors were 0.192–0.289. In this report, the rTEM values for intraobserver errors were 0.034–0.035 and those for interobserver errors were 0.018–0.019, which were lower than in these two reports. It is possible that these errors were reduced using semi-automatic measurement software.
Table 8.
Outline of previous and present studies having performed simple linear regression analysis for stature estimation with maximum length of the femur whose length was measured using radiographic images
| Author | Subject | Equipment | Side | Sex | Stature estimation formula | Correlation coefficient | R2 | SEE (cm) | Intra-OE (%) | Inter-OE (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Present study | Japanese | Computed tomography | Right | Male (n = 150) | y = 2.667x + 52.355 | - | 0.7053 | 3.664 | 0.035 | 0.018 |
| Female (n = 150) | y = 2.682 x + 51.321 | - | 0.7049 | 3.667 | ||||||
| Left | Male (n = 150) | y = 2.434 x + 57.802 | - | 0.686 | 3.456 | 0.034 | 0.019 | |||
| Female (n = 150) | y = 2.428 x + 57.895 | - | 0.6989 | 3.384 | ||||||
| Chiba et al. [44] | Japanese | Computed tomography | Right | Male (n = 116) | y = 2.670 x + 50.987 | - | 0.654 | 3.847 | 0.108 | 0.205 |
| Female (n = 108) | y = 2.702 x + 46.624 | - | 0.768 | 3.29 | ||||||
| Left | Male (n = 116) | y = 2.748 x + 47.259 | - | 0.653 | 3.85 | 0.247 | 0.289 | |||
| Female (n = 108) | y = 2.646 x + 48.733 | - | 0.76 | 3.34 | ||||||
| Hasegawa et al. [37] | Japanese | X-ray photography | Right | Male (n = 92) | y = 2.42 x + 63.32 | 0.895 | 0.8010* | 3.77 | - | - |
| Female (n = 342) | y = 2.31 x + 62.05 | 0.809 | 0.6545* | 3.03 | ||||||
| Left | Male (n = 92) | y = 2.49 x + 60.30 | 0.903 | 0.8154* | 3.83 | - | - | |||
| Female (n = 342) | y = 2.28 x + 63.37 | 0.813 | 0.6610* | 3.00 | ||||||
| Hishmat et al. [40] | Japanese | Computed tomography | Right | Male (n = 150) | y = 2.61 x + 52.17 | 0.73 | 0.5329* | 4.83 | 0.149 | 0.192 |
| Female (n = 109) | y = 2.86 x + 38.48 | 0.83 | 0.6889* | 4.29 | ||||||
| Left | Male (n = 150) | y = 2.47 x + 58.04 | 0.72 | 0.5184 | 4.72 | 0.277 | 0.201 | |||
| Female (n = 109) | y = 2.87 x + 37.42 | 0.81 | 0.6561* | 4.49 | ||||||
| Nishio [42] | Japanese | Computed tomography | Right | Male (n = 215) | y = 3.20 x + 27.81 | 0.8967 | 0.8041* | 4.32 | - | - |
| Female (n = 120) | y = 3.36 x + 20.22 | 0.8784 | 0.7716* | 4.12 | ||||||
| Left | Male (n = 215) | y = 3.11 x + 31.13 | 0.8841 | 0.7816* | 4.60 | - | - | |||
| Female (n = 120) | y = 3.15 x + 29.00 | 0.8591 | 0.7381* | 4.39 | ||||||
| Zhang et al. [63] | Danish | Computed tomography | Right | Male (n = 41) | y = 2.23 x + 70.70 | - | 0.52 | 4.4 | - | - |
| Female (n = 37) | y = 2.13 x + 69.26 | - | 0.75 | 3.5 | ||||||
| Left | Male (n = 41) | y = 2.19 x + 72.17 | - | 0.51 | 4.4 | - | - | |||
| Female (n = 37) | y = 2.07 x + 72.03 | - | 0.74 | 3.6 | ||||||
| Lee et al. [39] | Korean | Computed tomography | Right | Male (n = 155) | y = 2.593 x + 54.081 | 0.85 | 0.722* | 3.305 | - | - |
| Female (n = 153) | y = 2.82 x + 41.926 | 0.89 | 0.792* | 3.417 | ||||||
| Left | Male (n = 155) | y = 2.610 x + 54.081 | 0.859 | 0.737* | 3.214 | - | - | |||
| Female (n = 153) | y = 2.842 x + 40.776 | 0.886 | 0.785* | 3.468 | ||||||
*The values in the R2 segments are not presented in the reports but were calculated by the square of the correlation coefficient presented with them for ease of comparison.
SEE standard error of the estimate, intra-OE and Inter-OE r-TEMs of intraobserver and interobserver errors, respectively.
Compared with previous reports [37, 40, 42, 44] of Japanese cadavers, the results of R2 and SEE in this study were either better or at least not inferior; therefore, the stature estimation formulae determined in this study could be useful in forensic medical practice. Compared with previous reports providing stature estimations using CT images of Japanese femurs [40, 42, 44], the present study observed the lowest SEE in males, whereas the SEE in females was the second lowest after Chiba et al. [44], and the difference was < 0.2 cm. In their report, MLF was manually measured by reproducing the conventional anthropological measurement method using a CT arbitrary cross-section reconstruction image. Although it may be highly applicable to conventional bone measurements, their measurement method is complicated and time consuming, taking approximately 140 s for measuring MLF, and approximately 440 s for measuring the 5 measurements needed for single side written in the research [44]. In contrast, the semi-automatic measurement method examined in this study is much simpler and faster. It took approximately 40 s from manual marking to displaying 41 measurements, and approximately 280 s from launching this application to displaying all the results. This time period includes measurements of both sides of the femur and includes the time required for 3D model reconstruction. Since the semi-automatic measurement method reduced the measurement error and shortened the measurement time, it is expected that if a fully automatic measuring method is developed, it will be possible to measure with smaller errors and shorter measurement time than the results of this study currently show.
Hasegawa et al. [37] showed lower SEE values in females than those observed in this study (difference, > 0.3 cm), and their report showed the best results in terms of SEE in Japanese subjects, as shown in Table 8 [37, 40, 42, 44]. However, the SEE in males was slightly higher than that observed in males in this study. In addition, the difference in SEE between males and females was 0.74 and 0.83, which was greater than difference in this study (0.003 and 0.072). Hasegawa et al. [37] provided stature estimation formulae using an X-ray photograph of a living human. The difference between this report and theirs might be because their patients were alive, the radiation imaging device was different, and the number of female samples was higher than that of the male samples in their study.
Comparison of the present study with those of Zhang et al. [63] and Lee et al. [39] is complicated because the subjects are different, but our results were superior to those of Zhang et al. [63] and slightly inferior to those of Lee et al. [39]. Zhang et al. [63] studied a smaller number of cadavers than this study; therefore, the difference might be due to the sample size. Meanwhile, Lee et al. [39] had more cadavers with age of 41–60 years (65.8% for men and 45.1% for women) than our report (50.0% for men and 30.0% for women). They might have obtained better results of stature estimation formulae than this study, whose age groups of cadavers were scattered because their stature estimation formulae were adapted to the age groups that comprised most of their cadavers. The difference in age composition ratio, CT equipment, or image reconstruction software may have affected the results.
Many reports have shown that MLF is useful for stature estimation, consistent with our finding that stature estimation with MLF showed the best performance. However, it is impossible to measure MLF if only part of the femur remains. In this study, stature estimation using LAP showed the second lowest SEE. This suggests that LAP would be useful for stature estimation if the MLF cannot be measured, for example, if only the lower part of the femur remains. Although some reports provided stature estimation formulae using measurements of the lower part of the femur [29, 44, 64, 65], no report has suggested that LAP is useful for stature estimation. The high values of SEE for LAP and the three measurements, C-ML, C-LAP, and C-MAP, were not negligible. However, of all the studies that performed stature estimation using the measurements of the lateral side of the femur, only Chiba et al. [44] calculated SEE. They reported that the SEEs calculated from femoral epicondylar breadth (linear distance between projection points of the most medial and lateral epicondyles projected vertically to the horizontal) was 5.620–6.300. Compared to their study, SEEs calculated from LAP showed better results, and SEEs calculated from other measurements were not inferior. Since there are few comparison targets, further research on stature estimation using the measurements of the distal part of the femur is desirable in future studies.
Among the 41 measurements that were semi-automatically measured in the present study, group 2 measurements had large intraobserver and interobserver errors outside the permissible range. Descriptive statistics for the measurements corresponding to group 2 are shown in Online Resource 1. There are several possible reasons for the higher measurement errors in group 2 measurements. Group 2–1 measurements were based on information from the edge of the reconstructed 3D CT model. Therefore, the slight difference in construction due to the manual removal of calcified blood vessels and cartilage might have resulted in a large error. Group 2–2 measurements, except MAP, had smaller values than those of group 1, as shown in Table 4 and Online Resource 1. Therefore, the error caused by manual operation might have had a significant influence on these measurements. MAP had similar values to those of group 1 measurements, but it also had higher measurement errors. Unlike C-ML, C-LAP, and C-MAP, MAP is measured without creating a cross section at the lower part of the femur. The deformation of the knee joint, including the distal end of the femur, might have occurred in most of the cadavers in this study because primary knee osteoarthritis often occurs in people over 50 years old [66, 67]. This change may have made it difficult for the AI software to have identified them. In some cadavers, the software used in this study mistakenly recognized the knee cartilage and patella as part of the femur when it identified the femur, and the structure other than the femur had to be manually removed. This manual operation might have caused higher measurement errors. In addition, MAP had a larger measurement error than LAP, which was also measured without creating a cross section. This may be because osteoarthritis occurs more frequently on the medial side than on the lateral side [64].
The residual plots indicated that the two measurements, MLF and LAP, were good models for calculating regression equations. The other three measurements were difficult to adopt for the regression equations, because of the large outliers and a small range of predicted values, especially in the residual plots using single-sex. This may be attributed to the small range of the three measurements.
This study has several limitations. The measurements useful in other reports, such as the femoral diaphysis length, physiological length, or bicondylar length [13, 29, 65, 68, 69], were not measured because the semi-automatic measurement application was not configured to measure them. Furthermore, the application was developed by Fujifilm, including measurements selection. The femurs measured in this study were collected only from cadavers with soft tissue, so further studies examining the difference between digital and analog measurements are warranted. Femur deformation due to aging was not considered. In this research, the stature of the cadavers was recalculated in AS, and the estimation formulae were assessed, but since the actual stature was measured only once, intra- and inter-observer errors were not evaluated for the stature. Age-stratified analysis was not performed because of the insufficient sample size in this study. In addition, this study was performed using images captured with two types of CT equipment. Further studies comparing and examining images acquired with different CT devices are warranted.
Conclusion
This study provided the first stature estimation formulae based on a 3D CT model of modern Japanese femurs using a simple and rapid semi-automatic measurement software. For stature estimation with this method, MLF was the best, and LAP was the second-best measurement using 41 total measurements. These formulae can be useful in forensic investigations.
Supplementary Information
Below is the link to the electronic supplementary material.
Author contribution
All authors contributed to the conception and design of the study. Material preparation, data collection, and analysis were performed by Kei Kira and Fumiko Chiba. The first draft of the manuscript was written by Kei Kira, and all authors commented on the previous versions of the manuscript. All authors read and approved the final manuscript.
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
Code sharing not applicable to this article as no codes were generated or analyzed during the current study.
Declarations
Ethics approval
The experimental protocol was approved by the Ethical Review Board of Chiba University (2987) and the University of Tokyo (10835–1).
Consent to participate
This study provided sufficient protection of the privacy of the patients and their families as per the Japanese Protection Guideline of Personal Information on Research Publication in Legal Medicine, and the requirements of informed consent from the next of kin was waived by the Ethical Review Board.
Consent for publication
This study provided sufficient protection of the privacy of the patients and their families as per the Japanese Protection Guideline of Personal Information on Research Publication in Legal Medicine, and the requirements of informed consent from the next of kin was waived by the Ethical Review Board.
Conflict of interest
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Pearson K. IV. Mathematical contributions to the theory of evolution.—V. On the reconstruction of the stature of prehistoric races. Phil Trans R Soc Lond A. 1899;192:169–244. doi: 10.1098/rsta.1899.0004. [DOI] [Google Scholar]
- 2.Breitinger E. Zur Berechnung der Körperhöhe aus den langen Gliedmaßenknochen. Anthropol Anz. 1937;14:249–274. [Google Scholar]
- 3.Trotter M, Gleser GC. The effect of ageing on stature. Am J Phys Anthropol. 1951;9:311–324. doi: 10.1002/ajpa.1330090307. [DOI] [PubMed] [Google Scholar]
- 4.Trotter M, Gleser GC. Estimation of stature from long bones of American Whites and Negroes. Am J Phys Anthropol. 1952;10:463–514. doi: 10.1002/ajpa.1330100407. [DOI] [PubMed] [Google Scholar]
- 5.Olivier G, Aaron C, Fully G, Tissier G. New estimations of stature and cranial capacity in modern man. J Hum Evol. 1978;7:513–518. doi: 10.1016/S0047-2484(78)80020-7. [DOI] [Google Scholar]
- 6.Zeybek G, Ergur I, Demiroglu Z. Stature and gender estimation using foot measurements. Forensic Sci Int. 2008;181:54.e1–54.e5. doi: 10.1016/j.forsciint.2008.08.003. [DOI] [PubMed] [Google Scholar]
- 7.Duyar I, Pelin C. Body height estimation based on tibia length in different stature groups. Am J Phys Anthropol. 2003;122:23–27. doi: 10.1002/ajpa.10257. [DOI] [PubMed] [Google Scholar]
- 8.Mullins RA, Albanese J. Estimating biological characteristics with virtual laser data. J Forensic Sci. 2018;63:815–823. doi: 10.1111/1556-4029.13621. [DOI] [PubMed] [Google Scholar]
- 9.Asadujjaman M, Al Noman SN, Molla MBA. Stature estimation from foot anthropometric measurements in Bangladeshi population. Ir J Med Sci. 2020;189:365–372. doi: 10.1007/s11845-019-02048-x. [DOI] [PubMed] [Google Scholar]
- 10.Mahakkanukrauh P, Khanpetch P, Prasitwattanseree S, Vichairat K, Troy Case DT. Stature estimation from long bone lengths in a Thai population. Forensic Sci Int. 2011;210:279.e1–279.e7. doi: 10.1016/j.forsciint.2011.04.025. [DOI] [PubMed] [Google Scholar]
- 11.Zhang K, Luo YZ, Fan F, Zheng JQ, Yang M, Li T, Pang T, Zhang J, Deng ZH. Stature estimation from sternum length using computed tomography-volume rendering technique images of western Chinese. J Forensic Leg Med. 2015;35:40–44. doi: 10.1016/j.jflm.2015.07.003. [DOI] [PubMed] [Google Scholar]
- 12.Giurazza F, Del Vescovo R, Schena E, Cazzato RL, D’Agostino F, Grasso RF, Silvestri S, Zobel BB. Stature estimation from scapular measurements by CT scan evaluation in an Italian population. Leg Med (Tokyo) 2013;15:202–208. doi: 10.1016/j.legalmed.2013.01.002. [DOI] [PubMed] [Google Scholar]
- 13.Giurazza F, Del Vescovo R, Schena E, Battisti S, Cazzato RL, Grasso FR, Silvestri S, Denaro V, Zobel BB. Determination of stature from skeletal and skull measurements by CT scan evaluation. Forensic Sci Int. 2012;222:398.e1–398.e9. doi: 10.1016/j.forsciint.2012.06.008. [DOI] [PubMed] [Google Scholar]
- 14.Villa C, Hansen MN, Buckberry J, Cattaneo C, Lynnerup N. Forensic age estimation based on the trabecular bone changes of the pelvic bone using post-mortem CT. Forensic Sci Int. 2013;233:393–402. doi: 10.1016/j.forsciint.2013.10.020. [DOI] [PubMed] [Google Scholar]
- 15.Lorkiewicz-Muszyńska D, Przystańska A, Kociemba W, Sroka A, Rewekant A, Żaba C, Paprzycki W. Body mass estimation in modern population using anthropometric measurements from computed tomography. Forensic Sci Int. 2013;231:405.e1–405.e6. doi: 10.1016/j.forsciint.2013.05.017. [DOI] [PubMed] [Google Scholar]
- 16.Chiba F, Makino Y, Motomura A, Inokuchi G, Torimitsu S, Ishii N, Sakuma A, Nagasawa S, Saitoh H, Yajima D, Hayakawa M, Odo Y, Suzuki Y, Iwase H. Age estimation by multidetector CT images of the sagittal suture. Int J Legal Med. 2013;127:1005–1011. doi: 10.1007/s00414-013-0883-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Torimitsu S, Makino Y, Saitoh H, Ishii N, Yajima D, Inokuchi G, Motomura A, Chiba F, Yamaguchi R, Hoshioka Y, Iwase H. Determination of sex on the basis of hyoid bone measurements in a Japanese population using multidetector computed tomography. Int J Legal Med. 2018;132:907–914. doi: 10.1007/s00414-017-1728-x. [DOI] [PubMed] [Google Scholar]
- 18.Torimitsu S, Makino Y, Saitoh H, Sakuma A, Ishii N, Yajima D, Inokuchi G, Motomura A, Chiba F, Yamaguchi R, Hashimoto M, Hoshioka Y, Iwase H. Sexual determination based on multidetector computed tomographic measurements of the second cervical vertebra in a contemporary Japanese population. Forensic Sci Int. 2016;266:588.e1–588.e6. doi: 10.1016/j.forsciint.2016.04.010. [DOI] [PubMed] [Google Scholar]
- 19.Torimitsu S, Makino Y, Saitoh H, Sakuma A, Ishii N, Yajima D, Inokuchi G, Motomura A, Chiba F, Yamaguchi R, Hashimoto M, Hoshioka Y, Iwase H. Stature estimation in a contemporary Japanese population based on clavicular measurements using multidetector computed tomography. Forensic Sci Int. 2017;275:316.e1–316.e6. doi: 10.1016/j.forsciint.2017.02.037. [DOI] [PubMed] [Google Scholar]
- 20.Torimitsu S, Makino Y, Saitoh H, Sakuma A, Ishii N, Inokuchi G, Motomura A, Chiba F, Hoshioka Y, Iwase H. Estimation of sex in Japanese cadavers based on sternal measurements using multidetector computed tomography. Leg Med (Tokyo) 2015;17:226–231. doi: 10.1016/j.legalmed.2015.01.003. [DOI] [PubMed] [Google Scholar]
- 21.Torimitsu S, Makino Y, Saitoh H, Sakuma A, Ishii N, Hayakawa M, Inokuchi G, Motomura A, Chiba F, Hoshioka Y, Iwase H. Stature estimation in Japanese cadavers based on the second cervical vertebra measured using multidetector computed tomography. Leg Med (Tokyo) 2015;17:145–149. doi: 10.1016/j.legalmed.2014.11.003. [DOI] [PubMed] [Google Scholar]
- 22.Chiba F, Makino Y, Motomura A, Inokuchi G, Torimitsu S, Ishii N, Kubo Y, Abe H, Sakuma A, Nagasawa S, Saitoh H, Yajima D, Hayakawa M, Miura M, Iwase H. Age estimation by quantitative features of pubic symphysis using multidetector computed tomography. Int J Legal Med. 2014;128:667–673. doi: 10.1007/s00414-014-1010-4. [DOI] [PubMed] [Google Scholar]
- 23.Jeong Y, Jantz LM. Developing Korean-specific equations of stature estimation. Forensic Sci Int. 2016;260:105.e1–105.e11. doi: 10.1016/j.forsciint.2015.12.048. [DOI] [PubMed] [Google Scholar]
- 24.Trotter M, Gleser GC. A re-evaluation of estimation of stature based on measurements of stature taken during life and of long bones after death. Am J Phys Anthropol. 1958;16:79–123. doi: 10.1002/ajpa.1330160106. [DOI] [PubMed] [Google Scholar]
- 25.Auerbach BM, Ruff CB. Stature estimation formulae for indigenous North American populations. Am J Phys Anthropol. 2010;141:190–207. doi: 10.1002/ajpa.21131. [DOI] [PubMed] [Google Scholar]
- 26.Monum T, Prasitwattanseree S, Das S, Siriphimolwat P, Mahakkanukrauh P. Sex estimation by femur in modern Thai population. Clin Ter. 2017;168:e203–e207. doi: 10.7417/T.2017.2007. [DOI] [PubMed] [Google Scholar]
- 27.Ruff C. Body size prediction from juvenile skeletal remains. Am J Phys Anthropol. 2007;133:698–716. doi: 10.1002/ajpa.20568. [DOI] [PubMed] [Google Scholar]
- 28.Feldesman MR. Femur/stature ratio and estimates of stature in children. Am J Phys Anthropol. 1992;87:447–459. doi: 10.1002/ajpa.1330870406. [DOI] [PubMed] [Google Scholar]
- 29.Brits DM, Bidmos MA, Manger PR. Stature estimation from the femur and tibia in Black South African sub-adults. Forensic Sci Int. 2017;270:277.e1–277.e10. doi: 10.1016/j.forsciint.2016.10.013. [DOI] [PubMed] [Google Scholar]
- 30.Sládek V, Macháček J, Ruff CB, Schuplerová E, Přichystalová R, Hora M. Population-specific stature estimation from long bones in the early medieval Pohansko (Czech Republic) Am J Phys Anthropol. 2015;158:312–324. doi: 10.1002/ajpa.22787. [DOI] [PubMed] [Google Scholar]
- 31.Wilson RJ, Herrmann NP, Jantz LM. Evaluation of stature estimation from the database for forensic anthropology. J Forensic Sci. 2010;55:684–689. doi: 10.1111/j.1556-4029.2010.01343.x. [DOI] [PubMed] [Google Scholar]
- 32.Dayal MR, Steyn M, Kuykendall KL. Stature estimation from bones of South African whites. Afr J Sci. 2008;104:124–128. [Google Scholar]
- 33.Andou M. Nihonjin (seijin) no shishikotsu no keisoku ni oite. Kokka Igaku Zasshi. 1923;434:101–120. [Google Scholar]
- 34.Fujii A. On the relation of long bone length of limbs to stature. Juntendoudaigaku Taiikugakubu Kiyo. 1960;3:49–61. [Google Scholar]
- 35.White TD, Black MT, Folkens PA. Human osteology. 3. New York: Academic Press; 2011. [Google Scholar]
- 36.Sağir M. Estimation stature from X-rays of metacarpals in the Turkish population. Anthropol Anz. 2006;64:377–388. doi: 10.1127/anthranz/64/2006/377(inTurkish,withEnglishabstract). [DOI] [PubMed] [Google Scholar]
- 37.Hasegawa I, Uenishi K, Fukunaga T, Kimura R, Osawa M. Stature estimation formulae from radiographically determined limb bone length in a modern Japanese population. Leg Med (Tokyo) 2009;11:260–266. doi: 10.1016/j.legalmed.2009.07.004. [DOI] [PubMed] [Google Scholar]
- 38.Cui JH, Luo YZ, Chang YF, Peng Z, Deng LP, Zhang K, Deng ZH (2019) Stature estimation of Sichuan Han females based on X-ray photography of total lower limbs. Fa Yi Xue Za Zhi 35:11–16. 10.12116/j.issn.1004-5619.2019.01.003 (in Chinese, with English abstract) [DOI] [PubMed]
- 39.Lee S, Gong HH, Hyun JY, Koo HN, Lee HY, Chung NE, Choi YS, Yang KM, Ha Choi BH. Estimation of stature from femur length measured using computed tomography after the analysis of three-dimensional characteristics of femur bone in Korean cadavers. Int J Legal Med. 2017;131:1355–1362. doi: 10.1007/s00414-017-1556-z. [DOI] [PubMed] [Google Scholar]
- 40.Hishmat AM, Michiue T, Sogawa N, Oritani S, Ishikawa T, Fawzy IA, Hashem MA, Maeda H. Virtual CT morphometry of lower limb long bones for estimation of the sex and stature using postmortem Japanese adult data in forensic identification. Int J Legal Med. 2015;129:1173–1182. doi: 10.1007/s00414-015-1228-9. [DOI] [PubMed] [Google Scholar]
- 41.Imai N, Funayama K, Suzuki H, Tsuchiya K, Nozaki A, Minato I, Miyasaka D, Endo N. Stature estimation formulae based on bony pelvic dimensions and femoral length. Homo. 2020;71:111–119. doi: 10.1127/homo/2020/1116. [DOI] [PubMed] [Google Scholar]
- 42.Nishio H. Stature estimation based on the lengths of the long bones of the extremities according to post-mortem computed tomography. Res Pract Forensic Med. 2013;56:223–235. [Google Scholar]
- 43.Zech WD, Näf M, Siegmund F, Jackowski C, Lösch S. Body height estimation from post-mortem CT femoral F1 measurements in a contemporary Swiss population. Leg Med (Tokyo) 2016;19:61–66. doi: 10.1016/j.legalmed.2016.02.004. [DOI] [PubMed] [Google Scholar]
- 44.Chiba F, Makino Y, Torimitsu S, Motomura A, Inokuchi G, Ishii N, Hoshioka Y, Abe H, Yamaguchi R, Sakuma A, Nagasawa S, Saito H, Yajima D, Fukui Y, Iwase H. Stature estimation based on femoral measurements in the modern Japanese population: a cadaveric study using multidetector computed tomography. Int J Legal Med. 2018;132:1485–1491. doi: 10.1007/s00414-018-1834-4. [DOI] [PubMed] [Google Scholar]
- 45.De Mendonça MC. Estimation of height from the length of long bones in a Portuguese adult population. Am J Phys Anthropol. 2000;112:39–48. doi: 10.1002/(SICI)1096-8644(200005)112:1<39::AID-AJPA5>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 46.Meadows L, Jantz RL. Estimation of stature from metacarpal lengths. J Forensic Sci. 1992;37:147–154. doi: 10.1520/JFS13222J. [DOI] [PubMed] [Google Scholar]
- 47.Telkka A. On the prediction of human stature from the long bones. Acta Anat (Basel) 1950;9:103–117. doi: 10.1159/000140434. [DOI] [PubMed] [Google Scholar]
- 48.Radoinova D, Tenekedjiev K, Yordanov Y. Stature estimation from long bone lengths in Bulgarians. Homo. 2002;52:221–232. doi: 10.1078/0018-442x-00030. [DOI] [PubMed] [Google Scholar]
- 49.Arroyo M, Freire M, Ansotegui L, Rocandio AM. Intraobserver error associated with anthropometric measurements made by dietitians. Nutr Hosp. 2010;25:1053–1056. doi: 10.3305/nh.2010.25.6.4854. [DOI] [PubMed] [Google Scholar]
- 50.Mueller WH, Malina RM. Relative reliability of circumferences and skinfolds as measures of body fat distribution. Am J Phys Anthropol. 1987;72:437–439. doi: 10.1002/ajpa.1330720404. [DOI] [PubMed] [Google Scholar]
- 51.Jamaiyah H, Geeta A, Safiza MN, Khor GL, Wong NF, Kee CC, Rahmah R, Ahmad AZ, Suzana S, Chen WS, Rajaah M, Adam B (2010) Reliability, technical error of measurements and validity of length and weight measurements for children under two years old in Malaysia. Med J Malaysia 65 Supplement A:131–137 [PubMed]
- 52.Wright DB, Herrington JA. Problematic standard errors and confidence intervals for skewness and kurtosis. Behav Res Methods. 2011;43:8–17. doi: 10.3758/s13428-010-0044-x. [DOI] [PubMed] [Google Scholar]
- 53.McGee M. Case for omitting tied observations in the two-sample t-test and the Wilcoxon-Mann-Whitney test. PLoS ONE. 2018;13:e0200837. doi: 10.1371/journal.pone.0200837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kim HY. Statistical notes for clinical researchers: assessing normal distribution (2) using skewness and kurtosis. Restor Dent Endod. 2013;38:52–54. doi: 10.5395/rde.2013.38.1.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bilić-Zulle Lidija. Comparison of methods: passing and Bablok regression. Biochem Med (Zagreb) 2011;21(1):49–52. doi: 10.11613/bm.2011.010. [DOI] [PubMed] [Google Scholar]
- 56.Leiner T, Rueckert D, Suinesiaputra A, Baeßler B, Nezafat R, Išgum I, Young AA. Machine learning in cardiovascular magnetic resonance: basic concepts and applications. J Cardiovasc Magn Reson. 2019;21:61. doi: 10.1186/s12968-019-0575-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rueckel J, Reidler P, Fink N, Sperl J, Geyer T, Fabritius MP, Ricke J, Ingrisch M, Sabel BO. Artificial intelligence assistance improves reporting efficiency of thoracic aortic aneurysm CT follow-up. Eur J Radiol. 2021;134:109424. doi: 10.1016/j.ejrad.2020.109424. [DOI] [PubMed] [Google Scholar]
- 58.Mayo RC, Kent D, Sen LC, Kapoor M, Leung JWT, Watanabe AT. Reduction of false-positive markings on mammograms: a retrospective comparison study using an artificial intelligence-based CAD. J Digit Imaging. 2019;32:618–624. doi: 10.1007/s10278-018-0168-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Leite AF, Van Gerven AV, Willems H, Beznik T, Lahoud P, Gaêta-Araujo H, Vranckx M, Jacobs R. Artificial intelligence-driven novel tool for tooth detection and segmentation on panoramic radiographs. Clin Oral Investig. 2021;25:2257–2267. doi: 10.1007/s00784-020-03544-6. [DOI] [PubMed] [Google Scholar]
- 60.Sinagra E, Badalamenti M, Maida M, Spadaccini M, Maselli R, Rossi F, Conoscenti G, Raimondo D, Pallio S, Repici A, Anderloni A. Use of artificial intelligence in improving adenoma detection rate during colonoscopy: might both endoscopists and pathologists be further helped. World J Gastroenterol. 2020;26:5911–5918. doi: 10.3748/wjg.v26.i39.5911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Li X, Tian D, Li W, Dong B, Wang H, Yuan J, Li B, Shi L, Lin X, Zhao L, Liu S. Artificial intelligence-assisted reduction in patients’ waiting time for outpatient process: a retrospective cohort study. BMC Health Serv Res. 2021;21:237. doi: 10.1186/s12913-021-06248-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hassan AE, Ringheanu VM, Rabah RR, Preston L, Tekle WG, Qureshi AI. Early experience utilizing artificial intelligence shows significant reduction in transfer times and length of stay in a hub and spoke model. Interv Neuroradiol. 2020;26:615–622. doi: 10.1177/1591019920953055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zhang Q, Paz AR, Banner J, Jørkov MLS, Villa C. Stature estimation from postmortem CT femoral maximum length in contemporary Danish population. J Forensic Sci. 2020;65:930–938. doi: 10.1111/1556-4029.14254. [DOI] [PubMed] [Google Scholar]
- 64.Miyasaka T, Saito M, Kurosaka D, Ikeda R, Yamanaka S, Marumo K. Impact of posterior femoral condylar cartilage and posterior intercondylar distance on rotation of femoral component in total knee arthroplasty. BMC Musculoskelet Disord. 2020;21:498. doi: 10.1186/s12891-020-03537-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Menéndez Garmendia AM, Sánchez-Mejorada G, Gómez-Valdés JA. Stature estimation formulae for Mexican contemporary population: a sample based study of long bones. J Forensic Leg Med. 2018;54:87–90. doi: 10.1016/j.jflm.2017.12.019. [DOI] [PubMed] [Google Scholar]
- 66.Garstang SV, Stitik TP (2006) Osteoarthritis: epidemiology, risk factors, and pathophysiology. Am J Phys Med Rehabil 85 (11) Supplement: S2-S11; quiz S12. 10.1097/01.phm.0000245568.69434.1a [DOI] [PubMed]
- 67.Mine K, Nakayama T, Milanese S, Grimmer K. The effectiveness of braces and orthoses for patients with knee osteoarthritis: a systematic review of Japanese-language randomised controlled trials. Prosthet Orthot Int. 2017;41:115–126. doi: 10.1177/0309364616640926. [DOI] [PubMed] [Google Scholar]
- 68.Bidmos MA. Estimation of stature using fragmentary femora in indigenous South Africans. Int J Legal Med. 2008;122:293–299. doi: 10.1007/s00414-007-0206-2. [DOI] [PubMed] [Google Scholar]
- 69.Anzellini A, Toyne JM. Estimating the stature of ancient high-altitude Andean populations from skeletal remains of the Chachapoya of Peru. Am J Phys Anthropol. 2020;171:539–549. doi: 10.1002/ajpa.23977. [DOI] [PubMed] [Google Scholar]
- 70.Zhang Y, Wang X, Shao Y, Xia Q. The orientation of the surgical epicondylar axis varies in varus and non-varus knees in the coronal plane. Knee Surg Sports Traumatol Arthrosc. 2018;26:2580–2586. doi: 10.1007/s00167-016-4386-5. [DOI] [PubMed] [Google Scholar]
- 71.Berger RA, Rubash HE, Seel MJ, Thompson WH, Crossett LS. Determining the rotational alignment of the femoral component in total knee arthroplasty using the epicondylar axis. Clin Orthop Relat Res. 1993;286:40–47. doi: 10.1097/00003086-199301000-00008. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Code sharing not applicable to this article as no codes were generated or analyzed during the current study.