Support vector machine based emissions modeling using particle swarm optimization for homogeneous charge compression ignition engine

Abstract

The internal combustion engine faces increasing societal and governmental pressure to improve both efficiency and engine out emissions. Currently, research has moved from traditional combustion methods to new highly efficient combustion strategies such as Homogeneous Charge Compression Ignition (HCCI). However, predicting the exact value of engine out emissions using conventional physics-based or data-driven models is still a challenge for engine researchers due to the complexity the of combustion and emission formation. Research has focused on using Artificial Neural Networks (ANN) for this problem but ANN’s require large training datasets for acceptable accuracy. This work addresses this problem by presenting the development of a simple model for predicting the steady-state emissions of a single cylinder HCCI engine which is created using an metaheuristic optimization based Support Vector Machine (SVM). The selection of input variables to the SVM model is explored using five different feature sets, considering up to seven engine inputs. The best results are achieved with a model combining linear and squared inputs as well as cross correlations and their squares totaling 26 features. In this case the model fit represented by R² values were between 0.72 and 0.95. The best model fits were achieved for CO and CO₂, while HC and NO_x models have reduced model performance. Linear and non-linear SVM models were then compared to an ANN model. This comparison showed that SVM based models were more robust to changes in feature selection and better able to avoid local minimums compared to the ANN models leading to a more consistent model prediction when limited training data is available. The proposed machine learning based HCCI emission models and the feature selection approach provide insight into optimizing the model accuracy while minimizing the computational costs.

Introduction

Improving internal combustion engine efficiency and reducing their emissions has the potential to improve air quality in urban centers and reduce greenhouse gas emissions. This has led to governments around the world to introducing ever more stringent environmental legislation leading automobile manufactures to turn to new combustion methods in an attempt to meet these targets. Homogeneous Charge Compression Ignition (HCCI) is a low temperature internal combustion engine mode that has the potential to significantly reduce engine-out emissions and fuel usage.^1,2 HCCI is characterized by compression induced autoignition of a lean homogeneous air-fuel mixture.³ Reduced wall heat losses due to the reduced combustion temperature and short combustion duration provide HCCI with improved fuel efficiency benefits compared to conventional combustion modes.^4–7

HCCI has shown promising engine out emissions reductions, however, the lack of a direct timing control is a major control and modeling challenge.^8–11 Furthermore, increased Hydrocarbon (HC) and Carbon Monoxide (CO) emissions have also been observed.¹² The main combustion mechanism for HCCI is compression induced autoignition of a premixed charge, leading to a high dependency on the in-cylinder gas mixture properties. To meet current and the upcoming emission regulations a deep understanding of HCCI engine emission formation is essential. To capture the behavior of HCCI combustion, various simulation models including stochastic, multi-zone and physical models have been developed to predict the gas exchange and combustion processes.^13–16 These models are beneficial as they provide accurate results over a wide operating range while requiring minimal validation data especially for engine performance parameters.¹⁷ However, predicting the exact value of engine out emissions using conventional physics-based models is still a challenge for engine researchers due to the complexity of combustion and emission formation modeling.^18,19 Furthermore, detailed physical models are typically too computationally intensive for use in real-time engine applications and are often linearized around a specific operating point for implementation in processor based engine controllers.^20,21 This has led researchers to consider machine learning (ML) based methods which help to provide an accurate model while minimizing the computational requirements.

ML techniques have been widely used for addressing engine performance, emission modeling and control.^22–24 To this end, different ML methods have been tested and used for HCCI performance, combustion phasing, and emission modeling using an Artificial Neural Network (ANN),^25–29 Extreme Learning Machine (ELM),^30–33 Bayesian Neural Network (BNN),³⁴ Deep Neural Networks (DNN),³⁵ and Least Squared Support Vector Machine (LS-SVM).^36–38 Among these methods, most researchers have focused on the prediction of engine performance, consisting of Indicated Mean Effective Pressure (IMEP) and CA50 (crank angle where 50% of heat energy has been released)^{27,30–33,36–38} while a limited number of researchers have studied emission prediction.^25,26,28,29 ANN has been the ML method of choice and has been widely used for emission and performance prediction for Spark Ignition (SI) and Compression Ignition (CI) engines.^28,39–41 This has led researchers to consider ANN the baseline ML method for engine modeling and control implementation. However, to create an accurate model ANN requires a large data set which requires significant engine testing time and results in high testing costs.

One of the most powerful machine learning methods that has shown remarkable accuracy in the prediction of Internal Combustion Engine (ICE) emissions and performance is Support Vector Machine (SVM).^{22,23,39,42,43} SVM is a machine learning approach which has been used for both classification and regression problems.^44,45 By providing the SVM with a set of input and output pairs, it approximates a hyperplane to retrieve a pattern that exists between given inputs and the corresponding outputs. For HCCI, SVM has been used to predict combustion phasing, misfire, and high pressure rise rates.⁴⁶ For example, it has accurately predicted CA50 with an error of 1.9% for transient load changes,⁴⁶ and cyclic combustion variability.⁴⁷ Transit Linear Parameter Varying (LPV) based models were developed to predict CA50 and IMEP.^36–38 The accurate prediction capabilities and low computational requirements of SVM has proven it is a powerful technique for predicting the complex and highly nonlinear phenomena of other systems and this study looks to apply this strategy to emission formation in HCCI engines and compare the results to ANN. SVM has been used to predict the performance and emissions of SI^48,49 and diesel^22,23,42,43 engines but to date has not been comprehensively investigated for HCCI emissions prediction.

Hyperparameter tuning, is typically the most tricky part of every machine learning approach. In ANN, a grid search for the number of neurons and number of hidden layers is usually used to find optimal hyperparameters. Depending on the depth of the network, a random search could be added during optimization.²⁶ Metaheuristic approaches were also used to tune ANN hyperparameters such as Particle Swarm Optimization (PSO)^50,51 and Genetic Algorithm (GA).⁵² Compared with GA, PSO is a relatively new heuristic search method based on collaborative behavior and swarming in biological populations. Both GA and PSO are population-based search approaches that depend on information sharing among their population members. Although PSO and GA have a similar performance in terms of the accuracy of the solution, it has been proven that PSO is computationally more efficient, and requires fewer parameters that need to be defined for optimization.^53,54 In SVM, there are three main parameters to tune which are tolerated error, kernel function parameters, and regularization coefficient. In this study, the PSO algorithm is used to tune these hyperparameters.

In this paper, a SVM technique is used to find correlations between key manipulated variables of an HCCI engine and the engine out emissions. First the linear SVM and nonlinear SVM will be compared to an ANN model for four engine out emissions. Second, a detailed investigation into the feature selection will be performed to identify which engine inputs should be used for SVM design. Then finally, the chosen model will be tested for its prediction capabilities. Knowledge about the correlation between process inputs and emissions can be then used in future control applications for HCCI model based emissions control strategies.

With the overall goal of creating a control oriented emissions prediction model for HCCI combustion. The main contributions of this work can be summarized as follows:

• Developing a novel homogeneous charge compression ignition emission model using metaheuristic optimization based SVM,

• Implementing particle swarm optimization method for optimizing SVM hyperparameters,

• Analyzing feature sets based on physical understanding of the HCCI combustion process for each engine out emission component (CO, CO₂, HC, and NO_x),

• Evaluating the linear and nonlinear kernels for SVM and providing a detailed comparison to an artificial neural network,

• Proposing an accurate steady state simple emissions model design for future control applications.

Experimental setup

A Single Cylinder Research Engine (SCRE) outfitted with a fully variable Electro-Magnetic Valve Train (EMVT) is used to collect the experimental data. The flexibility of the valve timing allows for engine operation with various valve strategies including symmetric Negative Valve Overlap (NVO), which is used in this paper. Symmetric NVO is chosen where Exhaust Valve Closing (EVC) and Intake Valve Opening (IVO) are varied evenly around gas exchange Top Dead Center (TDC). This ensures that no intake or exhaust re-breathing takes place. The NVO duration can be changed every cycle if desired using this valve train.

Fuel is directly injected into the SCRE through a piezoelectric outward-opening hollow cone injector. Conventional European Research Octane Number (RON) 96 gasoline containing 10% ethanol is used and the fuel pressure is maintained at 100 bar. Cylinder pressure is measured by a Kistler 6041 piezoelectric pressure transducer which is used to calculate the Indicated Mean Effective Pressure (IMEP) as in Heywood et al.⁵⁶ The air-fuel equivalence ratio $\lambda$ is measured by a production Bosch wide-band oxygen sensor.

The exhaust gas measurement is done using two measurement devices. The first is an Eco Physics CLD700REht for Nitrogen Oxide (NO) and Oxides of Nitrogen (NOx) measurement and the second is a Rosemount NGA 2000 which provides measurements of unburnt Hydrocarbons (HC), Carbon Monoxide (CO), Carbon Dioxide (CO₂), and Oxygen (O₂) concentration. The emission analysis equipment provides an averaged emission reading due to the transport delay and mixing during transport. Therefore, the emissions values presented are average emissions over a 30 s measurement for a steady state operating point. The specifications of the emission measurement system are provided in Table 1 with full details provided in Gordon et al.¹⁰

Table 1.

Accuracy of emissions measurement system.⁵⁵

Gas	Maximum	Detection level	Resolution	Accuracy
NOx	10,000 ppm	0.1 ppm	0.1 ppm	1% of reading
uHC	5%	0.04 ppm	0.1 ppm	1% of reading
CO (low)	2500 ppm	0.1ppm	0.1 ppm	1% of reading
CO (high)	10%	0.1%	0.1%	1% of reading
CO2	18%	0.1%	0.1%	1% of reading
O2	25%	0.1%	0.1%	1% of reading

It is well understood that HCCI has a narrow operating range and performs best within a specific operating conditions.^57–59 At first this appears as a disadvantage, however, with the transition to hybrid and electric range extender applications a few efficient load and speed operating points are acceptable as the electric systems are used to handle transient loads. To simulate a steady state operating point the engine is operated in a conditioned environment that keeps rotational speed, load, intake pressure and temperature, oil and coolant temperature, and exhaust pressure constant to minimize the effect of these confounding variables. As only one load and speed is selected this helps to reduce the experimental space in order to show the effectiveness of the proposed SVM based model. The engine geometry and chosen operating condition are listed in Table 2.

Table 2.

Single cylinder research engine parameters.¹⁰

Parameter	Value
Displacement volume	0.499 l
Stroke	90 mm
Bore	84 mm
Compression ratio	12:1
Exhaust valve opening	160° aTDC
Intake valve closing	545° aTDC
Intake/exhaust pressure	1014 ± 4 mbar
Oil and coolant temperature	100 ± 1°C
Engine speed	1500 ± 5 rpm
Fuel rail pressure	100 ± 2 bar
Intake temperature	52 ± 1°C

Active input factors to the HCCI combustion process include injected fuel mass, injection timing, and valve timings. These variables were chosen to be varied as they significantly affect the combustion process and the resulting engine out emissions at a given load and speed operating point. They also significantly affect the combustion stability of the HCCI process which has a significant effect on the engine out emissions.^10,60 As the HCCI process is extremely sensitive to operating conditions a relatively small change in input parameters results in a significant change in engine output parameters. These engine input parameters have also been explored in previous works regarding HCCI emissions modeling.⁴⁰ The variation in engine inputs can be seen in Table 3.

Table 3.

Variation in HCCI engine input parameters.

Engine Input	Min	Max	Mean
SOI (°aTDC)	455.9	495	473.4
$m_f$ (mg)	2.7	2.96	2.86
NVO (°)	173	201.6	187.7

Methodology

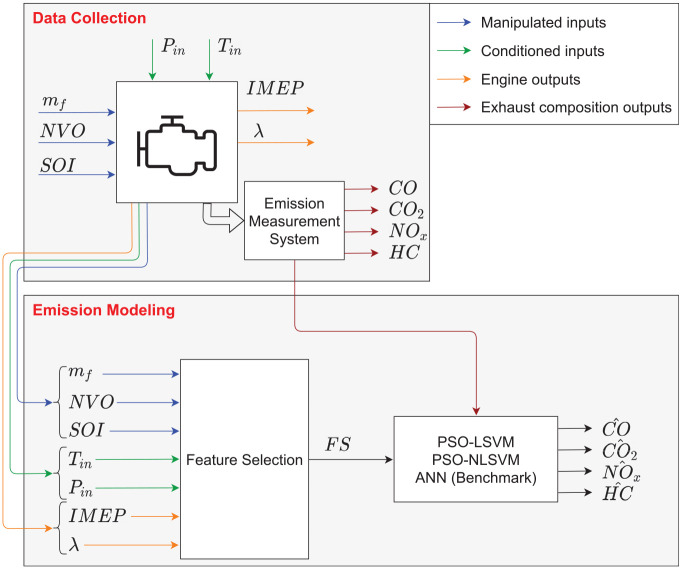
In this section, the main methodology of this study will be discussed. First, the required data for emission modeling of the HCCI engine was collected as discussed in Section 2. Figure 1 schematically shows the data collection and emission modeling. During data collection, fuel amount ( $m_f$ ), negative valve overlap duration ( $\mathrm{NVO}$ ), and start of fuel injection ( $\mathrm{SOI}$ ) are system’s main inputs while intake pressure ( $P_{\mathrm{in}}$ ) and intake temperature ( $T_{\mathrm{in}}$ ) are conditioned to keep them constant during data collection. The power output of the engine is represented by IMEP and the operating points are chosen to keep the output load approximately constant for all tests. There is a slight variation in IMEP over the operating range of 3.5 ± 0.2 bar. However, as IMEP is held relatively constant over the sweep of $m_f$ , SOI, and NVO inputs this results in varying combustion efficiency and a trade-off between different emissions.

Figure 1.

Schematic of data collection and proposed emission modeling using PSO-based LSVM and NLSVM.

Then, $\lambda$ , CO, CO2, NOx, and HC emission were collected. All manipulated and conditioned input and engine output variables in the emission modeling section are given to a data-driven system as inputs. Then different feature sets by interpolation of these inputs are created, and these features are the main inputs of the PSO-based SVM method. In this study, both Nonlinear SVM (NLSVM) and Linear SVM (LSVM) are considered for emission modeling using different feature sets, and PSO is used to optimize the hyperparameters of both the LSVM and NSVM. This method has been compared with the benchmark ML emission modeling, Artificial Neural Network (ANN) as proposed in literature.²⁶

Support vector machine

The main idea of the regression form of SVM, also called Support Vector Regression (SVR) is to find an optimal hyperplane, $\mathbf{y}\mathbf{(}{\mathbf{u}}_{\mathbf{i}}\mathbf{)}$ , such that $\mathbf{y}\mathbf{(}{\mathbf{u}}_{\mathbf{i}}\mathbf{)}$ is as flat as possible and it has the maximum deviation of $ϵ$ for all training data.⁴⁵ In other words, the optimization problem is to find the flattest function with the maximum error tolerance $ϵ$ . Therefore, the optimal hyperplane which describes the training data, { ${\mathbf{u}}_{\mathbf{i}},{\mathbf{z}}_{\mathbf{i}}$ }, can be defined as:

$$\begin{array}{c}\mathbf{y}\mathbf{(}{\mathbf{u}}_{\mathbf{i}}\mathbf{)}={\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}+\mathbf{b}\hfill \end{array}$$ (1)

where ${\mathbf{u}}_{\mathbf{i}}$ and ${\mathbf{z}}_{\mathbf{i}}$ are input and target of the training data and $\mathbf{w}$ and $\mathbf{b}$ are found by solving the SVM algorithm for regression problems. The optimization problem to find the optimum hyperplane $\mathbf{y}\mathbf{(}{\mathbf{u}}_{\mathbf{i}}\mathbf{)}$ is defined as:

$$\begin{array}{c}\begin{array}{cc}\mathrm{Minimize}:\hfill & \frac{1}{2}||\mathbf{w}|{|}_2^2\hfill \\ \multicolumn{1}{c}{\mathrm{Subject}\mathrm{to}:}& \{\begin{array}{c}{\mathbf{z}}_{\mathbf{i}}-{\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}-\mathbf{b}\le ϵ\hfill \\ \multicolumn{1}{c}{{\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}+\mathbf{b}-{\mathbf{z}}_{\mathbf{i}}\le -ϵi=1,...,n}\end{array}\hfill \end{array}\hfill \end{array}$$ (2)

where the flatest function is achieved by minimizing $\frac{1}{2}||\mathbf{w}|{|}_2^2$ and the tolerance is achieved by solving for the defined constraints. A schematic of SVM regression is shown in Figure 2 where the main objective of SVM is shown as the orange line estimating a proper function by the maximum deviation of $ϵ$ .

Figure 2.

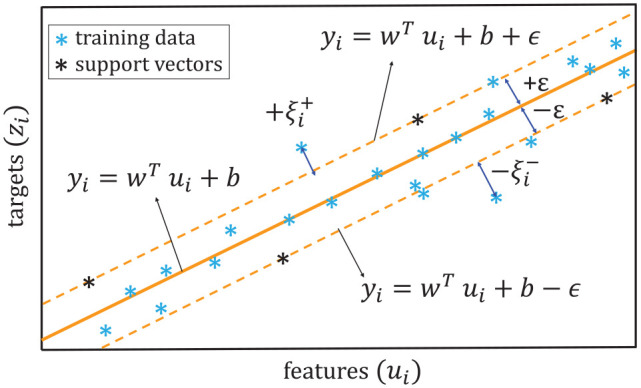
SVM regression and support vectors (based on Norouzi et al.²²).

For those data points within a defined tolerance ( $ϵ$ ), $\mathbf{y}\mathbf{(}{\mathbf{u}}_{\mathbf{i}}\mathbf{)}$ has been found such that it predicts all pairs of learning data within a defined error. If all the data points lay within the defined tolerance, the optimization problem is feasible. However, occasionally the algorithm cannot converge within the defined constraints and the current optimization problem becomes infeasible. To overcome the infeasibility of equation (2), a penalty variable ( ${\zeta }_i$ ) or so called slack variable has been added to the original optimization problem as:

$$-ϵ-{\zeta }_i^{-}\le {\mathbf{z}}_{\mathbf{i}}-{\mathbf{y}}_{\mathbf{i}}\le ϵ+{\zeta }_i^{+}$$ (3)

To consider these penalty variables, the Soft Margin Loss Function (SMLF) has been added to optimization problem which is defined as⁶¹:

$$\begin{array}{c}\begin{array}{cc}\mathrm{Minimize}:\hfill & \frac{1}{2}||\mathbf{w}|{|}_2^2+C\sum _{i=1}^n({\zeta }_{\mathbf{i}}^{+}+{\zeta }_{\mathbf{i}}^{-})\hfill \\ \multicolumn{1}{c}{\mathrm{Subject}\mathrm{to}:}& \{\begin{array}{c}{\mathbf{z}}_{\mathbf{i}}-{\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}-\mathbf{b}\le ϵ+{\zeta }_{\mathbf{i}}^{+}\hfill \\ \multicolumn{1}{c}{{\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}+\mathbf{b}-{\mathbf{z}}_{\mathbf{i}}\le ϵ+{\zeta }_{\mathbf{i}}^{-}i=1,...,n}\\ \multicolumn{1}{c}{{\zeta }_{\mathbf{i}}^{-},{\zeta }_{\mathbf{i}}^{+}\ge 0}\end{array}\hfill \end{array}\hfill \end{array}$$ (4)

where $C$ is a regulatory parameter to set the trade off between tolerated error and the smoothness of the model.

To consider constraints in the optimization problem the Lagrangian function is calculated as

$$\begin{array}{c}\multicolumn{1}{c}{L=\frac{1}{2}||\mathbf{w}|{|}_2^2+C\sum _{i=1}^N({\zeta }_i^{-}+{\zeta }_i^{+})}\\ -\sum _{i=1}^N{\alpha }_i^{+}(-{\mathbf{z}}_{\mathbf{i}}+{\mathbf{y}}_{\mathbf{i}}+ϵ+{\zeta }_i^{+})-\sum _{i=1}^N{\mu }_i^{+}{\zeta }_i^{+}\hfill \\ -\sum _{i=1}^N{\alpha }_i^{-}({\mathbf{z}}_{\mathbf{i}}-{\mathbf{y}}_{\mathbf{i}}+ϵ+{\zeta }_i^{-})-\sum _{i=1}^N{\mu }_i^{-}{\zeta }_i^{-}\hfill \end{array}$$ (5)

where ${\alpha }_i^{+}$ , ${\alpha }_i^{-}$ , ${\mu }_i^{+}$ , and ${\mu }_i^{-}$ are the non-negative Lagrangian Multipliers. The Lagrangian is solved by calculating the partial differential with respect to the optimization variables as

$$\frac{\partial L}{\partial \mathbf{w}}=0\to w=\sum _{i=1}^N({\alpha }_i^{+}-{\alpha }_i^{-}){\mathbf{u}}_{\mathbf{i}}$$ (6a)

$$\frac{\partial L}{\partial \mathbf{b}}=0\to \sum _{i=1}^N({\alpha }_i^{+}-{\alpha }_i^{-})=0$$ (6b)

$$\frac{\partial L}{\partial {\zeta }_i^{+}}=0\to {\alpha }_i^{+}+{\mu }_i^{+}=C$$ (6c)

$$\frac{\partial L}{\partial {\zeta }_i^{-}}=0\to {\alpha }_i^{-}+{\mu }_i^{-}=C$$ (6d)

where equations (6a)–(6c) are SVM expansion, bias constraints, and the box constraint, respectively.²² By substituting equations (6a)–(6d) into equation (5) the Quadratic Programming (QP) problem can be defined by

$$\begin{array}{c}\mathrm{Minimize}:L=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N({\alpha }_i^{+}-{\alpha }_i^{-})({\alpha }_j^{+}-{\alpha }_j^{-}){{\mathbf{u}}_{\mathbf{i}}}^T{\mathbf{u}}_{\mathbf{j}}\hfill \\ -\sum _{i=1}^N({\alpha }_i^{+}-{\alpha }_i^{-}){\mathbf{z}}_{\mathbf{i}}+ϵ\sum _{i=1}^N({\alpha }_i^{+}+{\alpha }_i^{-})\hfill \\ \mathrm{Subject}\mathrm{to}:\{\begin{array}{c}\sum _{i=1}^N({\alpha }_i^{+}-{\alpha }_i^{-})=0\hfill \\ \multicolumn{1}{c}{0\le {\alpha }_i^{+}\le C}\\ \multicolumn{1}{c}{0\le {\alpha }_i^{-}\le C}\end{array}\hfill \end{array}$$ (7)

which can be used in a compact version following⁶²:

$$\begin{array}{c}\mathrm{Minimize}:\frac{1}{2}{\alpha }^T\mathcal{H}\alpha +f^T\alpha \hfill \\ \mathrm{Subject}\mathrm{to}:A_{\mathrm{eq}}\alpha =B_{\mathrm{eq}}\hfill \end{array}$$ (8)

where

$$\begin{array}{c}\alpha =\left[\begin{array}{c}{\alpha }^{+}\hfill \\ \multicolumn{1}{c}{{\alpha }^{-}}\end{array}\right],\mathcal{H}=\left[\begin{array}{c}H-H\hfill \\ \multicolumn{1}{c}{-HH}\end{array}\right],f=\left[\begin{array}{c}-{\mathbf{z}}_{\mathbf{i}}+ϵ\hfill \\ \multicolumn{1}{c}{{\mathbf{z}}_{\mathbf{i}}+ϵ}\end{array}\right],\hfill \\ H=\left[{{\mathbf{u}}_{\mathbf{i}}}^T{\mathbf{u}}_{\mathbf{j}}\right],{\mathbf{A}}_{\mathbf{eq}}=[1...1-1...-1],{\mathbf{B}}_{\mathbf{eq}}=\left[0\right]\hfill \end{array}$$ (9)

In order to calculate $\mathbf{b}$ , the Karush–Kuhn–Tucker (KKT) conditions are used where^63,64:

$${\alpha }_i^{+}(-{\mathbf{z}}_{\mathbf{i}}+{\mathbf{y}}_{\mathbf{i}}+ϵ+{\zeta }_i^{+})=0$$ (10a)

$${\alpha }_i^{-}({\mathbf{z}}_{\mathbf{i}}-{\mathbf{y}}_{\mathbf{i}}+ϵ+{\zeta }_i^{-})=0$$ (10b)

$${\mu }_i^{+}{\zeta }_i^{+}=(C-{\alpha }_i^{+}){\zeta }_i^{+}$$ (10c)

$${\mu }_i^{-}{\zeta }_i^{-}=(C-{\alpha }_i^{-}){\zeta }_i^{-}$$ (10d)

must be fulfilled at the optimum point. Based on these equations, only five following cases are possible as

$${\alpha }_i^{+}={\alpha }_i^{-}=0$$ (11a)

$$0<{\alpha }_i^{+}<C,{\alpha }_i^{-}=0$$ (11b)

$$0<{\alpha }_i^{-}<C,{\alpha }_i^{+}=0$$ (11c)

$${\alpha }_i^{+}=C,{\alpha }_i^{-}=0$$ (11d)

$${\alpha }_i^{-}=C,{\alpha }_i^{+}=0$$ (11e)

To find the support vector, where $|{\mathbf{z}}_{\mathbf{i}}-{\mathbf{y}}_{\mathbf{i}}|$ is exactly equal to $ϵ$ , only $0<{\alpha }_i^{+}<C,{\alpha }_i^{-}=0$ and $0<{\alpha }_i^{-}<C,{\alpha }_i^{+}=0$ must be fulfilled. Therefore, $\mathbf{b}$ can be calculated as

$$\mathbf{b}=\frac{1}{|S|}\sum _{i\in S}^S({\mathbf{z}}_{\mathbf{i}}-{\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}-\mathrm{sign}({\alpha }_i^{+}-{\alpha }_i^{-})ϵ)$$ (12)

where $S$ represents the support vector set based on equations (18) and (19) as:

$$S=\{i|0<{\alpha }_i^{-}+{\alpha }_i^{+}<C\}$$ (13)

Therefore, by solving equations (12) and (8) and substituting $\mathbf{w}$ and $\mathbf{b}$ into equation (1), $\mathbf{y}\mathbf{(}{\mathbf{u}}_{\mathbf{i}}\mathbf{)}$ is obtained as²²:

$$\begin{array}{c}\multicolumn{1}{c}{\mathbf{y}\mathbf{(}\mathbf{u}\mathbf{)}=\sum _{i=1}^N({\alpha }_i^{+}-{\alpha }_i^{-}){{\mathbf{u}}_{\mathbf{i}}}^T\mathbf{u}}\\ +\frac{1}{|S|}\sum _{i\in S}^S({\mathbf{z}}_{\mathbf{i}}-{\mathbf{w}}^T{\mathbf{u}}_{\mathbf{i}}-\mathrm{sign}({\alpha }_i^{+}-{\alpha }_i^{-})ϵ)\hfill \end{array}$$ (14)

Kernel tricks

Although the structure of the dot product in equation (14), is a simple linear kernel, however, it fails to capture any nonlinear behavior of the process. Therefore, by replacing the linear kernel with a nonlinear kernel, using so called kernel tricks, brings nonlinear pattern recognition at a reasonable computational cost.⁶⁵ Thus, the inner product of equation (14), ${{\mathbf{u}}_{\mathbf{i}}}^T{\mathbf{u}}_{\mathbf{j}}$ , is replaced by nonlinear kernel as $K({\mathbf{u}}_{\mathbf{i}},{\mathbf{u}}_{\mathbf{j}})$ . In this study the RBF (Radial basis function) kernel function is used as

$$\begin{array}{cc}K({\mathbf{u}}_{\mathbf{i}},{\mathbf{u}}_{\mathbf{j}})\hfill & =\exp (\frac{||{\mathbf{u}}_{\mathbf{i}}-{\mathbf{u}}_{\mathbf{j}}|{|}_2^2}{2{\sigma }^2})\hfill \end{array}$$ (15)

where $\sigma$ is the Gaussian variance and $||.|{|}_2$ is the two norm. Therefore, the prediction function, $\mathbf{y}$ is calculated as⁶⁵:

$$\begin{array}{c}\mathbf{y}=\sum _{i=1}^n({\alpha }_i^{+}-{\alpha }_i^{-})K({\mathbf{u}}_{\mathbf{i}},\mathbf{u})+\mathbf{b}\hfill \end{array}$$ (16)

This study examines different interpolations of different features that also play the precise role of the polynomial kernel. Therefore, three main kernel types, including linear, RBF, and polynomial are considered in this study.

Hyperparameters optimization: Particle swarm optimization (PSO)

To calculate the hyperparameters for both the LSVM and the NLSVM, Particle Swarm Optimization (PSO) has been used. The LSVM and NLSVM hyperparameters are $(C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}})$ and $(C_{\mathrm{NLSVM}},{ϵ}_{\mathrm{NLSVM}},\sigma )$ , respectively. PSO is an optimization method that optimizes a candidate solution iteratively with regard to the given cost or merit function.^66,67 To train the SVM models, a total of 70 engine operating points were available. Then 80% of the data was used for training, 10% for cross-validation, and 10% as test data. Cross-validation data is used to tune the hyperparameters of the optimization methods. The cost function to find the LSVM and NLSVM is defined based on the Mean Square Error (MSE) of training and cross validation datasets. Hence, the hyperparameter calculation is defined as the following optimization problem:

$$\begin{array}{c}[C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}}]=\arg \min (\frac{1}{n_{\mathrm{tr}}}\sum _{i=1}^{n_{\mathrm{tr}}}(z_{\mathrm{tr},i}-y_{\mathrm{tr},i}{)}^2\hfill \\ +\frac{1}{n_{\mathrm{cv}}}\sum _{i=1}^{n_{\mathrm{cv}}}(z_{\mathrm{cv},i}-y_{\mathrm{cv},i}{)}^2)\hfill \\ [C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}},\sigma ]=\arg \min (\frac{1}{n_{\mathrm{tr}}}\sum _{i=1}^{n_{\mathrm{tr}}}(z_{\mathrm{tr},i}-y_{\mathrm{tr},i}{)}^2\hfill \\ +\frac{1}{n_{\mathrm{cv}}}\sum _{i=1}^{n_{\mathrm{cv}}}(z_{\mathrm{cv},i}-y_{\mathrm{cv},i}{)}^2)\hfill \end{array}$$ (17)

Where $C_{\mathrm{LSVM}}$ and $C_{\mathrm{NLSVM}}$ are the regulatory parameters for linear SVM and nonlinear kernel SVM, respectively. The index $\mathrm{tr}$ and $\mathrm{cv}$ represent training and cross-validation data set and $n$ denotes number of data points in the data-set (i.e. $n_{\mathrm{tr}}$ is number of training data points). The tolerated error for linear SVM is ${ϵ}_{\mathrm{LSVM}}$ and for nonlinear kernel SVM is ${ϵ}_{\mathrm{NLSVM}}$ . The target data and prediction data are illustrated by $z$ and $y$ , respectively and $\sigma$ is the Gaussian variance of RBF kernel. The PSO algorithm was used to solve for the hyperparameters. The PSO-based SVM algorithm is shown in Algorithm 1 and Algorithm 2 for linear and RBF kernel of SVM, respectively. The number of particles in the swarm set for both the LSVM and NLSVM model is set to 200 while the maximum iteration number is limited to 400 and 600 for LSVM and NLSVM, respectively.

Algorithm 1: PSO based linear kernel SVM algorithm

Result: HCCI emission model: $\mathbf{y}\mathbf{(}\mathbf{u}\mathbf{)}$ training data set: $\{\mathbf{u},\mathbf{z}\};$ splitting data set: training $\{{\mathbf{u}}_{\mathrm{tr}},{\mathbf{z}}_{\mathrm{tr}}\}$ , cross-validation   $\{{\mathbf{u}}_{\mathrm{cv}},{\mathbf{z}}_{\mathrm{cv}}\}$ , and test $\{{\mathbf{u}}_{\mathrm{ts}},{\mathbf{z}}_{\mathrm{ts}}\};$ Random hyperparameters: $C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}};$ Run Quadratic Programming of equation (11) to calculate ${\alpha }^{-}$  and ${\alpha }^{+};$ Calculate support vector sets based on equation (13) Calculate model based on random hyperparameters using  Equation (14) Set PSO options: $\mathtt{MaxIteration}{\mathtt{s}}^{\mathtt{1}}$ ,   $\mathtt{MaxStallIteration}{\mathtt{s}}^{\mathtt{2}}$ , $\mathtt{FunctionToleranc}{\mathtt{e}}^{\mathtt{3}}$ ,  and $\mathtt{SwarmSiz}{\mathtt{e}}^{\mathtt{4}}$ ; whilei∈ $\mathtt{MaxIterations}$ or $d_5$ over   $\mathtt{MaxStallIterations}$ ≥ $\mathtt{FunctionTolerance}$  do   Calculate cost function:    $\begin{array}{c}J(C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}})=(\frac{1}{n_{\mathrm{tr}}}\sum _{i=1}^{n_{\mathrm{tr}}}(z_{\mathrm{tr},i}-y_{\mathrm{tr},i}{)}^2+\hfill \\ \frac{1}{n_{\mathrm{cv}}}\sum _{i=1}^{n_{\mathrm{cv}}}(z_{\mathrm{cv},i}-y_{\mathrm{cv},i}{)}^2)\hfill \end{array}$   Run PSO algorithm to minimize $J(C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}})$ and    find hyperparameters   Update hyperparameters: $C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}}$   Run Quadratic Programming of equation (11) to calculate ${\alpha }^{-}$    and ${\alpha }^{+}$   Calculate support vector sets based on equation (13)   Calculate model based on Updated hyperparameters    using equation (14)    $\mathtt{i}=i+1$  end 1. Maximum number of iterations for optimization ( $=400$ ), 2. Positive integer ( $=20$ ), 3. Non-negative scalar: Iterations end when the relative change in cost function value over the last MaxStallIterations iterations is less than FunctionTolerance $=1e-6$ , 4. Number of particles in the swarm $=200$ , 5. Relative change

Algorithm 2: PSO based RBF kernel SVM algorithm

Result: HCCI emission model: $\mathbf{y}\mathbf{(}\mathbf{u}\mathbf{)}$ training data set: $\{\mathbf{u},\mathbf{z}\}$ splitting data set: training $\{{\mathbf{u}}_{\mathrm{tr}},{\mathbf{z}}_{\mathrm{tr}}\}$ , cross-validation   $\{{\mathbf{u}}_{\mathrm{cv}},{\mathbf{z}}_{\mathrm{cv}}\}$ , and test $\{{\mathbf{u}}_{\mathrm{ts}},{\mathbf{z}}_{\mathrm{ts}}\}$ Random hyperparameters: $C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}},\sigma$ Run Quadratic Programming of equation (11) to calculate ${\alpha }^{-}$  and ${\alpha }^{+}$ Calculate support vector sets based on equation (13) Calculate model based on random hyperparameters using  Equations (15) and (16) Set PSO options: $\mathtt{MaxIteration}{\mathtt{s}}^{\mathtt{1}}$ ,   $\mathtt{MaxStallIteration}{\mathtt{s}}^{\mathtt{2}}$ , $\mathtt{FunctionToleranc}{\mathtt{e}}^{\mathtt{3}}$ ,  and $\mathtt{SwarmSiz}{\mathtt{e}}^{\mathtt{4}}$ ; whilei∈ $\mathtt{MaxIterations}$ or $d_5$ over   $\mathtt{MaxStallIterations}$ ≥ $\mathtt{FunctionTolerance}$  do   Calculate cost function:    $\begin{array}{c}J(C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}},\sigma )=(\frac{1}{n_{\mathrm{tr}}}\sum _{i=1}^{n_{\mathrm{tr}}}(z_{\mathrm{tr},i}-y_{\mathrm{tr},i}{)}^2+\hfill \\ \frac{1}{n_{\mathrm{cv}}}\sum _{i=1}^{n_{\mathrm{cv}}}(z_{\mathrm{cv},i}-y_{\mathrm{cv},i}{)}^2)\hfill \end{array}$   Run PSO algorithm to minimize $J(C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}},\sigma )$    and find hyperparameters   Update hyperparameters: $C_{\mathrm{LSVM}},{ϵ}_{\mathrm{LSVM}},\sigma$   Run Quadratic Programming of equation (11) to calculate ${\alpha }^{-}$    and ${\alpha }^{+}$   Calculate support vector sets based on equation (23)   Calculate model based on Updated hyperparameters    using equations (25) and (26)    $\mathtt{i}=i+1$  end 1. Maximum number of iterations for optimization ( $=600$ ), 2. Positive integer ( $=20$ ), 3. Non- negative scalar: Iterations end when the relative change in cost function value over the last MaxStallIterations iterations is less than FunctionTolerance $=1e-6$ , 4. Number of particles in the swarm $=200$ , 5. Relative change

Artificial neural network (ANN)

In this study, the proposed methods will be compared to the conventional ANN methods presented in literature. A feed-forward backpropagation network with single hidden layer and 15 neurons in each hidden layer using Levenberg–Marquardt backpropagation training method has been used in this study. This model with the same structure and number of neurons was previously developed for a single cylinder HCCI Ricardo engine.²⁶ This is a relatively shallow network which was chosen as there is a limited amount of data available. The model training has been completed using the same parameters as used in Rezaei et al.²⁶

Feature selection: Physical insights

A steady state emissions model is developed to predict the steady-state HCCI engine emissions values of carbon dioxide (CO₂), carbon monoxide (CO), unburnt hydrocarbons (HC), and nitrogen oxides (NO_x). The structure of the model is defined by equation (1) where $\mathbf{w}$ and $\mathbf{b}$ are obtained by solving the SVM algorithm for a given training data set, { $\overline{\mathbf{u}},\mathbf{z}$ }. Here, $\overline{\mathbf{u}}$ is the normalized Feature Set (FS). In total five different FS are tested. The training target set, $\mathbf{z}$ , is defined based on measured steady-state CO₂, CO, HC, and NO_x values. To develop the model, 70 experimental data points are available where 56 points (80%) are used to train the model and 14 (20%) points to test the model.

Due to the lack of direct ignition control in HCCI, unlike conventional spark ignition in gasoline engines, the start of combustion depends on the in-cylinder conditions including pressure, temperature and gas mixture. However, these factors can only be influenced indirectly. The inputs used in this publication to set cylinder conditions and therefore affect the combustion are: Negative Valve Overlap ( $\mathrm{NVO}$ ); Injected Fuel Mass per cycle ( $m_f$ ); and Start of Injection ( $\mathrm{SOI}$ ).

Symmetric NVO is used to change the percentage of fresh air and exhaust gas within the cylinder, called Exhaust Gas Recirculation (EGR). This changes both the amount of oxygen in the cylinder as well the temperature of the cylinder charge. Generally, a lean mixture is desired for reduced NO_x emissions, however, at very lean mixtures the fuel flammability limit of the fuel may be exceeded leading to combustion instability which results in high cyclic variability and increased HC emissions. NVO also impacts the cylinder temperature after compression, where a higher cylinder temperature results in an earlier auto-ignition process. The injected fuel mass directly changes the amount of fuel that is added to the cylinder. However, it is important to note that some unburnt fuel is transferred between cycles due to the trapped EGR within the cylinder. As shown in¹⁷ the amount of transferred fuel changes depending on the combustion efficiency of the last cycle. The start of injection impacts the mixture homogeneity and can lead to stratified mixtures. This has an impact on the start of combustion as well as the emissions levels. These three parameters were chosen to be varied as they provide a wide range of cylinder conditions before combustion.

Additional factors that are held as constant as possible are: intake temperature ( $T_{\mathrm{in}}$ ); intake pressure ( $P_{\mathrm{in}}$ ); and indicated mean effective pressure ( $\mathrm{IMEP}$ ) which is representative of applied engine load. $\mathrm{IMEP}$ , $T_{\mathrm{in}}$ , and $P_{\mathrm{in}}$ are active input factors to the HCCI process but they were controlled for this measurement set to reduce the number of input variables. These three factors are included to account for unwanted fluctuations, and to provide a meaningful comparison between different operating conditions. For modeling in this work the measured lambda value is used, however, it can also be accurately estimated using measured intake air flow and injected fuel demand or calculated using an online gas exchange model making it a causal variable which is useful for future control applications.¹⁷

The first sets use seven inputs to create a linear model, L7. A first extension of the FS is considering cross correlations between the variables ( $m_f\times \mathrm{NVO},m_f\times \mathrm{SOI},\mathrm{NVO}\times \mathrm{SOI},\lambda \times \mathrm{NVO},\lambda \times \mathrm{SOI},\lambda \times m_f$ ) resulting in the L13 FS. The cross correlations with $T_{\mathrm{in}}$ , $P_{\mathrm{in}}$ , and $\mathrm{IMEP}$ are not taken into account as to not over interpret the effect of possible fluctuations. Then higher order correlations are also considered by adding the squares of the input variables, FS S14. Additionally, two more FS are added (S20 and S26) that consider the square of the cross correlations. Details of the five FS’s can be found in Table 4. From a machine learning point of view, these FS’s plays the exact role of a polynomial feature set. The only difference is that the redundant higher dimensional feature has been removed based on physical insight expertise.

Table 4.

Features $u_1-u_{26}$ for the five different feature sets L7–S26. $u_1-u_7$ are linear features, $u_8-u_{14}$ are squared features, $u_{15}-u_{20}$ are cross correlations, and $u_{21}-u_{26}$ are the squared cross correlations.

name → feature ↓	L7	L13	S14	S20	S26
$u_1=m_f$	x	x	x	x	x
$u_2=\mathrm{NVO}$	x	x	x	x	x
$u_3=\mathrm{SOI}$	x	x	x	x	x
$u_4=T_{\mathrm{in}}$	x	x	x	x	x
$u_5=P_{\mathrm{in}}$	x	x	x	x	x
$u_6=\mathrm{IMEP}$	x	x	x	x	x
$u_7=\lambda$	x	x	x	x	x
$u_8=m_f^2$			x	x	x
$u_9=\mathrm{NV}{O}^2$			x	x	x
$u_{10}=\mathrm{SO}{I}^2$			x	x	x
$u_{11}=T_{\mathrm{in}}^2$			x	x	x
$u_{12}=P_{\mathrm{in}}^2$			x	x	x
$u_{13}=\mathrm{IME}{P}^2$			x	x	x
$u_{14}={\lambda }^2$			x	x	x
$u_{15}=m_f\times \mathrm{NVO}$		x		x	x
$u_{16}=m_f\times \mathrm{SOI}$		x		x	x
$u_{17}=\mathrm{NVO}\times \mathrm{SOI}$		x		x	x
$u_{18}=\lambda \times \mathrm{NVO}$		x		x	x
$u_{19}=\lambda \times \mathrm{SOI}$		x		x	x
$u_{20}=\lambda \times m_f$		x		x	x
$u_{21}=(m_f\times \mathrm{NVO}{)}^2$					x
$u_{22}=(m_f\times \mathrm{SOI}{)}^2$					x
$u_{23}=(\mathrm{NVO}\times \mathrm{SOI}{)}^2$					x
$u_{24}=(\lambda \times \mathrm{NVO}{)}^2$					x
$u_{25}=(\lambda \times \mathrm{SOI}{)}^2$					x
$u_{26}=(\lambda \times m_f{)}^2$					x

L stands for linear and S stands for squared.

As the dimensions and the range of the features are quite different, all of the features should be normalized to improve the training performance.⁶⁸ Here the min-max normalization method is used to normalize the features

$$\overline{\mathbf{u}}=\frac{\mathbf{u}-\min (\mathbf{u})}{\max (\mathbf{u})-\min (\mathbf{u})}$$ (18)

All of features from Table 4 are normalized for ANN and SVM methods to eliminate relative orders of magnitude difference between the features. By solving the SVM algorithm for the training data set, { $\overline{\mathbf{u}},\mathbf{z}$ }, the approximate function, ${\mathbf{y}}_{\mathbf{ss}}$ is obtained to predict the steady-state values of CO₂, CO, HC, and NO_x.

Results and discussion

To illustrate the method, the model for the CO emissions will be discussed in detail with the other emissions being similar. The recorded data points are randomly split into three sections where 80% of the collected data is used as training data to develop the models. Then 10% of the data is used for model cross-validation. Training and cross-validation data sets are used to train the model and calculate hyperparamters. In LSVM and NLVM, as discussed in 3.4, the PSO algorithm is employed to calculate the hyperparameters by solving the optimization problem of equation (17). The same training and cross-validation data are used to train an ANN model using Levenberg–Marquardt algorithm. The remaining 10% of the data is allocated for assessment of the models where the same data is used for assessing all models including LSVM, NLSVM, and ANN. To do this, the randomly chosen data points for each of the three data sets is then kept constant between all models and feature sets to allow for a fair comparison.

To rate the model quality the coefficient of determination ( $R^2$ ) is used. It is defined by

$$R^2=1-\frac{\sum {(z_i-y_i)}^2}{\sum {(z_i-\overline{z})}^2}$$ (19)

with $z_i$ being a measured value in the data set, $y_i$ being the models response to the accompanying $z_i$ and $\overline{z}$ being the mean of the measured data. The closer the $R^2$ value is to 1 the better the model fits the data. The $R^2$ estimate of the relationship between the dependent variables based on an independent variable may fail to tell the goodness of fit. Therefore, the Normalized Root Mean Square Error (NRMSE) is used to capture the error between the model and actual values. The Normalized version of RMSE is used to remove the dependency of RMSE to scale output and generalize the model easily. NRMSE is defined by $\frac{\mathrm{RMSE}}{\sigma }$ where $\sigma$ is the standard deviation and $\mathrm{RMSE}$ is defined as $\mathrm{RMSE}=\sqrt{\frac{{\Sigma }_{i=1}^n(y_i-\hat{y})}{n}}$ where $y_i$ is experimental value and $\hat{y}$ is predicted value. This criteria provides a good representation of how far the model prediction is away from the real data. Therefore, the lower the NRMSE the closer the model is to the real value. Both of these methods help to quantify the model fit.

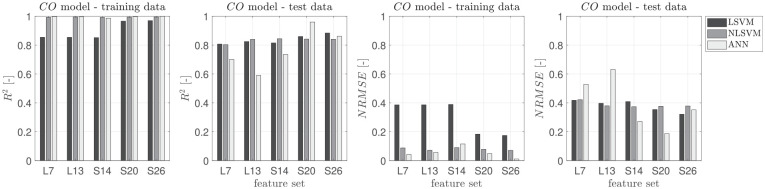
Figure 3 shows both the $R^2$ and NRMSE values for the training and test data for the CO model. As expected the $R^2$ and NRMSE values are the best for the training data as the models were trained on this data set. As the model has never been trained on the testing data this reduced prediction accuracy is expected and provides the best representation of the model fit.

Figure 3.

Comparison between $R^2$ and Normalized RMSE values for CO for NLSVM and LSVM with benchmark ANN method designed based on Rezaei et al.²⁶ in dependence of the different feature sets.

Model comparison

When comparing the coefficients of determination ( $R^2$ ) of the LSVM, NLSVM, and ANN models in Figure 3 a few key differences can be seen. First, when only considering the training data the NLSVM and ANN models result in an improved $R^2$ value over the simplified LSVM model. Although this does not result in a significantly improved model prediction performance when given the test data. Actually, the LSVM outperforms the ANN model in most feature sets. Showing that the ANN model can suffer from over fitting which is not seen with the simple LSVM model when presented with unknown training data. This problem with a small network, such as conventional ANN, can be reduced when using large datasets; however, when limited data is available the traditional machine learning algorithms such as SVM show a better prediction capability.²²

When comparing the different feature sets, all the three models result in fairly consistent prediction accuracy even as the number of features is increased. This is especially true for both linear and non-linear SVM models which only vary by 12.0% and 14.1% $R^2$ as the number of features is increased from 7 to 26. This is likely the result of the SVM algorithm always converging to the global minimum while the ANN model can converge to a local minimum as seen by the decrease in ANN model performance going from L7 to L13. The convergence of the ANN model is highly dependent of the initial choice of weights and bias values. This guarantee of global convergence is one the major advantages of the SVM method.^7,22,42,69 The main reason for global optimization is that SVM uses Quadratic programming, which includes optimizing a function according to linear constraints. As ANN uses Gradient descent, it makes ANN sensitive to randomization of weights parameters. This means that if initial weights put cost function close to a local minimum, the accuracy of the model will never increase past a certain threshold.³⁹ To avoid this, each ANN model is trained in a loop with multiple randomization values, where the randomization is reset until it reaches acceptable accuracy.

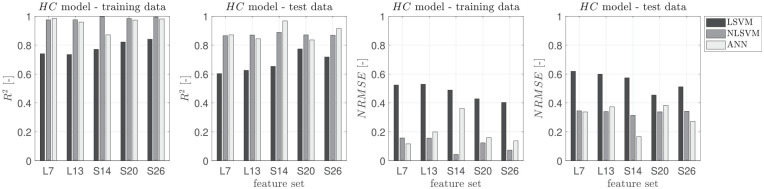
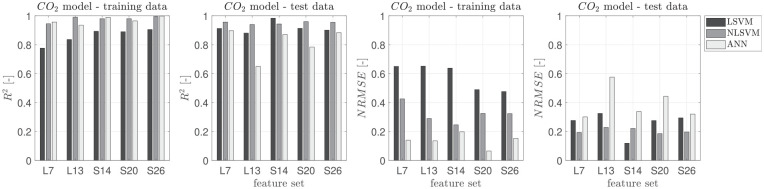
The findings from CO emissions can then be extended to HC, NO_x, and CO₂ as shown in Figures 4 to 6. The trends seen between modeling methods vary slightly between specific emissions as expected due to the physical differences in their production mechanism. To do this, a Criterion for Methods Selection (CMS), $J_{\mathrm{CMS}}(R^2)$ , is defined as

Figure 4.

Comparison between $R^2$ and Normalized RMSE values for HC for NLSVM and LSVM with benchmark ANN method designed based on Rezaei et al.²⁶ in dependence of the different feature sets.

Figure 6.

Comparison between $R^2$ and Normalized RMSE values for CO₂ for NLSVM and LSVM with benchmark ANN method designed based on Rezaei et al.²⁶ in dependence of the different feature sets.

$$J_{\mathrm{CMS}}(R^2)={\overline{R}}_{(\mathrm{FS})}^2-\sigma (R_{(\mathrm{FS})}^2)$$ (20)

Figure 5.

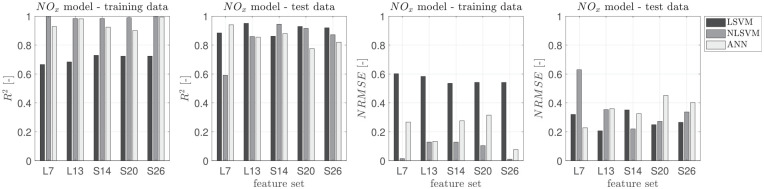
Comparison between $R^2$ and Normalized RMSE values for NO_x for NLSVM and LSVM with benchmark ANN method designed based on Rezaei et al.²⁶ in dependence of the different feature sets.

where $\sigma (R_{(\mathrm{FS})}^2)$ is standard deviation of $R^2$ and ${\overline{R}}_{(\mathrm{FS})}^2$ is average value of $R^2$ for selected feature set, L7, L13, S14, S20, and S26. Table 5 shows criterion for method selection, $J_{\mathrm{CMS}}(R^2)$ . This represents the lower bound of one standard deviation of uncertainty of the model fit. This helps to select a model with the best fit while ensuring the robustness of the model to changing feature sets. The goal is to have the value closest to 1. Here the best model fit score is highlighted in green and the worst is shown in red.

Table 5.

Criteria for method selection.

$\mathrm{CMS}(R^2)$	LSVM	NLSVM	ANN
$\mathbf{CO}$	0.809	0.818	0.641
$\mathbf{HC}$	0.612	0.864	0.838
$\mathbf{N}{\mathbf{O}}_{\mathbf{x}}$	0.877	0.710	0.799
$\mathbf{C}{\mathbf{O}}_2$	0.884	0.944	0.725

Here three of the four emissions are best represented using the NLSVM model and the other is best fit using LSVM. This shows that the SVM based models provide a stable prediction over the range of feature sets considered. A detailed analysis of the feature set will be performed next.

Feature selection

One important aspect to training the ML methods is the proper feature selection. It is important to include any features that have a correlation to the outputs of interest. However, the addition of extra features increase the model complexity and training time which is undesirable for real-time model implementation. Figure 3 shows the effect of feature selection on the model performance for CO emissions. Each feature set increases in the number of features from left to right.

The best $R_{\mathrm{training}}^2$ value in all cases occurs for FS L7 ( $R_{\mathrm{ANN}}^2=0.999$ ), while $R_{\mathrm{test}}^2$ is maximized at S20 ( $R_{\mathrm{ANN}}^2=0.959$ ) for the ANN model. The $R^2$ values are all very close for the training data at approximately $R^2\approx 0.98$ , however, a significant difference can be seen between the $R^2$ values of the test dataset. Generally as more features are added model performance improves as seen in Figure 3 in the test data for the ANN model. As the feature set is increased from L7 to S26 a continued increase can be seen, with the exception of L13 which has a decreased model performance with the training data using the ANN model. Improved model performance does not necessarily result from increased features.

For CO emissions the best model performance on the test data occurs when using the ANN model with S20 feature set. However, for simplified control purposes the L7 feature set using the NLSVM model provides good a prediction capability with a 15.6% reduction in model fit, $R_{\mathrm{test}}^2$ . As the main goal is to provide a real-time model for control applications this simplified and robust NLSVM prediction model is the desired choice for CO emissions prediction.

This feature analysis can then be extended extended to HC, NO_x, and CO₂ as seen in Figures 4 to 6. To compare the increased feature sets to the base feature set ( $\mathrm{FS}=L7$ ) a percent accuracy increase in $R^2$ value is defined, as Criterion for Feature Selection (CFS), $J_{\mathrm{CFS}}(R^2)$ , as:

$$J_{CFS}(R^2)=\frac{R_{FS}^2-R_{L7}^2}{R_{L7}^2}\times 100\%$$ (21)

This provides the relative increase in performance compared to the simplest model with lambda for the model type selected previously. Table 6 shows the improvement based on different feature sets. Here the simplest model is chosen that provides a significant increase in prediction performance ( $\mathrm{\Delta }{R}^2>2\%$ ).

Table 6.

Criteria for feature selection.

	Feature set	NLSVM- $\mathbf{CO}$ (%)	NLSVM- $\mathbf{HC}$ (%)	LSVM- $\mathbf{N}{\mathbf{O}}_{\mathbf{x}}$ (%)	NLSVM- $\mathbf{C}{\mathbf{O}}_2$ (%)
$J_{\mathrm{CFS}}(R^2)$	FS = L13	4.53	0.41	7.56	−1.75
	FS = S14	5.12	2.60	−2.57	−1.38
	FS = S20	4.78	0.59	5.09	0.34
	FS = S26	4.66	0.28	4.02	−0.17
	Selected FS	L13	L7	L13	L7

Overall, proper feature selection is required to gain the maximum model performance. This does not mean including any and all features but rather a proper feature exploration and selection is required. In this study, the emission model for control purposes for CO, HC, NO_x, and CO₂ are NLSVM-L13, NLSVM-L7, LSVM-L13, and NLSVM-L7, respectively. This shows that the inclusion of more features does not necessarily result in better model prediction performance. Additionally, this shows that based on the data collected there is not a single modeling method that should be used for all emissions.

Optimization and model training time

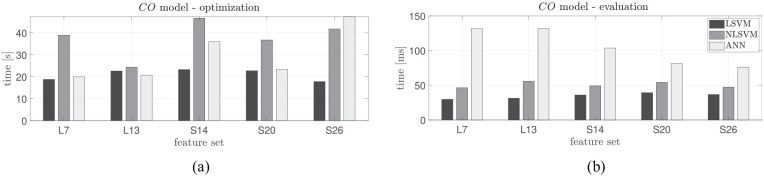
As the propose of the proposed emissions models is hardware implementation, it is necessary to evaluate their time requirements. To evaluate this possible problem the time it takes for optimization of the hyperparameters and evaluation of the model based on optimized hyperparameters are evaluated for the CO model as shown in Figure 7(a) and (b). As shown in Figure 7(a), PSO-based NSVM requires more optimization time than LSVM. Part of this increase is because more optimization variables need to be determined using PSO compared with LSVM. As shown, ANN has a optimization time that is between NSVM and LSVM. For the ANN model, the optimization time includes multiple ANN training runs to reduce the effect of the randomized starting weights as described in the “Model Comparison” section. However, in addition to this optimization time the ANN model also requires a grid search between the number of neurons and the hidden layer size that can add up to a significant computation time. However, as in this study, the structure of the ANN is chosen based on a benchmark model for comparison purposes based on Rezaei et al.²⁶ we did not require the grid search. The optimization part of modeling, even for the ANN grid search, does not affect the real-time implementation for two main reasons: (1) in real-time, only the already trained model is evaluated and (2) even with online learning, that is, updating model in real-time, the model will be updated based on optimized hyperparameters.

Figure 7.

Optimization and evaluation time comparison between LSVM, NSVM, and ANN: (a) CO – optimization time and (b) CO – evaluation time.

The model evaluation time is based on already optimized hyperparameters and this evaluation time plays a crucial role in real-time implementation. As shown in Figure 7(b), LSVM needs 67% and 32% lower evaluation time compared to ANN and NLSVM, respectively. NLSVM also takes 52% lower computation time than ANN. These results can be extended to the other NO_x, CO₂, and $\mathrm{HC}$ models which result in an average reduction in evaluation time for the LSVM model of 64% and 28% compared to the ANN and NLSVM models, respectively. On average for the four emissions the NLSVM requires 45% lower evaluation time than the ANN model.

Chosen model performance

The model type and feature set selected in the previous sections for each of the four emissions are evaluated compared against the experimental data. Figure 8(a) to (d) show the prediction performance of the selected models along with a $\pm 5\%$ band shown in red.

Figure 8.

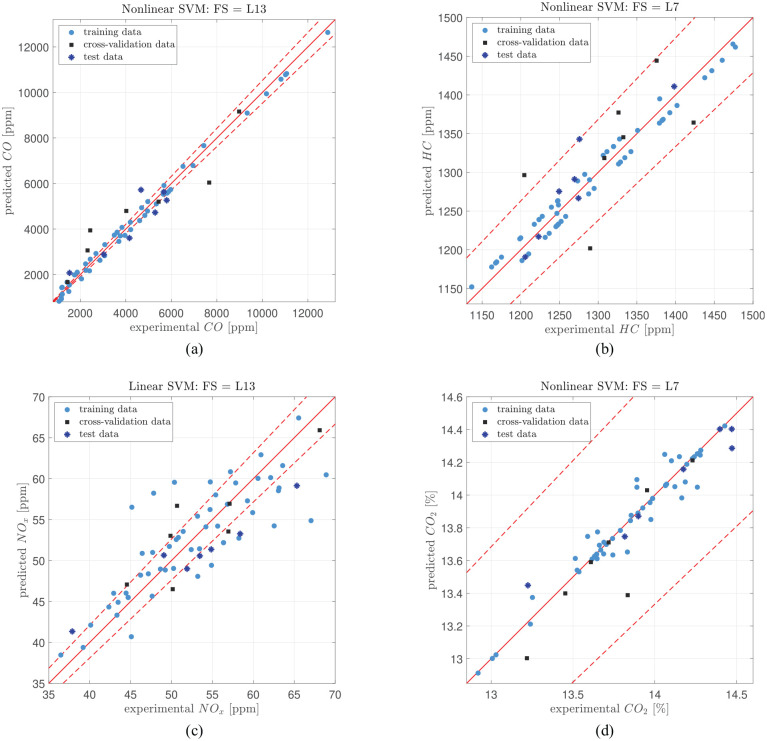
Actual versus experimental- HCCI emission model. Dashed red line represent ± 5% of experimental data value: (a) CO – NLSVM – L13 – actual versus experimental, (b) HC – NLSVM – L7 – actual versus experimental, (c) NOx – LSVM – L13 – actual versus experimental, and (d) CO2 – NLSVM – L7 – actual versus experimental.

The CO₂ model has all predicted values within the $\pm 5\%$ error bands. For the CO, HC and NO_x models there is 56%, 97%, and 56% of the data points within the error bands, respectively. For the CO model there is a relatively large spread in the cross-validation and test data. However, as there is a large spread in the CO levels over the testing data points the model is still able to provide the modeling trends.

The NO_x model has a larger spread in all of the data points. This could be a result of the low level of NO_x emissions from 35 to 70 ppm and the stochastic variation in the HCCI combustion that is not captured in the steady state modeling. A single or only a few cycles within a measurement can greatly increase the average emissions levels.

Conclusions

This paper shows the effect of different machine learning approaches and feature sets on the model quality for HCCI emissions prediction. The goal of this work was to select an accurate model while also selecting the simplest model that still has an acceptable prediction capability for future realtime control implementation. First, linear and non-linear SVM models were compared to a traditional ANN model. This comparison showed for a small data set that SVM based models were more robust to changes in feature selection and better able to avoid local minimums compared to ANN leading to a more consistent model prediction. For each of the four emissions examined the best model type was determined by taking the highest average $R^2$ value less the variance in $R^2$ over the various feature sets. This led to the NLSVM being selected for three of the emissions and LSVM for NO_x prediction.

Then the individual feature sets were examined. The base feature sets were extended by multiplying individual features together to explore in-feature interactions. By comparing the individual features with the base feature set (L7) the feature set with an improved accuracy that is acceptable given the increase in model complexity was chosen. In this study, the emission models chosen for control purposes for CO, HC, NO_x, and CO₂ are NLSVM-L13, NLSVM-L7, LSVM-L13, and NLSVM-L7, respectively. The NO_x and CO models have the largest prediction error while the HC and CO₂ models are quite accurate. The NO_x model produced the least accurate results however it was still able to capture the trends in NO_x production.

The presented SVM approach allows for emissions predictions that could be used as the basis for future real-time control applications. The inclusion of offline and online trained SVM models in engine controllers allows for real-time adaption to system aging and changes in operating conditions. Using the modeling methods identified in this work additional operating points can be tested and modeled. Additionally, the presented SVM model could be enhanced with the addition of a transient emissions model to better calculate engine out emissions during rapid load and speed changes. Implementing hybrid emission modeling by combining data-driven models with a physical-based model that provides more features from the physics of system through a chemical kinetics mechanism will be next step of this study to improve the emission model further.

Appendix

Notation

P_in Intake Pressure

T_in Intake Temperature

Λ Air-fuel Equivalence Ratio

ANN Artificial Neural Network

BNN Bayesian Neural Network

CA50 Crank angle where fifty percent of heat energy has been released

CFS Criterion for Feature Selection

CI Compression Ignition

CMS Criterion for Methods Selection

CO Carbon Monoxide

CO₂ Carbon Dioxide

DNN Deep Neural Networks

EGR Exhaust Gas Recirculation

ELM Extreme Learning Machine

EMVT Fully Variable Electro-magnetic Valve Train

EVC Exhaust Valve Closing

FS Feature Set

GA Genetic Algorithm

HC HydrocarbonHCCI Homogeneous Charge Compression Ignition

ICE Internal Combustion Engine

IMEP Indicated Mean Effective Pressure

IVO Intake Valve Opening

LSVM Linear Support Vector Machine

ML Machine Learning

MSE Mean Square Error

NLSVM Nonlinear Support Vector Machine

NO_x Nitrogen Oxide

NRMSE Normalized Root Means Square Error

NVO Symmetric Negative Valve Overlap

PSO Particle Swarm Optimization

RBF Radial Basis Function

RON Research Octane Number

SCRE Single Cylinder Research Engine

SOI Start of Fuel Injection

SVM Support Vector Machine

SVR Support Vector Regression

TDC Top Dead Center