Abstract
Ni-promoted indium oxide (In2O3) is a promising catalyst for the selective hydrogenation of CO2 to CH3OH, but the nature of the active Ni sites remains unknown. By employing density functional theory and microkinetic modeling, we elucidate the promoting role of Ni in In2O3-catalyzed CO2 hydrogenation. Three representative models have been investigated: (i) a single Ni atom doped in the In2O3(111) surface, (ii) a Ni atom adsorbed on In2O3(111), and (iii) a small cluster of eight Ni atoms adsorbed on In2O3(111). Genetic algorithms (GAs) are used to identify the optimum structure of the Ni8 clusters on the In2O3 surface. Compared to the pristine In2O3(111) surface, the Ni8-cluster model offers a lower overall barrier to oxygen vacancy formation, whereas, on both single-atom models, higher overall barriers are found. Microkinetic simulations reveal that only the supported Ni8 cluster can lead to high methanol selectivity, whereas single Ni atoms either doped in or adsorbed on the In2O3 surface mainly catalyze CO formation. Hydride species obtained by facile H2 dissociation on the Ni8 cluster are involved in the hydrogenation of adsorbed CO2 to formate intermediates and methanol. At higher temperatures, the decreasing hydride coverage shifts the selectivity to CO. On the Ni8-cluster model, the formation of methane is inhibited by high barriers associated with either direct or H-assisted CO activation. A comparison with a smaller Ni6 cluster also obtained with GAs exhibits similar barriers for key rate-limiting steps for the formation of CO, CH4, and CH3OH. Further microkinetic simulations show that this model also has appreciable selectivity to methanol at low temperatures. The formation of CO over single Ni atoms either doped in or adsorbed on the In2O3 surface takes place via a redox pathway involving the formation of oxygen vacancies and direct CO2 dissociation.
Keywords: CO2 hydrogenation, In2O3, Ni, mechanism, oxygen vacancy
1. Introduction
Anthropogenic CO2 emissions due to combustion of fossil fuels constitute a serious environmental threat because of their negative impact on the climate such as global warming, rise in sea level, and ocean acidification.1−3 One of the most attractive strategies to reduce these emissions is to close the carbon cycle by recycling CO2 captured from combustion processes or directly from the air, followed by its conversion into chemical feedstocks and fuels. This can be achieved by converting CO2 with hydrogen obtained from renewable resources.4−6 The use of carbon in a circular manner can eventually lead to the replacement of fossil fuels with renewable resources for covering the energy demand. Besides effectively mitigating emissions, CO2 hydrogenation products can be used to synthesize important chemical feedstocks. In the overall context of sustainability, methanol is particularly attractive because it can be directly used as a fuel and a building block to produce a wide range of chemicals such as formaldehyde, dimethyl ether, olefins, and hydrocarbon fuels.7−9
Currently, large-scale methanol production is based on the conversion of synthesis gas (CO/CO2/H2) over Cu/ZnO/Al2O3 catalysts at typical temperatures and pressures of 473–573 K and 50–100 bar, respectively.10,11 Challenges arise, however, in the hydrogenation of CO2 to CH3OH. The commercial Cu-based catalyst shows significant activity for the reverse water–gas-shift reaction (rWGS), leading to the formation of unwanted CO.12 Moreover, the catalyst is prone to sintering, decreasing the activity.13,14 Many efforts have been made to identify other catalyst formulations more suitable for the hydrogenation of CO2 to CH3OH.15−21 Among these, indium oxide (In2O3) was recently introduced as a promising catalyst for CO2 hydrogenation to methanol, especially when supported on ZrO2.22−25 Several density functional theory (DFT) studies emphasize the role of oxygen vacancies in the mechanism of CO2 hydrogenation to methanol on In2O3.26−31 Although In2O3 enables high selectivity toward methanol by suppressing the competitive rWGS reaction, CO2 conversion is limited by the low activity of indium oxide in dissociating molecular H2. To enhance the rate of hydrogen activation, several metal promoters have been investigated. Rui et al. showed that the addition of small Pd nanoparticles can enhance methanol synthesis.32 Supporting DFT calculations indicated that small Pd clusters increase the rate of H2 activation, resulting in a larger amount of H atoms at the metal–oxide interface.33 Frei et al. proposed that single-atom (SA) Pd doped inside the In2O3 lattice can stabilize clusters of a few Pd atoms on the In2O3 surface, enhancing H2 activation and, therefore, CH3OH productivity.25 Similar results have been reported for Pt-promoted In2O3.34−36 Given their price, it would be advantageous to replace Pd and Pt with earth-abundant metals like first-row transition metals. Earlier investigations have shown that adding Co37 and Cu38 to In2O3 can enhance the activity of In2O3 for methanol synthesis. More recently, Jia et al. prepared a highly dispersed Ni/In2O3 catalyst with significantly enhanced CO2 conversion compared to the unpromoted oxide while preserving high methanol selectivity.39 Notably, no methane was found in the product stream. In another study, Snider et al. suggested that the higher activity of bimetallic Ni–In catalysts for CO2 hydrogenation to CH3OH compared to In2O3 is due to the synergistic interactions between a Ni–In alloy and In2O3.40 Furthermore, Frei et al. reported that highly dispersed InNi3 patches formed on the In2O3 surface increase methanol production by supplying neutral H species, whereas Ni SAs were active for the rWGS.41 Shen et al. investigated the DFT pathways of CO2 hydrogenation to methanol on a Ni4/In2O3 model catalyst, demonstrating that oxygen vacancies are involved in CO2 hydrogenation, followed by hydrogenation of adsorbed CO2 to methanol.42 In a recent experimental study, we showed that Ni/In2O3 catalysts prepared using flame spray pyrolysis synthesis have enhanced CH3OH synthesis activity compared to that of bare In2O3.43 X-ray photoelectron spectroscopy, X-ray absorption spectroscopy, and electron paramagnetic resonance analyses of the used catalysts suggest that the working state of the catalyst corresponds to SAs or clusters of a few atoms of Ni dispersed on the In2O3 surface. However, differentiating the catalytic role of single Ni atoms and small clusters was challenging, meaning that the exact nature of Ni species in the active sites of Ni/In2O3 catalysts remains unclear. Supporting DFT calculations indicate that Ni promotion of methanol synthesis from CO2 on In2O3 is mainly due to low-barrier H2 dissociation, yet the mechanism of CO2 conversion to methanol has not been explored so far.
In the present study, we employ DFT in combination with genetic algorithms (GAs) and microkinetic modeling to systematically investigate the nature of the active sites and the mechanism of CO2 hydrogenation to methanol on Ni/In2O3. To understand the nature of the active site, we consider the following three model systems: (i) SA doped in and (ii) SA adsorbed on In2O3(111) and (iii) a Ni8 cluster placed on a In2O3(111) surface. GAs are used to identify optimum structural models for supported clusters, while DFT calculations are used to determine the elementary reaction steps for CO2 conversion to CH3OH, CO, and H2O. On the basis of these first-principles data, we construct microkinetic models to predict the CO2 consumption rate and the product distribution as a function of temperature, as well as surface coverages, reaction orders, and apparent activation energies. We perform a sensitivity analysis of the kinetic network to identify the elementary steps that control the rate of CO2 consumption and CH3OH selectivity. We herein show the factors underlying different activity and selectivity patterns on Ni/In2O3 model catalysts during CH3OH synthesis from CO2 hydrogenation, highlighting that small clusters are the most active and selective form of Ni for obtaining the desired methanol product, whereas on Ni SA models, the competing rWGS is preferred, wherein CO2 is hydrogenated to CO and H2O.
2. Computational Methods
2.1. DFT Calculations
All DFT calculations were conducted using the projector augmented wave (PAW) method44 and the Perdew–Burke–Ernzerhof45 exchange–correlation functional, as implemented in the Vienna ab initio simulation package (VASP) code.46,47 Solutions to the Kohn–Sham equations were calculated using a plane-wave basis set with a cut-off energy of 400 eV. The semi-core 5s and 5p states of In were treated explicitly as valence states within the scalar-relativistic PAW approach. All calculations were spin-polarized. The Brillouin zone was sampled using a 3 × 3 × 1 Monkhorst–Pack grid. Electron smearing was employed using Gaussian smearing with a smearing width (σ) of 0.1 eV. We chose the In2O3(111) surface termination because it is more stable than the (110) and (100) surfaces, as shown in a previous computational study.48 The stoichiometric In2O3(111) surface was modeled as a 2D slab with periodic boundary conditions. A 20.0 Å vacuum region was introduced in the c-direction to avoid the spurious interaction with neighboring super cells. It was verified that the electron density approached zero at the edges of the periodic super cell in the c-direction. In all calculations, the bottom two layers were frozen, while the top two layers were allowed to perturb. The supercell has dimensions of 14.57 Å × 14.57 Å × 26.01 Å. The In2O3(111) slab consisted of 96 O atoms and 64 In atoms distributed in four atomic layers on top of which the Ni species were placed.
The global minimum (GM) structure of In2O3-supported Ni clusters of either 6 or 8 atoms (Ni6 and Ni8) was determined by an in-house written GA procedure based on the earlier approach of Hammer et al.49,50 In this procedure, evolutionary processes including cross-over and mutation were employed to generate new candidate structures, whose geometry was optimized using the conventional conjugate-gradient method. This resulted in increasingly more stable clusters while maintaining a statistically diverse population to ensure that sufficiently distinct new candidates could be generated. The algorithm was seeded using 12 randomly generated clusters. Each iteration of the algorithm produced a new generation of clusters until population stagnation was observed, that is until no new clusters stabler than the existing clusters in the population pool were found. For the Ni8-cluster, a total of 513 structures were generated, of which the 201 most stable clusters were selected for further analysis. For the Ni6-cluster, 136 stable candidates were identified out of 346 structures obtained in total. The structure with the lowest energy in the pool of candidates was designated as the GM structure. To better understand the structures obtained with the GA, a statistical analysis based on Boltzmann statistics and a similarity analysis based on the minimum Hilbert–Schmidt (HS) norm were employed. In the latter, a distance matrix for each cluster was produced, wherein each matrix element represents the distance between any two atoms in a single cluster. The similarity between any two clusters in the set can then be expressed as the minimum HS norm of the difference of their distance matrices, wherein the minimum is established by evaluating all possible permutations over the indices for one of the distance matrices.
The influence of oxygen vacancies on the reaction energetics was investigated by removing oxygen atoms from the In2O3(111) lattice. The energy required to remove surface oxygen to form a vacancy (ΔEOv) was calculated using either O2 or H2O as the reference, according to the following two equations for the oxygen vacancy formation energy
| 1 |
| 2 |
Where Edefective slab is the electronic energy of the catalyst containing one oxygen vacancy,
and Estoichiometric slab is the reference
energy of the stoichiometric slab. 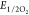 ,
, 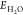 , and
, and 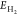 are the DFT-calculated energies
of gas-phase
O2, H2O, and H2, respectively. Herein,
we include the electronic energy, the zero-point energy (ZPE) correction,
and a finite temperature correction of translational and rotational
energies of each gas-phase molecule.
are the DFT-calculated energies
of gas-phase
O2, H2O, and H2, respectively. Herein,
we include the electronic energy, the zero-point energy (ZPE) correction,
and a finite temperature correction of translational and rotational
energies of each gas-phase molecule.
The stable states in the chemo-kinetic network were calculated using the conjugate-gradient algorithm. Transition states were determined using the climbing-image nudged elastic band method.51 A frequency analysis was performed to all states. Specifically, it was verified that stable states have no imaginary frequencies and transition states have a single imaginary frequency in the direction of the reaction coordinate.52 The Hessian matrix in this frequency analysis was constructed using a finite difference approach with a step size of 0.0015 Å for the displacement of individual atoms along each Cartesian coordinate. The corresponding normal mode vibrations were also used to calculate the ZPE correction and the vibrational partition functions.
Partial density of state (pDOS) and projected crystal orbital Hamiltonian population (pCOHP) analyses are conducted to analyze the electronic structure of each Ni/In2O3 model catalyst using the Lobster package.53,54 The atomic charges of Ni atoms were calculated using the Bader charge method.55
2.2. Microkinetic Simulations
Microkinetic simulations were conducted based on the DFT-calculated activation barriers and reaction energies to investigate the kinetics of CO2 hydrogenation to methanol. The chemo-kinetic network was modeled using a set of ordinary differential equations involving rate constants, surface coverages, and partial pressures of gas-phase species. Time-integration of the differential equations was conducted using the linear multistep backward differential formula method with a relative and absolute tolerance of 10–8.56−58
For the adsorption processes, the net rate of a gas-phase species i was calculated as
| 3 |
where θ* and θi are the fraction of free sites and the fraction of coverage species i, respectively. ki,ads/des is the rate constant for the adsorption/desorption process, and Pi is the partial pressure of species i.
To derive a rate for the adsorption processes, we assumed that the adsorbate loses one translational degree of freedom in the transition state with respect to the initial state. From this assumption, the rate of adsorption derived from transition state theory can be expressed as follows
| 4 |
where Ast and mi are the effective area of an adsorption site and the molar mass of the gas species, respectively. P and T are the total pressure and temperature, respectively, and kB is the Boltzmann constant. The gas-phase entropy of the adsorbates was calculated using the thermochemical Shomate equation as given by
| 5 |
where S0 is the standard molar entropy.59 The parameters A–G from eq 5 were obtained from the NIST Chemistry Webbook.60 For the corresponding desorption processes, we assumed that the species gains two translational degrees of freedom and three rotational degrees of freedom in the transition state with respect to the initial state. From this assumption, the rate of desorption derived from transition state theory can be expressed as follows
| 6 |
Herein, kdes is the rate constant for the desorption of the adsorbate, h is the Planck constant, σ is the symmetry number and is equal to 1, θrot is the rotational temperature, and ΔEads is the desorption energy. The value of Ast is equal to 9 × 10–19 m–2.
Finally, the rate constant (k) of an elementary reaction step is given by
| 7 |
where Q≠ and Q are the partition functions of the activated complex and its corresponding initial state, respectively, and ΔEact is the ZPE-corrected activation energy.
To identify the steps that control the CO2 consumption rate and the product distribution, we employed the concepts of the degree of rate control (DRC) developed by Kozuch and Shaik61,62 and popularized by Campbell63 as well as the degree of selectivity control (DSC).63−65
Herein, the DRC coefficient is defined as
| 8 |
A positive DRC coefficient indicates that the elementary reaction step is rate-controlling, whereas a negative coefficient suggests that the step is rate-inhibiting. When a single elementary reaction step has a DRC coefficient of 1, this step is identified as the rate-determining step.
The DSC quantifies the extent to which a particular elementary reaction step influences the selectivity for certain products. The DSC of a particular key component is expressed as
| 9 |
where XSC,i,c is the DSC of product c due to a change in the kinetics of the elementary reaction step i, and ηC is the selectivity toward a key product (methanol in this work). Note that the relationship between DRC and DSC coefficients is given by
| 10 |
3. Results and Discussion
3.1. Structure of Ni/In2O3 Models
The understand the nature of the active sites for Ni/In2O3 in CO2 hydrogenation to methanol, three model systems were considered, namely SA of Ni either (i) doped in the In2O3(111) surface (denoted as Ni1-doped) or (ii) adsorbed on the In2O3(111) surface (Ni1-adsorbed) and a cluster of (iii) 8 Ni atoms adsorbed on top of the In2O3(111) surface (Ni8-cluster). The models are shown in Figure 1. We also compare our Ni8 cluster with a smaller Ni6 cluster obtained at the same level of theory. To determine the most stable location of Ni for the Ni1-doped In2O3(111) model system, the energy of substituting an In atom for a Ni atom was calculated. The reported substitution energies (Esub) are given with respect to bulk Ni and In by
| 11 |
where 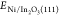 is the energy of each Ni1-doped
In2O3(111) surface, EIn,bulk, ENi,bulk, and
is the energy of each Ni1-doped
In2O3(111) surface, EIn,bulk, ENi,bulk, and  are the energies
of In bulk, Ni bulk, and
In2O3(111) surface models, respectively. The
resulting substitution energies for all the doping positions are collected
in Table S1. DFT calculations indicate
that Ni substitution is favored in position 1 as shown in Figure 1a (Esub = −0.35 eV). Ni prefers a nearly perfect octahedral
coordination by oxygen in the first metal layer of the structure (position
1). The six sites nearest to position 1 are slightly less stable (i.e.,
with substitution energies ∼+0.15 eV compared to position 1)
due to a slight distortion of the octahedral environment around the
Ni substituent. Compared to these sites, substitution at other positions
in the first metal layer is unfavorable, with substantially larger
exchange energies. We also studied the possibility of substituting
an In atom in the bulk of In2O3 with a Ni atom
(Figure S2a). Our calculations indicate
that the substitution of a Ni SA in subsurface layers is unfavorable
(Esub = +0.51 eV). We also evaluated the
possibility of replacing a second In atom in the surface (Figure S2b) and found that this is also unfavorable
(Esub = +0.59 eV). These findings are
in line with a previous study on Pd-doped In2O3.25
are the energies
of In bulk, Ni bulk, and
In2O3(111) surface models, respectively. The
resulting substitution energies for all the doping positions are collected
in Table S1. DFT calculations indicate
that Ni substitution is favored in position 1 as shown in Figure 1a (Esub = −0.35 eV). Ni prefers a nearly perfect octahedral
coordination by oxygen in the first metal layer of the structure (position
1). The six sites nearest to position 1 are slightly less stable (i.e.,
with substitution energies ∼+0.15 eV compared to position 1)
due to a slight distortion of the octahedral environment around the
Ni substituent. Compared to these sites, substitution at other positions
in the first metal layer is unfavorable, with substantially larger
exchange energies. We also studied the possibility of substituting
an In atom in the bulk of In2O3 with a Ni atom
(Figure S2a). Our calculations indicate
that the substitution of a Ni SA in subsurface layers is unfavorable
(Esub = +0.51 eV). We also evaluated the
possibility of replacing a second In atom in the surface (Figure S2b) and found that this is also unfavorable
(Esub = +0.59 eV). These findings are
in line with a previous study on Pd-doped In2O3.25
Figure 1.
(a) Substitution energy of In/Ni substitution in In2O3. The coloring of In atoms at the surface represents the energy associated with their replacement by Ni (Esub). Position 1 marks the most stable substitution site. (b) Adsorption energy of Ni SAs on In2O3(111). The coloring of the atoms at the surface represents their adsorption energy (Eads). Position 1 marks the most stable adsorption site. Energy minima structures obtained by the GA for gas-phase (c,e) and supported (d,f) Ni8 and Ni6 clusters, respectively. Red: O; gray: In; green: Ni.
The preferred location of a Ni SA on the In2O3(111) surface is bridging between two lattice oxygens (Figure 1b). The adsorption energies for all investigated sites are reported in Table S2. In its most stable configuration, the Ni–O distances are r(Ni–Oα) = 1.79 Å and r(Ni–Oβ) = 1.81 Å (Figures 1b and S3b). In its least stable adsorption configuration (position 6), Ni coordinates to a single oxygen atom and an In atom. The Ni–O and Ni–In distances are 2.14 and 2.54 Å, respectively. The Ni–O distance increases from 1.79 to 2.14 Å from the most stable to the least stable adsorption configuration, in line with a weaker binding of the Ni SA with the surface. In general, more stable configurations feature multiple Ni–O bonds. Furthermore, we determined barriers for the diffusion of a single Ni atom between stable adsorption sites (Table S3). Migration from position 1 to position 3 (Figure 1b) is associated with a barrier of 95 kJ/mol and is endothermic by 21 kJ/mol. Migration from position 3 to position 4 has a higher barrier (165 kJ/mol) and is endothermic by 11 kJ/mol. Lastly, migration from position 4 to position 5 is associated with a barrier of 142 kJ/mol and is endothermic by 65 kJ/mol.
In a recent experimental study on Ni/In2O3, it was found that Ni is present in a clustered form under reducing reaction conditions.43 These clusters were relatively small in optimized catalysts, as no methane was observed during CO2 hydrogenation. Methane was only formed at much higher Ni loading, where Ni nanoparticles were present on In2O3. To model small Ni clusters, we used clusters containing either 8 or 6 Ni atoms (Ni8 and Ni6, respectively) on the In2O3(111) surface as a compromise between computational tractability and a reasonable description of supported metal clusters that often adopt a bilayer structure.49 For comparison, we also determined the most stable structure of clusters in the gas phase of the Ni8 and Ni6 clusters (Figure 1c,e, respectively). The DFT-based GA identified 201 and 136 stable candidate structures for the Ni8 and Ni6-cluster models, respectively. The algorithm did not find new configurations that were significantly different from the energy minimum within an energy threshold of 0.1 eV after 57 and 36 genetic iterations for the Ni8 and Ni6-cluster models, respectively. The minimum-energy structures for gas-phase and supported Ni8 and Ni6 clusters are shown in Figure 1c–f respectively. In the gas phase, the most stable free clusters adopt a square bipyramidal shape, in line with an earlier computational study.66 The most stable supported Ni8 cluster obtained by our DFT-GA (Figure 1d) consists of a bilayer structure where 6 Ni atoms form the bottom layer, with the other two Ni atoms placed on threefold sites of the first Ni layer. For the supported Ni6 cluster (Figure 1f), 5 Ni atoms form the bottom layer, and the sixth Ni atom is placed on a threefold site. The different shapes of the Ni clusters in the gas phase and on the In2O3(111) support are caused by strong metal-support interactions (MSI) between Ni and In2O3. Such MSI were quantified by computing the cohesive energy per Ni atom of the GA-optimized Ni8 clusters in the gas phase and supported on In2O3 (Table S4). Placing the Ni8 cluster on the (111) surface of In2O3 increases the cohesive energy from 268 kJ/mol/atom for the gas-phase cluster to 358 kJ/mol/atom for the cluster on the In2O3 support. For a Ni6-cluster, the stabilization effect is slightly higher (111 kJ/mol/atom).
The stability of the supported Ni clusters can be further evaluated by determining the barrier needed to remove a single Ni atom from the cluster via migration on the In2O3 surface. We performed such DFT calculations and reported the results in Tables S5 and S6. Removing a Ni atom from a Ni6 cluster has a barrier of 201 kJ/mol and is endothermic by 179 kJ/mol. For the Ni8-cluster, the corresponding values are 232 and 192 kJ/mol. Thus, it is clear that the redispersion of Ni clusters into SAs is prohibitive from the kinetic and thermodynamic points of view.
To determine whether other configurations of the Ni clusters will also contribute to the catalytic performance, we analyzed the Boltzmann probability distribution for the structures (Section S3.2 of the Supporting Information). This analysis demonstrated that, for both clusters, one other structure occurs with a sufficiently large contribution at a reaction temperature at 400 K. Based on a structural similarity analysis (Table S7), it was found that this structure is nearly the same as the minimum energy structure for both the Ni6 and Ni8-cluster models. Accordingly, we focused only on the minimum energy structure of the Ni8 cluster in the following.
The electronic structure of the Ni/In2O3 models can be compared on the basis of the pDOS (Figure S6). In all cases, overlap between Ni 3d and O 2p orbitals is observed. The In 4d orbitals are core orbitals and, therefore, do not show appreciable overlap with O 2p or Ni 3d orbitals. For optimized, doped, and adsorbed SA models, the calculated Bader charges of the Ni atoms are +1.26 and +0.66 |e|, respectively. The Bader charge analysis further shows that Ni8 clusters on In2O3(111) carry a cumulative charge of +1.07 |e| (Table S8 and Figure S7a). The six Ni atoms located at the bottom layer of the cluster carry a positive charge, while the two Ni atoms adsorbed on top carry a slightly negative charge. Thus, for all models, there is a net flow of electrons from Ni to the O atoms of the In2O3 surface.
3.2. Oxygen Vacancy Formation
The role of oxygen vacancies (Ov) on the In2O3 surface has been emphasized for the adsorption and activation of CO2.26−28 To assess how the addition of Ni affects the formation of such vacancies, we compared the energy required to form such Ov (EOv, in eV) for the Ni/In2O3 surfaces with unpromoted In2O3 (Figure 2). The computed energies are referenced to gaseous O2. On the bare In2O3(111) surface (Figure 2a), the energy needed to remove an oxygen atom ranges from 1.8 to 3.0 eV, in line with previous calculations.48,67 We also calculated the Ov formation energies with respect to H2O because oxygen vacancies are usually formed in the presence of H2. In this case, the EOv lies between −0.65 and 0.99 eV.
Figure 2.
Oxygen vacancy formation energies (EOv) for the 12 surface oxygens on (a) bare In2O3, (b) Ni1-doped in and (c) Ni1-adsorbed on In2O3, (d) Ni6-cluster, and (e) Ni8-cluster. The coloring of the 12 surface oxygen atoms represents their EOv. Ni atoms are colored in dark gray, while all other atoms are colored in light gray. The Ni species are highlighted inside dashed circles.
Doping In2O3 with a Ni SA (Figure 2b) lowers the energy for Ov formation significantly. Values for EOv referenced to O2 lie between 0.94 and 1.86 eV. Considering H2O formation, oxygen vacancy formation is exothermic for all surface oxygens considered (EOv between −1.58 and −0.66 eV). As can be seen from Figure 2b, the O atoms bonded to Ni are more easily removed than O atoms bonded to In. In its most stable doping position, the Ni–O bond distance is 1.94 Å, which is 0.25 Å shorter than the In–O distance measured for an In atom occupying the same lattice position on the bare oxide. This suggests that doping a smaller Ni atom in In2O3 leads to lattice contraction bringing the O atoms closer to each other. This enhances electron–electron repulsion between the relatively large electron clouds around the negatively charged O atoms, weakening the Ni–O bonds, and thereby explaining the lower EOv. Adsorbing a Ni atom on top of the In2O3 (Figure 2c) significantly increases the oxygen vacancy formation energy, resulting in EOv values between 3.42 and 4.41 eV referenced to O2 and between 0.89 and 1.87 eV referenced to H2O. For a supported Ni6 cluster (Figure 2d), oxygen vacancy formation via direct thermal desorption of O2 lies between 2.65 and 3.52 eV. With respect to H2O formation, EOv values lie between 0.12 and 1.16 eV. For a supported Ni8 cluster (Figure 2e), similar values are found for oxygen vacancy formation energies via direct thermal desorption (2.48–3.51 eV). Thus, adsorbed Ni phases increase the oxygen vacancy formation energy compared to the reference pristine In2O3 case. This is in line with our knowledge that the Ni–O bond (396 kJ/mol) is stronger than the In–O bond (346 kJ/mol).68
A more careful inspection of Figure 2b–d shows that, for each of the Ni-promoted surfaces, formation of vacancies is easier for oxygens directly bonding to Ni species than for O atoms bonding only to In atoms. To understand this point, we performed a pCOHP analysis of the Ni–O and In–O bonds (Figure S8), where we compare the stoichiometric In2O3 surface with Ni-promoted ones. On In2O3 (Figure S8a), the character of In–O interactions is bonding. For all Ni-promoted surface models (Figure S8b–i), the pCOHP exhibits antibonding Ni–O and In–O interactions close to the Fermi level for oxygen atoms adjacent to Ni. This explains why less energy is needed to remove these oxygens compared to oxygens at larger distances from Ni. We infer that the addition of Ni to In2O3 causes electron transfer from Ni to O, which results in the formation of antibonding N–O and In–O interactions. Furthermore, Bader charge analysis shows that, upon formation of an oxygen vacancy, the excess charge is redistributed mainly to the nearest Ni atom from the cluster (Figure S7b). In this way, Ni atoms can contribute to stabilizing the oxygen-defective Ni/In2O3 surface, resulting in easier formation of vacancies at the Ni/In2O3 interface. In summary, with respect to the stoichiometric In2O3 surface, only the Ni1-doped model features more exothermic oxygen vacancy formation energies, whereas the other Ni/In2O3 models feature more endothermic oxygen vacancy formation energies. To understand whether oxygen vacancies will be formed on these models, we investigate the DFT pathways of oxygen vacancy formation via surface reduction by H2 and perform microkinetic simulations (vide infra).
3.3. Elementary Reaction Steps
We performed DFT calculations to elucidate the reaction mechanism of CO2 hydrogenation to methanol (CH3OH), carbon monoxide (CO), and water (H2O). No methane is observed during CO2 hydrogenation experiments for a Ni/In2O3 catalyst with a low Ni loading.32,34 To verify that CO2 methanation on small In2O3-supported Ni clusters is difficult, we studied direct and H-assisted CO dissociation to assess whether the second C–O bond scission is facile. The reaction network explored in this study is depicted in Figure 3. Based on previous computational studies, we investigate specific pathways for the formation of oxygen vacancies via H2O, for the formation of CH3OH via formate, and for the rWGS pathway leading to CO.24,70,71 The latter can take place either via direct cleavage of one C–O bond in CO2 or via an H-assisted pathway involving the COOH intermediate. In addition, a pathway via the CO intermediate toward CH3OH has been included for the Ni1-adsorbed and Ni8-cluster model surfaces.
Figure 3.
Full kinetic networks for CO2 hydrogenation to CO and CH3OH for (a) Ni1-doped, (b) Ni1-adsorbed, and (c) Ni8-cluster models. Orange: oxygen vacancy formation pathway; blue: formate pathway to CH3OH; green: CO hydrogenation pathway to CH3OH; red: rWGS to CO; gray: adsorption/desorption elementary steps. The numbers correspond to the elementary reaction steps as listed in Tables S9a–c.
We will discuss the elementary reaction steps in this network for the Ni1-doped, Ni1-adsorbed, and Ni8-cluster model surfaces and highlight the main trends in activation energies and transition-state structures. We also compare key elementary reaction steps for the formation of CO, CH4, and CH3OH between Ni6 and Ni8 clusters. The activation barriers are given with respect to the most stable adsorbed state for each intermediate. All the elementary reaction steps along with the corresponding forward and backward activation energies are tabulated in the Supporting Information in Section S7 (Tables S9a–c). The geometries corresponding to the initial, transition, and final states are reported in Sections S8–S10 of the Supporting Information.
3.3.1. Methanol Synthesis on Ni1-Doped In2O3
We first discuss the reaction energetics of CO2 hydrogenation to methanol over the Ni1-doped system. The reaction network is shown in Figure 3a and the corresponding potential energy diagram (PED) in Figure 4a. The geometries of initial, transition, and final states can be found in Section S8. H2 dissociation on the Ni1-doped In2O3(111) surface (step 1) is homolytic, similar to the In2O3 surface and leads to the formation of two OHδ+ groups.72 This step has an activation energy of 70 kJ/mol and is exothermic by ΔEr = −294 kJ/mol, indicative of the high stability of the surface hydroxyl groups. The relatively high barrier for H2 activation can be understood by considering that the surface O anions cannot stabilize the negatively charged H atoms during dissociation.43 Subsequent water formation has a barrier of 163 kJ/mol and is endothermic by 137 kJ/mol. H2O desorption (ΔEdes = 80 kJ/mol; step 3) completes oxygen vacancy formation. Overall, the process of oxygen vacancy formation is associated with a reaction energy of −80 kJ/mol and an activation barrier of 70 kJ/mol with respect to gas-phase H2.
Figure 4.
PEDs of the conversion of CO2 and H2 to CO, CH3OH, and H2O on (a) Ni1-doped, (b) Ni1-adsorbed, and (c) Ni8-cluster model. Reaction barriers are reported in the X/Y format, wherein X corresponds to the forward barrier and Y to the backward barrier. All energies are given in kJ/mol. Orange: oxygen vacancy formation pathway; blue: formate pathway to CH3OH; green: CO hydrogenation pathway to CH3OH; red: rWGS (direct or H-assisted) to CO.
Next, CO2 adsorbs at the oxygen vacancy (step 4). The carbon atom coordinates to a lattice oxygen instead of the Ni SA, which is due to the steric hindrance around Ni due to its location on the surface. The adsorption energy of CO2 is exothermic by ΔEads = −103 kJ/mol. Dissociative adsorption of another H2 molecule (step 5) leads to two hydroxyl groups adjacent to CO2. This step has an activation energy of 104 kJ/mol and is exothermic by ΔEr = −22 kJ/mol. CO2 hydrogenation to HCO2 + H (step 6) proceeds by proton migration from an adjacent hydroxyl species with a forward activation energy of 165 kJ/mol (ΔEr = 8 kJ/mol). Another proton migration step leads to H2CO2 (step 7) with a forward barrier of 313 kJ/mol (ΔEr = 287 kJ/mol). Notably, high activation energies are associated with the formation of a bond between a slightly positively charged C atom and the H atom of the OH group, which is also positively charged, in line with a previous work on In2O3.24 The possibility of hydrogenating one of the O atoms in HCO2 giving HCOOH was also investigated. However, no TS could be found for this elementary step because the HCOOH moiety does not adsorb stably on the surface. No TS has also been found for the direct dissociation of H2CO2 into CH2O + O. However, the CH2O intermediate can be obtained from H2CO2H dissociation. After dissociative adsorption of another H2 molecule (step 8; Eact = 71 kJ/mol, ΔEr = −32 kJ/mol), one of the two oxygens of H2CO2 is protonated (step 9) to form H2CO2H + H (Eact = 49 kJ/mol, ΔEr = 42 kJ/mol). The subsequent cleavage of a C–O bond of H2CO2H yields CH2O and a OH moiety, which occupies the oxygen vacancy (step 10). This step has an activation energy of 97 kJ/mol and is exothermic by 140 kJ/mol. Next, the CH2O moiety is hydrogenated to CH3O via proton migration from a neighboring OH group (step 11). This step is endothermic by 49 kJ/mol and has a forward activation energy of 117 kJ/mol. Finally, CH3O is hydrogenated by the hydroxyl species obtained from H2CO2H dissociation, forming methanol, which immediately desorbs (step 12). This concerted elementary step has an activation energy of 102 kJ/mol and is exothermic by ΔEr = −19 kJ/mol. Finally, oxygen migration (step 13) restores the initial stoichiometric surface. This step has an activation energy of 120 kJ/mol and is endothermic by ΔEr = 85 kJ/mol.
CO is observed during experiments on Ni/In2O3 as a by-product of the rWGS reaction (Figure 4a, red). On the Ni1-doped model, CO can be formed via a redox mechanism involving the formation of H2O (steps 1–3), adsorption of CO2 on an oxygen vacancy (step 4), and subsequent dissociation and desorption of CO (step 14). The energy penalty associated with replenishing one oxygen vacancy by CO2, thus restoring the stoichiometric surface, is 234 kJ/mol. Ye et al. observed that the same process on an In2O3(110) model surface has a barrier of 1.4 eV.27,28 The higher barrier for our model is in keeping with the result that doping In2O3 with Ni results in a more exothermic oxygen vacancy formation energy. A hydrogen-assisted rWGS pathway to CO via the COOH intermediate is generally also followed. We explored this pathway for the Ni1-doped model; however, no TS could be found for the dissociation of COOH into CO and OH as there is no active site to accept the OH.
3.3.2. Methanol Synthesis on Ni1-Adsorbed In2O3
Next, we discuss the mechanism of CO2 hydrogenation over the Ni1-adsorbed system. The reaction network is shown in Figure 3b and the PED in Figure 4b. The geometries of initial, transition, and final states can be found in Section S9. On this surface, H2 is heterolytically dissociated to form a NiHδ− and a OHδ+ species (step 1), as we reported in another study.43 This step is mildly activated (Eact = 19 kJ/mol) and exothermic by −36 kJ/mol. Notably, H2 dissociation has a lower activation energy compared to the formation of two OH groups, as found for the Ni1-doped system (Eactdoped = 70 kJ/mol). Next, the formation of an oxygen vacancy proceeds by H migration from the Ni–H moiety to form H2O (step 2). This step has an activation energy of 93 kJ/mol and a reaction energy of +27 kJ/mol. Water desorption from the surface (step 3) is associated with a desorption energy of 177 kJ/mol. The overall barrier and reaction energy of oxygen vacancy formation with respect to gas-phase H2 on this surface amount to 150 kJ/mol, which is considerably higher than the corresponding values for the Ni1-doped surface (70 and −80 kJ/mol, respectively).
CO2 adsorbs in the oxygen vacancy, coordinating with the Ni SA (step 4). In its most stable adsorption configuration, the carbon atom of CO2 binds to the Ni atom (ΔEads = −144 kJ/mol). A second H2 molecule can dissociate, forming two OH species (step 5). Homolytic dissociative adsorption of H2 is preferred because of the steric hindrance of the Ni atom, which is also involved in Ni–C bonds with adsorbed CO2. This step has an activation energy of 19 kJ/mol and is exothermic by ΔEr = −36 kJ/mol. Along the formate pathway to methanol (steps 6–11), first a H species migrates from the lattice oxygen to the Ni SA and hydrogenates CO2 to form HCO2 (step 6). This step has a forward activation energy of 66 kJ/mol and is slightly exothermic (ΔEr = −2 kJ/mol). The subsequent hydrogenation to H2CO2 (step 7) has a forward activation energy of 114 kJ/mol (ΔEr = 80 kJ/mol). Notably, the formation of a C–H bond on the Ni1-adsorbed model is easier than on the Ni1-doped model. This can be ascribed to the hydride character of the H atom adsorbed to Ni. Next, the cleavage of a C–O bond in the H2CO2 intermediate takes place (step 8, Eact = 101 kJ/mol, ΔEr = 33 kJ/mol), leading to CH2O and an O atom, the latter healing the oxygen vacancy. After adsorption of another H2 molecule (step 9; Eact = 19 kJ/mol; ER = −36 kJ/mol), the CH2O moiety is hydrogenated to CH3O (step 10; Eact = 55 kJ/mol ER = −79 kJ/mol). Finally, CH3O hydrogenation to methanol and its subsequent desorption (step 11) take place in a single elementary reaction step with an activation energy of 61 kJ/mol.
On the Ni1-adsorbed model surface, methanol can also be obtained via CO hydrogenation, as seen in Figure 3b. This involves steps 12–15 in the CO hydrogenation pathway, followed by steps 9–11 in the formate pathway. Upon adsorption on an oxygen vacancy, CO2 can directly dissociate (step 12) into CO and O (Eact = 81 kJ/mol, ER = 3 kJ/mol), where the O replenishes the oxygen vacancy, restoring the stoichiometric surface. From this state, CO is further hydrogenated to HCO (step 14) after adsorption of another H2 molecule (step 13; Eact = 19 kJ/mol; ER = −36 kJ/mol). Herein, CO hydrogenation to HCO has an activation energy of 71 kJ/mol (ER = 6 kJ/mol). Subsequently, HCO is hydrogenated to CH2O (step 15), which has a barrier of 177 kJ/mol and is endothermic by 142 kJ/mol. The resulting CH2O fragment is part of the formate pathway and, thus, its subsequent hydrogenation of methanol can proceed via this pathway.
The CO by-product can be obtained via formation of H2O (steps 1–3), followed by direct cleavage of the C–O bond in CO2 and subsequent desorption of CO from a stoichiometric surface (steps 12 and 20). The desorption of CO from a stoichiometric surface is associated with a barrier of 121 kJ/mol. In addition, a H-assisted rWGS pathway was investigated. After adsorption of CO2 on an oxygen vacancy (step 5) and dissociative adsorption of H2 (step 6), protonation of CO2 takes place (step 16), yielding COOH (Eact = 82 kJ/mol; ER = 13 kJ/mol). Next, COOH dissociates (step 17) into CO and OH (Eact = 45 kJ/mol, ER = 20 kJ/mol). OH hydrogenation to form water (step 18) is associated with an activation energy of 140 kJ/mol and is endothermic by −58 kJ/mol. Finally, desorption of CO and H2O (steps 19 and 3) proceeds with desorption energies of 51 and 177 kJ/mol, respectively, closing the catalytic cycle.
3.3.3. Methanol Synthesis on Ni8-Cluster In2O3
The network diagram and PEDs of CO2 conversion to CH3OH and CO on the Ni8-cluster model are depicted in Figures 3c and 4c, respectively. The geometries of initial, transition, and final states can be found in Section S10. H2 adsorbs molecularly on the nanocluster (ΔEr = −49 kJ/mol) and then homolytically dissociates into H atoms (Eact = 22 kJ/mol, ΔEr = −40 kJ/mol). Overall, the process of H2 activation (step 1) is exothermic by −89 kJ/mol. Notably, H2 activation on the Ni8-cluster model is more facile than on the SA models, which is expected for a Ni cluster with a metallic character. Next, one interfacial O atom can be hydrogenated to form H2O. The barriers for the two consecutive hydrogenation steps are 152 kJ/mol (step 2) and 140 kJ/mol (step 3). Water desorption from the surface (step 4) costs 80 kJ/mol. The oxygen vacancy formation involves overall reaction and activation energies of −22 and 57 kJ/mol, respectively, with respect to gas-phase H2. On the oxygen-defective surface, CO2 adsorbs (ΔEads = −120 kJ/mol; step 5) at the metal–oxide interface with the carbon coordinating to a lattice oxygen next to two Ni–H fragments. From this state, CO2 can be hydrogenated to methanol via a formate intermediate (steps 7–12). First, CO2 is hydrogenated to HCO2 by a Ni–H species (step 7), which is exothermic by −25 kJ/mol and has an activation energy of 95 kJ/mol. Next, HCO2 is hydrogenated to H2CO2 (step 8) by another Ni–H species. This step features the highest forward barrier of the formate pathway (Eact = 177 kJ/mol) and is endothermic by ΔEr = 138 kJ/mol. Next, cleavage of a C–O bond in the H2CO2 intermediate yields CH2O and O (step 9), the latter replenishing the oxygen vacancy. This elementary reaction step has a barrier of 52 kJ/mol and is exothermic by ΔEr = −30 kJ/mol. After adsorption of another H2 on the Ni8 cluster (step 10; ΔEr = −89 kJ/mol), two further hydrogenation steps toward CH3O and CH3OH with activation energies of 83 kJ/mol (step 11; ΔEr = 41 kJ/mol) and 124 kJ/mol (step 12; ΔEr = −39 kJ/mol), respectively, lead to methanol. Desorption of methanol costs 35 kJ/mol (step 13).
Besides H-assisted CO2 dissociation via the formate intermediate, C–O bond scission can also proceed in a direct fashion following oxygen vacancy formation. Herein, the vacancy is healed upon C–O bond scission in adsorbed CO2. CO2 can adsorb on the Ni8 cluster with a slightly lower adsorption energy of ΔEads = −88 kJ/mol than on the vacancy (−120 kJ/mol). Subsequent dissociation of CO2 adsorbed on the cluster results in an O atom that heals the oxygen vacancy and adsorbed CO. This reaction has a barrier of 114 kJ/mol and is exothermic by 30 kJ/mol (step 14). This barrier is higher than the corresponding barrier over the Ni1-adsorbed system (Eact, adsorbed = 81 kJ/mol). CO is a precursor for methanol synthesis along the CO-hydrogenation pathway (Figures 3c and 4c, green). After CO2 dissociation, CO can either desorb (ΔEads = −130 kJ/mol; step 28), which would be representative of an alternative rWGS pathway to the one discussed below or be hydrogenated to either HCO (Eact = 150 kJ/mol; step 16) or COH (Eact = 235 kJ/mol; step 17). HCO can be hydrogenated toward HCOH (step 18). This step is endothermic by 30 kJ/mol and features a barrier of 69 kJ/mol. Alternatively, HCOH can also be formed from COH by hydrogenation involving a barrier of 211 kJ/mol (step 20; ΔEr = 50 kJ/mol). HCOH can subsequently be hydrogenated to H2COH (step 22; ΔEr = −52 kJ/mol) and then to CH3OH (step 23). These two hydrogenation steps have activation energies of Eact = 111 kJ/mol and Eact = 76 kJ/mol, respectively.
To verify our hypothesis that CO2 methanation on small In2O3-supported Ni clusters does not occur, we computed the barriers for direct and H-assisted CO dissociation. These steps are most likely the rate-limiting steps in CO2 methanation.73 The barriers for these steps are reported in Table S10, and the structures of the TS can be found in Table S11. We can compare these results to data for CO dissociation pathways on extended surfaces of Ni by Sterk et al.73 Compared to Ni(110), direct cleavage of the C–O bond on a Ni8-cluster model is associated with a very high barrier (Eact = 312 kJ/mol for the cluster vs Eact = 150 kJ/mol for Ni(110)). On the Ni8 cluster, the barrier of H-assisted CO dissociation via an HCO intermediate of 174 kJ/mol is more facile than the barrier for direct CO dissociation. However, this barrier is still significantly higher than the one computed for Ni(110) (Eact = 117 kJ/mol). It is likely that the structure of the Ni8-cluster model would also lead to high barriers for alternative CO dissociation reactions involving COH, H2CO, and H3CO intermediates due to the absence of step-edge sites, in line with the expectations based on experimental evidence.43
In line with the Ni1-adsorbed model, on the Ni8-cluster model, CO can be obtained via formation of H2O (steps 1–4), followed by direct cleavage of the C–O bond in CO2 and subsequent desorption of CO from a stoichiometric surface (steps 14 and 28, respectively). The desorption of CO from a stoichiometric surface has a barrier of 130 kJ/mol. Finally, we discuss the formation of CO from CO2 via the H-assisted rWGS pathway. Herein, one of the oxygen atoms of the CO2 molecule is protonated to form COOH (step 24) with an activation energy of 62 kJ/mol. This step is endothermic by 48 kJ/mol. In turn, COOH can dissociate on the Ni8 cluster into CO and OH (step 25; Eact = 66 kJ/mol). This step is exothermic by 59 kJ/mol. The resulting hydroxyl fragment is hydrogenated to H2O (step 26; Eact = 122 kJ/mol). Finally, H2O and CO desorb, leaving a vacancy on the surface with ΔEdes of 80 and 114 kJ/mol, respectively.
3.4. Microkinetic Simulations
3.4.1. Overall Kinetics
To compare the catalytic performance of different Ni/In2O3 models, we compute the CO2 hydrogenation reaction rate employing microkinetic simulations and the DFT reaction energetics. The active sites in our model consist of either isolated single Ni atoms, that is, either the Ni1-adsorbed or the Ni1-doped model or clusters (Ni8- and Ni6-cluster models) stabilized on the In2O3 support. We do not take migration of intermediates between the active sites into account. Co-adsorbed species are modeled as distinct varieties of a single active site. In this approximation, all elementary reaction steps are unimolecular, with the exception of the adsorption and desorption steps. A detailed list of the elementary reaction steps is provided in the Supporting Information.
The CO2 consumption rate and the CH3OH selectivity as a function of temperature are plotted in Figure 5 for the three systems considered. The turnover frequencies (TOF) toward CH3OH and CO are given in Figure S9. As can be seen from Figure 5a, the Ni1-doped and Ni8-cluster models exhibit the highest CO2 consumption rate below 275 °C. Above 300 °C, the Ni1-adsorbed and Ni1-doped systems are more active than the Ni8-cluster model. From Figure 5b, it can be seen that the CH3OH selectivity for the Ni8 cluster is 95% at 200 °C. With increasing temperature, the rate of CO formation increases faster than the rate of methanol formation (Figure S9a,b), resulting in a decrease in methanol selectivity. Above 350 °C, CO becomes the main reaction product, in line with experimental results. Both the Ni1-adsorbed and Ni1-doped models show negligible CH3OH selectivity (Figure 5b), indicating that these two models are mainly active for the rWGS reaction.
Figure 5.
(a) CO2 consumption rate (s–1) and (b) CH3OH selectivity as a function of temperature on different models (p = 50 bar, H2/CO2 ratio = 5).
To highlight the promoting effect of Ni on In2O3, we constructed a microkinetic model for unpromoted In2O3 based on the published DFT data of Frei et al.24 The resulting predictions in terms of activity and selectivity are provided in Figure S10. These data clearly show the promoting effect of Ni clusters on In2O3 for CO2 hydrogenation at relevant temperatures. Notably, these results are qualitatively in line with the experimental results published by Jia et al.39 Overall, this implies that the Ni8–In2O3 model presents the highest methanol reaction rate in line with our earlier experimental work.69
We also verified that methane formation on the Ni8-cluster model is unlikely by performing microkinetic simulations using the barrier for direct CO dissociation calculated on the Ni8 cluster (312 kJ/mol) and using the data by Sterk et al.73 for the C–H coupling steps. Sensitivity analysis shows that appreciable methane selectivity takes place only if the activation energy of the CO dissociation step is below 60 kJ/mol (Figure S11).
The results in terms of coverage, apparent activation energy (Eapp), and reaction orders as a function of temperature are given in Figure 6. The coverages in Figure 6a–c should be interpreted as the fraction of time the system spends in a particular state (i.e., the time average). According to the ergodicity principle in statistical thermodynamics, this equals the fraction of active sites that are in a particular state (i.e., the ensemble average). The Ni8 cluster (Figure 6a) predominantly resides in the HCO2 + H state at lower temperatures (200 °C < T < 300 °C). The reaction order in H2 (Figure 6d) is positive, while the reaction order in CO2 is close to zero. A higher H2 partial pressure is beneficial because it increases the rate of hydrogenation of HCO2 to methanol. As the surface is dominated by a CO2-derived intermediate, further increasing the CO2 partial pressure will not increase its coverage and the reaction rate, explaining the close to zero reaction order in this reactant. The kinetic parameters for the Ni8-cluster model lie within the range of values reported in the experimental literature for In2O3. For instance, Frei et al. reported a positive reaction order in H2 (0.33) and a close-to-zero order for CO2 at 250 °C.72 We find that, with increasing temperature, the reaction order in H2 decreases and the one in CO2 increases. This is because the oxygen vacancy state becomes the dominant state at high temperature (Figure 6a, in gray). In the limit of the empty surface, a higher partial pressure of CO2 results in a higher coverage with reaction intermediates, increasing the CO2 turnover rate. This behavior is also reflected in the Eapp trend (Figure 6d). The Eapp is approximately constant below 400 °C and decreases at higher temperature. This reflects a change in the changing coverages. By comparing Figure 6a,d, it can be seen that the decrease in the apparent activation energy goes together with an increase in the oxygen vacancies, resulting in a higher coverage of CO2. The exothermic energy of CO2 adsorption (ΔEads = −120 kJ/mol) lowers the apparent activation energy of the overall reaction. The computed Eapp for the Ni8-cluster model is in line with the experimental values reported on Ni/In2O3 (80 kJ/mol between 200 and 300 °C).39 We also performed simulations with either CO or CH3OH as the key component to better understand the decrease of the Eapp with decreasing temperature (Figure S12). On the Ni8-cluster, the Eapp for CH3OH synthesis is lower than the one for CO production (Figure S12a), in line with the selectivity trend depicted in Figure 5b. The trends in kinetic parameters as shown in Figure 6a,d for the Ni8 cluster are also in keeping with the changing selectivity from CH3OH to CO. To further understand these aspects, we investigate these trends in more detail with a DRC and a flux analysis (vide infra).
Figure 6.
Surface state of the model catalysts (a–c), reaction orders and apparent activation energies (d−f) with CO2 as the key component as a function of temperature.
For the Ni1-adsorbed model (Figure 6b), at lower temperature, the dominant surface state features two adsorbed H species (NiH + H) on a stoichiometric Ni1–In2O3(111) surface. Subsequent water desorption along the oxygen vacancy formation pathway is associated with a relatively high barrier (ΔEdes, H2O = 177 kJ/mol). This step is the most difficult one along the most favorable pathway, as can be seen in Figures 3b and 4b. As a result, the NiH + H state is dominant. With increasing temperatures, H2O desorption will be easier, resulting in more vacancies, where CO2 can adsorb. This results in a decreasing contribution of the NiH + H state in favor of intermediates in the CO2 hydrogenation pathway, such as CO2 + 2H and HCO2 + H. The reasons behind the latter two states being dominant can be understood from Figure 3b. CO2 binds strongly to the surface (ΔEads = −144 kJ/mol), and subsequent hydrogenation of CO2 to HCO2 has a low activation energy of only 66 kJ/mol (step 6 in Figure 3b), whereas the subsequent hydrogenation step to H2CO2 has a considerably higher activation energy of 114 kJ/mol (step 7 in Figure 3b). Consequently, the HCO2 + H state together with the CO2 + 2H state, which only differ by 2 kJ/mol, are found to be the dominant states.
At low temperatures, the reaction orders in both CO2 and H2 (Figure 6e) are close to zero. Under these conditions, the reaction is limited by the rate of H2O removal, which is the last step toward oxygen vacancy formation (step 3 in Figure 3b). The rate of H2O desorption is not affected by the partial pressure of H2 and CO2. A temperature increase thus results in the formation of oxygen vacancy and CO2 adsorption (Figure 6b). Under these conditions, an increased partial pressure of H2 leads to a higher rate of H adsorption which, together with the presence of adsorbed CO2, results in CO2 + 2H and HCO2 + H states becoming dominant. However, these elementary reaction steps proceed toward a branch in the kinetic network away from the dominant product (CO). Thus, under these conditions, the reaction order in H2 is negative.
For the Ni1-adsorbed model, Eapp (Figure 6e) is constant at 175 kJ/mol for temperatures below 300 °C. This value corresponds to the desorption energy of H2O. As the temperature increases, the Eapp decreases. On this model, the Eapp for the CH3OH product is higher than the Eapp for the CO by-product (Figure S12b), in line with the selectivity trend depicted in Figure 5b. Together, these findings suggest that oxygen vacancy formation controls the overall reaction rate at low temperatures while, at high temperatures, either CO2 activation or hydrogenation are limiting the overall rate. These aspects can be better appreciated by means of a DRC analysis (vide infra).
When Ni is doped inside In2O3 (Figure 6c), the surface is predominantly in the CO2 + 2H and HCO2 + H working states. Although CO2 hydrogenation to HCO2 is possible on the catalyst’s surface, further hydrogenation toward methanol is limited by the high barrier for HCO2 hydrogenation to H2CO2 (Eact = 313 kJ/mol, ΔEr = 287 kJ/mol). The reaction order in CO2 is zero because the dominant working state (either CO2 + 2H or HCO2 + H) already corresponds to intermediates derived from CO2. The reaction order in H2 is negative at low temperature, indicating that a higher partial pressure of H2 would push the network away from the dominant pathway. On the Ni1-doped model, the Eapp (Figure 6f) is constant to a value of 130 kJ/mol in the explored temperature range. In line with the Ni1-adsorbed model, on the Ni1-dopped system, the Eapp for the CH3OH product is higher than the Eapp for the CO by-product (Figure S12c).
3.4.2. Rate and Selectivity Control of the Reaction Network
In this section, we discuss in detail the reaction network that leads to CH3OH and CO formation from CO2 hydrogenation on the three Ni/In2O3 models. We identify the elementary steps that control the overall CO2 consumption rate and the CH3OH selectivity and investigate how these steps change with reaction temperature. For this purpose, we conduct a sensitivity analysis based on Campbell’s DRC63 and DSC.65,74 Under zero extent of reaction, the sum of the DRC coefficients is conserved at one.75 The DSC quantifies the extent to which a particular elementary reaction step influences the selectivity of certain products for which methanol is of our primary interest. Note that the sum of the DSC values of all elementary reaction steps for a single product equals zero.64
3.4.2.1. Ni8-cluster
The DRC and DSC analyses for the Ni8-cluster model are reported in Figure 7a,b, respectively. From these figures, it can be seen that at low temperatures (200 °C < T < 300 °C), the rate of CO2 consumption is almost exclusively controlled by the rate of HCO2 hydrogenation to H2CO2 (step 8 in Figure 7c), which has the highest activation energy in the dominant pathway as seen from Figure 7c (pathway highlighted in red). Other elementary steps, such as CH2O and CH3O hydrogenation (steps 11 and 12 in Figure 7c), control the kinetics to a smaller extent. These results are consistent with the positive reaction order in H2 and a reaction order in CO2 of zero (Figure 6d). A higher partial pressure of H2 would increase the concentration of Ni–H states necessary for the hydrogenation reactions, thus enhancing the overall rate, whereas a change in the partial pressure of CO2 would not affect these reactions. The DSC analysis (Figure 7b) shows that the same elementary steps that are controlling the rate are also controlling methanol selectivity. An increased rate of HCO2 hydrogenation (step 8) would result in a higher flux in the route toward methanol, benefiting its formation at the expense of CO formation. With increasing temperatures, a change in the selectivity from methanol to CO is observed (Figure 5b), which is reflected by the DRC analysis. Herein, the DRC coefficient of HCO2 hydrogenation to H2CO2 decreases as a function of temperature, whereas the DRC coefficient of OH hydrogenation to H2O (step 26 in Figure 7c) increases. This last step pertains to the rWGS branch in the kinetic network. Thus, this step is observed to inhibit the selectivity toward methanol. Figure 7b shows that, at higher temperatures, the steps of CH2O hydrogenation to CH3O and its further hydrogenation to CH3OH (steps 11 and 12, respectively) control the selectivity to the desired methanol product. These two steps require more Ni–H species to occur than HCO2 hydrogenation (step 8). However, Ni–H species are less abundant at high temperature, as we previously observed (Figure 6a), suggesting that steps requiring less surface hydrogen, like the ones pertaining the rWGS pathway, are facilitated at high temperature. This can explain the observed shift in selectivity toward CO and is also consistent with the decrease in the computed reaction orders in H2 (Figure 6d). To confirm the effect of H2 partial pressure on CH3OH selectivity, we performed a simulation with a H2/CO2 ratio of 1:5 (instead of 5:1) and observed that the selectivity to CH3OH decreases to 20% at 250 °C (Figure S13). Thus, the selectivity shift to CO observed at high temperatures can be explained by the lower availability of Ni–H species at such temperatures.
Figure 7.
DRC (a) and DSC (b) with CO2 as the key component as a function of temperature for the Ni8-cluster model. (c,d) Reaction network analysis (left) and dominant pathways (right) for CO2 hydrogenation to CH3OH, CO, and H2O. (c) T = 250 °C and (d) T = 400 °C (ptot = 50 bar, H2/CO2 = 5). The numbers in the arrows are molar reaction rates (s–1) and are normalized with respect to the amount of adsorbed CO2. The pathways with the highest molar fluxes are highlighted in red in the right part of the figure.
Figure 7c,d shows the flux analysis at low and high temperatures, respectively. Following the pathways with the largest molar fluxes readily reveals the dominant kinetic pathway at those conditions (highlighted in red). At low temperatures (Figure 7c), the dominant pathway corresponds to methanol formation via formate, whereas at high temperatures (Figure 7d), the dominant pathway shifts to the H-assisted rWGS route. This is consistent with the activity and selectivity trends predicted by the microkinetic model. The reaction flux diagram also shows that the pathway of CO hydrogenation to methanol features significantly lower rates (2.20 × 10–14 mol s–1; steps 14–23) than the formate pathway (2.65 × 10–5 mol s–1; steps 7–12), indicating that it is not taken. Indeed, hydrogenation of CO to HCO and CO to COH is associated with activation energies of 150 and 235 kJ/mol, respectively, while CO desorption is associated with a lower barrier of ΔEdes = 130 kJ/mol. Therefore, the desorption of CO is more favorable than its further hydrogenation to methanol. Concerning the formation of CO, Figure 7c,d shows that direct CO2 dissociation has lower rates (2.61 × 10–8 mol s–1; step 14) as compared to the H-assisted rWGS pathway (4.79 × 10–6 mol s–1; step 24). This difference can be ascribed to the higher activation energy for direct CO2 dissociation as compared to its hydrogenation to COOH (114 and 62 kJ/mol, respectively), which makes the H-assisted rWGS more facile.
3.4.2.2. Ni1-doped and Ni1-adsorbed
From Figure 5b, it was established that neither the Ni1-doped nor the Ni1-adsorbed models produce methanol. As such, we only consider the DRC and flux analyses as the DSC analysis will evidently only show coefficients close to zero for all elementary reaction steps.
The DRC analysis and reaction flux analysis for the Ni1-adsorbed model are shown in Figure 8a,b. At low temperatures, the CO2 consumption rate is mostly controlled by the rate of H2O desorption (step 3) because this elementary step has the highest barrier among the steps pertaining to the oxygen vacancy formation pathway (ΔEdes = 177 kJ/mol). This result is consistent with the surface state of the catalyst featuring mostly adsorbed hydrogen species (NiH + H, in Figure 6b), which is a state that precedes H2O formation. At higher temperatures (T > 275 °C), the formation of oxygen vacancies and subsequent adsorption of CO2 result in a decrease in the DRC coefficient of H2O desorption in favor of CO2 dissociation (step 12), which becomes the dominant rate-controlling step. An increased rate of CO2 dissociation (step 12) would result in a higher rate toward the main product CO. As can be seen in Figure 8b, the branch of the mechanism going toward CO2 hydrogenation via the formate pathway features considerably lower rates than the one proceeding toward CO2 dissociation (2.10 × 10–6 and 6.68 × 10–2 s–1, respectively). The formate pathway is not taken because the steps of H2CO hydrogenation to H2CO2 (step 7) and its further dissociation into CH2O and O (step 9) are highly activated and endothermic, resulting in an overall reaction energy and barrier of 150 and 172 kJ/mol, respectively. The dominant pathway (highlighted in red in Figure 8b, right) on the Ni1-adsorbed model proceeds thus via direct dissociation of CO2, yielding CO, which desorbs from the surface, closing the rWGS catalytic cycle. In line with the Ni8-cluster model, the pathway of CO hydrogenation to methanol is not taken (steps 13–15 in Figure 8b). This is due to the step of HCO hydrogenation to CH2O being associated with a high activation energy (Eact,f = 177 kJ/mol) and being endothermic (ΔEr = 142 kJ/mol). Concerning the formation of CO, the direct dissociation of CO2 is preferred over the H-assisted rWGS (6.54 × 10–2 and 1.05 × 10–4 s–1, respectively). This is because the H-assisted rWGS pathway is limited by the activation energy of OH hydrogenation (Eact = 140 kJ/mol), which is significantly higher than that of the CO2 dissociation and subsequent CO desorption elementary steps (81 and 121 kJ/mol, respectively).
Figure 8.
DRC analysis with CO2 as the key component as a function of temperature for (a) Ni1-adsorbed and (c) Ni1-doped model surfaces. Reaction network analysis (left) and dominant pathways (right, highlighted in red) for CO2 hydrogenation to CH3OH, CO, and H2O for (b) Ni1-adsorbed and (d) Ni1-doped model surfaces. (T = 250 °C, ptot = 50 bar, H2/CO2 = 5). The numbers in the arrows are molar reaction rates (s–1) and are normalized with respect to the amount of adsorbed CO2. The pathways with the highest molar fluxes are highlighted in red.
The DRC analysis and reaction flux analysis for the Ni1-doped model are shown in Figure 8c,d, respectively. The elementary reaction step of CO2 dissociation and CO desorption (step 14) has a DRC coefficient of 1; thus, it is the rate-determining step (RDS) in the mechanism under the explored temperature range (Figure 8c). This step is rate determining because it has the highest activation energy in the rWGS pathway (Figures 3a and 4a). The dominant pathway for the Ni1-doped model at T = 250 °C (Figure 8d right highlighted in red) involves the hydrogenation of CO2 to CO via a mechanism involving the formation of an oxygen vacancy (steps 1–3), adsorption of CO2 on an oxygen vacancy (step 4), subsequent formation of CO, and healing of the vacancy (step 14). Concerning the formation of CH3OH, negligible reaction fluxes for the formate pathway are found (3.43 × 10–26 s–1), in line with the TOFCH3OH computed by the microkinetic model (Figure S7a). This is due to the high activation energy associated with the hydrogenation of HCO2 to H2CO2 (Eact = 313 kJ/mol, ΔEr = 287 kJ/mol), which makes methanol formation unfavorable.
3.5. General Discussion
The present study provides new insights into the role of promoting Ni species in the In2O3-catalyzed hydrogenation of CO2 to methanol. Methanol formation involves oxygen vacancies in the In2O3 support. Frei et al. reported oxygen vacancy formation on a In2O3(111) surface via homolytic dissociation of molecular hydrogen forming two surface OH groups, followed by water formation and desorption.72 Oxygen vacancy formation has an overall barrier of 67 kJ/mol with respect to gas-phase H2.48 Heterolytic H2 dissociation on this surface was found to have a similar overall barrier.76 The presence of a Ni8-cluster on the In2O3 surface results in a lower overall barrier (57 kJ/mol), whereas when a single Ni atom is either doped in or adsorbed onto the In2O3(111) surface, higher overall barriers are found (70 and 150 kJ/mol, respectively). Since the Ni6 cluster has the same metallic character and interface with In2O3 as the Ni8-cluster, we infer that the overall barriers to oxygen vacancy formation on the two clusters should be similar. Thus, oxygen vacancies are likely to be present under reaction conditions of methanol synthesis. Their formation and role in the reaction mechanism were explicitly taken into account in the microkinetic models for methanol synthesis based on DFT calculations covering reaction mechanisms involving methanol formation via formates and CO.
On the Ni8-cluster model, at relatively low temperatures, the rate of CO2 consumption is mainly limited by the elementary step of HCO2 hydrogenation to H2CO2. The main reaction pathway to methanol on the Ni8 cluster is via low-barrier C–O bond dissociation in a H2CO2 intermediate. This results in a high methanol selectivity at low temperatures. With increasing temperatures, the selectivity shifts to CO in line with experimental observations.39,43 The dependence of the selectivity on the temperature is associated with the availability of NiHδ− species. The analysis of the surface coverages shows that, at relatively low temperature, hydrides mainly occupy the surface, favoring hydrogenation reactions. With increasing temperatures, the coverage of surface hydrogen rapidly decreases, as it is used to reduce the surface by creating oxygen vacancies. Since the rWGS reaction requires only two hydrogenation steps, whereas methanol formation requires four, the former reaction becomes dominant under surface-hydrogen-lean conditions.
The outcomes of the simulations might be affected by the size and shape of the cluster. For this reason, we compare our Ni8 cluster with a smaller Ni6-cluster, which was also obtained with our DFT-based GA. We looked into key elementary reaction steps that are limiting the rate for the formation of CH4, CO, and CH3OH based on the microkinetic analysis for CO2 hydrogenation on the supported Ni8-cluster. The forward and backward activation energies for these steps are reported in Table S12, and the structures of IS, TS, and FS are depicted in Table S13. As can be seen from Table S12, the forward and backward activation energies of the Ni6 cluster are comparable to those obtained for the Ni8-cluster. Based on these results, we constructed a microkinetic model for the Ni6-cluster, assuming that all the other elementary reaction steps are the same as for the Ni8-cluster. The results highlighted in Figure S13 show that also the Ni6 cluster exhibits significant selectivity to CH3OH at low temperature (50% at 200 °C). This indicates that the choice of an eight-atom cluster is sufficiently representative for small In2O3-supported Ni clusters.
We also briefly discuss here our results in comparison to the findings recently reported by Shen et al., who investigated DFT possible pathways of CO2 hydrogenation to methanol on Ni4/In2O3 model catalysts.42 In line with our work, interfacial oxygen vacancies not only contribute to the adsorption of CO2 but also facilitate the hydrogenation of intermediate species to methanol. Shen et al. speculated on the basis of energy diagrams that the formation of CO from CO2, followed by its hydrogenation to methanol, is favored over the formate pathway. This is at odds with our finding from microkinetic simulations that CO2 hydrogenation to methanol involves formates.
For the Ni1-adsorbed system, H2 dissociation is heterolytic, resulting in NiHδ− and OHδ+ species. On this model, oxygen vacancy formation is endothermic and is furthermore kinetically limited by H2O desorption. As oxygen vacancy formation is endothermic, healing the oxygen vacancy is favorable, resulting in a relatively low barrier for direct CO2 dissociation into CO and O, with the latter healing the vacancy. This, together with the lower availability of NiHδ− species, results in a preference for CO formation over hydrogenation to methanol, explaining the predicted high CO selectivity. In line with our work, Frei et al. suggested that Ni SA on In2O3 would be active for the rWGS reaction.41
The Ni1-doped system also does not lead to methanol. For this model, the abundance of OHδ+ species causes high activation energies for the formation of C–H bonds, as also reported in a previous work on In2O3.24 For instance, a barrier of 313 kJ/mol is associated with HCO2 hydrogenation to H2CO2, making methanol formation unfavorable. Furthermore, because of the doped configuration of Ni, there is steric hindrance preventing the carbon atom from effectively bonding to Ni. This prevents the direct involvement of Ni in the catalytic reaction. The dominant pathway on the Ni1-doped model features the formation of CO via a redox pathway involving the formation of an oxygen vacancy, the adsorption of CO2 on such a vacancy, and subsequent dissociation yielding CO. On this model, the elementary step of CO2 dissociation is the investigation of the RDS in the temperature range.
4. Conclusions
Using DFT to compute the electronic structure and reaction energy diagrams and construct the input for microkinetic simulations, we investigated the promoting role of Ni on In2O3 for CO2 hydrogenation to methanol. As the exact location and nuclearity of the Ni promoter in Ni/In2O3 catalysts are unknown, we considered three representative model systems: (i) a single Ni atom doped in the In2O3(111) surface, (ii) a Ni atom adsorbed on In2O3(111), and (iii) a small cluster of eight Ni atoms adsorbed on In2O3(111). With respect to the pristine In2O3(111) surface, the Ni8-cluster model offers a lower overall barrier to oxygen vacancy formation, whereas the Ni1-doped and Ni1-adsorbed models feature higher overall barriers. Microkinetic simulations reveal that significant methanol formation occurs only for the Ni8-cluster model. The metallic cluster allows for facile H2 activation, providing hydride (Ni–H) species needed for the formation of oxygen vacancies in In2O3 and hydrogenation reactions of adsorbed surface intermediates. Methanol synthesis at intermediate temperatures involves the hydrogenation of CO2 adsorbed on an oxygen vacancy to a H2CO2 intermediate (formate pathway). At higher temperatures, the lack of Ni–H species at the surface results in a shift of the selectivity to CO via a mechanism involving a COOH intermediate. On the Ni8-cluster model, high barriers associated with either direct or H-assisted CO activation inhibit methane formation. We compared our Ni8 cluster with a smaller Ni6 cluster also obtained with our DFT-based GA. Our DFT calculations show similar barriers for key rate-limiting steps for the formation of CO, CH4, and CH3OH for the two clusters. Based on this, we investigated the kinetics of the Ni6 cluster with microkinetic modeling and found appreciable selectivity to methanol at low temperatures. Therefore, we conclude that our choice of an eight-atom cluster is sufficiently representative for a small In2O3-supported Ni cluster. When a single Ni atom is adsorbed on the In2O3 surface, CO is the main product because a relatively low barrier for direct CO2 dissociation is available. When a single Ni atom is doped in the In2O3 surface, the acidic nature of the H atoms adsorbed on the oxygen anions of In2O3 results in high activation barriers for CO2 hydrogenation reactions, precluding methanol formation.
Acknowledgments
The authors acknowledge NWO and SurfSARA for providing access to computational resources used to carry out the DFT calculations reported in this work. This work was supported by the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation program funded by the Ministry of Education, Culture and Science of the Government of the Netherlands. This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 801359.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscatal.2c04872.
Detailed description of the stability of the Ni SA-doped and adsorbed model, an analysis of the structures obtained with the DFT-based GA, electronic structure and Bader charge analysis of Ni/In2O3 models, full DFT dataset of the mechanisms investigated, geometries of elementary reaction steps, further microkinetic simulations, comparison with a Ni6-cluster, and the coordinates of the models (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- González-Garay A.; Frei M. S.; Al-Qahtani A.; Mondelli C.; Guillén-Gosálbez G.; Pérez-Ramírez J. Plant-to-Planet Analysis of CO2-Based Methanol Processes. Energy Environ. Sci. 2019, 12, 3425–3436. 10.1039/C9EE01673B. [DOI] [Google Scholar]
- Kondratenko E. V.; Mul G.; Baltrusaitis J.; Larrazábal G. O.; Pérez-Ramírez J. Status and Perspectives of CO2 Conversion into Fuels and Chemicals by Catalytic, Photocatalytic and Electrocatalytic Processes. Energy Environ. Sci. 2013, 6, 3112. 10.1039/c3ee41272e. [DOI] [Google Scholar]
- Dias V.; Pochet M.; Contino F.; Jeanmart H. Energy and Economic Costs of Chemical Storage. Front. Mech. Eng. 2020, 6, 21. 10.3389/fmech.2020.00021. [DOI] [Google Scholar]
- Álvarez A.; Bansode A.; Urakawa A.; Bavykina A. V.; Wezendonk T. A.; Makkee M.; Gascon J.; Kapteijn F. Challenges in the Greener Production of Formates/Formic Acid, Methanol, and DME by Heterogeneously Catalyzed CO2 Hydrogenation Processes. Chem. Rev. 2017, 117, 9804–9838. 10.1021/acs.chemrev.6b00816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong J.; Yang X.; Wu Z.; Liang B.; Huang Y.; Zhang T. State of the Art and Perspectives in Heterogeneous Catalysis of CO2 Hydrogenation to Methanol. Chem. Soc. Rev. 2020, 49, 1385–1413. 10.1039/c9cs00614a. [DOI] [PubMed] [Google Scholar]
- Jiang X.; Nie X.; Guo X.; Song C.; Chen J. G. Recent Advances in Carbon Dioxide Hydrogenation to Methanol via Heterogeneous Catalysis. Chem. Rev. 2020, 120, 7984–8034. 10.1021/acs.chemrev.9b00723. [DOI] [PubMed] [Google Scholar]
- Gumber S.; Gurumoorthy A. V. P.. Methanol Economy Versus Hydrogen Economy. Methanol; Elsevier, 2018; pp 661–674. [Google Scholar]
- Olah G. A. Beyond Oil and Gas: The Methanol Economy. Angew. Chem., Int. Ed. 2005, 44, 2636–2639. 10.1002/anie.200462121. [DOI] [PubMed] [Google Scholar]
- Goeppert A.; Czaun M.; Jones J. P.; Surya Prakash G. K.; Olah G. A. Recycling of carbon dioxide to methanol and derived products - closing the loop. Chem. Soc. Rev. 2014, 43, 7995–8048. 10.1039/c4cs00122b. [DOI] [PubMed] [Google Scholar]
- Baltes C.; Vukojevic S.; Schuth F. Correlations between Synthesis, Precursor, and Catalyst Structure and Activity of a Large Set of CuO/ZnO/Al2O3 Catalysts for Methanol Synthesis. J. Catal. 2008, 258, 334–344. 10.1016/j.jcat.2008.07.004. [DOI] [Google Scholar]
- Sehested J. Industrial and Scientific Directions of Methanol Catalyst Development. J. Catal. 2019, 371, 368–375. 10.1016/j.jcat.2019.02.002. [DOI] [Google Scholar]
- Behrens M. Promoting the Synthesis of Methanol: Understanding the Requirements for an Industrial Catalyst for the Conversion of CO2. Angew. Chem., Int. Ed. 2016, 55, 14906–14908. 10.1002/anie.201607600. [DOI] [PubMed] [Google Scholar]
- Nakamura J.; Choi Y.; Fujitani T. On the Issue of the Active Site and the Role of ZnO in Cu/ZnO Methanol Synthesis Catalysts. Top. Catal. 2003, 22, 277–285. 10.1023/A:1023588322846. [DOI] [Google Scholar]
- Fichtl M. B.; Schlereth D.; Jacobsen N.; Kasatkin I.; Schumann J.; Behrens M.; Schlögl R.; Hinrichsen O. Kinetics of Deactivation on Cu/ZnO/Al2O3 Methanol Synthesis Catalysts. Appl. Catal., A 2015, 502, 262–270. 10.1016/j.apcata.2015.06.014. [DOI] [Google Scholar]
- Wang J.; Li G.; Li Z.; Tang C.; Feng Z.; An H.; Liu H.; Liu T.; Li C. A Highly Selective and Stable ZnO-ZrO2 Solid Solution Catalyst for CO2 Hydrogenation to Methanol. Sci. Adv. 2017, 3, e1701290 10.1126/sciadv.1701290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C.-S.; Melaet G.; Ralston W. T.; An K.; Brooks C.; Ye Y.; Liu Y. S.; Zhu J.; Guo J.; Alayoglu S.; Somorjai G. A. High-Performance Hybrid Oxide Catalyst of Manganese and Cobalt for Low-Pressure Methanol Synthesis. Nat. Commun. 2015, 6, 6538. 10.1038/ncomms7538. [DOI] [PubMed] [Google Scholar]
- Posada-Pérez S.; Viñes F.; Ramirez P. J.; Vidal A. B.; Rodriguez J. A.; Illas F. The bending machine: CO2 activation and hydrogenation on δ-MoC(001) and β-Mo2C(001) surfaces. Phys. Chem. Chem. Phys. 2014, 16, 14912–14921. 10.1039/c4cp01943a. [DOI] [PubMed] [Google Scholar]
- Kunkel C.; Viñes F.; Illas F. Transition Metal Carbides as Novel Materials for CO2 Capture, Storage, and Activation. Energy Environ. Sci. 2016, 9, 141–144. 10.1039/c5ee03649f. [DOI] [Google Scholar]
- Duyar M. S.; Tsai C.; Snider J. L.; Singh J. A.; Gallo A.; Yoo J. S.; Medford A. J.; Abild-Pedersen F.; Studt F.; Kibsgaard J.; Bent S. F.; Nørskov J. K.; Jaramillo T. F. A Highly Active Molybdenum Phosphide Catalyst for Methanol Synthesis from CO and CO 2. Angew. Chem., Int. Ed. 2018, 57, 15045–15050. 10.1002/anie.201806583. [DOI] [PubMed] [Google Scholar]
- Fiordaliso E. M.; Sharafutdinov I.; Carvalho H. W. P.; Grunwaldt J. D.; Hansen T. W.; Chorkendorff I.; Wagner J. B.; Damsgaard C. D. Intermetallic GaPd2 Nanoparticles on SiO2 for Low-Pressure CO2 Hydrogenation to Methanol: Catalytic Performance and in Situ Characterization. ACS Catal. 2015, 5, 5827–5836. 10.1021/acscatal.5b01271. [DOI] [Google Scholar]
- Studt F.; Sharafutdinov I.; Abild-Pedersen F.; Elkjær C. F.; Hummelshøj J. S.; Dahl S.; Chorkendorff I.; Nørskov J. K. Discovery of a Ni-Ga Catalyst for Carbon Dioxide Reduction to Methanol. Nat. Chem. 2014, 6, 320–324. 10.1038/nchem.1873. [DOI] [PubMed] [Google Scholar]
- Frei M. S.; Mondelli C.; Cesarini A.; Krumeich F.; Hauert R.; Stewart J. A.; Curulla Ferré D.; Pérez-Ramírez J. Role of Zirconia in Indium Oxide-Catalyzed CO2 Hydrogenation to Methanol. ACS Catal. 2020, 10, 1133–1145. 10.1021/acscatal.9b03305. [DOI] [Google Scholar]
- Frei M. S.; Mondelli C.; Pérez-Ramírez J. Development of In2O3-Based Catalysts for CO2-Based Methanol Production. Chimia 2020, 74, 257–262. 10.2533/chimia.2020.257. [DOI] [PubMed] [Google Scholar]
- Frei M. S.; Capdevila-Cortada M.; García-Muelas R.; Mondelli C.; López N.; Stewart J. A.; Curulla Ferré D.; Pérez-Ramírez J. Mechanism and Microkinetics of Methanol Synthesis via CO2 Hydrogenation on Indium Oxide. J. Catal. 2018, 361, 313–321. 10.1016/j.jcat.2018.03.014. [DOI] [Google Scholar]
- Frei M. S.; Mondelli C.; García-Muelas R.; Kley K. S.; Puértolas B.; López N.; Safonova O. V.; Stewart J. A.; Curulla Ferré D.; Pérez-Ramírez J. Atomic-Scale Engineering of Indium Oxide Promotion by Palladium for Methanol Production via CO2 Hydrogenation. Nat. Commun. 2019, 10, 3377. 10.1038/s41467-019-11349-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Q.; Ye J.; Liu C.; Ge Q. In2O3as a promising catalyst for CO2utilization: A case study with reverse water gas shift over In2O3. Greenhouse Gases: Sci. Technol. 2014, 4, 140–144. 10.1002/ghg.1401. [DOI] [Google Scholar]
- Ye J.; Liu C.; Ge Q. DFT Study of CO2 Adsorption and Hydrogenation on the In2O3 Surface. J. Phys. Chem. C 2012, 116, 7817–7825. 10.1021/jp3004773. [DOI] [Google Scholar]
- Ye J.; Liu C.; Mei D.; Ge Q. Active Oxygen Vacancy Site for Methanol Synthesis from CO2 Hydrogenation on In2O3(110): A DFT Study. ACS Catal. 2013, 3, 1296–1306. 10.1021/cs400132a. [DOI] [Google Scholar]
- Cao A.; Wang Z.; Li H.; Nørskov J. K. Relations between Surface Oxygen Vacancies and Activity of Methanol Formation from CO2 Hydrogenation over In2O3 Surfaces. ACS Catal. 2021, 11, 1780–1786. 10.1021/acscatal.0c05046. [DOI] [Google Scholar]
- Wang J.; Zhang G.; Zhu J.; Zhang X.; Ding F.; Zhang A.; Guo X.; Song C. CO2 Hydrogenation to Methanol over In2O3-Based Catalysts: From Mechanism to Catalyst Development. ACS Catal. 2021, 11, 1406–1423. 10.1021/acscatal.0c03665. [DOI] [Google Scholar]
- Posada-Borbón A.; Grönbeck H. A First-Principles-Based Microkinetic Study of CO2Reduction to CH3OH over In2O3(110). ACS Catal. 2021, 11, 9996–10006. 10.1021/acscatal.1c01707. [DOI] [Google Scholar]
- Rui N.; Zongyuan W.; Kaihang S.; Ye J.; Liu C. CO2 hydrogenation to methanol over Pd/In2O3: effect of Pd and oxygen vacancy. Appl. Catal. B. 2017, 218, 488–497. 10.1016/j.apcatb.2017.06.069. [DOI] [Google Scholar]
- Ye J.; Liu C.; Mei D.; Ge Q. Methanol Synthesis from CO2 Hydrogenation over a Pd4/In2O3 Model Catalyst: A Combined DFT and Kinetic Study. J. Catal. 2014, 317, 44–53. 10.1016/j.jcat.2014.06.002. [DOI] [Google Scholar]
- Sun K.; Rui N.; Zhang Z.; Sun Z.; Ge Q.; Liu C. J. A highly active Pt/In2O3 catalyst for CO2 hydrogenation to methanol with enhanced stability. Green Chem. 2020, 22, 5059–5066. 10.1039/d0gc01597k. [DOI] [Google Scholar]
- Sun K.; Rui N.; Shen C.; Liu C. J. Theoretical Study of Selective Hydrogenation of CO2 to Methanol over Pt4/In2O3 Model Catalyst. J. Phys. Chem. C 2021, 125, 10926–10936. 10.1021/acs.jpcc.1c00638. [DOI] [Google Scholar]
- Han Z.; Tang C.; Wang J.; Li L.; Li C. Atomically Dispersed Ptn+ Species as Highly Active Sites in Pt/In2O3 Catalysts for Methanol Synthesis from CO2 Hydrogenation. J. Catal. 2021, 394, 236. 10.1016/j.jcat.2020.06.018. [DOI] [Google Scholar]
- Bavykina A.; Yarulina I.; Al Abdulghani A. J.; Gevers L.; Hedhili M. N.; Miao X.; Galilea A. R.; Pustovarenko A.; Dikhtiarenko A.; Cadiau A.; Aguilar-Tapia A.; Hazemann J.-L.; Kozlov S. M.; Oud-Chikh S.; Cavallo L.; Gascon J. Turning a Methanation Co Catalyst into an In–Co Methanol Producer. ACS Catal. 2019, 9, 6910. 10.1021/acscatal.9b01638. [DOI] [Google Scholar]
- Shi Z.; Tan Q.; Tian C.; Pan Y.; Sun X.; Zhang J.; Wu D. CO2 Hydrogenation to Methanol over Cu-In Intermetallic Catalysts: Effect of Reduction Temperature. J. Catal. 2019, 379, 78–89. 10.1016/j.jcat.2019.09.024. [DOI] [Google Scholar]
- Jia X.; Sun K.; Wang J.; Shen C.; Liu C. jun. Selective Hydrogenation of CO2 to Methanol over Ni/In2O3 Catalyst. J. Energy Chem. 2020, 50, 409–415. 10.1016/j.jechem.2020.03.083. [DOI] [Google Scholar]
- Snider J. L.; Streibel V.; Hubert M. A.; Choksi T. S.; Valle E.; Upham D. C.; Schumann J.; Duyar M. S.; Gallo A.; Abild-Pedersen F.; Jaramillo T. F. Revealing the Synergy between Oxide and Alloy Phases on the Performance of Bimetallic In-Pd Catalysts for CO2 Hydrogenation to Methanol. ACS Catal. 2019, 9, 3399–3412. 10.1021/acscatal.8b04848. [DOI] [Google Scholar]
- Frei M. S.; Mondelli C.; García-Muelas R.; Morales-Vidal J.; Philipp M.; Safonova O. V.; López N.; Stewart J. A.; Ferré D. C.; Pérez-Ramírez J. Nanostructure of Nickel-Promoted Indium Oxide Catalysts Drives Selectivity in CO 2 Hydrogenation. Nat. Commun. 2021, 12, 1960. 10.1038/s41467-021-22224-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen C.; Bao Q.; Xue W.; Sun K.; Zhang Z.; Jia X.; Mei D.; Liu C. jun. Synergistic Effect of the Metal-Support Interaction and Interfacial Oxygen Vacancy for CO2 Hydrogenation to Methanol over Ni/In2O3 Catalyst: A Theoretical Study. J. Energy Chem. 2022, 65, 623–629. 10.1016/j.jechem.2021.06.039. [DOI] [Google Scholar]
- Zhu J.; Cannizzaro F.; Liu L.; Zhang H.; Kosinov N.; Filot I. A. W.; Rabeah J.; Brückner A.; Hensen E. J. M. Ni-In Synergy in CO2 Hydrogenation to Methanol. ACS Catal. 2021, 11, 11371–11384. 10.1021/acscatal.1c03170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758. 10.1103/physrevb.59.1758. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initiomolecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. 10.1103/physrevb.49.14251. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Albani D.; Capdevila-Cortada M.; Vilé G.; Mitchell S.; Martin O.; López N.; Pérez-Ramírez J. Semihydrogenation of Acetylene on Indium Oxide: Proposed Single-Ensemble Catalysis. Angew. Chem., Int. Ed. 2017, 56, 10755–10760. 10.1002/anie.201704999. [DOI] [PubMed] [Google Scholar]
- Chang M. W.; Zhang L.; Davids M.; Filot I. A. W.; Hensen E. J. M. Dynamics of Gold Clusters on Ceria during CO Oxidation. J. Catal. 2020, 392, 39–47. 10.1016/j.jcat.2020.09.027. [DOI] [Google Scholar]
- Vilhelmsen L. B.; Hammer B. A Genetic Algorithm for First Principles Global Structure Optimization of Supported Nano Structures. J. Chem. Phys. 2014, 141, 044711. 10.1063/1.4886337. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Jónsson H. Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points. J. Chem. Phys. 2000, 113, 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- Heidrich D.; Quapp W. Saddle Points of Index 2 on Potential Energy Surfaces and Their Role in Theoretical Reactivity Investigations. Theor. Chim. Acta 1986, 70, 89–98. 10.1007/bf00532206. [DOI] [Google Scholar]
- Nelson R.; Ertural C.; George J.; Deringer V. L.; Hautier G.; Dronskowski R. LOBSTER : Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. 10.1002/jcc.26353. [DOI] [PubMed] [Google Scholar]
- Maintz S.; Deringer V. L.; Tchougr A. L.; Dronskowski R. LOBSTER: A Tool to Extract Chemical Bonding from Plane-Wave Based DFT. Comput. Chem. 2016, 37, 1030. 10.1002/jcc.24300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu M.; Trinkle D. R. Accurate and Efficient Algorithm for Bader Charge Integration. J. Chem. Phys. 2011, 134, 064111. 10.1063/1.3553716. [DOI] [PubMed] [Google Scholar]
- Brown P. N.; Byrne G. D.; Hindmarsh A. C. VODE: A Variable-Coefficient ODE Solver. SIAM J. Sci. Comput. 1989, 10, 1038. 10.1137/0910062. [DOI] [Google Scholar]
- Byrne G. D.; Hindmarsh A. C. Stiff ODE Solvers: A Review of Current and Coming Attractions. J. Comput. Phys. 1987, 70, 1–62. 10.1016/0021-9991(87)90001-5. [DOI] [Google Scholar]
- Byrne G. D.; Hindmarsh A. C. A Polyalgorithm for the Numerical Solution of Ordinary Differential Equations. ACM Trans. Math Software 1975, 1, 71–96. 10.1145/355626.355636. [DOI] [Google Scholar]
- Shomate C. H. A Method for Evaluating and Correlating Thermodynamic Da Ta. J. Phys. Chem. A 2002, 58, 368–372. 10.1021/j150514a018. [DOI] [Google Scholar]
- NIST Chemistry WebBook, https://webbook.nist.gov/chemistry/ (accessed Feb 1, 2022).
- Kozuch S.; Shaik S. A Combined Kinetic–Quantum Mechanical Model for Assessment of Catalytic Cycles: Application to Cross-Coupling and Heck Reactions. J. Am. Chem. Soc. 2006, 128, 3355–3365. 10.1021/ja0559146. [DOI] [PubMed] [Google Scholar]
- Kozuch S.; Shaik S. Kinetic-Quantum Chemical Model for Catalytic Cycles: The Haber–Bosch Process and the Effect of Reagent Concentration. J. Phys. Chem. A 2008, 112, 6032–6041. 10.1021/jp8004772. [DOI] [PubMed] [Google Scholar]
- Campbell C. T. The Degree of Rate Control: A Powerful Tool for Catalysis Research. ACS Catal. 2017, 7, 2770–2779. 10.1021/acscatal.7b00115. [DOI] [Google Scholar]
- Filot A. W.Introduction to Microkinetic Modeling; Technische Universiteit Eindhoven, 2017. [Google Scholar]
- Stegelmann C.; Schiødt N. C.; Campbell C. T.; Stoltze P. Microkinetic Modeling of Ethylene Oxidation over Silver. J. Catal. 2004, 221, 630–649. 10.1016/j.jcat.2003.10.004. [DOI] [Google Scholar]
- de Amorim R. V.; Batista K. E. A.; Nagurniak G. R.; Orenha R. P.; Parreira R. L. T.; Piotrowski M. J. CO, NO, and SO Adsorption on Ni Nanoclusters: A DFT Investigation. Dalt. Trans. 2020, 49, 6407–6417. 10.1039/d0dt00288g. [DOI] [PubMed] [Google Scholar]
- Qin B.; Li S. First Principles Investigation of Dissociative Adsorption of H2 during CO2 Hydrogenation over Cubic and Hexagonal In2O3 Catalysts. Phys. Chem. Chem. Phys. 2020, 22, 3390–3399. 10.1039/c9cp05867b. [DOI] [PubMed] [Google Scholar]
- Li Y.; Xu W.; Liu W.; Han S.; Cao P.; Fang M.; Zhu D.; Lu Y. High-Performance Thin-Film Transistors with Aqueous Solution-Processed NiInO Channel Layer. ACS Appl. Electron. Mater. 2019, 1, 1842–1851. 10.1021/acsaelm.9b00377. [DOI] [Google Scholar]
- Zhu J.; Cannizzaro F.; Liu L.; Zhang H.; Kosinov N.; Filot I. A. W.; Rabeah J.; Brückner A.; Hensen E. J. M. Ni-In Synergy in CO2 Hydrogenation to Methanol. ACS Catal. 2021, 11, 11371–11384. 10.1021/acscatal.1c03170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye J.; Liu C.; Mei D.; Ge Q. Active Oxygen Vacancy Site for Methanol Synthesis from CO2 Hydrogenation on In2O3(110): A DFT Study. ACS Catal. 2013, 3, 1296–1306. 10.1021/cs400132a. [DOI] [Google Scholar]
- Ye J.; Liu C.; Ge Q. DFT Study of CO2 Adsorption and Hydrogenation on the In2O3 Surface. J. Phys. Chem. C 2012, 116, 7817–7825. 10.1021/jp3004773. [DOI] [Google Scholar]
- Frei M. S.; Capdevila-Cortada M.; García-Muelas R.; Mondelli C.; López N.; Stewart J. A.; Curulla Ferré D.; Pérez-Ramírez J. Mechanism and Microkinetics of Methanol Synthesis via CO2 Hydrogenation on Indium Oxide. J. Catal. 2018, 361, 313–321. 10.1016/j.jcat.2018.03.014. [DOI] [Google Scholar]
- Sterk E. B.; Nieuwelink A. E.; Monai M.; Louwen J. N.; Vogt E. T. C.; Filot I. A. W.; Weckhuysen B. M. Structure Sensitivity of CO2Conversion over Nickel Metal Nanoparticles Explained by Micro-Kinetics Simulations. J. Am. Chem. Soc. 2022, 2, 2714. 10.1021/jacsau.2c00430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegelmann C.; Andreasen A.; Campbell C. T. Degree of Rate Control: How Much the Energies of Intermediates and Transition States Control Rates. J. Am. Chem. Soc. 2009, 131, 8077–8082. 10.1021/ja9000097. [DOI] [PubMed] [Google Scholar]
- Filot A. W.Introduction to Microkinetic Modeling; Technische Universiteit Eindhoven, 2017. [Google Scholar]
- Qin B.; Li S. First Principles Investigation of Dissociative Adsorption of H2 during CO2 Hydrogenation over Cubic and Hexagonal In2O3 Catalysts. Phys. Chem. Chem. Phys. 2020, 22, 3390–3399. 10.1039/c9cp05867b. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.











