Hydrodynamic clustering of two finite-length flagellated swimmers in viscoelastic fluids

Abstract

Clustering of flagellated microswimmers such as sperm is often mediated by hydrodynamic interactions between them. To better understand the interaction of microswimmers in viscoelastic fluids, we perform two-dimensional simulations of two swimming sheets, using a viscoelastic version of the smoothed dissipative particle dynamics method that implements the Oldroyd-B fluid model. Elasticity of sheets (stiff versus soft) defines two qualitatively different regimes of clustering, where stiff sheets exhibit a much more robust clustering than soft sheets. A formed doublet of soft sheets generally swims faster than a single swimmer, while a pair of two stiff sheets normally shows no speed enhancement after clustering. A pair of two identical swimmers is stable for most conditions, while differences in the beating amplitudes and/or frequencies between the two sheets can destroy the doublet stability. Clustering of two distinct swimmers is most stable at Deborah numbers of De = τω ≈ 1 (τ is the relaxation time of a viscoelastic fluid and ω is the beating frequency), in agreement with experimental observations. Therefore, the clustering of two swimmers depends non-monotonically on De. Our results suggest that the cluster stability is likely a dominant factor which determines the cluster size of collectively moving flagellated swimmers.

1. Introduction

Synchronization and clustering of dynamic appendages, such as flagella and cilia, is a common phenomenon in many biological systems. Sperm cells interact when they are in the close proximity of each other to form pairs, triplets and even large clusters [1–6]. Chlamydomonas algae exhibit an in-phase synchronization of their two beating flagella in order to swim straight and fast [7–10]. Helical flagella of Escherichia coli bacteria self-organize into a bundle to swim straight, but can be disentangled to reorient [11–13]. In the respiratory system, an ensemble of cilia can beat and synchronize to generate flows which transport mucus [14,15]. In all these examples, the synchronization and clustering of swimmers and their appendages are critical for a proper functioning of different biological systems.

Theoretical analyses, experiments and simulations have confirmed that the synchronization of external appendages and clustering of swimmers can be achieved purely through hydrodynamic interactions between them [2,16–19]. In the limit of zero Reynolds number (i.e. no inertia), the kinematic reversibility of Stokes flow would prevent the synchronization of inextensible symmetric flagella [20,21]. However, this symmetry can be broken by various factors, such as inertia [22–24], flagella elasticity [25–27], fluid elasticity [28,29] and waveform asymmetry [20,30]. Therefore, for most biological systems, hydrodynamic interactions nearly always facilitate the synchronization of active external appendages and interactions between swimmers.

Synchronization and clustering of microswimmers within a fluid-like environment are also instrumental for the collective behaviour of microorganisms and artificial swimmers, which has recently attracted a lot of scientific attention directed at the understanding of relevant physical mechanisms and potential biomedical applications [31–33]. Clustering of microswimmers is dominated by short-range (within a swimmer size) interactions between them, since inter-swimmer distances within a cluster are generally small [3,34]. For instance, swimming sperms can form multicellular clusters due to hydrodynamic interactions between them [3–5]. Interestingly, the clustering of sperms is enhanced in non-Newtonian viscoelastic fluids in comparison to sperm behaviour in Newtonian viscous fluids, which likely arises from the effect of fluid elasticity [5,35]. A further important question is the stability of sperm clusters with respect to differences in the swimming behaviour of different sperm cells, as experimental observations [5] clearly show that sperm clusters are very dynamic with a frequent interchange in their cell content. Therefore, a possible reason affecting the clustering of sperm cells and the stability of sperm clusters is an intrinsic variability in the swimming properties of sperm cells, including differences in their flagellum length and beating patterns [6].

To better understand clustering of sperm-like swimmers, we perform a systematic investigation of the clustering of two finite-length sheets with and without a head. Our primary focus is on the clustering properties of two swimmers in viscoelastic fluids represented by the Oldroyd-B fluid model. We employ a viscoelastic version of the smoothed dissipative particle dynamics (SDPD) method [36,37] to model fluid-like environment and an actuated elastic sheet model in two-dimensional (2D) simulations. We find that the elasticity of sheets (stiff versus soft) results in two qualitatively distinct regimes of clustering, where stiff sheets generally show a much more robust clustering than soft sheets. Fluid elasticity can enhance as well as reduce the interaction strength, depending on sheet properties, inter-sheet distance and fluid viscoelastic characteristics. Even though a formed doublet of two identical swimmers is generally stable for most conditions, the stability can be destroyed through relatively small differences in swimmer properties, such as the beating amplitude and frequency. The swimmer clustering results are corroborated well by inter-sheet force measurements for various conditions, and contribute toward better understanding of the collective behaviour of flagellated microswimmers such as sperm.

Our numerical study primarily focuses on the generic effects of sheet elasticity and fluid viscoelasticity for the propulsion of flagellated beating microswimmers. In this respect, sperm cells are best for comparison, since they propel in a similar way to our swimmer model and, therefore, hydrodynamic interaction mechanisms are likely similar [3,6,38]. Another limitation of our study is that we consider only 2D motion of microswimmers, while the propulsion of biological microorganisms is generally three-dimensional (3D). For the example of sperm cells, we expect that in 3D the interaction strength should be weaker than in 2D due to an additional degree of freedom. However, it is worth mentioning that a 2D representation may not be appropriate for some flagellated microswimmers, such as E. coli bacteria which have helical flagella rotated by internal motors [11,39]. In this example, not only is the propulsion strategy different from that for beating flagella, but also the generated 3D flow field is important for swimmer interactions with each other and encountered surfaces [40–42].

This article is organized as follows. Section 2 provides all necessary details about the employed simulation method and swimmer modelling. Section 3.1 presents swimming properties of a single sheet, while §3.2 discusses the dynamic attraction and clustering process of two swimmers. In §3.3, we study changes in the swimming properties of a clustered pair in comparison to those of a single swimmer. Section 3.4 discusses the cluster stability of two swimmers with respect to differences in their swimming behaviour, and §3.5 provides measurements of inter-sheet forces as a function of separation distance in order to better rationalize the observed clustering behaviour. Finally, we conclude in §4.

2. Methods and models

2.1. Viscoelastic Oldroyd-B fluid

SDPD [36] is a particle-based hydrodynamics method commonly used for mesoscopic simulations. SDPD is derived through the discretization of Navier–Stokes equation and includes consistent thermal fluctuations [43]. The standard SDPD method [36] models viscous Newtonian fluids and requires an extension for non-Newtonian fluids. We use a viscoelastic extension of the SDPD method which implements the Oldroyd-B model [37]. In this model, every fluid particle contains N_p polymer molecules. These polymer molecules are not explicitly simulated, but represented by a conformation tensor that characterizes polymer extension through the second moment of the end-to-end distance distribution function. The conformation tensor is defined as

$${\mathit{c}}_i=\frac{1}{N_{\mathrm{p}}}\sum _a^{N_{\mathrm{p}}}{\mathit{q}}_a{\mathit{q}}_a,$$ 2.1

where q_a is the end-to-end distance of the ath polymer within the fluid particle i.

Using the GENERIC formalism [44,45], evolution equations for particle position, velocity, energy and conformation tensor have been derived in a thermodynamically consistent way [37]. When a Hookean dumbbell model is used to represent polymers, the resulting SDPD method corresponds to the Oldroyd-B model of viscoelastic fluids. For a thermally isotropic system, the motion equations are given by [37]

$$\begin{array}{rl}& {\dot{\mathit{r}}}_i={\mathit{v}}_i,\\ & m_i{\dot{\mathit{v}}}_i={\displaystyle \sum _j({\mathit{F}}_{ij}^C+{\mathit{F}}_{ij}^D+{\tilde{\mathit{F}}}_{ij}),}\\ & {\mathit{F}}_{ij}^C=(\frac{{\mathit{\Pi }}_i}{d_i^2}+\frac{{\mathit{\Pi }}_j}{d_j^2})\cdot F_{ij}{\mathit{r}}_{ij},\\ & {\mathit{F}}_{ij}^D=-{\gamma }_{ij}[{\mathit{v}}_{ij}+({\mathit{e}}_{ij}\cdot {\mathit{v}}_{ij}){\mathit{e}}_{ij}],\\ & {\tilde{\mathit{F}}}_{ij}={\sigma }_{ij}(d{\overline{\mathit{W}}}_{ij}^s+\frac{1}{3}tr[d{\mathit{W}}_{ij}]\mathbf{1})\cdot \frac{{\mathit{e}}_{ij}}{\mathrm{\Delta }t}\\ \mathrm{and}& {\dot{\mathit{c}}}_i^{\mu {\mu }^{\prime }}=\frac{1}{d_i}{\mathit{c}}_i^{\mu \nu }{\mathit{\kappa }}_i^{\nu {\mu }^{\prime }}+\frac{1}{d_i}{\mathit{c}}_i^{{\mu }^{\prime }\nu }{\mathit{\kappa }}_i^{\nu \mu }+\frac{1}{\tau }({\delta }^{\mu {\mu }^{\prime }}-{\mathit{c}}_i^{\mu {\mu }^{\prime }})+\frac{d{\tilde{\mathit{c}}}_i^{\mu {\mu }^{\prime }}}{\mathrm{\Delta }t},\end{array}$$ 2.2

where r_i, v_i and m_i are the position, velocity and mass of particle i, respectively; ${\mathit{F}}_{ij}^C$, ${\mathit{F}}_{ij}^D$ and ${\tilde{\mathit{F}}}_{ij}$ are conservative, dissipative and stochastic forces between particles i and j, respectively; r_ij = r_i − r_j, v_ij = v_i − v_j and e_ij = r_ij/r_ij. The local particle number density d_i is defined as $d_i=\sum _j{W}_{ij}$ with a smoothing kernel function W_ij = W(r_ij) that vanishes beyond a cut-off radius r_c and determines a non-negative function F_ij through the equation ${\mathrm{\nabla }}_i{W}_{ij}=-r_{ij}{F}_{ij}$. ${\mathit{\Pi }}_i$ is the pressure tensor, $d{\mathit{W}}_{ij}$ is a matrix of independent Wiener increments, $d{\overline{\mathit{W}}}_{ij}^s$ is its traceless symmetric part and Δt is the time step. The dissipative and random coefficients γ_ij and σ_ij are given by

$${\gamma }_{ij}=\frac{5\eta }{3}\frac{F_{ij}}{d_i{d}_j}\mathrm{and}{\sigma }_{ij}=2\sqrt{k_{B}T{\gamma }_{ij}},$$ 2.3

where η is the dynamic viscosity, T is the temperature and k_B is the Boltzmann constant. The last expression in equation (2.2) defines dynamics of the conformation tensor, where ${\mathit{\kappa }}_i^{\mu \nu }=\sum _j{F}_{ij}{\mathit{r}}_{ij}^{\mu }{\mathit{v}}_{ij}^{\nu }$ is the velocity gradient tensor, τ is the relaxation time of polymers and $d\tilde{\mathit{c}}$ is the noise term. The pressure tensor ${\mathit{\Pi }}_i$ depends on the conformation tensor as

$${\mathit{\Pi }}_i=p_i^s\mathbf{1}+N_{\mathrm{p}}{d}_i{k}_{B}T(\mathbf{1}-{\mathit{c}}_i),$$ 2.4

where the fluid pressure $p_i^s$ is determined by the equation of state $p_i^s=p_0{(d_i/d_0)}^{\alpha }-p_b$ (p₀, α and p_b are selected constants) [46]. This viscoelastic SDPD model has two contributions to the total fluid viscosity η = η_s + η_p, including solvent η_s and polymer η_p components. The polymer contribution is given by η_p = N_pk_BTd₀τ and can easily be adjusted through the parameters N_p and τ. This formulation reduces to the standard SDPD method for Newtonian fluids by setting ${\mathit{\Pi }}_i=p_i^s\mathbf{1}$.

The standard SDPD [36] and viscoelastic SDPD [37] methods presented above do not conserve angular momentum. However, angular momentum conservation can be important for fluid–particle models to produce physically correct results [47,48]. Therefore, a further SDPD extension [47] that imposes the conservation of angular momentum in simulations is employed here. Each particle is supplied with a spin variable ψ_i, and an additional dissipative rotational force between particles is given by

$${\mathit{F}}_{ij}^R=-{\gamma }_{ij}\frac{{\mathit{r}}_{ij}}{2}\times ({\psi }_i+{\psi }_j).$$ 2.5

The inclusion of ${\mathit{F}}_{ij}^R$ into equation (2.2) leads to the modification of γ_ij as [47]

$${\gamma }_{ij}=\frac{20\eta }{7}\frac{F_{ij}}{d_i{d}_j}.$$ 2.6

The evolution equation for ψ_i is given by

$${\dot{\psi }}_i=\frac{1}{2I_i}\sum _j{\mathit{r}}_{ij}\times {\mathit{F}}_{ij},$$ 2.7

where F_ij is the total force between particles i and j, and I_i is the moment of inertia.

The final equations of motion for the viscoelastic fluid model are

$$\begin{array}{rl}& {\stackrel{.}{\mathit{r}}}_i={\mathit{v}}_i,\\ & m_i{\stackrel{.}{\mathit{v}}}_i=\sum _j\left[{\displaystyle \frac{{\mathrm{\Pi }}_i}{d_i^2}+{\displaystyle \frac{{\mathrm{\Pi }}_j}{d_j^2}}}\right]\cdot F_{ij}{\mathit{r}}_{ij}-{\displaystyle \frac{20\eta }{7}\sum _j{\displaystyle \frac{F_{ij}}{d_i{d}_j}}\left[{\mathit{v}}_{ij}+({\mathit{e}}_{ij}\cdot {\mathit{v}}_{ij}){\mathit{e}}_{ij}+{\displaystyle \frac{{\mathit{r}}_{ij}}{2}\times ({\mathit{\psi }}_i+{\mathit{\psi }}_j)}\right]}\\ & +2\sum _j\sqrt{k_{B}T{\displaystyle \frac{20\eta }{7}{\displaystyle \frac{F_{ij}}{d_i{d}_j}}}}\left(d\overline{{\mathcal{W}}_{ij}^s}+{\displaystyle \frac{1}{3}tr[d{\mathcal{W}}_{ij}]\mathbf{1}}\right)\cdot {\displaystyle \frac{{\mathit{e}}_{ij}}{dt},}\\ & {\stackrel{.}{\mathit{c}}}_i^{\mu {\mu }^{\mathrm{\prime }}}={\displaystyle \frac{{\mathit{c}}_i^{\mu \nu }}{d_i}\sum _j{F}_{ij}{\mathit{r}}_{ij}^{\nu }{\mathit{v}}_{ij}^{{\mu }^{\mathrm{\prime }}}+{\displaystyle \frac{{\mathit{c}}_i^{{\mu }^{\mathrm{\prime }}\nu }}{d_i}\sum _j{F}_{ij}{\mathit{r}}_{ij}^{\nu }{\mathit{v}}_{ij}^{\mu }+{\displaystyle \frac{1}{\tau }({\delta }^{\mu {\mu }^{\mathrm{\prime }}}-{\mathit{c}}_i^{\mu {\mu }^{\mathrm{\prime }}})+{\displaystyle \frac{d{\tilde{\mathit{c}}}_i^{\mu {\mu }^{\mathrm{\prime }}}}{dt}}}}}\\ \mathrm{and}& {\stackrel{.}{\mathit{\psi }}}_i={\displaystyle \frac{1}{2I_i}\sum _j{\mathit{r}}_{ij}\times {\mathit{F}}_{ij}.}\end{array}\}$$ 2.8

The equations of motion are integrated using the velocity-Verlet algorithm [49]. In this work, the smoothing kernel is represented by the 2D Lucy function [50]:

$$W(r)=\frac{5}{\pi r_c^2}(1+3\frac{r}{r_c}){(1-\frac{r}{r_c})}^3.$$ 2.9

In simulations, thermal fluctuations are neglected by setting k_BT = 1.6 × 10⁻⁷. The noise term of conformation tensor is also omitted. Therefore, the SDPD method is essentially reduced to the SPH method with the Oldroyd-B extension. All parameters of the modelled fluid can be found in table 1.

Table 1.

Basic fluid and swimmer parameters. The reference parameters represent parameter magnitudes most frequently used in simulations, and are used for the non-dimensionalization of all simulation parameters, such that the performed simulations can easily be reproduced.

parameter	value
reference length rc (cut-off radius)	1.6
reference viscosity ηref	6.25
reference mass density ρref	6.25
unit of thermal energy kBT	1.6 × 10−7
particle number density d0	$16/r_c^2$
fluid density ρ/ρref	1.0
fluid viscosity η/ηref	9.6
polymer viscosity ηp/ηref	6.4
time step Δt/tref	0.00078
EoS pressure parameter p0/pref	261.4
static pressure (p0 − pb)/pref	32.8
EoS exponent α	7
length of a sheet L/rc	9.375 or 18.75
thickness of a sheet dth/rc	0.75
radius of the head Rh/rc	1.0
wavenumber of the travelling wave krc	3π/(L/rc)
harmonic bond coefficient ζl/ζref	1228.8
amplitude of the oscillating equilibrium angle θb/π	0.067
coefficient for the harmonic angle potential ${\zeta }_b^{\theta }/{\zeta }_{\mathrm{ref}}^{\theta }$	480.0
dimension of the simulated system Lx/rc × Ly/rc	18.75 × 18.75 for short sheets (L/rc = 9.375)
	37.5 × 37.5 for long sheets (L/rc = 18.75)
position constraint strength ζs/ζref	8192.0
orientation constraint strength ${\zeta }_t^{\theta }/{\zeta }_{\mathrm{ref}}^{\theta }$	10240.0

The Oldroyd-B model is one of the simplest models for viscoelastic fluids, which contains nonlinear viscoelasticity. There also exist studies of microswimmer propulsion in linear viscoelastic fluids (e.g. Maxwell model) [51,52], which suggest that moderate linear viscoelasticity (i.e. moderate Deborah number) has little impact on the propulsion of sperm-like swimmers. We expect that nonlinear terms in a non-Newtonian constitutive relationship are probably not negligible when considering beating flagella, since both the strength of locomotion of a single flagellum and the interaction forces between two flagella scale quadratically with the amplitude of oscillatory motion [28,53]. Despite its simplicity, the Oldroyd-B model allows us to study the importance of fluid viscoelasticity for swimmer clustering. It should also represent basic aspects of a viscoelastic mucus, a natural environment of sperm cells.

2.2. Model of a swimmer

A sheet model is represented by a collection of particles assembled in three layers in 2D, as shown in figure 1. These particles are interconnected by harmonic springs with an energy E = ζ_l (r − r₀)², where ζ_l is the spring stiffness and r₀ is the equilibrium length. The middle layer of sheet particles is subjected to a harmonic angle potential with the energy $E={\zeta }_b^{\theta }{(\theta -{\theta }_0)}^2$, where ${\zeta }_b^{\theta }$ is the bending coefficient and θ₀ is the equilibrium angle. To prescribe dynamic bending (or beating) of the sheet, the equilibrium angle is a function of both time and position as

$${\theta }_0={\theta }_b\sin (ks-\omega t),$$ 2.10

where θ_b is the amplitude of oscillating equilibrium angle, k is the wavenumber of the travelling wave, s is a curvelinear coordinate along the sheet centreline and ω is the angular frequency. Equation (2.10) results in an imposed travelling wave along the sheet, as shown in figure 1c,d. In some simulations, a head is attached to the beating sheet, as illustrated in figure 1b,d. The connection between the sheet and the head is also facilitated by harmonic bonds. Similarly to our previous study [24], the swimmers are fully embedded into the modelled fluid, and have the same number density as that of fluid particles. Thus, the interaction between fluid and swimmer particles is the same as that between different fluid particles. This results in no-slip boundary conditions for the fluid at the swimmer surface.

Figure 1.

(a) Illustration of the sheet model constructed from particles (blue dots) interconnected by springs. L is the sheet length. (b) Illustration of a swimmer model with a head. R_h is the head size. (c) Snapshot of an actuated sheet. The inset shows the configuration of the particles and springs with θ representing the angle between neighbouring springs in the middle layer. (d) An actuated swimmer with an attached head.

Sheet bending stiffness κ can be estimated as [24]

$$\kappa ={\zeta }_l{l}_0^3+2{\zeta }_b^{\theta }{l}_0,$$ 2.11

where l₀ is the equilibrium length between interconnected particles in the middle layer. Note that this approximation becomes inaccurate when deformation of the sheet is large.

In some simulations, the position and orientation of the swimmers are fixed for the purpose of measuring hydrodynamic forces between the two swimmers. Position of a swimmer is controlled by a spring connecting the centre of mass r_CM of the swimmer and a prescribed anchoring position r₀ with the restoration force calculated as

$${\mathit{F}}_{\mathrm{res}}=-{\zeta }_s({\mathit{r}}_{\mathrm{CM}}-{\mathit{r}}_0),$$ 2.12

where ζ_s is the spring stiffness. The restoration force is uniformly distributed to all particles forming the swimmer. Furthermore, the orientation of a swimmer is controlled by a similar method. For a prescribed orientation ϕ₀ (in radians with respect to the x-axis), and the current orientation ϕ, whose value is found from a linear regression of the sheet particles, a restoration torque is computed as

$$T_{\mathrm{res}}=-{\zeta }_t^{\theta }(\varphi -{\varphi }_0),$$ 2.13

where ${\zeta }_t^{\theta }$ is the restoration torque coefficient. A force with a magnitude of $T_{\mathrm{res}}/\sum (|{\mathit{r}}_i-{\mathit{r}}_{\mathrm{CM}}|)$ is applied to all particles of the sheet in the direction perpendicular to r_i − r_CM, where r_i is the position of the ith particle of the sheet.

2.3. Simulation setup

In all cases, the simulation domain L_x × L_y is periodic in both dimensions. The cut-off radius is fixed at r_c = 1.6 and used as a basic length scale. Fluid resolution characterized by the number density $d_0=16/r_c^2$ is kept the same in all simulations. Furthermore, we introduce a reference mass density ρ_ref = 6.25 and dynamic viscosity η_ref = 6.25, which define a mass scale $m_{\mathrm{ref}}={\rho }_{\mathrm{ref}}{r}_c^2$ and a time scale $t_{\mathrm{ref}}=r_c^2{\rho }_{\mathrm{ref}}/{\eta }_{\mathrm{ref}}$. Similarly, further reference scales are introduced for the frequency ω_ref =1/t_ref, velocity v_ref = r_c/t_ref, force $F_{\mathrm{ref}}=r_c^3{\rho }_{\mathrm{ref}}/t_{\mathrm{ref}}^2$, pressure $p_{\mathrm{ref}}=r_c^2{\rho }_{\mathrm{ref}}/t_{\mathrm{ref}}^2$, spring stiffness ${\zeta }_{\mathrm{ref}}=r_c^2{\rho }_{\mathrm{ref}}/t_{\mathrm{ref}}^2$, angle potential strength ${\zeta }_{\mathrm{ref}}^{\theta }=r_c^4{\rho }_{\mathrm{ref}}/t_{\mathrm{ref}}^2$ and flexural rigidity ${\kappa }_{\mathrm{ref}}=r_c^5{\rho }_{\mathrm{ref}}/t_{\mathrm{ref}}^2$. Table 1 shows parameters that are normally used in simulations. When other parameter values are used, they are explicitly specified in the text. Selection of the resolution and smoothing parameters (d₀ and r_c) is justified through two convergence tests: (i) unsteady flow above an oscillating plate and (ii) a waving sheet with a prescribed waveform. These tests are presented in appendix A, and show that simulation results are independent of the choice of d₀ and r_c.

The simulation system is characterized by three non-dimensional numbers: (i) Sperm number defined as Sp = (ηω/κk³)^1/3, (ii) Deborah number De = τω and (iii) Reynolds number defined as Re = f b²ρ/η, where f = ω/(2π) and b is the wave amplitude. Sp quantifies the dimensionless ratio of fluid to bending stresses, De characterizes fluid elasticity and Re quantifies the importance of inertia. Even though Reynolds numbers are generally small for microswimmers, inertial effects may not always be neglected, as reported in other swimmer studies [22–24,54].

3. Results and discussion

3.1. Swimming speed of a single swimmer

Analytical prediction [53] for an infinitely long Taylor sheet suggests that its swimming speed decreases with increasing fluid elasticity or De as

$$\frac{U_{NN}}{U_N}=\frac{1+{\eta }_s/\eta {\mathrm{De}}^2}{1+{\mathrm{De}}^2},$$ 3.1

where $U_N=\frac{1}{2}\omega b^{2}k$ is the swimming velocity in a Newtonian fluid. However, when sheet flexibility is also considered, fluid elasticity can actually enhance the swimming speed [55]. For large enough Sp, an increase in De monotonically results in a larger speed. The transition from hindered to enhanced propulsion occurs when ${\mathrm{Sp}}^3>1/(2\sqrt{\beta })$, where β = η_s/η. In the limit of Sp ≫ 1, the ratio between U_NN and U_N becomes [55]

$$\frac{U_{NN}}{U_N}=\frac{1+{\eta }_s/\eta {\mathrm{De}}^2}{1+{({\eta }_s/\eta )}^2{\mathrm{De}}^2}.$$ 3.2

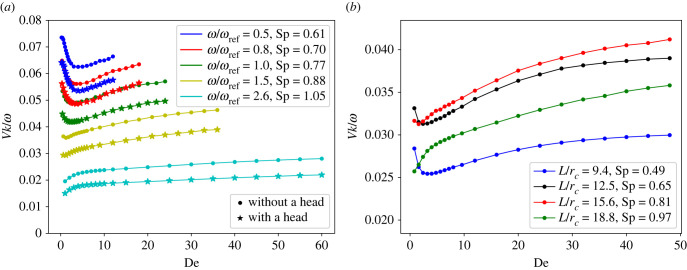
To compare theoretical predictions with simulations, the motion of a finite-length sheet is modelled for different De and Sp. Figure 2a shows the dependence of the swimming speed V on De for different beating frequencies. At low Sp with increasing De, the swimming velocity first decreases, reaching a minimum at De ≈ 1, and then increases. However, at high Sp, the swimming velocity monotonically increases with De. The presence of a head attached to the sheet does not affect this trend, but reduces the swimming speed V due to an increased resistance of the swimmer with the head. The critical Sperm number, at which the minimum in swimming velocity disappears, is close to 0.88 in figure 2a. According to the theory in [55], the critical Sp is $1/{(2\sqrt{\beta })}^{1/3}=0.86$, in a good agreement with our simulation results. Figure 2b shows the same transition from partial hindrance of swimmer speed to a monotonic enhancement, where Sp is increased through an increase of the sheet length. Here, the critical Sp is close to 0.81, in a good agreement with the theoretical prediction of 0.86 [55]. Since β is fixed in all simulations, sheets with Sp > 0.86 will be referred to as soft sheets further in the text, and otherwise as stiff sheets.

Figure 2.

(a) Swimming velocity V of a single swimmer (with and without a head) as a function of De for various beating frequencies. The sheet length is L/r_c = 18.75. (b) Swimming velocity of a swimmer without a head for different sheet lengths. Simulation domain dimensions are fixed at L_x/r_c × L_y/r_c = 37.5 × 37.5 and ω/ω_ref = 2.05. In all simulations, ρ/ρ_ref = 0.125 and the bending stiffness of the sheet is κ/κ_ref ≈ 281.1.

The existence of a minimum swimming velocity as a function of De at low Sp has also been demonstrated in simulations of undulating Caenorhabditis elegans with a stroke asymmetry [56,57]. This non-monotonic velocity dependence on De [57] is attributed to fluid viscoelasticity, which results in a non-monotonic behaviour of the beating amplitude for moderately soft sheets [56–58]. However, previous studies [56,57] also report that the velocity behaviour becomes monotonic when the sheet is very soft, in agreement with our simulation results. Furthermore, the dependence of swimming speed in figure 2 agrees well with experimental results [59] on flexible sperm-like swimmers in a glucose-based Boger fluid, where fluid elasticity was found to monotonically enhance the swimmer’s propulsion.

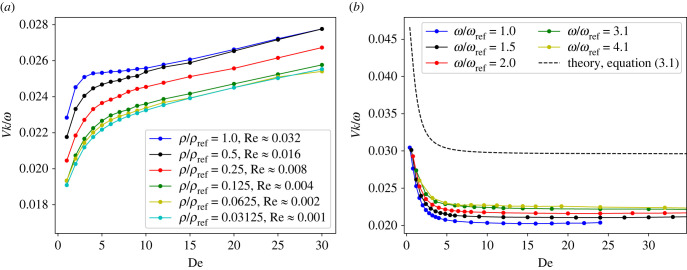
To test the possible effect of inertia in our model, we performed a number of simulations for different Re by changing the fluid density. Figure 3a shows swimming velocity for various Re, and demonstrates that Re does not affect the trend of monotonically increasing V as a function of De. Furthermore, for ρ/ρ_ref ≤ 0.125 (Re ≤ 0.004), the simulation results become independent of Re, representing the Stokes limit. Also, the limit of Sp = 0 is studied by prescribing the motion of sheet particles as a pure sine wave, travelling on an inextensible sheet (more details can be found in appendix A and [24]). Figure 3b shows that at Sp = 0, fluid viscoelasticity significantly impedes the propulsion speed, which decreases monotonically with increasing De. This suggests that the non-monotonic dependence of swimming velocity on De at large enough Sp is a result of the interaction between sheet elasticity and fluid viscoelasticity. Note that the curves for different ω in figure 3b do not collapse onto a single curve even after scaling by ω, which is the case for an infinite Taylor sheet. Finally, the sheet of a finite length swims significantly slower than an infinite sheet.

Figure 3.

(a) Effect of inertia on swimming velocity V for different Re as the fluid density ρ is changed. V becomes independent of Re for ρ/ρ_ref ≤ 0.125. Here, L/r_c = 18.75, ω/ω_ref = 2.56, Sp = 1.05 and Δt/t_ref = 7.8 × 10⁻⁴, 3.9 × 10⁻⁴, 3.9 × 10⁻⁴, 1.95 × 10⁻⁴, 9.8 × 10⁻⁵, 4.9 × 10⁻⁵ for ρ/ρ_ref = 1.0, 0.5, 0.25, 0.125, 0.0625, 0.03125, respectively. (b) Swimming velocity in the limit of Sp = 0 achieved by prescribing the motion of the sheet. Here, L/r_c = 12.5, L_x/r_c × L_y/r_c = 25 × 25, kr_c = 2π/(L/r_c), b/r_c = 0.625 and kb = 0.314.

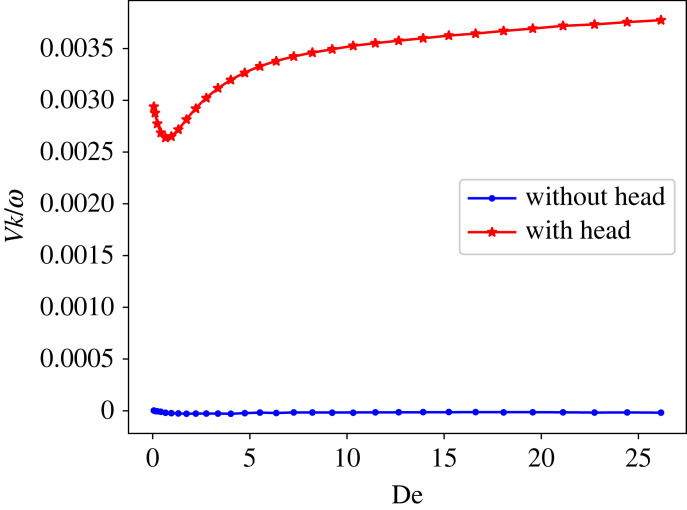
At zero Reynolds number, kinematic reversibility does not allow a swimmer to attain net displacement in a Newtonian fluid if the deformation is reciprocal, which is known as the Purcell’s scallop theorem [60]. However, experiments [61] and theories [62,63] suggest that in a non-Newtonian fluid, net propulsion should be possible for a reciprocal deformation. To test the scallop theorem in simulations, the beating of a sheet with reciprocal deformation is employed, where the equilibrium angle within the sheet is prescribed as

$${\theta }_0={\theta }_b\sin (ks)\sin (\omega t).$$ 3.3

In this case, there is no travelling wave, and sheet bending is reciprocal. Figure 4 shows the swimming velocity of the sheet with a reciprocal deformation as a function of De. The blue curve represents the swimming velocity of the sheet without a head, which is zero for all De values. This indicates that fluid viscoelasticity does not successfully break the symmetry in the case of a headless sheet, and the scallop theorem remains valid. The red curve in figure 4 corresponds to velocity of the sheet with an attached head, which has a non-vanishing propulsion for all De. In this case, the deformation of the swimmer is not reciprocal due to the presence of the head, even though the sheet bending is reciprocal. Note that the swimming velocity is much smaller than when a travelling wave is imposed. Furthermore, the swimming velocity does not vanish at De ≈ 0, indicating that symmetry breaking and a net propulsion in this case are due to the presence of the head rather than fluid viscoelasticity. However, fluid viscoelasticity for a headed swimmer does have a significant effect on the swimming velocity, which exhibits a non-monotonic trend as a function of De, qualitatively similar to that in figure 2 for stiff sheets.

Figure 4.

Velocity of a single swimmer beating through a reciprocal deformation in a viscoelastic fluid. Here, ρ/ρ_ref = 0.125, L/r_c = 18.75, ω/ω_ref = 1.53 and Sp = 0.88.

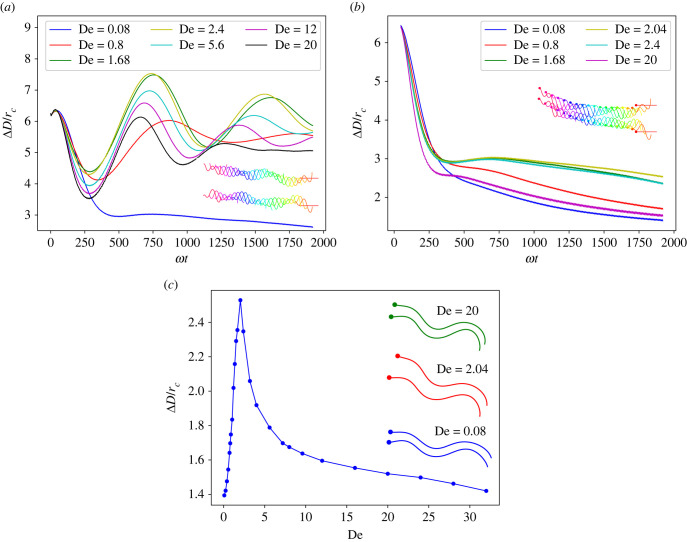
3.2. Dynamic clustering of two identical sheets

A beating sheet with a head is a pronounced pusher, and a sheet without the head is still a pusher, though a much weaker one [64]. In the far field, two sheets induce two force dipoles attracting each other with their flow field decaying as 1/r². However, when two sheets are close enough, their interaction is more complex than the attraction between two force dipoles. In fact, the short-range interaction and present noise likely dominate the collective behaviour of flagellated microswimmers [34]. Therefore, we investigate the short-range interaction between two sheets in order to better understand their clustering.

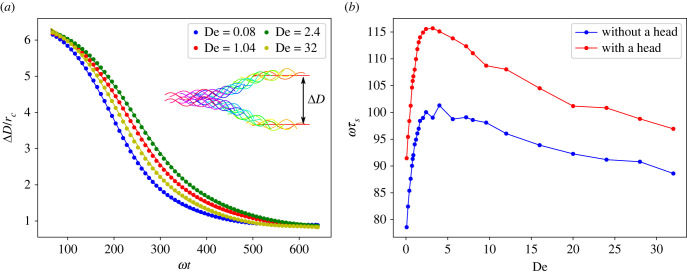
We start with two identical sheets placed parallel to each other and separated by a distance d that is smaller than their length, and explore their dynamic clustering due to hydrodynamic interactions. Figure 5a shows that the inter-swimmer distance ΔD for two relatively stiff sheets at Sp = 0.49 decreases with time until it comes to a stable fixed value that is independent of De. The inset in figure 5a illustrates the dynamic approach of two sheets toward each other. Evolution of the inter-swimmer distance can be characterized by a clustering time τ_s computed by fitting the solution of a modified Adler equation [24,26,65] to the temporal evolution of ΔD from simulations as

$$\mathrm{\Delta }D=A{\tan }^{-1}(\tan ({\psi }_0/2)\hspace{0.17em}{\mathrm{e}}^{-t/{\tau }_s})+C,$$ 3.4

where A and C are fitting parameters and ψ₀ is the initial phase difference between the two swimmers (here, it is just another parameter to be fitted). Solid lines in figure 5a demonstrate that fits with equation (3.4) to the simulation data are very good. The dependence of τ_s on De is presented in figure 5b. As De increases, the clustering time first increases reaching a peak at De ≈ 2–3, and then decreases. The Newtonian limit at De = 0 corresponds to the fastest clustering of two swimmers. Simulations of swimmers with and without a head show that the head slows down the clustering process. However, the qualitative behaviour of τ_s as a function of De is not affected by the presence of the head.

Figure 5.

(a) Evolution of the distance ΔD between two stiff sheets over time for different De. Dots correspond to simulation data, while solid lines are fits using equation (3.4). Inset shows a dynamic clustering process for De = 2.4, where sheets swim from the right to the left. Various colours represent different times of the sheet positions. (b) Dependence of the characteristic clustering time τ_s on De. For all cases, L/r_c = 9.375, ω/ω_ref = 2.05, κ/κ_ref = 281.1 and Sp = 0.49.

For soft sheets at Sp = 0.97, the dynamic clustering is much less robust. Figure 6a shows that the distance between two soft sheets does not monotonically decrease over time for most of De values. In fact, the distance ΔD oscillates and may become even larger than its initial value. The inset in figure 6a illustrates this oscillating process, in which the sheets periodically attract and repel each other. Interestingly, the presence of swimmer heads favours a stable distance regardless of the value of De, as shown in figure 6b. Independently, whether the head is present or not, the fluid elasticity significantly affects the oscillation/clustering process. For the case without a head, the strongest oscillations in ΔD occur at De ≈ 2, while in the Newtonian limit (De = 0.08), the sheets reach a stable distance. Figure 6c presents the final distance between two clustered sheets with a head. ΔD is largest at De ≈ 2, indicating that clustering interactions are weakest around De ≈ 2.

Figure 6.

(a) Evolution of the distance between two soft sheets without a head. Inset demonstrates trajectories of the sheets at De = 1. Various colours represent different times of the sheet positions. (b) The presence of heads facilitates stable clustered distance between two swimmers. Inset illustrates the clustering process at De = 1. Various colours represent different times of the sheet positions. (c) For sheets with heads, the final distance between the two sheets depends on fluid elasticity. Inset shows several snapshots of two clustered sheets. In all cases, L/r_c = 18.75, ω/ω_ref = 2.05, κ/κ_ref = 281.1 and Sp = 0.97. In all insets, the swimming direction of the sheets is from the right to the left.

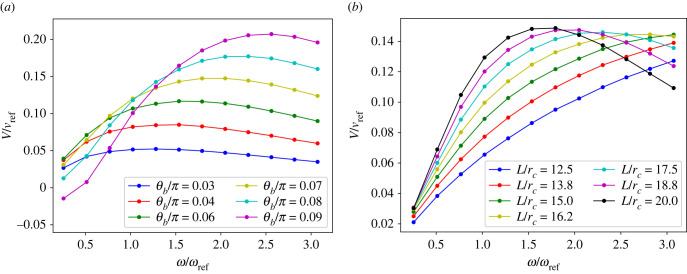
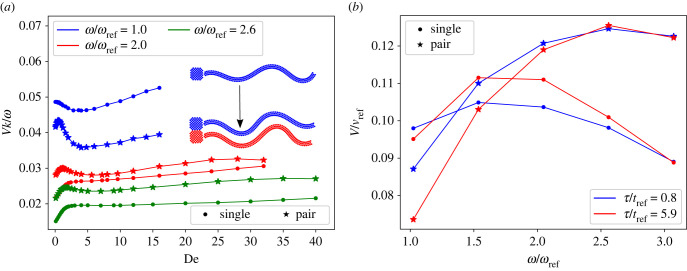
3.3. Swimming characteristics before and after clustering

Early experiments with bull spermatozoa [1] have shown that sperm clustering leads to changes in their beating pattern, including an increase in the beating frequency, wave amplitude and the swimming speed. Theoretical analysis of two infinite elastic Taylor sheets shows that the wave amplitude of the sheets varies with a change in their phase difference, and the maximal amplitude occurs when the phase difference vanishes [28]. Recent experiments also demonstrate that as the distance between two flagella decreases, the flagellar waveform exhibits a systematic change [17]. For biological swimmers, clustering often enhances the propulsion of a formed cluster [1,66]. A theoretical prediction for two Taylor sheets is that the synchronized state corresponds to a minimum energy-dissipation rate [16,25,28]. In reality, it is of course possible that after a cluster is formed, the swimmers adapt their beating frequency and amplitude through some feedback mechanism. Currently, it is unclear whether the observed boost in propulsion of clustered swimmers comes from the possible active adjustment or due to the clustered configuration or both. Here, the prescribed driving of the sheets is kept unchanged before and after clustering, while the overall propulsion of a formed pair is examined.

Figure 7 presents a comparison of the swimming velocity of a single swimmer and a clustered doublet. The primary observation is that at low beating frequencies (corresponding to stiff single sheets or low Sp), clustered sheets swim slower than a single one, but at high enough beating frequencies (representing soft single sheets or large Sp), clustering enhances the propulsion speed of a pair. Furthermore, the monotonic behaviour of V with increasing De at high ω for a single swimmer becomes non-monotonic after the cluster is formed, as shown in figure 7a. Figure 7b shows that the maximum propulsion velocity as a function of ω increases and shifts toward larger ω values after clustering. Note that several properties are changed for a clustered doublet.

• (i) Viscous friction on the doublet is larger than that on a single swimmer due to an increased thickness of the doublet swimmer, as shown in the inset of figure 7a.
• (ii) The beating amplitude increases after clustering through an increase of the average amplitudes of the two dominant modes, as shown in figure 7c.
• (iii) The doublet becomes effectively stiffer after it is formed, because the clustering results in a larger second moment of area for the cross-section section of the swimmer/doublet.

The competition between an increased viscous resistance and beating amplitude after clustering explains the reduction in propulsion of a doublet at small frequencies and the enhancement of velocity at large ω. At low frequencies, the sheets are effectively stiff, and an increase in the beating amplitude is small (see figure 7c), not allowing to overcome the effects of an increased viscous resistance of the formed doublet. At large enough ω, the sheets become effectively soft, and the effect of an increased beating amplitude on the doublet speed dominates over the increased viscous resistance, such that the clustered pair swims faster than single swimmers. Furthermore, an effective stiffening of the doublet accounts for changes in the V–De curves in figure 7. For example, a non-monotonic dependence of V on De for a pair results from the fact that after clustering, the sheets have effectively a lower Sp in comparison to that before the clustering. As shown in §3.1, a decrease in Sp can affect the V–De relation, such that V becomes non-monotonic with a minimum at De ≈ 1. After a cluster is formed, Sp decreases due to an increased second moment of area for the cross-section section of the doublet, which may lead to a significant slowing down of the clustered doublet.

Figure 7.

(a) Swimming velocity of a single swimmer in comparison with that of a clustered doublet for different beating frequencies and De. Inset shows a snapshot of a single swimmer and a formed pair. (b) The swimming velocity as a function of ω for several τ. v_ref = r_c/t_ref. (c) Average amplitude of the two dominant modes as a function of De. B = (B₁ + B₂)/2, where B_i is the amplitude of the ith mode determined by the principal component analysis [67] of the waveforms. For all cases, L/r_c = 18.75. For the single swimmer, $\mathrm{Sp}=0.77,0.97\hspace{0.17em}\mathrm{and}\hspace{0.17em}1.05$ when $\omega /{\omega }_{\mathrm{ref}}=1.02,2.05\hspace{0.17em}\mathrm{and}\hspace{0.17em}2.56$, respectively.

To better support the arguments above, figure 8 shows the dependence of swimming velocity for a single swimmer on beating amplitude and sheet length. Figure 8a demonstrates that an increase in the beating amplitude leads to an increase in V and a shift of the maximum velocity toward larger ω values (i.e. the saturation frequency increases). Figure 8b shows that a decrease in the sheet length (or decrease in Sp) results in the maximum V to shift toward larger ω values. As the length of the sheet decreases, the beating amplitude also decreases, but the maximum in V remains nearly unaffected by a change in Sp. Therefore, the phenomenon shown in figure 7b, that the maximum V becomes larger and shifts toward larger ω values after clustering, is a direct result of the increased beating amplitude and the decreased effective elasticity of a doublet after the cluster is formed. Note that in experiments, bovine sperm cells may change their beating frequency upon clustering [1], which could contribute to an increase of the saturation frequency.

Figure 8.

(a) Dependence of V on the beating amplitude for a single swimmer. Here, τ/t_ref = 5.9, L/r_c = 18.75 and v_ref = r_c/t_ref. (b) Swimming velocity as a function of the sheet length. Here, τ/t_ref = 5.9.

For swimmers with a head, the clustering results do not change qualitatively, as shown in figure 9. There are only two minor differences: (i) the velocity of a doublet is smaller in the case with heads, due to an increase in the viscous resistance resulting from the presence of heads and (ii) enhancement of the swimming velocity is generally smaller for headed swimmers, while the reduction in V is larger. The main reason for the second difference is that the presence of a head prevents close alignment of the sheets, as there is always a gap between the clustered sheets. This gap reduces hydrodynamic inter-sheet interaction, and, therefore, weakens the velocity enhancement after the cluster is formed.

Figure 9.

(a) Swimming velocity of a single swimmer with a head in comparison with two clustered headed swimmers for different beating frequencies and De. Inset shows a snapshot of a single swimmer and a formed pair. (b) The swimming velocity as a function of ω for several τ. For all cases, L/r_c = 18.75. For the single swimmer, $\mathrm{Sp}=0.77,0.97\hspace{0.17em}\mathrm{and}\hspace{0.17em}1.05$ when $\omega /{\omega }_{\mathrm{ref}}=1.02,2.05\hspace{0.17em}\mathrm{and}\hspace{0.17em}2.56$, respectively.

3.4. Stability of a clustered doublet

Experiments on the collective behaviour of bovine sperm cells indicate that fluid viscoelasticity promotes clustering of the sperm cells in the regime of De ≤ 2 [5], such that the mean cluster size first increases and then decreases with increasing De. At the first glance, this seems to be qualitatively different from our results in §3.2, where it is shown that the clustering time is the largest at De ≈ 1. However, other properties such as the stability of a formed pair can play an important role in determining the cluster size in addition to the clustering time. Biological swimmers are never identical to each other and can have substantial differences in their swimming characteristics, which may result in a temporary attraction rather than a stable cluster formation. For instance, experiments show that formed clusters are dynamic, such that the swimmers can switch from one cluster to another [5]. Furthermore, swimmer clusters can constantly appear and disappear. To better understand cluster stability, we investigate the effect of viscoelasticity on the stability of formed clusters.

Even though a formed pair of two identical swimmers appears to be stable, differences in the swimmer geometry or propulsion can affect the doublet stability. To examine doublet stability, we perform simulations which start with a perfectly clustered pair, but there are imposed differences in the driving forces (or bending amplitudes) of the two sheets. For relatively stiff sheets with Sp = 0.43, figure 10a,b demonstrates that fluid viscoelasticity affects the cluster stability for the amplitude difference of Δθ_b/π = 0.061 between the two swimmers. For this difference in propulsion, the sheets stay together only when De ≈ 1, and separate otherwise. Furthermore, the clustered configuration of two distinct swimmers has generally a worse alignment of sheets in comparison to the case of two identical swimmers, as shown in the inset of figure 10a. For soft sheets with Sp = 1.02 and Δθ_b/π = 0.0092, figure 10c,d illustrates that De ≈ 1 also leads to a stable cluster, while for other values of De, the doublet might become unstable. Note that the soft sheets align well after clustering with a nearly zero distance between them (see the inset of figure 10c).

Figure 10.

Cluster stability of two sheets with a prescribed difference Δθ_b in their driving amplitude. Trajectories for stiff sheets with Sp = 0.43 and Δθ_b/π = 0.061 at (a) De = 1.02 and (b) De = 1.8. Trajectories for soft sheets with Sp = 1.02 and Δθ_b/π = 0.0092 at (c) De = 1 and (d) De = 2. (a,c) Insets show clustered configurations. For cases (a) and (b), L/r_c = 9.375 and ω/ω_ref = 1.54. For cases (c) and (d), L/r_c = 18.75 and ω/ω_ref = 2.56. Various colours represent different times of the sheet positions. In all simulations, ζ_l/ζ_ref = 1638.4 and κ/κ_ref = 304.

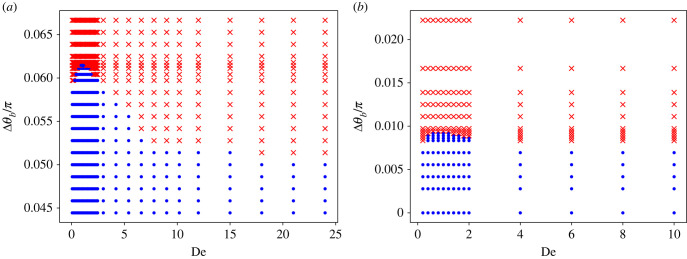
Cluster stability diagrams for stiff and soft sheets as a function of Δθ_b and De are shown in figure 11. The larger the driving force difference, the more likely the formed pair is unstable. Fluid elasticity also affects the cluster stability, which is best at De ≈ 1, and becomes worse for smaller and larger De values. The cluster stability diagram for soft sheets (Sp = 1.02) in figure 11b is qualitatively similar to the case of stiff sheets in figure 11a. However, the clustered configuration is less stable for soft sheets than for stiff sheets. Thus, sheet elasticity reduces the stability of a doublet. Fluid elasticity has a similar effect on the cluster stability of both stiff and soft sheets, with De ≈ 1 resulting in the most stable cluster formation. These results are consistent with experimental observations of the cluster formation by sperm cells [5], where the clustering is enhanced around De ≈ 1.

Figure 11.

(a) Cluster stability diagram for stiff sheets as a function of Δθ_b and De. De ≈ 1 represents the most stable condition. Here, L/r_c = 9.375, ω/ω_ref = 1.54, ζ_l/ζ_ref = 1638.4, κ/κ_ref = 304 and Sp = 0.43. (b) Cluster stability diagram for soft sheets as a function of Δθ_b and De. Here, L/r_c = 18.75, ω/ω_ref = 1.54, ζ_l/ζ_ref = 1638.4, κ/κ_ref = 304 and Sp = 1.02. The dots denote a stable cluster, while the crosses correspond to an unstable cluster.

3.5. Inter-sheet forces

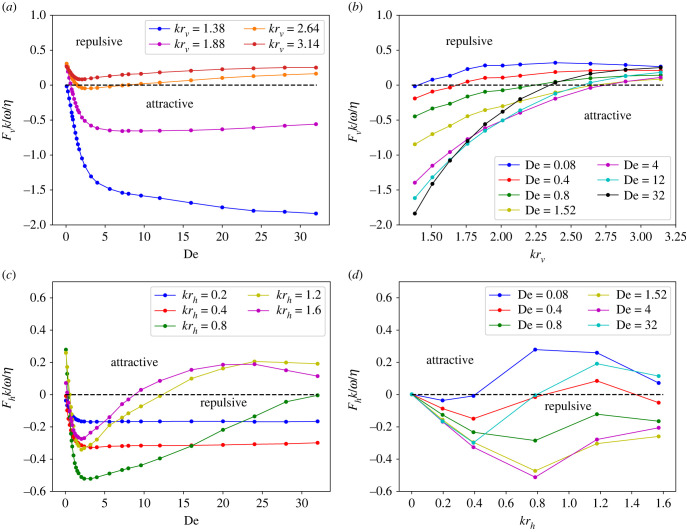
To better support the clustering results, hydrodynamic forces between two sheets are measured in simulations where the position and orientation of the sheets with respect to each other are fixed. Figure 12 shows inter-sheet forces for two identical stiff sheets with the same orientation but varying vertical and horizontal distances between them. For all vertical distances r_v between the sheets, figure 12a,b shows that the vertical forces in the normal to sheet direction are attractive, and favour clustering. The attraction forces decrease with increasing inter-sheet distance. Fluid elasticity also influences the measured forces, with a minimum attraction force at De ≈ 1–2, which is consistent with the longest clustering time in figure 5. The simulation results show that the vertical force decays as $1/r_v^{\alpha }$, where α ∈ [3.6, 4.3].

Figure 12.

Hydrodynamic forces between two stiff sheets. (a) Vertical force F_v on the upper sheet as a function of De for different separation distances r_v and a fixed horizontal difference r_h = 0. (b) Vertical force on the upper sheet as a function of separation distance r_v. Inset illustrates the positioning of two sheets, for which the distances r_v and r_h remain fixed. (c) Horizontal force F_h on the upper sheet as a function of De for different horizontal distances r_h and a fixed vertical distance kr_v = 2.01. (d) Horizontal force on the upper sheet as a function of r_h. For all cases, L/r_c = 9.375, ω/ω_ref = 2.05 and Sp = 0.49.

Figure 12c,d presents interaction force for varying horizontal distances r_h. For small distances (kr_h ≤ 1.6), the horizontal forces between two sheets are attractive regardless of the value of De. However, if r_h is large enough, large De magnitudes lead to repulsive forces. The transition between the attractive and repulsive horizontal forces shifts to smaller De with increasing r_h (see figure 12c). Note that the vertical forces remain attractive for all r_h values. Figure 12d shows that the attractive horizontal forces have a maximum at kr_h ≈ 1.3, independent of De. For small kr_h ≤ 0.8, the effect of fluid elasticity is rather weak, while for kr_h > 0.8, De significantly influences horizontal forces between the sheets.

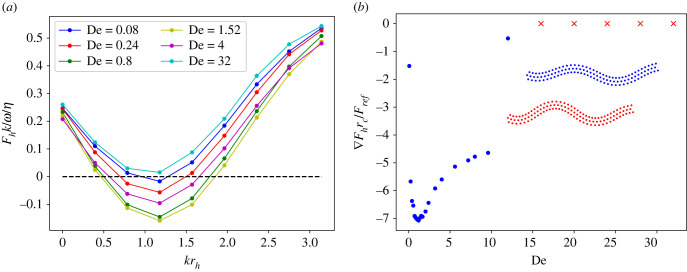
Force measurements for two identical soft sheets are shown in figure 13. In comparison with the case of stiff sheets, for which vertical forces are always attractive, the vertical forces for soft sheets change sign from being attractive to repulsive. Figure 13a,b presents vertical forces for several r_v and De (here, r_h = 0). For small De, vertical forces are generally repulsive for most distances r_v. An increase in De results in F_v becoming attractive. These attractive forces are monotonically increasing with De for small r_v, but have a maximum at large r_v. If r_v is large enough (e.g. kr_v = 3.14), the vertical force becomes dominantly repulsive again. The forces in horizontal direction for a fixed vertical distance of kr_v = 1.88 are shown in figure 13c,d. The dependence of F_h on r_h and De is rather complex with multiple transitions between attractive and repulsive forces. In general, both increase and decrease in De can cause the repulsive forces F_h to become attractive, and this is more likely to happen when the distance r_h is large. The maximum repulsive forces in the horizontal direction appear within the range De ∈ [1, 4].

Figure 13.

Hydrodynamic forces between two soft sheets. (a) Vertical force F_v on the upper sheet as a function of De for different separation distances r_v and a fixed horizontal difference r_h = 0. (b) Vertical force on the upper sheet as a function of r_v. (c) Horizontal force F_h on the upper sheet as a function of De for different horizontal distances r_h and a fixed separation distance kr_v = 1.88. (d) Horizontal force on the upper sheet as a function of r_h. For all cases, L/r_c = 18.75, ω/ω_ref = 2.05 and Sp = 0.97.

The force measurements above are consistent with the clustering results in §3.2. For example, when the sheets are stiff, they attract each other independently of De. When the sheets are soft, they may also repel each other, depending on their relative position and fluid elastic properties. However, the force measurements do not seem to explain that the distance between two clustered soft sheets can oscillate for some conditions (see figure 6a), which could occur through a periodic switch between inter-sheet repulsion and attraction. A possible explanation of this observation is the fact that during the dynamic clustering process, orientation of the sheets can change (see the inset in figure 6a), so that they are not always moving in parallel. To illustrate the importance of relative orientation, figure 14 shows force measurements between two sheets having a small tilt in their relative orientation, which may change the direction of inter-sheet forces. Change in the force sign due to a small tilt is clearly present for soft sheets, while the stiff sheets are much more robust to such perturbations. Thus, the oscillation in inter-sheet distance of a clustered pair is likely caused by the dynamic change in the relative position and orientation of the two sheets.

Figure 14.

Vertical force on the upper sheet for a configuration with a non-zero tilt in the relative orientation of the two sheets. Inset illustrates the orientation of tilted sheets. Vertical and horizontal distances are fixed at kr_v = 3.14 and r_h = 0.0. Here, L/r_c = 18.75, ω/ω_ref = 2.05 and Sp = 0.97.

Despite the complexity in swimmer interactions, the force measurements provide a robust explanation for the cluster stability in §3.4. When two sheets separate as a result of the asymmetry in their beating amplitude, one of them always swims faster than the other one and the relative displacement along the swimming direction becomes larger than the vertical separation. Therefore, the horizontal inter-sheet forces mainly control the clustering and separation. Figure 15a presents horizontal forces between two asymmetric stiff sheets (Sp = 0.49) for fixed Δθ_b/π = 0.0223 and kr_v = 2.76. The force curves show that there are two fixed points where F_h = 0, and the horizontal separation distance with a smaller r_h is the stable point at which the clustering is successful. The cluster stability can be measured through the force gradient $\mathrm{\nabla }{F}_h$ at the stable fixed points, so that the clustering is more stable for larger values of the gradient. Figure 15b presents the horizontal force gradients at the stable fixed points for different De, supporting that the most stable condition is at De ≈ 1. This result is in excellent agreement with the stability diagram in figure 11a. Figure 16 presents F_h and $\mathrm{\nabla }{F}_h$ for soft sheets (Sp = 0.97) with fixed Δθ_b/π = 0.0054 and kr_v = 1.88. Unlike the case of stiff sheets where the stable fixed points correspond to large enough r_h (kr_h > 0.4), for soft sheets the stable r_h is generally very close to zero. This fact explains the difference in relative sheet position between the insets of figure 10a,c. Absolute value of the horizontal force gradient has a maximum at De ≈ 4 and decreases slightly after this maximum, in agreement with the smooth stability line in figure 11b. Note that the position of the maximum is not exactly at De = 1.

Figure 15.

(a) Horizontal force between two asymmetric stiff sheets. (b) Horizontal force gradient at the stable fixed points. Blue dots depict stable fixed points, while red crosses denote no existence of stable fixed points at the corresponding De. Inset illustrates the two clustered sheets. In all cases, L/r_c = 9.375, ω/ω_ref = 2.05, kr_v = 2.76, Δθ_b/π = 0.0223 and Sp = 0.49.

Figure 16.

(a) Horizontal force between two asymmetric soft sheets. (b) Horizontal force gradient at the stable fixed points. Blue dots depict stable fixed points, while red crosses denote no existence of stable fixed points in the proximity of r_h = 0 at the corresponding De. Inset illustrates the two clustered sheets. In all cases, L/r_c = 18.75, ω/ω_ref = 2.05, kr_v = 1.88, Δθ_b/π = 0.0054 and Sp = 0.97.

4. Summary and conclusion

In our previous work [24], the synchronization of two infinite sheets in viscoelastic fluids was studied. One of the main results is that fluid viscoelasticity leads to strong synchronization forces for large beating amplitudes and Deborah numbers De > 1, suggesting a strong clustering of swimmers under these conditions. In this study, interactions of two finite-size free swimmers (i.e. closer to real swimmers) are investigated and the fluid-mediated interactions between them are found to be rather weak. Further investigated aspects include the influence of sheet elasticity, an attached head, the stability of two clustered swimmers and the swimmer characteristics after pair formation. The key findings are summarized in table 2.

Table 2.

Key findings.

property	sheet	obtained results
speed of a single swimmer	stiff sheet	the speed first decreases, and then increases with increasing De
	soft sheet	the speed monotonically increases with increasing De
dynamic clustering	stiff sheets	both headed and headless swimmers form clusters
		cluster formation is slowest for De ≈ 2–3
	soft sheets	the distance between headless swimmers oscillates in viscoelastic fluids
		the oscillation is strongest at De ≈ 2 headed swimmers cluster, with the slowest clustering time at De ≈ 2
inter-sheet forces	stiff sheets	the traverse force is attractive $F_v\sim 1/r_v^4$ with a minimum at De ≈ 1–2
		the longitudinal force is attractive at small longitudinal distances,
		but becomes repulsive at large longitudinal distances and large De
	soft sheets	frequent transitions between sheet attraction and repulsion for De > 0
		inter-sheet distances and tilt angles affect the sign of these forces
properties after clustering	stiff sheets	the speed decreases after clustering
	soft sheets	the speed increases after clustering
		the monotonic increase in the V–De curve becomes non-monotonic
cluster stability of distinct swimmers	stiff sheets	clusters are most stable at De ≈ 1
	soft sheets	clusters are most stable at De ≈ 1
inter-sheet forces between distinct swimmers	stiff sheets	the force gradient at a stable point is largest at De ≈ 1
	soft sheets	the force gradient at a stable point is largest at De ≈ 2–3

Our simulations show that both fluid viscoelasticity and sheet elasticity significantly affect the clustering of two swimmers, including their clustering time, changes in their swimming behaviour after the doublet is formed, the stability of the cluster and the inter-sheet forces. For a relatively stiff sheet ($\mathrm{Sp}\lesssim 0.86$), an increase in fluid elasticity first impedes its speed and then results in its increase, with a minimum velocity at De ≈ 1. For a soft sheet ($\mathrm{Sp}\gtrsim 0.86$), the swimming speed is a monotonically increasing function of fluid elasticity. Therefore, soft sheets have the slowest speed in a Newtonian fluid at De = 0.

Two stiff sheets generally attract each other, with the weakest attraction strength (or the longest clustering time) corresponding to De ≈ 2–3. Attractive interactions between two sheets in the vertical direction decay relatively fast with the inter-sheet distance r_v, such that $F_v\sim 1/r_v^{\alpha }$ with α ≈ 4. Clustering of two soft sheets is much less robust, often showing a time-dependent oscillating distance between the two sheets. This behaviour can be explained by frequent transitions between sheet attraction and repulsion, which depend on relative inter-sheet distances and tilt angles. At low Sp, the clustering of two sheets generally exhibits a decrease of the doublet speed, as a result of a larger viscous resistance of the pair in comparison to a single swimmer. At large Sp, the speed of a doublet after clustering is increased due to an enhancement in the beating amplitude of the pair. Furthermore, the clustering leads to stiffening of the doublet swimmer in comparison to a single swimmer, such that the relationship between the doublet speed and De shifts toward swimming of a stiffer swimmer after the cluster is formed. Swimmers with a head show a qualitatively similar behaviour, with a reduced swimming velocity in comparison to the case without a head due an additional viscous friction from the head.

Despite the fact that two identical swimmers successfully cluster, the stability of a doublet can substantially be affected by differences in the sheet properties, such as beating frequency, wave amplitude and relative tilt angle between the two sheets. For instance, already a relatively small difference in the driving amplitude of two sheets ($\mathrm{\Delta }{\theta }_b/\pi \gtrsim 0.06$) results in no stable clustering of the pair. Furthermore, a tilt angle of a few degrees in the relative orientation of two sheets can lead to repulsion between them. Note that the cluster formation is most stable at De ≈ 1, which has been confirmed through the calculation of interaction force gradients at stable fixed points for different De. In conclusion, the doublet stability of two distinct swimmers is robust only for small differences between the sheets, which experience weak attractive or repulsive hydrodynamic interactions depending on various conditions.

In the context of collective behaviour of multiple swimmers, the effect of fluid viscoelasticity can be quite complex, as fluid viscoelasticity often affects non-monotonically interaction forces and the stability of swimmer clustering. Consistently with experiments on enhanced clustering of bovine sperms in viscoelastic fluids [5], our simulations show that the stability of clustered swimmers is enhanced at De ≈ 1. However, sperm clusters are dynamic, such that sperms can leave a cluster or new cells can join it, which is likely due to differences in the sperm properties, such as different beating amplitudes and frequencies, flagellum lengths and stiffnesses. As a result, the differences in swimmer properties lead to distinct local flow fields around interacting swimmers, affecting their hydrodynamic coupling and determining their clustering potential.

Appendix A. SDPD convergence tests

Convergence tests for the SDPD method have been performed for two problems: (i) an unsteady flow above an oscillating plate (the second Stokes problem) and (ii) a waving sheet with a prescribed waveform. For the first problem, the flow is governed by the following equations:

$$\begin{array}{rl}& \rho \frac{\mathrm{\partial }{v}_x}{\mathrm{\partial }t}={\eta }_s\frac{\mathrm{\partial }{v}_x^2}{\mathrm{\partial }{y}^2}+\frac{{\eta }_p}{\tau }\frac{\mathrm{\partial }{c}_{xy}}{\mathrm{\partial }y},\\ & \frac{\mathrm{\partial }{c}_{xx}}{\mathrm{\partial }t}=2c_{xy}\frac{\mathrm{\partial }{v}_x}{\mathrm{\partial }{v}_y}+\frac{1}{\tau }(1-c_{xx})\\ \mathrm{and}& \frac{\mathrm{\partial }{c}_{xy}}{\mathrm{\partial }t}=\frac{\mathrm{\partial }{v}_x}{\mathrm{\partial }y}-\frac{c_{xy}}{\tau }.\end{array}\}$$ A 1

These governing equations are subject to boundary conditions given by

$$v_x=V\sin (\omega t),y=0\hspace{0.17em}\text{or}\hspace{0.17em}y=L_y.$$ A 2

Here, for convenience, the velocity boundary conditions are imposed at both y = 0 and y = L_y. In SDPD, this setup is achieved by using periodic boundary conditions in the y-direction. The initial conditions are given by

$$\begin{array}{rl}& v_x=0,\hspace{0.17em}\text{for}\hspace{0.17em}t=0,\hspace{0.17em}0\le y\le L_y,\\ & c_{xx}=1.0,\text{for}\hspace{0.17em}t=0,\hspace{0.17em}0\le y\le L_y\\ \mathrm{and}& c_{xy}=0.0,\text{for}\hspace{0.17em}t=0,\hspace{0.17em}0\le y\le L_y.\hspace{0.17em}\end{array}\}$$ A 3

Equations (A1) are first solved in the domain 0 ≤ y ≤ L_y using a finite-difference method (Crank–Nicolson method). Oscillation of a monitored point at L_y/2 is recorded. Then, the same problem with identical parameters is solved using our SDPD implementation. The oscillation of the monitored point at L_y/2 is compared between the two methods using the L₁ error:

$$L_1=\frac{1}{N}\sum _t^N|x_f\hspace{0.17em}(t)-x_s(t)|,$$ A 4

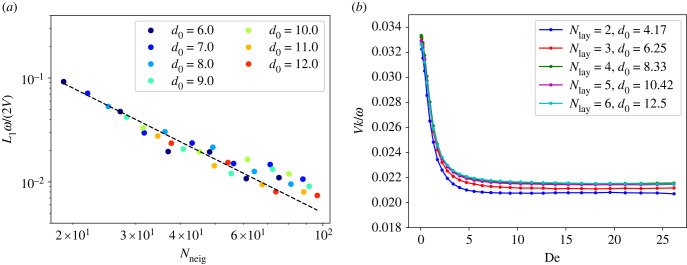
where x_f is the position determined from the finite-difference scheme, x_s is the position determined from the SDPD simulation and N is the number of samples. We obtain N = 400 equidistant samples from the first four oscillation periods. To test the convergence of the SDPD simulation, both the cut-off radius and the number density of particles are varied. The L₁ errors for different r_c and d₀ are shown in figure 17a. For the SDPD/SPH method, errors vanish when d₀ → ∞, N_neig → ∞ and h → 0 [69], where N_neig is the number of neighbour particles within the smoothing length h. Figure 17a demonstrates that the L₁ errors reduce with increasing d₀ and r_c, and scale with N_neig as $L_1\propto N_{\mathrm{neig}}^{-1.72}$. For all simulations in this article, the resolution $d_0=16/r_c^2$ and the cut-off radius r_c = 1.6 were used, which is a reasonable choice based on the convergence results in figure 17.

Figure 17.

SDPD convergence tests. (a) L₁ error for the second Stokes problem, where solutions from a finite-difference scheme and the SDPD method are compared. The dashed line indicates the slope of $L_1\propto N_{\mathrm{neig}}^{-1.72}$. The errors are normalized by the oscillation magnitude 2V/ω. Here, ρ/ρ_ref = 1, η_s/η_ref = 9.6, η_p/η_ref = 6.4, τ/t_ref = 15.6, ω/ω_ref = 0.32, V/v_ref = 0.8, L_y/l_ref = 12.5 (note that the reference values in table 1 are used with the reference length l_ref fixed at 1.6), and De = 5.0. (b) Convergence test for the waving sheet problem, showing the swimming velocity. Here, L/r_c = 12.5, L_x/r_c × L_y/r_c = 25 × 25, kr_c = 2π/(L/r_c), ω/ω_ref = 1.5 and b/r_c = 0.625.

The second problem for testing the convergence of SDPD is a finite-size waving sheet. The employed actuation sheet model explicitly depends on the discretization resolution. If the bending stiffness κ of the sheet is finite, a modification in the sheet resolution would necessarily affect the bending stiffness, which makes it difficult to study the convergence for soft sheets. Therefore, the case of κ = ∞ (S_p = 0) is only considered here, as the waveform of the sheet is prescribed and no internal beating actuation is needed. When a sine wave y(x, t) = bsin (kx − ωt) travels along the sheet, the motion of sheet particles in the frame of the swimming sheet is given by

$$\begin{array}{rl}& v_x=\frac{\omega }{k}-Q\cos \theta ,v_y=-Q\sin \theta ,\\ & \tan \theta =bk\cos (kx-\omega t+\varphi )\\ \mathrm{and}& Q=\frac{\omega }{2\pi k}{\displaystyle {\int }_0^{2\pi }{(1+b^2{k}^2{\cos }^2\xi )}^{1/2}\mathrm{d}\xi ,}\end{array}\}$$ A 5

where v_x and v_y are the particle velocities. Motion of the SDPD particles representing the sheet is imposed using equation (A 5), which results in driving the surrounding fluid flow. Then, the swimming velocity of the sheet is equal to the far-field flow velocity. To test the convergence of swimming velocity as a function of fluid resolution, the number of particle layers (N_lay) within the sheet representation is varied with the sheet thickness and length fixed. In this case, the number density of fluid particles cannot be altered arbitrarily, since we have to guarantee that the number of layers within the sheet representation is an integer. Therefore, d₀ is changed according to the number of layers N_lay. Figure 17b presents the swimming velocity for different sheet resolutions as a function of De. As the number of layers in the sheet representation is increased, the velocity results converge for all De values. For the lowest resolution (d₀ = 4.17), the largest error is about 6% with respect to the converged velocity values. For a good balance between the computing cost and accuracy, d₀ = 6.25, N_lay = 3 was selected for all simulations in this work.

Data accessibility

The code necessary to reproduce the findings of this study can be accessed at https://github.com/mokchie/lammps_flagellated_swimmer.git. Input scripts for all simulations and post-processing scripts for the data analysis used in this study can be accessed at https://github.com/mokchie/clustering_swimmers.git.

Authors' contributions

C.M.: formal analysis, investigation, software, visualization, writing—original draft; D.A.F.: conceptualization, supervision, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

C.M. acknowledges funding by the China Scholarship Council (CSC) and German Academic Exchange Service (DAAD) through the Sino-German (CSC-DAAD) Postdoc Scholarship Program.