Comparing COVID-19 Case Prediction Between ARIMA Model and Compartment Model — China, December 2019–April 2020

Abstract

Introduction

To compare the performance between the compartment model and the autoregressive integrated moving average (ARIMA) model that were applied to the prediction of new infections during the coronavirus disease 2019 (COVID-19) epidemic.

Methods

The compartment model and the ARIMA model were established based on the daily cases of new infection reported in China from December 2, 2019 to April 8, 2020. The goodness of fit of the two models was compared using the coefficient of determination (R²).

Results

The compartment model predicts that the number of new cases without a cordon sanitaire, i.e., a restriction of mobility to prevent spread of disease, will increase exponentially over 10 days starting from January 23, 2020, while the ARIMA model shows a linear increase. The calculated R² values of the two models without cordon sanitaire were 0.990 and 0.981. The prediction results of the ARIMA model after February 2, 2020 have a large deviation. The R² values of complete transmission process fit of the epidemic for the 2 models were 0.964 and 0.933, respectively.

Discussion

The two models fit well at different stages of the epidemic. The predictions of compartment model were more in line with highly contagious transmission characteristics of COVID-19. The accuracy of recent historical data had a large impact on the predictions of the ARIMA model as compared to those of the compartment model.

The outbreak of coronavirus disease 2019 (COVID-19) at the end of 2019 has caused a global pandemic and presents a major challenge to human health and survival. Accurately predicting the incidence of the COVID-19 epidemic can help distribute medicine and other health resources, take prompt and effective control measures, and suppress the spread of the epidemic. The compartment model divides the population into different compartments categorized by their epidemiological status. Ordinary differential equations were used to express the continuous dynamic changes among different compartments. Different epidemic processes of infectious diseases were simulated by adjusting the differential equations. The autoregressive integrated moving average (ARIMA) model is a time series prediction method that uses autocorrelation analysis of time series data to identify patterns of change and predict future points in the series. Previous research studies (1-4) have applied these two models in predicting COVID-19 epidemics, but few have compared them. Therefore, this study aims to compare the performance of the two models during the early COVID-19 outbreak in China. According to the timing of intervention measures and their effects, this paper divides the timeline of the epidemic into 3 stages: 1) Stage 1 from December 2, 2019, when the first case was reported, to January 22, 2020, when few interventions were taken during this stage; 2) Stage 2 from January 23 to February 1, 2022, when cordon sanitaire was implemented during this stage; 3) Stage 3 from February 2 to April 8, 2022, when centralized isolation and expanded testing were applied during this stage (details are provided in Supplementary Materials and Supplementary Figure S1, available in https://weekly.chinacdc.cn/).

METHODS

Data Source

The COVID-19 infection data was extracted from the Infectious Disease Reporting System of Chinese Center for Disease Control and Prevention from December 2, 2019 to April 8, 2020. The data included the reported onset date of the infection, which is the date when an infected person reported symptoms such as fever, cough, and other respiratory symptoms, and the clinical severity of each infected person, which ranged from asymptomatic, mild, moderate, severe, and critical. After excluding asymptomatic infections, a total of 81,102 confirmed cases were sorted to obtain the number of daily new cases. This was used to construct time series models and compartment models as well as to evaluate their fit and predictive effects. The population data for the same period were collected from the official website of the National Bureau of Statistics (5).

Comparison Between Two Models

First, this study compared the effects of the two models in fitting the complete transmission process of the epidemic. Second, the study compared the predictions of the number of new cases without cordon sanitaire by the two models. Finally, the study compared predictions without centralized isolation and expanded testing by two models.

Comparison of Model Fitting

The coefficient of determination (R²) was used to compare the fitting of the model. The formula is as follows:

1

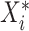is the true value in moment 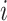, 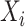is the predicted value in moment 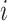, and 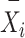is the mean of true values.

Data Analysis

Packages “aTSA,” “forecast,” and “BayesianTools” in the R software (version 4.0.5, R Foundation for Statistical Computing, Vienna, Austria) were used to construct the ARIMA model and the compartment model and to predict new infections. P<0.05 was considered statistically significant (α=0.05).

RESULTS

For the compartment model, the parameters of the Stages 1–3 of the model (more details are provided in Supplementary Materials, Supplementary Table S1, and Supplementary Figure S2, available in https://weekly.chinacdc.cn/) were used to simulate the complete transmission process of the epidemic. The results are shown in Figure 1A. For the ARIMA model, the unit root test was performed on the onset sequences of Stages 1–3, and the results showed that the sequences were stationary. The autocorrelation coefficient and partial correlation coefficient of the stationary series are shown in Supplementary Figure S3A and S3B (available in https://weekly.chinacdc.cn/). The p=1–3 and q=1–3 of the onset sequence of the Stages 1–3 were preliminarily determined; the results of the residual white noise test on the 9 initially determined alternative models are shown in Supplementary Table S2 (available in https://weekly.chinacdc.cn/). According to the principle of Bayesian Information Criterion (BIC) minimization, ARIMA (1,2,1) was selected as the optimal model for the onset sequence of Stages 1–3. The optimal model was used to simulate complete transmission process of the epidemic and was compared with the compartment model (Figure 1B). The calculated R² values of the compartment model and the ARIMA model were 0.964 (P<0.001) and 0.933 (P<0.001), respectively.

Figure 1.

Comparison of the two models. (A) The results of the compartment model in fitting the complete transmission process of the epidemic; (B) The results of the ARIMA model in fitting the complete transmission process of the epidemic; (C) The prediction results of the compartment model without cordon sanitaire implemented; (D) The prediction results of the ARIMA model without cordon sanitaire implemented; (E) The prediction results of the compartment model without centralized isolation and expanded testing implemented; (F) The prediction results of the ARIMA model without centralized isolation and expanded testing implemented; (G) The prediction results of the ARIMA model without centralized isolation and expanded testing implemented after excluding outliers.

Note: Due to the abnormally high number of daily new cases reported on February 1, 2020, the prediction results of the ARIMA model after February 2, 2020 showed a rapid increase. After excluding the outlier, the prediction of daily new cases will decrease.

Abbreviation: ARIMA=autoregressive integrated moving average.

For the compartment model in Stage 1, the parameters from Stage 1 were used to predict the number of new COVID-19 cases during the 10 days starting from January 23, 2020 (i.e., first 10 days in Stage 2) with the assumption that no cordon sanitaire was implemented in China (Figure 1C). For the ARIMA model, after 3 differences in the Stage 1 incidence sequence, the unit root test showed that the sequence had been stationary. The autocorrelation coefficient and partial correlation coefficient of the stationary series are shown in Supplementary Figure S3C and S3D. The p=0 and q=1–3 of the first-stage onset sequence were preliminarily determined, and the results of the residual white noise test for the 3 preliminarily determined alternative models are shown in Supplementary Table S2. According to the principle of minimizing BIC, ARIMA (0,3,3) was chosen as the optimal model of the Stage 1 onset sequence. The optimal model was used to compare the prediction of incidence over the same period of time with that of the compartment model (Figure 1D). The prediction of the two models demonstrated that the number of new COVID-19 cases would increase if no cordon sanitaire was taken after January 23, 2020. The number of daily cases predicted by the compartment model showed an exponential increase. The ARIMA model, however, showed a linear increase, which did not reflect the high transmissibility of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) virus. The R² of the compartment model and the ARIMA model were 0.990 (P<0.001) and 0.981 (P<0.001), respectively.

For the compartment model, the parameters of the Stage 1–2 were applied to predict the number of new cases during the 10 days starting from February 2, 2020 (i.e., first 10 days in Stage 3) with the assumption of no centralized isolation and expanded testing being adopted (Figure 1E). After taking the three differences of the Stage 1–2 onset sequence for the ARIMA model, the unit root test showed that the sequence had been stationary. The autocorrelation coefficient and partial correlation coefficient of the stationary series are shown in Supplementary Figure S3E and S3F. The p=1–3 and q=0 of the onset sequences of Stage 1–2 were preliminarily determined; the residual white noise test results of the 3 initially determined alternative models are shown in Supplementary Table S2. According to the principle of BIC minimization, ARIMA (2,3,0) was selected as the optimal model of Stage 1–2 onset sequence. This optimal model was used to predict incidence outside the modeling sequence for the same duration, and the result was compared with the compartment model (Figure 1F). Due to the abnormally high number of cases reported in a single day on February 1, the results of the ARIMA model had a large deviation and showed a rapid increase. After excluding this outlier, the results of re-fitting the ARIMA model are shown in Figure 1G. The R² values of the compartment model and the ARIMA model, without excluding outliers, were 0.969 (P<0.001) and 0.948 (P<0.001), respectively. After excluding outliers, the R² of the ARIMA model was 0.937.

DISCUSSION

Appropriate predictions can help authorities promptly adjust control strategies and allocate medical resources. The compartment model and the ARIMA model are used by numerous researchers in the prediction of COVID-19. Taking the early COVID-19 epidemic in China as an example, the predictions of the compartment model and the ARIMA model at different stages of the epidemic were compared and both models fit well at different stages of the epidemic. Furthermore, the predictions of the compartment model are in line with the highly contagious transmission characteristics of the COVID-19. In addition, since the ARIMA model is a prediction method that considers the changing trends of past values over time and predicts future values by fitting the mathematical model with historical data, the accuracy of recent historical data has a relatively large impact on the results of model extrapolation. Based on the numbers of daily new cases and parameters supported by existing literature, the compartment model can be calibrated using Markov chain Monte Carlo (MCMC) algorithm, allowing its predictions to be relatively less affected by outliers.

Although the ARIMA model does not perform as well as the compartment model in terms of predicting COVID-19, it is important to consider that the novel coronavirus is still in the process of dynamic evolution in the future. With this in mind, the parameters of the compartment model can also change accordingly and are difficult to obtain. Meanwhile, the accurate simulation of model has high requirements for the selection of parameters. Compared with the compartment model, the ARIMA model only needs time series data to build a forecasting model, which is easy to implement and has high accuracy for short-term forecasting. It can be quickly applied to forecasting COVID-19.

The compartment model divides the population into different compartments, with the dynamics of these compartments described by ordinary differential equations. Researchers can incorporate different compartments and parameters into the model to more accurately simulate transmission patterns and epidemiological characteristics of the novel coronavirus. Compared with the ARIMA model, which replaces various influencing factors with time, the compartment model can analyze the impact of population movement, vaccination, isolation measures, and other interventions on disease transmission. Therefore, when predicting COVID-19, it is necessary to comprehensively consider the advantages of different models and choose the best model based on existing conditions.

This study was subject to at least two limitations. First, there were no real-world values to compare with the models’ predictions on the temporal trends of the numbers of daily new cases in specific hypothetical scenarios. Therefore, the accuracy of predictions could not be compared using mean absolute error (MAE) and root mean squared error (RMSE). Second, as a result of dynamic changes in epidemic-related influencing factors — such as prevention and control measures, medical resources, and viral transmissibility, etc. — neither the compartment model nor the ARIMA model could guarantee the accuracy of their long-term predictions. It is necessary to constantly update data to improve their prediction accuracy.

SUPPLEMENTARY MATERIAL

Compartment Model

Under the framework of the susceptible-exposed-infectious-recovered (SEIR) model, pre-symptomatic cases (P), asymptomatic infected cases (A), hospitalized patients (H), and shelter-isolated infected persons (Iq) were added to simulate the transmission pattern of coronavirus disease 2019 (COVID-19) at different stages (Supplementary Figure S1). According to the different interventions that were taken at different stages, different compartments and parameters were introduced to establish a multi-stage infectious disease compartment model.

The reported onset date of the first case of COVID-19 infection, December 2, 2019, was set as the starting date of the model. The initial value of the model is set to S=59,170,000, I=1, E=P=A=H=R=0. The model parameters were obtained from two kinds of sources. Some parameters were obtained according to previous studies. Other parameters were estimated by the Markov chain Monte Carlo algorithm (MCMC) (1) (Supplementary Table S1).

Compartment Model Structures and Parameters

A compartment model was developed to simulate the full-spectrum dynamics of COVID-19 in China between December 2, 2019 and April 8, 2020. The resident population of Hubei Province in 2018 was used as the initial susceptible population, and the inter-provincial population movement during the Chunyun, or Spring Festival travel period, in Hubei Province was not considered in the analysis. The reasons are as follows:

1. In the period of Stage 1, most infections occurred in Hubei Province.

2. During the Chunyun (January 10 to January 22, 2020), the outflow population in Hubei Province were isolated in their homes for a long time (i.e., after January 23, 2020).

3. According to the report of the China-World Health Organization (WHO) joint investigation expert group, community transmission outside Hubei Province was very limited and most of it was in family clusters (2).

The model structure is illustrated in Supplementary Figure S1.　

Figure S1.

Schematic diagram of the COVID-19 transmission in the compartment model. (A) At Stage 1 and Stage 2; (B) At Stage 3.

Note: S is the numbers of susceptible population. E is the exposed state with latent infection. A is the asymptomatic infected cases (i.e., people who never develop symptoms). P is the pre-symptomatic cases. Although there is no pre-symptomatic phase for asymptomatic individuals, P was treated as a transitional phase in order to distinguish between the non-infectious latent period and the infectious pre-symptomatic state. I is the confirmed cases with symptoms. H is the hospitalized patients who are hospitalized because of worsening symptoms. Iq is the confirmed cases who are detected because of expanded testing and isolated in the square cabin. R is the recovered patients.

Model Structure

The ordinary differential equations are as follows:

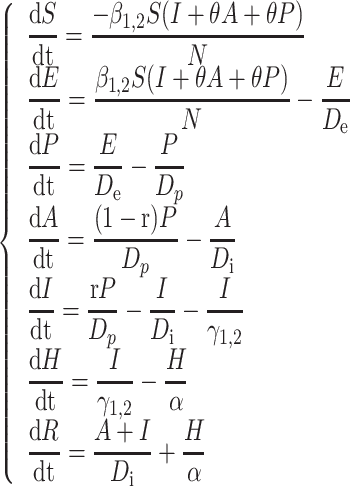Formula S1 indicates the differential equations for COVID-19 transmission during Stage 1 and Stage 2, and Formula S2 indicates the differential equations for COVID-19 transmission during Stage 3 where parameter 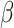is the transmission rate for the confirmed cases with symptoms. Pre-symptomatic and asymptomatic cases were assumed to be less infectious compared to people suffering from symptoms with a relative risk 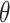. r is proportion of symptomatic infected cases among all infected cases; D_e is the latent period; D_p is the pre-symptomatic infectious period; D_i is the asymptomatic, mild, and moderate infectious period; is the duration from illness onset to hospitalization; 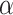is the time to recovery for confirmed cases; 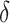is the duration from testing to isolation; 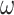is detection rate of asymptomatic infections; and b is proportion of isolation in the square cabin among all symptomatic infections.

All model parameters are summarized in Supplementary Table S1. This system dynamics model is implemented in the R software (version 4.0.5; R Core Team, Vienna, Austria).

Table S1. Definition and value of parameters.

Model parameters	Meaning	Value	Sources
Abbreviation: MCMC=Monte Carlo Markov Chain.
	Transmission rate (Stage 1)	1.598	MCMC calibration
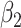
	Transmission rate (Stage 2)	0.376	MCMC calibration
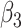
	Transmission rate (Stage 3)	0.127	MCMC calibration
r	Proportion of symptomatic infected cases	20.0%	(3)
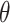
	Relative transmission risk for pre-symptomatic and asymptomatic infections	30.0%	(4)
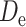
	Duration of latent period	2.9 days	(5)
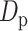
	Duration of infectious pre-symptomatic state	2.3 days	(5–6)
	Infectious period for asymptomatic, mild, and moderate infections	7.0 days	(7)
	Duration from illness onset to hospitalization (Stage 1 and Stage 2)	6.0 days	(5)
	Duration from illness onset to hospitalization (Stage 3)	2.0 days	(5)
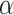
	Time to recovery for the confirmed cases	10.0 days	(8)
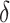
	Duration from testing to isolation	2.0 days	(9)
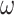
	Detection rate of asymptomatic infections	54.7%	MCMC calibration
b	Proportion of isolation in the square cabin among all symptomatic infections	9.6%	(10–11)

Model Calibration

To estimate parameters (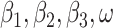), the Metropolis–Hastings Markov Chain Monte Carlo (MCMC) algorithm was used. The Delayed Rejection Adaptive Metropolis (DRAM) sampler from the BayesianTools R package was also used. Calibration target is numbers of daily new cases, which was extracted from The Infectious Disease Reporting System of the Chinese Center for Disease Control and Prevention from December 2, 2019 (i.e., date of onset of the first reported infection) to April 8, 2020. It was assumed that the observed number of daily new cases in which individuals experienced symptom onset on day d — denoted as k_d — follows a Poisson distribution with rate 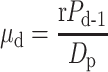, in which P_d−1 is the expected number of pre-symptomatic cases on day (d−1). The likelihood function is

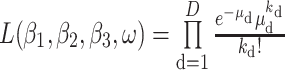In MCMC sampling, a non-informative flat was set prior of Unif (0,2) for 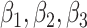and Unif (0,1) for . After a burn-in period of 50,000 iterations, MCMC sampling was continued for an additional 100,000 iterations and MCMC samples were selected at every 10 iterations to avoid auto-correlation. Means of the model parameters are presented in Supplementary Table S1. Supplementary Figure S2 shows a histogram of the posterior distributions.

Figure S2.

Posterior distributions of Markov Chain Monte Carlo samples for calibrated model parameters. (A) For β₁; (B) For β₂; (C) For β₃; (D) For ω.

ARIMA Model

The ARIMA model was established in 4 steps (12). 1) Time series stabilization. The model requires that the fitted time series be stable, that is, the mean and variance of the series do not change over time. If the original series is not stable, it needs to be made into a stationary series by means of difference. The time series diagram and unit root test can be used to judge whether the series is stationary. 2) Model identification. Autocorrelation function (ACF) and partial autocorrelation function (PACF) were drawn from the sequence that meets the stationarity requirement after the difference. The values of p and q in the model were preliminarily determined according to its truncation or tailing situation, and multiple alternative models were fitted. 3) Model diagnosis. To check whether the model was effective, the sufficiency of information extraction was tested. The Ljung-Box residual white noise test was carried out on the candidate model. A non-white noise fitting residual sequence indicated that there were still relevant factors that had not been extracted and needed to be excluded. 4) Model optimization. According to the Bayesian Information Criterion (BIC), the model with the minimum value of BIC function was the optimal model.　

Figure S3.

The ACF and PACF graphs. (A) ACF for Stages 1–3; (B) PACF for Stages 1–3; (C) ACF for Stage 1; (D) PACF for Stage 1; (E) ACF for Stages 1–2; (F) PACF for Stages 1–2.

Abbreviation: ACF=autocorrelation function; PACF=partial autocorrelation function.

Table S2. Residual white noise test and BIC value of alternative models.

Stages	Alternative models	Whether the model was effective	BIC value
Note: "−" means not applicable. Abbreviation: BIC=Bayesian Information Criterion; ARIMA=autoregressive integrated moving average.
1	ARIMA (0,3,1)	No	−
	ARIMA (0,3,2)	No	−
	ARIMA (0,3,3)	Yes	597.69
1–2	ARIMA (1,3,0)	No	−
	ARIMA (2,3,0)	Yes	862.97
	ARIMA (3,3,0)	No	−
1–3	ARIMA (1,2,1)	Yes	1,796.24
	ARIMA (2,2,1)	Yes	1,797.92
	ARIMA (3,2,1)	Yes	1797.63
	ARIMA (1,2,2)	Yes	1797.47
	ARIMA (2,2,2)	Yes	1799.20
	ARIMA (3,2,2)	Yes	1799.50
	ARIMA (1,2,3)	Yes	1798.30
	ARIMA (2,2,3)	Yes	1797.16
	ARIMA (3,2,3)	Yes	1801.48

REFERENCES

• Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian data analysis. 3rd ed. New York: Chapman and Hall. 2013. https://www.taylorfrancis.com/books/mono/10.1201/b16018/bayesian-data-analysis-david-dunson-donald-rubin-john-carlin-andrew-gelman-hal-stern-aki-vehtari.

• Shi YC. China-WHO joint investigation expert group: community transmission is limited in other provinces outside Hubei, mostly family clustered outbreaks. 2022. https://news.ifeng.com/c/7uKcoSNfqfQ. [2022-07-11]. (In Chinese).

• He ZY, Ren LL, Yang JT, Guo L, Feng LZ, Ma C, et al. Seroprevalence and humoral immune durability of anti-SARS-CoV-2 antibodies in Wuhan, China: a longitudinal, population-level, cross-sectional study. Lancet 2021;397(10279):1075 − 84. http://dx.doi.org/10.1016/S0140-6736(21)00238-5.

• Chen Y, Wang AH, Yi B, Ding KQ, Wang HB, Wang JM, et al. Epidemiological characteristics of infection in COVID-19 close contacts in Ningbo city. Chin J Epidemiol 2020;41(5):667 − 71. http://dx.doi.org/10.3760/cma.j.cn112338-20200304-00251. (In Chinese).

• Hao XJ, Cheng SS, Wu DG, Wu TC, Lin XH, Wang CL. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 2020;584(7821):420 − 4. http://dx.doi.org/10.1038/s41586-020-2554-8.

• Li Q, Guan XH, Wu P, Wang XY, Zhou L, Tong YQ, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med 2020;382(13):1199 − 207. http://dx.doi.org/10.1056/NEJMoa2001316.

• Prem K, Liu Y, Russell TW, Kucharski AJ, Eggo RM, Davies N. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health 2020;5(5):e261 − 70. http://dx.doi.org/10.1016/S2468-2667(20)30073-6.

• Shao P, Shan YJ. Beware of asymptomatic transmission: study on 2019-nCoV prevention and control measures based on extended SEIR model. bioRxiv. 20202020 − 1. http://dx.doi.org/10.1101/2020.01.28.923169.

• Kucharski AJ, Klepac P, Conlan AJK, Kissler SM, Tang ML, Fry H, et al. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study. Lancet Infect Dis 2020;20(10):1151 − 60. http://dx.doi.org/10.1016/S1473-3099(20)30457-6.

• China TSCI. Fighting covid-19: China in action. People's Daily. http://to.china-embassy.gov.cn/eng/sgxw/202006/t20200608_57786.htm. [2020-6-8].

• Bai M, Liu XQ, Wu WQ, Sun K, Huang X, Jin HZ. Clinical characteristics of 472 cases of novel coronavirus pneumonia in Wuhan Jiangan Makeshift (Fangcang) Hospital. Clin Focus 2020;35(4):297-301. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2020&filename=LCFC202004002. (In Chinese).

• Wang Y. Time series analysis with R. Beijing: China Renmin University Press. 2015. http://find.nlc.cn/search/showDocDetails?docId=-4764597708139708653&dataSource=ucs01&query=%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97%E5%88%86%E6%9E%90. (In Chinese).

Funding Statement

Supported by the National Natural Science Foundation of China (No. 82041023)