SDEGen: learning to evolve molecular conformations from thermodynamic noise for conformation generation

Abstract

Generation of representative conformations for small molecules is a fundamental task in cheminformatics and computer-aided drug discovery, but capturing the complex distribution of conformations that contains multiple low energy minima is still a great challenge. Deep generative modeling, aiming to learn complex data distributions, is a promising approach to tackle the conformation generation problem. Here, inspired by stochastic dynamics and recent advances in generative modeling, we developed SDEGen, a novel conformation generation model based on stochastic differential equations. Compared with existing conformation generation methods, it enjoys the following advantages: (1) high model capacity to capture multimodal conformation distribution, thereby searching for multiple low-energy conformations of a molecule quickly, (2) higher conformation generation efficiency, almost ten times faster than the state-of-the-art score-based model, ConfGF, and (3) a clear physical interpretation to learn how a molecule evolves in a stochastic dynamics system starting from noise and eventually relaxing to the conformation that falls in low energy minima. Extensive experiments demonstrate that SDEGen has surpassed existing methods in different tasks for conformation generation, interatomic distance distribution prediction, and thermodynamic property estimation, showing great potential for real-world applications.

In this paper, we developed a novel conformation generation model, termed SDEGen, learning how a molecule evolves in a stochastic dynamics system starting from noise and eventually relaxing to the conformation that falls into low energy minima.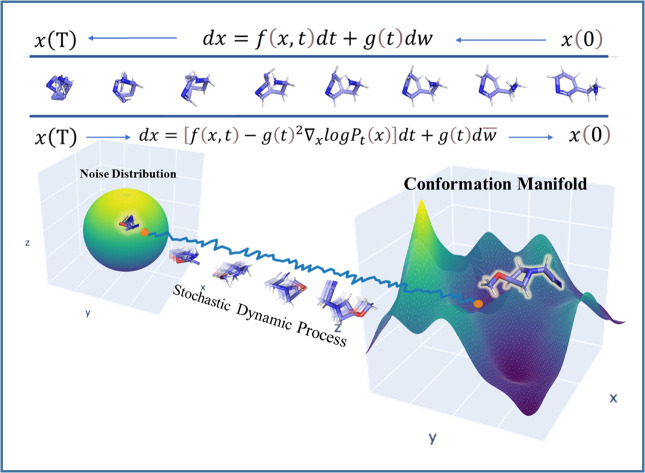

Introduction

The conformation of a molecule represents the 3D coordinates of all the atoms in a molecule. It is well acknowledged that in statistical dynamics, we know everything about a macroscopic system if we can search for all the corresponding microstates, i.e., geometries. Therefore, it is quite essential to obtain all the possible conformations for studied systems to solve complicated biomolecule-involved problems such as structure-based drug design. For example, the quality and diversity of the 3D conformations of a molecule are crucial for various tasks in drug discovery, such as three-dimensional quantitative structure–activity relationships (3D-QSAR),¹ pharmacophore searching,² molecular docking,³ and thermodynamic calculations.⁴

Experimental techniques for 3D structure determination, including X-ray crystallography, cryo-electron microscopy (Cryo-EM) and nuclear magnetic resonance (NMR) spectroscopy, have made continuing progress, but typically they can only provide a single or several static snapshots for the studied system.⁵ Moreover, all these experiments are time-consuming and costly. Therefore, economical computational methods are needed to generate a series of conformations of molecules to study their dynamical evolution. Existing computational approaches for molecular conformation generation mainly rely on molecular dynamics (MD)⁶ and distance geometry (DG).^7,8 In MD, the conformational state of a molecule is sequentially updated based on the forces acting on each atom, starting from an initial state and a chosen approach for force computation. There are three classes of approaches to calculating the forces on atoms according to their theoretical principles: ab initio methods,⁹ density functional theory (DFT),¹⁰ and molecular mechanics (MM) based on empirical force fields.^11–13Ab initio methods and DFT are challenging to be applied to large systems due to extensive computational cost. MM based on empirical force field is much faster than the former two, but it has been considered to give a crude approximation of molecular potential energy.¹⁴ In DG, a randomly sampled set of atomic coordinates is refined against distance constraints to generate rough 3D conformations. However, the estimation of the distance matrix obtained based on traditional triangular constraints is still too coarse, resulting in low-quality conformations.¹⁵ Therefore, generating more natural and diverse low-energy conformations is still a long-standing challenge.

With the advances of artificial intelligence (AI) technologies in recent years, 3D deep generative models have been utilized for conformation generation. In 2019, Mansimov and coworkers reported the first attempt to generate 3D conformations in Cartesian coordinates using the Variational AutoEncoder (VAE) architecture.¹⁷ Subsequently, researchers adopted the idea of DG into conformation generation by changing the learning objective from the distribution in Cartesian coordinates to the distribution in the distance matrix representation, followed by the reconstruction of the 3D conformations of molecules with improved performance.^18,19 Two contemporary works reported by Ganea et al.²⁰ and Xu et al.¹⁹ can generate conformations in an end-to-end fashion via geometry elements assembly and bi-level programming, respectively. The state-of-the-art (SOTA) score-based method ConfGF²¹ reported by Shi et al. learns the pseudo-force on each atom and obtains new conformations via Langevin Markov chain Monte Carlo (MCMC) sampling. Its performance on the GEOM-Drugs²² dataset is comparable to that of the rule-based method called experimental-torsion-knowledge distance geometry (ETKDG), which is the default conformation generation model implemented in RDKit.²³ Two other methods that are developed more recently exhibit promising performances: one is DMCG,²⁴ which directly manipulates Cartesian coordinates, and the other is torsional diffusion,²⁵ which searches the conformations in the torsional space. Except the generative model framework, reinforcement learning has been used to generate conformations by scanning all accessible torsion angles.^26,27 Furthermore, Luo and coworkers extended the method of ConfGF named DGSM to enhance its performance on the GEOM-Drugs dataset²⁸ by randomly adding non-bonded edges to graph structures. In conclusion, most of these methods have better performance than the ETKDG approach on the small molecule dataset GEOM-QM9 with the number of atoms less than nine, but there is still a lot of room for improvement in GEOM-Drugs, which is more closely related to the application scenarios of drug design.

Here, inspired by recent advances in generative modeling²⁹ and stochastic dynamics,³⁰ we developed a conformation generation model, SDEGen, based on stochastic differential equations (SDE) using a deep generative model (Fig. 1). Different from the regression scheme, our model can generate not only one energetically favorable conformation but also a series of locally optimal conformations, in consistent with the real thermodynamic environment. Three benchmarks for conformation generation, interatomic distance distribution analysis and thermodynamic property prediction were designed to evaluate the accuracy and diversity of the generated conformations by using the metrics including Coverage (COV) and Matching (MAT) of molecular geometry, Max Mean Discrepancy (MMD) of interatomic distance distribution and Mean Absolute Error (MAE) of energy. The results show that SDEGen beats most competitive models on the GEOM-Drugs dataset across almost every tested metric used for benchmarking. In particular, SDEGen outperforms all the competitors on both the COV and MAT metrics to the GEOM-Drugs dataset after force-field refinement. For the interatomic distances, SDEGen beats the other models on 4 out of 6 metrics and achieves comparable results on the other one. Furthermore, with regards to the prediction of thermodynamic properties, the ensemble properties of conformations generated by SDEGen are closest to the results of the DFT calculation (∼2 kJ mol⁻¹), which brings benefits to structure-based drug design with more accuracy and effectiveness. By testing on the generated conformations of a randomly selected molecule, we observed an excellent coverage of almost all local minima on the energy landscape at the DFT level, including but not limited to where the crystal structure conformation falls in. Further tests on 12 more molecules with diverse sizes (up to 12 rotatable bonds) are conducted at the semi-empirical level, which also demonstrate good coverage of most energetically favorable regions. Finally, our model can sample conformations ten times faster than the score-based SOTA method ConfGF, showing powerful application prospects in the real world.

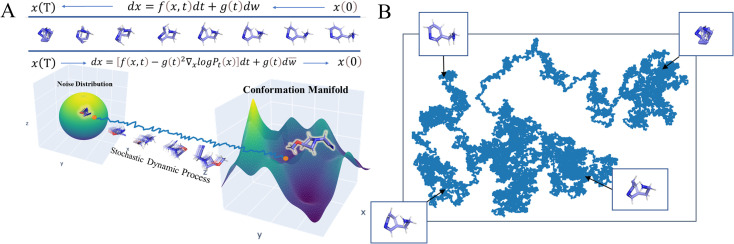
Fig. 1. Physical illustration of (A) conformation generation based on Stochastic Differential Equations (SDEGen) that evolves through the dynamical system, and (B) the evolvement of the random noise to the thermodynamically stable arrangement of atoms.

Results and discussion

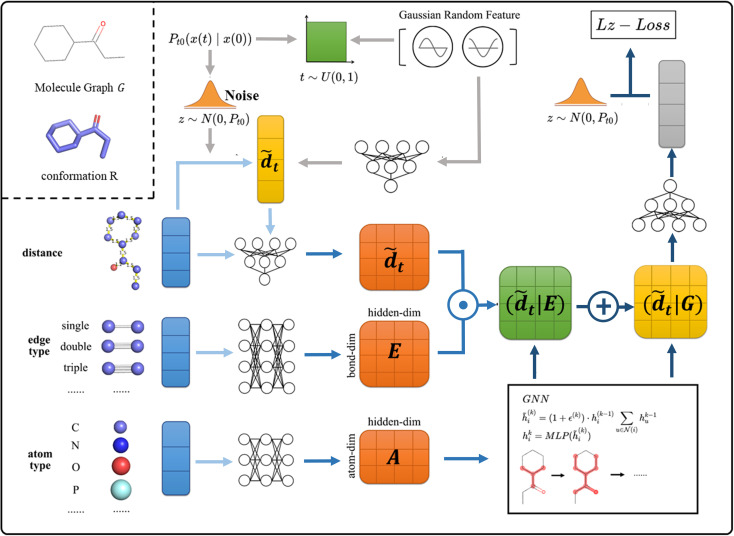
As shown in Fig. 2, in SDEGen, after randomly selecting a time step, the thermodynamic noise at that time is added to the initial interatomic distances, and then an embedding of the high-dimensional space together with the edge information is added to form the distance embedding conditional on the topological features, i.e., (d̃|E). At the same time, the attributes of atoms are also embedded and are sent to the Graph Isomorphism Networks(GIN)³¹ combined with (d̃|E) for feature extraction. After three iterations of graph message passing, the final distance features conditional on molecule Graph (d̃|G) are formed. Finally, we map (d̃|G) into the vector of dimension one and compute the L₂ loss with the original noise. This process is repeated many times at various molecules and time between [0,1] until convergence. The empirical force field-based energy optimization is embedded in the last step to fine-tune the conformations obtained by the stochastic dynamics system. Through the well-trained SDEGen network, the random samples can be evolved to thermodynamically stable conformations. The Euler–Maruyama³² solver, predictor-corrector scheme,³³ and ODE-Solver can be used to generate conformations. The details of SDEGen are described in the Method Section.

Fig. 2. The framework of SDEGen. At training time, given the graph G and conformation R, we: (1) sample the time from [0,1] uniform distribution and utilize the Gaussian random feature to encode the time information to the model, then this temporal feature is mapped together with the perturbed distance to form the d̃ (2) Map the edge(E) and atom(A) features from molecules to form corresponding embeddings (light blue and slightly darker blue arrows) (3) utilize the GNN model to encode the graph structure to the model (d̃|G) and train the SDEGen network with denoising score matching (dark blue arrows). The procedure amounts to learning the evolutionary state of the molecule in the stochastic dynamics system at the given time.

Physical illustration and model comparison

We schematically construct the physical intuition for the SDEGen model (Fig. 1). The phase space of a molecule is approximately 3N dimensions, where N is the number of the atoms in the molecule, and each point in the phase space represents a conformation. Due to the energy constraints, molecular conformations are not discrete and uniformly distributed in the phase space. The possible conformations of a molecule are distributed over the low-dimensional manifold in the high-dimensional phase space. Our initial sampling is randomly sampled in the high-dimensional phase space. It then evolves through the dynamical system, represented by the stochastic differential equation dx = f(x,t)dt + g(t)dw, to the low-dimensional manifold of the original data distribution, forming our final molecular conformation (Fig. 1A). This map in the phase space can be understood as a motion guided by the given force field, and our stochastic differential equation can be viewed as a dynamically driven approach. As illustrated in Fig. 1B, one can imagine scattering a handful of particles into the water, and the positions of the particles obey a random distribution at first. As the particles continue to collide with the water molecules, their final position distribution will tend to be thermodynamically stable. In the language of mapping, this dynamics process can be understood as a diffeomorphism from a D-dimensional hypersphere in 3N-dimensional space to another D-dimensional complex manifold in 3-dimensional space. Fig. S1 and S2† show some examples visually generated by SDEGen and other methods.

Quality of generated conformations

The mean and median of COV and MAT scores were evaluated on both the GEOM-QM9 and GEOM-Drugs datasets for SDEGen and other competitive methods, implying that the comparison was made between the conformations generated by the model and the ensemble of the quantum-computed conformers. The COV represents how much the set of quantum-computed conformations can be covered by the set of generated conformations for a given RMSD threshold: the higher, the better; while the MAT measures how similar the generated and the training QM-level conformations are: the lower, the better. The specific definition and an illustrative example of the metrics COV and MAT, standing for the diversity and accuracy of the generated conformation cluster under a given RMSD threshold, could be found in the ESI† (Part 0). The comparison of different conformation generation models is hardly straightforward because of the different training and evaluation settings used in different work. Here we have done exhaustive experiments to compare five competitive models (i.e., ConfGF, RDKit, DMCG, CGCF, and ConfGFDist) with the same dataset and settings, as shown in Table 1. SDEGen shows excellent performance on all four metrics on both datasets with force-field refinement, and achieves SOTA results on the GEOM-Drugs dataset. All the parameters were untuned. Interestingly, we observe that the performance of DMCG decreases after the force-field refinement, especially on GEOM-Drugs (dropping from 95.36 and 100.0 to 87.02 and 97.73 of mean and median COV). The subsequent experiments on the bond distribution and thermodynamic properties also support this observation. That may be because the DMCG model is designed to directly predict Cartesian coordinates trained through data enhancement, which does not meet the requirements of SE (3)-equivariance originally and causes the overfitting. At the same time, SDEGen embeds the geometry constraints by modeling the three-hop distance, contributing to more robust performance after the force-field refinement. We would like to suggest such refinement as a standard step for conformation generation tasks, just like how it serves in solving crystal or cryo-EM structures, to fine-tune the generated conformations into the nearest stationary point on the specified potential energy surface, and to check the quality of the generated structures, which also fits for the meet of the downstream tasks in real-world applications. In contrast to ConfGF, SDEGen is a multiple-stage approach, which is generally believed to be inferior to the end-to-end model,³⁴ but it still achieved an overall victory on the two datasets with the force-field refinement settings. Additionally, compared with DGSM that concerns long-range interactions by adding non-bonded edges stochastically, our model achieved better COV and MAT scores with consideration of three-hop distances, which correspond to the truncation value for the calculations of the direct interactions in MM methods.³⁵

COV and MAT scores of the different methods on the GEOM-QM9 and GEOM-Drugs datasets with Merck molecular force field refinement. The threshold δ was set to 0.5 Å for QM9 and 1.25 Å for Drugs.

Dataset	Method	COV(%) (↑)		MAT(Å) (↓)
		Mean	Median	Mean	Median
QM9	RDKit	81.82	85.98	0.3027	0.2564
	CGCF	83.48	86.70	0.2984	0.2694
	ConfGF	90.99	95.76	0.2648	0.2691
	ConfFDist	83.80	86.72	0.2658	0.2618
	DMCG	96.14	99.55	0.2035	0.2002
	SDEGen	92.40	96.51	0.2034	0.1918
Drugs	RDKit	70.47	77.08	1.2069	1.1080
	CGCF	72.41	74.09	1.1198	1.1017
	ConfGF	86.39	89.86	0.8554	0.8347
	ConfFDist	81.08	88.37	0.9624	0.9368
	DMCG	87.02	97.73	0.8794	0.8693
	SDEGen	92.00	98.51	0.7892	0.7665

Distribution of interatomic distances

The interatomic distances contain not only the bond lengths between atoms with covalent bonds but also auxiliary bonds, i.e., two-hop and three-hop distances (1–3 bond and 1–4 torsion interactions). As shown in Fig. 3B, the distribution of the interatomic distances roughly shows three peaks corresponding to the three hop bonds, which presents more structural information (including bond angels and bond dihedrals) than the trivial bond length distribution, without being too redundant like the distance matrix evaluated in RDKit. The metric MMD employed here is a kernel-base statistical test to determine whether the given two distributions are the same. The low MMD value indicates similar interatomic distributions. As shown in Table 2, although the 3D reconstruction process has compromised the estimation of distance distribution, SDEGen still yielded impressive results on all the metrics. In particular, SDEGen outperformed ConfGF in Single-median, Pair-median, all-median, and Pair-mean metrics, and still reached comparable results in Single-mean (0.3943 vs. 0.3684) and all-mean (0.6249 vs. 0.6091) metrics. It is noted that the performance of DMCG on this task falls short of the SDEGen and ConfGF models despite its superior performance on the above-mentioned conformation generation evaluation task. The comparison of SDEGen with other DG-inspired methods (i.e.,GraphDG and CGCF) indicates that SDEGen could learn smooth distance distributions conditional on different types of atoms and chemical bonds, demonstrating the plausibility of the conformations generated by SDEGen from another perspective.

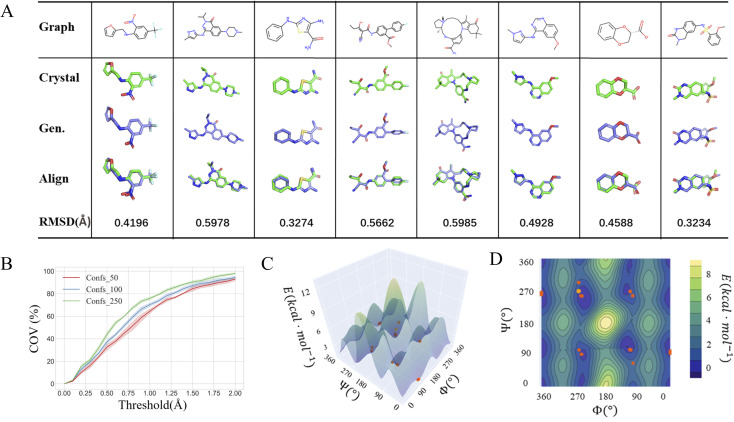
Fig. 3. (A) Comparison of generated conformations with the crystal conformations of representative molecules including macrocyclic and chiral ones; (B) the relationship between the crystal conformation coverage and the RMSD threshold within different numbers of the generated conformation of all molecules. The potential energy surface with (C) 3D and (D) 2D presentations of a randomly selected molecule scanned at DFT level. The yellow dot represents the crystal conformation and the orange dots represent the generated conformations.

The mean and median MMD of the interatomic distances distribution of different methods compared with the test set. Single: individual distances p(d_ij|G), Pair: pairwise distances p(d_ij,d_uv|G), All: all distances p(d|G).

Method	Single		Pair		All
	Mean	Median	Mean	Median	Mean	Median
RDKit	3.4513	3.1602	3.8452	3.6827	4.0866	3.7519
DMCG	4.5088	5.0245	5.2494	5.8464	5.8464	6.3546
CVGAE	4.1789	4.1762	4.9184	5.1856	5.9747	5.9928
GraphDG	0.7645	0.2346	0.8920	0.3287	1.1949	0.5485
CGCF	0.4490	0.1786	0.5509	0.2734	0.8703	0.4447
ConfGF	0.3684	0.2358	0.4582	0.3206	0.6091	0.4240
SDEGen	0.3943	0.1037	0.4518	0.1762	0.6249	0.2742

Prediction of thermodynamic properties

Thermodynamic property prediction needs a comprehensive understanding of the macroscopic states of a system. In this task, each conformation corresponds to a microscopic thermodynamic state, and these conformations are aggregated as an ensemble for a specific molecule to represent a thermodynamic system. The more comprehensive microstates considered in thermodynamic calculations, the more accurate the prediction can be. Following this principle, we evaluated the thermodynamic properties of the conformation ensemble generated by SDEGen and its representative opponents (i.e., RDKit, CGCF, ConfGF, and DMCG). The results in Table 3 show that the ensemble properties of the conformations generated by SDEGen are closest (∼2 kJ mol⁻¹) to those obtained by DFT calculations. Among all the results, SDEGen performed considerably better than the classical method RDKit (∼50 kJ mol⁻¹) on this task, implying that the stochastic dynamics method we developed does learn the molecular thermodynamic evolution process with quantum accuracy. In contrast, CGCF performs poorly (50–2500 kJ mol⁻¹) on this task due to its insufficient capability to learn the multi-model conformational manifolds. ConfGF and DMCG perform much better than the above two, but SDEGen still beats all the baselines in all the metrics and achieves the accuracy of quantum chemistry for conformation generation.

The MAE of ensemble thermodynamic properties among different methods (units: kJ mol⁻¹).

Method	Ē	E min	Δ	Δεmin	Δεmax
RDKit	70.928	46.473	27.531	52.887	18.387
CGCF	2456.7	195.94	197.38	902.02	56.323
DMCG	8.0016	8.1336	13.355	16.262	17.188
ConfGF	3.6643	3.3657	5.5305	13.355	4.8476
SDEGen	2.6406	2.9219	4.4440	12.036	4.5742

Searching for crystal and other thermodynamically stable conformations

The conformations of small-molecule ligands in the bound states suggested by their experimentally determined structures deposited in Protein Data Bank (PDB³⁶), are usually regarded as the gold standard in structure-based drug design. In most cases, these near-native conformations fall in the vicinity of the local minima, judging by the free-energy landscape of the molecule in its free state. One of our expectations for the model is that the multiple local minima could be captured so that the natural crystal conformations determined experimentally would be included in the generated conformation ensemble. To test this capability, we treated the Platinum dataset³⁷ as another external test set. The platinum dataset contains 4626 structures extracted from a total of over 347 k co-crystallized ligand structures stored in PDB by filtering out low-quality co-crystallized ligand structures (resolution > 2.0 Å) according to a set of well-designed criteria. We used the SDEGen model trained on GEOM-Drugs to generate the molecular conformations in the Platinum dataset and compared them with their original crystal conformations. The superimposed structures as well as their RMSDs of representative molecules including macrocyclic and chiral ones are shown in Fig. 3A.

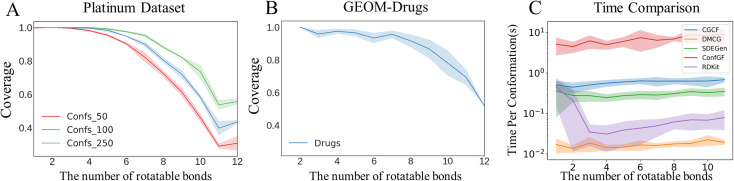
As shown in Fig. 3B, among over 85% cases, the conformations generated by our SDEGen can cover the crystal structures in the Platinum dataset (with an RMSD threshold of 1.5 Å). Moreover, the crystal conformation coverage did not increase with the increase of the number of the generated conformations in the ensemble, highlighting the model's good robustness. In general, one can reach more than 75% probability of covering the crystal conformations by generating 50 conformations for a molecule, and ∼80% probability by generating 100 conformations.

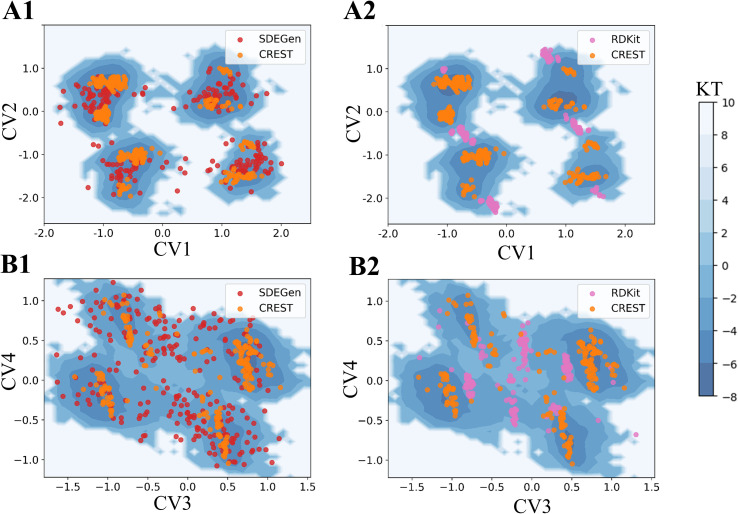
To further illustrate the quality of the conformations generated by SDEGen, we performed several case studies to test the coverage of all low-energy conformations, probably including but not limited to the crystal structures, for both QM9-level and drugs-level molecules. Firstly, we selected a molecule with two rotatable bonds from the ligand library of PDB³⁶ and scanned the potential energy values of each conformation as the function of two rotation angles at the DFT level. The orange dots on the potential energy surface in Fig. 3C and D represented the conformations generated by SDEGen, and the yellow dot represented the crystal conformations. It is found that all the 50 conformations generated by SDEGen fall into multiple wells on the potential energy landscape, and cover almost all the captured local minima. It means that the generated 50 conformations can depict most of the potential wells for the tested molecule; meanwhile, the crystal conformation also fell into one of the potential wells covered by our generated conformations, not surprisingly. More examples through semi-empirical x-TB calculations can be found in the ESI† for additional illustration (Fig. S3†). Moreover, we also explored the system of druglike molecules containing 12 rotatable bonds. Fig. 4 shows that the distribution sampled by SDEGen (red dots) allows adequate exploration of the conformational space of the molecule, and most of the sampled points are concentrated near the dominant conformation obtained by quantum chemistry computation (orange dots). Compared with the points sampled by RDKit (pink dots), the sample points from SDEGen are more uniformly distributed on the energy surface. Combined with the more accurate prediction of thermodynamic properties achieved by the previous experiment, we believe that the SDEGen could generate a representative and uniformly sampled ensemble. Treating these generated conformations as the inputs to downstream tasks can broaden the representative of energetically favorable conformations, thus fully expressing the molecule's druggability and reducing the likelihood of missing potential active compounds in lead discovery.

Fig. 4. Free energy surfaces of the two Drugs-level molecules (A) and (B) with 12 rotatable bonds estimated by x-TB based metadynamics. (A1) and (B1) are the comparisons between SDEGen and CREST(GEOM-Drugs) samples; (A2) and (B2) are the comparisons between RDKit and CREST samples. CV is the abbreviation of collective variable, which is the reduced coordinate used for visualization. The specific definition is in the appendix.†.

Discussion about limitations

Although SDEGen achieved good results in the Platinum dataset, the generated conformations for several molecules (about 16.0%) still did not cover the crystal conformations (RMSD threshold 1.5 Å). We attribute the failure cases to the following two reasons. Firstly, it is not easy for the model to handle large systems due to the existence of high degrees of freedom. According to Fig. 5A, the model's performance on Platinum decreases with the increase of the number of rotatable bonds. The same happens with GEOM-Drugs (Fig. 5B), implying that the long-range interactions in these relatively large systems (molecules with 8 or more rotatable bonds) need special consideration. Secondly, the conformations in Platinum are influenced by other biomolecules, whereas SDEGen only counts the internal interactions in molecules. To be specific, the Platinum dataset comprises ligands with protein-bound ligand conformations from the PDB. At the same time, the training set is generated from the DFT calculations without any consideration of the protein pocket environment. Given that protein pockets would exert some kinds of non-bonded interactions on the ligands, i.e., the probability distribution of the small molecule conformation is changed by its binding with the protein (or other effector molecules). Hence the more flexible the molecules, the greater the perturbation by the protein pocket environment. Consequently, it is not surprising to observe that the COV-threshold curve of Platinum falls a little faster than that of GEOM-Drugs, owing to external interaction exerted on Platinum's molecules. We summarize the possible direction for boosting the limitations into two folds: (1) embedding physical/chemical/biological constraints to help the model learn the intrinsic physics behind a large amount of data. (2) Considering multi-scale modeling to capture higher-level interactions, as a famous saying goes, ‘More is Different’,³⁸ which is applied to the phenomenon we met here.

Fig. 5. Coverage vs. number of rotatable bonds on the (A) Platinum and (B) GEOM-Drugs datasets. Notation Confs in (A) denotes the number of the generated conformations of a molecule. (C) Comparison of conformation generation times for competitive models.

Conformation generation speed

Sampling speed is another perspective we should focus on beyond the quality of conformation ensembles. In real-world applications, downstream tasks such as pharmacophore mapping and conformational search require a large number of conformers, i.e., 50 conformers per molecule. To prove the potential application value of SDEGen, we conducted the time cost experiment over Intel(R) Xeon(R) Gold 5218 CPU with 30 CPU cores. We divided the molecules in GEOM-Drugs based on different rotatable bonds and recorded the time used for generating a single conformation by different methods. Fig. 5C shows that SDEGen achieved comparable generation speed, about ten times faster than the score-based SOTA model, ConfGF. RDKit generates conformations at a rate of about 0.1 s a piece; meanwhile, another VAE-based SOTA method, DMCG, generates conformations at a rate of about 0.01 s a piece, which is the fastest model in the baselines. However, considering the quality of the generated conformations, the thermodynamic properties of the conformational system and other factors, we still believe that SDEGen is a competitive model.

Model comparison

The underlying math of SDEGen is dx = f(x,t)dt + g(t)dw. In fact, if we made g(t) = 0, this stochastic dynamical system would degenerate to an ordinary differential system dx = f(x,t)dt, which is utilized for constructing the CGCF model. One possible reason why our model works well is that the presence of the stochastic term gives the model a better chance of jumping out of the local optimum. To be specific, the score-based SOTA method ConfGF performed annealing Langevin dynamics to learn the gradient field of molecular conformations, generating samples through given different temperature scales. Nevertheless, since SDEGen learns the ∇ log p (gradient of the probability distribution of the evolution of the particle over time) for the given interval, implying that one can use any classical integer method or any given step size to evolve this dynamical procedure from the beginning to the end. That is one of the reasons why SDEGen generates samples faster. Compared with another SOTA model, DMCG, which utilizes VAE as its backend, the SDEGen enjoys a lower number of model's parameters (∼8 M vs. 1283 M) and the ability to compute likelihoods through the ODE solver, implying an additional application to the enhanced importance sampling.

Conclusions

In this study, we exploit the physical intuition and the latest generative model architecture to learn the stochastic dynamics evolution of atoms starting from a random atomic distribution and eventually relaxing to conformations near the energy optimum. This model surpasses most AI-based conformation generation models in terms of generated conformation quality under real-world application settings, interatomic distance distribution and thermodynamic property prediction. For example, as to the conformation generation quality for drug-like molecules, our model scores best on the COV and MAT metrics with force-field refinement for the drug-like molecules. Besides, our SDEGen model is about ten times faster than the closely related model, ConfGF, which is crucial to generate a large number of conformations for large-scale virtual screening in real scenarios. In the application section, we found that SDEGen can quickly search for the conformations in the crystal structures of small molecules in the Platinum dataset with 80 percent probability. Furthermore, the energy surfaces for both small and large molecules were explored to illustrate that SDEGen could search for the local region which contains the crystal structure and locate other energetically favorable potential wells uniformly.

Method

Data representation

In this study, a molecular graph is represented as an undirected 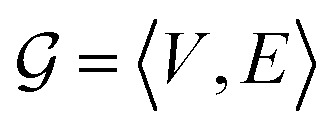, where V = {V₁,V₂,…,V_|V|} is the set of atoms of the molecule, and 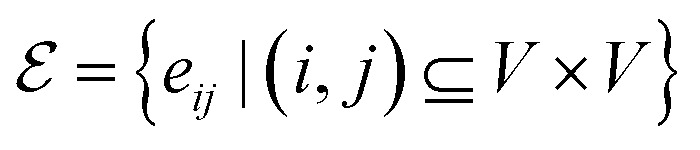is the set of bonds in the molecule. Each atom v_i ∈ V is associated with some atom's attributes, such as element type and atomic coordinates. Each bond 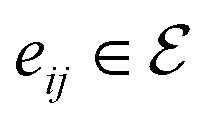is associated with a chemical bond type and a scalar 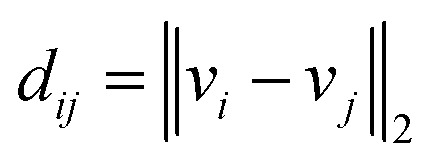denoting the Euclidean distance between the atomic positions of v_i and v_j. As the chemical bonds in a molecule would not suffice to characterize a molecule conformation and cannot express the local interactions within a molecule, we expand our molecule graph to an extended graph by adding auxiliary bonds. The two-hop edges and three-hop edges can be viewed as incorporating bond and dihedral angles information into a 2D graph, i.e., the 1–3 angle interaction and the 1–4 dihedral angle interaction. This technique helps the model capture neighboring features in a molecule and conveys the chemical knowledge that covalent bonds can transmit atomic interaction, where the cutoff setting is always 3. Hereafter, we assume all molecular graphs are extended unless stated.

Generative model based on stochastic differential equation

SDEGen is based on the generative model,^29,39 which aims at learning the process of perturbating a given data distribution to random noise. We can smoothly mold random noise into data for sample generation by reversing this process. This process of perturbating data can be modeled as the solution to an Ito SDE:

dx = f(x,t)dt + g(t)dw 1

where 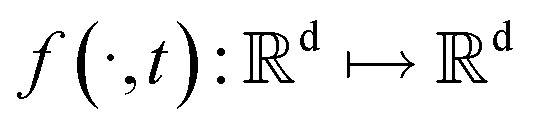is a vector valued function called the drift coefficient of x(t), and 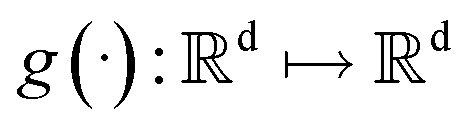is a scalar function known as the diffusion coefficient of x(t). w is the brownian motion. This formula represents the process of adding noise to the data distribution to another complex distribution that contains no information on data distribution, such as a Gaussian distribution. The reverse process has been proved to satisfy a reverse-time SDE:³²

dx = [f(x,t) − g(t)²∇_x log Pt(x)]dt + g(t)dw̄ 2

where w̄ is a standard Wiener process when time flows back from T to 0. Once the gradient of each marginal distribution, ∇_x log P_t(x), is known for all t, then we can derive the reverse stochastic process and simulate it to sample from the data distribution. So our goal is to train a network 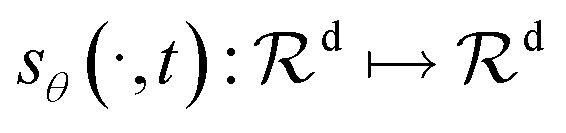to approximate ∇_x log P_t(x).

To estimate ∇_x log P_t(x), we can train a time-dependent model s_θ(x,t) by:

3

where 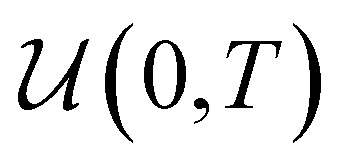is a uniform distribution over [0,T], p_t(x) is the probability density of x(t), p_0t(x(t)∣x(0)) denotes the transition kernel from x(0) to x(t), and denotes a positive weighting function. In the objective, the expectation over x(t) can be estimated with empirical means over data samples from p₀. The expectation over x(t) can be estimated by sampling from p_0t(x(t)|x(0)), which is efficient when the drift coefficient f(x,t) is affine. The weight function λ(t) is typically chosen to be inversely proportional to 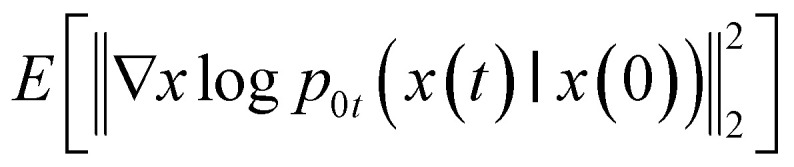. After the network s_θ(x,t) is trained, samples could be generated by solving the reverse-time SDE equation with Euler–Maruyama sampler or predictor-corrector sampler.

Symmetry

Symmetry is ubiquitous in physics systems. Formally, a function 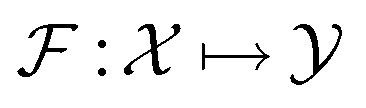being equivariant can be represented as follows:

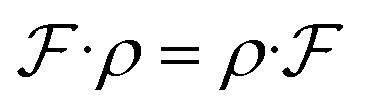4

where ρ is a transformation function, e.g., rotation. Eqn.(7) says that applying the ρ on the input has the same effect as applying it to the output. In our problem, we find that molecular conformations under Cartesian coordinate are not roto-translational invariance. One approach to tackle this issue is to do normalization;⁴⁰ another approach is to redesign this task based on physical intuition. Inspired by a traditional conformation generation method, Distance Geometry(DG), the target can be transformed from learning P_t(R_i|G) to learning P_t(d_i|G), we except:

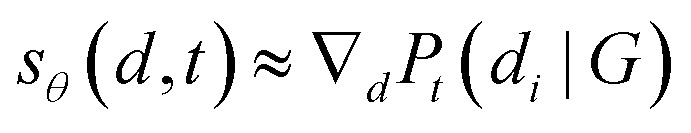5

where s_θ is the network, d is the distance between atoms in a molecule, G is a molecule graph. For generalization and elegant reasons, we explicitly embed such equivariance into the model architecture.

Based on the above discussion, the framework of SDEGen could be summarized in two stages. Firstly, it learns a conditional probability distribution P(D|G,t) utilizing a generative model scheme based on the SDE. Secondly, it reconstructs the 3D Cartesian conformations from the P(D|G,t) obtained in the first stage.

Specifically, we chose the form of the stochastic differential equation:

dx = σ^t dw̄, t ∈ [0,1] 6

In this case, the transition kernel is

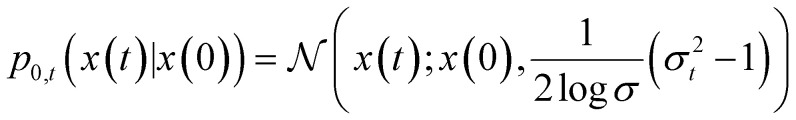7

and the weighting function is

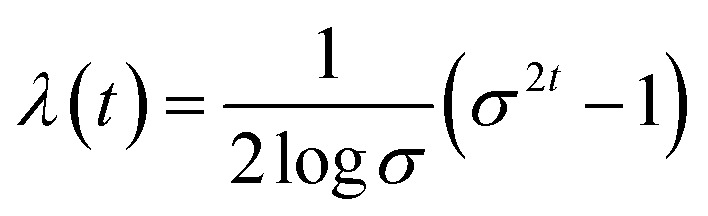8

when s is large, the prior distribution p_i=1 can be approximated in the following form:

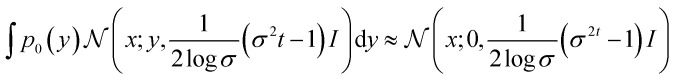9

The eqn (9) indicates that the prior distribution to be chosen is approximately independent of the data distribution and is easy to sample from. Solving this SDE numerically, we can smoothly transform the data x(0) to a simple white noise x(1).

dx = −σ^2t∇_x log P_t(x)dt + σt dw̄ 10

In this setting, we aim to learn a conditional network to jointly estimate the gradient of perturbed data on all-time steps, which means s_θ(d̃,t) ≈ ∇d̃ log Pt(d̃|G). Since 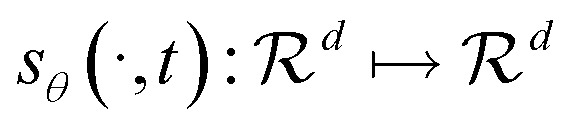, we can formulate the first stage of conformation generation as an edge regression problem.

Given a molecule graph G and its corresponding set of atomic distances 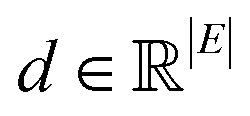, we embed the atomic attributes and the corresponding auxiliary bond attributes into a low-dimensional space using a Multilayer Perceptron(MLP)

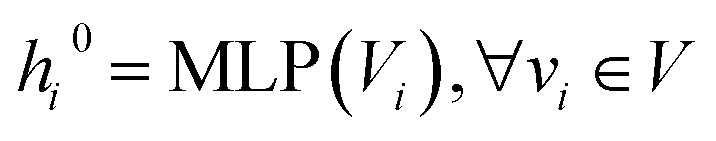11

At the same time, in order to embed the time information so that the network can condition on t, the Gaussian random feature²⁹ is used as an encoding for time step t. Specifically, for a given time step t, the corresponding Gaussian random features are:

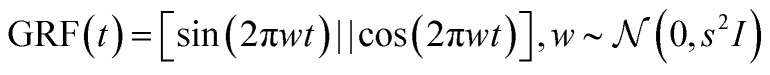12

where ‖ denotes the vector concatenation operation and s is a fixed number. Using the method of adding Gaussian random features to the embedding layer, we can encode time information into our network.

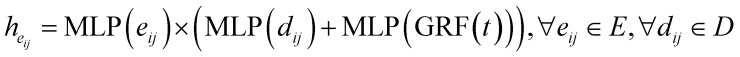13

We then use a graph neural network to update atom embeddings. We choose Graph Isomorphism Network (GIN)³¹ as the GNN module. Since GIN is a provably maximally powerful GNN under the neighborhood aggregating framework. At each layer of GIN, atom embeddings are updated by aggregating messages from neighboring atoms and bonds:

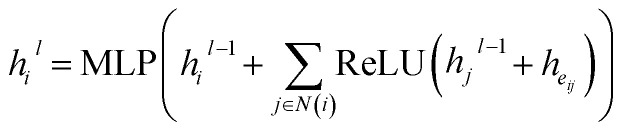14

where N(i) denotes ith atom's neighbors. After 3 rounds of message passing, we derive the final bond embedding by concatenating the corresponding atom embeddings for each bond as follows:

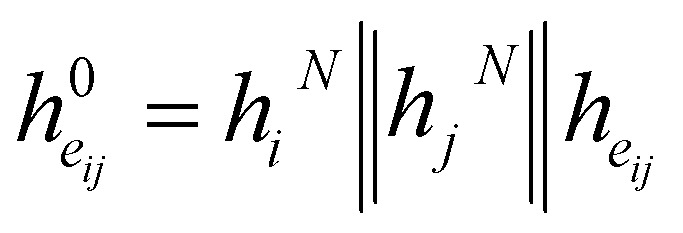15

where 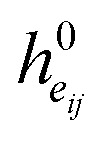denotes the final embeddings of bond e_ij ∈ E. Finally, we use an MLP function to parameterize the SDE network, i.e.

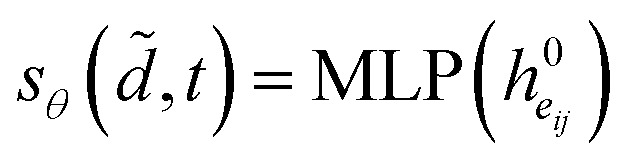16

We can rescale the output of the SDE network by 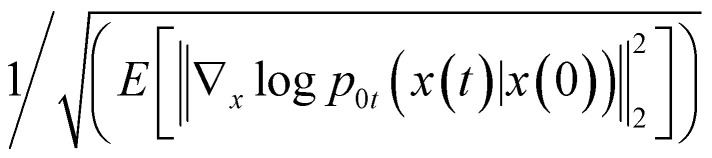to help capture the norm of the actual gradient. Based on the above discussion, the whole loss function takes the form as follows

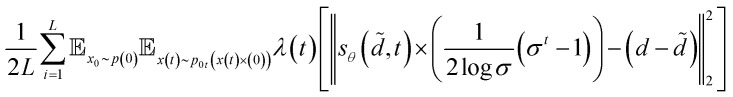17

At this point, all expectations can be computed by Monte Carlo estimation.

By the way, we also added the Exponential Moving Average (EMA)⁴¹ algorithm to SDEGen and trained a better robust model.

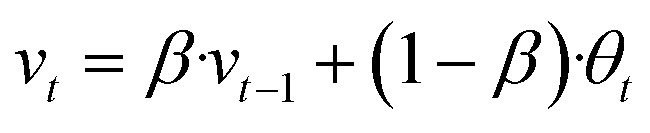18

where θ_t is the model parameters at time t, v_t is the average of the model parameters, and β is the weighted weight value, which is set to 0.999 in our model. The performance of the SDEGen model with EMA algorithms was proved to be greatly improved, especially on the small molecule dataset GEOM-QM9. The probable reason for this improvement is that the randomness introduced by the procedure of adding noise to molecular conformations is averaged out by EMA, a temporal ensembling method that allowed our final model to incorporate more historical states in the learning process. So more molecular structures will be attached attention in the final trained model.

Conformation generation

SDE solver & Langevin dynamics

Given a molecule graph and a well-trained SDE network, the generation process of molecular conformations is performed by numerically solving the stochastic differential eqn (2), i.e., reconstructing the distribution of each atom's position from a noise distribution. For the numerical solver, we use the predictor-corrector scheme,^29,42 which leverages the additional information, an estimate of the gradient of p_x(x(t)) via the network, to reduce the error of the numerical SDE solver and improve sample quality. This solver is in two steps. Based on a simple discretization to the SDE, the first step is solving the Euler–Maruyama equation, replacing dt with Δt and dw with 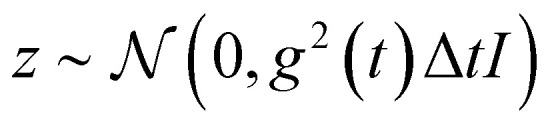. When applied to our reverse-time SDE, we can obtain the following equation:

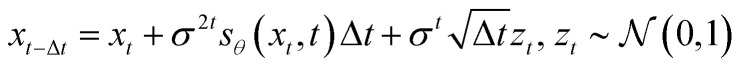19

Then, to improve the accuracy of the solution, n steps Langevin MCMC would be implemented as the second step.

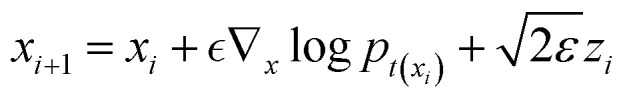20

Finally, the conformation would be sampled from Gaussian distribution, and then the PC solver would integrate the SDE in the reverse time direction to obtain the reconstructed conformation. This modified sampling scheme ensures that the sample fully converges to the probability distribution under the given time at each step of solving the SDE equation, reducing the risk of a spatial clash of conformations.

ODE solver

For eqn (2), there exists an ordinary differential equation

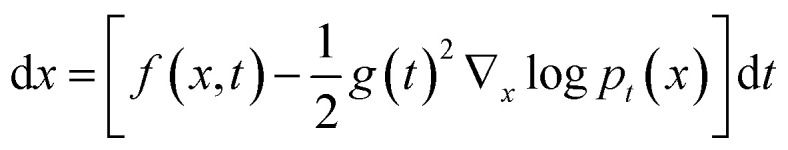21

which shares the same marginal probability density p_t(x) with eqn (2). Therefore, we can solve this differential equation through classical integrated algorithms to sample the new energetically favorable conformations and track how the probability evolves after the sampling procedure.

We obtained the likelihood of conformation with the following equation:

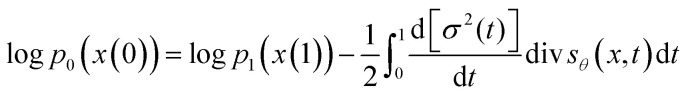22

Through this by-product of the ODE sampler, the weights of the samples generated by SDEGen are known. Furthermore, combined with the energy function we define, we can use the SDEGen as an importance sampler to overcome the so-called rare event problem in molecular simulation. But this section is beyond conformation generation. We only provide a demo version code to the interested readers and leave it for a future adventure. The molecule conformations, after evolving through the stochastic system, will fall near the local optimal point, and then we use deterministic optimization to make it converge further.

Experiments

To thoroughly evaluate the performance of SDEGen, we compare it with multiple competitive methods on multiple benchmark datasets with the various tasks.

Tasks and metrics

Quality of generated conformations

In this task, we generated twice the number of conformations as its benchmark conformations for each molecular graph in the test set following conventions.^19,21,43 We then computed the COV and MAT between the generated and benchmark conformations. As the fundamental metric for our conformation evaluation, we used root mean square deviation (RMSD), a standard measure of the difference between two conformations in MD simulations analysis.

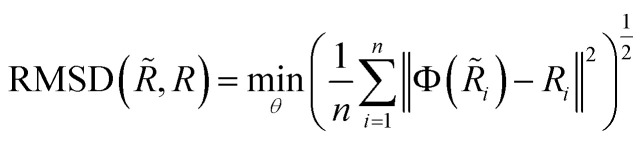23

where n is the number of heavy (non-hydrogen) atoms and Φ is an alignment function that aligns two conformations by rotation and translation. Following,¹⁹ the COV and MAT used to quantify the quality of conformations are defined as follows:

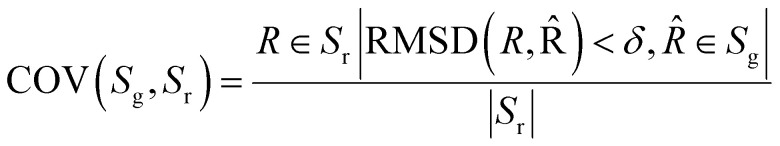24

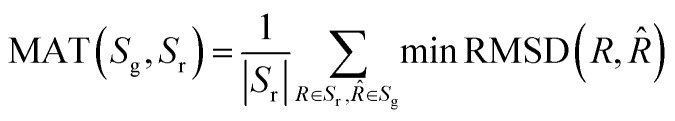25

where S_g and S_r are generated and reference molecular conformation ensembles, respectively. δ is a given RMSD threshold. While COV is effective to assess the diversity and detect the model-collapse phenomenon, MAT is a complement to measure how close the generated conformations and the reference conformations. In general, a higher COV score represents greater diversity performance, while a lower MAT score represents better accuracy of the generated conformations. An illustrative example is prepared in the appendix† for better understanding.

Distribution of interatomic distances

Since the covalent bond lengths are insufficient to represent the information of three-dimensional geometry, we consider the interatomic distances measured in the second task, including the bond lengths (1–2 connection) and 1–3 and 1–4 connections. This consideration amounts to measuring the direct local interactions between atoms that drive the atoms to relax to the real-world thermodynamic distribution from a random distribution. In this task, we sampled 1000 conformations for each test molecule as pseudo-trajectories, and then calculated the MMD between the two distributions using a Gaussian kernel. In specific, for each molecule in the test set, we evaluated distributions of all distances p(d|G) (All), pairwise distances p(d_ij,d_uv|G) (Pair), and individual distances p(d_ij|G) (Single).

Prediction of Thermodynamic Properties

As mentioned earlier, a macroscopic thermodynamic property of an ensemble is obtained by weighting all accessible microscopic states. For each molecule in the test set, we utilized PyScf⁴⁴ with DFT(M06-2X/def2-TZVPP) to calculate electron energy and HOMO–LUMO for each generated and benchmark conformation. We then computed the MAE metric for macroscopic thermodynamic properties by statistical averaging. The ensemble properties considered here include average energy Ē, lowest energy E_min, highest energy E_max, average HOMO–LUMO gap Δ , minimum gap Δε_min, maximum gap Δε_max. The mean absolute error (MAE) was used for measuring the accuracy of property prediction.

Datasets

Three well-known datasets, GEOM-QM9, GEOM-Drugs²² and ISO17,^45–47 were used. GEOM-QM9 is a small molecule dataset containing neutral molecules with up to nine atoms, not counting hydrogen. GEOM-Drugs is a drug-like molecule dataset whose molecule species are accessed as part of AICures.⁴⁸ These conformers were generated with the CREST⁴⁹ program, which adopts semi-empirical DFT to generate reliable and accurate structures. Following the²¹ sampling scheme, the resulting split is 40 000 molecules in the training set with 200 000 conformations and 200 molecules in the test set with 22 408 and 14 324 conformations for GEOM-QM9 and GEOM-Dugs, respectively. The molecules in the ISO17 dataset were randomly drawn from the largest set of isomers in the QM9 dataset, which consists of molecules with a fixed composition of atoms(C₇O₂H₁₀). These conformers were generated with the Fritz–Haber Institute ab initio simulation package (FHI-aims),⁵⁰ reaching a higher level of accuracy than the DFT method. So this dataset was assigned to evaluate the interatomic distance distribution task. The default split results in the training set with 357 621 conformations of 167 molecules and the test set with 73 071 conformations of 30 molecules.

Baselines

We tested our model compared with a classical rule-based method and other ML-based methods. The rule-based method is ETKDG,⁸ the default program in RDKit for molecular conformation generation. The other AI-based method go as follows: CVGAE,¹⁶ GraphDG,¹⁸ CGCF,¹⁹ ConfGF,²¹ DMCG²⁴ and DGSM.¹⁸ Among these methods, we focus on the ConfGF since it is the SOTA method built upon the score-based generative model, achieving impressive results on both GEOM-QM9 and GEOM-Drugs datasets. Although DGSM is an improved version of ConfGF, we still have no access to its source code until now, so the reported performance²⁸ in its original paper was used in our study. It is noted that the official codes of GraphDG and CVGAE are utilized old versions of Tensorflow,⁵¹ which does not match the version of our machine. However, these two methods are not our main competitors, so we just extract these results from the ConfGF²¹ paper.

Data and code availability

The data and source code of this study is freely available at GitHub (https://github.com/HaotianZhangAI4Science/SDEGen) to allow replication of the results.

Author contributions

H. Zhang and S. Li contributed to the main code and wrote the manuscript. J. Zhang and Z. Wang performed the experiment. J. Wang and D. Jiang provided partial codes of this work. Z. Bian and Y. Zhang helped perform the analysis with constructive discussions. Y. Deng and J. Song contributed to the visualization and technique support. T. Hou and Y. Kang provided essential financial support and conception, and were responsible for the overall quality.

Conflicts of interest

There are no conflicts to declare.