Minimal Nucleation State of α-Synuclein Is Stabilized by Dynamic Threonine−Water Networks

Abstract

The first structures of α-synuclein (αSyn) fibrils have recently been solved. Here, we use a unique combination of molecular dynamics simulation strategies to address the minimal nucleation size of the 11-amino acid NAC protofibril solved by X-ray and to interrogate the dynamic behavior of unexpected crystal waters in the steric zipper. We found that protofibrils of >8 chains are thermodynamically stabilized due to protection of the fibril core from solvent influx and ordering of the end strands by the fibril core. In these stable oligomers, water molecules resolved in the crystal structure freely exchange with bulk solvent but are, on average, stably coordinated along the β-sheet by inward-facing Thr72 and Thr75. We confirm the persistence of this water coordination via simulations of the full-length Greek-key structure solved by NMR and speculate that these Thr–water networks are important in the context of enhanced fibril nucleation in the familial A53T mutation.

Graphical Abstract

The presence of insoluble amyloid fibrils is a notable histological characteristic of multiple neurodegenerative diseases.^1,2 Misfolded α-synuclein (αSyn), a protein that is abundant in neurons but normal function of which is not well-characterized,³ has been identified as the filamentous component of Lewy bodies. These insoluble inclusions are found in brain tissue of patients with Parkinson’s disease, dementia with Lewy bodies, multiple systems atrophy, Alzheimer’s disease and numerous other less characterized α-synucleinopathies.^4–6 Oligomers of αSyn–capable of seeding and elongating into mature fibrils–have been shown to be neurotoxic in in vivo models, where toxicity correlates with increased rate of fibril formation.⁷

In vitro experiments have shown that αSyn fibril assembly proceeds via two distinct phases: (1) a concentration dependent lag phase and (2) an exponential elongation phase.⁸ The lag phase is rate-limited by the nucleation of seeding competent αSyn assemblies. These assemblies can be thought of as the smallest assemblies for which the rate of monomer addition exceeds the rate of dissociation.⁹ In thermodynamic terms, a nucleus is said to have formed when the change in free energy of monomer addition is less (more favorable) than the change in free energy of dissociation. Absent molecular scale details and structures, it has been impossible to estimate with any confidence either the minimal oligomeric size (copy number) or the key molecular interactions that are required to stabilize a nascent αSyn fibril nucleus. Such information will be crucial in future attempts to rationally design drugs that, rather than disrupting mature fibrils, target the early stages of oligomerization.

Two high-resolution structures of αSyn fibrils haven recently been published,^10,11 providing the first molecular scale platform for rational thermodynamic analysis of the nucleation process. The first structures were from nanocrystals of an 11-amino acid sequence, termed the NACore (nonamyloid component core, residues A₆₈VATVGTVVAG₇₈) and a 10-amino acid sequence, termed PreNAC (residues 47 to 56).¹¹ Despite its short length, the authors demonstrated that the NACore sequence is the minimal entity necessary to recapitulate fibrillization kinetics and toxicity present in full length αSyn.¹¹ The high-resolution (1.4 Å) structures for the NACore and PreNAC protofibrils revealed a pair of apposed β-sheets, forming a steric zipper. In the case of NACore, surprisingly, crystal waters were found to coordinate with two threonine residues in what had been presumed to be a cloistered hydrophobic interface.¹¹ This raises the interesting possibility that specific water–Thr interactions may play a central role in stabilizing αSyn oligomers.

More recently, a high-resolution NMR structure of full length αSyn fibrils (residues 1 to 140) was published. The structure is defined by a core “Greek Key” motif of apposed β-sheets that span the NAC domain.¹⁰ Although there are important differences between the crystal NMR structures, there are enough similarities to prompt comparative analysis of certain features. In particular, as NMR does not resolve coordinated waters, it is important to determine if the waters present in the NACore crystal structure are also partnered with Thr residues in the full-length fibril, something we address in this study.

The present work, which relies on molecular simulation techniques, is a first attempt to assess the size of the critical nucleus for fibril formation. The discovery of the NACore fibril crystal structure permits atomistic modeling of the molecular level events underlying the formation and stability of disease-causing aggregates. From a computational thermodynamics perspective, the key distinguishing feature of this study is its focus on breakdown, rather than formation, of putative fibrils. Even at high concentration, fibril formation is a slow process, on the time scale of all-atom simulation, since most of the time is spent waiting for a new monomer to arrive at the correct location and assume a conformation that is competent to bind. In kinetics terminology, k_on contains a significant component that is not interesting or system specific but rather is simply governed by diffusion (either in real space or in conformation space). By contrast, k_off is unimolecular and thus is governed entirely by the molecular motions of the oligomer itself. By examining the dissolution of putative fibrils, we have estimated the minimum oligomer size that leads to metastable structures resembling that found mesoscopically in the crystal. This study uses two molecular dynamics strategies for the NACore structure, namely, brute force and replica-exchange molecular dynamics simulations, to investigate the molecular level details that connect the initial stages of nucleation to the elongation phase of fibril growth. A simulation of the Greek key structure is then used to interrogate whether the crystal waters found in the NACore structure are also present and stable in the full-length fibril.

The kinetic stability of NACore fibrils of varying oligomeric size was determined using multiple independent brute force molecular dynamics simulations for each size. Twenty replicas of each system were simulated, and collectively the results presented here are for ~35 μs of total simulation time (Supplemental Table S1). Figure 1 shows the kinetic stability of small NACore fibrils as a function of fibril size, ranging from 4 to 18 monomers (2 to 9 dimers). As indicated schematically in Figure 1A, for each different fibril assembly, dimer number is shown on the y-axis, with the average kinetic stability for each dimer unit across all simulations reported via a heat-map (yellow = all native crystal contacts preserved, black = <50% native crystal contacts). Figure 1B reports the results of the six different oligomer sizes we tested. The smallest fibrils (4 monomers) lose their native contacts within a few nanoseconds on average, indicating that they are not even metastable on the molecular dynamics time scales. Moreover, even the native contacts that are present are not indicative of native-like structure; rather, the complex twists and distorts and is better characterized as a hydrophobic globule than a fibril. The 6-mer (3 dimers) is slightly more stable, and the central dimer in particular retains some native-like structure for ~25 ns, on average. The 8-mer and 10-mer systems begin to show evidence of stability of the overall fibril, with the 10-mer having a persistently stable core. The longest protofibrils (14 and 18 monomers) are stable on the time scales considered in this study, with all but the end dimers retaining nearly all of their native contacts. Moreover, visual assessment of the simulations confirms that the structures are far more fibril-like throughout the trajectories, some of which were as long as 500 ns. It is important to recognize that these results are the average of a large number of independent trajectories; dissolution kinetics can only be reliably assessed from an ensemble, not from a single instantiation.

Figure 1.

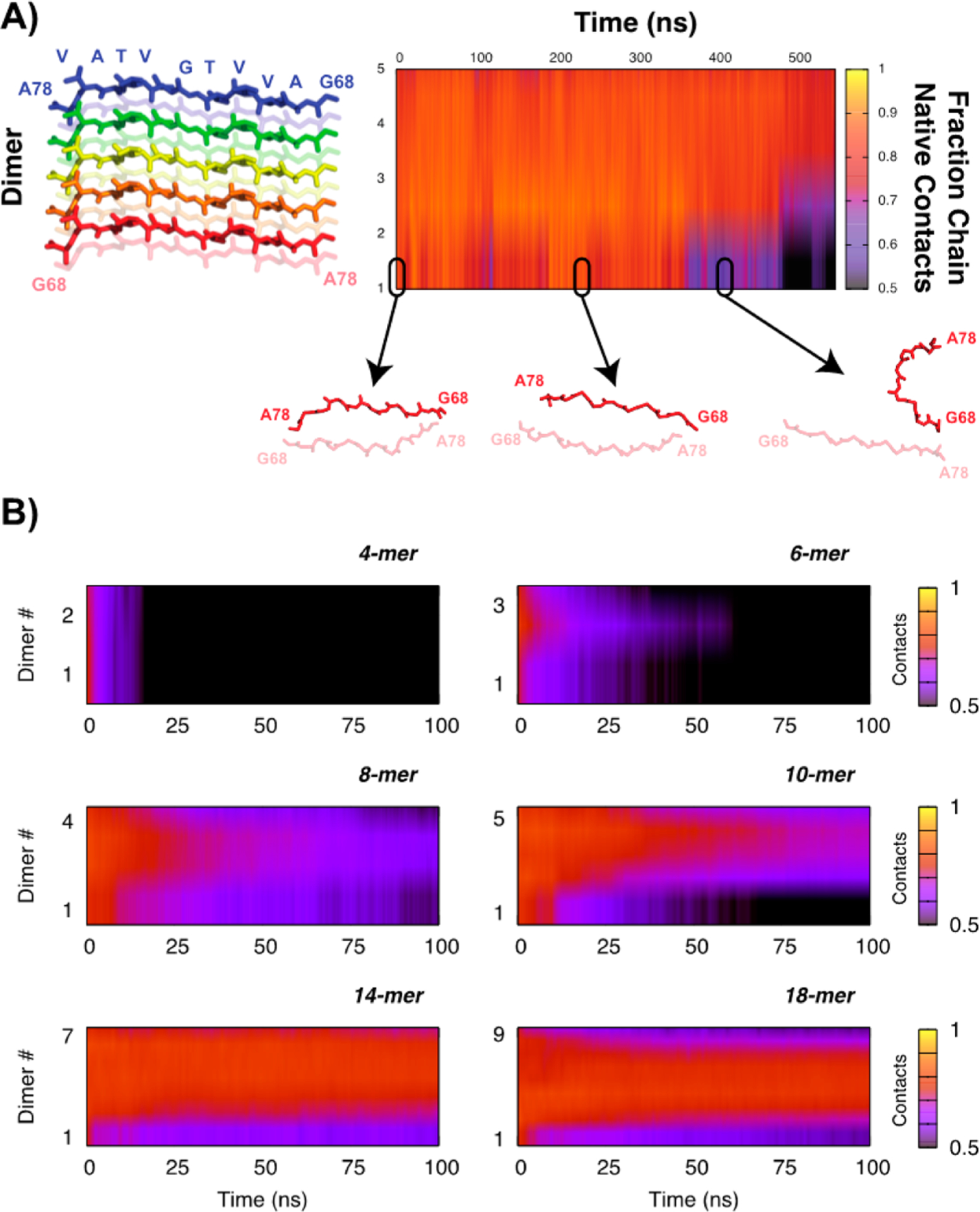
(A) Data from a single 10-mer replica (5-dimers) showing the orientation of the dimers along the y-axis in the plot and representative structures for a single dimer depicting its dissociation and corresponding fractional native contacts. (B) Kinetic stability of the fibrils as a function of fibril size, averaged over 20 replicas. Similarity to the crystal structure is quantified using the average fractional native contact per dimer (1 indicates all native contacts are present, 0 means none of the contacts from the crystal structure are present).

To further establish the minimal oligomerization number required for αSyn NACore nucleation, specifically to determine if the 8-mer and 10-mer observed in Figure 1B are in fact stable, we followed the method of De Simone et al.¹² In particular, systems of oligomers comprised of 4 to 10 monomers were simulated using replica exchange molecular dynamics (REMD). REMD is an enhanced sampling technique that increases the sampling of conformational space by increasing the rate of thermodynamic barrier crossing (e.g., monomer dissociation). Three independent simulations of each 4- to 10-mer system were simulated with 16 temperature replicates. We used the distance from each end-monomer to its nearest neighboring monomer as the metric that best reflects the stability of the fibril. An end-monomer that samples a narrow range of distances from its nearest neighbor, close to that of the crystal structure (7.2 Å, Figure 2A), indicates stability, while one that samples a wide range of distances from its nearest neighbor (>7.2 Å) indicates instability.

Figure 2.

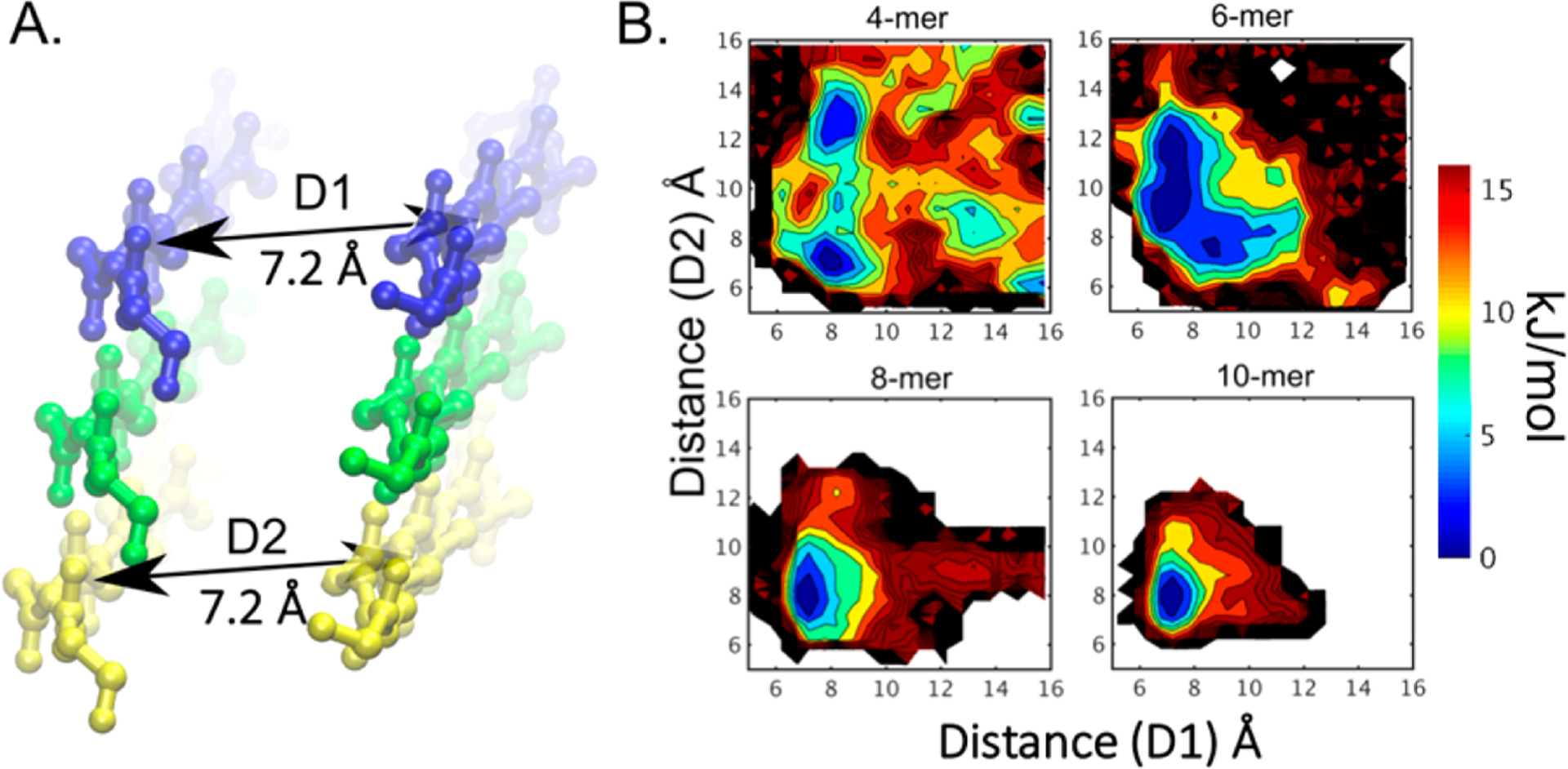
Two-Dimensional free energy projections of NACore oligomer dissolution. (A) Snapshot from the 6-mer system illustrating the distance metrics (D1 and D2) that characterize the average distance between the monomers, comprising a dimer, at each end of the fibril. (B) Two-dimensional free energy estimates, determined through MBAR analysis, illustrate average distances, D1 and D2, and free energy (color-map) defined relative to the observed global minimum. All systems show rough symmetry in x/y and have a free energy minimum at ~7.2 Å. As more strands are added, the free energy minimum becomes increasingly focused, and the free energy gradient for strand separation becomes steeper. Uncolored regions of the contour plot show unsampled regions of the conformational landscape.

Free energy estimation (Figure 2B and Supplemental Figure S1) was performed using the Multistate Bennet Acceptance Ratio (MBAR) analysis.¹³ MBAR analysis uses system information from all 16 temperature replicates (not just the lowest temperature replica) to determine an estimate of the free energy. Systems comprised of 9 or 10 subunits displayed a single free energy minimum centered at the crystal structure distance of 7.2 Å, with a depth of at least 15 kJ/mol (see Figure 2B). Additional minima appear with 8 subunits, separated from the crystal minimum by at most 11 kJ/mol. With 7 subunits or fewer the conformational landscape becomes broad and comparatively flatter. Multiple free-energy minima arise, but the minimum at 7.2 Å is conspicuously missing or displaced, indicating that the fibril spontaneously disintegrates at these smaller sizes.

Free energy projection was also determined from the state probability histograms of the systems at the lowest temperature (see Supplemental Figure S2). Results from the free energy projections are characteristically similar to the MBAR analysis. When examined separately, the three independent REMD simulations produced similar free energy projections (Supplemental Figure S2). Examining the free energy projections for every temperature replicate of the 4-mer, 6-mer, 8-mer, and 10-mer systems (Supplemental Figures S3–S6) highlights a transition that occurs between the 6-mer and 8-mer system (Supplemental Figures S4 and S5, respectively). Moreover, for systems with 8 or more monomers, the free energy well corresponding to the crystal structure becomes steeper and narrower at increasing temperatures, indicating a substantial entropic component resulting in increased stability in fibrils of these sizes. Thus, collectively, the combined brute-force and REMD simulations strongly suggest that the minimal nucleation size of αSyn NACore protofibrils is ≥8 monomers.

The hydrophobic nature of the NAC domain is essential for driving the aggregation of αSyn fibrils.¹⁴ Thus, it was somewhat surprising that the NACore crystal structure contains waters coordinating with threonine (Thr72 and Thr75, red spheres in Figure 3A), where most steric zipper motifs are completely dry.¹¹ We examined the NACore trajectories for the presence and stability of water within the crystal lattice. Figure 3A shows the water occupancy from a 7-dimer (14-mer) simulation. The discrete sites highlighted in the water density correlate nicely with the waters identified in the crystal structure. What is most interesting is that these waters exchange rapidly with the bulk solvent over the course of the simulation; typical lifetimes are on the order of a few nanoseconds. However, Figure 3A shows that the crystal water sites have high occupancy as long as the fibril is relatively native-like. The simulated protofibril, from which the data in Figure 3 was derived, maintained cohesiveness for nearly half of a microsecond before one end dissociated, and the average backbone RMSD to the starting crystal-based structure was 2.2 Å. To further test the role of these crystal waters in fibril stability, REMD was performed on the 10-mer fibril system with crystal waters omitted (10-mer “dry” system). MBAR analysis and free energy projections (Figure 3B and Supplemental Figure S7) highlight significant instability within the fibril. Instead of a clearly defined global minimum in the normal system (Figure 3B, left), the “dry” 10-mer system samples a much broader range of conformational space with multiple local free energy minima (Figure 3B, right). This result suggests that these dynamic, structural waters are stabilizing the core of the fibril structure.

Figure 3.

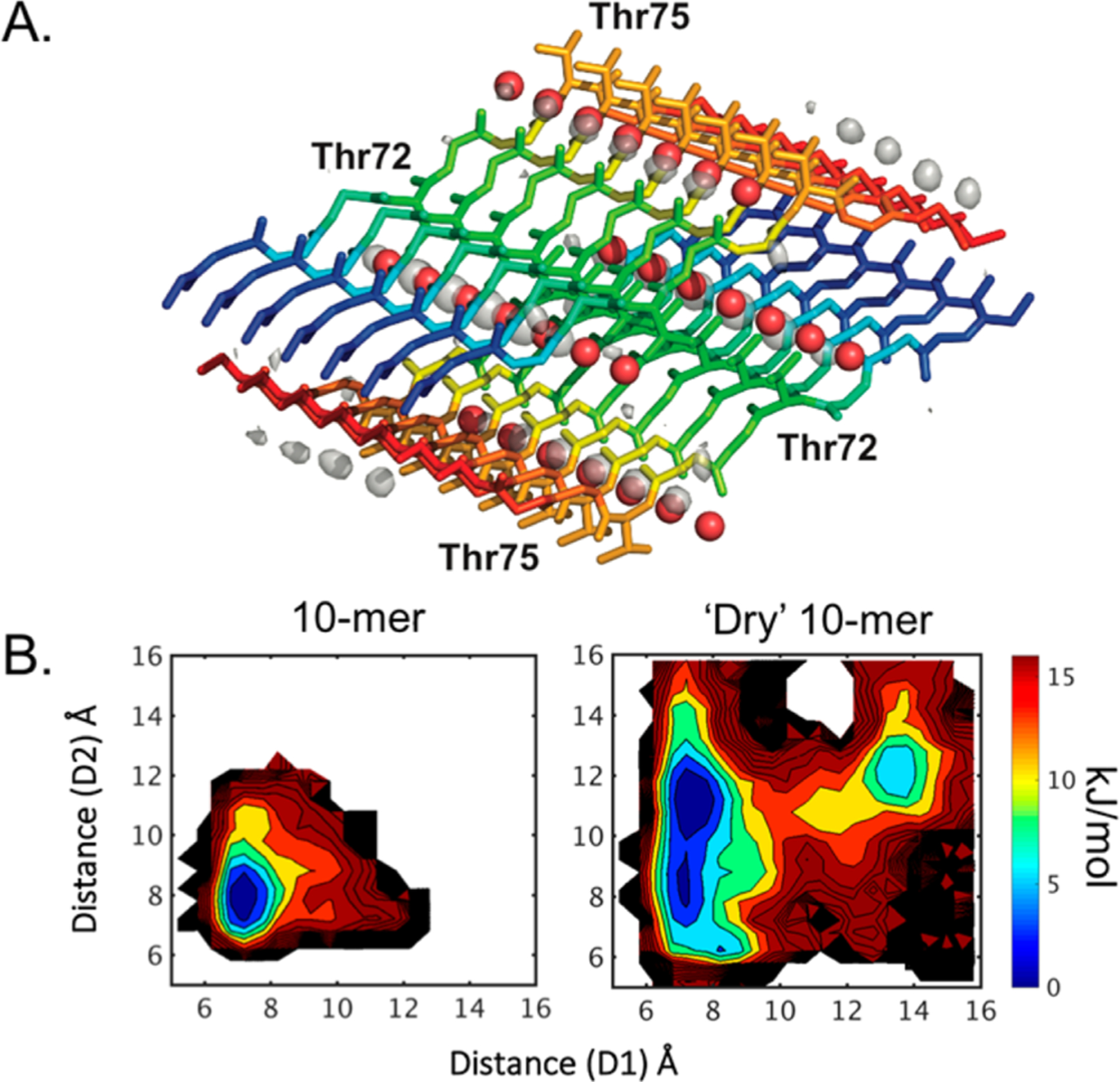
(A) Water occupancy in a 7-dimer (14-mer) simulation, contoured at twice the bulk solvent density. The backbone color corresponds to the index along the chain for each monomer (e.g., blue for the first glycine to red for the final alanine). The crystal waters are shown as red spheres. The differences in positions are due to the average MD structure not exactly matching the crystal structure. (B) REMD free energy estimate from MBAR analysis for the 10-mer fibril, simulated with (left) and without (right, “Dry”) crystal waters.

The Greek-Key NMR structure of a full-length αSyn fibril provides the more physiologically relevant system through which to validate the existence of this threonine–water coordination within αSyn hydrophobic core. However, because that system is significantly larger than the NACore, computational limitations prevented us from performing stability calculations. Because NMR structures do not contain any structural waters, the equilibrated simulations provide clear evidence regarding the propensity of waters to hydrate the hydrophobic core. To limit computational cost, we simulated the structured residues within the Greek-Key (residues 29–98) and analyzed the water density near threonine residues within the NACore domain (Thr72 and Thr75). Figure 4A shows a representative snapshot from the equilibrated trajectory. There is a large hydrated water cavity that occupies Thr72, whereas Thr75 interacts directly with Thr92 and a continuous tube of water. Upon close inspection (Figure 4B), Thr75 participates in an extensive hydrogen-bond network throughout the fibril core. The tube of water is surrounded by an otherwise hydrophobic pocket formed by Val71 and the methyl group from the side chain of Thr92. This Thr72–water network persists throughout the simulation and over the full length of the fibril (Supplemental Table S2), with waters dynamically exchanging but ever present, similar to our finding with the NACore nanocrystal simulations.

Figure 4.

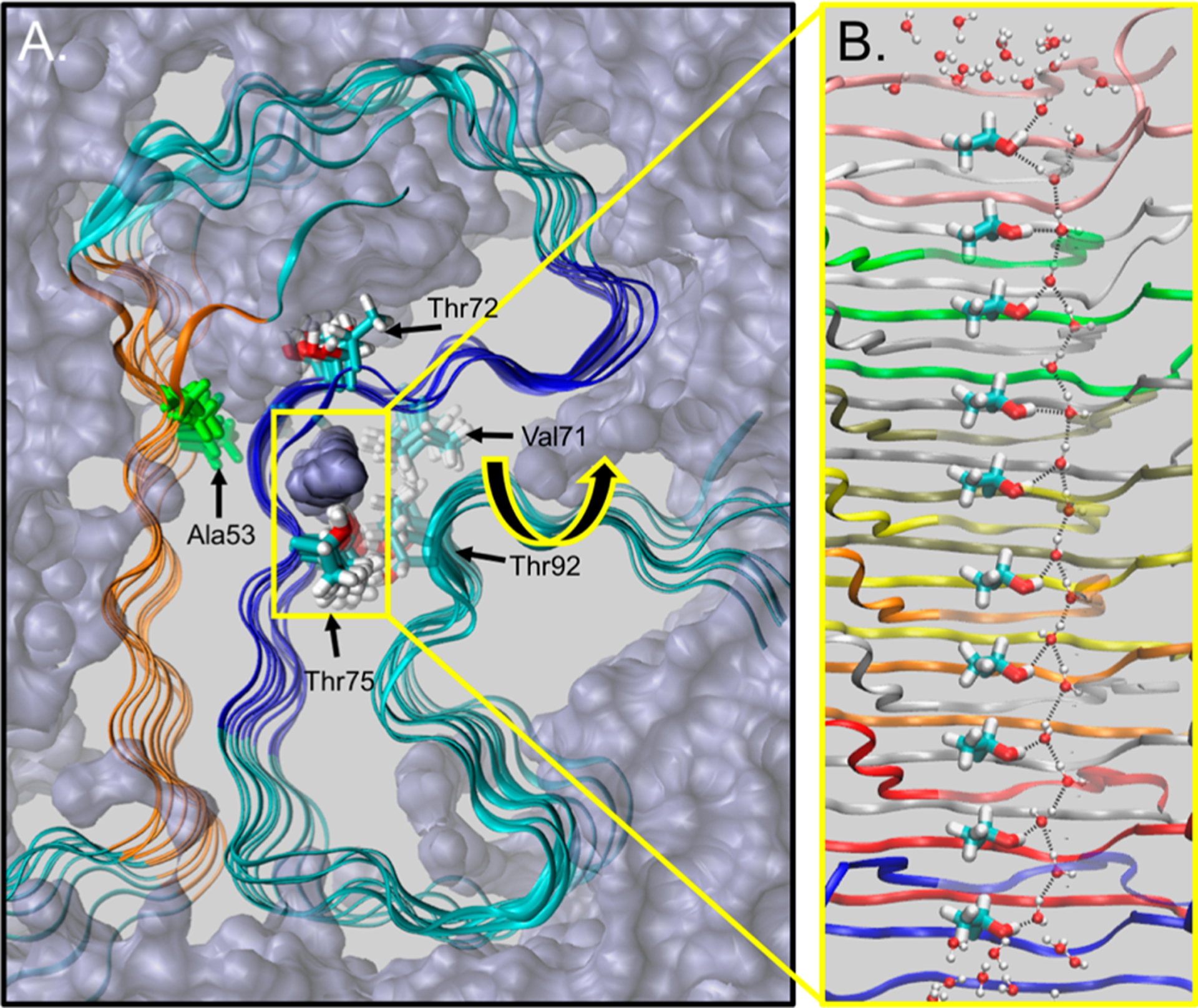
Threonine–water hydrogen bond network within the Greek-Key structure. (A) snapshot from a simulation of a 10-mer Greek-Key fibril (residues 29–98) where water molecules (purple, volume filling) and protein backbone (green with PreNAC in orange and NACore in blue) illustrated. The NACore residues, Thr72 and Thr75 (bold coloring) and proximal residues Val71 and Thr92 (translucent), as well as disease related Ala53 (green) are highlighted. A tunnel of water coordinates with Thr75, within a hydrophobic pocket of the Greek-Key fibril. (B) A snapshot illustrating the Thr75–water hydrogen bond network that extends throughout the Greek-Key lattice.

Our results suggest that fibril stability is driven by two phenomena: (1) the coordination of dynamic, structural waters, which in turn (2) confers order to the end-monomers. Rodriguez et al. noted the unusual presence of water molecules coordinated by inward-facing threonine residues¹¹ and our simulations recapitulate this finding in a dynamic system. In addition, we find that these waters are more likely to be found in simulated conformations that are most closely aligned to the crystal structure, indicating that they play a structural role in fibril stability. To further test this, an additional REMD simulation of the 10-chain fibril was run without the crystal waters, and the results are unambiguous: without crystal waters, the fibril is destabilized compared to the 10-mer with crystal waters (Figure 3B), confirming the critical role of structural waters in fibril stability.

In both sets of simulations (NACore, Figure 3, and Greek-Key, Figure 4), we observed water coordination with threonine. These findings suggest, speculatively, that the A53T familial mutation might result in further water stabilization within the fibril core through a hydrogen bond network.^10,11 Implications for this increase in stabilized water may extend to changes in fibrillization kinetics, as the A53T mutation undergoes more rapid fibrillization kinetics than wild-type αSyn. Based on our findings, we hypothesize that the more rapid kinetics for A53T are driven, at least in part, through a minimization of the desolvation penalty for adding an additional αSyn monomer.

Finally, fibrils containing at least 14 monomers are, on average, stable for more than 100 ns, and all fibrils containing at least 8 chains are dramatically more stable than those containing fewer. The second-order rate constant for fibril elongation has been estimated experimentally to be 1–2 mM⁻¹ s⁻¹,¹⁵ meaning that for a 100 μM solution, the average rate of monomer addition is ~1 per 8 s.¹⁶ While molecular dynamics simulations cannot approach these time scales directly, our modeling results have still shed light on the molecular mechanisms underlying the stabilization of short protofibrils from sub-nanosecond time-scales to those approaching 1 μs. Increased stability is not expected to extrapolate to ever-increasing fibril lengths, as at a certain size, the existing fibril will appear infinitely long to the added monomer. Future simulations could determine the structural correlation distance along the long-axis of longer fibrils.

COMPUTATIONAL METHODS

Kinetic stability simulations were performed using NAMD 2.11¹⁷ with the CHARMM36¹⁸ force field. SPME¹⁹ was used for the electrostatics, along with a 10 Å VDW cutoff. The system temperature was held at 310 K using Langevin dynamics, integrated with a 2 fs time-step. Bond lengths were constrained using RATTLE.²⁰ System construction, management, and analysis were all performed using LOOS²¹ and NAMD 2.11. The conventional molecular dynamics simulations were performed on the BlueGene/Q at the Center for Integrated Research Computing at the University of Rochester. In total, approximately 36 μs of molecular dynamics simulations were performed (see Supplemental Table S1). Molecular visualizations were made using PyMOL.²²

System construction for NACore nanocrystal simulations consisted of creating putative fibrils containing from 2 to 9 dimers by extending the crystallographic dimer along the fibril axis along with the crystal waters,¹¹ Twenty replicas of each system were then assembled by embedding the fibril in a water box, which in turn was built from a 16 Å cubic water box that had been randomized by 1 ns of unrestrained molecular dynamics (MD) simulation. After an initial energy minimization, the backbone atoms and crystal waters were restrained with a 20 kcal/(mol·Å²) harmonic potential while the system was heated to 310 K. The restraints were gradually reduced to 0, followed by 1 ns of unrestrained MD before switching to the production simulation. The NPT ensemble was used throughout. No restraints were placed upon the crystal waters during the production simulation; they were free to exchange with the bulk.

Initial preprocessing, solvation, and counterion seeding for the Greek-Key αSyn structure (2N0A.pdb) was performed using VMD’s psf-gen and solvation utility.²³ Energy minimization, restraints, and production runs were similar to those used for the NACore fibril assemblies.

The state of the putative-fibril (i.e., whether it had begun to dissociate) was characterized using a custom tool built using the LOOS simulation analysis library.^21,24 The fraction of native-like interchain backbone contacts was computed on a per-chain basis, using the crystal structure as a reference, with a contact cutoff of 10 Å. There should be some degree of hysteresis in the termini that is tolerable, for example, a monomer can partially dissociate and rapidly reform. Therefore, when a chain had sustained fractional contacts below 50%, the fibril was deemed to have begun to fall apart or was sufficiently noncrystal-like and the trajectory was terminated. This measure leads to trajectories of different lengths, so the fractional contact data was normalized such that the final fractional-contacts for a trajectory were replicated (by appending) until all trajectories were the same length. Finally, since the two monomers in each dimer are chemically equivalent, the fractional contact statistic was averaged to form a dimer native-contact that is used in subsequent graphs and analysis.

Water density analysis was performed using the density tools suite from LOOS. The density histogram was constructed using a 0.5 Å grid, smoothed by convolving with a Gaussian kernel, and then contoured at approximately twice the bulk density contour level. Water-contact lifetimes and exchanges were assessed using tools from LOOS.

The most common fibril conformation is not the crystal-like structure, but one that exhibits some twist along the fibril axis. One concern with using the crystal native-contacts as a reference is to what extent this biases our results should the crystal structure not be representative of the true native state. To assess this, we created a set of “rescue” systems by taking the longest stable structure from each production system and using it as a seed for the original construction method. Here, only 10 replicas were made. The same trajectory normalization procedure was also used. In these cases, the reference structure used was the stable MD structure not the crystal structure. A similar stability trend and sharp transition between 3-dimers and 4-dimers resulted as was found in the original simulations.

Replica exchange molecular dynamics (REMD) was run using NAMD 2.8.²⁵ The NACore region of α-synuclein was constructed using the crystal information provided in Rodriguez et al.¹¹ NACore oligomers with 4, 5, 6, 7, 8, 9, and 10 monomers were simulated with sufficient explicit TIP3²⁶ water (>9000) to prevent periodic image interactions when a monomer became fully separated. Importantly, crystal structure waters were left in place. Simulations were carried out using the velocity Verlet algorithm.²⁷ Long-range electrostatics were calculated using the particle mesh Ewald²⁸ method with a 1.5 Å grid spacing and fourth order interpolation. Temperature and pressure (1 atm) were maintained using the Langevin integrator and Langevin piston methods,²⁹ respectively. Covalent bonds involving hydrogen were constrained using RATTLE.³⁰ Each system was equilibrated by restraining α-carbons at 1, 0.1, and 0.01 kcal/(mol·Å²) and simulating for 1 × 10⁶ steps at each stage. For REMD simulation, each system was simulated in triplicate, with 16 replicates per run, simulated at temperatures of 300–348 K. Exchanges were attempted every 500 steps, and simulations were carried out for at least 10⁵ steps per replicate. A summary of exchange efficiency for one independent run of each system is presented in Supplemental Figure S8. Each independent REMD trajectory spanned a minimum of 8 × 10⁷ steps (160 ns). This was sufficient to get broad sampling but was not so long that we observed total disintegration of the fibril. A trajectory frame was written at every exchange attempt. Analysis followed that of De Simone et al.¹² We started by sorting the structures by temperature and exporting the system coordinates and the system potential energy at each exchange attempt. The distance between each of the two “edge” strands and its nearest diagonal binding partner (measured from centers of mass of residues T72, G73, and V74) in the fibril was determined using LOOS. The histogram distribution of state probabilities was calculated using the first 10⁵ frames, converted to free energy using Boltzmann’s equation, and plotted as a 2D free energy projection.

Hydrogen bond occupancy was performed using the built in LOOS hbonds tool with (bond length ≤ 4 Å, bond angle ≤ 30°).