Universal and non-universal features of musical pitch perception revealed by singing

Summary

Musical pitch perception is argued to result from nonmusical biological constraints, and thus to have similar characteristics across cultures, but its universality remains unclear. We probed pitch representations in residents of the Bolivian Amazon – the Tsimane’, who live in relative isolation from Western culture – as well as US musicians and non-musicians. Participants sang back tone sequences presented in different frequency ranges. Sung responses of Amazonian and US participants approximately replicated heard intervals on a logarithmic scale, even for tones outside the singing range. Moreover, Amazonian and US reproductions both deteriorated for high frequency tones even though they were fully audible. But whereas US participants tended to reproduce notes an integer number of octaves above or below the heard tones, Amazonians did not, ignoring the note “chroma” (A, B, etc.). Chroma matching in US participants was more pronounced in US musicians than non-musicians, was not affected by feedback, and was correlated with similarity-based measures of octave equivalence as well as the ability to match the absolute f0 of a stimulus in the singing range. The results suggest the cross-cultural presence of logarithmic scales for pitch, and biological constraints on the limits of pitch, but suggest that octave equivalence may be culturally contingent, plausibly dependent on pitch representations that develop from experience with particular musical systems.

eToC Blurb

Jacoby et al. use sung reproduction of tones to explore pitch perception cross-culturally. US and native Amazonian listeners exhibit deterioration of pitch at high frequencies, and logarithmic mental scaling of pitch. However, sung correlates of octave equivalence are undetectable in Amazonians, suggesting effects of culture-specific experience.

Introduction

Music is present in every known culture, suggesting that it is a consequence of human biology [1]. Consistent with this idea, some structural and functional properties of music are present to a considerable extent across cultures [2, 3]. On the other hand, other structural features and uses of music vary considerably from place to place [4, 5]. There is thus longstanding interest in the physical, biological, and cultural influences that shape music. Most perceptual research, however, has exclusively been conducted on listeners from Western cultures, leaving critical gaps in our knowledge of the potential effects of culture-specific experience on musical behavior. Here we examine cross-cultural similarities and differences in the perception of pitch, a key ingredient in most forms of music.

The use of pitch in Western (and at least some non-Western) music is marked by three defining characteristics. First, note-to-note intervals that are equal on a logarithmic scale are heard as equivalent [6]. Second, music is composed of notes from a limited range, beyond which pitch perception deteriorates [6-8]. Third, individual notes separated by octaves are heard as musically equivalent [9-14]. All three of these features have an established basis in perception for Western listeners. But because they are also prominent in the structure of Western music, their origins have remained uncertain, with plausible explanations in terms of (presumptively universal) non-musical biological constraints as well as culture-specific musical experience.

The perceptual equivalence of intervals on a logarithmic scale could reflect the mapping between frequency and place on the cochlea, which is approximately logarithmic over at least part of the frequency range [15, 16]. But the equivalence could also derive from our experience with Western music, in which the same melodic motifs are routinely replicated in different pitch ranges (registers) according to a logarithmic scale. The limits on pitch perception observed in Western listeners [6, 7, 17] have likewise been proposed to reflect the upper limit of phase locking in the auditory nerve [18-20]. But because the fundamental frequencies (f0s) of Western musical instruments do not exceed about 4 kHz [21], the limits of pitch perception could alternatively reflect the limits of the f0s we experience. And the tendency of Western listeners to judge tones separated by an octave as similar could derive from pitch mechanisms [22-25] adapted to the harmonic frequency spectra of mammalian vocalizations [26] (which are maximally similar for sounds separated by an octave), but could alternatively be internalized from Western music, in which the octave is structurally prominent. These alternatives are not mutually exclusive, and could interact in complex ways. However, it remains possible that some factors matter more than others, and that some do not matter at all.

The origins of musical pitch remain unclear in part because pitch representations have rarely been studied experimentally in non-Western cultures [27-32]. Cross-cultural observations have largely been limited to ethnomusicological studies of the structure of musical systems around the world or the analysis of recorded material [33]. There are many examples of logarithmic scales in other cultures [34-36], and of pitches separated by an octave being notated in the same way [37, 38]. There are also claims of cross-cultural tendencies to harmonize in octaves [2]. There is thus some reason to think that logarithmic scales and octave-based pitch systems might be favored by factors that influence the evolution of musical systems. One possibility is that the biology of the auditory system predisposes certain perceptual equivalencies. But any such predispositions might not influence perception without appropriate musical experience. Moreover, constraints on the production of music could also be critical, for instance due to the ease with which simple frequency ratios can be reliably produced on simple musical instruments (by bisecting strings, for instance). These considerations raise the possibility that pitch perception could be influenced by exposure to particular musical systems, rather than the other way around. We explored these issues through experiments testing the universality of musical pitch perception across cultures with divergent musical experiences.

We probed musical pitch representations by asking human listeners to sing back pitch intervals produced in different registers (Figure 1). The design was inspired by the classic experiment of Attneave and Olson [6], who asked participants to adjust a stimulus in a particular frequency range to match their memory of the National Broadcasting Corporation call sign. We instead presented pitch intervals in different frequency registers, and asked participants to reproduce them using voiced pitches within their singing range, which is confined to about an octave for most people. The instructions were to “copy” what was heard, with the goal of revealing the factors determining similarity and fidelity of internal pitch representations. We found this task to be natural and easy to explain to untrained participants, which is essential for cross-cultural testing, particularly with participants with little formal education. In particular, our task was much less arduous than a variety of psychophysical alternatives, including the adjustment paradigm of Attneave and Olson.

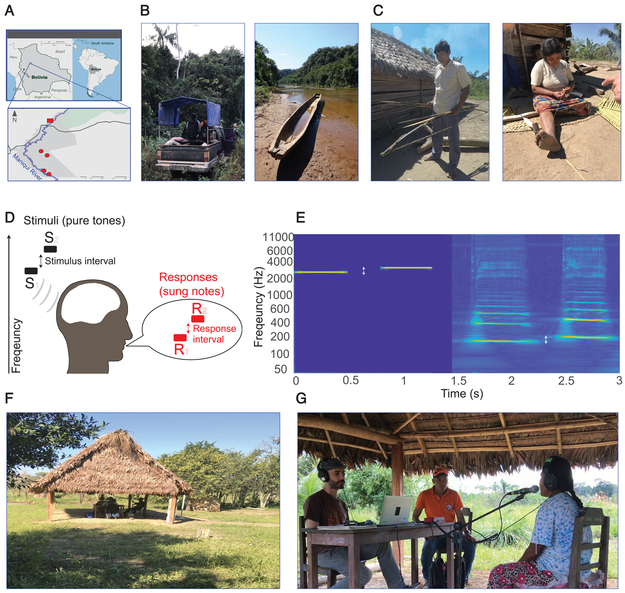
Figure 1. Singing Reproduction Paradigm.

A. Tsimane’ territory. Map shows the four villages in which the experiments in this paper were conducted. Inset shows the region where many Tsimane’ villages are located. B. We reached the villages Mara and Moseruna by truck from the town of San Borja (left). The upriver villages of Iñañare and Anachere were reached by canoe (right). C. The Tsimane’ maintain a traditional way of living, but occasionally travel to nearby towns (e.g. San Borja) to trade and buy goods, and thus typically wear clothing from industrialized society. D. Experimental paradigm. Participants heard sequences of two tones and sung back a reproduction of what they heard. E. Spectrograms showing example stimulus and response. Stimuli were typically pure tones in a particular frequency range. Participants sung back two notes within their singing range. F. Photographs of experimental setup in the field. Experiments were generally conducted under communal roofed structures that we selected to be distant from other community activities on the days that we tested, to minimize noise. G. Experimental session. Participants listened to tones via closed headphones and sung into a microphone. A translator (here in an orange shirt) provided verbal instructions to participants. Related to Figure S1.

We tested individuals residing in the US along with members of the Tsimane’, a farmer-forager society native to the Bolivian Amazon rainforest (Figures 1A and 1C). The Tsimane’ live in relative isolation from Western music and culture [39]. The villages in which we tested lack electricity and running water, and the residents’ exposure to Western culture was mostly limited to occasional trips into nearby towns to trade for supplies. Their own music consists of melodies with a small range and fewer distinct pitches compared with Western music [40], and appears to lack group performances and harmony [41] (see ‘Background information on the Tsimane’ and their music’, Methods). In our previous work, we found pronounced differences between the Tsimane’ and Western participants in aesthetic judgments of consonance and dissonance [41], and in mental representations of rhythm [42], consistent with our impression that their musical experience is very different from that of typical Western listeners, and providing evidence for the effects of this experience. However, we also observed similarities in perceptual sensitivity to harmonicity and roughness [41], and in the tendency to favor integer ratio rhythms [42]. The Tsimane’ thus seem a promising group in which to investigate potential cross-cultural similarities and differences in musical pitch perception.

Results

In the main experiments, listeners were presented with pairs of pure tones (single frequencies), and were instructed to sing back what they heard (Figures 1D and 1E). The f0s of the reproduced notes were extracted from the recorded audio (Figure 1E). To address the cross-cultural presence of logarithmic scaling, range limits, and octave equivalence in musical pitch perception, we analyzed this same basic experiment (the design of which is schematized in Figure S1 and described in detail in the Methods) in three ways. To assess the mental scaling of pitch, we compared the sung reproductions to the heard intervals assuming several candidate scales, and evaluated which best predicted listeners’ reproductions. To investigate the limits of pitch, we measured the accuracy of reproductions as a function of the stimulus frequency register. To test for octave equivalence, we compared the position within the octave (the “chroma”) of the stimulus notes to the reproduced notes. In addition to the main experiment described in the following three results sections, we conducted a number of experiments for replication and control purposes.

Mental scaling of musical intervals

Consider an example in which the stimulus tones have frequencies of 800 and 900 Hz, respectively. Suppose that participants reproduce the first tone within their singing range (say around 160 Hz). If listeners represented the tones using the logarithmic scale for pitch (as in Western music), we would expect that the second note would be produced at about 180 Hz, matching the frequency ratio of 9/8 (and thus the difference on a logarithmic scale). By contrast, if listeners used a scale based on the frequency-to-place mapping of the ear (the Mel [43], Bark [44], and ERB-number [45] scales are each different proposals for this mapping), they would instead match the difference in the place of excitation on the cochlea, which would yield a different reproduction of the second tone (e.g. 217 Hz for the Mel scale). Different mental scales thus predict different reproductions (Figure 2A).

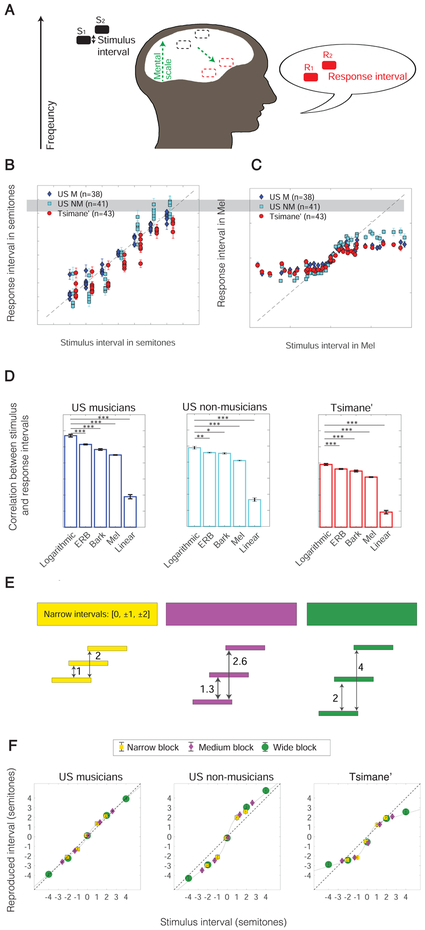
Figure 2. Log Frequency Scale is Present Cross-culturally.

A. Schematic of experiment design. Participants heard tones in one of eight different frequency registers and reproduced them in their singing range, presumably using an internal scale to map the stimulus interval onto their response interval. B. Stimulus and mean response intervals measured with a logarithmic scale, for US non-musician and Tsimane’ participants. Each data point plots the mean reproduced interval for a particular stimulus interval, stimulus register, and participant group. Error bars plot SEM across participants. C. Stimulus and mean response intervals measured with the Mel scale. D. Correlation between stimulus and response intervals when measured with five common scales. Asterisks denote statistically significant differences (*: p<.05; ***: p<.001). Error bars plot within-subject SEM across participants (see Figure S2 for scatter plots of the correlations for individual participants). E. Design of control experiment in which the range of stimulus intervals varied across three sections of the experiment. F. Stimulus and response intervals for the three groups, measured with a logarithmic scale. Every data point plots the mean reproduced interval for a particular stimulus interval in one of the three sections, averaged across registers to facilitate comparison between sections. The same stimulus interval generated similar response intervals across experiment sections with different ranges of intervals, indicating that listeners were not simply fitting the heard intervals into their comfortable singing range irrespective of their actual size. Curves denote parametric model fits to the data (a linear combination of sigmoid and a linear function).

Figures 2B and 2C show the stimulus and mean reproduction intervals for both participant groups from the main experiment (Experiment 1), expressed using logarithmic and Mel scales. A scale that perfectly predicted participants’ responses would yield data points exactly on the diagonal. It is apparent that the logarithmic scale is a much better predictor of responses. To summarize the goodness of fit for each of the candidate scales, we measured the correlation between stimulus and response pitch intervals expressed in each scale. As shown in Figure 2D, the logarithmic scale fitted the data significantly better than any of the alternatives for all three groups (p<.02 in all cases, via paired t-test).

One possible concern with the results of Figures 2B-D is that participants could have simply mapped the stimulus intervals within a block onto their comfortable singing range. Under this view, participants would sing intervals on the large side of what they are comfortable producing when they hear an interval that is large within the block. Hence, the correlation between stimulus and response intervals under a logarithmic scale could be the result of having used stimulus intervals in semitones that approximately span the comfortable singing range.

To control for this possibility, the same participants completed an additional experiment (Experiment 2; Figure 2E). In each of the three sections of this experiment the intervals were drawn from sets covering different ranges: 0, ±1, ±2; 0, ±2, ±4; or 0, ±1.3, ±2.6. If participants’ reproductions are in fact a reflection of a consistent internal scale, the response to a particular stimulus interval should be similar irrespective of whether the stimulus interval is large or small within the experiment section. The results (Figure 2F) indeed show no significant difference between the reproductions of the 2-semitone intervals in the narrow and wide sections for any of the three groups (+2 semitones, p>0.16 in all cases, t-test; −2 semitones, p>0.07 in all cases). Moreover, the reproductions for the larger ascending interval in each section were significantly different for all three groups (2, 2.6, and 4 semitones; p<0.001 for all groups, ANOVA), as were the reproductions of the large descending intervals (−2, −2.6, and −4 semitones; p<0.001 for all groups). In addition, data from each of the three experiment sections could be fitted as well by a stimulus-response curve fitted to all the data as by curves fitted to the data for the individual sections (p=0.51, 0.54 and 0.51 for Tsimane’, US non-musicians, and US musicians, respectively), indicating that the stimulus-response mapping was relatively independent of the interval range of the section. It is also apparent that both groups exhibit systematic biases in their reproductions depending on the interval (the difference between stimulus and response intervals varied with the stimulus interval; p<0.001 for all groups, ANOVA). In particular, sung intervals seem to be “pulled” toward the major second. However, the key point for the purposes of this experiment is that these biases are similar across the three sections. The results are consistent with the use of a single mental scale that is approximately logarithmic for all participant groups, at least over the range of intervals that we were able to test.

Limits of pitch

To assess the limits of pitch across cultures, we measured the accuracy of sung reproductions as a function of the stimulus frequency register. We expected that reproduction accuracy would deteriorate in Westerners for very high frequencies (above ~5kHz), due to the perceptual impairments documented in prior work [6-8].

To get a sense of the range of musical pitch the Tsimane’ likely experience, we recorded the f0 ranges of every instrument we could find in two of the villages where we ran the experiments (six flutes and one stringed instrument resembling a violin; Figure 3A). The Tsimane’ instruments were limited to f0s below 2 kHz (Figure 3B), in contrast to Western instruments, some of which produce f0s up to around 4 kHz (Figure 3C). Moreover, we observed informally that Tsimane’ songs typically reside in the lower end of the range of their instruments. If the limits of pitch reflect the range of experienced musical pitches, one might expect the Tsimane’ to exhibit a different upper limit than Westerners.

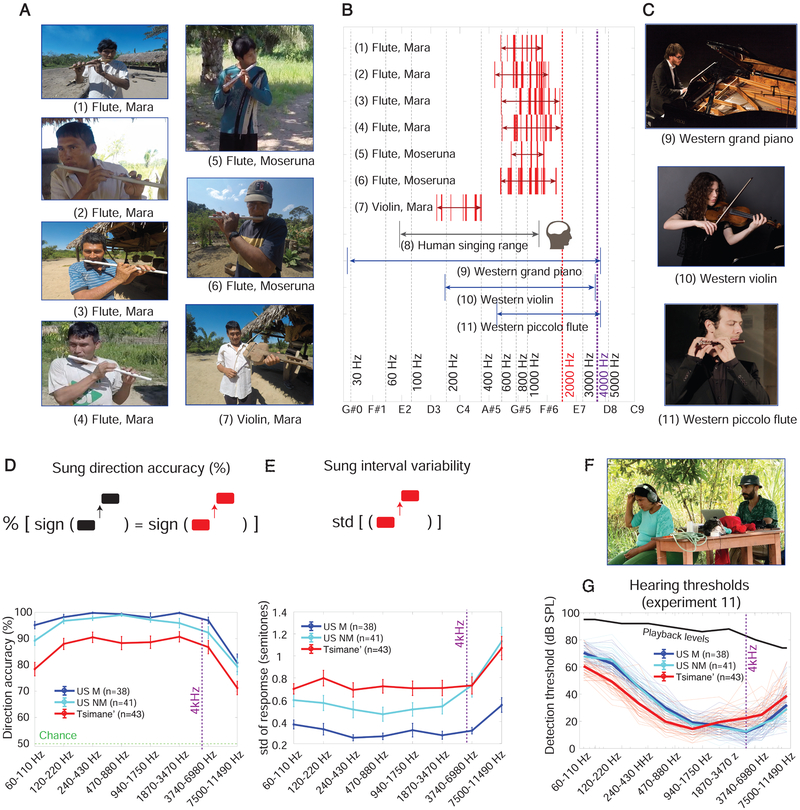
Figure 3. Limits of Pitch Perception Are Shared Across Cultures.

A. Photographs of Tsimane’ instruments from the two villages in which the experiments were conducted. B. Pitch ranges of Tsimane’ and a small subset of common Western instruments. C. Photographs of Western instruments. D. Accuracy of the direction of sung reproductions as a function of stimulus frequency. Error bars here and in E plot SEM across participants. E. Variability of reproduced intervals as a function of stimulus frequency. F. Photograph of diotic detection threshold measurements in the field. G. Measured detection thresholds (bottom). Thin lines show thresholds for individual participants; bold lines show group averages. Stimulus levels from the sung reproduction experiments are shown in black for comparison. Related to Figure S2.

The stimulus tones were presented in one of eight registers spanning most of the audible hearing range (60-11,500 Hz). Registers were octave-spaced with center frequencies ranging from 80 Hz (octave 1) to 10,248 Hz (octave 8). The target intervals were ±1, ±2, ±3 semitones, presented in random order. We assessed the accuracy of reproduction via two measures: the proportion of trials on which the direction of the pitch interval (up or down) was correct, and the variability of the reproductions of the same interval. Variability was analyzed (rather than the mean absolute error in the produced interval) to avoid assuming a particular scale (variability was also used by Attneave and Olson [6]). However, results were similar when absolute error (in semitones) was analyzed instead.

As shown in Figure 3D and 3E, the two measures of accuracy exhibited similar trends. Direction accuracy and interval variability showed significant main effects of group (direction: F(119,2)=18.8 p<0.001 η_p=0.24; variability: F(119,2)=18.65 p<0.001 η_p = 0.23) and register (F(494.11,4.15)=52.31 p<0.001 η_p=0.30; F(545.8,4.58)=22.60 p<0.001 η_p=0.16), with only a small interaction marginally significant for variability (direction: F(494.11,8.3)=1.02 p=0.42 η_p =0.02, variability: F(545.8,9.17) p=0.027 η_p =0.034). These results indicate that the dependence of accuracy on register was similar for the three groups.

The register main effects were driven by the highest frequency register, for which performance was significantly worse by both measures than in all other registers (p<0.001 for paired comparisons with all other registers for both direction and variability). Direction accuracy was also significantly lower for the lowest register compared with registers 2-7 (p<0.017), consistent with prior measurements of frequency discrimination thresholds in Westerners [17], though the variability measure did not show a comparable effect. See Figure S2 for results for individual stimulus intervals.

To ensure that the results were not due to poor audibility at high frequencies, we measured pure tone detection thresholds as a function of frequency in both groups (Figure 3F). Participants who exhibited signs of hearing loss (elevated thresholds) were removed from the analysis (see Methods). For the analyzed participants, all stimuli were presented at least 10 dB above detection threshold, indicating that performance impairments at high frequencies are not because the tones were inaudible (though they were closer to threshold for the lowest and highest frequency registers, which could contribute to poorer performance). The results are instead consistent with biological constraints on the upper limit of pitch, potentially due to the breakdown of phase locking when stimulus frequencies are sufficiently high [46].

Octave equivalence – chroma matching

As a test of whether participants heard tones separated by an integer number of octaves as similar, we analyzed the difference between the chroma of the stimulus and response (Figure 4A). Stimulus frequencies were projected onto the singing range (by adding or subtracting the integer number of octaves that placed them less than half an octave from the sung response), and the chroma difference was calculated as the difference between the projected stimulus and the sung response, in semitones (Figure 4B). Because singing accuracy was reduced for the highest and lowest frequency ranges, we restricted the analysis to registers 2-6 (of 8) (see Figure S3 for results for individual registers). We analyzed all trials where the stimulus was outside the singing range of the participant (defined as those trials where the absolute value of the mean difference between stimulus and response f0 exceeded six semitones).

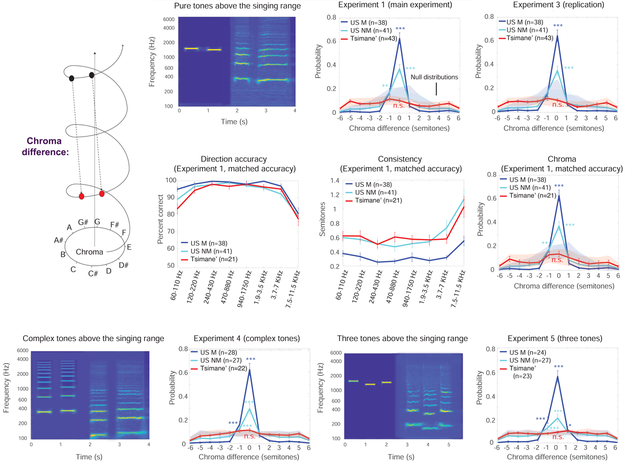
Figure 4. Chroma Matching Varies Across Cultures.

A. Schematic of analysis procedure. Stimulus frequencies were projected onto the singing range and compared to the reproduced f0, yielding the difference in semitones between the stimulus and response f0 modulo 12 (“chroma difference”). B. Spectrogram of example stimulus and response when stimulus was outside the singing range. C. Histograms of stimulus-response chroma difference from the main experiment (described as Experiment 1 in the Methods). Error bars plot SEM across participants. We found that chroma difference histograms were similar for the first and second tones, and all histograms presented in this paper pool the data across tones (i.e., treating them as independent trials). The shaded areas denote the null distribution of the chroma difference histogram for each participant group, computed from histograms of permuted datasets in which the stimulus-response correspondence was randomized. Note that because the stimulus chroma values were not uniformly distributed (see Methods) this null distribution was not uniform. The null distribution also depended on the consistency of produced pitches, so if participants produced a constant pitch regardless of the stimuli, the null histogram would have a peak around the corresponding chroma. Asterisks denote proportions that are significantly higher than would be expected if there were no relationship between the stimulus and response chroma (*: p<.05; **: p<.01; ***: p<.001). D. Histograms of stimulus-response chroma difference from the replication experiment (described as Experiment 3 in the Methods). Same conventions as B. E&F. Direction accuracy (E) and interval variability (F) from Experiment 1 for the best 50% of Tsimane’ participants (selected via direction accuracy) in Experiment 3. US musician and non-musician data are replotted from Figure 3 for ease of comparison. G. Chroma difference histogram from Experiment 1 for the three groups, restricting Tsimane’ participants to the 50% most accurate (such that accuracy was approximately matched to US non-musicians). H. Spectrogram of example stimulus and response for complex tone stimulus. I. Chroma difference histograms for complex tone stimuli (Experiment 4). J. Spectrogram of example stimulus and response for the three tone experiment. K. Chroma difference histograms for the three note stimuli (Experiment 5). Related to Figures S3 and S4.

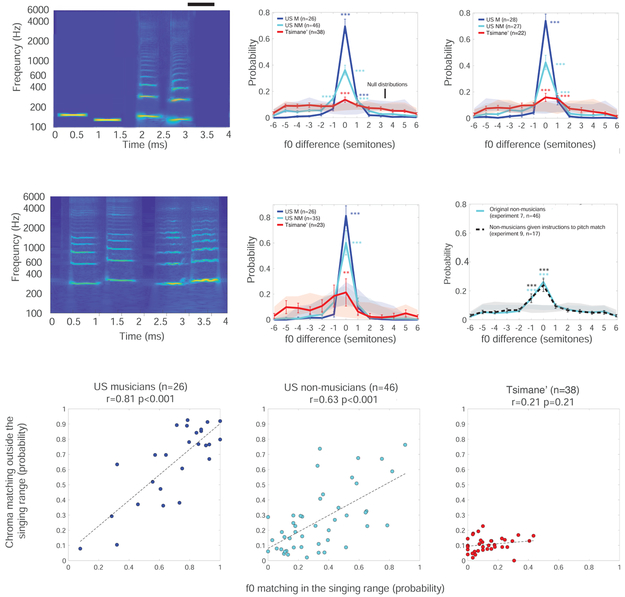
Figure 4C shows the histogram of chroma differences between the stimuli and responses of Experiment 1. For both groups of US participants, the histogram had a peak at 0 that was much higher than would be expected by chance (p<0.001, via bootstrap). This peak indicates a tendency to match the pitch chroma of the stimulus despite the large difference in absolute pitch between stimulus and response. These results substantiate the phenomenon of octave equivalence in Western listeners, but also show that it is substantially stronger in musicians (p<0.001, via bootstrap), at least when measured in this way.

In contrast to US participants, Tsimane’ participants did not exhibit significant chroma matching for tones outside the singing range (Figure 4C; p=0.75). We replicated the results in an additional experiment in which we attempted to make the task easier (Experiment 3). We eliminated the highest and lowest stimulus registers (in which chroma matching was not evident in Westerners; Figure S3; leaving only registers 2-6), and presented the intervals in increasing/decreasing order of size (to reduce uncertainty for the participants). The goal was to maximize the chances of seeing chroma matching in the Tsimane’. Despite these changes the results were similar (Figure 4D): US participants again showed significant chroma matching for tones above the singing range (musicians: p<.0.001; non-musicians: p<0.001), but the Tsimane’ participants did not (p=0.68 for the three registers above the singing range).

To address the possibility that the lack of chroma matching in the Tsimane’ might reflect the lower overall accuracy of their reproductions (Figures 3D and 3E), we separately analyzed the top 50% of Tsimane’ participants when ranked according to their sung direction accuracy in independent data (from experiment 3). This group of Tsimane’ participants was approximately matched in accuracy and variability to the US non-musician participants (Figures 4E and 4F), but showed no significant chroma matching (Figure 4G). It thus appears that the group differences cannot be explained by differences in accuracy – Tsimane’ with good relative pitch abilities nonetheless did not chroma match.

To test whether the Tsimane’ participants were attempting to match the absolute f0 of the stimulus instead of the chroma, we measured the mean response f0 as a function of stimulus register. This analysis revealed that all groups were somewhat biased by the absolute stimulus f0, with higher reproduced f0s for the high registers than for the low registers (Figure S4). However, these effects were modest, and actually strongest in US non-musicians, who tended to use falsetto voice for higher stimulus registers. When US non-musicians were excluded there was no group by register interaction (F(239,3.1)=0.5 p=0.83 η_p=0.006), indicating that the Tsimane’ participants were no more biased by the absolute stimulus f0 than the US musicians, in whom chroma matching was strong. This result suggests that the absence of chroma matching in the Tsimane’ is not because they were trying to match the absolute f0 rather than the chroma.

To test whether the results would be different with stimuli containing multiple frequencies that are more similar to human vocal sounds, we repeated the experiment with harmonic complex tone stimuli (Figure 4H). The results (Figure 4I) were similar to those with pure tones: frequent chroma matching in US musicians (p<0.001), reduced chroma matching in US non-musicians (significantly different from musicians, p<0.001, but above chance, p<0.001), and no detectable chroma matching in the Tsimane’ group (p=0.19).

We also tested whether the results would be different with three-note stimuli, that might be thought to sound more unambiguously musical than two note sequences (Figure 4J). The results (Figure 4K) were similar to those obtained with two notes, with the same pattern across groups, and no detectable chroma matching in Tsimane’ participants (p=0.11).

Octave equivalence – similarity rating

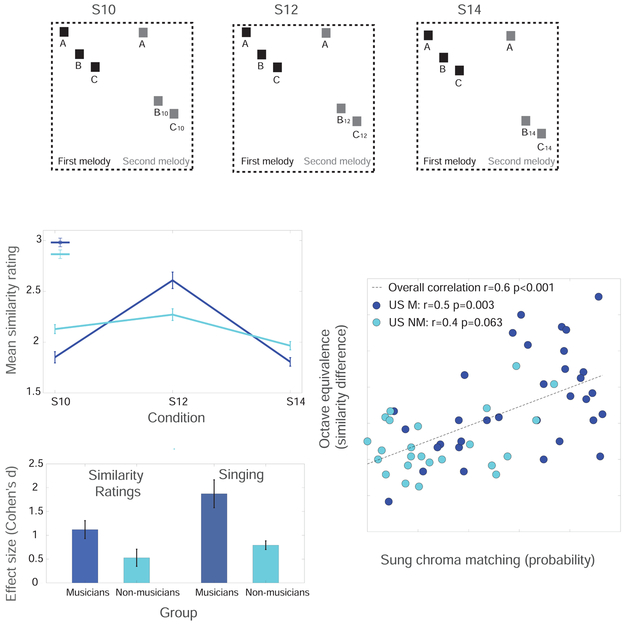
One natural concern is that because our task involves production it might not fully reflect latent perceptual representations. To compare the results of our singing paradigm to a more traditional measure of octave equivalence, we replicated an experiment by Demany and Armand [47] in which participants rated the similarity of pairs of melodies (Experiment 6). The last two tones of the second melody were transposed by either 10 (a seventh), 12 (an octave), or 14 (a ninth) semitones (Figure 5A). This paradigm was ill-suited to a cross-cultural experiment due to the need to explain the notion of similarity, so we ran it only on our US participants.

Figure 5. Similarity Ratings.

A. Schematic of main experimental conditions and task (Experiment 6). The last two notes of the second melody were transposed downward by 10, 12, or 14 semitones. B. Mean similarity ratings for US musicians and non-musicians. C. Scatter plot of octave equivalence as measured by similarity ratings and chroma matching. D. Comparison of octave equivalence effect sizes for musicians and non-musicians from similarity ratings and singing. Related to Figure S5.

We summarized an individual’s octave equivalence in this paradigm as the difference between the rating of the octave condition from the mean of the ratings of the seventh and ninth conditions. Musicians showed robust evidence of octave equivalence (Figure 5B; p<.001, t-test). This measure of octave equivalence was non-zero for non-musicians (Figure 5B; p=.02), but was smaller than for musicians. Cohen’s d was 1.12 for musicians and 0.53 for non-musicians (these values were significantly different, p=0.0017, bootstrap). Most importantly for our purposes, the rating difference of octave transpositions was strongly correlated across participants with the tendency to chroma match in a separate singing experiment performed by the same participants (r=0.59, p<0.001, correlation between the rating difference and the proportion of trials with a chroma difference less than 0.5 semitones; Figure 5C). This relationship suggests that chroma matching during singing taps the perceptual effect that has classically been associated with octave equivalence. However, the effect size of sung chroma matching was larger than the effect size of the similarity rating difference for octave transpositions (p<0.001, bootstrap) Figure 5D; this result held even when the number of trials per participant was equated across the two experiments; p<0.001). This result suggests that singing is arguably a more sensitive measure of the classical octave equivalence effect, and that the weaker effects in the Tsimane’ and in non-musicians are unlikely to be an artifact of production limits or task understanding.

Octave equivalence – relation to f0 matching

The chroma analyses in Figure 4 examined sung responses to tones outside the singing range (operationalized as trials where the absolute difference between response and stimulus f0 was larger than 6 semitones), to probe perceptual similarity of pitches across different registers. However, the same analysis can be performed for stimuli in the singing range (Figure 6A; analogously operationalized as cases where the response was within +/−6 semitones of the stimulus), revealing any tendency to match the absolute f0 of the stimulus. This analysis is shown for pure tones (from Experiment 4) and complex tones (Experiment 5) in Figure 6B. Although the Tsimane’ had a statistically significant tendency to reproduce the stimulus f0 (pure: p<0.001; complex: p=0.0078), the f0 matching results are strikingly similar to those for chroma matching. For both pure and complex tones, f0 matching was common in US musicians, less prevalent in US non-musicians (p<0.001, bootstrap), and barely evident in Tsimane’ (though statistically significant). We replicated these general trends in an additional experiment using sung notes as stimuli (Figure 6C), and found similar effects (Figure 6D). We also conducted an experiment using US non-musicians in which they were explicitly instructed to match the stimulus pitch (Experiment 9), and saw similar results to those observed without instruction (Figure 6E; there was no significant difference in f0 matching when compared to US non-musicians in experiment 7, p=0.77). These results suggest that f0 matching varies across individuals, and that it is stronger in individuals with more musical experience. Moreover, the variations in f0 matching seem unlikely to reflect differences in how individuals choose to respond, as some participants remained unable to pitch match even when explicitly asked to do so.

Figure 6. Relation of Chroma Matching to f0 Matching.

A. Spectrogram of example trial from Experiment 7 with pure tone stimulus in the singing range of a participant. B. Histogram of difference between stimulus and response f0 for trials in the singing range. Shaded region plots 95% confidence intervals on null distribution computed via bootstrap. C. Histogram of the difference between stimulus and response f0 for trials in the singing range (complex tones; Experiment 4). D. Spectrogram of example trial from Experiment 8, with a sung stimulus in the participant’s singing range. E. Results of Experiment 8 (same format as B). F. Results of Experiment 9, in which participants were instructed to match the pitch of the stimulus (same format as B). G. Scatter plots of f0 matching and chroma matching, plotted separately for each group. The dashed line shows the best linear fit to the data.

To gain insight into the relationship between chroma matching and f0 matching, we computed their correlations across individuals, separately for the three groups of participants (Figure 6F). f0 and chroma matching were strongly correlated for both groups of US participants (US musicians: r=0.81, p<0.001; US non musicians: r=0.63, p<0.001), but not for Tsimane’ (r=0.21, p=0.21; because there was essentially no measurable chroma matching in any Tsimane’ individual, and little f0 matching). In US participants f0 matching was also correlated with the similarity rating measure of octave equivalence from Experiment 6 (r=0.45, p=0.0004). These results suggests a relationship between the representations enabling chroma matching and those enabling the reproduction of the absolute f0 of a stimulus.

Octave equivalence – feedback

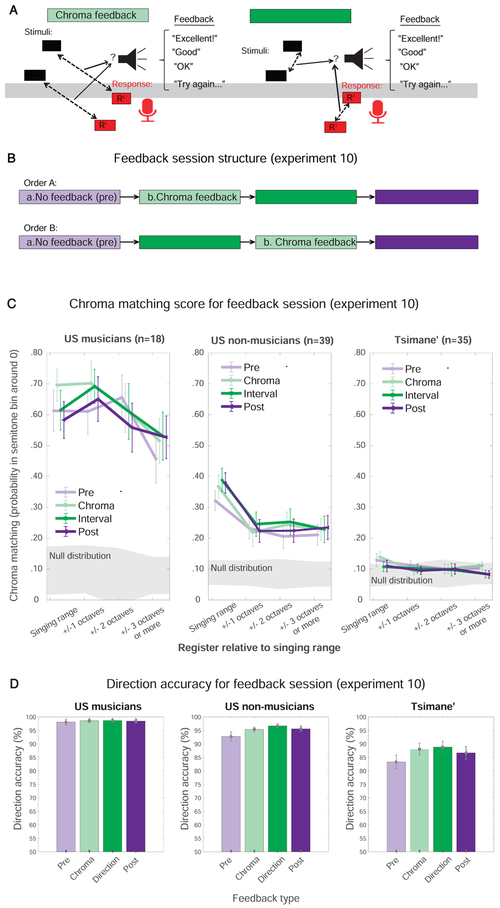
Because the experiments in which we assessed chroma matching did not explicitly instruct the participants how to respond, the variation in chroma matching could in principle be explained by a difference in how participant groups interpreted the task. The fact that f0 matching differences between groups were largely unaffected by explicit instructions to pitch match is inconsistent with this interpretation, but we nonetheless conducted an additional experiment to try to coach participants to chroma match (Figure 7A). The experiment consisted of four blocks, the second and third of which provided feedback based on how well participants matched either the relative pitch (interval) or chroma of the stimulus (Figure 7B). Feedback was provided in the form of pre-recorded spoken phrases in the participant’s native language (English or Tsimane’) immediately after each of the sung trials.

Figure 7. Effect of Feedback (Experiment 10).

A. Schematic of how feedback was determined from response, for direction (left) and chroma (right) blocks. B. Schematic of experiment structure. Listeners completed four blocks. The first and last had no feedback, like the rest of the experiments described in this paper. The middle two blocks had feedback based either on direction or chroma, in random order. C. Chroma matching in the four blocks for each group, binned according to the register difference between stimulus and response. Asterisks denote statistically significant differences from chance (i.e., the null distribution). In left and middle panels, asterisks apply to all data points. In the right panel, asterisks apply to the singing range condition only. D. Direction accuracy in the four blocks for each group.

As shown in Figures 7C-7D, the feedback had little effect: the Tsimane’ group showed weak tendencies to pitch match to stimuli in their singing range and did not chroma match outside of it, irrespective of the feedback. Indeed, we found no significant effect of block, and no block by group interaction (F(245.6,2.76)=1.27 p=0.284 η_p²=0.014; F(245.6,5.52)=1.08 p=0.37 η_p²=0.024). Although this result leaves open the possibility that some alternative method of training might increase chroma matching, the collective evidence suggests that explicit instructions or coaching have little influence on either pitch or chroma matching, at least on the short time scale of an experimental session. If someone were able to hear notes separated by integer numbers of octaves as similar and simply was choosing not to base their responses on this similarity, one would think that the feedback would have caused them to alter their behavior. The results suggest that the lack of chroma matching in the Tsimane’, and the reduced chroma matching in US non-musicians, is not due to a difference in the interpretation of the task, and rather reflects some more fundamental difference in the underlying perceptual representations.

Discussion

We introduced sung reproduction as a method for studying pitch perception, and used it cross-culturally to address the universality of three notable features of musical pitch perception in Westerners. We found that two aspects of pitch perception were shared between the Tsimane’ and US participants. Despite vast differences in the music that they experience, both groups reproduced frequency intervals that were roughly consistent with an internal scale for pitch that is logarithmically related to frequency. Sung reproductions of pitch intervals in all three groups were accurate over a wide range: from ~100-4000 Hz, extending far above the human vocal range. Moreover, reproductions in all groups deteriorated in accuracy for stimuli that were very high or very low in frequency, plausibly because of shared biological constraints on the extraction of pitch. But whereas US participants exhibited a reliable tendency to replicate the position of stimulus tones within the octave, the Tsimane’ did not. Moreover, this tendency to “chroma match” was substantially stronger in US participants with substantial musical experience, was correlated strongly with perceptual similarity measures of octave equivalence, and was not altered by our attempts to coach people to chroma match using feedback or by explicit instructions. The results are consistent with the presence of biological constraints on some aspects of musical pitch perception and behavior, but suggest that others (namely, octave equivalence) are not universal, and plausibly depend on experience with particular musical systems.

Relation to other methods

Prior evidence for octave equivalence has come predominantly from similarity ratings of tones [14, 48] and recognition of octave-scrambled melodies [12, 13] by Western participants. However, in both cases the results have occasionally been inconsistent [14, 49, 50] and/or absent for non-musicians [51]. There are also reports that listeners who are conditioned to respond to particular frequencies generalize to an adjacent octave [10, 52], though we failed to replicate the more recent of these studies in pilot experiments. It is also well established that trained musicians can reliably adjust one tone to be an octave apart from another [53]. Our results for Western listeners are consistent with these previous findings, as well as with prior evidence for logarithmic interval representations [6], and the dependence of pitch fidelity on stimulus frequency [6, 7], but have the advantage of being applicable and robust even in non-musicians. Indeed, sung chroma matching produced larger effect sizes in both US groups compared to a classical measure of octave equivalence based on similarity ratings. The sensitivity of the method could reflect the ethologically valid musical behavior [54] involved in the task. In particular, the requirement to sing may help non-musicians tap into musical pitch representations that are otherwise more readily accessible to musicians.

On the other hand, the dependence of the method on singing raises the possibility that production constraints could influence the results. For instance, singing may introduce an additional, production-related source of variability [55]. We found that data pooled over a set of trials reveal clear octave specificity with semitone resolution even for non-musicians (who presumably are not expert singers), but in contexts requiring sub-semitone distinctions, production noise could limit measurement resolution.

Another possible production-related concern is that because singing produces harmonic sounds, chroma matching could potentially be explained by the strategy of choosing an f0 with an overtone that matches the stimulus. Two aspects of our results argue against overtone matching. First, substituting complex tone stimuli for pure tone stimuli did not alter the results (Figure 4I), despite the considerable change in the number of stimulus frequencies a participant could in principle match to. Second, chroma matching did not vary much with the stimulus register provided the stimuli were below the upper limit of pitch (Figure S3, Figure. 7C). Because the number of overtones per octave increases with frequency (for a harmonic tone with fixed f0), if participants were overtone matching without regard to octave relationships, then the proportion of trials with a chroma-matched response should have decreased with the stimulus register (because only the 2^nd, 4^th, and 8^th harmonics would produce a chroma-matched response, the odds of matching the chroma decrease with register under this strategy). These pieces of evidence suggest that chroma matching in Westerners does not simply reflect explicit spectral similarity between stimuli, consistent with prior evidence for octave equivalence.

Alternative interpretations

Perhaps the most important production-related consideration is whether the variation in results across groups and individuals could reflect differences in some aspect of task performance that is not exclusively perceptual. One potential concern is that the task (copying the stimulus) could be open to interpretation, with different individuals or groups employing different strategies. We addressed this concern by attempting to coach participants to chroma match, and found this had no measurable effect. We also addressed the related possibility that the Tsimane’ might have tried to match the absolute stimulus register rather than the chroma, but found that they were no more biased by register than US participants. The Tsimane’ could instead have focused on matching the direction of the pitch change between notes, ignoring chroma, but then one might have expected the feedback manipulation to alter their behavior. Moreover, it is not obvious why prioritizing relative pitch differences would interfere with chroma matching (indeed, successfully matching chroma should in general make it easier to replicate relative pitch changes, consistent with the increased accuracy of US musicians). We also attempted to alter the behavior of US participants by explicitly asking them to pitch match, and found this had no measurable effect. These observations are consistent with our anecdotal sense that non-musicians are not aware of their chroma matching behavior, and do not employ a conscious strategy when performing the task.

A second alternative interpretation is that the differences between groups and individuals reflect their ability to coordinate production with perception [56]. For instance, consider the group and individual differences in the tendency to match the stimulus f0 of stimuli in the singing range. Although the Tsimane’ exhibited statistically significant f0 matching in these conditions, the effect was much reduced relative to that for US participants. Moreover, many US non-musicians also did not exhibit f0 matching, consistent with prior results [56, 57]. If one assumes that all listeners have perceptual representations of the absolute stimulus f0, this result might be interpreted as evidence that the Tsimane’, and some US individuals, have trouble translating their perceptual representations into a motor program for their voice. One might by extension suppose that the variation in chroma matching is similarly not exclusively perceptual.

The main evidence against this view is that in US participants, a purely perceptual measure of octave equivalence was strongly correlated with the extent of chroma matching (r=0.59), and with the extent of f0 matching (r=0.45). We also note that the above premise of universal perceptual representations of absolute f0 is not well supported even in Westerners. This is because psychophysical assays of pitch perception almost always involve a comparison between two or more sounds, and thus can be performed using relative pitch; psychophysical measures of absolute f0 perception are rare [58]. It thus remains possible that people by default compute relative pitch and do not retain a representation of the absolute f0, in which case it would be difficult to pitch match, or to chroma match. Octave equivalence could result from representations of absolute f0 that depend on experiential factors and vary across individuals and groups. By contrast, relative pitch, as indexed by accurate reproduction of the direction and approximate magnitude of note-to-note intervals, appears to be more clearly universal (though it is clearly refined with musical expertise). Our results could thus reflect a dissociation between representations of absolute and relative f0, with octave equivalence a byproduct of absolute f0 representations. This proposal remains speculative at present, but is broadly consistent with evidence that pitch perception involves multiple mechanisms whose contribution apparently varies across stimuli and tasks [58], and that could be differentially enhanced by different types of musical experience.

The counterargument to this perceptual interpretation of our results is that the only unambiguous links between chroma matching and perception are in US participants, leaving the possibility that the distinct behavior of the Tsimane’ reflects their ability to coordinate production with perception. To maintain this view one would have to suppose that the production differences across groups are specific to absolute f0 and chroma, because we were able to equate relative pitch abilities across groups (Figure 4E-G). But we acknowledge that our results leave room for this possibility. Future work with other perceptual tasks related to absolute f0, or with brain measures that do not require an explicit response, could help to more definitively resolve this issue.

Cross-cultural variation in chroma and f0 matching

Regardless of the interpretation, we have documented a pronounced difference in musical behavior across cultures. The cross-cultural variation we observed in chroma and f0 matching seems likely to reflect a dependence on particular types of musical experience (because it is not obvious what other difference in the lives of the Tsimane’ would give rise to the differences in results, and because we found musical training in Westerners to be predictive of these effects). Octave equivalence may thus provide an example where pitch perception is shaped by musical systems and/or behavior rather than the other way around. Because there are many differences between the musical experience of the Tsimane’ relative to typical Western listeners, we can only speculate as to the features of musical systems that might underlie the cross-cultural differences we observed. It is possible that perceptual octave equivalence only emerges in the presence of an octave-based musical system with a large melodic range, which the Tsimane’ appear to lack. It may also depend on experience with harmony, which the Tsimane’ apparently do not encounter very often [41]. It could also emerge as a side effect of men and women, or children and adults, needing to sing in a coordinated way.

It likewise remains to be seen whether musical experience could explain previous evidence for octave equivalence in young French infants [47], which at face value might seem inconsistent with the idea that octave equivalence emerges from exposure to a musical system. However, we also cannot exclude the possibility (suggested by the original authors) that there is some perceptual equivalence at birth that fades if a listener does not experience the appropriate musical system. Our results also do not speak to the reasons for the worldwide prevalence of the octave in musical systems [33]. One possibility is that octaves are easy to produce reliably on simple instruments, and thus form an “attractor point” for the evolution of scale systems.

We also emphasize that the peripheral auditory representations of tones separated by octaves are likely to be more similar than those of tones separated by non-octave intervals regardless of culture, due to mathematical properties of the octave that are preserved by the ear. Thus, for musical systems in which similarity relations across registers matter, the octave remains a natural choice. However, the availability of these cues should not be confused with their actual effect on perception. It is possible that acoustic cues favoring octave equivalence are universally available and that these cues often (but not always) influence the development of musical systems over generations. However, if a given group of listeners is not sufficiently exposed to music with structure related to the cue (for example, in music limited to a narrow melodic range), the cue may have a negligible effect on perception. This idea is consistent with historical fluctuations in the importance of the octave within Western music [59]. For example, the notation of ninth century chant, which also featured a very narrow vocal range, equated notes separated by a perfect fifth rather than an octave [60]. Our results also suggest a dissociation between octave equivalence and (approximate) logarithmic scales for pitch. Under the assumption of a single internal scale for pitch, octave equivalence entails a logarithmic scale, but the reverse need not be the case [48]. The Tsimane’ may provide an example of how logarithmic scales can exist without perceptual octave equivalence.

Biological constraints on pitch

Our results provide new evidence for biological constraints on pitch. Although the deterioration of pitch at high frequencies has long been speculated to relate to the breakdown of phase locking [18-20], definitive evidence has remained elusive. This is partly because the limits of pitch had only been documented in members of Western society, in which the limits of pitch perception match the f0 range of music. Our results do not implicate a particular physiological mechanism, but suggest that the limits of pitch are somewhat invariant to the range of pitches we experience. Although the Tsimane’ are but one additional culture, the consistent pitch limits we observed more clearly implicate a biological constraint, particularly given the differences we have observed between Western and Tsimane’ individuals in other aspects of pitch and music perception [41, 42].

We have revisited classic issues in musical pitch perception with a simple experimental paradigm that is well suited for cross-cultural experiments. Our work with the Tsimane’ has revealed both similarities and differences with Western listeners, underscoring the insights that can be obtained with experiments in non-Western cultures, and by using production to reveal perceptual representations.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Nori Jacoby (nori.jacoby@ae.mpg.de). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Participants

We recruited 215 participants from three groups for each experiment: US participants with extensive experience playing a musical instrument or singing (“musicians”); US participants with little musical experience (“non-musicians”); and Tsimane’ participants with little musical experience. The experiments with Tsimane’ participants were run during two different trips to the field and thus did not all have the same sets of participants; the partial overlap between participants in different experiments is indicated in Table S2.

We recruited Tsimane’ participants from four villages: Mara, Moseruna, Anachere and Iñañare. Mara and Moseruna were relatively remote (about a two day’s walk from the closest town, San Borja, and accessible by truck only during the dry months of the year). Anachere and Iñañare were only accessible by a two-day trip upriver in a motor canoe. The villages did not have electricity or running water. We included only participants who had not lived in a city for more than six months.

We recruited two types of US participants (musicians and non-musicians), all of whom were fluent English speakers. All experiments in the US were run in New York City, except for experiment 8, which was run in Boston. The demography and results of US participants from the two different cities were nearly identical. Musical experience was assessed via self-reported number of years spent playing a musical instrument or singing.

The musician cohort comprised 38 participants living in New York City with over 10 years of experience playing a musical instrument or singing (18 female, mean age = 32.6 years, SD = 11.5, range 18-69). The mean musical experience of this group was 20.2 years, SD= 6.45 range = 10-38). The non-musician cohort comprised 91 participants with up to three years of experience playing an instrument or singing (42 female, mean age 34.5 years, SD=9.2, range 20-59), recruited in New York (n = 74) and in Boston (n = 17). This group had mean musical experience of 0.80 years (SD 1.0 range = 0-3). Of these, 45 reported that they had never played an instrument or sung on a regular basis.

Tsimane’ participants had varied degree of musical experience and none, as mentioned earlier, regarded music as a profession (n = 86, 54 females; mean age =27.5 years, range = 18-54). Of these, 65 reported that they had never played an instrument or sung. Table S1 provides the demographic details of all experiments and Table S2 details the overlap between the populations across experiments. Sample size estimation is described in the “QUANTIFICATION AND STATISTICAL ANALYSIS” section of the STAR Methods. Note that experiment 11 (Diotic pure tone detection thresholds) was included as part of the session for each of the experiments and as such was run on every participant (to eliminate participants who might be unable to hear the stimuli, as described above). The data plotted in Figure 3G are from the 122 participants from Experiments 1-3.

All participants provided informed consent in accordance with the Columbia University Institutional Review Board and the Massachusetts Institute of Technology Committee on the Use of Humans as Experimental Subjects.

Background on the Tsimane’ and their music

The Tsimane’ are an indigenous people of lowland Bolivia, comprising about 17,000 individuals who live in about 120 small villages along the branches of the Maniqui and Apere rivers (Figure 1A). They subsist mostly on hunting, fishing, and farming (Figure 1B). The Tsimane’ have traditional indigenous music, familiarity with which varies across individuals. To the best of our knowledge, traditional songs were sung by individuals one at a time, generally without instrumental accompaniment. As reported by Riester [40], their song melodies are characterized by small intervals, often approximately two or three semitones, and a narrow vocal range. There is little evidence for musical transposition in Tsimane’ music, and as a result it was unclear a priori whether they would use a logarithmic scale for pitch. Song lyrics are usually allegorical, and frequently rely on animals to describe human social situations. Other songs describe spiritual or mythological content.

In addition to their knowledge of traditional music, nowadays most Tsimane’ villagers are somewhat familiar with religious Christian hymns, which many learn from missionaries. These hymns are monophonic and sung in Tsimane’. They are similar to traditional Tsimane’ music and other indigenous songs of the region in two additional respects: they rely on small intervals and encompass a relatively narrow vocal range. Group singing appears to be uncommon, irrespective of whether the material is traditional songs or hymns. Musicianship as occurs in Western and other cultures also appears to be rare [64]. Tsimane’ individuals never reported receiving compensation for playing music, and never mentioned any formal musical training or apprenticeship. However, some individuals own a musical instrument and play it in church or at home. Some individuals also report that they sing in weekly church ceremonies. The degree of participation in these kinds of activities varies considerably between individuals and communities. However, as described quantitatively below (“Participants” section), the majority of participants in each experiment reported that they never played a musical instrument and that they rarely sing.

Over the course of our recent trips to the Tsimane’ territory, it has become apparent that the region is undergoing rapid modernization. Changes are evident even year to year, due to a push by the Bolivian government to provide modern services to the indigenous peoples. Some villages now have electricity (when we first visited the region in 2011 this was not the case). Evangelism has also spread to many villages (though Christian missionaries have been in the region since the 1950s). Until recently, radios were extremely rare in Tsimane’ villages due to the limited availability of batteries, but their usage has increased across the Bolivian lowlands in recent years. The Tsimane’ villagers often listen to a missionary radio station, as it is widely used to communicate messages to remote villages. Our experiments were specifically limited to villages that remain relatively remote and that lack electricity, but some participants owned radios.

METHOD DETAILS

General Procedures

Sound presentation and response measurement

The sung reproduction experiments all had the same format, consisting of a series of trials in which two or three tones were presented, after which participants responded by singing two or three notes that were supposed to replicate the stimulus as well as possible. The participant was seated in front of a microphone facing the experimenter (Figure 1G). All stimuli were presented through Sennheiser HD 280 Pro headphones. Sung responses were recorded with a Shure SM58 microphone mounted on a microphone stand and connected to a Focusrite Scarlett 2i2 USB sound card.

f0 extraction of sung notes

After the stimulus presentation was finished, we began recording the microphone input. The recording was terminated after 1950 ms except for experiments 5 (three notes) and 8 (sung notes) where the recording durations were 2620 and 2350 ms, respectively (see Table S3). We ran an automatic f0 extraction algorithm on the recorded audio immediately following each trial. The f0 extraction algorithm was designed to find long segments of voiced vocal output (corresponding to sung notes) and to estimate their fundamental frequency (f0). Trials were considered valid when the algorithm detected exactly two voiced segments (for two note experiments) or exactly three voiced segments (for experiment 5) and the extraction met our quality assurance heuristic criteria (see below). To avoid missing data, if the trial was invalid we immediately tried to collect another response for the same condition (up to four attempts; see section “General experiment structure,” below).

f0 extraction was performed using a custom MATLAB script based on the yin algorithm [61], with the detection range (the free parameter of the yin algorithm) set to 65.4-523.2 Hz for male participants and 130.8-1046.4 Hz for female participants. Yin outputs the estimated fundamental frequency for each time point within the recording, and an aperiodicity value between 0 and 1 (ratio of aperiodic to total power) that should be low for periodic sound segments.

We performed a sliding average of the aperiodicity value over a 10-ms rectangular window. We then extracted continuous voiced segments that could potentially correspond to sung tones by selecting those segments for which the smoothed aperiodicity value was continuously smaller than a threshold of 0.3.

We estimated the amplitude envelope of each of the extracted audio segments as the maximum absolute value of the waveform within a rectangular sliding window of 10 ms. This envelope was used for the remaining steps in the note finding procedure. We first located peaks in the envelope using MATLAB’s findpeaks function, and then located the beginning and the end of the voiced segment corresponding to each peak.

To locate the end of the segment corresponding to a peak, we found the earliest point in time ${\mathrm{t}}_{\mathrm{i}}^{\mathrm{end}}$ that satisfied the conditions of (a) having a level of −22 dB or lower relative to the level of the peak and (b) the level of all points within 195 ms after ${\mathrm{t}}_{\mathrm{i}}^{\mathrm{end}}$ (within the window of $[{\mathrm{t}}_{\mathrm{i}}^{\mathrm{end}},{\mathrm{t}}_{\mathrm{i}}^{\mathrm{end}}+195]$), remained smaller than the −22 dB threshold. Similarly, we detected the beginning of the segment ${\mathrm{t}}_{\mathrm{i}}^{\mathrm{beg}}$ as the latest time point before the peak where the level within the window ([${\mathrm{t}}_{\mathrm{i}}^{\mathrm{beg}}-25$, ${\mathrm{t}}_{\mathrm{i}}^{\mathrm{beg}}$]), was lower than −22 dB relative to the level of the peak.

To ensure accurate f0 extraction given our field conditions, we further processed the extracted voiced segments using a number of additional heuristics that proved effective in pilot experiments. We found that sung notes were almost always longer than 200 ms, and that shorter voiced segments were usually due to detection errors. We therefore filtered the resulting set of segments by ignoring those with an overall duration of less than 185 ms. We also noticed that participants were less stable in f0 near the beginning and end of a sung note. We therefore discarded the first and last 75 ms of each segment and computed the median of yin’s f0 estimates within the trimmed segment. We also noticed that certain participants sometimes had a “cracked voiced” that produced unstable f0 detection, often resulting in some part of the sung note being assigned an f0 an octave higher or lower. We eliminated such unstable segments by excluding segments where more than 1/3 of the duration of the trimmed segment had an f0 estimate that was more than 6 semitones away from the median. The trial counted as valid when these procedures resulted in two (or three, for Experiment 5) voiced segments, and the median f0 of the trimmed segments was taken as the response. Otherwise the trial was considered invalid.

Optimizing experimental conditions

Because the Tsimane’ villages lack enclosed spaces (let alone soundproof booths), there was inevitably some degree of background noise during the experimental sessions. We made efforts to optimize listening conditions by selecting locations that were as distant as possible from potential acoustic disturbances from community activities (Figure 1F). When required, we also hired a community member to keep children and animals out of earshot from the experimental stations. To minimize the audibility of the background noise that remained, we used circumaural headphones that attenuated external sounds (Sennheiser HD-280 Pro). To maximize the signal-to-noise-ratio of the recorded responses, we used a directional dynamic microphone (Shure SM-58) and positioned it on a microphone stand directly in front of the participant (Figure 1G).

To ensure that participants were comfortable with the experimental session and understood the task instructions, all sessions were accompanied by a native Tsimane’ translator (Figure 1G). The translators had typically spent considerable time in nearby Bolivian towns, and were fluent in Spanish as well as Tsimane’. To ensure the accuracy of task instructions, they were initially translated into Tsimane’ by one translator, written down, backtranslated by another translator, and iteratively edited during two weeks of pilot testing in four additional Tsimane’ villages (Manguito, Arenales, Campo Bello, and Jamanchi). All experimenters learned the relevant Tsimane’ phrases to ensure that the translators were consistent and accurate in their work. These field procedures were developed and perfected to the extent possible in our earlier work [41, 42].

Experimental conditions in the US

Experiments in the US were run in way that matched the conditions in Bolivia as closely as possible. Participants were seated in front of the experimenter. We did not use a translator, as all US participants were fluent in English. To imitate the acoustic conditions in Bolivia we also did not use an isolated soundbooth, but instead ran the experiment in a room within the university.

Stimuli

Each trial presented two or three tones separated by 300 ms of silence.

Pure tones (Experiments 1-3, 5, 7, 9, and 10)

Each pure tone was 500 ms in duration with 50 ms linear attack and decay ramps. The stimulus level varied with tone frequency in order to approximately equate loudness (Table S3). Pure tones with different parameters were used for the melodic similarity experiment (see description of Experiment 6 below)

Complex tones (Experiment 4)

The complex tones contained harmonics 1 through 10, in sine phase, with harmonic amplitudes scaled by −12 dB/octave. The duration and temporal envelope were the same as for the pure tones. The stimulus level varied with tone f0 in order to approximately equate loudness (Table S3).

Sung stimulus (Experiment 8)

Stimuli were generated from notes produced by two singers (the two authors N.J. and M.J.M.). The singers produced short /a/ vowels lasting 500-800 ms. See further description of Experiment 8 below.

General Experiment Structure

Each experiment consisted of a series of “blocks” presented in random order, each of which presented stimuli within a single frequency register (Figure S1A). In some experiments these blocks were organized into “sections” that differed in some way.

Each block contained a number of “sub-blocks” corresponding to different f0 intervals (conditions) presented in random order (Figure S1B). On each trial, the participant heard the stimulus and tried to reproduce it by singing. The condition was repeated at least two but not more than four times: participants moved onto the next condition after successfully completing two valid trials (trials where the f0 extraction algorithm was able to extract exactly two sung tones, as explained in the “f0 extraction of sung notes” section). Two valid repetitions were collected in over 98% of the sub-blocks. The stimuli presented in each repetition were identical (same tone frequencies). However, the presented tone frequencies varied from condition to condition as described below (different for different experiments).

The stimulus f0s of the first tone in each condition were roved in one of two different ways, depending on the experiment, as described in the next section. In experiments 1-3, within each block each trial began from the same starting frequency (Y^b). In experiments 4-5 and 7-10 the starting frequency was roved across sub-blocks (i.e., it was constant across the repetitions within each sub-block but varied across sub-blocks).

Roving details

In experiments 1-3 the starting f0 for a block was uniformly randomized from a logarithmic scale within a window of ±2.5 semitones around the center of the register (X^b). Formally, if Y^b and X^b are represented in a semitone scale then:

$${\mathrm{Y}}^{\mathrm{b}}~\mathrm{U}[{\mathrm{X}}^{\mathrm{b}}-2.5,{\mathrm{X}}^{\mathrm{b}}+2.5]$$

Every trial presented two stimulus tones: the first was fixed across the block, and the second was determined by the condition, with the first and second tone forming a specific f0 interval for each condition. Formally, we denote the first and second tones of condition i within block b and repetition t by S¹ _b,i,t and S² _b,i,t respectively. Then

$$\begin{gathered} {\mathrm{S}}^1{}_{b,i,t}={\mathrm{Y}}^{\mathrm{b}} \\ {\mathrm{S}}^2{}_{b,i,t}={\mathrm{Y}}^{\mathrm{b}}+{\mathrm{I}}^{\mathrm{i}} \end{gathered}$$

where the interval Iⁱ is determined by the condition i, and Y^b is roved (randomized) once per block (i.e., stimulus frequency register) and per participant.

Similarly, we denote by R¹ _b,i,t and R² _b,i,t the response corresponding to S¹ _b,i,t and S² _b,i,t, respectively. We also denote by ${\mathrm{I}}_{b,i,t}^{\mathrm{R}}$ the response interval:

$${\mathrm{I}}_{b,i,t}^{\mathrm{R}}={{\mathrm{R}}^2}_{b,i,t}-{{\mathrm{R}}^1}_{b,i,t}$$

The experiment therefore is completely characterized by the block frequency range centers ([X_b]_b=1,..,m) and the list of conditions or stimulus intervals ([I_i]_i=1,..,n). Table S3 provides these parameters for each experiment.

In experiments 4-10, the first tone was roved every condition rather than once per block (Figure S1C). In addition, we increased the range of roving of the first tone to +/−6 semitones in order for the resulting stimuli to have a uniform chroma distribution. The starting tone Y^b,i of block b and condition i was randomized as follows:

$${\mathrm{Y}}^{b,i}~\mathrm{U}[{\mathrm{X}}^{\mathrm{b}}-6,{\mathrm{X}}^{\mathrm{b}}+6]$$

The two stimuli of condition i within block b and repetition t thus had f0s given by:

$$\begin{gathered} {{\mathrm{S}}^1}_{b,i,t}={\mathrm{Y}}^{b,i} \\ {{\mathrm{S}}^2}_{b,i,t}={\mathrm{Y}}^{b,i}+{\mathrm{I}}^{\mathrm{i}} \end{gathered}$$

Experiment 5 was similar to experiment 4 but included three tones. The first tone was randomized every sub-block: Y^b,i~U[X^b − 6, X^b + 6]. In addition, the two intervals ${\mathrm{I}}_{\mathrm{i}}^1$ and ${\mathrm{I}}_{\mathrm{i}}^2$ were randomized every sub-block ${\mathrm{I}}_{\mathrm{i}}^1$, ${\mathrm{I}}_{\mathrm{i}}^2~\mathrm{U}[-4.5,4.5]$

The three stimulus tones were:

$$\begin{gathered} {{\mathrm{S}}^1}_{b,i,t}={\mathrm{Y}}^{b,i} \\ {{\mathrm{S}}^2}_{b,i,t}={\mathrm{Y}}^{b,i}+{\mathrm{I}}_{\mathrm{i}}^1 \\ {{\mathrm{S}}^3}_{b,i,t}={\mathrm{Y}}^{b,i}+{\mathrm{I}}_{\mathrm{i}}^1+{\mathrm{I}}_{\mathrm{i}}^2 \end{gathered}$$

Table S3 provides the parameters for all the singing experiments.

Experiment 1 (pure tones in all registers)

This experiment was the main experiment of the paper, featuring tones in all 8 registers (60 Hz to 11.5 kHz), so that all three main analyses (Figs. 2-4) could be performed. Each frequency register was presented in random order; within a register the intervals were presented in a random order without replacement before proceeding to the next register. The stimulus intervals were 0, ±1, ±2, ±3 semitones. The frequency of the first of the two tones was roved across blocks (i.e. registers) but kept the same within a block (Figure S1A-B).

Experiment 2 (scaling control experiment)

This experiment was used as a control experiment for the scaling analysis of experiment 1, testing the effect of the interval set used on interval reproductions. The experiment contained three sections presented in a randomized order. Each section presented one set of intervals (0, ±1, ±2 semitones, 0, ±2, ±4 semitones, or 0, ±1.3, ±2.6 semitones; see Table S3). Because of the large number of conditions we only used four frequency registers 2-5 (between 120 and 1500 Hz). Within a section, the trials for a given frequency register were presented within a single block in random order. These blocks were randomly ordered within the section. As in Experiment 1, the frequency of the first of the two tones was roved across blocks (and participants) but kept the same within a block (Figure S1A-B).

Experiment 3 (replication)

This experiment aimed to afford the best conditions for observing chroma matching, and served in this paper to replicate the results of Experiment 1. We only used frequency registers 2-6, where frequencies were not too high (above 3 kHz) or too low (below 120 Hz). To make the task even easier for participants, the conditions (intervals) were presented in one of two ascending or descending orders, counterbalanced across participants ([0, 1, 2, 3, 4, 0, −1, −2, −3, −4, 0] or [0, −1, −2, −3, −4, 0, 1 2, 3, 4, 0]), as in Experiment 0. The frequency of the first of the two tones was roved across blocks but kept the same within a block (Figure S1A-B).

Experiment 4 (complex tones)

Experiment 4 tested the effect of altering the tone from pure to complex. This experiment included larger roving of the first tone (+/−6 semitones) in order for the resulting stimuli to have a uniform chroma distribution. In addition, the first tone was roved every condition rather than once per block; therefore the first tone was not constant within each block (Figure S1C). We used frequency registers 2-6.

Experiment 5 (three notes)

Experiment 5 tested whether participants were better at chroma matching when producing short melodies with three tones (compared with two tones in all other experiments). In each sub-block the first tone was randomized Y^b,i~U[X^b − 6, X^b + 6]. In addition, the two intervals I¹ and I² were randomized I¹, I²~U[−4.5, 4.5]

The three stimulus tones were:

$$\begin{gathered} {{\mathrm{S}}^1}_{b,i,t}={\mathrm{Y}}^{b,i} \\ {{\mathrm{S}}^2}_{b,i,t}={\mathrm{Y}}^{b,i}+{\mathrm{I}}^1 \\ {{\mathrm{S}}^3}_{b,i,t}={\mathrm{Y}}^{b,i}+{\mathrm{I}}^1+{\mathrm{I}}^2 \end{gathered}$$

The procedure was otherwise identical to all previous two tones experiments. We used frequency registers 2-6.

Experiment 6 (melodic similarity rating)

Experiment 6 (Figure 5) measured octave equivalence with a more conventional similarity rating paradigm. Each participant competed the similarity rating task as well as an accompanying singing task with pure tone stimuli, so that the results of the two paradigms could be directly compared (in Figure 5C). The singing task was identical to Experiment 7 (see below). The two tasks were completed in random order. The entire experiment was run before or after sessions 2 and 3 (order randomized across participants). The design and parameters of the similarity rating experiment were adapted from a previous publication [47]. Every trial presented two different melodies, each composed of three pure tones. Participants were asked to rate the similarity of the two melodies on a scale of 1-4. Because we were not confident that we could translate the notion of “similarity rating” for Tsimane’, we ran the experiment exclusively on US participants.

In the critical test conditions (Figure 5), the two melodies had the same contour (sequence of increases and decreases), but the two last tones of the second melody were shifted down in pitch by a minor seventh (10 semitones), an octave (12 semitones), or a major ninth (14 semitones). Participants experiencing perceptual octave equivalence would be expected to rate the pairs of melodies in the octave shift condition as more similar than melodies in the minor seventh or major ninth conditions. We included additional control conditions in which the two melodies were either identical or differed in their contour (these were not included in Demany and Armand’s original design, but were added to ensure task comprehension in case an octave effect was weak or absent in the shift conditions). Consistent with previous literature, participants were indeed highly sensitive to contour changes (see Figure S5).

The two melodies ([A₁, A₂, A₃] and [A₄, A₅, A₆]) were separated by 1000 ms of silence with each tone lasting 281 ms with 10 ms linear attack and decay ramps and an inter-tone interval of 375 ms.

The melodies were composed from random intervals that varied from trial to trial to avoid trial-to-trial priming effects and thus facilitate a longer experimental session, increasing power. The tone of the first melody (A₁) was randomized uniformly on a logarithmic scale from a frequency range of +/− 2 semitones around a central frequency of 736.7 Hz. Following Demany and Armand [47], both intervals were descending, and were randomized uniformly on a logarithmic scale: I₁ = A₁ – A₂ = U(5.15,7.15) semitones, and I₂ = A₁ – A₃ = U(9.39,11.39) semitones.

The experiment began with a practice block containing 12 trials to familiarize participants with the experiment. Participants then completed two test blocks in randomized order, one with the control conditions (melodies that were identical or that differed in contour), and one with the three different shifts. In all cases, the first tone of the second melody was identical to that of the first melody (A₄ = A₁).

The pitch-shift test block shifted the last two tones of the second melody by 0, 10, 12, or 14 semitones. Namely:

$${\mathrm{A}}_4={\mathrm{A}}_1,{\mathrm{A}}_5={\mathrm{A}}_2-\mathrm{S}={\mathrm{A}}_1-{\mathrm{I}}_1-\mathrm{S},{\mathrm{A}}_3-\mathrm{S}={\mathrm{A}}_1-{\mathrm{I}}_2-\mathrm{S}$$

where S ∈ {0,10,12,14}. Each of four conditions was repeated 12 times (48 trials total), each time with a different random initial melody ([A₁, A₂, A₃]).

In the changing contour block, the second melody of a trial preserved the interval magnitudes of the first melody (I₁ and I₂) but changed the contour to all four options, namely:

$${\mathrm{A}}_4={\mathrm{A}}_1,{\mathrm{A}}_5={\mathrm{A}}_1\pm {\mathrm{I}}_1,{\mathrm{A}}_6={\mathrm{A}}_1\pm {\mathrm{I}}_2$$

Each of four conditions was repeated eight times (32 trials total) each time with a different random initial melody ([A₁, A₂, A₃]).

The practice stimuli contained pairs of melodies that were identical, or that contained a small (4 semitone) or a large (10 semitone) increase in the second tone of the second melody.

The conditions are summarized in Table S4. Results for control conditions are provided in Figure S5.

Experiment 7 (roving pure tones)

Experiment 7 was identical in its parameters to experiment 4 (complex tones) but used pure tones. Like experiments 4-6, the first tone was roved +/− 6 semitones across conditions (Figure S1C), and we used frequency registers 2-6.

Experiment 8 (sung stimulus)

Experiment 8 tested the effect of using sung notes as the stimulus. The stimuli were pairs of recorded sung notes. The stimulus register was reduced to the typical male and female sung vocal ranges (specified below), and the range of roving was reduced so that the stimuli best matched natural singing:

$${\mathrm{Y}}^{b,i}~\mathrm{U}[{\mathrm{X}}^{\mathrm{b}}-2.5,{\mathrm{X}}^{\mathrm{b}}+2.5]$$

There were two sections: 8a, using unmanipulated recordings of sung notes, the results of which we analyze and present in this paper, and 8b, in which sung notes were artificially f0-flattened and shifted to obtain the needed note f0s. The results of section 8b were similar to those of 8a and we omit them for brevity and because 8a was more naturalistic and thus a better control experiment for our purposes in this paper.

In section 8a stimuli were generated from notes produced by two singers (the two authors N.J. and M.J.M.). The singers produced short /a/ vowels using a procedure designed to cover the logarithmic scale at eighth-tone intervals. The singer would hear a pure tone randomly selected from the set of f0s desired for the stimulus set (eighth-tones ranging from 196 Hz to 523 Hz for the female singer and 100 Hz to 262 Hz for the male singer), and would attempt to reproduce the stimulus pitch. The same f0 extraction algorithm used for the experiments automatically identified the average sung f0. If the sung f0 met the criteria for a successful response (as described in the “f0 extraction of sung notes” section), the recording was saved and the closest stimulus f0 was removed from the set (provided that the sung f0 was within an eighth-tone from that stimulus f0). This process was repeated until there was a sung note within an eighth-tone from every f0 in the set. The resulting sung vowels were 500-800 ms in duration.

During the experiment the stimulus f0s were sampled from the distributions described above, and the sung notes with closest f0s to the sampled f0s were used for the stimulus. The stimulus f0 intervals thus deviated slightly from the target values, but these deviations were less than a quartertone.

Experiment 9 (explicit instructions)

Experiment 9 tested whether explicit instructions to sing back the stimulus pitches would alter the results. The experiment was identical to Experiment 7, except that participants were told: “Please sing the same pitches (same notes) that you hear”. We ran the experiment exclusively on US participants, as we were not confident that we could translate the verbal instructions to match the stimulus pitches. This experiment was run on a separate cohort of US non-musicians (in Boston, whereas all other experiments were run in New York). However, we found no measurable difference between the results of this cohort and the other groups of NYC non-musicians.

Experiment 10 (interval and chroma feedback)

Experiment 10 (Figure 6) was intended to test whether explicit feedback provided after each trial would alter the extent of chroma matching. The experiment was divided into four sections: (10a) pre-test without feedback, (10b) chroma feedback, (10c) interval feedback, (10d) post-test without feedback. Section 10a was always first and section 10d was always last. We did not provide feedback in these two sections. These two sections were identical to experiment 7 (roving pure tones; Figure S1C). The order of the intermediate sections (10b and 10c, where feedback was provided) was randomized (Figure 7B).

In the feedback sections (10b and 10c), after each trial, the computer script automatically analyzed the trial and provided feedback. The feedback (e.g. “excellent!”) was provided by a short recorded phrase in English or Tsimane’ (for US and Bolivian participants, respectively). To emphasize that sections 10b and 10c contained different tasks (matching the chroma or matching the interval, respectively) we used different voices for the two sections. For each language we recorded two speakers (one female and one male) and used one of the speakers for the chroma feedback section (10b) and the other for the interval feedback section (10c), with the assignment randomized across participants.

Before each section (10b and 10c), participants were provided with instructions informing them that a human voice would now provide feedback. Following this, we provided a short training section (one block) with the same structure as 4b or 4c, but with the stimulus confined to the singing range (see Table S3). After the first of the two feedback sections, participants were informed that the feedback would be given by a different person, and performed another training block within the singing range.

The four possible feedback responses were “Excellent!”, “Good”, “OK,” and “Try again” (in English, or in translations to Tsimane’). We avoided negative feedback (e.g. “Bad”) to avoid discouraging Tsimane’, who we had observed fail to chroma match in experiments 1-3. The feedback “try again” was reserved for trials in which the number of valid recorded tones was not exactly two (see “f0 extraction” below). The other feedback responses reflected the accuracy of the participants’ response according to one of two metrics. In experiment 10b (“chroma feedback”), the feedback depended on the chroma difference between the stimulus and response tones, while in experiment 10c (“interval feedback”) the feedback only depended on the interval accuracy.

We defined the stimulus interval and response interval as I^S = S² – S¹ and I^R = R² – R¹. Similarly, we defined the chroma difference of the tone j between stimulus S^j and response R^j: c^j = mod₁₂(R^j − S^j + 6) − 6 where j = 1,2. The criteria for the different feedback responses are summarized in Table S5.

The stimulus tones were drawn from registers 2-6. Each frequency register was presented in random order; within a register the intervals were presented in a random order without replacement before proceeding to the next register. The stimulus intervals were 0, ±1, ±2, ±3 semitones.

Experiment 11 (pure tone detection thresholds)

To verify that all stimuli in the experiments were clearly audible, we performed a field version of an audiometry screening, measuring diotic pure tone detection thresholds (Figures 3F-3G). As in the sung reproduction experiments, we presented pure tones at different frequencies (from 60 Hz to 11.5 kHz) presented simultaneously to both ears (at the same level). The tones were presented in 10 randomly ordered blocks. Each block repeatedly presented a single frequency from a set of ten: 60, 125, 250, 500, 1000, 2000, 4000, 6000, 8000, and 11500 Hz. The experimenter adjusted the intensity of these tones, attempting to determine the faintest tone of this frequency that the participant could reliably hear. Participants responded to a tone by raising their finger (Figure 3F).

Sounds were initially presented at a comfortable but high level (Table S3). Participants were seated facing away from the experimenter to avoid non-auditory cues to the tone presentations. Sounds were played out over Sennheiser HD 280 Pro circumaural headphones and a Mac laptop computer. The headphones were selected for their sound attenuation properties (because the test was administered outside, there was always some amount of background noise from wind, insects, and other animals). The audio presentation system was calibrated ahead of time with a GRAS 43AG Ear & Cheek Simulator connected to a Svantek SVAN 977 audiometer, enabling tone presentation at the desired sound pressure level.

The audiometry experiment took about 10 minutes to complete. All participants in US and Bolivia completed the same experiment. We excluded 9 Tsimane’ participants and 9 NYC participant whose thresholds were within 10 dB of the tone presentation levels used in the sung reproduction experiments. For the remaining participants, the tone levels were on average 27.3 dB above detection thresholds (range of 10-40 dB).

Session Structure

The 11 experiments were grouped into four distinct testing sessions. All sessions lasted about 90 minutes, including at least two breaks. All experimental sessions began with a fixed sequence of “warm up” experiments to familiarize participants with the general method. Participants took part in no more than one session each day. The time between sessions ranged from one day to 13 months. Session 1 (experiments 1-3) was mainly run during 2017, but additional participants were recruited in 2018. Most participants that participated in session 1 also participated in sessions 2 and 3 (run during 2018). Table S2 summarizes the overlap between experiments.

1. Demography:

Each session began with a demographic survey. Answers were entered into a computer interface by the experimenter, aided by the Tsimane’ translator.

2. Initial demonstration:

The translator provided a Tsimane’ translation of the following sentence: “The experimenter will make a sound and the translator will copy it. Then, the experimenter will make it again and you will copy it”. This verbal description was followed by a demonstration: the experimenter sang two tones at an identical pitch (a unison). The translator then repeated the two tones as best as he could. The experimenter then repeated the tones once more, signaling to the participant to repeat the tones. The process was repeated until participants were comfortable with the flow of the experimental trial format.

3. Training to sing with a microphone:

The translator provided a Tsimane’ translation of the following sentence: “Now we both are going to use the microphone. I will make a sound and you will copy it.” The experimenter demonstrated the usage of a microphone by singing into another microphone on the experimenter’s desk, and participants were supposed to mimic the experimenter and sing into the main microphone. To avoid priming the participant with a particular frequency, experimenters wore headphones, heard a series of tones that were randomized by the computer, and sang these tones.

4. Training to sing with headphones:

The participant was then familiarized with the use of headphones. Most Tsimane’ participants had not used headphones in the past, and it was important that they felt comfortable with them before we proceeded. We first let the participant hold and manipulate the headphones to help them understand that they were not fragile. The translator then helped the participant position the headphones comfortably on their ears. The translator provided a Tsimane’ translation of the following sentence: “Now the computer will make the sound and you will repeat them”. The computer played two randomized tones within the singing range (see Table S3 for the randomization specification). The participant replicated the tones by singing. The experimenter waited for the participant to respond before initiating the next stimulus.

5. Training to sing continuously (Experiment 0):

This part of the training session was intended to acquaint the participant with the temporal flow of the experiment. This familiarity was important for reducing the overall duration of the experiment and to minimize fatigue. Tones were presented within the singing range (register 2 for male participants and register 3 for female participants). The conditions (intervals) were presented in one of two ascending/descending orders, counterbalanced across participants ([0, 1, 2, 3, 4, 0, −1, −2, −3, −4, 0] or [0, −1, −2, −3, −4, 0, 1, 2, 3, 4, 0]). If a participant had trouble providing timely sung responses, the experimenter and translator repeated the instruction and this part of the session was repeated.

6. Passive exposure to high and low frequencies.

This part of the training session was intended to familiarize the participant with pure tones above and below the singing range. Up to this point in the session, all tones had been within the singing range. To ensure that participants were not surprised to hear tones in other frequency registers, we played a few tones lower (between 69 and 92 Hz) and higher (between 2217 and 2960 Hz) than the singing range. Participants were instructed to listen to the tones without making a response. The translator then explained that the next experiment would have tones of this kind, but the participant would always need to respond in “their normal and comfortable singing voice”.

Division of experiments into sessions

Session 1 consisted of Experiments 3, 2, 1, and 11 in that order. Session 2 consisted of Experiments 10 and 11, in that order, followed or preceded by Experiment 6 when run in New York. Session 3 consisted of Experiments 4, 5, 7 and 8, in random order, followed by 11, followed or preceded by Experiment 6 when run in New York. Because of the duration of the session, some Tsimane’ participant participated only in some of the experiments. The number of participants and the overlap between participants in the experiments within this session are detailed in Table S2. Session 4 consisted of Experiments 8, 9, 7, and 6, an additional experiment not described here, and 11, in that order. Session 4 additionally moved step 6 of the session warm up (presenting example high frequency stimuli) to after Experiment 8, to avoid the possibility that hearing these high frequency stimuli might somehow interfere with the ability to pitch match to stimuli in the singing range.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical Details

Scale comparison (Figures 2B and 2C)

We compared the response and stimulus intervals measured according to different scales. Namely, if ${\mathrm{I}}_{\text{semitones}}^{\mathrm{R}}={{\mathrm{R}}^2}_{b,i,t}-{{\mathrm{R}}^1}_{b,i,t}$ is the response interval measured in semitones, then the response interval measured in Hz is given by: ${\mathrm{I}}_{\mathrm{Hz}}^{\mathrm{R}}=2\frac{{\mathrm{I}}_{\text{semitones}}^{\mathrm{R}}}{12}$.

Similarly, we compared differences in the ERB-number [45], Bark [44, 62], and Mel [43] scales. If f_Hz is the frequency in Hz, then f_Hz values represented in the three scales are given by the following formulae:

$$\begin{gathered} {\mathrm{f}}_{\mathrm{ERB}}=21.4\cdot {\log }_{10}\left(1+\frac{4.37\cdot {\mathrm{f}}_{\mathrm{Hz}}}{1000}\right)=6.442\cdot {\log }_2\left(1+\frac{{\mathrm{f}}_{\mathrm{Hz}}}{228.8330}\right) \\ {\mathrm{f}}_{\mathrm{Mel}}=1127\cdot \log \left(1+\frac{{\mathrm{f}}_{\mathrm{Hz}}}{700}\right)=2595\cdot {\log }_{10}\left(1+\frac{{\mathrm{f}}_{\mathrm{Hz}}}{700}\right)=781.18\cdot {\log }_2\left(1+\frac{{\mathrm{f}}_{\mathrm{Hz}}}{700}\right) \\ {\mathrm{f}}_{\text{bark}}=\{\begin{array}{c}\hfill z\hfill \\ \hfill 0.85\ast z+0.3\hfill \\ \hfill 1.22\ast z-4.422\hfill \end{array}\begin{array}{c}\hfill 2\le z\le 20.1\hfill \\ \hfill z<2\hfill \\ \hfill z>20.1\hfill \end{array}\phantom{\}}\text{where}z=26.81\cdot \frac{{\mathrm{f}}_{\mathrm{Hz}}}{(1960+{\mathrm{f}}_{\mathrm{Hz}})}-0.53 \\ \approx 13\cdot \text{atan}(0.00076\cdot {\mathrm{f}}_{\mathrm{Hz}})+3.5\cdot \text{atan}\left({\left(\frac{{\mathrm{f}}_{\mathrm{Hz}}}{7500}\right)}^2\right) \end{gathered}$$

To compare these scales to the internal scale dictating participants’ responses, we computed the response differences in each of the scales and compared it with the stimulus interval measured in that same scale.

Scaling model comparison (Figure 2D)

We used the Spearman correlation, corrected for attenuation [63] using split-half reliability. We computed the split-half reliability of the response interval r_r from the two repetitions of the same interval within the sub-blocks (corrected for the split sample size with the Spearman-Brown correction). Because the stimulus interval is given without error, its reliability is 1, such that the attenuated correlation (r’) is computed from the correlation of response and stimulus interval (r) as: $\mathrm{r}’=\mathrm{r}∕\sqrt{1\cdot {\mathrm{r}}_{\mathrm{r}}}$. We estimated the correlation for each participant and model (logarithmic, ERB-number, Bark, Mel, and linear). We then performed a series of planned comparisons between the logarithmic scale and the three other scales via a paired t-test on the correlations measured for individual subjects. Error bars in Figure 2D plot within-subject SEM - the SEM across participants of the difference between the correlation for a particular scale from the average correlation for the five scales, computed separately for each participant.

Analysis of Experiment 2 (Figure 2F)

Produced intervals were averaged across repetitions and registers, obtaining a single value for each participant, interval, and condition. Namely, for each participant j, condition c, and interval i, we computed the average response interval ${\mathrm{E}}_{b,t}\left({\mathrm{I}}_{b,i,t}^{\mathrm{R}}\right)$ in semitones, and compared it with the produced intervals (I^S(i, c)). Error bars in Figure 2F represent the standard error of these values across different participants.

To assess whether a single scale could account for participants’ responses across the three blocks, each of which had a different range of intervals, we fit functions to the data. We fitted a parametric “global” model that takes into account only interval size ${\stackrel{‒}{\mathrm{I}}}^{\mathrm{R}}(\mathrm{j},\mathrm{i},\mathrm{c})={\mathrm{f}}_{\theta }(\mathrm{i})+{ϵ}_{j,i,c}$, where ϵ_j,i,c is the residual that is not accounted by the model, and compared it to an alternative set of models fitted separately for each block, namely ${\stackrel{‒}{\mathrm{I}}}^{\mathrm{R}}(\mathrm{j},\mathrm{i},\mathrm{c})={\mathrm{g}}_{{\theta }_{\mathrm{c}}}(\mathrm{i})+{{ϵ}^{\prime }}_{j,i,c}$.

To compare the models, we split the participants into two equal size groups, training both models on the first half of the data and testing them on the second half (quantified by the percent of explained variance). We did this for 20,000 splits of the participants, and then compared the mean variance explained by the second model to the distribution of variance explained by the first model. The analysis was performed separately for Tsimane’ (2F) and NYC participants (2G).

We fitted the data in Figure 2F with functions that could accommodate the fact that they do not follow a simple linear trend. We noticed that small interval reproductions scaled roughly like a sigmoid function, whereas larger intervals approximated a linear trend. As a parametric model, we therefore used a linear combination of a sigmoid function and a linear trend line, which we found fit the data well. Formally:

$${\mathrm{f}}_{\theta }(\mathrm{i})=\mathrm{a}\frac{1}{1+{\mathrm{e}}^{-\mathrm{bi}}}+(\mathrm{ci}+\mathrm{d})$$

This model explained 67.0% and 68.8% of the variance in left-out data for the Tsimane’ and NYC participants, respectively. There was no difference in the variance explained when parametric models were fitted to individual blocks (sigmoid linear: p= 0.50, 0.55 for Tsimane’ and NYC, respectively), suggesting that participants used the same scale irrespective of the range of intervals encountered in a block.

Reproduction accuracy (Figures 3D and 3E)

Direction accuracy was defined as the proportion of responses with the same direction (up/down) as the stimulus, namely:

$$\mathrm{p}\left[\mathrm{sign}({{\mathrm{R}}^2}_{b,i,t}-{{\mathrm{R}}^1}_{b,i,t})==\mathrm{sign}\left({{\mathrm{S}}^2}_{b,i,t}-{{\mathrm{S}}^1}_{b,i,t}\right)\right]$$

For this analysis, we excluded unisons (whose direction is undefined), and averaged over repetitions and intervals, thereby obtaining the direction accuracy of each register (b) for every participant:

$$\mathrm{d}(\mathrm{b})={\mathrm{E}}_{\mid \mathrm{i}\mid \ge 1,\mathrm{t}}\left[1_{\mathrm{sign}({{\mathrm{R}}^2}_{b,i,t}-{{\mathrm{R}}^1}_{b,i,t})=\mathrm{sign}({{\mathrm{S}}^2}_{b,i,t}-{{\mathrm{S}}^1}_{b,i,t})}\right]$$

Error bars in Figure 3D show the standard error of d(b)computed across participants.

We quantified reproduction variability as the standard deviation of the reproduced interval across the two trials of a condition:

$${{\mathrm{e}}^{\prime }}_{b,i}={\mathrm{std}}_{\mathrm{t}}\left({{\mathrm{R}}^2}_{b,i,t}-{{\mathrm{R}}^1}_{b,i,t}\right)$$

We excluded sub-blocks where the standard deviation was extremely large (e′_b,i > 6 semitones), and computed the average accuracy for every register b and participant:

$$\mathrm{e}(\mathrm{b})={\mathrm{E}}_{\mid \mathrm{i}\mid \ge 1}({{\mathrm{e}}^{\prime }}_{b,i})={\mathrm{E}}_{\mid \mathrm{i}\mid \ge 1}\left[{\mathrm{std}}_{\mathrm{t}}\left({{\mathrm{R}}^2}_{b,i,t}-{{\mathrm{R}}^1}_{b,i,t}\right)\right]$$

Error bars in Figure 3E show the standard error of e(b) computed across participants.

Chroma difference analysis (Figure 4)

Chroma difference was defined as the difference between a stimulus tone and a response note modulo 12. Formally:

$${{\mathrm{c}}^{\mathrm{j}}}_{b,i,t}={\mathrm{mod}}_{12}\left({{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\mathrm{S}}^{\mathrm{j}}}_{b,i,t}+6\right)-6$$

A chroma difference of 0 corresponds to the stimulus and response having the same chroma (the same note name in Western musical notation; Figure 4A). We summarized the measured chroma differences with their histogram:

$$\mathrm{h}(\mathrm{i})=\mathrm{p}\left(\mathrm{i}-\frac{1}{2}\le {{\mathrm{c}}^{\mathrm{j}}}_{b,i,t}<\mathrm{i}+\frac{1}{2}\right)$$

These histograms were computed separately for different registers (Figure S3) or combined over all registers. In the latter case, we only included stimuli that were distant from the response by more than 6 semitones:

$$\mathrm{h}(\mathrm{i})=\mathrm{p}\left(\phantom{\mid }\mathrm{i}-\frac{1}{2}\le {{\mathrm{c}}^{\mathrm{j}}}_{b,i,t}<\mathrm{i}+\frac{1}{2}\mid \mid {{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\mathrm{S}}^{\mathrm{j}}}_{b,i,t}\mid >6\right)$$

The histogram contained the chroma difference for all of the notes on a trial, treated independently. Results were similar if just the first note was analyzed.

Error bars of the histograms in Figures 4C, 4D, 4G, 4I and 4K were computed by bootstrapping N=20,000 datasets by sampling participants with replacement.

To obtain the null distributions used to evaluate statistical significance of the peaks at 0 (Figures 4C, 4D, 4G, 4I and 4K), we created shuffled bootstrapped datasets, described in the following sections.

We also checked for peaks at other values of the chroma difference (corresponding to consistent transposition by something other than an integer number of octaves), using the same bootstrapping procedure but for f0 differences modulo other integers. There were never significant peaks off of zero for the Tsimane’.

Chroma analysis: Experiments 1-3

To create a bootstrapped dataset we sampled participants with replacement. Then for each participant we computed chroma differences using the stimulus parameters of either the previous block (in which case the first block was paired with the last block) or the next block (in which case the last block was paired with the first block). In other words, we chose one of two possible shuffles for each participant:

$${\mathrm{b}}^{\prime }=\mathrm{mod}(\mathrm{b}+1,\mathrm{m})$$

or

$${\mathrm{b}}^{\prime }=\mathrm{mod}(\mathrm{b}-1+\mathrm{m},\mathrm{m})$$

where m is the total number of blocks in the experiment. We then computed the reshuffled chroma difference, namely:

$${{\tilde{\mathrm{c}}}^{\mathrm{j}}}_{b,i,t}={\mathrm{mod}}_{12}\left({{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{{\mathrm{S}}^{\mathrm{j}}}_{\mathrm{b}\prime }}_{,i,t}+6\right)-6$$

where S^j _b′i,t is the stimulus of the previous or next block b′.

We then sampled conditions with replacement, creating histograms as with the real data:

$$\tilde{\mathrm{h}}(\mathrm{i})=\mathrm{p}\left(\mathrm{i}-\frac{1}{2}\le {{\tilde{\mathrm{c}}}^{\mathrm{j}}}_{b,i,t}<\mathrm{i}+\frac{1}{2}\right)$$

Note that this null distribution is not uniform. To accommodate vocal production constraints, in Experiments 1-3 we used stimuli within a limited frequency range which therefore were not uniformly distributed over chroma. The distribution width was determined by the randomization of the first tone within the block (±2.5 semitones around the center frequency of the range, as described in Table S3). Given that the responses were also not uniform (see Figure S5 for the distribution of responses), the difference $({{\tilde{\mathrm{c}}}^{\mathrm{j}}}_{b,i,t}={\mathrm{mod}}_{12}\left({{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\tilde{\mathrm{S}}}^{\mathrm{j}}}_{b,i,t}+6\right)-6)$ was likewise non-uniform. We used bootstrapping to distinguish the contributions to the histogram that arose from the consistency between the responses (R^j _b,i,t) and stimuli (S^j _b,i,t), and contributions to the histogram that were determined by the non-uniform response distribution and that could therefore be reproduced if the stimulus-response correspondence was randomized $({{\tilde{\mathrm{S}}}^{\mathrm{j}}}_{b,i,t})$.

Chroma analysis: Experiments 4, 7-10

The process was identical to that for experiments 1-3, but because the initial tone was randomized in every condition, we used the previous or next conditions rather than block for the shuffling. Formally:

$${\mathrm{i}}^{\prime }=\mathrm{mod}(\mathrm{i}+1,\mathrm{n})$$

or

$${\mathrm{b}}^{\prime }=\mathrm{mod}(\mathrm{b}-1+\mathrm{n},\mathrm{n})$$

where n is the total number of conditions. In this case, the shuffled chroma is defined as:

$${{\tilde{\mathrm{c}}}^{\mathrm{j}}}_{b,i,t}={\mathrm{mod}}_{12}\left({{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{{\mathrm{S}}^{\mathrm{j}}}_{{b,i}^{\prime }}}_{,t}+6\right)-6$$

We generated 20,000 bootstrapped datasets in this way. We performed the following procedure in order to obtain a p-value quantifying the significance of the histogram at a chroma difference of 0: for each dataset we computed the histogram value for a chroma difference of zero semitones (h(0)) and compared it to the distribution of peaks within the bootstrapped datasets $(\tilde{\mathrm{h}}(0)))$. The shaded areas in Figure 4 are 95% confidence intervals of the bootstrapped null distribution of the histogram $(\tilde{\mathrm{h}}(\mathrm{i}))$. Effect sizes of the peak at 0 were estimated using Cohen’s d. Namely, we computed the difference in means between the response and null distribution and divided it by the pooled standard deviation: $\mathrm{d}=\frac{\mathrm{E}(\mathrm{h}(0))-\mathrm{E}(\tilde{\mathrm{h}}(0))}{\sqrt{\mathrm{var}(\mathrm{h}(0))+\mathrm{var}(\tilde{\mathrm{h}}(0))}}$.

Chroma analysis: Experiment 5

The process was identical to the analysis of two notes but we averaged the histograms over the three notes. We also analyzed the histograms of chroma difference separately for each note (first, second, and third); the individual histograms produced nearly identical results and were thus omitted.

Accuracy matching (Figures 4E-4G)

To check that group differences in chroma matching did not merely reflect a difference in accuracy, we used the data from experiment 3 to select Tsimane’ participants whose interval reproduction variability was better than the median. To obtain the results in Figures 4E-4G, we analyzed the data for the selected participants from Experiment 1 (i.e., a separate experiment within the same session, to avoid non-independence). Figures 4E and 4F display their direction accuracy and interval variability, respectively. Figure 4G shows the chroma matching histogram for this subpopulation.

Similarity ratings (Figure 5)

In the analysis of the similarity rating experiment (Figure 5B) we focused mainly on the three conditions (S10, S12, S14) where the two melodies had the same contour but where the two last tones of the second melody were shifted by 10,12, or 14 semitones. Figure S5 shows the results for all other conditions. Effect sizes (Figure 5D) were computed as the mean difference between the rating for condition S12 and the mean of the rating of S10 and S14, divided by the standard deviation of this difference across participants. Effect sizes for singing experiments were computed as explained above (in “Chroma difference analysis” section). Following Demany and Armand [47], to generate a measure of octave equivalence for individual participants (Figure 5C), we subtracted the average ratings for conditions S10 and S14 from the mean rating for condition S12. Figure 5C plot this score against the tendency to chroma match when singing (the probability of chroma differences within the range of +/− 0.5 semitones), measured in a separate experiment section with the same participants.

F0 matching and chroma matching (Figure 6)

To obtain measures of how well each participant pitch matched and chroma matched, we divided trials into those where the stimulus was close to a participant’s vocal range and those where it was not. Specifically, to measure f0 matching we constrained the analysis to all trials of a given participant where the stimulus and response f0 difference was smaller in absolute value than 6 semitones. We then computed histograms of the f0 difference as before:

$${\mathrm{h}}_{\mathrm{p}}(\mathrm{i})=\mathrm{p}\left(\phantom{\mid }\mathrm{i}-\frac{1}{2}\le {{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\mathrm{S}}^{\mathrm{j}}}_{{b,i}^{\prime },\mathrm{t}}<\mathrm{i}+\frac{1}{2}\mid \mid {{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\mathrm{S}}^{\mathrm{j}}}_{b,i,t}\mid \le 6\right)$$

The participant score for f0 matching was this histogram value at 0 semitones (h_p(0)).

To provide a similar measure for chroma matching, we computed the chroma histogram value at zero semitones for trials where the response-stimulus f0 difference was larger (in absolute value) than 6 semitones:

$${\mathrm{h}}_{\mathrm{c}}(\mathrm{i})=\mathrm{p}\left(\phantom{\mid }\mathrm{i}-\frac{1}{2}\le {{\mathrm{c}}^{\mathrm{j}}}_{b,i,t}<\mathrm{i}+\frac{1}{2}\mid \mid {{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\mathrm{S}}^{\mathrm{j}}}_{b,i,t}\mid >6\right)$$

The participant score for chroma matching was this histogram value at 0 semitones (h_c(0)).

Feedback session (Figure 7)

Figure 7C shows the results for feedback sessions. We binned the data based on the number of octaves between stimulus and response. We denote by d^j _b,i,t the number of octaves separating the stimulus and response, namely:

d^j _b,i,t was k octaves if and only if

$$-6+12\cdot \mathrm{k}\le {{\mathrm{R}}^{\mathrm{j}}}_{b,i,t}-{{\mathrm{S}}^{\mathrm{j}}}_{{b,i}^{\prime },t}<6+12\cdot \mathrm{k}.$$

Formally, the Chroma score displayed in Figure 7C is:

$${\mathrm{C}}_{\mathrm{k}}=100\cdot \mathrm{p}(\mid {{\mathrm{c}}^{\mathrm{j}}}_{b,i,t}\mid <\frac{1}{2}\mid {{\mathrm{d}}^{\mathrm{j}}}_{b,i,t}=\pm \mathrm{k}).$$

Note that C₀ is the f0 matching score of the previous section (C₀ = 100 · h_p(i = 0))

Figure 7D shows the direction accuracy for the different conditions.

Instrument analysis

During our visit to the villages of Mara and Moseruna in 2017, we documented the musical instruments in the villages. We asked individuals who own and play musical instruments to demonstrate their playing, and recorded them using a Hero-5 GoPro camera. Since Mara is a relatively small village (19 households, 91 individuals) we comprehensively documented all musical instruments in the village, which totaled four different flutes, one three-string instrument resembling a violin, and two drums. In Moseruna, a larger and more geographically distributed village, we documented two flutes and one drum. In each case we asked participants to play the highest tones that their instrument is able to produce. These recordings were analyzed by a f0 extraction algorithm (based on the yin algorithm [61]; see below). For each instrument we computed all produced f0s and extracted the minimum and maximum produced f0 (Figures 3A-B). None of the documented musical instruments produced an f0 higher than 2 kHz. Ranges for Western instruments are based on [21]. Tsimane' musicians analyzed and presented in Figures 3A (images and video/audio recordings taken with permission): Fidel Canchi Cuata (1,7), Martin Canchi Majoyete (2,3,4), Espiritu Majoyete Masa (2,4), Fidel Vie Canchi (5), Angelito Maito Temba (6). Images of western musicians in Figures 3C (taken with permission): Imri Talgam (9), Carmel Raz (10), Roy Amotz (11).

Sample Sizes

Following pilot experiments with Tsimane’ participants that suggested that octave equivalence would, if anything, be the weakest of the three main effects we hoped to test, we based sample sizes on power analyses of this effect. Specifically, we estimated the number of participants necessary to detect an octave equivalence effect that was half as large as that found in the US non-musician participants with a probability exceeding 90%. The criterion for significance in this analysis was based on the deviation of the empirical histogram of stimulus-response chroma distance from the null-hypothesis histogram (see below). Therefore, to estimate the required number participants we simulated datasets with variable numbers of participants by sampling with replacement from the NYC participant data. In each of the simulated datasets we replaced 50% of the participants’ data with shuffled data in which the stimulus assignment was randomized. This procedure is equivalent to reducing the effect size by a factor of two. For each of these simulated datasets we evaluated whether the dataset yielded a significant peak compared with the null distribution, using a .05 significance threshold. We repeated this process 20,000 times, yielding a curve relating the sample size to the proportion of data sets yielding a significant result. The smallest sample size that produced significant results in 90% of the cases was N = 17 participants. We ran at least this many participants in each experiment.

Statistical Methods

For the analysis of Figure 2D, we computed Pearson correlations for each participant (r values corrected for attenuation, as explained in the above section “Scaling model comparison”) between the stimulus and response intervals measured by five different scales (logarithmic, ERB-number, Bark, and Mel). To compare the significance of the difference between pairs of scales in Experiment 1 (for example, between the logarithmic and linear scales) we used a one-tailed paired t-test applied to the r-scores of all participants within a group.

To compare the productions of ±2 semitone within the narrow and wide blocks of Experiment 2 (Figures 2F and 2G), we used a two-tailed paired t-test. The test was applied to the mean produced interval of each participant for the two conditions, measured in semitones. To compare the productions of the large intervals in each block we ran repeated measure ANOVAs using IBM’s SPSS (v.25). Greenhouse-Geisser correction was applied when Mauchly's Test of Sphericity showed significant results; otherwise we did not apply a correction.

To test whether the data from the three block types could all be well fitted by the same stimulus-response curve (Figures 2F and 2G), we computed the percent of the variance explained by a sigmoid-linear function (see Methods section “Analysis of Experiment 2”) fitted to the combined data from the three blocks (once per group). We then compared this number to the mean of the percent of variance explained by models fitted to the individual block. In order to obtain the significance level, we performed bootstrapping (20,000 repetitions, with participants sampled randomly with replacement) and compared the explained variance for the all-data model to the null distribution for the single-block models. To test for biases in the reproductions we analyzed the same data after pooling over interval size from all 3 blocks, using a repeated measures ANOVA on the bias (response interval - stimulus interval).

To compare the fidelity of pitch representations across frequency registers (Figure 3) we computed direction accuracy and interval variability for each participant and register. We then applied a repeated measure ANOVA. To compare particular registers, we used a one-tailed t-test with Bonferroni correction.

For the analysis of Figure 4, we computed histograms of chroma difference from all trials for all participants. We then obtained a null distribution via bootstrapping (20,000 repetitions, with participants sampled randomly with replacement; see Methods for details), from which we computed p values. These p values were then Bonferroni corrected for multiple comparisons. Effect sizes of the peak at 0 were estimated using Cohen’s d. Namely, we computed the difference in means between the response and null distribution and divided it by the pooled standard deviation. To compare chroma matching across groups, we computed bootstrap distributions for the peak at 0 in the chroma difference histogram, resampling participants with replacement. P-values were estimated by comparing the mean of one group against the bootstrap distribution for another group. To compare the extent to which the absolute stimulus f0 biased responses (Figures S4B and S4D), we performed ANOVAs with participant group, gender, and stimulus f0 as factors.

For the analysis of Figure 5B we averaged the ratings for each condition; error bars represent standard error across participants. To evaluate octave equivalence we computed the mean rating for the octave condition minus the mean of the ratings for the seventh and ninth conditions, and compared this to zero with t-tests across participants. Effect size was computed as the mean of this difference divided by the standard deviation of the difference. Error bars represent the standard deviation of this effect size measure from bootstrapped samples (20,000 repetitions, with participants sampled randomly with replacement). To compare effect sizes between groups or experiments, we used these bootstrap distributions. P-values were estimated by comparing the mean of one group/experiment against the bootstrap distribution for another group/experiment. Correlations in Figure 5C are Pearson correlations between the scores.

For the analysis of Figure 5D, we used 36 trials (3 conditions × 12 repetitions) to compute the effect size for the melodic similarity experiment, whereas the number of trials used to compute the effect size for the accompanying singing experiment was 48 (4 registers beyond the singing range × 6 conditions × 2 repetitions). To ensure that the difference in effect size between the two experiments was not merely due to the different number of trials, we reanalyzed the data by taking only one repetition from each condition of the singing experiment, resulting in 24 trials per participant. As indicated in the main text, this did not substantially affect the results and the singing experiment again showed a significantly larger effect size than the melodic similarity experiment (p<0.001).

Figures 6B, 6C, 6E and 6F (measuring f0 matching to stimuli in the singing range) are based on the same procedure as Figure 4. Figure 6G was generated using measures analogous to those used in Figure 5C. The f0 matching score was defined as the proportion of trials with an absolute f0 difference less than 0.5 semitones. P-values for comparison across groups/experiments were estimated by comparing the mean of one group/experiment against the bootstrap distribution for another group/experiment.

Figure 7C was generated using the procedure for Figure 4, but instead of plotting the full histogram pooling across registers, we plotted the proportion of trials with a chroma difference in the zero semitone bin, as a function of the feedback condition and stimulus register (as explained above in the section “Feedback session (Figure 7)”). Significance was estimated used the same bootstrapping procedure as for Figure 4. We corrected for multiple comparisons with the Bonferroni correction. Figure 7D shows the mean direction accuracy averaged across registers for each of the feedback conditions and groups (see above in section "Reproduction accuracy (Figure 3D and 3E)"). The error bars plot standard errors across participants.

DATA AND CODE AVAILABILITY

Original data from all experiments is available online: https://osf.io/dw39v/?view_only=ef7509ef8781466180984d0d7fe6e433

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Raw and analyzed data	This paper	https://osf.io/dw39v/?view_only=ef7509ef8781466180984d0d7fe6e433
Software and Algorithms
MATLAB	Mathworks	https://www.mathworks.com/
Psychtoolbox	Psychtoolbox.org	http://psychtoolbox.org/

Highlights.

• Pitch perception was probed cross-culturally with sung reproduction of tone sequences

• Mental scaling of pitch was approximately logarithmic for US and Amazonian listeners

• Pitch perception deteriorated similarly in both groups for very high frequency tones

• Sung correlates of octave equivalence varied across cultures and musical expertise