Computational platform for doctor–artificial intelligence cooperation in pulmonary arterial hypertension prognostication: a pilot study

Abstract

Background

Pulmonary arterial hypertension (PAH) is a heterogeneous and complex pulmonary vascular disease associated with substantial morbidity. Machine-learning algorithms (used in many PAH risk calculators) can combine established parameters with thousands of circulating biomarkers to optimise PAH prognostication, but these approaches do not offer the clinician insight into what parameters drove the prognosis. The approach proposed in this study diverges from other contemporary phenotyping methods by identifying patient-specific parameters driving clinical risk.

Methods

We trained a random forest algorithm to predict 4-year survival risk in a cohort of 167 adult PAH patients evaluated at Stanford University, with 20% withheld for (internal) validation. Another cohort of 38 patients from Sheffield University were used as a secondary (external) validation. Shapley values, borrowed from game theory, were computed to rank the input parameters based on their importance to the predicted risk score for the entire trained random forest model (global importance) and for an individual patient (local importance).

Results

Between the internal and external validation cohorts, the random forest model predicted 4-year risk of death/transplant with sensitivity and specificity of 71.0–100% and 81.0–89.0%, respectively. The model reinforced the importance of established prognostic markers, but also identified novel inflammatory biomarkers that predict risk in some PAH patients.

Conclusion

These results stress the need for advancing individualised phenotyping strategies that integrate clinical and biochemical data with outcome. The computational platform presented in this study offers a critical step towards personalised medicine in which a clinician can interpret an algorithm's assessment of an individual patient.

Short abstract

High-throughput biomarker screening and machine learning (ML) are promising new technologies that could revolutionise the way doctors screen PAH patients. Principles of game theory combined with ML modelling would allow doctor–ML collaboration. https://bit.ly/3FvbXJD

Introduction

Pulmonary arterial hypertension (PAH) is a highly morbid disease characterised by complex pathobiology and variable clinical presentation [1]. The availability of numerous approved [2] and emergent [3] PAH medications has expanded treatment options used clinically to limit morbidity and prevent premature death. However, pharmacotherapeutic initiation and dose escalation is guided by risk assessment [4], emphasising the importance of data and algorithms that clarify prognosis in individual patients. In turn, pathogenetic and phenotypic heterogeneity across the PAH spectrum introduce unique challenges to precision-based risk stratification methods.

Several validated risk estimation tools are now available for PAH and have transformed clinical decision-making by allowing evidence-based prognostication at point-of-care [5, 6], but these algorithms consider a relatively narrow range of variables that can't account for disease heterogeneity [7–9]. Utilising machine-learning algorithms allows contemporary calculators to compute risk estimates from robust datasets that can include thousands of circulating biomarkers [10, 11] across diverse PAH populations, thereby expanding the gamut of patient-specific measurements available for compiling risk estimates. However, a clinician utilising these complex multivariate models on a patient would only be presented with a numeric risk score without any explanation of how the model reached its calculation. Therefore, these models require an analytic strategy to generate an intuitive readout that explains how each marker contributed to the final prediction, which would mark a significant advance towards individualising clinical decision-making in PAH.

The overall goal of this project was to showcase a computational platform that 1) integrates big data inclusive of biological and clinical parameters to generate a composite risk profile and 2) ranks the contribution of all patient parameters to the computed risk score for an individual patient (using game theory). Combining these two mathematical principles for risk stratification is positioned to advance the use of artificial intelligence for personalised clinical decision-making in PAH.

Methods

To demonstrate the aforementioned computational platform for doctor–machine interaction in PAH prognostication, we utilised the dataset presented in Sweatt et al. [7] (referred to here as the case study dataset) to train a random forest model that predicts the probability of death/transplant within 4 years. Once a suitably accurate model was developed, we then applied game theory principles [12] to explain overall model structure and showcase how a clinician could interpret the prediction for a specific patient.

Case study dataset: study population and design

The study analysed data from a prospective observational cohort of 281 PAH patients evaluated at Stanford University (Stanford, CA, USA) who had banked peripheral blood samples between 2008 and 2014. This dataset has been described extensively [7]. Within this cohort, 114 patients were known to be alive and transplant-free before the 4-year follow-up, but not evaluated beyond this point. Therefore, this study considers 167 patients (demographics shown in table 1) with a documented 4-year outcome (n=93 transplant-free survival versus n=74 death or lung transplantation), where the 4-year cut-off was chosen to achieve a roughly 50% event rate, because machine-learning algorithms tend to produce erroneous classifiers when trained on imbalanced datasets.

TABLE 1.

Stanford cohort patient characteristics in high 4-year risk and low 4-year risk groups. Continuous data are compared using a t-test and categorical variables by Chi-squared test

	High 4-year risk	Low 4-year risk	Two-tailed p-value
Sample size	74	93
Age (years)	52.7±15.5	47.0±14.3	0.015
Female (%)	71.6	75.3
Race
White	42	53	0.992
Asian	10	24
Hispanic	11	11
Black	5	3
Other	6	2
PAH subtype
Connective tissue disease	25	27	0.997
Idiopathic PAH	19	27
Drug and toxins	13	15
Congenital heart disease	8	17
Portopulmonary hypertension	8	4
Hereditary PAH	1	3
NYHA functional class
Class I	4	5	0.942
Class II	11	42
Class III	46	37
Class IV	13	9
Haemodynamics
mPAP (mmHg)	50.8±16.2	50.9±16.6	0.969
PVR (dyn·s·cm−5)	11.2±7.14	11.3±6.59	0.925
Cardiac index (L·min−1·m−2)	2.27±0.82	2.24±0.67	0.795
Mean right atrial pressure (mmHg)	9.70±6.33	7.89±4.78	0.037
PCWP (mmHg)	12.2±5.72	10.5±4.09	0.027
Timing from
Diagnosis (years)	3.1±3.9	4.5±5.4	0.053
Symptom onset (years)	4.4±4.8	6.0±5.4	0.051
Therapy
Treatment-naïve	23	28	0.999
Monotherapy	21	28
Dual therapy	22	26
Triple therapy	8	11

Data are presented as n or mean±sd, unless otherwise stated. PAH: pulmonary arterial hypertension; NYHA: New York Heart Association; mPAP: mean pulmonary artery pressure; PVR: pulmonary vascular resistance; PCWP: pulmonary capillary wedge pressure.

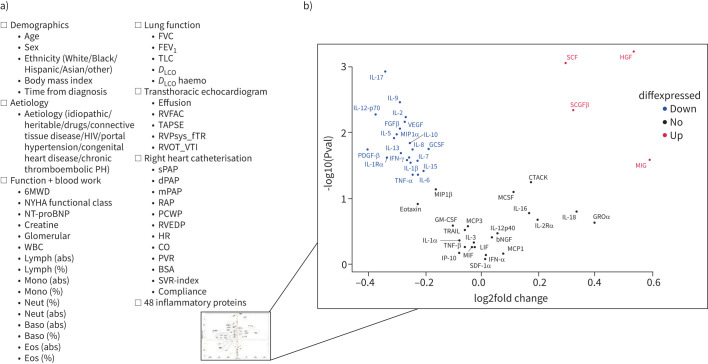
For each patient, the model was trained on 93 patient parameters (figure 1a; all variables defined in table 2) which included 1) demographics; 2) PAH subgroup; 3) functional metrics and standard clinical bloodwork; 4) invasive haemodynamic measurements; 5) lung function measurements; 6) selected echocardiographic parameters; and 7) an exploratory proteomic immune panel of 48 cytokines, chemokines and growth factors measured using a Bio-Plex multiplex immunoassay (Bio-Rad, Hercules, CA, USA) (figure 1b).

FIGURE 1.

a) An outline of all biomarkers considered; b) volcano plot showing all circulating proteins considered with fold change (concentration in high-risk patients/concentration in low-risk patients) in high 4-year risk, relative to low 4-year risk. Proteins in red and blue represent those that were statistically higher or lower (p<0.05), respectively, and with a |foldchange| >1. PH: pulmonary hypertension; 6MWD: 6-min walk distance; NYHA: New York Heart Association; NT-proBNP: N-terminal pro-brain natriuretic peptide; WBC: white blood cells; lymph: lymphocytes; abs: absolute; mono: monocytes; neut: neutrophils; baso: basophils; eos: eosinophils; FVC: forced vital capacity; FEV₁; forced expiratory volume in 1 s; TLC: total lung capacity; D_LCO: diffusing capacity of the lung for carbon monoxide; D_LCO haemo: D_LCO adjusted for haemoglobin during pulmonary function testing; RVFAC: residual volume fractional area change at transthoracic echocardiogram (TTE); TAPSE: tricuspid annular plane systolic excursion; RVPsys_fTR: right ventricle (RV) systolic pressure computed from tricuspid regurgitation; RVOT_VTI: RV outflow tract velocity time integral at TTE; sPAP: systolic pulmonary arterial pressure; dPAP: diastolic pulmonary arterial pressure; mPAP: mean pulmonary arterial pressure; RAP: right atrial pressure; PCWP: pulmonary capillary wedge pressure; RVEDP: RV end-diastolic pressure; HR: heart rate; CO: cardiac output; PVR: pulmonary vascular resistance; BSA: body surface area; SVR: systemic vascular resistance.

TABLE 2.

Table of variables used in this study

	Description	Units
Age		years
6MWD	6-min walk distance	m
MSWT	Modified shuttle-walk test distance	m
e6MWD	Estimated 6MWD: 0.7225 × MSWT + 70.769	m
NT-proBNP	Circulating N-terminal B-type natriuretic peptide	pg·mL−1
Creatine	Serum creatine concentration	pg·mL−1
Glomerular	Glomerular filtration rate	mL·min−1·1.73m−2
WBC	CBC white blood cell count	×103 cells·mm−3
Lymph (abs)	CBC differential absolute lymphocytes count	×103 cells·mm−3
Lymph (%)	CBC differential percent lymphocytes count among all WBCs	%
Mono (abs)	CBC differential absolute monocyte count	×103 cells·mm−3
Mono (%)	CBC differential percent monocyte count among all WBCs	%
Neut (abs)	CBC differential absolute neutrophil count	×103 cells·mm−3
Neut (%)	CBC differential percent neutrophil count among all WBCs	%
Baso (abs)	CBC differential absolute basophil count	×103 cells·mm−3
Baso (%)	CBC differential percent basophil count among all WBCs	%
Eos (abs)	CBC differential absolute eosinophil count	×103 cells·mm−3
Eos (%)	CBC differential percent eosinophil count among all WBCs	%
FVC	Forced vital capacity during PFT	%
FEV1	Forced expiratory volume in 1 s during PFT	%
TLC	Total lung capacity during PFT within	%
D LCO	Diffusion capacity of the lung for carbon monoxide during PFT	%
DLCO haemo	DLCO adjusted for haemoglobin during PFT	%
Effusion	Pericardial effusion observed at TTE	mm
RVFAC	RV fractional area change at TTE	%
TAPSE	Tricuspid annular plane systolic excursion	cm
RVPsys_fTR	RV systolic pressure computed from tricuspid regurgitation	mmHg
RVOT_VTI	RV outflow tract velocity time integral at TTE	cm·s−1
sPAP	Systolic pulmonary arterial pressure	mmHg
dPAP	Diastolic pulmonary arterial pressure	mmHg
mPAP	Mean pulmonary arterial pressure	mmHg
RAP	Right atrial pressure	mmHg
PCWP	Pulmonary capillary wedge pressure	mmHg
RVEDP	RV end-diastolic pressure	mmHg
HR	Heart rate	beats·min−1
CO	Cardiac output	mL·s−1
PVR	Pulmonary vascular resistance	Wood units
BSA	Body surface area	m2
SVR-index	Systemic vascular resistance index	(Wood units2)·m−2
Compliance	(sPAP−dPAP)/stroke volume	mmHg·mL−1
HGF	Hepatocyte growth factor	AU
SCF	Stem cell factor	AU
IL-2	Interleukin 2	AU
IL-9	Interleukin 9	AU

Abs: absolute value; CBC: complete blood count; PFT: pulmonary function test within 3 months; TTE: transthoracic echocardiogram; RV: right ventricle; AU: arbitrary units.

Feature engineering

Of the 93 patient parameters, four categorical parameters (sex, ethnicity, PAH subgroup and presence of pericardial effusion) were one-hot-encoded (i.e. coding categorical variables as binary vectors) [13] to arrive at a dataset with 167 observations and 104 features.

The dataset had 863 (<5% of total data matrix) missing values. For continuous variables that were distributed normally, each missing value was replaced with the feature mean. For categorical variables or continuous variables that were not distributed normally, the missing values were replaced with the feature mode.

To reduce the dimension of the original dataset, we performed recursive feature elimination (RFE) (10 000 trees trained at each iteration; each tree is allowed four decision splits; 3% of the least important features are removed at each iteration), as described in [14] (using Matlab 2020b, Mathworks). The variable set producing the lowest out-of-bag classification error [15] contained 23 features, which was too high for a predictive model with 167 observations. Therefore, we allowed the RFE algorithm to run until <10 features remained, thus producing a final data matrix with nine features.

Developing the final predictive model and validation

A final random forest model (with 10 000 trees based on plateaued out-of-bag classification error; each tree was allowed to grow to a maximum depth of four generations) was trained on 80% of the observations, with 20% withheld for (internal) validation (using “sklearn” library [13] in Python 3.9.6). An additional external validation cohort of 38 PAH patients from the University of Sheffield, collected from the Sheffield Pulmonary Vascular Disease Unit between 2008 and 2014, was also utilised to assess model performance. Therefore, the results of this study reference the internal validation cohort (20% of the Stanford cohort (table 1), withheld for testing) and the external validation cohort (the Sheffield cohort; supplementary material O2, trained on 100% of the Stanford patients).

Because the overall objective of this study was to showcase model interpretability, and there is no point in interpreting a model that is not sufficiently accurate, we compare the performance of the final trained random forest model against the REVEAL 2.0 calculator [6] as a standard for sufficient model accuracy. All sensitivity/specificity values reported in the manuscript were computed by generating a receiver operating curve (ROC) for computed probability values (when evaluating the random forest model) or REVEAL 2.0 risk score.

Random forest model interpretability

In 1951, Lloyd Shapley built on the concept of game theory by deriving an equation for the marginal contribution of a single player in a cooperative game [16], which won him the Nobel Prize in economics. The Shapley value is computed for each player in a cooperative game to fairly determine the marginal contribution of that player, which, through interaction between players, might be different from the player's individual score. This concept has been expanded to “explain” the marginal contribution of each feature in multivariate tree-based machine-learning models [12], which allows for both global (how input features rank and contribute to the overall model prediction) and local (how input features rank and contribute to an individual model prediction) interpretability of feature contribution and interaction.

SHAP values and the reported plots that use them were computed using the TreeExplainer SHAP package in Python [12]. Even though the direct computation of Shapley values would be too computationally expensive, especially as the number of considered features would be increased, the computational pipeline outlined [12] is fast for even high-dimensional problems, and guarantees “local accuracy” and “consistency” [17]. Global model structure was explored using violin plots. Local model interpretability (defined as the degree that a human can understand the cause of a model's decision), used to understand the model prediction for a specific patient, was assessed using violin plots and decision plots.

Results

Random forest model of risk (a case study)

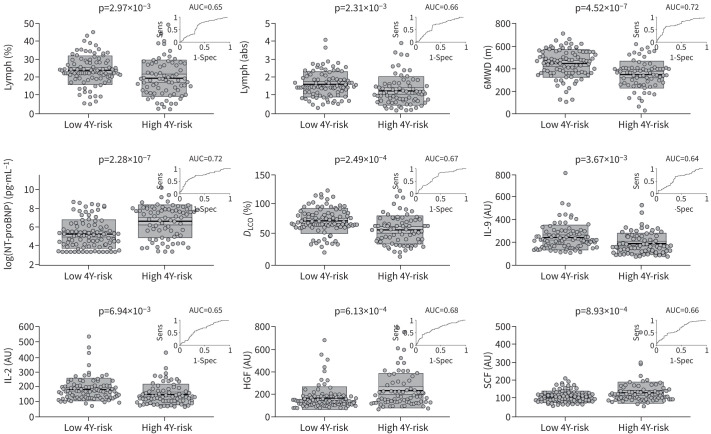
After performing RFE, the final model consisted of nine features: 1) 6-min walk distance (6MWD); 2) diffusing capacity of the lung for carbon monoxide; 3) N-terminal pro-brain natriuretic peptide (NT-proBNP); 4) lymphocytes (%); 5) lymphocytes (absolute); 6) interleukin (IL)-9; 7) IL-2; 8) stem cell factor; and 9) hepatocyte growth factor, which all had significantly different means between high-risk and low-risk patients (figure 2; all variables defined in table 2). The area under the ROC curve (AUC) shown in figure 2 revealed that all nine markers fairly discriminated high-risk versus low-risk patients, but the discrimination accuracy is considerably improved by combining all nine into a multivariate model (figure 3). It is critical to note that we are not suggesting that these nine features be clinically utilised based on this relatively small patient cohort. Although we are encouraged by the fact that our RFE algorithm identified markers commonly accepted as prognostic, these metrics would need to be validated in larger prospective studies. An expanded discussion of these results is available in supplementary material O1.

FIGURE 2.

Mean comparison between low 4-year risk group and high 4-year risk group for each of the nine markers chosen through recursive feature elimination. Each plot shows raw data, mean, 95% CI (light shading), 1sd (dark shading). An inset in each plot shows the receiver operating curve for that marker along with the area under the curve (AUC). Lymph: lymphocytes; sens: sensitivity; spec: specificity; high 4Y-risk: high 4-year risk of death or need for transplant; low 4Y-risk: low 4-year risk of death; abs: absolute; 6MWD: 6-min walk distance; NT-proBNP: N-terminal pro-brain natriuretic peptide; D_LCO: diffusing capacity of the lung for carbon monoxide; IL: interleukin; AU: arbitrary units; HGF: hepatocyte growth factor; SCF: stem cell factor.

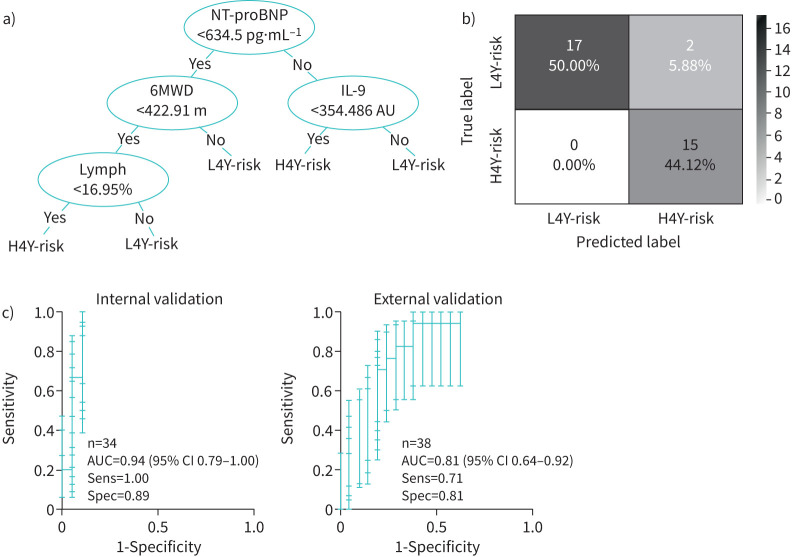
FIGURE 3.

a) An example decision tree randomly chosen from the 10 000 trees trained in the random forest model. b) Confusion matrix showing the accuracy of the random forest model at predicting mortality in internal validation cohort. c) Receiver operating curves (with error bars for each pointwise sensitivity calculation found by sampling 1000 bootstrap replicas) for the internal and external validation cohorts. AUC: area under receiver operating curve; H4Y-risk: high 4-year risk of death or need for transplant; L4Y-risk: low 4-year risk of death.

For the internal validation cohort (figure 3b), the random forest model accurately predicted 15 out of 17 patients as high risk. The model's computed probability of 4-year all-cause mortality risk in the internal validation cohort produced an AUC of 0.94 (95% CI 0.79–1.00), with a sensitivity and specificity of the random forest model of 1.00 and 0.89, respectively (figure 3c). Pointwise confidence intervals on the sensitivity were computed using vertical averaging from 1000 sampled bootstrap replicas. For the external validation cohort, which used an estimate of the 6MWD and serum NT-proBNP measurements (supplementary material O2), the model revealed an AUC of 0.81 (95% CI 0.64–0.92) and sensitivity and specificity of 0.71 and 0.81, respectively (figure 3c).

Global and local interpretability of the random forest model

Given that the random forest model has 10 000 trained decision trees, it's not possible to intuitively understand what parameters are driving model prediction and how they influence the overall computed score, which is referred to as the “global model structure”. While there have been numerous methods proposed for evaluating global model structure (e.g. ranking feature importance [18]), our approach can also be applied to an individual patient (described in the next section).

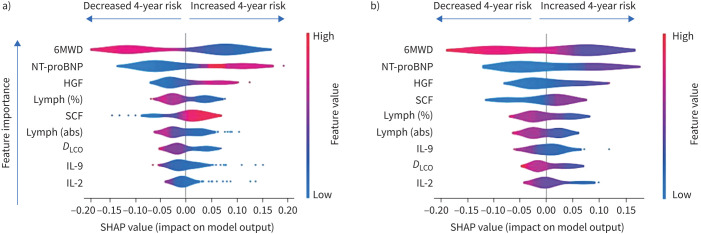
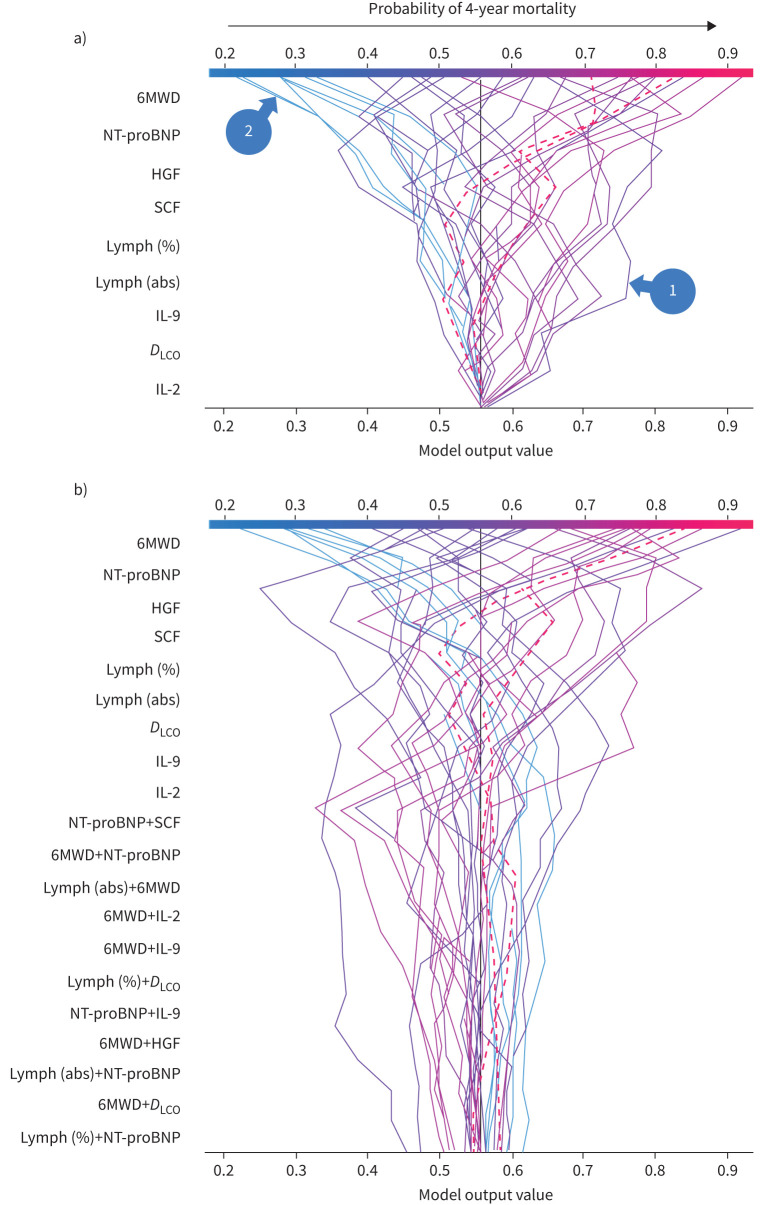
Figure 4 shows a violin summary plot of SHAP values for the training (figure 4a) and internal validation (figure 4b) datasets. The top three features are the same in both datasets, suggesting a consistent global model structure between the training and validation cohorts. The features listed are those identified as “most important” through RFE and ordered along the vertical axis based on global feature importance in the random forest model. A single dot represents a patient, and the width of the violin is representative of the number of patients that fall into that region. As an example, based on the limited case study presented here, the violin plots shown in figure 4 allows us to conclude that a high 6MWD can reduce the probability of death in 4 years by up to 20%, but the long tail towards positive SHAP values seen for IL-2 and IL-9 would suggest that, even though they are at the bottom of the global importance plot, these cytokine levels could be extremely important for certain individuals.

FIGURE 4.

Global and local model interpretability: summary violin plot of SHAP values using a) the training dataset and b) the internal validation dataset. 6MWD: 6-min walk distance; NT-proBNP: N-terminal pro-brain natriuretic peptide; HGF: hepatocyte growth factor; lymph: lymphocytes; SCF: stem cell factor; abs: absolute; D_LCO: diffusing capacity of the lung for carbon monoxide; IL: interleukin.

Local interpretability of the trained random forest model for a specific patient

When asking a trained random forest model to make a risk prediction for a new incoming patient, the algorithm runs that new patient's data through the 10 000 trees that were generated during the training process. Each tree classifies the patient as high or low risk, and the algorithm then takes a majority vote to make its prognosis. The numerical divide of how each tree voted also offers an estimate of probability, although a calibration plot showed that, for the case study dataset considered here, the model probability values were overly conservative and unresponsive to Platt's scaling [19], probably due to a small validation cohort. Therefore, if a clinician is interested in knowing how each patient measurement contributed to the risk score, it is not possible for a human to make sense of this prediction from 10 000 decision trees.

Figure 5a shows decision plots for the internal validation cohort with dashed lines representing the two patients who were incorrectly predicted to have a high 4-year risk of mortality (note that the feature order is identical to figure 4b). The vertical axis lists the features in order of importance for that specific cohort of patients, so the order might be different if some patients were removed or if only one patient was being considered.

FIGURE 5.

Decision plot of for the 34 patients withheld for (internal) validation. Each line corresponds to a given patient, and hidden lines correspond to the two misclassified patients. Plots a) with and b) without interactions. 6MWD: 6-min walk distance; NT-proBNP: N-terminal pro-brain natriuretic peptide; HGF: hepatocyte growth factor; SCF: stem cell factor; lymph: lymphocytes; abs: absolute; IL: interleukin; D_LCO: diffusing capacity of the lung for carbon monoxide.

Decision plots are used to show how a model (for any individual patient or for combined patients) reaches the predicted 4-year risk score. All decision tree lines start at the same point (at a risk score of 0.55 in figure 5a) along the bottom horizontal axis, which represents the baseline predicted score before any of the features were considered. The SHAP values (i.e. the change in the score in response to a specific feature) accumulate from the base value to arrive at the random forest model's final score on the top horizontal axis.

Case example 1

In figure 5a, we focus on two random patients, indicated by arrows. Both patients had relatively normal 6MWD and NT-proBNP and, therefore, based on the current approach to risk stratification, might be expected to harbour similar risk profiles. However, patient 1 had abnormally low IL-2 and IL-9 levels based on comparisons in Sweatt et al. [7] (figure 2), which in spite of normal exercise tolerance and markers of heart failure, put them firmly in the high-risk group. Alternatively, all nine metrics for patient 2 were in the normal range, thus resulting in assignment to the low-risk group.

Figure 5b shows a decision tree for the internal validation cohort that considers the cumulative effect of first-order interactions between the features. Here we see that interactions can certainly drive the final risk score for some patients, but are all ranked as the “least important” features for the model output when the entire internal validation cohort is considered. For this reason, and because considering interactions significantly complicate the interpretability of the final model, we omit them for single-patient analysis in figure 6.

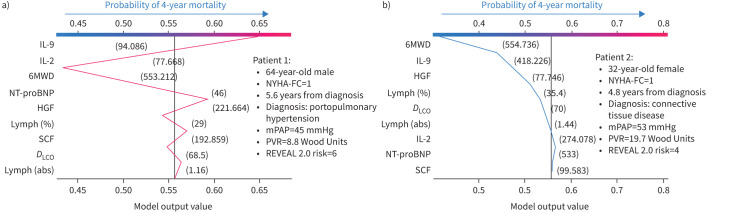
FIGURE 6.

Decision plots for two randomly selected patients show a graphical example of how a clinician can interpret the model prediction for a specific patient. The plot also shows that features ranked for an individual prediction can be notably different than the global model structure. IL: interleukin; 6MWD: 6-min walk distance; NT-proBNP: N-terminal pro-brain natriuretic peptide; HGF: hepatocyte growth factor; lymph: lymphocytes; SCF: stem cell factor; D_LCO: diffusing capacity of the lung for carbon monoxide; abs: absolute; NYHA-FC: New York Heart Association functional class; mPAP: mean pulmonary arterial pressure; PVR: pulmonary vascular resistance.

Case example 2

Figure 6a and b shows decision plots for two randomly selected patients from the internal validation cohort. Here we see that both patients were assigned a New York Heart Association functional class (NYHA-FC) of 1 with a similar REVEAL 2.0 risk score, but patient 1 had a mortality event within 4 years of study enrolment. The random forest model trained in this case study accurately predicted patient 1 to be in the high-risk group, driven primarily by circulating levels of IL-2 and IL-9, despite low-risk 6MWD and NT-proBNP. The profile for patient 2 included all nine markers within the low-risk range, corresponding to correct assignment to the low-risk group.

Discussion

Prior reports using trained machine learning models (e.g. random forest models) in PAH have been effective for identifying biomarkers that contribute to risk estimation across patient cohorts [20–22]. However, these algorithms produce a single classification or score when asked to make a prediction for a specific patient, so the clinician might be hesitant to make treatment decisions based on “black box” predictions. Therefore, if the clinician can interact with the algorithm and ranking of the parameters in the final decision is graphically presented (using decision plots), that clinician would be better suited to generate a treatment strategy based on the algorithm's assessment or possibly overrule the algorithm based on their own clinical intuition.

In this paper, we use a case study to introduce a platform that generates a graphical explanation of the random forest model's prognosis for an individual PAH patient (a step towards personalised medicine). Because the cohort available for our case study had a limited number of patients for model training, we utilised RFE to reduce the 93 available patient measurements to nine. We then showed in two validation cohorts that our random forest model's accuracy was comparable to the REVEAL 2.0 calculator (an expanded discussion on comparing against the REVEAL 2.0 calculator is available in supplementary material O3).

Global interpretability studies showed that the general structure of the trained random forest model heavily skewed towards known prognostic markers of PAH (e.g. exercise tolerance and heart failure). However, the violin plots for most of the circulating inflammatory markers in figure 4 had long tails, suggesting that they could also be a major driver of the prognostic score for some patients. This is confirmed by decision plots for the entire internal validation cohort (figure 5), which showed that, consistent with multiple prior studies [10, 11, 23, 24], inflammatory markers and their occasional interaction with other metrics can heavily influence the prognosis. This is also seen when looking at individual decision plots from randomly selected patients in figure 6. As an example, patient 1 was placed in a low-risk category based on NYHA-FC and REVEAL 2.0 score, which don't consider biomarkers of inflammation. However, the random forest model (trained with circulating markers of inflammation) correctly classified this patient as high risk and the decision plot shows that it was the decreased levels of circulating cytokines that drove that prognosis. Interestingly, both IL-2 and many other inflammatory cytokines are known to be upregulated in PAH patients, relative to controls [7, 25–27], but are reduced in PAH patients with poor survival. This would suggest that the presence of these markers could be protective and that the time course of cytokine levels is itself prognostic, but this would need to be explored in future studies.

A major limitation of the current study was the relatively modest cohort available for model training and (internal and external) validation. This also prevented us from evaluating whether our model was sufficiently calibrated, because calibration curves require a large number of samples [28]. Future studies will re-evaluate our results in a larger cohort, but here we focused on showcasing the computational pipeline for doctor–algorithm interaction.

The external validation utilised in our study offers both a strength and a weakness. Even though 6MWD was estimated from modified shuttle-walk test distance and NT-proBNP was measured in serum, we were encouraged to find that the model still performed reasonably well. However, this inconsistency required us to focus on an internal validation dataset within the main manuscript, which can suffer from the same confounding biases as the training cohort and present an overinflated view of model performance.

Conclusion

In this study, we present a novel computational pipeline for clinician–algorithm interaction in PAH risk assessment using a case study of prospectively analysed patients. This approach can be expanded to consider hundreds and even thousands of patient measurements, thus introducing a critical step towards implementing big data and artificial intelligence into clinical decision-making and entering the era of personalised medicine.

Supplementary material

Please note: supplementary material is not edited by the Editorial Office, and is uploaded as it has been supplied by the author.

Supplementary material 00484-2022.SUPPLEMENT ^{(825.2KB, pdf)}