Abstract
Neuromorphic computing is expected to achieve human-brain performance by reproducing the structure of biological neural systems. However, previous neuromorphic designs based on synapse devices are all unsatisfying for their hardwired network structure and limited connection density, far from their biological counterpart, which has high connection density and the ability of meta-learning. Here, we propose a neural network based on magnon scattering modulated by an omnidirectional mobile hopfion in antiferromagnets. The states of neurons are encoded in the frequency distribution of magnons, and the connections between them are related to the frequency dependence of magnon scattering. Last, by controlling the hopfion’s state, we can modulate hyperparameters in our network and realize the first meta-learning device that is verified to be well functioning. It not only breaks the connection density bottleneck but also provides a guideline for future designs of neuromorphic devices.
A learn-to-learn physical neural network is constructed on the scattering phenomenon between magnons and 3D magnetic texture.
INTRODUCTION
Topological solitons have been extensively studied in field theory (1, 2). It was not until recently that their magnetic versions showed great potential for future electronic devices (3–8). Magnetic solitons are robust due to their topological nature and are easy to manipulate using various techniques based on fields, currents, photons, etc. (9–12). One of the successful examples is skyrmions. Observed in a vast diversity of magnetic materials, they have been developed into devices and circuits for a range of applications operating even at room temperature (13, 14).
Among the applications of magnetic solitons, nonconventional computing attracts us the most for being unexplored in traditional electronics, especially neuromorphic computing (15–18). Various synaptic devices based on magnetic solitons are proposed as the building blocks for neural networks, and most of them are designed in the light of the leaky-integrate-fire model. In some of those proposals, the position of the domain wall or the size of the skyrmion plays the role of the electric potential in a neuron (16, 17). The domain or the skyrmion is expanded in the presence of an input current or shrinks to its original size as a result of a certain energy descent when the current is withdrawn. In another design, skyrmions function as neurotransmitters, which would trigger a spiking signal once their concentration in the detecting area has reached a certain level (18).
However, these practices are confronted with an emergent requirement called meta-learning. In addition to modulating weights and biases in a neural network, meta-learning requires taking the network structure or other metadata under training as well. It reduces manual labor in model training, helps us escape the overfit trap, improves training efficiency, and, lastly, makes machine learning more available in various real-life scenarios (19–23). Despite all these advantages, this requirement would be difficult to realize at a hardware level without adding extra circuit complexity. During circuit design, a neural network is usually decomposed into the basic units that can be directly replaced by electronic devices. Under current practice, the basic unit is a synapse, and the network structure is implemented by physical connections between them. As a result, the network structure is hardwired, and it entails an additional controller to program these connections at a software level, forcing the circuit designer to choose between inflexibility and unnecessary complexity. Besides, since all the synaptic devices are inevitably distributed and manufactured in a plane, their connection density becomes so limited that it is almost impossible for the circuit to achieve performance as high as that of a human brain, in which neurons are densely connected.
To tackle the above problem, we introduce the concept of magnon scattering. It is based on a reflection on two customary ways of thinking prevailing in current practice. First, instead of concentrating on the implementation of synapses, we should pay more attention to seeking a physical process equivalent to neural network structure. Second, following this idea, instead of regarding magnetic solitons merely as signal carriers, we should develop their potential value for representing network structure. Here, we propose magnons as the signal carriers and their scattering by a magnetic soliton as the physical process for substituting the network structure. Since magnons are not exclusive particles like magnetic solitons, it is therefore possible to break the connection density bottleneck by building multiple channels of different frequencies in parallel. These advantages make them a more ideal carrier than magnetic solitons. The frequency spectrum of magnons will be used to encode multidimensional signals, and in this view, the magnon scattering can be seen as a nonlinear map between these signals, which implicitly has the structure of a neural network. To obtain an adjustable neural network, the scattering pattern should be easily modulated by controlling the state of the soliton.
The flexibility required by meta-learning is lastly settled by selecting hopfions as the kind of magnetic solitons responsible for causing the magnon scattering. Skyrmions are excluded because they cause relatively constant scattering results due to their simple spin configuration. Hopfions, instead, are fully qualified to satisfy our needs. Discovered in 1975 as a group of three-dimensional (3D) soliton solutions of the Skyrme-Faddeev model (24, 25), they have been demonstrated either theoretically or experimentally in several magnetic systems such as chiral magnets (26–29), frustrated magnets (30, 31), magnetic multilayers (32), and ferromagnets with high-order exchange interactions (33). As knot-shaped solitons, hopfions host such a rich variety of 3D configurations that even their topological classification becomes a complicated question. This complexity provides a scattering characteristic pathological enough to serve as a neural network. The most important point is that, as an anisotropic object in 3D space, a hopfion has all the degrees of freedom of a 3D rigid body, a set of state parameters that are simple but complete enough for modulating the neural network through the pathological scattering characteristic. However, up until now, the intricate dynamics of hopfions has not been fully explored (34–37). Recent research on hopfions driven by spin transfer torque has revealed the “exotic dynamics” of hopfions, including translation, rotation, and dilation (35). However, none of them has reached the level of omnidirectional motion in 3D or programmable velocity control for all degrees of freedom in 3D. The constrained motion of a hopfion places a restriction on the number of its state parameters, represses the “gene expression” of hopfions’ scattering properties and, therefore, should be settled before the meta-learning framework is constructed. Spin-wave polarization, an additional degree of freedom emerging from antiferromagnetism, is used to achieve omnidirectionality and to simplify the velocity control mechanism.
Here, we implement a meta-learning framework using magnon scattering modulated by the omnidirectional motion of a hopfion. The omnidirectional motion is realized on the basis of a first study into the hopfion-driving effect of spin-wave polarization in antiferromagnets. An empirical relationship is displayed geometrically between the velocity of the hopfion and the spin-wave polarization, and it results in a simple scheme where the velocity of a hopfion is encoded in two spin-wave sources. Four 3D trajectories of the hopfion are shown in ascending order of complexity to demonstrate the power of the encoding scheme. The frequency dependence of hopfions’ motion is also studied for the later use of the frequency spectrum of magnons. On the basis of all these preparatory investigations, the meta-learning framework is realized. Signals are carried by the frequency spectrum of magnons, and the neural network is built into the scattering process, which can be modulated by the position and altitude of the hopfion. The framework is applied to predicting periodic and chaotic signals, and the prediction turns out to be of high accuracy, indicating the well functionality of our approach.
RESULTS
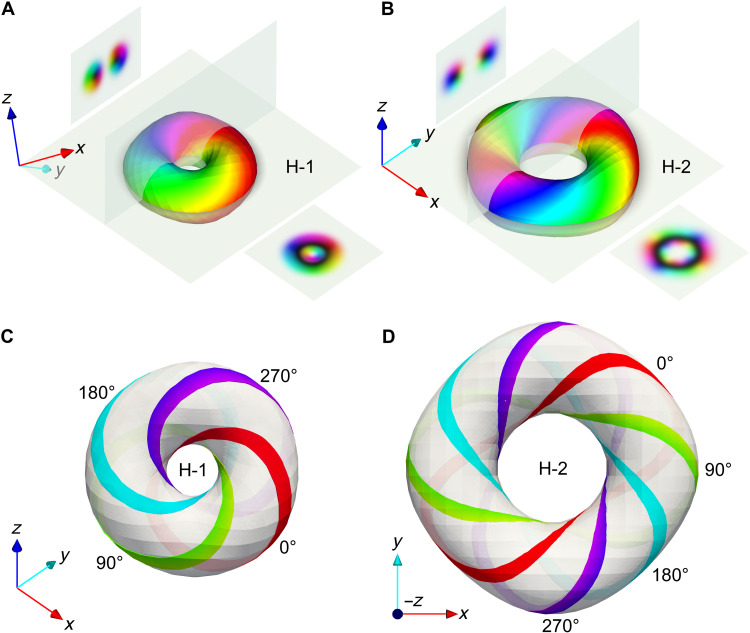
The existence and stability of hopfions in frustrated antiferromagnets can be derived from a general field theory model in the continuum limit (30, 38, 43, 44). The Hamiltonian is given in Methods, and the stable spin configurations of hopfions with the Hopf indices 1 (H-1) and 2 (H-2) are shown in Fig. 1. The spin configuration and the calculation of the Hopf index are given in the Supplementary Materials. From Fig. 1, we can see the difference in orientation between H-1 and H-2 hopfions, a phenomenon reported in (33). This is caused by the configuration of high-order exchange interaction, which is anisotropic and nonquadratic in our system.
Fig. 1. Spin configurations of hopfions in the lowest-energy state.
(A and B) Isosurfaces nz = 0 of (A) an H-1 hopfion and (B) an H-2 hopfion. The direction of the Neel field is represented by colors in the hue, saturation, and lightness (HSL) color space. The pale green planes are the xy and yz planes. The top left insets are the yz slices of the hopfions, and the bottom right insets are the xy slices of the hopfions. It can be seen from the axis orientation that the H-1 hopfion is oriented toward the direction, while the H-2 hopfion is oriented toward the [001] direction. (C and D) Preimages of the Neel vectors with xy angles of 0°, 90°, 180°, and 270° for (C) the H-1 hopfion and (D) the H-2 hopfion. The white torus represents the isosurface nz = 0.
Polarization dependence of hopfion dynamics
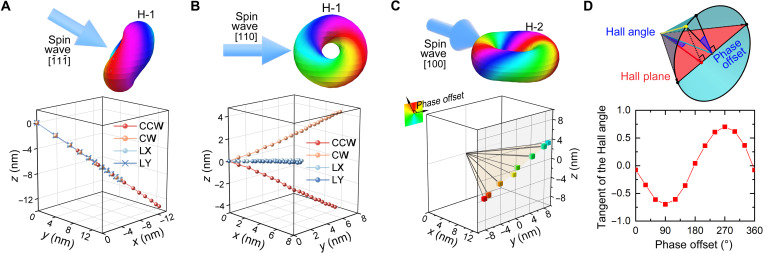
We start to search for treasure buried in hopfion dynamics that may help accomplish the goal of omnidirectional motion, and, lastly, spin-wave polarization, an additional degree of freedom emerging only in antiferromagnets, comes to our attention. Our major concern is to figure out the soliton-driving effect of spin-wave polarization. A spin wave needs two other parameters to specify: the incident direction and the frequency. These parameters should be carefully chosen so that the polarization dependence of a hopfion’s motion is both visible and enlightening. To find suitable values, micromagnetic simulations of hopfions’ motion are performed for spin waves incoming from two specific directions: one is parallel to the rotation axis of the hopfion and the other is perpendicular. Four kinds of polarization are selected as samples for the preliminary study: counterclockwise circular polarization (CCW-C), clockwise circular polarization (CW-C), linear polarization in the x direction (LX), and the y direction (LY). Linear combinations of these modes comprise all the first-order spin-wave modes. Higher-order spin waves, which cannot be decomposed into these four kinds of polarization, are not considered here. The hopfion under simulation is of configuration P = 1 and Q = 1 (and thus H = 1), and its rotation axis is in the direction due to the anisotropic exchange interaction (see Fig. 1A). The frequency of spin waves is set to 440 GHz.
The simulation results are shown in Fig. 2. When the spin waves are incoming along the rotation axis, that is, along the direction, the hopfion is pushed along the incident direction of the waves regardless of polarization (see Fig. 2A). The velocities for most kinds of polarization are the same except for CCW-C, in which case the velocity is about times as much as any of the other three. As we turn the incident direction from the rotation axis to that which is parallel to the torus plane, like [110] as we select, the polarization dependence of hopfions’ motion becomes obvious (see Fig. 2B). The trajectories under linearly polarized waves (L-waves) are still parallel to the incoming direction, while the two trajectories under circularly polarized waves (C-waves) begin to deviate from it and lastly become “a pair of wings” on its two sides. If we keep turning the incident direction around until it reaches the direction, the case will be similar to the initial one, except that the hopfion will move in the opposite direction and the CW-C wave will now be the most powerful one. In summary, when the incident direction of spin waves is along , the polarization dependence becomes sufficiently apparent, and the trajectory variation involves as many degrees of freedom as possible.
Fig. 2. Polarization dependence of hopfions’ motion.
(A) Trajectories of H-1 hopfions driven by spin waves with different kinds of polarization incoming along the direction. The spin waves are excited by a time-varying magnetic field of amplitude 2.0 T and a frequency of 440 GHz. (B) Trajectories of H-1 hopfions driven by spin waves with different kinds of polarization incoming along [110]. The spin waves are excited by a magnetic field of amplitude 5.0 T and a frequency of 440 GHz. (C) Displacements of H-2 hopfions driven by spin waves whose phase offset cycles were from 0° to 360° in a step of 30°. The phase offset for each point is represented by a color with a distinctive hue. The Hall plane is highlighted in pale yellow. The spin waves are propagating along [100]. The exciting magnetic field is the same as the one in (B). (D) Geometric picture of polarization dependence. The top shows the mapping from the phase offset to the Hall angle. The red plane denotes the Hall plane. The light cyan cone with its apex at the origin exhibits the area the imaginary displacement may pass through. The yellow vector with a yellow ending point represents the imaginary displacement given the azimuthal angle or, in other words, the phase offset. The actual displacement, represented by a red vector with a red ending point, turns out to be the projection of the imaginary displacement onto the Hall plane. The bottom shows the measured function between the phase offset and tanαHall, which is direct evidence for the picture shown in the top.
Before a further study is carried out, we need to quantify the concept of polarization. We focus on those spin waves that can be decomposed into LX and LY waves with the same amplitude and frequency. The polarization of the waves is then represented by the phase offset between these two components. For instance, CW-C and CCW-C are represented respectively by phase offsets of 90° and 270°.
A series of simulations are performed to explore the relationship between the phase offset of the incident waves and the velocity of the hopfion. To measure the position of the hopfion easily, the simulations are performed for H-2 hopfions instead of the H-1 hopfions used previously. The rotation axis of an H-2 hopfion is aligned to the z axis, and its torus plane is parallel to the xy plane (see Fig. 1B). As a result, the incident waves can be emitted from one side of the magnet and propagate along the x axis, one of the major propagating directions of spin waves, if the incident direction is required to be parallel to the torus plane of the hopfion.
As the phase offset evolves in cycles, the trajectory of the hopfion along with its end point swings up and down like a pendulum on a certain plane (the orange plane in Fig. 2C). To facilitate an easily accessible discussion, we call this plane the Hall plane and define the effective Hall angle as the angle between the moving direction of the hopfion and the incoming direction of the spin wave (see the top of Fig. 2D). It can be seen from Fig. 2C that all the displacements share the same x component, indicating that the longitudinal velocity of the hopfion is constant while the transverse velocity varies with the polarization.
The geometric picture given in the top of Fig. 2D may be useful to deepen our understanding. Imagine a cone with its apex at the initial position of the hopfion and its axis along the incident direction of the spin wave (the cyan cone in the top of Fig. 2D). The two C-wave–driven trajectories of the hopfions are designated as generating lines of the cone, and therefore, their angle is the aperture of the cone. In this picture, the Hall plane is the conic section crossing these two generating lines, and the Hall angle of a trajectory is the angle between this trajectory and the cone’s axis. In this way, the Hall angle must be smaller than half of the aperture, and it reaches its maximum when the incident wave is circularly polarized.
To elucidate the geometric meaning of the phase offset, a polar coordinate system is defined on the cone’s base. The polar axis is the diameter perpendicular to the Hall plane so that the final positions of the hopfions driven by CW-C and CCW-C waves have polar angles of 90° and 270°, respectively. The trajectory of the hopfion can be treated as the projection of a generating line onto the Hall plane, and the corresponding displacement (the red vector in the top of Fig. 2D) as the projection of the vector covered by the generating line (we name it the “imaginary” displacement and represent it by the yellow vector in the top of Fig. 2D). We find that the azimuthal angle of the imaginary displacement (where the north pole is the positive direction of the x axis) is exactly the phase offset leading to the actual displacement. More formally, if a spin-wave source has the complex form
| (1) |
then the Hall angle αHall is dependent on the phase offset in the following way, which is confirmed by the diagram shown in Fig. 2D
| (2) |
where is the Hall angle for C-waves. A more general case is considered where the spin waves have the complex form
| (3) |
In this case, the Hall angle will be scaled down as
| (4) |
while the transverse velocity is kept independent of θ. It turns out that Eqs. 1 and 2 are a special case of Eqs. 3 and 4, where θ = 0. As we will see in a later discussion on magnon scattering, the oscillation of the hopfion’s trajectory in the Hall plane results from the competition between magnons with opposite polarizations being scattered toward different directions. In a detailed derivation presented in the Supplementary Materials, antiferromagnetic spin waves are decomposed into two kinds of circularly polarized magnons that drive the hopfion toward opposite sides of a plane. The phase offset is found to describe the relative amplitude between these two components and therefore becomes a bridge between the spin-wave polarization and the hopfion’s moving direction. This treatment can explain the oscillation perfectly and is used to provide a solution for omnidirectional motion. The relationship expressed in Eq. 2 will radically simplify the programming procedure of a trajectory arbitrarily given for the hopfion to move along.
Omnidirectional motion in 3D space
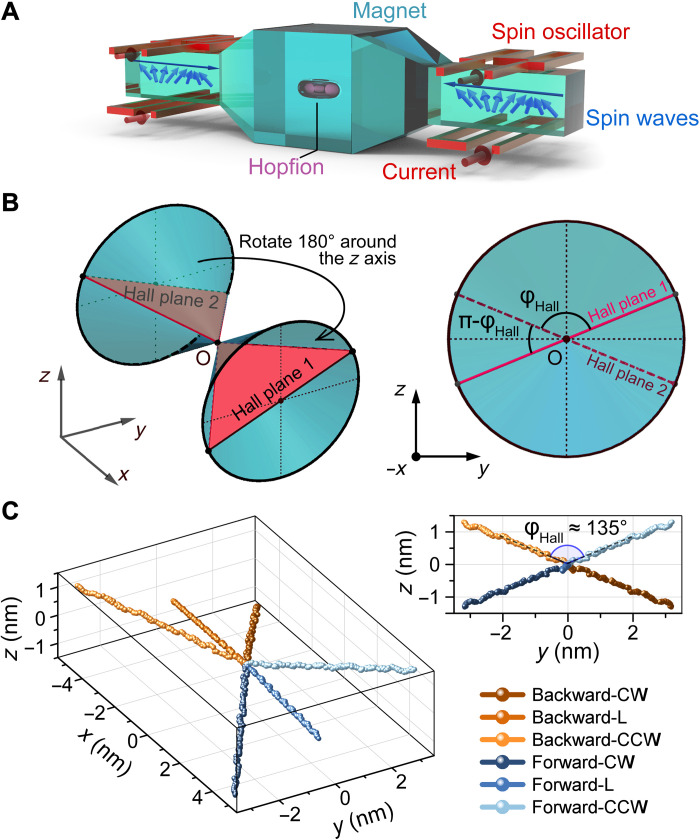
Next, we are going to achieve the motion of a hopfion with unconstrained degrees of freedom step by step. Simply speaking, this is achieved by a compound motion driven by two independent spin-wave beams. Spin-wave sources are put on both sides of the hopfion so that the spin waves emanating from the two sides can propagate face to face along the x axis (see Fig. 3A). The two non-coplanar Hall planes corresponding to these two spin-wave sources are used to span a 3D space (see Fig. 3B). These two planes form a plane angle of 135° at a frequency of 440 GHz (see Fig. 3C), enabling us to move the hopfion in any direction in 3D space.
Fig. 3. Mechanism for realizing omnidirectional motion of a hopfion in the 3D space.
(A) Proposed experimental setup for omnidirectional motion. The cyan glass is the magnet, in the center of which a violet torus is embedded, representing the hopfion. The red wires are the antennae responsible for inducing exciting magnetic fields from currents. The two antennae above the magnet are used to excite LX waves, while the two below the magnet are used to excite LY waves. The four antennae are distributed on both sides of the magnet and constitute a pair of spin-wave sources. The spin waves are released using sub-terahertz spin oscillators (45–48). (B) Non-coplanar Hall planes of the two spin-wave sources. The cyan cones denote the cones of imaginary displacements. The red planes are the Hall planes. (C) Trajectories of hopfions driven by spin waves of different kinds of polarization emanating from each of the two spin-wave sources. These results confirm the prediction in (B).
We first achieve a spin-wave driving scheme permitting arbitrary motion in the xy plane by considering the parametric equations of a unit circle in 2D skew coordinates
| (5) |
where is the angle of two coordinate axes, and e1,2 is the basis of the coordinate system. The spin waves coming from the two sources are both in the form of Eq. 1. We set the amplitudes of the two sources to the same value so that their forces on the hopfion cancel out in the x direction. Note that the transverse forces exerted by the two sources form an angle of 135° ( = Hall) and constitute a basis of a skew coordinate system (see Fig. 4A). Using Eq. 5, the total force on the yz plane is decomposed into two components, which can be tuned separately by varying the polarization of each source. According to Eq. 2, where the transverse velocity under certain waves is shown to be proportional to the sine of the phase offset, the phase offsets of the two sources (1,2) can be set directly to the arguments of the two sine functions in Eq. 5 if we try to move the hopfion toward a certain azimuthal angle (ϕ)
| (6) |
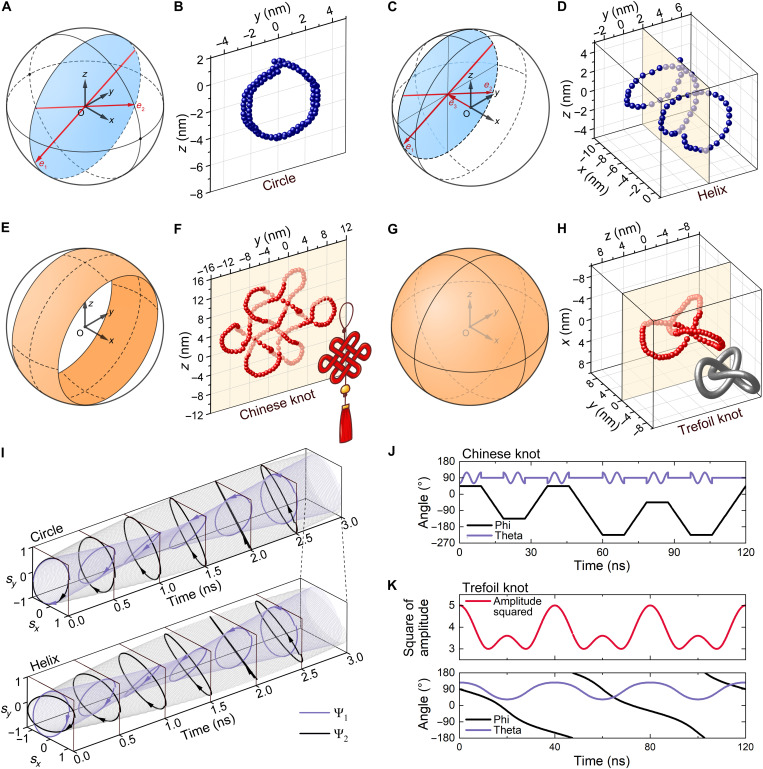
Fig. 4. Example trajectories of hopfions and their spin-wave configurations.
(A, C, E, and G) Direction range of velocity the hopfion covers during the motion, which is extended from a circle to the entire unit sphere. The red arrows in (A) and (C) denote the basis of the skew coordinate system. (B, D, F, and H) Complex trajectories that the hopfion moves along, including (B) a circle, (D) a helix, (F) a Chinese knot, and (H) a trefoil knot. These examples are organized in ascending order of complexity. (I) Waveforms of the incident waves applied in (B) (top) and (D) (bottom). Ψ2 in the two panels is the same, while Ψ1 in the bottom is an elongated version of Ψ1 in the top. (J) Direction of the instantaneous velocity for realizing the Chinese knot. (K) Instantaneous velocity for realizing the trefoil knot.
This allows us to program any planar trajectory with ease. Consider θ to be a linear function in time. We obtain a trajectory in the shape of a circle (see Fig. 4B and movie S1).
We expand our approach to a 3D situation. Realizing a helix-shaped trajectory might be the most intuitive approach to omnidirectional motion, for a velocity along any direction can be seen as a point on the unit sphere, and a vertical cross section of this sphere can be seen as the set of all the tangent vectors on a certain helix (see Fig. 4C). All we need is an extra tunable velocity in the longitudinal direction, which has been realized in Eqs. 3 and 4. A helix-shaped trajectory is thus achieved on the basis of the circle’s case (see Fig. 4D and movie S2): The first source (ψ1) is the same as the one in the circle’s case (Eq. 1), while the second (ψ2) is replaced by Eq. 3
| (7A) |
| (7B) |
Although the transverse forces coming from the two sources are both subject to the same limit, the total longitudinal force exerted on the hopfion is out of balance and provides a stable velocity along the x axis. A comparison between the spin-wave configurations for a circle and that of a helix is shown in Fig. 4I.
However, the formulae generalized from the helix trajectory are piecewise and have little connection with the commonly used representation of 3D vectors. They might be sufficient for a Chinese knot (see Fig. 4, E to F, and movie S3) but are incompetent for greater complexity. On these grounds, we construct a spin-wave configuration in the form of spherical coordinates, which we commonly use (see Fig. 4G). To move the hopfion toward the direction of azimuthal angle ϕ and polar angle θ with a velocity of A2 units, we set the spin-wave sources to
| (8A) |
| (8B) |
where θHall is an intrinsic scattering parameter subject to . At the frequency of 440 GHz, φHall = 135°, , θHall = 75.76°, and tan(θHall/2) = 0.7780.
The correctness of this configuration is based on the same principle underlying Eqs. 3 and 4 (see the Supplementary Materials for proof). Using the above equations, we achieve a trajectory in the shape of a trefoil knot (see Fig. 4H and movie S4). The geometric parameters of the trefoil knot as well as the Chinese knot are given in Fig. 4 (J to K), and the designated trajectories can be easily generated by substituting them into Eqs. 8A and 8B. This embodies the convenience and flexibility of the spin-wave configuration in Eqs. 8A and 8B and symbolizes that our objective of omnidirectional motion of a hopfion in 3D space has been accomplished successfully.
Frequency dependence of magnon scattering
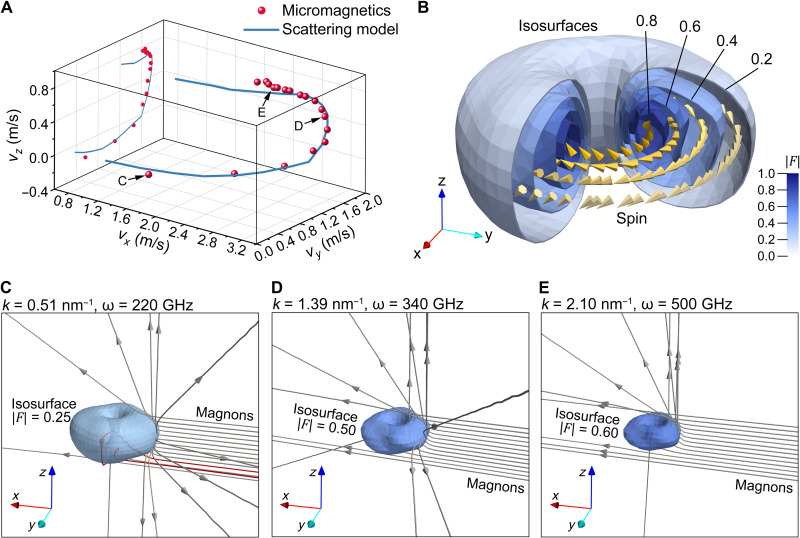
Before multidimensional signals are encoded in the frequency spectrum of magnons, it is necessary to study the frequency dependence of magnon scattering. Magnons are treated as wave packets so that they can be treated as classical particles in phase space with a position and a velocity. The mechanism hidden behind magnon scattering is verified by the hopfion dynamics it causes. We measure the displacement of a hopfion in magnon-driven micromagnetic simulations for frequencies from 240 to 560 GHz in a step of 20 GHz, extract the normalized velocity from the data (see the Supplementary Materials for more details), and plot them in Fig. 5A as red dots. In addition, a linear model of magnon scattering is developed in the Supplementary Materials, enabling us to calculate the magnon-driven velocity of a hopfion driven by polarized magnons. The velocity calculated from the model is shown in Fig. 5A as the blue curve. The results from the model and the simulation are consistent with each other, and both have shown the nonlinearity relationship between the frequency of the magnons and the velocity of the hopfion. It is also noteworthy that the frequency dependence implies the control of the Hall plane, another aspect besides the control of the Hall angle by polarization. The azimuthal angle of the Hall plane (/2) is a monotonically increasing function of the wave frequency, despite the function being quite nonlinear and hence less convenient for velocity control than polarization dependence.
Fig. 5. Frequency dependence of magnon scattering.
(A) Velocities of hopfions driven by CCW-C waves at different frequencies. The red points denote the values of the velocities obtained from micromagnetic simulation for frequencies from 220 to 560 GHz in a step of 20 GHz. The blue line is the velocity calculated from the magnon-hopfion interaction model. Both of them are projected onto the yz plane to show their relative position from the side view. (B) Emergent magnetic field F of a hopfion. The isosurfaces of ∣F∣ with values of 0.2, 0.4, 0.6, and 0.8 are exhibited in an increasing depth of blue. The direction of F on the equatorial plane in each shell is represented by a chain of yellow cones. (C to E) Paths of certain magnons in the real space for three specifically selected frequencies. The wave number k and the frequency ω are labeled at the top of each figure. The color depth of a isosurface indicates the magnitude of ∣F∣. The magnitude of the field F on these isosurfaces is no more than it is required to reflect all the magnons. The gray trajectories with arrows on them are the paths of magnons, which are scattered by the field. Some of them are painted red to distinguish themselves from their neighbors. The positions of these arrows are a snapshot of all the outgoing magnons at the same simulation time.
The frequency dependence can be qualitatively explained by the particle-like properties of spin-wave packets described by our model. It is found that the topography of the field F or, to be more specific, the shape and configuration of isosurfaces of ∣F∣ as Fig. 5B shows, plays an important role in determining the frequency dependence of magnon scattering. To expose the scattering process hidden behind the dependence, three frequencies (220, 340, and 500 GHz) are chosen from different parts of the band (see Fig. 5, C to E, and movies S5 to S7). For frequencies as low as 220 GHz (see Fig. 5C and movie S5), the incoming magnons are scattered strongly, some of which are even captured by the emergent magnetic field and experience a period of irregular motion before escape (the red tube in Fig. 5C). As the frequency increases to 340 GHz (see Fig. 5D and movie S6), the momentum of magnons increases, and as a result, the magnons can approach the core region of the hopfion more easily instead of being scattered by its outer region. The field F in the core region is different from that in the outer region in both magnitude and orientation: The field in the core region is stronger and is oriented moderately upward while that in the outer region is weaker and is oriented mostly downward (see Fig. 5B). As a result, the scattering in the core region causes a substantial momentum exchange in the positive direction of the z axis, explaining the upraising curve between 220 and 500 GHz. When the frequency finally enters the high band in which it becomes higher than 340 GHz (see Fig. 5E and movie S7), the magnons become so powerful that they can straightly pierce through the whole region. The scattering cross section begins to shrink and the velocity of the hopfion declines, especially in the x direction.
Another important point is that the scattering process is both dispersive and nonlinear thanks to the magnetic frustration in our system. The reflection caused by ∣F∣ isosurfaces changes the wave number of a magnon. This can be derived from the arrows in Fig. 5 (C to E), which indicate that magnons travel different distances in the same period of time. Without the magnetic frustration, the fictitious magnetic field would cause only deflection of the incident direction but not result in any kind of wave number change. Now that the scattering process is dispersive, there must be a multiple scattering phenomenon of magnons, whether it is strong or weak (the red trajectory in Fig. 5C shows a magnon scattered multiple times). This introduces another kind of nonlinearity into the system, which is necessary for constructing a neural network.
Neural network with meta-learning
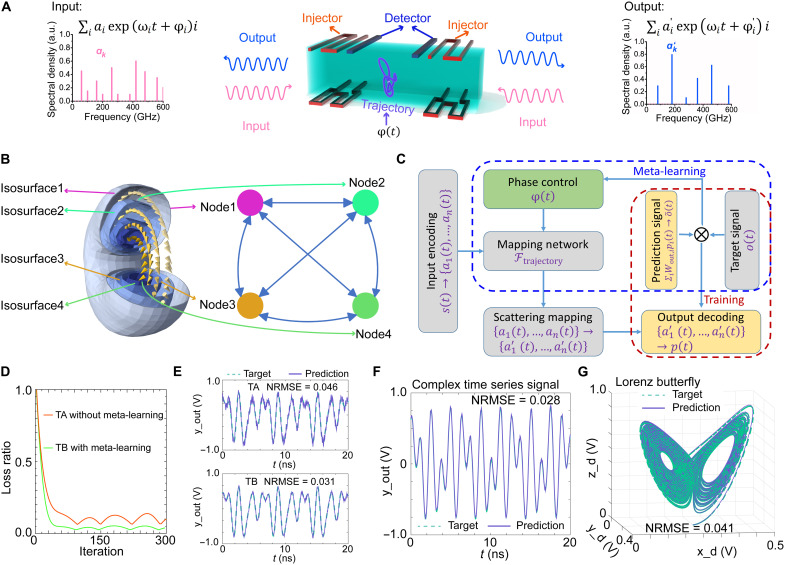
The scattering process of magnons by hopfion can be seen as the nonlinear mapping layer of a physical neural network. The input and output signals are stored respectively in the incoming and outgoing magnons. As shown in Fig. 6A, the input signal {a1, …, an} is encoded in the amplitudes of n discrete frequencies {ω1, …, ωn} carefully chosen from the whole spectrum. In this notation, an oscillating spin experiencing the incident spin waves can be expressed as , where ak and k are respectively the amplitude and phase of each frequency. Both {ak} and {k} vary relatively slowly compared to ωkt. When a magnon tries to cross the hopfion region, it is scattered by the fictitious magnetic field and has a probability of entering the detection area. The magnon detector can detect the scattering spectrum at a certain region so that the oscillating macrospin in this region can be described as . The output signal can be then extracted from it using the Fourier transformation. The nonlinearity of magnon scattering originates from the magnon interaction arising from the frustrated exchange as well as the multiple scattering phenomenon, leading to frequency interference. If the amplitude of each frequency is seen as a neuron in a neural network, the scattering process will function as the synaptic connections between these neurons (see Fig. 6B). To summarize the argument, the scattering process is appropriate for the role of signal mapping pertaining to a neural network.
Fig. 6. Meta-learning neural network based on magnon scattering by a hopfion.
(A) Schematic of the meta-learning neuromorphic device. The process of magnon scattering by the hopfion is used to implement the neural network. Carrying the input signal shown in the left frequency spectrum, magnons are injected into the device through the injector antenna. The scattered magnons are received at the detector antenna and are decoded to the right spectrum to obtain the output signal in arbitrary units (a.u.). (B) Correspondence between the neural network nodes and the isosurfaces of the hopfion. The amplitude of magnons of each frequency can be seen as a node in a neural network. The connections between nodes can be treated as the scattering spectrum of magnons. The connections starting from the same node can be seen as an isosurface of the hopfion. (C) Flowchart of the meta-learning framework. The blue dashed circle denotes the meta-learning step, and the red dashed circle denotes the linear regression step. (D) Normalized loss function (loss ratio) convergence curves for the test task. The red line represents the test without meta-learning. The green line represents the test with meta-learning. (E) Prediction result for the test task without and with the multitask training. Normalized root mean square error (NRMSE) is used to estimate the prediction accuracy. (F and G) Our device performs so well in complex time series tasks that the NRMSE reaches 0.028 for (F) the periodic signal and 0.041 for (G) the Lorenz-like chaotic time series.
Meta-learning requires the training of hyperparameters in a neural network, which here corresponds to the modulation of the scattering pattern (19, 49, 50). Note that the pattern is determined by the state parameters of the hopfion ω, i.e., the degrees of freedom related to the omnidirectional motion, in the way pointed out in the previous analysis of magnon scattering. The magnon scattering at a certain frequency mainly happens at the corresponding isosurface of the hopfion (see Fig. 6B), whose position and altitude vary simultaneously with those of the hopfion. According to our achievement of omnidirectional motion, these state parameters can be dynamically tuned by the polarizations of two spin-wave sources. Hence, the network can be trained by controlling the polarization of spin-wave sources. The training process can be visualized as the hopfion drawing a trajectory in the magnet until it eventually settles down at a specific position. In conclusion, a direct scattering problem is formulated to show how the state parameters of the hopfion determine the network mapping function. The remaining task is to solve the corresponding inverse scattering problem, which is accomplished in the Supplementary Materials using state space searching combined with numerical simulation.
The flowchart of a practical meta-learning framework is shown in Fig. 6C. Given an input signal s(t) and target signal o(t) (note that t here varies slowly with respect to the oscillating frequency of magnon), the framework will learn to build a temporally variant neural network to obtain a prediction signal in the following way. In the input layer of the physical neural network, st is encoded into the frequency spectrum of the incident waves {a1, …, an}. Then, it is mapped by the nonlinear scattering process to the spectrum of the scattered waves , which is decoded and transformed into a vector pt. The final prediction value is produced by the output layer through a linear transformation , where wout is the weights of the output layer. After the prediction value is compared with the standard signal, the back propagation is carried out with two levels of optimization. The two levels are represented in Fig. 6C by a red dashed circle and a blue dashed circle, respectively. The first level is to optimize wout with a fixed ω using linear regression. It aims to find the linear combination of pt closest to the target signal ot (39, 40). This level of optimization is analogous to regular training in a traditional neural network (48). The second is to train the hyperparameter ω as well as φi for meta-learning (19). In this level, the nonlinear mapping is adjusted by controlling the hopfion’s state through the phases of magnons. Once ω is selected, wout will be immediately optimized to produce the minimum prediction error, which is then used to estimate the performance of ω. In conclusion, the first level is used to estimate the performance of the meta-learning by matching the output values with the target signal, while the second level is used to search for the optimal mapping function, which can be observed as a specific trajectory of hopfion.
Our framework meets the requirements of meta-learning. Its meta-learning performance can be verified in multitask scenario (19). The training task family consists of four trigonometric signals, ; the neural network will learn the four tasks for meta-training. After that, we set a test task, , to test the learning capability of the meta-trained neural network. The learning results with and without meta-training by task family are compared and shown in Fig. 6 (D and E). To visualize the learning speed of the neural network, we plot the loss function convergence curves for the test tasks in Fig. 6D. The test noted as Task B (TB) (neural network with meta-training) takes less time for the loss function to decline than Task A (TA) (neural network without meta-learning), indicating that our neural network has been adjusted to a state more suitable for trigonometric signal prediction after learning similar tasks. To characterize the prediction accuracy, the normalized root mean square error (NRMSE) is used as a metric. From Fig. 6E, we can see that the prediction accuracy of the test task is improved as well, indicating that the experience of learning task family can help improve the prediction accuracy in the test task. As a summary, both the learning speed and the prediction accuracy become higher after meta-training by multitasks, demonstrating the meta-learning performance in multitask scenario. The performance of our network is also estimated for complex learning tasks. The results of numerical experiments show that the hopfion-based meta-learning network has a strong learning capability when using meta-learning (19, 49, 50). It can be seen from Fig. 6 (F and G) that the accuracy reaches a high level not only for a periodic scalar signal but even a chaotic vectorial signal, which is regarded as a touchstone for neural networks. Our device successfully eliminates the complex physical links between nodes in traditional neural network implementation, allowing us to create a high-density neural network with meta-learning.
DISCUSSION
Here, we first study the polarization-dependent motion of a hopfion and the frequency-dependent scattering of magnons by a hopfion. We unveil the hopfion-driving effect of spin-wave polarization by associating it with the Hall angle of the hopfion. The relationship is so simple that it enables efficient programming of a hopfion’s trajectory. In light of this, we devised a way to achieve omnidirectional motion in 3D space. A series of trajectories are constructed step by step in ascending order of complexity: first, a circle with its tangent velocity limited in a coordinate plane; second, a helix with an extra velocity perpendicular to that plane; third, a Chinese knot as a natural extension to the helix; and lastly, a trefoil knot involving omnidirectional motion. We further propose a linear model for predicting magnon-driven velocities for different solitons, and it has been confirmed by the frequency dependence of the hopfion’s motion. Under the eikonal approximation, spin waves are dealt with as particles moving in the emergent magnetic field, and the motion of a soliton is understood as a phenomenon of momentum exchange between these particles and the soliton. Our model highlights the wave-particle duality of spin waves and can explain the results of frequency dependence well.
On the basis of these mechanisms, we propose a method for neuromorphic computing using the omnidirectional motion of a hopfion and nonlinear magnon-hopfion scattering. The states of neuron nodes in the neural network, including the input signals, are encoded into the frequency distribution of magnons, and the connections between these neurons are built into the scattering of magnons. The frequency distribution has intrinsically infinite degrees of freedom, permitting a high connection density. The nonlinearity of the scattering process meets the requirements of neuromorphic computing. The meta-learning is realized by using the 3D omnidirectional motion of the hopfion. During the network training, the position of the hopfion is tuned to generate the proper scattering pattern, which results in the optimal network hyperparameters. In this way, our design circumvents the problems in the way of conventional neuromorphic devices, such as the connection density bottleneck and hardwired neural network structure. The whole neural network is now implemented with a single device instead of an array of elementary units. As the device is scaled down greatly, the power consumption is reduced to a large extent as well.
Last, the structures of hopfions are reminiscent of proteins or DNA in structural biology. Hopfions have knot-like structures, and it can be very complicated for them to consist of more than one loop. Their knot-like structure reminds us of peptides in a protein or DNA for their topological equivalence to intertwining strings. The exchange interaction can be used to glue spins from different parts of a hopfion together, playing the same role as hydrogen bonds play in forming the secondary structure of a biomacromolecule. In some situations, the magnetic interaction becomes as strong as the bonds of amino acid side chains in a protein, on which a complex 3D shape or, in terms of structural biology, “tertiary structure” is built. It has been confirmed decades ago that the functional diversity of proteins is closely connected with their structural complexity, implying a great potential of hopfions in achieving complex logic operations. Our work on precise manipulation of hopfions is the first step to fulfilling this potential, and it opens the door to the possibility of biological-like information processing in the future.
METHODS
Micromagnetic simulation
We use MuMax3 (41) for micromagnetic simulation. MuMax3 is built on the finite-difference method for solving the Landau-Lifshitz-Gilbert equation. To simulate a frustrated antiferromagnets, the energy functional is
| (9) |
where M is the magnetization of either sublattice, m is the unit vector of the net magnetization, χ is the magnetic susceptibility, and n is the Neel field or the staggered magnetization. In general, , where J is the spin density of either sublattice. The material parameters A, B, and Kz are the second-order exchange stiffness, the fourth-order exchange stiffness, and the anisotropy energy, respectively. These parameters are configured as follows: A = 1 × 10−14 J · m−1, Kz = 1 × 104 J · m3, and Bμν is a scalar with the value of 3.1 × 10−32 J · m. The high-order exchange interaction is discretized and added as a custom-effective field. For a scalar Bμν, the custom field in the grid point i looks like
| (10) |
where mi(j) stands for the unit vector of spin at cell i(j), and denotes the set of the kth nearest neighbors of i. The source code, which is originally published in (42), is shown in the Supplementary Materials with detailed comments.
Measurement of the displacement of a hopfion
The displacement of hopfions is measured by applying the phase correlation algorithm to the z component of magnetization. The rotation angle of hopfions, thanks to the rotational symmetry of torus-like hopfions, can be simply extracted from the change in the azimuthal angle of spin, where the north pole is defined as the positive direction of the z axis.
Acknowledgments
Funding: We would like to acknowledge the support of the National Natural Science Foundation of China (grant nos. 62122008, 61971024, and 51901008) and the International Mobility Project (grant no. B16001). M.K. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) projects 403502522 (SPP 2137 Skyrmionics) and 268565370 (SFB TRR173 projects A01 and B02) as well as TopDyn and the Horizon 2020 Framework Program of the European Commission under project ERC-2019-SyG no. 856538 (3D MAGiC).
Author contributions: Y.Z. planned and supervised the project. Z.Z. and K.L. performed the numerical simulations. Z.Z., K.L., A.B., and K.X. carried out the theoretical analysis. Z.Z., K.L., and Y.Z. wrote the manuscript. M.K. and W.Z. contributed to the proposed concept and helped with writing the manuscript. All authors discussed the results and commented on the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Sections S1 to S5
Figs. S1 to S10
References
Other Supplementary Material for this : manuscript includes the following:
Movies S1 to S7
REFERENCES AND NOTES
- 1.R. Friedberg, T. D. Lee, A. Sirlin, Gauge-field non-topological solitons in three space-dimensions (II). Nucl. Phys. B. 115, 32–47 (1976). [Google Scholar]
- 2.M. Rho, A. S. Goldhaber, G. E. Brown, Topological soliton bag model for baryons. Phys. Rev. Lett. 51, 747–750 (1983). [Google Scholar]
- 3.G. Finocchio, F. Büttner, R. Tomasello, M. Carpentieri, M. Kläui, Magnetic skyrmions: From fundamental to applications. J. Phys. D Appl. Phys. 49, 423001 (2016). [Google Scholar]
- 4.A. Fert, V. Cros, J. Sampaio, Skyrmions on the track. Nat. Nanotechnol. 8, 152–156 (2013). [DOI] [PubMed] [Google Scholar]
- 5.S. M. Mohseni, S. R. Sani, J. Persson, T. N. A. Nguyen, S. Chung, Y. E. Pogoryelov, P. K. Muduli, E. Iacocca, A. Eklund, R. K. Dumas, S. Bonetti, A. Deac, M. A. Hoefer, J. Åkerman, Spin torque–generated magnetic droplet solitons. Science. 339, 1295–1298 (2013). [DOI] [PubMed] [Google Scholar]
- 6.J. Zázvorka, F. Jakobs, D. Heinze, N. Keil, S. Kromin, S. Jaiswal, K. Litzius, G. Jakob, P. Virnau, D. Pinna, K. Everschor-Sitte, L. Rózsa, A. Donges, U. Nowak, M. Kläui, Thermal skyrmion diffusion used in a reshuffler device. Nat. Nanotechnol. 14, 658–661 (2019). [DOI] [PubMed] [Google Scholar]
- 7.Y. Zhou, M. Ezawa, A reversible conversion between a skyrmion and a domain-wall pair in a junction geometry. Nat. Commun. 5, 4652 (2014). [DOI] [PubMed] [Google Scholar]
- 8.X. Zhang, M. Ezawa, Y. Zhou, Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 5, 9400 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.M. A. P. Gonçalves, C. Escorihuela-Sayalero, P. Garca-Fernández, J. Junquera, J. Íñiguez, Theoretical guidelines to create and tune electric skyrmion bubbles. Sci. Adv. 5, eaau7023 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.N. Romming, A. Kubetzka, C. Hanneken, K. von Bergmann, R. Wiesendanger, Field-dependent size and shape of single magnetic skyrmions. Phys. Rev. Lett. 114, 177203 (2015). [DOI] [PubMed] [Google Scholar]
- 11.J. Iwasaki, M. Mochizuki, N. Nagaosa, Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 8, 742–747 (2013). [DOI] [PubMed] [Google Scholar]
- 12.M. Finazzi, M. Savoini, A. R. Khorsand, A. Tsukamoto, A. Itoh, L. Duo, A. Kirilyuk, T. Rasing, M. Ezawa, Laser-induced magnetic nanostructures with tunable topological properties. Phys. Rev. Lett. 110, 177205 (2013). [DOI] [PubMed] [Google Scholar]
- 13.O. Boulle, J. Vogel, H. Yang, S. Pizzini, D. de Souza Chaves, A. Locatelli, T. O. Menteş, A. Sala, L. D. Buda-Prejbeanu, O. Klein, M. Belmeguenai, Y. Roussigné, A. Stashkevich, S. M. Chérif, L. Aballe, M. Foerster, M. Chshiev, S. Auffret, I. M. Miron, G. Gaudin, Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotechnol. 11, 449–454 (2016). [DOI] [PubMed] [Google Scholar]
- 14.S. Woo, K. Litzius, B. Krüger, M.-Y. Im, L. Caretta, K. Richter, M. Mann, A. Krone, R. M. Reeve, M. Weigand, P. Agrawal, I. Lemesh, M.-A. Mawass, P. Fischer, M. Kläui, G. S. D. Beach, Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016). [DOI] [PubMed] [Google Scholar]
- 15.J. Grollier, D. Querlioz, K. Y. Camsari, K. Everschor-Sitte, S. Fukami, M. D. Stiles, Neuromorphic spintronics. Nat. Electron. 3, 360–370 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.K. Yue, Y. Liu, R. K. Lake, A. C. Parker, A brain-plausible neuromorphic on-the-fly learning system implemented with magnetic domain wall analog memristors. Sci. Adv. 5, eaau8170 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.S. Luo, N. Xu, Z. Guo, Y. Zhang, J. Hong, L. You, Voltage-controlled skyrmion memristor for energy-efficient synapse applications. IEEE Electron Device Lett. 40, 635–638 (2019). [Google Scholar]
- 18.K. M. Song, J. S. Jeong, B. Pan, X. Zhang, J. Xia, S. Cha, T. E. Park, K. Kim, S. Finizio, J. Raabe, J. Chang, Y. Zhou, W. Zhao, W. Kang, H. Ju, S. Woo, Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 3, 148–155 (2020). [Google Scholar]
- 19.T. Hospedales, A. Antoniou, P. Micaelli, A. Storkey, Meta-learning in neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 44, 5149–5169 (2022). [DOI] [PubMed] [Google Scholar]
- 20.R. Vilalta, Y. Drissi, A perspective view and survey of meta-learning. Artif. Intell. Rev. 18, 77–95 (2002). [Google Scholar]
- 21.K. Hsu, S. Levine, C. Finn, Unsupervised Learning via Meta-Learning; https://arxiv.org/abs/1810.02334 (2018).
- 22.A. Luedtke, M. Carone, N. Simon, O. Sofrygin, Learning to learn from data: Using deep adversarial learning to construct optimal statistical procedures. Sci. Adv. 6, eaaw2140 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.A. Rajeswaran, C. Finn, S. M. Kakade, S. Levine, Meta-learning with implicit gradients. Adv. Neural Inf. Process Syst. Title. 32, 97817 (2019). [Google Scholar]
- 24.V. E. E. Korepin, L. D. Faddeev, Quantization of solitons. Theor. Math. Phys. 25, 1039–1049 (1975). [Google Scholar]
- 25.L. D. Faddeev, Some comments on the many-dimensional solitons. Lett. Math. Phys. 1, 289–293 (1976). [Google Scholar]
- 26.J. S. Tai, I. I. Smalyukh, Static Hopf solitons and knotted emergent fields in solid-state noncentrosymmetric magnetic nanostructures. Phys. Rev. Lett. 121, 187201 (2018). [DOI] [PubMed] [Google Scholar]
- 27.J. S. B. Tai, P. J. Ackerman, I. I. Smalyukh, Topological transformations of Hopf solitons in chiral ferromagnets and liquid crystals. Proc. Natl. Acad. Sci. U.S.A. 115, 921–926 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.P. Sutcliffe, Hopfions in chiral magnets. J. Phys. A: Math. Theor. 51, 375401 (2018). [Google Scholar]
- 29.R. Voinescu, J. S. B. Tai, I. I. Smalyukh, Hopf solitons in helical and conical backgrounds of chiral magnetic solids. Phys. Rev. Lett. 125, 057201 (2020). [DOI] [PubMed] [Google Scholar]
- 30.I. L. Bogolubsky, Three-dimensional topological solitons in the lattice model of a magnet with competing interactions. Phys. Lett. A 126, 511–514 (1988). [Google Scholar]
- 31.P. Sutcliffe, Skyrmion knots in frustrated magnets. Phys. Rev. Lett. 118, 247203 (2017). [DOI] [PubMed] [Google Scholar]
- 32.N. Kent, N. Reynolds, D. Raftrey, I. T. G. Campbell, S. Virasawmy, S. Dhuey, R. V. Chopdekar, A. Hierro-Rodriguez, A. Sorrentino, E. Pereiro, S. Ferrer, F. Hellman, P. Sutcliffe, P. Fischer, Creation and observation of Hopfions in magnetic multilayer systems. Nat. Commun. 12, 1562 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.F. N. Rybakov, N. S. Kiselev, A. B. Borisov, L. Döring, C. Melcher, S. Blügel, Magnetic hopfions in solids. APL Mater. 10, 111113 (2022). [Google Scholar]
- 34.X. S. Wang, A. Qaiumzadeh, A. Brataas, Current-driven dynamics of magnetic hopfions. Phys. Rev. Lett. 123, 147203 (2019). [DOI] [PubMed] [Google Scholar]
- 35.Y. Liu, W. Hou, X. Han, J. Zang, Three-dimensional dynamics of a magnetic hopfion driven by spin transfer torque. Phys. Rev. Lett. 124, 127204 (2020). [DOI] [PubMed] [Google Scholar]
- 36.L. Bo, L. Ji, C. Hu, R. Zhao, Y. Li, J. Zhang, X. Zhang, Spin excitation spectrum of a magnetic hopfion. Appl. Phys. Lett. 119, 212408 (2021). [Google Scholar]
- 37.D. Raftrey, P. Fischer, Field-driven dynamics of magnetic Hopfions. Phys. Rev. Lett. 127, 257201 (2021). [DOI] [PubMed] [Google Scholar]
- 38.S. Grytsiuk, J.-P. Hanke, M. Hoffmann, J. Bouaziz, O. Gomonay, G. Bihlmayer, S. Lounis, Y. Mokrousov, S. Blügel, Topological-chiral magnetic interactions driven by emergent orbital magnetism. Nat. Commun. 11, 511 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.M. Lukoševičius, J. Herber, Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 3, 127–149 (2009). [Google Scholar]
- 40.J. C. Gartside, K. D. Stenning, A. Vanstone, H. H. Holder, D. M. Arroo, T. Dion, F. Caravelli, H. Kurebayashi, W. R. Branford, Reconfigurable training and reservoir computing in an artificial spin-vortex ice via spin-wave fingerprinting. Nat. Nanotechnol. 17, 460–469 (2022). [DOI] [PubMed] [Google Scholar]
- 41.A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez, B. V. Waeyenberge, The design and verification of MuMax3. AIP Adv. 4, 107133 (2014). [Google Scholar]
- 42.V. M. Kuchkin, K. Chichay, B. Barton-Singer, F. N. Rybakov, S. Blügel, B. J. Schroers, N. S. Kiselev, Geometry and symmetry in skyrmion dynamics. Phys. Rev. B 104, 165116 (2021). [Google Scholar]
- 43.T. Dombre, N. Read, Nonlinear σ models for triangular quantum antiferromagnets. Phys. Rev. B 39, 6797–6801 (1989). [DOI] [PubMed] [Google Scholar]
- 44.C. Naya, D. Schubring, M. Shifman, Z. Wang, Skyrmions and hopfions in three-dimensional frustrated magnets. Phys. Rev. B 106, 094434 (2022). [Google Scholar]
- 45.S. Wienholdt, D. Hinzke, U. Nowak, THz switching of antiferromagnets and ferrimagnets. Phys. Rev. Lett. 108, 247207 (2012). [DOI] [PubMed] [Google Scholar]
- 46.R. Cheng, D. Xiao, A. Brataas, Terahertz antiferromagnetic spin hall nano-oscillator. Phys. Rev. Lett. 116, 207603 (2016). [DOI] [PubMed] [Google Scholar]
- 47.J. Li, C. B. Wilson, R. Cheng, M. Lohmann, M. Kavand, W. Yuan, M. Aldosary, N. Agladze, P. Wei, M. S. Sherwin, J. Shi, Spin current from sub-terahertz-generated antiferromagnetic magnons. Nature 578, 70–74 (2020). [DOI] [PubMed] [Google Scholar]
- 48.G. Marcucci, D. Pierangeli, C. Conti, Theory of neuromorphic computing by waves: Machine learning by rogue waves, dispersive shocks, and solitons. Phys. Rev. Lett. 125, 093901 (2020). [DOI] [PubMed] [Google Scholar]
- 49.M. Andrychowicz, M. Denil, S. G. Colmenarejo, M. W. Hoffman, D. Pfau, T. Schaul, B. Shillingford, N. de Freitas, Learning to learn by gradient descent, in Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS’16), Barcelona, Spain, 5 to 10 December 2016, pp. 3988–3996. [Google Scholar]
- 50.C. Finn, P. Abbeel, S. Levine, Model-agnostic meta-learning for fast adaptation of deep networks, in Proceedings of the 34th International Conference on Machine Learning (ICML’17), Sydney, NSW, Australia, 6 to 11 August 2017, pp. 1126–1135. [Google Scholar]
- 51.S. H. Oh, S. K. Kim, K. J. Xiao, K. J. Lee, Bidirectional spin-wave-driven domain wall motion in ferrimagnets. Phys. Rev. B 100, 174403 (2019). [Google Scholar]
- 52.P. Shen, Y. Tserkovnyak, S. K. Kim, Driving a magnetized domain wall in an antiferromagnet by magnons. J. Appl. Phys. 127, 223905 (2020). [Google Scholar]
- 53.S. K. Kim, K. Nakata, D. Loss, Y. Tserkovnyak, Tunable magnonic thermal Hall effect in skyrmion crystal phases of ferrimagnets. Phys. Rev. Lett. 122, 057204 (2019). [DOI] [PubMed] [Google Scholar]
- 54.P. Yan, A. Kamra, Y. Cao, G. E. Bauer, Angular and linear momentum of excited ferromagnets. Phys. Rev. B 88, 144413 (2013). [Google Scholar]
- 55.S. K. Kim, Y. Tserkovnyak, O. Tchernyshyov, Propulsion of a domain wall in an antiferromagnet by magnons. Phys. Rev. B 90, 104406 (2014). [Google Scholar]
- 56.G. Tanaka, T. Yamane, J. B. Héroux, R. Nakane, N. Kanazawa, S. Takeda, H. Numata, D. Nakano, A. Hirose, Recent advances in physical reservoir computing: A review. Neural Netw. 115, 100–123 (2019). [DOI] [PubMed] [Google Scholar]
- 57.F. Zhou, W. Bin, Z. Li, Deep Meta-Learning: Learning to Learn in the Concept Space; https://arxiv.org/abs/1802.03596 (2018).
- 58.J. Gladikowski, M. Hellmund, Static solitons with non-zero Hopf number. Phys. Rev. D 56, 5194–5199 (1997). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Sections S1 to S5
Figs. S1 to S10
References
Movies S1 to S7