Abstract
Acoustic waves exert forces when they interact with matter. Shaping ultrasound fields precisely in 3D thus allows control over the force landscape and should permit particulates to fall into place to potentially form whole 3D objects in “one shot.” This is promising for rapid prototyping, most notably biofabrication, since conventional methods are typically slow and apply mechanical or chemical stress on biological cells. Here, we realize the generation of compact holographic ultrasound fields and demonstrate the one-step assembly of matter using acoustic forces. We combine multiple holographic fields that drive the contactless assembly of solid microparticles, hydrogel beads, and biological cells inside standard labware. The structures can be fixed via gelation of the surrounding medium. In contrast to previous work, this approach handles matter with positive acoustic contrast and does not require opposing waves, supporting surfaces or scaffolds. We envision promising applications of 3D holographic ultrasound fields in tissue engineering and additive manufacturing.
Ultrasound fields from multiple acoustic holograms permit the assembly of matter in arbitrary 3D shapes.
INTRODUCTION
One-shot fabrication of polymer structures has recently been proposed as a manufacturing concept, in which a whole three-dimensional (3D) object is formed in one shot (1). In this case, the object’s 3D shape has to be defined by a suitable intensity distribution of the generating light field, e.g., by a photo-initiated polymerization reaction. However, it is difficult to shape optical fields in a compact 3D volume at once using conventionally available devices and spatial light modulators. We refer to compact 3D fields as those that exhibit feature sizes over similar length scales in all three dimensions. For a projected image, the achievable lateral resolution scales with 1/NA and the axial resolution with 1/NA2, where NA is the numerical aperture (2). Thus, to create compact 3D holographic images, the optimal working distance should be about half the aperture diameter, so that NA ≈ 1. Such high numerical apertures are thus far only practicable for illuminating microscopic target volumes. Examples for optical computer-generated holography (CGH) at larger dimensions have correspondingly lower NAs, and the resulting images are stretched by several orders of magnitude in the beam propagation direction (3, 4), which limits their use for fabrication purposes of compact objects. Proposed solutions to this problem are thus far based on the nonlinear activation of a photoinitiator. One promising approach is the sequential illumination from varying angles into a rotating chamber to obtain projected tomography (5–7). In this case, it is necessary that the chemical cross-linker activates only when the accumulated light dose exceeds a certain threshold (7). Recently, this concept has been demonstrated to also work within lightly scattering media such as cell suspensions and using a cytocompatible photoinitiator (8). An alternative approach, called xolography (9), is based on two-photon excitation with different wavelengths and consequently allows separation into two beams: one illuminating a plane with a focused lightsheet and the second beam projecting the corresponding cross section of the object on that plane. Since both excitation wavelengths are necessary, the polymerization reaction is only initiated in one plane at a time. It stands to reason that both methods, however, still generate the 3D fields in a serial manner and not in a single step.
An alternate approach to light is to use sound fields that exert acoustic forces for assembly. This approach has the distinct advantage that the material of interest, such as particles or cells, is directly manipulated. Furthermore, the application of ultrasound at the intensities used here is cytocompatible and does not warrant the use of chemical additives such as photoinitiators. Acoustic particle assembly shows promise for rapid prototyping (10) and application in cell cultures (11) but has thus far been limited to 2D assembly close to boundaries (12, 13) or point-like tweezing in air (14, 15) and water environments (16, 17). These tweezing methods require phase discontinuities in the focal region, which complicates their extension toward extended traps. Alternatively, standing waves can be used to assemble cells in 2D into regular patterns (18, 19) or colloidal microparticles in 3D (20), but here, the patterns are generally highly symmetric. Prisbrey et al. (21) have examined the use of a closed cavity whose surface is fully lined by transducer elements to assemble particles in a fluid volume. They found solutions for a selection of 3D traps using the boundary element method. However, the geometric constraints imposed by opposing transducers and inevitable reflections in this closed environment limit the attainable shapes to mode geometries highly dependent on the container shape, i.e., cubic symmetries.
Here, we present a method to realize the first one-step 3D assembly of matter into arbitrary shapes using ultrasound by combining multiple acoustic holograms. In particular, we show that neither counterpropagating waves nor phase discontinuities are required to trap particles in 3D. Our method thus not only allows assembly into arbitrary 3D forms but also confers flexibility in the experimental setup as all acoustic sources can be placed on one side of the projected field. That leaves room for experimental intervention, i.e., the addition of sample material, the integration with other processes, and access for optical characterization and imaging. We demonstrate the practicability of our compact 3D fields by assembling different classes of matter—namely, solid particles, biological cells, and hydrogel beads—into 3D shapes in one shot.
RESULTS
Computation of compact 3D holographic fields
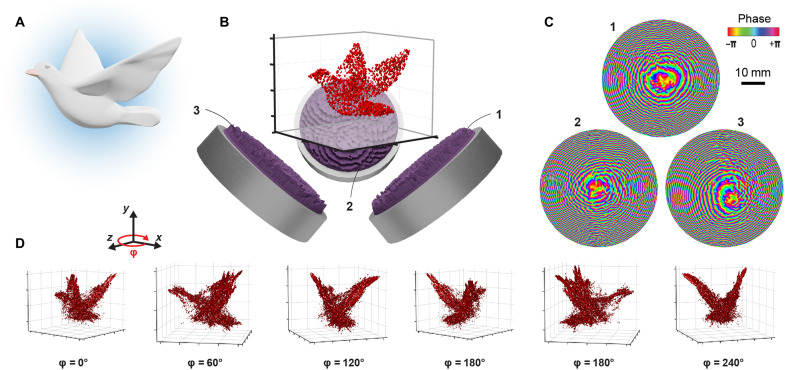
The wavelengths of waterborne ultrasound at megahertz frequencies are about three orders of magnitude larger than those of visible light. The experimental dimensions and aperture sizes that we use in practice, however, are of the same order. For this reason, the axial and radial resolutions scale favorably, and we achieve similar resolution in all three spatial directions. Superposition of concurrent fields from different angles leads to high-fidelity acoustic fields due to a wider range of accessible wave vectors (essentially a much larger numerical aperture). Figure 1 shows the general concept and workflow. The target object (Fig. 1A) is first converted and transferred to the computation volume (Fig. 1B). Depending on the problem at hand, the number and orientation of the holograms and transducers are chosen and placed relative to the target. In practice, we found orthogonal placement as the most convenient, because it is very space efficient and enables faster computation of the combined fields. See fig. S1 for renderings of two configurations. Then, we compute phase maps for all holograms using an optimization algorithm (Fig. 1C). In this exemplary simulation, three transducers with a frequency of 3.5 MHz and a diameter of 50 mm are used. Results for the generated 3D pressure fields in the shape of the target are shown in Fig. 1D, and more examples can be found in the Supplementary Materials (figs. S2 to S4). The pressure images in the shape of the 3D target will drive the assembly process.
Fig. 1. Concept to form compact acoustic 3D pressure images.
The target 3D shape (A) is scaled and converted into a voxel representation (B). The number of necessary holograms as well as their position and orientation relative to the target are chosen as part of the design process. Each hologram is placed on an ultrasound transducer that emits a plane wave at a fixed frequency. (C) Our CGH routine finds the optimal phase maps for each hologram. (D) Reconstruction of the ultrasound pressure amplitude emanating from the transducer-hologram sources (1, 2, and 3) and projecting into the 3D volume shows good results, displayed here as isosurfaces at 40% of the maximum pressure.
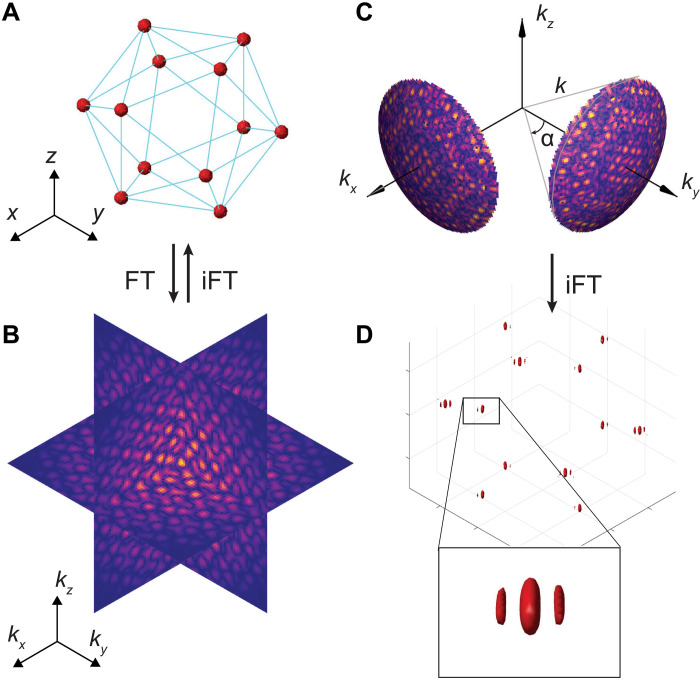
The synthesis of 3D fields forming a target volume or shape is challenging and an active research topic in CGH (4, 22). The goal of CGH is to find the spatial phase and amplitude distribution of an incident wavefront that will, upon diffraction, form the target image. The goal is achieved by optimizing the output acoustic field under the experimental constraints, such as the incident beam profile and wave shaping modalities. The latter indicates whether the amplitude or the phase (or both) can be controlled. CGH methods for 2D images are well advanced; however, accessing the third dimension poses the additional problem that often the optical or acoustic waves have to propagate across regions with highly varying intensities while energy conservation has to be preserved. Some desired 3D target images may thus not be physically realizable, only via a different geometry. As we show here, an effective way to quickly infer the feasibility of volumetric fields without having to undertake time-consuming volumetric wave propagation calculations is to analyze the 3D spatial frequency spectrum of the target object (23). Figure 2A shows an exemplary field of focal spots (regions where high intensity is desired) arranged so as to form the vertices of a regular icosahedron. Its 3D Fourier transform (FT) (Fig. 2B) corresponds essentially to a decomposition into plane waves, each represented by their wave vector k. Thus, for monochromatic illumination (insonification) with wavelength λ0, this spectrum has to be limited to the surface of a sphere, the Ewald sphere, whose radius is equal to the wave number ∣k∣ = k0 = 2π/λ0. However, sources of light or sound are restricted in space. The finite aperture of a real source thus further constrains the wave vectors to a cone of opening angle α, which is given by the dimensions of the source (Fig. 2C). Back transformation of this limited spectrum using the inverse FT (iFT) reveals one possible solution to the initial field. We call this approach the Fourier constraint method (FCM). Alternatively, solutions can be found by varying the complex phases of points in the spatial field, which then determines the hologram that is to be used in conjunction with the source. The same procedure can be extended to multiple transducers with their respective holograms in arbitrary (source) orientations and configurations. An example for the spectrum limited to two holograms along the x and y directions, respectively, can be seen in Fig. 2C. The iFT reveals the resulting field in Fig. 2D, where characteristic intensity (pressure) nodes around the foci are visible. Other configurations are shown in fig. S5.
Fig. 2. Field synthesis in Fourier space.
(A) Exemplary 3D arrangement of focal points at the vertex locations of an icosahedron and (B) its spatial frequency spectrum. (A) and (B) are linked via the (inverse) 3D FT, indicated by FT (or iFT). (C) The spectrum is limited to the Ewald surface of a monochromatic wave with wave number k = 2π/λ and two sources with limited aperture size (opening angle α). (D) The resulting field with a close-up view on a single spot.
Iterating through these steps to compute a hologram has been termed a 3D variant of the Gerchberg-Saxton (GS) algorithm in optical CGH (3, 24). However, this is not directly applicable in the case of ultrasound, which we will use for assembly. In ultrasound, the near field needs to be considered in contrast to the far field typically encountered in optics, where the source and target are related by a simple FT. Before source constraints can be applied, it becomes necessary to propagate the wave from the image to the hologram plane. This propagation is accomplished in a straightforward manner using the angular spectrum method applied to the limited spectrum, which is contained on the section of the Ewald surface with regard to the opening angle of the source. The FCM delivers very good results for fields that consist only of collections of focal points. However, one difficulty for it [and including GS and its derived iterative angular spectrum approach (12, 25)] is to achieve uniform amplitude over extended regions, which is particularly desirable for acoustic traps making up lines, surfaces, or volumes. To improve the homogeneity of amplitudes over extended traps, we therefore resorted to parallel computation of the volumetric field using the angular spectrum method combined with a gradient-based optimization procedure. Nonconvex optimization has been used previously in this context with pioneering work done by Zhang et al. (26). Similar in spirit, Marzo et al. (14) used gradient-based optimization to improve the stiffness of their traps. Further details can be found in Materials and Methods. In summary, our approach is suitable for holographic reconstruction in the acoustic near field and allows for arbitrary numbers of holograms at user-defined positions and orientations to generate complex 3D pressure patterns in space.
Directed 3D assembly of microparticles
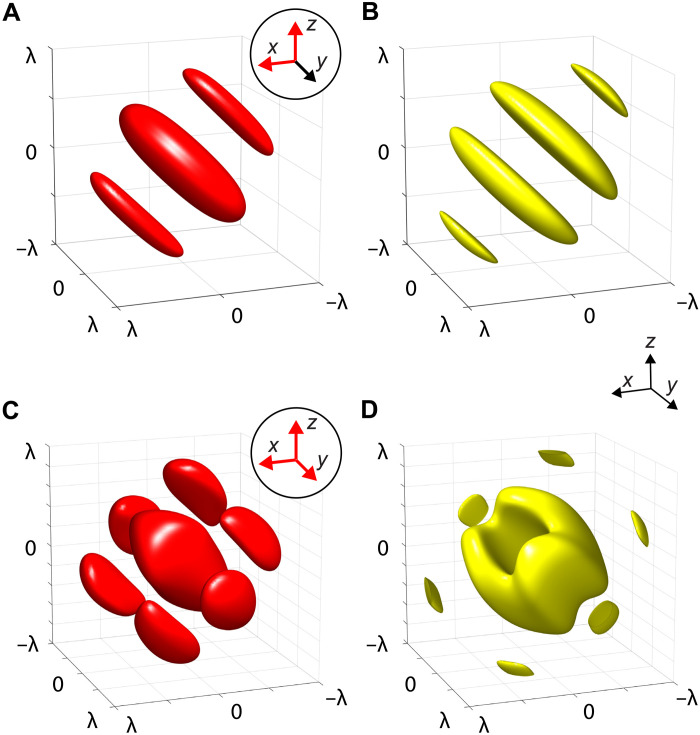
Structured acoustic fields have long been used to trap and assemble microparticles (27, 28). In this work, however, we use an overlooked configuration. Instead of counterpropagating (i.e., standing) waves or single-beam setups, we use the superimposed foci of multiple beams. This results in interference around the foci and allows tweezing of positive acoustic contrast particles at nodes between the high-amplitude interference fringes. In the following, we intend to illustrate the trapping with two exemplary configurations. A popular measure to gauge the attainable trapping potential in acoustics is the Gor’kov radiation potential because of its straightforward computation (see Materials and Methods) (29), which has been extended to complex structured fields (30) and arbitrarily shaped particles (31). Figure 3 visualizes two examples of superimposed beams: Two (Fig. 3A) or three (Fig. 3C) beams are focused to a point at the origin (0,0,0) coming from orthogonal directions corresponding to the axes highlighted in red in the insets. The Gor’kov potential is defined in such a way that particles experience a force toward the potential’s minima. Therefore, the opposite sign of the potential is displayed as isosurfaces in Fig. 3 (B and D). In this way, the closed surfaces resemble the approximate form of particle aggregates in a superimposed focal spot. The particles used in this work (e.g., silica gel) have positive acoustic contrast in water, which means that the minima of the Gor’kov potential coincide with the sound pressure nodes. It should be noted here that these traps do not constitute a single connected potential well that the particles fall into. Because of the interference patterns, the trapping regions span multiple pressure nodes in proximity to the focal points, leading to a striped appearance of the assembled structures. The spacing between stripes can consequently be reduced by using higher ultrasound frequencies.
Fig. 3. Particle-trapping potential around the mutual focal spot of multiple focused beams.
Beam directions are indicated by red arrows in the circular insets. (A) Normalized intensity distribution at the focus of two beams pointed in the X and Z directions (isosurfaces at 0.25 · max {I}) and (B) the particle-trapping sites indicated by the negative Gor’kov potential − (isosurfaces at −0.25 · min {}). (C and D) Intensity distribution (isosurfaces at 0.1 · max {I}) and negative Gor’kov potential (isosurfaces at −0.25 · min {}) for three focused beams in the X, Y, and Z directions. All dimensions are normalized by wavelength λ, and the potentials have been computed for a silica gel particle with radius ap = λ/10.
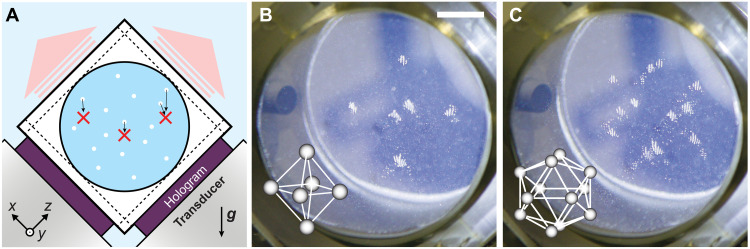
Trapping of solid particles in specified locations in 3D has been demonstrated by arranging trapping sites at vertices of the platonic bodies. In this experiment, two holograms were computed for two source beams intersecting at 90°, as shown in the schematic in Fig. 4A. A photo of this setup can be seen in fig. S6. A removable cubic container was filled with a suspension of porous silica gel spheres in water and placed so that it rested directly on the holograms. Its faces were covered with acoustically transparent windows and therefore allowed the ultrasound field to propagate through the container with minimal reflection. The holograms were computed so that an acoustic image forms at the center of the container. At the start of the experiment, the cube was shaken manually and then placed on the rig. The microparticles quickly sedimented under the influence of gravity; however, particles that traversed the trapping sites around each focal point were retained by the acoustic radiation force. Figure 4 (B and C) shows photographs of the final trapping state for an octahedron and an icosahedron, respectively. Movie S1 shows the assembly process in real time. The gallery containing all other platonic solids can be found in fig. S7. All trapping sites were successfully populated with particles in our experiments, and the trapped particle clusters appear visually as predicted in Fig. 3.
Fig. 4. Trapping of silica gel microspheres with ultrasound at specified points in 3D.
(A) Schematic of the experimental setup (2.25 MHz) using two holograms and a removable particle container. After initial resuspension by shaking, the particles (white dots) sediment under gravity g until they pass a trapping site (red cross). The trap locations represent vertices of platonic solids: (B) octahedron and (C) icosahedron. Scale bar, 10 mm.
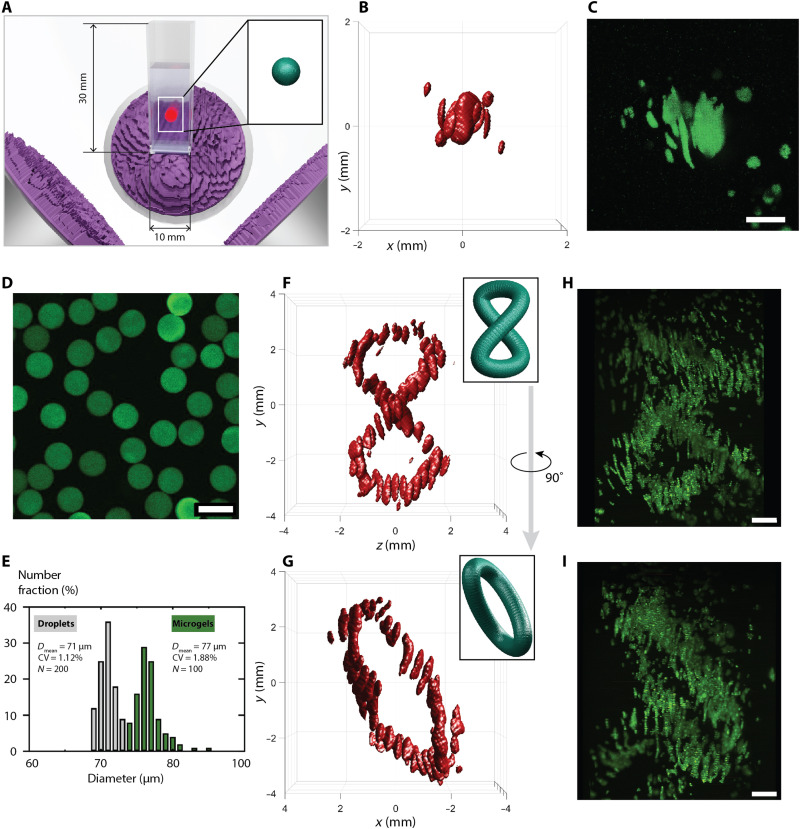
The combination of beams from orthogonal directions (causing highly varying wave vectors) causes interference patterns with pressure nodes that can be used to trap and assemble matter with a positive acoustic contrast. This is useful as most materials, including cells, have a positive acoustic contrast in water (polydimethylsiloxane is an exception). Figure 5 shows assemblies of biological cells (C2C12 mouse myoblasts) and microscopic hydrogel beads [gelatin methacrylate (GelMa)]. The assembled particles and cells were fixed in a slow-curing hydrogel medium, which leaves enough time for excess particles to settle before solidification. The experiments were performed inside square cuvettes, which were aligned to the transducers so that the target field is projected toward the center of the medium (Fig. 5A and fig. S8). The first demonstration is the assembly of biological cells to an extended spherical volume. Figure 5 (B and C) shows the simulated sound intensity field and the final cell assembly, respectively. We recorded and confirmed the 3D structure of the sample using a custom-built laser-sheet fluorescence imaging setup, a schematic of which is shown in fig. S9. Note here that the assembly does not form a closed 3D sphere but rather fills the volume with intertwined nodal surfaces similar to those seen in Fig. 3D. Hydrogel beads labeled with a fluorescent dye were fabricated on a microfluidic platform as reported in Materials and Methods. A fluorescence microscope image and their size distribution before (droplets) and after curing (μGels) can be seen in Fig. 5 (D and E, respectively). It can be seen that the hydrogel beads swell by a small amount relative to the droplet size before curing. However, the microfluidic fabrication method leads to a narrow and well-controlled size distribution. The beads can also be readily loaded with a cargo, for instance, with cells. We then computed the holograms to obtain a compact figure eight curve and used the same experimental setup to assemble the hydrogel beads. Figure 5 (F and G) illustrates the simulated sound intensity fields in front view and side view, respectively. The thresholds for the isosurfaces have been chosen in a way to visually reflect the achieved asemblies. Note that acoustic trapping itself is similarly threshold based, since particles are held at positions that provide a minimum of trapping force. By changing the input power to the transducers, the particle aggregates become larger or smaller as well. Laser-sheet images of the same sample are shown corresponding to the views in Fig. 5 (H and I). Animations of the reconstructed 3D structures for the different experiments can be seen in movie S3, and a series of photos in fig. S10 further illustrates the process. There, hydrogel beads were left to sediment through either the enabled ultrasonic field (projecting a helix) or no field at all.
Fig. 5. 3D holographic assembly of cells and microgel beads.
(A) The compact 3D sound image formed by three 2.25-MHz ultrasound transducers and associated holograms is focused into a standard cuvette. Inset shows the target field, in this example, an extended spherical volume, where (B) and (C) show the simulated sound intensity I (isosurface at 0.09 · max {I}) and a 3D fluorescence image stack of assembled C2C12 mouse myoblasts, respectively. (D) Microscope image of fluorescent microgels. (E) Size distribution of microgels before and after curing. CV, cofficient of variation. (F and G) Simulated sound intensity field of a distorted figure eight curve shown in front view and turned 90° around the vertical axis. Sound intensity isosurfaces at 0.16 · max {I}. (H and I) Assembly of microgels shown according to the views in (F) and (G). Scale bars, 100 μm (D) and 1 mm (all others).
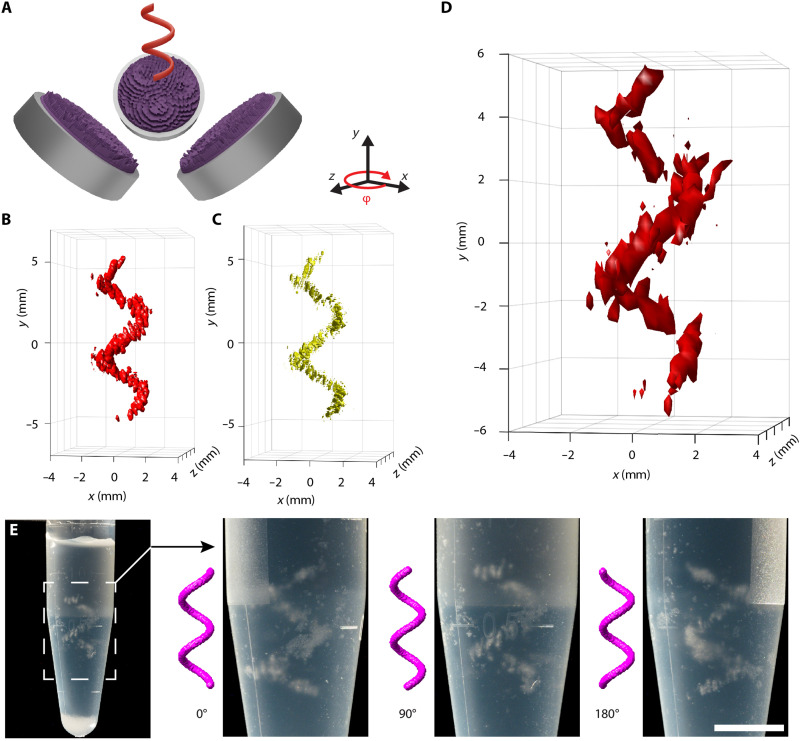
Figure 6 shows a rendering of the 3D assembly of silica gel microparticles in the shape of a helix, with the setup and target placement illustrated in Fig. 6A, where the sample tube has been omitted for clarity. The simulated intensity distribution of this field can be seen in Fig. 6B, and the corresponding Gor’kov radiation force potential can be seen in Fig. 6C. We measured the sound pressure field in the experiment by scanning a hydrophone through the region of interest. To avoid excessive heating of the transducers during this time-consuming measurement, the transducers were driven at lower electrical power (0.5 W, about 1/10 of the power used in the trapping experiments). The acquired volumetric data (Fig. 6D) confirm the successful reconstruction of the holographic 3D shape. In this case, the maximum measured pressure was 55 kPa. Because we found the transducers to respond linearly over the whole experimental range, we use this data point to estimate the maximum pressure amplitude during trapping experiments to be about 175 kPa. The acoustic assembly was fixed using the two-part hydrogel kit as in the previous experiments. Figure 6E shows the assembly of silica gel particles captured from varying angles to demonstrate its 3D character.
Fig. 6. 3D assembly of silica gel beads with holographic ultrasound fields.
(A) Arrangement of three sources (2.25 MHz) and target field (sample container hidden). (B) Intensity distribution (isosurface at 0.16 · max {I}) of the simulated field and its (C) radiation force potential for silica gel particles (isosurfaces at −0.1 · min {}). (D) Hydrophone measurement of the sound pressure field. Isosurfaces at 0.4 · max {p} = 21.6 kPa. (E) Photo of the fixed 3D assembly of silica gel particles in cross-linked hydrogel. Subsequent images show rotated close-up views. Scale bar, 5 mm.
DISCUSSION
In summary, we introduced a concept for generating compact 3D acoustic pressure shapes through superposition of fields from multiple acoustic holograms. To compute the fields in 3D, we initially used an FCM, which is sufficient to generate point-like targets. Furthermore, FCM is useful as a fast and intuitive way to gauge the feasibility whether certain target shapes can be generated with a particular configuration of holograms. To obtain traps beyond points that extend along lines in space, one needs to resort to a gradient-based optimization of the phase profile. To this aim, we devised an alternative computational method based on nonconvex optimization that minimizes the mean squared error between the generated field and the target field via a projected gradient descent scheme. Note that closely related approaches to nonconvex optimization have been proposed by Zhang et al. (26) and subsequently been taken up by Chakravarthula et al. (32). However, these works consider standard single-source optical holograms. Here, we show how to obtain complex 3D pressure shapes using multiple acoustic sources and holograms. The compact acoustic fields that we created experimentally using the computed holograms allowed us to rapidly assemble matter into arbitrary 3D shapes. We have demonstrated this concept with silica gel particles, biological cells, and also hydrogel beads in setups consisting of two or three transducers, where each is fitted with one hologram. The assemblies were fixed in a hydrogel phase for subsequent analysis. Our compact 3D acoustic fields trap and assemble particles simultaneously around specified points or along curved lines in a bulk suspension and even inside conventional sample tubes and cuvettes. Note that the assembly happens in parallel in a single step. The only time-limiting factors currently are (i) the removal of untrapped particles or cells in the regions with low acoustic exposure and (ii) cross-linking the hydrogel medium. In future work, we intend to optimize this process using carefully designed cross-flows or container movements. The hydrogel can further be modified with a photoinitiator, which would enable fast polymerization upon exposure to light. Therefore, the method presented here is orders of magnitude faster than serial bioprinting, and crucially, the fabrication time in our method does not depend on the size of the object. Multiple holograms can thus be used to obtain arbitrary shapes and objects that are not subject to any symmetry constraints, provided a corresponding hologram can be computed that encodes the object’s shape. The complexity of the 3D shapes that can be formed will depend on a number of parameters, including the number of holograms (three is better than two), the frequency where higher frequencies make for finer features (but this is ultimately limited by absorption and streaming), and the nature of the constituent particulate matter that is being assembled, which needs to have a suitable contrast factor such that the acoustic radiation force can counter sedimentation. One design goal is therefore to increase both the transducer frequency and its aperture. Furthermore, in practice, the size of the assembly is largely limited by the output power of the available transducers. Trapping the same type of particles over extended volumes approximately scales P ∝ d3, with d being a characteristic length of the target. To achieve the assembly of objects such as the dove in Fig. 1 requires transducers with high frequencies and sustained acoustic output power.
Because of the versatility and ability to accommodate different materials, our method shows promise for fabrication of scaffolds or directly assembling biological tissue. We foresee applications of compact high-fidelity 3D ultrasound fields in medical therapy, targeted drug delivery, and neurostimulation. The effects of ultrasound in these emerging fields have already been shown and are investigated by many research groups (33). Furthermore, the directed 3D assembly of matter is a promising avenue for rapid prototyping and, in particular, for tissue engineering.
MATERIALS AND METHODS
Angular spectrum method
The angular spectrum method (34) provides an efficient way to propagate electromagnetic or acoustic fields between parallel and aligned planes by means of fast FTs. Given the value of a 3D complex valued field in a plane z = zi, i.e., , we can obtain the field in a different plane via multiplication with a corresponding propagator function in Fourier space (34). To this aim, let the spatial frequency spectrum of the wave in the plane at zi be obtained via a 2D FT of the field
| (1) |
| (2) |
Let denote the wave number of a single frequency wave with wavelength λ. The propagator function, relating fields at z0 and z1 in Fourier space, can be written as (35)
| (3) |
Then, the propagated field can be related to the original field via a linear operator Az0 → z1 : ℂℝ2 → ℂℝ2
| (4) |
| (5) |
where 2D and are the Fourier and iFT in 2D, respectively.
From the unitarity of the propagator function in Eq. 3 combined with the unitarity of the FT, we can conclude that Az0 → z1 itself is a unitary operator, i.e., (Az0 → z1)*Az0 → z1 = Az1 → z0Az0 → z1 = I, where (Az0 → z1)* denotes the adjoint operator.
In practice, for computational purposes, one can only consider the field p(x, y, z) in a discretized finite volume with dimensions nx × ny × nz, where ni denotes the number of pixels in dimension i. We denote the discretized field, which can be expressed as a 3D tensor, as p ∈ ℂnx × ny × nz and analogously the field in the transducer plane at z = z0 as a 2D tensor pz0 ∈ ℂnx × ny. Moreover, we overload notation and define the action of the propagation operator Az0 → z1 on the discretized field as a mapping ℂnx × ny → ℂnx × ny in which the continuous FTs are substituted by discrete FTs. Now, as we only consider the field in a finite volume, generally, not all wave vectors originating in the plane at z = z0 are able to reach the plane at any other z = z1. One can account for this phenomenon by introducing a cutoff in the frequency domain that is usually determined by some heuristics (36). Our implementation relies on the procedure described in the following. Suppose that we have a circular aperture with diameter lA and the image plane of interest is in distance z from the aperture. Moreover, the image has transversal extend ltarget, and its center is aligned with the center of the aperture. A simple geometric consideration shows that in order for a wave vector k = (kx, ky, kz) originating at the phase modulating device to reach the image volume, its x and y components must fulfill
| (6) |
The frequency cutoff can then be implemented in a modified propagator defined as
| (7) |
where θ is the Heaviside step function, and we defined . Note that this frequency filter removes the unitarity of the forward operator A so we can no longer assume .
This means that, due to the consideration of a finite volume, some energy will be lost between planes and, consequently, that propagation is not reversible, i.e., .
While the angular spectrum method provides a way to propagate a field from one plane to another, it can be readily extended to propagate one field into multiple planes and back, respectively. By slicing a 3D target image into a number of 2D planes, this allows us to deploy the framework for 3D holography. For a 3D target volume sliced into nz discrete planes of dimension nx × ny at z = zi, i = 1, …, nz, we define the 3D discretized propagation operator A : ℂnx × ny → ℂnx × ny × nz as the direct sum of propagation operators Az0 → zi between pairs of planes at (z0, zi)
| (8) |
where is to be interpreted as a concatenation of the field in the nz planes pzi ∈ ℂnx × ny along the third dimension, which yields a tensor p ∈ ℂnx × ny × nz. Correspondingly, the adjoint operator A* : ℂnx × ny × nz → ℂnx × ny is given by
| (9) |
which for i = 1, …, n picks the ith plane of the image volume, reverses the propagation from z0 to zi, and subsequently sums over all backward-propagated contributions with equal weight.
As described above, the angular spectrum method requires the planes of interest to be parallel and aligned. In multitransducer settings, this translates into the requirement that the transducers are placed orthogonal to each other. While, in practice, a roughly orthogonal setting is often already required for space reasons, our optimization methods described in the following can be used in nonorthogonal settings by resorting to a propagation operator defined via pointwise wave propagation based on carrying out the diffraction integral.
Computation of holograms
Phase-only CGH is concerned with finding the optimal phase relation ϕ ∈ ℝnx × ny of the sound pressure field in the hologram plane p0 = ueiϕ ∈ ℂnx × ny so that the propagated field matches a desired amplitude g ∈ ℝnx × ny × nz at some distance from the transducer. Here, we assume the transducer to be located at z0 = 0 and to have a fixed amplitude u ∈ ℝnx × ny independent of the phase modulation ϕ. The fields in the hologram (or transducer) plane and the target volume are related by a linear operator A : ℂnx × ny → ℂnx × ny × nz, which can be implemented, e.g., using the angular spectrum method (see the previous section). Correspondingly, the inverse propagation from the target volume to the transducer plane is described by the adjoint operator A* : ℂnx × ny × nz → ℂnx × ny. Mathematically, the problem is an inverse problem consisting of two amplitude constraints: (i) In the transducer plane, the field p0 = ∣p0∣ eiϕ is required to have the amplitude u imposed by the transducer ∣p0∣ = u, and (ii) in the image volume, the target amplitude g from ∣Ap0∣ = g should be produced. The degrees of freedom of this optimization problem lie in the phase ϕ.
Fourier constraint method
Assume that we want to generate a 3D amplitude profile g(x, y, z) using a transducer that emits a wave field p(x, y, z) with wavelength λ. For the purpose of presentation, we describe the algorithm on the level of field variables p(x, y, z) instead of their discretization p ∈ ℂnx × ny × nz. The discretized version follows directly by going over to discrete FTs and adapting the constraint set accordingly. For a physical wave field with wave number k = 2π/λ, all allowed wave vectors k = (kx, ky, kz) lie on a so-called Ewald sphere with radius k and . As the wave field is emitted by a transducer with a designated propagation direction, e.g., in the positive z direction, we obtain the additional constraint kz ≥ 0. Moreover, with a finite aperture, not all wave vectors originating at the transducer plane can reach the image volume, which, as argued in the previous section, can be expressed with a heuristic constraint Eq. 6. As a result, all allowed wave vectors lie within a patch E on one half of the Ewald sphere defined as
| (10) |
Let 3D[p](kx, ky, kz) denote the FT of the field p. Then, we can formulate the problem as finding a solution in the intersection of the target amplitude constraint set G and Fourier space constraint set F defined respectively as
| (11) |
| (12) |
In general, F ∩ G = ∅; however, this problem has a form suitable for a GS-like alternating projection scheme to compute an approximate solution (37, 38). Note that the following procedure has been proposed previously in (23). Starting with a random initial field in Fourier space , the algorithm proceeds by repeating the following steps.
1) Projecting the iterate on the set of fields G with the desired target amplitude by taking the iFT and setting the amplitude to g while keeping the phase to obtain p.
2) Projecting the iterate p on the set of physically realizable fields F by taking the FT 3D[p] and setting the field to zero outside the relevant patch E on the Ewald sphere to obtain .
Finally, the result can be transformed back into real space using an iFT. Using, e.g., the angular spectrum method, the field can be propagated to the transducer plane to obtain the corresponding phase profile that needs to be realized in the hologram. As here, we are interested in holograms from multiple transducers. Each transducer corresponds to a patch E in Fourier space. Using the linearity of the (inverse) FT allows us to transform the information lying on the different patches into real space separately and thus allows us to separate the contributions from the transducers in real space. With the separated real-space fields at hand, we can simply propagate each field to the corresponding transducer plane to obtain the required phase profiles.
The Fourier constraint approach has the drawback that while it takes into account the direction and geometrical properties of the transducers, their amplitudes do not enter the iterative hologram computation. Instead of ensuring physical consistency between the transducer amplitude, which is a constraint on a single plane, and the produced field consisting of nz planes, the FCM only focuses on ensuring physical consistency between the nz 2D planes in z direction. For 3D CGH, it has been observed in practice that taking into account the transducer amplitudes has a small but non-negligible impact on the quality of the result. Therefore, for more complex fields, we resort to a gradient-based optimization procedure that explicitly takes into account the transducer amplitudes as described in the following section.
Gradient descent optimization
Gradient-based optimization schemes have been deployed in the context of CGH (26, 32, 39). These methods generally optimize the phase pattern ϕ ∈ ℝnx × ny in the hologram plane by minimization of a real-valued error measure 𝓁[h(ϕ), g] between the generated field h(ϕ) and the target g, where h describes the functional relationship between the phase pattern ϕ and the produced amplitude field in the target volume. Typically, this is solved with first-order optimization methods, such as the limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm (26) or gradient descent (32, 39). Instead of solving the unconstrained optimization problem in real variables, we opt for a closely related but different approach by solving a constrained optimization problem over the complex field in the transducer plane p0 ∈ ℂnx × ny with the constraint ∣p0∣ = u, where u ∈ ℝnx × ny represents the transducer amplitude, so that the problem becomes
| (13) |
The numerical solution of this problem with continuous optimization tools requires the computation of the gradient of the loss function with respect to the decision variables. However, because the objective in Eq. 13 is a real-valued function of a complex variable, it cannot be differentiated in the standard complex analysis sense as it is nonholomorphic (i.e., not complex differentiable). Instead, in analogy to previous works (32, 39), we resort to Wirtinger subdifferential calculus (40) to extract meaningful gradients; see, e.g., (41), for a comprehensive introduction.
For simplicity of notation, we substitute the field variable p ∈ ℂnx × ny with a vectorized version p ∈ ℂnx · ny in the following. For a general pressure field p = pr + ipi ∈ ℂnx · ny with pr, pi ∈ ℝnx · ny, we denote the convex conjugate variable as . We define the Wirtinger differential operators (41)
| (14) |
where pr and pi are treated as independent variables. Consider the loss as a function of the complex field directly, i.e., let L : ℂnx · ny → ℝ be a real-valued function on a complex domain such that L(p) = 𝓁( ∣Ap∣ , g). Then, the optimality conditions are given as dL = 0, where the Wirtinger differential dL is defined as (41)
| (15) |
| (16) |
In the last step, we defined the Wirtinger gradient of L with respect to p as . For computational purposes, can be treated like a normal partial derivative. Using the chain rule of multivariate calculus, we thus obtain the Wirtinger (sub-)gradient of L as
| (17) |
| (18) |
| (19) |
where ∘ denotes the element-wise or Hadamard product. Note that several modern automatic differentiation frameworks including Tensorflow (42) return Wirtinger gradients by default when trying to differentiate real-valued objectives with respect to complex variables and thus conceal this additionally required complexity.
Having defined a meaningful gradient, we can solve Eq. 13 by deploying the simple projected gradient descent scheme detailed in Algorithm 1. Therein, U(p) ≔ u ∘ p / ∣p∣ is the Euclidean projection onto the constraint set U. In the case of the square loss
| (20) |
we have ∇x𝓁(x, g) = x − g, and Eq. 19 simplifies to
In contrast to the gradient-based optimization methods of related works (26, 32) that directly optimize the phase pattern ϕ, our optimization on the level of the complex field variable p bears a close connection to the famous GS algorithm (37). To see this, consider the optimization of the square loss in our framework using a fixed step size τ = 0.5. Now, under the assumption of a unitary propagation operator A (which is violated in practice; see the “Angular spectrum method” section), the projected gradient descent update rule becomes
| (21) |
In words, this implies the following steps: (i) Propagate the field to the target volume and set the amplitude to the target amplitude while keeping the phase, and (ii) propagate the field back to the transducer plane and set the amplitude to the transducer amplitude while keeping the phase. These are exactly the steps taken by the GS method (37). Therefore, our method can be understood as a variant of the GS algorithm that uses adaptive step sizes and correctly takes into account the nonunitarity of the propagation operator.
Acoustic radiation force potential
We use the Gor’kov radiation force potential to identify the trapping sites for microparticles (14, 29). It is defined as the potential of conservative radiation forces, F = −∇, and consequently, particles are pushed toward and trapped at the local minima of . Computation is straightforward if we compute the acoustic velocity v from the sound pressure distribution p as v = ∇p/iρmω with , angular frequency ω = 2πf, and frequency f. Then
| (22) |
| (23) |
| (24) |
where a is the particle radius, ρ is the density, and c is the speed of sound. Subscripts m and p refer to the material properties of the medium or particle, respectively. The Gor’kov potential is valid for a ≪ λ and fields dissimilar to plane traveling waves, which is the case here (29).
The sonomechanical properties of silica gel can be calculated in the long-wavelength regime as an effective medium (43), because the pore sizes are much smaller than the acoustic wavelength. From the material datasheet, we estimate a pore volume fraction of 70% and assume that all pores are filled with water, which gives cp = 1415 ms−1 and ρp = 1498 kgm−3. These values result in a positive acoustic contrast factor Γ = C0/3 + C1/2 = 0.21 in water, which means that the minima of and thus the particle-trapping sites coincide with sound pressure nodes (44). The acoustic contrast factor for C2C12 mouse myoblasts was not possible for us to obtain. However, biological cells are known to have positive acoustic contrast, and some examples are reported to lie in the range of 0.14 to 0.25 (45).
Synthesis of GelMA
GelMA was synthesized on the basis of a slightly adapted protocol from Yue et al. (46). Briefly, 10 g of gelatin from cold water fish skin (Sigma-Aldrich, Germany) was dissolved in 100 ml of Dulbecco’s phosphate-buffered saline (DPBS) at 50°C, followed by adding 8 ml of methacrylic anhydride (94%; Sigma-Aldrich, Germany) dropwise. The mixture was reacted for 2 hours under magnetic stirring at 50°C after which the reaction was stopped with a twofold dilution of warm DPBS, followed by dialysis for 5 days using a membrane (12 to 14 kDa Mw cutoff) at 40°C to remove impurities, such as unreacted methacrylic anhydride. Last, the solution was freeze-dried to yield a white foam and stored at 4°C until further use.
Fabrication of GelMA beads
Freeze-dried GelMA was dissolved in a mixture of DPBS, rhodamine 6G (Sigma-Aldrich, Germany) at a concentration of 1 mg ml−1, and the photoinitiator lithium-phenyl-2,4,6-trimethylbenzoylphosphinate (Sigma-Aldrich, Germany) to yield photopolymerizable GelMA solutions [10% (w/v)]. To prepare GelMA microgels, the GelMA solution was used as a dispersed phase, while 1% (w/w) of perfluoropolyether-PEG (polyethylene glycol) block copolymer fluorosurfactants (Ran Biotechnologies Inc, USA) dissolved in HFE 7500 oil (3M, USA) was used as a continuous phase to prepare a water-in-oil emulsion. Both phases were individually injected into the inlet microchannels of a step emulsification microfluidic device using syringe pumps at constant flowrates to obtain droplets of 70 μm in diameter. The surfactant-stabilized GelMA droplets were then polymerized in solution using a 10-W ultraviolet (UV) lamp, collected in a microcentrifuge tube, and stored at 4°C until further use. Confocal images were taken using an LSM900 (0.75% laser power, 700-V gain, excitation/emission of 488/512 nm; Zeiss, Germany), and the size of the droplets/particles was determined manually or by using ImageJ software.
Acoustic assembly
All transducers were custom-built with 2.25-MHz center frequency. The first version was acquired from the company Precision Acoustics (UK) and had an active aperture of 45 mm. Recently, we designed and fabricated our own transducers with the same frequency, an active aperture of 50 mm, and integrated air-cooling system, which allows continuous operation over longer time periods. The transducers were mounted on a 3D-printed mechanical rig in orthogonal arrangement so that their axes intersect in the center of a cubic volume with 60-mm side length. The holograms were fabricated using a 3D printer (Objet Connex 260, Stratasys, Israel) in VeroClear material and placed directly on the transducer faces using vacuum grease (Dow Corning, USA) or water as contact layer. For the particle-trapping experiments, the whole transducer setup was submerged in an open-topped water tank (600 mm × 300 mm × 300 mm) filled with degassed, deionized water.
Different containers were used for particle-trapping experiments. The platonic point traps were assembled inside a 3D-printed cube (side length, 60 mm) with circular openings on all sides that were covered with transparency sheets (approximately 100 μm thick) to allow unimpeded transmission of the ultrasound waves and visual inspection. The windows had a diameter of 45 mm. The assemblies of biological cells and hydrogel capsules were performed inside UV-Vis cuvettes made of polystyrene. The helix was assembled from silica gel spheres (75 to 200 μm, Sigma-Aldrich, Germany) inside sample tubes (size, 1.5 ml; Eppendorf, Germany).
Because of manufacturing tolerances and varying impedances, each transducer was driven through a separate electric channel, including the function generator (AFG1022, Tektronix, USA) and amplifier (75A2 or 2200L, Electronics & Innovation, USA). The function generators were synchronized to a common clock. During trapping experiments, each transducer was driven at approximately 5-W electrical power to assemble silica gel particles. The volumetric hydrophone scans were performed at reduced input power of about 0.5 W per channel. Photos were taken using a single-lens reflex camera (EOS 60D, Canon, Japan) with macro lens (LAOWA 100 mm f/2,8 2:1 Ultra Macro APO, Venuslens, China).
Laser lightsheet fluorescence imaging
We built a custom laser lightsheet fluorescence imaging setup to reconstruct the samples’ 3D structure from sectional fluorescent images. A schematic of the setup can be found in fig. S9. The light source is a green laser (532 mm, Coherent, USA). Its beam is expanded via lens pair L1 and L2 with focal lengths of −25 and 25 mm, respectively, and sent through a pin hole P (100 μm). That beam is then shaped into a light sheet using lens L3 (125 mm) and cylindrical lens L4 (200 mm). The sample is fixed in a UV-vis cuvette, which is mounted on a motorized three-axis stage (PT3/M-Z8, Thorlabs, Germany) and scanned through the beam in 10-μm steps. The imaging path provides a small magnification of ×1.2 onto a camera sensor (1800 U-2050m, Allied Vision), and the emitted light is separated by a longpass filter with a cutoff wavelength of 550 nm. Lenses L5 and L6 are achromatic doublets with 100- and 120-mm focal lengths, respectively. All lenses, filter, and pinhole were purchased from Thorlabs. During the scan, the stage pauses at each step until an image is taken and stored on a computer. The resulting image stack is then processed through ImageJ to reconstruct the 3D object.
Acknowledgments
We thank S. Pashapour and the microfluidic core facility at the Institute for Molecular Systems Engineering and Advanced Materials (IMSEAM) at Heidelberg University for the microfluidic device fabrication. We thank J. P. Spatz for support and helpful discussions.
Funding: The research was, in part, supported by the European Research Council under the ERC Advanced Grant Agreement HOLOMAN (no. 788296), the joint research innovation grant by the Max Planck Society and the Fraunhofer Society (AKUSTOGRAMME), and the German Research Foundation [Deutsche Forschungsgemeinschaft (DFG)] under Germany’s Excellence Strategy via the Excellence Cluster 3D Matter Made to Order (EXC-2082/1-390761711).
Author contributions: K.M. and P.F. initiated the project and developed the concept. K.M., M.S., and S.S. performed the experiments and measurements. H.K. developed the optimization algorithm and wrote the software. S.S. and C.F. fabricated hydrogel beads. C.D. designed and built the ultrasound transducers. I.P., D.S., B.S., and P.F. supervised the project. K.M., H.K., and P.F. wrote the paper. All authors approved the final version of the manuscript.
Competing interests: K.M. and P.F. are inventors on a patent related to this work granted by the European Patent Office (EP 3034281 B1). The authors declare that they have no other competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Figs. S1 to S10
Other Supplementary Material for this : manuscript includes the following:
Movies S1 to S3
REFERENCES AND NOTES
- 1.M. Shusteff, A. E. M. Browar, B. E. Kelly, J. Henriksson, T. H. Weisgraber, R. M. Panas, N. X. Fang, C. M. Spadaccini, One-step volumetric additive manufacturing of complex polymer structures. Sci. Adv. 3, eaao5496 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.T. Latychevskaia, Lateral and axial resolution criteria in incoherent and coherent optics and holography, near- and far-field regimes. Appl. Optics 58, 3597–3603 (2019). [DOI] [PubMed] [Google Scholar]
- 3.G. Whyte, J. Courtial, Experimental demonstration of holographic three-dimensional light shaping using a Gerchberg–Saxton algorithm. New J. Phys. 7, 117 (2005). [Google Scholar]
- 4.G. Makey, O. Yavuz, D. K. Kesim, A. Turnali, P. Elahi, S. Ilday, O. Tokel, F. O. Ilday, Breaking crosstalk limits to dynamic holography using orthogonality of high-dimensional random vectors. Nat. Photonics 13, 251–256 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.P. N. Bernal, P. Delrot, D. Loterie, Y. Li, J. Malda, C. Moser, R. Levato, Volumetric bioprinting of complex living-tissue constructs within seconds. Adv. Mater. 31, e1904209 (2019). [DOI] [PubMed] [Google Scholar]
- 6.D. Loterie, P. Delrot, C. Moser, High-resolution tomographic volumetric additive manufacturing. Nat. Commun. 11, 852 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.B. E. Kelly, I. Bhattacharya, H. Heidari, M. Shusteff, C. M. Spadaccini, H. K. Taylor, Volumetric additive manufacturing via tomographic reconstruction. Science 363, 1075–1079 (2019). [DOI] [PubMed] [Google Scholar]
- 8.J. Madrid-Wolff, A. Boniface, D. Loterie, P. Delrot, C. Moser, Controlling light in scattering materials for volumetric additive manufacturing. Adv. Sci. 9, 2105144 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.M. Regehly, Y. Garmshausen, M. Reuter, N. F. Konig, E. Israel, D. P. Kelly, C. Y. Chou, K. Koch, B. Asfari, S. Hecht, Xolography for linear volumetric 3D printing. Nature 588, 620–624 (2020). [DOI] [PubMed] [Google Scholar]
- 10.K. Melde, E. Choi, Z. Wu, S. Palagi, T. Qiu, P. Fischer, Acoustic fabrication via the assembly and fusion of particles. Adv. Mater. 30, 1704507 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Z. Ma, A. W. Holle, K. Melde, T. Qiu, K. Poeppel, V. M. Kadiri, P. Fischer, Acoustic holographic cell patterning in a biocompatible hydrogel. Adv. Mater. 32, 1904181 (2020). [DOI] [PubMed] [Google Scholar]
- 12.K. Melde, A. G. Mark, T. Qiu, P. Fischer, Holograms for acoustics. Nature 537, 518–522 (2016). [DOI] [PubMed] [Google Scholar]
- 13.Y. Gu, C. Chen, J. Rufo, C. Shen, Z. Wang, P. H. Huang, H. Fu, P. Zhang, S. A. Cummer, Z. Tian, T. J. Huang, Acoustofluidic holography for micro- to nanoscale particle manipulation. ACS Nano 14, 14635–14645 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.A. Marzo, S. A. Seah, B. W. Drinkwater, D. R. Sahoo, B. Long, S. Subramanian, Holographic acoustic elements for manipulation of levitated objects. Nat. Commun. 6, 8661 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.A. Marzo, B. W. Drinkwater, Holographic acoustic tweezers. Proc. Natl. Acad. Sci. U.S.A. 116, 84–89 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.D. Baresch, J. L. Thomas, R. Marchiano, Observation of a single-beam gradient force acoustical trap for elastic particles: Acoustical tweezers. Phys. Rev. Lett. 116, 024301 (2016). [DOI] [PubMed] [Google Scholar]
- 17.A. Franklin, A. Marzo, R. Malkin, B. W. Drinkwater, Three-dimensional ultrasonic trapping of micro-particles in water with a simple and compact two-element transducer. Appl. Phys. Lett. 111, 094101 (2017). [Google Scholar]
- 18.J. P. K. Armstrong, J. L. Puetzer, A. Serio, A. G. Guex, M. Kapnisi, A. Breant, Y. Zong, V. Assal, S. C. Skaalure, O. King, T. Murty, C. Meinert, A. C. Franklin, P. G. Bassindale, M. K. Nichols, C. M. Terracciano, D. W. Hutmacher, B. W. Drinkwater, T. J. Klein, A. W. Perriman, M. M. Stevens, Engineering anisotropic muscle tissue using acoustic cell patterning. Adv. Mater. 30, e1802649 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.J. P. K. Armstrong, E. Pchelintseva, S. Treumuth, C. Campanella, C. Meinert, T. J. Klein, D. W. Hutmacher, B. W. Drinkwater, M. M. Stevens, Tissue engineering cartilage with deep zone cytoarchitecture by high-resolution acoustic cell patterning. Adv. Healthc. Mater. , e2200481 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.M. Caleap, B. W. Drinkwater, Acoustically trapped colloidal crystals that are reconfigurable in real time. Proc. Natl. Acad. Sci. U.S.A. 111, 6226–6230 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.M. Prisbrey, J. Greenhall, F. G. Vasquez, B. Raeymaekers, Ultrasound directed self-assembly of three-dimensional user-specified patterns of particles in a fluid medium. J. Appl. Phys. 121, 014302 (2017). [Google Scholar]
- 22.R. Piestun, J. Shamir, Synthesis of three-dimensional light fields and applications. Proc. IEEE 90, 222–244 (2002). [Google Scholar]
- 23.G. Shabtay, Three-dimensional beam forming and Ewald’s surfaces. Opt. Commun. 226, 33–37 (2003). [Google Scholar]
- 24.H. Chen, Y. Guo, Z. Chen, J. Hao, J. Xu, H.-T. Wang, J. Ding, Holographic optical tweezers obtained by using the three-dimensional Gerchberg–Saxton algorithm. J. Opt. 15, 035401 (2013). [Google Scholar]
- 25.S. Mellin, G. Nordin, Limits of scalar diffraction theory and an iterative angular spectrum algorithm for finite aperture diffractive optical element design. Opt. Express 8, 705–722 (2001). [DOI] [PubMed] [Google Scholar]
- 26.J. Zhang, N. Pégard, J. Zhong, H. Adesnik, L. Waller, 3D computer-generated holography by non-convex optimization. Optica 4, 1306–1313 (2017). [Google Scholar]
- 27.B. W. Drinkwater, Dynamic-field devices for the ultrasonic manipulation of microparticles. Lab Chip 16, 2360–2375 (2016). [DOI] [PubMed] [Google Scholar]
- 28.A. Ozcelik, J. Rufo, F. Guo, Y. Gu, P. Li, J. Lata, T. J. Huang, Acoustic tweezers for the life sciences. Nat. Methods 15, 1021–1028 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.L. P. Gor’kov, On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys. Dokl. 6, 773–775 (1962). [Google Scholar]
- 30.O. A. Sapozhnikov, M. R. Bailey, Radiation force of an arbitrary acoustic beam on an elastic sphere in a fluid. J. Acoust. Soc. Am. 133, 661–676 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.T. S. Jerome, M. F. Hamilton, Born approximation of acoustic radiation force and torque on inhomogeneous objects. J. Acoust. Soc. Am. 150, 3417–3427 (2021). [DOI] [PubMed] [Google Scholar]
- 32.P. Chakravarthula, Y. Peng, J. Kollin, H. Fuchs, F. Heide, Wirtinger holography for near-eye displays. ACM Trans. Graph. 38, 1–13 (2019). [Google Scholar]
- 33.A. G. Athanassiadis, Z. Ma, N. Moreno-Gomez, K. Melde, E. Choi, R. Goyal, P. Fischer, Ultrasound-responsive systems as components for smart materials. Chem. Rev. 122, 5165–5208 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.J. W. Goodman, Introduction to Fourier Optics (Roberts & Co. Publishers, ed. 3, 2005). [Google Scholar]
- 35.D. L. Liu, R. C. Waag, Propagation and backpropagation for ultrasonic wavefront design. IEEE Trans. Sonics Ultrason. 44, 1–13 (1997). [DOI] [PubMed] [Google Scholar]
- 36.K. Matsushima, T. Shimobaba, Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields. Opt. Express 17, 19662–19673 (2009). [DOI] [PubMed] [Google Scholar]
- 37.R. W. Gerchberg, W. O. Saxton, A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246 (1972). [Google Scholar]
- 38.R. Escalante, M. Raydan, Alternating Projection Methods (Society for Industrial and Applied Mathematics, 2011). [Google Scholar]
- 39.E. J. Candes, X. Li, M. Soltanolkotabi, Phase retrieval via wirtinger flow: Theory and algorithms. IEEE Trans. Inf. Theory 61, 1985–2007 (2015). [Google Scholar]
- 40.W. Wirtinger, Zur formalen Theorie der Funktionen von mehr komplexen Veränderlichen. Math. Ann. 97, 357–375 (1927). [Google Scholar]
- 41.R. Remmert, Theory of Complex Functions, Graduate in Texts Mathematics (Springer, 1991). [Google Scholar]
- 42.M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu, X. Zheng, TensorFlow: Large-scale machine learning on heterogeneous systems (2015); tensorflow.org.
- 43.J. G. Berryman, Long‐wavelength propagation in composite elastic media I. Spherical inclusions. J. Acoust. Soc. Am. 68, 1809–1819 (1980). [Google Scholar]
- 44.H. Bruus, Acoustofluidics 7: The acoustic radiation force on small particles. Lab Chip 12, 1014–1021 (2012). [DOI] [PubMed] [Google Scholar]
- 45.D. Hartono, Y. Liu, P. L. Tan, X. Y. Then, L. Y. Yung, K. M. Lim, On-chip measurements of cell compressibility via acoustic radiation. Lab Chip 11, 4072–4080 (2011). [DOI] [PubMed] [Google Scholar]
- 46.K. Yue, G. Trujillo-de Santiago, M. M. Alvarez, A. Tamayol, N. Annabi, A. Khademhosseini, Synthesis, properties, and biomedical applications of gelatin methacryloyl (GelMa) hydrogels. Biomaterials 73, 254–271 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S10
Movies S1 to S3