Muscarinic Acetylcholine Receptors Modulate HCN Channel Properties in Vestibular Ganglion Neurons

Abstract

Efferent modulation of vestibular afferent excitability is linked to muscarinic signaling cascades that close low-voltage-gated potassium channels (i.e., KCNQ). Here, we show that muscarinic signaling cascades also depolarize the activation range of hyperpolarization-activated cyclic-nucleotide gated (HCN) channels. We compared the voltage activation range and kinetics of HCN channels and induced firing patterns before and after administering the muscarinic acetylcholine receptor (mAChR) agonist oxotremorine-M (Oxo-M) in dissociated vestibular ganglion neurons (VGNs) from rats of either sex using perforated whole-cell patch-clamp methods. Oxo-M depolarized HCN channels' half-activation voltage (V_1/2) and sped up the rate of activation near resting potential twofold. HCN channels in large-diameter and/or transient firing VGN (putative cell bodies of irregular firing neuron from central epithelial zones) had relatively depolarized V_1/2 in control solution and were less sensitive to mAChR activation than those found in small-diameter VGN with sustained firing patterns (putatively belonging to regular firing afferents). The impact of mAChR on HCN channels is not a direct consequence of closing KCNQ channels since pretreating the cells with Linopirdine, a KCNQ channel blocker, did not prevent HCN channel depolarization by Oxo-M. Efferent signaling promoted ion channel configurations that were favorable to highly regular spiking in some VGN, but not others. This is consistent with previous observations that low-voltage gated potassium currents in VGN are conducted by mAChR agonist-sensitive and -insensitive channels. Connecting efferent signaling to HCN channels is significant because of the channel's impact on spike-timing regularity and nonchemical transmission between Type I hair cells and vestibular afferents.

SIGNIFICANCE STATEMENT Vestibular afferents express a diverse complement of ion channels. In vitro studies identified low-voltage activated potassium channels and hyperpolarization-activated cyclic-nucleotide gated (HCN) channels as crucial for shaping the timing and sensitivity of afferent responses. Moreover, a network of acetylcholine-releasing efferent neurons controls afferent excitability by closing a subgroup of low-voltage activated potassium channels on the afferent neuron. This work shows that these efferent signaling cascades also enhance the activation of HCN channels by depolarizing their voltage activation range. The size of this effect varies depending on the endogenous properties of the HCN channel and on cell type (as determined by discharge patterns and cell size). Simultaneously controlling two ion-channel groups gives the vestibular efferent system exquisite control over afferent neuron activity.

Introduction

The mammalian vestibular system detects head motions across a wide range of amplitudes and frequencies. Low- and high-frequency head movements are encoded by two vestibular afferent groups that differ in excitability and spike-timing (Sadeghi et al., 2007; Eatock and Songer, 2011). Afferents that spike at regular intervals have lower detection thresholds for low-frequency head movements, while irregular afferents have lower detection thresholds for all other frequencies. Afferent excitability and spike-timing reflect, in part, the complement of ion channels expressed by the neurons. In vitro studies have identified low-voltage gated potassium channels (e.g., Kv1 and KCNQ) and hyperpolarization-activated cyclic-nucleotide gated (HCN) channels as critical regulators of afferent spike-timing (e.g., Kalluri et al., 2010; Horwitz et al., 2014). These two ion channel groups have voltage-gated properties that make currents available between resting potential and voltage threshold, where they can influence the summation of synaptic events (Meredith et al., 2012) and action potential generation.

Vestibular afferents receive input from an extensive network of primarily cholinergic efferent neurons, which increase afferent excitability by activating muscarinic acetylcholine receptors (mAChRs). The resulting signaling cascades increase afferent excitability by shutting down low-voltage activated potassium currents carried by KCNQ channels (Pérez et al., 2009; Sadeghi et al., 2009; Holt et al., 2017; Raghu et al., 2019). Here, we consider whether muscarinic signaling cascades also affect HCN channels in vestibular afferent neurons. This is a possibility because the second messenger cascades initiated by mAChR activation include phosphatidylinositol 4,5-bisphosphate (PIP₂) and cAMP (Zhang et al., 2003; Hughes et al., 2007), which are known modulators of HCN channels (Wainger et al., 2001; Pian et al., 2007).

HCN channels conduct an inward, hyperpolarization-activated Na⁺/K⁺ current (I_H) that controls pace-making in the heart and brain (Pape and McCormick, 1989; DiFrancesco, 1993; Biel et al., 2009). The I_H current has received significant attention in the vestibular system for its putative role in shaping spike-timing regularity (Horwitz et al., 2014; Yoshimoto et al., 2015). HCN channels are also thought to contribute to nonquantal transmission, a nonchemical form of communication (Yamashita and Ohmori, 1991; Songer and Eatock, 2013; Highstein et al., 2014) by which ion channels found on the inner surface of afferent terminals resistively couple sensory hair cells to vestibular afferent neurons (Contini et al., 2020; Govindaraju et al., 2023). In either of these cases, HCN can only shape neuronal responses when its current, I_H, is available between rest and threshold. Because in vitro characterizations of HCN channels show the channel activation is typically very hyperpolarized (Chabbert et al., 2001; Almanza et al., 2012; Meredith et al., 2012; Ventura and Kalluri, 2019), here we tested whether efferent signaling may bring the channel's activation to a voltage range where it can impact spike activity.

We recorded from dissociated and briefly cultured vestibular ganglion neurons (VGNs), the cell bodies of vestibular afferents. We treat cell bodies as proxies for the afferent terminals since they express similar ion channels and efferent receptors as found at afferent terminals (Pérez et al., 2009; Holt et al., 2017; Ventura and Kalluri, 2019). For example, the impact of mAChR on KCNQ channels was first identified in somatic recordings (Pérez et al., 2009), and subsequently verified as impacting afferent function (Schneider et al., 2021). Also, the accessibility of isolated cell bodies makes it feasible to apply perforated-patch clamping techniques, which preserve the second messengers that are important for HCN function and the intracellular signaling cascades that are likely triggered by efferent inputs. The recordings were made in VGN in the second to third postnatal weeks (mean at P15) to allow developmental upregulation of HCN (e.g., Yoshimoto et al., 2015) and KCNQ channels (e.g., Rocha-Sanchez et al., 2007). Although still an immature system, both regular firing and irregular firing patterns are well represented within the in vivo responses of vestibular afferents at this age range (Curthoys, 1979).

Our results show that the activation range of HCN channels can be depolarized by activating mAChRs. These results suggest that, in addition to their well-known impact on spike rate (Goldberg et al., 1984; Holt et al., 2017), vestibular efferents also may control spike-timing regularity by both suppressing irregularity-promoting KCNQ channels and enhancing regularity-promoting HCN channels. We also show that the sensitivity of HCN channels to modulation varied by VGN cell type. The shifts in HCN channel activation range were more pronounced in VGN with small- to medium-diameter cell bodies that responded to steady current injection with sustained-spike trains and less pronounced in large-diameter VGNs that responded with transient firing patterns. Given previous work linking cell size and in vitro firing patterns with irregular/regular firing afferent groups (Kevetter and Leonard, 2002; Kalluri et al., 2010), the greater sensitivity of HCN channels to cholinergic modulation in the cell bodies of putative regular firing afferents (small-diameter sustained firing VGN) suggests that efferent modulation may impact both firing rate (as previously shown) (Sadeghi et al., 2009; Holt et al., 2017) and the regularity of spike-timing.

Materials and Methods

Preparations

Data were recorded from the superior portion of the vestibular ganglion of Long-Evans rats of either sex aged postnatal day (P)9-22 (P0, birth day). The cell bodies of afferents emerging from the utricle, lateral, and horizontal cristae comprise the superior ganglion. Functional diversity in afferent response properties, as indicated by regular and irregular afferents, is found in all three epithelia. The inferior ganglion was explicitly excluded from this study since we have found that disassociation is more difficult when it is included. All animals were handled and housed in accordance with National Institutes of Health's Guide for the care and use of laboratory animals. All animal procedures were approved by the University of Southern California Institutional Animal Care and Use Committee. Chemicals were obtained from Sigma-Aldrich unless otherwise specified. Temporal bones were dissected from the animals in chilled and oxygenated Leibowitz medium supplemented with 10 mm HEPES (L-15 solution). The superior part of the vestibular ganglia was detached from the distal and central nerve branches and separated from the otic capsule. Bone fragments, debris, and any remaining connective tissue were removed from the surface of the ganglia. Two ganglia from 1-2 litter-matched animals of either sex were pooled together. Ganglia were then incubated at 37°C in L-15 medium solution with 0.05% collagenase and 0.25% trypsin for 20-40 min, depending on age of the animal. We chose this enzymatic cocktail since it appears to preserve cell size and age-dependent ion channel function that is consistent with other methods that do not rely on enzymatic treatment (Risner and Holt, 2006; Rocha-Sanchez et al., 2007; Kalluri et al., 2010; Meredith and Rennie, 2015; Ventura and Kalluri, 2019). For example, KCNQ channels are found in patch-clamp recordings in both enzymatically treated ganglion cells and nonenzymatically treated afferent terminals (Pérez et al., 2009; Kalluri et al., 2010; Meredith and Rennie, 2015). Consistent with the electrophysiology, immunohistochemistry indicates a spatiotemporal variation in KCNQ channel expression in vestibular afferent cell bodies and terminals (Rocha-Sanchez et al., 2007).

After enzymatic treatment, ganglia were then washed sequentially in fresh L-15 solution, and culture medium (see below). Somata were dissociated in culture medium by triturating through a series of polished Pasteur pipettes and allowed to settle onto 1% polyethyleneimine-coated glass coverslips. Culture dishes contained bicarbonate-buffered culture medium (MEM, Invitrogen), supplemented with 10 mm HEPES, 5% FBS, and 1% penicillin–streptomycin (Invitrogen). The culture medium was titrated with NaOH to a pH of 7.35. Cells were incubated for 16-24 h in 5% CO₂/95% air at 37°C. Short-term incubation tends to remove supporting and satellite cells, clears debris from enzyme treatment, allows cells to adhere to the substrate, and promotes successful recordings as the animals entered the second postnatal week and beyond.

Electrophysiology

Cells were viewed at 40× using an inverted microscope (Zeiss, Axiovert 135 TV) fitted with Nomarski optics. A MultiClamp 700B amplifier, Digidata 1440 board, and pClamp 10.7 software (MDS; RRID:SCR_011323) were used to deliver, record, and amplify all signals. Recording pipettes were fabricated using filamented borosilicate glass. Pipettes were fire polished to yield an access resistance between 4 and 8 mΩ. Recording pipettes were coated with Parafilm (Bemis) to reduce pipette capacitance.

The properties of ion channels were studied using perforated-patch methods. The contents of the perforated-patch internal solution contained the following (in mm): 75 K₂SO₄, 25 KCl, 5 MgCl₂, 5 HEPES, 5 EGTA, 0.1 CaCl₂, and titrated with 1 m KOH to a pH of 7.4 and an osmolality of 260-270 mmol/kg. Amphotericin B (240/ml; Sigma-Aldrich) was dissolved in DMSO and added to the perforated-patch solution on day of recording. This allowed passage of small monovalent ions while preventing larger molecules from dialyzing.

The series resistance was estimated in voltage-clamp using the built-in series resistance estimation function on the MultiClamp. Series resistance ranged between 8 and 35 mΩ. Recordings with higher series resistance were excluded from analysis. Although series resistance tends to be higher in perforated patch than in ruptured patch, the same cutoff value of 35 mΩ has been used in our previous studies (Ventura and Kalluri, 2019). Series resistance was typically left uncompensated with voltage errors corrected offline. Electrophysiology recordings show command voltages as indicated in the figures. Corrected voltages for input/output functions were calculated by the following equation:

$$V_{corrected}=V_{command}-R_s{I}_{ss}$$

where R_s is the series resistance, I_ss is the steady-state current during the conditioning step.

Half-activation voltages are reported after applying this correction. We assessed the influence of series resistance on V_1/2 in a subset of 4 cells in which we measured V_1/2 both before and after applying 50% series resistance compensation. Online compensation reduced series resistance by an average of 8.8 ± 2.2 mΩ relative to the uncompensated condition. Given the slow activation and long-duration protocol, estimates of V_1/2 were similar with and without online series resistance compensation (mean V_1/2 uncompensated = −96.6 ± 5.0 mV, V_1/2 50% compensated = −97.4 ± 6.3 mV, paired t test, t₍₃₎ = −0.5, p = 0.64, N = 4).

During any given perforated-patch recording, series resistance is expected to drift as the number of perforations fluctuates. Here we report data from cells in which series resistance was relatively stable before and after drug application (Rs_pre-drug – Rs_post-drug = 1.8 ± 1.2 mΩ, t₍₂₀₎ = −1.5, paired t test, p = 0.1536, N = 21). In addition, we found that series resistance had no effect on V_1/2 (r₍₄₅₎ = −0.11, p = 0.45, N = 47).

Whole-cell capacitance was estimated online using the built-in estimation circuitry on the MultiClamp amplifier. Online calculation of capacitance (C_m) was verified offline by analyzing recordings of capacitive currents in response to small depolarizing voltages. We measured C_m by first fitting a single exponential to the transient current evoked by a 5 mV depolarizing step and measuring the membrane time constant (τ_m). C_m was calculated by dividing τ_m by the series resistance. Input resistance (R_in) was calculated from voltage changes in response to a hyperpolarizing 10 or 20 pA step in current-clamp mode.

Recordings were made at room temperature (25°C-27°C) and in an external bath continuously perfused with fresh oxygenated L-15 media. Perforated patch internal solution had junction potentials of 5.0 mV, which was computed with JPCalc (Barry, 1994) as implemented by pClamp 10.7 and left uncorrected. Only recordings in which the cell had formed a giga-ohm seal were used. Recording stability was monitored by measuring resting potential, input resistance, series resistance, and size of action potential. Significant fluctuations in these values within each experimental condition were indicative of an unhealthy cell and/or compromised recording and were not included in our dataset.

Pharmacology

Ten or 100 μm solutions of the mAChR agonist oxotremorine-M (Oxo-M) were prepared on the day of the experiment by dilution in L-15. The effect of Oxo-M on I_H was similar at both doses (average shift in I_H V_1/2 with 10 μm Oxo-M = 3.8 ± 1.1, n = 4, 100 μm = 3.6 ± 1.1, n = 17, Student's t test, t₍₂₀₎ = 0.16, p = 0.89, n = 21). Therefore, we pooled both concentrations for our statistical analyses. The lack of any differences between the low- and high-dose concentrations suggests that there were no off-target effects of Oxo-M, although this could be tested with atropine in a future study. In the experiments that used linopirdine, a 250 μm stock solution was prepared in DMSO and then diluted in L-15 10 μm on the day of the experiment. Drugs were applied via pressurized superperfusion system (Warner Instruments). Measurements of I_H were made at least 5 min after exposure to any drug.

I_H activation parameters

We studied the voltage-dependent activation of I_H using a voltage-clamp tail-current protocol (see Fig. 1). The protocol begins with a 1.7 s conditioning voltage step, followed by a 100 mV “tail-step” for 300 ms and finally returns to −60 mV for 100 ms. The conditioning voltage step was incremented by 5 mV to range between −135 and −40 mV. A 15 s delay was implemented between each step to allow enough time for HCN channels to close completely before starting the next voltage step.

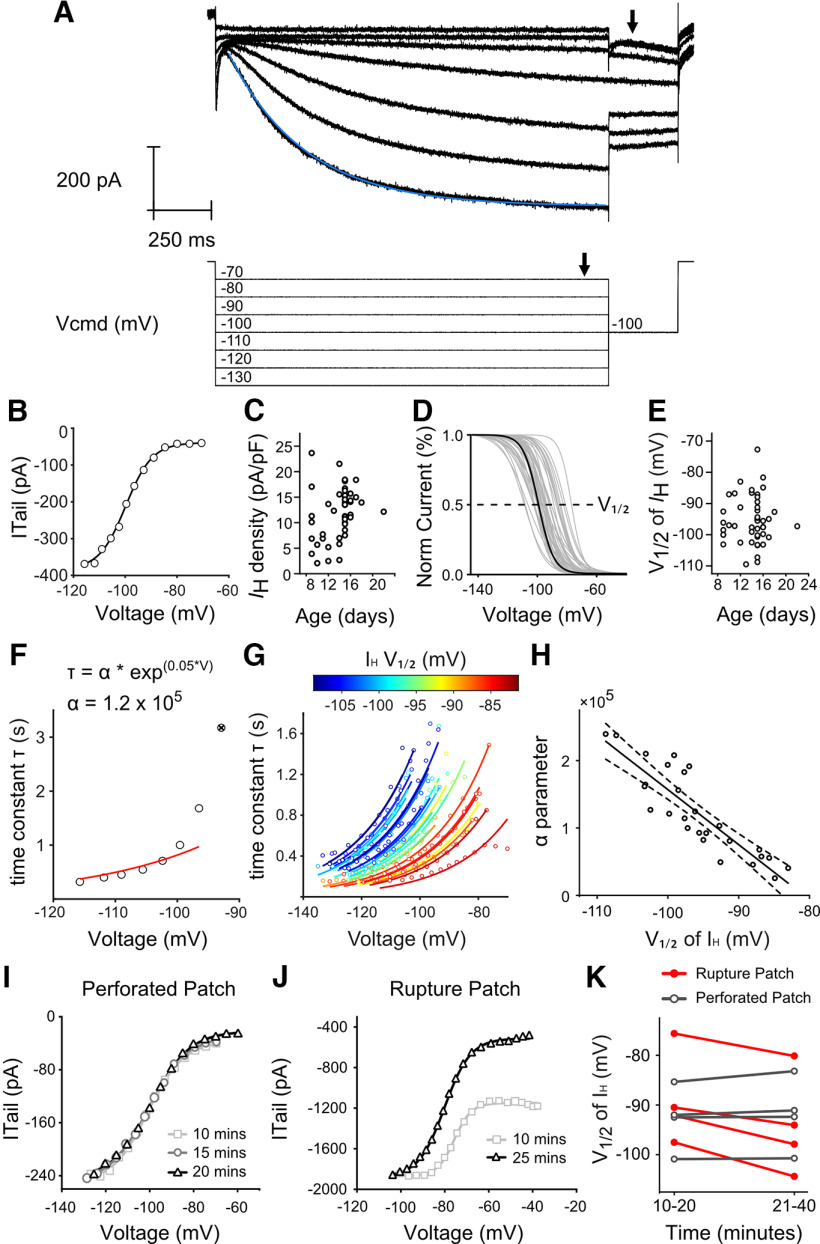
Figure 1.

VGNs have HCN channels with diverse voltage-gated activation properties. A, Currents activated from voltage steps from −130 to −70 mV in a single cell. A single-exponential fit in blue is overlaid on the current response to each conditioning step (example exponential fit is shown in blue). B, I_H activation measured as the magnitude of the tail current (arrowhead in A, top) as a function of the conditioning voltage step (arrowhead in A, bottom). I_H activation curves were fit by Boltzmann function from Equation 1 (dotted curve). C, Current density of I_H varied from 2.1 to 23.6 pA/pF. There was no relationship between current density and age of animal. D, I_H activation curves fit by Boltzmann function were normalized to the maximum conductance of I_H. Gray curves represent the activation curves measured in 47 cells. Bold curve represents the activation curve for cell shown in A and B. E, The half-activation voltage (V_1/2) of I_H varied from −109.5 to −76.4 mV. Like current density, V_1/2 was not related to age. F, Current responses were fit with an exponential line (exponential fit of current response to −130 mV step is shown in blue in A). The time constant τ from the exponential fits of the cell shown in A is plotted with the voltage step on the x axis. A single-parameter exponential described in Equation 2 was used to fit the τ value/voltage relationship in this cell (dotted line). Point labeled with X was excluded from fitting since it exceeded the duration of the stimulus (1.7 s). G, Fits of the τ value/voltage relationship for each cell. Points and lines are color-coded according to the V_1/2 of each individual cell, with the most depolarized V_1/2 values in red and the most hyperpolarized V_1/2 values in blue. H, The α parameter, which describes the steepness of the fits in I_H activation rate, is shown for each cell plotted against the V_1/2 of I_H. I, Tail currents from a single neuron assessed at three different time points using the perforated patch technique. J, Tail currents from a different single neuron assessed at two different time points using the rupture patch technique. K, Shift in the half-activation voltage of I_H (V_1/2) after short (10-20 min) and long (21-40) intervals in perforated patch and rupture patch recording conditions. In rupture-patch recording conditions, V_1/2 hyperpolarized over time (p = 0.0006, n = 4, Tukey–Kramer HSD).

We chose to make all measurements with a 1.7 s conditioning step. Although even longer steps would allow more current to activate and reach its true steady state, the extreme hyperpolarization significantly increases the cell's risk of dying during recording (Ventura and Kalluri, 2019). Therefore, we chose this step duration to allow us to repeat the protocol in several pharmacological conditions.

The voltage-dependent activation of I_H is characterized by plotting the amplitude of current flowing at 100 ms after the start of the tail step (I_tail) against the conditioning voltage (V_con). This is a measure of the slow component of I_H rather than the fast instantaneous component. Measurements of I_tail were taken 100 ms into the tail step to avoid contamination from other low-voltage gated currents, particularly during the most positive voltage steps (−60 to -40mV). These data were fit with a Boltzmann function (Eq. 1):

$$I_{tail}=\frac{I_{max}}{1+\left({\text{exp}}^{\frac{V1/2-Vcon}{k}}\right)}+C$$ (1)

where I_max is the maximum current of the Boltzmann function, V_con is the conditioning voltage, V_1/2 is the half-activation potential, k is the slope factor, and C is a constant. To ensure adequate fitting, the range of V_con was adjusted in each cell to ensure that the I_H current saturated at the most negative potentials. Only Boltzmann fits with correlation coefficients of ≥0.95 were retained to ensure that the voltage activation properties were well described.

The time course for I_H current activation was estimated by fitting the current evoked at the −135 to −70 mV conditioning step with a single exponential. Fits were not attempted for more positive steps because I_H currents are small and there was a potential for contamination by other currents activating. All fits were obtained after a 60 ms delay from the start of the voltage step. Only fits with a correlation coefficient ≥0.95 were retained. The τ value was used to estimate the time course of I_H activation. Values greater than the 1.7 s I_H-testing protocol, which were often observed at the smallest voltage steps (±10 mV), were discarded since these values cannot be assumed to be accurate since they exceeded the length of the protocol. To estimate the effect of Oxo-M on the voltage activation speed of HCN channels, the τ values across multiple voltage steps were fit with a simple exponential equation shown in Equation 2.

$$\text{τ}=\alpha *{\text{exp}}^{(0.05*V)}$$ (2)

This equation allowed us to quantify the relationship between τ and voltage step as a single model parameter, α. We fit τ values only as far as they increased with depolarizing voltage. Only fits with a correlation coefficient ≥0.80 are included in figures and our analyses. The true dependence on voltage is likely more complicated than can be captured by this single exponential. However, this fit has the advantage in allowing us to plot the relationship between the voltage dependence of activation kinetics and V_1/2 using a single simple parameter (α).

Experimental design and statistical analyses

All data were analyzed with pClamp 10 software (Clampfit; MDS Analytical Technologies). Statistical analysis was done with Origin Pro (OriginLab; RRID:SCR_014212) and/or JMP Pro 13 (SAS Institute; RRID:SCR_014242). Statistical significance was estimated with Student's t test when comparing between groups. Assumptions of equal variance and normality were assessed before running t tests with Levene's and Kolmogorov–Smirnov tests, respectively. For assessment of bimodal distributions, we defined the midpoint of the bimodal distribution as the point of maximum overlap between two gaussians that were fit to each mode. One-way ANOVAs were applied and followed by a post hoc Tukey's HSD analysis, as required, to drug condition on V_1/2. Since the distribution of V_1/2 in each firing pattern was not normally distributed, median V_1/2 values in these groups were reported and compared using Kruskal–Wallis and Steel–Dwass as the related post hoc test. A two-way repeated-measures ANOVA and Tukey's HSD post hoc test were applied to compare time-related drift in V_1/2 in perforated and ruptured-patch recording conditions. A linear mixed model was used to compare the I_H kinetics parameter, α, in control and Oxo-M conditions while controlling for V_1/2. We used a threshold value of 0.05 for all statistical tests. Significant p values of <0.05 are indicated in figures with asterisks. Descriptive statistics are reported as mean ± SEM.

Results

We present whole-cell, perforated patch-clamp recordings from cultured VGN of rats aged postnatal day (P)9 to P22 (n = 84). Firing pattern was assessed in all recorded cells, and I_H was characterized in 47 of the 84 cells. Although we present all available data over the full age range, most of the data (59 of 84 cells) are from P15 ± 1 d. We first describe the diversity of HCN current characteristics in VGN and its sensitivity to recording conditions. Second, we present data on whether HCN channels in VGN are sensitive to muscarinic signaling cascades using the muscarinic agonist Oxo-M. Third, we characterize HCN channel sensitivity to muscarinic signaling cascades in relation to cell type as defined by firing pattern and somatic size. Finally, we examine the impact of muscarinic signaling cascades on firing patterns. Table 1 summarizes the number of cells and age ranges included in each analysis.

Table 1.

Summary of the number of cells and age ranges included in each analysis

Data collected	Control (n, n15±1)	Linopirdine (n, n15±1)	Oxo-M (n, n15±1)	Linopirdine + Oxo-M (n, n15±1)
Firing pattern	Total n = 84, 59	Total n = 10, 5	Total n = 21, 11	Total n = 12, 6
	Transient (n = 43, 31)	Transient (n = 5, 3)	Transient (n = 13, 8)	Transient (n = 4, 3)
	Sustained-A (n = 5, 4)	Sustained-A (n = 1, 0)	Sustained-A (n = 1, 0)	Sustained-A (n = 1, 0)
	Sustained-B (n = 25, 18)	Sustained-B (n = 3, 2)	Sustained-B (n = 6, 2)	Sustained-B (n = 4, 2)
	Sustained-C (n = 11, 6)	Sustained-C (n = 1, 0)	Sustained-C (n = 1, 1)	Sustained-C (n = 3, 1)
IH voltage activation range	Total n = 47, 29	Total n = 8, 5	Total n = 21, 11	Total n = 12, 6
	Transient (n = 29, 19)	Transient (n = 5, 3)	Transient (n = 13, 8)	Transient (n = 4, 3)
	Sustained-A (n = 1, 0)	Sustained-A (n = 1, 0)	Sustained-B (n = 1, 0)	Sustained-A (n = 1, 0)
	Sustained-B (n = 11, 7)	Sustained-B (n = 3, 2)	Sustained-B (n = 6, 2)	Sustained-B (n = 4, 2)
	Sustained-C (n = 6, 3)	Sustained-C (n = 1, 0)	Sustained-C (n = 1, 1)	Sustained-C (n = 3, 1)
HCN channel activation rate	Total n = 47, 29	Total n = 9, 5	Total n = 22, 11	Total n = 11, 5
	Transient (n = 29, 19)	Transient (n = 5, 3)	Transient (n = 12, 6)	Transient (n = 4, 3)
	Sustained-A (n = 1, 0)	Sustained-B (n = 3, 2)	Sustained-A (n = 1, 0)	Sustained-A (n = 1, 0)
	Sustained-B (n = 11, 7)	Sustained-C (n = 2, 0)	Sustained-B (n = 8, 4)	Sustained-B (n = 3, 1)
	Sustained-C (n = 6, 3)	Data not shown	Sustained-C (n = 1, 1)	Sustained-C (n = 3, 1)

Diversity in the activation properties of HCN channels in the vestibular ganglion

We assessed two properties of HCN channel activation that are known to be modifiable: voltage activation range and voltage-dependent rate of activation. An example of the voltage activation of I_H currents is shown in Figure 1A. The voltage dependence of I_H is apparent when the magnitude of the current measured during the tail step (Fig. 1A, top, arrow) is plotted as a function of the conditioning voltage step (Fig. 1A, bottom, arrow). These current–voltage activation curves (Fig. 1B) are sigmoidal in shape and fit by a Boltzmann equation (Fig. 1B, dashed line; see Eq. 1). I_H activation curves derived from this protocol closely approximate those measured by pharmacologically isolating I_H using HCN channel blockers like CsCl or ZD7288 (Ventura and Kalluri, 2019).

The size of the maximum I_H tail current (I_max) ranged from as large as 703 pA to as small as 38 pA (mean = 261.6 ± 22.9 nA, SD = 156.8 nA, n = 47). To account for variations in cell size, Figure 1C plots I_H current density as a function of age. Regression analysis showed that there was no dependence of I_H current density on age between P9 and P22 (r₍₄₅₎ = 0.22, p = 0.70, n = 47, Fig. 1C). The Boltzmann fits were normalized by I_max to allow direct comparison of the activation range from different cells (Fig. 1D, example from Fig. 1A,B, bolded). The voltage at which half of the I_H current is active (V_1/2) is indicated in Figure 1D as a dotted line. V_1/2 ranged from as positive as −76 mV to as negative as −110 mV (average V_1/2 = −95.5 ± 1.1 mV, SD = 7.2 mV, n = 47). V_1/2 did not change with age (r₍₄₅₎ = 0.03, p = 0.83, n = 47; Fig. 1E).

The activation rate of I_H depends on the size of the conditioning voltage step; with more negative steps activating the current more quickly than more positive steps. To quantify the relationship between voltage and activation rate, we fit a single exponential curve with a time constant (τ) to the I_H trace during each of the long conditioning voltage steps (V) (Fig. 1A, blue curve overlaid on current response to −130 mV hyperpolarizing step). Figure 1F shows the relationship between τ and the command voltage steps V in the same cell shown in Figure 1A. τ values were smallest (i.e., I_H activated more quickly) in response to the largest hyperpolarizing steps, while τ values were largest (i.e., I_H activated more slowly) at the smallest steps. τ values that exceeded the duration of the hyperpolarizing step (1.7 s) were excluded from the exponential fit as they could not be assumed to be accurate (Fig. 1F, crossed out point).

The slowing down of I_H activation at more depolarized voltages is a general feature of I_H kinetics as illustrated in 27 cells (Fig. 1G). However, the sensitivity of τ to V is highly variable as I_H activation slowed down more in some cells than in others. To quantify the sensitivity of τ to V, we fit τ(V) with an exponential function with a free parameter α (see equation in Fig. 1F; Eq. 2). α reflects the steepness of τ(V) and therefore how quickly the channel activates across a range of membrane potentials. In Figure 1F, the fit for the example cell is shown with the dashed line; and in Figure 1G, the fits for the remaining cells are shown.

The sensitivity of τ to V is dependent on the voltage activation range. Figure 1G color-codes exponential fits according to the half-activation voltage of I_H (V_1/2). Cells with more depolarized V_1/2 (red) have smaller values for τ(V) and faster activation rates than cells with hyperpolarized V_1/2 (blue). To quantify this covariance, we plotted α against V_1/2 (Fig. 1F; see Eq. 2). Larger values of α correspond to τ values that increase more quickly (i.e., activate more slowly) as the conditioning steps approach the half-activation voltage. As illustrated in Figure 1H, α is inversely dependent on V_1/2 (r₍₂₅₎ = −0.88, p < 0.0001). This is consistent with other HCN studies that have linked faster activation rates to depolarized V_1/2 (Almanza et al., 2012; Ventura and Kalluri, 2019).

The range of V_1/2 values seen here is broader than in previous studies (Almanza et al., 2012; Ventura and Kalluri, 2019). These studies mostly recorded using rupture-patch methods in which the intracellular composition is subject to dialysis with the contents of the recording pipette. Such dialysis may impact the concentration of intracellular second messengers, such as cAMP, and thus reduce cell-to-cell variability in the activation range of HCN channels. Figure 1I, J illustrates the stability of V_1/2 in an individual cell during recordings using perforated patch compared with the instability and long-term hyperpolarization of V_1/2 in a second cell using ruptured patch methods. In perforated patch, the estimates of I_H currents are stable over the duration of the recording session, both in current magnitude and in V_1/2 (Fig. 1I). In contrast, there is considerable drift over time in both the current magnitude and V_1/2 when recordings were made in rupture-patch (Fig. 1J). In all four cells recorded using the ruptured patch technique, V_1/2 shifted in the hyperpolarizing direction after less than an hour, whereas V_1/2 remained stable in all cells recorded using the perforated-patch technique (Fig. 1K, V_1/2 shift perforated patch = −0.8 ± 0.5 mV, p = 0.56, n = 4, V_1/2 shift rupture patch = −5.2 ± 0.7 mV, p = 0.0006, n = 4, Tukey–Kramer HSD). The remaining data are reported for recordings made using perforated-patch methods exclusively.

Activating mAChRs depolarizes the activation range of HCN channels via a KCNQ-independent mechanism

To test whether activating muscarinic receptors influences the voltage-gated properties of HCN channels, we measured the voltage activation of I_H currents under different pharmacological conditions (Fig. 2A,B). First, we characterized I_H in a control solution (Fig. 2A1,B1). Next, in some cells, we switched the bath solution to contain Oxo-M (Fig. 2A2), a muscarinic receptor agonist known to close KCNQ channels in VGN by activating a G-protein-coupled signaling cascade. In other cells, we first added a KCNQ channel blocker, linopirdine (Lino; Fig. 2B2) before switching to a cocktail containing both Lino and Oxo-M (Lino+Oxo-M; Fig. 2B3). In order to maximize the number of successful recordings, we continued recording from new cells after Lino, Oxo-M, or Lino+Oxo-M were introduced into the bath. In these not-naive cases, a control-condition recording was not available for a paired comparison before and after treatment.

Figure 2.

Activation of mAChRs depolarizes the voltage activation range of I_H. A, Currents activated from voltage steps from −140 to −60 mV in a single before and after Oxo-M (A1,A2) and in a single cell in control, linopirdine, and linopirdine and Oxo-M conditions (B1,B2,B3). C–E, Data from the individual neuron shown in A. F–H, The neuron from B. C, I_H activation curves were fit by a Boltzmann function before (light gray squares) and after Oxo-M (black triangles). D, The fractional activation of I_H plotted as a function of the conditioning voltage step. E, Each point represents a single V_1/2 measurement with lines connecting each cell before (square) and after Oxo-M (triangle). The average shift of all cells is drawn in bold. V_1/2 in 11 of 12 neurons shifted in the depolarized direction (*p = 0.0015, paired t test). F, I_H activation curves were fit by Boltzmann function in control (light gray squares), linopirdine (dark gray circles), and after Oxo-M (black triangles). G, The fractional activation of I_H plotted as a function of the conditioning voltage step. H, Each point represents a single V_1/2 measurement at baseline (square), after linopirdine (circle), and then after administration of both linopirdine and Oxo-M (triangle). The average shift of all cells is drawn in bold. Linopirdine had no effect on V_1/2, while the cocktail containing linopirdine and Oxo-M shifted the activation range in the depolarizing direction (*p = 0.0236, Tukey's HSD).

Activating the muscarinic receptor via Oxo-M enhanced HCN channels by shifting the activation range of I_H in the depolarizing direction. Figure 2C shows the voltage activation of the I_H current in control and drug conditions for the cell shown in Figure 2A. The I_H half-activation voltage, V_1/2, is shown as a dotted line in Figure 2D. The voltage-dependent activation of I_H shifted in the depolarizing direction in 11 of the 12 cells tested (Fig. 2E). The extent of the depolarizing shift was variable from cell to cell; in some cells, V_1/2 shifted by as much as 5.8 mV in the depolarizing direction; while in other cells, V_1/2 shifts were more modest. The overall effect on I_H was a significant positive shift of 2.3 ± 0.6 mV (paired t test, t₍₁₁₎ = 4.2, p = 0.0015, n = 12). This depolarizing shift was consistent across the whole voltage range as the steepness of the fractional activation of I_H (the slope factor, k) was unaffected (k_control = 6.16 ± 0.58, k_Oxo-M = 6.24 ± 0.39 mV, t₍₁₁₎ = 0.25, p = 0.81, paired t test). Similarly unchanged were I_max, the maximum I_H tail current (I_{max control} = 203.2 ± 31.8 pA, I_{max Oxo-M} = 212.5 ± 31.2 pA, t₍₁₁₎ = 1.65, p = 0.13, paired t test), and the constant C (C_control = −257.2 ± 33.0, C_Oxo-M = −267.3 ± 33.8 pA, t₍₁₁₎ = 1.6, p = 0.13, paired t test). Therefore, Oxo-M induced a depolarizing shift in the voltage activation range, while the shape of the I_H current's voltage sensitivity remained consistent.

Activation of mAChR is known to reduce potassium currents carried by KNCQ channels (Pérez et al., 2009; Brown, 2010; Holt et al., 2017). To test whether directly blocking the KCNQ channels had a similar impact on the activation of HCN channels, we characterized I_H activation with the KCNQ channel blocker linopirdine in the bath. Voltage activation of the I_H current in all three experimental conditions for the cell from Figure 2E is shown from the tail conductance and normalized currents in Figure 2F and Figure 2G, respectively. Linopirdine depolarized resting potential by 5.7 ± 1.2 mV (t₍₈₎ = 19.6, p = 0.0022, paired t test, n = 9), which is consistent with the closure of KCNQ channels. Figure 2F shows V_1/2 in all cells as the bath solution transition

Linopirdine had no effect on V_1/2 (ΔV_1/2 = −0.18 ± 1.9 mV; Tukey–Kramer HSD, p = 0.9953). Oxo-M shifted V_1/2 in the depolarizing direction relative to baseline V_1/2 linopirdine (ΔV_1/2 = 5.77 ± 1.9, p = 0.0236, Tukey–Kramer HSD). These results show that Oxo-M shifts I_H activation in the depolarizing direction independently of its effect on closing KCNQ channels. Since we found that linopirdine has no effect on HCN channels, cells that received the cocktail of linopirdine plus Oxo-M are pooled together with the Oxo-M group, unless otherwise noted.

Activating mAChRs increases the speed of HCN channel activation

We next examined whether muscarinic signaling cascades also affect the activation rate of HCN channels. Since cells with more depolarized V_1/2 in control conditions also have faster activation kinetics (Fig. 1H), we tested whether the mAchR triggered depolarization in V_1/2 also accelerated the activation rate.

Figure 3 shows evoked currents in a single cell before (Fig. 3A) and after Oxo-M (Fig. 3B). We characterized the activation time course τ(V) (defined in Fig. 1) in 40 cells in control and Oxo-M conditions of which 14 were tested in both (Fig. 3C, blue and red symbols, respectively). In the Oxo-M condition (red curves) compared with control condition (blue curves), τ(V) is shifted to the right, has overall smaller values across all voltage steps (V), and is less sensitive to changes in voltage. The parameter, α, derived from exponential fits to τ(V) is shown in Figure 3D. Cells that received Oxo-M reported α values that were 20% smaller than cells in control solution, which reflects a significant speeding of activation rates. In 14 cells in which I_H kinetics were assessed before and after Oxo-M, Oxo-M significantly reduced α in 9 (t₍₁₃₎ = −2.56, p = 0.0236, N = 14, paired t test). The variance of $\alpha$ was also reduced in the Oxo-M condition (SD_control = 6.4 × 10⁴, SD_Oxo-M = 3.9 × 10⁴, F_(1,52) = 7.52, p = 0.0084, Levene's Test, N = 54). Given that the net tendency is for α to become smaller, this reduction in variance may reflect the limit to how quickly the channels can activate.

Figure 3.

mAChR agonists increase the rate of HCN channel activation. A, B, Currents activated from voltage steps from −130 to −70 mV in a single cell in control solution (A, black) and in Oxo-M (B, red). C, The time constant τ derived from fits to whole-cell currents is plotted as a function of the command voltage step (V). A single-parameter exponential described in Equation 2 was used to fit the τ(V) for each cell. τ(V) recorded in the control condition is shown in blue lines and squares. Cells from the Oxo-M condition are shown in red lines and triangles. D, α from Equation 2 is plotted for each cell before (blue squares) and after Oxo-M (red triangles). Thin lines connect individual cells. Bold line indicates the mean difference in α. Oxo-M increased the activation rate of I_H as indicated by the reduction in α (*p = 0.0236). E, τ(V) in control solution. F, τ(V) in Oxo-M. Points and lines are color-coded according to V_1/2, with the most depolarized V_1/2 values in red and the most hyperpolarized V_1/2 values in blue. G, α values plotted against the V_1/2 of each cell on the x axis in control (blue squares) and Oxo-M (red triangles) conditions. Straight lines indicate linear regression, and 95% CI estimates of control and Oxo-M groups in black and red, respectively. H, α and V_1/2 measurement pairs from 14 individual cells tested before (blue squares) and after (red triangles) Oxo-M administration. Arrows are drawn between two data points in each cell. Linear regressions from G are shown in dotted lines in H.

Figure 3E, F shows τ(V) in control and Oxo-M conditions with individual curves colored according to V_1/2 (blue to red as V_1/2 becomes more depolarized). The depolarizing shift in V_1/2 by Oxo-M is evident in Figure 3F by the decrease in the number of cells with hyperpolarized V_1/2 in blue and an increase in the number of cells with depolarized V_1/2 in red. As evident by the smooth progression of color in the plots of τ(V) versus V_1/2, there remains a clear correlation between V_1/2 and τ(V) in both conditions. This is clearly quantified by linear regression plots for α versus V_1/2 in Figure 3G (r_control(25) = −0.88, p < 0.0001, N = 27, r_Oxo-M(25) = −0.83, p < 0.0001, n = 27). When controlling for V_1/2, we found no effect of Oxo-M on the activation-rate parameter α (F_(1,50) = 0.72, p = 0.47). This suggests that the change in α is related to the overall depolarization of V_1/2 in the Oxo-M condition.

The possibility of an upper limit to the speed of activation is evident in the paired comparisons shown in Figure 3H. Cells with the most hyperpolarized V_1/2 and slowest activation kinetics in control conditions had the largest changes in activation kinetics in response to Oxo-M. Here we plot α in 14 cells that were tested before and after Oxo-M administration. Of the two cells with the largest change in α, both had V_1/2 values that were relatively hyperpolarized before mAChR activation (negative to −100 mV). In contrast, two cells with depolarized V_1/2 values (positive to −100 mV) had large changes in V_1/2 without a corresponding reduction in α.

HCN channel properties covary with firing pattern and cell size

Next, we tested whether V_1/2, τ(V), and the sensitivity of these properties to mAChR activation varied by VGN subgroups. Two criteria were used to classify VGN subgroups: (1) cell size (as inferred from capacitance measurements) and (2) firing patterns in response to current injection. We considered cell size because afferents with larger cell bodies and axon diameters more commonly originate from the central regions of sensory epithelia where they are more likely to synapse with Type I hair cells and produce irregular-timed spike patterns in vivo (Lysakowski and Goldberg, 1997; Leonard and Kevetter, 2002). Also, immunohistochemistry suggests that HCN channel isoforms are differentially enriched in large and small-diameter somata; the isoform containing the HCN2 subunit is more common in large-diameter ganglion somata (Almanza et al., 2012). We also tested whether the activation properties of HCN channels differ by in vitro firing pattern because previous studies linked them to in vivo firing patterns (Kalluri et al., 2010; Hight and Kalluri, 2016) and suggested that HCN channels contribute to spike-timing regularity (e.g., Horwitz et al., 2014; Yoshimoto et al., 2015).

Defining vestibular ganglion neuron subgroups based on firing patterns and cell size

VGNs respond to simple current injection with diverse firing patterns (Iwasaki et al., 2008; Kalluri et al., 2010). VGNs with these diverse firing patterns and their distributions of cell size are shown in Figure 4A–D. We broadly classified VGNs as either transient firing (N = 43) or sustained firing (N = 41) according to criteria described by Kalluri et al. (2010). Transient firing VGNs produce a single action potential in response to 500 ms current steps that reach or exceed spike threshold (Fig. 4A1). The responses of sustained firing VGN are more variable because of variations in the size of low-voltage activated potassium currents and sodium currents (Hight and Kalluri, 2016). Although firing patterns are dependent on continuous variations in underlying ion channel composition and thus it is difficult to define the boundaries between firing pattern subgroups, we qualitatively grouped sustained firing neurons into three broad subgroups. Sustained-A neurons fire continuously throughout the current step (Fig. 4B1, N = 5). Sustained-B neurons fire multiple action potentials that increase in frequency at larger current steps (Fig. 4C1, N = 25). Sustained-C neurons fire a single action potential followed by voltage oscillations (Fig. 4D1, N = 11). In all VGNs, large negative current steps produced a sharp hyperpolarization followed by a slow depolarization. The resulting voltage “sag” indicates the activation of net inward currents through HCN channels (see Fig. 4A1–D1, arrows).

Figure 4.

Vestibular ganglion neurons are heterogeneous with different firing patterns in response to depolarizing current steps. Large hyperpolarizing current steps produce a voltage sag (arrow) driven by the hyperpolarization-activated mixed cationic current (I_H). Scale bars are consistent throughout all traces. Depolarizing current steps are the closest 20 pA current step to threshold in each trace. A1, Transient firing neurons fire a single action potential at the onset of suprathreshold depolarizing current steps. The amplitude of the positive current step necessary to reach threshold is shown below each trace. Dashed line indicates −60 mV. A2, Size distribution of transient firing neurons was measured from C_m. B1, Sustained-A neurons fire continuously throughout the current step. B2, Size distribution of sustained-A firing neurons. C1, Sustained-B neurons fire multiple action potentials after the onset of the depolarizing current steps and are rapidly adapting. C2, Size distribution of sustained-B firing patterns. D1, Sustained-C neurons fire a single action potential followed by voltage oscillations. D2, Size distribution of sustained-C neurons. E, Top, Firing patterns in all cells (n = 81) plotted against age in postnatal days. Transients are shown as blue triangles (n = 40), sustained-A as gray asterisks (n = 5), sustained-B as red squares (n = 26), and sustained-C as green circles. Cells aged P15 ± 1 d are represented as empty shapes, while points from all other ages are filled in. Bottom, Size distribution overlaid with two Gaussian distributions fit to each peak. The two distributions intersect at 26 pF. F1, Firing pattern of all 81 cells according to their age in postnatal days. Gray area highlights the postnatal day 15 shown in F2. F2, Size distribution of cells recorded at exactly 15 d of age.

Membrane capacitance is an indirect measure of somatic size. As shown in previous studies, VGNs come in a variety of sizes (Limón et al., 2005). Cell size in transient firing and sustained-A firing VGN was broadly distributed (Fig. 4A2,B2), although only 5 sustained-A firing cells were recorded in this study. Most sustained firing VGNs were classified as sustained-B or sustained-C firing (36 of 41) and were generally small (Figs. 4C2,D2). Although the distribution of sizes for transient firing neurons was broad, they were, on average, larger than sustained firing VGN (Transient C_m = 26.1 ± 1.6 pF, N = 43, Sustained-A/B/C C_m = 20.6 ± 1.4 pF, N = 41, t₍₈₃₎ = 2.81, p = 0.0106, Student's t test). That large cells tend to be transient firing is consistent with previous studies (Kalluri et al., 2010; Ventura and Kalluri, 2019).

Figure 4E1 shows the number of cells recorded within each firing pattern subgroup by age and cell size. Transient firing was the most prevalent firing pattern encountered in this study (N = 43), while sustained-A firing patterns were rarely encountered at this age range (N = 5). Sustained-A firing patterns are more frequently encountered in the first postnatal week than seen here (Kalluri et al., 2010; Ventura and Kalluri, 2019).

Across all ages and firing patterns, we observed transient and sustained firing patterns in both large and small somata (Fig. 4E). Here, we defined cells with capacitance >26 pF as large cells. This value was determined by fitting two gaussians to the bimodal distribution of cell size; 26 pF was the intersection of these two Gaussian distributions. This value is consistent with other studies that defined large cells as having capacitance >30 pF (Limón et al., 2005; Mercado et al., 2006; Almanza et al., 2012). Large cells were mostly transient firing (20 of 27 total), while small cells were more often sustained firing (34 of 57).

The broad range of cell size and firing patterns is not an artifact of sampling from a wide range of ages. We observed a similarly broad variety of cell sizes and firing patterns from cells recorded at a single age point (at p15, highlighted in gray in Fig. 4F1). Among p15 cells, cell size was bimodally distributed with all cell sizes and firing patterns represented (Fig. 4F2, N = 44). The relationship between firing pattern and cell size is present in this limited age range. For example, most large somata were transient firing (15 of 20), and more than half of all small somata were sustained firing (15 of 24). Therefore, the diversity in firing patterns and cell size did not result from the wide age range in our dataset. Nevertheless, in this figure and in all figures that follow, cells aged P15 ± 1 d are represented as empty shapes while filled in shapes represent cells of all other ages.

The dependence of I_H activation range and kinetics on firing pattern

Figure 5A shows four representative examples of I_H current responses in VGNs with transient, sustained-A, sustained-B, and sustained-C firing patterns. Figure 5B shows the current–voltage relationship from the tail currents in the same four cells. Transient, sustained-A, sustained-B, and sustained-C firing cells had I_H currents of 293.9 ± 29.6 pF (SD = 159.5, N = 29), 224.5 pF (N = 1), 246.3 ± 50.7 (SD = 168.1, N = 11), and 140.1 ± 21.3 (SD = 52.2, N = 6), respectively. I_H current densities were similar across all firing pattern subgroups (current density transient = 12.5 ± 1.0 pA/pF, N = 29, current density sustained-A/B/C = 10.6 ± 1.0, N = 18). Although sustained-A firing patterns are rarely found during the second to third postnatal weeks, the I_H current density in the one sustained-A cell we recorded from is like that of the other sustained firing cells.

Figure 5.

Heterogeneity of I_H activation properties as a function of firing pattern and cell size. A, Currents activated from voltage steps from −135 to −60 mV followed by a −100 mV tail step from four representative different neurons with different firing patterns. B, C, Data from the individual neurons shown in A. A large transient firing neuron is shown in A1, sustained-A firing neuron in A2, sustained-B firing neuron in A3, and sustained-C firing neuron in A4. The sustained-A example shown in A2 is the only cell in this group. In the same neurons, (B) tail currents and (C) I_H activation curves fit by Boltzmann function and normalized to the maximum conductance of I_H are shown. D, Violin plots and individual data points on a normal distribution of V_1/2 of I_H in each firing pattern group are shown. Cells aged 15 ± 1 d are indicated as empty shapes. V_1/2 is more depolarized in transient firing neurons than sustained-B neurons (*p = 0.0213, Steel–Dwass method) and sustained-C neurons (*p = 0.0013). Cells in which the V_1/2 of I_H was positive of −95 mV were designated as HCN-depolarized (gold area of graph), and cells with I_H activation ranges more negative than −95 mV were grouped as HCN-hyperpolarized (gray area of graph). E, Distribution of V_1/2 values in all 47 cells. The two peaks of the distribution were fit with separate normal distributions. The two distributions intersect at −91.5 mV. Cells with V_1/2 more hyperpolarized than −91.5 mV are colored in gray, and cells with V_1/2 more depolarized than −91.5 mV are colored in gold. F, V_1/2 is shown plotted against cell size (Capacitance). Firing patterns are represented by shapes shown in D. Cells above dashed line were classified as HCN-depolarized, and cells below dashed line were HCN-hyperpolarized. G, C_m distribution in transient firing (top) and sustained-A, -B, and -C firing (bottom) cells. The number of cells classified as HCN-depolarized is shown in the histogram in gold, while cells defined as HCN-hyperpolarized are shown in gray. H, A single exponential was fit to each conditioning step from −135 to −60 mV from cells in each firing pattern, and the time constant τ from each step is plotted as a function of voltage. Cells with transient firing patterns are shown in blue triangles, sustained-A in gray asterisks, sustained-B in red squares, and sustained-C in green circles. I, τ constant in all cells is shown as either HCN-depolarized (gold line and circles, n = 13, 9 of which were age P15 ± 1 d) or HCN-hyperpolarized (gray line and circles, n = 34, 21 of which were age P15 ± 1 d).

As shown in the normalized I_H currents in Figure 5C, the cell with the transient firing pattern had a more depolarized V_1/2 than the example cells with sustained firing patterns. Cells with different firing patterns differed in V_1/2 (H₍₂₎ = 13.2, N = 47, p = 0.0014, Kruskal–Wallis test, Fig. 5D). V_1/2 in most transient firing cells (22 of 29) was more depolarized than almost all (16 of 18) sustained firing cells. Overall, transient firing cells had more depolarized V_1/2 (mean = −93.2 ± 1.0 mV, median = −94.4, N = 29) than sustained-B (mean = −97.3 ± 2.9 mV, median = −100.0 mV, N = 11, p = 0.0213, Steel–Dwass method), sustained-C cells (mean = −103.2 ± 2.0 mV, median = −102.5 mV, N = 6, p = 0.0013), and a sustained-A cell (V_1/2 = −97.3 mV).

When data from all firing patterns are pooled, the distribution of V_1/2 values is bimodal (Fig. 5E). We defined the midpoint of the bimodal distribution as the point of maximum overlap (here −91.5 mV) between two gaussians that were fit to each mode. We classified any cell with an I_H activation range more positive than −91.5 mV as HCN-depolarized and those with I_H activation more negative than −91.5 mV as HCN-hyperpolarized (Fig. 5D,E, to the right and above the dotted lines, respectively). Most cells (34 of 47) had V_1/2 values that were more negative than −91.5 mV and were accordingly classified as HCN-hyperpolarized cells. Thirteen of the 47 cells were classified as HCN-depolarized, and all but two of them had transient firing patterns. Of the two HCN-depolarized cells that were not transient firing, both were sustained-B firing and had the most depolarized V_1/2 of all cells recorded. Figure 5F shows that the two sustained-B firing cells in the HCN-depolarized group were also among the largest cells, whereas many cells with the most hyperpolarized V_1/2 were among the smallest.

We further illustrate how V_1/2 relates to both firing pattern and cell size; we plotted the distribution of cell size for transient and sustained firing VGNs (Fig. 5G). Different colored bars represent the number of cells in each firing pattern group that were classified as either HCN-depolarized (yellow) or HCN-hyperpolarized (gray). The HCN-hyperpolarized group contained a mix of both transient and sustained firing cells, while cells in the HCN-depolarized group were almost exclusively transient firing (11 of 13). Transient firing, HCN-depolarized cells were mostly moderate- to large-sized, while sustained firing cells tended to be small and mostly have hyperpolarized HCN channels, except for the two large cells with sustained firing cells as noted above. Overall, HCN-depolarized cells were larger than HCN-hyperpolarized cells regardless of firing pattern (C_m HCN-depolarized: 30.8 ± 2.6 pF, N = 13; C_m HCN-hyperpolarized: 19.0 ± 1.3 pF, N = 34; t₍₄₆₎ = 20.9, p < 0.0001). These results show that both cell size and transient firing patterns are associated with depolarized V_1/2. It remains to be tested whether this variability in V_1/2 is related to a previously described size dependence in HCN channel isoform expression (Almanza et al., 2012).

Figure 5H shows the τ(V) (voltage-dependent activation rate of I_H current) for transient- and sustained-A, -B, -C firing cells (blue triangles, gray asterisk, red squares, and green circles, respectively). As with V_1/2, τ(V) is not simply related to firing pattern. While many transient firing cells have fast activation time constants, many transient firing cells also had slow activation. Similarly, most sustained-spiking cells had relatively slow activation, but the two large sustained-B cells noted above had very fast activation (arrowheads). Consistent with the analysis in Figure 3, Figure 5J shows that HCN-depolarized cells have faster activation kinetics than HCN-hyperpolarized cells. Therefore, HCN channels in cells with depolarized V_1/2 activate more quickly.

Muscarinic modulation of I_H alters firing pattern in only some VGN

Given that the activation properties of HCN channels vary according to VGN firing pattern and size, an important question is whether there is a correlated sensitivity to mAChR activation. We first examined how firing patterns are altered by mAChR activation in 9 cells that were sequentially exposed to all three bath solutions: control, linopirdine, and linopirdine plus Oxo-M. On average, resting membrane potential (RMP) depolarized by 5.7 ± 1.3 mV in response to linopirdine and then another 2.0 ± 3.4 mV following the application of the linopirdine plus Oxo-M cocktail (Fig. 6A). Linopirdine shifted RMP in the depolarizing direction in 7 of the 9 cells, while no effect on RMP was observed in the remaining 2. Unlike the linopirdine-alone condition, the response to linopirdine + Oxo-M was mixed; RMP shifted in the hyperpolarizing direction in 3 cells and shifted in the depolarizing direction in 3 cells.

Figure 6.

Heterogeneity in the impact of activation mAchR on firing patterns. A, RMP is plotted for each cell before, after linopirdine, and after linopirdine and Oxo-M. Thin lines connect individual cells. Bold line and data points indicate the average change RMP in each condition. B, RMP in each condition for transient (blue triangles) and sustained-C (green circles) firing cells only. C, RMP in each condition for cells with sustained-B firing patterns (red squares). D1, Large transient firing cell that saw no change in firing pattern despite a moderate positive shift in I_H activation range. D2, Sustained-B with moderate effect. D3, Sustained-B with large effect. Voltage response are shown in a stacked array separated by 10 mV. Dashed horizontal line drawn at −60 mV in all three cells. Traces are shown at baseline control (light gray), after linopirdine (dark gray), and after linopirdine and Oxo-M (black). The cell in D3 was held at −59 mV in both lino and lino+oxo conditions. E1, The cell shown in D3 fired spontaneously following linopirdine administration. Cell was not spontaneously active in the control condition. Blue bars above the trace represent the period in which firing pattern regularity was assessed in E2. Although the spontaneous activity is concatenated into a single trace, there was a 1 s delay between sweeps that is represented by the blue bars. E2, The spontaneous activity shown in E1 is shown with each line indicating a separate trace. Note the presence of spike failure as indicated by the black arrows. RMP in control condition is shown as a dotted horizontal line. F1, The cell shown in D3 also fired spontaneously following administration of linopirdine and Oxo-M. The period of spontaneous activity was continuous and lacked periods of quiescence. F2, The spontaneous activity shown in F1 is shown with each line indicating a separate sweep. Note the reduction in spike failure and the increase in the regularity of spikes after Oxo-M is added to the bath. G, The spontaneous activity shown in E and F was used to construct a histogram for each interspike interval following linopirdine (light gray) as well as linopirdine and Oxo-M (dark gray). The variability of the interspike interval of the spontaneous activity was reduced following linopirdine and Oxo-M compared with linopirdine alone. This increase in regularity is reflected in the decrease in coefficient of variability (CV) from 0.33 after Lino to 0.06 after Lino+Oxo.

To understand the diversity of the RMP response to linopirdine + Oxo-M, we grouped cells according to their firing pattern. Figure 6B shows that RMP in both transient firing and sustained-C cells shifted in the hyperpolarizing direction in 3 of 6 cells while the remaining 3 saw little or no change. In contrast, RMP dramatically depolarized in 2 of 3 sustained-B firing cells with a minor depolarization observed in the third (Fig. 6C). These results suggest that RMP in sustained-B firing cells depolarizes in response to HCN depolarization because they have little remaining I_KL to counter the addition of inward current. In contrast, enhancing the activation of HCN channels can stimulate the further activation of residual I_KL currents in other cells, thus stabilizing or hyperpolarizing the resting potential (consistent with the predictions of modeling in Ventura and Kalluri, 2019).

Figure 6D1 shows an example of a large, transient firing cell in all three bath conditions. In this cell, Oxo-M shifted the I_H voltage activation range by ∼5 mV. However, the firing pattern was virtually unchanged after adding linopirdine as well as after adding Oxo-M. Transient firing patterns are defined by a mixture of Kv1 and KCNQ-mediated low-voltage activated potassium currents (Pérez et al., 2009; Kalluri et al., 2010). Presumably, the low-voltage activated potassium current in this cell is either dominated by Kv1 or is not completely blocked by linopirdine and Oxo-M. Therefore, the transient firing pattern is maintained. In contrast, in cells with sustained-B firing patterns, I_KL is likely comprised in larger part by KCNQ channels (Kalluri et al., 2010; Hight and Kalluri, 2016) that are sensitive to both Oxo-M and linopirdine (Suh et al., 2004). As predicted by modeling, in the absence of I_KL, HCN channels steadily depolarize the membrane potential, thereby bringing the cell closer to threshold and producing more action potentials (Ventura and Kalluri, 2019). As an example of this additional impact of HCN channels, Figure 6D2 shows a sustained-B VGN with an I_H voltage activation range that shifted in the depolarizing direction by 3-5 mV, but in this case the cell generated four more spikes near threshold after exposure to Oxo-M relative to when the cell was in control and linopirdine bath conditions.

In some neurons, V_1/2 shifted even more dramatically in the presence of Oxo-M (e.g., by nearly 18 mV in the cell shown in Fig. 6D3). The addition of Oxo-M to the bath solution also further depolarized the RMP to −43 mV. Initially, resting potential depolarized so much (from −66 to −43 mV) that the cell was unable to fire an action potential in response to step current injection. The inability to fire an action potential from depolarized RMPs is likely because of sodium channel inactivation since the cell fired successfully when first held at −56 mV (Fig. 6D3, dark gray and black traces). Notably, the cell's firing pattern in response to current injection converted from sustained-B to sustained-A. This transition is expected if the closure of KCNQ channels eliminates nearly all I_KL components.

The neuron from Figure 6D3 eventually became spontaneously active during the linopirdine condition (Fig. 6E1,E2). Although spontaneously active, the firing pattern showed some burstiness as periods of spontaneous activity were interrupted by periods of quiescence (Fig. 6E1). Even after selecting the most consistently active periods of spontaneous activity for analysis (Fig. 6E1, blue bars), some spikes failed to fully form and we observed the occasional spike failure (Fig. 6E2, bottom, black arrows). After adding Oxo-M, the cell fired spontaneously for longer durations than with linopirdine only (Fig. 6F1). In addition, these periods of spontaneous activity lacked the spike failures observed following the application of linopirdine alone (Fig. 6F2).

Figure 6G shows the interspike interval histograms in the linopirdine-only and linopirdine + Oxo-M conditions. The addition of Oxo-M both decreased the average interspike interval (i.e., increased the overall spike rate) and produced a striking increase in the regularity of spike intervals (CV_Lino = 0.33, CV_Lino+Oxo = 0.06). In this case, the Oxo-M condition produced the most regular firing we have recorded in vitro, and the CV value is comparable to the most regular firing patterns observed in vivo (Goldberg et al., 1990; Ventura and Kalluri, 2019). Therefore, the muscarinic receptor agonist, Oxo-M, boosted the regularity of spiking to beyond that which resulted from simply closing KCNQ. This is likely because of the enhanced activation of HCN channels on top of the near-complete closure of KCNQ channels. These three examples illustrate how HCN channel's impact on firing patterns is contextually dependent on the presence of other ion channels and how the vestibular efferents can have dramatic impact on afferent firing patterns via their dual control over KCNQ and HCN currents.

Small, sustained firing VGNs have biased sensitivity to I_H modulation

We considered whether cells of different size and step-evoked firing pattern also differed in the sensitivity of their HCN channels to mAChR signaling. Accordingly, we first compared the relationship between cell size and V_1/2 before and after Oxo-M (Fig. 7A,B). Before Oxo-M, large cells have more depolarized V_1/2 than smaller cells (Fig. 7A, blue). The correlation is reflected in simple polynomial regression shown in blue (r₍₄₅₎ = 0.59, p < 0.0001, r² = 0.35, n = 47). After Oxo-M, there was no correlation between cell size and V_1/2 (r₍₄₀₎ = 0.14, p = 0.67, Fig. 7A, red). This is because V_1/2 in small cells was depolarized in the Oxo-M condition relative to control. This is clearer in individual cells where paired comparisons are made before and after Oxo-M, as shown in Figure 7B. The largest depolarizing shifts are observed in small cells.

Figure 7.

Small size and sustained firing patterns are associated with increased sensitivity to I_H modulation. A, V_1/2 shown plotted against cell size in control and Oxo-M conditions. Straight lines indicate linear regression, and 95% CI estimates of control and Oxo-M groups in blue and red, respectively. B, V_1/2 and C_m measurement pairs from 21 individual cells tested before (blue) and after (red) Oxo-M administration. Arrows are drawn between two data points in each cell. Linear regressions from A are shown in dotted lines in B. C, Left, Line series are shown with each point representing a single V_1/2 measurement at baseline and after Oxo-M was added to the bath in 21 cells. Lines and points are color-coded according to firing pattern with transients (blue lines and triangles), sustained-C (green lines and circles), and sustained-B (red lines and squares) shown. Cells at 15 ± 1 d are shown as empty shapes. Right, The size of the Oxo-M-induced shift in V_1/2 is shown in transient firing cells (blue triangles), sustained-B (red squares), and sustained-C (green circles). Oxo-M shifted V_1/2 more in sustained-B cells significantly more compared with both sustained-C (p = 0.0397, Tukey's HSD) and transient firing cells (p = 0.0053).

Since we showed in Figure 4 that cell size and firing pattern are related, we also examined whether cells with different firing patterns (as determined in control condition) had HCN channels with different sensitivities to mAChR activation. We limited this comparison to cells that were recorded before and after Oxo-M since blocking KCNQ promotes sustained or spontaneous firing in some cells. Figure 7C shows the effect of Oxo-M in cells with each firing pattern. Transient firing cells had HCN channels with a depolarized V_1/2 before (V_1/2: −95.0 ± 1.4 mV) and after Oxo-M (V_1/2: −92.7 ± 1.2 mV). We observed a moderate depolarization after Oxo-M in this group (V_1/2 shift: 2.3 ± 0.5 mV). In contrast, HCN channels in cells with sustained-C firing patterns had hyperpolarized V_1/2 (V_1/2: −102.5 ± 0.04 mV) and were insensitive to Oxo-M (V_1/2: −101.4 ± 1.9 mV, V_1/2 shift = 1.1 ± 1.8 mV, N = 2). In contrast to both transient and sustained-C firing cells, cells with sustained-B firing pattern had both hyperpolarized V_1/2 in control conditions (V_1/2: −102.1 ± 3.9 mV) as well as a dramatic shift in V_1/2 following mAChR activation (8.6 ± 2.7 mV, N = 5). The average shift in V_1/2 following mAChR was significantly greater in sustained-B cells compared with both sustained-C (p = 0.0397, Tukey's HSD) and transient firing cells (p = 0.0053). Together, these results suggest that the greatest sensitivity of I_H to muscarinic signaling cascades is biased toward a population of small- to medium-sized sustained-B firing neurons. Given the proposed connection between this group and regular firing afferents, we suggest that these cells have the latent capacity to produce highly regular firing.

Discussion

An endogenous mechanism for depolarizing HCN channels

HCN channels are thought to contribute to vestibular afferent signaling by promoting nonquantal transmission (e.g., Contini et al., 2020) and driving regular spike-timing (Horwitz et al., 2014). However, previous in vitro characterizations from isolated ganglion neurons indicated that the HCN current, I_H, is mostly unavailable for shaping vestibular neuron activity (Hight and Kalluri, 2016) because of its hyperpolarized voltage activation range (Chabbert et al., 2001; Almanza et al., 2012). In vitro experiments also show that the activation range of HCN channels in vestibular afferents can be depolarized into a physiologically useful range by artificially elevating the concentration of intracellular second messengers like cAMP (e.g., Meredith et al., 2012; Horwitz et al., 2014; Ventura and Kalluri, 2019). Such modulation of HCN can dramatically alter patterns of afferent activity in immature neurons (Horwitz et al., 2014). Our results identified a natural mechanism for depolarizing the activation range of HCN channels through intracellular signaling cascades that are targeted by the cholinergic efferent system. Given recent evidence that cholinergic vestibular efferents are tonically active (Raghu et al., 2019), I_H may be more available to shape afferent activity in vivo than indicated by previous in vitro characterizations.

mAChRs impact the voltage activation range of I_H presumably by triggering g-protein coupled signaling cascades that affect the availability of intracellular cAMP and/or PIP₂ (Robinson and Siegelbaum, 2003; Pian et al., 2007). Whether mAChR activation upregulates or downregulates intracellular cAMP or PIP₂ theoretically depends on which mAChR receptor subtype is activated; all five mAChRs (M1-M5) are expressed in vestibular neurons (Li et al., 2007). The odd numbered M1, M3, and M5 receptor subtypes couple to the Gαq/11 G-protein to activate PIP₂ (Brown, 2010) and likely depolarize the activation range of HCN channels. For example, activation of M1 receptors in expression systems depolarizes the activation range of I_H through a PIP₂-related mechanism (Pian et al., 2007). The M2 and M4 subtypes release Gi/Go G-proteins that can either inhibit or stimulate cAMP activity (Dittman et al., 1994; Michal et al., 2001; Harvey and Belevych, 2003). Increasing and decreasing cAMP concentration in VGN shifts the I_H activation range in the depolarizing and hyperpolarizing directions, respectively (Almanza et al., 2012; Ventura and Kalluri, 2019). The diverse sensitivities to mAchR activation that we observed in VGN could, in part, result from the variety of M receptors known to be expressed in VGN. Thus, whether mAChR-dependent modulation of HCN channels in VGN is mediated by cAMP, PIP₂, or some combination of both messengers is yet unclear since the different M receptors may recruit multiple signaling pathways.

Here we found that the activation range and activation kinetics of HCN channel currents are more variable than previously characterized in vestibular ganglion. The half-activation voltage of I_H ranged from −76 mV to −110 mV. Previous studies did not find I_H activation ranges as depolarized as −76 mV in VGN (Chabbert et al., 2001; Almanza et al., 2012; Yoshimoto et al., 2015; Ventura and Kalluri, 2019). The likely difference between the present and previous studies is that here we used perforated-patch methods to characterize I_H; 8 cells across two previous studies compared with 47 cells in this study used perforated-patch (Almanza et al., 2012; Ventura and Kalluri, 2019). Rupture-patch techniques used in previous studies cause the intracellular composition to dialyze with the contents of the recording pipette. The resulting time-dependent rundown in second messengers likely hyperpolarizes the activation range of HCN and reduces the cell-to-cell variability in HCN channel properties reported here.

I_H activation range in VGN is cell size and firing pattern-dependent

Our results provide novel insight into how cell-type categories overlap with HCN channel properties. That VGNs are remarkably diverse in their cell size, discharge pattern, and ion-channel composition was established by previous studies (Iwasaki et al., 2008; Kalluri et al., 2010; Almanza et al., 2012; Yoshimoto et al., 2015; Hight and Kalluri, 2016; Ventura and Kalluri, 2019). This diversity is present across a wide range of postnatal ages (P0-P21), with and without enzymatic treatment (Risner and Holt, 2006; Kalluri et al., 2010; Yoshimoto et al., 2015; Ventura and Kalluri, 2019), and at recordings made at afferent somata and terminals (Songer and Eatock, 2013). Thus, although the biophysical properties of vestibular ganglion change with maturation (e.g., Almanza et al., 2012; Ventura and Kalluri, 2019), heterogeneity in cell sizes and firing patterns is present in early postnatal days and persists with maturation.

HCN channel isoform diversity may be a factor contributing to the cell-to-cell variability in HCN channel properties reported here. The HCN channel includes four isoforms that differ in their voltage activation range, activation rate, and cAMP sensitivity (Robinson and Siegelbaum, 2003). All four HCN isoforms are expressed in vestibular afferents with HCN3 and HCN4 being less expressed than the HCN1 and HCN2 isoforms (Almanza et al., 2012). These HCN channel isoforms with HCN2 and HCN4 subunits are strongly activated by cAMP, while those with the HCN3 subunit are inhibited (Robinson and Siegelbaum, 2003).

That the half-activation voltage and activation kinetics of I_H vary by cell size is consistent with immunohistochemistry showing preferential enrichment for HCN1 and HCN2 isoforms in large-diameter VGN (Almanza et al., 2012). In expression systems, HCN1 isoforms are noted to have more depolarized half-activation voltages, faster activation kinetics, and less sensitivity to cAMP than other HCN channel isoforms (Altomare et al., 2003). This may, in part, account for why the HCN currents in large and transient firing VGN had more depolarized half-activation voltages and faster kinetics under baseline conditions and were less sensitive to depolarization via mAChR activation.

Functional significance

Efferent control of I_H is significant because of the relevance of HCN channels to two hallmark features of vestibular afferent signaling: nonquantal transmission and spike-timing regularity.

Modulation of nonquantal transmission

HCN channels are believed to contribute to a form of fast (nonquantal) transmission between vestibular hair cells and the calyceal synapses of vestibular afferents (Contini et al., 2020). Recent work suggests that nonquantal transmission results when K⁺ released from Type I hair cells accumulates in the narrow synaptic cleft of the calyx and flows into the afferent neuron through the low-voltage gated ion channels found on the calyx inner face. This ultrafast inward current is thought be conducted through either HCN (Contini et al., 2020) and/or low-voltage-gated potassium channels (Govindaraju et al., 2023). Regardless of whether HCN channels provide a direct pathway for current flow or raise the RMP of the postsynaptic calyx to place it within the activation range of the potassium channels, the relative impact of HCN channels to nonquantal transmission is dependent on the channel's activation range. Our results show that large VGN with predominantly transient firing patterns, which are likely the somata of irregular firing calyx afferents from the central zones of vestibular epithelia (Kevetter and Leonard, 2002), have HCN channels that are naturally more depolarized than HCN channels in small ganglion neurons which likely belong to regular firing peripheral zone afferents. Such depolarized voltage activation range might favor a greater contribution of HCN channels to nonquantal transmission.

By controlling the ion channels active near resting potential (i.e., KCNQ and HCN channels), efferent signaling has the potential to shape nonquantal transmission in vestibular afferents. Efferent terminals synapse with the outer face of the calyx (Lysakowski and Goldberg, 1997), which express muscarinic M1, M2, M4, and M5 receptors (Li et al., 2007). To control nonquantal transmission, mAChRs on the outer face would have to impact the ion channels found on the inner face of the calyx. Calyx terminal recordings have shown that HCN channels are sensitive to intracellular cAMP concentration, although whether efferents are capable of modulating cAMP levels is not known (Meredith et al., 2012). However, it is plausible that mAchR activation impacts remotely located HCN and KCNQ on the inner face of the calyx through intracellular signaling cascades.

Dual impact of mAchR on KCNQ and HCN channels is necessary for promoting regularity

The depolarizing currents of HCN channels are believed to be instrumental toward generating the strikingly regular interspike intervals found in many vestibular afferents (Horwitz et al., 2014; Yoshimoto et al., 2015). This is akin to HCN channels' role in cardiac pacemaking (DiFrancesco and Tromba, 1988). Evidence supporting this hypothesis is that (1) highly regular-spike patterns become more prevalent with postnatal development (Curthoys, 1979) as HCN channel expression grows and matures (Yoshimoto et al., 2015) and (2) spike-timing regularity is sensitive to pharmacological manipulation of HCN channel activity in neonatal vestibular afferents (Horwitz et al., 2014).

Although HCN channels promote pace-making in other systems (Pape and McCormick, 1989; DiFrancesco, 1993), their impact on vestibular afferent spike-timing likely depends on whether the afferent also expresses low-voltage activated potassium channels. Vestibular ganglion neurons containing low-voltage gated potassium currents produce irregular-timed spike patterns in response to simulated synaptic currents (Kalluri et al., 2010). Ventura and Kalluri (2019) showed that HCN channels amplify transient firing and irregular firing patterns in dissociated vestibular ganglion neurons by shifting the membrane potential toward the activation range of potassium channels (Ventura and Kalluri, 2019). Indeed, HCN channels are known to similarly interact with low-voltage gated potassium currents in auditory brainstem neurons to enhance transient firing (Oertel et al., 2000; Rothman and Manis, 2003; McGinley and Oertel, 2006; Cao and Oertel, 2011; Khurana et al., 2012). Thus, HCN channels enhance transient-spiking and irregular-timed spiking in neurons that contain I_KL, even when the HCN channel activation is depolarized by artificially increasing the intracellular concentration of cAMP (Ventura and Kalluri, 2019). In a model, Ventura and Kalluri (2019) demonstrated that HCN channels could only promote regular-timed firing in simulated neurons that do not have I_KL.

Most mature vestibular ganglion neurons are likely to have some I_KL because of the upregulation of KCNQ channels with maturation (Rocha-Sanchez et al., 2007). This suggests that a developmental upregulation of HCN channels alone is unlikely to account for the increased prevalence of regular spiking with maturation. However, since vestibular efferent neurons are believed to be tonically active (Sadeghi et al., 2009; Raghu et al., 2019), the simultaneous closure of KCNQ channels and enhancement of HCN channels via the muscarinic receptor cascade provide a plausible scenario for promoting highly regular firing.

Our results suggest that spike-timing regularity may not be a fixed property for all vestibular neurons, but dynamically regulated by efferent inputs. Efferent activity may promote ion channel configurations that favor both regular and irregular spike-timing, depending on the balance between low-voltage gated potassium currents and the activation range of HCN currents. How might modulation of HCN channels impact spike-timing in different afferent types? In neurons that express low-voltage gated currents primarily through KCNQ channels (likely neurons contacting peripheral zones; of the epithelium), simultaneously closing KCNQ and enhancing HCN channels would promote regular-timed spiking because the efferent signaling squelches most of the low-voltage gated potassium currents while also amplifying the contribution of the pace-making currents from HCN. These neurons may fire at either regular or irregular intervals depending on efferent input. Spike-timing regularity may be less flexible in other neurons if they contain low-voltage gated potassium channels (e.g., Kv1) (Iwasaki et al., 2008; Kalluri et al., 2010), which are not as easily closed by activating mAChR signaling. However, because mAChR activation triggers a complex sequence of second messenger cascades, it is possible that other ion channels besides KCNQ and HCN are also impacted. For example, muscarinic signaling cascades have been shown to both inhibit and activate a plethora of other ion channels, including inward rectifying potassium channels (for review, see Brown, 2018). However, in VGN, the muscarinic signaling cascades seems to be targeting KCNQ channels, but no other outward potassium currents (Pérez et al., 2009).

The closure of KCNQ would increase the firing rate, but I_KL components that are resistant to closure would still drive transient-spiking in response to injected current steps and produce irregular firing patterns in response to synaptic drive (as predicted by modeling) (Ventura and Kalluri, 2019). Thus, the impact of efferent-mediated modulation is likely to be more nuanced than previously appreciated because it affects two ion channel groups that shape spike-timing. Our results show that HCN channels are targeted by the same muscarinic signaling cascades that are already known to close KCNQ channels (Pérez et al., 2009; Holt et al., 2017). The dual impact of the cholinergic pathway on two ion channel groups that are known to be important for regulating spike-rate and timing highlights the complex mechanisms by which vestibular efferents can modify the activity of vestibular afferents. Future studies are needed to test whether the neuro-modulatory mechanisms identified at the somata are recapitulated at afferent terminals where efferent synapses are found.