Abstract
Objectives
This study aimed to assess stress distribution in 5-unit fixed partial dentures (FPDs) with a pier abutment and rigid (RC) and nonrigid connectors (NRCs) with the canine rise and group function occlusal schemes by finite element analysis (FEA).
Materials and Methods
In this FEA study, a geometrical model of the maxilla with natural teeth and periodontal ligament (PDL) was three-dimensionally designed and meshed by ANSYS and Pro/Engineer software programs. A 5-unit FPD was then designed to replace the lost first premolar and first molar teeth; the second premolar served as a pier abutment, and the canine and second molar served as terminal abutments. Two FPDs were designed with RC and NRC. Each FPD was analyzed with the canine rise and group function occlusal schemes (a total of 4 models). The first and second molars (180 N), premolars (120 N), and canine (80 N) teeth were subjected to progressive vertical and oblique (12-degree) loads, and maximum von Mises stress and strain in teeth and connectors were calculated for each model.
Results
The models had 73704 elements and 137732 nodes. The connector design and occlusal scheme had significant effects on stress distribution in FPDs. The highest von Mises stress (73.035 MPa) was recorded in FPD with RC and group function occlusal scheme. The lowest von Mises stress (0.004 MPa) was recorded in FPD with NRC and canine rise occlusal scheme.
Conclusion
Oblique forces created greater stress, and FPD with NRC and canine rise occlusal scheme decreased stress in FPD and increased stress in the tooth crown.
1. Introduction
Considering the high prevalence of partial and complete edentulism in adults, replacement of the lost teeth is a common task for dental clinicians [1]. Some partially edentulous patients require the replacement of the lost teeth with fixed partial dentures (FPDs) with a pier abutment [2]. A Pier abutment is a natural tooth located between two edentulous spaces and terminal abutments, which supports an FPD. For instance, the second premolar can serve as a pier abutment when the first premolar and first molar teeth are lost [3]. Obviously, the optimal function of FPDs depends on balanced stress distribution in the pier abutment and terminal abutments.
Rigid connectors (RCs) are commonly used for FPDs [1]. When occlusal loads are applied to the connectors, the pier abutment can serve as a support, and result in debonding of the terminal abutment with lower retention, leading to restoration fracture and treatment failure [2]. Thus, FPDs with RCs may not be an appropriate treatment option for the replacement of two lost teeth with one pier abutment, because The amount of load applied to the anterior part may be different from the posterior part, causing the destruction of the prosthesis, tooth decay, pulp irritation, and ultimately the need for root canal treatment, causing prolonged pain and discomfort to the patient [4–12]. Also, failure may occur due to differences in the physiological mobility of the teeth in the anterior and posterior regions [13]. Thus, nonrigid connectors (NRCs) have been proposed to decrease the risk of failure [2, 14]. NRCs transfer stress to the supporting bone instead of its concentration in the connector [15]. However, NRCs have drawbacks as well, such as greater bone loss around the pier abutment, higher cost, and requiring a longer time for fabrication [16].
Occlusion is a highly debated topic in the fabrication of FPDs. In lateral movements of the mandible, the mandibular posterior teeth come out of centric occlusion with the opposing teeth. This movement is guided by the condyle in the posterior region and follows a lateral downward path in the anterior region as dictated by the anterior guidance [17, 18]. The dental occlusal scheme is conventionally divided into four groups anterior guidance, canine rise, partial group function, and group function. In the canine rise occlusal scheme, only the maxillary and mandibular canine teeth are in contact in lateral excursive movements while in group function, only the posterior teeth are allowed to be in contact during lateral movements, and at least canine and two premolars at the working side should be in contact with the opposing teeth [19]. Sidana [17] and other supporters of the group function occlusal scheme believe that occlusal wear in this scheme is a compensatory coping mechanism that results in optimal stress distribution for an appropriate functional relationship [17].
Clinical assessment of stress concentrated in prosthetic components or transferred to the supporting tissue is almost impossible. However, since the success of prosthetic restorations is influenced by biomechanical properties, measurement of these stresses is critical [2, 20]. Photo-elastic models are important tools for the assessment of stress distribution in different systems. Nonetheless, these models are made of plastic material, and cannot precisely simulate the biological behavior of tissues. Thus, the pattern of stress distribution in the enamel, dentin, and pulp, and the nonlinear behavior of the periodontal ligament cannot be simulated. Finite element analysis (FEA) provides new insight into tooth biomechanics, and can three-dimensionally simulate the behavior of many dental structures with different shapes and properties under different loading conditions [2]. Modi et al. [2] evaluated stress distribution in a 5-unit FPD with a pier abutment under constant and progressive loads. They designed FPDs with RC and NRC and applied vertical and oblique loads to them. They showed different patterns of stress distribution under vertical and oblique loads and revealed that NRC decreased stress in restoration and increased stress in crestal bone. Oruc et al. [21] used FEA to assess stress distribution in a 5-unit FPD with pier abutment and RC and NRC. The second molar and canine teeth served as terminal abutments, and the second premolar served as a pier abutment with a mesial and distal connector. They showed that NRC at the distal of the second premolar resulted in less stress concentration following the application of 50 N static load to the cusps. Jiang et al. [22] assessed the durability of two resin-bonded FPDs with RC and NRC by the wear test. The first premolar and second molar teeth served as abutments for 4-unit FPDs. NRC was placed at the distal of the first premolar. The models underwent thermal cycles and mechanical loading. The results showed that NRC decreased the stress between tooth and wing since it allowed independent movement of the two separate prosthetic components, and increased the durability and clinical service of FPD. Although some articles suggest the application of new materials for force distribution in the dental prosthesis, changes in the design of the prosthesis can also be important in this distribution [23].
Implant-tooth-supported fixed partial prostheses can cause changes in marginal bone loss under the effect of changes of occlusal forces [24] and the available studies on stress distribution in 5 unit FPDs with a pier abutment and RC and NRC did not address the role of different occlusal schemes in stress distribution. In addition, the finite element articles on this subject exclusively examine the restoration of the mandible, but the direction of the occlusal forces in the maxilla and mandible is different [25]. Thus, this study aimed to assess stress distribution in maxillary 5-unit FPDs with a pier abutment and RC and NRC with the canine rise and group function occlusal schemes by FEA.
2. Materials and Methods
In this FEA study, a geometrical model of the maxilla was designed by ANSYS (ANSYS Inc.; Houston, TX, USA) and Pro/Engineer (Parametric Technology Corporation, USA) software programs. Approval was obtained from the Isfahan University of Medical Sciences ethics committee (IR.MUI.RESEARCH.REC.1400.344).
2.1. Modeling in Mimics and 3Matic Software Programs
The bone, teeth, metal framework, and connectors were modeled in Mimics and 3Matic software programs. For this purpose, cone-beam computed tomography scans with 1 mm slice interval were imported to Mimics. A 3D model of the maxillary canine, first and second premolar, and first and second molar is simulated based on the information obtained from Wheelers's dental anatomy, physiology, and occlusion [26, 27]. External shapes of the roots were generated from the textbook [27]. A cement-retained Straumann CARES titanium abutment with a gingival height of 1.5 mm and a Straumann bone level tapered (BLT) implant with a diameter of 4.1 mm and a height of 10 mm were designed and positioned in the maxillary canine site. The implant was presumed to be completely osseointegrated. The tooth was prepped conventionally for a PFM restoration. The crowns were composed of Ni-Cr alloy and porcelain and zinc phosphate cement used for both the tooth and implant. The segmentation tool was used to create masks for the teeth, maxilla, and PDL, and then Calculate 3D feature was used to design a 3D model of the components. All components were then exported in STL format and converted to STP format in Geomagic software by reverse engineering.
2.2. Analysis in ANSYS Software
After the conversion of all geometries to STP format, they were imported to ANSYS software.
The designed geometrical model had natural teeth, PDL, and maxillary bone three-dimensionally. The model was then meshed in the software and the mechanical properties of the materials were also uploaded for stress analysis. In FEM analysis, the stress distribution is commonly specified as von Mises stress, which could be maximum and minimum principal stress or principal strain. A formula is used to calculate the von Mises stress in three planes: the x-axis, the y-axis, and the z-axis. A 5-unit FPD was designed for the replacement of a lost first premolar and first molar. The second premolar served as a pier abutment, and the canine and second molar teeth served as terminal abutments. Two FPDs were simulated one with RC and the other one with NRC. To simulate NRCs, Shillingburg's dovetail design was used on the distal surface of the pier abutment. Next, each designed model was analyzed with two different occlusal schemes, namely canine rise and group function (a total of 4 models).
2.3. Boundary Conditions for Canine Rise Occlusal Scheme
To simulate the canine rise occlusal scheme, an 80 N load was applied to the canine tooth first vertically, and then with 12-degree angulation. The upper surface of the maxilla was fixed.
2.4. Boundary Conditions for Group Function Occlusal Scheme
Loads equal to 80 N, 120 N, 120 N, 180 N, and 180 N were applied to the canine, first premolar, second premolar, first molar, and second molar teeth, respectively, to simulate the group function occlusal scheme. The loads were first applied vertically, and then with 12-degree angulation. The upper surface of the maxilla was fixed [2].
2.5. Meshing
The total number of elements of the model was 73,704 tetrahedral elements, and the total number of nodes was 137,372 nodes. All materials were considered homogeneous, isotropic, and linearly elastic.
2.6. Sensitivity Analysis of Meshing
A sensitivity analysis curve was drawn to ensure the independence of results from the size of the meshing and the number of elements. For this purpose, the number of elements was increased (the size of elements decreased) and the von Mises stress value was read. The stress (MPa) curve was drawn based on the number of elements. The curve became flat when the number of elements reached 73,704. Thus, this value was considered as the optimal number of elements for meshing.
2.7. Properties of the Materials
Table 1 presents the mechanical properties of the materials used in this study according to the available literature [2, 28].
Table 1.
Mechanical properties of the materials used in this study.
| Component | Young's modulus (MPa) | Poisson's ratio |
|---|---|---|
| Cortical bone | 13700 | 0.3 |
| Cancellous bone | 1370 | 0.3 |
| Cobalt-chromium metal framework | 206000 | 0.33 |
| Porcelain | 82800 | 0.35 |
| PDL | 69 | 0.45 |
| Tooth | 18000 | 0.33 |
| Nonrigid connector | 110000 | 0.33 |
Next, maximum von Mises stress, maximum shear stress, maximum von Mises strain, and maximum shear strain around the teeth and connectors were calculated for the four models and compared.
3. Results
3.1. FPD with NRC and Canine Rise Occlusal Scheme (Figure 1)
Figure 1.
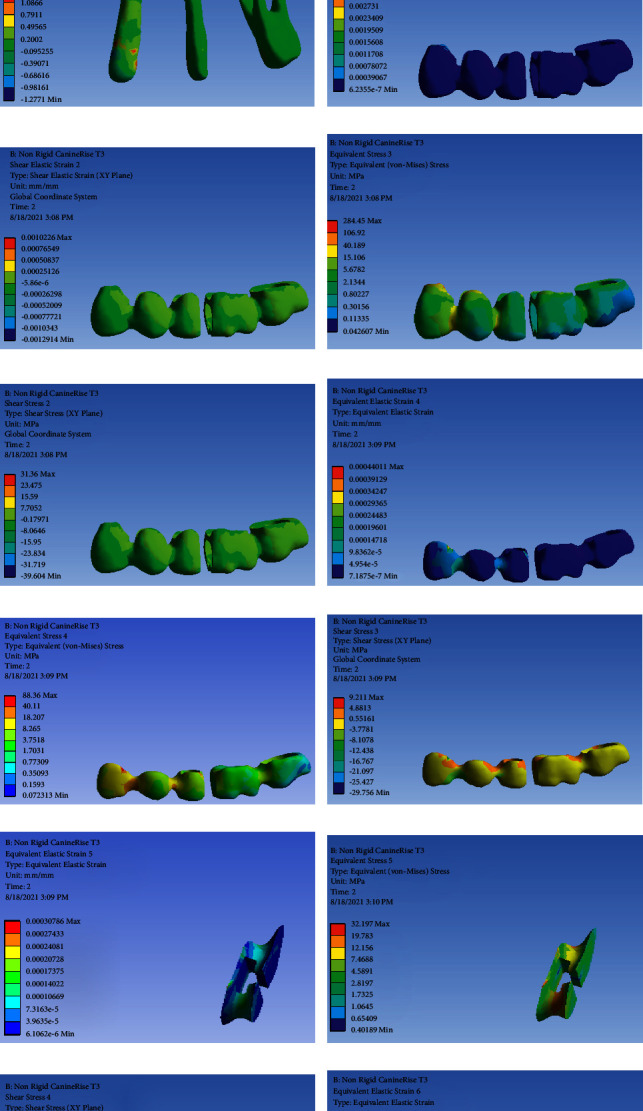
FPD with NRC and canine rise occlusal scheme: (a) strain distribution in the entire model, (b) von Mises stress distribution in the entire model, (c) strain distribution in abutments, (d) von Mises stress distribution in abutments, (e) shear stress distribution in abutments, (f) strain distribution in FPD, (g) strain distribution in FPD, (h) von Mises stress distribution in FPD, (i) shear stress distribution in FPD, (j) strain distribution in the metal framework, (k) von Mises stress distribution in the metal framework, (l) shear stress distribution in the metal framework (m) strain distribution in the connector, (n) von Mises stress distribution in the connector, (o) shear stress in the connector, (p) strain distribution in the connector, (q) von Mises stress distribution in the connector, and (r) shear stress distribution in the connector.
Table 2 presents the von Mises stress and strain values in FPD with NRC and canine rise occlusal scheme.
Table 2.
Von Mises stress (MPa) and strain values in FPD with NRC and canine rise occlusal scheme.
| Variable | Component | Maximum value | Location of maximum value | Minimum value | Location of minimum value |
|---|---|---|---|---|---|
| Stress | Entire model | 17.657 | The mesial surface of the first premolar and the distal surface of the canine | 0.004 | The occlusal surface of the second molar |
| Tooth | 5.3259 | The buccal surface of the canine | 0.0208 | The occlusal surface of the second molar | |
| FPD | 40.189 | The mesial surface of the first premolar and the distal surface of the canine | 0.0426 | The occlusal surface of the second molar | |
| Metal framework | 40.11 | The mesial surface of the first premolar and the distal surface of the canine | 0.1593 | The occlusal surface of the second molar | |
| Connector | 15.216 | The mesial surface of the connector | 1.06 | The distal superior surface of the connector | |
|
| |||||
| Strain | Entire model | 0.006 | The distal surface of the canine and mesial surface of the first premolar | 1.991 | The occlusal surface of the second molar |
| Tooth | 0.0002 | The lingual surface of the canine | 1.529 | The occlusal surface of the second molar | |
| FPD | 0.007 | The lingual surface of the canine | 6.235 | The occlusal surface of the first and second molars | |
| Metal framework | 0.0003 | The distal surface of the second premolar | 7.187 | The occlusal surface of the first and second molars | |
| Connector | 0.0002 | The buccal inferior surface of the connector | 3.963 | The lingual superior surface of the connector | |
3.2. FPD with NRC and Group Function Occlusal Scheme (Figure 2)
Figure 2.

FPD with NRC and group function occlusal scheme: (a) strain distribution in the entire model, (b) von Mises stress distribution in the entire model, (c) strain distribution in abutments, (d) von Mises stress distribution in abutments, (e) shear stress distribution in abutments, (f) strain distribution in FPD, (g) von Mises stress distribution in FPD, (h) shear stress distribution in FPD, (i) strain distribution in the metal framework, (j) von Mises stress distribution in the metal framework, (k) shear stress distribution in the metal framework, (l) strain distribution in the connector, (m) von Mises stress distribution in the connector, (n) shear stress distribution in the connector, (o) strain distribution in the connector, (p) von Mises stress distribution in the connector, and (q) shear stress distribution in the connector.
Table 3 presents the von Mises stress and strain values in FPD with NRC and group function occlusal scheme.
Table 3.
Von Mises stress (MPa) and strain values in FPD with NRC and group function occlusal scheme.
| Variable | Component | Maximum value | Location of maximum value | Minimum value | Location of minimum value |
|---|---|---|---|---|---|
| Stress | Entire model | 67.888 | The distal surface of the second premolar and the mesial surface of the first molar | 0.077 | The occlusal surface of the second molar |
| Tooth | 32.501 | The mesial surface of canine and second premolar | 0.525 | The distal root of the second molar | |
| FPD | 69.035 | The buccal surface of the canine | 0.886 | The distal surface of the second molar | |
| Metal framework | 63.959 | The distal surface of the canine | 8.006 | The buccal surface of the second molar | |
| Connector | 59.802 | Mesial surface | 2.0625 | Superior, distal and buccal surface of the connector | |
|
| |||||
| Strain | Entire model | 0.020 | The buccal surface of the second premolar | 4.462 | The occlusal surface of the entire FPD |
| Tooth | 0.001 | The buccal surface of the canine and second premolar | 1.924 | The occlusal surface of the second molar | |
| FPD | 0.003 | The distal surface of the canine | 9.569 | The occlusal surface of the entire FPD | |
| Metal framework | 0.001 | The distal surface of the canine | 1.909 | The occlusal surface of the entire framework | |
| Connector | 0.001 | The buccal surface of the connector | 2.4223 | The distal surface of the connector | |
3.3. FPD with RC and Canine Rise Occlusal Scheme (Figure 3)
Figure 3.
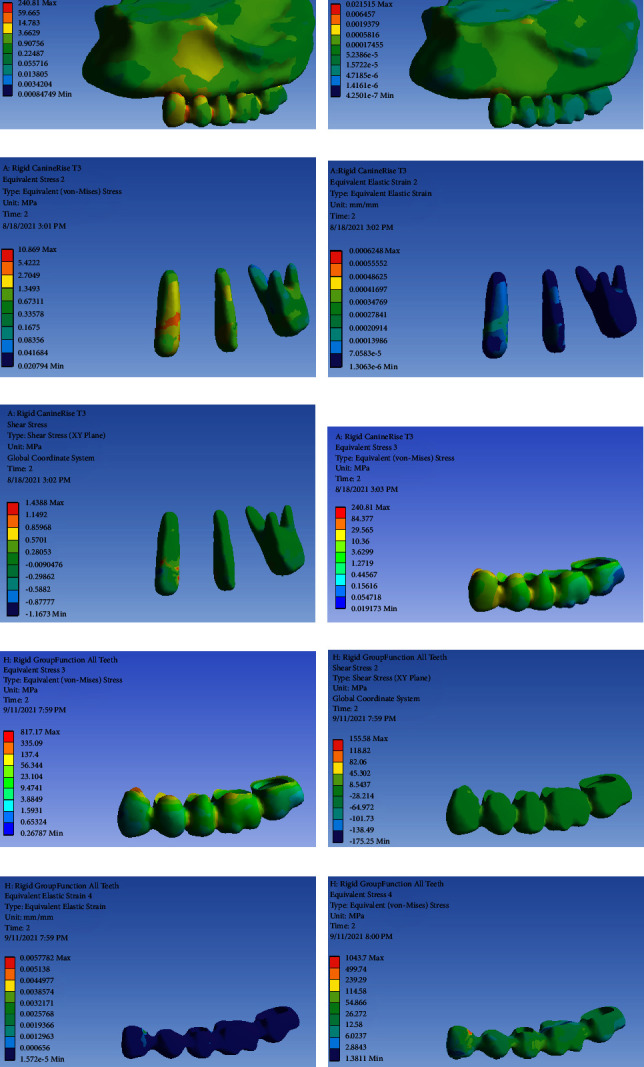
FPD with RC and canine rise occlusal scheme: (a) von Mises stress distribution in the entire model, (b) strain distribution in the entire model, (c) von Mises stress distribution in abutments; (d) strain distribution in abutments, (e) shear stress distribution in abutments, (f) von Mises stress distribution in FPD, (g) strain distribution in FPD and shear stress distribution abutments, (h) strain distribution in the metal framework, (i) von Mises stress distribution in metal framework, and (j) shear stress distribution in the metal framework.
Table 4 presents the von Mises stress and strain values in FPD with RC and canine rise occlusal scheme.
Table 4.
Von Mises stress and strain values in FPD with RC and canine rise occlusal scheme.
| Variable | Component | Maximum value | Location of maximum value | Minimum value | Location of minimum value |
|---|---|---|---|---|---|
| Stress | Entire model | 59.665 | The distal surface of the canine and mesial surface of the first premolar | 0.003 | The occlusal surface of the second premolar |
| Tooth | 5.422 | The buccal surface of the canine | 0.083 | The lingual root of the second molar | |
| FPD | 29.565 | The buccal surface of the canine | 0.054 | The occlusal surface of first and second molars | |
| Metal framework | 38.361 | The distal surface of the canine | 0.045 | The distal surface of the second molar | |
|
| |||||
| Strain | Entire model | 0.0005 | The distal surface of canine and first premolar | 4.718 | The buccal surface of the first and second molars |
| Tooth | 0.0002 | The buccal surface of the canine | 7.058 | The terminal surface of all roots | |
| FPD | 0.0006 | Mesial surface of the canine | 4.250 | Occlusal surface of entire FPD | |
| Metal framework | 0.0002 | The distal surface of the canine and mesial surface of the first premolar | 5.321 | The occlusal surface of first and second molars | |
3.4. FPD with RC and Group Function Occlusal Scheme (Figure 4)
Figure 4.
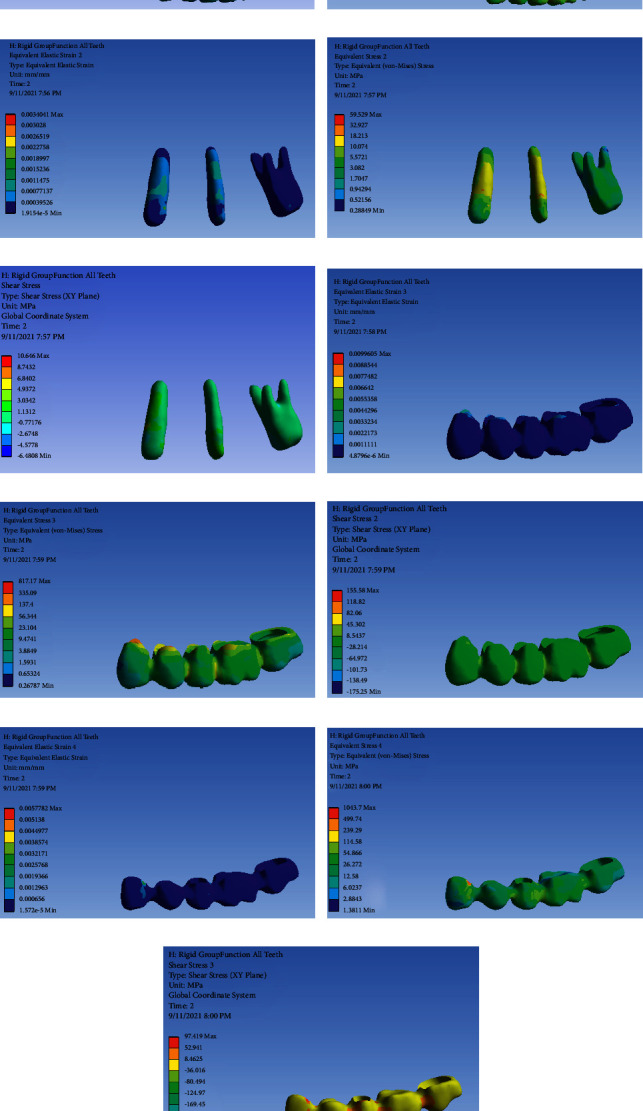
FPD with RC and group function occlusal scheme: (a) strain distribution in the entire model, (b) von Mises stress distribution in the entire model, (c) strain distribution in abutments, (d) von Mises stress distribution in abutments, (e) shear stress in abutments, (f) strain distribution in FPD, (g) von Mises stress distribution in FPD, (h) shear stress distribution in FPD, (i) strain distribution in the metal framework, (j) von Mises stress distribution in the metal framework, and (k) shear stress distribution in the metal framework.
Table 5 presents the von Mises stress and strain values in FPD with RC and group function occlusal scheme.
Table 5.
Von Mises stress and strain values in FPD with RC and group function occlusal scheme.
| Variable | Component | Maximum value | Location of maximum value | Minimum value | Location of minimum value |
|---|---|---|---|---|---|
| Stress | Entire model | 73.035 | The buccal surface of the first premolar and first molar | 1.352 | The occlusal surface of the second molar |
| Tooth | 32.927 | The buccal surface of the second premolar | 0.288 | The distal root of the second molar | |
| FPD | 56.344 | The lingual surface of the canine | 0.653 | The mesial surface of the canine and occlusal surface of the second molar | |
| Metal framework | 114.58 | The mesial surface of the first molar and the distal surface of the second premolar | 2.884 | The occlusal surface of the second molar | |
|
| |||||
| Strain | Entire model | 0.002 | The distal surface of the second premolar | 1.2661e − 5 | The mesial surface of the canine and occlusal surface of the second molar |
| Tooth | 0.001 | The buccal surface of the canine | 1.915 | The occlusal surface of the second molar | |
| FPD | 0.004 | The lingual surface of the canine | 0.001 | The mesial surface of the second molar | |
| Metal framework | 0.002 | The distal surface of the canine | 1.572 | The occlusal surface of the second molar | |
4. Discussion
According to Badwaik and Pakhan [26] each restoration should be able to withstand functional and parafunctional forces applied in the oral cavity. This factor should be taken into account in the fabrication of FPDs. If the loads applied to dental abutments exceed the physiological tolerance threshold of the supporting bone, they can cause bone loss and lead to treatment failure [29]. Thus, the treatment plans should include strategies to minimize such stresses. FEA can greatly help in this regard [30]. This study assessed stress distribution in 5-unit FPDs with a pier abutment and RC and NRC with the canine rise and group function occlusal schemes by FEA. The results showed that connector design had a significant effect on stress distribution in 5-unit FPD with pier abutment. The use of NRCs slightly decreased the level of stress in FPD at the site of connector attachment and cervical margin of restoration but increased the stress at the level of alveolar bone. According to Misch [31], in conventional FPDs, the male part of NRC is usually at the mesial surface of the posterior artificial tooth while the female part is located at the distal of the natural tooth abutment; this design prevents mesial movement of the connector [31].
With respect to stress and strain distribution in the abutments, the highest von Mises stress in the abutments (32.927 MPa) was noted on the buccal surface of the second premolar in both RC and NRC while minimum von Mises stress (0.0208 MPa) was recorded on the occlusal surface of second molar in FPD with NRC and canine rise occlusal scheme. Comparison of stress distribution in different designs showed high-stress concentration in the connectors and cervical part of the abutments, particularly the pier abutment. Stress concentration was recorded on root surfaces and the apical part. Nonetheless, NRC decreased the level of stress. This was specifically true when an NRC was placed at the distal of the pier abutment and decreased maximum stress concentration in the pier abutment. This design caused no stress accumulation in the anterior abutment with posterior loading, and vice versa. This finding may indicate the role of NRC in the prevention of the lever effect in a 5-unit FPD. Also, the stress level of the second molar was lower than that of the pier abutment and canine tooth, which may be explained by the larger periodontal area of the molar tooth compared with canine [32, 33] which may improve stress distribution as explained by Oruc et al. [21].
With respect to stress and strain distribution in FPDs, the highest von Mises stress value (63.959 MPa) was recorded on canine tooth crown in the use of NRC with group function occlusal scheme while the lowest von Mises stress (0.0426 MPa) was recorded on the occlusal surface of the second molar crown in use of NRC and canine rise occlusal scheme. In the present study, FPDs were subjected to progressive loads to simulate the mean masticatory forces applied in vivo. The present results were in agreement with those of Yoda et al. [34] who reported higher occlusal forces in the posterior region. According to their study, 180 N load was applied to molar teeth, 120 N to premolars, and 80 N to the canine tooth in the present study. This type of loading was practiced to more precisely simulate the masticatory forces applied to restorations in the clinical setting [20].
With respect to stress and strain distribution in the connectors, the maximum von Mises stress value (59.802 MPa) in NRCs was recorded in FPD with group function occlusion, and the minimum value (1.06 MPa) was noted in canine rise occlusion. The present results showed minimum stress in NRC with posterior loading condition, which was in line with previous findings [14, 25]. Ferencz [35] reported that resin-bonded FPDs with NRCs enabled independent movement of components, and were successful in the short term. Nonetheless, due to the placement of an NRC at the mesial surface of the abutment or distal surface of the anterior abutment, excessive stress concentration occurs in the anterior terminal abutment. A molar tooth has a larger periodontal surface than a canine [36] as explained earlier [37], and it may serve as an advantage for the molar tooth. Thus, stress concentration in the anterior abutment, compared with a posterior abutment, is less desirable. The present study showed stress concentration in canine with this particular location of NRC. Considering all the above, it may be stated with certainty that NRCs can decrease stress at the connectors and cervical part of FPDs but at the expense of increased stress in the crown, which subsequently increases the risk of bone loss [38–40]. The results of FEA are reported by the von Mises stress values, which indicate the entire stress in the field, and are considered as an index for possible trauma [25]. Since connectors are the site of maximum stress concentration in FPDs, NRCs are recommended [37, 41], and were simulated in the present study.
Concerning stress and strain distribution in bone, maximum von Mises stress in bone (73.035 MPa) was recorded in FPDs with RC and group function scheme while minimum value (0.004 MPa) was recorded in FPDs with NRC and canine rise scheme. Yoda et al. [34] performed photoelastic analysis on the bone with NRCs and reported that stress concentration points varied depending on the location of NRCs. The present results were in line with their findings. They also added that FPDs with RCs distributed the stresses homogenously and vertically, and NRCs located at the distal surface of the canine and mesial surface of molar teeth caused uniform stress distribution. Consistent with their findings, the present results revealed more uniform stress distribution in the loading of all teeth in FPDs with RC. Stress distribution in the use of NRCs located at the distal surface of the canine and mesial surface of the molar tooth was similar to the use of RC and group function loading. RC and NRC have differences in stress distribution and concentration in the supporting bone [34, 37, 40]. Stress distribution in bone in the present study was similar to previous findings [34, 37, 40]. FPDs with RC and pier abutments can serve as a lever, and create a high-stress concentration in pier abutments, which can result in excessive movements in terminal abutments and their subsequent damage. Thus, NRCs can be used to eliminate the role of pier abutments as support [37]. Ideally, an NRC should be located at the distal surface of the pier abutment [14, 25].
The occlusal scheme is the most important factor which should be taken into account prior to treatment to maximize the possibility of a favorable prognosis [8, 28]. According to the present results, NRC with a canine rise occlusal scheme would be the optimal design for a 5-unit FPD with a pier abutment.
This study had some limitations. Due to its nature, all components were considered homogeneous, isotropic, and linearly elastic [33], which is not the case in the clinical setting. Also, the results were compared qualitatively. In total, the inherent limitations of FEA should be considered when interpreting the results. Also, due to the in vitro design of the study, the results cannot be directly generalized to the clinical setting. Future studies on additional loading conditions on the occlusal surface and connectors or research on more demanding crown materials including zirconia crowns and the effect of these forces on this type of crown material are needed, considering the properties of zirconia and its challenging adhesion to the teeth [42]. Moreover, the most common location of NRC on the abutment was simulated in this study [14]. Future studies may focus on other designs of NRCs and their effect on stress distribution.
5. Conclusion
The NRC generated less stress than RC in this study. Oblique forces created greater stress, and maximum stress was noted in the canine abutment. Deformation was greater in pier abutments (compared with terminal abutments), and in RC (compared with NRC). Stress was greater in pier abutment and NRC, compared with RC. The FPD with NRC and canine rise occlusal scheme decreased stress in FPD and increased stress in the tooth crown, and can be suggested as the best design for a 5-unit FPD with pier abutment.
Acknowledgments
This article was fully funded by the authors.
Data Availability
The data are available through a request from the corresponding author: Amirhossein Fathi, Email: amir_alty@yahoo.com.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- 1.Hongsathavij R., Yosvimol Kuphasuk K. Effectiveness of platelet-rich fibrin in the management of pain and delayed wound healing. European Journal of Dermatology . 2017;11(4):192–195. doi: 10.4103/ejd.ejd_346_16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fathi A., Atash R., Fardi E., Ahmadabadi M. N., Hashemi S. Comparison of the outcomes and complications of three-unit porcelain-fused-to-metal tooth-implant-supported prostheses with implant-supported prostheses: a systematic review and meta-analysis. Dental Research Journal . 2023;20(3) doi: 10.4103/1305-7456.156847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Akulwar, Suryakanth R., Kodgi A. Non-rigid connector for managing pier abutment in FPD : a case report. Journal of Clinical and Diagnostic Research . 2014;8(7) doi: 10.7860/JCDR/2014/9710.4572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Akmal N. L. H. B. I., Jain A. R. Knowledge, awareness and practice on cantilever abutment among dental students and practitioners–A survey. Research Journal of Pharmacy and Technology . 2018;11(7):3067–3076. doi: 10.5958/0974-360x.2018.00564.4. [DOI] [Google Scholar]
- 5.Pesun I. J. Intrusion of teeth in the combination implant‐to‐natural‐tooth fixed partial denture: a review of the theories. Journal of Prosthodontics . 1997;6(4):268–277. doi: 10.1111/j.1532-849x.1997.tb00107.x. [DOI] [PubMed] [Google Scholar]
- 6.Gross M., Laufer B. Z. Splinting osseointegrated implants and natural teeth in rehabilitation of partially edentulous patients. Part I: laboratory and clinical studies. Journal of Oral Rehabilitation . 2008;24(11):863–870. doi: 10.1111/j.1365-2842.1997.tb00287.x. [DOI] [PubMed] [Google Scholar]
- 7.Misch C. M., Ismail Y. Finite element stress analysis of tooth‐to‐implant fixed partial denture designs. Journal of Prosthodontics . 1993;2(2):83–92. doi: 10.1111/j.1532-849x.1993.tb00388.x. [DOI] [PubMed] [Google Scholar]
- 8.Özçelik T. B., Ersoy A. E. An investigation of tooth/implant‐supported fixed prosthesis designs with two different stress analysis methods: an in vitro study. Journal of Prosthodontics . 2007;16(2):107–116. doi: 10.1111/j.1532-849x.2007.00176.x. [DOI] [PubMed] [Google Scholar]
- 9.Breeding L. C., Dixon D. L., Sadler J. P., McKay M. L. Mechanical considerations for the implant tooth-supported fixed partial denture. The Journal of Prosthetic Dentistry . 1995;74(5):487–492. doi: 10.1016/s0022-3913(05)80350-6. [DOI] [PubMed] [Google Scholar]
- 10.Chee W. W., Mordohai N. Tooth‐to‐implant connection: a systematic review of the literature and a case report utilizing a new connection design. Clinical Implant Dentistry and Related Research . 2009;12(2):122–133. doi: 10.1111/j.1708-8208.2008.00144.x. [DOI] [PubMed] [Google Scholar]
- 11.Schlumberger T. L., Bowley J. F., Maze G. I. Intrusion phenomenon in combination tooth-implant restorations: a review of the literature. The Journal of Prosthetic Dentistry . 1998;80(2):199–203. doi: 10.1016/s0022-3913(98)70110-6. [DOI] [PubMed] [Google Scholar]
- 12.Shadmehr E., Hashemi S., Hashemi S. S., Goudarzi A., Khademi A. The the effect of adding clonidine to articaine and epinephrine on post-treatment pain: a randomized clinical trial study. Iranian Endodontic Journal . 2021;16(4):210–216. doi: 10.22037/iej.v16i4.33555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kuruvila A., Joseph S., Jayalekshmi N. L., Menon S. K. The key to the management of pier abutment: an alternative approach. Journal of International Oral Health . 2017;9(3):p. 136. [Google Scholar]
- 14.Banerjee S., Khongshei A., Gupta T., Banerjee A. Non-rigid connector: the wand to allay the stresses on abutment. Contemporary Clinical Dentistry . 2011;2(4):p. 351. doi: 10.4103/0976-237x.91802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Akulwar R. S., Kodgi A. Non-rigid connector for managing pier abutment in FPD: a case report. Journal of Clinical and Diagnostic Research . 2014;8(7):ZD12–ZD13. doi: 10.7860/JCDR/2014/9710.4572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saurav B., Khongshei A., Gupta T., Banerjee A. Non-rigid connector : the wand to allay the stresses on abutment. Contemporary Clinical Dentistry . 2011;2(4):351–354. doi: 10.4103/0976-237X.91802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sidana V., Pasricha N., Makkar M., Bhasin S. Group function occlusion. International Journal of Oral Science . 2012;3(3):124–128. doi: 10.4103/0976-6944.111173. [DOI] [Google Scholar]
- 18.Parnia F., Moslehi Fard E., Sadr K., Motiagheny N. Pattern of occlusal contacts in eccentric mandibular positions in dental students. Journal of Dental Research, Dental Clinics, Dental Prospects . 2008;2(3):85–89. doi: 10.5681/joddd.2008.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Akören A., Karaačaçliočlu L. Comparison of the electromyographic activity of individuals with canine guidance and group function occlusion. Journal of Oral Rehabilitation . 1995;22(1):73–77. doi: 10.1111/j.1365-2842.1995.tb00213.x. [DOI] [PubMed] [Google Scholar]
- 20.Eraslan O., Sevimay M., Usumez A., Eskitascioglu G. Effects of cantilever design and material on stress distribution in fixed partial dentures - a finite element analysis. Journal of Oral Rehabilitation . 2005;32(4):273–278. doi: 10.1111/j.1365-2842.2004.01429.x. [DOI] [PubMed] [Google Scholar]
- 21.Oruc S., Eraslan O., Tukay H. A., Atay A. Stress analysis of effects of nonrigid connectors on fixed partial dentures with pier abutments. The Journal of Prosthetic Dentistry . 2008;99(3):185–192. doi: 10.1016/s0022-3913(08)60042-6. [DOI] [PubMed] [Google Scholar]
- 22.Jiang H., Tan J., Wang X. Z. Wear test of 4-unit posterior resin bonded fixed partial dentures with non-rigid connector. Beijing Da Xue Xue Bao . 2012;44(1):84–87. [PubMed] [Google Scholar]
- 23.Reda R., Zanza A., Galli M., De Biase A., Testarelli L., Di Nardo D. Applications and clinical behavior of BioHPP in prosthetic dentistry: a short review. Journal of Composites Science . 2022;6(3):p. 90. doi: 10.3390/jcs6030090. [DOI] [Google Scholar]
- 24.Akça K., Uysal S., Çehreli M. C. Implant–tooth‐supported fixed partial prostheses: correlations between in vivo occlusal bite forces and marginal bone reactions. Clinical Oral Implants Research . 2006;17(3):331–336. doi: 10.1111/j.1600-0501.2005.01169.x. [DOI] [PubMed] [Google Scholar]
- 25.Shillingburg H. T., Sather D. A. Fundamentals of Fixed Prosthodontics . Berlin, Germany: Quintessence Pub; 2012. [Google Scholar]
- 26.Badwaik P., Pakhan A. Non-rigid connectors in fixed prosthodontics: current concepts with a case report. Journal of Indian Prosthodontic Society . 2005;5(2):99–102. doi: 10.4103/0972-4052.16879. [DOI] [Google Scholar]
- 27.Juloski J., Radovic I., Goracci C., Vulicevic Z. R., Ferrari M. Ferrule effect: a literature review. Journal of Endodontics . 2012;38(1):11–19. doi: 10.1016/j.joen.2011.09.024. [DOI] [PubMed] [Google Scholar]
- 28.Burak Özcelik T., Ersoy E., Yilmaz B. Biomechanical evaluation of tooth‐and implant‐supported fixed dental prostheses with various nonrigid connector positions: a finite element analysis. Journal of Prosthodontics . 2011;20(1):16–28. doi: 10.1111/j.1532-849x.2010.00654.x. [DOI] [PubMed] [Google Scholar]
- 29.Singh V., Das S., Sharma N. K. Iodoform: a boon in disguise. Open Journal of Stomatology . 2012;02(4):322–325. doi: 10.4236/ojst.2012.24055. [DOI] [Google Scholar]
- 30.Nitzan D. On the genesis of “dry socket”. Journal of Oral and Maxillofacial Surgery . 1983;41(11):706–710. doi: 10.1016/0278-2391(83)90185-4. [DOI] [PubMed] [Google Scholar]
- 31.Misch C. E. Dental Implant Prosthetics . Maryland Heights, Missouri: Mosby; 2005. [Google Scholar]
- 32.Hedström L., Sjögren P. Effect estimates and methodological quality of randomized controlled trials about prevention of alveolar osteitis following tooth extraction: a systematic review. Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology & Endodontics . 2007;103(1):8–15. doi: 10.1016/j.tripleo.2006.01.007. [DOI] [PubMed] [Google Scholar]
- 33.Goodacre C. J., Campagni W. V., Aquilino S. A. Tooth preparations for complete crowns: an art form based on scientific principles. The Journal of Prosthetic Dentistry . 2001;85(4):363–376. doi: 10.1067/mpr.2001.114685. [DOI] [PubMed] [Google Scholar]
- 34.Yoda N., Liao Z., Chen J., Sasaki K., Swain M., Li Q. Role of implant configurations supporting three‐unit fixed partial denture on mandibular bone response: biological‐data‐based finite element study. Journal of Oral Rehabilitation . 2016;43(9):692–701. doi: 10.1111/joor.12411. [DOI] [PubMed] [Google Scholar]
- 35.Ferencz J. L. The use of non-rigid connectors for long span ceramo-metal fixed partial dentures. New York Journal of Dentistry . 1978;48(9):287–291. [PubMed] [Google Scholar]
- 36.Shillingburg H. T., Fisher D. W. Nonrigid connectors for fixed partial dentures. Journal of The American Dental Association . 1973;87(6):1195–1199. doi: 10.14219/jada.archive.1973.0552. [DOI] [PubMed] [Google Scholar]
- 37.Wheeler R. Dental Anatomy, Physiology, and Occlusion . Philadelphia USA: WB Saunders Company; 1974. [Google Scholar]
- 38.Blum I. Contemporary views on dry socket (alveolar osteitis): a clinical appraisal of standardization, aetiopathogenesis and management: a critical review. International Journal of Oral and Maxillofacial Surgery . 2002;31(3):309–317. doi: 10.1054/ijom.2002.0263. [DOI] [PubMed] [Google Scholar]
- 39.Ting M., Faulkner R. J., Donatelli D. P., Suzuki J. B. Tooth-to-Implant–Supported fixed partial denture: a comprehensive overview of systematic reviews. Implant Dentistry . 2019;28(5):490–499. doi: 10.1097/id.0000000000000901. [DOI] [PubMed] [Google Scholar]
- 40.Lin C. L., Wang J. C., Chang W. J. Biomechanical interactions in tooth–implant‐supported fixed partial dentures with variations in the number of splinted teeth and connector type: a finite element analysis. Clinical Oral Implants Research . 2008;19(1):107–117. doi: 10.1111/j.1600-0501.2007.01363.x. [DOI] [PubMed] [Google Scholar]
- 41.Kawarizadeh A., Bourauel C., Jäger A. Experimental and numerical determination of initial tooth mobility and material properties of the periodontal ligament in rat molar specimens. The European Journal of Orthodontics . 2003;25(6):569–578. doi: 10.1093/ejo/25.6.569. [DOI] [PubMed] [Google Scholar]
- 42.Fathi A., Hashemi S., Tabatabaei S. S., Mosharraf R., Atash R. Adhesion to Zirconia: an umbrella review. International Journal of Adhesion and Adhesives . 2023;122 doi: 10.1016/j.ijadhadh.2023.103322.103322 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data are available through a request from the corresponding author: Amirhossein Fathi, Email: amir_alty@yahoo.com.


