Impact of collagen-like peptide (CLP) heterotrimeric triple helix design on helical thermal stability and hierarchical assembly: A coarse-grained molecular dynamics simulation study

Abstract

Collagen-like peptides (CLP) are multifunctional materials garnering a lot of recent interest from the biomaterials community due to their hierarchical assembly and tunable physicochemical properties. In this work, we present a computational study that links the design of CLP heterotrimers to the thermal stability of the triple helix and their self-assembly into fibrillar aggregates and percolated networks. Unlike homotrimeric helices, the CLP heterotrimeric triple helices in this study are made of CLP strands of different chain lengths that result in ‘sticky’ ends with available hydrogen bonding groups. These ‘sticky’ ends at one end or both ends of the CLP heterotrimer then facilitate inter-helix hydrogen bonding leading to self-assembly into fibrils (clusters) and percolated networks. We consider the cases of three sticky end lengths - two, four, and six repeat units - present entirely on one end or split between two ends of the CLP heterotrimer. We observe in CLP heterotrimer melting curves generated using coarse grained Langevin dynamics simulations at low CLP concentration that increasing sticky end length results in lower melting temperatures for both one and two sticky ended CLP designs. At higher CLP concentrations, we observe non-monotonic trends in cluster sizes with increasing sticky end length with one sticky end but not for two sticky ends with the same number of available hydrogen bonding groups as the one sticky end; this nonmonotonicity stems from the formation of turn structures stabilized by hydrogen bonds at the single, sticky end for sticky end lengths greater than four repeat units. With increasing CLP concentration, heterotrimers also form percolated networks with increasing sticky end length with a minimum sticky end length of four repeat units required to observe percolation. Overall, this work informs the design of thermoresponsive, peptide-based biomaterials with desired morphologies using strand length and dispersity as a handle for tuning thermal stability and formation of supramolecular structures.

I. Introduction

Bio-inspired and biologically derived materials exhibit complex morphologies at multiple length scales. In synthetic biomimetic materials this complex multi-scale structure often is obtained through a combination of tailored design of the building block (e.g., polypeptide composition and sequence, oligonucleic acid composition and sequence, cellulose derivatives, etc.) and the directed-/self-assembly of these building blocks. Additionally, both the building block and the assembled structures can be altered through triggers from external stimuli such as temperature, pH, light, and salt concentration.^1–7 One class of bio-inspired building blocks are collagen-like peptides (CLPs), also known as collagen-mimetic peptides (CMPs). CLPs are biopolymers consisting of repeat units of amino acid triplets, (X-Y-G), where X and Y typically are proline (P) and hydroxyproline (O), respectively, inspired by human collagen I. Like native (natural) collagen, CLPs exhibit structures at different length scales: three CLP strands hybridize to form a triple helix,^{8, 9} and these CLP triple helices assemble to form fibrils and networks in aqueous solutions.^10–13 CLP triple helices are thermoresponsive because at low temperatures three single CLP strands associate via inter-strand hydrogen bonding to form a stable triple helix and at high temperatures the hydrogen bonds dissociate causing the ‘melting’ of the triple helix. The multi-length scale hierarchical structures and the thermoresponsive nature of CLPs make them useful as biomaterials for drug delivery^14–17 and scaffolds for cell culture and tissue engineering applications^18–21. To achieve controlled assembly, however, there is still a need for simple designs and approaches for forming supramolecular structures where strand length or dispersity afford opportunities but are less explored than chemical identity.

Going beyond the canonical CLP designs, recent advances in controlled peptide synthesis have enabled synthesis of heterotrimeric triple helices,^22–28 which are CLP triple helices with heterogeneity in length and/or amino acid sequences in the two or three CLP strands that form the triple helix. In past studies, AAB and ABC heterotrimeric helices have been formed and stabilized by the formation of salt bridges^{24, 29–31} (e.g., lysine-aspartate or lysine-glutamate salt bridges), repulsive electrostatic interactions²⁵, and cation-π interactions²². For example, Hartgerink and coworkers synthesized and analyzed the stability of AAB and ABC heterotrimers composed of (DOG)₁₀, (PKG)₁₀, and (POG)₁₀ strands.²⁹ They observed that an ABC heterotrimer (i.e., a triple helix made of (DOG)₁₀, (PKG)₁₀, and (POG)₁₀ strands) exhibited a melting temperature comparable to that of a (POG)₁₀ homotrimer even though D and K residues occurred 20 times in the heterotrimeric helix and have been shown to destabilize the helix compared to P and O residues. In other studies, CLP heterotrimers have been designed to mimic the glycine mutations present in either the α1 or α2 chains of type I collagen; this was accomplished utilizing an electrostatic recognition motif in three chains that can force the interactions of any three peptides, such as AAA, AAB, and ABC heterotrimers.³² Two major challenges in synthesizing heterotrimers are that the same peptide strands, ABC, can form competing homotrimeric helices (e.g., AAA, BBB, or CCC) and can also arrange in different helical registers: e.g., an ABC heterotrimer would have 27 possible registers (e.g., ABC, ACB, or BAC) where A, B, or C can be present in the leading, middle, or lagging strand positions. Therefore, experimental studies of heterotrimers frequently show multiple melting transitions due to a mixture of homotrimers and heterotrimers present in solution.^{22, 32} Other studies, however, have successfully designed heterotrimers that selectively form a single register via lateral salt bridges involving non-natural amino acids,²⁸ repulsive interactions involving aspartate side chains,²⁵ and high content of arginine due to the ability of the arginine side chain to hydrogen bond with backbone carbonyls of other peptide chains³⁰. These studies highlight the approaches for forming heterotrimers and their utility for forming complex morphologies and supramolecular structures (e.g., via charged ‘sticky ends’ involving salt bridges³¹).

One can also find ‘sticky’ ends in homotrimeric triple helices such that sticky ended approaches have been more widely studied in homotrimeric rather than heterotrimeric triple helix designs.³³ For example, Hartgerink and co-workers have proposed that lysine-aspartate salt bridges create an offset, sticky-ended homotrimeric triple helix.³⁴ Furthermore, they theorized that the salt bridges force a configuration such that only one-third of the possible lysine-aspartate pairs are satisfied within a single triple helix and the remaining two-third of the salt bridges are satisfied through intrahelical interactions that form an assembled infinitely long triple helical fiber. Due to the fibrous morphology of the aggregates, the ‘sticky end’ in each collagen triple helix could not be elucidated using any biophysical tool available.^{31, 34} Raines and co-workers have intentionally synthesized sticky-ended homotrimeric triple helices in which the three strands are held in a staggered arrangement by disulfide bonds.³⁵ Results from atomic force microscopy (AFM), transmission electron microscopy (TEM), circular dichroism (CD), and dynamic light scattering (DLS) showed that these sticky-ended (POG)-based triple helices self-assembled without salt bridges to form micrometer-long fibrils that mimic the structure and thermal behavior of natural collagen. Other studies of (POG)-based CLP polymers formed by native chemical ligation have shown the formation of a dense network of fibers 10-20 nm in diameter and microns in length due to the presence of sticky ends.³⁶ Paramonov et al. hypothesized that the polydispersity of the peptide strands resulted in sticky ended (POG)-based triple helices, thus leading to supramolecular assembly without the need for salt bridge formation. Since the sticky ends were a result of dispersity, there were no means to control the length of the resulting sticky ends. Therefore, this leaves opportunities for simulation approaches to explore and understand the impact of dispersity in the context of sticky ends with the overarching goal of forming hierarchical structures via self-assembly.

While there have been multiple experimental studies focused on CLP homotrimeric versus heterotrimeric triple helices with and without sticky ends in dilute solutions,^{31, 35, 37} few studies have explored the multiscale assembly of such systems to form supramolecular networks. Similarly, computational tools have only been used to predict melting temperatures of CLP homotrimeric triple helices³⁸ and heterotrimeric triple helices in dilute solutions³⁹ and not explored the multi-length scale assembly of CLP strands to triple helices and the assembly of those triple helices into fibrils/networks. Atomistic simulation studies have explored triple helix stability as a function of sequence length,⁴⁰ amino acid substitutions,⁴¹ and amino acid stereochemistry⁴². Due to the intractable simulation times required to observed melting, many of these studies quantified triple helix stability in terms of key atomic structural rearrangements and interactions, such as root mean square deviations (RMSD) of the peptide backbone, helical twist, and water-mediated hydrogen bonding.⁴³ For example, the work of Raman et al. has shown using atomistic simulations that aspartic acid residues destabilize the triple helix due to increased chain flexibility, and their impact on inter-molecular hydrogen bonding and reorganization of the water structure surrounding the triple helix.⁴¹ However, there is currently a lack of atomistic simulation studies on CLP self-assembly at length scales beyond the triple helix due to the computational expense involved in simulating assembled systems with atomistic resolution.^44–46

Coarse-grained simulations, on the other hand, are well suited to observe CLP melting as compared to atomistic simulations because of their reduced degrees of freedom. For example, the CLP coarse-grained model of Condon and Jayaraman reproduces the directionality of hydrogen bonding interactions within the CLP triple helix.⁴⁷ Recently, we performed simulations using this CLP coarse-grained model to predict thermal stability of homotrimeric triple helices with natural and non-natural amino acid substitutions (e.g., Lysine substitution for hydroxyproline, allylyoxycarbonyl (alloc) functionalized lysine residues for crosslinking in hydrogel systems) and found qualitative agreement with experimentally observed melting temperatures as a function of CLP design (i.e., amino acid substitutions).⁴⁸ Other CG models designed by Buehler and coworkers are based on the MARTINI forcefields and can determine mechanical and structural properties of CLPs such as elastic moduli and persistence lengths.^44–46 These CG models do not capture the inter-strand N-H to C=O hydrogen bonding pattern found in collagen triple helical structures which dictates the thermal stability of the triple helix and drives higher-order assembly beyond the triple helix (e.g., assembly of sticky ended helices into fibrils). Therefore, the CLP coarse-grained model of Condon and Jayaraman model that captures intra- and inter- helix hydrogen bonds is the appropriate choice for molecular dynamics simulation studies of CLP assembly at larger length and time scales, which is the focus of this paper.

In this paper we use the CLP coarse-grained model of Condon and Jayaraman model to study thermal stability and assembly of CLP heterotrimeric triple helices. Each triple helix has one or two ‘sticky’ ends because the three CLP strands in each triple helix is of same sequence (i.e., POG repeat units) but differ in chain lengths, thus exposing hydrogen bonding groups (i.e., prolines and glycines) at these sticky ends to allow for inter-helix hydrogen bonding and assembly into fibrils and supramolecular networks. Therefore, in this work we expand on the POG-based sticky ended designs previously explored in homotrimeric systems and apply them to heterotrimeric systems by incorporating dispersity in chain length for a range of CLP triple helical designs. This approach highlights the ability of simulations to explore CLP systems which are often difficult to synthesize such that we can achieve specified differential chain lengths with the goal of generating design rules linking triple helix design to their hierarchical assembly.

This paper is organized as follows. In section II, we describe the details of simulation methods (atomistic and CG), systems simulated and computational analysis. In section III, we present first the results from our CG simulation work of CLP heterotrimers which then motivate our atomistic simulations. Finally, we summarize our results in the conclusion section.

II. Methods

A. Coarse-Grained (CG) CLP simulations.

We use the CG CLP model of Condon and Jayaraman⁴⁷ (Figure 1a) to study CLP heterotrimers and predict their hierarchical assembly. This is a phenomenological CG model developed to reproduce CLP triple helix dimensions (end-to-end distance and diameters) and the trends in CLP helix melting temperatures seen in experiments.⁴⁷ For example, recent work by Kloxin, Jayaraman, and co-workers has shown semi-quantitative agreement between melting curves obtained from the CG CLP model of Condon and Jayaraman and experimental melting curves for CLP triple helices with uncharged, charged, and non-natural amino acids.⁴⁸ (see Figure S1)

Figure 1.

Coarse-grained representations and amino acid sequences of CLP heterotrimeric triple helices with one or two sticky ends. (a) Model of a (POG) triplet with bonded interactions shown by lines and angles connecting coarse grained beads. (b) Model of two (POG) triplets showing their dihedral angles. For the coarse-grained representation, proline backbone beads (PB) are colored blue, hydroxyproline backbone beads are orange, glycine backbone beads are green, and proline hydrogen bonding (PH) and glycine hydrogen bonding (GH) beads are yellow. Full coarse- grained representations and amino acid sequences are shown for (c) a one sticky ended and (d) two sticky ended design.

In our CG CLP model, each (POG) repeat is represented as a chain of CG beads: a proline backbone (PB) bead, a proline H-bond (PH) acceptor bead, a hydroxyproline backbone bead (OB), a glycine backbone (GB) bead, and a glycine H-bond (GH) donor bead. All backbone (BB) beads have a diameter of 1.0 σ and a mass of 3.0 m while all H-bond beads have a diameter of 0.3 σ and a mass of 1.0 m. All distances are defined in terms of σ = 0.5 nm and all masses in terms of an arbitrary m as the simulations are not intended to capture the correct dynamics of these CLP systems. All energy terms are defined in terms of ε = 0.1 kcal/mol.

In each CLP chain, adjacent BB beads are connected via a harmonic bond potential with a bond length of 0.5 σ and force constant of 1000 ε/σ². Each H-bond bead is connected to its “parent” BB bead via a harmonic bond potential with a bond length of 0.37 σ and force constant of 1000 ε/σ². The SHAKE algorithm is used to constrain all BB-HB bond lengths.⁴⁹ To account for the rigidity of the polyproline type II conformation of the CLP strands,¹⁰ we include a harmonic angle potential between three adjacent BB beads with the angle constant set at 20 ε/radian² and equilibrium bond angle set at 180° (i.e., π radians). To ensure that H-bond formation occurs perpendicular to the backbone, a H-bond bead-parent BB bead-adjacent BB bead angle potential is implemented with a force constant of 300 ε/radian² and equilibrium angle of 90°. To ensure the directionality of H-bond beads with respect to neighboring H-bond beads along the same strand, we incorporate two H-bond bead—BB bead—BB bead—H-bond bead dihedral angle potentials,

$$U^{dih}\left(\phi \right)=k_d\left(1+\text{cos}(\phi -{\phi }_0)\right)$$ (1)

in which the dihedral constant k_d is set at 15 ε and the reference dihedral, φ₀ is set at –120° for (GH-GB-PB-PH) dihedrals and 120° for (PH-PB-GB-GH) dihedrals.

Non-bonded H-bond donor (D) - acceptor (A) interactions are modeled using the Lennard-Jones (LJ) potential,⁵⁰

$$U_{D-A}^{HB}\left(r\right)={\epsilon }_{D-A}^{HB}\left[{\left(\frac{{\sigma }^{HB}}{r}\right)}^{12}-{\left(\frac{{\sigma }^{HB}}{r}\right)}^6\right]$$ (2)

where ${\epsilon }_{HB}^{D-A}$ is the interaction strength between D and A beads and is set at 50.4 ε and σ^HB is the diameter of a H-bond bead. All other pairwise interactions besides the H-bond donor-acceptor interactions for CLP beads are modeled using the purely repulsive, Weeks-Chandler-Andersen (WCA) potential.⁵¹

$$U_{ij}\left(r\right)=\{\begin{array}{ll}4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r}\right)}^6\right]+{\epsilon }_{ij}& ;r<2^{\frac{1}{6}}{\sigma }_{ij}\\ 0& ;otherwise\end{array}$$ (3)

where σ_ij is the arithmetic mean of the diameters of beads i and j, and ε_ij, the interaction strength, is set at 1.0 ε. For donor-donor and acceptor-acceptor interactions, σ_ii is set at 0.7 σ instead of 0.3 σ to ensure that a donor HB bead only forms an H-bond with a single HB acceptor bead, and vice versa.

As the model we use in this study is a phenomenological CG model rather than a chemistry-specific bottom-up CG model, the choice of form of pair-wise interaction potentials is not rooted in chemistry but rather a choice of a mathematical expression of the U(r) that reproduces the desired phenomenon. Such phenomenological CG models are widely used in soft materials modeling by many groups studying biopolymers with dominant hydrogen bonding (e.g., DNA and peptides) or colloids with patchy attractive sites in implicit solvent. Jayaraman and co-workers⁵² have shown that it is the combination of LJ potentials, repulsive interactions between pairs of donors and pairs of acceptors, and relative bead sizes and placements that reproduces the effectively directional and donor-acceptor specific interactions like hydrogen bonding.

In this study, we focus on CLP heterotrimeric triple helices that differ in chain lengths between CLP strands forming each triple helix resulting in sticky ends (Figure 1c and 1d). We study both one sticky ended (Figure 1c) and two sticky ended (Figure 1d) heterotrimeric triple helices. We define two families of peptides, the (POG)₁₀ and (POG)₁₂ families, each with a fixed total number of (POG) repeat units per triple helix. The (POG)₁₀ family has a total number of 30 (POG) repeat units per helix while the (POG)₁₂ family has a total of 36 (POG) repeat units per helix. We investigate heterotrimeric triple helices of varying sticky end length, Δ, while keeping the total number of hydrogen bonding groups per helix, i.e. (POG) units, constant within each family to ensure that differences in assembly or morphology are due to differences in the architecture of the helix rather than an increase or decrease in the number of hydrogen bonding sites. For the (POG)₁₀ family, we define sequences of (POG)_10+Δ-(POG)₁₀-(POG)_10-Δ where the length of the leading strand within the triple helix is increased by Δ repeat units and the lagging strand’s length is decreased by Δ repeat units. Therefore, Δ creates an offset which results in a sticky ended triple helix. In this work, we explore Δ = 2, 4, and 6. Similarly, for the (POG)₁₂ family we define sequence of (POG)_12+Δ-(POG)₁₂-(POG)_12-Δ. For a one sticky ended design, the entire offset (Δ) is placed on a single end of the helix while for a two sticky ended design half of the offset is placed on each side of the helix. Therefore, for the same value of Δ both a one sticky ended helix and two sticky ended helix each have the same total sticky end length (or same number of available hydrogen bonding sites). We have also included a table of peptide designs and solutions conditions (Table S1) explored in this study. The design parameters explored in this study such as sticky end lengths, CLP concentrations, and CLP chain lengths (i.e., (POG) families) are based on previously published studies by Hartgerink and co-workers^{31, 34} and Kloxin and co-workers,^{48, 53} including ongoing peptide synthesis by Kloxin and co-workers and others in the field for producing collagen mimetic materials.

We perform Langevin dynamics simulations in the NVT ensemble using the LAMMPS simulation package.⁵⁴ For all systems, the initial configuration is created by randomly placing intact CLP triple helices in a cubic simulation box of size 110 σ with periodic boundary conditions. Details of the number of CLP triple helices as a function of CLP concentration are shown in Table S2. Our simulation box size of 110σ is considerably larger than the triple helix sizes explored in this study and the range of interactions. For example, the end-to-end distance of a (POG)₁₂ triple helix is 16.88σ⁴⁷ and our model only includes short-ranged potentials with a cutoff distance of 2.5σ and no long-ranged electrostatic interactions. In all Langevin simulations the friction coefficient is set to 10 τ (where 0.001 τ is approximately 6 fs) guided by previous work with similar systems.⁵⁵ A two-level RESPA⁵⁶ integrator is also used so that non-bonded and bonded interactions are integrated with a time step of 0.001 τ and 0.0005 τ, respectively. All systems are first equilibrated for 10⁸ time steps followed by a 10⁷ time steps long production run during which data is collected every 100,000 time steps.

To quantify the stability of the CLP triple helix in CG simulations, we define the ensemble average fraction of inter-strand glycine (G) triplets that are intact, f_intact. An inter-strand G triplet refers to three G BB beads that are all part of separate strands and are located at the same relative position along the triple helix. Moreover, the triplet is counted as intact if the maximum distance between any pair of G BB beads is less than 3 σ. Therefore, a plot of f_intact vs. reduced temperature, T*, would describe the stability of the CLP triple helix at different temperatures; the melting temperature, T_m*, is defined as the value of T* for which f_intact = 0.5.

To quantify the higher-order assembly of CLP triple helices into aggregates and fibrils, we calculate the radius of gyration of each cluster of CLP heterotrimeric triple helices, R_g,cluster, and the number of helices per cluster, N_{helix,cluster}. Two triple helices are considered as being part of the same cluster if there exists at least a single hydrogen bond between the two helices with a hydrogen bond defined as a pair of PH and GH beads that are separated by a distance of 0.45σ or less. By looping through all triple helices, we identify clusters as collection of triple helices that satisfy the above criterion. Then, the radius of gyration of each cluster of CLP heterotrimeric triple helices, R_g,cluster, is calculated as

$$R_{g,cluster}=\sqrt{\frac{1}{N}{\sum }_i|r_i-r_{COM}{|}^2}$$ (4)

where N is the number of CLP beads in the cluster, r_i, is the position of bead i, and r_com is the cluster’s center of mass. We quantify weighted probability distributions of R_g,cluster and N_{helix,cluster} such that the probability of each bin is weighted by its respective value (R_g,cluster or N_{helix,cluster}). We focus on clusters with at least two helices per cluster and calculate weighted distributions of R_g,cluster and N_{helix,cluster} and label this calculation as the ‘assembled’ calculation. Next, we generate weighted probability distributions of R_g,cluster and N_{helix,cluster} for clusters in which there is only a single, free triple helix and label the calculation as the ‘free’ calculation. Finally, we consider all clusters with at least one helix (free triple helix) or more (assembled triple helix) and label these weighted probability distributions of R_g,cluster and N_{helix,cluster} as the ‘combined’ distributions. In this work, we only emphasize the qualitative trends in how the aggregate sizes increase or decrease as a function of CLP design rather than numerical values as the absolute value of the aggregate sizes (e.g., number of CLPs in a cluster and the radius of gyration) are a function of the number of CLP helices simulated.

We also note that our CG model assumes that hydrogen bonding is the dominant mechanism via which these sticky-ended (POG)-based heterotrimers assemble and neglects other interactions such as hydrophobic and π-π stacking interactions that have been shown to drive side-side helical assembly in other CLP systems. This assumption results in fibrillar clusters with diameters matching those observed for a single triple helix. The extent to which interactions such as hydrophobicity influence self-assembly depends on solvent quality: for example, Raines and co-workers³⁵ have shown experimentally for similar (POG)-based sticky ended heterotrimeric designs that triple helices assembled head-tail based on hydrogen bonding and did not observe any side-side assembly or hydrophobic interactions between helices due to their choice of solvent, i.e., solutions of acetic acid, methanol, and mixtures of acetic acid and methanol. Therefore, our CG model best represents these types of solvent conditions in which hydrogen bonding is dominant. Other experimental studies have also shown that π-π stacking interactions are important for homotrimeric, (POG)-based CLPs with termini including aromatic groups such as phenyl and pentafluorophenyl^{67, 68} and have reported stacking interactions which result in self-assembly. In this work, our CG model best represents CLPs with neutral termini and does not account for chemistries with aromatic end groups inspired by experimental reports of (POG)-based CLPs without modified termini (i.e., non-aromatic termini) and with blunt ended designs which form triple helices but do not assemble to form fibrillar structures.⁶⁷

Finally, to characterize the formation of a percolated network, we first determine the maximum cluster size (i.e., maximum number of helices per cluster) in the original configuration, then replicate the image of the configuration in the x, y, and z directions and re-evaluate the maximum cluster size for the larger configuration. If the size of any cluster in the new replicated configuration is larger than the largest cluster of the original configuration, we record that configuration as being percolated. This procedure ensures that the network spans the simulation box and is also connected to its periodic copies across periodic boundary conditions. We conduct this calculation over a number of configurations, marking each configuration as either percolated (τ_perc = 1) or not percolated (τ_perc = 0); we report the ensemble average fraction of configurations in a percolated state, <τ_perc>.

For all simulation results, error bars show the standard deviation obtained from three trials in which the data from all three trials (i.e., all frames) are pooled and the standard deviation of the pooled values is reported.

B. Atomistic CLP simulations.

To investigate the propensity of CLP strands to form turn structures, atomistic molecular dynamics simulations are performed using the GROMACS 4.6.7 simulation package.⁵⁷ All initial (GPO)₆ single CLP strand configurations are obtained using the Interactive Triple-Helical collagen Building Script (THeBuScr)⁵⁸ by generating homotrimeric (GPO)₆ polyproline type II triple helices and deleting the middle and lagging strands. Since the goal of these atomistic simulations is to investigate the propensity of a single CLP strand to form turn structures, only one strand with a polyproline type II helix is necessary.

For each CLP sequence, a single CLP strand is solvated in water and an appropriate number of Na+ and Cl- counterions are added to achieve net charge neutral systems. All sequences are simulated using a cubic simulation box size of size 15 nm. Each system is energy minimized using a steepest descent method with the maximum force tolerance level set as 900 KJ mol⁻¹ nm⁻¹. MD simulations are performed using the Gromos53a6 forcefield⁵⁹ and the SPC water model⁶⁰ in the NPT ensemble at 300 K and 1 bar for 102 ns. A time step of 2 fs is used for the numerical integration and bonds involving hydrogen atoms are constrained using the LINCS method.⁶¹ Temperature and pressure are maintained constant using the stochastic velocity rescaling method⁶² and Berendsen barostat⁶³, respectively, with time constants of 1.0 and 2.0 ps respectively. All electrostatic interactions are modeled using the particle-mesh Ewald (PME) method using fourth-order cubic interpolation.⁶⁴

Secondary structures are assigned using the STRIDE algorithm⁶⁵ for all four CLP systems with varying end group functionalization. We study four systems: 1) a single (GPO)₆ strand with a positively charged N-terminus (NH₃⁺) and negatively charged C-terminus (COO⁻), 2) a single (GPO)₆ strand with an uncharged N-terminus (NH₂) and uncharged C-terminus (COOH), 3) a single (GPO)₆ strand with a positively charged N-terminus (NH₃⁺) and uncharged C-terminus (COOH), and 4) a single (GPO)₆ strand with an uncharged N-terminus (NH₂) and negatively charged C-terminus (COO⁻). Furthermore, we quantify the fraction of amino acids participating in turn structures, f_res, as a function of time and ensemble averaged fraction of configurations in which each, unique residue forms turn structures, <f_turn>. All simulation snapshots are obtained using Visual Molecular Dynamics (VMD).⁶⁶

III. Results and Discussion

In this work, we study the effects of dispersity in terms of CLP strand lengths within a triple helix on the thermal stability of the CLP heterotrimer helix and the assembly of CLP heterotrimeric helices. Such helical designs facilitate exposure of hydrogen bonding groups (i.e., prolines and glycines) at the ends of the helices (i.e., ‘sticky ends’) and allow for inter-helix hydrogen bonding and assembly into fibrils and supramolecular networks. Moreover, we expand on the POG-based sticky ended designs previously explored in homotrimeric systems^{35, 36} and apply them to heterotrimeric systems by incorporating dispersity in chain length for a range of CLP triple helical designs. Specifically, we examine the impact of CLP heterotrimer design, namely, sticky end length, Δ, number of sticky ends, and (POG) family on the thermal stability (i.e., melting temperature) and the assembly of the CLP heterotrimeric helices. We define two families of peptides, the (POG)₁₀ and (POG)₁₂ families, each with a fixed total number of (POG) repeat units per triple helix to ensure that differences in assembly or morphology are due to differences in the architecture of the helix rather than an increase or decrease in the number of hydrogen bonding sites. The (POG)₁₀ family has a total number of 30 (POG) repeat units per helix while the (POG)₁₂ family has a total of 36 (POG) repeat units per helix. We investigate heterotrimeric triple helices of varying sticky end length, Δ, while keeping the total number of hydrogen bonding groups per helix, i.e. (POG) units, constant within each family.

First, we examine the impact of Δ and (POG) family on the thermal stability of the CLP heterotrimeric triple helix. In Figure 2 we present the melting curves of CLP heterotrimers obtained from CG MD simulations for one sticky ended heterotrimeric triple helices at low CLP concentrations of 0.3 mM. For both the (POG)₁₀ and (POG)₁₂ families of heterotrimers, as sticky end length (Δ) increases the melting temperature (i.e., T_m* in reduced units) decreases. Since the total number of (POG) repeat units is held constant within a single helix for all cases of Δ, a longer Δ would result in fewer intra-helix hydrogen bonds and therefore a lower T_m*. Previous computational studies on CLP homotrimers have shown that fewer intra-helix hydrogen bonds lead to lower melting temperature.⁴⁸ We also observe that an increase from Δ = 0 to Δ = 6 leads to a larger reduction in T_m* for the (POG)₁₀ as compared to the (POG)₁₂ family. Since the (POG)₁₂ family has a greater total number of (POG) repeat units as compared to the (POG)₁₀ family (36 versus 30 units), the same Δ leads to a larger reduction in the percentage of intra-helix hydrogen bonds for the (POG)₁₀ versus (POG)₁₂ family. Therefore, a larger reduction in the percentage of hydrogen bonds results in a larger reduction in thermal stability of the triple helix (T_m*) for the (POG)₁₀ family.

Figure 2.

Melting curves of CLP heterotrimers obtained from CG MD simulations for one sticky ended heterotrimeric triple helices for sticky end lengths, Δ, of 2, 4, and 6 for (a) the (POG)₁₀ family and (b) (POG)₁₂ family. All melting curves are obtained at a CLP concentration of 0.3 mM.

The results seen for one sticky ended triple helices in Figure 2, namely a reduction in T_m* with increasing Δ and a larger shift in T_m* for the (POG)₁₀ versus (POG)₁₂ family, are also seen for two sticky ended helices (see Figure S2 a and b). We also do not observe statistically significant differences between the melting temperatures for a one- or two-sticky ended design for the same Δ and (POG) family. Therefore, the major design parameters which impact the melting temperatures of these POG-based heterotrimeric triple helices are the sticky end length, Δ, and the number of (POG) repeat units, i.e., the (POG) family.

We note that melting temperature calculators³⁹ parameterized using experimental melting temperatures compiled from multiple research studies can provide insight in terms of the impact of sticky ends (i.e., staggered helical registers) on the melting temperature of the triple helix. Recently, Hartgerink and co-workers have developed a melting temperature calculator for CLP homotrimeric and heterotrimeric triple helices that can assign melting temperatures to blunt-ended and staggered, sticky triple helices. For a (POG)₈ triple helix, the blunt-ended triple helix with acetylated and amidated termini has a melting temperature of 51.13 °C while all other sticky ended version have lower melting temperatures. For example, a (POG)₈ triple helix with a stagger of b+7 and c+2, such that the middle strand is shifted relative to the leading strand by 7 repeat units and lagging strand is shifted relative to the leading strand by 2 repeat units, has a melting temperature of 38.97 °C. Therefore, these results are in qualitative agreement with the melting curves obtained from our CG simulations and the impact of sticky end length, Δ, on the melting temperature of the triple helix such that larger Δ result in lower melting temperatures. Also, such melting temperature calculators can evaluate the impact of staggered registers on the melting temperature but cannot evaluate the melting temperatures of heterotrimers with differential chain lengths. Therefore, there is significant insight to be gained from using CG models to investigate the impact of peptide designs with differential chain lengths on the thermal stability of the triple helix.

Next, we investigate the higher order assembly of CLP heterotrimeric triple helices into larger aggregates and fibrils as a function of heterotrimer design at temperatures below the melting temperature of the triple helix (T* = 3.0) at a CLP concentration of 1 mM.

For the one sticky ended (POG)₁₂ family, the weighted probability distributions of the radius of gyration of CLP clusters, R_g,cluster, as a function of sticky end length, Δ, are shown in Figure 3. The radius of gyration calculation considering all clusters with one or more triple helix per cluster is labeled as the ‘combined’ R_g,cluster calculation (Figure 3a). For Δ = 2 and 4, we observe two peaks in the weighted probability distribution of R_g,cluster while for Δ = 6 we see only one peak. We also observe that the tails of the weighted R_g,cluster distributions [i.e., value of R_g,cluster P(R_g,cluster) at larger R_g,cluster] are larger for Δ = 4 than for Δ = 2 and 6. This trend of a larger tail for Δ = 4 than for Δ = 2 and 6 is also seen in (Figure 3b) the weighted probability distributions of number of helices per cluster (N_{helix,cluster}). To understand these results better, we decompose the R_g,cluster calculation into an ‘assembled’ calculation in which we only consider CLP clusters with at least two CLP triple helices per cluster and a ‘free helix’ calculation in which we only consider free (unclustered) single triple helices. This decomposition shows us that the two peaks in Δ = 2 and 4 weighted probability distribution of R_g,cluster arise from the distinct sizes of the free (unassembled) helices and assembled clusters. In the ‘assembled’ weighted distributions of R_g,cluster (Figure 3c) and N_{helix,cluster} (Figure 3d) we observe the larger value of tails for Δ = 4 as compared to 2 and 6 while in the ‘free’ weighted R_g,cluster distributions, larger Δ leads to a larger helix size (Figure 3e). These ‘assembled’ and ‘free’ weighted distributions confirm that this non-monotonicity in cluster sizes with sticky end length arises from clusters rather than free helix size. Moreover, for Δ = 6 in Figure 3, there is a peak in the assembled case at R_g,cluster = 10σ but this peak does not occur in the combined case. For the combined case, all clusters containing at least a single triple helix or more (N ≥ 1) are considered. Therefore, for Δ = 6 there is a significant number of clusters with N = 1 (i.e., free helices) versus assembled clusters (N > 1) and the peak in the combined distribution corresponds to the peak in the free helix distribution at R_g,cluster ~ 7.5σ. We note that the weighted probability in the combined distribution for Δ = 6 at R_g,cluster = 10σ is still nonzero, indicating that there are clusters corresponding to the same size (peak) observed in the assembled distribution, but such clusters are observed with less frequency as compared to the free helix R_g peak.

Figure 3.

Weighted probability distributions of radii of gyration, R_g,cluster, and number of helices per cluster, N_{helix,cluster}, of CLP heterotrimers obtained from CG MD simulations for the one sticky ended (POG)₁₂ family at a CLP concentration of 1 mM at T* = 3.0. Distributions of (a) R_g,cluster and (b) N_{helix,cluster} for clusters of CLP heterotrimers with at least 1 helix per cluster. Distributions of (c) R_g,cluster and (d) N_{helix,cluster} for clusters of CLP heterotrimers with at least 2 helices per cluster. (e) R_g,helix distribution for clusters made up of a single ‘free’ triple helix.

In contrast to the one sticky ended CLP, for the two sticky ended (POG)₁₂ family (Figure 4), we see a monotonic effect of Δ on the cluster sizes of CLP heterotrimeric triple helices (Figure 4 a–d) and free triple helices (Figure 4e) such that longer sticky ends result in larger radii of gyration (R_g,cluster) and number of helices per cluster (N_{helix,cluster}). The radius of gyration of clusters of CLP heterotrimeric triple helices (Figure 4a) and number of helices per cluster (Figure 4b) follow a monotonic trend with increasing Δ for clusters with at least one triple helix per cluster, and do not show larger tails in the distributions for Δ = 4 versus 2 and 6, as seen for a one sticky ended design (Figure 3). The same monotonic trend with increasing Δ is also seen for clusters with at least two triple helices per cluster for R_g,cluster (Figure 4c) and N_{helix,cluster} (Figure 4d). For the two sticky ended (POG)₁₂ family, we also observe that a larger Δ results in a larger “free” helix (Figure 4e), mirroring the results for a one sticky ended design. Therefore, we only observe a nonmonotonic effect of Δ on cluster sizes for a one-sticky ended design but not a two-sticky ended design for CLP heterotrimers. We observe the same nonmonotonic (Figure S3 a, c, e) and monotonic trends (Figure S3 b, d, e) for the one sticky and two sticky end designs, respectively, in the (POG)₁₀ family as well. For the (POG)₁₀ family, there is however no significant dependence of free triple helix sizes (i.e., R_g,helix distributions) on the sticky end length, Δ (Figure S3 e and f).

Figure 4.

Weighted probability distributions of radii of gyration, R_g,cluster, and number of helices per cluster, N_{helix,cluster}, of CLP heterotrimers obtained from CG MD simulations for the two sticky ended (POG)₁₂ family at a CLP concentration of 1 mM at T* = 3.0. Distributions of (a) R_g,cluster and (b) N_{helix,cluster} for clusters of CLP heterotrimers with at least 1 helix per cluster. Distributions of (c) R_g,cluster and (d) N_{helix,cluster} for clusters of CLP heterotrimers with at least 2 helices per cluster. (e) R_g,helix distribution for clusters made up of a single “free” triple helix.

To explain the trends observed for CLP cluster sizes (R_g,cluster and N_{helix,cluster}) in Figures 3 and 4, we quantify the number of inter-helix hydrogen bonds per helix as a function of Δ, CLP concentration, and number of sticky ends (Figure 5). For a one sticky ended design, for both the (POG)₁₀ and (POG)₁₂ families, at low CLP concentrations (1 and 2.5 mM), there is a nonmonotonic effect of Δ on the number of inter-helix hydrogen bonds (Figure 5a and b) in agreement with the nonmonotonic trend seen in their R_g,cluster and N_{helix,cluster} analyses in Figure 3. Since these CLP heterotrimers associate via inter-helix hydrogen bonds to form clusters, a larger number of inter-helix hydrogen bonds would potentially lead to larger CLP assemblies (N_{helix,cluster}), assuming that an increase in inter-helix hydrogen bonds results in more unique, helix-helix contacts as opposed to a larger number of hydrogen bonds between a single pair of helices. We also observe a monotonic effect of Δ on the inter-helix hydrogen bonds (Figure 5c and d) for the two sticky ended design, in agreement with the monotonic trend seen in their R_g,cluster and N_{helix,cluster} analyses in Figure 4. Furthermore, we observe that for Δ = 4 the CLP triple helices form fewer intra helix hydrogen bonds than Δ = 2 and 6 at low CLP concentrations for one sticky ended design (Figure S4 a and b); in contrast for two sticky ended design, increasing Δ leads to decreasing number of intra-helix hydrogen bonds per helix (Figure S4 c and d). Since the total number of (POG) repeat units is held constant while Δ is varied, an increase in inter-helix hydrogen bonds is compensated by a decrease in intra-helix hydrogen bonds; thus, the intermediate sticky end length (Δ = 4) forms the most inter-helix hydrogen bonds for a one sticky ended design at low CLP concentrations (1 mM) as compared to the other sticky end lengths at the expense of forming fewer intra-helix hydrogen bonds.

Figure 5.

Inter-helix hydrogen bonds per helix as a function of CLP concentration, sticky end length, Δ, and number of sticky ends obtained from CG MD simulations for a one sticky ended design (a,b) and two sticky ended design (c,d) at T* = 3.0. Inter-helix hydrogen bonds per helix are also shown for the (POG)₁₀ family (a,c) and (POG)₁₂ family (b,d).

To understand the underlying reason for the above results in Figures 3–5, we look for clues in the representative snapshots from CG MD simulations of CLP heterotrimers at infinite dilution (0 mM) as a function of Δ and number of sticky ends. We see that CLPs with a single sticky end and Δ = 6 form loops at the sticky end (Figure 6) while we see no such loop formation for Δ = 2 or 4. The formation of these loop structures would inhibit the formation of inter-helix hydrogen bonds, thus leading to smaller CLP clusters for Δ = 6 for a one sticky ended design than for Δ = 4 which does not exhibit these loops.

Figure 6.

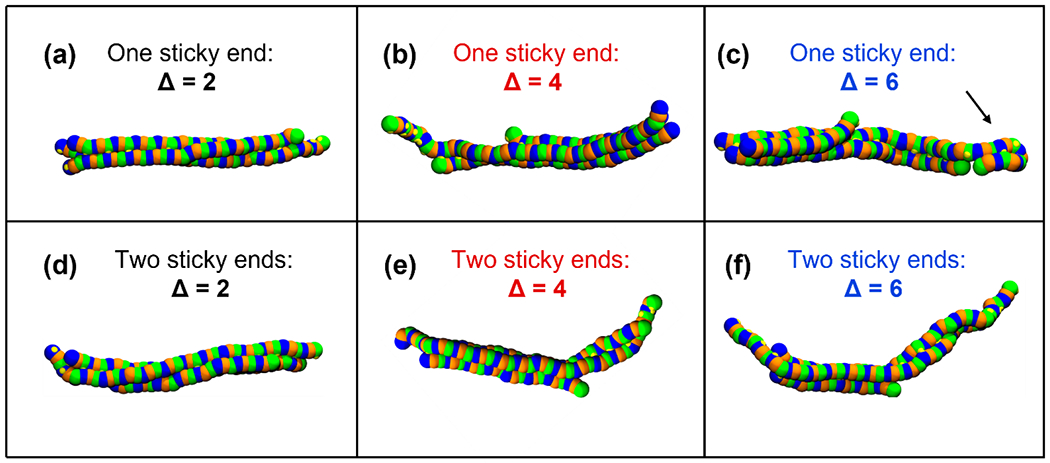
Simulation snapshots of CLP heterotrimers obtained from CG MD simulations at a CLP concentration of ~0 mM (infinite dilution) for (a,b,c) a one-sticky ended design and (d,e,f) a two sticky ended design at T* = 3.0. Snapshots are shown for (a,d) Δ = 2, (b,e), Δ = 4, and (c,f) Δ = 6. The loop formation is seen in part c and denoted with a black arrow.

We also quantify the fraction of CLP strands participating in loop structures, f_strands, (Figure S5) at low CLP concentrations (e.g., 1 mM) and observe that all one sticky ended designs for Δ = 6 show a similar propensity to form loops while Δ = 2 and 4 do not form loops. We also observe loop formation at Δ = 6 only for a one sticky ended design and not the corresponding two sticky ended design which has a shorter sticky length of Δ = 3 on both ends. Therefore, the non-monotonic effect of Δ on CLP cluster sizes (R_g,cluster, N_{helix,cluster}) and inter- and intra-helix hydrogen bonding for a one-sticky ended design can be attributed to the formation of loops for the longest sticky ends. We also observe smaller end-to-end distances (R_ee) with increasing Δ for both a one sticky ended, and two sticky ended design (Figure S6).

Strikingly, at higher CLP concentrations (e.g., 5 mM), for one sticky ended CLPs we do not observe a nonmonotonic effect of the sticky end length, Δ, on CLP cluster sizes (Figure 7a and Figure 7b). The loss of nonmonotonicity can be attributed to a loss of loop structures as sticky ends prefer to interact with sticky ends on neighboring triple helices than within the same CLP strands as the system becomes more crowded. We confirm a decrease in the fraction of CLP strands participating in loops, <f_strands>, at higher CLP concentrations for both the one sticky ended (POG)₁₀ and (POG)₁₂ families in Figure S5. Moreover, this hypothesized higher propensity to interact with neighboring helices is confirmed with the number of inter-helix hydrogen bonds per helix at high CLP concentrations (4 and 5 mM) data (Figure 5a and b); as Δ increases the number of inter-helix hydrogen bonds increases. As expected, increasing Δ leads to larger clusters (combined, assembled, and free helix) for a two sticky ended triple helix at 5 mM (Figure 7d–f), in agreement with distributions obtained at 1 mM (Figure 4) and the number of inter-helix hydrogen bonds at high CLP concentrations (Figure 5 c and d).

Figure 7.

Weighted probability distributions of radii of gyration, R_g,cluster of CLP heterotrimers obtained from CG MD simulations for the one sticky ended (a-c) and two sticky ended (d-f) (POG)₁₂ families at a CLP concentration of 5 mM at T* = 3.0. Distributions of R_g,cluster for clusters of CLP heterotrimers with at least 1 helix per cluster (a,d), clusters of CLP heterotrimers with at least 2 helices per cluster (b,e), and clusters made up of a single “free” triple helix (c,f).

To simply confirm that the formation of loop structures at the sticky ends of CLP heterotrimeric triple helices is not an artifact of the CG model, we perform atomistic simulations of CLP single strands with 6 repeat units to match the sticky ends of the one sticky ended heterotrimers with Δ = 6. In this work, we examine four systems with different end groups to ensure that our atomistic simulation results are generalizable regardless of the experimental synthesis method chosen and that the end group charge does not bias the formation of loop (turn) structures. We simulate systems containing uncharged and/or charged termini such as: 1) a single (GPO)₆ strand with a positively charged N-terminus (NH₃⁺) and negatively charged C-terminus (COO⁻), 2) a single (GPO)₆ strand with an uncharged N-terminus (NH₂) and uncharged C-terminus (COOH), 3) a single (GPO)₆ strand with a positively charged N-terminus (NH₃⁺) and uncharged C-terminus (COOH), and 4) a single (GPO)₆ strand with an uncharged N-terminus (NH₂) and negatively charged C-terminus (COO⁻). For each system, the CLP strand has an initial structure of a polyproline II helix and simulation snapshots indicate the formation of turn structures (loops) at the end of production simulations (Figure 8 a and b). We quantify the fraction of residues participating in turn structures (f_res) as a function of time using the STRIDE algorithm⁶⁵ (Figure 8c) and observe that all four systems with different end groups form the same fraction of turn structures, in agreement with simulation snapshots. We also quantify the ensemble averaged fraction of configurations in which each unique residue forms turn structures (<f_turn>) and observe that all residues show a similar propensity to form turn structures within error (Figure S7). This confirms that the turn structures are not an artifact of the CG model and are observed in atomistic structures.

Figure 8.

Representative simulation snapshots obtained of (GPO)₆ single strands (a,b) and secondary structure analyses obtained using the STRIDE algorithm⁶⁵ for four (GPO)₆ systems obtained using atomistic simulations (c). Snapshots are shown at the end of 100 ns of production simulations for (a) a (GPO)₆ strand with a positively charged N-terminus, NH₃⁺, and negatively charged C-terminus, COO⁻ and (b) a (GPO)₆ strand with a charge neutral N-terminus, NH₂, and charge neutral C-terminus, COOH. (c) Fraction of amino acids participating in turn structures, f_res, as a function of time for four different end group functionalizations for (GPO)₆ strands.

At lower CLP concentrations (1 – 5 mM), simulation snapshots show small clusters of heterotrimers but do not reveal the formation of percolated network structures (Figure S8). For a one sticky ended design, we observe head-to-tail assembly due to the splay of the triple helix even at the non-sticky end which exposes hydrogen bonding beads of proline and glycines and thus, allows the formation of linear head-to-tail assembly of CLP triple helices. At 20 mM for the one sticky ended (POG)₁₂ family, as sticky end length Δ increases, we observe the emergence of bimodal, weighted (assembled) R_g,cluster distributions (Figure 9a). For example, for Δ = 4 and 6 there are two populations of cluster sizes, a smaller cluster size with R_g,cluster ~ 10σ and another larger cluster size with R_g,cluster comparable to half of the simulation box size (55 σ). Simulation snapshots (Figure 9 b–d) show the presence of smaller and larger clusters for Δ = 4 and 6 in contrast to only small clusters observed for Δ = 2. We also confirm that the clusters for Δ = 4 and 6 are percolated; we confirm this by testing if the largest cluster formed spans the simulation box and connects to its periodic image across periodic boundary conditions (Table S3). We also confirm that for cases with bimodal distributions that the system will not evolve into a single peak by monitoring the average number of CLP triple helices per cluster as a function of simulation time steps during each of the three trials of productions simulations which fluctuates around an average value during the production run (Figure S9).

Figure 9.

Weighted probability distributions of radii of gyration, R_g,cluster of CLP heterotrimers for the (POG)₁₂ family obtained from CG MD simulations for the one-sticky ended design at a CLP concentration of 20 mM (a) and representative simulation snapshots at T* = 3.0, (b,c,d). Distributions of R_g,cluster are shown for clusters of CLP heterotrimers with at least 2 helices per cluster. Simulation snapshots are shown for (b) Δ = 2, (c) Δ = 4, and (d) Δ = 6 and are color coded based on cluster ID.

Like the (POG)₁₂ family, at 20 mM for the one sticky ended design, we observe a bimodal distribution of smaller and larger clusters (Figure 10a) for the (POG)₁₀ family for Δ = 4 and 6. Simulation snapshots show the presence of small clusters for Δ = 2 (Figure 10b) and large clusters for Δ = 4 (red cluster in Figure 10c and Figure S10) and Δ = 6 (red cluster in Figure 10d) extending in multiple dimensions. Additional percolation analyses for Δ = 4 and 6 confirm that the largest cluster spans the simulation box and is connected to its periodic image across periodic boundary conditions (Table S3). Therefore, we observe that the minimum sticky end length required to observe percolation is four sticky ended repeat units (Δ = 4) and is independent of (POG) family for the chain lengths examined in this study.

Figure 10.

Weighted probability distributions of radii of gyration, R_g,cluster of CLP heterotrimers for the (POG)₁₀ family obtained from CG MD simulations for the one-sticky end design at a CLP concentration of 20 mM (a) and representative simulation snapshots at T* = 3.0 (b,c,d). Distributions of R_g,cluster are shown for clusters of CLP heterotrimers with at least 2 helices per cluster. Simulation snapshots are shown for (b) Δ = 2, (c) Δ = 4, and (d) Δ = 6 and are color coded based on cluster ID.

For two sticky ends, in the (POG)₁₀ family (Figure S11) we observe that increasing Δ also results in the formation of a spanning cluster at Δ = 4 and 6 as shown by the bimodal weighted assembled R_g,cluster distribution (Figure S11a). Simulation snapshots show a network-like architecture for Δ = 4 and 6 (Figure S10c and d) and percolation analyses (Table S4) confirm that the spanning cluster is connected across periodic boundary conditions. Moreover, simulations show that two sticky ended systems result in a larger number of helices per cluster with increasing sticky end length, Δ, as compared to a one sticky ended design at a CLP concentration of 20 mM for the (POG)₁₀ family (Figure S12 a). This shows that switching from a one to a two sticky ended design results in clusters with more helices per cluster and a higher propensity for network assembly. Like the (POG)₁₀ family, for the (POG)₁₂ family increasing the number of sticky ends has a minimal effect on the weighted assembled R_g,cluster distributions (Figure S13) with a greater number of helices per cluster for the two versus one sticky ended design (Figure S12 b). Like the one sticky ended (POG)₁₀ and (POG)₁₂ families, simulation snapshots also confirm the formation of percolated, multidimensional networks for Δ = 4 and 6. Overall, we observe that the sticky end length, Δ, and number of sticky ends are the main design parameters which can be used to engineer CLP heterotrimers which self-assemble to form gels and percolated networks such that longer Δ and two sticky ends, would be preferred to promote assembly.

IV. Conclusion

We have used coarse-grained (CG) molecular dynamics simulations to link the design of CLP heterotrimers made of CLP strands that vary in the number of (POG) repeat units to the thermal stability of the CLP heterotrimeric triple helix and their assembly at varying concentrations. Due to the different lengths of (POG) repeats in each of the three CLP strands forming a triple helix, there are dangling strand ends at either one or both sides of the triple helix. We call the exposed hydrogen bonding groups at these dangling ends ‘sticky’ ends as they can hydrogen bond with other unbonded hydrogen bonding groups.

Melting curves obtained from CG simulations showed that increasing sticky end length, Δ, while keeping the total number of (POG) repeat units, resulted in lower thermal stability of the helices, marked by lower melting temperatures. CLP heterotrimeric triple helices with fewer total (POG) repeat units showed a larger reduction in melting temperature with increasing Δ as compared to triple helices with more (POG) repeat units. A reduction in melting temperature with increasing Δ was observed for CLP heterotrimers for both one and two sticky ended design. Simulations of dilute solutions (e.g., 1 mM) showed assembly of CLP heterotrimers into clusters with a nonmonotonic effect of sticky length Δ on CLP cluster size observed for systems with one sticky ended design but not for a two sticky ended design with a sticky length of Δ/2 on both ends of the heterotrimers. The nonmonotonicity was attributed to a reduction in the number of inter-helix hydrogen bonds per helix for systems with the longest sticky ends because of the formation of intra-strand turn structure at the sticky end for longer sticky lengths; the possibility of formation of turn structures for CLP single strands was confirmed using atomistic simulations. Simulations of concentrated solutions showed a loss of nonmonotonicity of cluster sizes with increasing sticky end lengths at higher CLP concentration due to helices preferring to form inter-helix hydrogen bonds than intra-helix (loop) turn structures. At higher concentrations (20 mM), simulations showed the formation of percolated, multi-dimensional networks of CLP heterotrimers at large Δ; a minimum sticky end length of four repeat units (Δ = 4) was required for percolation. Going from one sticky end to two sticky ends resulted in spanning CLP clusters with a greater number of helices per cluster suggesting a greater propensity for a two sticky ended design to form percolated networks.

Overall, this work highlights the utility of computational tools in exploring large design spaces in order to examine how peptide design impacts self-assembly, from triple helical stability to supramolecular network formation. This work can therefore be used to inform new system designs and streamline the discovery of new, biomimetic platforms for a range of biomedical applications.