A Guide to the Continuous Constant pH Molecular Dynamics Methods in Amber and CHARMM [Article v1.0]

Abstract

Like temperature and pressure, solution pH is an important environmental variable in biomolecular simulations. Virtually all proteins depend on pH to maintain their structure and function. In conventional molecular dynamics (MD) simulations of proteins, pH is implicitly accounted for by assigning and fixing protonation states of titratable sidechains. This is a significant limitation, as the assigned protonation states may be wrong and they may change during dynamics. In this tutorial, we guide the reader in learning and using the various continuous constant pH MD methods in Amber and CHARMM packages, which have been applied to predict pK_a values and elucidate proton-coupled conformational dynamics of a variety of proteins including enzymes and membrane transporters.

1. Introduction

1.1. Background

Solution pH is tightly regulated in biological environments [1]. In normal adult cells, intracellular pH_i is about 7.2 and extracellular pH_e is about 7.4 [2]; however, in cancer cells, the pH gradient is reversed, which promotes cancer progression, metabolic adaptation, and metastasis [2, 3]. Virtually all proteins depend on pH to maintain their structure and function [1, 4]. A small change in pH can perturb the functions of many enzymes. For example, SARS coronavirus main proteases have the maximal cleavage activity in a narrow pH range around 7.0 [5]. Below the optimum pH, the active site collapses due to the protonation state change of a histidine [5, 6]. The function of human β-secretase 1 peaks at pH 4.5, [7]; at low or high pH the protonation state of the catalytic dyad changes, which results in the closure of the “flap” that lies above the active site and blockage of substrate entrance [8]. Solution pH is also an important parameter in the creation of dynamic, stimuli-responsive materials [9]. For example, pH triggers the formation of hydrogel films from the biopolymer chitosan [10]; addition of surfactants allows the chitosan film to be reconfigured via a second pH signal to achieve different mechanical properties [11].

In a conventional molecular dynamics (MD) simulation, solution pH is implicitly taken into account by fixing the protonation states of titratable sites according to the experimental pK_a values of model compounds (or peptides) or traditional pK_a calculations based on a static structure. Traditional pK_a methods include empirical approaches, e.g., PropKa [12], Rosetta [13], Poisson-Boltzmann solvers MCCE [14], APBS/PDB2PQR [15], DelPhiPKa [16], H++ [17], and other variants [18]. These tools are fast; however, the predicted protonation states are often incorrect for deeply buried sites [19], enzyme active sites [20], transmembrane proteins [21], and cysteines or lysines in general [22–24]. Also, even assuming an accurate assignment of protonation states at the beginning of MD, the conformational changes sampled by the simulation may modify the electrostatic environment around the titratable groups, changing their protonation states. To account for the direct coupling between conformational dynamics and protonation state changes and to offer more accurate pK_a predictions, constant pH MD methods have been developed.

Over the past two decades, much progress has been made in the development of constant pH MD methods. In a discrete (also known as stochastic) constant pH MD (DpHMD), the MD trajectory is periodically interrupted by the Metropolis Monte-Carlo (MC) sampling of protonation states [25–29]. Here, protonation and deprotonation of titratable groups is sampled discretely, assuming one of the two states. Besides the advantage that only physical (protonated and deprotonated) states are sampled, the DpHMD method based on the hybrid MD/MC scheme is conceptually simple and practically straightforward to implement. In contrast, the continuous constant pH MD (CpHMD) [30–35] treats the protonation states of ionizable sites using an auxiliary set of continuous titration coordinates based on an extended Hamiltonian λ-dynamics approach [36]. This method allows the system to escape local energy minima by transiently accessing the partially protonated states. Although sampling the unphysial intermediate states is a major caveat, the CpHMD method offers significantly faster convergence for coupled residues, and importantly it can be readily extended to all-atom simulations. The faster convergence arises from the fact that at every MD step the λ values of all titratable sites are updated, whereas in a typical DpHMD implementation, the protonation state of a single residue is attempted at each MC step.

Development of an all-atom DpHMD algorithm based on the hybrid MD/MC approach is challenging, as in explicit solvent a switch in protonation state leads to a large change in electrostatic energy, which results in a nearly complete rejection of the MC move [29]. This problem, which is due to the lack of overlap between explicit solvent configurations for the protonated and deprotonated states [29], has been tackled by introducing a free energy calculation [37] or a short non-equilibrium MD (neMD) [28, 29, 38] (see later discussion).

In an implicit-solvent constant pH scheme, sampling of both conformational dynamics and protonation states is performed using a continuum electrostatic model, typically a generalized Born (GB) model. Implementations of this scheme in the CHARMM package [39] include the GBMV-[40] and GBSW- [41] based CpHMD [30–32] methods. Implementations in the Amber package [42] include the OBC-GB [43] based DpHMD [26] and the GBNeck2-based CpHMD [44, 45] methods.

In a hybrid-solvent constant pH scheme, conformational sampling is conducted with explicit solvent, while a continuum model e.g., GB or Poisson-Boltzmann (PB), is used to sample protonation states, i.e., calculating the solvation forces on the λ particles for the CpHMD methods or the energy changes due to protonation-state changes for the DpHMD methods. Implementations of this scheme include the first DpHMD method based on PB/TIP3P [25] for GROMACS [46], the GBSW/TIP3P based CpHMD method [33] in CHARMM [39], and the OBC-GB/TIP3P based DpHMD method [27] in Amber [42]. Note, the GBSW/TIP3P based CpHMD method [33] was extended to the treatment of transmembrane systems [21] by incorporating a membrane GBSW model [47].

An all-atom or fully explicit-solvent constant pH scheme removes the dependence on a continuum model in that it samples both conformational and protonation states in explicit solvent. An all-atom CpHMD method called CPHMD^MSλD [48] was implemented by the Brooks group in the BLOCK module of the CHARMM package [39] as a part of the multi-site λ-dynamics (MSλD) functionality [49]. Most recently, the Brooks group developed a standalone GPU program called basic lambda dynamics engine (BLaDE) [50], which enables GPU-accelerated MSλD and constant pH simulations. The first all-atom particle mesh Ewald (PME) CpHMD method was implemented by the Shen group in CHARMM [39], as an extension to the GBSW and hybrid-solvent CpHMD methods in the PHMD module [34, 35, 51]. To compensate for the net charge fluctuation due to proton titration, the Shen group introduced co-titrating ions [34] or water [51]. Most recently, the all-atom PME CpHMD method was implemented in Amber (version Amber22 [52]) by the Shen group [53]. A λ-dynamics based all-atom CpHMD implementation was also developed by the Grubmüller group [54, 55] in the GROMACS package [46], although the method has not been validated for a large number of proteins yet. The proper treatment of tautomer states and the use of PME for λ dynamics remain to be addressed.

To circumvent the aforementioned configuration overlap problem in a DpHMD framework, Bürgi and van Gunsteren used thermodynamic integration (TI) to calculate the titration free energy change for the MC move [37]; however, TI calculations are computationally costly and do not readily converge. Recently, an all-atom DpHMD method based on a hybrid neMD/MC scheme has been implemented in NAMD [56] by the Roux group [29, 38]. This approach, which was originally proposed by Stern [28], has the flavor of both TI and λ dynamics methods, as it utilizes a (λ) coupling parameter in a neMD trajectory to gradually change the protonation state thus allowing solvent to adjust [29, 38]. Analogous to the titratable ion or water approach of the Shen group [34, 51], the hybrid neMD/MC implementation of the Roux group used the chemical transformation between a counterion and water to maintain charge neutrality of the system [29]. Interestingly, while the Roux group reported that charge neutrality acts as a constraint and decreases the acceptance ratio in the MC steps [29, 38], the Shen group observed a slow down in convergence of protonation state sampling [35, 51]. Having reviewed the various constant pH methods, the remainder of the tutorial will focus on the CpHMD implementations developed by the Shen group.

While accurate prediction of protonation states or pK_a values is a goal, a major application of constant pH MD is to elucidate the mechanisms of pH-dependent or proton-coupled conformational dynamics. One can argue that the latter can also be studied by conventional fixed-protonation-state MD using simulations with different protonation states. While this may well be true when the switch of one protonation state is involved, the problem becomes intractable when the number N of titratable sites is large because the number of possible protonation states increases as 2^N. Furthermore, the identity of the titratable site responsible for proton-coupled conformational changes is often unclear, which makes the fixed-protonation-state approach unfeasible. Importantly, by running fixed-protonation-state MD one cannot obtain the pK_a value for the conformational transition [21, 57–59], which can be compared with experiment to validate the microscopic details revealed by simulation.

Table 1 summarizes the applications of the implicit-, hybrid-, and fully explicit-solvent CpHMD methods developed in the Shen group. The implicit-solvent GBSW- and GBNeck2-CpHMD methods have been mainly applied to pK_a predictions of proteins [23, 32, 45, 60, 61], while the hybrid-solvent and all-atom CpHMD methods have been additionally applied to elucidate the mechanisms of pH-dependent or proton-coupled conformational processes, e.g., protein unfolding [62], structure-function relationships of proteases and kinases [6, 8, 63–65], protein/ligand binding [66–68], conformational activation of transmembrane channels and transporters [21, 58, 69], and materials [10, 11]. A recent application of GBNeck2-CpHMD method is the prediction of nucleophilic cysteine and lysine sites for targeted covalent drug design [6, 22, 24, 65, 70]. In this tutorial, we will discuss GBNeck2-CpHMD in Amber [20, 45], hybrid-solvent [33], and particle-mesh Ewald (PME) all-atom CpHMD [35] in CHARMM [39].

Table 1. Applications of the continuous constant pH MD (CpHMD) methods.

GBSW-CpHMD [31, 32], hybrid-solvent [33] and membrane-enabled hybrid-solvent [21] CpHMD methods are implemented in CHARMM [39]. The GRF [34, 51] and PME [35] based all-atom CpHMD methods are also implemented in CHARMM [39] and they can be used with co-titrating ions [34] or water [51]. GBNeck2-CpHMD [44, 45] method is implemented in Amber18 [42]. The pH replica-exchange protocol [33] was used for all applications except for those with GBSW-CpHMD where the temperature replica-exchange protocol [32] was used. All implementations except for GBNeck2-CpHMD are for CPU computing.

System	Topic	Method	Reference
Soluble proteins
Benchmark proteins	pKa calculations	GBSW	[32, 60]
SNase	Blind pKa predictions for 87 engineered mutant proteins	GBSW	[61]
Peptides and mini-proteins	pH-dependent folding mechanisms	GBSW	[71–73]
Benchmark proteins	pKa calculations	Hybrid	[33]
NTL9, BBL	Unfolded states and unfolding mechanism	Hybrid	[62, 74]
SNase	pKa calculation for a deeply buried lysine; proton-coupled opening of the site	Hybrid	[75]
Spider silk protein	pH sensing residues for dimerization	Hybrid	[57]
BACE1, BACE2, cathepsin D, renin, plasmepsin D	Acid/base roles of the catalytic dyad; binding-induced protonation state change of the in-hibitor; pH-dependent conformational dynamics; proton-coupled dynamics of binding site water; pH-dependent inhibitor binding free energy calculations	Hybrid	[8, 64, 66–68, 76, 77]
c-Src Kinase	Proton-coupled conformational change of the DFG motif	Hybrid	[63]
Benchmark proteins	pKa calculations for Asp/Glu/His	All-atom	[35]
Various enzymes	Prediction of proton donor and nucleophile and physical determinants	Hybrid	[20]
Benchmark proteins	pKa calculations for Asp/Glu/His/Cys	GBNeck2	[44, 45]
Various kinases	Prediction and rationalization of reactive Lys and Cys	GBNeck2	[22, 24, 70]
Coronavirus papain-like proteases	Protonation states of His/Cys; proton-coupled conformational dynamics	GBNeck2	[65]
Coronavirus main proteases	Protonation states of His and Cys; proton-coupled conformational change of the binding site	GBNeck2	[6]
Transmembrane proteins
Proton channel M2	Proton-coupled channel opening/closing	Membrane-hybrid	[69]
Sodium/proton antiporter NhaA	Identification of proton binding residues; proton-coupled conformational changes	Membrane-hybrid	[21, 59]
Efflux pump AcrB	Identification of proton binding residues; proton-coupled conformational transitions	Membrane-hybrid	[58]
μ-opioid receptor	pKa calculation	Membrane-hybrid	[78, 79]
Materials
Various surfactants	pKa calculation in micelle	GBSW and hybrid	[80]
Fatty acid	pKa calculation in micelle and bilayer	All-atom	[81]
Fatty acid	pH-dependent micelle/bilayer formation	Hybrid	[82, 83]
Peptide	pH-dependent unfolding of β-sheets; phase transition pKa	All-atom	[84]
Polysaccharide chitosan	Glucosamine titration; pH-dependent dissociation of a model crystallite; phase transition pKa; pH-dependent interaction with a surfactant	All-atom	[10, 11]

1.2. The continuous constant pH molecular dynamics framework

In the CpHMD framework [30, 31], each titratable residue is assigned a titration coordinate λ_i, which is bound between 0 and 1, representing the (physical) protonated and deprotonated states, respectively. To satisfy the bounds, λ_i is expressed as a function of θ in the work of Shen group,

$${\lambda }_i={\text{sin}}^2{\theta }_i,$$ (1)

where θ_i can take on any value and is the underlying coordinate that is assigned fictitious mass (see below). The functional form of λ (Eq. 1) is somewhat arbitrary. In fact, in the MSλD based CpHMD method [49] as well as the λ-dynamics based CpHMD implementation in GROMACS [54, 55], λ is expressed using different functional forms of θ.

Since λ continuously evolves between 0 and 1, in simulation analysis we apply cutoffs to define protonated (λ^P < 0.2) and deprotonated states (λ^U > 0.8). Having the titration coordinate in place, we use an extended Hamiltonian to allow the simultaneous propagation of spatial (real) and titration (virtual) coordinates:

$$\mathscr{H}\left(\left\{{\mathit{\text{r}}}_a\right\},\left\{{\theta }_i\right\}\right)=\frac{1}{2}\sum _a{m}_a{\dot{\mathit{\text{r}}}}_a^2+\frac{1}{2}\sum _i{m}_i{\dot{\theta }}_i^2+U^{\text{int}}\left(\left\{{\mathit{\text{r}}}_a\right\}\right)+U^{\text{hybr}}\left(\left\{{\mathit{\text{r}}}_a\right\},\left\{{\theta }_i\right\}\right)+\sum _i{U}^{*}\left({\theta }_i\right),$$ (2)

where r_a refers to the (x,y,z) coordinates of atom a, and θ_i refers to the titration coordinate of titratable residue i. The two first terms of Eq. 2 give the kinetic energies of real atoms and virtual λ particles. U^int represent the titration-independent bonded and non-bond energies. We note that the force field parameters of some residue types (e.g., carboxylates) may depend on the protonation state; however, in the CpHMD [31, 33, 35, 44, 45, 48] as well as the hybrid MD/MC based DpHMD [26, 27] implementations the bonded parameters are fixed in one of the protonation states. This is a limitation that needs to be addressed in the future.

The fourth term, U^hybr, describes the non-bond energies, which are dependent on both spatial and titration coordinates. For the particle-mesh Ewald (PME) all-atom CpHMD [35] U^hybr includes only Coulomb and van der Waals (vdW) energies, while for the implicit- and hybrid-solvent CpHMD methods U^hybr also includes the generalized Born (GB) energy:

$$U^{\text{hybr}}\left(\left\{{\mathit{\text{r}}}_a\right\},\left\{{\theta }_i\right\}\right)=U^{\text{elec}}\left(\left\{{\mathit{\text{r}}}_a\right\},\left\{{\theta }_i\right\}\right)+U^{\text{vdW}}\left(\left\{{\mathit{\text{r}}}_a\right\},\left\{{\theta }_i\right\}\right)+U^{\text{GB}}\left(\left\{{\mathit{\text{r}}}_a\right\},\left\{{\theta }_i\right\}\right)$$ (3)

The dependence of the electrostatic energy on the titration coordinates arises from the requirement that the partial atomic charges on the titrating residue are linearly interpolated between the values in the deprotonated and protonated states with respect to λ:

$$q_j\left({\lambda }_i\right)=\left(1-{\lambda }_i\right)q_j^{\text{prot}}+{\lambda }_i{q}_j^{\text{unprot}},$$ (4)

where q_j refers to the partial charge of an atom j in the titrating residue i. As to vdW energies, the interactions involving a titratable proton are linearly attenuated with respect to λ:

$$U_{ij}^{\text{vdW}}\left({\mathit{\text{r}}}_i,{\mathit{\text{r}}}_j,{\lambda }_j\right)=\left(1-{\lambda }_i\right)U_{ij}^{\text{vdW}*}\left({\mathit{\text{r}}}_i,{\mathit{\text{r}}}_j\right),$$ (5)

where i is the index for the titratable proton, j is the index for all other atoms, and $U_{ij}^{\text{vdW}*}$ refers to the protonation independent vdW interaction energy. If both i and j are titratable protons, the interaction is linearly attenuated by the λ values of both:

$$U_{ij}^{\text{vdW}}\left({\mathit{\text{r}}}_i,{\mathit{\text{r}}}_j,{\lambda }_i,{\lambda }_j\right)=\left(1-{\lambda }_i\right)\left(1-{\lambda }_j\right)U_{ij}^{\text{vdWW}*}\left({\mathit{\text{r}}}_i,{\mathit{\text{r}}}_j\right).$$ (6)

Note, the vdW energy correction is small and typically neglected in constant pH methods except for the CpHMD methods implemented in CHARMM and Amber [31, 33, 35, 44, 45].

Finally, the last term in Eq. 2 only affects titratable groups and is consisted of three biasing potentials:

$$U^{*}\left({\theta }_i\right)=-U^{\text{mod}}\left({\lambda }_i\right)+U^{\text{barr}}\left({\lambda }_i\right)+U^{\text{pH}}\left({\lambda }_i\right)\text{.}$$ (7)

The first biasing potential U^mod describes a potential of mean force (PMF) of model titration along the λ-coordinate, where the model represents a fully solvent-exposed amino acid, i.e., a blocked single amino acid or a small peptide in solution. According to the linear response theory, model PMF is (in GB solvent) or can be approximated (in explicit solvent) as a quadratic function:

$$U^{\text{mod}}\left({\lambda }_i\right)=A{\left({\lambda }_i-B\right)}^2.$$ (8)

Here A and B are parameters that can be determined through free energy calculation methods, such as thermodynamic integration (TI, see section Parameterization). By analogy, in the case of coupled double-site titration [31], e.g., histidine or carboxylic acid, the model PMF is second order in both λ and x, where x is a coordinate that represents the tautomer interconversion. The two-dimensional PMF can be written as a bivariate polynomial,

$$U^{\text{mod}}\left({\lambda }_i,x_i\right)=a_0{\lambda }_i^2{x}_i^2+a_1{\lambda }_i^2{x}_i+a_2{\lambda }_i{x}_i^2+a_3{\lambda }_i^2+a_4{x}_i^2+a_5{\lambda }_i{x}_i+a_6{\lambda }_i+a_7{x}_i+a_8.$$ (9)

Here $x_i={\text{sin}}^2{\theta }_i^x$ is bound between 0 and 1, where ${\theta }_i^x$ is the underlying unbound variable.

U^barr, the second biasing potential in Eq. 7, describes a barrier or penalty potential in the center of the titration coordinate,

$$U^{\text{barr}}\left({\lambda }_i\right)=-4\beta {\left({\lambda }_i-\frac{1}{2}\right)}^2,$$ (10)

where β is a parameter that determines the height of the barrier. Adding the barrier potential serves to increase the sampling time at the end-point states (e.g., λ < 0.2 or λ > 0.8) and therefore minimizing the unphysical vdW and electrostatic interactions associated with mixed state (e.g., 0.2 ≤ λ ≤ 0.8).

U^pH, the last term of Eq. 7 describes the pH dependence of the deprotonation free energy and is given by

$$U^{\text{pH}}\left({\lambda }_i\right)=\mathit{\text{ln}}(10)k_{B}T\left(\text{pH}-\text{p}{K}_a^{\text{mod}}\right){\lambda }_i,$$ (11)

where k_B is the Boltzmann constant, T is the system temperature, and pK_a^mod is the model pK_a for the titratable residue i.

1.3. Scope

This tutorial mainly covers two CpHMD methods that have been extensively validated and applied to various real-life problems: 1) the hybrid-solvent CpHMD [33] in CHARMM [39] and 2) the GBNeck2 implicit-solvent CpHMD [44, 45] in Amber [42]. Currently, fully patched Amber 18 and 20 released versions are supported. GBNeck2-CpHMD patches to them can be downloaded from our cphmd-patches repository. Details about how to apply them are described on that repository page. The CHARMM hybrid-solvent CpHMD currently supports CPUs only, but the Amber GBNeck2-CpHMD supports both CPU or GPU computing. We strongly recommend running the CpHMD simulations via the pH replica-exchange protocol to significantly accelerate convergence of pK_a’s and conformational sampling; however, if desired, a single pH simulation or a set of independent pH simulations can also be conducted.

In addition to the above two methods, we will briefly discuss the PME all-atom CpHMD method implemented in CHARMM for CPU computing [35] and in Amber for GPU computing (Harris, Liu, and Shen, unpublished data). We note, this tutorial does not cover the GBSW implicit-solvent CpHMD method in CHARMM [30–32, 85], which is available for both CPU and GPU computing. The GBSW-CpHMD method with the temperature replica-exchange protocol has been extensively validated for protein pK_a predictions and pH-dependent conformational dynamics.

2. Prerequisites

CpHMD is a specialized MD technique, so the user should have some familiarity with MD simulations and especially with the Amber or CHARMM packages. Users having experience with other MD engines, such as GROMACS [86], NAMD[87], or OpenMM [88] are encouraged to go through the introductory tutorials for Amber or CHARMM to get started. Before running a CpHMD simulation, it is important to know the research objective. If the objective is to predict the pK_a values of soluble proteins or their protonation states at a certain pH condition, we recommend the GPU-accelerated GBNeck2-CpHMD in Amber [45], as the pK_a’s converge rapidly and the accuracies for titrating Asp, Glu, His, Cys, and Lys (in solvent-exposed and buried sites) have been validated using a large number of proteins (see references in Table 1). If the objective is to investigate the detailed proton-coupled conformational dynamics, proton transfer, protein-ligand binding/unbinding, or transmembrane proteins, we currently recommend the hybrid-solvent CpHMD [33], as the accuracy has been extensively validated in terms of pK_a values and description of proton-dependent conformational dynamics (see example applications in Table 1), although speed is limited due to the use of CPUs. We note, a GPU-accelerated all-atom PME CpHMD implementation in Amber22 [52] has been recently released by us [53] and holds a promise to offer more accurate description of proton-coupled conformational dynamics for heterogeneous systems such as protein-ligand complexes and transmembrane proteins. Like all computational chemistry calculations, it is important to know the system of interest before attempting any simulations. With such knowledge, one an properly choose the salt concentration, temperature, pH range, and titratable residue types to use in CpHMD. Also, the research objective dictates the simulation length. For example, to predict protonation states, simulation can be run until the unprotonated fractions at all pH are converged, typically 10–50 ns per replica. If however, a large conformational transition is of interest, the simulation should be much longer.

2.1. Background knowledge

Knowledge of classical MD is required to understand what we can and cannot achieve through a MD simulation. The user should also understand the parameters used in energy minimization, heating, equilibration, and production runs. Of course, chemistry knowledge of pH, pK_a, and protonation states and how they may impact the physical properties of the specific biological or material system is essential for obtaining meaningful results.

CpHMD simulations are run on a workstation or high-performance computing (HPC) cluster under a Linux operating system. The user is expected to have a good knowledge of Linux commands for accessing and editing files, submitting jobs to servers, and retrieving simulation result files. Shell script and preferably also Python skills are required for pre- and post-processing files. For simulations on a HPC cluster, the user is required to be familiar with the specific batch scheduler and queuing system, e.g., SLURM (Simple Linux Universal Resource Manager), SGE (Sun Grid Engine), or PBS (Portable Batch System). The user is expected to know commands for submitting and checking the status of jobs. The user is also expected to set environmental variables required for the specific MD engine. Nowadays, a CpHMD job can also be performed on a workstation with a single or multiple GPUs. In this case, the user is required to use commands such as ‘nvidia-smi’ to check the GPU status and ‘nvcc -version’ to check the CUDA version as well. The user can use any data visualisation tool(s), but matplotlib in Python and Jupyter notebooks are recommended in our analysis tool set.

2.2. Software/system requirements

For GBNeck2-CpHMD, Amber16 is the minimum version. Requirements for installing Amber can be found in the Amber website. For the GPU version (pmemd.cuda), a Nvidia GPU card with at least compute compatibility sm3.0 should be installed with the latest driver. A version of CUDA required by Amber needs to be installed. After successfully installing CUDA, it is important to set three environmental variables in Linux. CUDA_HOME and LD_LIBRARY_PATH must point to the directories where the desired CUDA version is installed. We also need to specify CUDA_VISIBLE_DEVICES to GPU device indices. For example,

$ export CUDA_HOME=/usr/local/cuda−10.1 
$ export LD_LIBRARY_PATH=/usr/local/cuda−10.1/lib64 
$ export CUDA_VISIBLE_DEVICES=0,1

These variables will direct the Linux system to use the CUDA 10.1 version installed in the /usr/local directory. In the example above two GPU cards are available, and the indices 0 and 1 for CUDA_VISIBLE_DEVICES indicate the first and second GPU to use, respectively. Following installation of Amber, the user should set the environmental variable AMBER-HOME to the Amber installation folder.

$ export AMBERHOME=/path_to_Amber_version_xx/

Before preparing CpHMD inputs of a protein system, we need to clean up and fix problems in the PDB file, e.g., removing non-protein atoms, adding missing residues and atoms, and fixing non-canonical amino acid residues. To do that, we can use the Perl script convpdb.pl in mmtsb tool set [89] or pdbfixer in OpenMM [88]. For example, the following commands can be used to fix the file 1vii.pdb downloaded from RCSB (www.rcsb.org) [90].

$ convpdb.pl −nohetero −fixcoo −renumber 1 −out amber −chain A −segname 1 vii.pdb

or

$ pdbfixer −−add−atoms=heavy
−−keep−heterogens=none −−add−residues 
−−replace −nonstandard 1 vii.pdb

Alternatively, we can use a homology modeling software such as SWISS-MODEL [91] to fix those problems especially when the number of continuously missing residues is large [91].

The next step is to add capping ligands ACE and NH2 to the N- and C-terminus and to modify ASP, GLU and HIS to AS2, GL2, and HIP residues if these residue types are set as titratable. For AS2 and GL2, a library file phmd.lib and a force field modification file frcmod.phmd are included in Ambertools after version 19 [42], or we can load them to tLeap/Leap from the directory containing the two files. The last step is to use tLeap/Leap in Amber/ Ambertools to generate topology and parameter files. Our cphmd-prep tool set uses the pdbfixer tool for the first step and can do all the aforementioned steps to prepare GBNeck2-CpHMD compatible input files.

We use a Python-based asynchronous replica exchange implementation for GPU pH replica-exchange simulations. Scripts in cphmd-analysis are used for analyzing CpHMD related files, including convergence checking, pK_a calculation, and replica-exchange profiling. Some simple trajectory based analysis such as RMSD can also be done, but the users can use any tools, e.g., CPPTRAJ [92], PTRAJ [92], VMD [93], and MDAnalysis [94].

A suggestion to use Python dependent packages is to use Anaconda or Miniconda. With them, the user can create a virtual environment specific for CpHMD related calculations. For example, after installing Anaconda or Miniconda, we can type

$ conda create −−name cphmd python=3.7

Note that we choose Python version 3.7 because the OpenMM package currently only supports up to Python 3.7. Activate the environment named ‘cphmd’ by

$ conda activate cphmd

Many packages can be installed through the conda and pip tool.

$ conda install −c omnia pdbfixer parmed
$ conda install −c conda−forge ambertools mdanalysis matplotlib
$ conda install −c anaconda numpy scipy pandas
$ pip install f90nml

Whenever the user wants to do some calculations or analysis related to CpHMD, they can activate this ‘cphmd’ virtual environment and use the installed tools without causing conflict with other software.

For running the hybrid-solvent CpHMD [33] in CHARMM [39] you will need to follow the installation instructions in the CHARMM documentation. We suggest including the MPI and the Hamiltonian replica exchange options.

$ ./install.com gnu xxlarge M mpif90 +CMPI +REPDSTR +ASYNC_PME +GENCOMM

If you want to install CHARMM on a local workstation for building and preparing systems or for running a single pH simulation, you can use the following installation command.

$ ./install.com gnu xxlarge

3. Workflow for the hybrid-solvent CpHMD in CHARMM

The hybrid-solvent CpHMD method makes uses of explicit solvent for conformational dynamics and a GB model for propagating protonation states [33]. As all MD simulations, CpHMD consists of three stages: system preparation, equilibration, and production. We will explain each stage using a specific protein as an example. To follow along, the tutorial files for soluble proteins can be downloaded from our GitLab website cphmd-tutorial/hphmd_charmm and for transmembrane proteins, the tutorial files can be downloaded from cphmd-tutorial/memb_hphmd_charmm. We will use the pH replica-exchange protocol [33] in all the examples.

3.1. System Preparation

To demonstrate CpHMD simulations of soluble proteins without retaining the crystal waters, we use the mini-protein BBL as an example. The tutorial files for system preparation can be found in the directory bbl_sys_prep.

Step 1. Prepare a protein structure with dummy hydrogens.

First, we retrieve the coordinates of a protein structure from Protein Data Bank[90], e.g., BBL (PDB: 1w4h [95]). A homology modeling tool such as SWISS-MODEL[91] can be used to add any missing atomic coordinates. Next, we convert the PDB file from the standard PDB format to the CHARMM PDB format using the MMTSB tool command [89] convpdb.pl or a user supplied script followed by a shell command “sed” to change all histidine residue names to HSP to facilitate titration.

$ perl convpdb.pl −out charmm22 −segnames −renumber 1 1w4h.pdb | sed ” s/HSD/HSP/g”
>start. pdb

Here, the output PDB file is formatted for CHARMM (-out charmm22); the segment names are included in the output (-segnames); the residue identification numbers (resid) are renumbered starting at 1; and the input file is “1w4h.pdb.” The CHARMM default tautomer for His is HSD. Changing HSD to HSP indicates to the CpHMD program that histidine is titratable (see later discussion of the parameter file). Although all resid have been renumbered starting from 1, this does not have to be the case. Next we add hydrogen atoms to the protein using the HBUILD facility[96] in CHARMM [39].

To allow titration of Asp and Glu sidechains, we place dummy hydrogens on both carboxylate oxygens. Note, the dummy atoms do not interact with each other and only one is turned on when Asp/Glu is protonated [31]. The dummy hydrogens are placed in the syn position, because it is considered more favorable than the anti position (see discussion in Ref [31]). To prevent the dummy hydrogens from moving to the anti position, in which case nonnative hydrogen bonds may form and a neutral dummy may lose the ability to gain charge, in the CpHMD specific force field parameter file, the C–O bond rotation energy barrier is increased from the standard 0.5 to 6.0 kcal/mol (see discussion in Ref [31]).

Following the addition of hydrogens, a brief energy minimization is performed to correct unfavorable positions. Here 50 steps of steepest descent (SD) and 10 steps of adopted basis Newton-Raphson (ABNR) are used, whereby a harmonic restraint with the force constant of 50 kcal/mol/Ų is placed on the heavy atoms. In many experiments, the N- and C-terminal ends of the protein are truncated and require capping. For N-terminus we use CH₃CO (patch ACE), and for C-terminus we use NH₂ (patch CT2) or NHCH₃ (patch CT3). In special cases, the free ionized forms, ${\text{NH}}_3^{+}$ and COO^–, are used and can be set titratable when CpHMD is turned on. The input file step1_add_h_prot.inp is an example of how to perform these steps on BBL and can be run with the following command.

$ charmm − i step1_add_h_prot.inp −o step1.out

The example input also checks for disulfide bonds using a sulfur-to-sulfur distance cutoff of 2.5 Å. After running any input file, make sure to visualize the output structure to confirm all the dummy hydrogens and additional features are correctly constructed.

Step 2. Prepare a solvated system

Now we move to protein solvation by first building a large water box of the desired size. This is done by generating a plane of small cubic water boxes along the x- and y-axes, and then stacking the planar water boxes along the z-axis. CHARMM toppar directory contains the cubic water box made of preequilibrated TIP3P waters. The size of the large water box is calculated based on the longest dimension of the protein and a padding space between the protein and the edges of the water box. We recommend having at least ~10 Å padding in x, y, and z directions. The large cubic water box is then reshaped to a truncated octahedron by removing waters in all eight corners. The input file step2a_make_waterbox.inp is used to construct the octahedron water box.

$ charmm − i step2a_make_waterbox.inp −o step2_make_waterbox.out

Once the water box is built, the protein is placed at the center and water molecules within 2.8 Å of the protein heavy atoms are deleted.

The solvated system is subject to energy minimization to release unfavorable contacts. First, the protein heavy atoms are fixed and the system undergoes energy minimization using SD and ABNR for 50 steps each. Next, a five-stage minimization is conducted with the harmonic constants of 100, 50, 25, 5, and 0 kcal/mol on the protein heavy atoms using 50 steps of SD and 100 steps of ABNR in each stage. The input file step2b_solvate.inp can be used.

$ charmm − i step2b_solvate.inp −o step2b_solvate.out

Again, always remember to visualize the system and make sure the system has been constructed to your expectations.

3.2. System preparation that includes crystal waters

In some cases the X-ray structure contains water molecules and it is desirable to keep them, e.g., those in the enzyme active site. A tutorial showing how to set up a system with crystal waters can be found in the directory crys_wat_system_prep. Here we use a small protein, staphylococcus nuclease (SNase), as an example, as the X-ray structure (PDB ID: 3hzx) contains crystal waters. To keep the crystal waters, just a few additional steps are needed. First, move all the water molecules into a separate PDB file and make sure the file is properly formatted with the correct column names and column spacing. In the tutorial the crystal water coordinates have been exported into the the file xwat_original.pdb; however, this file needs to be reformatted for use in CHARMM. The Python script mod_xwat.py reformats this file to xwat_.pdb. We should note that most error messages involving the handling of crystal waters are due to the PDB file not being properly formatted.

Since the crystal waters resolved in a X-ray structure do not contain hydrogen positions, they can be added using the CHARMM input file step1b_add_h_crys_wat.inp. With hydrogens added to the protein and crystal waters, the two sets of coordinates need to be combined using the CHARMM input file step1c_merge_prot_crys_wat.inp. The rest of the system preparation is very similar to that without crystal waters. The only difference to note is when you solvate the system you can merge the segids of the crystal waters (segid: XWAT) with the bulk water (segid: SOLV) using the following command.

JOIN XWAT SOLV renumber
RENAME SEGID SOLV sele segid XWAT end

Keep in mind this needs to be done after the deletion of water that overlaps with the protein; otherwise you run the risk of accidentally removing some crystal waters. An example input file is step2b_solvate_crys_wat.inp.

3.3. System preparation for transmembrane proteins

Due to the presence of a lipid bilayer, the preparation of transmembrane proteins for CpHMD simulations requires additional steps. We divide the preparation into the initial and final stages. The initial preparation is for fixed-charged equilibration, whereas the final preparation is for CpHMD simulations. The related files can be accessed from the directories initial_system_prep and final_system_prep.

To begin the initial system preparation, a solvated protein-membrane system is built. We start by retrieving the protein structure from the database OPM (Orientations of Proteins in Membranes), which properly orients the protein in the lipid bilayer using theoretical calculations and experimental data.[97] Just like for soluble proteins, any missing residues need to be added. Here we adopt the standard protonation states, i.e., Asp(−), Glu(−), Cys(0), Lys(+), and Arg(+). As the solution or model pK_a of His is 6.54 [98], which is within one unit of the physiological pH, special attention needs to be given to its protonation (singly or doubly protonated) and tautomeric state (HSD or HSE) by considering the nearby hydrogen bonding and/or salt-bridge interactions. Like soluble proteins, the N- and C-terminal ends may be capped or if necessary the charged forms may be used.

With the complete protein structure (all heavy atom positions are in place), we use the script step1_genpsf.inp to build hydrogen positions followed by a short energy minimization in the GB implicit-solvent model to adjust any energetically unfavorable hydrogen positions. Next, we build the rest of the system and equilibrate the lipid bilayer following the CHARMM-GUI protocol [99] for placing the lipids, solvating the system, and adding ions. The input files for these steps can be found in the directory step1-5. Below we will briefly go through the steps.

After the protein structure is prepared, we place it at the origin and estimate its cross section using the script step2.1_orient.inp. The next step is to add water to the pore of the protein using the script step2.2_pwat.inp. To determine the system dimensions the script step3.1_size.inp is used. This script also estimates the lipid type area and the number of lipids required to be placed between the protein boundary and the periodic boundary. Approximately 4 to 5 lipids should be placed between the protein and the periodic boundary. Additionally, the script calculates the thickness of the water layer above and below the lipid bilayer. With the dimensions of the system determined, the lipid heads using big dummy spheres are placed to estimate the positions of the lipids in the bilayer. This is accomplished by step3.2_packing.inp. Next, the dummy spheres are replaced with lipid molecules from a library of randomized conformations using the script step4.1_lipid.inp. In this example, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) is used, but if other lipids are desired, the libraries of randomized conformations of lipid molecules can be found in the CHARMM-GUI Archive - Individual Lipid Molecule Library.

After the lipid bilayer is built, a rectangular water box is generated using the script step4.2_waterbox.inp, which solvates the protein/membrane complex. Next, the number of ions required to achieve the desired salt concentration is calculated, and the ions are randomly placed in the slabs of water above and below the membrane. In the final step, all of the system components are combined using the script step5_assembly.inp.

We now relax the assembled protein/membrane system in six stages with gradually reduced harmonic restraints using the fixed-charge MD CHARMM-GUI scripts in the directory step6. Following the system relaxation, a much longer (100 ns) simulation in the NPT ensemble is required to fully equilibrate the lipid bilayer. The protein heavy atoms are harmonically restrained during the simulation. The progress of the bilayer equilibration is monitored by the calculation of three properties: surface area per lipid, bilayer thickness, and lipid order parameters [100, 101]. The system is considered equilibrated when these properties plateau with the simulation time. Since this can be performed on any scalable or GPU-enabled MD engine using a standard protocol, we leave this step up to the user.

Following the fixed-charge equilibration of the lipid bilayer, we move to the final system preparation. Here, we prepare the protein for CpHMD titration by adding dummy hydrogens. Example input files can be found in the directory final_system_prep. The first step to break the final snap shot from the bilayer equilibration into separate components (protein, bilayer, bulk water, pore water, and ions). We add hydrogens using the script step1a_add_h.inp. PSF and CRD files are generated for the rest of the system components with the following scripts: step1b_genpsf_memb.inp, step1c_genpsf_water_bulk.inp, step1d_genpsf_water_pwat.inp, step1e_genpsf_ion_sod.inp, and step1f_genpsf_ion_cla.inp. Once all the PSF and CRD files have been made, the rest of the system can be rebuilt using the script step2_assemble.inp.

3.4. Equilibration of soluble proteins

Equilibration of soluble proteins for CpHMD is performed at a single pH in several stages. An example input for the BBL protein is equil_hphmd.inp. Since CpHMD is turned on during equilibration, titratable residues must be chosen. In the example here, Asp, Glu, and His are allowed to titrate because of the pH range used in the production simulation. The crystal structure pH condition or physiological pH 7.4 can be used. We specify the physiological ionic strength of 0.15 M and temperature of 298 K. Before invoking the PHMD module for CpHMD simulation, we need to call GBSW using the following command.

GBSW HYBRID SGAMMA 0.005 NANG 50 CONC 0.15 − SELE protein END 

Here, SGAMMA (default 0.005) is the non-polar surface tension coefficient, NANG (default 50) is the number of angular integration points, and CONC (default 0.15) is the ionic strength in M. Except for CONC, which the user may change according to the specific problem, the default parameters should be used.

Now we invoke PHMD and set related options using the following command.

PHMD PAR 23 WRI 25 PH 7.4 NPRI 5000 PHFRQ 5 
MASS 10.0 BARR 2.0 BETA 5.0 TEMP 298 LAM −
SELE RESN ASP. or. RESN GLU. or. RESN HSP end

Here PH is the simulation pH (default 7); NPRI is the frequency of printing lambda values (5000 means 10 ps); PHFRQ is the update frequency for the lambda coordinates (default 5); TEMP is the temperature for λ dynamics (default 298); MASS is the fictitious mass of the λ particles (default 10); BARR is the quadratic barrier height (default 2.0 and is overwritten by the values specified in the parameter file phmd.inp); BETA is the friction coefficient for lambda dynamics (default 5.0); LAM tells the PHMD module to output lambda values; and SELE specifies the types of residues allowed to titrate (default all residues in phmd.inp file). Except for PH, NPRI, and SELE options, the default parameters should be used.

The length of each stage depends on the system and should be adjusted accordingly. In the BBL example equil_hphmd.inp, the heating/equilibration stages were run for 20 ps, because the system is very small and stable. First, the system is heated in the NVT ensemble, and next four stages of equilibration are performed in the NPT ensemble with decreasing harmonic restraints on the heavy atom positions, e.g., 5.0, 1.0, 0.1, and 0 kcal/mol/Ų. The idea here is to slowly relax the system by removing any high energy contacts and to allow for the initialization of protonation states at the specified pH (e.g., 7). Note, the equilibration time for the mini-protein BBL is short, and one can adjust it accordingly for larger proteins.

3.5. Equilibration of transmembrane proteins

Now three short equilibration steps can be performed using CpHMD at a single pH. Example inputs are in the directory cphmd_equil. As for a soluble protein, the specified pH should be the pH used in the experiment (e.g., crystal growth, NMR, etc) or physiological pH. In the first step, the CpHMD simulation is performed in the NVT ensemble with a harmonic force constant of 1.0 kcal/mol/Ų for 0.1 ns using step0.1_equil.inp. In the second step, the CpHMD simulation is performed in the NPT ensemble using step0.2_equil.inp. In the third step, the simulation (step0.3_equil.inp) continues in the NPT ensemble for 0.8 ns with all restraints are removed. We note, the membrane-enabled CpHMD simulation makes use of the membrane GBSW model [47].

GBSW HYBRID SGAMMA 0.0 NANG 50 CONC 0.15 −
TEMP 310 TMEMB 30 MSW 2.5 −
RCYLN 15 SELE solu END

The options TMEMB, MSM, and RCYLN are used to specify a low dielectric slab in the GBSW model with a high dielectric cylinder centered in the protein. TMEMB specifies the slab thickness (Å) and should be set to the average difference in the Z positions of the lipid C2 atoms from the top and bottom leaflets. This will vary for different lipid types. MSM specifies the half membrane switching length for the dielectric transition between the low-dielectric slab and the bulk solution; the default is 2.5 Å. Finally, RCYLN is the radius of a high dielectric water cylinder placed in the center of the protein; it should be set to an appropriate value such that the water cylinder covers the entire protein but does not overlap with lipids as much as possible. Although no positional restraints are placed on the protein, we recommend using a cylindrical restraint with a harmonic force constant of 0.1 kcal/mol/Ų to prevent the protein from a lateral drift. This can be done using the MMFP facility in CHARMM [39].

3.6. Production

The CpHMD production stage is similar for soluble and transmembrane proteins. The only difference is that the GBSW command includes additional options for the lipid bilayer (see discussion of the equilibration steps) for transmembrane protein simulations. An example input for the production run of a soluble protein is prod_hphrex.inp. A similar production input for a transmembrane protein is prod_hphrex.inp. An example job submission file for a HPC cluster is hphrex.qsub.

To begin the production run one must choose a pH range and number of pH replicas. The proper choice of the pH range depends on the research objective. For example, the pH range of 1.5–6.5 was used in the hybrid-solvent CpHMD study of the pH-dependent structure function relationship of the endosomal protein BACE1 in which the catalytic aspartyl residues play a central role [8]. On the other hand, the pH range 4–8 was used in the membrane-enabled hybrid-solvent CpHMD study of the pH-dependent conformational activation of the transmembrane M2 channel, whereby the titration of four histidines modulates the conformation of the channel [69]. Next, one needs to choose the total number of pH replicas. The spacing of the pH conditions needs to be close enough such that sufficient exchange probabilities (e.g., at least 20%) are obtained. To obtain good overlap between potential energy distributions of neighboring replicas a pH spacing of 0.5 and sometimes even 0.25 is required. Other aspects to consider are the number of available CPUs on the HPC and how many CPUs can be allocated to each replica. Simulations with CHARMM do not scale well past 8 CPUs, so for a job using 16 replicas we recommend requesting a total of 128 CPUs with 8 CPUs for each replica. We recommend making exchange attempts every 1000 MD steps. A typical pH replica-exchange CpHMD simulation has an average exchange ratio of ~40%, but if the exchange ratios are too low, more replicas can be added to fill in the spacing between replicas. To achieve optimum performance in enhanced sampling, several replicas should move across all pH conditions.

To use pH-based replica exchange in CHARMM, one can use the REPD module.

REPD NREP 8 PHMD EXLM FREQ 5000 UNIT 17

Here, the REPD command initiates replica exchange, and NREP states the number of replicas to use (in this case 8). PHMD EXLM states this is a special type of Hamiltonian exchange (i.e., pH-based) and allows for the exchange of pH conditions of two adjacent replicas. FREQ states the frequency of an exchange attempt.

Then, to run several replicas in parallel, CHARMM reads in a rep.cmd file for each pH replica with the syntax, rep.cmd_0, rep.cmd_1, to rep.cmd_(NREPS), using the following command in the input file.

$ stream rep.cmd

Notice this command lacks the ‘_0’ portion of the name. In each of the rep.cmd file you will have the command that states the pH environment of the replica.

PHMD RESPH OLDPH @crysph NEWPH @ph PKATEMP @temp

Here OLDPH is the pH used in the equilibration and NEWPH is the pH of the replica. Finally, PKATEMP should be set to the same temperature of the simulation. The rest of the replica exchange set up follows a standard MD run in CHARMM. Production run inputs for BBL (prod_hphrex.inp and rep.cmd) can be used to run one 2 ns stage of pH-Replica Exchange CpHMD.

3.7. General settings for MD and CpHMD in CHARMM

For all simulations the protein is represented by CHARMM22/CMAP force field.[102, 103] Note, the current CpHMD methods are not compatible with the CHARMM36 protein force field. For solvent the CHARMM modified TIP3P water model is used. For ions or lipid molecules the CHARMM36 force fields are used [100]. The van der Waals energies are calculated with a switching function from 10 to 12 Å and a cutoff at 14 Å. All simulations are conducted under periodic boundary conditions. The PME method [104] is used to calculate the long-range electrostatic energies and forces with a real space calculation cutoff of 12 Å and 1 Å grid spacing, and a 6th-order spline interpolation. The non-bond neighbor list is updated heuristically. Additionally, the SHAKE [105] algorithm is used to constrain all bonds involving hydrogens to allow for a 2-fs time step. For NPT simulations, the temperature is maintained with the Nóse-Hoover thermostat [106, 107]. The pressure is maintained with the Langevin piston pressure-coupling algorithm [108]. For the CpHMD simulations, the default GBSW radii [109, 110] are used for the protein. For small molecules, the generic atomic radii in the GBSW file may be used upon user verification. A CpHMD parameter file phmd.inp contains the model reference pK_a values and the parameters in the titration potential of mean force for Asp, Glu, His, Cys, and Lys. Parameters for additional titratable groups can be obtained by following the steps discussed in section Parameterization.

4. Workflow for all-atom PME CpHMD in CHARMM

Minor modifications to the workflow for hybrid-solvent CpHMD are needed to set up and run all-atom PME CpHMD simulations in CHARMM [35]. The example inputs for simulations of BBL are downloadable from ephmd_charmm. To maintain charge neutrality during the all-atom PME CpHMD simulation, titratable water molecules [51] (or co-ions [34] in an earlier version) should be added. Specifically, each acidic (Asp or Glu) or basic residue (His or Lys) is coupled with one titratable water that can convert to a hydroxide (TIPU) or hydronium (TIPP). Details are explained in Ref [51]. Together with salt ions, titratable water molecules are placed in the water box using the input script step3_add_ions_titr.inp.

To run an all-atom PME CpHMD simulation, make sure the command GBSW is NOT invoked before calling PHMD. The additional options need to be added in the PHMD command to specify the residue names of titratable water (TIPU and TIPP) and the total number as well as residue IDs of the coupled pairs. For example, in the BBL simulation, 3 Asp, 3 Glu, and 2 His are titratable, and they are coupled to 8 titratable water molecules.

PHMD PAR 23 WRI 25 PH 7.0 NPRI 5000 PHFRQ 5
MASS 10.0 BETA 5.0 TEMP 298 LAM −
sele resn ASP. Or. resn GLU. or. TIPU. or. 
resn HSP. or. TIPP end −
qcouple 8 −
resi 4 resc 4789 −
resi 16 resc 4790 −
resi 20 resc 4791 −
resi 36 resc 4792 −
resi 37 resc 4793 −
resi 39 resc 4794 −
resi 17 resc 4771 −
resi 41 resc 4772

Here resn TIPU and TIPP declare the two types of titratable water. The option qcouple 8 specifies a total number of 8 coupled pairs. Following qcouple, residue IDs for the titratable group (e.g., resi 4) and co-titrating water (e.g., resc 4789) are listed. Note, all co-titrating pairs need to be specified manually.

5. Workflow for implicit-solvent CpHMD in Amber

Here we discuss how to run GBNeck2-CpHMD [44, 45] simulations in Amber. The related files can be found in the GitLab directory cphmd-tutorial/gphmd_Amber.

5.1. Preparation of structure and input files

To simplify system preparation for GBNeck2-CpHMD simulations, we recommend the user to download and install a tool set CpHMD-prep. Once installed, the shell script cphmd_prep.sh can be called to prepare the structure and input files for running CpHMD.

Before explaining cphmd_prep.sh, we briefly explain the important CpHMD specific files and options in Amber. Similar to CpHMD simulations in CHARMM (section 3.1), we first convert the PDB file to the Amber format, cap the terminal groups, and change the names of titratable Asp, Glu, and His residues to AS2, GL2, and HIP, respectively. We then add dummy hydrogens to AS2 and GL2. Besides the standard Amber force field files, tleap requires two CpHMD specific files for building topology and parameters: frcmod.phmd, which specifies the modifications of bonded parameters for AS2 and GL2, and phmd.lib, which contains the definitions of AS2 and GL2. For GBNeck2-CpHMD, set the PBradii to mbondi3 in tleap (see later discussion of modifications). For running CpHMD, an additional file gbneck2_input.parm is needed, which contains the partial charges and van der Waals energy flags of the protonated/deprotonated forms of the titratable residues as well as the parameters of the model titration PMFs (see section 7).

To run CpHMD, the pmemd.cuda command should contain several CpHMD options. The option -phmdparm reads in the aforementioned CpHMD parameter file gbneck2_input.parm. The option -phmdin reads in a CpHMD job control file, which specifies various options for CpHMD simulations. We note, except for MaskTitrRes(:) (titratable residue types, e.g., ‘AS2’, ‘GL2’, ‘HIP’, ‘CYS’, ‘LYS’) and Mask-TitrResTypes (number of titratable residues, e.g., 5), the default settings in the phmdin file should be kept. Finally, if specified the option -phmdstrt reads in a CpHMD restart file. We should also point out that for CpHMD runs, the Amber mdin files are similar to those for the fixed-charge MD using GBNeck2 implicit solvent and Langevin dynamics. The two CpHMD specific flags are iphmd and solvph. For GBNeck2-CpHMD, iphmd should be set to 1 and solvph should be set to the desired pH condition.

Now we explain the shell script cphmd_prep.sh.

cphmd_prep. sh
[−pdb|−−pdbid] | [− fil |−−filename] 
[−cha|−−chainid]
[−mod|−−modelid]
[−con|−−conc]
[− tim|−−time]
[−tem|−−temp]
[−dph]
[− phl|−−phlow]
[−phu|−−phup]
[− res|−−restype]
[−run|−−runmode]
[−h|−−help]

If specified, the option -pdb|–pdbid reads in a PDB ID and downloads the corresponding structure from RCSB. If no PDB ID is given, the option -fil|–filename reads in a PDB file. The option -cha|–chainid specifies the chain ID to include in simulations (default ‘A’). If specified, the option -mod|– modelid reads in a rotamer model ID (e.g., A or B) in the PDB file. The following options are related to the simulation: -con|–conc specifies the ionic strength in M (default 0.15); -tim|–time specifies the simulation length in ns for each pH condition (default 10); -tem|–temperature specifies the simulation temperature in K (default 300); -phl|–phlow specifies the lowest pH (default 6.5); -phu|–phup specifies the highest pH (default 9.0); -phi|–pHintvl specifies the pH interval for calculating the individual simulation pH conditions between phlow and phup; -res|–restype specifies the amino acid residue types allowed to be titratable (default ‘Asp Glu His Cys Lys’); and -rm|–runmode specifies the type of simulation (‘async’ for asynchronous pH replica exchange, ‘rex’ for synchronous pH replica exchange, and ‘ind’ for independent pH simulations). Finally, -t|–test offers a test option (‘t’ means temporary files will be kept for checking) and -h|–help displays the usage and options.

cphmd_prep.sh accepts either a PDB ID or a user-prepared PDB file and calls PDBFixer in OpenMM[88] to extract the desired chain, add missing heavy atoms or residues and the terminal capping groups (CH₃CO and NH₂). Note, ions, ligands, waters, and unspecified chains from the PDB file are removed. Once the PDB file is cleaned up, tleap in Amber (or Ambertools) is used to build the positions of hydrogen as well as dummy hydrogen atoms according to the specified titratable residue types. As required by GBNeck2-CpHMD, [44, 45] the GB input radii of HD1/HE2 of His, SG of Cys, OD1/OD2 of Asp, and OE1/OE2 of Glu are changed to 1.17, 2.00, 1.40, and 1.40 Å respectively, and the interactions between the dummy carboxylate hydrogens in Asp/Glu are excluded. cphmd_prep.sh automatically generates input files as well. Below we give two examples.

Example 1. Predict the pK_a’s of the EGFR kinase given a PDB ID.

Here we wish to predict the pK_a’s and the protonation states of His, Cys, and Lys at the physiological pH 7.4.

$ cphmd_prep.sh −pdb 5U8L −mod A −phl 5.5 −phu 9.5 −res ‘His Cys Lys’

Here 5U8L is the PDB ID. We omit chain ID, because 5U8L contains only one chain (default is chain A), but we specify the model A (there are two rotamer models in the PDB file). For PDB file containing NMR models, a specific model can be selected using the -m flag. The pH range is 5.5 to 9.5, which extends 2 pH units above and below the physiological pH 7.4. Since the (default) pH interval is 0.5 units, the total number of simulation pH conditions is 9. In this example, simulation length (-l|–simlength), temperature (-tp|–temperature), and ionic strength (-i|–ionic) are set to the respective default values of 10 ns, 300 K, and 0.15 M.

Upon execution, cphmd_prep.sh generates a file ‘cphmd_prep.log’ and a folder 5U8L, which contains the files listed in the aforementioned checklist. ‘cphmd_prep.log’ contains the information of the job control parameters and also the names of the files generated for the current job. Inside the folder 5U8L, there are multiple files with names like 5U8L_chainA_A_TAG.EXT with different tags TAG and extensions EXT. ‘5U8L’ is the PDB ID provided, ‘chainA’ refers to chain A, and ‘A’ is the rotamer model ID provided. Tags include mini for minimization, equil* for different equilibration steps, and prod for production. Extensions include pdb for the PDB file, rst7 for the Amber rst7 coordinate file, parm for the Amber parm7 parameter file, mdin for the Amber input file, and phmdin for CpHMD control parameter file. We can also specify multiple chains. For example, if we want to include both chain A and chain B, the command option -cha ‘A B’ can be used, and the file names will start with 5U8L_chainAB. All files in the folder ‘5U8L’ are also zipped as cphmd_inputs.zip.

Example 2. Predict the pK_a’s of the protein Snase given a PDB file.

$ cphmd_prep.sh − fil 3BDC. pdb −mod A −phl 1.0 −phu 12.0 −tim 4

Here the script takes a PDB filename and the simulations are conducted in a wider pH range from 1.0 to 12.0. With a default interval of 0.5 units, this amounts to 23 simulation pH conditions. Since the model pK_a’s of Asp/Glu are 3.7/4.3 and the model pK_a of Lys is 10.4, this pH range typically allows the titration of all default residue types ‘Asp Glu His Cys Lys’. For this reason, the residue type (-type) is omitted. Another difference from Example 1 is that a much shorter simulation length of 4 ns (-tim 4) is specified. This is because only a rough estimate of the pK_a values is desired. Similar files are generated as in Example 1; however, there are 14 extra Amber input files due to the additional pH conditions. All related files can be found here 3BDC.

Several additional files are generated by cphmd_prep.sh. apHREX.py is a Python script for running asynchronous pH replica exchange simulations if -run is not specified or specified as async. The related file cphmd.groupfile is an Amber style for specifying individual replica files in pH replica-exchange simulations. Finally, the file README contains all the commands for successfully running GBNeck2-CpHMD simulations for the current job.

5.2. Running GBNeck2-CpHMD simulations

Here we discuss the protocol of running GBNeck2-CpHMD simulations using the two examples discussed above. All commands for minimization, equilibration, and production can also be found in the file README.

Energy minimization

The energy minimization is performed with the input file ending with ‘_mini.mdin’, e.g., 3BDC_chainA_A_mini.mdin for SNase. During minimization, a harmonic restraint with the force constant of 50 kcal mol⁻¹ Å⁻² is placed on all protein heavy atoms, except for the terminal and capping residues where all atoms are allowed to move. The minimization lasts 1000 steps, using the steepest descent and conjugate gradient algorithms for the first and second 500 steps, respectively. To run minimization, we call pmemd.MPI or pmemd.cuda if Amber 20 [111] or a later version is used.

$ export name= ‘3 BDC_chainA_A’
$ mpirun −n 4
$AMBERHOME/ bin/pmemd.MPI −O
− i ${name} _mini. mdin −c ${name}. rst7
−p ${name}. parm7 −ref ${name}. rst7
−r ${name} _mini. rst7 −o ${name} _mini. out

Here, ‘-n 4’ specifies 4 CPU cores. Note, a large number of processors may be specified if hardware allows. The ‘-ref’ option specifies the reference coordinate file (3BDC_ModelA_A_fixed.rst7). The ‘-l’ option specifies the initial coordinate file. It is omitted here, since it the same as the reference file. If minimization runs error free, a timing info is given out and two files are generated: the file 3BDC_ModelA_A_fixed_mini.out contains the printed energies, and *_mini.rst7 is the restart coordinate file for the next step equilibration.

Equilibration

Following minimization, we perform a four-stage equilibration to relax the protein structure at physiological pH 7.5 (or the crystallization pH). Note, for implicit-solvent simulations heating is not required. During the four-stage equilibration (2000 steps each), the harmonic force constant on the heavy atoms is gradually reduced from 5.0, 2.0, 1.0, to 0.0 kcal/mol/Ų. CpHMD is turned on by setting the iphmd keyword to 1 (GBNeck2-CpHMD) in the Amber input file.

Using SNase as an example, the first equilibration stage is run with the following command:

$ export name= ‘3 BDC_chainA_A’
$ $AMBERHOME/bin/pmemd.cuda −O
− i ${name} _equil1.mdin −c ${name} _mini.rst7
−p ${name}.parm7 −ref ${name} _mini.rst7
−r ${name} _equil1.rst7 −o ${name} _equil1.out
−x ${name} _equil1.nc −phmdin ${name}.phmdin 
−phmdparm gbneck2_input.parm
−phmdout ${name} _equil1.lambda 
−phmdrestrt ${name} _equil1.phmdrst
$ sed − i ‘ s/QPHMDStart = .true. ,/QPHMDStart
= .false. , /g’ ${name}. phmdin 
$ sed − i ‘ s /PHMDRST/PHMDSTRT/g ’
${name}.phmdrst

Here, 3BDC_chainA_A_mini.rst7 generated by the minimization step is used as the initial (-c) and reference (-ref) coordinates. The Amber job input file 3BDC_chainA_A_equil1.mdin file specifies simulation length, restraints, and other MD control parameters. 3BDC_chainA_A.phmdin contains job control parameters for GBNeck2-CpHMD. gbneck2_input.parm, which is a common file for GBNeck2-CpHMD simulations, contains the model pK_a values and titration parameters. 3BDC_chainA_A_equil1.rst7 is the restart file that contains coordinates and velocities. 3BDC_chainA_A_equil1.phmdrst is the corresponding CpHMD restart file that contains the λ values and velocities. 3BDC_chainA_A_equil1.out contains the energy information. 3BDC_chainA_A_equil1.lambda contains the λ coordinates, although it is of little use since they are from the equilibration run. The two ‘sed’ commands modify the names for the next step.

For the rest of the equilibration stages, the same commands are used but file names should be changed. For example, we should replace ‘equil1’ and ‘mini1’ with ‘equil2’ and ‘mini2’ for the second equilibration step, and use 3BDC_chainA_A_equil1.rst7 as the initial and reference coordinate file. In addition, we need to use a new -phmdstrt flag and use 3BDC_chainA_A_equil1.phmdrst as a CpHMD restart file. After all four equilibration stages are completed, files with the names *equil4* are generated.

The above example uses pmemd.cuda, but we can also use pmemd.MPI if no GPU is available. The only modification is to replace ‘$AMBERHOME/bin/pmemd.cuda’ with ‘mpirun -n 16 $AMBERHOME/bin/pmemd.MPI’ in the command, assuming 16 cores can be used for the simulation.

Production

For production runs, we can use either independent pH, synchronous pH replica exchange, or asynchronous pH replica exchange. For independent pH runs, the simulation at different pH conditions are run independently either on the same or different machines. The running order is arbitrary, and we collect all the output files together for data analysis. The input files can be generated using cphmd_prep.sh with –run ind. For SNase, the production run is invoked with the following command:

$ export name= ‘3 BDC_chainA_A ’
$ $AMBERHOME/ bin/pmemd. cuda −O
− i ${name}_pH7.5 _prod. mdin
−c ${name} _equil4. rst7 −p ${name}. parm7
−r ${name}_pH7.5 _prod1. rst7
−o ${name}_pH7.5 _prod1. out
−x ${name}_pH7.5 _prod1. nc
−phmdin ${name}. phmdin
−phmdparm gbneck2_input. parm
−phmdstrt ${name} _equil4. phmdrst 
−phmdout ${name}_pH7.5 _prod1. lambda 
−phmdrestrt ${name}_pH7.5 _prod1. phmdrst 
− inf pH7. 5. mdinfo

The restart files generated by equilibration step 4 are used as starting files for the production run. No reference file is needed. Along with *.out, *.rst7, *.nc (trajectory), and *.phmdrst files, λ coordinates are saved in 3BDC_chainA_A_fixed_pH*_prod1.lambda. For the command above, we again use pmemd.cuda but we can also run on CPUs with pmemd.MPI. All input files for this example can be found in gphmd_snase_phind.

pH replica-exchange simulations usually converge much faster and thus require less simulation time than independent pH simulations [23, 33, 45]. The traditional replica-exchange algorithm allows each replica to run in parallel and data exchange is synchronized. The pH replica-exchange protocol is executed similarly as the temperature replica-exchange protocol in Amber, i.e., we need a group file that contains the commands and inputs for every pH condition and then mpirun is called. The commands in the group file are quite similar to those for the independent pH runs. The input files can be generated using cphmd_prep.sh with the option -run rex. For example,

mpirun −np 64
$AMBERHOME/bin/pmemd. MPI −ng 16
−groupfile cphmd.groupfile

Note that we use 4 processes for a single pH replica and a total of 64 processes are needed (-np 64) given the number of pH conditions (-ng 16) in the Snase example command. For using mpirun for CpHMD, we should make sure that each pH replica runs on a single node so that there is only minimal data exchange between nodes if the whole job spreads across multiple node. Supposing we have a CPU cluster consisting of 64-core nodes, we should make sure the number of pH replicas is a factor of 64. This example uses pmemd.MPI to run on CPU clusters. If we have a GPU cluster, we can replace the ‘-np 64 $AMBERHOME/bin/pmemd.MPI -ng 16’ with ‘-np 1 $AMBERHOME/bin/pmemd.cuda.MPI -ng 16’. However, if the number of GPUs is less than 16, it might not work properly. The input files can be found in the gphmd_snase_phrex folder.

The traditional replica-exchange algorithm was designed for CPU based HPC clusters, where a large number of processors are available such that all replicas can be run in parallel. However, the latter condition cannot be always met for today’s GPU workstation or even HPC cluster, i.e., the number of GPUs is smaller than the number of replicas. Thus, we implemented an asynchronous pH replica-exchange algorithm, [65] in which each replica is run consecutively and data exchange is performed after all replicas are run. The users can download the related Python program async_ph_replica_exchange that allows an arbitrary number of pH replicas to be run on an arbitrary number of GPUs.

A Python script apHREX.py generated by cphmd_prep.sh with ‘-run async’ is called to run the asynchronous pH replica-exchange simulations for 3BDC.

$ export name= ‘3 BDC_chainA_A ’
$ python apHREX. py 2000
template_$ {name} _prod. mdin ${name}. parm7 
gbneck2_input. parm ${name}. phmdin 
${name}_cphmd ${name} _equil4. rst7
1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
5.0 5.5 6.0 6.5 7.0 7.5 8.0 8.5
9.0 9.5 10.0 10.5 11.0 11.5 12.0

Output files, including the standard Amber outputs, lambda files, and trajectory files, are concatenated on the fly according to the pH conditions instead of replicas in the pHREX method. These files are stored in the 3BDC_chainA_A_cphmd subdirectory. The input files for this example can be found in gphmd_snase_aphrex.

Other relevant settings

For optimum performance in pK_a prediction, the default settings in GBNeck2-CpHMD should be followed. Currently, the Amber ff14SB force field is recommended for proteins. A Langevin thermostat with the collision frequency of 1 ps⁻¹ is used to maintain the temperature for λ dynamics. A non-bond cutoff of 999 Å (i.e., no cutoff) is used. Files should be saved infrequently to avoid IO that substantially slows down simulations on the GPUs. The default frequency of saving λ files every 1000 MD steps is designed for simulations of 10 ns per replica. For longer simulations, less frequent saving should be used. If analysis of conformational dynamics is desired, a saving frequency of every 10,000 MD steps (20 ps with a 2-fs time step) is recommended for a simulation of 10 ns per replica. However, if only pK_a’s are desired, trajectory saving should be set to the frequency of restart file writing, e.g., 500,000 MD steps (1 ns with a 2-fs time step) or even larger depending on the wall clock time of the simulation (aiming at writing restart file once or twice a day). Writing to the Amber log file should be avoided or as infrequent as possible.

6. Post-simulation analysis

CpHMD simulations allow the user to determine the protonation states of all titratable sites at the simulation pH conditions, the pK_a values, or pH- or proton-coupled conformational dynamics. Below we will discuss these aspects.

6.1. Determination of protonation states and pKa values

The lambda file contains the time evolution of λ (titration state) and x (tautomeric state) coordinates of titratable groups. These data allow us to determine the protonation states at specific pH, calculate the pK_a values and tautomer states, and monitor convergence of protonation-state sampling. As an example, Fig. 2 shows the time evolution of λ for Cys481 in the BTK kinase at different pH conditions.

Figure 2. Time series of the λ value for Cys481 in the BTK kinase.

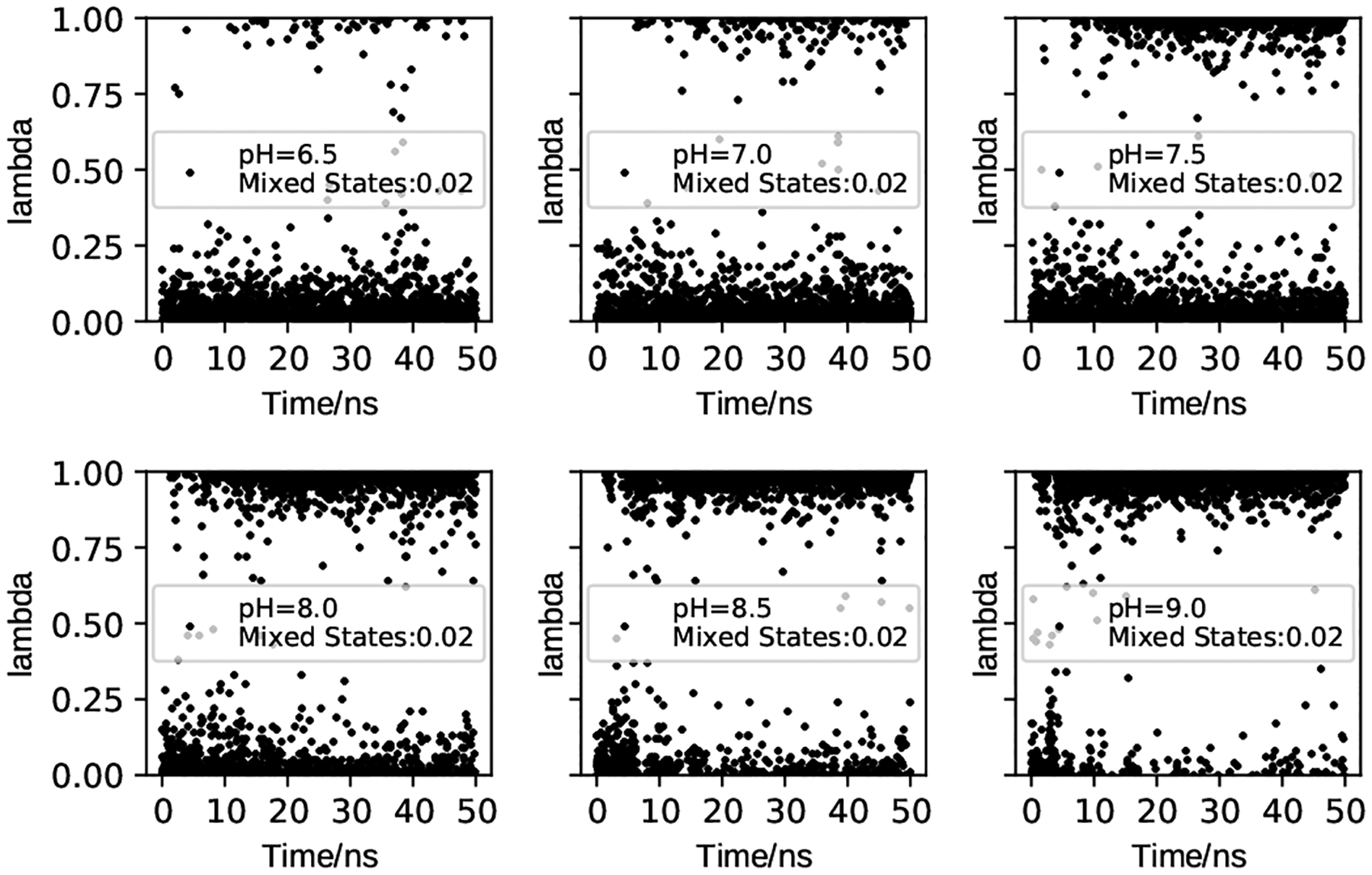
The data were saved every 20 ps (taken from Ref [112]). The pH conditions and fractions of mixed states (0.2 ≤ λ ≤ 0.8) are given. The plots show that the protonation-state sampling at all pH conditions converge after ~10 ns.

To facilitate analysis of the lambda files, we developed a Python tool cphmd_anal.py. This tool returns plots of the time series of unprotonated fractions and fitting of the unprotonated fractions to obtain pK_a’s (see discussion below). For a trajectory at a specific pH, we can count the number of frames where a titratable residue i is in the protonated or unprotonated state, which is defined as λ_i < 0.2 or λ_i > 0.8, respectively. The unprotonated fraction of the residue (S_i) is calculated as

$$S_i=\frac{N_i^{\text{Unprot}}}{N_i^{\text{Prot}}+N_i^{\text{Unprot}}},$$ (12)

where $N_i^{\text{Prot}}$ and $N_i^{\text{Unprot}}$ are the number of protonated and unprotonated frames, respectively. Plotting the time series of the S_i value informs convergence of the protonation state sampling (Fig. 1, step 5). Once convergence is reached, the pK_a of residue i can be obtained by fitting the S_i values at all simulation pH to the generalized Henderson-Hasselbalch equation,

$$S_i=\frac{1}{1+{10}^{n{\left({\text{pK}}_{\text{a},i}-\text{pH}\right)}^{\prime }}}$$ (13)

where n is the Hill coefficient. The resulting best fit is referred to as the titration curve (Fig. 1, step 5). A significant deviation of n from 1 indicates cooperativity (n > 1) or anti-cooperativity (n < 1) with a neighboring residue. We note, in the past, λ_i < 0.1 and λ_i > 0.9 were used for defining the protonated and unprotonated states [31, 32]; however, our extensive studies (based on more than 100 proteins) showed that the calculated pK_a value is not sensitive to the cutoff.

Figure 1.

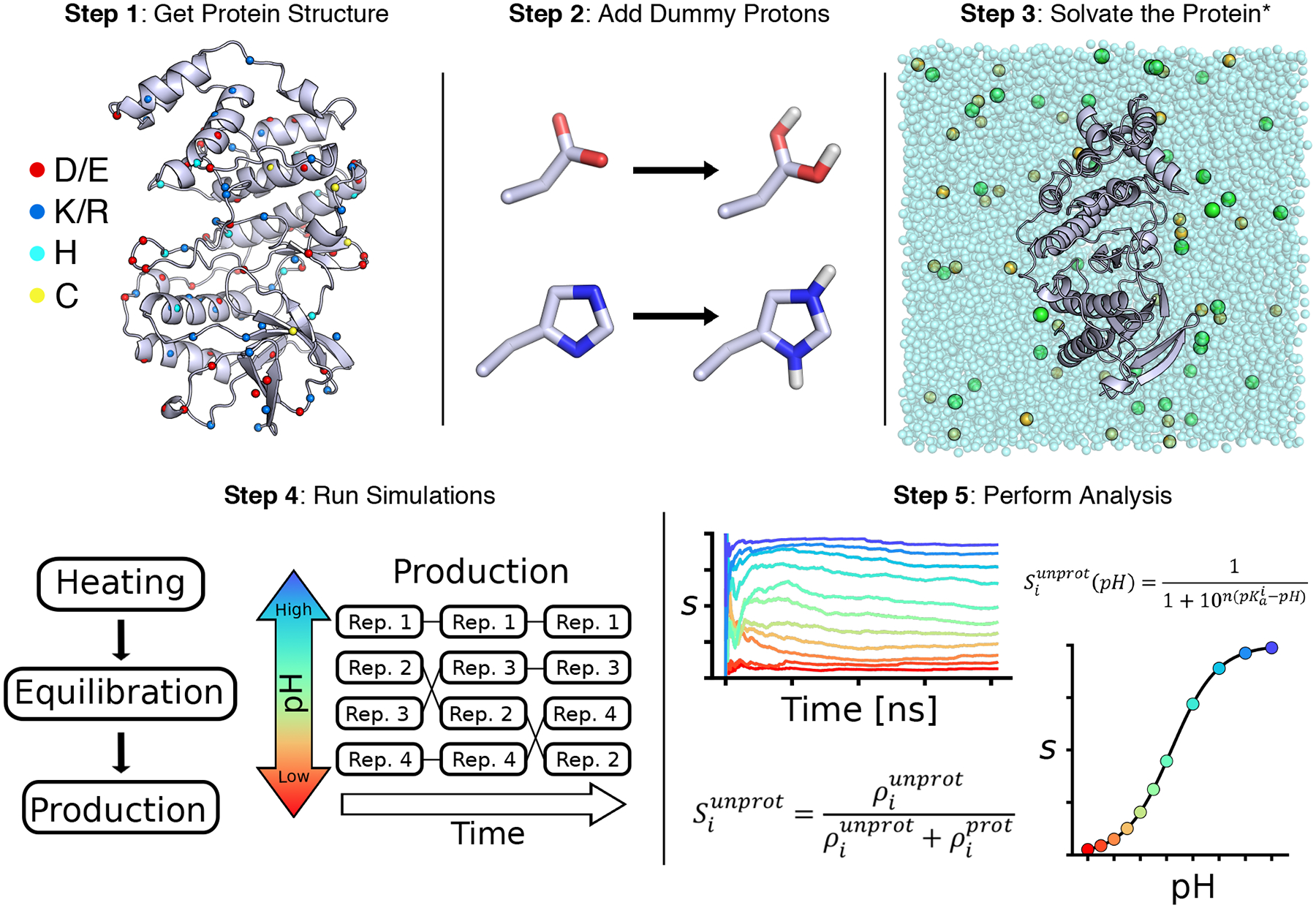
Overview of the CpHMD workflow

6.2. Analysis of proton-coupled conformational dynamics and rationalization of the calculated pK_a values

A major application of CpHMD simulations is elucidation of pH-dependent or proton-coupled conformational dynamics, which in turn rationalizes the calculated pK_a values. This practice can be best explained using an example. The pH replica-exchange GBNeck2-CpHMD simulations of the BTK kinase [112] gave a pK_a of about 7.5 for Cys481, which is one unit lower than the model pK_a of cysteine – the pK_a value of an isolated cysteine fully exposed to solvent. Analysis of the pH replicas (i.e., trajectories at different pH conditions) revealed that Cys481 accepts hydrogen bonds (h-bond) from Asn481 and Thr410 when it is in the deprotonated thiolate state (Fig. 3a). Note, these h-bonds are absent in the crystal structure (PDB 3pj3). Following this observation, we plotted the deprotonated fractions of Cys481 at different pH conditions (Fig. 3b) and the occupancies of the h-bond formation between Cys481 and Asn484 or Thr410 (Fig. 3c). A comparison between the pH-dependent deprotonation and h-bond formation demonstrates that the two are correlated, i.e., deprotonation of Cys481 is coupled to the h-bond formation. It also suggests that the pK_a downshift of Cys481 relative to the model value can be attributed to the stabilization of the deprotonated thiolate state by the h-bond formation with Asn484 and Thr410. We note, while implicit-solvent based CpHMD simulations have been successfully applied to pK_a predictions and rationalization, hybrid-solvent and all-atom CpHMD simulations offer more accurate description of conformational dynamics. We refer the user to the studies listed in Table 1 as examples.

Figure 3. An example analysis of proton titration of a cysteine and coupling with conformational dynamics.

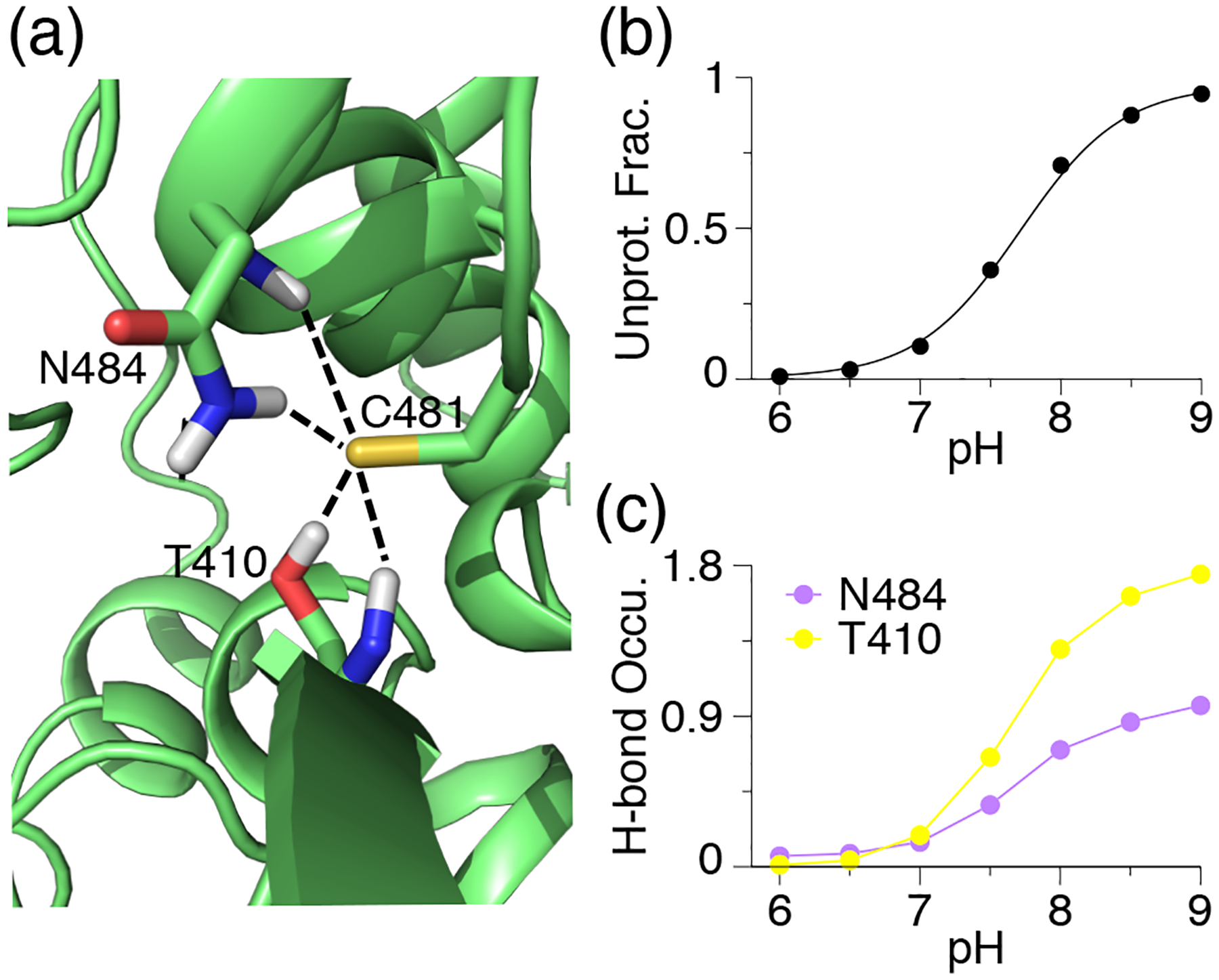
(a) A zoomed-in view of the structural environment of Cys481 in the BTK kinase taken from the trajectory at pH 9. The h-bonds with Asn484⋯ Cys481 and Thr410⋯ Cys481 are shown. The pH 9 replica is used. (b) The unprotonated fractions of Cys481 at different pH conditions. The titration curve represents the best fit to the Henderson-Hasselbalch equation. (c) Occupancy of the h-bond formation between Cys481 thiolate and Asn484 or Thr410 at different pH conditions. Reprinted with permission from Liu, Zhan et al.[112] Copyright 2021 American Chemical Society.

7. Parameterization of model titration

CpHMD is a relative free energy simulation approach, whereby the potential of mean force (PMF) of deprotonation of a titratable amino acid in the protein environment is calculated relative to that of a reference, i.e., a model compound or peptide in solution [30, 31]. Model compounds, which were used in the early development of CpHMD methods [30, 31, 35], are blocked single amino acid residues CH₃CO-X-NH₂ or CH₃CO-X-CONH₂, where X represents a titratable amino acid. In the development of the hybrid-solvent CpHMD [33] and GBNeck2-CpHMD [44, 45], model peptides CH₃CO-AAXAA-NH₂ were used to take advantage of recent experimental data [98, 113]. Since in the CpHMD simulation, a model PMF is subtracted, simulation of a model compound or peptide should return a zero PMF at the pH value equal to the model pK_a. In other words, protonated and deprotonated states are sampled with equal probabilities (S ≈ 0.5). To ensure this is the case, the model PMF needs to be accurately determined.

To obtain the model PMF U^mod, we use a free energy simulation method called thermodynamics integration, in which the mean forces at different values of θ (for single site titration) or θ and x for double site titration are calculated and then analytically integrated to obtain U^mod. The single site titration model is applied to Cys and Lys. The latter has equivalent protons, so one is selected for titration. There are two types of double site titration model. His sidechains have two titratable nitrogens with different microscopic pK_a’s, while carboxylate sidechains (Asp and Glu) have two titratable oxygens but identical microscopic pK_a’s. These three titration models require different forms of U^mod and methods of fitting.

7.1. Protocol of parameterization for single site model titration

For running TI simulations to obtain parameters, we set the options prlam to FALSE, prderiv to TRUE, and phtest to TRUE in the phmdin file, vph_theta to 0 in the phmdstrt file. For a single site titration model (e.g., Cys and Lys), we run CpHMD simulations at θ_i = (0.4, 0.6, 0.785, 1.0, 1.2, 1.4.). Each simulation is run for 10 ns, from which the mean forces 〈 ∂U/∂θ|_θi〉 are calculated. Fitting of the mean forces to the following analytic form of ∂U/∂θ (Eq. 14) returns the two parameters A and B (Fig. 4).

Figure 4.

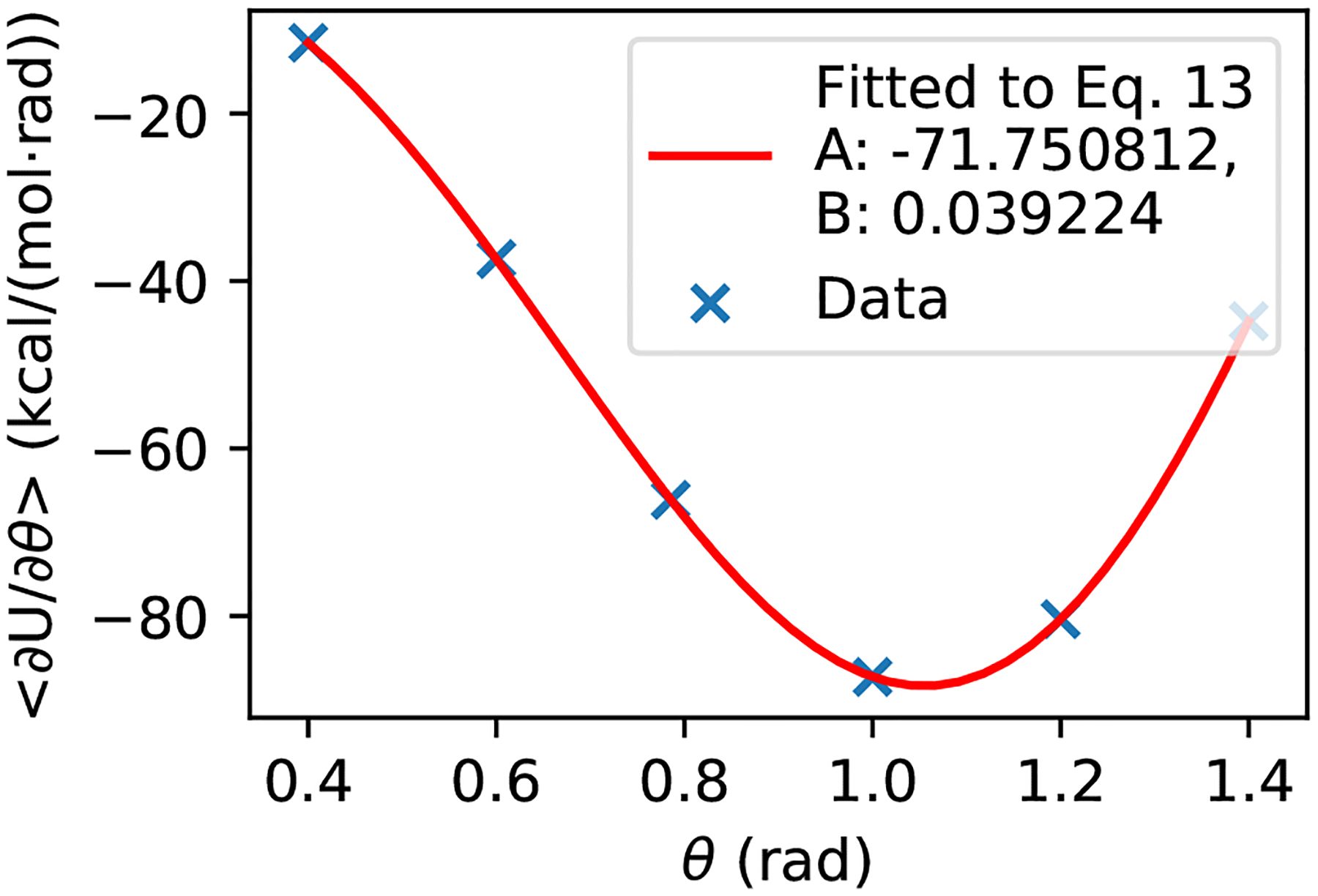
Example of fitting A and B parameters for a single site titration model.

$$\frac{\partial U}{\partial \theta }=2A\text{\hspace{0.17em}sin}(2\theta )\left({\text{sin}}^2\theta -B\right).$$ (14)

As an example, Fig. 4 shows the fitting result for the GBNeck2-CpHMD titration of Cys model peptide. We note, related to error propagation. fitting should be performed in the θ space (and not in the transformed λ space) to minimize fitting errors.

Protocol of parameterization for histidine model titration

For a double site titration model with two different microscopic pK_a’s (e.g. His), the two-dimensional PMF (Eq. 9) can be reduced to the following form [31],

$$U^{\text{mod}}=A_{10}{\lambda }^2{x}^2+2\left(A_1{B}_1-A_0{B}_0\right)\lambda x+2\left(A_0{B}_0-A_1{B}_1-A_{10}{B}_{10}\right){\lambda }^{2}x+A_1{\lambda }^2-2A_1{B}_1\lambda ,$$ (15)

where λ = sin²θ and x = sin²θ^x. The six parameters A₀, B₀, A₁, B₁, A₁₀, and B₁₀ are the parameters in the quadratic functions that describe the one-dimensional processes [31]. A₀ and B₀ correspond to HIP ⇌ HID, i.e., titration at Nϵ; A₁ and B₁ correspond to HIP ⇌ HIE, i.e., titration at Nδ; and A₁₀ and B₁₀ correspond to the tautomer interconversion HIE ⇌ HID.

Step 1. To obtain A₀ and B₀, we run TI simulations by fixing θ^x at 0 (λ = 0, HID, Nδ is protonated), varying θ at (0.0, 0.2, 0.4, 0.6, 0.785, 1.0, 1.2, 1.4, 1.5708), and fitting the resulting mean forces to the following one-dimensional function,

$$\frac{\partial U}{\partial \theta }=2A_0\text{\hspace{0.17em}sin}(2\theta )\left({\text{sin}}^2\theta -B_0\right).$$ (16)

Step 2. To obtain A₁ and B₁, we run TI simulations by fixing θ^x at 1.5708 (λ = 1, HIE, Nδ is protonated), varying θ at (0.0, 0.2, 0.4, 0.6, 0.785, 1.0, 1.2, 1.4, 1.5708), and fitting to the following one-dimensional function,

$$\frac{\partial U}{\partial \theta }=2A_1\text{\hspace{0.17em}sin}(2\theta )\left({\text{sin}}^2\theta -B_1\right).$$ (17)

Step 3. To obtain A₁₀ and B₁₀, we run TI simulations by fixing θ at 1.5708 (λ = 0, HIP, doubly protonated His), varying θ_x at (0.0, 0.2, 0.4, 0.6, 0.785, 1.0, 1.2, 1.4, 1.5708) and fitting the resulting mean forces to the following one-dimensional function,

$$\frac{\partial U}{\partial {\theta }^x}=2A_{10}\text{\hspace{0.17em}sin}\left(2{\theta }^x\right)\left({\text{sin}}^2{\theta }^x-B_{10}\right).$$ (18)

Protocol of parameterization for carboxylic acid model titration

For double site titration models with two identical microscopic pK_a’s (e.g., Asp and Glu), the two-dimensional PMF (Eq. 9) can be reduced to the following form [31],

$$U^{\text{mod}}\left({\lambda }_i,x_i\right)=\left(R_1{\lambda }_i^2+R_2{\lambda }_i+R_3\right){\left(x_i+R_4\right)}^2+R_5{\lambda }_i^2+R_6{\lambda }_i$$ (19)

where R₁, …, R₆ are parameters that can be determined via one-dimensional fitting.

Step 1. To generate the data for fitting, we run TI simulations at the combinations of θ value of 0.0, 0.4, 0.6, 0.785, 1.0, 1.2, or 1.4 and θ^x value of 0.0, 0.4, 0.6, 0.785, 1.0, 1.2, 1.4, or 1.5708.

Step 2. We obtain A and B parameters at each value of θ, A(θ) and B(θ), by fitting 〈∂U/∂θ_x〉 at different θ^x values to the derivative of the quadratic function,

$$\frac{\partial U}{\partial {\theta }^x}=2A(\theta )\text{\hspace{0.17em}sin}\left(2{\theta }_x\right)\left({\text{sin}}^2{\theta }_x-B(\theta )\right),$$ (20)

where A(θ) and B(θ) are the θ-dependent parameters.

Step 3. We obtain A and B parameters at each value of θ^x, A(θ^x) and B(θ^x), by fitting 〈 ∂U/∂θ〉 at different θ values,

$$\frac{\partial U}{\partial \theta }=2A\left({\theta }^x\right)\text{sin}(2\theta )\left({\text{sin}}^2\theta -B\left({\theta }^x\right)\right),$$ (21)

where A(θ^x) and B(θ^x) are the parameters.

Step 4. We obtain R₁, R₂, and R₃ by fitting A(θ_i) to

$$A(\theta )=R_1{\text{sin}}^4\theta +R_2{\text{sin}}^2\theta +R_3,$$ (22)

Step 5. We set R₄ = 0.5, because the two titrating sites are identical. We then obtain R₅ by fitting A(θ^x) to

$$A\left({\theta }^x\right)=a_0{\text{sin}}^4{\theta }^x+a_1{\text{sin}}^2{\theta }^x+R_5,$$ (23)

and obtain R₆ by fitting B(θ^x) to

$$B\left({\theta }^x\right)=a_0{\text{sin}}^4{\theta }^x+a_1{\text{sin}}^2{\theta }^x+R_6,$$ (24)

7.2. Scripts for TI simulations and parameterization

To facilitate TI simulations and parameter fitting, we implemented a Shell script heat_equil_prod_param.sh and a Python program cphmd_parm_fit.py. Here we use Cys to illustrate the usage.

$. /min.scr cys
$. /heat_equil_prod_param.sh cys

After minimization, heating, equilibration, and production thermodynamic integration, we obtain ∂U/∂θ values saved in files with the extension .lambda as in the folder single (single site titration). We then call the Python script to fit the A and B parameters.

$ python cphmd_parm_fit.py single

Four files are generated: du.data, du.fit, du.png, and cphmd.parm. du.data contains the mean force data, du.fit contains the detailed fitting results, du.png is the plot of the fitting (Fig. 4), and cphmd.parm contains the A and B parameters that can be directly copied and pasted into the standard CpHMD parameter file. The instructions for parameterization of different models are described in the folder parameterization and the example results are included, as in the folders single, his, and carboxyl.