Disentangled Representation Learning for OCTA Vessel Segmentation With Limited Training Data

Abstract

Optical coherence tomography angiography (OCTA) is an imaging modality that can be used for analyzing retinal vasculature. Quantitative assessment of en face OCTA images requires accurate segmentation of the capillaries. Using deep learning approaches for this task faces two major challenges. First, acquiring sufficient manual delineations for training can take hundreds of hours. Second, OCTA images suffer from numerous contrast-related artifacts that are currently inherent to the modality and vary dramatically across scanners. We propose to solve both problems by learning a disentanglement of an anatomy component and a local contrast component from paired OCTA scans. With the contrast removed from the anatomy component, a deep learning model that takes the anatomy component as input can learn to segment vessels with a limited portion of the training images being manually labeled. Our method demonstrates state-of-the-art performance for OCTA vessel segmentation.

I. Introduction

Optical coherence tomography (OCT) angiography (OCTA) is an noninvasive imaging modality with applications in various retinal and neurological diseases. It provides detailed visualizations of the retina’s vascular structure [1]–[7] and foveal avascular zone (FAZ) [8], [9]. Although OCTA data are acquired as volumes, for a variety of reasons including the presence of so-called projection artifacts [10], [11], it is common to project selected slabs into en face images for analyzing macular OCTA images [5]–[7]. The resulting two standard OCTA en face images depict the superficial vascular plexus (SVP), which incorporates the ganglion cell layer (or lies within the ganglion cell layer and nerve fiber layers), and the deep vascular plexus (DVP), which incorporates the inner nuclear layer [12]–[15].

Quantitative studies of en face OCTA images usually require segmentation of the retinal vessels and capillaries. Different methods for segmenting OCTA images have been explored in recent years [16]–[24]. In particular, supervised trained deep learning methods have drawn a lot of attention, because of their success in many related applications. However, manually segmenting capillaries in OCTA images is extremely time-consuming and obtaining a sufficient number of such pixel-level annotations for supervised training of deep networks is impractical,¹ especially when it must be done for different scanners. Moreover, for many scans identifying capillaries is impossible due to the limited image resolution and the presence of noise and artifacts. For this reason, existing publicly available datasets mainly focus on large vessels [23] with limited capillary delineation [25]. An example scan with its manual delineation from the ROSE dataset [25] is given in Fig. 1. Although, we can see numerous capillaries in the zoomed-in view of the image, most of them are not included in the manual delineation.

Fig. 1.

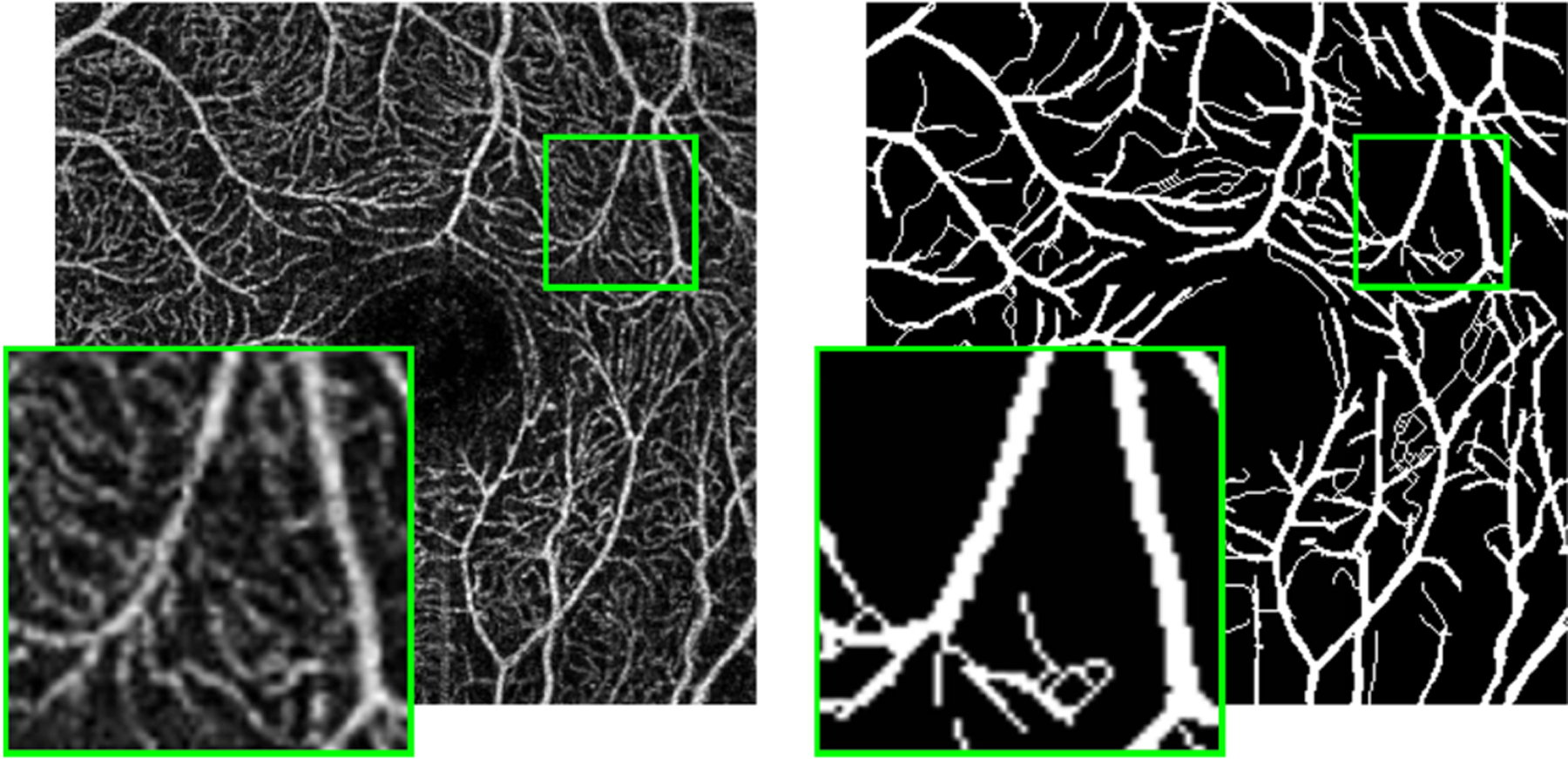
An example subject from the ROSE dataset [25]. The Optovue SVP scan is shown on the left, with its pixel-level annotation shown on the right. For each image, a zoomed-in view for the region inside the green box is shown in the bottom left corner.

While vessel and capillary delineations require a great deal of manual labor and time to acquire, it is relatively easy to acquire multiple unlabeled OCTA images of the same subject’s eye from the same or different scanners [8], [18], [19], [21], [26]. In this work, we consider those repeated scans as paired data. Although there are inherent scanner differences, those repeated scans from the same eye should have similar anatomy but different artifacts and are corrupted by independent noise. When examining such paired scans, we can identify vessels and capillaries from their shared intensity pattern; conversely, inconsistent patterns are usually associated with noise and artifacts. For example, Fig. 2 shows two Optovue scans and one Heidelberg scan from the same eye. The green boxes in the three scans, also shown zoomed up, cover the same region of the macula. Although different noise and artifacts are present, we can readily identify very similar capillary structures in the zoomed-up views; some of these are highlighted for clarity. Although we could not practically require such multiple scans to be available for each future subject, in this paper we show how to take advantage of such paired images, available for many past subjects, to help train a segmentation algorithm that requires only one scan as input and tends to ignore artifacts, noise, and contrast variations.

Fig. 2.

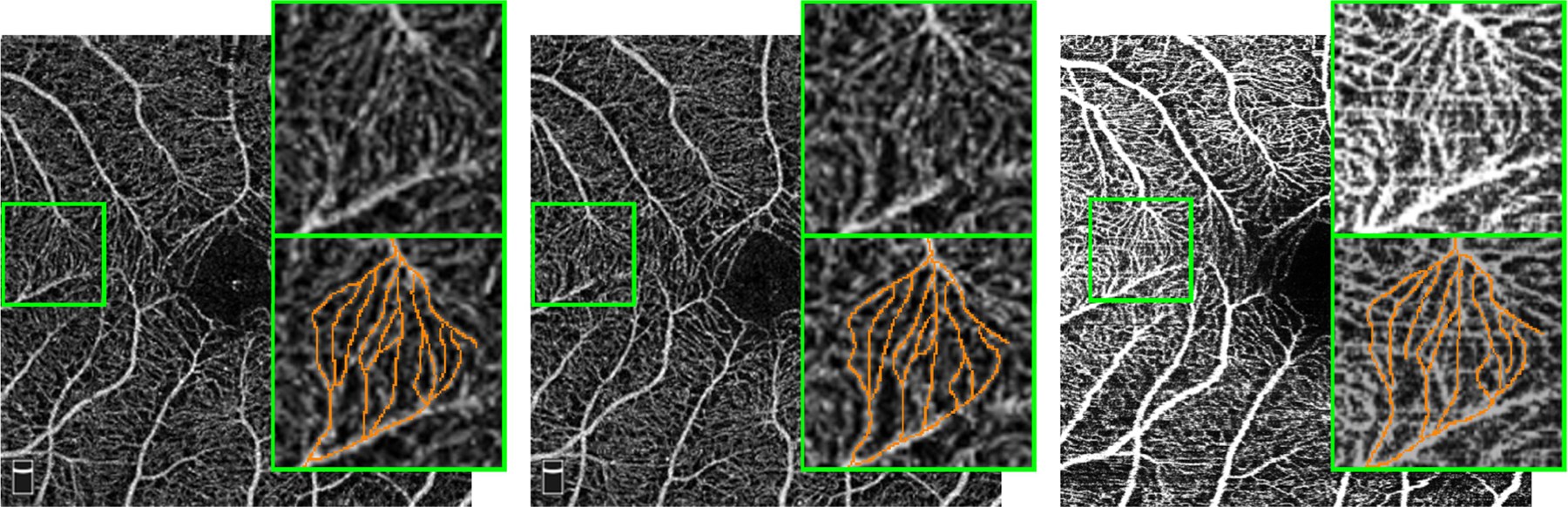
Two Optovue scans (left and middle), and one Heidelberg scan (right) of the same eye are shown. In the upper right corner of each sub-image, we show the zoomed regions highlighted by the green box. A manual tracing for some capillaries are provided in the lower right corner of each image; not every recognizable capillary is highlighted for clarity in the figure. The three scans are not registered.

The proposed method, named Artifacts and Contrast Robust Representation for OCTA Semi-supervised Segmentation (ACRROSS), disentangles the anatomy and contrast in OCTA images for accurate segmentation of vessels and capillaries. ACRROSS is trained using two datasets: one dataset with unlabeled registered paired OCTA images and the other with a very limited set of manual labels. ACRROSS learns to disentangle an OCTA image into separate contrast and anatomy components by identifying shared structures in the paired OCTA images. While learning to do this, it also learns to segment capillaries and vessels from the anatomy component using a limited set of manual delineations. In experiments, we first use two publicly available datasets of OCTA images, ROSE [25] and OCTA-500 [23]; the manual delineations in both datasets focused on large vessels with limited capillary delineations. We show that ACRROSS trained with only patches of manual delinations (total area used was less than a single scan) can achieve comparable or even better accuracy than the comparison methods that trained on the entire dataset. We also built an in-house dataset with capillary level delineations and show quantitatively that detailed capillary segmentation can be achieved without a large amount of manual delineations. Since FAZ segmentation is closely related to the segmentation of capillaries, we also show that based on our segmentation results, a simple post-processing approach can segment the FAZ with close to state-of-the-art performance.

II. Related Work

Several works have explored the use of deep learning methods for OCTA vessel segmentation. A U-net [27] architecture was used by Morgan et al. [28] for vessel and FAZ segmentation in SVP images from two scanners. Mou et al. [22], [29] proposed an attention module for vessel segmentation, and applied it to OCTA images. Pissas et al. [30] proposed an iterative approach for 8 × 8 mm SVP scans. Li et al. [23], [24] and [31] proposed to directly output 2D vessel maps and FAZ segmentations from 3D OCTA images. Hu et al. [32] investigated segmenting 3D vessels from the 3D OCTA volumes; Yu et al. [33] proposed a method for segmenting vessels from 2D OCTA images and estimated the depth information for the segmented vessels to facilitate 3D vessel analysis. All of the previous supervised methods require a significant amount of training data with corresponding manual delineations. More recently, Xu et al. [34] proposed a partially-supervised method that used 3% to 5% of the training data compared with other supervised methods. In contrast, our method needs less than 2% of manually delineated scans used by supervised methods to achieve similar performance. Unlike our previous work [21], which uses a dedicated encoder and decoder structure for each scanner, the majority of the network weights in ACRROSS are shared across different scanners. Thus, ACRROSS requires less computational resources and can be easily extended to multiple scanners without additional computational overhead.

The design of a semi-supervised method usually depends on the availability of weak labels. For brain lesion segmentation, unsupervised image translation between healthy and disease subjects was used [35], [36]. Zhou et al. [37] used disease severity grading to learn lesion attention maps for semi-supervised segmentation. Semi-supervised learning based on disentanglement has been previously used for both classification and segmentation. Robert et al. [38] designed an autoencoder structure with two encoders to separate a class-specific component and a complementary component. The two components were combined by a decoder to reconstruct the unlabeled input image, and classification is learned from the class-specific component. For segmenting cardiac cine magnetic resonance (MR) images, a similar structure was used by Chartsias et al. [39], where the outputs of two encoders are interpreted as spatially and non-spatially dependent components. In both methods, a self-reconstruction loss is used for learning the disentanglement. However, self-reconstruction and segmentation may play contradictory roles in feature extraction [38]. This is crucial for segmentation tasks, because a self-reconstruction loss reinforces the noise and allows artifacts to be learned as part of the anatomy representation. Although our method also reconstructs the encoder’s input image, we avoid this problem by learning the disentanglement from paired images, which have different noise and artifacts.

Several methods for disentangled representation learning use autoencoders [40]. Zhang et al. [41] used the encoder to learn a label-irrelevant spatial component along with a non-spatial embedding code conditioning. Dewey et al. [42] and related works [43], [44] proposed an encoder-decoder network structure for disentangling MR image modality and anatomy. Although they did not explicitly use a conditioning network, the modality vector learned from the encoder feeds into their decoder as a condition, and therefore, their method can be interpreted as a modified conditional variational autoencoder (CVAE). In fact, the two-encoder structure used in Chartsias et al. [39] is also a CVAE, where the spatial component branch serves as the conditioning. ACRROSS is different from the above methods in two important aspects. First, all three methods in [39], [42], and [41] seek to disentangle a subject specific anatomy component that is spatially dependent from a scanner-specific contrast component that is non-spatially dependent. Because of the spatially-varying contrast in OCTA images, we chose to disentangle two spatially dependent components. This allows us to model the contrast and artifacts regionally. Second, in [41] and [42] the anatomical component is the latent representation of the CVAE, which requires sampling during training. On the other hand, we have chosen the anatomical component to be the conditioning. With this choice, we avoid independently sampling the anatomy representation at each pixel location, which produces less noisy anatomy representations and consequently is beneficial for the segmentation task.

III. Method

A. Overview

As shown in Fig. 3(a), our proposed model consists of four networks: an encoder, a decoder, a conditioning network (CN), and a segmenter. The CN and the segmenter branch performs the segmentation. During supervised training, a cross-entropy loss computed between the output of the segmenter and manual delineations can be back-propagated to both the CN and segmenter. However, when the number of training data samples is small, supervised training can lead to unsatisfactory results during test time. This is especially true for OCTA images, where different artifacts and contrast variations in unseen images cannot be fully covered in the training dataset. To address this problem, we introduced two additional networks: an encoder and a decoder. The encoder, decoder, and CN together form a CVAE that uses a second dataset of unlabeled, registered, paired OCTA scans for training. With the additional components, the CN learns to extract a contrast-disentangled anatomy representation for the segmenter to use. As a preview, a test time example result, which uses only the CN and the segmenter to generate, is shown in Figs. 3(b) and 3(c). Methodological details of our approach are provided in the following sections.

Fig. 3.

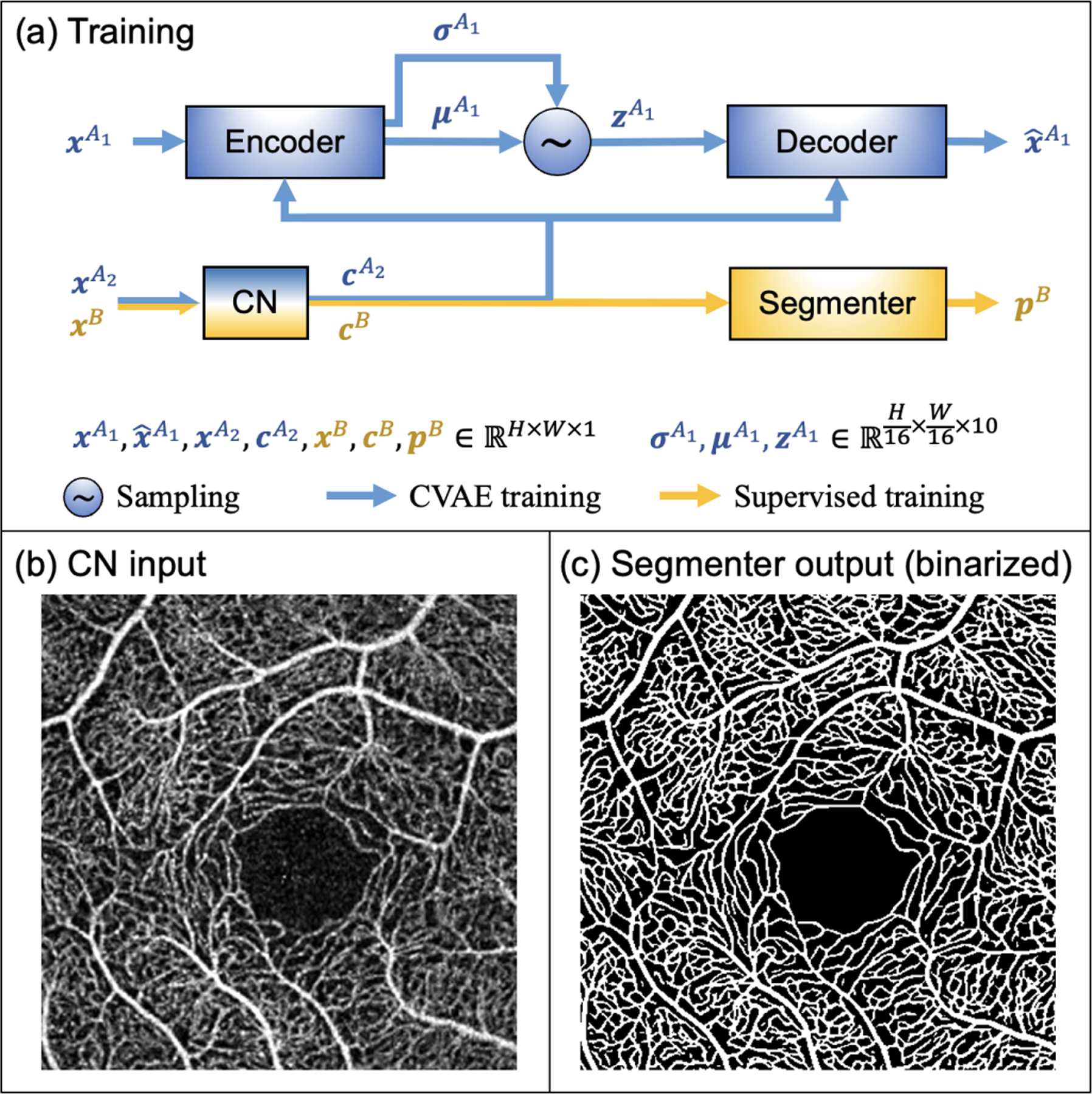
(a) An overview of the training process of the proposed method. The dimension of each variable are provided, with H and W being the height and width of the original scan. The blue and yellow paths indicate CVAE and supervised training flow, respectively, with the CN being shared by both. As a preview, an example of test time input (b) and segmentation result (c) are provided. The model was trained using the XJU-CVAE and the XJU-MD subsets (see Sec. IV for complete details).

B. Conditional Variational Autoencoder

Consider $x^{A_1}$ and $x^{A_2}$ as an unlabeled pair of registered OCTA scans acquired from the same eye. These images could be from the same or different scanners, but to avoid anatomical changes they should be acquired within a few days of each other. The CVAE framework assumes that the encoder’s input x can be reconstructed by the decoder from a latent representation z given the conditioning c. Specifically for ACRROSS, an OCTA scan $x^{A_1}$ is reconstructed from $z^{A_1}$ given the conditioning $c^{A_2}$ (see Fig. 3). The superscript indicates that $z^{A_1}$ is learned from $x^{A_1}$ but $c^{A_2}$ is extracted from its paired scan $x^{A_2}$. In theory, the encoder and the decoder approximate the posterior and likelihood distributions $q\left(z^{A_1}|x^{A_1};c^{A_2}\right)$ and $p\left(x^{A_1}|z^{A_1};c^{A_2}\right)$ with a parametric encoder q_ϕ and a parametric decoder p_θ, respectively. Similar to a variational autoencoder (VAE) [45], a CVAE can be trained using the negative variational lower bound given by

$${ℒ}_{CVA\text{E}}=-E_{q\varphi }\left[\log p_{\theta }\right]+D_{KL}\left(q_{\varphi }\parallel p\left(z\prime \right)\right),$$ (1)

where p(z′) is assumed to be a multivariate Gaussian. The first term in (1) is the expectation of the log posterior, which has a similar effect as a mean squared error loss that encourages reconstruction of $x^{A_1}$. The second term in (1) is the Kullback–Leibler divergence between the two distributions and can be thought of as a regularization term acting on the learned latent representation z.

The architectures of the encoder and decoder are shown in Fig. 4. The encoder with four max-pooling layers compresses $x^{A_1}$ by a factor of 16 in each spatial dimension. The outputs of the encoder are interpreted as the mean ${\mu }^{A_1}$ and standard deviation ${\sigma }^{A_1}$ of a multivariate Gaussian that characterizes the distribution of the latent representation. Samples ($z^{A_1}$ ‘s) of this distribution are generated by following [45] for training the decoder. The number of channels in ${\mu }^{A_1}$ and ${\sigma }^{A_1}$ is a hyper-parameter that determines the compression rate of the encoder-decoder branch. In this work, we use 10 channels, but we found the result to be similar when using between 4 and 32 channels. Accordingly, each 16 × 16 block from the input is represented by a vector of length 10.

Fig. 4.

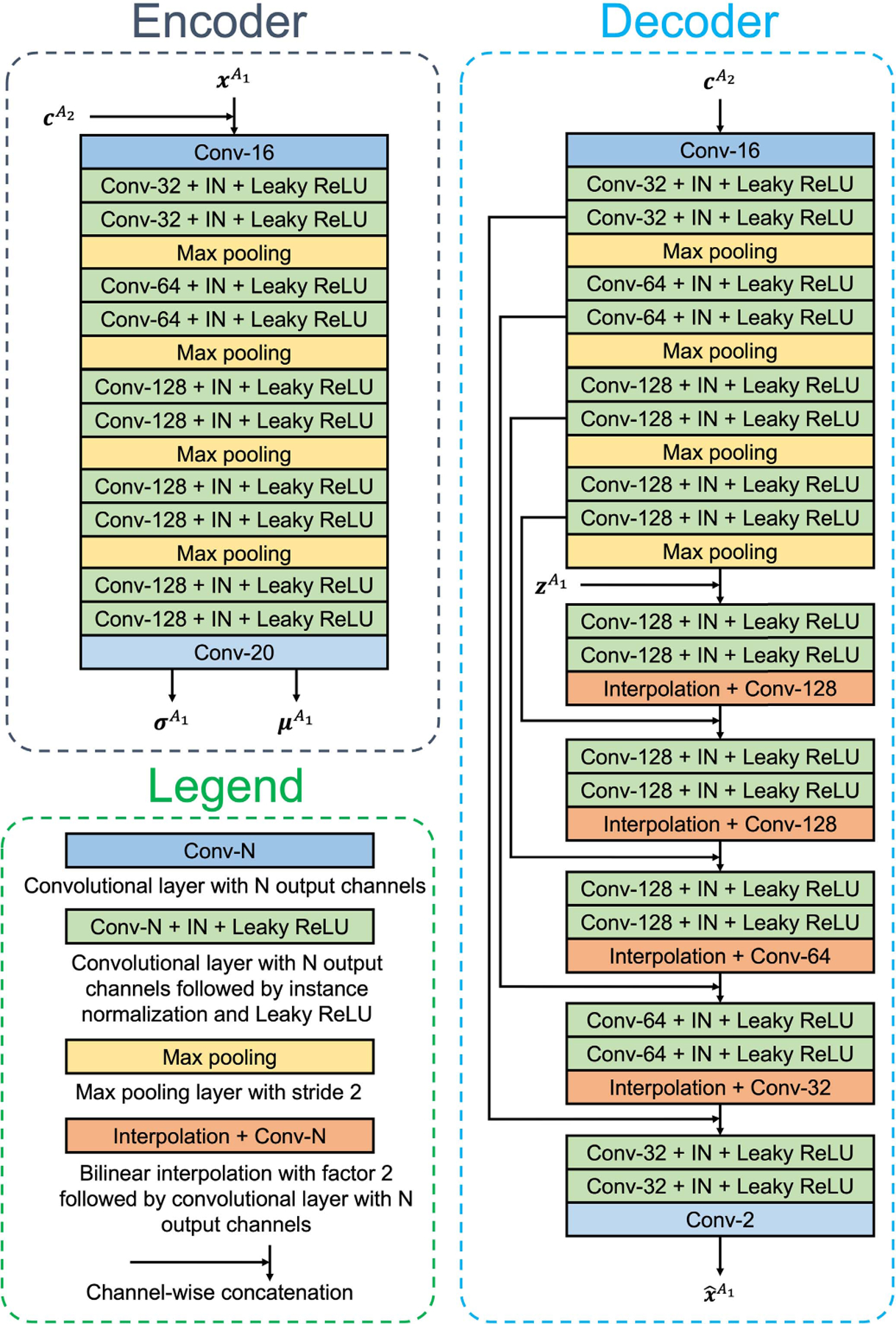
Detailed architecture of the encoder and decoder. All convolutional layers used in this work have a kernel size of 3 × 3 and padding of size one.

C. Anatomy-Contrast Disentanglement

A CVAE is generally considered to be a generative model where diverse samples for a particular class can be generated from the decoder by sampling the learned latent representation and input the samples to the decoder with the class label as conditioning. In contrast, ACRROSS uses a CVAE to learn the disentanglement of an anatomy component and a contrast component from paired scans. For an OCTA image, the anatomy component captures the vessels and capillaries whereas the contrast component captures the representation of the vessels and capillaries that makes those anatomy distinguishable from noise or background. This is achieved by the novel training strategy we adopted: instead of manually assigning a conditioning, ACRROSS uses a feed-forward CN to learn a conditioning from $x^{A_2}$; thus, the decoder uses two sources of information— $z^{A_1}$ from the encoder and $c^{A_2}$ from the CN—to reconstruct $x^{A_1}$ Similar to the common autoencoder structure with a bottleneck, $z^{A_1}$ will be a lossy compressed representation of $x^{A_1}$ given its limited capacity. With the use of $c^{A_2}$, we can guide the encoder to focus on compressing local contrast information.

We designed the conditioning variable $c^{A_2}$ to have the same spatial dimension as $x^{A_1}$. Since $z^{A_1}$ can only encode limited information from $x^{A_1}$, if some of the information is also contained in $c^{A_2}$, then the full capacity of $z^{A_1}$ can be used for information specific to $x^{A_1}$. When we use registered paired OCTA images as input to the encoder and CN, respectively, then this information comprises the local contrast, noise, and artifacts of $x^{A_1}$. The encoder can confidently ignore the vascular structures in producing $z^{A_1}$ because the decoder can expect that information to come from $c^{A_2}$, which has a much larger capacity. Therefore, the encoder and CN learn to cooperate for a better reconstruction of $x^{A_1}$. In particular, the CN learns to extract vessels and capillaries that $x^{A_2}$ shares with $x^{A_1}$ so that the encoder can focus on the local contrast, artifacts, and noise that are only accessible from $x^{A_1}$. Otherwise, the redundant information in $z^{A_1}$ further limits its representation power, which would result in a higher reconstruction loss.

Importantly, we did not design an architecture that would learn the conditioning information from $x^{A_1}$. If we were to try it this way, then the CN and decoder would simply learn an identity mapping to perfectly reconstruct $x^{A_1}$ without needing $z^{A_1}$. Methods with such an alternative design require constraints to achieve disentanglement, e.g., forced binarization for the conditioning [42] or an additional cycle-consistency loss [39].

Once trained, the CN can extract the vascular structures that are shared between $x^{A_1}$ and $x^{A_2}$, but in fact it predicts the intensity patterns from $x^{A_2}$ that are useful to reconstruct $x^{A_1}$ without actually observing $x^{A_1}$. This is beneficial at test time because the CN can remove the contrast, noise, and artifacts from $x^{A_2}$ that are irrelevant for reconstructing $x^{A_1}$ without the need of a paired scan as input to the encoder.

D. Semi-Supervised Segmentation

The representation learned by the CN greatly reduces the contrast variations from OCTA images caused by either the OCTA algorithms or contrast-related artifacts. This allows the use of a segmenter network with just two convolutional layers to segment vessels from the conditioning. For training, we use a dataset of OCTA images with manual delineations. An image x^B goes through the segmentation path (the CN and segmenter) to produce p^B, as shown in Fig. 3(a), and the cross entropy loss ${ℒ}_{CE}$ is computed between p^B and the manual delineation. This supervised training procedure injects our preference into the segmentation model, e.g., the thickness of the vessels to be segmented or the minimum intensity to be considered as foreground. As shown in Sec. IV, different manual delineations lead to different results, but the same CVAE training procedure is used.

During each forward pass, both ${ℒ}_{CVAE}$ and ${ℒ}_{CE}$ are calculated using the two datasets, then the combination of the two losses is back-propagated to update the parameters in all sub-networks. The ${ℒ}_{CVAE}$ has effects on the encoder, decoder, and CN, whereas ${ℒ}_{CE}$ has effects on the segmenter and CN. After training, only the CN and the segmenter—i.e. no paired images—are needed for segmentation of an OCTA image. Unlike other sub-networks in the proposed method, the CN is the most flexible component. Because it is used for generating the conditioning, the only requirement for the CN is to preserve the spatial dimension of the input. Therefore, any previously proposed dense prediction network can be used for the CN. In our experiments, we report the results of two versions of the proposed method using two previously proposed network structures for our CN: U-Net [27] and CS-Net [29].

IV. Experiments

A. Datasets

The performance of vessel segmentation was evaluated on two publicly available datasets, OCTA-500 [24] and ROSE [25], both with manual delineation of vessels, and a proprietary dataset, XJU [18]. All training and evaluations were carried out on OCTA scans representing the superficial vascular plexus (SVP). We constructed a subset of unlabeled registered paired OCTA scans from the XJU dataset for CVAE training; this subset is termed XJU-CVAE. Taking advantage of the paired data for reliable delineation of capillaries, we built a subset of manually delineated scans from the XJU dataset; this subset is termed XJU-MD. We also use the manual delineations for FAZ from both the OCTA-500 and the OCTAGON [46] datasets to demonstrate how our trained vessel segmentation model can be used for FAZ segmentation. The details of each dataset are provided below.

1). XJU:

Scans from Angiovue (RTVue XR Avanti, Optovue, Inc. Fremont, CA), Angioplex (Cirrus HD-5000, Zeiss Meditec. Dublin, CA), Triton (Topcon DRI OCT Triton, Topcon, Japan) and Spectralis OCT2 module (Heidelberg Engineering, Germany) were included [18]. Each eye was scanned twice on the Topcon, Zeiss, and Optovue scanners and once on the Heidelberg scanner. For each eye, all seven scans were registered to a designated Optovue scan by a deformable transformation using ANTs [47]. The registered scans were manually reviewed and 138 out of 146 eyes were found to be successfully registered. The 8 failure cases were caused by major artifacts or field of view differences between the scans.

2). XJU-CVAE:

From the 138 successfully registered scans in the XJU dataset, we randomly selected 110 eyes for CVAE training in ACRROSS. Each training sample is a pair of different OCTA images randomly selected from the seven repeats.

3). XJU-MD:

From the remaining 28 successfully registered eyes in the XJU dataset, we randomly selected four eyes (22 scans) for manual delineation. Each scan was divided into patches of size (1/64)^th of the image and a set of such patches were randomly selected for delineation. To improve the delineation quality in regions with noise and artifacts, potential capillaries were verified by comparing with its repeated scans in the same location. All delineations were reviewed by a second person and corrected if necessary. In total 48 patches were delineated (13 Heidelberg, 13 Optovue, 11 Topcon, 11 Zeiss), an example of which can be seen in Fig. 10. The total area of these 48 patches is approximately equal to 3/4 the area of a single scan. Despite the relative small total area finally delineated, the overall task–including initial labeling, verification with repeat scans, and independent review–was extraordinarily time-consuming; ultimately taking eight weeks to complete with rater fatigue also being a handicap.

Fig. 10.

Examples of applying our model (trained on XJU-MD) on scans from XJU-MD, OCTA-500, and ROSE-1. The supervised training does not use any examples from OCTA-500 or ROSE-1. Our trained model can produce detailed capillary segmentation for scans from OCTA-500 and ROSE-1 that is previously not available in the OCTA-500 and ROSE-1 manual delineations.

4). OCTA-500:

All 200 subjects (No. 10301—No. 10500) with 3 mm × 3 mm SVP scans from the OCTA-500 dataset [24] are included in our experiments. The data were collected using a commercial 70 kHz SD-OCT (RTVue-XR, Optovue, CA). We use the maximum projection map between internal limiting membrane (ILM) and outer plexiform layer (OPL) because it was used for vessel delineations. We followed the same training, validation, and testing split as in [24] (No. 10301—10440 for training; No. 10441—10450 for validation; and No. 10451—10500 for testing). For each scan, a manual delineation of FAZ is also provided.

5). ROSE-1:

All 39 scans in the ROSE-1 subset of the ROSE dataset [25] are included in our experiments. For each subject, we used the 3 mm × 3 mm SVP scans and their corresponding manual delineations. The ROSE-2 subset is not included, because it only contains centerline-level annotations of vessels. All 39 scans were acquired on a RTVue XR Avanti SD-OCT system (Optovue, USA). As specified in [25], 30 selected scans were used for training and 9 were used for testing.

6). OCTAGON:

OCTAGON [46] is a publicly available dataset for FAZ segmentation; it includes 55 SVP 3 mm × 3 mm scans acquired from a Topcon device (DRI OCT Triton) and their manual FAZ segmentations.

B. Illustration of Disentanglement

In Fig. 5, we show some additional results for the same eye as in Fig. 3 produced by ACRROSS. In addition to the Optovue scan from Fig. 3, we also show its registered paired Heidelberg scan. To produce each contrast-removed conditioning result (c^B in Fig. 3(a)), an original scan is provided as input (x^B in Fig. 3(a)) to the CN. With the contrast largely removed, we can easily see the capillary structure in this intermediate result. The segmentation result for each scan is produced from the conditioning using the segmenter followed by binarization at a 0.5 threshold. Because the CN is robust to contrast variations, the loss-of-signal-strength artifact that can be seen in the Heidelberg scan has minimum impact on the conditioning. This allows us to observe a very similar vascular pattern in the segmentation results even in the artifact-affected region.

Fig. 5.

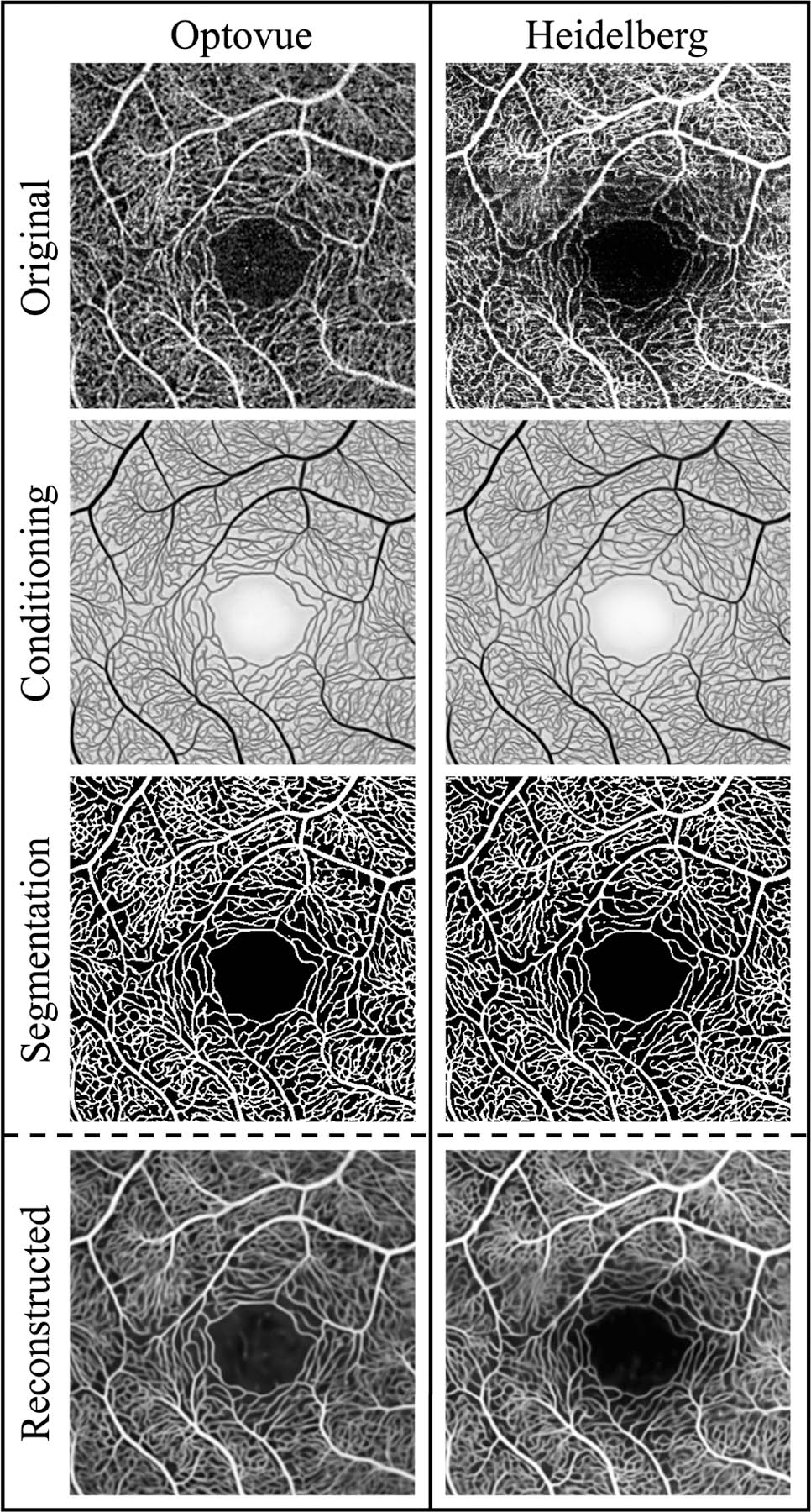
An example of the inputs and outputs from ACRROSS. The two columns represent the processing of two different scanner manufacturers: Optovue and Heidelberg. From top to bottom, the rows are the original input OCTA images, the conditioning, the corresponding segmentation, and the reconstruction of the input. The two scans are registered. The XJU-MD subset is used for supervised training.

Although typically not used after training is complete, it is instructive to see a reconstructed image (${\widehat{x}}^{A_1}$ in Fig. 3(a)) from a registered paired set of scans. The reconstructed image shown in the bottom left of Fig. 5 is generated using the Optovue scan as $x^{A_1}$ and the Heidelberg scan as $x^{A_2}$ (i.e. the contrast component from the Optovue scan and the anatomy component from the Heidelberg scan.). The reconstructed image shown in the bottom right of Fig. 5 uses the opposite assignment. It is clear from these two reconstructed images that artifacts are encoded in the variable $z^{A_1}$, which comes from the image $x^{A_1}$. This visualization confirms the effect of disentanglement and reinforces our contention that ACRROSS segmentation results are not greatly affected by artifacts.

C. Metrics for Vessel Segmentation

To evaluate the performance of vessel segmentation algorithms, the following metrics are calculated between the manual delineation and the segmentation results produced by each algorithm:

• Area under the ROC curve: AUC;

• Accuracy: ACC = (TP + TN)/(TP + TN + FP + FN);

• Kappa score: KAPPA = (ACC − p_e)/(1 − p_e);

• False discovery rate: FDR = FP/(FP + TP);

• G-mean score: $GMEAN=\sqrt{sensitivity\times sensitivity}$;

• Dice coefficient: DSC = 2 × TP/(FP + FN + 2 × TP),

where TP, TN, FP, FN represent the True Positives, True Negatives, False Positives, and False Negatives, respectively, and p_e = ((TP+FN)(TP+FP)+(TN+FP)(TN+FN))/(TP+TN + FP + FN)². Sensitivity and specificity are computed as TP/(TP + FN) and TN/(TN + FP), respectively. These metrics are also reported in [25]. All the p-values reported were computed using a paired, two-sided Wilcoxon signed rank test (null hypothesis: the difference between paired values comes from a distribution with zero median).

D. Implementation Details

Our model was implemented using Pytorch, and all networks were trained using the Adam optimizer with a learning rate of 4 × 10⁻⁴ and weight decay of 1 × 10⁻⁶. When there is a corresponding validation dataset available, the training terminates when the validation loss stops decreasing; otherwise the number of training epochs was determined empirically. Specifically, the OCTA-500 dataset has its own validation dataset, and for our semi-supervised ROSE-1 experiment the unused images serve as the validation dataset. Our other experiments use an empirically determined number of training epochs. During CVAE training, the CN may take scans from different manufacturers as input. To handle the contrast difference, the inputs of CN are processed by four convolutional layers (with LeakyReLU activation), which learn a different set of weights for each scanner. It has been shown previously that such dedicated sub-networks can improve network generalizability [50]. The source code for this work is currently proprietary while under review for potential commercialization.

In all experiments, ACRROSS used the XJU-CVAE for CVAE training (batch size of 8) and a dataset with manual delineations (OCTA-500, ROSE-1, or XJU-MD) for supervised training (batch size of 2). Because each loss term is calculated separately before the combined loss is back-propagated, scanners used in CVAE training are not required to be used for supervised training. For example, ACRROSS can be trained using XJU-CVAE with scans from four scanners together with OCTA-500, which only has Optovue scans. For each of our three datasets, the test time procedure for new unseen images is the same. This procedure is depicted as the yellow portion of our network in Fig. 3(a). First, we pass the unseen image, x^B, through the condition network CN to generate the conditioning, c^B. The conditioning is then passed to the segmentation network to generate, p^B, which is then binarized to generate a segmentation (threshold at 0.5 intensity value). All the comparison methods were concatenated with the same segmenter network as in ACRROSS and trained using the same settings except for those methods that cannot use the unlabeled XJU-CVAE subset.

E. Supervised Vessel Segmentation on OCTA-500

We first used all 140 scans from the OCTA-500 training set to test the performance of the proposed method in a fully supervised setting. We provided two versions of ACRROSS using different network architectures as the conditioning network: ACRROSS(CS-Net) used CS-Net and ACRROSS (U-net) used U-net. For the comparison methods, we included U-net [27], nnU-Net [49], R2U-Net [48] and CS-Net [29]. For training U-net, R2U-Net, and CS-Net, we used the same hyper-parameters as our methods for fair comparison. nnU-Net was originally designed for 3D images with the ability to automatically determine its hyper-parameters, we followed an example provided by the authors to make it work for 2D images. The results on the 50 test scans are summarized in Table I. Our methods (ACRROSS(CS-Net) and ACRROSS (U-net)) produce comparable or better results when measured by AUC, and ACRROSS(U-net) is significantly better than all comparison methods in terms of DSC (p-value < 0.001).

TABLE I.

Comparison of the Vessel Segmentation Results for 50 Superficial Vascular Plexus en face Test Scans (Mean ± Std. Dev.) From the octa-500 Dataset, Using All Training Images (140 Scans) for Supervised Training. Bold Numbers Indicate the Best Mean Value

Method	AUC	ACC	GMEAN	KAPPA	DSC	FDR
R2U-Net [48]	0.994 ± 0.005	0.985 ± 0.003	0.939 ± 0.020	0.876 ± 0.027	0.884 ± 0.026	0.117 ± 0.059
U-net [27]	0.992 ± 0.006	0.988 ± 0.002	0.944 ± 0.016	0.902 ± 0.021	0.909 ± 0.020	0.078 ± 0.029
nnU-Net [49]	0.980 ± 0.009	0.987 ± 0.002	0.940 ± 0.014	0.896 ± 0.021	0.902 ± 0.020	0.082 ± 0.029
CS-Net [29]	0.995 ± 0.003	0.987 ± 0.002	0.941 ± 0.015	0.892 ± 0.021	0.900 ± 0.020	0.092 ± 0.033
ACRROSS(CS-Net)	0.995 ± 0.004	0.986 ± 0.003	0.940 ± 0.018	0.887 ± 0.022	0.895 ± 0.021	0.096 ± 0.044
ACRROSS(U-net)	0.997 ± 0.003	0.988 ± 0.003	0.944 ± 0.018	0.906 ± 0.022	0.912 ± 0.021	0.069 ± 0.035

F. Semi-Supervised Vessel Segmentation on OCTA-500

To test the semi-supervised setting when there are fewer training samples, we decreased the number of training data used for supervised training from N = 140 subjects to N = 20 and N = 4 in two additional experiments. Further reduction in the number of training samples may cause a high variance in repeated experiments where training samples with different quality and variety are selected. To address this problem, we divided the total area of each scan into 8×8 square patches and treated one patch instead of one scan as a training sample. This is implemented by only computing the cross-entropy loss inside the selected patches. However, we still input the entire image into the network to make sure the normalization layers work properly. We first randomly select 4 scans, and then 32, 16, and 8 patches are randomly selected from each of the 4 scan as training data. As a result, the total number of patches used in this three additional experiments are P = 128, P = 64, and P = 32, equivalent to N = 2, N = 1, and N = 0.5 subjects in terms of total area that is used. For example, the total area for P = 32 is (32/(8 × 8)) subjects, which is equivalent to half a scan.

To further reduce the randomness in the result, each experiment was run three times with different random seeds and the same set of random seeds were used for all methods. We evaluated the performance of U-net [27], CS-Net [29], and ACRROSS(U-net) on the 50 test scans. The results of the three repeats are combined (50 × 3 data points) and reported in Fig. 6 (a) and (b). We can see that for AUC and DSC, ACRROSS consistently produces better results across all sets of experiments with different amount of training data. This can also be seen from the example shown in Fig. 7, where only large vessels were segmented because the manual delineations for OCTA-500 do not include capillaries. When measured by AUC, the proposed method ACRROSS(U-net) trained with 32 patches produces comparable results to the U-net trained with 20 subjects (p-value = 0.995) and CS-Net trained with 140 subjects (p-value = 0.324). It is significantly better than CS-Net trained with 20 subjects (p-value < 0.001). We also observed that for all methods, N = 4 underperforms P = 128, although the latter case uses less area during training. This may be analogous to training using 2D slices outperforming training using 3D volumes, when the number of subjects is small [51].

Fig. 6.

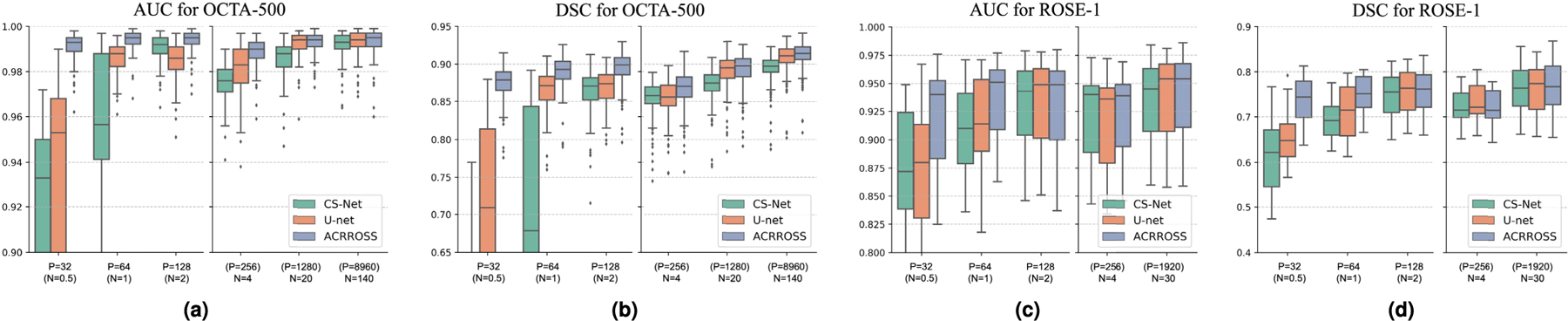
The box plots of the area under the ROC curve (AUC) and Dice coefficient (DSC) for the segmentation results produced by CS-Net [29], U-net [27], and ACRROSS(U-net) when trained using different amounts of training data. The amount of training data used is indicated on the horizontal axes. Each plot is divided into two parts, with the left part shows the results when trained using patches as training samples and the right part shows the results when trained using scans as training samples. The total area used for training in P = 32, P = 64, and P = 128 are equal to N = 0.5, N = 1, and N = 2 subjects, respectively. For training with scans, the equivalent number of patches are also shown. The results for the OCTA-500 dataset are shown in (a) and (b) and the results for the ROSE-1 dataset are shown in (c) and (d).

Fig. 7.

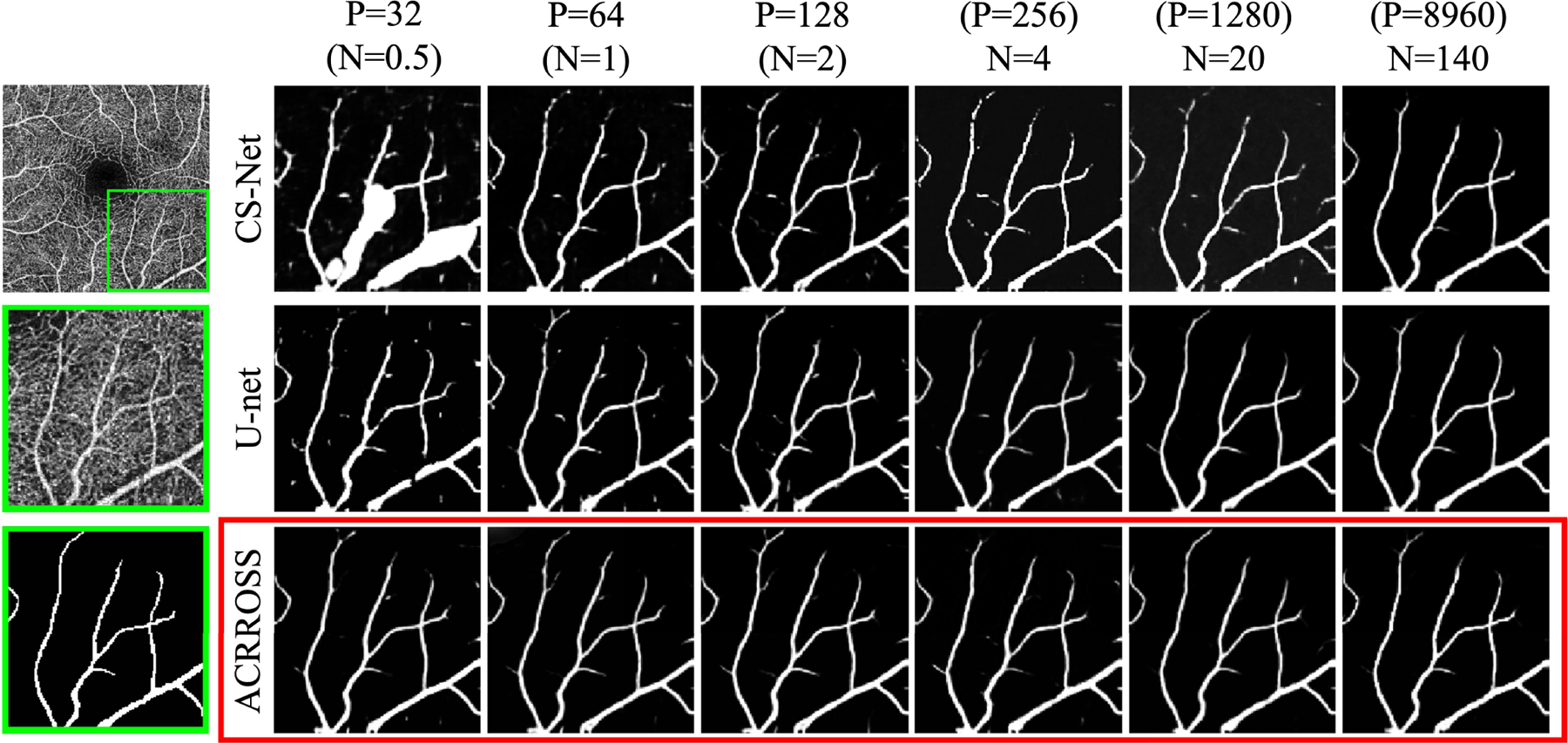
Examples of test result from the OCTA-500 dataset when training with a different number of samples. Leftmost column shows the original image (top) and the zoomed-in region (middle), along with its corresponding manual delineation (bottom). The predicted vessel probability maps of CS-Net [29] (row 1), U-net [27] (row 2), and ACRROSS(U-net) (row 3) are shown in the right columns. See the text for an explanation of P and N.

G. Ablation Study

We conducted ablation studies on the OCTA-500 dataset. We first trained ACRROSS without the Kullback-Leibler divergence loss in Eq. 1. The removal of this regularization reduced the CVAE to an autoencoder structure (AE). We also investigate the impact of using dedicated sub-networks as input layers for CN (see Sec. IV-D). In Fig. 8, we compared the DSC of these two methods against the original ACRROSS, where we denote the version without the use of dedicated sub-networks as “w/o DA”. In all experiments, the models were trained in the same way as described in Sec. IV-F. The results show that both the Kullback-Leibler divergence loss in Eq. 1 and the dedicated sub-networks improve the segmentation results, especially in the semi-supervised setting.

Fig. 8.

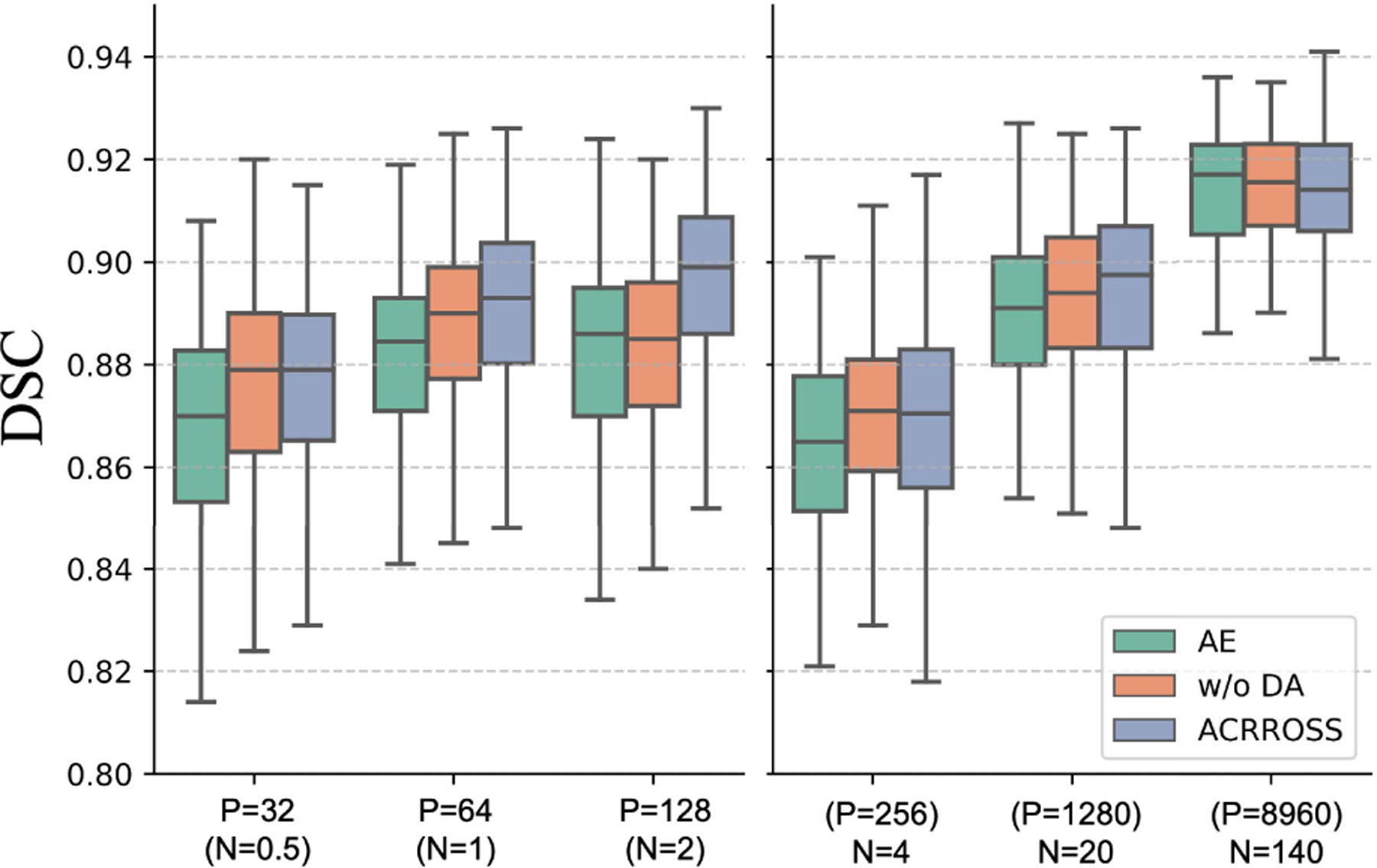
The results of the ablation study using OCTA-500 dataset.

H. Reproducibility Test

We test the reproducibility of ACRROSS under different contrasts in supervised and semi-supervised settings. The training follows the strategy described in Sec. IV-F. The trained models were then applied to the XJU-MD dataset, in which seven repeated scans from four scanners were captured for each eye (see Sec. IV-A). Because all manually delineated scans in the OCTA-500 dataset come from Optovue scanners, we separately compared the segmentation results between the two Optovue scans (i.e. intra-Optovue) and the segmentation results between the first Optovue scan and other contrast scans (i.e. inter-Optovue), which include scans from Heidelberg, Topcon and Zeiss. We calculated the DSC and reported the averaged numbers in Fig. 9. The results from U-net and CS-Net were also included for reference. Since all the scans were registered, if the segmentations are consistent we would anticipate a higher DSC; which means better reproducibility of the algorithm across the various scanners. It can be seen from Fig. 9 that the intra-Optovue experiments generally have a better consistency compared with the inter-Optovue experiments. This is expected because supervised training only include Optovue scans. For CS-Net and U-Net, we observed decreasing consistency—lower DSC scores—of their results as we reduce the amount of training data. In contrast, the results produced by ACRROSS are not affected by the amount of supervised training data.

Fig. 9.

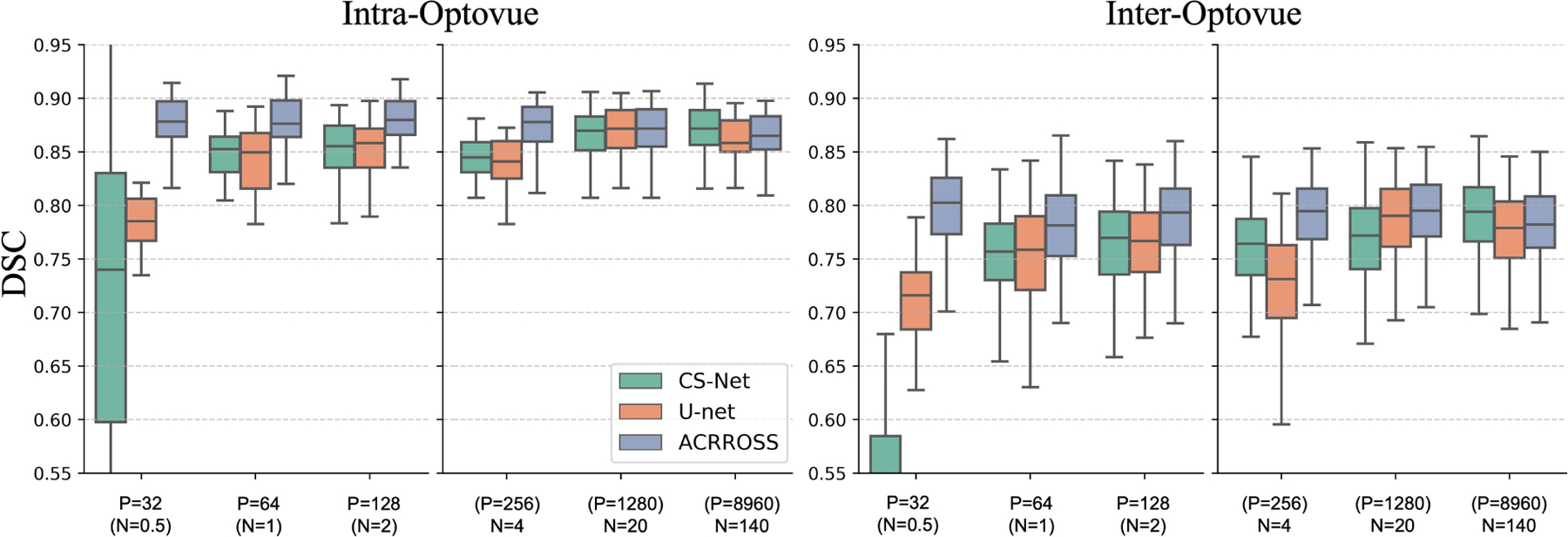
The results of the reproducibility test for CS-Net, U-net, and ACRROSS when trained with different amounts of training data from the OCTA-500 dataset. The DSC between the two Optovue scans are shown on the left (intra-Optovue) and the DSC between the first Optovue scan and scans from other scanners are shown on the right (inter-Optovue).

I. Supervised Vessel Segmentation on ROSE-1

The ROSE-1 subset provides delineations for large vessels as well as some capillaries. We used the provided training and testing split where all 30 training samples in the dataset were used for supervised training and test results were computed on the 9 held-out scans. We observe that our method produces comparable or better results in terms of AUC (see Table II) and, when measured by the DSC, ACRROSS(U-net) results are significantly better than all comparison methods (p-value < 0.005).

TABLE II.

Comparison of the Vessel Segmentation Results for Superficial Vascular Plexus en face Scans (Mean ± Std. Dev.), Using All Thirty Scans From rose-1 Training Set for Supervised Training. Bold Numbers Indicate the Best Mean Value

Method	AUC	ACC	GMEAN	KAPPA	DSC	FDR
R2U-Net [48]	0.931 ± 0.038	0.917 ± 0.026	0.821 ± 0.062	0.708 ± 0.069	0.757 ± 0.054	0.158 ± 0.042
U-net [27]	0.938 ± 0.037	0.922 ± 0.025	0.834 ± 0.061	0.727 ± 0.067	0.773 ± 0.052	0.147 ± 0.042
nnU-Net [49]	0.935 ± 0.040	0.924 ± 0.026	0.836 ± 0.056	0.734 ± 0.069	0.779 ± 0.054	0.141 ± 0.034
CS-Net [29]	0.932 ± 0.037	0.920 ± 0.027	0.832 ± 0.053	0.724 ± 0.069	0.771 ± 0.052	0.155 ± 0.023
OCTA-Net [25]	0.944 ± 0.031	0.922 ± 0.027	0.828 ± 0.048	0.726 ± 0.067	0.772 ± 0.051	0.142 ± 0.023
ACRROSS(CS-Net)	0.937 ± 0.037	0.921 ± 0.026	0.830 ± 0.062	0.721 ± 0.069	0.768 ± 0.055	0.151 ± 0.039
ACRROSS(U-net)	0.945 ± 0.033	0.924 ± 0.026	0.852 ± 0.053	0.743 ± 0.067	0.788 ± 0.051	0.165 ± 0.030

J. Semi-Supervised Vessel Segmentation on ROSE-1

To test the semi-supervised setting where there are insufficient training samples, we randomly selected 4 subjects for training and, to further reduce the training data, we used the same patch sampling technique as in our OCTA-500 experiments. Specifically, 4 subjects were randomly selected and then a total of P = 32, P = 64, and P = 128 patches were randomly selected from the 4 subjects (8, 16, and 32 patches from each) so that the total areas used in training are equivalent to N = 0.5, N = 1, and N = 2 subjects. The performances were evaluated on the same 9 held-out scans. We compared with the results from U-net and CS-Net that were trained under the same setting. Each method was trained three times with different random seeds and the same set of random seeds were used for all methods. The results of the three repeats were combined (9 × 3 data points) and averaged performances were reported in Fig. 6 (c) and (d). In addition, we compared with three semi-supervised methods in Table III, including: 1) Mean teacher (MT), a consistency-based semi-supervised learning approach [52] modified for the segmentation task [34]; 2) MixMatch, a data augmentation based semi-supervised method [53]; and 3) PSL, a recently proposed patch-based semi-supervised method that combined MixMatch and active learning [34]. These results were originally reported in [34]. For each method, the area of manually delineated data used for training relative to the total area of all scans in the training dataset was also reported in Table III. When using 3.3% of the manual delineation, our method outperformed MT [52] and MixMatch [53] and was comparable to PSL [34]. The minimum amount of training data PSL tested on was 3.3%, however, ACRROSS achieves comparable results with only 1.7% of the training data and without involving the iterative training and labeling process in PSL.

TABLE III.

Comparison of Semi-Supervised Vessel Segmentation Results for ROSE-1 Dataset

Method	Training data %	ACC	DSC
U-net [27]	1.7%	0.877	0.660
CS-Net [29]	1.7%	0.818	0.616
U-net [27]	3.3%	0.891	0.712
CS-Net [29]	3.3%	0.883	0.695
MT [52]	3.3%	0.883	0.666
MixMatch [53]	3.3%	0.908	0.730
PSL [34]	3.3%	0.912	0.748
ACRROSS	1.7%	0.911	0.736
ACRROSS	3.3%	0.910	0.749

TABLE IV.

Comparison of the Mean Jaccard Indexes for 3 mm × 3 mm SVP Scans (Mean ± Std. Dev.). the Previous Methods Have Not Reported Their Standard Deviations. Bold Numbers Indicate the Best Mean Value in That Row

	Díaz et al [46]	Lu et al. [54]	Ours
Healthy	0.82	0.87	0.83 ± 0.07
Diabetic	0.83	0.82	0.85 ± 0.08

K. Semi-Supervised Vessel Segmentation on XJU-MD

Although ROSE-1 has 39 subjects with manual delineation, in many cases the delineation does not align well with the true capillaries, as shown in Figs. 1 and 10. Our experiments using the OCTA-500 and ROSE-1 datasets show that high accuracy results can be achieved with the proposed method using very few manual delineations for training. For accurate segmentation of OCTA images at the capillary level, the proposed method was trained on an in-house dataset with manual delineations (XJU-MD).

Given the limited number of manually labeled patches (48 patches), we used 47 patches (73.4% the area of one scan) for supervised training. We provide the qualitative result of the remaining patch in Fig. 10. To avoid potential data leakage issue, none of the other patches from this eye were used for training. Since XJU-MD contains scans from Heidelberg, Optovue, Topcon, and Zeiss, we were also able to apply the trained model on scans from both the OCTA-500 and ROSE-1 datasets without using any scans or manual delineations from those datasets during training. Qualitative results on scans from OCTA-500 and XJU-MD are shown in the two additional rows in Fig. 10. Despite the site differences between the training (XJU-MD) and testing (OCTA-500 and ROSE-1) data, ACRROSS is able to provide detailed capillary segmentation that is previously not available in the manual delineation for OCTA-500 and ROSE-1.

L. FAZ Segmentation

The FAZ is the avascular region around the fovea. If the capillaries are accurately detected, a simple post-processing algorithms can be used to provide an accurate segmentation of the FAZ. Accordingly, we applied a morphological closing operation to our vessel segmentation result and found the FAZ as the largest connected component in the background (see Fig. 11). We compared our FAZ segmentation results to two FAZ segmentation methods [46], [54]. Despite the simplicity of our post-processing steps, we achieved similar results in terms of Jaccard Index (see Table IV). The OCTA-500 dataset also contains manual delineations of the FAZ that we could compare to. Our post-processing based FAZ segmentation has a mean DSC of 0.954 ± 0.025 and a Jaccard Index of 0.912 ± 0.044, which is close to the performance of several supervised trained deep learning methods reported in [24]. Note that our training used the manually delineated patches from the XJU-MD, without any examples or FAZ masks from OCTAGON or OCTA-500. This result suggests that our vessel segmentation model can accurately detect the capillaries around the FAZ. We note that the current post-processing method is not suitable for many disease cases as non-perfusion areas can be falsely detected as the FAZ by our use of the largest connected component. However, it demonstrates the potential for achieving accurate FAZ segmentation in healthy controls without the need of extra manual delineations of the FAZ for supervised training.

Fig. 11.

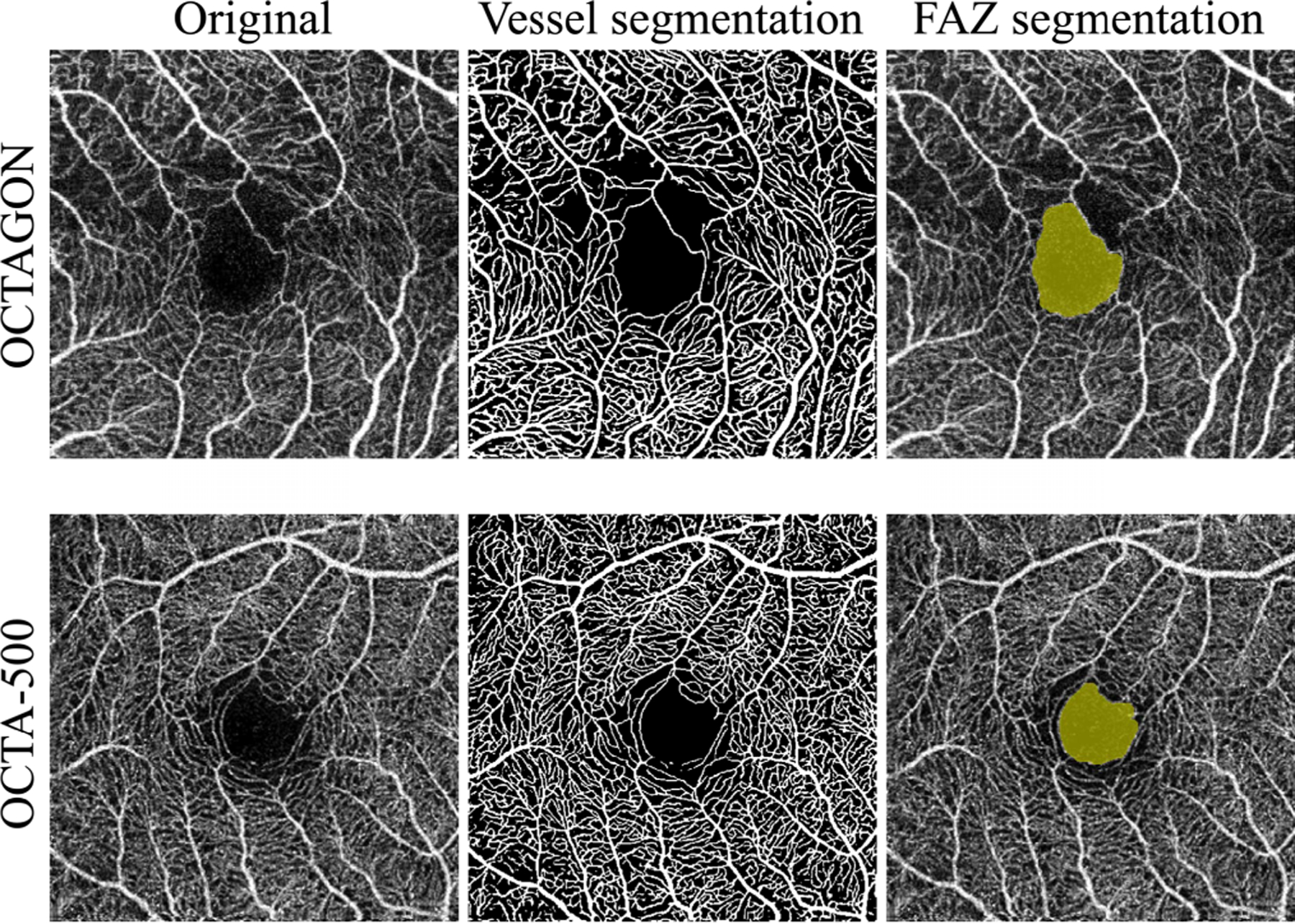
Examples of FAZ segmentations for a Topcon scan from OCTAGON dataset [46] and an Optovue scan from OCTA-500 dataset [24]. The corresponding vessel segmentations and FAZ segmentations are shown in the middle and right column.

V. Discussion and Conclusion

We proposed a deep network architecture called ACRROSS for disentangling local contrast and vascular structures from en face OCTA images so that retinal vessel and capillary segmentation can be learned with limited manual delineations.

ACRROSS is closely related to our previously reported method [21] called VICCE. The CVAE training in ACRROSS can be considered as the cross-scanner synthesis in VICCE but applied to the CN and decoder. Also, both methods can be interpreted as special cases of unsupervised representation learning [55] where similar anatomy representations are extracted from the paired scans. Without the negative samples that are commonly used in unsupervised representation learning, VICCE forces the representation learned from one scan to be able to synthesize its paired scan in order to avoid the model collapse problem. This, however, implicitly assumes that the underlying anatomical information is identical in both scans, which is generally not true since there are inherent hardware and software differences between different scanners. Alternatively, ACRROSS uses the extra input (z) during CVAE training to encode the scan-specific information, which includes the scan-specific anatomy. For example, a layer segmentation error can cause more vessels to be included in the SVP projection map, but this will not affect the segmentation result because those extra vessels are considered scan-specific and encoded in z. In contrast, scanner-specific anatomy is encoded in c, because it is shared by repeated scans from the same scanner.

Generally, supervised training with diverse data is a preferred way to learn the variability in a real data distribution. By learning the disentanglement from the unlabeled data, ACRROSS reduces the requirement of diverse training samples in labeled data. In particular, we found when using the OCTA-500 dataset that training using 128 patches selected from 4 scans (with 32 patches per scan) is comparable to using 128 patches selected from 32 scans (with 4 patches per scan). The learned disentanglement also shows the potential for transferring the knowledge of manual delineations from one dataset to another. Our method trained using the OCTA-500 dataset and the XJU-CVAE subset can segment Topcon scans from the OCTAGON dataset without using any manual delineations from Topcon scans. Notice that this is different from the concept of domain adaption because the CVAE training uses unlabeled Topcon scans to learn the disentangled representation.

Despite these advantages, ACRROSS and similar disentangled representation learning methods are limited to segmentation tasks where all structures are labeled. Otherwise, extra manual delineations are needed to separate the labeled structures from the unlabeled structures. Essentially, the labeled and unlabeled structures determined by the manual delineation become entangled components in the conditioning. In such tasks [39], the segmentation cannot take full advantage of the disentangling. Another limitation of our method is the over-segmentation problem, in which some noise is falsely recognized as capillaries. This is observed when applying our model trained on healthy subjects to disease cases. This phenomenon is related to the artifact-affected scans in the XJU-CVAE dataset. As paired scans are unlikely to be affected by the same imaging artifact, the CVAE training allows artifacts like loss-of-signal-strength to be disentangled from the anatomy representation and recover the capillaries in the affected area. This is undesirable, however, when the subject experiences a true loss of capillaries. Since the training dataset only consists of healthy subjects, ACRROSS may interpret missing capillaries in disease cases as an artifact. This problem can likely be solved by including paired disease cases in the CVAE training or excluding regions affected by artifacts in healthy subjects, though further investigation is needed.

Our experiments are limited to 3 mm × 3 mm SVP scans because we find it difficult to acquire consistent and reliable manual segmentations for the DVP; also 3D OCTA data with manual delineations are currently unavailable. In practice, acquiring repeated scans from one scanner is more common than repeat scans from different scanners. Therefore, we experimented with training ACRROSS using only Optovue scans. In this case, ACRROSS still outperforms the comparison methods, but including scans from another scanner can significantly improve the results. Whether the inclusion of multiple scanners helps disentangled representation learning or is simply a result of the fact that more scans prevent over-fitting is a subject for future research.