Elucidating the Mechanisms of Dynamic and Robust Control of the Liver Homeostatic Renewal Process: Cell Network Modeling and Analysis

Abstract

Recent experimental investigations of liver homeostatic renewal have identified high replication capacity hepatocyte populations as the primary maintainers of liver mass. However, the molecular and cellular processes controlling liver homeostatic renewal remain unknown. To address this problem, we developed and analyzed a mathematical model describing cellular network interactions underlying liver homeostatic renewal. Model simulation results demonstrate that without feedback control, basic homeostatic renewal is not robust to disruptions, leading to tissue loss under persistent/repetitive insults. Consequently, we extended our basic model to incorporate putative regulatory interactions and investigated how such interactions may confer robustness on the homeostatic renewal process. We utilized a Design of Experiments approach to identify the combination of feedback interactions that yields a cell network model of homeostatic renewal capable of maintaining liver mass robustly during persistent/repetitive injury. Simulations of this robust model indicate that repeated injury destabilizes liver homeostasis within several months, which differs from epidemiological observations of a much slower decay of liver function occurring over several years. To address this discrepancy, we extended the model to include feedback control by liver nonparenchymal cells. Simulations and analysis of the final multicellular feedback control network suggest that achieving robust liver homeostatic renewal requires intrinsic stability in a hepatocellular network combined with feedback control by nonparenchymal cells.

Introduction

Mammalian tissue maintenance is accomplished through a program of homeostatic renewal involving adult cells, stem cells, and subpopulations of cells that display characteristics of both stem and adult cells, so-called “stem-cell-like” cells, that are becoming increasingly recognized for their importance in homeostatic renewal. While all tissues share common renewal mechanisms, certain tissues, such as the intestinal epithelium, have higher turnover rates (∼5 days), while other tissues such as intercostal skeletal muscle turn over at a much slower rate (∼30 years), with most of this turnover occurring through homeostatic renewal.¹ In multiple organs, the cell types, signaling pathways, and gene regulatory networks contributing to homeostatic renewal have been fully characterized (e.g., intestinal epithelium;² colonic crypt;³ muscle;⁴ pancreatic islets;⁵ and lung alveoli⁶). In the case of the liver, the components of the network involved in the renewal process were largely unknown until recent experimental studies began to shed light on the abundance of cell types that underlie homeostatic maintenance of liver tissue.

Multiple lines of research have identified diverse populations that appear to participate in liver homeostatic renewal. How they work together to maintain liver cell populations, however, remains incompletely understood. A brief summary of the current understanding of liver homeostatic renewal based on recent research follows. Recently, researchers have shown that precursor cells located near the central vein (Axin2+ “stem-cell-like” cells) and mature hepatocytes located in the remainder of the parenchyma (Axin2– hepatocytes) continuously turn over in the liver during homeostatic renewal.⁷ Additionally, a population of precursor cells (Sox9 expressing “hybrid hepatocytes”) can replenish liver tissue following mild chronic damage.⁸ Another population of hepatocytes (Tert expressing cells) are distributed throughout liver tissue and can also populate a significant fraction of liver tissue over time.⁹ Still another population of biliary originated precursor cells can repopulate liver tissue following induced hepatocyte senescence, potentially mimicking a homeostatic renewal process.¹⁰ Whether (and to what extent) stem cells participate in the homeostatic renewal of hepatocytes in the liver remains an open question.¹¹ Taken together, these results suggest a homeostatic renewal scheme in which a fraction of highly self-renewing hepatocytes (SR_high) that may have precursor-like properties give rise to the majority of lower-rate self-renewing hepatocytes (SR_low) to replenish the tissue continually, thus contributing to the homeostatic maintenance of liver mass and function (Figure 1A).

Figure 1.

Homeostatic renewal model. (A) Model schematic showing two populations of hepatocytes: SR_high and SR_low. Each population can replicate, or die, at distinct specified rates, and while SR_high cells can transition to SR_low cells, the reverse cannot occur. (B) Phase plane representation of steady-state behavior of the model showing multiple steady states but no stable attractor. Blue arrows represent the sign of the local derivative in the y-direction; the local derivative in the x-direction is zero everywhere. (C) In response to a transient increase in the cell death rate (in this specific simulation an increase of 50% for 30 days), the system shifts to a new steady state. (D) Phase-plane representation of steady-state model behavior in response to a transient 50% increase in the cell death rate lasting 30 days. The initial steady state is 0.95 and 0.05 for SR_high and SR_low cells, respectively. During the transient cell death rate increase, the cell population sizes decrease to a new, lower steady state.

This characterization of the system exposes a conceptual challenge: the two-population system of SR_high and SR_low cell populations described above is not robust to disruptions and can lead to a continued loss of tissue under a persistent mild insult, yet the liver can maintain function for a prolonged period even when exposed to various toxins and injuries repeatedly over this period. Reconciling this contradiction between nature and our understanding of it necessitates the existence of a yet-unidentified robust homeostatic renewal process governing maintenance of liver tissue during routine exposure to a toxic environment. The necessity for a robust process of homeostatic renewal requires the answer to several questions that currently remain unanswered.

• How are the dynamics of proliferation, death, and transformation of constituent cell types coordinated to yield homeostasis?

• How is the liver’s documented robustness of the renewal process achieved?

• Which network interactions confer robustness to insults on the liver so that it can maintain tissue health over a long period of time?

The current study is focused on addressing these questions using a mathematical model to derive insights into the operational principles of liver homeostatic renewal. We postulate a set of feedback control loops in the cellular network and develop mathematical models describing these interactions. We use a Design of Experiments-based approach to evaluate the relative contribution of these control loops to the overall robustness of the renewal process in the face of persistent and repetitive insults. Finally, we extend the network model further to incorporate control loops corresponding to liver nonparenchymal cells and evaluate the putative contributions of these interactions to the fine-tuned control of the liver homeostatic renewal process. While these mechanisms are by no means exhaustive, they represent a reasonable biological “search space” for archetypal mechanisms that are likely to contribute to homeostatic renewal based on mechanisms proposed in the liver and in other organs.²⁻⁷

Materials and Methods

Model Development

Homeostatic Renewal Base Model

Our objective is to provide a mathematical description of homeostatic renewal in the liver that will enable a quantitative investigation of how different types of feedback control mechanisms influence the dynamics of tissue renewal. To this end, we developed a mathematical model of liver homeostatic renewal based on currently available mechanistic details including recent results demonstrating that tissue renewal is governed by two populations: high-rate self-renewal (SR_high) and low-rate self-renewal hepatocytes (SR_low).^7,8,10

We described the dynamics of SR_high and SR_low hepatocyte populations during homeostatic renewal with ordinary differential equations arising from ensemble material/population balances. Although the biological processes of cell replication and cell death are intrinsically stochastic at the individual cell level, it has been shown in vitro and in vivo(12−14) that at the population level, these processes can be represented adequately well using deterministic ensemble continuum modeling.

Our modeling scheme begins with exponential growth of a single self-renewing hepatocyte population, with a proliferation rate equal to k_prol, as follows

1

where [SR] is the population level of the self-renewing hepatocytes.

Eq 1, however, results in unchecked growth of hepatocytes under all conditions. We therefore introduce a death term (governed by the death rate, k_death) to balance the self-renewal. When k_prol equals k_death, the system is at equilibrium, and the population of hepatocytes is stable, see eq 2.

2

While eq 2 describes a single hepatocyte population, our model encompasses two such populations, a fast self-replicating population (SR_high) and a slow self-replicating population (SR_low). Applying eq 2 to these populations yields eqs 3–4.

3

4

In this modeling scheme, the sizes of the two cell populations of interest are governed by a balance between the respective proliferation and cell death rates. The rates of cell proliferation of SR_high and SR_low populations are described by constants, k_prol^high and k_prol, respectively, with corresponding rates of cell death described by constants k_death^high and k_death. An additional feature of our model is that SR_high cells are constitutively transformed to SR_low cells at a constant transition rate, k_T. This introduces a first order term in the equations describing the transition between states, k_T[SR_high]. Consequently, balances on SR_high and SR_low cell populations, respectively, give rise to the following equations:

5

6

Incorporating Feedback

As described by eqs 5 and 6 above, the system of SR_high and SR_low cells in such a feedforward network is not robust to disruptions. By contrast, biological liver function can recover from a variety of acute and chronic insults. This suggests the presence of stabilizing feedback mechanisms that endow the network with robustness characteristics. In the absence of consensus experimental information about such feedback mechanisms, we proposed three plausible mechanisms that we incorporated into our modeling framework, as putative contributors to liver homeostatic renewal.

Model A: Implicit Competition within Hepatocyte Populations (i.e., Population Size Capacity Constraint)

Model A describes a modification to the baseline exponential growth model with transition between cell populations (eqs 5–6). In this scheme, hepatocytes within a subpopulation compete for limited resources, potentially including nutrients, space, or cofactors. Such competition for limited resources, which affects both population’s ability to proliferate, is represented using logistic growth equations, g([SR_high]) and g([SR_low]), as follows

7

8

where K_cap^high and K_cap are the carrying capacities, or average population sizes given the available nutrients and resources, for SR_high cells and SR_low cells, respectively. In these equations, the carrying capacities were chosen to be 1.5× the steady-state value of the tissue since infiltration of greater than 50% of hepatocytes by fat occurs rarely, as seen in only 33% of morbidly obese patients.¹⁵

These carrying capacities are then incorporated into the equations governing the system of hepatocyte renewal (eqs 5 and 6) in place of exponential growth (i.e., the terms k_prol^high [SR_high] and k_prol [SR_low]), as shown below:

9

10

Model B: Negative Feedback of SR_low Hepatocytes on SR_high Cell Self-Renewal (i.e., Product Inhibition of Proliferation)

Model B describes a modification to the baseline exponential growth model with transition between cell populations (eqs 5–6); note, model B does not build on top of model A. In this scheme, SR_high cells sense and respond to the total number of functional hepatocytes in the liver by modifying their proliferation rate. Specifically, the proliferation rate of SR_high cells slows down as the number of functional hepatocytes in the liver increases, and the proliferation rate of SR_high cells increases when the number of functional hepatocytes in the liver decreases. To this end, a new parameter, k_env^prol, is introduced, which represents the effect of the tissue microenvironment on SR_high cell proliferation. In this formulation, a larger hepatocyte population size conditions the microenvironment to slow SR_high proliferation, leading to the term . Since the total proliferative hepatocyte population is composed of both SR_high and SR_low cells, the term becomes , leading to eq 11.

11

Additionally we introduce k_A, an autosuppression parameter, which corresponds to the relative contribution of SR_high cells to the impaired SR_high cell proliferation, compared to the contribution of SR_low cells. Therefore, the base homeostatic renewal model (eqs 5 and 6) is adjusted according to this change in SR_high proliferation.

12

13

The value of k_A was arbitrarily set to 0.1 as we reasoned that SR_high cells would have a larger proportional feedback on their own proliferation than SR_low cells, due in part to spatial proximity. Later, we used local and global sensitivity analyses to evaluate the effect of choosing how k_A = 0.1 on our model predictions.

Model C: Negative Feedback of SR_low Cells on SR_high Cell Transition (i.e., Product Inhibition of Cellular Transitions)

Model C describes another modification to the baseline exponential growth model with transition between cell populations (eqs 5–6); note, model C does not build on top of model A nor model B. This scheme corresponds to the case where the SR_low cell population size influences the transition rate of SR_high cells as follows. As the SR_low cell population size increases, the transition signal (k_env^T) is diluted, and the observed transition rate, k_T, decreases according to the proportion of the transition signal to the SR_low cell population. Oppositely, as the SR_low cell population size decreases, the transition rate increases according to the same proportion, which is described by the following term modifying k_T, , as shown in eqs 14–15.

14

15

Model D: Exogenous Cells Contributing to the SR_high Cell Population (e.g., Stem Cell Dependent Renewal)

Model D describes our final modification to the baseline exponential growth model with transition between cell populations (eqs 5–6); note, model D does not build on top of models A, B, or C. The most widely studied process of homeostatic renewal in multiple organs is stem cell-dependent renewal, although some organs, such as the pancreas, renew by self-replication rather than through stem cell differentiation.^5,16,17 In the liver, it has been assumed widely that self-replication largely governs homeostatic renewal of hepatocytes; however, emerging evidence suggests that stem cells also contribute to hepatocyte renewal under certain conditions.^11,18 Consequently, we simulated the presence of an exogenous population of cells that contribute to the SR_high cell population. We represented the effect of contributions to the SR_high cell population from an exogenous population of cells by including an additional term in the equation for SR_high cell growth, f([SR_high]) (eq 16), which describes exogenous-based cell replacement of SR_high cells at low liver masses. For the specific formulation of f([SR_high]), we chose an inverse exponential (eq 18); the fit parameters in this term were chosen such that at steady state the exogenous cells no longer contribute to the SR_high population, but they contribute exponentially to renewal when the SR_high cell population size falls below a certain threshold (set at ∼4% of liver mass in this model).

16

17

18

It should be noted that this exogenous population is not limited only to stem cells. It has been shown¹⁹ that while stem cells can be an important class of contributors to cell renewal, they are not the only contributors. Experimental evidence suggests that other exogenous cell types may contribute to liver renewal, including hybrid hepatocytes,^8,20,21 biliary cells (capable of transdifferentiation into hepatocytes and vice versa),^22,23 and hepatic stellate cells (via mesenchymal to epithelial transition into hepatocytes),^24,25 any of which could contribute to the effect of an exogenous cell population on homeostatic renewal.

Parameter Identification and Constraints

A comprehensive description of how appropriate values are determined for the parameters in the model is available in the Supporting Information. Table 1 lists the parameter values for the base homeostatic renewal model and for the robust model, which incorporates multiple feedback control loops.

Table 1. Parameter Values for the Base and Robust Model Formulations.

parameter/model	base	robust
kprolhigh	0.071429	0.214258
Kcaphigh	--	0.075
Kcaplow	--	1.425
kprollow	0.035714	0.107129
kdeathhigh	0.0375	0.044629
kdeathlow	0.0375	0.044629
kT	0.033887	0.169629
kenvprol	--	0.434961
kenvT	--	0.95
kA	--	0.1
C1	--	--
C2	--	--
kRenew	--	--

Model Selection for Robustness

We employed a systematic approach based on statistical design of experiments (DOE) to investigate the system behavior under all possible combinations of feedback mechanisms. We characterized system recovery in response to a wide variety of disturbances: specifically, (a) a transient (30 day) increase in cell death rate, (b) decrease in cell death rate, (c) increase in proliferation rate, and (d) decrease in proliferation rate. In the “experimental design”, we considered each feedback mechanism to be a factor with one of two levels: 1 (present) or 0 (absent). With four postulated feedback mechanisms, the result is a 2⁴ full factorial design or 16 distinct configurations, ranging from no feedback mechanism to a combination of all four proposed feedback mechanisms and all other possible combinations in between. We then simulated system responses to the transient disturbances listed above and quantified each response with the “total robustness” metric in eqs 25 and 26 (Results section), defined as the reciprocal of the total recovery volume. For each case investigated, we calculated a recovery volume by determining the area of the total SR_high and SR_low cell population size displacements (in a two-dimensional phase plane) and multiplying this area by the total recovery time. The total recovery volume was then obtained as the sum of the individual recovery volumes for each disturbance. Not every human is biologically the same, and the regulatory mechanisms governing tissue behavior are likely to be subjected to patient-to-patient variability in genomic makeup, transcriptional regulation, and proteomic regulation. We therefore also investigate how robust the model is to slight deviations corresponding to potentially different regulatory mechanisms of homeostasis renewal in different patients by varying the following parameters to carrying capacities (K_cap^high, K_cap), proliferation rates (k_prol^high, k_prol, k_env^prol), death rates (k_death, k_death^low), transition rates (k_T, k_env), and the area parameter (k_A) We simulated a total of 10 individual patients by creating 9 additional parameter sets, one for each of the above state’s parameters, by sampling the value of each parameter from a normal distribution with a mean at the nominal value and a standard deviation that is 1% of the nominal value, simulating a small change in nominal tissue function across patients. We then repeated the full 2⁴ design for each parameter set. We analyzed the resulting data on total robustness using Analysis Of Variance (ANOVA) to identify which feedback mechanisms contributed significantly to homeostatic renewal robustness following transient disturbances.

Nonparenchymal Cell Controllers

Control by nonparenchymal cells was implemented within the Matlab ODE solver using proportional-plus-integral (PI) controllers that generate control action 1 (CA₁), which influences the environmental contribution to proliferation (k_env^prol), and control action 2 (CA₂), which influences the transition rate (k_env), according to the following differential equations.

19

20

These control actions (CA₁ and CA₂) affect the hepatocyte equations as follows:

21

22

Here, SR_high^ss and SR_low are the steady-state population sizes of SR_high and SR_low, respectively, set to values of 0.95 and 0.05 for the simulations described in this manuscript. The PI controller parameters were selected using the automatic tuning function in the Simulink platform (Mathworks, Natick, MA) and are available in Table 2.

Table 2. Control System Parameters.

controller	P	I	N
kenvprol NPC	37.5	20.8	100
kenvT NPC	15.9	2.5	100

Model Simulation and Reproducibility

All simulations were carried out using Matlab and Simulink (Mathworks, Natick, MA). The model ODEs were integrated using the function ode15s. Model files are available for download from GitHub (https://github.com/Daniel-Baugh-Institute/LiverHomeostaticRenewalModel) and are also available in the Supporting Information. Self-assessment of the Ten Simple Rules for Credible Practice in Modeling and Simulation in Healthcare was performed and is included in the Supporting Information.²⁶

Results

Feedback Control Is Required to Maintain a Stable Steady-State Level of Hepatocytes

First, we implemented a model of liver homeostatic renewal based on known information from experimental studies. The model consisted of two hepatocyte populations differentiated by self-renewal capacity – high self-renewal hepatocytes (or SR_high cells) and low self-renewal hepatocytes (or SR_low cells) – and no feedback mechanisms.^7,8,10 In this scheme, both SR_high cells and SR_low cells can proliferate, with each cell type subject to a constitutive cell death rate (Figure 1A; eqs 5 and 6); additionally, SR_high cells can transform or differentiate into SR_low cells. In all cases, purely mass action kinetics is assumed for cell proliferation, death, and transformation of SR_high cells into SR_low cells.

Phase-plane analysis of the system dynamics under these conditions revealed that in the absence of feedback interactions, the initial steady state is unstable (Figure 1B). At steady state, and are equal to zero in the equations governing SR_high and SR_low population size behavior (eqs 5 and 6), which rearrange as follows.

23

24

Note from these equations that unless (k_prol^high – k_death – k_T) = 0 and (k_T + k_prol^low – k_death) = 0, the only steady-state values of the SR_high and SR_low population sizes will be zero, leading to a steady state with no liver cells.

Consequently, under these conditions, any change to SR_high and SR_low population sizes will result in a steady state where the SR_high and SR_low populations are zero. In other words, the system is unable to maintain homeostasis in the hepatocyte populations following any challenge that leads to cell death. The system is entirely unable to recover from any perturbation of any magnitude, even transient ones, regardless of duration. For example, Figure 1C shows the response of the system to a transient insult (50% increase in cell death rate lasting for 30 days). This transient increase in cell death rate causes a transient decrease in the populations of both SR_high cells and SR_low cells, moving toward the steady state of zero cells. Once the insult is removed, cell growth and death are rebalanced, leading to a new steady state with smaller population sizes. Since within the mathematical framework considered here the liver does not recover from lost hepatocyte mass following a transient insult (Figure 1D), repetitive transient injuries will drive the system toward complete loss of hepatocytes over time, resulting in liver failure. These results demonstrate that feedback control is required to maintain hepatocyte population sizes in the face of one or more injuries causing cell death. Note that this analysis does not take into consideration liver regeneration following major mechanical or chemical insults. In those cases, the mechanisms involved are not thought to play a role in liver homeostatic renewal or liver response to the minor insults investigated in this study.

Different Types of Feedback Controls Result in Distinct Dynamics of Hepatocyte Renewal

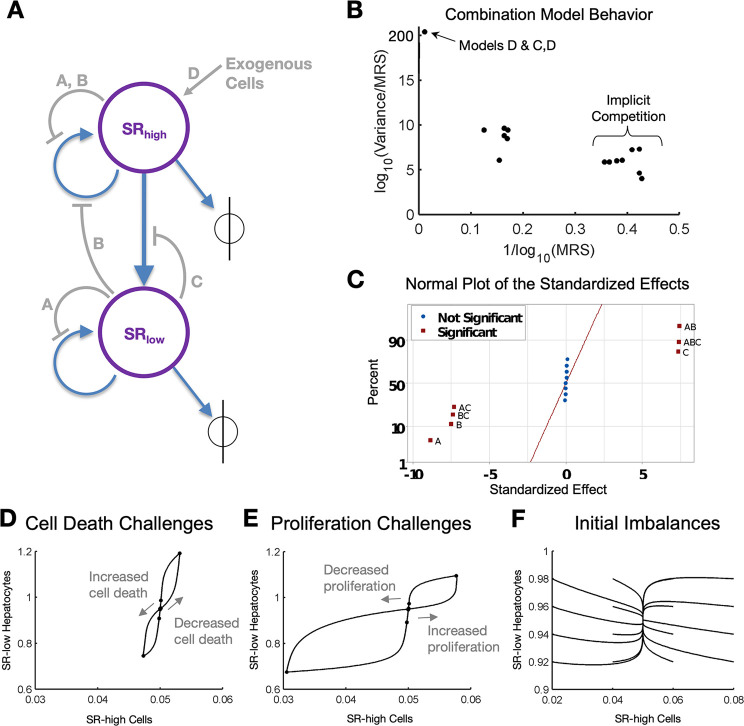
Next, we modified the network model to incorporate feedback. Specifically, we consider four distinct feedback mechanisms representing the following physiological phenomena: (A) population size capacity constraints, (B) inhibition of proliferation, (C) inhibition of SR_high transformation, and (D) recruitment of SR_high cells from sources external to liver tissue (Figure 2A). We investigated the ability of these potential feedback mechanisms, individually or in combination, to confer stability on the system in the face of repetitive insults. Our analysis, described in detail in the Supporting Information (see Figures S1–S5), showed that each feedback mechanism produced a different steady state and dynamic behavior. To summarize, the feedback mechanism in model A leads to inverse behavior between cell population size and growth rate, as one grows the other falls. Steady-state analysis shows the presence of three possible steady states: (1) the initial steady state; (2) a steady state where all SR_low cells have died, but SR_high cells maintain liver mass at a level of only 5% of nominal mass; and (3) a steady state where all SR_high cells have died, but SR_low cells repopulate and maintain the liver tissue at 95% of nominal mass. Model B feedback is directly affected by the proliferation rate of SR_high cells; a decrease in the proliferation rate of SR_high increases the number of functional hepatocytes in the liver, while an increase in the proliferation rate of SR_high cells decreases the number of functional hepatocytes. Model B has only one steady state, which is at the initial hepatocyte population sizes. Model C feedback influences the transition rate of SR_high cells to SR_low cells through SR_high cell sensing. This is the only model to exhibit a single, unstable steady state at the initial population sizes. Finally, Model D shows the effect of stem cell dependence on homeostatic renewal. This model, like that of Model A and B, also exhibits a stable steady state at the initial population sizes.

Figure 2.

Incorporating feedback mechanisms. (A) Network model schematic modified to include the physiological phenomena of (A) population size capacity constraints, (B) inhibition of proliferation, (C) inhibition of SR_high transformation, and (D) recruitment of SR_high cells from sources external to liver tissue. (B) Robustness of system response to multiple transient disturbances (plotted as MRS) and variance in simulated patient response with altered physiological parameters. The systems that responded with the largest MRS (highest robustness) also showed the smallest normalized variance in response to altered parameters. (C) ANOVA shown as a plot of standardized effects resulted in significant feedback mechanisms A, B, and C as did their interactions. However, feedback D and its interactions did not affect model output significantly. (D) Robust model (Model A+B+C) response to transiently increased and transiently decreased cell death (1.5× and 0.5× nominal value for 30 days). (E) Robust model response to transiently increased and transiently decreased proliferation (1.5× and 0.5× nominal value for 30 days). (F) Robust model response to initial population imbalances shows that multiple starting conditions converge to a steady state. Points represent t = 0, 10, 40, and 60 days followed by every 30 days until 1 year, at which points represent each subsequent year. Gray arrows represent the direction of motion on the phase plane. MRS is the Mean Recovery Score, which is the sum of the recovery volumes for all disturbances.

Combinations of Feedback Mechanisms Result in a Renewal System That Is Robust to Multiple Biological Perturbations

From an evolutionary point of view, a system that is able to respond to many perturbations (i.e., optimized for robustness) is preferable to a system that maintains maximum functional efficiency at one condition but is unable to respond well to challenges (i.e., optimized for efficiency). Examples of biological systems that appear to be optimized for robustness include protein coding,²⁷ DNA damage repair,²⁸ and even whole transcriptional systems.²⁹ We postulated that a homeostatic renewal process that is optimized for robustness to disturbances will allow the liver to maintain a steady mass even in the face of toxic challenges. Consequently, we investigated which combination of feedback mechanisms will show the most robust recovery following multiple types of perturbations, referring to the resulting model as the “robust model” in the subsequent analyses.

We employed a systematic design of experiment-based (DOE) approach, as described in the “Model selection for robustness” section of the Materials and Methods, to explore all possible combinations of feedback interactions to determine which model is the most robust. Detailed results of the DOE analysis are shown in Supporting Information Table S3. We used the metrics in eqs 25 and 26 below to quantify and evaluate the model’s response to multiple individual disturbances

25

26

where N_{perturbations} = 4, and the recovery volume for each disturbance is computed as the volume of the hypercube of deviation in the SR_high cells and SR_low cells multiplied by the recovery time.

In addition to performing the DOE using nominal parameter values, we also created 9 additional parameter sets to evaluate the robustness of each model to parameter variations. This approach allowed us to identify a model that is robust to physiological and parametric disturbances. Subsequent analysis of the results using ANOVA allowed us to determine which feedback mechanisms affect model behavior significantly. We found that combination models that included implicit competition (Model A) were able to recover from physiological disturbances with the highest degree of robustness and lowest variance caused by parametric changes (Figure 2B). The ANOVA results indicated that the responses with all combinations of feedback interactions in models A (implicit competition), B (product inhibition of proliferation), and C (product inhibition of transitions) were significant but that of model D (exogenous populations) was not significant (Figure 2C). Therefore, we included in our robust model all feedback interactions except the contribution from exogenous populations (Model D), yielding the following robust model:

27

28

We simulated the response of the robust model to cell death challenges (Figure 2D), proliferation challenges (Figure 2E), and imbalanced initial conditions (Figure 2F). We found that the renewal system described by the robust model can recover from transient cell death and proliferation challenges with relatively small deviations in cell numbers compared to the response under individual feedback mechanisms. Most of the recovery occurred within the initial 20 days following the end of the physiological challenge. Additional analysis of the robust model may be found in the Supporting Information (see Figures S6–S13).

Model Simulations Capture Experimentally Observed Dynamics of Liver Renewal after Stem Cell Transplantation under Induced Hepatocyte Senescence

Having developed a model of homeostatic renewal that is robust to individual, transient disturbances, next we evaluated our model’s ability to capture experimentally observed behavior of liver homeostatic renewal. It has been shown that, under normal conditions, stem cells are not required for homeostatic renewal. However, recent research showed that stem cells are able to repopulate the mouse liver when hepatocyte senescence is induced using βNF.¹⁰ With this treatment, approximately 99% of the hepatocytes in the liver (presumably both SR_high cells and SR_low cells) were unable to replicate. The livers were then dosed with additional βNF to induce liver damage and subsequent mass recovery, with the result that the livers recovered their original mass in 90 days. Cell lineage tracing showed that the new hepatocytes originated from stem cells.

To enable investigations into the case of system behavior following induced hepatocyte senescence, we introduced stem cell renewal (model D) into our robust model. Previous model analyses under normal conditions showed that the effect of stem cell proliferation on homeostatic renewal is not significant. Therefore, we investigated the model response to challenges, with and without stem cell renewal (Figure S7). As we expected, the inclusion of stem cell renewal does not change model response behavior or response timing. We simulated induced senescence in the liver by including two additional, nonreplicating populations of hepatocytes: senescent SR_high cells and senescent SR_low cells. For simplicity, we assume that the population sizes of senescent SR_high and SR_low cells remain at 5% and 95% of the senescent hepatocyte population, respectively. It is unclear whether senescent SR_high cells can transition to senescent SR_low cells; therefore, for simplicity, we decided not to include such a transition parameter in the model.

The resulting modified model equations are shown below in eqs 29–31.

29

30

31

Here H^s is the level of senescent hepatocytes, SR_Tot^high is the sum of senescent and nonsenescent SR_high cells ([SR^high] + 0.05x [H^s]), and SR_Tot is the sum of senescent and nonsenescent SR_low cells ([SR^low] + 0.95x [H^S]). Since SR_high and SR_low cell death rates are equal in our model, we arbitrarily chose to use k_death^high for the senescent hepatocyte cell death rate. The following simulations of homeostatic renewal following induced hepatocyte senescence in the absence of other insults and following a toxic injury to 40% of the liver are shown in Figure 3.

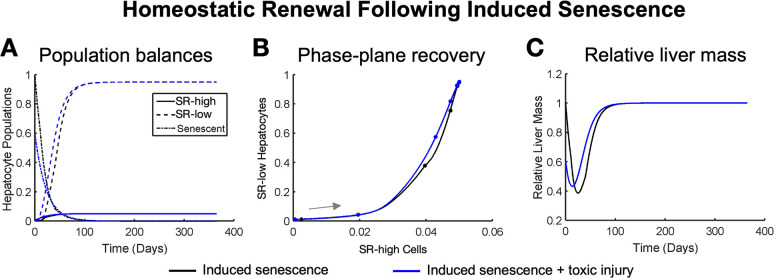
Figure 3.

Homeostatic renewal recovers liver mass when hepatocytes become senescent and are coupled with a large cell death event, shown here using (A) hepatocyte population balances, (B) phase-plane recovery, and (C) relative liver mass recovery. Researchers have shown complete renewal 90 days postinjury, which is consistent in our model.¹⁰ Induced senescence without damage is represented by black lines, and induced senescence with 40% of hepatocytes removed (toxic injury) is represented by blue lines. Our model predicts that stem cells become active even without an additional cell death challenge but that the time frame of recovery is slightly longer (∼120 days to recovery). Points represent t = 0, 10, 40, and 60 days followed by every 30 days until 1 year, at which points represent each subsequent year. Gray arrows represent the direction of motion on the phase plane.

We found that constitutive cell death alone was enough to trigger stem cell renewal into SR_high cells followed by a repopulation of hepatocytes with nonsenescent cells (Figure 3A, black lines). With no additional insult, the liver recovers its replicating cells fully in approximately 120 days (Figure 3A, black lines), with SR_high cells beginning to recover more quickly than SR_low cells (Figure 3B, black line). However, our model simulations predict that a significant amount of liver mass will be lost before stem cells are able to produce a population of replicating cells large enough to overcome constitutive cell death (Figure 3C, black lines). When the additional insult of a 40% toxic shock is introduced to the induced senescence, the liver responds in a very similar way. However, repopulation of the liver with replicating cells begins more rapidly (Figure 3A, blue lines). Although the phase trajectory of recovery is similar in the two cases, introducing an additional insult speeds recovery in our simulations (Figure 3B, blue line). Adding the additional insult decreases the maximum liver mass lost (45% remaining as opposed to 39%) and speeds recovery time (90 days as opposed to 120 days) (Figure 3C, blue line). This simulated recovery time following dual insults matches the recovery time previously observed experimentally (10).

Frequency Analysis Shows That High Insult Frequencies Impair Homeostatic Renewal

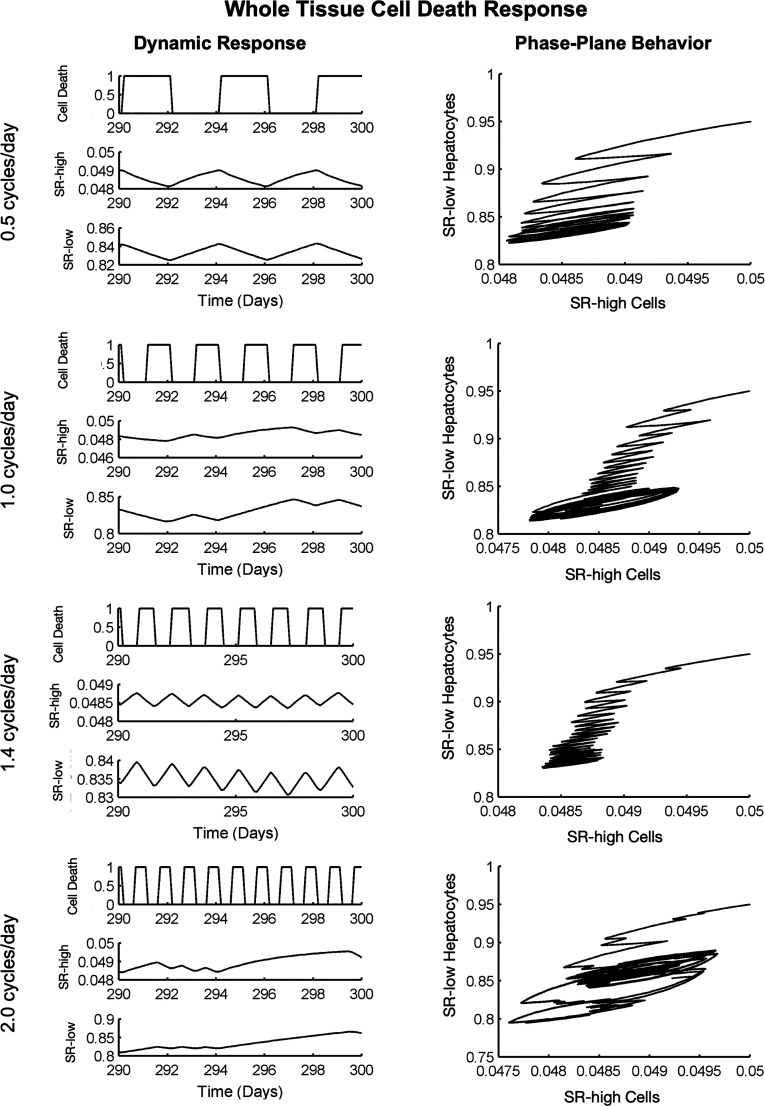
Thus far, our analyses have involved only a single challenge to liver function. However, chronic liver diseases are caused by persistent, repetitive challenges that occur over the course of years or decades. To investigate how such chronic insults affect homeostatic renewal, we simulated the cell death rate as a sinusoidal input with a variety of frequencies and analyzed the predicted response of SR_high and SR_low cells. Figure S8 depicts the behavior of the cell death rate over the course of 1 week at different frequencies, interpreted in the context of a common toxin (alcohol) introduced into the liver. For example, a frequency of f = 2.0 cycles/day corresponds to a daily alcohol binge leading to a peak in cell death once per day (Figure S8). We investigated the model’s response when SR_high cells are selectively targeted (Figure S9), when SR_low cells alone are selectively targeted (Figure S10), and when cell death rates of both cell populations change (Figure S11). In all cases, the system response to cell death challenges begins to destabilize at around a frequency of 2.0 cycles/day.

Realistically, toxic challenges likely do not cause sinusoidal changes to cell death but rather a transient increase in cell death rate while the toxin is active. As an alternative, we used step functions occurring at different frequencies to simulate the insult (Figure 4) and found that, following this type of insult, the system often falls into an attractor cycle that deviates from the steady state. Furthermore, as the insult frequency increases, the system is progressively less able to maintain a stable attractor state. It is possible that such a sustained deviation from healthy balances could contribute to disease progression in the face of persistent insults, but more research is needed to confirm or refute this possibility.

Figure 4.

Simulating multiple, pulsatile whole liver cell death events. At low frequencies (f < 2.0 cycles/day), the liver is able to recover between cell death events. At high frequencies (f ∼ 2.0 cycles/day and above), the hepatocyte populations are unable to recover between events, and population sizes become unstable. In this figure a “Cell Death” value of 0 represents no external cell death challenge (only the intrinsic cell death rate).

The previous analyses focused on the effect of varying frequencies of insult with the total magnitude of the insult remaining constant. However, chronic diseases may result from a specific insult magnitude occurring at varying frequencies. Such an insult pattern would be expected to increase total damage at high frequencies. Indeed, our investigation of this type of insult showed that low frequency cell death events allow for system recovery, while higher frequencies do not, resulting instead in attractor states below nominal population sizes (Figure S12). We also investigated the effects of changing the magnitude of damage per cell death event for a given frequency (Figure S13) and found that while the qualitative phase behavior of the system is governed by the frequency of insult, the magnitude of that response depends on the magnitude of insult.

Nonparenchymal Cell Mediated Processes Can Enhance Disturbance Rejection

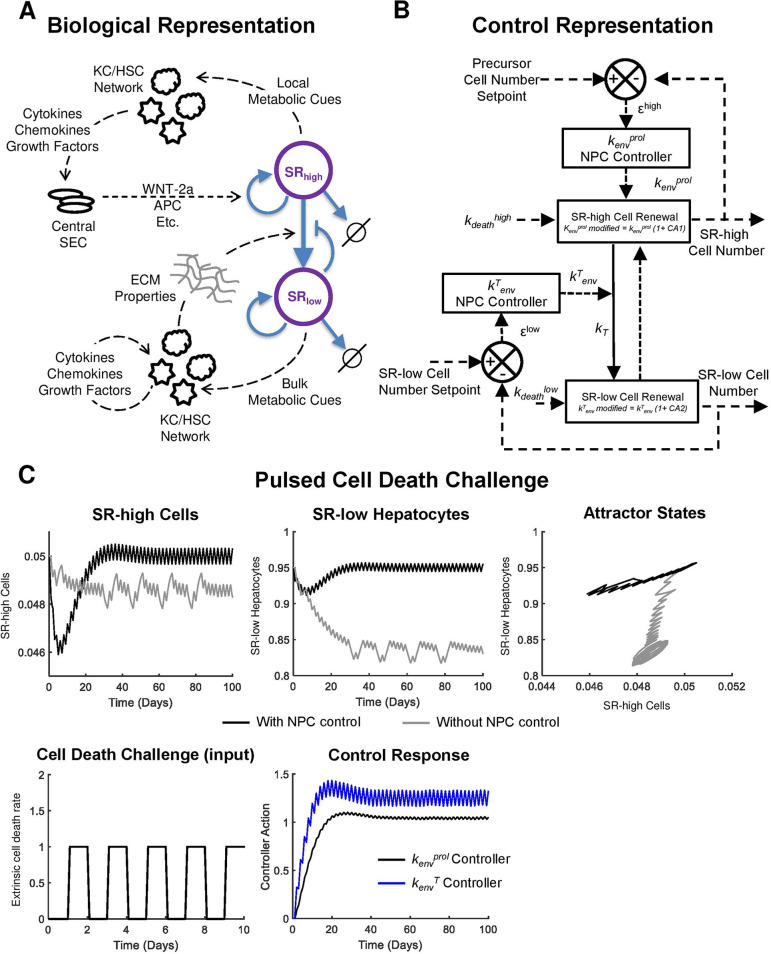
In the robust model of liver homeostatic renewal, a periodic cell death challenge results in functional liver mass below steady-state population sizes. However, in chronic liver diseases, like alcoholic or nonalcoholic fatty liver disease, total liver mass is maintained or increased (due to the accumulation of hepatic fat). In light of this apparent discrepancy, we postulate that nonparenchymal cell mediated regulation of the liver microenvironment also contributes to homeostatic maintenance of hepatocytes. The structure of our homeostatic renewal model suggests two places where the nonparenchymal cell network could modulate homeostatic renewal dynamics (Figure 5A). This may occur first by modifying the tissue microenvironment local to the central vein. The pericentral nonparenchymal cell network could modify the behavior of local sinusoidal endothelial cells, leading to altered secretion of factors promoting central SR_high cell renewal (These factors include WNT-2a and others.). Second, a nonparenchymal cell network could modulate homeostatic renewal by changing the bulk properties of the liver extracellular matrix. This could lead to a change in transition rate of SR_high cells to SR_low cells by altering the molecular diffusion of protransition and antitransition molecules through the tissue. Nonparenchymal cell modulation of the tissue microenvironment adds an additional layer of control to homeostatic renewal such that the hepatocellular network has intrinsic stability and external control to maintain tissue functional mass.

Figure 5.

Nonparenchymal cell control of hepatocyte homeostatic renewal. (A) Model schematic representing the biological process underlying the control system. Dashed lines represent a flow of information, while solid lines represent a flow of mass. (B) A control systems representation of liver homeostatic renewal controlled by nonparenchymal cell networks. In this representation, an increase or decrease in cell death rate disturbs normal homeostatic renewal. The proliferation (k_env^prol) and transformation (k_env^T) rates are modified by the nonparenchymal controllers as shown in eqs 21 and 22. Dashed lines represent a flow of information, while solid lines represent a flow of mass. (C) Ability of the nonparenchymal cell network controller to mitigate the effects of a periodic cell death challenge (increasing extrinsic cell death rate 1 day every other day). Controller action causes an attractor state with minimal deviation around the steady state. In the absence of nonparenchymal cell control, hepatocyte populations fall into an attractor cycle below steady-state population size.

A control system representation of this scheme is shown in Figure 5B. For a complete description of the model including nonparenchymal cell control, see the Supporting Information. PI controllers were used to represent the nonparenchymal cell networks. Tuned controller parameters are given in Table 2, where the k_env^prol controller generates control action 1 (CA₁), which modifies the effect of the parameter k_env through a multiplication factor (1 + CA₁) as per eq 21. The k_env^T controller generates control action 2 (CA₂), which modifies the effect of the parameter k_env through a multiplication factor (1 + CA₂).

The addition of nonparenchymal cell control to the system allows for smaller overall deviation from steady state when homeostatic renewal is disturbed. Transient disturbances result in a deviation from nominal values for both cell populations at the start and end of the disturbance as the microenvironment must return to homeostasis (Figure S14). The magnitude of deviation caused to SR_high cells following the disturbance is similar with and without nonparenchymal cell control, while the deviation caused to SR_low hepatocytes (which make up the bulk of the liver) is much lower when nonparenchymal cell control is incorporated in the model.

We explored how nonparenchymal cell control of homeostatic renewal is affected by induction of cellular senescence. The complete set of differential equations governing homeostatic renewal with nonparenchymal cell control and hepatocyte senescence can be found in the Supporting Information (equations S17–S21). This implementation of the model also produces a robust response resulting in complete liver mass recovery when senescence is induced with and without simulated toxic injury (Figure S16A-C). We also simulated highly attenuated NPC control if their feedback control signals are reduced to 1% of their healthy levels to examine the effect on homeostatic cell numbers when considering senescent hepatocytes. Still, there was a robust response resulting in complete liver mass recovery (Figure S16D-F). The time frame of liver mass recovery is slightly shorter with toxic injury as seen in the original implementation of the model with induced senescence alone (Figure 3). Additionally, the model with NPC control and induced senescence results in faster overall liver mass recovery as compared to the model with induced senescence alone (Figure S16, Figure 3).

During a periodic pulsatile increase in the cell death rate in the absence of nonparenchymal cell control, both SR_high and SR_low cell populations oscillate well below the healthy steady-state value (Figure 5C, gray lines). However, when nonparenchymal cell control is available to modulate renewal dynamics, there is a transient decrease in cell populations, capable of recovering in approximately 30 days. Following this transient decrease, cell populations oscillate near the steady state (Figure 5C, gray lines). Both a control action corresponding to an early increase in control parameters followed by a control action of oscillation about higher values are necessary to drive the system to an oscillation near the steady state (Figure 5C). In this simulation, cell death events occur for 1 day every other day (Figure 5C). The controller responses also have a frequency of approximately one cycle per day. This is not an unreasonable frequency for the controller governing k_env^prol, as cytokine profiles can change more rapidly than daily. This also not an unreasonable frequency for the controller governing k_env, as the transition between SR_high cells and SR_low cells may be governed by a gradient of responsiveness to a growth-maintaining factor (for example, responsiveness to WNT-2a in the specific high self-renewal case of Axin2+ cells). Such responsiveness to a self-replication maintaining factor may be due to (a) central endothelial cell-derived factors promoting stability of SR_high cell population, (b) diffusivity of these factors governed by matrix stiffness and pressure gradients, and (c) motility of hepatocytes across sinusoids that could also be governed by matrix cues, all of which can change within a day. A more complete characterization of the control system and a discussion of the resulting biological insights are available in the Supporting Information (see Figures S15–S19).

Discussion

Our model-based analyses suggest that multiple feedback control mechanisms must be active during tissue homeostatic renewal in the liver. Simulations of our mathematical model in the absence of feedback control show that homeostatic renewal leads to a tissue incapable of reaching steady state and unable to respond to disturbances. In contrast, simulations of homeostatic renewal with multiple types of feedback control mechanisms result in a tissue that can respond robustly to several different disturbances, both transient and periodic. Intrinsic stability caused by multiple feedback mechanisms within hepatocytes alone, however, is not enough to handle a sustained disturbance to homeostatic renewal, such as increased cell death caused by a sustained viral infection. In addition to intrinsic stability, there must be an external control that maintains hepatocyte populations in such a condition. We propose that control of the extracellular microenvironment by a network of nonparenchymal cells acts as such a control circuit.

Our model was able to capture the experimentally observed behavior of the liver following induced hepatocyte senescence. Following induced senescence and toxic damage to a large portion of the liver, recovery of its original hepatocyte populations and overall mass occurred in approximately 90 days. Furthermore, based on our model structure, we believe that several observations have value for future experimental investigation. Our first observation was that although all of the replicating hepatocytes come from stem cells in the induced senescence study, based on our model simulations, it is possible that only SR_high cells are generated directly from stem cells. Second, based on our model structure, it is possible that replicating SR_low hepatocytes are generated predominantly from transitioning SR_high cells. Lastly, according to model simulations, it is possible that induced senescence without any additional damage will result in stem cell activation and differentiation; however, the time to repopulate the liver with replicating cells will be longer, on the order of 120 days (as opposed to 90 days with an additional injury). Our model is able to accurately capture the observations from cell-tagging experiments which demonstrate that cells with higher replication rates (SR_high) have stem-cell-like features and yield daughter cells with lower replication rates (SR_low) that lack stem-cell-like features.⁷

Our model implicates control of homeostatic renewal by nonparenchymal cells as an important contributor to maintaining liver mass during chronic challenges. Many liver diseases are chronic issues and may affect the behavior of the nonparenchymal cell network. This can be seen by the number of liver diseases that result in fibrosis and cirrhosis if left untreated.³⁰ Recent work has shown that chronic alcoholism shifts the balances of nonparenchymal cell populations.³¹ Future studies could investigate extracellular matrix properties during chronic insults to determine how these properties could influence nonparenchymal cell balances. Additionally, our study used only the automatic controller tuning in Matlab. A more robust control strategy could better control cell populations and may more realistically represent the underlying biology.

Conclusion

Our study takes the first steps toward generating an integrated view of liver homeostatic renewal in the context of intercellular networks. Maintaining balances among cellular populations appears to be critical in conserving a healthy homeostatic renewal process. It is likely that interactions between parenchymal and nonparenchymal cells, among cell populations, and with the extracellular matrix are important for governing homeostatic renewal. Additionally, nonparenchymal cell control of the tissue microenvironment is likely spatial in nature, leading to unique control actions depending on the needs of the tissue within a local environment.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.iecr.2c03579.

• Supplemental text–supplemental materials and methods, results, figures, and tables; self-assessment of our model–our model’s conformance to Ten Simple Rules of Credible Practice in Modeling and Simulation in Healthcare; and Matlab code (PDF)

Author Contributions

Conceptualization, R.V.; Methodology, D.C., B.A.O., and R.V.; Software, D.C.; Formal Analysis, D.C.; Resources, D.C. and R.V.; Writing – Original Draft Preparation, D.C.; Writing – Review& Editing, D.C., A.M., R.V., and B.A.O.; Visualization, D.C. and R.V.; Supervision, R.V. and B.A.O.; Project Administration, R.V. and B.A.O.; Funding Acquisition, D.C., R.V., and B.A.O.

The authors would like to acknowledge financial support for this study from the National Institute on Alcohol Abuse and Alcoholism (R01 AA018873, T32 AA007463, and F31 AA030214) and the National Institute of Biomedical Imaging and Bioengineering (U01 EB023224). The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

The authors declare no competing financial interest.