Fractional telegraph equation under moving time-harmonic impact

Abstract

The time-fractional telegraph equation with moving time-harmonic source is considered on a real line. We investigate two characteristic versions of this equation: the “wave-type” with the second and Caputo fractional time-derivatives as well as the “heat-type” with the first and Caputo fractional time-derivatives. In both cases the order of fractional derivative 1 < α < 2. For the time-fractional telegraph equation it is impossible to consider the quasi-steady-state corresponding to the solution being a product of a function of the spatial coordinate and the time-harmonic term. The considered problem is solved using the integral transforms technique. The solution to the “wave-type” equation contains wave fronts and describes the Doppler effect contrary to the solution for the “heat-type” equation. Numerical results are illustrated graphically for different values of nondimensional parameters.

1. Introduction

In 1876, Heaviside [1] (see also historical notes in the books [2,3]) in his research on telegraph cables obtained the telegraph equation

$$A\frac{{\partial }^{2}u}{\partial t^2}+B\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial x^2}-bu.$$ (1)

It turns out that Eq. (1) describes various processes in different fields of study: electrical transmission [1-4], heat and mass transfer [5-8], random models [9,10], pressure in pulsatile blood flow in arteries [11,12], the velocity field in the Reyleigh problem for a Maxwell fluid [13], cosmic ray transport [14], biology [11,15], economics [16], etc. (the additional references can be found in the abovementioned publications).

Originally, the sought-for function u was interpreted in terms of the voltage or current on an electrical transmission line, and the coefficients A, B, D, and b were expressed in terms of the resistance, inductance, conductance, and capacitance. For different physical processes, the function u and the coefficients A, B, D, and b have the corresponding interpretation and associated physical dimensions.

For example, if we treat Eq. (1) as the damped wave equation

$$\frac{{\partial }^{2}u}{\partial t^2}+B\frac{\partial u}{\partial t}=c^2\frac{{\partial }^{2}u}{\partial x^2}-bu,$$ (2)

then the wave propagation speed has the physical dimension [c] = m/sec, the friction coefficient [B] = 1/sec, and [b] = 1/sec².

If we correlate Eq. (1) with the heat conduction (diffusion) equation,

$$A\frac{{\partial }^{2}u}{\partial t^2}+\frac{\partial u}{\partial t}=a\frac{{\partial }^{2}u}{\partial x^2}-bu,$$ (3)

then the thermal diffusivity coefficient has the physical dimension [a] = m²/sec, the additional time parameter [A] = sec, and [b] = 1/sec.

In the context of the theory of heat (mass) transport, the hyperbolic transfer equation was obtained by several authors. Fock [17] derived the evolution equations for total particles densities in the form of the hyperbolic transfer equation. Davydov [18] modified the standard diffusion equation and obtained the hyperbolic transfer equation in the context of the molecular diffusion (see also [19]). Cattaneo [20,21] and Vernotte [22] generalized the Fourier constitutive equation for the heat flux

$$\mathbf{q}+A\frac{\partial \mathbf{q}}{\partial t}=-k\text{grad}u$$ (4)

and obtained the telegraph equation

$$A\frac{{\partial }^{2}u}{\partial t^2}+\frac{\partial u}{\partial t}=a\Delta u.$$ (5)

It should be emphasized that Eq. (4) can be rewritten in the time-nonlocal form with the “short-tale memory” exponential kernel

$$\mathbf{q}(t)=-\frac{k}{A}{\int }_0^t\text{exp}\left(-\frac{t-\tau }{A}\right)\text{grad}u(\tau )\mathrm{d}\tau .$$ (6)

The fractional calculus (the theory of integrals and derivatives of non-integer order) has numerous applications in mechanics, physics, geophysics, rheology, engineering, chemistry, geology, biology, bio-engineering, finance, and medicine (see [23-32] among many others). For example, Ezzat et al. considered theory of thermoelasticity [33], thermo-viscoelasticity [34], magneto-thermoelasticity [35], and magneto-hydrodynamics [36] based on the fractional heat conduction.

It should be noted that time-fractional operators describe memory effects, space-fractional operators represent the long-range interaction. Recall the main notions of the fractional calculus [23,24]. The Riemann-Lioville fractional integral of order α is defined as

$$I^{\alpha }f(t)=\frac{1}{\Gamma (\alpha )}{\int }_0^t(t-\tau {)}^{\alpha -1}f(\tau )\mathrm{d}\tau ,t>0,\alpha >0,$$ (7)

and has the following Laplace transform rule

$$ℒ\{I^{\alpha }f(t)\}=\frac{1}{s^{\alpha }}{f}^{\ast }(s),$$ (8)

where Γ(α) is the gamma function, the asterisk denotes the transform, s is the Laplace transform variable.

The Riemann–Liouville derivative of the fractional order α

$$\begin{gathered} D_{RL}^{\alpha }f(t)=\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}\left[\frac{1}{\Gamma (n-\alpha )}{\int }_0^t(t-\tau {)}^{n-\alpha -1}f(\tau )\mathrm{d}\tau \right], \\ t>0,n-1<\alpha <n, \end{gathered}$$ (9)

for its Laplace transform requires the knowledge of the initial values of the fractional integral I^n–αf (t) and its derivatives of the order k = 1, 2, … , n – 1:

$$ℒ\{D_{RL}^{\alpha }f(t)\}=s^{\alpha }{f}^{\ast }(s)-\sum _{k=0}^{n-1}{D}^k{I}^{n-\alpha }f(0^{+})s^{n-1-k},n-1<\alpha <n.$$ (10)

The Caputo fractional derivative of order α

$$\begin{gathered} D_C^{\alpha }f(t)\equiv \frac{{\mathrm{d}}^{\alpha }f(t)}{\mathrm{d}{t}^{\alpha }}=\frac{1}{\Gamma (n-\alpha )}{\int }_0^t(t-\tau {)}^{n-\alpha -1}\frac{{\mathrm{d}}^{n}f(\tau )}{\mathrm{d}{\tau }^n}\mathrm{d}\tau , \\ t>0,n-1<\alpha <n, \end{gathered}$$ (11)

for its Laplace transform rule requires the initial values of a given function and its derivatives of integer order:

$$ℒ\{D_C^{\alpha }f(t)\}=s^{\alpha }{f}^{\ast }(s)-\sum _{k=0}^{n-1}{f}^{(k)}(0^{+})s^{\alpha -1-k},n-1<\alpha <n.$$ (12)

If care is taken, equations containing the Caputo derivative can be recast to those with the Riemann-Liouville derivative and vice versa according to the following formula

$$D_{RL}^{\alpha }f(t)=D_C^{\alpha }f(t)+\sum _{k=0}^{n-1}\frac{t^{k-\alpha }}{\Gamma (k-\alpha +1)}{f}^{(k)}(0^{+}),n-1<\alpha <n.$$ (13)

Compte and Metzler [37] considered four possible generalizations of the telegraph Eq. (5) with the Riemann-Liouville fractional derivative:

$$\frac{\partial u}{\partial t}+\zeta D_{RL}^{1+\alpha }u=a\frac{{\partial }^{2}u}{\partial x^2},0<\alpha <1,$$ (14)

$$D_{RL}^{\alpha }u+\zeta D_{RL}^{2\alpha }u=a\frac{{\partial }^{2}u}{\partial x^2},1∕2<\alpha <1,$$ (15)

$$D_{RL}^{\alpha }u+\zeta \frac{{\partial }^{2}u}{\partial t^2}=a\frac{{\partial }^{2}u}{\partial x^2},1<\alpha <2,$$ (16)

$$D_{RL}^{\alpha }u+\zeta D_{RL}^{1+\alpha }u=a\frac{{\partial }^{2}u}{\partial x^2},0<\alpha <1.$$ (17)

Atanackovic et al. [38] investigated a generalized telegraph equation with two Riemann-Liouville fractional derivatives. This equation can be written as

$$A{D}_{RL}^{\alpha }u+B{D}_{RL}^{\beta }u=D\frac{{\partial }^{2}u}{\partial x^2},0<\beta <\alpha \le 2.$$ (18)

It follows from Eq. (13) that for functions with zero initial conditions, the difference between the Riemann-Liouville and Caputo definitions disappears.

Equation (18) with two Caputo derivatives can be obtained as a consequence of the constitutive equation for the heat flux (see [30,39,40]):

$$B{I}^{1-\beta }\mathbf{q}+A\frac{{\partial }^{\alpha -1}\mathbf{q}}{\partial t^{\alpha -1}}=-k\text{gradu}u,1<\alpha \le 2,0<\beta \le 1,$$ (19)

or

$$\mathbf{q}(t)=-\frac{k}{A}{\int }_0^t(t-\tau {)}^{\alpha -2}{E}_{\alpha -\beta ,\alpha -1}\left[-\frac{B}{A}(t-\tau {)}^{\alpha -\beta }\right]\text{gradu}u(\tau )\mathrm{d}\tau ,$$ (20)

where E_α,β is the generalized Mittag-Leffler function in two parameters:

$$E_{\alpha ,\beta }(z)=\sum _{n=0}^{\infty }\frac{z^n}{\Gamma (\alpha n+\beta )},\alpha >0,\beta >0,z\in C.$$ (21)

It is evident that physical dimensions of coefficients arising in equations containing differential and integral operators of fractional order differ from those appearing in equations with the corresponding operators of the integer order (see the discussion above). We can interprete the coefficients A and B in Eqs. (18)-(20) as having the physical dimensions [A] = sec^α−1 and [B] = sec^β−1. If we introduce some time parameter τ₀, then we may assume that $A={\tau }_0^{\alpha -1}$ and $B={\tau }_0^{\beta -1}$. The choice of notation A and B or ${\tau }_0^{\alpha -1}$ and ${\tau }_0^{\beta -1}$ for these coefficients is only a question of custom, a question of convenience or a question of habitude. Both notations are used in the literature, and the statement of the paper [41] about dimensional inconsistency of coefficients in time-fractional constitutive equations for the flux q in the papers [42-44] is quite incorrect. In fact, the theory presented in [41] is a modification of the thermoelasticity theory based on the time-fractional telegraph equation for temperature proposed in [39].

Different choices of the coefficients A and B and the orders of derivatives α and β allow one to obtain different particular cases of the time-fractional telegraph equation. A variety of problems for different versions of the time-fractional telegraph equation were considered in [45-50], among others. Numerical methods for solving fractional telegraph equation were proposed in [51-54] (see also [55,56]).

Ångström [57] was the first to investigate the heat conduction equation under the time-harmonic impact. An extensive literature on the so-called “oscillatory diffusion” can be found in [58,59]. The Ångström approach to measurement of material thermal properties still attracts the attention of researchers (see, for example, [60,61] and references therein).

It was shown in [62] that the telegraph equation has two harmonic wave solutions: temporally attenuated and spatially periodic (TASP) and spatially attenuated and temporally periodic (SATP). The standard telegraph equation with the time-harmonic source was considered in [63]. In the present paper, we develop the results of previous authors’ investigations [62,63] and study the time-fractional telegraph equation with moving time-harmonic source on a real line. Two characteristic versions of this equation are investigated: the “wave-type” with the second and Caputo fractional time-derivatives as well as the “heat-type” with the first and Caputo fractional time-derivatives. In both cases the order of fractional derivative 1 < α < 2. Numerical results are illustrated graphically for different values of nondimensional parameters introduced for both versions.

2. Fractional telegraph equation on a real line with moving time-harmonic source

2.1. The fractional telegraph equation of the “wave-type”

Consider the fractional telegraph equation of the “wave-type” with the time-harmonic source moving with the velocity v

$$\begin{gathered} \frac{{\partial }^{2}u}{\partial t^2}+{\zeta }_{\alpha }\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=c^2\frac{{\partial }^{2}u}{\partial x^2}-bu+Q_0\delta (x-vt){\mathrm{e}}^{i\omega t}, \\ -\infty <x<\infty ,1<\alpha <2, \end{gathered}$$ (22)

under zero initial conditions

$$t=0:u=0,$$ (23)

$$t=0:\frac{\partial u}{\partial t}=0.$$ (24)

The exponential Fourier transform with respect to the spatial coordinate x and the Laplace transform with respect to time t give the solution in the transform domain

$${\tilde{u}}^{\ast }(\xi ,s)=\frac{Q_0}{\sqrt{2\pi }}\frac{1}{s-i(\omega +v\xi )}\frac{1}{s^2+{\zeta }_{\alpha }{s}^{\alpha }+c^2{\xi }^2+b},$$ (25)

where the tilde denotes the Fourier transform, ξ is the transform variable.

Taking into account that

$${ℒ}^{-1}\left\{\frac{1}{s-i(\omega +v\xi )}\right\}={\mathrm{e}}^{i(\omega +v\xi )t}$$ (26)

and denoting

$${ℒ}^{-1}\left\{\frac{1}{s^2+{\zeta }_{\alpha }{s}^{\alpha }+c^2{\xi }^2+b}\right\}=G_W(\xi ,t),$$ (27)

after inverting the integral transforms using the convolution theorem, we get

$$u(x,t)=\frac{Q_0}{2\pi }{\int }_{-\infty }^{\infty }{\int }_0^t{G}_W(\xi ,\tau ){\mathrm{e}}^{-i[x-v(t-\tau )]\xi }{\mathrm{e}}^{i\omega (t-\tau )}\mathrm{d}\tau \mathrm{d}\xi$$ (28)

or, taking into account that G_W (ξ, τ) is an even function with respect to the Fourier transform variable ξ,

$$u(x,t)=\frac{Q_0}{\pi }{\int }_0^{\infty }{\int }_0^t{G}_W(\xi ,\tau )\cos \{[x-v(t-\tau )]\xi \}{\mathrm{e}}^{i\omega (t-\tau )}\mathrm{d}\tau \mathrm{d}\xi .$$ (29)

The representation of G_W (ξ, τ) amenable for numerical calculation is obtained using a method described by Beyer and Kempfle [64]. To evaluate the inverse Laplace transform, we bend the Bromwich path of integration into the equivalent Hankel path, a loop which starts from −∞ along the lower side of the negative real axis, encircles a small circle in the positive direction and ends at −∞ along the upper side of the negative real axis. In this case

$$s=r{\mathrm{e}}^{\pm i\pi },s^2=r^2,s^{\alpha }=r^{\alpha }[\cos (\alpha \pi )\pm i\sin (\alpha \pi )]$$ (30)

and

$${ℒ}^{-1}\left\{\frac{1}{s^2+{\zeta }_{\alpha }{s}^{\alpha }+c^2{\xi }^2+b}\right\}=K_1(\xi ,t)+K_2(\xi ,t).$$ (31)

Here

$$\begin{gathered} K_1(\xi ,t)=-\frac{1}{\pi }\Im \mathrm{m}{\int }_0^{\infty }\frac{{\mathrm{e}}^{-rt}}{r^2+{\zeta }_{\alpha }{r}^{\alpha }[\cos (\alpha \pi )+i\sin (\alpha \pi )]+c^2{\xi }^2+b}\mathrm{d}r \\ =\frac{\sin (\alpha \pi )}{\pi }{\int }_0^{\infty }\frac{{\zeta }_{\alpha }{r}^{\alpha }{\mathrm{e}}^{-rt}}{[r^2+{\zeta }_{\alpha }{r}^{\alpha }\cos (\alpha \pi )+c^2{\xi }^2+b{]}^2+[{\zeta }_{\alpha }{r}^{\alpha }\sin (\alpha \pi ){]}^2}\mathrm{d}r, \end{gathered}$$ (32)

$$K_2(\xi ,t)=\frac{2{\mathrm{e}}^{-\Psi t}}{p^2+q^2}[p\cos (\Omega t)+q\sin (\Omega t)],$$ (33)

where s_1,2 are simple, conjugate complex zeros of the denominator in Eq. (31)

$$s^2+{\zeta }_{\alpha }{s}^{\alpha }+{\xi }^2+b=0$$ (34)

on the principal branch of s^α (−π < arg s < π):

$$s_{1,2}=-\Psi \pm i\Omega .$$ (35)

These zeros are placed in the open left half-plane (ψ > 0 , Ω > 0) and

$$p\pm iq=2s_{1,2}+\alpha {\zeta }_{\alpha }{s}_{1,2}^{\alpha -1}.$$ (36)

Let L be the characteristic length. We introduce the following nondimensional quantities

$$\begin{gathered} \stackrel{‒}{x}=\frac{x}{L},\stackrel{‒}{t}=\frac{c}{L}t,\stackrel{‒}{\omega }=\frac{L}{c}\omega ,\stackrel{‒}{v}=\frac{v}{c}, \\ \stackrel{‒}{b}=\frac{L^2}{c^2}b,{\stackrel{‒}{\zeta }}_{\alpha }=\frac{L^{2-\alpha }}{c^{2-\alpha }}{\zeta }_{\alpha },\stackrel{‒}{u}=\frac{c^2}{L{Q}_0}u. \end{gathered}$$ (37)

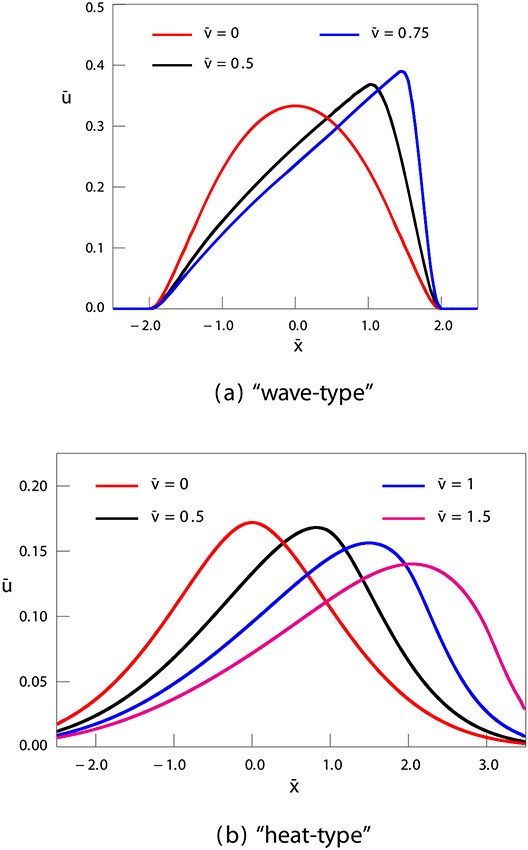
The results of numerical calculation of the real part of the solution (29) are presented in Figs. 1a-5a for different values of the order of derivative α and different values of nondimensional parameters (37).

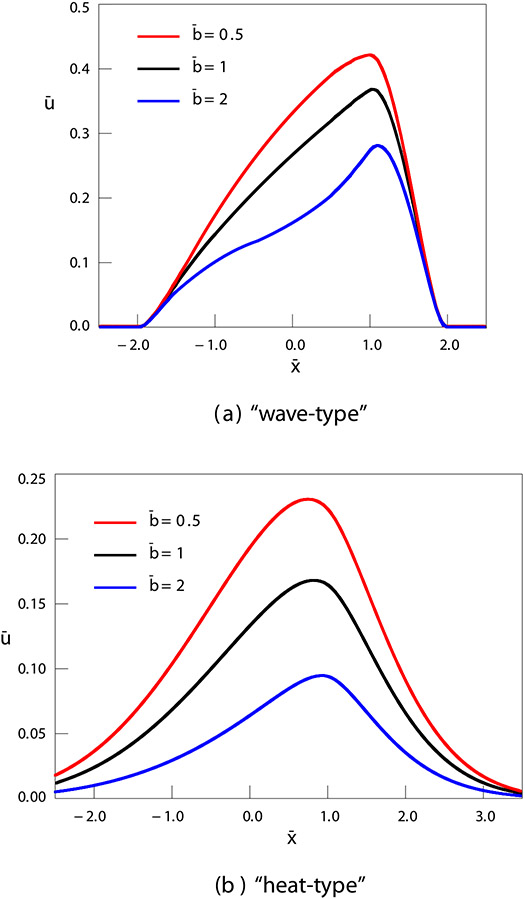
Fig. 1.

Dependence of the solution on distance for various values of nondimensional velocity of the source. The results of computer simulation for the values of parameters α = 1.5, $\stackrel{‒}{\omega }=\pi ∕4$, $\stackrel{‒}{b}=1$, ${\stackrel{‒}{\zeta }}_{\alpha }=0.5$. $\stackrel{‒}{t}=2$. (a) – solution (29); (b) – solution (41).

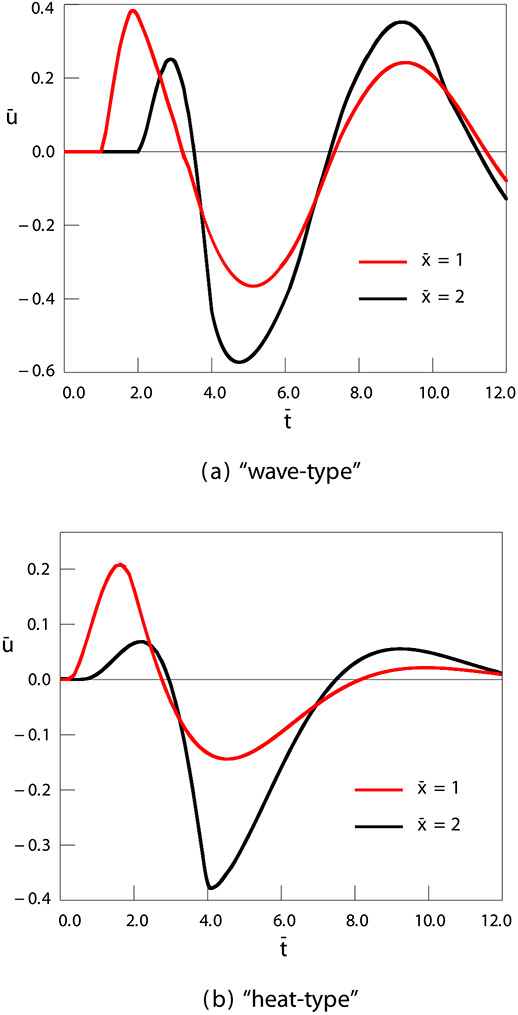
Fig. 5.

Dependence of the solution on time for various values of the spatial variable. The results of computer simulation for the values of parameters α = 1.5, $\stackrel{‒}{v}=0.5$, $\stackrel{‒}{\omega }=\pi ∕4$, ${\stackrel{‒}{\zeta }}_{\alpha }=0.5$, $\stackrel{‒}{b}=1$. (a) – solution (29); (b) – solution (41).

2.2. The fractional telegraph equation of the “heat-type”

Next we study the fractional telegraph equation of the “heat-type” with moving time-harmonic source:

$$\begin{gathered} \frac{\partial u}{\partial t}+{\zeta }_{\alpha }\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=a\frac{{\partial }^{2}u}{\partial x^2}-bu+Q_0\delta (x-vt){\mathrm{e}}^{i\omega t}, \\ -\infty <x<\infty ,1<\alpha <2, \end{gathered}$$ (38)

under zero initial conditions

$$t=0:u=0,$$ (39)

$$t=0:\frac{\partial u}{\partial t}=0.$$ (40)

The exponential Fourier transform with respect to the spatial coordinate x and the Laplace transform with respect to time t result in the solution

$$u(x,t)=\frac{Q_0}{\pi }{\int }_0^{\infty }{\int }_0^t{G}_H(\xi ,\tau )\cos \{[x-v(t-\tau )]\xi \}{\mathrm{e}}^{i\omega (t-\tau )}\mathrm{d}\tau \mathrm{d}\xi ,$$ (41)

where

$$G_H(\xi ,t)={ℒ}^{-1}\left\{\frac{1}{s+{\zeta }_{\alpha }{s}^{\alpha }+c^2{\xi }^2+b}\right\}=K_1(\xi ,t)+K_2(\xi ,t),$$ (42)

$$\begin{gathered} K_1(\xi ,t)=\frac{\sin (\alpha \pi )}{\pi }{\int }_0^{\infty } \\ \times \frac{{\zeta }_{\alpha }{r}^{\alpha }{\mathrm{e}}^{-rt}}{[-r+{\zeta }_{\alpha }{r}^{\alpha }\cos (\alpha \pi )+c^2{\xi }^2+b{]}^2+[{\zeta }_{\alpha }{r}^{\alpha }\sin (\alpha \pi ){]}^2}\mathrm{d}r, \end{gathered}$$ (43)

$$K_2(\xi ,t)=\frac{2{\mathrm{e}}^{-\Psi t}}{p^2+q^2}[p\cos (\Omega t)+q\sin (\Omega t)],$$ (44)

S_1,2 are simple, conjugate complex zeros of the denominator in Eq. (42)

$$s+{\zeta }_{\alpha }{s}^{\alpha }+{\xi }^2+b=0$$ (45)

on the principal branch of s^α

$$s_{1,2}=-\Psi \pm i\Omega ,\Psi >0,\Omega >0,$$ (46)

and

$$p\pm iq=1+\alpha {\zeta }_{\alpha }{s}_{1,2}^{\alpha -1}.$$ (47)

In this case, we introduce the nondimensional quantities

$$\begin{gathered} \stackrel{‒}{x}=\frac{x}{L},\stackrel{‒}{t}=\frac{a}{L^2}t,\stackrel{‒}{\omega }=\frac{L^2}{a}\omega ,\stackrel{‒}{v}=\frac{L}{a}v, \\ \stackrel{‒}{b}=\frac{L^2}{a}b,{\stackrel{‒}{\zeta }}_{\alpha }=\frac{a^{\alpha -1}}{L^{2\alpha -2}}{\zeta }_{\alpha },\stackrel{‒}{u}=\frac{a}{L{Q}_0}u. \end{gathered}$$ (48)

The results of numerical calculations of the real part of the solution (41) are presented in Figs. 1b-5b for different values of nondimensional parameters (48).

3. Discussion

For moving time-harmonic source, in the case of fractional telegraph equation of the “wave-type” there are two wave fronts and there appears the Doppler effect. Indeed, at least for small times t (the large values of the Laplace transform variable s), from Eqs. (25) and (28) we have the expression for the real part of the solution:

$$\Re \mathrm{e}u(x,t)=\{\begin{array}{cc}0,\hfill & -\infty <x<-ct,\hfill \\ \frac{Q_0}{2c\omega }\sin \left(\frac{c}{c+v}\omega t+\frac{\omega x}{c+v}\right),\hfill & -ct<x<vt,\hfill \\ \frac{Q_0}{2c\omega }\sin \left(\frac{c}{c-v}\omega t-\frac{\omega x}{c-v}\right),\hfill & vt<x<ct,\hfill \\ 0,\hfill & ct<x<\infty .\hfill \end{array}\phantom{\}}$$ (49)

It follows from Eq. (49) that there are two wave fronts at x = –ct and at x = ct, and the obtained solution describes the Doppler effect: at one side the angular frequency is

$${\omega }_1=\frac{c}{c+v}\omega ,$$ (50)

at another side the angular frequency equals

$${\omega }_2=\frac{c}{c-v}\omega .$$ (51)

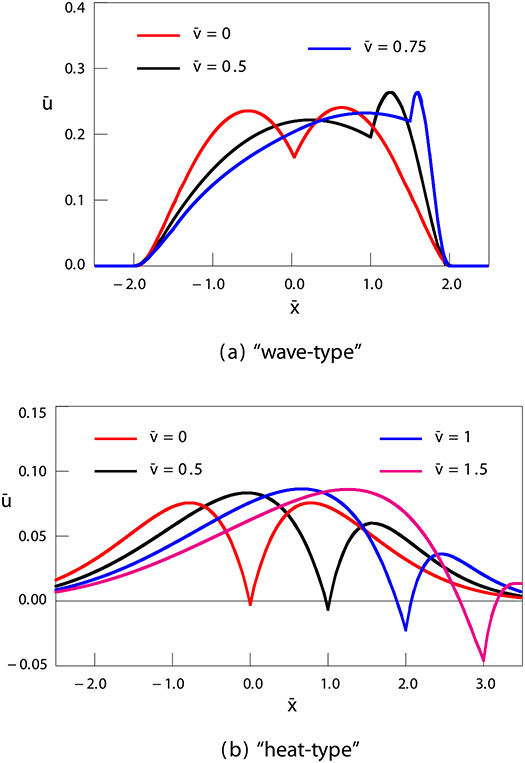
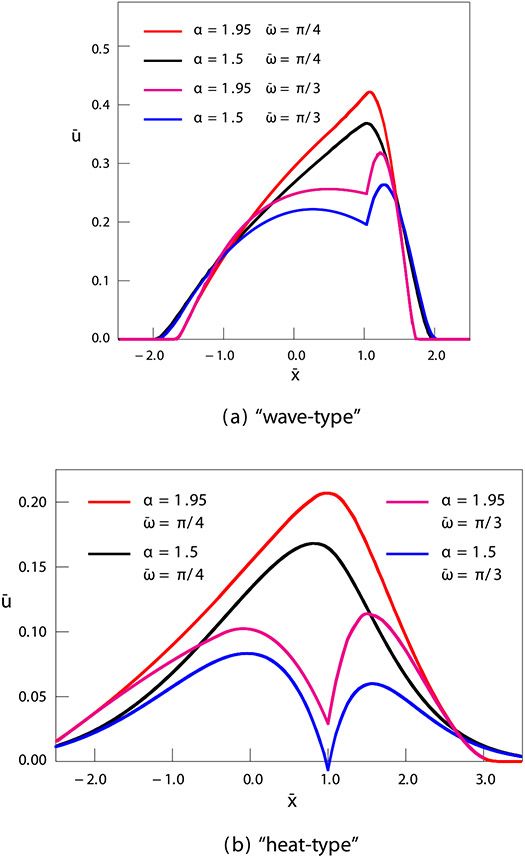
In the case of fractional telegraph equation of the “heat-type” the signal propagates with the infinite velocity with no Doppler effect. It should be noted that for equations of different types, we have introduced different definitions of nondimensional velocity (compare Eqs. (37) and (48)). For the fractional telegraph equation of the “wave-type” 0 ≤ v < c ($(0\le \stackrel{‒}{v}<1)$), we do not consider the source movement with the “supersonic velocity” v > c ($v>c(\stackrel{‒}{v}>1)$); for the fractional telegraph equation of the “heat-type”, there is no limitation on v. For some values of frequency, at $\stackrel{‒}{x}=\stackrel{‒}{v}\stackrel{‒}{t}$ there appear kinks on the curves describing the solution. Such kinks are clearly demonstrated in Figs. 2 and 4. In graphical representation of numerical results, we have used different scales due to large differences in wave amplitudes for various values of the nondimensional parameters.

Fig. 2.

Dependence of the solution on distance for various values of nondimensional velocity of the source. The results of computer simulation for the values of parameters α = 1.5, $\stackrel{‒}{\omega }=\pi ∕3$, $\stackrel{‒}{b}=1$, ${\stackrel{‒}{\zeta }}_{\alpha }=0.5$, $\stackrel{‒}{t}=2$. (a) – solution (29); (b) – solution (41).

Fig. 4.

Dependence of the solution on distance for various values of the order of fractional derivative. The results of computer simulation for the values of parameters $\stackrel{‒}{v}=0.5$, ${\stackrel{‒}{\zeta }}_{\alpha }=0.5$, $\stackrel{‒}{t}=2$, $\stackrel{‒}{b}=1$. (a) – solution (29); (b) – solution (41).

In the case of fractional telegraph equations it is impossible to consider the so-called “quasi-steady-state” solution corresponding to the representation of the sought-for function u(x, t) as a product of a function of the spatial coordinate U(x) and the time-harmonic term

$$u(x,t)=U(x){\mathrm{e}}^{i\omega t}$$ (52)

as for the fractional order Caputo derivative (11) of the exponential function, we have [65]

$$\frac{{\mathrm{d}}^{\alpha }{\mathrm{e}}^{\lambda t}}{\mathrm{d}{t}^{\alpha }}={\lambda }^{\alpha }{\mathrm{e}}^{\lambda t}\frac{\gamma (n-\alpha ,\lambda t)}{\Gamma (n-\alpha )}\ne {\lambda }^{\alpha }{\mathrm{e}}^{\lambda t},$$ (53)

where γ(a, x) is the incomplete gamma function

$$\gamma (a,x)={\int }_0^x{\mathrm{e}}^{-t}{t}^{a-1}\mathrm{d}t.$$ (54)

The “quasi-steady-state” solution can be considered for the time-fractional telegraph equation in which the Caputo derivative of the fractional order α is defined with the lower terminal at −∞ (see [66]). But in this case it is impossible to study problems with initial conditions.

The derived solutions can be successfully used when the source term can be expanded into a Fourier series. In this case the solution can be represented as a superposition of harmonic terms. The obtained results can also have medical applications (see, for example, [67]).

Fig. 3.

Dependence of the solution on distance for various values of the parameter $\stackrel{‒}{b}$. The results of computer simulation for the values of parameters α = 1.5, $\stackrel{‒}{\omega }=\pi ∕4$, $\stackrel{‒}{v}=0.5$, ${\stackrel{‒}{\zeta }}_{\alpha }=0.5$, $\stackrel{‒}{t}=2$. (a – solution (29); (b – solution (41).