Abstract
Cortical neuronal populations can use a multitude of codes to represent information, each with different advantages and trade-offs. The auditory cortex represents sounds via a sparse code, which lies on the continuum between a localist representation with different cells responding to different stimuli, and a distributed representation, in which each stimulus is encoded in the relative response of each cell in the population. Being able to dynamically shift the neuronal code along this axis may help with certain tasks that require categorical or invariant representations. Cortical circuits contain multiple types of inhibitory neurons which shape how information is processed within neuronal networks. Here, we asked whether somatostatin-expressing (SST) and vasoactive intestinal peptide-expressing (VIP) inhibitory neurons may have distinct effects on population neuronal codes, differentially shifting the encoding of sounds between distributed and localist representations. We stimulated optogenetically SST or VIP neurons while simultaneously measuring the response of populations of hundreds of neurons to sounds presented at different sound pressure levels. SST activation shifted the neuronal population responses toward a more localist code, whereas VIP activation shifted them towards a more distributed code. Upon SST activation, sound representations became more discrete, relying on cell identity rather than strength. In contrast, upon VIP activation, distinct sounds activated overlapping populations at different rates. These shifts were implemented at the single-cell level by modulating the response-level curve of monotonic and nonmonotonic neurons. These results suggest a novel function for distinct inhibitory neurons in the auditory cortex in dynamically controlling cortical population codes.
INTRODUCTION
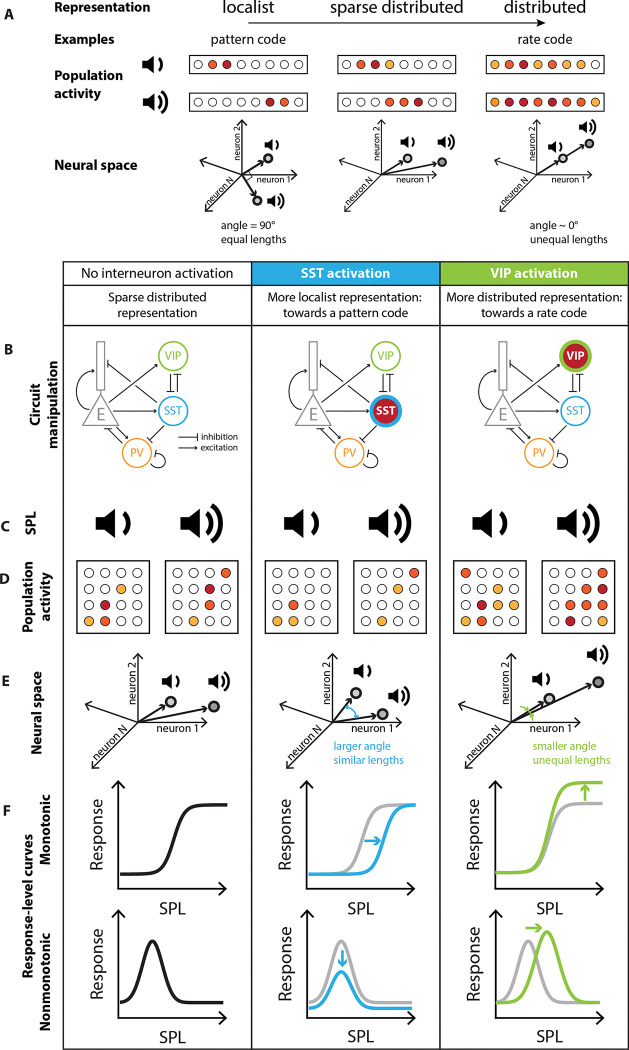
Within any specific brain region, neurons form intricate networks, which represent sensory information. A sensory stimulus elicits activity in a subset of neurons in a network. A neuronal network can use a multitude of codes to represent information. A stimulus can be encoded discretely with a localist, pattern-separated representation, in which a specific group of neurons represents a specific stimulus, and different stimuli elicit activity in different groups of neurons (Figure 1A, Supplementary Figure S1). Such localist representations have the advantage of discreteness: they can separate stimuli in different categories. Alternatively, in a distributed representation, stimulus-evoked activity can be distributed across the network, such that the relative activity of neurons within a group represent different stimuli (Figure 1A, Supplementary Figure S1). An example of a distributed representation is a rate code, in which the firing rate of the active neurons represent a continuously varying stimulus feature, such as intensity or sound location (Belliveau et al., 2014). Distributed representations have the advantage of invariance: a small change in stimulus parameter will elicit a small variation in the neural response. Along the auditory pathway, the coexistence of neurons with monotonic and nonmonotonic response-level curves indicates that sound pressure level is represented by both localist and distributed codes (Schreiner et al., 1992; Tan et al., 2007; Watkins and Barbour, 2011; Wu et al., 2006). More generally, stimulus representation within neural networks is mixed between local and distributed codes, in so-called sparse distributed representations, with both the level of activity and identity of activated neurons encoding the stimulus (Figure 1A) (Hromádka et al., 2008; Rolls and Tovee, 1995; Vinje and Gallant, 2000; Wixted et al., 2014). Based on the environmental and behavioral demands, it may be beneficial for neuronal representations to shift dynamically towards a more localist or a more distributed representation of a stimulus feature.
FIGURE 1: Predictions for testing for differential control of localist and distributed representations of sounds by inhibitory neurons.
A. A schematic of localist versus distributed neuronal codes. For additional implementations of these codes, see Figure S1. B. Neuronal circuit manipulation: Optogenetic stimulation of SST and VIP neurons in Auditory Cortex (simplified connectivity circuit). C. Noise bursts at different sound pressure levels (SPL) were presented to an awake mouse. D. For each sound pressure level, some neurons responded (filled circles) while many cells didn’t respond (empty circles). E. The response to different sound pressure levels can be described in the neural space by the separation angle between the mean population vectors and the length separating them. F. Changes to the representation of sound pressure level at the population level are implemented through changes to the response-level curve of each neuron. Gray: baseline; blue: response transformation with SST activation; green: response transformation with VIP activation.
Sensory cortical neuronal networks are comprised of multiple subtypes of neurons, including excitatory and inhibitory neurons. Inhibitory neurons can be divided into multiple sub-classes, including somatostatin-expressing (SST) and vasoactive intestinal peptide-expressing (VIP) neurons, which mutually inhibit each other (Campagnola et al., 2022). The activity of these neurons modulates stimulus representations in Auditory Cortex (AC). Specifically, activating SST neurons reduces and decorrelates cortical activity (Chen et al., 2015), sharpens frequency tuning of AC neurons (Phillips and Hasenstaub, 2016) and contributes to surround suppression (Lakunina et al., 2020) and adaptation to stimulus context (Natan et al., 2017, 2015). By contrast, VIPs disinhibit excitatory neurons (Millman et al., 2020), largely via their projections onto SST neurons (Pfeffer et al., 2013; Pi et al., 2013), without affecting frequency tuning (Bigelow et al., 2019) and can enable high-excitability states in the cortex (Jackson et al., 2016). VIP neurons furthermore are affected by neuromodulators (Chen et al., 2015; Fu et al., 2014; Zhang et al., 2014). Theoretically, inhibitory neurons in the sensory cortex may mediate the effect of neuromodulators in shifting the population responses between more localist and distributed representations (Haga and Fukai, 2021; Hertäg and Sprekeler, 2019a; Honey et al., 2017; King et al., 2013). Here, we hypothesized that SST and VIP neurons, with their differential effect on stimulus-evoked activity, may differentially mediate a localist or distributed representation, respectively.
To test this hypothesis, we studied the representation of noise bursts presented at different sound pressure levels in AC by imaging the responses of populations of hundreds of neurons while simultaneously activating SST or VIP neurons optogenetically (Figure 1B, Figure 2). First, we tested whether sound pressure level was best represented in the neural population by a localist or a distributed code and whether the code changed with SST or VIP activation (Figure 1C, D). We expected that SST neurons, which provide direct inhibition to excitatory cells and thus reduce sound responses, may promote a sparser, more localist representation while VIP neurons, which mediate disinhibition and thus lead to a more global activation of the network, may shift the network towards a more distributed representation. Next, we tested how the representation of sound pressure level changed in the neuronal space with and without SST and VIP activation (Figure 1E). We expected SST neurons to increase the separation angle between population vectors to different sound pressure levels, thereby shifting the population towards a more local code. We expected that VIP neurons may decrease the separation angle while strengthening the magnitude of response, shifting the encoding of sound pressure level towards a distributed representation. Finally, we tested whether and how changes in the response-level curves of monotonic and nonmonotonic individual neurons upon SST or VIP activation mediated the changes in representation at the population level (Figure 1F). We expected that activation of SSTs, which mediate surround suppression would narrow the bandwidth of individual cells and decrease overlap in responses between monotonic and nonmonotonic neurons. By contrast, we expected that activating VIPs, which amplify sound responses in excitatory neurons, potentially mediating the effects of neuromodulators, would broaden the bandwidth and increase the overlap between different neurons’ bandwidth.
FIGURE 2: EXPERIMENTAL SET UP AND OPTOGENETIC STIMULATION OF INTERNEURON POPULATIONS.
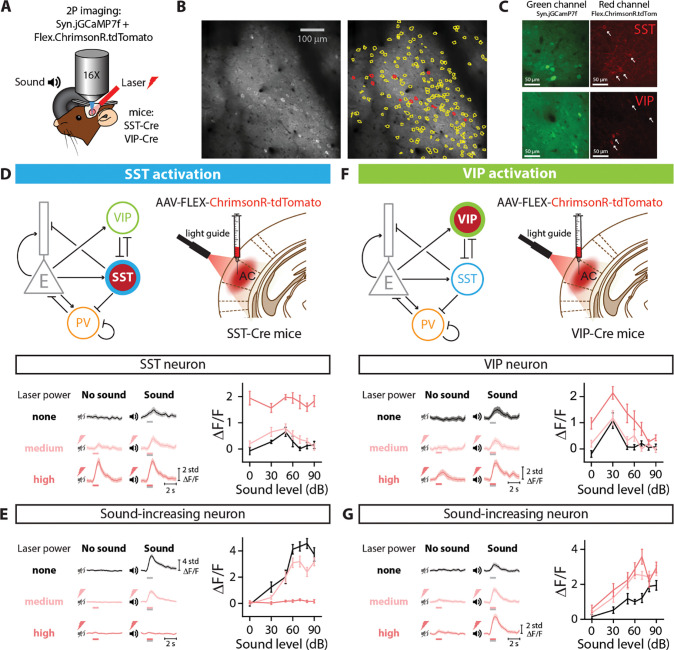
A. Two-photon imaging and laser stimulation through the round window of a mouse injected with viruses encoding Syn.jGCaMP7f and Flex.ChrimsonR.tdTomato in the left Auditory Cortex. Flex.ChrimsonR.tdTomato is injected in AC of SST-Cre and VIP-Cre mice, and is activated by a 635-nm laser. The mouse lines used were SST-Cre x Cdh23+/+ and VIP-Cre x Cdh23+/+. A speaker delivers a broadband noise stimulus at sound pressure levels within 0–90 dB to the right ear. B. Cell tissue with two-photon imaging in the green channel (left) and cell identification (right) using Suite2p software, with yellow lines delineating cell borders, and red lines indicating the neurons expressing ChrimsonR.tdTomato. C. Signal in the green channel (left panels) and red channel (right panels) of a SST-Cre mouse (top panels) and an VIP-Cre mouse (bottom panels). Cells identified as VIP or SST interneurons are indicated with an arrow (see Methods). D. (Top) diagrams for optognetic manipulation circuit and experimental set-up. (Bottom left) Response of a SST neuron to no sound and sound stimulation (50 dB) when activating SST neurons with different laser powers. (Bottom right) Average fluorescence over a 1-s fixed time window as a function of sound pressure level for the example cell in the left panel. E. (Left) Response of a sound-increasing neuron to no sound and sound stimulation (70 dB) when activating SST neurons with different laser powers. (Right) Average fluorescence over a 1-s fixed time window as a function of sound pressure level for the example cell in the left panel. F. (Top) diagrams for optognetic manipulation circuit and experimental set-up. (Bottom l eft) Response of a VIP neuron to no sound and sound stimulation (70 dB) when activating VIP neurons with different laser powers. (Bottom right) Average fluorescence over a 1-s fixed time window as a function of sound pressure level for the example cell in the left panel. G. (Left) Response of a sound-increasing neuron to no sound and sound stimulation (70 dB) when activating VIP neurons with different laser powers. (Right) Average fluorescence over a 1-s fixed time window as a function of sound pressure level for the example neuron in the left panel. For all panels, black, pink and red colors correspond to no laser power (0 mW/mm2), medium laser power (~0.3 mW/mm2) and high laser power (~3.5 mW/mm2), respectively (see Methods for power calibration). The gray and red bars below the example traces in panels D-G indicate the presence of the sound and laser stimulus, respectively.
RESULTS
SST and VIP activation modulate the response of sound-increasing neurons
To investigate whether and how distinct classes of inhibitory neurons in AC, SSTs and VIPs, mediate localist or distributed representations of stimuli by cortical neurons, we imaged Calcium activity of neurons in AC of awake, head-fixed mice presented with sounds while activating SSTs or VIPs using sub-millisecond optogenetic manipulation with Chrimson (Figure 2A) (Klapoetke et al., 2014). We monitored calcium activity by measuring fluorescence of GCaMP expressed in hundreds of neurons at a time (VIP-Cre mice: 3321 neurons over 16 recordings, SST-Cre mice: 2284 neurons over 13 recordings) and identified the cells expressing the opsin through co-expression of tdTomato (Figure 2B and 2C). This approach allowed us to quantify the transformations of sound representations within a large population of cortical neurons driven by SST or VIP activation.
We first confirmed that the optogenetic manipulations produced expected responses. SST neurons directly inhibit excitatory cells and other cells within the neural population, and so we expected that optogenetic manipulation would increase SST neuronal activity, but decrease the responses of other cells. By contrast, VIP cells mostly inhibit other inhibitory neurons (Campagnola et al., 2022), and therefore we expected the VIP activation would increase both VIP neuronal activity and provide a release of inhibition to other cells in the network. In SST-Cre mice, a representative SST neuron increased activity at all sound pressure levels with laser power (example neuron, ***plaser=1.8e-13, GLME, Figure 2D). The change in the response of a representative non-SST neuron to SST activation was sound level-dependent, with a decrease at most sound pressure levels for the medium laser power. Sound responses were abolished with strong SST activation at the high laser power (plaser=0.74, ***plaser:sound=1.0e-14, GLME, Figure 2E). In VIP-Cre mice, the response of a representative VIP neuron increased at all sound pressure levels with laser power and the increase was sound-level dependent (example neuron, ***plaser=1.8e-7, *plaser:sound=1.1e-2, GLME, Figure 2F). The activity of a representative non-VIP neuron increased at most sound pressure levels during activation of VIPs, with a larger increase at the high than medium laser power (*plaser=1.5e-2, GLME, Figure 2G). As a control, we injected mice with Flex.tdTomato instead of the opsin in VIP-Cre x Cdh23 mice (n=5), and verified that laser stimulation of AC in the absence of the opsin did not lead to significant changes in the neuronal responses of VIP neurons (plaser=0.20, GLME, Supplementary Figure S2A) and non-VIP neurons (plaser=0.64, GLME, Supplementary Figure S2B). These representative effects of SST or VIP activation are consistent with previous reports of their connectivity, suggesting that the activation method worked as expected.
The representation of sound pressure level is more localist with SST activation and more distributed with VIP activation
We next tested whether sound pressure level was best represented in the neural population by a localist or distributed code, and whether and how SST and VIP activation shifted the population responses between theses modes. We characterized the response of each cell over its optimal time window for each sound and laser combination (Figure 3 panels A and F; see Methods) and the response of each population to any stimulus combination over its fixed time window (Figure 3 panels B-C and G-H, see Methods).
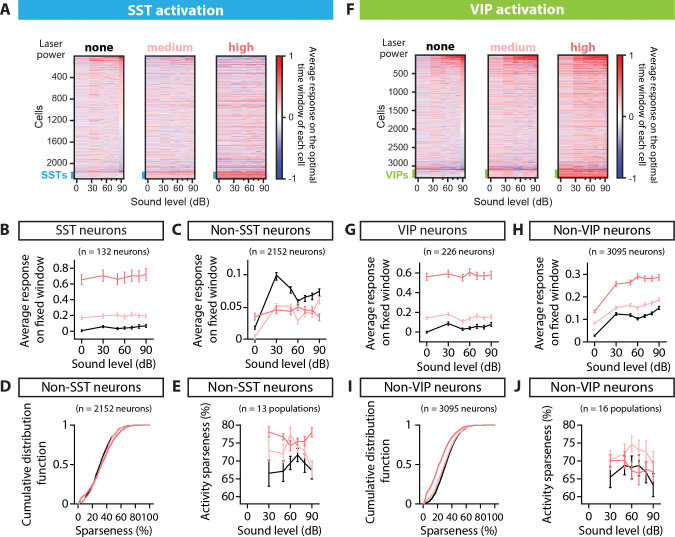
FIGURE 3: POPULATION RESPONSE TO SST AND VIP ACTIVATION AND SPARSENESS.
A. Rasters of the average fluorescence versus sound pressure level for all neurons imaged in the SST-Cre mice, calculated over the optimal time window for each cell and each sound and laser condition (see Methods). Rasters from left to right correspond to SST activation with no laser power, medium laser power and high laser power. The thick blue line at the bottom of each raster indicates the SST interneurons. Cells are ordered given their response at 90dB and no laser power. B. Average fluorescence over a 1-s fixed window as a function of sound pressure level for the whole population of SST neurons recorded (132 neurons), when the SST population is activated. C. Average fluorescence over a 1-s fixed window as a function of sound pressure level for the whole population of non-SST neurons recorded (2152 neurons), when the SST population is activated. D. Cumulative distribution function of sparseness for the population of non-SST neurons, when the SST population is activated. E. Average activity sparseness as a function of sound pressure level for each population of neurons (SST neurons excluded), when the SST population is activated. F. Rasters of the average fluorescence versus the sound pressure level for all neurons imaged in the VIP-Cre mice, calculated over the optimal time window for each cell and each sound and laser condition (see Methods). Rasters from left to right correspond to VIP activation with no laser power, medium laser power and high laser power. The thick green line at the bottom of each raster indicates the VIP interneurons. Cells are ordered given their response at 90dB and no laser power. G. Average fluorescence over a 1-s fixed window as a function of sound pressure level for the whole population of VIP neurons recorded (226 neurons), when the VIP population is activated. H. Average fluorescence over a 1-s fixed window as a function of sound pressure level for the whole population of non-VIP neurons recorded (3095 neurons), when the VIP population is activated. I. Cumulative distribution function of sparseness for the population of non-VIP neurons, when the VIP population is activated. J. Average activity sparseness as a function of sound pressure level for each population of neurons (VIP neurons excluded) when the VIP population is activated. For all panels, black, pink and red colors correspond to no laser power (0 mW/mm2), medium laser power (~0.3 mW/mm2) and high laser power (~3.5 mW/mm2), respectively (see Methods for power calibration).
Because SSTs directly inhibit excitatory cells, we hypothesized that SST activation would lead to fewer neurons responding at increasing sound pressure levels, reflective of a sparser, more localist stimulus representation. During the SST activation, the average response of SST neurons increased at all sound pressure levels (n=132 SST neurons, ***plaser<1e-100, GLME, Figure 3A–B), whereas non-SST neurons exhibited a mix of decreased and increased responses (Figure 3A). The overall effect of SST activation on the population of non-SST neurons was sound-dependent, with a significant interaction term between sound and laser amplitude, but not laser alone (n=2152 neurons, plaser=0.20, ***plaser:sound=2.2e-10, GLME, Figure 3C). The average response-level curve for non-SST neurons shifted downwards for the medium laser power, and at a high laser power, the modulation of the population’s response by sound was lost with an average response to silence equal to the average response to sounds, consistent with expectations for a more localist distribution (Polley et al., 2004).
To further assess the representation of sound pressure level in the neuronal population, we studied two characteristics of sparse distributed representations: (1) each neuron responds only to a few stimuli (high sparseness) and (2) only a few neurons respond to each stimulus (high activity sparseness). To measure how many stimuli a neuron responds to, we computed the sparseness of each non-SST neuron (see Methods). The sparseness of non-SST neurons increased for 70% of the neurons, with a significant increase from 31% to 33% upon SST activation (median, n=2152 neurons, ***plaser=7.1e-4, GLME, Figure 3D), indicating that neurons responded to fewer stimuli. To measure how many neurons responded to each stimulus, we computed the activity sparseness for each population of non-SST neurons, which is the ratio of neurons that are not active in response to a given stimulus, compared to silence at a given laser power. The activity sparseness increased significantly upon SST activation (n=13 populations, **plaser=1.6e-3, GLME, Figure 3E), indicating that at each successive sound pressure level, there were fewer non-SST neurons that were active.
Because VIPs provide a release of SST inhibition on excitatory cells, we hypothesized that VIP activation would lead to more neurons active in response to each sound level and with stronger responses, reflective of a more distributed stimulus representation. When VIP neurons were activated, the average response of VIP neurons increased at all sound pressure levels (n=226 VIP neurons, ***plaser<1e-100, GLME, Figure 3F–G). Non-VIP neurons similarly exhibited an increase in response, both in silence and to sounds at different sound pressure levels (Figure 3F). The average response-level curve for non-VIP neurons shifted upwards at all sound pressure levels as VIP neurons were activated (n=3095 neurons, ***plaser<1e-100, GLME, Figure 3H). At all laser powers, the modulation of the population’s response by sound was maintained: the population average to sounds was higher than to silence. Neuronal sparseness decreased for all neurons, with a significant decrease from 32% to 22% upon VIP activation (median, n=3095 neurons, ***plaser<1e-100, GLME, Figure 3I), indicating that each neuron responded more equally to the different sound pressure levels. The activity sparseness measured from silence at a given laser power did not change upon VIP activation (n=16 populations, plaser=0.44, GLME, Figure 3J), indicating that the same number of neurons showed an increase in response at each sound pressure level from silence at a given laser power. Consistent with the overall increase in responses with VIP activation in silence, the activity sparseness measured from silence at no laser power significantly decreased (Supplementary Figure S3).
Overall, SST activation led to weaker and sparser responses in the population, with neurons responding to fewer stimuli and each stimulus eliciting a response in fewer neurons. This suggests that SST activation shifts the population responses toward a more localist stimulus representation. By contrast VIP activation leads to a global increase in the neural population’s response, along with each neuron responding to more stimuli. This suggest that VIP activation leads to a more distributed stimulus representation.
Sound pressure level is represented more discretely or continuously in the neural population with SST or VIP activation, respectively.
There are various ways that a neuronal network can implement a localist or distributed representation of a sensory feature. For example, a distributed code may rely on the magnitude of response of the population of neurons (rate code, Figure 1A) or on the relative response of each cell (Supplementary Figure S1). To investigate this, we examined next the properties of the representation of sound pressure level upon SST and VIP activation in the neuronal space. We computed the mean population vector from 0dB at a given laser amplitude to each nonzero sound pressure level at that laser amplitude (Figure 4A), and computed the separation angle between pairs of mean population vectors at the same laser power (Figure 4B), as well as the length of mean population vectors between pairs of sounds (Figure 4C).
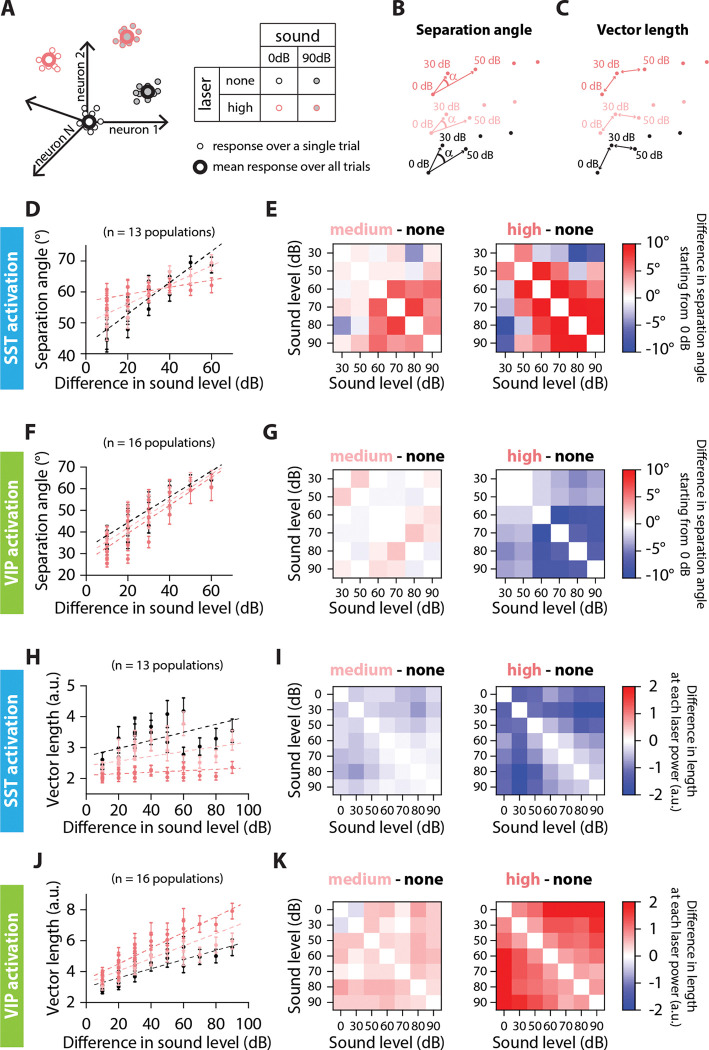
FIGURE 4: SEPARATION ANGLE AND VECTOR LENGTH ARE DIFFERENTIALLY CONTROLLED BY SST AND VIP ACTIVATION.
A. Schematic representation of the population’s response to sound and laser stimulation, for single trials (small dots) and the average response over all trials (large dots). Sound pressure level is represented by the shading of the dot, laser power by the outline of the dot. We simplify the representation of the population’s response to two dimensions, keeping only the color code for the laser power. This simplified representation is then used schematically in panels B and C and in Supplementary Figure S4. B. Low-dimensional schematic of the separation angle between mean population vectors to each sound pressure level at a given laser power, starting from 0dB at each laser power. C. Low-dimensional schematic of the vector length of mean population vectors between sound pressure levels at a given laser power. D. Separation angle between pairs of mean population vectors to different sound pressure levels as a function of the difference in sound pressure level for no, medium and high laser powers of SST activation (circles). The dotted lines are the result from the GLME fit at the different laser powers of SST activation. E. Confusion matrix of the difference in separation angle between pairs of sound stimuli from medium (left) or high (right) laser power to no laser power of SST activation. F. Separation angle between pairs of mean population vectors to different sound pressure levels as a function of the difference in sound level for no, medium and high laser powers of VIP activation (circles). The dotted lines are the result from the GLME fit at the different laser powers of VIP activation. G. Confusion matrix of the difference in separation angle between pairs of sound stimuli from medium (left) or high (right) laser power to no laser power of VIP activation. H. Length of the mean population vector between pairs of sound pressure levels as a function of the difference in sound pressure level for no, medium and high laser powers of SST activation (circles). The dotted lines are the result from the GLME fit at the different laser powers of SST activation. I. Confusion matrix of the difference in vector length between pairs of sound stimuli from medium (left) or high (right) laser power to no laser power of SST activation. J. Length of the mean population vector between pairs of sound pressure levels as a function of the difference in sound pressure level for no, medium and high laser powers of VIP activation (circles). The dotted lines are the result from the GLME fit at the different laser powers of VIP activation. K. Confusion matrix of the difference in vector length between pairs of sound stimuli from medium (left) or high (right) laser power to no laser power of VIP activation. For all panels, black, pink and red colors correspond to no laser power (0 mW/mm2), medium laser power (~0.3 mW/mm2) and high laser power (~3.5 mW/mm2), respectively (see Methods for power calibration).
The separation angle (Vinje and Gallant, 2000) computes the angle between the mean population vectors to two different sound pressure levels taking 0dB at each laser power as the origin (Figure 4B). A smaller angle indicates the population vectors are more collinear, meaning similar neurons respond to the different stimuli, although perhaps with differing magnitude. A larger angle indicates that there is less overlap between the populations of neurons responding to each stimulus (Figure 1D–E).
When there is no interneuron activation, the separation angle increased with the difference in sound level (Figure 4D and F, black circles), indicating that there is less overlap in the groups of neurons responding to sounds with a large difference in sound pressure level than a small difference in sound pressure level. Upon SST activation, the curve flattened around 60°, meaning that there was an increase in separation angle for small differences in sound pressure level, and a decrease in separation angle for large differences in sound pressure level (dotted lines correspond to GLME estimates, ***plaser=1.6e-17, ***pΔsound=2.3e-31, ***plaser:Δsound=3.6e-13, GLME, Figure 4D and Figure S4A). On average, the difference in separation angle between sound pairs from medium or high laser to no laser was positive, at 3.7° ± 1.7° for the high laser power (mean ± s.e.m, 15 angles, Figure 4E). This indicates that the population vectors to the different tested sound pressure levels were more equally distributed in the neuronal space. There is, however, still an overlap between groups of neurons responding to different sound pressure levels, as a fully orthogonal coding of sound pressure level would lead to a 90° separation angle. In contrast, upon VIP activation, the separation angle decreased equally for all differences in sound pressure level (dotted lines correspond to GLME estimates, **plaser=6.1e-3, ***pΔsound=6.9e-13, plaser:Δsound=0.47, GLME, Figure 4F and Figure S4B). On average, the difference in separation angle between sound pairs from medium or high laser to no laser was negative, at − 4.6° ± 0.7° degrees at the high laser power (mean ± s.e.m, 15 angles, Figure 4G). This indicates that the population vectors to the different tested sound pressure levels were more collinear, with more overlap between groups of neurons responding to different sound pressure levels with VIP activation.
The vector length computes the Euclidian norm of the mean population vector between two sound pressure levels at a given laser power (Figure 4C). A small length indicates that the responses to two different stimuli are close in the neural space, either due to small magnitudes of response, to small differences in separation angle or both, whereas a large length indicates that there is a large difference in magnitude, in separation angle or both. Therefore, we tested whether SST and VIP activation differentially affected the Euclidian norm.
Upon SST activation, the vector length decreased for all sound pressure level differences to about 2 a.u. at high laser power, along with a decrease in the slope of the GLME estimate by 81% at high laser power (dotted lines correspond to GLME estimates, ***plaser=2.9e-6, ***pΔsound=1.6e-8, ***plaser:Δsound=3.8e-4, GLME, Figure 4H and Figure S4C). The average change in length from medium or high laser power to no laser was negative, at −1.00 ± 0.10 a.u. for the high laser power (mean ± s.e.m, 21 lengths, Figure 4I). Upon VIP activation, the vector length increased for all sound pressure level differences, and the slope of the GLME estimate also increased by 72% at high laser power (dotted lines correspond to GLME estimates, *plaser=1.2e-2, ***pΔsound=6.1e-5, ***plaser:Δsound=1.5e-6, GLME, Figure 4J and Figure S4D). The average change in length from medium or high laser power to no laser was positive, at 1.27 ± 0.12 a.u. for the high laser power (mean ± s.e.m, 21 lengths, Figure 4K).
Combined with the differences in the separation angle, these results point to emergence of two types of coding: Upon SST activation, the encoding of sound pressure level resembles a localist pattern coding where the magnitude of response is less relevant than the identity of responding cells: the strength of response is reduced and similar for all sound pressure levels, but the population vectors are more spread out in neuronal space, indicating that there is less overlap between groups of neurons responding to different sound pressure levels. Upon VIP activation, the encoding of sound pressure level resembles a rate code, which is a type of distributed representation in which the varying strength of the whole population encodes a continuously varying parameter of the stimulus. Therefore, VIP activation promotes the strength of response more than the identity of responding neurons: there is more overlap between the groups of neurons responding to different sound pressure levels, but the strength of response is increased.
Response-level curves of sound-modulated cells exhibit a narrower response upon SST activation, and a broader response upon VIP activation
We next tested how the shifts in stimulus representation mediated by SST and VIP neurons at the scale of the neural population are implemented at the single-cell level by analyzing the changes with SST or VIP activation in response-level curves of single neurons responding positively to sound. Some AC neurons exhibit increased responses with increased sound pressure levels (monotonic response-level curve) while others are tuned with a peak response to a specific sound pressure level (nonmonotonic response-level curve) (Phillips et al., 1995; Schreiner et al., 1992; Wu et al., 2006). We classified cells depending on their Monotonicity Index (MI, see Methods) and fit response functions of monotonically responding cells with a Sigmoid function (Figure 5, Supplementary Figure S5A, see Methods) and those of non-monotonically responding cells with a Gaussian function (Figure 6, Supplementary Figure S5B, see Methods). We then tested how the parameters of the fits change with interneuron activation.
FIGURE 5: SINGLE-CELL FITS OF RESPONSE-LEVEL CURVES FOR MONOTONIC CELLS.
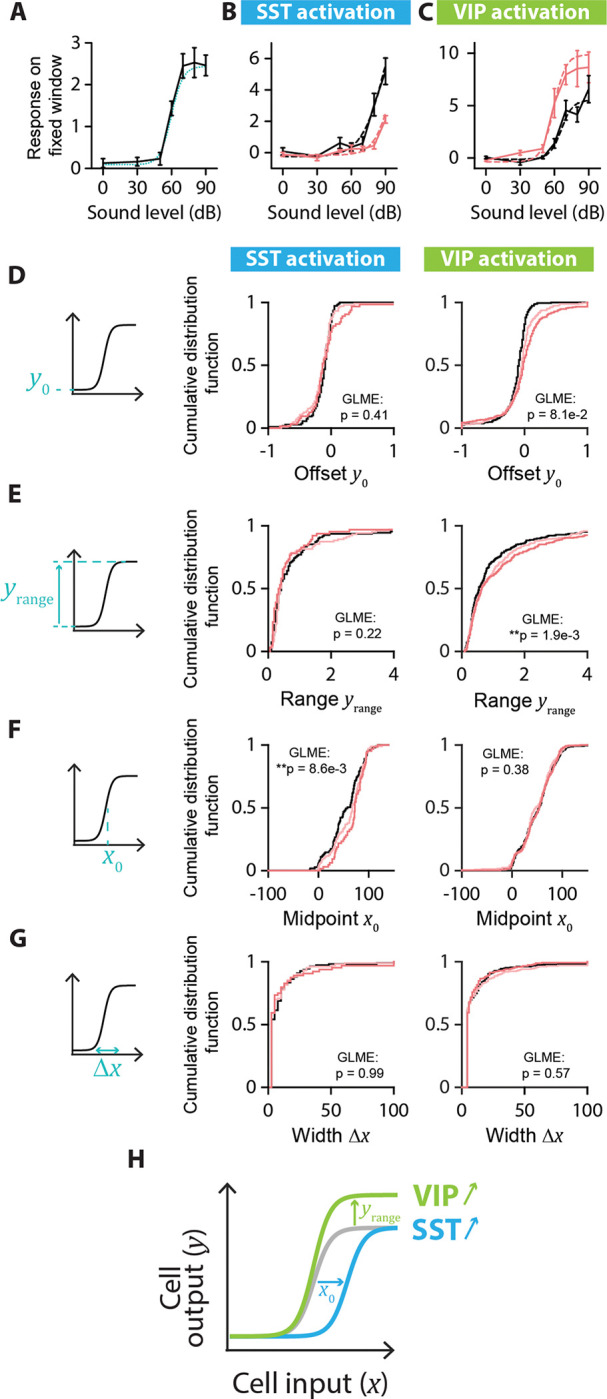
A. Example neuron with a monotonic response-level curve (solid black line) with a sigmoid fit (dotted blue line). The parameters for the sigmoid fit are: Offset amplitude y0 = 0.1; Range yrange = 2.4; Midpoint x0 = 60 dB; Width Δx = 5 dB. B. Example of changes to the response-level curve of a sound-increasing monotonic neuron upon SST activation. Response-level curves (solid lines) are fit by sigmoid functions (dotted lines) at no (black lines) and high (red lines) laser powers of SST activation. The parameters for the sigmoid fit are, for no SST activation: y0 = −0.3; yrange = 13.4; x0 = 93 dB; Δx = 11 dB; and for SST activation: y0 = −0.2; yrange = 8.6; x0 = 96 dB; Δx = 8 dB. C. Example of changes to the response-level curve of a sound-increasing monotonic neuron upon VIP activation. Response-level curves (solid lines) are fit by sigmoid functions (dotted lines) at no (black lines) and high (red lines) laser powers of VIP activation. The parameters for the sigmoid fit are, for no VIP activation: y0 = −0.1; yrange = 5.6; x0 = 66 dB; Δx = 5 dB; and for VIP activation: y0 = −0.4; yrange = 9.9; x0 = 60 dB; Δx = 5 dB. D. Schematic showing the offset amplitude y0 parameter of the sigmoid fit (left panel) and cumulative distribution function of y0 for monotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. E. Schematic showing the amplitude range yrange parameter of the sigmoid fit (left panel) and cumulative distribution function of yrange for monotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. F. Schematic showing the midpoint x0 parameter of the sigmoid fit (left panel) and cumulative distribution function of x0 for monotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. G. Schematic showing the width Δx parameter of the sigmoid fit (left panel) and cumulative distribution function of Δx for monotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. H. Schematic of the mean significant changes to the response-level curve of a monotonic sound-increasing cell (gray line) upon SST (blue line) and VIP (green line) activation. For all panels, black, pink and red colors correspond to no laser power (0 mW/mm2), medium laser power (~0.3 mW/mm2) and high laser power (~3.5 mW/mm2), respectively (see Methods for power calibration). For all panels, the statistical test GLME was performed on the distributions at the three different levels of interneuron activation, with n.s. corresponding to non-significant, * corresponds to p<0.05, ** corresponds to p<0.01, *** corresponds to p<0.001. There are n=109, n=103 and n=64 sound-increasing monotonic cells fit at no, medium and high laser powers of SST activation, respectively. There are n=267, n=239 and n=269 sound-increasing monotonic cells fit at no, medium and high laser powers of VIP activation, respectively.
FIGURE 6: SINGLE-CELL FITS OF RESPONSE-LEVEL CURVES FOR NONMONOTONIC CELLS.
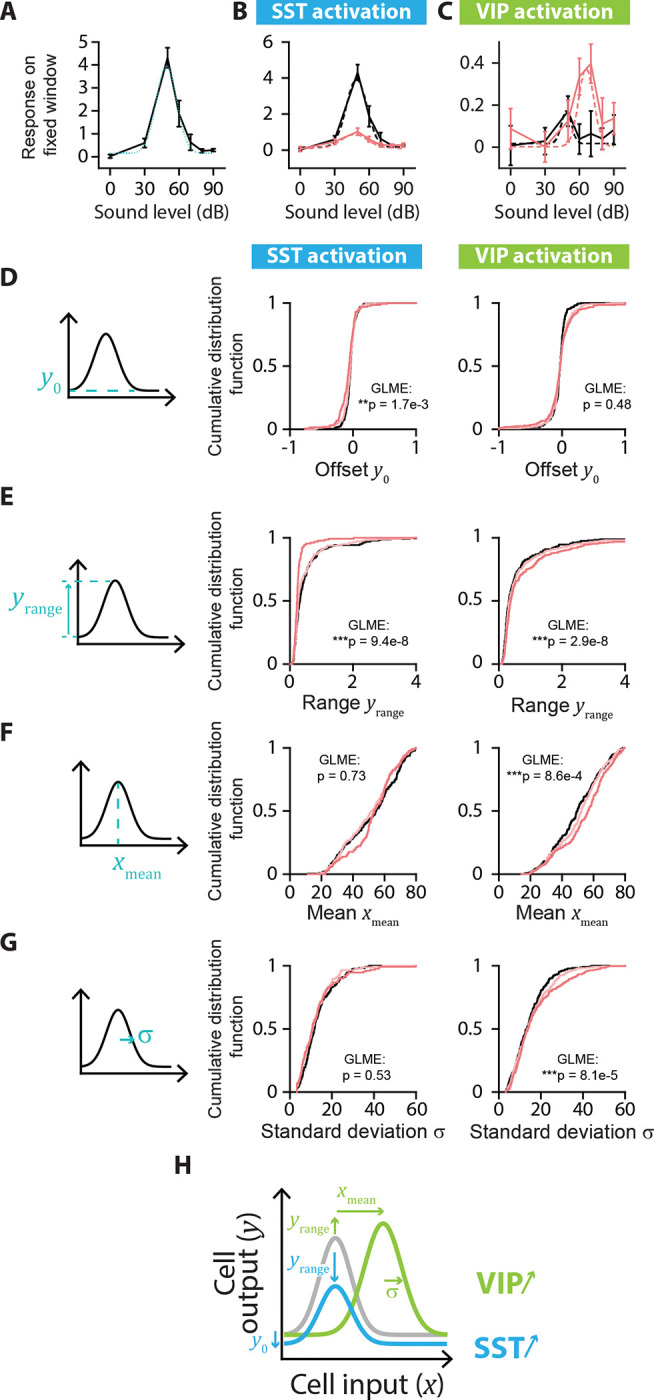
A. Example neuron with a nonmonotonic response-level curve (solid black line) with a Gaussian fit (dotted blue line). The parameters for the Gaussian fit are: Offset amplitude y0 = 0.15; Range yrange = 3.8; Mean xmean = 49 dB; Standard Deviation s = 9 dB. B. Example of changes to the response-level curve of a sound-increasing nonmonotonic neuron upon SST activation. Response-level curves (solid lines) are fit by Gaussian functions (dotted lines) at no (black lines) and high (red lines) laser powers of SST activation. The parameters for the Gaussian fit are, for no SST activation: y0 = 0.2; yrange = 3.8; xmean = 49 dB; σ = 9 dB; and for SST activation: y0 = 0.1; yrange = 0.8; xmean = 47 dB; σ = 11 dB. C. Example of changes to the response-level curve of a sound-increasing nonmonotonic neuron upon VIP activation. Response-level curves (solid lines) are fit by Gaussian functions (dotted lines) at no (black lines) and high (red lines) laser powers of VIP activation. The parameters for the Gaussian fit are, for no VIP activation: y0 = 0.0; yrange = 0.2; xmean = 49 dB; σ = 4 dB; and for VIP activation: y0 = 0.0; yrange = 0.4; xmean = 66 dB; σ = 7 dB. D. Schematic showing the offset amplitude y0 parameter of the Gaussian fit (left panel) and cumulative distribution function of y0 for nonmonotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. E. Schematic showing the amplitude range yrange parameter of the Gaussian fit (left panel) and cumulative distribution function of yrange for nonmonotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. F. Schematic showing the mean xmean parameter of the Gaussian fit (left panel) and cumulative distribution function of xmean for nonmonotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. G. Schematic showing the standard deviation σ parameter of the Gaussian fit (left panel) and cumulative distribution function of σ for nonmonotonic sound-increasing neurons at different laser powers of SST (middle panel) and VIP (right panel) activation. H. Schematic of the mean significant changes to the response-level curve of a nonmonotonic sound-increasing cell (gray line) upon SST (blue line) and VIP (green line) activation. For all panels, black, pink and red colors correspond to no laser power (0 mW/mm2), medium laser power (~0.3 mW/mm2) and high laser power (~3.5 mW/mm2), respectively (see Methods for power calibration). For all panels, the statistical test GLME was performed on the distributions at the three different levels of interneuron activation, with n.s. corresponding to non-significant, * corresponds to p<0.05, ** corresponds to p<0.01, *** corresponds to p<0.001. There are n=224, n=175 and n=130 sound-increasing nonmonotonic cells fit at no, medium and high laser powers of SST activation, respectively. There are n=243, n=278 and n=310 sound-increasing nonmonotonic cells fit at no, medium and high laser powers of VIP activation, respectively.
We first characterized the responses of sound-modulated cells that exhibited a monotonic response-level curve by fitting this curve for individual cells at different levels of laser power (Figure 5A–C). Out of the four sigmoidal fit parameters (Figure 5D–G, middle panels), only the midpoint of the sigmoid fit exhibited a significant change upon SST activation from 58 dB at no laser power to 73 dB at high laser power (median values, n=109; 103 and 64 neurons for no, medium and high laser power, respectively; offset: plaser=0.41; range: plaser=0.22; midpoint: **plaser=8.6e-3; width: plaser=0.99; GLME, Figure 5D–G, middle panels). With VIP activation, only the range of the sigmoid fit showed a significant increase (n=267, 239 and 269 neurons for no, medium, and high laser power, respectively; offset: plaser=0.081; range: **plaser=1.9e-3; midpoint: plaser=0.38; width: plaser=0.57; GLME, Figure 5D–G, right panels). Thus, SST activation leads to monotonic response-level functions that are shifted rightwards towards higher sound pressure levels, leading to responses to a narrower range of sounds at higher sound pressure levels. VIP activation expanded the neuronal response-level curves upwards, leading to responses for a broader range of sound pressure levels (Figure 5H).
We then characterized the responses of sound-modulated cells that exhibited a nonmonotonic response-level curve by fitting this curve for individual cells at different levels of laser power (Figure 6A–C). Whereas the mean and standard deviation of the Gaussian fit remained unchanged (mean: plaser=0.73; standard deviation: plaser=0.53; GLME, Figure 6F–G, middle panels), the offset and the range of the Gaussian fit decreased with SST activation (n=224, 175 and 130 neurons for no, medium and high laser power, respectively; offset: **plaser=1.7e-3; range: ***plaser=9.4e-8; GLME, Figure 6D–E, middle panels). The offset of response did not change with VIP activation (offset: plaser=0.48, GLME, Figure 6D, right panel), whereas the range increased significantly as well as the Gaussian mean and standard deviation (n=243, 278 and 310 neurons for no, medium and high laser power, respectively; range: ***plaser=2.9e-8; mean: ***plaser=8.6e-4; standard deviation: ***plaser=8.1e-5; GLME, Figure 6E–G, right panels). Thus, SST activation leads to nonmonotonic response-level functions that were shifted downwards with a decreased range of responses, leading to responses above noise level to a narrower range of sound pressure levels. VIP activation shifted the neuronal response-level curves rightwards with an increased range of response, leading to increased peak responses at higher sound pressure levels (Figure 6H).
These results demonstrated that SST activation promotes a more localist representation of sound pressure level at the population scale by changes to the response-level curves of sound-modulated neurons that elicited responses above noise level over a narrower range of sound pressure levels, and increasing separation between the sound pressure levels covered by monotonic and nonmonotonic neurons. In contrast, VIP activation promotes a more distributed representation of sound pressure level by broadening response-level curves of single neurons and increasing the overlap between the sound pressure levels covered by monotonic and nonmonotonic neurons.
Could the changes to the fit parameters of sound-modulated cells (Figure 5 and Figure 6) explain the differential effect of SST and VIP activation on the separation angle and length between mean population vectors to different sound pressure levels (Figure 4)? To answer this question, we constructed a qualitative model including a monotonic and a nonmonotonic cell, with response-level fit parameters for no and high laser power taken as the mean parameters from the data in Figure 5 and Figure 6 for no and high laser power (Supplementary Figure S6A–B). With this simple two-cell population, we could qualitatively reproduce the increase in separation angle upon SST activation and the decrease in separation angle upon VIP activation over the range of sound pressure levels we tested (Supplementary Figure S6D–F), and similarly the decrease in vector length upon SST activation and the increase in vector length upon VIP activation (Supplementary Figure S6G–I). Thus, the changes to the fit parameters observed in Figures 5–6 can explain the change in representation of sound pressure levels observed in Figure 4.
Overall, when neither SST or VIP neurons are activated, the neural population encodes different sound pressure levels using two strategies: the identity of the responsive cells (different cells respond to different sound pressure levels, discrete encoding of sound pressure level) and the strength of the neural response (continuous encoding of sound pressure level). When SST neurons are activated, the neural population shifts towards a more localist representation of sound pressure level. Specifically, the encoding of sound pressure level relies more on the identity of the responsive cells and less on the magnitude of response: there is less overlap between populations of cells responding to different sound pressure levels, but the strength of response is similar for all sound pressure levels. This can be explained with the narrower bandwidths of response, albeit of reduced magnitude, of both monotonic and nonmonotonic sound-increasing cells with SST activation. By contrast, when VIP neurons are activated, the neural population shifts towards a more distributed representation of sound pressure level. Specifically, the encoding of sound pressure level by the magnitude of the neural response is enhanced, while the representation by different cell groups declines: the neural responses are of higher magnitude and over a higher range, but there is more overlap between neurons responding to different sound pressure levels. This can be explained with the larger and broader responses of monotonic and nonmonotonic sound-increasing neuronal responses with VIP activation.
DISCUSSION
In this study, we set out to test whether and how distinct inhibitory neurons modify the neuronal code for the representation of sound pressure level. From a sparse distributed representation of sound pressure level, activation of one class of inhibitory neurons, SSTs, led to a sparser, more localist representation (Figure 3D–E), where sound pressure level is encoded in discrete steps by distinct groups of neurons (Figure 4D) with a similar low strength (Figure 4H). By contrast, activation of another class of inhibitory neurons, VIPs, led to a more distributed representation (Figure 3I–J), with more overlap between the cell populations responding to different sound pressure levels (Figure 4F): sound pressure level is encoded continuously by varying the strength of response of a large group of neurons (Figure 4J). These shifts in representation are implemented at the single-neuron level through changes to the response-level function of monotonic (Figure 5) and nonmonotonic neurons (Figure 6). SST activation shifts the response-level curves of sound-modulated neurons by further separating the sound pressure levels that monotonic and nonmonotonic neurons represent (Figure 5H and 6H). With VIP activation, the changes to the response-level curves of sound-modulated neurons allow for stronger responses and more overlap in bandwidth between monotonic and nonmonotonic neurons (Figure 5H and 6H). SST and VIP inhibit each other and thus control the processing of sound to either promote a representation of sound pressure levels based on the identity of responsive neurons, which may help with discrimination between stimuli, or based on the strength of response, which may help with detectability of weak stimuli.
Our experiments show that SSTs shift the network’s state towards a more localist representation of sound pressure level, whereas VIPs shift it towards a more distributed representation of sound pressure level. A defining feature of the auditory cortex is sparse coding (DeWeese et al., 2003), which can lead to both distributed and localist representations. Neural population responses have been measured at various positions along the localist to distributed representation spectrum across many features and areas, (such as memory: (Wixted et al., 2014), sound (Hromádka et al., 2008), sound localization (Belliveau et al., 2014; Lesica et al., 2010), vision (Christensen and Pillow, 2022) ) and can change dynamically along the spectrum (Honey et al., 2017; Kato et al., 2015; Kuchibhotla et al., 2017). Localist versus distributed representations, modulated by the relative strength of global (SST) versus local (PV or VIP) inhibition respectively (Haga and Fukai, 2021; Hertäg and Sprekeler, 2019b), may provide support for neural computations such as discreteness versus invariance (Kuchibhotla and Bathellier, 2018), segmentation versus concatenation (Haga and Fukai, 2021), integration of bottom-up versus top-down information (Hertäg and Sprekeler, 2019b; Honey et al., 2017). The two types of interneurons receive neuromodulatory inputs and may dynamically change the network’s state towards one or the other type of representation for a given task: SST activation may help with tasks requiring focused attention such as discriminating different stimuli (Lee and Middlebrooks, 2011) or detecting in noise (Lakunina et al., 2022), by sharpening tuning, decreasing the activity for non-relevant stimuli, and enhancing the information-per-spike (Phillips and Hasenstaub, 2016). In contrast, VIP activation may help with tasks requiring receptive-attention such as active sensing (Gentet et al., 2012) or detecting small stimuli by amplifying weak signals (Millman et al., 2020), increasing detectability (Cone et al., 2019) without however increasing the stimulus-response mutual information (Bigelow et al., 2019). As distinct inhibitory populations can be recruited during different behaviors, their ability to transform the neuronal code can be advantageous to brain function. Combined, our results provide for a novel level of understanding of the function of inhibitory neurons in population neuronal dynamics.
Our results build on the previous studies of the effect of SST activation and VIP activation on neural responses measured at single-cell level to develop a population-level understanding of the function of these neurons within the neuronal networks. Previous work found that SST decreases the activity of the neural population to sounds (Natan et al., 2017; Phillips and Hasenstaub, 2016), and leads to a rightward shift of monotonic response-level curves (Wilson et al., 2012), while VIP, through a disinhibitory circuit, increases the activity of the population (Pfeffer et al., 2013; Pi et al., 2013; Zhang et al., 2014). We built on these studies by testing the representation of sound pressure level by the neural population and whether sound pressure level is encoded by discrete populations or by the strength of response. Interestingly, the connectivity between cortical neurons is largely conserved across layers, primary and non-primary cortices, sensory and non-sensory areas (Campagnola et al., 2022; Douglas and Martin, 2004; Markram et al., 2004; Yu et al., 2019), with SST and VIP mutually inhibiting each other as a common motif: perhaps the change in representation we observe along the sound level feature upon SST or VIP activation extends to other stimulus features, sensory and non-sensory alike.
Our results expand on the results of previous studies that measured more general effects of interneuron modulation. The changes to the response-level curves (Figures 5 and 6) we measured upon SST or VIP activation can explain how the frequency-response functions of neurons in AC change with interneuron modulation. The excitatory and inhibitory inputs to pyramidal cells of AC are frequency-tuned (Isaacson and Scanziani, 2011; Kato et al., 2017; Li et al., 2013), and intracortical inhibition further shapes the tuning (Wu et al., 2008). From the response-level curves, we can plot the response with interneuron activation versus without and thus predict within which range of amplitudes we can expect multiplicative or additive effects to the frequency tuning curve. Previous studies have shown that SST activation leads to either subtractive, divisive or a combination of both subtractive and divisive effects on the frequency tuning curve (Phillips and Hasenstaub, 2016; Seybold et al., 2015; Wilson et al., 2012). Our data is consistent with these results: for monotonic neurons, SST activation can lead to divisive and/or subtractive effects at a low range of sound amplitudes and for nonmonotonic neurons, SST activation leads to both divisive and subtractive effects (Supplementary Figure S7). Previous studies have also shown that VIP activation leads to an additive shift in the frequency tuning curve (Bigelow et al., 2019; Pi et al., 2013) and similarly SST inactivation leads to a multiplicative or additive shift mostly (Phillips and Hasenstaub, 2016). Our data can explain these results as well, with multiplicative effects for monotonic neurons and a range of additive and multiplicative effects for nonmonotonic neurons (Supplementary Figure S7). Our results can help explain results that used a narrower set of frequencies than our stimuli.
Nonmonotonic neurons in AC either can have their nonmonotonicity inherited from the nonmonotonic excitatory input into those cells while the monotonic inhibitory input, which shows a peak in delay at the cell’s best pressure level, sharpens the nonmonotonicity (Wu et al., 2006) or can be constructed de novo with an imbalance between excitatory and inhibitory inputs (Tan et al., 2007; Wu et al., 2006). This means that for some of the nonmonotonic cells we recorded from, the input into the cell does not covary with the sound pressure level, and so for these cells, we are not assessing the input-output function of the cell through the response-level curve, rather how inhibition further shapes the already intensity-tuned input. From our experiments, we observe that SST activation decreases the range of response of nonmonotonic neurons but does not change the sound pressure level of peak response nor the width of response (Figure 6). This may indicate that SST activation does not change the timing of the inhibitory input into the nonmonotonic cells, but rather the overall strength of inhibition across all sound pressure levels. In contrast, VIP activation leads to a shift of the sound pressure level of peak response towards higher levels, along with a broadening of the response and an increase in the range of response (Figure 6). This could simply be explained if VIP activation changes the timing of the inhibition, with the delay between excitatory and inhibitory inputs peaking at a higher sound pressure level.
A limitation of our study is that we are measuring the response only from a subset of neurons from layer 2/3 while broadly stimulating all SST or VIP neurons across different cortical layers. Our sound stimulus is a broadband white noise stimulus which also broadly stimulates many neurons (Bandyopadhyay et al., 2010). In our approach to testing the role of different interneuron subtypes in sound pressure level representation, we designed the stimulus such that sound-responsive cells across the network would have a uniform increase in inhibition from a given subtype of neurons, without spatial disparities. Thus, the broad optogenetic activation of the inhibitory neuron subtypes is well matched to the broadband white noise stimulus. With a frequency-tuned stimulus, a more local optogenetic stimulation of interneuron activation might be better suited. We targeted layer 2/3 neurons which largely transmit the signal to higher cortical areas (Douglas and Martin, 2004), and therefore serve as output units of auditory cortex. However, neurons across the cortical column may perform additional computations in other layers, which would be interesting to record in future experiments.
In our experiments, we tested the results of SST or VIP activation on the representation of sound pressure level at the neural level, and an important next step will be to investigate whether the changes in neural representation of sound pressure level correlate with behavioral effects. One approach would be to image the activity of SST neurons while a mouse is engaged in a task that may require SST activation, or similarly VIP neurons. SST activation may be involved in tasks leading to a sharpening in the neural tuning properties, or to a filtering out of irrelevant stimuli through the overall decrease in firing rate, such as discrimination tasks and signal-in-noise tasks (Christensen et al., 2019; Kuchibhotla et al., 2017; Lakunina et al., 2022; Lee and Middlebrooks, 2011; Otazu et al., 2009). VIP activation may be involved in tasks requiring amplification of weak signals, such as a detection at threshold task or active sensing (Bennett et al., 2013; Cone et al., 2019; Fritz et al., 2003; Gentet et al., 2012; Kato et al., 2015; Millman et al., 2020). A second approach would be to measure how SST or VIP activation changes the performance of a mouse engaged in a task. In a detection task, we may expect that detection thresholds increase with SST activation and decrease with VIP activation, as seen in the Visual Cortex (Cone et al., 2019). In a discrimination task or detection of sounds in background task, we may expect SST activation to increase the performance, while VIP activation may decrease or not affect performance: SST inactivation decreases performance in the detection of sounds in background noise (Lakunina et al., 2022), and at the neural level, VIP activation decreases “encoding efficiency” (Bigelow et al., 2019) while SST activation may increase it (Phillips and Hasenstaub, 2016). It should be noted that the dichotomy between the functional roles of SST and VIP might not be so clear cut: VIPs and SSTs may cooperate to simultaneously amplify relevant stimuli and filter out irrelevant stimuli, respectively, or VIP may be more active for weak stimuli and SST for loud stimuli (Dipoppa et al., 2018; Karnani et al., 2016; Kuchibhotla et al., 2017; Mesik et al., 2015; Millman et al., 2020; Zhang et al., 2014).
METHODS
Animals
We performed experiments in fourteen adult mice (7 males and 7 females), which were crosses between Cdh23 mice (B6.CAST-Cdh23Ahl+/Kjn, JAX: 002756) and Sst-Cre mice (Ssttm2.1(cre)Zjh/J, JAX: 013044; n=5 in experimental group) or Vip-IRES-Cre mice (Viptm1(cre)Zjh/J, JAX: 010908; n=4 in experimental group, n=5 in control group). Mice had access to food and water ad libitum and were exposed to light/dark on a reversed 12h cycle at 28°C. Experiments were performed during the animals’ dark cycle. Mice were housed individually after the cranial window implant. All experimental procedures were in accordance with NIH guidelines and approved by the Institutional Animal Care and Use Committee at the University of Pennsylvania.
Surgery procedures
Mice were implanted with cranial windows over Auditory Cortex following a published procedure (Wood et al., 2022). Briefly, mice were anesthetized with 1.5–3% isoflurane and the left side of the skull was exposed and perforated by a 3mm biopsy punch over the left Auditory Cortex. We injected in that region 3×750nL of an adeno-associated virus (AAV) mix of AAV1.Syn.GCaMP (6m: Addgene 100841 or 7f: Addgene 104488; dilution 1:10 ~ 1×1013 GC/mL) and AAV1.Syn.Flex.Chrimson.tdTomato (UNC Vector Core; dilution 1:2 ~ 2×1012 GC/mL). In the control mice, we injected a mix of AAV1.Syn.jGCaMP7f (Addgene 104488; dilution 1:10 ~ 1×1013 GC/mL) and AAV1.Syn.Flex.tdTomato (Addgene 28306; dilution 1:100–1:20 ~ 2×1011 – 1×1012 GC/mL) in VIP-Cre mice. We then sealed the craniotomy with a glass round window, attached a head plate to the mouse and let it recover for 3–4 weeks. After habituating the mouse to being head fixed for 3 days, we mapped the sound-responsive areas of the brain and located Auditory Cortex using wide field imaging, then performed two-photon imaging in Auditory Cortex. If we recorded from a mouse several times, we changed the location or depth within layer 2/3 of Auditory Cortex in order to not image the same neurons twice.
Two-photon imaging
We imaged neurons in layer 2/3 of Auditory Cortex of awake, head-fixed mice (VIP-Cre mice: 3321 neurons over 16 recordings, SST-Cre mice: 2284 neurons over 13 recordings) using the two-photon microscope (Ultima in vivo multiphoton microscope, Bruker) with a laser at 940nm (Chameleon Ti-Sapphire). The fluorescence from the tissue went consequentially through a Primary Dichroic long pass (620 LP), through an IR Blocker (625 SP), through an Emission Dichroic Long pass (565 LP) which separated the light in two beams. The shorter wavelengths went through an additional bandpass filter (525/70) before being captured by a PMT (“green channel”); the longer wavelengths went through a bandpass filter (595/50) before being captured by a PMT (“red channel”). This set up was used to minimize the contamination of the green channel by the optogenetic stimulus at 635nm. There was nevertheless some bleedthrough during the optogenetic stimulus which was small enough not to saturate the green channel, and thus the activity of neurons could be recorded continuously without interruption during optogenetic stimulation. The pixels that were contaminated by the optogenetic stimulation were removed before processing the recordings with Suite2p. We imaged a surface of 512×512 pixels2 at 30Hz.
Optogenetic laser: Power calibration
We first calibrated the laser power by measuring the curve of command voltage versus output power for the laser (Optoengine LLC, MRL-III-635–300mW). The laser’s peak frequency was 635nm. Prior to every recording, we calibrated the laser power at the tissue level as follows: we used an empty cannula to reduce the power of the laser by a factor 10–15 and positioned the optical fiber on the objective so it would shine a spot of 1mm diameter centered on the focal point of the objective. Thus, the calibrated power at the imaging plane was for the medium laser power: 0.3 ± 0.09 mW/mm2 (mean ± std, n=29; range: 0.14–0.47 mW/mm2) and for the high laser power: 3.4 ± 1.0 mW/mm2 (mean ± std, n=29; range: 1.6–5.3 mW/mm2).
Identification of interneurons being stimulated
We started each recording by taking a 2600 frame video both in the green and the red channels (thus imaging GCaMP and tdTomato). As tdTomato is not dependent on the cell activity, any modulation in the signal in the red channel is due to bleedthrough from the GCaMP. We plotted for all cells the raw signal from the red channel versus the signal from the green channel and did a linear fit to extract the bleedthrough coefficient. We then subtracted the bleedthrough in the red signal and calculated the average fluorescence of the processed red signal for every cell. We then z-scored the signal of the red channel to the background fluorescence and selected the cells with a fluorescence higher than 2 σ (standard deviation of the background) as the targeted interneurons. The percentage of cells labeled as VIP or SOM interneurons with this criterion was consistent with the percentage of VIP or SOM expected within cortex (Rudy et al., 2011).
Stimulus presentation
We presented combinations of sound and optogenetic stimuli. The auditory stimulus consisted in 1-s long click trains of 25-ms pulses of broadband white noise (range 3–80 kHz) at 10Hz, at 7 sound pressure levels within 0–90 dB SPL (0; 30; 50; 60; 70; 80; 90 dB SPL). The optogenetic stimulus consisted in a 1-s long pulse train of 635nm laser with 5-ms pulses at 20 Hz, at 3 amplitudes with no, medium or high laser power (see power at tissue level in section Optogenetic laser: Power calibration). The two stimuli were presented simultaneously, with the optogenetic stimulus preceding the sound stimulus by 20 ms (Blackwell et al., 2020) for maximal optogenetic effect, the inter-stimulus interval was 5 s. All 21 combinations of sound and optogenetic stimuli were presented randomly and with 10 repeats per combination.
Analysis of single-cell activity: Optimal time window versus fixed time window
For each trial of a stimulus, the response was defined as the mean ΔF/Fstd over the baseline one-second window fluorescence Fbaseline preceding the stimulus: ΔF/Fstd = (F − mean(Fbaseline))/std(Fbaseline), with F the fluorescence of the cell. Optimal window: In order to compute the best responses across different neurons, which may respond with different time courses, we defined the optimal window of neuronal response of each neuron for each stimulus combination as the one-second window for which the average response most reliably differs from the baseline activity. The optimal time window was selected as the 1-s averaging window which maximized the sensitivity index (d’) between [0–1s] and [4–5s]. Fixed window: In order to compare how neuronal responses changed with laser stimulation, all parameters similar besides that one, we defined the fixed window of neuronal response for each recording (one window for all stimulus combinations) as the one-second window with the largest number of responsive neurons. The fixed time window was selected as the 1-s averaging window which maximized the number of cells with a significant response to at least one of the stimuli pairs for each recording compared to the pre-stimulus fluorescence (paired t-test, p<0.01 with multiple comparison correction).
Sparseness of a neuron’s response and activity sparseness of a population of neurons
To quantify how many stimuli a neuron responds to, we calculated the sparseness of each neuron adapted from (Vinje and Gallant, 2000):
where ri is the average response of a neuron to the ith sound pressure level calculated over its optimal time window minus the neuron’s lowest response to any combination of sound pressure level and laser activation, and n is the number of sound pressure levels. We subtracted the lowest response of each neuron to the response at a given sound amplitude and laser power to adapt this measure to fluorescence data. Indeed, this sparseness measure can only be computed with positive responses and is usually computed with the firing rate of each neuron (Rolls and Tovee, 1995; Vinje and Gallant, 2000). A sparseness value of 0% indicates that a neuron’s responses to all sound pressure levels are equal, and a sparseness value of 100% indicates that a neuron only responds to one sound pressure level.
To quantify how many neurons in a population are active in response to a given stimulus, we calculated the activity sparseness of each population (Willmore and Tolhurst, 2001) at a given sound level pressure and laser power as the ratio of neurons that had an increase in response above threshold from silence at the same laser power. The threshold was set as the standard deviation of the population’s response to no sound and no laser power and the response was calculated over each neuron’s optimal time window. An activity sparseness value of 0% indicates that all neurons in a population are active, and a value of 100% indicates that none of the neurons are active.
Separation angle and Vector length
To quantify whether mean population vectors were collinear in the neuronal space, we calculated the separation angle between mean population vectors adapted from (Vinje and Gallant, 2000). For each recording, we computed the mean population vectors at each laser power from 0dB to each non-zero sound pressure level (Figure 4A). We then computed the angle between each pair of mean population vectors at a given laser power (Figure 4B), and represented the mean ± s.e.m (Figure 4D and F) or the mean difference in separation angle from a given laser power to no laser power (Figure 4E and G) across recordings for each sound pair. To quantify whether mean population responses were close in the neuronal space, we computed the vector length between mean population vectors (Figure 4C). For each recording, we computed the mean population vectors at each laser power between all pairs of sound pressure levels (Figure 4A). We then computed the Euclidian norm of each mean population vector at a given laser power (Figure C), and represented the mean ± s.e.m (Figure 4H and J) or the mean difference in vector length from a given laser power to no laser power (Figure 4I and K) across recordings for each sound pair.
Fitting of response-level curves
Mean response curves and the standard error of the mean (s.e.m) for every neuron were determined by averaging over the fixed-time window its responses to all 10 trials of each sound pressure level. Thus, for a given cell we constructed three response curves, one for every light condition.
To characterize responses as monotonic or nonmonotonic, we first normalized the response curves such that abs(max(response)) ≤ 1 and computed the monotonicity index (MI). This metric refers to the relative responses at higher stimulus levels (Watkins and Barbour, 2011) and was calculated from the mean curve as
| (1) |
where responsemax_level is the response to 90 dB which is the highest level of sound presented and responsespontaneous is the spontaneous response measured at 0 dB. A response curve was classified as nonmonotonic if its MI was less than 0.3 and monotonic if it was greater than 0.7. We refrain from a hard cutoff at 0.5 since preliminary analysis of the response curves indicated that due to stochasticity both monotonic and nonmonotonic curves may have MI values between 0.3 and 0.7. Furthermore, note that a given cell could change its monotonicity in the presence of optogenetic stimulation.
After determining the monotonicity of the neural response, we fitted the monotonic and nonmonotonic curves with a 4-parameter sigmoid function and a 4-parameter Gaussian function, respectively. The sigmoid function is given by the equation,
| (2) |
while the Gaussian function can be written as,
| (3) |
y refers to the response curve, y0 is the offset response, yrange is its range in amplitude, x0 is the x value of the sigmoid midpoint and Δx denotes the width of the sigmoid. In the Gaussian, the parameter y0 is the offset response. The amplitude, mean and standard deviation of the Gaussian are denoted by yrange , xmean and σ, respectively, and have their regular interpretations. During the fitting procedure, we minimize (1 – McFadden pseudo R-squared) using the Powell optimizer (scipy.minimize.optimize in Python). The formula for this error value is,
| (4) |
Assuming is gaussian with the experimentally computed response average as its mean value and the response s.e.m as its standard deviation, we can rewrite the formula as,
| (5) |
We chose the McFadden R-squared since it allows us to account for different values of s.e.m at the different intensities. The regular R-squared equation constrains the s.e.m values to be equal at all intensities. A cell’s response curve is considered well fit by its respective function if the Mcfadden R2 is greater than 0.8. Due to the nonlinear nature of our optimization we chose 16 random starting points for the optimizer and cells fitted using 2 or more of the starting conditions were characterized using the fitting curve which had the highest R2 value. For neurons whose mean response curve MI lay between 0.3 and 0.7 we follow a similar procedure but fit the curve with both the sigmoid and Gaussian functions to find the better fitting function. Furthermore, we constrain the mean of all our Gaussian fits to lie between 10 and 80 dB. Response curves with means less than 10 dB or greater than 80 dB were recharacterized using the sigmoid function since only one sound pressure level data point (0 dB or 90 dB) is insufficient to adequately distinguish if the cell is monotonic or nonmonotonic. Roughly ~5% of the total response curves (combined across all three light conditions) were refitted in this manner. Lastly, we tested if the fitting curve was overfitted to the empirical sound intensities by calculating a new variable – interpolated error. The interpolated sigmoid/Gaussian curve is constructed by interpolating the fitted curve at the intermediate sound pressure levels – (15, 40, 55, 65, 75, 85) dB. The interpolated error is the regular R-squared value evaluated using the equation,
| (6) |
yinterpolated levels refers to the Gaussian/sigmoid equations (2, 3) computed at the sound pressure levels 0, 15, 30, 40, 50, 55, 60, 65, 70, 75, 80, 85, and 90 dB. When computing statistics on different parameters we remove neurons with interpolated error less than 0.25 for both the Sigmoid and Gaussian fits. This threshold allows us to select at least 90% of the fitted curves.
Statistics
All responses are plotted as mean ± s.e.m (standard error of the mean) with the number of measurements above the figure. We tested significance with a Generalized Linear Mixed Effects (GLME) Model with the matlab function fitglme, using laser power, sound pressure level and the interaction term between laser power and sound pressure level as fixed-effect terms and cell identity or session number as grouping variables. All results from the statistical analyses are reported in: Statistics Table in Supplementary Information.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Dr. Anna Schapiro for helpful discussions. The authors also thank the members of the Geffen laboratory for helpful discussions and advice. This work was supported by NIDCD R01DC015527, R01DC014479, NINDS R01NS113241 to MNG.
Footnotes
CONFLICT OF INTEREST
The authors declare no competing interests.
REFERENCES
- Bandyopadhyay S., Shamma S.A., Kanold P.O., 2010. Dichotomy of functional organization in the mouse auditory cortex. Nat Neurosci 13, 361–368. 10.1038/nn.2490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belliveau L.A.C., Lyamzin D.R., Lesica N.A., 2014. The Neural Representation of Interaural Time Differences in Gerbils Is Transformed from Midbrain to Cortex. Journal of Neuroscience 34, 16796–16808. 10.1523/JNEUROSCI.2432-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett C., Arroyo S., Hestrin S., 2013. Subthreshold Mechanisms Underlying State-Dependent Modulation of Visual Responses. Neuron 80, 350–357. 10.1016/j.neuron.2013.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigelow J., Morrill R.J., Dekloe J., Hasenstaub A.R., 2019. Movement and VIP Interneuron Activation Differentially Modulate Encoding in Mouse Auditory Cortex. eNeuro 6, ENEURO.0164–19.2019. 10.1523/ENEURO.0164-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwell J.M., Lesicko A.M., Rao W., De Biasi M., Geffen M.N., 2020. Auditory cortex shapes sound responses in the inferior colliculus. eLife 9, e51890. 10.7554/eLife.51890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campagnola L., Seeman S.C., Chartrand T., Kim L., Hoggarth A., Gamlin C., Ito S., Trinh J., Davoudian P., Radaelli C., Kim M.-H., Hage T., Braun T., Alfiler L., Andrade J., Bohn P., Dalley R., Henry A., Kebede S., Alice M., Sandman D., Williams G., Larsen R., Teeter C., Daigle T.L., Berry K., Dotson N., Enstrom R., Gorham M., Hupp M., Dingman Lee S., Ngo K., Nicovich P.R., Potekhina L., Ransford S., Gary A., Goldy J., McMillen D., Pham T., Tieu M., Siverts L., Walker M., Farrell C., Schroedter M., Slaughterbeck C., Cobb C., Ellenbogen R., Gwinn R.P., Keene C.D., Ko A.L., Ojemann J.G., Silbergeld D.L., Carey D., Casper T., Crichton K., Clark M., Dee N., Ellingwood L., Gloe J., Kroll M., Sulc J., Tung H., Wadhwani K., Brouner K., Egdorf T., Maxwell M., McGraw M., Pom C.A., Ruiz A., Bomben J., Feng D., Hejazinia N., Shi S., Szafer A., Wakeman W., Phillips J., Bernard A., Esposito L., D’Orazi F.D., Sunkin S., Smith K., Tasic B., Arkhipov A., Sorensen S., Lein E., Koch C., Murphy G., Zeng H., Jarsky T., 2022. Local connectivity and synaptic dynamics in mouse and human neocortex. Science 375. 10.1126/science.abj5861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen N., Sugihara H., Sur M., 2015. An acetylcholine-activated microcircuit drives temporal dynamics of cortical activity. Nat Neurosci 18, 892–902. 10.1038/nn.4002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen A.J., Pillow J.W., 2022. Reduced neural activity but improved coding in rodent higher-order visual cortex during locomotion. Nat Commun 13, 1676. 10.1038/s41467-022-29200-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen R.K., Lindén H., Nakamura M., Barkat T.R., 2019. White Noise Background Improves Tone Discrimination by Suppressing Cortical Tuning Curves. Cell Reports. 10.1016/j.celrep.2019.10.049 [DOI] [PubMed] [Google Scholar]
- Cone J.J., Scantlen M.D., Histed M.H., Maunsell J.H.R., 2019. Different inhibitory interneuron cell classes make distinct contributions to visual contrast perception. eNeuro. 10.1523/ENEURO.0337-18.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWeese M.R., Wehr M., Zador A.M., 2003. Binary spiking in auditory cortex. J Neurosci 23, 7940–7949. 10.1523/JNEUROSCI.23-21-07940.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dipoppa M., Ranson A., Krumin M., Pachitariu M., Carandini M., Harris K.D., 2018. Vision and Locomotion Shape the Interactions between Neuron Types in Mouse Visual Cortex. Neuron. 10.1016/j.neuron.2018.03.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas R.J., Martin K.A.C., 2004. Neuronal Circuits of the Neocortex. Annual Review of Neuroscience 27, 419–451. 10.1146/annurev.neuro.27.070203.144152 [DOI] [PubMed] [Google Scholar]
- Fritz J., Shamma S., Elhilali M., Klein D., 2003. Rapid task-related plasticity of spectrotemporal receptive fields in primary auditory cortex. Nat Neurosci 6, 1216–1223. 10.1038/nn1141 [DOI] [PubMed] [Google Scholar]
- Fu Y., Tucciarone J.M., Espinosa J.S., Sheng N., Darcy D.P., Nicoll R.A., Huang Z.J., Stryker M.P., 2014. A cortical circuit for gain control by behavioral state. Cell 156, 1139–1152. 10.1016/j.cell.2014.01.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentet L.J., Kremer Y., Taniguchi H., Huang Z.J., Staiger J.F., Petersen C.C.H., 2012. Unique functional properties of somatostatin-expressing GABAergic neurons in mouse barrel cortex. Nat Neurosci 15, 607–612. 10.1038/nn.3051 [DOI] [PubMed] [Google Scholar]
- Haga T., Fukai T., 2021. Multiscale representations of community structures in attractor neural networks. PLOS Computational Biology 17, e1009296. 10.1371/journal.pcbi.1009296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertäg L., Sprekeler H., 2019a. Amplifying the redistribution of somato-dendritic inhibition by the interplay of three interneuron types. PLoS Computational Biology. 10.1371/journal.pcbi.1006999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertäg L., Sprekeler H., 2019b. Amplifying the redistribution of somato-dendritic inhibition by the interplay of three interneuron types. PLoS Comput Biol 15, e1006999. 10.1371/journal.pcbi.1006999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey C.J., Newman E.L., Schapiro A.C., 2017. Switching between internal and external modes: A multiscale learning principle. Network Neuroscience 1, 339–356. 10.1162/NETN_a_00024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hromádka T., DeWeese M.R., Zador A.M., 2008. Sparse Representation of Sounds in the Unanesthetized Auditory Cortex. PLOS Biology 6, e16. 10.1371/journal.pbio.0060016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacson J.S., Scanziani M., 2011. How inhibition shapes cortical activity. Neuron 72, 231–243. 10.1016/j.neuron.2011.09.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson J., Ayzenshtat I., Karnani M.M., Yuste R., 2016. VIP+ interneurons control neocortical activity across brain states. Journal of Neurophysiology 115, 3008–3017. 10.1152/jn.01124.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karnani M.M., Jackson J., Ayzenshtat I., Sichani X.H., Manoocheri K., Kim S., Yuste R., 2016. Opening holes in the blanket of inhibition: Localized lateral disinhibition by vip interneurons. Journal of Neuroscience 36, 3471–3480. 10.1523/JNEUROSCI.3646-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato H.K., Asinof S.K., Isaacson J.S., 2017. Network-Level Control of Frequency Tuning in Auditory Cortex. Neuron. 10.1016/j.neuron.2017.06.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato H.K., Gillet S.N., Isaacson J.S., 2015. Flexible Sensory Representations in Auditory Cortex Driven by Behavioral Relevance. Neuron. 10.1016/j.neuron.2015.10.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King P.D., Zylberberg J., DeWeese M.R., 2013. Inhibitory Interneurons Decorrelate Excitatory Cells to Drive Sparse Code Formation in a Spiking Model of V1. J. Neurosci. 33, 5475–5485. 10.1523/JNEUROSCI.4188-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klapoetke N.C., Murata Y., Kim S.S., Pulver S.R., Birdsey-Benson A., Cho Y.K., Morimoto T.K., Chuong A.S., Carpenter E.J., Tian Z., Wang J., Xie Y., Yan Z., Zhang Y., Chow B.Y., Surek B., Melkonian M., Jayaraman V., Constantine-Paton M., Wong G.K.-S., Boyden E.S., 2014. Independent optical excitation of distinct neural populations. Nat Methods 11, 338–346. 10.1038/nmeth.2836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuchibhotla K., Bathellier B., 2018. Neural encoding of sensory and behavioral complexity in the auditory cortex. Current Opinion in Neurobiology 52, 65–71. 10.1016/j.conb.2018.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuchibhotla K.V., Gill J.V., Lindsay G.W., Papadoyannis E.S., Field R.E., Sten T.A.H., Miller K.D., Froemke R.C., 2017. Parallel processing by cortical inhibition enables context-dependent behavior. Nat Neurosci 20, 62–71. 10.1038/nn.4436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakunina A.A., Menashe N., Jaramillo S., 2022. Contributions of Distinct Auditory Cortical Inhibitory Neuron Types to the Detection of Sounds in Background Noise. eneuro 9, ENEURO.0264–21.2021. 10.1523/eneuro.0264-21.2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakunina A.A., Nardoci M.B., Ahmadian Y., Jaramillo S., 2020. Somatostatin-expressing interneurons in the auditory cortex mediate sustained suppression by spectral surround. Journal of Neuroscience. 10.1523/JNEUROSCI.1735-19.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C.-C., Middlebrooks J.C., 2011. Auditory cortex spatial sensitivity sharpens during task performance. Nat Neurosci 14, 108–114. 10.1038/nn.2713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesica N.A., Lingner A., Grothe B., 2010. Population Coding of Interaural Time Differences in Gerbils and Barn Owls. Journal of Neuroscience 30, 11696–11702. 10.1523/JNEUROSCI.0846-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L., Li Y., Zhou M., Tao H.W., Zhang L.I., 2013. Intracortical multiplication of thalamocortical signals in mouse auditory cortex. Nat Neurosci 16, 1179–1181. 10.1038/nn.3493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H., Toledo-Rodriguez M., Wang Y., Gupta A., Silberberg G., Wu C., 2004. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci 5, 793–807. 10.1038/nrn1519 [DOI] [PubMed] [Google Scholar]
- Mesik L., Ma W.P., Li L.Y., Ibrahim L.A., Huang Z.J., Zhang L., Tao H.W., 2015. Functional response properties of VIP-expressing inhibitory neurons in mouse visual and auditory cortex. Frontiers in Neural Circuits 9. 10.3389/fncir.2015.00022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millman D.J., Ocker G.K., Caldejon S., Kato I., Larkin J.D., Lee E.K., Luviano J., Nayan C., Nguyen T.V., North K., Seid S., White C., Lecoq J., Reid C., Buice M.A., de Vries S.E.J., 2020. VIP interneurons in mouse primary visual cortex selectively enhance responses to weak but specific stimuli. eLife 9, 1–22. 10.7554/eLife.55130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natan R.G., Briguglio J.J., Mwilambwe-Tshilobo L., Jones S.I., Aizenberg M., Goldberg E.M., Geffen M.N., 2015. Complementary control of sensory adaptation by two types of cortical interneurons. eLife 4, e09868. 10.7554/eLife.09868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natan R.G., Rao W., Geffen M.N., 2017. Cortical Interneurons Differentially Shape Frequency Tuning following Adaptation. Cell Reports 21, 878–890. 10.1016/j.celrep.2017.10.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otazu G.H., Tai L.-H., Yang Y., Zador A.M., 2009. Engaging in an auditory task suppresses responses in auditory cortex. Nat Neurosci 12, 646–654. 10.1038/nn.2306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeffer C.K., Xue M., He M., Huang Z.J., Scanziani M., 2013. Inhibition of inhibition in visual cortex: The logic of connections between molecularly distinct interneurons. Nature Neuroscience. 10.1038/nn.3446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips D.P., Semple M.N., Kitzes L.M., 1995. Factors shaping the tone level sensitivity of single neurons in posterior field of cat auditory cortex. Journal of Neurophysiology 73, 674–686. 10.1152/jn.1995.73.2.674 [DOI] [PubMed] [Google Scholar]
- Phillips E.A., Hasenstaub A.R., 2016. Asymmetric effects of activating and inactivating cortical interneurons. eLife 5, e18383. 10.7554/eLife.18383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pi H.J., Hangya B., Kvitsiani D., Sanders J.I., Huang Z.J., Kepecs A., 2013. Cortical interneurons that specialize in disinhibitory control. Nature 503, 521–524. 10.1038/nature12676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polley D.B., Heiser M.A., Blake D.T., Schreiner C.E., Merzenich M.M., 2004. Associative learning shapes the neural code for stimulus magnitude in primary auditory cortex. Proceedings of the National Academy of Sciences 101, 16351–16356. 10.1073/pnas.0407586101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls E.T., Tovee M.J., 1995. Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. Journal of Neurophysiology 73, 713–726. 10.1152/jn.1995.73.2.713 [DOI] [PubMed] [Google Scholar]
- Rudy B., Fishell G., Lee S., Hjerling-Leffler J., 2011. Three groups of interneurons account for nearly 100% of neocortical GABAergic neurons. Developmental Neurobiology 71, 45–61. 10.1002/dneu.20853 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiner C.E., Mendelson J.R., Sutter M.L., 1992. Experimental Brain Research Functional topography of cat primary auditory cortex: representation of tone intensity, Exp Brain Res. [DOI] [PubMed] [Google Scholar]
- Seybold B.A., Phillips E.A.K., Schreiner C.E., Hasenstaub A.R., 2015. Inhibitory Actions Unified by Network Integration. Neuron 87, 1181–1192. 10.1016/j.neuron.2015.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan A.Y.Y., Atencio C.A., Polley D.B., Merzenich M.M., Schreiner C.E., 2007. Unbalanced synaptic inhibition can create intensity-tuned auditory cortex neurons. Neuroscience 146, 449–462. 10.1016/j.neuroscience.2007.01.019 [DOI] [PubMed] [Google Scholar]
- Vinje W.E., Gallant J.L., 2000. Sparse Coding and Decorrelation in Primary Visual Cortex During Natural Vision. Science 287, 1273–1276. 10.1126/science.287.5456.1273 [DOI] [PubMed] [Google Scholar]
- Watkins P.V., Barbour D.L., 2011. Rate-level responses in awake marmoset auditory cortex. Hearing Research 275, 30–42. 10.1016/j.heares.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willmore B., Tolhurst D.J., 2001. Characterizing the sparseness of neural codes. Network: Computation in Neural Systems 12, 255–270. 10.1080/net.12.3.255.270 [DOI] [PubMed] [Google Scholar]
- Wilson N.R., Runyan C.A., Wang F.L., Sur M., 2012. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature 488, 343–348. 10.1038/nature11347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wixted J.T., Squire L.R., Jang Y., Papesh M.H., Goldinger S.D., Kuhn J.R., Smith K.A., Treiman D.M., Steinmetz P.N., 2014. Sparse and distributed coding of episodic memory in neurons of the human hippocampus. Proceedings of the National Academy of Sciences 111, 9621–9626. 10.1073/pnas.1408365111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood K.C., Angeloni C.F., Oxman K., Clopath C., Geffen M.N., 2022. Neuronal activity in sensory cortex predicts the specificity of learning in mice. Nat Commun 13, 1167. 10.1038/s41467-022-28784-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G.K., Arbuckle R., Liu B., Tao H.W., Zhang L.I., 2008. Lateral Sharpening of Cortical Frequency Tuning by Approximately Balanced Inhibition. Neuron 58, 132–143. 10.1016/j.neuron.2008.01.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G.K., Li P., Tao H.W., Zhang L.I., 2006. Nonmonotonic Synaptic Excitation and Imbalanced Inhibition Underlying Cortical Intensity Tuning. Neuron 52, 705–715. 10.1016/j.neuron.2006.10.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J., Hu H., Agmon A., Svoboda K., 2019. Recruitment of GABAergic Interneurons in the Barrel Cortex during Active Tactile Behavior. Neuron. 10.1016/j.neuron.2019.07.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S., Xu M., Kamigaki T., Do J.P.H., Chang W.C., Jenvay S., Miyamichi K., Luo L., Dan Y., 2014. Long-range and local circuits for top-down modulation of visual cortex processing. Science. 10.1126/science.1254126 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.