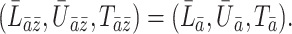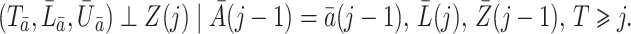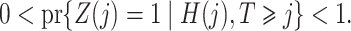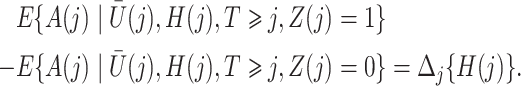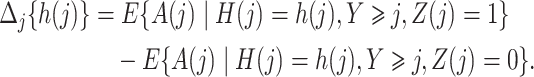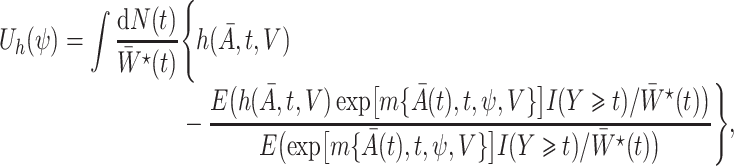Summary
Robins (1998) introduced marginal structural models, a general class of counterfactual models for the joint effects of time-varying treatments in complex longitudinal studies subject to time-varying confounding. Robins (1998) established the identification of marginal structural model parameters under a sequential randomization assumption, which rules out unmeasured confounding of treatment assignment over time. The marginal structural Cox model is one of the most popular marginal structural models for evaluating the causal effect of time-varying treatments on a censored failure time outcome. In this paper, we establish sufficient conditions for identification of marginal structural Cox model parameters with the aid of a time-varying instrumental variable, in the case where sequential randomization fails to hold due to unmeasured confounding. Our instrumental variable identification condition rules out any interaction between an unmeasured confounder and the instrumental variable in its additive effects on the treatment process, the longitudinal generalization of the identifying condition of Wang & Tchetgen Tchetgen (2018). We describe a large class of weighted estimating equations that give rise to consistent and asymptotically normal estimators of the marginal structural Cox model, thereby extending the standard inverse probability of treatment weighted estimation of marginal structural models to the instrumental variable setting. Our approach is illustrated via extensive simulation studies and an application to estimating the effect of community antiretroviral therapy coverage on HIV incidence.
Keywords: Causal inference, Instrumental variable, Marginal structural model, Observational study, Survival analysis, Unmeasured confounding
1. Introduction
Robins (1998, 2000) introduced a new class of counterfactual models, known as marginal structural models, that encode the joint causal effects of time-varying treatments subject to time-varying confounding. Marginal structural models are particularly powerful, as they estimate the causal effects of time-dependent treatments in the presence of time-dependent confounders that are affected by prior treatments. For identification of marginal structural model parameters, Robins (1998, 2000) relied on a sequential randomization assumption, also known as sequential exchangeability, which rules out unmeasured confounding of treatment assignment over time. Applications of marginal structural models abound in the health and social sciences (see, e.g., Robins et al., 2000; Hernán et al., 2001; Cole & Hernán, 2008; Cerdá et al., 2010).
Right-censored data are of common occurrence in epidemiological studies where, due to censoring, the clinical outcome may not always be observed. In such settings, marginal structural models extend to time-dependent Cox models. Unlike standard time-dependent Cox models, marginal structural Cox models (Hernán et al., 2000) allow for adjustment of time-varying confounders through the use of inverse probability of treatment weighting, and thus can be employed to estimate the causal effects of time-varying treatments in the presence of time-varying confounders; see de Keyser et al. (2014), Karim et al. (2014) and Ali et al. (2016) for recent applications of marginal structural Cox models in clinical studies.
However, sequential randomization can seldom be guaranteed in observational studies, even if one adjusts for a large number of covariates in an effort to make the assumption credible. The instrumental variable method (Goldberger, 1972; Imbens & Angrist, 1994; Angrist et al., 1996; Wooldridge, 2010) is a well-known approach to estimating causal effects subject to unmeasured confounding in observational studies. An instrumental variable is defined as a pre-treatment variable that is independent of all unmeasured confounders, and does not have a direct causal effect on the outcome other than through the treatment. In a double-blind placebo-controlled randomized trial, random assignment is a common example of an ideal instrumental variable for the causal effect of treatment when some patients fail to comply with the assigned treatment, provided that double-blinding is maintained. To our knowledge, Michael et al. (2020) were the first to consider identification and estimation of marginal structural mean models in the context of a time-varying treatment and a time-varying instrumental variable. However, additional challenges arise with censored survival data, which were not addressed by Michael et al. (2020).
The first formal instrumental variable approach for right-censored survival outcomes was proposed by Robins & Tsiatis (1991), who parameterized the treatment effect under a structural accelerated failure time model. The approach, which applies to both point and time-varying treatments, can be challenging to implement in practice, because of the need for artificial censoring in order to estimate the structural model parameters (Robins & Tsiatis 1991; Joffe et al., 2012). More recently, Li et al. (2015) and Tchetgen Tchetgen et al. (2015) considered estimating the conditional hazard difference under an additive hazard model (Aalen, 1989). Tchetgen Tchetgen et al. (2015) also considered instrumental variable estimation for a Cox structural model under rare disease. MacKenzie et al. (2014) considered instrumental variable estimation of a marginal structural Cox model for point exposure, but their estimator generally fails to be consistent as their proposed estimating equation fails to be unbiased. Martinussen et al. (2017b) developed instrumental variable estimators under a semiparametric structural cumulative survival model, which is closely related to the additive hazard model of Li et al. (2015) and Tchetgen Tchetgen et al. (2015). In contrast, Martinussen et al. (2017a) and Sørensen et al. (2019) considered estimating the causal hazard ratio among the treated. The literature on instrumental variable methods for complier causal effect is also well developed for survival data (e.g., Loeys et al., 2005; Cuzick et al., 2007; Nie et al., 2011; Yu et al., 2015; Kianian et al., 2019). However, to date none of these approaches has been extended to time-varying settings, although some progress was made by Yende-Zuma et al. (2019) under somewhat restricted conditions, including that the unmeasured confounder cannot be an effect of prior treatment.
In fact, many instrumental variables that have been used in point exposure studies are often valid time-varying instrumental variables in settings where longitudinal data are available. For instance, in many well-established longitudinal observational studies such as the Multicenter AIDS Cohort Study and the Women’s Interagency HIV Study, both HIV treatment assignment information and treatment adherence information between follow-up visits are routinely collected, and therefore treatment assignment is a potential time-varying instrumental variable for the causal effects of time-varying antiretroviral therapy actually taken on HIV-related outcomes. Validity of treatment assignment as an instrumental variable relies on the assumption that confounding by indication can be fully accounted for, an assumption which is well justified in the literature (Robins et al., 2000; Hernán et al., 2001). Nowadays, even if not measured directly, adherence information is routinely inferred from pharmacy data in large electronic medical records when studying the causal effects of time-varying treatments on a variety of disease outcomes beyond HIV. Other examples of a common instrumental variable that is also inherently time-varying include physician treatment preference as physician preferences evolve with clinical practice and needs (Brookhart & Schneeweiss), distance from nearest college as individuals move over time, distance to nearest needle exchange program (Frangakis et al., 2004), calendar period (Cain et al., 2009), and differential distance between the nearest low-level and nearest high-level neonatal intensive care units in analyses of the causal effects of delivery at a high- versus low-level neonatal intensive care unit on birth outcomes (Zubizarreta et al., 2013; Yang et al., 2014). We acknowledge that sometimes instrumental variables may be related to initiating a treatment, but not adhering to it, so one should exercise caution in selecting a valid time-varying instrumental variable.
In this paper, we adopt an instrumental variable approach and establish sufficient conditions for identification of marginal structural Cox model parameters encoding the joint effects of binary time-varying treatments by leveraging a binary time-varying instrumental variable when the sequential randomization assumption fails to hold. Our identifying conditions extend those of Wang et al. (2022) to the longitudinal treatment setting, and require that in each risk set no unobserved confounder interacts with the instrumental variable in its additive effects on the treatment process. Our proposed semiparametric estimators extend standard inverse probability of treatment weighted estimation, which is the most popular method of estimating marginal structural Cox models under the sequential randomization assumption, by incorporating time-varying instrumental variables through a modified set of weights. We formally establish identification of our modified weighted estimating equations, and we provide asymptotic theory that allows, in the absence of model misspecification, valid inference about the marginal structural Cox model parameters.
2. Marginal structural Cox models
2.1. Notation
We first introduce some notation. Continuous time is denoted by 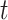 and is measured in weeks or months since the beginning of a subject’s follow-up. The index
and is measured in weeks or months since the beginning of a subject’s follow-up. The index 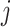 is often used to indicate an integer number of weeks or months, and
is often used to indicate an integer number of weeks or months, and 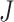 denotes the administrative end of follow-up. Let
denotes the administrative end of follow-up. Let 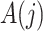 and
and 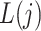 denote, respectively, a binary treatment taken by a subject and a vector of relevant prognostic factors for the survival outcome in the time interval (
denote, respectively, a binary treatment taken by a subject and a vector of relevant prognostic factors for the survival outcome in the time interval (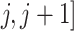 , where
, where 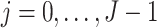 . We assume that
. We assume that 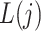 temporally precedes
temporally precedes 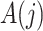 . Although time
. Although time 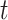 is treated as continuous, we assume that recorded data on the treatment and prognostic factors do not change except at integer times. For any time-dependent variable
is treated as continuous, we assume that recorded data on the treatment and prognostic factors do not change except at integer times. For any time-dependent variable 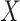 , we let
, we let 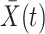 denote the history of that variable up to time
denote the history of that variable up to time 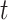 . For example, the covariate process up to
. For example, the covariate process up to 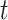 is
is 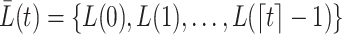 , where
, where 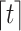 denotes the smallest integer greater than or equal to
denotes the smallest integer greater than or equal to 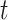 . Furthermore, let
. Furthermore, let 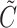 be the censoring time,
be the censoring time, 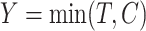 the observed time and
the observed time and 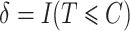 the censoring indicator, where
the censoring indicator, where 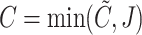 . Throughout the paper, except where necessary, we will suppress the subscript indexing the individual because we assume that the observed data of each subject are drawn independently from a distribution common to all subjects.
. Throughout the paper, except where necessary, we will suppress the subscript indexing the individual because we assume that the observed data of each subject are drawn independently from a distribution common to all subjects.
Figure 1 gives a causal graph representation of longitudinal confounding. The Markov property encoded in this graph implies that a node is independent of nondescendants conditional on its parents. Bi-directed edges into the covariate process 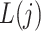 and outcome
and outcome 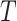 indicate the possibility that there are unmeasured common causes confounding their association. As pointed out by Robins (1997), a standard Cox model of the joint effects of treatment on time to event, which would typically condition on
indicate the possibility that there are unmeasured common causes confounding their association. As pointed out by Robins (1997), a standard Cox model of the joint effects of treatment on time to event, which would typically condition on 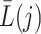 , is subject to collider bias, and therefore bound to incorrectly report a causal effect linking treatment to the event time even under the sharp null hypothesis of no causal effect. This potential flaw of standard regression models motivated Robins (1998) to develop a marginal structural model as a principled way of circumventing this difficulty. Importantly, he assumed that there are no unmeasured common causes of the treatment process and the outcome
, is subject to collider bias, and therefore bound to incorrectly report a causal effect linking treatment to the event time even under the sharp null hypothesis of no causal effect. This potential flaw of standard regression models motivated Robins (1998) to develop a marginal structural model as a principled way of circumventing this difficulty. Importantly, he assumed that there are no unmeasured common causes of the treatment process and the outcome 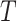 , hence encoding sequential randomization, which we formally define in § 2. Thus, under a data-generating mechanism consistent with Fig. 1, the joint causal effect of treatment on
, hence encoding sequential randomization, which we formally define in § 2. Thus, under a data-generating mechanism consistent with Fig. 1, the joint causal effect of treatment on 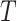 would in fact be point-identified under a nonparametric model for the observed data using the g-formula of Robins (1997).
would in fact be point-identified under a nonparametric model for the observed data using the g-formula of Robins (1997).
Fig. 1.
A causal graph of longitudinal confounding with bi-directed arrows.
We conclude this subsection by introducing counterfactuals which are key to defining marginal structural models. Neyman (1923) proposed using counterfactual outcomes to define the causal effects of time-independent treatments in randomized experiments. Rubin (1974) further used potential outcomes in the analysis of causal effects of time-independent treatments in observational studies. Robins (1986, 1987) proposed a formal counterfactual theory of causal inference that extends Neyman’s time-independent treatment theory to longitudinal studies with both direct and indirect effects, and time-varying treatments and confounders. For a specific fixed treatment history 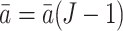 ,
, 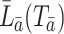 is defined to be the random vector representing a subject’s covariate process had the subject been treated with the particular treatment regime
is defined to be the random vector representing a subject’s covariate process had the subject been treated with the particular treatment regime 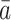 rather than with their observed treatment history;
rather than with their observed treatment history;  is defined to be the subject’s time to death had the subject been treated with the particular treatment regime
is defined to be the subject’s time to death had the subject been treated with the particular treatment regime 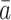 . Throughout the paper, we assume that the future cannot cause the past; for example,
. Throughout the paper, we assume that the future cannot cause the past; for example, 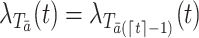 and
and 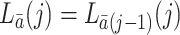
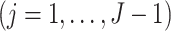 .
.
2.2. Identification of marginal structural Cox models under the sequential randomization assumption
Suppose that we are interested in estimating the parameter 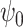 indexing a marginal structural Cox model which encodes the causal effect of all potential treatment histories,
indexing a marginal structural Cox model which encodes the causal effect of all potential treatment histories,
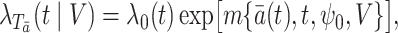 |
(1) |
where 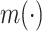 is a known function satisfying
is a known function satisfying 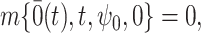
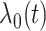 is an unspecified baseline hazard function and
is an unspecified baseline hazard function and 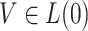 are baseline covariates. Suppose that we observe data
are baseline covariates. Suppose that we observe data 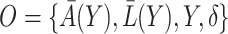 . We denote by
. We denote by 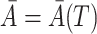 and
and 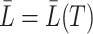 the treatment history and covariate history up to failure, respectively. In this section, we assume an independent censoring mechanism, i.e.,
the treatment history and covariate history up to failure, respectively. In this section, we assume an independent censoring mechanism, i.e., 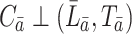 . Three important assumptions are sufficient for the identification of
. Three important assumptions are sufficient for the identification of  from the observed data in marginal structural Cox models.
from the observed data in marginal structural Cox models.
First, we make the standard consistency assumption that  almost surely, which means that the observed failure time corresponds to the potential failure time under a potential intervention that sets the treatment process to the observed treatment history.
almost surely, which means that the observed failure time corresponds to the potential failure time under a potential intervention that sets the treatment process to the observed treatment history.
The next assumption is the well-known sequential randomization assumption proposed in Robins (1998),
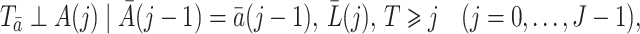 |
(2) |
where the term 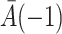 is defined as an empty set throughout the paper. This assumption generalizes the assumption of ignorable treatment assignment (Rosenbaum & Rubin, 1983) to longitudinal studies with time-varying treatments and confounders. It says that conditional on the treatment history up to time
is defined as an empty set throughout the paper. This assumption generalizes the assumption of ignorable treatment assignment (Rosenbaum & Rubin, 1983) to longitudinal studies with time-varying treatments and confounders. It says that conditional on the treatment history up to time  and recorded covariates up to time
and recorded covariates up to time 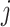 , the treatment at time
, the treatment at time 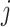 is independent of the counterfactual outcome
is independent of the counterfactual outcome  . The sequential randomization assumption holds if all common causes of
. The sequential randomization assumption holds if all common causes of 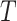 and
and  are included in
are included in 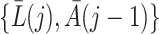 , thereby ruling out unmeasured confounding of the treatment process as encoded in graph of Fig. 1.
, thereby ruling out unmeasured confounding of the treatment process as encoded in graph of Fig. 1.
Finally, we make the following treatment positivity assumption:
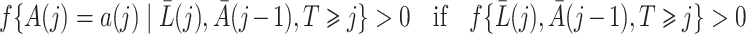 |
for 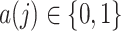
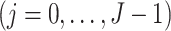 . This assumption states that, conditional on the observed history, there is a positive probability of receiving either treatment value at any given time. This assumption makes it possible to draw inferences about longitudinal treatment comparisons encoded in the marginal structural models.
. This assumption states that, conditional on the observed history, there is a positive probability of receiving either treatment value at any given time. This assumption makes it possible to draw inferences about longitudinal treatment comparisons encoded in the marginal structural models.
We define the time-varying weights
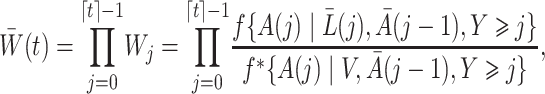 |
(3) |
where 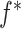 is a user-specified function of the treatment process
is a user-specified function of the treatment process 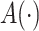 . Robins (1998) showed that
. Robins (1998) showed that  in (1) is the solution to the weighted estimating equation
in (1) is the solution to the weighted estimating equation
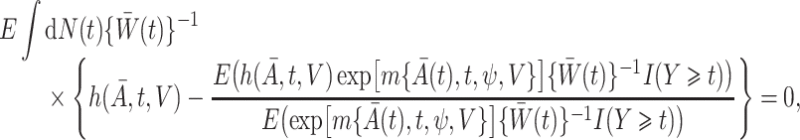 |
where 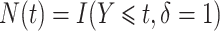 is the counting process for the outcome variable, and
is the counting process for the outcome variable, and 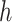 is a vector-valued function which has the same dimension as the causal parameter of interest
is a vector-valued function which has the same dimension as the causal parameter of interest  . In particular, given the marginal structural Cox model
. In particular, given the marginal structural Cox model
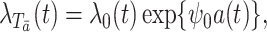 |
(4) |
and taking 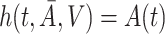 ,
, 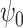 is the solution to the weighted estimating equation
is the solution to the weighted estimating equation
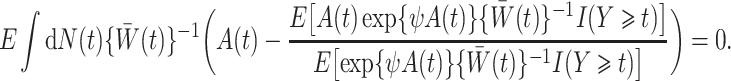 |
The weights 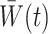 are generally unknown and need to be estimated from the observed data. Hernán et al. (2001) proposed using pooled logistic regression to estimate a model for the treatment process in both the numerator and the denominator of
are generally unknown and need to be estimated from the observed data. Hernán et al. (2001) proposed using pooled logistic regression to estimate a model for the treatment process in both the numerator and the denominator of 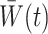 . The estimator obtained by substituting
. The estimator obtained by substituting 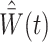 for
for 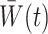 and evaluating expectations under the empirical distribution, is
and evaluating expectations under the empirical distribution, is 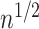 -consistent and asymptotically linear under standard regularity conditions, including
-consistent and asymptotically linear under standard regularity conditions, including 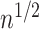 -consistency of an estimator for the treatment process
-consistency of an estimator for the treatment process 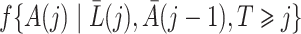 .
.
3. Instrumental variable identification and inference of marginal structural Cox models
3.1. Identification
It is not always possible to ensure that a sufficiently rich set of variables 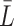 was collected for sequential randomization to hold. With this in mind, suppose that
was collected for sequential randomization to hold. With this in mind, suppose that 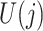 denotes an unobserved common cause of
denotes an unobserved common cause of 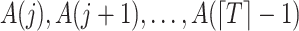 and
and 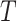 , such that (2) fails. Therefore, the treatment process is endogenous, i.e., subject to unmeasured confounding. On the other hand, suppose that one has observed a time-varying instrumental variable
, such that (2) fails. Therefore, the treatment process is endogenous, i.e., subject to unmeasured confounding. On the other hand, suppose that one has observed a time-varying instrumental variable 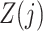 which satisfies the instrumental variable conditions described below. We develop a method of leveraging such an instrumental variable process to identify and estimate the marginal structural Cox model parameter
which satisfies the instrumental variable conditions described below. We develop a method of leveraging such an instrumental variable process to identify and estimate the marginal structural Cox model parameter 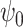 .
.
A variety of instrumental variable models have been discussed in the literature on point treatment cases; see Swanson et al. (2018) for a comprehensive review. In the following, we adopt the latent counterfactual instrumental variable model described in Swanson et al. (2018) for the proposed method. Specifically, we consider a setting like the one depicted in Fig. 2, where the sequential randomization assumption fails to hold, as we allow unmeasured time-varying covariates that confound the treatment process. Suppose that 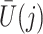 is a common cause of
is a common cause of 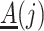 and
and 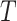 , where
, where 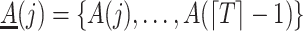 . We make the following assumption of latent sequential randomization.
. We make the following assumption of latent sequential randomization.
Fig. 2.
A causal graph of longitudinal confounding with unobserved confounders.
Assumption 1
(Latent sequential randomization). We have that
.
Denote the observed data by 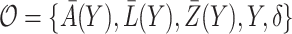 . A binary time-varying instrumental variable
. A binary time-varying instrumental variable 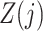 is observed just prior to
is observed just prior to 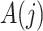 , but after
, but after 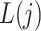
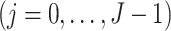 and satisfies the following time-varying instrumental variable conditions for
and satisfies the following time-varying instrumental variable conditions for 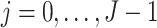 .
.
Assumption 2
(Instrumental variable relevance). We have that
with the history process defined as
.
Assumption 3
(Exclusion restriction). We have that
Assumption 4
(Instrumental variable independence). We have that
Assumption 5
(Instrumental variable positivity). We have that
Assumptions 2–4 are core instrumental variable conditions, while Assumption 5 is needed for nonparametric identification (Greenland, 2000; Hernán & Robins, 2006). Assumption 2 requires that the instrumental variable be associated with the treatment conditional on the history process. Assumption 2 does not rule out confounding of the 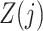 -
-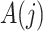 association by an unmeasured factor; however, if present, such a factor must be independent of
association by an unmeasured factor; however, if present, such a factor must be independent of 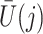 . We will refer to
. We will refer to 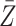 as causal instrumental variables when no such confounding is present. Assumption 3 states that there can be no direct causal effect of
as causal instrumental variables when no such confounding is present. Assumption 3 states that there can be no direct causal effect of 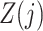 on
on 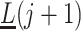 ,
, 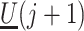 and
and  not mediated by
not mediated by 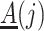 . Assumption 4 essentially says that the null direct causal effect of
. Assumption 4 essentially says that the null direct causal effect of 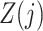 on
on  ,
, 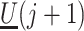 and
and  would be identified conditional on the history process if one could intervene and set
would be identified conditional on the history process if one could intervene and set 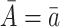 .
.
Finally, we also require the following condition that there is no additive interaction between 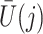 and
and 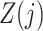 in a model for
in a model for  given
given 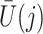 ,
, 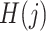 and
and 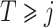 .
.
Assumption 6
(Independent compliance type). We have that
(5)
This assumption is a longitudinal generalization of the assumption made by Wang & Tchetgen Tchetgen (2018) and Wang et al. (2022) in the case of point exposure.
To interpret Assumption 6, suppose that the causal effect of 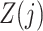 on
on 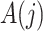 is unconfounded given
is unconfounded given 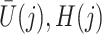 and
and 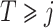 , i.e.,
, i.e.,
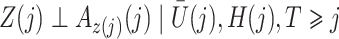 |
for 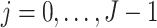 . Then
. Then
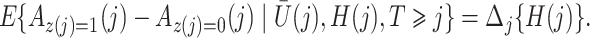 |
The causal interpretation is that, while the unmeasured confounders 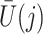 may confound the causal effects of
may confound the causal effects of 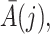
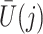 does not predict compliance type expressed in terms of an individual’s potential treatment status under hypothetical instrumental variable interventions
does not predict compliance type expressed in terms of an individual’s potential treatment status under hypothetical instrumental variable interventions 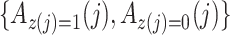 at any
at any 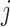 . Figure 3 gives a causal graph representation of longitudinal confounding with unobserved confounders
. Figure 3 gives a causal graph representation of longitudinal confounding with unobserved confounders 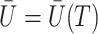 and causal instrumental variables
and causal instrumental variables 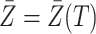 . In principle, we only require (5) so that
. In principle, we only require (5) so that 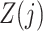 need not be a causal instrumental variable, i.e., the association between
need not be a causal instrumental variable, i.e., the association between 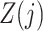 and
and 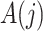 may be subject to uncontrolled confounding, provided the confounder is independent of
may be subject to uncontrolled confounding, provided the confounder is independent of 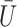 .
.
Fig. 3.
A causal graph of longitudinal confounding with unobserved confounders and instrumental variables.
Finally, we make a positivity assumption regarding censoring, namely 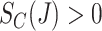 , and the following standard independent censoring assumption.
, and the following standard independent censoring assumption.
Assumption 7.
We have that
.
It may not always be reasonable to make such an independence assumption about loss-to-follow-up censoring; in fact, in § 5 we implement inverse probability of censoring weights that appropriately account for dependent censoring by time-varying covariates under the weaker condition 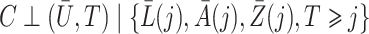 .
.
3.2. Identification of marginal structural Cox model parameters
Before presenting the main identification result, the following lemma states that under Assumptions 4 and 6, 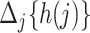 is empirically identified from the observed data.
is empirically identified from the observed data.
Lemma 1.
Under Assumptions 4 and 6, for
we have that
Next, we define the novel time-varying weights
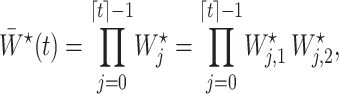 |
(6) |
where
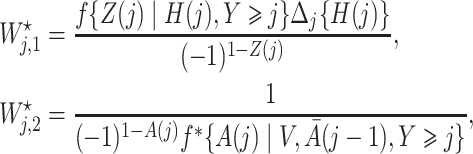 |
with 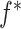 being user-specified, possibly empirically determined. Given that these weights can be identified from the observed data, we have the following theorem, which establishes that
being user-specified, possibly empirically determined. Given that these weights can be identified from the observed data, we have the following theorem, which establishes that 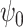 in marginal structural Cox model (1) is identified.
in marginal structural Cox model (1) is identified.
Theorem 1.
Suppose that consistency, positivity and Assumptions 1–7 hold. Then
solves the population moment equation
with
where
and
is a
-dimensional vector-valued function such that
is invertible.
3.3. Instrumental variable-based weighted estimator and large-sample properties
Theorem 1 motivates a weighted estimating equation of the parameter 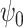 for the marginal structural Cox model defined in (1) in the presence of unmeasured confounding, i.e.,
for the marginal structural Cox model defined in (1) in the presence of unmeasured confounding, i.e., 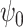 is the solution to the population estimating equation
is the solution to the population estimating equation
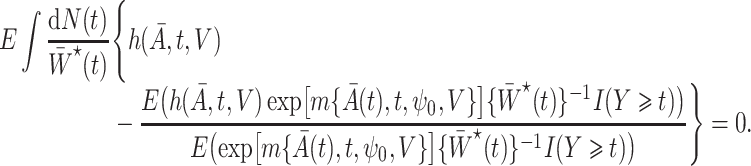 |
(7) |
However, the weights 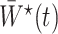 are unknown and need to be estimated from the observed data. We propose using various parametric models to estimate these densities. For example, one can estimate the densities
are unknown and need to be estimated from the observed data. We propose using various parametric models to estimate these densities. For example, one can estimate the densities  ,
, 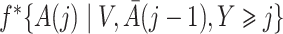 and
and 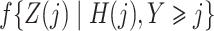 with the logistic regressions
with the logistic regressions
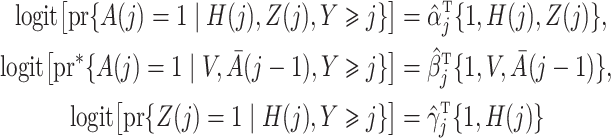 |
estimated by standard maximum likelihood. Let 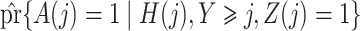 and
and  denote the maximum likelihood estimates of
denote the maximum likelihood estimates of  and
and 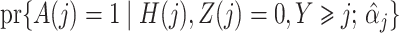 , respectively, and let
, respectively, and let 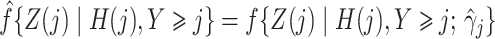 . The compliance type
. The compliance type 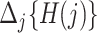 can then be estimated by
can then be estimated by
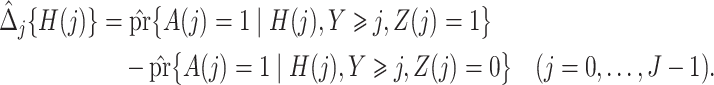 |
We denote the estimated weights by
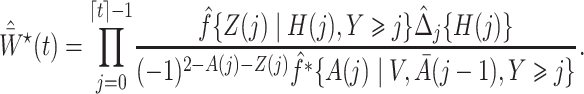 |
Our final estimator 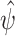 solves an empirical version of (7), where
solves an empirical version of (7), where 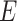 is replaced by
is replaced by 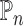 . By standard M-estimation theory,
. By standard M-estimation theory, 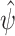 is asymptotically linear with first-order expansion
is asymptotically linear with first-order expansion
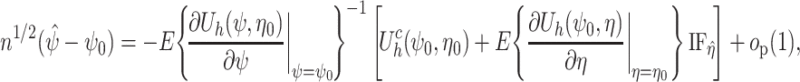 |
where
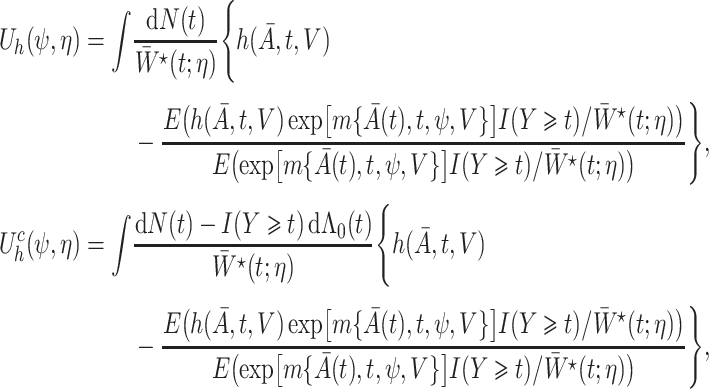 |
 ,
,  is the influence function of
is the influence function of  and
and 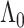 is the baseline cumulative hazard function. Confidence intervals can then be constructed, either using an estimate of the asymptotic variance of
is the baseline cumulative hazard function. Confidence intervals can then be constructed, either using an estimate of the asymptotic variance of 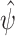 based on the influence function representation given above, or via the nonparametric bootstrap.
based on the influence function representation given above, or via the nonparametric bootstrap.
4. Simulation studies
4.1. Preliminaries
In this section we conduct simulation studies in a setting with 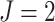 to compare the proposed estimator with existing estimators. As a benchmark, we consider an oracle weighted estimator of marginal structural Cox models, which uses the correctly specified weight
to compare the proposed estimator with existing estimators. As a benchmark, we consider an oracle weighted estimator of marginal structural Cox models, which uses the correctly specified weight 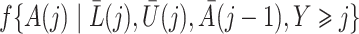 instead of
instead of 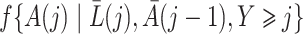 in (3). This oracle estimator is clearly not feasible in practice because
in (3). This oracle estimator is clearly not feasible in practice because  would not be observed. In addition, we implement both a marginal structural Cox model estimated via inverse probability of treatment weighting, incorrectly assuming the sequential randomization assumption given the
would not be observed. In addition, we implement both a marginal structural Cox model estimated via inverse probability of treatment weighting, incorrectly assuming the sequential randomization assumption given the  process, and a time-varying Cox model which directly adjusts for
process, and a time-varying Cox model which directly adjusts for  in the regression model.
in the regression model.
Generating failure time outcomes under a specific marginal structural Cox model is not straightforward. We adopt the approach developed in the 2006 PhD thesis of E. Tchetgen Tchetgen from Harvard University, which we outline in the next subsection.
4.2. Generating potential outcomes under a marginal structural Cox model
Let 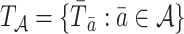 , with
, with 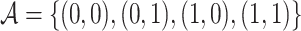 , denote a person’s set of potential outcomes. Under our identifying assumptions and the further condition that
, denote a person’s set of potential outcomes. Under our identifying assumptions and the further condition that
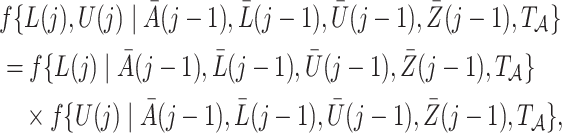 |
the full data 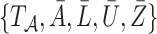 have a joint likelihood that factorizes as
have a joint likelihood that factorizes as
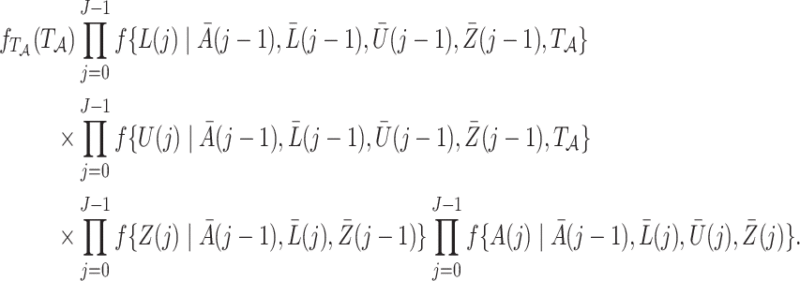 |
Suppose that we wish to generate 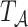 under the marginal structural Cox model
under the marginal structural Cox model
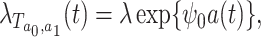 |
(8) |
where 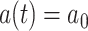 if
if 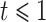 and
and 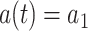 if
if 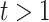 . In the Supplementary Material it is shown that, by generating
. In the Supplementary Material it is shown that, by generating 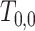 from an exponential density function with constant hazard
from an exponential density function with constant hazard 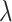 and then defining
and then defining 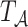 under the accelerated failure time model
under the accelerated failure time model
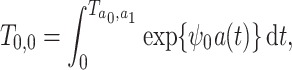 |
we obtain the marginal structural Cox model in (8). We further specify
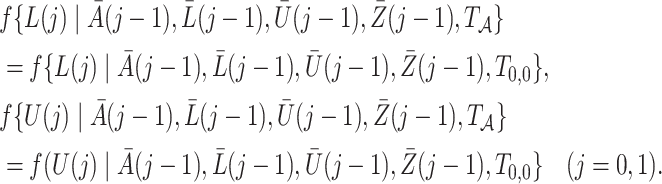 |
Upon generating 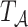 , we simulate the processes
, we simulate the processes 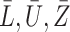 and
and 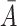 . The censoring time is generated independently, and the observed time and censoring indicator are defined as
. The censoring time is generated independently, and the observed time and censoring indicator are defined as 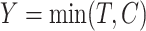 and
and 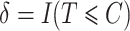 , respectively.
, respectively.
4.3. Simulation settings
We consider two settings, with  for the first scenario and
for the first scenario and 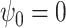 for the second scenario. In both scenarios, the random errors
for the second scenario. In both scenarios, the random errors 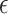 are generated from
are generated from 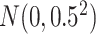 . The baseline hazard is
. The baseline hazard is 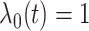 . For convenience, and with a slight abuse of notation, we omit the input argument of
. For convenience, and with a slight abuse of notation, we omit the input argument of 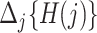 and write simply
and write simply 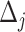 hereafter. The data-generating mechanism for the treatment and survival time is as follows:
hereafter. The data-generating mechanism for the treatment and survival time is as follows: 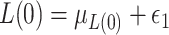 , where
, where 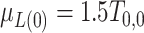 ;
; 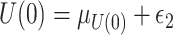 , where
, where 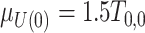 ;
; 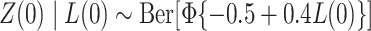 , where
, where 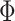 is the cumulative distribution function of the standard normal distribution;
is the cumulative distribution function of the standard normal distribution; 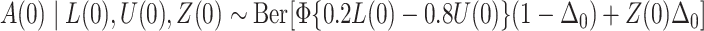 , where
, where 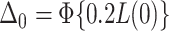 ;
; 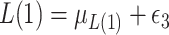 , where
, where 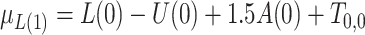 ;
; 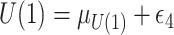 , where
, where 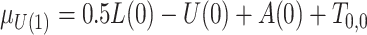 ;
; 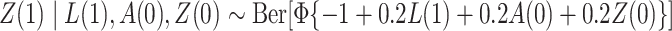 ; and
; and 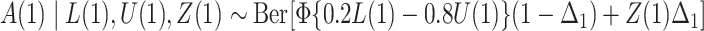 , where
, where 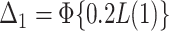 .
.
The censoring time is generated by 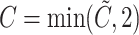 where
where 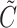 follows
follows 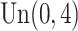 , yielding a censoring rate of approximately 40
, yielding a censoring rate of approximately 40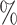 for the first scenario and 30
for the first scenario and 30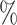 for the second scenario. We also perform a sensitivity analysis for different censoring rates in each scenario; the results are presented in the Supplementary Material. We consider sample sizes
for the second scenario. We also perform a sensitivity analysis for different censoring rates in each scenario; the results are presented in the Supplementary Material. We consider sample sizes 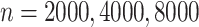 . Each simulation is repeated 500 times. We further perform sensitivity analyses for violation of various instrumental variable assumptions in each scenario; these results can be found in the Supplementary Material. In addition, we examine the empirical coverage of 95
. Each simulation is repeated 500 times. We further perform sensitivity analyses for violation of various instrumental variable assumptions in each scenario; these results can be found in the Supplementary Material. In addition, we examine the empirical coverage of 95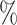 confidence intervals of
confidence intervals of 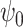 for both scenarios at sample size
for both scenarios at sample size 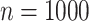 . The confidence intervals are obtained by nonparametric bootstrap with
. The confidence intervals are obtained by nonparametric bootstrap with 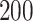 replications.
replications.
Both the standard inverse probability of treatment weighted estimator and our proposed weighted estimator of the marginal structural Cox model (4) require estimation of weights. The density functions 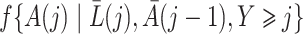 , and
, and 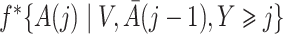 in (3) and (6) are estimated via maximum likelihood of time-specific logistic regression models,
in (3) and (6) are estimated via maximum likelihood of time-specific logistic regression models,
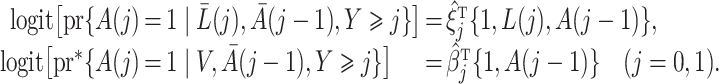 |
The conditional density of 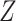 is estimated via maximum likelihood estimation using the model
is estimated via maximum likelihood estimation using the model
 |
where the  link function is the inverse standard normal cumulative distribution function. The data-generating mechanism specifies a model
link function is the inverse standard normal cumulative distribution function. The data-generating mechanism specifies a model 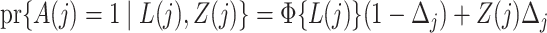 . Estimation of the compliance type is therefore performed via maximum likelihood estimation of the Bernoulli probability mass function for observations still at risk at time
. Estimation of the compliance type is therefore performed via maximum likelihood estimation of the Bernoulli probability mass function for observations still at risk at time 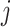 ,
,
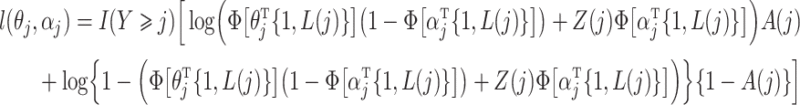 |
for 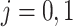 . Thus we obtain the estimated compliance type
. Thus we obtain the estimated compliance type 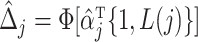 , where
, where 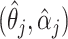 is the maximizer of
is the maximizer of 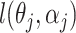 .
.
4.4. Simulation results
We plot the squared bias and mean squared error of the estimated causal parameter in Fig. 4 for the first scenario and Fig. 5 for the second scenario.
Fig. 4.
Scenario 1 simulation results: (a) Monte Carlo squared bias and (b) mean squared error of 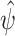 . The following methods are compared: a standard time-varying Cox model that adjusts for
. The following methods are compared: a standard time-varying Cox model that adjusts for  directly in the regression (red); the proposed instrumental variable estimator (green); standard inverse probability of treatment weighted estimation of the marginal structural Cox model under the sequential randomization assumption (blue); and oracle inverse probability of treatment weighted estimation of the marginal structural Cox model which includes
directly in the regression (red); the proposed instrumental variable estimator (green); standard inverse probability of treatment weighted estimation of the marginal structural Cox model under the sequential randomization assumption (blue); and oracle inverse probability of treatment weighted estimation of the marginal structural Cox model which includes 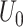 and
and 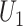 in the treatment model (purple).
in the treatment model (purple).
Fig. 5.
Scenario 2 simulation results: (a) Monte Carlo squared bias and (b) mean squared error of 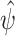 . The methods are the same as in Fig. 4.
. The methods are the same as in Fig. 4.
From Fig. 4(a) and Fig. 5(a) we see that the Cox proportional hazard model and standard weighted estimation of the marginal structural Cox model have severe bias, the former because there exist time-dependent confounders that are affected by previous treatments and unmeasured confounding, and the latter because of unmeasured confounding. Our proposed estimator outperforms both the Cox proportional hazard model and standard weighted estimation of the marginal structural Cox model, in terms of bias and mean squared error. The oracle weighted estimator of the marginal structural Cox model performs as well as the proposed method, and both the bias and the mean squared error converge to zero as the sample size increases. This confirms that our proposed instrumental variable approach performs nearly as well in terms of bias, as the infeasible inverse probability of treatment weighted estimator had 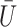 been observed, and can outperform the latter in terms of efficiency.
been observed, and can outperform the latter in terms of efficiency.
Table 1 reports empirical coverage percentages of 95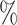 nonparametric bootstrap confidence intervals. The proposed instrumental variable method and the oracle inverse probability of treatment weighted estimator achieve the nominal coverage. However, the confidence intervals of both the standard weighted estimation of the marginal structural Cox model and the standard time-varying Cox proportional hazard model fail to attain nominal coverage.
nonparametric bootstrap confidence intervals. The proposed instrumental variable method and the oracle inverse probability of treatment weighted estimator achieve the nominal coverage. However, the confidence intervals of both the standard weighted estimation of the marginal structural Cox model and the standard time-varying Cox proportional hazard model fail to attain nominal coverage.
Table 1.
Coverage 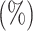 of
of 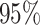 confidence intervals
confidence intervals
| iv | sra | sra.o | Cox | |
|---|---|---|---|---|
Scenario 1 ( ) ) |
96.4 | 87.4 | 93.6 | 67.2 |
Scenario 2 (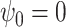 ) ) |
97.2 | 87.2 | 94.2 | 66.4 |
iv, the proposed instrumental variable estimator; sra, standard inverse probability of treatment weighted estimation of the marginal structural Cox model; sra.o, oracle inverse probability of treatment weighted estimation of the marginal structural Cox model; Cox, a standard time-varying Cox model.
5. Estimating the effect of community antiretroviral therapy coverage on HIV acquisition
We apply the proposed method to an HIV study analysed in Tanser et al. (2013), which found evidence that significant reduction of HIV incidence can be achieved by nurse-led, devolved, public-sector antiretroviral therapy, or ART, programmes in rural sub-Saharan African settings, where complete coverage of therapy under existing treatment guidelines has not yet been attained. The analysis in Tanser et al. (2013) was based on a standard time-varying Cox proportional model. Our goal is to examine whether unmeasured confounding biased the reported association between high coverage of ART and the decline in risk of HIV acquisition in rural KwaZulu-Natal, South Africa.
We reanalysed the dataset considered in Tanser et al. (2013), which comes from one of Africa’s largest population-based prospective cohort studies to follow up individuals who were HIV-uninfected at baseline. Our analysis is restricted to 6093 individuals who were enrolled in the study, were known to be HIV-negative on 5 June 2008, and had complete covariate and instrumental variable data. The objective of our analysis is to determine the joint effects of living in a high-coverage community at two time-points, 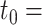 5 June 2008 and
5 June 2008 and 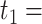 1 January 2011, on HIV incidence. The overall cumulative proportion of events for the outcome was 6.3
1 January 2011, on HIV incidence. The overall cumulative proportion of events for the outcome was 6.3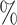 . We consider the following six time-varying covariates: number of partners in the past 12 months; current marital status; wealth index in terms of quintile; age and gender; location of residence; and community HIV prevalence. ART coverage is defined as the proportion of all HIV-infected individuals receiving ART at every location (Tanser et al., 2013). HIV prevalence and ART coverage of an individual’s surrounding community were determined for each year of observation. ART coverage and HIV prevalence around each individual were measured by means of a moving two-dimensional Gaussian kernel with a search radius of 3 km for each year of observation (Tanser et al., 2013). Here ART coverage is dichotomized at 30
. We consider the following six time-varying covariates: number of partners in the past 12 months; current marital status; wealth index in terms of quintile; age and gender; location of residence; and community HIV prevalence. ART coverage is defined as the proportion of all HIV-infected individuals receiving ART at every location (Tanser et al., 2013). HIV prevalence and ART coverage of an individual’s surrounding community were determined for each year of observation. ART coverage and HIV prevalence around each individual were measured by means of a moving two-dimensional Gaussian kernel with a search radius of 3 km for each year of observation (Tanser et al., 2013). Here ART coverage is dichotomized at 30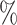 , i.e.,
, i.e., 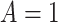 if ART coverage is 30
if ART coverage is 30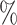 or more and
or more and 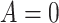 otherwise, such that 40
otherwise, such that 40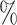 of
of 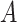 equals 1 over person-time.
equals 1 over person-time.
Our instrumental variable is defined in terms of travel distance to the nearest ART facility: 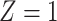 if the distance is less than 3.8 km and
if the distance is less than 3.8 km and 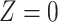 otherwise, such that 65
otherwise, such that 65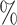 of
of 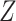 equals 1 over person-time. The travel distance to the closest ART facility is found to be strongly associated with ART coverage. The adjusted log odds ratios and 95
equals 1 over person-time. The travel distance to the closest ART facility is found to be strongly associated with ART coverage. The adjusted log odds ratios and 95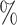 confidence intervals for the association between travel distance to the closest ART facility and community ART coverage are
confidence intervals for the association between travel distance to the closest ART facility and community ART coverage are 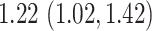 , and
, and 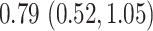 at
at 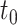 and
and 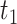 , respectively, which justify instrumental variable relevance, Assumption 2. Furthermore, it is reasonable to assume that the mechanism by which the local density of ART clinics, and therefore travel distance to the nearest ART clinic, affects HIV incidence is primarily through ART coverage, and so the exclusion restriction, Assumption 3, holds.
, respectively, which justify instrumental variable relevance, Assumption 2. Furthermore, it is reasonable to assume that the mechanism by which the local density of ART clinics, and therefore travel distance to the nearest ART clinic, affects HIV incidence is primarily through ART coverage, and so the exclusion restriction, Assumption 3, holds.
We specify the marginal structural model (4) and estimate the various models needed to construct standard inverse probability of treatment weighted weights, as well as our proposed instrumental variable weights under the following model specification:
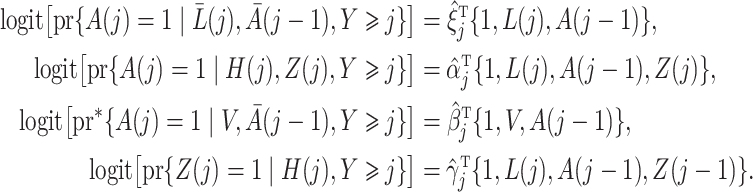 |
In the Supplementary Material we also consider incorporating weights that account for dependent censoring, by adapting the approach of Robins & Rotnitzky (1992) to our method under the assumption 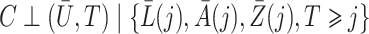 . This entails multiplying
. This entails multiplying 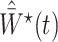 by an estimate of
by an estimate of
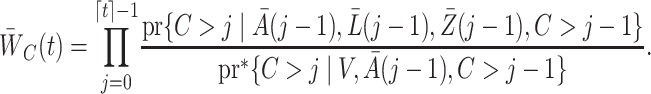 |
The results with and without censoring weights are similar, indicating no evidence of dependent censoring. We obtained point estimates and 95 confidence intervals of the hazard ratio, using the nonparametric bootstrap with 1000 replications for standard weighted estimation and instrumental variable estimation of the marginal structural Cox model. To attenuate the impact of extreme values of weights, we truncated the 2.5th and 97.5th percentiles of the weights for the proposed estimator (Cole & Hernán, 2008). The histogram of weights and the results for the untruncated weights are reported in the Supplementary Material. The untruncated instrumental variable weighted estimator yields a similar point estimate to that of the truncated instrumental variable weighted estimator, but wider confidence intervals, due to outliers in the distribution of estimated weights. As can be seen from Table 2, the instrumental variable point estimate is much smaller, which we interpret, under our instrumental variable assumptions, as appropriately accounting for unmeasured confounding; this suggests that Tanser et al. (2013) might have underestimated the true effect of ART coverage.
confidence intervals of the hazard ratio, using the nonparametric bootstrap with 1000 replications for standard weighted estimation and instrumental variable estimation of the marginal structural Cox model. To attenuate the impact of extreme values of weights, we truncated the 2.5th and 97.5th percentiles of the weights for the proposed estimator (Cole & Hernán, 2008). The histogram of weights and the results for the untruncated weights are reported in the Supplementary Material. The untruncated instrumental variable weighted estimator yields a similar point estimate to that of the truncated instrumental variable weighted estimator, but wider confidence intervals, due to outliers in the distribution of estimated weights. As can be seen from Table 2, the instrumental variable point estimate is much smaller, which we interpret, under our instrumental variable assumptions, as appropriately accounting for unmeasured confounding; this suggests that Tanser et al. (2013) might have underestimated the true effect of ART coverage.
Table 2.
Effect of community ART coverage on HIV acquisition
| sra | iv | |
|---|---|---|
| Hazard ratio | 0.45 | 0.19 |
95 confidence interval confidence interval |
(0.20, 0.92) | (0.06, 0.83) |
sra, standard inverse probability of treatment weighted estimation of the marginal structural Cox model; iv, the proposed instrumental variable estimator, with weights truncated at the 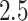 th and
th and 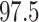 th percentiles.
th percentiles.
6. Discussion
The proposed method can be improved or extended in multiple ways. It would be of interest to look at truncation of the weights in simulations. Formal justification of truncating weights as a means of stabilizing inverse probability weighting analyses is currently lacking, and represents a fruitful avenue of future research. Another potential extension is in the direction of semiparametric efficiency and enhanced robustness against partial model misspecification of nuisance parameters. The efficient influence function for the proposed marginal structural model is significantly more complicated than that in the marginal structural mean model (Tchetgen Tchetgen et al., 2018), and its study is beyond the scope of this paper.
Supplementary Material
Acknowledgement
We thank the two reviewers, associate editor and editor for many useful comments which have led to an improved manuscript. Cui was supported in part by the National University of Singapore and Singapore Ministry of Education. Tchetgen Tchetgen was supported in part by the U.S. National Institutes of Health.
Contributor Information
Y Cui, Department of Statistics and Data Science, National University of Singapore, 6 Science Drive 2, 117546 Singapore.
H Michael, Department of Mathematics and Statistics, University of Massachusetts, 710 N. Pleasant Street, Amherst, Massachusetts 01003, U.S.A.
F Tanser, Lincoln Institute for Health, University of Lincoln, Brayford Way, Brayford Pool, Lincoln LN6 7TS, U.K.
E Tchetgen Tchetgen, Department of Statistics and Data Science, The Wharton School, University of Pennsylvania, 265 South 37th Street, Philadelphia, Pennsylvania 19104, U.S.A.
Supplementary material
The Supplementary Material includes proofs of the theoretical results and additional simulation scenarios.
References
- Aalen, O. O. (1989). A linear regression model for the analysis of life times. Statist. Med. 8, 907–25. [DOI] [PubMed] [Google Scholar]
- Ali, M. S., Groenwold, R. H. H., Belitser, S. V., Souverein, P. C., Martin, E., Gatto, N. M., Huerta, C., Gardarsdottir, H., Roes, K. C. B., Hoes, A. W.. et al. (2016). Methodological comparison of marginal structural model, time-varying Cox regression, and propensity score methods: The example of antidepressant use and the risk of hip fracture. Pharmacoepidemiol. Drug Safety 25, 114–21. [DOI] [PubMed] [Google Scholar]
- Angrist, J. D., Imbens, G. W. & Rubin, D. B. (1996). Identification of causal effects using instrumental variables. J. Am. Statist. Assoc. 91, 444–55. [Google Scholar]
- Brookhart, M. A. & Schneeweiss, S. (2007). Preference-based instrumental variable methods for the estimation of treatment effects: assessing validity and interpreting results. Int. J. Biostatist. 3, article no. 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cain, L. E., Cole, S. R., Greenland, S., Brown, T. T., Chmiel, J. S., Kingsley, L. & Detels, R. (2009). Effect of highly active antiretroviral therapy on incident AIDS using calendar period as an instrumental variable. Am. J. Epidemiol. 169, 1124–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerdá, M., Diez-Roux, A. V., Tchetgen Tchetgen, E. J., Gordon-Larsen, P. & Kiefe, C. I. (2010). The relationship between neighborhood poverty and alcohol use: Estimation by marginal structural models. Epidemiology 21, 482–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, S. R. & Hernán, M. A. (2008). Constructing inverse probability weights for marginal structural models. Am. J. Epidemiol. 168, 656–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuzick, J., Sasieni, P., Myles, J. & Tyrer, J. (2007). Estimating the effect of treatment in a proportional hazards model in the presence of non-compliance and contamination. J. R. Statist. Soc. B 69, 565–88. [Google Scholar]
- de Keyser, C. E., Leening, M. J. G., Romio, S. A., Jukema, J. W., Hofman, A., Ikram, M. A., Franco, O. H., Stijnen, T. & Stricker, B. H. (2014). Comparing a marginal structural model with a Cox proportional hazard model to estimate the effect of time-dependent drug use in observational studies: Statin use for primary prevention of cardiovascular disease as an example from the Rotterdam Study. Eur. J. Epidemiol. 29, 841–50. [DOI] [PubMed] [Google Scholar]
- Frangakis, C. E., Brookmeyer, R. S., Varadhan, R., Safaeian, M., Vlahov, D. & Strathdee, S. A. (2004). Methodology for evaluating a partially controlled longitudinal treatment using principal stratification, with application to a needle exchange program. J. Am. Statist. Assoc. 99, 239–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberger, A. S. (1972). Structural equation methods in the social sciences. Econometrica 40, 979–1001. [Google Scholar]
- Greenland, S. (2000). An introduction to instrumental variables for epidemiologists. Int. J. Epidemiol. 29, 722–9. [DOI] [PubMed] [Google Scholar]
- Hernán, M., Brumback, B. & Robins, J. (2000). Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology 11, 561–70. [DOI] [PubMed] [Google Scholar]
- Hernán, M. A., Brumback, B. & Robins, J. M. (2001). Marginal structural models to estimate the joint causal effect of nonrandomized treatments. J. Am. Statist. Assoc. 96, 440–8. [Google Scholar]
- Hernán, M. & Robins, J. (2006). Instruments for causal inference: An epidemiologist’s dream? Epidemiology 17, 360–72. [DOI] [PubMed] [Google Scholar]
- Imbens, G. W. & Angrist, J. D. (1994). Identification and estimation of local average treatment effects. Econometrica 62, 467–75. [Google Scholar]
- Joffe, M. M., Yang, W. P. & Feldman, H. (2012). G-estimation and artificial censoring: Problems, challenges, and applications. Biometrics 68, 275–86. [DOI] [PubMed] [Google Scholar]
-
Karim, M. E., Gustafson, P., Petkau, J., Zhao, Y., Shirani, A., Kingwell, E., Evans, C., Van Der Kop, M., Oger, J. & Tremlett, H. (2014). Marginal structural Cox models for estimating the association between
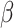 -interferon exposure and disease progression in a multiple sclerosis cohort. Am. J. Epidemiol. 180, 160–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
-interferon exposure and disease progression in a multiple sclerosis cohort. Am. J. Epidemiol. 180, 160–71. [DOI] [PMC free article] [PubMed] [Google Scholar] - Kianian, B., Kim, J. I., Fine, J. P. & Peng, L. (2019). Causal proportional hazards estimation with a binary instrumental variable. arXiv: 1901.11050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J., Fine, J. & Brookhart, A. (2015). Instrumental variable additive hazards models. Biometrics 71, 122–30. [DOI] [PubMed] [Google Scholar]
- Loeys, T., Goetghebeur, E. & Vandebosch, A. (2005). Causal proportional hazards models and time-constant exposure in randomized clinical trials. Lifetime Data Anal. 11, 435–49. [DOI] [PubMed] [Google Scholar]
- MacKenzie, T. A., Tosteson, T. D., Morden, N. E., Stukel, T. A. & O’Malley, A. J. (2014). Using instrumental variables to estimate a Cox’s proportional hazards regression subject to additive confounding. Health Serv. Outcomes Res. Methodol. 14, 54–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinussen, T., Nørbo Sørensen, D. & Vansteelandt, S. (2017a). Instrumental variables estimation under a structural Cox model. Biostatistics 20, 65–79. [DOI] [PubMed] [Google Scholar]
- Martinussen, T., Vansteelandt, S., Tchetgen Tchetgen, E. J. & Zucker, D. M. (2017b). Instrumental variables estimation of exposure effects on a time-to-event endpoint using structural cumulative survival models. Biometrics 73, 1140–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michael, H., Cui, Y., Lorch, S. & Tchetgen Tchetgen, E. (2020). Instrumental variable estimation of marginal structural mean models for time-varying treatment. arXiv: 2004.11769v2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neyman, J. (1923). On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statist. Sci. 5, 463–80. Translated from the Polish original by Dabrowska D. M. and Speed, T. P.. 1990. [Google Scholar]
- Nie, H., Cheng, J. & Small, D. S. (2011). Inference for the effect of treatment on survival probability in randomized trials with noncompliance and administrative censoring. Biometrics 67, 1397–405. [DOI] [PubMed] [Google Scholar]
- Robins, J. (1986). A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Math. Mod. 7, 1393–512. [Google Scholar]
- Robins, J. M. (1987). Errata to “A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect” Mathl Modelling 7(9–12), 1393–1512 (1986). Comp. Math. Appl. 14, 917–21. [Google Scholar]
- Robins, J. M. (1997). Causal inference from complex longitudinal data. In Latent Variable Modeling and Applications to Causality, Berkane, M. ed. New York: Springer, pp. 69–117. [Google Scholar]
- Robins, J. M. (1998). Marginal structural models. In Proc. 1997 American Statistical Association Section on Bayesian Statistical Science. Alexandria, Virginia: American Statistical Association, pp. 1–10. [Google Scholar]
- Robins, J. M. (2000). Marginal structural models versus structural nested models as tools for causal inference. In Statistical Models in Epidemiology, the Environment, and Clinical Trials, Halloran M. E. & Berry, D. eds. New York: Springer, pp. 95–133. [Google Scholar]
- Robins, J. M., Hernán, M. A. & Brumback, B. A. (2000). Marginal structural models and causal inference in epidemiology. Epidemiology 11, 550–60. [DOI] [PubMed] [Google Scholar]
- Robins, J. M. & Rotnitzky, A. (1992). Recovery of information and adjustment for dependent censoring using surrogate markers. In AIDS Epidemiology. Berlin: Springer, pp. 297–331. [Google Scholar]
- Robins, J. M. & Tsiatis, A. A. (1991). Correcting for non-compliance in randomized trials using rank preserving structural failure time models. Commun. Statist. A 20, 2609–31. [Google Scholar]
- Rosenbaum, P. R. & Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika 70, 41–55. [Google Scholar]
- Rubin, D. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 66, 688–701. [Google Scholar]
- Sørensen, D. N., Martinussen, T. & Tchetgen, E. T. (2019). A causal proportional hazards estimator under homogeneous or heterogeneous selection in an IV setting. Lifetime Data Anal. 25, 639–59. [DOI] [PubMed] [Google Scholar]
- Swanson, S. A., Hernán, M. A., Miller, M., Robins, J. M. & Richardson, T. S. (2018). Partial identification of the average treatment effect using instrumental variables: Review of methods for binary instruments, treatments, and outcomes. J. Am. Statist. Assoc. 113, 933–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanser, F., Barnighausen, T., Grapsa, E., Zaidi, J. & Newell, M.-L. (2013). High coverage of ART associated with decline in risk of HIV acquisition in rural KwaZulu-Natal, South Africa. Science 339, 966–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen, E. J., Michael, H. & Cui, Y. (2018). Marginal structural models for time-varying endogenous treatments: A time-varying instrumental variable approach. arXiv: 1809.05422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen, E. J., Walter, S., Vansteelandt, S., Martinussen, T. & Glymour, M. M. (2015). Instrumental variable estimation in a survival context. Epidemiology 26, 402–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, L. & Tchetgen Tchetgen, E. (2018). Bounded, efficient and triply robust estimation of average treatment effects using instrumental variables. J. R. Statist. Soc. B 80, 531–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, L., Tchetgen Tchetgen, E. J., Martinussen, T. & Vansteelandt, S. (2022). IV estimation of causal hazard ratio. arXiv: 1807.05313v2. [DOI] [PubMed] [Google Scholar]
- Wooldridge, J. M. (2010). Econometric Analysis of Cross Section and Panel Data. Cambridge, Massachusetts: MIT Press. [Google Scholar]
- Yang, F., Lorch, S. A. & Small, S. D. (2014). Estimation of causal effects using instrumental variables with nonignorable missing covariates: Application to effect of type of delivery NICU on premature infants. Ann. Appl. Statist. 8, 48–73. [Google Scholar]
- Yende-Zuma, N., Mwambi, H. & Vansteelandt, S. (2019). Adjusting the effect of integrating antiretroviral therapy and tuberculosis treatment on mortality for noncompliance: A time-varying instrumental variables analysis. Epidemiology 30, 197–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, W., Chen, K., Sobel, M. E. & Ying, Z. (2015). Semiparametric transformation models for causal inference in time-to-event studies with all-or-nothing compliance. J. R. Statist. Soc. B 77, 397–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zubizarreta, J. R., Small, D. S., Goyal, N. K., Lorch, S. & Rosenbaum, P. R. (2013). Stronger instruments via integer programming in an observational study of late preterm birth outcomes. Ann. Appl. Statist. 7, 25–50. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.