Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2024 Jan 1.
Published in final edited form as: J Biomech. 2022 Nov 25;146:111397. doi: 10.1016/j.jbiomech.2022.111397

Hyperelastic characterization reveals proteoglycans drive the nanoscale strain-stiffening response in hyaline cartilage

Kaitlin P McCreery a,b, Callan M Luetkemeyer a,*, Sarah Calve a,b, Corey P Neu a,b,*
PMCID: PMC9922104  NIHMSID: NIHMS1857644  PMID: 36469996

Abstract

Degenerative diseases such as osteoarthritis (OA) result in deterioration of cartilage extracellular matrix (ECM) components, significantly compromising tissue function. For measurement of mechanical properties at micron resolution, atomic force microscopy (AFM) is a leading technique in biomaterials research, including in the study of OA. It is common practice to determine material properties by applying classical Hertzian contact theory to AFM data. However, errors are consequential because the application of a linear elastic contact model to tissue ignores the fact that soft materials exhibit nonlinear properties even at small strains, influencing the biological conclusions of clinically-relevant studies. Additionally, nonlinear material properties are not well characterized, limiting physiological relevance of Young’s modulus. Here, we probe the ECM of hyaline cartilage with AFM and explore the application of Hertzian theory in comparison to five hyperelastic models: NeoHookean, Mooney-Rivlin, Arruda-Boyce, Fung, and Ogden. The Fung and Ogden models achieved the best fits of the data, but the Fung model demonstrated robust sensitivity during model validation, demonstrating its ideal application to cartilage ECM and potentially other connective tissues. To develop a biological understanding of the Fung nonlinear parameter, we selectively degraded ECM components to target collagens (purified collagenase), hyaluronan (bacterial hyaluronidase), and glycosaminoglycans (chondroitinase ABC). We found significant differences in both Fung parameters in response to enzymatic treatment, indicating that proteoglycans drive the nonlinear response of cartilage ECM, and validating biological relevance of these phenomenological parameters. Our findings add value to the biomechanics community of using two-parameter material models for microindentation of soft biomaterials.

Keywords: Atomic force microscopy, In situ, Cartilage, Extracellular matrix, Hyperelasticity

1. Introduction

Tissue engineering solutions require knowledge of micromechanical properties in synthetic and natural biomaterials. Biomechanical properties not only enable macroscale tissue function by supporting physical load, but also regulate cellular processes to the extent that changes in elasticity contribute to diseases like cancer or degenerative osteoarthritis (OA) (Kashani and Packirisamy, 2020; Maldonado and Nam, 2013; McLane and Ligon, 2016). In particular, articular cartilage and musculoskeletal tissues are organized to withstand physical loads which relies on heterogeneous composition, specific microstructural organization, and multiscale mechanical coupling (Armiento et al., 2018; Guo et al., 2022). Understanding and decoupling microscale biomaterial mechanics is fundamental for advancing early diagnosis for degenerative diseases, and developing tissue engineering solutions for extracellular matrix (ECM) degradation.

The mechanical behavior of cartilage is not only important in macroscale joint loading but also plays a crucial role in the health and long-term function of chondrocytes. Changes in ECM composition during the initiation of OA alter healthy cell function and resilience (Bonnans et al., 2014). Recent investigations revealed that cartilage mechanical function also depends on ECM composition (Ebrahimi et al., 2020; Wyse Jackson et al., 2022). The mechanical properties of hyaline cartilage arise from a dense collagen fiber network embedded in a solution of glycosaminoglycans (GAGs). GAGs are unbranched sugar polymers with repeating disaccharides which stabilize water by attracting cations to the ECM thereby increasing osmotic pressure. There are two main classes of GAGs: sulfated GAGs (chondroitin sulfate, dermatan sulfate, keratan sulfate, and heparan sulfate) and nonsulfated GAGs, like hyaluronan (also known as hyaluronic acid, or HA) (Roughley and Lee, 1994). Hyaluronan has a mobile form and can become immobilized by covalent bonding to other GAGs to form proteoglycans (PGs). Charge density in cartilage is therefore controlled by both fixed and mobile charges determined by the interaction between ECM components. Type II collagen fibrils give cartilage its tensile strength, particularly at its surface, and GAG content determines the compressive stiffness (Bank et al., 2000; Kempson et al., 1970). The composite proteoglycan-water solid contributes to osmotic swelling pressure, hydraulic permeability, and resistance to compressive and shear deformation (Heneghan and Riches, 2008). While we know that several pathologies reduce the stiffness of the ECM, contributions of specific ECM constituents to biomechanics, including nonlinear elastic behavior, is not understood. By degrading these components using enzymes targeting hyaluronan, GAG substrates, and collagen fibrils, functional relevance of ECM composition may be resolved.

Atomic Force Microscopy (AFM) is a powerful technique to directly measure micromechanical properties of the ECM as it can resolve microstructural changes. AFM indentation has been applied to study ECM development, degeneration, and cell-ECM interactions (McCreery et al., 2021; Wilusz et al., 2013; Xu et al., 2016a). When AFM is applied to biomaterials, a common approximation of material behavior is an elastic response, using Hertzian theory to approximate a compressive modulus. Given the complexity of ECM, the polymer mechanics of cartilage under microindentation are only partially captured by the linear elastic approximation of its indentation response. It is well known that soft material response to deformation is highly nonlinear, and the application of AFM to soft matter is complicated by the lack of practical nonlinear contact mechanics models. Analytical errors are inevitable when Hertzian theory is applied beyond the linear elastic range, rarely resolvable in soft materials like cells and tissues with stiffness < 5 kPa (Costa et al., 2006; Van Liedekerke et al., 2020). These errors vary in magnitude depending on AFM indentation parameters, substrate effects, and best-fit analyses, resulting in modulus approximations that vary by at least an order of magnitude in the literature (Harris and Charras, 2011; Kontomaris et al., 2022). Computational modeling has shown that certain hyperelastic models are better fits for indentations of soft tissues as a consequence of introducing a nonlinear material parameter (Lin et al., 2009). However, what physiological insights these models reveal about the structure/function relationships of tissues is not validated or defined.

Our objective was to compare models used to describe mechanics of biomaterials, assess their appropriateness for AFM indentations, and determine which ECM components give rise to stiffness vs nonlinear parameter values in hyaline cartilage (Fig. 1). We uncovered how composition is related to initial stiffness and nonlinear material properties by removing key ECM components using selective enzyme degradation and analyzing AFM data with hyperelastic models of soft material indentation. Furthermore, we assessed the sensitivity of model parameters to changes in ECM composition. This work is an applicable comparison of elastic and hyperelastic models to describe AFM data.

Fig. 1. Hyaline cartilage ECM composition and mechanical characterization with AFM.

Fig. 1.

Open in a new tab

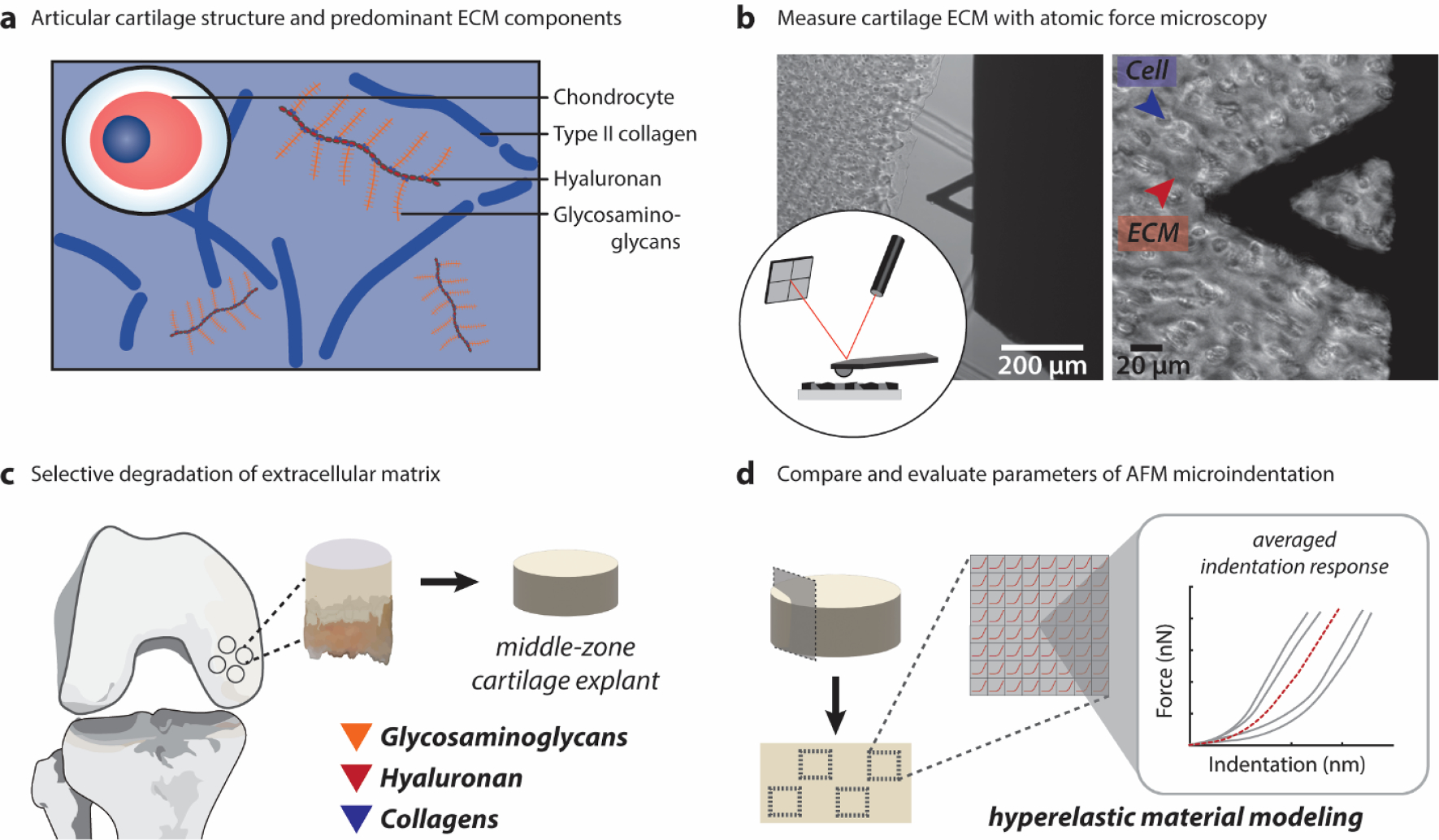
(A) The articular cartilage extracellular matrix consists predominantly of interacting type II collagen fibers and glycosaminoglycans. These components define both the structure and mechanical properties of the tissue. (B) Atomic force microscopy (AFM) is an established technique used to define micromechanical properties of the ECM network. Here, we use this technique with the assistance of optical microscopy to probe the cartilage ECM following enzymatic treatment. (C) In this work, bovine cartilage explants were co-cultured ex vivo with specific matrix-degrading enzymes targeting GAGs (chondroitinase ABC), hyaluronan (bacterial hyaluronidase), and the collagen matrix (purified collagenase). (D) Force-indentation vectors from each specimen were interpolated to calculate an average indentation response for comparative analysis of 6 different elastic and hyperelastic biomechanics models.

2. Methods

2.1. Cartilage specimen acquisition and tissue explant culture

Experimental methods are detailed in Appendix A. Briefly, bovine middle-zone cartilage explants (N = 6 for each group) were harvested and cultured in complete media. Tissue viability was maintained from collection to AFM testing to measure micromechanical properties of the native tissue without introducing effects from freeze-thaw cycles (Xu et al., 2016a) (Fig. 1B).

2.2. Targeted degradation of ECM components

Explants from each animal (N = 6) were randomly assigned to an enzyme treatment group or the control culture media group (Fig. 1C). Explants were cultured in control (media) or treatment (media + enzyme) for 44hrs at 37 °C with media changes every 24hrs. Treatment groups were (1) 100 U/mL purified collagenase (Worthington Biochem Corp., NJ, USA, LS005273), (2) 50 U/mL bacterial hyaluronidase (MP Biomedicals, USA, 320421), or (3) 0.1 U/mL chondroitinase ABC (chABC) (Sigma Aldrich, MO, USA, C2905) (Sigma, USA). The concentrations used here were based on previous studies (Chan et al., 2010; June and Fyhrie, 2009; Karhula et al., 2017; Nissi et al., 2016; Pastrama et al., 2019). Samples were rinsed 3 × with PBS and enzyme inhibitors (5 mM EDTA and 5 mM benzamidine HCL), then stored in PBS on ice until testing.

2.3. Parameter sweep simulations

To understand the influence of individual material parameters on the indentation response, simulations were performed in MATLAB using the approximate analytical force-indentation relationships determined by Lin et al. (2009) and Zhang et al. (2014), as reported in Table 1. For all model fits, a Hertzian relationship between the contact radius (a) and probe radius (R) was assumed

a=R12δ12

Table 1.

Force-indentation relationships for Hertzian and hyperelastic strain energy density functions.

Name Force (F) – indentation (δ) relationship Parameters See also
Hertz F=4ER12δ3231−ν2a=R1/2δ1/2 E (Hertz, 1882)
NeoHookean F=C10πa5−15Ra4+75R2a35Ra2−50R2a+125R3 C 10 (Lin et al., 2009)
Mooney-Rivlin F=C10πa5−15Ra4+75R2a35Ra2−50R2a+125R3+C01πa5−15Ra4+75R2a3−a3+15Ra2−75R2a+125R3 C10, C01 (Lin et al., 2009; Mooney, 1940)
Arruda-Boyce F=μ0RδδA0+∑i=13Ai+exp−λm/Bi Where Ai and Bi vary by δ/R, according to values in Supplementary Table 1. μ0, λm (Arruda and Boyce, 1993; Zhang et al., 2014)
Fung F=Bπa5−15Ra4+75R2a35Ra2−50R2a+125R3expba3−15Ra225R2a−125R3 B, b (Fung, 1967; Fung et al., 1979; Lin et al., 2009)
Ogden F=Bπa2α1−0.2aR−α2−1−1−0.2aRa−1 B, α (Lin et al., 2009; Ogden, 1972)
Open in a new tab

Lin and colleagues (2009) found that this equation is valid for hyperelastic materials while a/R ≤ 0.4. A range of 5 values for each parameter were used for simulations. For two parameter models, one parameter was fixed at the middle value while a sweep was performed on the other.

2.4. Imaging cartilage matrix organization

Half-plugs from each treatment group were frozen and stored at −20 °C. Following, 100 μm vibratome sections across the full thickness of each sample were obtained and labeled with immunofluorescence targeting type II collagen (Invitrogen, USA, MA5–13026). Tissues were fixed following antibody labeling and stained with DAPI and wheat germ agglutinin (WGA) (Fisher, MA, W21404). Staining was performed with picro-sirius red (PR) (Abcam, U.K., ab246832) to visualize collagen organization.

2.5. Indentation of the cartilage ECM via AFM

Cartilage samples were sectioned immediately following treatment prior to AFM testing, described in Appendix A.

A Keysight 5500 AFM (Keysight Technologies Inc., CA, USA) was combined with a Nikon Eclipse Ti wide-field inverted microscope (Nikon Instruments Inc., NY, USA), outfitted with a 40 × objective allowing for visualization of testing regions (Fig. 1B). The cartilage ECM was identified and optically aligned with the AFM probe. Four areas, each at least 1 mm apart, were selected and probed over 20 × 20 μm2 with 8 × 8 px2 indentations. For elastography images, spectroscopy resolution was 32 × 32 px2 indentations. A maximum applied load was chosen at ~ 90nN at 8 μm/s, corresponding to an average indentation depth of 224.84 ± 106.04 nm among all treated and control groups. Probe specifications include a cantilever with stiffness k = 0.382N/m and a borosilicate glass sphere tip with diameter = 2 μm (NovaScan, USA).

2.6. Post-processing of microindentation data

Indentation (force–displacement) curves were automatically processed in MATLAB to determine soft material contact point. The values of force and indentation depth were inferred from directly measurable quantities, the cantilever spring constant k, and knowledge of contact point. The bending position of the cantilever (d) and the position of the cantilever base (z) were used to determine the contact point with deflection (d0) and position (z0). Values for the applied load (F) and the indentation depth (δ) in the absence of attractive or repulsive forces are

F=k(d−d0)
δ=(z−z0)−(d−d0)

In each experimental group, all indentations over four regions per animal (>200 per explant) were processed to produce an average response curve for each biological replicate by interpolating with piecewise cubic hermite interpolating polynomial via the MATLAB function pchip, and force–displacement vectors were averaged respectively. Mean parameter values for each animal were calculated from interpolated average indentation response curves, and elastography pixel values were generated by fitting each indentation to the selected model (Fig. 1D).

2.7. Parameter identification

A custom MATLAB script was used to fit the analytical functions in Table 1 to force-indentation curves. Best-fit material parameters were identified for each model using a least-squares minimization approach, employing the function lsqnonlin. We assessed the fit quality of each model to the average indentation-response of each animal by calculating the sum square error (SSE), root mean square error (RMSE), and mean percent error (MPE). We assessed parameter identifiability by visualizing the cost function space and calculating parameter sensitivity matrices near the identified minima.

2.8. Assessment of parameter identifiability

Determining material parameters from contact mechanics models typically involves numerical approximation. However, numerical solutions from AFM are often influenced by experimental noise and error in contact point estimation. It is therefore important to consider the identifiability of the calculated parameters (Luetkemeyer et al., 2021). To examine this, sensitivity matrices (Sij) were constructed to the fit of a given model to the average response curve:

Sij=δ2ϕδεiδεj

where the diagonal element Sii is the sensitivity of the cost function ϕ to small perturbations in an identified parameter ξi. The off-diagonal element Sij is the cost function sensitivity to the paired relationship of perturbations for parameters ξi and ξj, which when small and outside the sensitivity range defined by the diagonal elements, indicate parameter covariance, meaning one or both are not identifiable.

2.9. Statistical tests

Statistical tests were all performed using R (R Core Team, 2013). Means across parameter values following treatments, and between model errors if SSE, RMSE, and MPE were each tested using one-way ANOVA and Tukey HSD post-hoc testing where appropriate (*p < 0.05, **p < 0.001).

3. Results

In this study, we probed the micromechanical properties of cartilage with AFM to quantify how ECM composition influences microindentation response (Fig. 1). Middle-zone hyaline cartilage is avascular and aneural, making it an ideal ex vivo model for studying tissue mechanics without introducing variability via freeze–thaw cycles, fixation, or cell death of residing chondrocytes (McCreery et al., 2020; Xu et al., 2016a). Preliminary measurements were carried out to identify indentation parameters, ensuring reproducibility of the measured results, by optimizing previously reported testing protocols (Wilusz et al., 2013; Wilusz and Guilak, 2014; Xu et al., 2016a). Indentation was optimized by slowing the ramp speed to reduce fluid-flow viscoelastic effects, and a constant setpoint force was maintained to consistently probe the ECM testing surface with minimum interaction with the sample.

We assessed the appropriateness of six different models applied to explants. Each model has one or two parameters that influence the mathematical behavior of indentation (Fig. 2). We began with the one-parameter Hertz model, commonly used for AFM data of biomaterials, and the NeoHookean model used to characterize nonlinear polymer materials (Ding et al., 2017). We further explored the Arruda-Boyce (AB), Fung, Mooney-Rivlin (MR), and Ogden models to develop a comprehensive overview of two-parameter models used to describe soft materials (Lin et al., 2009; Zhang et al., 2014).

Fig. 2. Changing material parameters alters indentation response curve behavior.

Fig. 2.

Open in a new tab

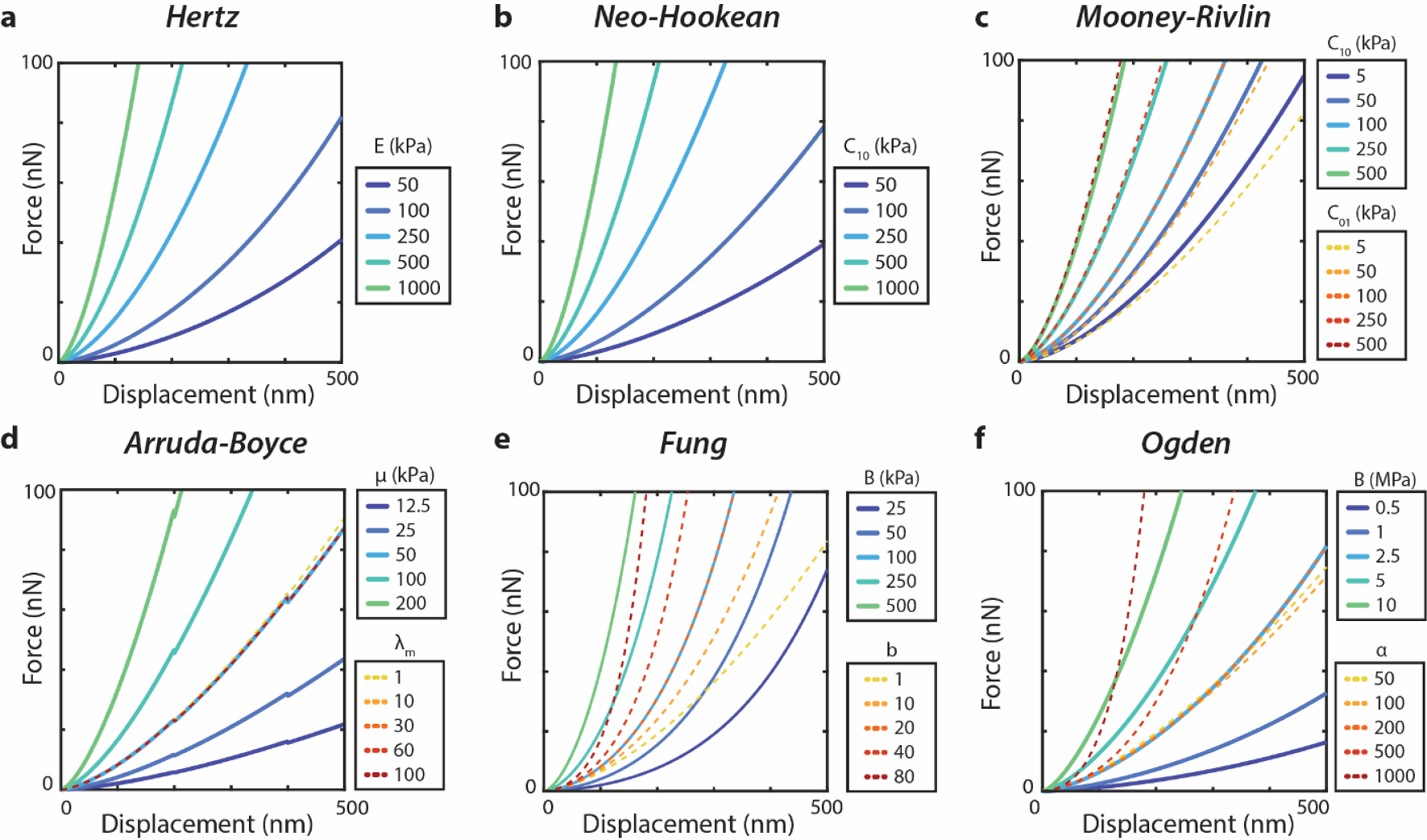
Simulated force–displacement curves during indentation with representative parameter sweep for (A) Hertz, (B) NeoHookean, (C) Arruda-Boyce, (D) Fung, (E) Mooney-Rivlin, and (F) Ogden models. For the second parameter sweep in two-parameter models (C-F), the first parameter is held constant at the chosen middle value. Values were determined with a fixed probe radius of 1 μm to correspond to experimental conditions later in this work.

The disruption of key ECM components was confirmed by staining cartilage sections to observe proteoglycans (WGA) and collagen fibril organization (picro-sirius red, COL2A1 IF) (Fig. 3). We observed reduced intensity of WGA staining in chABC and hyaluronidase-treated ECM, indicating a reduction of GAGs and selective degradation of the proteoglycan network (Fig. 3A). Reduction of PR histochemical staining in collagenase-treated samples confirmed disruption of the predominantly type II collagen matrix (Fig. 3B). Immunofluorescence of type II collagen demonstrated change in the collagen matrix organization, especially following hyaluronidase treatment. Treatment with chABC strongly depleted WGA signal, except in the chondron. Meanwhile, hyaluronidase eliminated WGA signal that co-localizes with the chondron.

Fig. 3. Fluorescent visualization of cartilage ECM following selective enzymatic digestion.

Fig. 3.

Open in a new tab

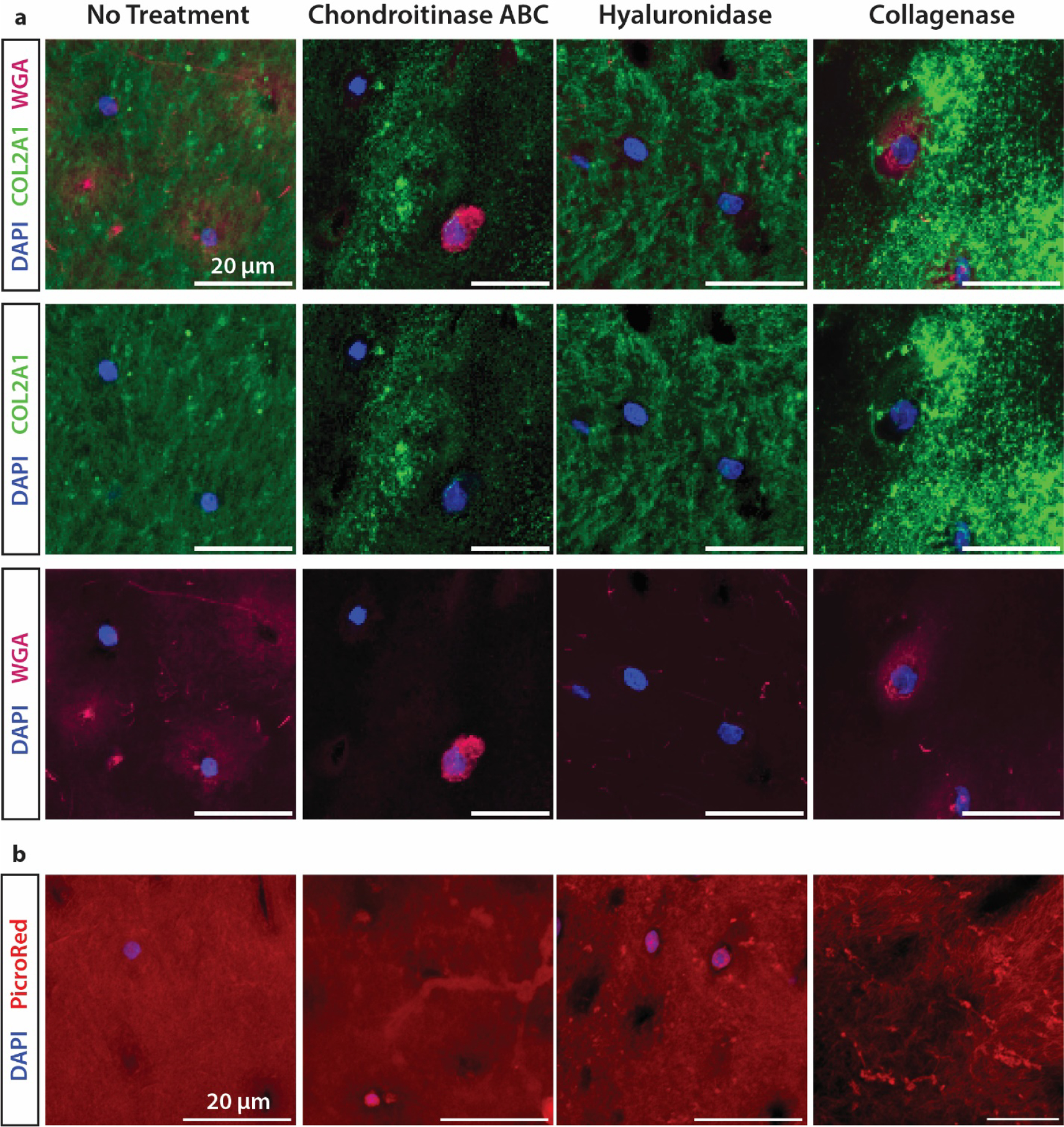
Change in intensity and consistency of immunofluorescent (A) and histological (B) fluorescent visualization of the collagen and proteoglycan networks. Staining was performed with WGA to visualize carbohydrates, and anti-collagen II antibody and picrosirius red to visualize the impact on the collagen matrix.

For AFM indentations per explant, force–displacement vectors were interpolated to calculate an average indentation-response. We analyzed these average indentation-response curves with each of 6 models to investigate the impact of ECM degradation on the best-fit parameter values. We compared parameters from one-parameter models (Fig. 4) and two-parameter models (Fig. 5). There was a statistically significant difference in each parameter between at least two groups of each the Hertz and NeoHookean parameters (**p < 0.001). Both chABC and hyaluronidase treatment significantly affected the Hertzian and NeoHookean moduli (**p < 0.001), but we observed no significant reduction following collagenase treatment (p = 0.466). Among two-parameter models, we found the same reduction observed in initial shear modulus (μ0) of the AB model and initial stiffness (B) of the Fung model (**p < 0.001). Furthermore, the nonlinear Fung parameter b significantly increased in chABC-treated cartilage (*p < 0.05) and in the hyaluronidase-treated cartilage (**p < 0.001).

Fig. 4. Single-parameter models are affected by enzymatic disruption of cartilage ECM.

Fig. 4.

Open in a new tab

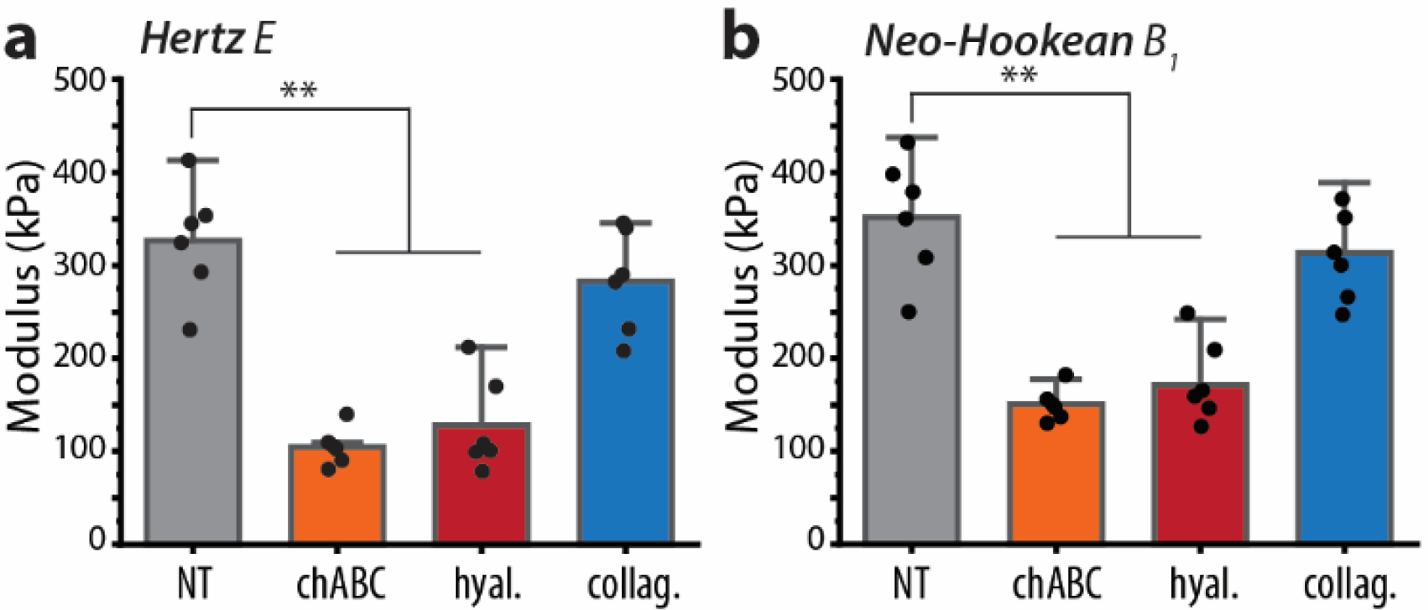
(A) Hertzian linear elastic and (B) NeoHookean hyperelastic models show similar parameter reduction effect on the cartilage ECM. Mean ± s.d., N = 6 animals average indentation response curves. **p < 0.001.

Fig. 5. Two-parameter hyperelastic models are affected by enzymatic disruption of cartilage ECM.

Fig. 5.

Open in a new tab

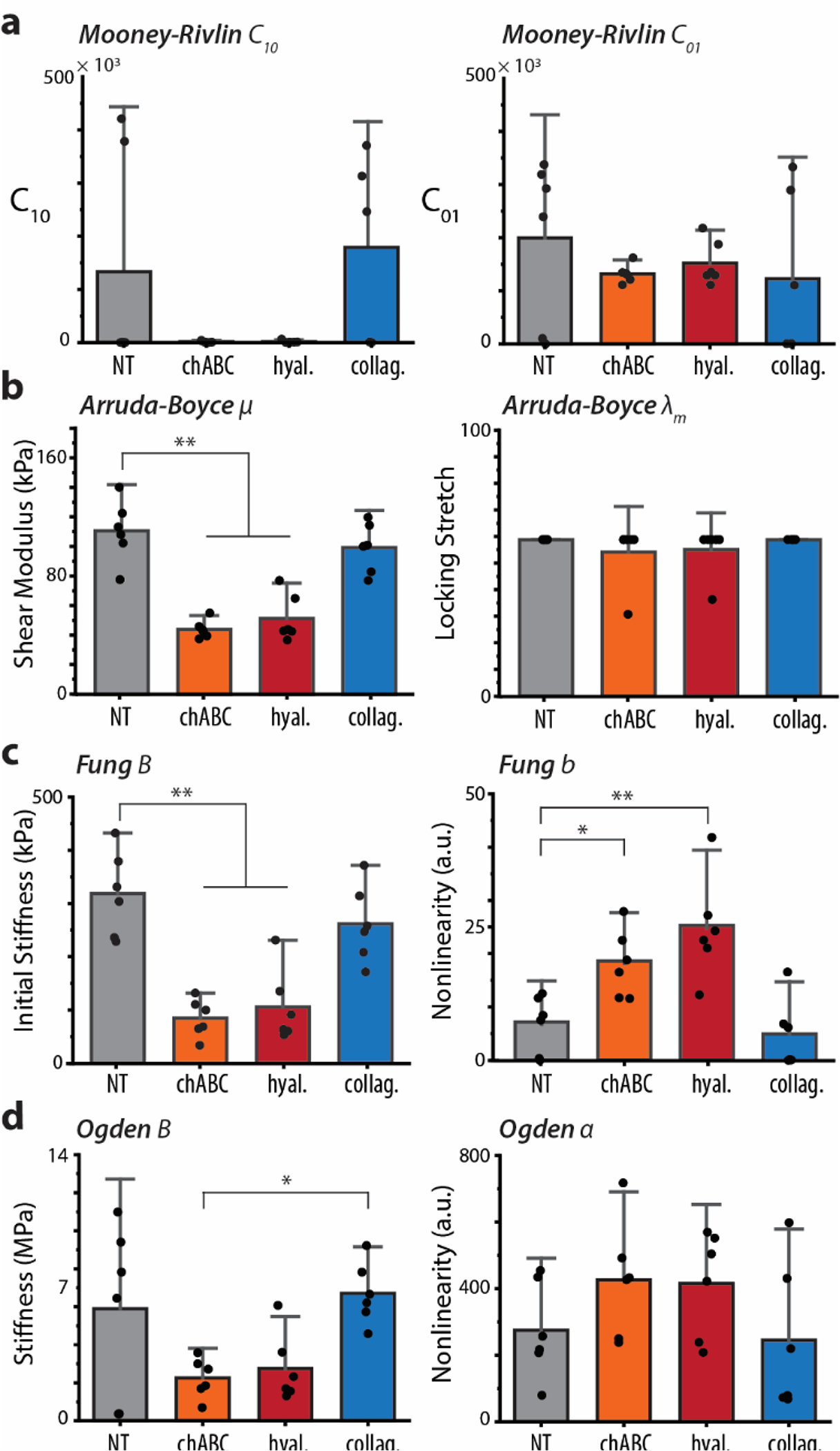
Two-parameter model parameters (A) Arruda-Boyce, (B) Fung, (C) Mooney-Rivlin, and (D) Ogden extracted from identical dataset of average indentation response curves. Significant differences were identified in both groups of the Fung model. Mean ± s.d., N = 6 animals average indentation response curves. *p < 0.05, **p < 0.001.

Fit quality to the average indentation-response was compared using SSE, RMSE, and MPE (Fig. 6). We found a significant difference between errors of each model fit (F = 18.33, p < 0.00001). The mean error of fits to the Fung and Ogden models was smaller than all other groups (**p < 0.001), but not significantly different from each other (p = 0.946). There were no significant differences between MPE, RMSE, or SSE resulting from fits to Hertz, NeoHookean, MR, and AB models. We expanded this analysis to assess if enzymatic treatment would influence fit quality, but the conclusion held that Fung and Ogden showed the least error (Supplemental Fig. 1).

Fig. 6. Model fit of cartilage ECM indentation to elastic and hyperelastic models.

Fig. 6.

Open in a new tab

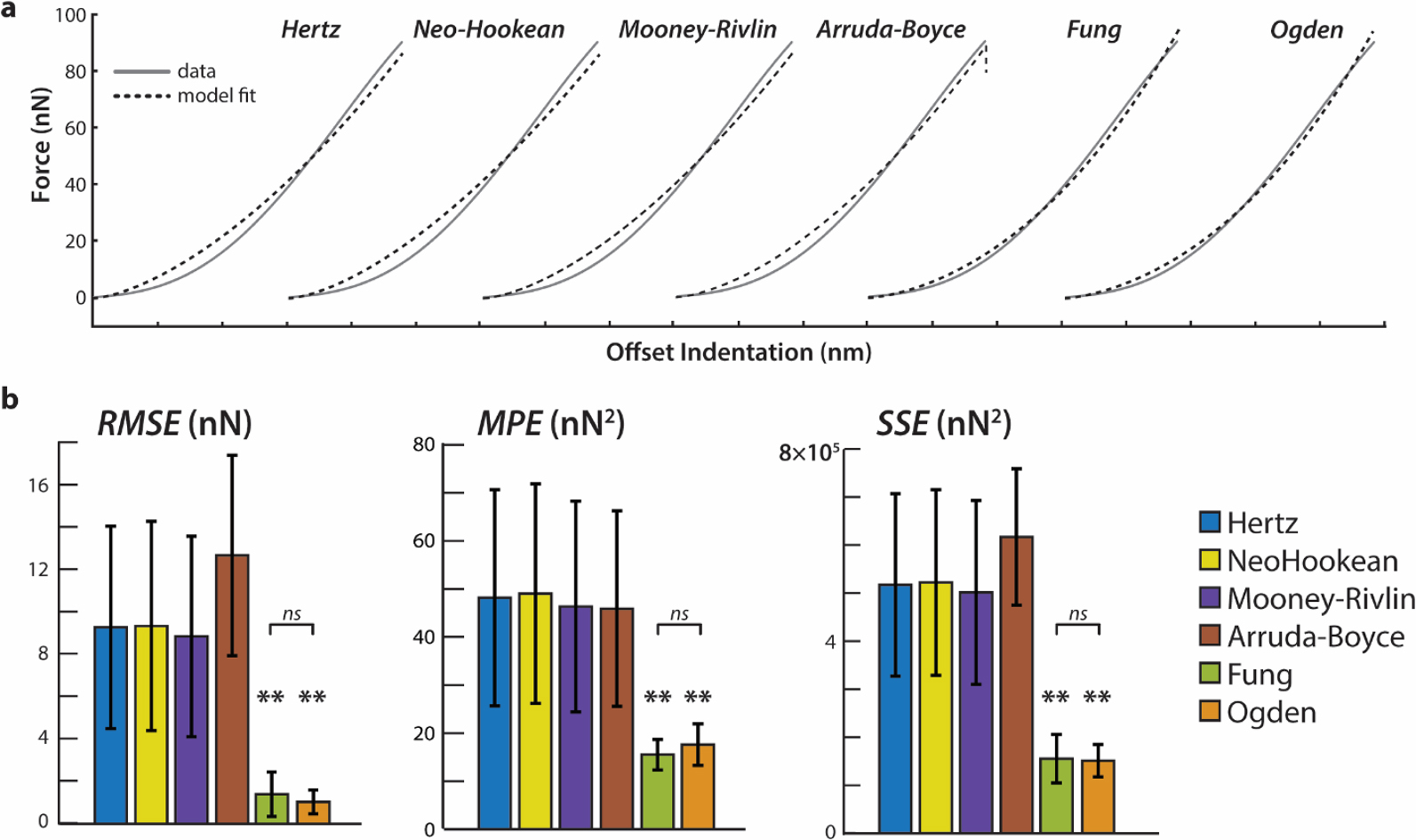
(A) Sample force–displacement data of untreated cartilage ECM indentation showing all data points in the indentation curve at the contact point. Data are plotted six times, with each set and model fit offset by 150 nm for clarity. (B) RMSE, MPE, and SSE for each model fit to untreated cartilage indentations. Fung (green) and Ogden (orange) models show the lowest residual error and are not significantly different from each other. Mean ± s.d., N = 6 animals average indentation response curves. *p < 0.05, **p < 0.001.

To better understand parameter identifiability when applying each model to indentation data, sensitivity matrices and cost-function visualizations of average response curves were constructed, and the representative results reported were consistent between specimens. The cost function spaces for AB and MR illustrated that one parameter in both models (λm and C01, respectively) is not identifiable (Fig. 7A, 7C). However, cost functions for the Fung and Ogden models consistently demonstrated unique solutions for Fung parameters B and b, and Ogden parameters B and α (Fig. 7B, 7D). Changes to the initial conditions did not significantly affect Fung and Ogden parameter solutions, with clear global minima for all treatment groups. Further investigation of parameter identifiability via sensitivity analysis showed that sensitivity for both the stiffness and nonlinear parameters were higher in the Fung model than the Ogden model without exhibiting parameter covariance.

Fig. 7. Assessment of parameter identifiability with sensitivity analysis and cost function visualization.

Fig. 7.

Open in a new tab

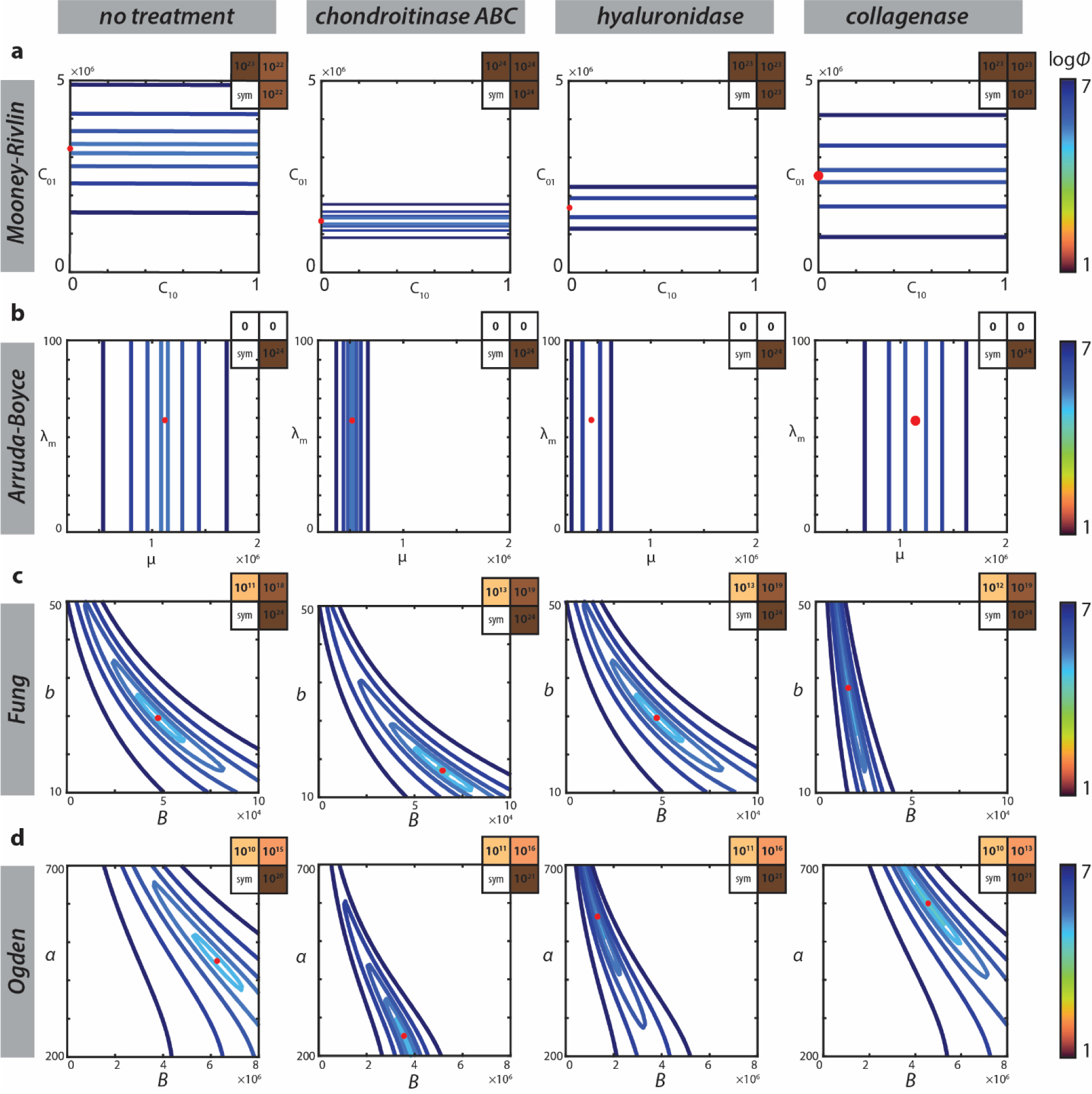
The cost function spaces for each two-parameter model indicate unique and identifiable global minima with respect to parameters in the Fung and Ogden models (B,D). However, the cost functions for both the Mooney-Rivlin and Arruda-Boyce models (A,C) exhibit little to no sensitivity with respect to one material parameter. The symmetric sensitivity matrices (upper right hand corners) for the Arruda-Boyce model confirms this finding. Sensitivity matrices for the Fung and Ogden models reveal greater identifiability of the Fung nonlinear parameter compared to the nonlinear parameter in the Ogden model.

Representative elastography data (1,024 spatially-mapped indentations) are presented as 20 × 20 μm2 maps in all four treatment groups (Fig. 8A). The Fung model was fit to these data to extract the initial stiffness parameter B and the nonlinear parameter b to capture their respective spatial distribution (Fig. 8B). The initial stiffness parameter of the Fung model exhibited very similar spatial patterning as the Hertz modulus for a given region, with slightly lower parameter values for the Fung initial stiffness approximation and greater regional contrast. Mapping of the nonlinear parameter showed distinctly different patterns in treatment groups.

Fig. 8. AFM elastography maps of best-fit model parameters.

Fig. 8.

Open in a new tab

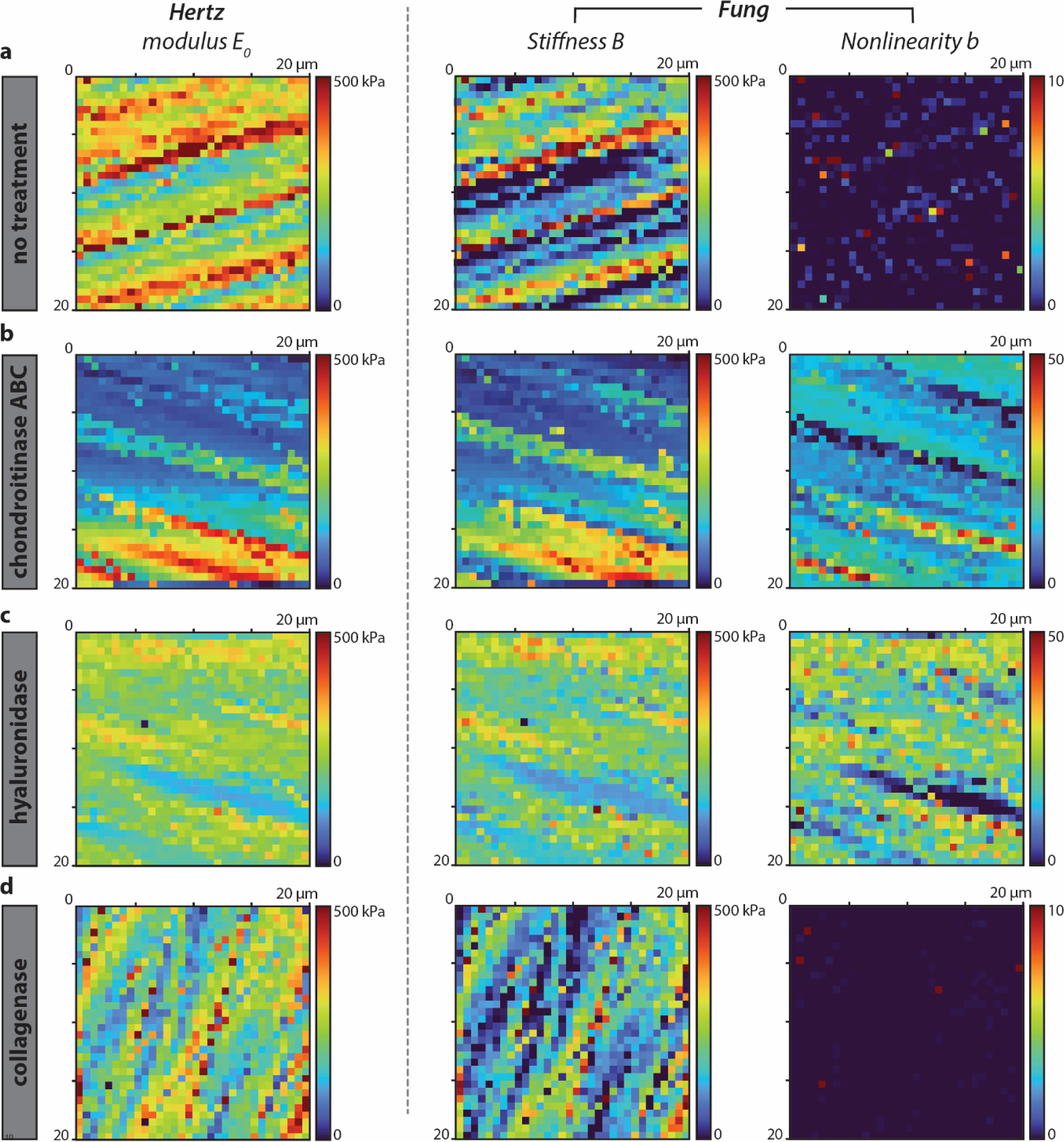
Material parameter maps were computed using the Hertz model and Fung model for a 20 × 20 μm2 region (32 × 32 px2) of bovine cartilage for (A) untreated cartilage and selective degradation with (B) chondroitinase ABC, (C) hyaluronidase, and (D) collagenase. Initial stiffness calculated with the Fung model demonstrates enhanced contrast compared to the compressive modulus calculated with the Hertz model. The dynamic range of AFM elastography is extended by including the nonlinear component, which provides insight into changes in proteoglycans, a significant mechanistic advance.

4. Discussion

The objective of this study was to compare commonly used models to describe indentation of biomaterials, assess their appropriateness for describing AFM indentations, and determine which ECM components give rise to changes in stiffness and nonlinear parameter values in hyaline cartilage. We found that the Fung and Ogden models demonstrated the lowest residual error for best-fits of the data, however, the Fung model displayed increased sensitivity for nonlinear parameter identification. Our findings suggest that Fung parameters are sensitive to changes in ECM proteoglycan composition and resulting organization, with stiffness decreasing and nonlinearity increasing upon disruption. Taken together, our results provide experimental context for the use of the Fung model to describe AFM indentation of biomaterials and suggest that nonlinearity in hyaline cartilage is determined by relative amounts of proteoglycans.

4.1. AFM analysis of soft materials

To understand changes in micromechanics associated with development, injury, and disease, AFM is a valuable tool to directly probe changes in stiffness. Advances in AFM over the last decade have facilitated its application to measure ECM properties in soft tissues including skin, tendon, neural tissue, and metastatic tumors (Cauble et al., 2020; Chen et al., 2021; Hartmann et al., 2020). For these applications, many biomechanics researchers employ the Hertz spherical contact equation and its assumption of linear elasticity at small strains to estimate an elastic modulus parameter for tissues (Bosnic et al., 2022; Stolz et al., 2004). Only recently have engineers demonstrated higher accuracy in modeling AFM force-indentation data with alternative models to the Hertz equation (Li et al., 2021; Zhang et al., 2014). The value of multi-parameter models to describe AFM data, and how they are related to biomaterial changes, have yet to be explored.

We found that the Fung and Ogden models exhibit the best fits to the biomaterial AFM indentation data, confirming published results (Li et al., 2021; Lin et al., 2009). Here, we determined that the Fung model exhibits low residual error and the highest sensitivity to its nonlinear parameter, exceeding the Ogden model. Our findings for Fung initial stiffness as a function of enzymatic treatment group follow the same trends as the change in elastic compressive modulus calculated from Hertzian theory, facilitating reasonable comparison of Fung stiffness data to previously reported values determined with Hertzian mechanics. Furthermore, fitting AFM data to the Fung model has the added value of a second computed parameter with a unique solution that resolves differences in a separate material property as a function of ECM composition and organization.

We note the limitation that some models that were not included in this study may perform comparatively or better than the Fung equation. Higher-order polynomials with more than two fitting parameters may better resolve differences in the AFM indentation response with the use of mechanically-derived parameters. Additionally, the presented models may vary in fit quality depending on the native tissue type. It was not our intent to conduct a comprehensive comparison of hyperelastic models nor soft tissue microindentation, and these areas are open to exploration with application to AFM data.

4.2. Potential roles of ECM networks in stiffness and nonlinearity

AFM is often applied to experimentally approximate stiffness during ECM development and degeneration (Ihnatouski et al., 2020; Wilusz et al., 2013; Xu et al., 2016b). It is understood that the value of the Hertz modulus E0 for a biomaterial has a critical effect on cell differentiation, cell spreading, metastasis, and even cell and nuclear mechanics (Dokukin et al., 2013; Hansen et al., 2007; McCreery et al., 2021; Takai et al., 2005). However, the realistic application of Hertzian theory to biomaterials is limited. Cartilage and other soft tissues are composed of interacting amorphous and fibrous networks that introduce nonlinear elastic mechanics to tissue, even at small strains. As a result, over-estimation of the elastic modulus is a normal consequence of using the Hertz equation, resulting from variable strain-stiffening of soft biomaterials. While modulus estimates work well in serving as a mechanical marker of biological change in published data, multi-parameter models provide a gateway for extracting more information from AFM data, particularly that proteoglycans can be mapped to a nonlinear indentation response.

A key finding of this work is that the indentation response is dependent on matrix composition, which was detected independently by both stiffness and nonlinearity parameters. In cartilage, type II collagen is considered to be the backbone of cartilage ECM and the primary determinants of macroscale mechanics (Tonti et al., 2021). However, our findings underscore the importance of non-collagenous ECM in compressive mechanical function. We found that disrupting GAGs in the cartilage ECM reduces matrix stiffness in agreement with published findings (Pastrama et al., 2019; Wilusz and Guilak, 2014). During AFM indentation, micro-compression from the probe causes various ECM components to interact with displaced water molecules and with each other. Aggrecan molecules trap water, restricting fluid outflow which generates increased resistance and likely results in compressive strain stiffening (Han et al., 2011). The proteoglycan matrix therefore plays a central role in compressive resistance via osmotic pressure and fixed charge density.

We observed that depletion of GAGs in the native cartilage ECM leads to an increase in the value of the Fung nonlinearity parameter, which one may think to attribute to time-dependent ECM characteristics. However, our results also indicated that nonlinearity was not significantly affected by indentation speeds spanning 0.5 μm/s to 50 μm/s (Appendix B, Supplementary Fig. 2), and so it is unlikely that fluid displacement under indentation is the sole mechanism controlling the nonlinear AFM indentation response. The strain-stiffening effect may arise from decreased fiber tension following ECM degradation, leading to an inherently more nonlinear elastic response of the fibers under microindentation. On the other hand, osmotic pressure and fluid-based swelling in the cartilage ECM stretches collagen fibers to resist buckling, leading to an increase in isotropic network stiffness and decreasing fiber anisotropy (Chen et al., 2022). GAG depletion and low osmotic pressure weakens the static tensile load on the ECM, which results in a relaxation of the collagen network (Wahlquist et al., 2017). Thus, one alternative explanation is that nonlinearity is linked to ECM isotropy, attributing Fung nonlinearity to changes in network organization.

Our results do not show a significant difference in Fung stiffness and nonlinearity parameters upon selective disruption of collagens via collagenase, despite fluorescent verification that the collagen matrix was disrupted. We speculate that this experiment or the nonlinearity parameter may not be sensitive to the disruption of collagens. However, following disruption of HA with hyaluronidase and sugar chains with chABC, Fung stiffness was reduced while nonlinearity significantly increased. Despite the specificity of bacterial hyaluronidase to HA and not GAG chains, we did not observe notable differences between chABC and hyaluronidase-treated groups. Hyaluronan interacts with elastin, GAGs, and collagens (Watkins, 2014), and so its biomechanical degradation may have a structural impact. These findings are consistent with widely observed phenomena that compressive resistance is reduced as proteoglycan content drops in early stages of OA (Jones et al., 2012), highlighting the role of proteoglycan aggregates in soft tissue mechanical behavior.

While the Fung model was previously adopted for describing microindentation behavior of cartilage (Lin et al., 2009), a physiological meaning of nonlinear parameter b had not yet been realized. The stress–strain relationship in the small-strain regime determines the initial stiffness parameter, but the nonlinear parameter describes the strain stiffening behavior observed at larger strains. Increased nonlinearity indicates greater strain stiffening at larger indentation depths which captures the nonlinear, region-dependent, and strain-dependent indentation response. The mechanism responsible for microindentation nonlinearity has not been realized and remains open to further investigation.

Our findings reveal both the initial stiffness and nonlinear response of hyaline cartilage are largely governed by proteoglycan content, with decreased proteoglycan content reducing stiffness (as reported elsewhere) and increasing compressive nonlinearity. Therefore, use of the Fung model (or other hyperelastic models) may be implemented in broader applications to describe in vivo elastography data (Chan et al., 2016; Lee et al., 2022) to aid in the early detection of OA and cartilage degeneration by (1) producing greater contrast in modulus maps compared to a linear elastic estimate, and (2) providing a nonlinear parameter estimate that may offer an early marker for cartilage damage and OA before stiffness is measurably reduced.

Supplementary Material

MMC1

Acknowledgements

We would like to acknowledge: Emily Miller and Soham Ghosh for recommendations in data collection and analysis. This work was funded by NIH grants R01 AR063712 and AR071359, and NSF CAREER grant 1349735. CML was supported by Schmidt Science Fellows, in partnership with the Rhodes Trust.

Appendix A. Experimental method details

Bovine knee joints from male calves (~1 week old) were obtained from Research 87 (MA, USA) within one day of euthanasia. Cylindrical osteochondral plugs with a diameter of 5 mm were aseptically extracted from the load-bearing medial femoral condyle and placed in complete media (DMEM) with 100 U/mL penicillin, 100 μg/mL streptomycin, 0.1 % BSA, and 50 μg/mL l-ascorbic-acid-2-phosphate to support chondrocyte viability (Khalafi et al., 2007). The surface and deep zones were identified under a stereoscope, positioned with a cutting jig, and removed using a feather blade (Ted Pella, CA, USA) to obtain 3 mm tall middle-zone cartilage explants. Explants were rinsed 3 × with DMEM and stabilized for 1 h (37 °C in 5 % CO2).

Following enzymatic treatment, cartilage samples were sectioned for AFM testing. Half-plugs were affixed to the sample holder of a Leica VT–1000S vibratome with 1 μL Loctite superglue. Smooth sections from the lateral sample surface with thickness 100 μm were mounted to an Ibidi μ–Dish 35 mm high (Ibidi LCC, Martinsried, Germany). A plastic (Thermanox) coverslip was glued to the imaging dish with < 0.5 μL cyanoacrylate (Loctite, Westlake, OH, USA) so that no glue would touch the tissue section. Samples were consistently hydrated with PBS.

Appendix B. Rate-dependency of parameter values

To further understand how strain rate influences model parameters, an independent experiment was performed with thawed cartilage samples (N = 3 animals). Vibratomed cartilage samples were indented in PBS at intervals of increasing indentation speeds: 0.5 μm/s, 2 μm/s, 10 μm/s, 25 μm/s, and 50 μm/s. Data were collected as 4 × 4px indentations over a scan area 20 × 20 μm2, with 5 min between scans.

ECM degradation by chondroitinase and hyaluronidase treatment resulted in an increase in the value of the Fung nonlinearity parameter. This quantified change of indentation response could be attributed to time-dependent indentation effects during experimentation, namely the speed of AFM indentation. We performed an independent experiment to track the effect of indentation speed on parameter values (Supplemental Fig. 2). Hertzian modulus trended upward, but not significantly (p = 0.0593). Meanwhile, Fung stiffness and nonlinear values were consistent or trended upward at higher speeds ≥ 25 μm/s, though were not significantly increased as a function of indentation speed (p = 0.3868, p = 0.6969). These results suggest that the stiffness and nonlinear parameters determined from AFM data are not significantly rate-dependent.

Appendix C. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jbiomech.2022.111397.

Footnotes

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

CRediT authorship contribution statement

Kaitlin P. McCreery: Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Callan M. Luetkemeyer: Writing – original draft, Supervision, Methodology, Formal analysis, Conceptualization. Sarah Calve: Writing – review & editing, Resources, Funding acquisition, Conceptualization. Corey P. Neu: Writing – review & editing, Supervision, Project administration, Funding acquisition, Conceptualization.

References

  1. Armiento AR, Stoddart MJ, Alini M, Eglin D, 2018. Biomaterials for articular cartilage tissue engineering: Learning from biology. Acta Biomater. 65, 1–20. 10.1016/j.actbio.2017.11.021. [DOI] [PubMed] [Google Scholar]
  2. Arruda EM, Boyce MC, 1993. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 41 (2), 389–412. [Google Scholar]
  3. Bank RA, Soudry M, Maroudas A, Mizrahi J, TeKoppele JM, 2000. The increased swelling and instantaneous deformation of osteoarthritic cartilage is highly correlated with collagen degradation. Arthritis Rheum. 43, 2202–2210. . [DOI] [PubMed] [Google Scholar]
  4. Bonnans C, Chou J, Werb Z, 2014. Remodelling the extracellular matrix in development and disease. Nat. Rev. Mol. Cell Biol. 15, 786–801. 10.1038/nrm3904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bosnic M, Rasoulian A, Brandon SCE, 2022. Investigating the effects of activation state and location on lower limb tissue stiffness. J. Biomech. 135, 111032 10.1016/j.jbiomech.2022.111032. [DOI] [PubMed] [Google Scholar]
  6. Cauble MA, Mancini NS, Kalinowski J, Lykotrafitis G, Moss IL, 2020. Atomic force microscopy imaging for nanoscale and microscale assessments of extracellular matrix in intervertebral disc and degeneration. JOR Spine 3, e1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chan DD, Cai L, Butz KD, Trippel SB, Nauman EA, Neu CP, 2016. In vivo articular cartilage deformation: noninvasive quantification of intratissue strain during joint contact in the human knee. Sci. Rep. 6, 19220. 10.1038/srep19220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chan SMT, Neu CP, Duraine G, Komvopoulos K, Reddi AH, 2010. Atomic force microscope investigation of the boundary-lubricant layer in articular cartilage. Osteoarthr. Cartil. 18, 956–963. 10.1016/j.joca.2010.03.012. [DOI] [PubMed] [Google Scholar]
  9. Chen X, Chen D, Ban E, Toussaint KC, Janmey PA, Wells RG, Shenoy VB, 2022. Glycosaminoglycans modulate long-range mechanical communication between cells in collagen networks. PNAS 119, e2116718119. 10.1073/pnas.2116718119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chen X, Hughes R, Mullin N, Hawkins RJ, Holen I, Brown NJ, Hobbs JK, 2021. Atomic force microscopy reveals the mechanical properties of breast cancer bone metastases. Nanoscale 13, 18237–18246. 10.1039/d1nr03900h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Costa KD, Sim AJ, Yin F-C-P, 2006. Non-Hertzian approach to analyzing mechanical properties of endothelial cells probed by atomic force microscopy. J. Biomech. Eng. 128, 176–184. 10.1115/1.2165690. [DOI] [PubMed] [Google Scholar]
  12. Ding Y, Xu G-K, Wang G-F, 2017. On the determination of elastic moduli of cells by AFM based indentation. Sci. Rep. 7, 45575. 10.1038/srep45575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dokukin ME, Guz NV, Sokolov I, 2013. Quantitative study of the elastic modulus of loosely attached cells in AFM indentation experiments. Biophys. J. 104, 2123–2131. 10.1016/j.bpj.2013.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ebrahimi M, Turunen MJ, Finnilä MA, Joukainen A, Kröger H, Saarakkala S, Korhonen RK, Tanska P, 2020. Structure-Function Relationships of Healthy and Osteoarthritic Human Tibial Cartilage: Experimental and Numerical Investigation. Ann. Biomed. Eng. 48, 2887–2900. 10.1007/s10439-020-02559-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fung YC, 1967. Elasticity of soft tissues in simple elongation. Am. J. Physiol. 213, 1532–1544. 10.1152/ajplegacy.1967.213.6.1532. [DOI] [PubMed] [Google Scholar]
  16. Fung YC, Fronek K, Patitucci P, 1979. Pseudoelasticity of arteries and the choice of its mathematical expression. Am. J. Physiol. 237, H620–H631. 10.1152/ajpheart.1979.237.5.H620. [DOI] [PubMed] [Google Scholar]
  17. Guo Y, Calve S, Tepole AB, 2022. Multiscale mechanobiology: Coupling models of adhesion kinetics and nonlinear tissue mechanics. Biophys. J. 121, 525–539. 10.1016/j.bpj.2022.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Han L, Grodzinsky AJ, Ortiz C, 2011. Nanomechanics of the Cartilage Extracellular Matrix. Annu. Rev. Mater. Res. 41, 133–168. 10.1146/annurev-matsci-062910-100431.Nanomechanics. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hansen JC, Lim JY, Xu L-C, Siedlecki CA, Mauger DT, Donahue HJ, 2007. Effect of surface nanoscale topography on elastic modulus of individual osteoblastic cells as determined by atomic force microscopy. J. Biomech. 40, 2865–2871. 10.1016/j.jbiomech.2007.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Harris AR, Charras GT, 2011. Experimental validation of atomic force microscopy-based cell elasticity measurements. Nanotechnology 22 (34), 345102. [DOI] [PubMed] [Google Scholar]
  21. Hartmann B, Marchi G, Alberton P, Farkas Z, Aszodi A, Roths J, Clausen-Schaumann H, 2020. Early Detection of Cartilage Degeneration: A Comparison of Histology, Fiber Bragg Grating-Based Micro-Indentation, and Atomic Force Microscopy-Based Nano-Indentation. Int. J. Mol. Sci. 21 (19), 7384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Heneghan P, Riches PE, 2008. The strain-dependent osmotic pressure and stiffness of the bovine nucleus pulposus apportioned into ionic and non-ionic contributors. J. Biomech. 41, 2411–2416. 10.1016/j.jbiomech.2008.05.025. [DOI] [PubMed] [Google Scholar]
  23. Hertz H, 1882. Ueber die Berührung fester elastischer Körper (On the contact of rigid elastic solids). J. für die reine und Angew. Math 92. [Google Scholar]
  24. Ihnatouski M, Pauk J, Karev D, Karev B, 2020. AFM-Based Method for Measurement of Normal and Osteoarthritic Human Articular Cartilage Surface Roughness. Mater. (Basel, Switzerland) 13. 10.3390/ma13102302. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jones EF, Schooler J, Miller DC, Drake CR, Wahnishe H, Siddiqui S, Li X, Majumdar S, 2012. Characterization of human osteoarthritic cartilage using optical and magnetic resonance imaging. Mol. Imaging Biol. 14, 32–39. 10.1007/s11307-011-0480-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. June RK, Fyhrie DP, 2009. Enzymatic digestion of articular cartilage results in viscoelasticity changes that are consistent with polymer dynamics mechanisms. Biomed. Eng. Online 8, 32. 10.1186/1475-925X-8-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Karhula SS, Finnilä MA, Lammi MJ, Ylärinne JH, Kauppinen S, Rieppo L, Pritzker KPH, Nieminen HJ, Saarakkala S, 2017. Effects of Articular Cartilage Constituents on Phosphotungstic Acid Enhanced Micro-Computed Tomography. PLoS One 12, e0171075. 10.1371/journal.pone.0171075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kashani AS, Packirisamy M, 2020. Cancer cells optimize elasticity for efficient migration. R. Soc. Open Sci. 7 (10), 200747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kempson GE, Muir H, Swanson SA, Freeman MA, 1970. Correlations between stiffness and the chemical constituents of cartilage on the human femoral head. Biochim. Biophys. Acta 215, 70–77. 10.1016/0304-4165(70)90388-0. [DOI] [PubMed] [Google Scholar]
  30. Khalafi A, Schmid TM, Neu C, Reddi AH, 2007. Increased accumulation of superficial zone protein (SZP) in articular cartilage in response to bone morphogenetic protein-7 and growth factors. J. Orthop. Res. 25, 293–303. 10.1002/jor.20329. [DOI] [PubMed] [Google Scholar]
  31. Kontomaris SV, Malamou A, Stylianou A, 2022. The Hertzian theory in AFM nanoindentation experiments regarding biological samples: Overcoming limitations in data processing. Micron 155, 103228. 10.1016/j.micron.2022.103228. [DOI] [PubMed] [Google Scholar]
  32. Lee W, Miller EY, Zhu H, Luetkemeyer CM, Schneider SE, Neu CP, 2022. High-frame-rate analysis of knee cartilage deformation by spiral dualMRI and relaxation mapping. bioRxiv 2022.03.11.483911. 10.1101/2022.03.11.483911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Li H, Li J, Yu S, Wu C, Zhang W, 2021. The mechanical properties of tibiofemoral and patellofemoral articular cartilage in compression depend on anatomical regions. Sci. Rep. 11, 6128. 10.1038/s41598-021-85716-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lin DC, Shreiber DI, Dimitriadis EK, Horkay F, 2009. Spherical indentation of soft matter beyond the Hertzian regime: numerical and experimental validation of hyperelastic models. Biomech. Model. Mechanobiol. 8, 345–358. 10.1007/s10237-008-0139-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Luetkemeyer CM, Scheven U, Estrada JB, Arruda EM, 2021. Constitutive modeling of the anterior cruciate ligament bundles and patellar tendon with full-field methods. J. Mech. Phys. Solids 156, 104577. [Google Scholar]
  36. Maldonado M, Nam J, 2013. The role of changes in extracellular matrix of cartilage in the presence of inflammation on the pathology of osteoarthritis. Biomed. Res. Int. 2013, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. McCreery KP, Calve S, Neu CP, 2020. Ontogeny informs regeneration: explant models to investigate the role of the extracellular matrix in cartilage tissue assembly and development. Connect. Tissue Res. 61 (3–4), 278–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. McCreery KP, Xu X, Scott AK, Fajrial AK, Calve S, Ding X, Neu CP, 2021. Nuclear Stiffness Decreases with Disruption of the Extracellular Matrix in Living Tissues. Small 17 (6), 2006699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. McLane JS, Ligon LA, 2016. Stiffened Extracellular Matrix and Signaling from Stromal Fibroblasts via Osteoprotegerin Regulate Tumor Cell Invasion in a 3-D Tumor in Situ Model. Cancer Microenviron. 9, 127–139. 10.1007/s12307-016-0188-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mooney M, 1940. A Theory of Large Elastic Deformation. J. Appl. Phys. 11 (9), 582–592. [Google Scholar]
  41. Nissi MJ, Salo E-N, Tiitu V, Liimatainen T, Michaeli S, Mangia S, Ellermann J, Nieminen MT, 2016. Multi-parametric MRI characterization of enzymatically degraded articular cartilage. J. Orthop. Res. 34, 1111–1120. 10.1002/jor.23127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ogden RM, 1972. Large deformation isotropic elasticity – on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. London. A. Math. Phys. Sci 326, 565–584. [Google Scholar]
  43. Pastrama M-I, Ortiz AC, Zevenbergen L, Famaey N, Gsell W, Neu CP, Himmelreich U, Jonkers I, 2019. Combined enzymatic degradation of proteoglycans and collagen significantly alters intratissue strains in articular cartilage during cyclic compression. J. Mech. Behav. Biomed. Mater. 98, 383–394. 10.1016/j.jmbbm.2019.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. R Core Team, 2013. R: A language and environment for statistical computing. R Foundation for Statistical Computing. [Google Scholar]
  45. Roughley PJ, Lee ER, 1994. Cartilage proteoglycans: structure and potential functions. Microsc. Res. Tech. 28, 385–397. 10.1002/jemt.1070280505. [DOI] [PubMed] [Google Scholar]
  46. Stolz M, Raiteri R, Daniels AU, VanLandingham MR, Baschong W, Aebi U, 2004. Dynamic elastic modulus of porcine articular cartilage determined at two different levels of tissue organization by indentation-type atomic force microscopy. Biophys. J. 86, 3269–3283. 10.1016/S0006-3495(04)74375-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Takai E, Costa KD, Shaheen A, Hung CT, Guo XE, 2005. Osteoblast elastic modulus measured by atomic force microscopy is substrate dependent. Ann. Biomed. Eng. 33, 963–971. 10.1007/s10439-005-3555-3. [DOI] [PubMed] [Google Scholar]
  48. Tonti O, Larson H, Lipp SN, Luetkemeyer CM, Makam M, Vargas D, Wilcox SM, Calve S, 2021. Tissue-specific parameters for the design of ECM-mimetic biomaterials. Acta Biomater. 132, 83–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Van Liedekerke P, Neitsch J, Johann T, Warmt E, Gonzàlez-Valverde I, Hoehme S, Grosser S, Kaes J, Drasdo D, 2020. A quantitative high-resolution computational mechanics cell model for growing and regenerating tissues. Biomech. Model. Mechanobiol. 19, 189–220. 10.1007/s10237-019-01204-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wahlquist JA, DelRio FW, Randolph MA, Aziz AH, Heveran CM, Bryant SJ, Neu CP, Ferguson VL, 2017. Indentation mapping revealed poroelastic, but not viscoelastic, properties spanning native zonal articular cartilage. Acta Biomater. 64, 41–49. 10.1016/j.actbio.2017.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Watkins J, 2014. Biomechanics of Musculoskeletal Adaptation. Compr. Biomed. Phys. 10, 1–37. 10.1016/B978-0-444-53632-7.01002-9. [DOI] [Google Scholar]
  52. Wilusz RE, Guilak F, 2014. High resistance of the mechanical properties of the chondrocyte pericellular matrix to proteoglycan digestion by chondroitinase, aggrecanase, or hyaluronidase. J. Mech. Behav. Biomed. Mater 38, 183–197. 10.1016/j.jmbbm.2013.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Wilusz RE, Zauscher S, Guilak F, 2013. Micromechanical mapping of early osteoarthritic changes in the pericellular matrix of human articular cartilage. Osteoarthr. Cartil. 21, 1895–1903. 10.1016/j.joca.2013.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Wyse Jackson T, Michel J, Lwin P, Fortier LA, Das M, Bonassar LJ, Cohen I, 2022. Structural origins of cartilage shear mechanics. Sci. Adv. 8 10.1126/sciadv.abk2805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Xu X, Li Z, Cai L, Calve S, Neu CP, 2016a. Mapping the Nonreciprocal Micromechanics of Individual Cells and the Surrounding Matrix Within Living Tissues. Sci. Rep. 6, 24272. 10.1038/srep24272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Xu X, Li Z, Leng Y, Neu CP, Calve S, 2016b. Knockdown of the pericellular matrix molecule perlecan lowers in situ cell and matrix stiffness in developing cartilage. Dev. Biol. 418, 242–247. 10.1016/j.ydbio.2016.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Zhang M-G, Cao Y-P, Li G-Y, Feng X-Q, 2014. Spherical indentation method for determining the constitutive parameters of hyperelastic soft materials. Biomech. Model. Mechanobiol. 13, 1–11. 10.1007/s10237-013-0481-4. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

MMC1
NIHMS1857644-supplement-MMC1.docx (1.2MB, docx)

RESOURCES