Enriched Random Forest for High Dimensional Genomic Data

Abstract

Ensemble methods such as random forest works well on high-dimensional datasets. However, when the number of features is extremely large compared to the number of samples and the percentage of truly informative feature is very small, performance of traditional random forest decline significantly. To this end, we develop a novel approach that enhance the performance of traditional random forest by reducing the contribution of trees whose nodes are populated with less informative features. The proposed method selects eligible subsets at each node by weighted random sampling as opposed to simple random sampling in traditional random forest. We refer to this modified random forest algorithm as ”Enriched Random Forest”. Using several high-dimensional micro-array datasets, we evaluate the performance of our approach in both regression and classification settings. In addition, we also demonstrate the effectiveness of balanced leave-one-out cross-validation to reduce computational load and decrease sample size while computing feature weights. Overall, the results indicate that enriched random forest improves the prediction accuracy of traditional random forest, especially when relevant features are very few.

1. Introduction

IN recent years unprecedented increase in structural and functional analysis of human genome have presented enormous opportunities and challenges for machine learning researchers. High-throughput genomic technologies such as gene expression micro-array, single nucleotide polymorphism (SNP) array, microRNA array, RNA-seq, ChIP-seq, and whole genome sequencing have enabled us to detect variations associated with increased risk of having a disease, with finer resolution than before. In genomics application, features usually correspond to genes, proteins (sequences), or single motifs, and the number of features is usually several thousands and higher. Lets say, n denote the number of training data samples and p the original feature dimension, then the raw features can be expressed as a set p-dimensional vectors: x(t) = [x₁(t), x₂(t), …, x_p(t)]^T, t = 1, 2, …, n. The feature dimension (p) is extremely high, where as the sample size (n), is often severely limited. For example, in gene expression microarray data, features represent gene expression coefficients corresponding to the abundance of mRNA in a sample, for a number of patients. Usually, there are very few samples (often less than 100 patients) and the number of features for each sample ranges from 6000 to 60,000. In this extreme of very few observations on very many features, classical regression framework is no longer applicable. Firstly, the small sample size could lead to over-fitting if all the features were to be used in the classification/regression model. Secondly, the highly correlated structure of genomics data violates the independent assumption of traditional statistical models. Lastly, many biological mechanisms involve gene-gene interactions or gene networks. Specifying such interaction effects in statistical models is not realistic for high-dimensional setting, especially the higher order interactions. Generally, a small portion of genome markers are associated with particular phenotype, and performing feature selection on the high-dimensional, correlated, and interactive genomics data require sophisticated methodology. Efficient and robust techniques such as deep-learning, that are widely applied in other functional domains, cannot address the challenge of “large p, small n” paradigm in biological Big Data.

With vast body of feature selection techniques, the need arises to determine which technique to use in a given situation. Based on the evaluation criteria, feature selection algorithms are classified into three categories: 1) filter approaches; 2) wrapper approaches; and 3) embedded approaches. A filter method is independent of any learning algorithm. It does not make use of a classifier, but rather attempts to find predictive subsets of features using simple statistics from the empirical distribution. For example, an algorithm that ranks features based on mutual information between the features and the class labels. Wrapper approaches, on the other hand, include a learning algorithm in the feature subset evaluation step. The learning algorithm is used as a “black box” by a wrapper to evaluate the goodness of the selected features. Given a classifier and a set of features, a wrapper method searches for subsets of the original feature vector, using cross-validation to compare the performance of the trained classifier on each tested subset. Filter algorithms are computationally less expensive and more general compared to wrapper algorithms. However, filters ignore the performance of the selected features on a classifier/learner. Wrapper algorithms achieve better performance than filter algorithms, but they may require orders of magnitude more computation time. In addition, in wrapper methods, repeated use of cross-validation on a single dataset can lead to uncontrolled growth in the probability of finding a feature subset that performs well on the validation data by chance alone. To this end, embedded methods combine both feature selection as well as classifier learning into a single process. Some embedded methods perform feature weighting based on regularization models with objective functions that minimize fitting errors and force the feature coefficients to be small or exactly zero. Methods such as penalized regression, tree-based approaches, and boosting have been applied to handle high-dimensional problems.

As pointed out in literature, an ideal feature selection algorithm should achieve an optimal trade-off between predictive performance, i.e., the capacity of identifying the most relevant/predictive features, and stability, i.e., the robustness of results with respect to changes in dataset composition. In a problem with over 7000 features, filtering methods have significantly smaller computational complexity compared to wrapper methods. Several studies that have analyzed microarray data have used filtering methods. Besides filter approaches, many studies have applied prediction-error-oriented wrapper methods in context of large feature space. However, in the “large p, small n” paradigm, it has been demonstrated that wrapper methods may induce over-fitting due to reduced number of instances and small ratio between the number of samples and number of features. It has been pointed out in the literature that methods performing regularization can address high dimensionality of the features by trimming the hypothesis space (i.e., the combinatorial space of feature subsets) and constraining the magnitude of the parameters.

In this paper, we discuss the ensemble learning paradigm and its extension to feature selection process. Particularly, we address the limitations of traditional random forests (RFs) in the “large p small n” setting and propose a novel method called Enriched Random Forest (ERF). Our proposed method enhances the traditional random forest by applying weighted random sampling, so that the chances of selecting less informative features are minimized. Odds of trees containing more informative features being included in the forest increases. Using our proposed approach, we obtain a higher number of better base learners, and thus resulting in better fit. Another novel aspect of this approach is the effectiveness of balanced leave-one-out cross validation to reduce computational load as well as decrease the sample size while computing feature weights. This work extends our preliminary work [1], and addresses the future research goals set forth therein.

The remainder of the paper is organized as follows. A discussion of the related work is presented in section 2. In section 3, we discuss the details of the proposed approach. The experimental evaluation of the proposed approach and discussion of the results are included in sections 4 and 5. The conclusion and future work are presented in section 6

2. Related Work

Feature selection is extremely important to address the large number of input features in high-dimensional supervised learning. It aims at selecting a subset of the original features, eliminating irrelevant and redundant features while achieving the best for a predetermined objective – the highest prediction accuracy. Feature selection is a difficult task mainly due to a large search space. For a dataset with p features, total number of possible solutions is 2^p. The task becomes more challenging as p becomes large and increases complexity of the problems. An exhaustive search for the best feature subset of a given dataset is practically impossible in most situations. Another important challenge of feature selection is to account for feature interaction problems. There can be two-way, three-way, or complex multi-way interactions among features. A feature, which is weakly relevant to the target concept by itself, could significantly improve the accuracy if it is used together with some complementary features. In contrast, an individually relevant feature may become redundant when used together with other features. The principal reasons for feature selection in genomics are: (i) finding co-expressed genes to build metabolic pathways; (ii) biological relevance of individual genes for clinical diagnosis; and (iii) enhancement of classifier performance. In addition, feature selection also help data visualization, reduction of measurements, storage requirements, as well as reduction of data processing time.

Feature selection methods have received much attention in the classification literature. Xing et al. [22], reported the application of feature selection methods to classification problem using microarray data. Their approach was a hybrid of filter and wrapper approaches. The authors applied a sequence of simple filters called Markov Blanket Filter, to identify feature subsets for each subset cardinality. Cross validation was performed to compare between the resulting subset cardinalities. All of the classifiers that were studied – generative Gaussian classifier, discriminative logistic regression classifier, k-NN classifier, performed significantly better in the reduced feature space than in the original feature space. The proposed method explicitly eliminated redundant features. The study also compared feature selection to regularization methods. Results showed that explicit feature selection yields classifiers that perform better than regularization methods. Feature selection and regularization are not mutually exclusive and it would be worth considering their combinations.

Computational methods for protein subcellular localization prefer knowledge-based methods (using gene ontology) over sequence-based methods. However, the gene ontology based predictors often lack interpretability and suffer from over-fitting due to the high dimensionality of feature vectors. Wan et al. [20] developed a multi-label predictor called mLASSO-Hum for large-scale prediction of human protein subcellular localization. In [20], the authors applied multi-label LASSO for both feature selection and classification. By using the one-vs-rest LASSO-based classifiers the authors found that only 87 out of more than 8000 gene ontology terms played significant roles in determining the subcellular localization. Based on these 87 essential terms, a depth-dependent hierarchical information-based method was used to incorporate the information from other non-essential terms into the feature vectors. These feature vectors were then presented to multi-label LASSO classifiers for classification. By using mLASSO-Hum, the authors obtained a sparse solution, and through the sparse solution, they could easily see which gene ontology terms played more significant roles in indicating whether a query protein belongs to a certain subcellular location or not. In another similar study [21], the authors applied a multi-label elastic net classifier called Mem-mEN, for predicting membrane proteins with single- and multi-label functional types. This study used a similar two-stage approach like mLASSO-Hum. The features selected in the first stage of training are then combined with other non-essential gene ontology terms to form final feature vectors that require another set of weights for achieving best classification performance. The authors pointed out that the key advantage of this two-stage approach is that it allows the construction of flexible application-oriented predictors. For example, in some applications, it is better to classify the selected features by nonlinear classifiers such as neural networks as opposed to linear classifiers such as LASSO or elastic net.

Another regularization based method proposed by Li et al. [15], used a two-stage procedure for simultaneously analyzing a large number of SNPs with a small number of samples. The method involved producing a ‘preconditioned’ response variable first using a supervised principle component analysis (PCA) and then formulating Bayesian lasso to select a subset of significant SNPs. The Bayesian lasso was implemented with a hierarchical model, in which scale mixtures of normal were used as prior distributions for the genetic effects and exponential priors were considered for their variances, and then solved by using the Markov chain Monte Carlo (MCMC) algorithm. The approach selected the lasso parameter by imposing a diffuse hyperprior and estimating it along with other parameters. The authors had validated their approach using a real dataset from the Framingham Heart Study. They had detected several significant genes that were associated with body mass index (BMI) which were also supported by the previous results about BMI-related SNPs. Zhang at al. [23] used somewhat similar PCA based approach and developed an inferential framework for gene set enrichment analyses which utilizes the temporal information based on functional principal component analysis, and decomposes the effects of overlapping genes by a functional extension of the elastic-net regression.

Genomics datasets contain highly correlated variables, many of them being irrelevant for classification purposes. Although feature selection methods identify these noisy variables, it is to be noted that the term relevant is meaningful only in context of the objective function of the applied classifier. In addition, these datasets present challenge due to a large number of gene expression values per experiment and a relatively small number of experiments. Czekaj et al. [7], demonstrated that the selected subsets of significant genes can vary in cardinality, and due to the redundancy (correlation) of genes, it is possible to select different minimal subsets of genes, necessary for classification. However, their interpretation ought to be made cautiously.

Guyon et al. [13], addressed the problem of selection of small subsets of genes from broad patterns of gene expression data. They used backward elimination procedure in linear Support Vector Machines (SVM), and referred to as SVM recursive feature elimination (SVM-RFE). Compared to other wrapper methods, SVM-RFE was scalable and efficient. Nested subsets of features were selected through sequential backward elimination, starting with all the feature variables and removing one feature at a time. At each step, the coefficients of the weight vector w of a linear SVM were used to compute the feature ranking score.The feature with the smallest ranking score was eliminated. The method was evaluated on two different cancer databases. Significant improvements were obtained over the baseline methods. The genes found by SVMs were biologically relevant in contrast to other methods that select genes correlated with the separation at hand and not relevant to the phenotype. Another similar study [14] described the notion of self-supervision and presented a method called vector index adaptative SVM (VIA-SVM) based on self-supervised feature selection. VIA-SVM was superior to SVM-RFE in two aspects: (i) it outperformed SVM-RFE at feature selection in low dimensions; and (ii) it automatically bounded the features within a smaller range. In addition, VIA-SVM was insensitive to the penalty factor in SVM training and avoided the need for a cut-off point to stop the feature selection process. Based on several experiments on microarray and SNPs data, VIA-SVM when combined with some filter provided substantial dimension reduction with significantly small decline in prediction accuracy.

Multi-classifier systems exploit the strengths of diverse classifier models to obtain enhanced performance by their combination. This approach is referred to as ensemble learning paradigm and has been extensively covered in pattern recognition and machine learning literature. In recent years, significant research efforts have explored the extension of this paradigm to the feature selection process. Pes et al. [18], studied the effects and potential benefits of ensemble feature selection in the context of biomarker discovery from high-dimensional genomics data. They evaluated the effects of a specific ensemble approach, namely data perturbation. Data perturbation combined multiple selectors that exploit the same core algorithm but are trained on different perturbed versions of the original data. In this study, the authors showed how the ensemble implementation improves the overall performance of the selection process, in terms of predictive accuracy and stability. Their results indicated that the beneficial impact of the ensemble approach is inversely proportional to the strength of the method. Only the least stable/effective methods gain advantage in computationally expensive ensemble setting. They also measured the impact of the ensemble approach on the composition of the selected feature subsets. It turned out that different methods, when used in the ensemble version, tend to produce similar subsets.

In [4], authors developed a framework for feature selection consisting of ensemble of filters and classifiers. Five filters based on different metrics were used. Each filter selected a different subset of features which was used to train and test a specific classifier. The outputs of these classifiers were then combined by simple voting. In this study, three well known classifiers were used for the classification task: C4.5, naive-Bayes, and instance based learner (IBL). The idea to use ensemble was to reduce the variability of selected features by using filters in different classification domains. The proposed method was evaluated using ten microarray data sets. The results obtained by the ensemble method achieved the lowest average error for each of the classifiers tested, showing the adequacy of the ensemble. In some specific cases, there was a filter that outperformed the ensemble. However, there was no better filter in general and the ensemble seemed to be the most reliable alternative for feature selection. The ensemble achieved best average error for the two classifiers C4.5 and IBL. IBL obtained the best error rates for 7 out of 10 data sets. For naive Bayes classifier, the results obtained by the ensemble in terms of average error was very close to the one obtained by best incremental ranked subset (BIRS).

Anaissi et al. [3], introduced ensemble SVM-Recursive Feature Elimination (ESVM-RFE) for gene selection that employed the concepts of ensemble and bagging used in random forest. The algorithm adopts backward elimination strategy to recursively eliminate features. The rationale for building ensemble SVM models using randomly drawn bootstrap samples from training set was to produce different feature rankings which would be subsequently aggregated as one feature ranking. Features were eliminated based upon the ranking of multiple SVM models instead of one particular model. The proposed approach addressed the problem of imbalanced datasets by constructing nearly balanced bootstrap samples. The results of this study showed that ESVM-RFE improved classification performance on five microarray datasets. When applied on the childhood leukemia dataset, ESVM-RFE obtained average 9% better accuracy than SVM-RFE, and 5% over traditional random forest. The genes selected by ESVM-RFE were further explored with Singular Value Decomposition (SVD) and significant clusters were found within the selected data. Similar approach was applied by Duan et al. [11] called multiple SVM-RFE which computes the feature ranking score from statistical analysis of the weight vectors of multiple linear SVMs trained on sub-samples of training data. The results demonstrated that the method selected better gene subsets than SVM-RFE and obtained improved classification accuracy on validation datasets.

Random forests (RF) is a popular tree-based ensemble learning method that is highly adaptive to the characteristics of the data and applies to “large p, small n” problems. RFs also account for correlation as well as interactions among feature variables. Chen et al. [6], reviewed the applications and progresses of RF for genomics data, including prediction, classification, variable selection, pathway analysis, genetic association, and unsupervised learning. The authors pointed out that a rigorous theoretical work of RF is needed. Its effectiveness in the non-standard small sample size and large feature space setting is not fully explored. Theoretical analysis should focus on asymptotic rates of convergence and answer questions, such as determining optimal values for RF parameters – mtry and nodesize, and provide ways to modify forests for improved prediction performance.

Uriarte et al. [8], investigated the use of RF for classification of microarray datasets, including multi-class problems. They developed a new method of gene selection based on RF. The study used simulated and nine microarray datasets to compare the performance of RF to other classification methods, such as diagonal linear discriminant analysis (DLDA), k-NN, and SVM. The goal of this method was to yield smaller subsets of non-redundant genes while preserving prediction accuracy. The proposed method selected genes by iteratively fitting RFs, and at each iteration building a new forest after discarding the genes with smallest variable importance. The selected set of genes was the one that produced smallest error rate. The method used bootstrap technique to assess the prediction error rates. Here, the authors did not recalculate variable importance at each step because it could result in severe over-fitting. After fitting all forests, the out-of-bag (OOB) error rates of those forests were compared. The method chose the solution with smallest number of genes whose error rate is within u standard errors of the minimum error rate of all forests. When u = 0, it selected the genes that lead to the smallest error rate, and when u = 1, it was similar to “1 s.e. rule” used in classification trees. The results showed that this method returned small sets of genes compared to alternative variable selection methods and did not include genes that were highly correlated. Besides, this study also examined the effects of changes in the parameters of random forest and the variable selection process. Deng et al. [9] proposed another approach called guided regularized random forest (GRRF) that performed feature selection based on the importance score from a RF built on the complete training data complemented with the information gain in a local node. The trees in GRRF are highly correlated and cannot be built in parallel. The authors addressed this limitation by using the importance scores from an RF and by having each tree built independently of one another in their subsequent method known as guided random forest (GRF) [10].

In [17], Nguyen applied a two-stage quality based sampling method in traditional RF.The method used p-value assessment to determine a cut-off point that separated the informative and non-informative features (SNPs) in two groups. The informative SNPs were further subdivided into two groups: highly informative and weak informative SNPs. When sampling the SNPs subspace for building the trees of a forest, only those SNPs from the highly and weak informative subgroups were considered. During each split at a node, the algorithm resulted in feature subspace that always contained highly informative SNPs. The authors had performed extensive experiments on two genome-wide SNP datasets and 10 gene datasets to demonstrate the effectiveness of this method. Their results indicated that the proposed method significantly reduced prediction errors and outperformed most state-of-art variants of RF. The approach enabled to generate more accurate trees with lower prediction error and avoided over-fitting.

Ge et al. [12], developed a feature selection algorithm based on correlation measurement, Maximal Information Coefficient (MIC). This method selected features associated with phenotype independently of each other and used nearest neighbor classification algorithm. Comparative study based on 17 datasets indicated that the method performed as well or better than existing methods, and significantly reduced the number of selected features. The selected features also appeared to have biomedical relevance to the phenotype in the literature.

In this paper, we propose a novel method called Enriched Random Forest (ERF), that performs feature selection by sampling the variables used to partition each node according to a given set of weights assigned to each variable. As pointed out previously, in traditional RF, simple random sampling is used for selecting the subset of eligible features at each node, thus almost all these subsets are likely to contain a preponderance of non-informative features. To overcome this limitation of traditional RF, ERF applies weighted random sampling, assigning lower weight to the less informative features. If the weights of all the variables are set to one then the algorithm becomes standard random forest and if the weight of a variable is set to zero then the variable will be excluded from the training data. To evaluate our method, we applied ERF to various gene expression dataset and compared its performance to that of traditional RF.

3. Methods

3.1. Enriched Random Forest

3.1.1. Background

Random Forest (RF) proposed by Breiman (2001) adds an additional layer of randomness to bagging that builds on large collection of de-correlated trees, and then average them. In addition to using different bootstrap samples for constructing each tree, in RF each node is split using the best split among all variables. The performance of RF is similar to boosting as well as they are simple to train and tune. The essential idea is to average many noisy but approximately unbiased models, and hence reduce the variance. Similar to bagging, RF also uses trees as the base learner, since they can capture complex interaction structures in the data, and if grown sufficiently deep, have relatively low bias. Also, trees are inherently noisy, so they benefit greatly from averaging.

In bagging, successive trees do not depend on earlier trees. Each tree is constructed independently using a bootstrap sample of the training data and is identically distributed (i.d.). Thus, the expectation of an average of B trees is the same as expectation of any one of them. This means the bias of bagged trees is the same as that of individual trees, and the only improvement can be achieved through variance reduction. An average of B i.i.d. random variables, each with variance σ², has variance $\frac{1}{B}{\sigma }^2$. If the variables are simply i.d. with positive correlation ρ, the variance of the average is:

$$\rho {\sigma }^2+\frac{1-\rho }{B}{\sigma }^2$$ (1)

As B increases, the second term diminishes, and the size of the correlation between pairs of bagged trees limits the benefits of averaging. To this end, RF improves variance reduction by reducing the correlation between the trees without increasing the variance too much. This is achieved in the tree growing process through random sampling of the predictor variables. When growing a tree on bootstrapped dataset, before each split, m ≤ p of the predictor variables are selected at random as candidate for splitting. For regression, the default value for m is $⌊\frac{p}{3}⌋$ and the minimum node size is five. For classification, the default value for m is $⌊\sqrt{p}⌋$ and the minimum node size is one. After B such trees are grown, the RF predictor (regression) is given by:

$${\widehat{f}}_{rf}^B(x)=\frac{1}{B}\sum _{b=1}^{B}T\left(x;{\Theta }_b\right)$$ (2)

When used for classification, random forest obtain a class vote from each tree, and then classifies using majority vote.

3.1.2. Out of Bag Samples

An important feature of RFs is its OOB samples. For each observation z_i = (x_i, y_i), random forest predictor is constructed by averaging only those trees corresponding to bootstrap samples in which z_i did not appear. An OOB error estimate is identical to that obtained by N-fold cross validation. Hence, unlike many other nonlinear estimators, RF can be fit in one sequence, with cross validation being performed on the way. Once, the OOB error stabilizes, the training can be terminated.

3.1.3. Variable Importance

RF also use the OOB samples to construct variable importance measure, to measure the prediction strength of each variable. When the b^th tree is grown, the OOB samples are passed down the tree, and the prediction accuracy is recorded. Then, the values for the j^th variable are randomly permuted in the OOB samples, and the accuracy is again computed. The decrease in accuracy as a result of this permuting is averaged over all trees, and is used as a measure of the importance of variable j in the RF.

3.1.4. Limitations of Random Forest

Although traditional RF works well in datasets with many features (large p), when the percentage of truly informative features is small, such as with DNA microarray data, its performance tends to decline significantly. In previous studies, Moechars et al. [16], and Raghavan et al. [19], illustrated this point using an experiment conducted to study whether mice whose Slc17A5 gene has been knocked out could be distinguished from wild type mice at the gene expression level. Gene expression measurements were taken on newborn (0-day-old) mice as well as on 18-day-old mice. At day 0, there were no obvious occurrence of any phenotypic variations in the knockout mice but subtle effects would have already begun at the cellular level. By day 18 phenotypic variations in the knockout mice are evident with observable morphological alterations such as defects in myelination. The separation of the 18-day-old mice is straightforward both physiologically and with gene expression data. On applying traditional RF, an out-of-bag error rate of less than 10% was obtained. On the other hand, it is a challenge to separate the newborn mice, not only physiologically, but even with gene expression data; the out-of-bag error rate for RF was over 50%.

Let us consider a situation with p features, of which only H are informative. Then, if at any node m features are selected by resampling randomly with equal weights, the probability distribution of the number of informative features selected is binomial with m trials and probability $\pi =\frac{H}{p}$. The mean number of informative features selected at each iteration is μ = πm. Since π is typically very small, so will μ be. For example, if H = 100, p = 10, 000 and m = p^1/2 = 100, the resulting μ is only one informative feature per node. The trees built using such nodes will have low accuracy and overall performance of the ensemble will suffer. Thus, in situation like this, traditional RF algorithm can be considerably enhanced by reducing the contribution of trees whose nodes are populated by less informative features. To some extent, this can be achieved by pre-filtering, but here we develop a novel adjustment that has demonstrated superior performance when applied on high dimensional genomics datasets with too few truly informative features. We choose eligible subsets for splitting at each node by weighted random sampling instead of simple random sampling, with the weights tilted in favor of the informative features. This results in Enriched Random Forest.

3.1.5. Enriched Random Forest Algorithm

Enriched Random Forest enhances the performance of traditional Random Forest method by reducing the contribution of trees whose nodes are populated by less informative features. ERF uses weighted random sampling instead of simple random sampling, so that less informative features are less likely to get selected and the odds of trees containing more informative features being included in the forest increases. Consequently, the ERF comprises of a higher number of better base learners, resulting in a better fit. ERF algorithm samples the variables used for partitioning each node according to a set of given weights assigned to each variable. If the weight of a variable is zero then the variable is excluded from the training set.

Given a training set X consisting of n observations, an outcome variable Y, and p features, a tree is constructed as follows: a feature x and a threshold t that splits X into two subsets that are maximally distinct according to a specified criterion are selected from all features of X and all possible values of t. The training set is then split into the two buckets X_L and X_R depending on whether or not x < t. This procedure is repeated with each of X_L and X_R using another (x, t) combination until no further splitting is possible. In a random forest, a tree, rather than being trained on the entirety of the training set, is trained on a sample of the n observations drawn at random with replacement from the complete set of n observations. Additionally, when determining which feature to split on at each node, only a subset of m of the p features (usually m = p^1/2) are considered eligible; this subset is drawn at random without replacement independently for each node from the complete set of p features. A RF is an ensemble of R number of such trees, where each tree is called a base learner. For classification, classes are assigned to test cases by majority vote: when given a test case, each tree assigns a class according to its classification rules; this information is then collated and overall the forest assigns the majority class to the test case. For regression, the outcome of a test case is predicted as the average of the values predicted by each tree. The novel aspect of ERF is it uses weighted random sampling instead of simple random sampling when selecting the subset of m features for splitting at each node. Weighting is done by scoring each feature based on its ability to separate the groups, e.g. via a t-test or chi-square test, and using these scores to assign weights, w_i, so those features that most separate the groups are assigned higher weights. Once the weights are determined, at any node, the subset of m eligible features is selected from the p features using weighted random sampling with the weights w_i. Below is an overview of our proposed method, followed by a detailed discussion of the feature scoring technique. Figure 1 illustrates the overall approach of ERF.

Fig. 1:

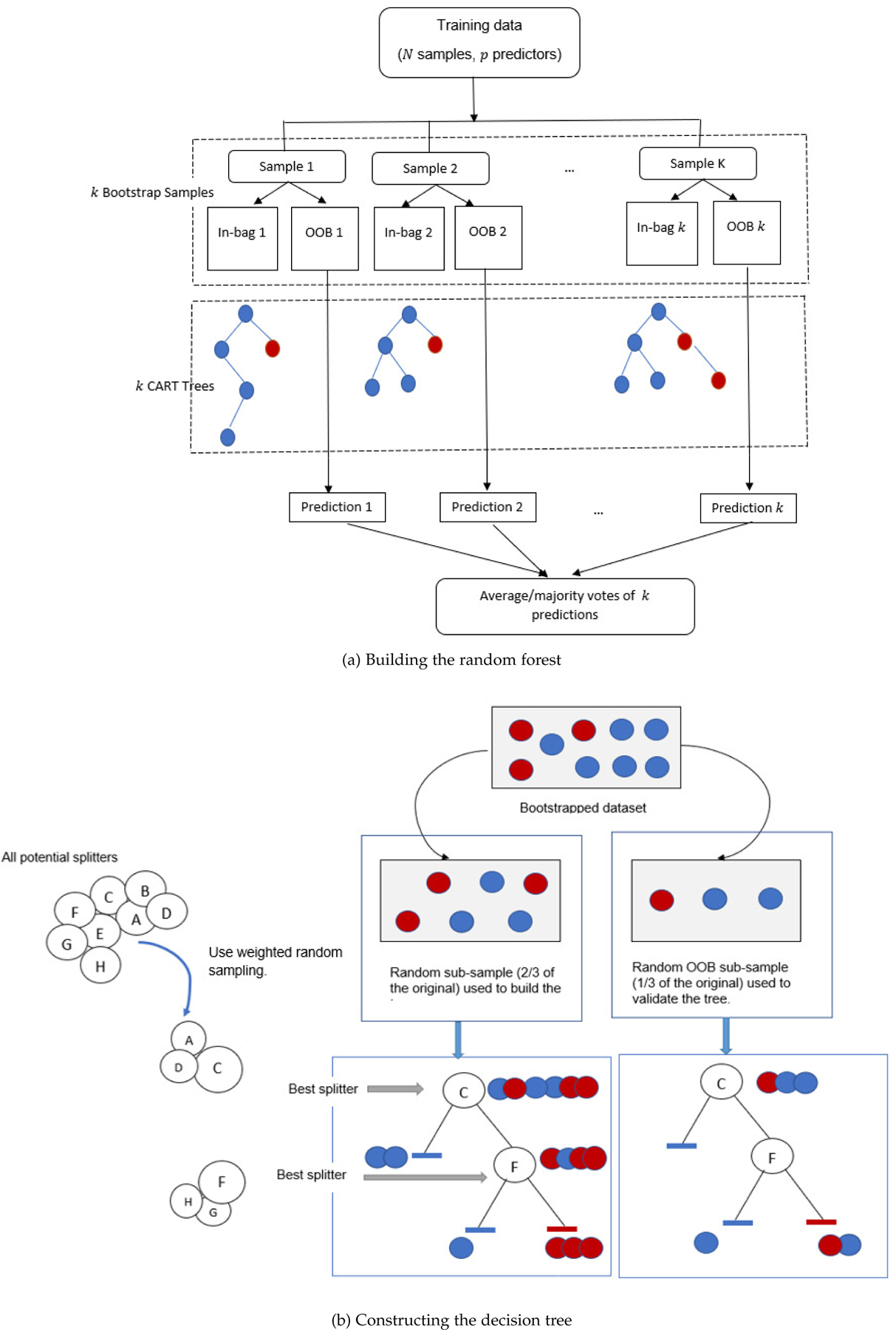
Enriched Random Forest

1. We split the given n observations with p variables randomly into two samples: in-bag samples (68% of n) and out-of-bag samples (32% of n).

2. Next, build a tree on the in-bag sample using the Classification and Regression Trees (CART) algorithm ( or use any alternative splitting criterion) with two modifications.

   1. To perform the split at each node, we use ”mtry” variables (usually $\sqrt{p}$ or $\frac{p}{3}$) selected using the weight vector of probabilities W.
   2. The complete tree is built without pruning.

3. We use the tree built using the in-bag samples to predict the outcome variable for the out-of-bag samples.

4. Steps 1–3 are repeated at least N = 1000 times and the out-of-bag predictions are stored in a matrix of dimension n × N where the entries for the in-bag observations of each column are missing values. If the response is categorical, we calculate for each row the most frequent prediction and assign that presiction to the observation of that row. In case of continuous response, the predicted value for each observation/row equals average of that row.

3.1.6. Weighting the Features

The key characteristic of ERF is to score each feature based on how well it separates the groups. Such score is generated by computing the correlation between the predictor variables and the response when both are of continuous numeric types. If the response is a binary variable and the predictor is continuous, we test each feature for a group mean effect using two sample t-test and one-way anova. When both response and predictor are categorical, we perform chi-square independence test to determine significant difference between the expected frequencies and the observed frequencies in one or more categories. Next, we obtain a p-value from these significance tests, small p-value indicates greater separation and large p-values indicate less separation. However, to weight using the p-values themselves would fail to take into account: (i) the multiplicity of the tests being performed; and (ii) the small sample sizes typical of microarray experiments. To adjust for the multiplicity problem, we compute the weights based on q-values, which are calculated from the p-values as: q_(i) = min_k≥1{min((p/k)p_(k), 1)}, where p_(i) and q_(i) are the p-value and q-value associated with the feature with i-th smallest p-value and p here denotes the number of features. The q-values provide false discovery rate (FDR) adjusted measures of significance for the features and are in the same order as the p-values. In addition, the use of q-values instead of p-values help lessen the likelihood of over-fitting in situations with no separation of the data into groups. If p-value based weights were used, some genes by chance would have small p-values and would be wrongly assigned higher weights. This would result in ERF mistakenly implying a separation. When using q-value based weights all genes would be assigned equal weights and ERF would not find a separation. The standard way to compute weights of the predictor variables is by computing negative logarithm of the q-values. For applying a steeper transformation if desired, we could also apply w_i = (1/q_(i) − 1). Based on these weights, features with less separability will get zero weight and features with high separability will get large weights. For further details regarding the use of q-values for calculating weights please refer to the experimental results presented by the authors in their preliminary work [1].Furthermore, to adjust for (ii), we used Conditional t-test (Ct) [2] instead of usual t-test since it is likely to generate a better ranking of features. The usual t-test has low power and thus have low discriminatory ability when the sample size is small.

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{Algorithm 1}\text{\hspace{0.17em}\hspace{0.17em}Algorithm for Enriched Random Forest\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}}\hfill \\ \begin{array}{l}\mathbf{Input:}\text{A training set }S\text{ = (}{x}_{\text{1}}\text{, }{y}_{\text{1}}\text{), }\dots \text{,(}{x}_N\text{, }{y}_N\text{), features }F\text{,}\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} and the number of trees in forest }B\end{array}\hfill \\ \mathbf{Output:}\text{ The learned forest }H\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}1: }\mathbf{function }EnrichedRandomForest(S,F)\hfill \\ Initialisation\text{:}\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}2: }H\leftarrow \varphi \hfill \\ LOOP\text{ Pr}ocess\text{:}\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}3:\hspace{0.17em}\hspace{0.17em}}\mathbf{for}i\text{\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}}B\mathbf{do}\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}4: \hspace{0.17em}\hspace{0.17em}}{S}^{\left(i\right)}\leftarrow \text{A bootstrap sample S}\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}5: }{h}_i\leftarrow RandomizedTreeLearn(S^{\left(i\right)},F)\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}6: } H\leftarrow H\cup \left\{h_i\right\}\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}7:\hspace{0.17em}}\mathbf{end for}\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}8:\hspace{0.17em}}\mathbf{return}H\hfill \\ \text{\hspace{0.17em}\hspace{0.17em}9:\hspace{0.17em}}\mathbf{end function}\hfill \\ \text{10: }\mathbf{function }RandomizedTreeLearn(S^{\left(i\right)},F)\hfill \\ \text{11: At each node}\hfill \\ \text{12: }W\leftarrow ComputeWeight(S^{\left(i\right)},F)\hfill \\ \text{13: }f\leftarrow Subsetof\text{\hspace{0.17em}F\hspace{0.17em}usin}gweightedrandomsampling\hfill \\ \text{14: Split\hspace{0.17em}on\hspace{0.17em}best\hspace{0.17em}feature\hspace{0.17em}in\hspace{0.17em}}F\hfill \\ \text{15: }\mathbf{return}\text{\hspace{0.17em}\hspace{0.17em}The\hspace{0.17em}learned\hspace{0.17em}tree }h\hfill \\ \text{16: }\mathbf{end function}\hfill \end{array}}}$$

We also highlight the fact that the error rates may be underestimated if the weights are calculated just once based on all the samples than if they are to be determined separately for each tree based on only the in-bag samples. However, the latter would increase computational burden and render the weights less well determined than if they had been calculated outside the loop using all the samples. In order to address this issue, here we implement another variant of ERF called ERF-CV that perform balanced leave-one-out cross-validation instead of bagging to lighten the computational load and to decrease the sample size when determining weights. Let J = R/n. In ERF-CV, in J of the R trees,one observation is set aside as out-of-bag test set, the weights are calculated based on the n − 1 in-bag cases which are used for building the tree. The prediction is done on the OOB case. The process is repeated with each of the other cases. As such, less computation is required by ERF-CV than ERF since the weights are calculated only n times rather than R times in this process.

4. Experimental Evaluation

We implemented the proposed approach on different microarray datasets to evaluate its effectiveness in both regression and classification setting as compared to the traditional RF.

4.1. Regresion

4.1.1. Dataset 1: RNA Data

This is an unpublished dataset containing gene expression of 25000 genes from 100 subjects diagnosed with lupus. The response variable is a clinical score that measures the activity and chronicity in lupus. Given the high dimensionality of the dataset, it is supposed that a lot of variables are non-informative and that there exist unknown groups of highly correlated predictors. Applying the ERF algorithm, we perform feature selection in way such that the subset of eligible features at each node contain a preponderance of truly informative features. We split the data into train and test sets based on i the suggested train and test indices included in the data file. Here, we compute “pseudo R-squared” as indicated by Breiman (2001) [5]. Generally, explained variance (R²) is defined as: $R^2=1-\sum \left({\left(\widehat{y}-\overline{y}\right)}^2\right)\sum \left({(\overline{y}-y)}^2\right)$, and takes value between 0 and 1. On the other hand “pseudo R-squared” is defined as: R² = 1−(Mean Squared Error)/var(y), which, mathematically can produce negative values. A simple interpretation of negative R², is that we are better off predicting any given sample as equal to overall estimated mean, indicating very poor model performance.

In random forests, there is no need for cross-validation or a separate test set to get an unbiased estimate of the test set error. It is estimated internally. Each tree is constructed using a different bootstrap sample from the original data. About one-third of the cases are left out of the bootstrap sample and not used in the construction of the k^th tree. Each case left out in the construction of the k^th tree is used to estimate the error. This are called out-of-bag samples. However, our implementation also provides the flexibility to carry out cross-validation applying hold-out approach. We compared our proposed method to traditional random forest using out-of-bag samples as well as hold-out approach. Table 1. illustrates the performance of enriched random forest in contrast to traditional RF when applied to the rnadata.

TABLE 1:

Predictive Performance of ERF and RF on RNA Data

	OUT-OF-BAG		HOLD-OUT SET
Methods	MSE	R 2	MSE	R 2
Enriched Random Forest	3.87	0.15	3.46	0.13
Traditional Random Forest	4.70	−0.08	3.86	−0.12

Figure 2 illustrates the performance of ERF and RF via scatterplots of the OOB predicted values versus the observed response values when applied to the above dataset.

Fig. 2:

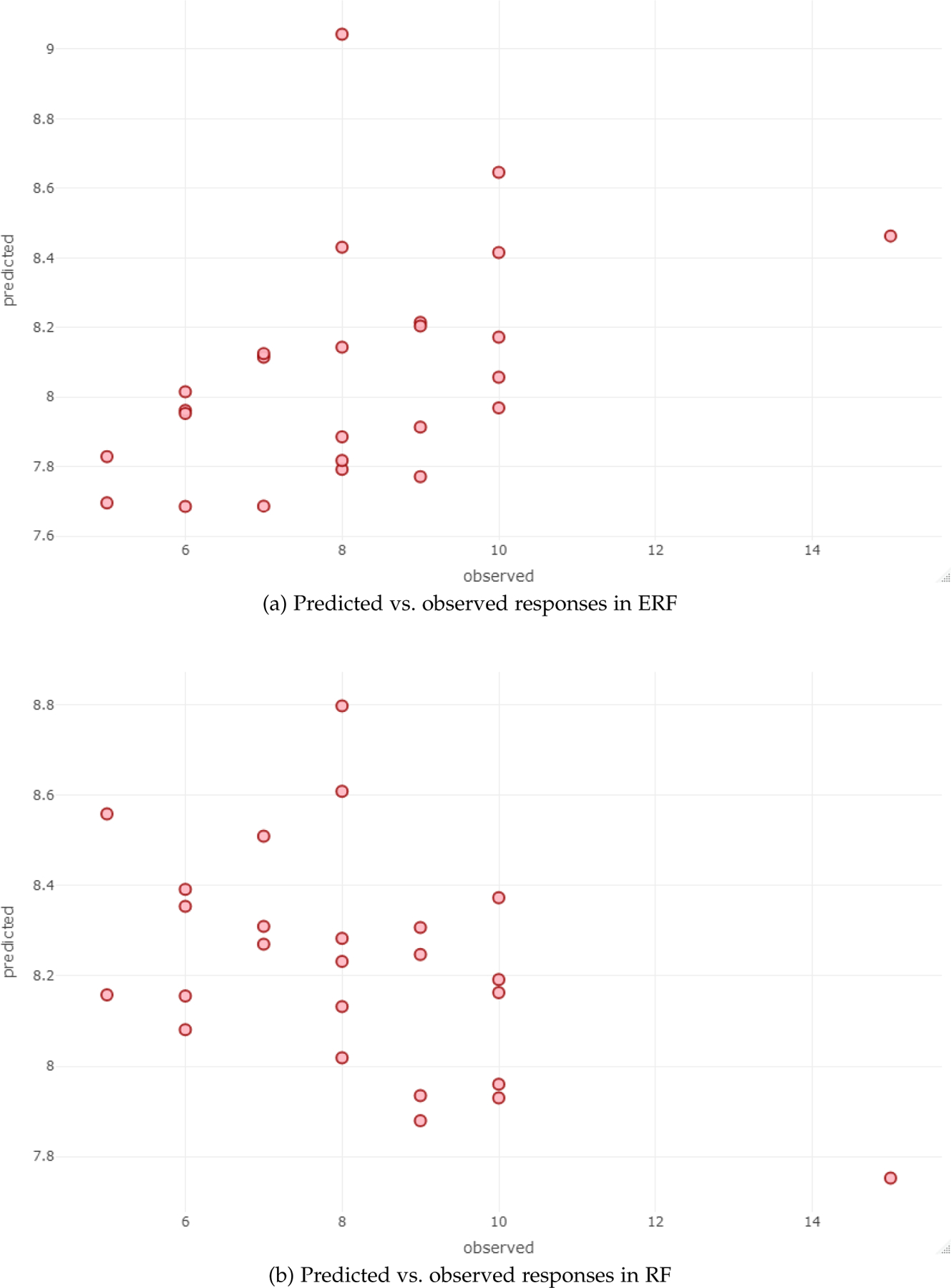
OOB Prediction vs. observed responses

4.1.2. Dataset 2: Toxicity Data

Next, we also applied the method on another similar gene expression data, liver.toxicity, available in the R package mixOmics. This is a real dataset from a study by Heinloth et al.(2004), in which four male rats of the inbred strain Fisher 344 were exposed to different doses of acetaminophen (non toxic dose 50 or 100mg/kg), moderate toxic dose (100mg/kg), and severe toxic dose (2000 mg/kg) in a controlled experiment. Necropsies were performed at different hours after exposure (6,18,24, and 48 hours) and the mRNA from the liver was extracted. In the original study, 10 clinical variables containing markers of liver injury were measured. However, the dataset used in our analysis contains: (i) a data frame, called gene, of size 64 rows representing the subjects and 3116 columns representing explanatory variables which are gene expression levels; and (ii) a vector, called clinic, with 64 rows and 1 column, which is the response variable and corresponds to the serum albumin level. Table 2. Illustrates the performance of enriched random forest in contrast to traditional RF when applied to the liver.toxicity data.

TABLE 2:

Predictive Performance of ERF and RF on Liver Toxicity Data

	OUT-OF-BAG		HOLD-OUT SET
Methods	MSE	R 2	MSE	R 2
Enriched Random Forest	0.04	0.4	0.02	0.7
Traditional Random Forest	0.05	0.24	0.02	0.62

4.2. Classification

4.2.1. Dataset 3: Slc17A5 Data

For classification task, we use the Slc17A5 Day 0, Slc17A5 Day 10, and Slc17A5 Day 18 data. These datasets capture gene expression measurements of 45,101 genes for 12 samples belonging to two separate classes taken on newborn, 10-day-old, and 18-day-old mice respectively. Slc17A5 Day 0 dataset is the primary dataset for our evaluation. The Slc17A5 Day 18 dataset, which has unequivocal separation of classes, is used to assess the performance of ERF when there is strong signal. The Slc17A5 Day 10 dataset captures an intermediate stage. In addition, we also created artificial datasets by random permutation of the Slc17A5 Day 0, Slc17A5 Day 10, and Slc17A5 Day 18 datasets. These datasets were used to verify that the method is not over-fitting. If the weighting is not done carefully, it is possible to find spurious classifications in datasets that have no true separation.

In classification, the out-of-bag data is used to get a running unbiased estimate of the classification error as trees are added to the forest. Each case left out in the construction of the k^th tree is included in the out-of-bag data to get a classification for the k^th tree. In this way, a test set classification is obtained for each case in about one-third of the trees. At the end, take the class that got most of the votes every time case i was in out-of-bag data. The proportion of times the predicted class is not equal to the true class of i averaged over all cases is the out-of-bag error estimate. Table 3. display the results of enriched random forest and traditional RF when applied to the Slc17A5 gene expression measured at day 0, day 10, and day 18.

TABLE 3:

Predictive Performance of ERF and RF on Slc17A5 Gene Expression Data

	Day 0	Day 10	Day 18
Methods	OOB Err. Rate	OOB Err. Rate	OOB Err. Rate
ERF	0.08	0	0
Traditional RF	0.58	0.47	0

The results on the permutated datasets are presented in Table 4.

TABLE 4:

Predictive Performance of ERF and RF on Slc17A5 Gene Expression Data

	Day 0	Day 10	Day 18
Methods	OOB Err. Rate	OOB Err. Rate	OOB Err. Rate
ERF	0.75	0.73	0.75
Traditional RF	1	0.8	0.83

We also performed similar experiments to compare the performances of ERF-CV and ERF on original and scrambled Slc17A5 Day 0 and Slc17A5 Day 18 data. Balanced leave-one-out cross validation was applied in ERF-CV. The error rates of ERF were 0.17 and 0.00 on original Slc17A5 Day 0 and Slc17A5 Day 18 datasets respectively. ERF-CV obtained 0.08 and 0.00 on original day 0 and day 18 data. On the other hand, on scrambled datasets ERF achieved an error rate of 0.83 and 0.68, while ERF-CV obtained 0.75 and 0.42 on day 0 and day 18 datasets respectively.

To further evaluate our method, we also compared the performance of ERF using a separate dataset (Slc17A5 Day 0) for training and a separate one (Slc17A5 Day 18) for testing. It was observed that ERF outperformed traditional RF in this scenario as well.

4.2.2. Dataset 4: SRBCT Data

Our method is also applicable when the response variable has multiple groups. Here, we applied our proposed method on the SRBCT data available in the R package mixOmics. This real classification dataset is a small version of the small round blue cell tumors of childhood data and contains the expression measure of genes measured on 63 samples. The dataset is composed of: (i) a data frame, called gene, of size 63 × 2308 which contains the 2308 gene expressions; and (ii) a response factor of length 63, called class, indicating the class of each sample (4 classes in total). To verify that our method is not over-fitting we performed y-randomization test. The values of response variable (class) are randomly ascribed (scrambled) to different samples, while the descriptors values (genes) are left intact. Scrambled data are then used for training the model. The test indicate the quality of obtained models in comparison to chance models derived from random data. The results are displayed in Table 5.

TABLE 5:

Predictive Performance of ERF-CV and ERF on Slc17A5 Data

	Original Data		Scrambled Data
Methods	ERF	ERF-CV	ERF	ERF-CV
Slc17A5 Day 0	0.17	0.08	0.83	0.75
Slc17A5 Day 18	0.00	0.00	0.68	0.42

5. Discussion

Enriched Random Forest works best when applied to datasets that have subtle signal. If the signal were strong or non-existent, both ERF and RF would produce essentially the same result. Table 1 and 2, display the results of ERF when applied to two such datasets RNA data and liver.toxicity data. They show that ERF outperforms traditional RF in terms of Mean Square Error (MSE) and R². When applied to the RNA data, ERF achieves out-of-bag MSE of 3.87 in contrast to traditional RF which achieves out-of-bag MSE of 4.70. The pseudo-R² of ERF was found to be 0.15 whereas for traditional RF it was −0.08. To account for the low pseudo-R² value, we also illustrated the performance of ERF and RF in Figure 2, using the OOB predictions versus the observed responses. We clearly observe that ERF obtain a better fit than RF. In hold-out set approach, ERF and traditional RF obtained MSE of 3.46 and 3.86 respectively. The pseudo-R² for ERF and RF were 0.13 and −0.12 respectively. As explained previously, negative value of R² indicate that we are better off predicting any given sample as equal to overall estimated mean, indicating very poor model performance. Therefore, ERF performs well in comparison to traditional random forest when the percentage of truly informative feature is very small (i.e., the signal is subtle). Traditional RF have little or no predictive power at all in such situation. Similarly, when applied on liver.toxicity data ERF obtained out-of-bag MSE of 0.04 and pseudo-R² of 0.4. Traditional RF, on the other hand, obtained out-of-bag MSE of 0.05 and pseudo-R² of 0.24. In hold-out set approach, MSE for both ERF and RF was found to be 0.02, and pseudo-R² of ERF and RF was found to be 0.7 and 0.6 respectively. When there is true signal in the data, enriched random forest performs equally consistent or better than standard random forest.

For classification task, we compare the out-of-bag error rates of ERF and traditional RF on three separate microarray datasets – Slc17A5 Day 0, Slc17A5 Day 10, and Slc17A5 Day 18. A good classifier should have low out-of-bag error rates for original datasets and high out-of-bag error rate for scrambled datasets. Table 3, display the results of ERF and traditional RF on the original Slc17A5 datasets. The out-of-bag error rates for ERF were 0.08, 0, and 0 when applied to Day 0, Day 10, Day 18 gene expression measurement data. Traditional RF obtained error rate of 0.58 on Day 0, 0.47 on Day 10, and 0 for Day 18 measurements. At day 0, the phenotypic variations in the knockout mice were very subtle and mostly at the cellular level. By day 18 phenotypic variations are evident with observable morphological alterations. The separation of the 18-day-old mice is therefore more straightforward as the genes are fully expressed. Day 10 is an intermediate stage in the development process. Table 4, illustrates the performance of ERF compared to traditional RF on scrambled datasets. The out-of-bag error rates for ERF were 0.75, 0.73, and 0.75 when applied to day 0, day 10, day 18 measurements data. Traditional RF had error rate of 1, 0.8, and 0.83 on day 0, day 10, and day 18 data. These high out-of-bag error rates validate that ERF does not over-fit unlike many other classifiers. In case of multiple groups, we evaluated our proposed approach using the SRBCT gene expression dataset. Our results indicate that both ERF and traditional RF perform equally well on this dataset, achieving an out-of-bag error rate of 0.01. To test for over-fitting, we performed y-randomization test and found that the out-of-bag error rate increased significantly – ERF (error rate = 0.67) and RF (error rate = 0.74). Our experiments also confirmed that ERF-CV performed equally compared to ERF and were both significant improvements over traditional RF. By large, the ERF and ERF-CV error rates were similar to each other. Thus, ERF-CV could be more useful in practice since it is less computationally intensive and less prone to small sample sizes.

In summary, when compared to the other state-of-art methods discussed in this paper, our proposed method have key advantages in “large p, small n” setting, especially when the percentage of truly informative features is extremely small. Regularization based methods such as LASSO and elastic net perform feature selection by imposing L₁ and (L₁+L₂) regularized constraints respectively on the weights associated with the features. Particularly, the L₁ constraint in LASSO forces the weights of some features to exactly zero, and hence produce a sparse solution, resulting in loss of some important information. Especially, when we have correlated features, LASSO arbitrarily selects only one feature from a group of several correlated features. For instance, in gene expression data the ideal gene selection method would eliminate the trivial genes and automatically include whole groups into the model once one gene among them is selected (“grouped selection”). LASSO does not address the grouped selection. To this end, elastic net uses a convex combination of L₁ and L₂ penalties that yield sparse representations similar to LASSO, while allowing the correlated features to be selected or deselected together as in grouped selection. The downside to these regularization based methods is that they introduce more hyper-parameters to be set, and this can be very expensive if we have a lot of them. RF and ERF on the other hand have only one hyper-parameter to be set: the number of features to randomly select at each node. Also, LASSO and elastic net are both linear models and are not suitable for modeling non-linear relationships observed in genomic datasets. As pointed out earlier, genomics data often involve gene-gene interactions and gene networks. Given the high-dimensional setting, it is not realistic to prespecify these feature interactions and especially if there are higher-order interactions. Regularization methods such as LASSO and elastic nets require to specify these interactions in the model and therefore are not suitable for high-dimensional genomic datasets. An important advantage of tree based methods such as ERF and RF is their ability to model non-linear relationships and capture interactions among the feature variables. Lastly, linear models as well as traditional RF tend to perform better when there are large number of features with very low ratio of signal to noise.

Another approach that has been discussed in related work is recursive feature elimination. RFE is based on the idea of repeatedly constructing a model (e.g., SVM-RFE) and choosing either the best or worst performing feature (for example based on coefficients), setting aside the selected feature and then repeating the process with rest of the features. This process is applied until all features in the dataset are exhausted. Features are ranked according to when they were eliminated. As such, it is a greedy optimization for finding the best feature subset. The stability of RFE depends heavily on the type of model that is used for feature ranking at each iteration. But, in the “large p, small n” paradigm, the performance of RFE methods decline significantly and also increase the risk of over-fitting.

6. Conclusion

In this paper, we proposed a novel approach to enhance the traditional random forest algorithm to better perform in ”large p, small n” paradigm. In contrast to the traditional RF, our proposed ERF method uses weighted random sampling to select subsets that has preponderance of informative features for splitting at each node. We extensively evaluated the effectiveness of our approach using several high-dimensional genomics datasets. Our main contribution is twofold: (i) We applied weighted random sampling instead of simple random sampling, so that chances of selecting less informative features are reduced and odds of tree containing more informative features being included in the forest increases. Overall, our results indicate that ERF outperformed traditional RF when the signal is subtle. This means that only a small fraction of the features are truly informative. In case where the signal is strong and the data is easily separable ERF performed consistently equally and better than traditional RF. (ii) We also demonstrated how ERF-CV perform balanced leave-one-out cross-validation instead of bagging to lighten the computational load and decrease the sample size when determining weights.

We have extended the work of Amartunga et. al [1] which discussed ERF only in the two-group classification context. Here, we have proposed an extension to the case of multiple groups. In addition, we incorporated the idea of applying ERF in regression setting. Our implementation also addresses the challenge associated with variables that have mixed data types. We have applied appropriate statistical significance tests based on the data type of the predictor and response variables. Our future work will focus on further improvement in the achieved accuracy of the prediction model. In multinomial classification, complexity grows as the features that separate any two groups could differ substantially from the features that separate any two other groups. A possible direction to pursue is to possibly involve collation of multiple pairwise analyses. We conjecture that this idea could be incorporated into other ensemble and machine learning techniques such as linear discriminant analysis, logistic regression, and SVM.

Currently, we are in the process of having our code as an R package that will implement the proposed methodology, thus making it widely available for use by other researchers.

TABLE 6:

Predictive Performance of ERF and RF on SRBCT Gene Expression Data

	Original Data	Scramled Data
Methods	OOB Err. Rate	OOB Err. Rate
ERF	0.01	0.67
Traditional RF	0.01	0.75

Biographies

Debopriya Ghosh, PhD, is a Senior Biostatistician at Janssen Research and Development, LLC. She received her PhD from Rutgers University and MS from Baylor University. She was awarded the NSF Northeast Big Data Innovation Young Innovators Fellowship by Columbia University.

Javier Cabrera, PhD, is a Professor of Statistics and Biostatistics at Rutgers University and Rutgers Robert Wood Johnson Medical School. He has published many papers and books on Biostatistics, Big Data for medical sciences, Functional Genomics, data mining Genomics data, Statistical computing and graphics, and computer vision. Fulbright fellow, Henry Rutgers fellow, and supported by grants from NSF, NIH, the RWJ foundation and the Qatar foundation.