Intramolecular Charge Transfer and Ultrafast Nonradiative Decay in DNA-Tethered Asymmetric Nitro- and Dimethylamino-Substituted Squaraines

Abstract

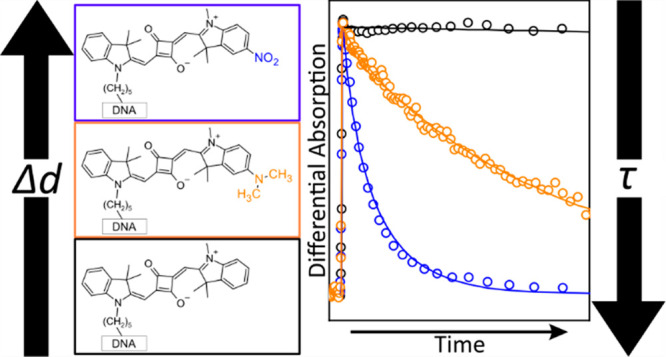
Molecular (dye) aggregates are a materials platform of interest in light harvesting, organic optoelectronics, and nanoscale computing, including quantum information science (QIS). Strong excitonic interactions between dyes are key to their use in QIS; critically, properties of the individual dyes govern the extent of these interactions. In this work, the electronic structure and excited-state dynamics of a series of indolenine-based squaraine dyes incorporating dimethylamino (electron donating) and/or nitro (electron withdrawing) substituents, so-called asymmetric dyes, were characterized. The dyes were covalently tethered to DNA Holliday junctions to suppress aggregation and permit characterization of their monomer photophysics. A combination of density functional theory and steady-state absorption spectroscopy shows that the difference static dipole moment (Δd) successively increases with the addition of these substituents while simultaneously maintaining a large transition dipole moment (μ). Steady-state fluorescence and time-resolved absorption and fluorescence spectroscopies uncover a significant nonradiative decay pathway in the asymmetrically substituted dyes that drastically reduces their excited-state lifetime (τ). This work indicates that Δd can indeed be increased by functionalizing dyes with electron donating and withdrawing substituents and that, in certain classes of dyes such as these asymmetric squaraines, strategies may be needed to ensure long τ, e.g., by rigidifying the π-conjugated network.

Introduction

Conjugated organic molecules, i.e., dyes, are of relevance to a broad number of fields, including light harvesting,¹⁻⁶ organic optoelectronics,⁷⁻⁹ and nanoscale computing.¹⁰⁻¹⁷ Dyes play a critical role in these applications due to their strong absorption of light, particularly in the visible spectral range. A key additional feature of dyes is the extent of and diversity to which their chemical structure can be modified to tailor their optical properties for target applications. For example, adding an electron donating or withdrawing substituent to one end of a conjugated network can increase the magnitude of the difference static (or permanent) dipole moment, i.e., Δd, which is the difference of the static excited- and ground-state dipole moments (i.e., d_e – d_g) and represents the degree of charge transfer concomitant with photoexcitation. For simplicity, such molecules are referred to as asymmetric dyes. Asymmetric dyes sometimes exhibit considerably broadened absorption spectra compared to symmetric dyes, which makes them attractive for applications in light harvesting^18,19 and organic optoelectronics.²⁰ Asymmetric dyes can also exhibit a large nonlinear optical response,²¹⁻²³ which makes them potentially useful as active media in optical switches.²⁴⁻²⁷

Another area of interest for asymmetric dyes is in quantum information science (QIS). Materials at the forefront of QIS currently include superconductors,²⁸⁻³¹ defects and impurities in solids,^32,33 semiconductor quantum dots,^34,35 and molecular spin systems.³⁶⁻⁴⁰ While considerable progress has been made in understanding and using molecular spin systems for QIS, an alternative, albeit much less explored, potential approach is to use molecular excitonic systems. Molecular excitonic systems leverage delocalized, collective electronic excitations^41,42 as the basic unit, and several recent works have theoretically evaluated their feasibility in QIS.⁴³⁻⁴⁵ The reason molecular excitonic systems can be used for QIS is because the molecular (Frenkel) exciton Hamiltonian is of the same form as the Hamiltonian describing multiparticle quantum walks that are universal to quantum computation.⁴⁶ The Frenkel exciton Hamiltonian accounts for two key interactions, single- and bi-exciton interaction,⁴⁷ that permit quantum entanglement and computing. The single-exciton interaction, which can be quantified via the excitonic hopping parameter (J), describes the ability of an exciton to delocalize in a wave-like manner across an aggregate. The bi-exciton interaction, which can be quantified via the exciton–exciton interaction energy (K), describes the strength of interaction between neighboring excitons. J governs the rate at which the exciton hops between sites along the aggregate, i.e., the frequency of the superposition that is the basic ingredient of entangled states and quantum bits, while K is required to form multiparticle entangled states and realize quantum parallelism.⁴⁸ In quantum information systems based on molecular excitons, the ability to realize quantum entanglement and perform quantum computations requires large excitonic interaction energies, i.e., large J and K. In contrast to many other materials platforms for QIS, a significant advantage of molecular excitonic systems is that J and K can be much larger than thermal energy, i.e., k_BT. As will be discussed in more detail below, dyes with large Δd, such as asymmetric dyes, are a prerequisite for large K.

In order to realize the molecular aggregate properties of J and K, it is necessary to assemble dye aggregate networks where a controlled number of dyes can be arranged in close proximity. One approach to controlling dye aggregation is deoxyribonucleic acid (DNA) templating.^17,49−68 DNA templating leverages the self-assembly of DNA, which is based on complementary pairing between four oligonucleotides. These simple design rules enable predictable and programmable assembly of DNA–dye nanostructures.⁶⁹ DNA nanostructures enable control over dye–dye positioning, a critical component of aggregation.^56,65,70 One such nanostructure, the four-armed DNA Holliday junction (HJ),^71,72 has been shown to support exciton delocalization in a variety of dye aggregate systems, including those composed of cyanines, squaraines, and squaraine rotaxanes.^70,73−81 DNA HJs are also advantageous for characterizing dye monomer photophysics by suppressing their spontaneous aggregation.

Why is it advantageous to characterize dye monomer photophysics? Because the magnitudes of J and K largely depend on electronic properties of the individual dyes that comprise the aggregates. Specifically, it is generally well-known that J is directly proportional to the square of the transition dipole moment (μ); it is less well recognized, however, that K is directly proportional to the square of Δd.⁴⁷ In general, dyes satisfy large J values by nature of a large μ. For example, μ of the prototypical cyanine dye Cy5 is ∼15–16 D (see, e.g., refs (82 and 83)) and aggregates of this dye have been assembled that exhibit a large J of ∼800 cm^–1 (∼0.1 eV).^73,75 Another example is evident in the case of the pyrene, a prototypical polycyclic aromatic hydrocarbon.⁸⁴ In the case of pyrene, its lowest energy electronic transition is only weakly allowed, i.e., ε_max ∼ 300 M^–1 cm^–1 (whose magnitude can serve as a proxy for μ; see, e.g., ref (85)), while its next higher energy electronic transition is more strongly allowed, i.e., ε_max ∼ 44 000 M^–1 cm^–1. This has profound consequences on excitonic coupling; whereas the higher energy electronic transition exhibits a pronounced redshift in its aggregated/crystalline form, little to no redshift is observed in the case of its lowest energy electronic transition. In contrast to μ, comparatively fewer dyes have large Δd. For example, while μ of Cy5 is relatively large (as highlighted above), its computed Δd is only ∼1 D,⁸³ which is equivalent to the value measured for a structurally analogous thiadicarbocyanine dye.^86,87 That said, it has been shown that control over the magnitude of Δd can be achieved by introducing electron donating and/or withdrawing substituents to π-conjugated dyes.^88,89 For example, a large Δd of ∼40 D was measured for a derivative of ß-carotene, a long-chain polyene incorporating a strongly electron withdrawing substituent on just one end.⁸⁹

In addition to μ and Δd, another important dye property is its excited-state lifetime (τ). Although dye monomers generally have long nanosecond-time scale lifetimes, a significant challenge in the field is that excited-state quenching via accelerated nonradiative decay generally occurs with aggregation.^56,58,76,77 As originally highlighted by Sundström and Gillbro, short monomer lifetimes may further compound this issue.⁹⁰

In this manuscript, the electronic structure and excited-state dynamics of a series of asymmetrically substituted indolenine-based squaraine monomers tethered to DNA HJs were examined. First, specific aspects of their electronic structure, i.e., Δd and μ, were calculated for the squaraine monomers using a combination of density functional theory (DFT) and time-dependent (TD) DFT. The electronic structure of the squaraine monomers was further examined, and their excited-state dynamics were initially surveyed via steady-state absorption and fluorescence spectroscopy. Next, the excited-state dynamics of solutions of the asymmetric squaraines were characterized via time-correlated single photon counting (TCSPC). Lastly, the excited-state lifetimes were quantified and mechanistic insights were gained into the excited-state dynamics via a combination of femtosecond visible (VIS) and near-infrared (NIR) transient absorption (TA) spectroscopy measurements along with modeling of the TA via global target analysis (GTA).

Methods

Synthetic Methods

Synthesis of Squaraines

Squaraines 1–4 were obtained from SETA BioMedicals (Urbana-Champaign, IL). The synthesis of 1 was previously reported.⁷⁸ The synthetic procedures for 2–4 are reported in Section S1.

Preparation of DNA-Tethered Squaraine Monomers

DNA oligonucleotides were purchased from Integrated DNA Technology (Coralville, IA). 1–4 were internally incorporated into the DNA oligonucleotides via a modified thymine nucleobase, and the resultant oligonucleotides were purified via dual high-performance liquid chromatography. Complementary DNA oligonucleotides without 1–4 were purified by standard desalting. The DNA oligonucleotides were dissolved in ultrapure water obtained from a Barnstead Nanopure (Thermo-Fisher Scientific, Waltham, MA) to form ∼100 μM stock solutions. Concentrations of DNA oligonucleotide solutions were determined via a NanoDrop One Microvolume UV–vis spectrometer (Thermo-Fisher Scientific, Waltham, MA) using calculated extinction coefficients (see, e.g., ref (77)). DNA HJs were prepared by combining equimolar amounts of the oligonucleotides into a buffer solution including 1× TBE 15 mM MgCl₂. The buffer solution was the same for all measurements, except in the case where the pH of the buffer solution was varied (as described in more detail below). Desired final concentrations depended on the measurement. All DNA HJs were allowed to hybridize at room temperature overnight with the exception of those used for pH-dependent steady-state absorption spectroscopy, which were subjected to a previously reported annealing process.⁷⁸Section S2 includes a table of the squaraine labeled and unlabeled DNA oligonucleotide sequences used to assemble the DNA HJ tethered squaraine monomers, along with mass spectra, confirming attachment of the squaraines to the DNA oligonucleotides.

Theoretical Methods

Density Functional Theory (DFT) and Time-Dependent (TD) DFT

DFT and TD DFT calculations were undertaken using Gaussian 16.⁹¹ Squaraine monomers were built by generating a SMILES string and a 3D geometry initially optimized using a UFF force field in RDkit.^92,93 The ground-state geometry was further optimized via electronic structure calculations in Gaussian 16.⁹¹ All DFT calculations were performed with the 6-31+G** basis set and the M06-2X exchange correlation functional.⁹⁴ These DFT parameters were chosen following an extensive survey of basis sets and exchange correlation functionals on squaraine molecules reported in our prior work and by Jacquemin et al.⁹⁵⁻⁹⁷ Excited-state data were calculated as the vertical excitation of the ground-state geometry, which was intended to recreate the nonequilibrium excited-state condition. The integral equation formalism polarizable continuum model^98,99 was used to estimate solvation effects for the squaraine dyes in water, assuming nonequilibrium solvation conditions for excited-state calculations.

Experimental Methods

Steady-State Absorption Spectroscopy

Steady-state absorption spectra were measured with either a Cary 5000 UV–vis–NIR spectrophotometer (Agilent Technologies, Santa Clara, CA) or a Cary 60 UV–vis spectrophotometer (Agilent Technologies, Santa Clara, CA). Scans were typically obtained in 1 nm steps, with 0.1 s averaging time, and over a spectral range of 230–800 nm. For steady-state absorption measurements, concentrations of 1.5 μM were used. pH-dependent absorption measurements were obtained by lowering or raising the pH of the standard buffer (8.38) over the range of 3 to 9 pH by adding solutions of HCl and NaOH, respectively. To lower the pH in coarse and fine adjustments, 6 and 1.5 M HCl solutions, respectively, were prepared by dissolving the appropriate amount of 10 N HCl (RICCA Chemical, Arlington, TX) in ultrapure water and diluting as needed. To increase the pH, solutions of NaOH at the same concentrations were prepared by dissolving the appropriate amount of powdered NaOH (Fisher Scientific, Waltham, MA) in ultrapure water and diluting as needed. The adjustment of the standard buffer solution (i.e., pH = 8.38) was carried out by adding 1 mL increments of the HCl or NaOH solutions until the desired pH was reached. The pH of the solutions was measured after the addition of each 1 mL increment with a SevenCompact pH/Ion probe meter (Mettler Toledo, Columbus, OH).

Steady-State Fluorescence Emission and Excitation Spectroscopy

Steady-state fluorescence emission and excitation were measured for solutions of 1–3 using a Fluorolog-3 spectrofluorometer (Horiba Scientific, Irvine, CA). Sample solutions were diluted to an optical density below ∼0.1 in the spectral range of 550–750 nm. For fluorescence emission (excitation) measurements, an excitation (detection) wavelength of 600 (660) nm was used. Fluorescence emission spectra were corrected for the wavelength-dependent detection response using the correction curve provided by the vendor.

Fluorescence Quantum Yield Measurements

Fluorescence quantum yield (FQY) measurements were measured using a Fluorolog-3 spectrofluorometer (Horiba Scientific). A solution of a 26 base pair (per oligonucleotide) DNA-duplex tethered Cy5 monomer, which has been shown to exhibit an FQY of ∼0.29,⁷⁶ was used as a relative fluorescence standard. The signal intensity was optimized for maximum counts while staying within the linear range of the setup by varying spectrofluorometer parameters, such as slit width, for the brightest solution. In the measurements, the brightest solution was the solution of the DNA-duplex tethered Cy5 monomer. The spectrofluorometer parameters were maintained constant for corresponding measurements of solutions of 1–3. The FQY was calculated via:¹⁰⁰

where the subscripts unk and ref refer to the unknown solution and the reference solution, respectively. The Φ terms are the FQY of the solutions, the I terms are the integrated fluorescence emission intensities, the A^λ terms are the absorbance of the solution at the fluorescence excitation wavelength (λ), and the n terms are the refractive indices of the solutions.

Time-Correlated Single Photon Counting (TCSPC)

TCSPC measurements were undertaken using a FluoTime 250 TCSPC spectrometer (PicoQuant, Berlin, Germany). A pulsed picosecond laser excitation source of 660 nm was used, and a detection wavelength of 700 nm was chosen. The repetition rate of the excitation laser was optimized for each sample, ranging from 26 to 60 MHz. With this excitation source, the instrument response function (IRF) of the spectrometer has a full-width at half-maximum of ∼80 ps. The solutions were contained in a 1 cm path length quartz cuvette (Starna Cells, Atascadero, CA) and had an optical density below ∼0.1 at 660 nm.

Femtosecond Visible (VIS) and Near-Infrared (NIR) Transient Absorption (TA) Spectroscopy

Femtosecond TA measurements were performed using a Ti:sapphire-based regeneratively amplified laser system (Coherent, Santa Clara, CA) as a light source. The laser system produces a 1 kHz pulse train of ∼100 fs, ∼5 mJ pulses centered at ∼800 nm. Pump and probe beams were generated by placing a beamsplitter at the output of the femtosecond laser amplifier. Pump wavelength generation was accomplished by routing the pump beam into an optical parametric amplifier (Coherent, Santa Clara, CA). The pump beam and a second 800 nm beam were directed into a commercial transient absorption spectrometer (Ultrafast Systems, Sarasota, FL). After passing through the delay stage, either a VIS or NIR continuum was generated from the 800 nm fundamental of the amplifier (Section S3). Temporal overlap between pump and probe beams was controlled by varying the path length of the probe beam via an internal delay stage. Within the spectrometer, pump and probe beams were routed to and spatially overlapped at the sample position. Pump fluences for VIS TA measurements ranged from ∼80 to ∼100 μJ cm^–2, while pump fluences for NIR TA measurements ranged from ∼160 to ∼200 μJ cm^–2. The relative polarization between the pump and probe was oriented at the magic angle, i.e., ∼54.7°, at the sample position. The pump pulse duration was previously determined to be ∼230 fs.⁷⁹ Solutions were contained in a 2 mm path length quartz cuvette (Starna Cells, Atascadero, CA). A magnetic stir bar was included in the cuvette and stirred using a magnetic stirrer (Ultrafast Systems, Sarasota, FL) for the duration of the measurement. Optical densities of samples ranged from ∼0.05 to ∼0.3 at the excitation wavelength.

Results and Discussion

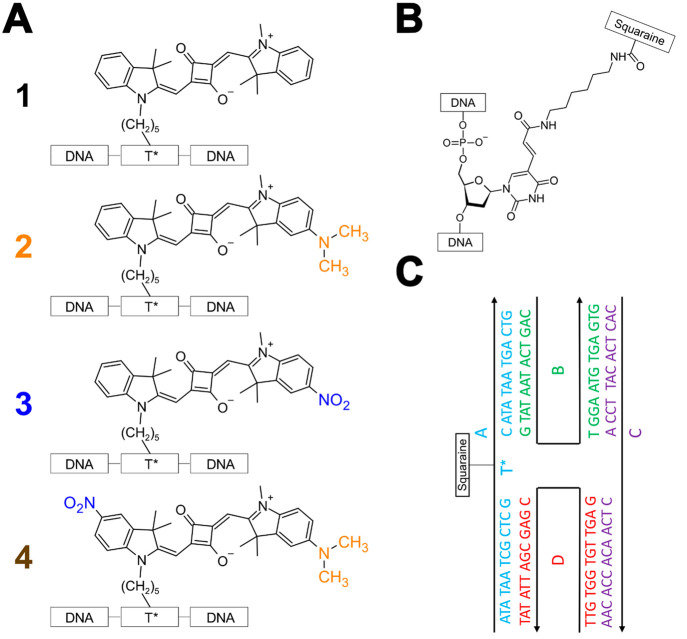
The indolenine-based squaraines at the focus of the study are shown in Figure 1A. Squaraine dyes, which are of great interest in nonlinear optics,^101−114 bioimaging,^109,113 sensing,^115−120 and supramolecular assembly,^5,121−126 were chosen due to their chemical tunability, structural stability, and large transition dipole moment amplitude.^{78,94,127−130} Unsubstituted symmetric squaraine 1 was used as a control. The synthesis and characterization of 1 has been reported previously.⁷⁸ To induce asymmetry, 1 was functionalized with dimethylamino and/or nitro groups that serve as strongly electron donating and electron withdrawing substituents, respectively. 2 and 3 feature electron donating and withdrawing substituents, respectively, on the indolenine ring opposite the linker to the DNA, while 4 features both substituents. Specifically, 4 features the electron withdrawing substituent on the indolenine ring on the side of the linker and the electron donating substituent on the indolenine ring on the side opposite the linker. Additional details of the synthesis and characterization of 2–4 are included in Section S1. Figure 1B displays the structure of the modified thymine linker used to incorporate the dyes into the oligonucleotide sequence. Figure 1C displays the “immobile” DNA HJ used as a scaffold to examine the electronic structure and excited-state dynamics of 1–4. Tethering 1–4 to DNA HJs is expected to suppress their aggregation (as is explained in further detail in Section S4) and permit characterization of their monomer photophysics. In the absence of such strategies, hydrophobic squaraines, such as 1,⁷⁸ are known to aggregate in aqueous solutions at concentrations as small as ∼1 μM.^131,132Section S5 describes how tethering the dyes to DNA in this manner is not expected to impact their intrinsic photophysics, largely because the dyes are expected to have appreciable conformational freedom.

Figure 1.

(A) Indolenine-based squaraines 1–4 at the focus of the study. 1 is unsubstituted symmetric squaraine, which is used as a control. 2 and 3 are functionalized with dimethylamino and nitro substituents, respectively, opposite the linker. 4is functionalized with a nitro substituent on the same side as the linker and a dimethylamino substituent on the side opposite the linker. To facilitate comparison between structures, the dimethylamino and nitro substituents are drawn in orange and blue, respectively. (B) Thymine base modified with a six-carbon linker (C6 dT) to incorporate dyes 1–4 into an oligonucleotide sequence. (C) Schematic representation of the “immobile” four-armed DNA Holliday junction (HJ) used as a scaffold to examine the electronic structure and excited-state dynamics of 1–4. The DNA HJ is composed of four oligonucleotide sequences labeled A, B, C, and D. 1–4 are incorporated into oligonucleotide A. The composition of each sequence, i.e., the nucleotides, are shown next to the black single-headed arrows. The black lines begin at the 5′ end and terminate at the 3′ end of the oligonucleotide, which is where the arrowhead is located.

The properties of 1–4 associated with their lowest-energy electronic transition, i.e., S₀ → S₁, were first characterized via theoretical calculations. As noted in the Introduction, large values of both the difference static dipole moment (Δd_theory) and the transition dipole moment (μ_theory) are needed to support entanglement in DNA-templated dye aggregate networks because of their role in the magnitude of K and J, respectively. Δd_theory and μ_theory were calculated via DFT and TD DFT. Table 1 shows that 1–4 exhibit a progressively increasing Δd_theory, which is as small as 0.26 D and as large as 2.15 D and in the order 1 < 2 < 3 < 4. These values are similar to the values of ∼2–3 D measured using electroabsorption (Stark) spectroscopy for seven distinct indolenine-based dicyanovinyl-substituted squaraine dyes synthesized by Würthner and co-workers and dissolved in dioxane;¹³³ it is noteworthy that, for these particular dyes, where the squarate moiety was functionalized,¹³⁴ Δd is orthogonal to μ (see, e.g., refs (125 and 133)). Δd_theory for 1–4 are also similar to the value of ∼1 D measured by Vauthey and co-workers for the matrix-field induced Δd in an aniline-based diethylamino-substituted squaraine dye embedded in polar and nonpolar polymers.¹³⁵ Additionally, Table 1 shows that 1–4 exhibit a large μ_theory of ∼15–16 D. Thus, μ_theory remains large even as Δd_theory is increased via the introduction of dimethylamino and/or nitro substituents. The trend in Δd_theory may be visualized by calculating electron density difference maps (EDDMs) for 1–4 (Figure 2). EDDMs depict the difference in electron density between initial and final states, i.e., how the electron density changes with photoexcitation. The EDDM of 1 shows that most of the change occurs near the center of the conjugated network. In contrast, the EDDMs of 2–4 show additional density change near the location of the electron donating and withdrawing substituents. As expected, a decrease and increase of electron density is observed when dimethylamino and nitro substituents, respectively, are present, and so, the EDDMs show that the spatial extent of the electron density difference varies in the order 1 < 2 < 3 < 4, which is consistent with the trend in Δd_theory.

Table 1. Theoretical Difference Static and Transition Dipole Moment Amplitudes of 1–4^a,b.

dye	Δdtheory (D)	μtheory (D)
1	0.26	14.7
2	0.67	15.2
3	1.83	15.3
4	2.15	15.9

^aFor 1, Δd and μ values were obtained from prior work.⁹⁴

^bThe theoretical difference static dipole moment (Δd_theory) and the transition dipole moment (μ_theory) were calculated via density functional theory and time-dependent density functional theory.

Figure 2.

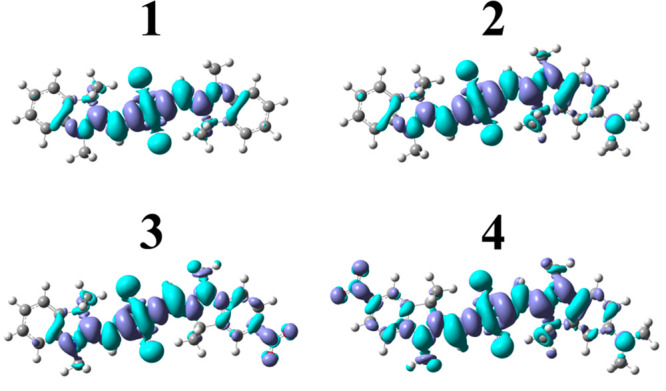
Calculated electron density difference density maps (EDDMs) for 1–4. Electron density differences are visualized at an isovalue of 0.0004 e^–/Bohr³. Regions of increased and decreased electron density are depicted in dark and light blue, respectively.

1–4 were subsequently characterized via steady-state absorption, fluorescence emission, and fluorescence excitation spectroscopy (Figure 3). The strongest absorption band of 1 peaks at ∼638 nm, and there is an additional vibronic absorption band evident at shorter wavelength peaking at ∼595 nm. The fluorescence emission spectrum, which exhibits mirror symmetry with respect to the absorption spectrum, features its most intense band at ∼650 nm along with an additional vibronic band appearing at longer wavelength and peaking at ∼710 nm. The Stokes shift of 1, defined as the difference in energy between the lowest-energy absorption and highest-energy emission bands, is ∼240 cm^–1. The Stokes shift reports on the energy lost by the system following photoexcitation, which can result from a combination of intra- and intermolecular processes. The values observed for 1 are generally consistent with those observed by Mass et al., who surveyed a series of six symmetrically substituted squaraines tethered to DNA.⁷⁸ Specifically, the authors observed the strongest absorption bands between 638 and 648 nm, the most intense fluorescence emission bands between 646 and 659 nm, and Stokes shifts ranging from ∼200 to 320 cm^–1.

Figure 3.

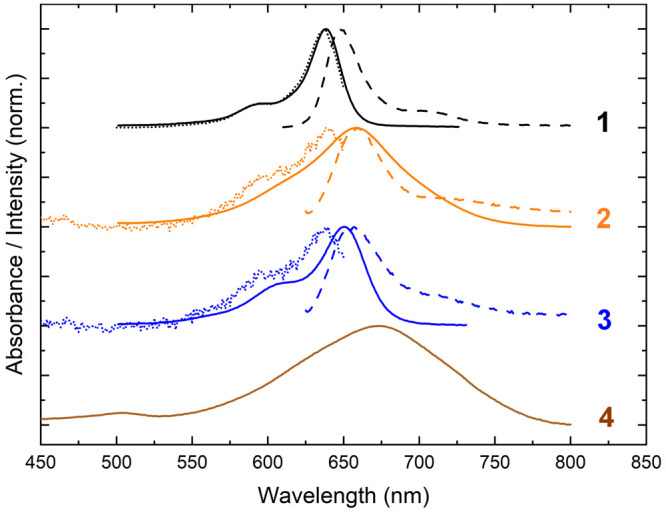
Steady-state absorption, fluorescence emission, and fluorescence excitation spectra of solutions of 1–4. Absorption spectra are shown with solid lines. Fluorescence emission (excitation) spectra are shown with dashed (dotted) lines and were obtained using an excitation (detection) wavelength of 600 (660) nm for 1–3. Due to weak fluorescence emission, it was not possible to measure the fluorescence emission and excitation spectra of 4. The concentration of the DNA–dye constructs for absorption and fluorescence spectroscopy was ∼1.3–1.5 and ∼0.2–0.4 μM, respectively.

The spectroscopic properties of asymmetric squaraines 2–4 deviate from the typical behavior exhibited by unsubstituted symmetric squaraine 1. The absorption spectra of 2 and 4 are red-shifted and significantly broadened relative to 1, with their strongest absorption bands at 658 and 672 nm, respectively. The absorption spectrum of 3 is red-shifted relative to 1, peaking at 650 nm with an additional vibronic band at 610 nm. 3 also exhibits broadened absorption bands relative to 1. Curiously, in the case of the squaraines including the dimethylamino substituent (2 and 4), the strongest absorption band is not the lowest-energy absorption band. Thus, the intensity of the vibronic progression is weighted more toward shorter-wavelength vibronic absorption bands, which indicates there is significant displacement between the ground and excited-state electronic potential energy surfaces for 2 and 4. In addition to the absorption spectra, the extinction spectra of 2–4 were measured and compared with the extinction spectrum of 1 (Section S6). Table 2 lists the maximum extinction coefficient (ε_max) and experimentally derived transition dipole moment amplitude (μ_exp) of 1–4. μ_exp was derived by integrating the extinction spectra plotted in units of cm^–1 (see, e.g., refs (136 and 137)). Interestingly, while ε_max varies in the order 1 > 2 > 3 > 4, all of the dyes exhibit a similar μ_exp of ∼11–12 D. As can be seen in the extinction spectra displayed in Section S6, this is because the integrated area of the extinction spectrum stays the same even though ε_max varies from ∼300 000 to ∼82 000 M^–1 cm^–1. Thus, μ_exp validates μ_theory; Δd_theory increases for 1–4, and both μ_theory and μ_exp are large.

Table 2. Maximum Extinction Coefficient and Experimentally Derived Transition Dipole Moment Amplitudes of 1–4^a.

dye	εmax (M–1 cm–1)	μexp (D)
1	300 000	11.9
2	180 000	12.3
3	110 000	11.2
4	82 000	11.5

^aThe experimental transition dipole moment (μ_exp) was calculated based on the integrated extinction spectrum (Section S6) as described in the literature^136,137 where the solvent refractive index was approximated to be that of water (1.3327).

Steady-state fluorescence excitation spectroscopy provides additional information on the homogeneous or heterogeneous nature of the solution. In the case of 1, the fluorescence excitation spectrum matches the absorption spectrum, which indicates the solution is homogeneous. That is, the solution consists of a single emitting species, whose absorption profile is represented in the steady-state absorption spectrum. In the case of 2 and 3, the fluorescence excitation spectra are blue-shifted compared with their corresponding absorption spectra. The fluorescence excitation and absorption spectra of 2 and 3 do not match, indicating that the solutions of 2 and 3 are heterogeneous. In the case of solutions of 2 and 3, the observations indicate that a large population of non- or weakly emissive dyes plays a primary role in the absorption properties of the solutions, whereas a small population of highly emissive dyes appears to dominate the fluorescence behavior.

One potential source of heterogeneity for 2 (and, by extension, 4) is that the dimethylamino substituent can exist in either a nonprotonated or protonated form. The nonprotonated form of the dimethylamino substituent has a lone pair of electrons on the nitrogen atom, which can be partially delocalized with the π-conjugated network and permit the dimethylamino group to adopt a trigonal planar geometry due to the sp²-hybridized nitrogen atom. In contrast, in the protonated form of the dimethylamino substituent, the lone pair of electrons is bound to a proton, which prevents its delocalization with the π-conjugated network and causes the dimethylamino group to adopt a tetrahedral out-of-plane geometry due to the sp³-hybridized nitrogen atom. To investigate whether the dimethylamino substituent exists in either nonprotonated or protonated forms in these solutions, absorption spectra were measured as a function of pH. Figure 4 displays the pH-dependent absorption spectra of a solution of 2. Above pH 5, 2 exhibits a broad, featureless absorption spectrum as displayed in Figure 3. At and below pH 5, 2 exhibits an absorption spectrum similar to 1, with a primary absorption peak at 635 nm and a vibronic shoulder at ∼590 nm. The absorption spectra exhibit a drastic change between pH 5 and 6, which is generally consistent with the pK_a of 5.2 expected for the protonated form of the dimethylamino substituent. This value for the pK_a is based on the pK_b of 8.8 of N,N-dimethylaniline measured at 25 °C (see, e.g., ref (138)) and the relationship between pK_a and pK_b, i.e., pK_a = 14 – pK_b. Based on these observations, the red-shifted, broadened absorption spectrum is assigned to the nonprotonated form of 2, whereas the more typical absorption spectrum (where the strongest absorption band is also the lowest energy absorption band) is assigned to the protonated form of 2.

Figure 4.

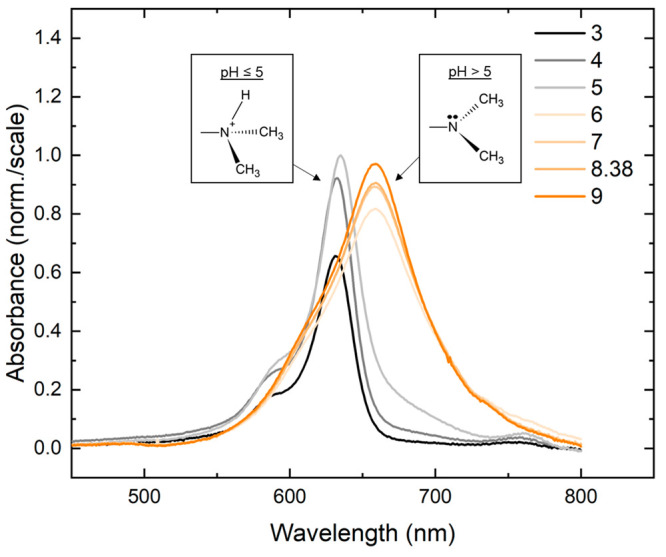
pH-dependent absorption spectra of solutions of 2. The pH was reduced and increased from 8.38, the standard pH of the buffer solution, by adding solutions of HCl or NaOH, respectively. At high pH, solutions of 2 exhibit a red-shifted and broadened absorption spectrum. At low pH, solutions of 2 exhibit an absorption spectrum typical of a dye monomer, i.e., similar to the absorption spectrum of 1. The inset displays schematics of the protonated and nonprotonated forms of the dimethylamino substituent at low and high pH, respectively. The concentration of the DNA–dye constructs was ∼1.4–1.7 μM.

The pH of the standard buffer sample was measured to be 8.38, which, assuming a pK_a of 5.2 for the protonated form of 2 and using the Henderson-Hasselbach equation, yields a non-negligible fraction of protonated dyes at 0.06%. To determine if these distinct subpopulations were present in the standard buffer sample, fluorescence excitation spectra were measured for solutions of 2 at a series of detection wavelengths. The detection wavelength-dependent fluorescence excitation spectra are presented in Figure 5. To characterize the entire absorption profile of the protonated and nonprotonated forms of 2, whose absorption profiles span the range of ∼525 to 750 nm (Figures 3 and 4), detection wavelengths from 695 to 760 nm were chosen for the measurements. At long detection wavelengths (above ∼740 nm), the fluorescence excitation spectrum largely matches the absorption spectrum of the nonprotonated form of 2. At shorter detection wavelengths, the fluorescence excitation spectrum more resembles the absorption spectrum of the protonated form of 2. Thus, the results indicate that the nonprotonated form of 2 and an emissive subpopulation, resembling the protonated form of 2, are present in standard buffer solutions of 2.

Figure 5.

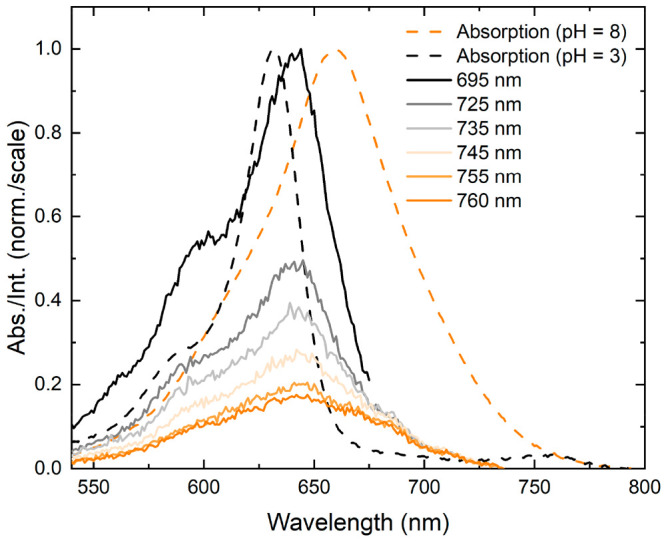
Detection wavelength-dependent fluorescence excitation spectra of solutions of 2. The fluorescence excitation spectra of solutions of 2 were collected at detection wavelengths spanning from 695 to 760 nm. The absorption spectra of a solution of 2 at pH 3 and at pH 8 are plotted as a dashed, black line and dashed, orange line, respectively. At short detection wavelengths, solutions of 2 exhibit behavior similar to the low pH solutions, and at long detection wavelength, solutions of 2 exhibit red-shifted, broadened excitation spectra characteristic of the high pH solution. The concentration of the DNA–dye constructs for absorption and fluorescence spectroscopy was ∼1.5 and ∼0.3 μM, respectively.

To evaluate the brightness of the different monomer solutions, relative fluorescence intensity measurements were performed. Figure 6 displays the relative fluorescence intensity of 1–3. As the figure shows, 1 exhibits the most intense fluorescence emission; thus, 1 is the brightest dye of the series. Thereafter, the fluorescence intensities follow the order I₁ ≫ I₂ > I₃. The results suggest that 2 and 3 exhibit increased nonradiative decay concomitant with dimethylamino and nitro substitution, respectively. To further evaluate the brightness of the different solutions, fluorescence quantum yield (FQY) measurements were performed using the prototypical cyanine dye Cy5 as a relative fluorescence quantum yield standard (Φ_F = 0.29; see, e.g., (67)). The FQYs of 1–3 are shown in Table 3 (and the fluorescence emission spectra used to calculate the FQYs are shown in Section S7). The FQY of 1, which is 0.24, is very similar to that of Cy5, indicating that 1 is a relatively bright dye. That is, radiative decay is able to effectively compete with nonradiative decay. As expected, the FQY of solutions of 2 and 3 vary in the order Φ₁ ≫ Φ₂ > Φ₃, with 2 and 3 exhibiting values of ∼10^–2 and 10^–3, respectively. Thus, as was concluded above, significant nonradiative decay pathways are introduced upon dimethylamino and nitro substitution.

Figure 6.

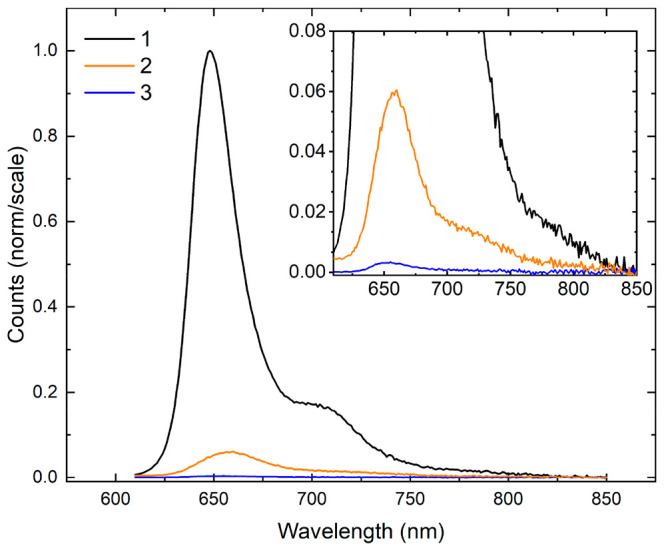
Relative fluorescence emission intensities of 1–3. The spectrum of 1 was normalized to its most intense emission feature, while the spectra of 2 and 3 were scaled using the normalization factor determined for 1. The inset displays a close-up of the relative fluorescence emission intensities of 2 and 3. The concentration of the DNA–dye constructs was ∼0.3 μM.

Table 3. Fluorescence Quantum Yield of 1–3^a.

dye	ΦF
1	0.24
2	10–2
3	10–3

^aThe fluorescence quantum yield (Φ_F) of 1–3 was determined using the cyanine dye Cy5 as a relative fluorescence quantum yield (FQY) standard (Φ_F = 0.29; see, e.g., ref (67)). Section S7 displays the steady-state fluorescence emission spectra used for the calculation.

To further investigate the nonradiative decay observed in the asymmetric squaraines, time-correlated single photon counting (TCSPC) measurements of 1–3 were performed. In TCSPC, the sample is excited with a picosecond pulsed laser and the amount of time between the excitation event and the detection of single emitted photons is measured. Figure 7 displays fluorescence decay traces obtained using excitation and detection wavelengths of 660 and 700 nm, respectively. The data and associated fits are depicted as open circles and solid lines, respectively. For 1, the fluorescence decay trace was well described by a single exponential function, yielding a lifetime of 2.4 ns. The fluorescence decay traces obtained for the asymmetric squaraines exhibited more complex profiles and, consistent with the relative fluorescence intensity and fluorescence quantum yield measurements, shorter lifetimes. The decay traces were well described by a biexponential decay function, with lifetimes and relative contributions given in Table 4. The shorter lifetime, which was instrument response limited (i.e., τ ≤ 80 ps), was associated with the larger amplitude (A₁ ≥ 0.95) for both 2 and 3. These decay components are assigned to the primary populations in the solutions. The second component, which exhibits a lifetime similar to 1, is assigned to a small subpopulation of long-lived dyes. In the case of 2, this subpopulation may originate, in part, from the protonated form of 2 (see, e.g., Figures 4 and 5).

Figure 7.

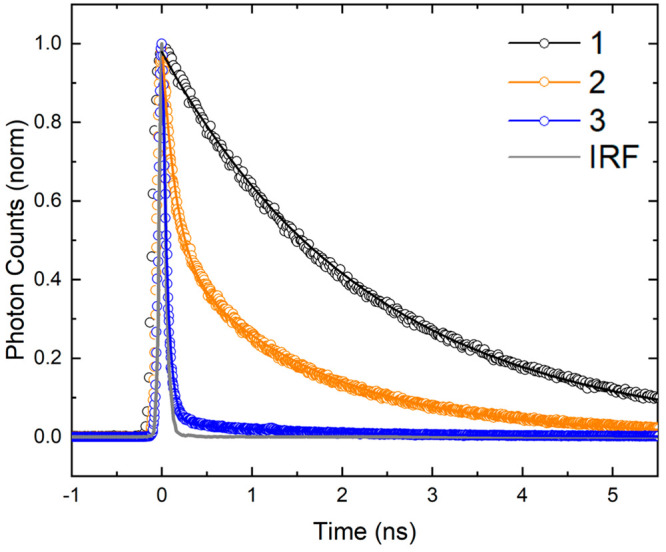
Time-correlated single photon counting characterization of solutions of 1–3. The solutions were excited at 660 nm, and fluorescence emission was detected at 700 nm. Open circles correspond to the experimental data, while the solid lines represent fits to the data. The fit for 1 was a single exponential function, while the fits for 2 and 3 were a biexponential function. In all cases, the exponential decay functions were convolved with the instrument response function (IRF). The IRF is shown in solid gray. The concentration of the DNA–dye constructs was ∼0.2 μM.

Table 4. Exponential Fitting Parameters for TCSPC Decay Kinetics of Solutions of 1–3^a.

dye	A1 (%)	τ1 (ns)	A2 (%)	τ2 (ns)
1		2.4
2	94.6	≤0.08	5.4	1.7
3	99.4	≤0.08	0.6	1.6

^aThe exponential fitting parameters include the lifetimes and amplitudes associated with each lifetime. The measurement of the short-lived lifetime of 2 and 3 was limited by the instrument response function, which was determined to be ∼80 ps. See Section S8 for further details of the analysis of the TCSPC decay kinetics.

The results of the TCSPC measurements are generally consistent with results of the FQY measurements. Specifically, the large FQY of solutions of 1, i.e., 0.24, is consistent with the solution being composed entirely of a long-lived, emissive population. The smaller FQY of solutions of 2, i.e., 10^–2, which is smaller by approximately an order-of-magnitude, is consistent with the presence of a large amplitude (i.e., 94.6%), short-lived, emissive population and a smaller amplitude (i.e., 5.4%), long-lived, emissive population. Lastly, the smallest FQY of solutions of 3, i.e., 10^–3, smaller than 2 by another order-of-magnitude, is consistent with an even larger amplitude (i.e., 99.4%), short-lived, emissive population and an even smaller amplitude (i.e., 0.6%), long-lived, emissive population. Thus, the TCSPC results confirm that significant nonradiative decay pathways are introduced upon dimethylamino and nitro substitution and additionally indicate that solutions of 2 and 3 contain small amounts of a long-lived, emissive population.

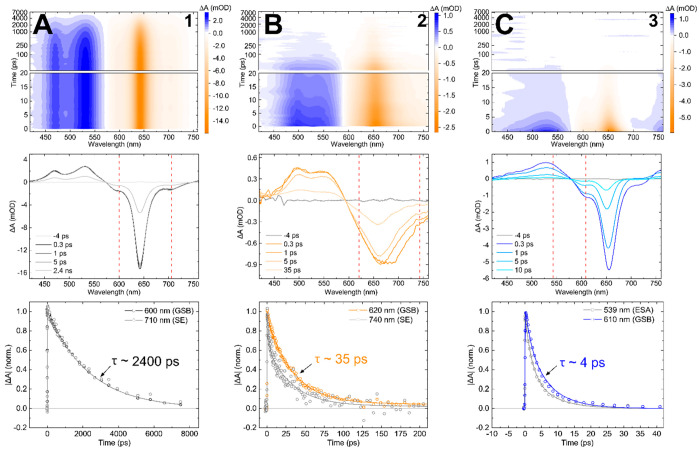
To gain additional insight into the excited-state dynamics of 1–3, femtosecond visible (VIS) transient absorption (TA) was employed. In femtosecond VIS TA, a narrowband pump pulse excites the constituents of the solution and a time-delayed, spectrally broadband probe pulse measures changes in the electronic structure. Figure 8 displays the femtosecond VIS TA of 1–3. The surface plot (top panel) of 1 shown in column A features long-lived, positive- and negative-going signals out to 7 ns. Selected TA spectra (middle panel) show distinct spectral features that undergo monotonic decay, as illustrated by the selected kinetic traces shown in the bottom panel. Based on the similar peak positions in the steady-state absorption and fluorescence spectra (Figure 3), the negative-going signals at ∼600, ∼650, and ∼720 nm bands observed in the selected spectra are assigned to ground-state bleach (GSB) features, a combination of GSB and stimulated emission (SE) features, and SE features, respectively. 1 also exhibits two positive-going bands at ∼470 and ∼530 nm that are assigned to excited-state absorption (ESA) features. The longevity of the TA signal of 1, which is evident from all panels in Figure 8A, is consistent with its high emissivity. Chowdhury et al. observed similar behavior for symmetric and highly emissive Cy5 and Cy5.5 monomers tethered to DNA HJs.⁷⁹

Figure 8.

Femtosecond visible transient absorption (TA) of 1, 2, and 3 collected with pump wavelengths of 640, 700, and 650 nm, respectively, at pump fluences of ∼80–100 μJ cm^–2. Columns A, B, and C plot the TA for 1, 2 and 3, respectively. The top row shows the TA surface plots for each dye, plotted with a linear time scale from 0 to 20 ps and a logarithmic time scale at time delays later than 20 ps. The middle row shows the TA spectra at selected time delays, and dashed red lines show the wavelengths of the selected kinetics. The bottom row shows the kinetics traces at selected probe wavelengths associated with different spectral features (i.e., excited-state absorption, stimulated emission, and ground-state bleach features). The plots of the kinetics traces include data, shown as open circles, along with fits, shown as solid lines, generated by performing a global target analysis on each data set. The concentration of the DNA–dye constructs was ∼1 μM.

In contrast to 1, the TA of 2 and 3 exhibits distinct excited-state dynamics (Figure 8B,C). The selected TA spectra of 2 and 3 exhibit negative-going signals that resemble their respective steady-state absorption spectra (Figure 3), where 2 has a broad band centered near ∼670 nm and 3 has a narrow band centered near ∼660 nm. Based on the similarity with the steady-state absorption spectra, these signals are assigned as GSB features. The selected TA spectra exhibit additional negative-going signals at ∼730 nm for 2 and at ∼710 nm for 3 at early time delays (i.e., 1 ps) that are assigned as SE features. Two broad, positive-going bands are observed at ∼490 and ∼580 nm for 2 and ∼460 and ∼530 nm for 3 that are assigned as ESA features. In stark contrast to 1, the TA of both 2 and 3 has largely decayed by 100 ps. Additionally, the selected kinetics of both 2 and 3 demonstrate different decay rates at different wavelengths, indicating that their excited-state dynamics may involve multiple steps.

To further characterize the excited-state dynamics of 1–3 and quantify their lifetimes, the femtosecond VIS TA was analyzed via global target analysis (GTA). GTA fits the time-resolved data at all wavelengths (i.e., globally) using time constants associated with the decay components of a targeted kinetic model.^139,140 The TA of solutions of 1 was modeled with a single-component kinetic scheme (Section S9), which yielded a time constant of ∼2.4 ns that is assigned to the excited-state lifetime of 1. This result is in excellent agreement with the TCSPC measurement (Figure 7 and Table 4). The TA of solutions of 2, measured at a pump wavelength of 700 nm to preferentially excite the nonprotonated form, is modeled by a sequential two-component kinetic scheme that yielded time constants of 4 and 32 ps (see, e.g., Table 5), which are assigned to the excited-state dynamics of the nonprotonated form of 2. When measuring at pump wavelengths of 650 nm where both forms of 2 are excited, a third time constant of 1.7 ns is observed that is assigned to the lifetime of a small subpopulation of long-lived dyes (see, e.g., Section S9). The TA of solutions of 3 was modeled using a three-component kinetic scheme, which yielded time constants of ≤300 fs and 4 ps, which are assigned to the excited-state dynamics of 3, while a third time constant of 1.6 ns was observed and assigned to a small contribution from a long-lived emission subpopulation. The shorter lifetime of 3 (i.e., ∼4 ps) compared with 2 (i.e., ∼30 ps) is consistent with the relative fluorescence intensity and FQY measurements (Figure 5 and Table 3). Furthermore, the short, picosecond lifetimes of 2 and 3 compared with the nanosecond lifetime of unsubstituted symmetric 1 reveal that both asymmetric dyes undergo rapid nonradiative decay to the ground state.

Table 5. Time Constants Derived via Global Target Analysis of Femtosecond Visible TA of Solutions of 1–3^a.

solution	λexc (nm)	τ1 (ps)	τ2 (ps)	τ3 (ps)
1	640	2400
2	700	4	32
2	650	3	35	1700
3	650	≤0.3	4	1600

^aDetails regarding global target analysis, including mathematical and physical justification for the number of components in the model, can be found in Section S9.

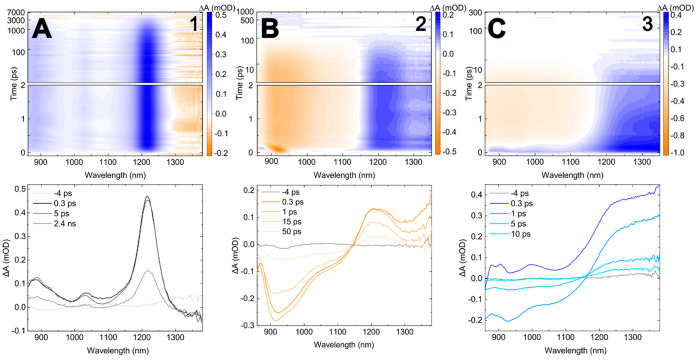
To further characterize the excited-state dynamics of the asymmetric squaraines, femtosecond near-infrared (NIR) TA measurements were performed. Femtosecond NIR TA measurements are advantageous because there are fewer overlapping signals in the NIR spectral range.^{79,80,141−143} Specifically, there are no overlapping GSB signals in the NIR spectral range because there is no steady-state absorption at these wavelengths (Figure 3); as such, key mechanistic insight can be gleaned. Figure 9 displays the femtosecond NIR TA of 1–3. The selected NIR TA spectra of 1 exhibit three distinct positive-going bands that are assigned to ESA features. Specifically, these ESA features are associated with a single electronic transition, where the primary (i.e., 0–0) band is at ∼1230 nm and higher-energy vibronic bands are at ∼1030 and ∼875 nm. The general profile of the NIR TA of 1 is consistent with the NIR TA of similar cyanine and squaraine rotaxane-based symmetric dyes.^79,80 In contrast to 1, the selected NIR TA spectra of 2 exhibit negative- and positive-going signals at wavelengths shorter and longer than ∼1150 nm, respectively. The negative-going signals are assigned to SE features, given that the absorption spectrum of 2 does not extend into the NIR. The positive-going signals are assigned to ESA features. Lastly, the NIR TA spectra of 3 at the earliest time delay (i.e., ∼100 fs) exhibit positive-going signals across the NIR range, similar to 1, which are assigned to ESA features. As the time delay increases, a negative-going signal grows in amplitude at wavelengths below ∼1150 nm at time delays prior to 1 ps. Similar to 2, the negative-going signal in 3 is assigned to a SE feature because 3 does not exhibit steady-state absorption in the NIR spectral range.

Figure 9.

Femtosecond near-infrared (NIR) transient absorption (TA) spectra of 1, 2, and 3 collected at pump wavelengths of 640, 700, and 650 nm, respectively, and pump fluences of ∼160–200 μJ cm^–2. Columns A, B, and C plot the NIR TA for 1, 2, and 3 respectively. The top row shows the TA surface plots, plotted on a linear time scale from 0 to 2 ps and a logarithmic time scale at delays longer than 2 ps. The bottom row shows selected TA spectra with time delays indicated in the legend. The concentration of the DNA–dye constructs was ∼1 μM.

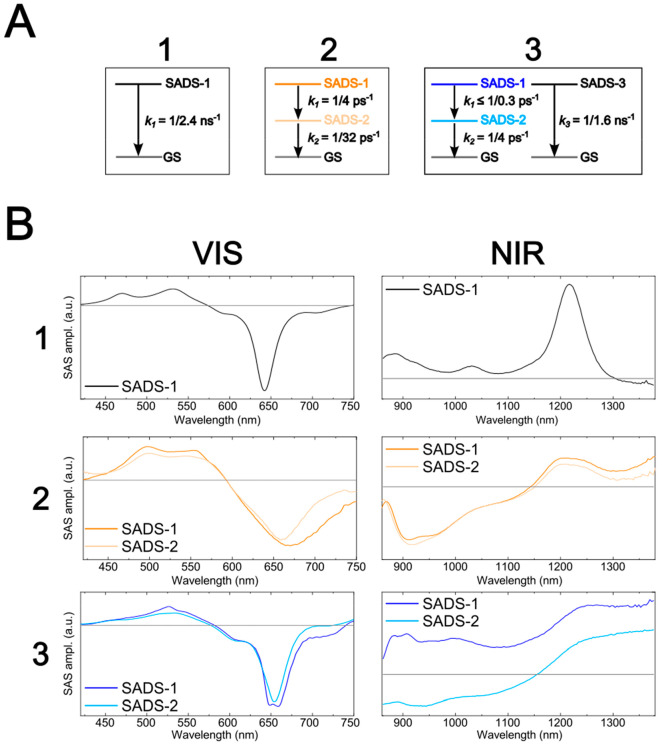
The femtosecond NIR TA measurements, in combination with the VIS TA measurements, provide key insights on the excited-state dynamics of the asymmetric squaraines. Physical interpretation of the dynamics can be facilitated via a GTA of the measurements. The kinetic schemes used for the GTA are based on those used for analyzing the VIS TA measurements (Figure 10A). Key to the analysis, species associated difference spectra (SADS) are generated for each population that contributes to the VIS and NIR TA. In the case of 1, Figure 10B shows that SADS-1 matches the VIS and NIR TA spectra displayed in Figures 8 and 9, respectively. In the case of 2 and 3, the VIS SADS-1 displays amplitude in the vicinity of their respective SE features at ∼730 nm, which is not present in VIS SADS-2. In the case of 2, NIR SADS-1 and SADS-2 do not exhibit considerable differences: both exhibit a broad SE feature below ∼1150 nm. Lastly, in the case of 3, there are distinct differences between NIR SADS-1 and SADS-2. Specifically, SADS-1 of 3 looks similar to SADS-1 of 1, which consists of only ESA features. In contrast, SADS-2 of 3 exhibits a broad SE feature below ∼1150 nm, which is more consistent with 2.

Figure 10.

(A) Kinetic schemes used to model the transient absorption (TA) of solutions of 1–3. The TA of solutions of 1, 2, and 3 was modeled according to a single-, two-, and three-component kinetic schemes, respectively. The two-component kinetic scheme used to model the TA of solutions of 2 involves a sequential transition of species associated difference spectrum (SADS)-1 into SADS-2 followed by the decay of SADS-2. The three-component kinetic scheme used to model the TA of solutions of 3 involves a sequential transition of SADS-1 into SADS-2 followed by the decay of SADS-2 along with a parallel decay of SADS-3. (B) The SADS of the TA of solutions of 1–3. The first column shows the VIS SADS, and the second column shows the NIR SADS. SADS-3 of solutions of 3, assigned to a small subpopulation of long-lived dyes, was omitted as it is not relevant to the excited-state dynamics of 3. Experiments were performed at pump wavelengths of 640, 700, and 650 nm for 1, 2, and 3, respectively.

The observations above are consistent with a mechanism in 2 and 3 where intramolecular charge transfer (ICT) is followed by rapid nonradiative decay to the ground state. For example, ICT is a process commonly observed in molecules with strong electron donating and withdrawing substituents where electron density is transferred between regions within the molecule following photoexcitation, particularly in polar solvents.¹⁴⁴ A prototypical example of such a molecule is 4-(N,N-dimethylamino)benzonitrile (DMABN), which is structurally similar to 2. Although certain details of the mechanism of ICT in DMABN are currently debated (i.e., several models involving different ICT conformations have been proposed to explain the excited-state dynamics^144−147), what is clear from these studies is that molecules that involve ICT exhibit dual-fluorescence behavior.^148−150 Specifically, dual fluorescence occurs when emission bands are observed in two distinct spectral regions: (i) at short wavelength, which is attributed to a locally excited (LE) state of the dye, and (ii) at long wavelength, which is attributed to an ICT state of the dye. (Another possible explanation of the observed dual fluorescence is excited-state proton transfer;¹⁵¹ however, this mechanism is ruled out for the nonprotonated form of 2 and for 3.) Clearly, there are many parallels with the dual-fluorescence behavior associated with ICT and the excited-state dynamics observed for 3. For example, the VIS and NIR TA (and SADS) shows clear signs of the loss and growth of SE on the few hundred femtosecond time scale in the VIS and NIR, respectively. Furthermore, at early times, the NIR TA (and SADS) of 3 exhibits broad ESA bands with peaks at ∼1230, ∼1030, and ∼900 nm, a profile strongly reminiscent to that of 1. This suggests that, following optical (i.e., vertical) excitation, 3 exhibits considerable LE character before transitioning to the ICT state. The dynamics of 2 can also be explained by the ICT model. Unlike in 3, the NIR SE band of 2 is present immediately following excitation. This observation is rationalized with an adiabatic representation of the excited-state wave function; strong coupling between the LE and ICT states results in a considerable admixture of ICT character in the overall excited-state wave function. As such, vertical excitation occurs to a state having considerably more ICT character than LE character. Following vertical excitation, a decay of the VIS SE band and growth of NIR SE band is observed in the VIS and NIR TA (and SADS) of 3 on the picosecond time scale. This is consistent with a decrease and increase of LE and ICT composition in the excited-state wave function, respectively, on a picosecond time scale concomitant with structural relaxation. Due to the presence of electron donating and withdrawing substituents, as well as the high polarity of the aqueous buffer in which the DNA-tethered asymmetric squaraine molecules are dissolved, it is therefore sensible to conclude that the excited-state dynamics of 2 and 3 involve ICT.

Perhaps the most striking observation related to 2 and 3 is that the ICT dynamics are followed by rapid relaxation to the ground state. To explain the rapid relaxation to the ground state, twisting motions of the indolenine rings on the periphery of the squaraine are invoked. Specifically, nonradiative decay rates are known to be considerably enhanced when the bonds of a π-conjugated network undergo twisting motions, which Turro et al. have described as the “free rotor” effect.⁸⁵ In molecular dyes subject to the “free rotor” effect, twisting motions of bonds along the π-conjugated network can raise and lower the energy of the ground adiabatic state and excited adiabatic state, respectively, such that rapid nonradiative decay mediated by nonadiabatic coupling can take place between the adiabatic states.^85,152 In these asymmetric squaraines, twisting motions of the dimethylamino/nitro groups and/or the indolenine rings may enhance the rate of internal conversion following ICT. In agreement with this interpretation, in a comprehensive survey of bis[4-(dimethylamino)phenyl]-substituted aniline-based squaraine and 18 of its derivatives, which are similar to 2, Law concluded that twisting motions of the aniline rings with respect to the squarate moiety mediated nonradiative decay of the ICT state.¹⁵³ Law’s conclusion was largely based on the observation that the FQY of ICT emission increased in solutions of squaraines featuring N-alkyl substituents of successively increasing length, where the presence of longer N-alkyl substituents was expected to reduce the rate of twisting motions. Law reached a similar conclusion in a comprehensive survey of 13 asymmetric aniline- and anisole-based squaraines,¹⁵⁴ and the same conclusion was independently made by Rettig and co-workers in a solvent- and temperature-dependent study of bis[4-(dimethylamino)phenyl]squaraine and its aza-crown-ether derivative.¹⁵⁵ Based on this interpretation, it is expected that minimizing twisting motions of rings peripheral to the squarate moiety in asymmetric squaraines may mitigate nonradiative decay and permit long excited-state lifetimes. For example, DeBoer and Schlessinger and subsequently Saltiel et al. were able to reduce the rate of internal conversion in derivatives of cis- and trans-stilbene, respectively, by structurally constraining the peripheral phenyl groups.^85,156,157 Thus, constraining twisting motions along the π-conjugated network of asymmetric dyes that undergo ICT may be a way to circumvent excited-state quenching while simultaneously increasing Δd.

Conclusions

In this work, the electronic structure and excited-state dynamics of a series of asymmetric indolenine-based squaraine monomers tethered to DNA were characterized in a polar solvent. Specifically, the asymmetric squaraine monomers were tethered to DNA HJs dissolved in an aqueous buffer. DFT and TD DFT calculations indicated that the addition of dimethylamino and nitro substituents to unsubstituted squaraine (1) successively increased Δd in the order 1 < 2 < 3 < 4, yet μ remained largely the same amplitude (in both theory and experiment). Relative fluorescence intensity, FQY, and TCSPC measurements indicated that 1 was highly emissive and exhibited a long excited-state lifetime. In contrast, the asymmetric squaraines exhibited less fluorescence emission and a shorter excited-state lifetime, indicating the presence of a significant nonradiative decay pathway. Femtosecond VIS and NIR TA measurements were undertaken to shed additional insight on the excited-state dynamics of the asymmetric squaraines. A GTA of the femtosecond VIS TA quantified the excited-state lifetimes of 1, 2, and 3, which were determined to be 2.4 ns, 35 ps, and 4 ps, respectively. Furthermore, the observation of the presence and growth of SE in the NIR and the simultaneous loss of SE in the VIS, i.e., dual fluorescence emission, suggests that the excited-state dynamics of the asymmetric squaraines involve ICT. Subsequent rapid nonradiative decay to the ground state is proposed to be mediated by twisting motions of the π-conjugated network of the asymmetric squaraines. Although new nonradiative decay pathways resulted in significant excited-state quenching (i.e., drastically reduced excited-state lifetimes), the addition of dimethylamino and nitro substituents increased Δd without adversely affecting μ, which is an important step toward achieving dye structures that simultaneously promote strong single- and bi-exciton interactions in molecular aggregates.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.2c06442.

• Additional details on squaraine synthesis and characterization, squaraine labeled and unlabeled DNA oligonucleotide sequences, femtosecond transient absorption probe continua spectra, extinction spectra, fluorescence quantum yield measurements, TCSPC decay kinetics analysis, and femtosecond transient absorption global target analysis (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Physical Chemistry of Quantum Information Science”.