Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 26;127(5):1264–1275. doi: 10.1021/acs.jpcb.2c07981

How Does Electronic Polarizability or Scaled-Charge Affect the Interfacial Properties of Room Temperature Ionic Liquids?

Sijia Chen 1, Gregory A Voth 1,*
PMCID: PMC9924258  PMID: 36701801

Abstract

graphic file with name jp2c07981_0009.jpg

The room temperature ionic liquid (RTIL) air–liquid interface plays an important role in many applications. Herein, we present molecular dynamics simulation results for the air–liquid interface of a common RTIL, 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl) imide, [C4mim][NTf2]. To elucidate the effects of electronic polarizability and scaled-charge ions on the properties of the RTIL air–liquid interface, we employ three different kinds of force fields: a nonpolarizable force field (FF) with united ion charges (FixQ), a nonpolarizable FF with scaled-charge by 0.8 (ScaleQ), and a polarizable FF (Drude). To identify whether the ions reside at the interface or not, the method of identification of the truly interfacial molecules is used. The structural and dynamical properties in the interfacial, subinterfacial, and central layers are evaluated. In general for bulk liquids, the FixQ model predicts too-ordered structures and too-sluggish dynamics, while the ScaleQ model can serve as a simple cure. However, the ScaleQ model cannot reproduce the results of the Drude model at the interface, due to an inappropriate scaled-down charge near the interface.

Introduction

Room temperature ionic liquids (RTILs) are a class of materials whose composition is solely made up of ions and primarily in the liquid state under ambient conditions. Unlike simple molten salts, the ions in RTILs are always bulky organic cations and polarizable inorganic or organic anions. The intrinsic asymmetry of the RTIL ions and complex interactions between them result in a wide range of different properties. However, they still share a number of properties, including excellent thermal stability, favorable organic and inorganic compound solvation behavior, negligible vapor pressure, and high selectivity, which makes them promising substitutes for traditional organic solvents.1,2 Given the large design possibilities of ionic liquids, there has been widespread interest in RTILs for many applications, like electrolytes in batteries, gas-capture media, reaction media in catalytic chemistry, etc.3−7 For example, ionic liquids are seen as promising candidates for capturing and separating greenhouse gases.8 A number of technologies for capturing CO2 have been developed during the past few decades, such as gas membrane separation and pressure swing absorption.9 However, most of them suffer from high energy consumption and may cause secondary pollution. On the other hand, considering the favorable physicochemical properties of RTILs, their high CO2 solubility, and especially their high designability, RTILs are seen as potential candidates for environment-friendly and cost-efficient CO2 capture media.8,10 In the process of capture and separation, the air–liquid interface plays an important role, as the chemical species needs to pass through the interface. Therefore, for this reason and a number of others, it is vital to understand the nature of the air/RTIL interface.

Recently, the structure of the air–liquid interface of ionic liquids has been investigated both computationally and experimentally.11−17 While many of these computational studies have using nonpolarizable force fields (FFs) with scaled-charge to improve the properties, the accuracy of the scaled-charge model remains an issue, especially for phase behavior and long-range ion–ion correlations.18,19 Moreover, a comprehensive benchmark for different FFs for predicting the interfacial properties of RTILs is still not available, and this is a goal of the present paper.

Previous studies in bulk liquid RTIL phases have found that while the fixed-charge model can predict accurate thermodynamic properties such as density and heat of vaporization, it fails to estimate the dynamical properties, for example self-diffusion coefficients and viscosities, which are always largely slower and higher, respectively, than the experimental values. By scaling down the atomic charges in the fixed-charge model to about 0.8 (aka the scaled-charge model), the sluggish dynamics can be resolved to some extent, and transport properties are improved compared to the results from the fixed-charge model while not increasing the computational cost compared to the classical fixed-charge model.20 However, the scaled-charge model has adverse effects on structural quantities, including lower liquid densities and lower heat of vaporization, and it does not improve the screening behavior and the dielectric response.19 By contrast, the polarizable FF can significantly improve thermodynamic and dynamical properties by explicitly considering the many-body interactions.21−23 There are different ways to implement polarizability effects, such as fluctuating charges,24 Drude oscillators,25 and induced point dipoles.26 Yan et al. were among the first to implement a polarizable FF for RTILs and demonstrated significant effects on their dynamics and interfacial properties.17,23 A detailed review has also recently been published on polarizable FFs for ionic liquids.21 Among these implementations, the Drude oscillator method is one of the most popular in the community and has been implemented in several molecular dynamics (MD) software packages, such as NAMD,27 LAMMPS,28 GROMACS,29 and OpenMM.30 While most of above models take the induced dipole interaction into account and often achieve success in simulating numerous systems, induced dipole models sometimes are not adequate to fully deal with the many-body interactions in more complex systems and may cause overpolarization.21 Therefore, there have recently been efforts to include higher-order induced moments in polarizable FFs, which enables better agreement between the polarizable FF and ab initio theory. A representative model among them is the AMOEBA–IL model,31,32 which considers up to the quadrupole (Q) term. In addition to the polarization effects, charge transfer may play a role in accurately simulating ILs.

Although there have been several popular polarizable FFs available for ionic liquids, many current studies still use nonpolarizable FFs, since they are more computationally efficient. In most cases, the polarizable FF is 5 to 10 times slower than the nonpolarizable FF. The accuracy of different kinds of FFs on RTIL interfacial properties has not been elucidated systematically. Although there have been some studies comparing different kinds of FFs, most of these comparisons are for bulk phases19 or IL mixtures33 instead of the liquid-vacuum interface.

To explicitly answer the above question on the physical accuracy of different FFs in predicting interfacial quantities, we examined several critical interfacial properties of [C4mim][NTf2], including surface tension, density profiles, survival time of interfacial ions, and the reorientation correlation function of ions, using three kinds of FFs: the fixed-charge model, the scaled-charge model, and the polarizable model. Our purpose is to analyze the behavior of different models on interfacial properties and also to determine if the ad hoc scaled-charge method can provide an acceptable alternative for polarizable FFs. While there are many FFs for ionic liquids, we choose to use the one developed by Canongia Lopes and Pádua (denoted here as CL&P), as it is one of the most popular, generic, and systematic FFs for ionic liquids.34 The fixed-charge model is the original CL&P FF, and the scaled-charge model was achieved by scaling down the atomic charges in the CL&P model by 0.8. Both CL&P model and its scaled-charge variant have been used widely to predict different RTIL properties.35−37 The polarizable FF we used in this study is the CL&Pol model, which is a polarizable successor to the CL&P model achieved by adding the polarization terms.38 The CL&Pol model implements the polarizability effect by the Drude oscillator, where Drude dipoles are formed by two harmonically coupled point charges of opposite sign, giving rise to an induced dipole when subject to an electric field. The CL&Pol model embodies a strategy in which researchers can transform the existing fixed-charge model into a polarizable model systematically and efficiently while keeping general applicability without the need for additional expensive first-principles calculations.

Most previous RTIL MD simulation studies have used the density profile as the criterion to distinguish the interfacial and bulk regions while assuming the interface is a steady flat plane. However, due to the intrinsic thermal fluctuations of the fluid interface, the instantaneous positions constantly change, which renders the above method more vague and inaccurate. To overcome such shortcomings, we instead used the method of identification of the truly interfacial molecules (ITIM),39 developed by Jedlovszky and co-workers, to probe interfacial ions and molecules. With the implementation of the ITIM analysis, we can categorize the ions into interfacial, subinterfacial, and central layers. There have also been a few previous papers applying the ITIM analysis to ionic liquid systems.12,40 In our present work, to elucidate how properties change in different layers and better compare results between FFs, our analysis is characterized by the layers, instead of an overall average value.

Methods

MD Simulations

The three FFs applied to predict interfacial properties are termed as follows:

  • FixQ: the original nonpolarizable CL&P model;34

  • ScaleQ: the CL&P model with all atomic charges scaled by a factor of 0.8;

  • Drude: polarizable CL&Pol model with the Drude oscillator.38

All MD simulations were performed in the LAMMPS MD software41 with the USER-DRUDE package. The initial configurations of the bulk phase simulation boxes for FixQ and ScaleQ models were generated by the FFTOOL42 and PACKMOL43 programs and contained 500/1000/1350 [C4mim][NTf2] ion pairs to form different thicknesses of the ionic liquid layer. The three different thicknesses are labeled as systems #1, #2, and #3, respectively. For each FF, all three systems (thicknesses) are simulated to investigate whether the thickness of the ionic liquid layer affects the properties. First, each simulation box was equilibrated under a constant NPT ensemble for 10 ns to converge the density, with a Nosé–Hoover thermostat and barostat to control the simulation temperature at 300 K and pressure at 1 atm, with update frequencies of 100 and 1000 fs, respectively. Then, the surface normal direction was elongated, so the ionic liquid slab occupied the middle with two vacuum phases above and below it, achieving two equivalent air–liquid interfaces. Next, the simulation box was re-equilibrated under a constant NVT ensemble for another 10 ns. Finally, the MD production run of 15 ns for FixQ and ScaleQ models was carried out. For the polarizable Drude model, we first took the final configuration of FixQ’s NPT equilibration step and polarized it with the POLARIZER44 tool. The equilibration process for the Drude model is similar to that of the FixQ and ScaleQ models but using the temperature-grouped dual-Nosé–Hoover (TGNH)45 thermostat (and barostat) in a constant NVT (or NPT) ensemble, with the relative motion of Drude particles (DPs) with respect to their Drude cores (DCs) regulated at a temperature of 1 K. The production runs for the Drude model were 10 ns. The final box size and liquid phase size are shown in Table 1. A representative snapshot of the MD simulation system is shown in Figure 1.

Table 1. Simulation Box Sizes and Liquid Phase Thicknesses Studied in This Paper.

System # Number of Ion Pairs Box dimensions (Å × Å × Å) Liquid Phase Thickness (Å)a Vacuum Phase Thickness (Å)
1 500 80.0 × 80.0 × 160.0 ∼40.0 ∼120.0
2 1000 78.3 × 78.3 × 200.0 ∼78.5 ∼121.5
3 1350 60.0 × 60.0 × 500.0 ∼190.0 ∼310.0
Open in a new tab
a

The thicknesses for different models with the same number of ion pairs have slight differences, due to the different densities of bulk phases. The values here are used for reference only.

Figure 1.

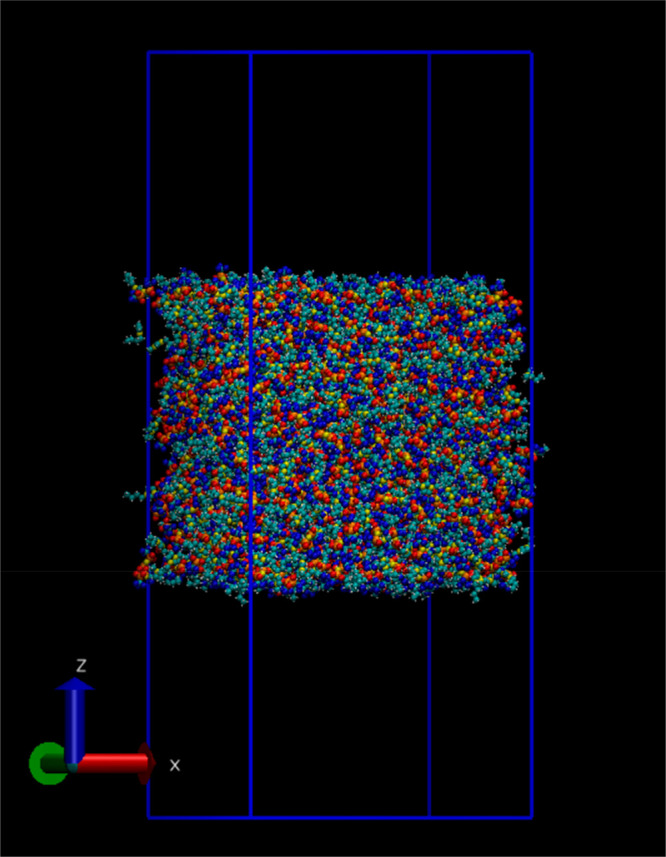
Figure 1

Open in a new tab

A representative MD simulation snapshot of the vacuum-liquid interface system of a typical room temperature ionic liquid (RTIL), 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([C4mim][NTf2]). The liquid phase thickness is about 80 Å, and the overall dimension of the simulation box is 78.3 × 78.3 × 200.0 Å.

The cutoff distance was set to 15 Å for both the Lennard-Jones and Coulombic interactions. Long-range Coulombic interactions were computed using a particle–particle particle-mesh (PPPM) solver with a cutoff precision of 10–5. The SHAKE algorithm was used to constrain bonds terminating in hydrogen atoms. The MD time step was 1 fs. For the Drude model, the mass of DPs was set at 0.4 g mol–1, and their charge was calculated based on their atomic polarizability. The Thole damping function46 was employed to reduce the Coulombic interactions at the short-range and avoid the “polarization catastrophe”.

ITIM Method

Most previous studies of the air–liquid interfacial properties determined the interfacial molecules by calculating the distance of the molecule to the Gibbs dividing interface. However, this method is ambiguous and relies largely on a preknowledge of the size of the molecules, which might be inaccurate, especially for asymmetric molecules and ions. To unambiguously detect the molecules that are truly located at the interface, as noted earlier Jedlovszky and co-workers have proposed a new method called identification of the truly interfacial molecules (ITIM).39 Here we provide a brief introduction to the ITIM method. By moving a fictitious probe sphere of a given radius along straight lines parallel to the surface normal from the vacuum phase to the liquid phase, we can identify interfacial atoms/molecules. Once a fictitious probe sphere touches the first actual atom, it stops, and the atom is marked as an interfacial atom. In this study, our focus is the interfacial cations and anions other than a single atom; therefore, the cation or anion to which the touched atom belongs will be marked as interfacial. Once all test lines have been traversed, we obtain a full list of the truly interfacial cations and anions. We can then identify the subinterfacial cations and anions by excluding already identified cations and anions and repeating the above procedure. Following the suggestion of Jedlovszky and co-workers,47 the size of atoms was approximated by their LJ parameters, and the radius of the fictitious probe sphere was set to 2 Å. The test lines were spaced 1.0 Å in the x and y directions. Using the above method, we determined the interfacial and subinterfacial cations and anions, termed as interfacial and subinterfacial layers, respectively. The rest of the cations and anions are labeled as the central layers.

Results and Discussion

Density Profile

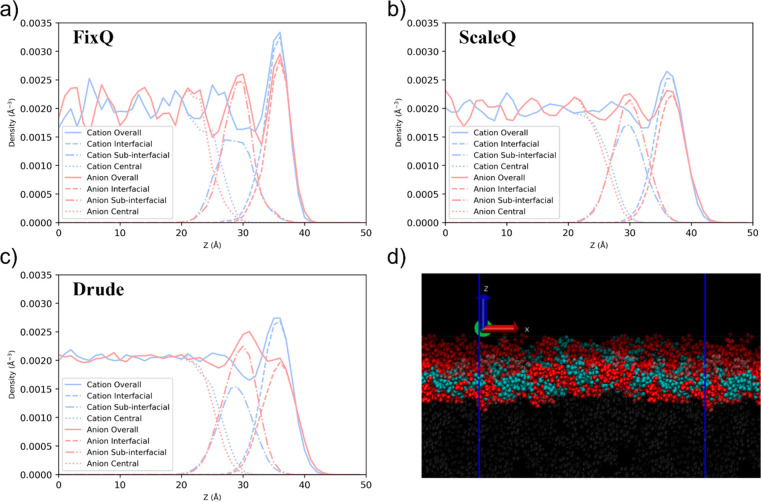
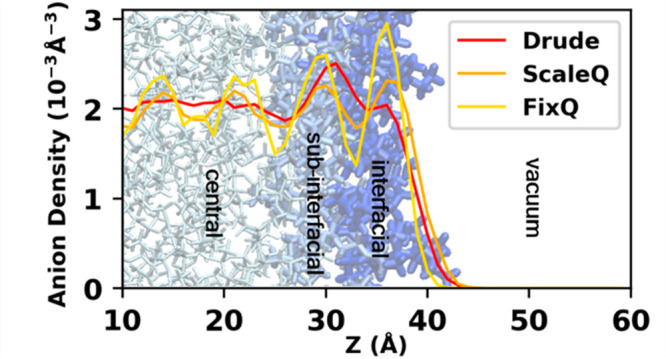
The number density profiles for the center of mass (COM) of cations and anions using different models are shown in Figure 2(a–c). The density profiles are computed by dividing the simulation boxes into slabs of width of 1 Å along the interface normal direction, namely the z-direction, to characterize the density behavior with respect to the interface normal, with the COM of the ionic liquid layer located at z = 0 Å. For clarity while not losing generality, only density profiles for system # 2 are shown here, and those for other systems can be found in the Supporting Information. Overall, the density shows strong oscillations for all three models, which extends to more than 40 Å. However, the oscillation intensity is different: while the FixQ model predicts the strongest fluctuation, the oscillation predicted by the Drude model is almost negligible in the central layer, and the ScaleQ model’s prediction is quite close to that of FixQ. The density oscillation directly results from the strong Coulombic interaction and hydrophobic effect. The FixQ model always overestimates the Coulombic interaction due to the neglect of the polarization effect. Although the ScaleQ model can mimic the polarization effect to some extent by scaling down the atomic charge, the polarization effect is more complicated. Nakajima et al.48 have compared the density profile predicted by a scaled-charge model with the experimental data by high-resolution Rutherford backscattering spectroscopy (HRBS). Their study shows that the simulation profiles show more pronounced structures than experiment. Although the scaled-charge model used in their paper is not exactly the same as the ScaleQ model used in this study, the tendency of predicting an overstructured system is often the case for a scaled-charge model. By contrast, the Drude model provides a more reasonable density profile for the ionic liquid.

Figure 2.

Figure 2

Open in a new tab

Number density profiles for the center of mass (COM) of cations and anions using (a) FixQ, (b) ScaleQ, and (c) Drude models for the [C4mim][NTf2], with a liquid phase thickness of 80 Å. The center of mass of the ionic liquid layer is located at z = 0 Å. The solid lines represent the overall density profiles of all ions, dashed lines for only interfacial ions, dash-dot lines for only subinterfacial ions, and dot lines for only central layer ions. Panel (d) shows a representative MD simulation snapshot. Transparent red and cyan space-filling models represent interfacial cations and anions, respectively, while solid red and cyan space-filling models represent subinterfacial cations and anions, respectively. Central ions are shown with transparent gray space-filling models.

Except for the density oscillation intensity, there are some other differences in the interfacial and subinterfacial layers. It can be clearly seen that all three models predict an enhanced density of cations at the interface. The highest density of cation at the interface using the FixQ model is higher than that using the ScaleQ or Drude model, ∼0.0034 vs ∼0.0027 Å–3. However, the behavior of the anion is quite different when using the three models. While the FixQ model predicts a higher density of the interfacial anions than that of the subinterfacial anions, the Drude model predicts that the anion achieves its highest density in the subinterfacial layer, and the interfacial density is even slightly lower than its bulk density. The ScaleQ model predicts a behavior somewhere between the previous two conditions.

Despite the ScaleQ model resolving the rigidity of cations at the interface to some extent, it still cannot predict a density profile of interfacial anions similar to that of the Drude model, which could lead to other different predictions of interfacial properties, which will be discussed later.

Orientational Preference

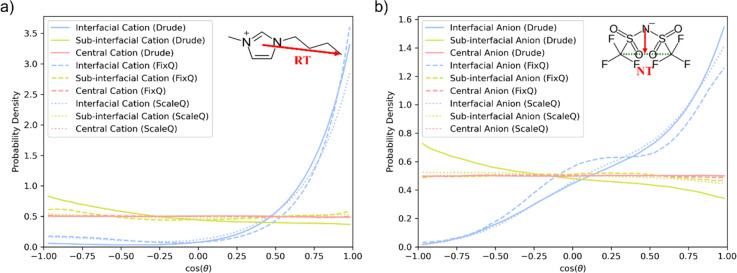
To characterize the orientational preference of the cations and anions in different layers, we defined two vectors: one for the cation, from the cation ring to terminating carbon (RT), and the other for the anion, from the anion nitrogen to the center of terminating carbons (NT), as shown in the inset panels of Figure 3(a,b), respectively. The probability density distribution of the angle between the vector RT/NT and the interface normal is calculated, as shown in Figure 3. Obviously, the vectors RT in the interfacial layer all show a large tendency to be perpendicular to the surface normal, which means that cations prefer to protrude their alkyl chains from the liquid to the vacuum phase and hide their charged head inside the liquid phase.17 This observation coincides with previous experimental results.49,50 The condition for an anion in the interfacial layer is akin to that of a cation, with one exception of the higher probability density near cos θ = 0 for the FixQ model. Considering the different conformations of the anion, trans or cis, the enhanced probability density near cos θ = 0 may be caused by a higher percentage of the trans-conformer of the anion in the FixQ simulation. Although the cis conformer is energetically unfavorable in the bulk phase,51 the surface energy can be lowered by exposing both CF3 groups to the vacuum. Nakajima et al.52 employed HRBS to study the surface structure of [Cxmim][NTf2] (x = 2, 4, 6) for the anion and found that the dominant configuration was the cis conformer for x = 2 and 4. However, if the oxygen atom in the [NTf2] is bonded to the hydrogen of the C2 carbon atom of the imidazolium ring, [NTf2] cannot have its CF3 group protrude into the vacuum and stays as the trans-conformer. Therefore, the possible reason for the higher percentage of the trans-conformer in the FixQ model is the strong hydrogen bond between the cation and the anion.

Figure 3.

Figure 3

Open in a new tab

Probability density distribution of cos(θ) in interfacial, subinterfacial, and central layers, where θ is the angle between a given vector (defined in the inserted panel) and the interface normal, for (a) a cation and (b) anion, respectively.

Within the subinterfacial layer, the Drude model predicts a slight orientational preference for cations and anions, which is seen in neither the FixQ nor ScaleQ models. This interesting phenomenon can be explained by the net charges of each layer with different models, as shown in Table 2. The net charges of a given layers are calculated by (1) integrating the density profiles of cations and anions in the layer, respectively, which gives the number of cations and anions in the layer, and (2) subtracting the number of anions from the number of cations. Although the Drude model predicts a lower overall density for the interfacial layer and subinterfacial layers than both FixQ and ScaleQ models, the absolute values of net charges of the interfacial layer and subinterfacial layers predicted by the Drude model are higher than those predicted by the FixQ model, by about 50% for the interfacial layer and 60% for the subinterfacial layer. The higher values of the Drude model are direct results of the enhanced cation density at the interface and the highest anion density at the subinterface. Although induced dipoles can screen part of the Coulombic interactions, the unscreened part may lead to the cations and anions reorienting their charged heads, forming a polar region between the interfacial and subinterfacial layer. It is an unusual phenomenon that the Drude model predicts an overall lower interfacial density but a higher net charge near the interface, which can significantly impact electrolyte properties, like electrical double layer (EDL) capacitance.

Table 2. Net Charges of the Interfacial and Subinterfacial Layers Using Different Force Fields.

Net Charge (e) Interfacial Layer Subinterfacial Layer
FixQ model +28.7 ± 2.4 –34.6 ± 3.6
ScaleQ model +21.0 ± 1.5 –26.5 ± 1.8
Drude model +41.3 ± 1.9 –56.5 ± 1.8
Open in a new tab

2D Radial Distribution Functions

To further investigate the structural properties of the interfacial layers, we computed the 2D radial distribution function (RDF)53 between ions’ COMs:

graphic file with name jp2c07981_m001.jpg 1

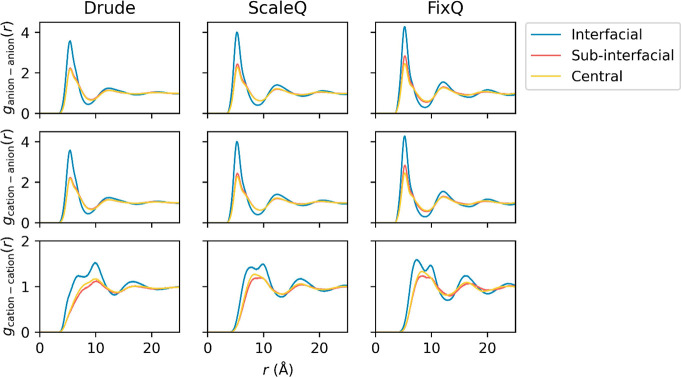
where Δz = 1 Å, ρregion is the average number density in each region, and rij is the 2D center-of-mass (COM) distance perpendicular to the interface normal between the ith and jth ions. Figure 3 shows the COM 2D RDF between anion–anion, cation–anion, and cation–cation in different layers using the three models. Obviously, a higher first peak always appears in the interfacial region than in other regions, no matter the model used. Since the coordination numbers of ions in the interfacial layer are much lower than those in other layers, the high first peak demonstrates that each ion tends to keep a similar coordination number to that in the bulk phase, by forming a local cluster.

In general, peaks in the FixQ’s 2D RDFs are more pronounced, which indicates a more ordered, crystal-like structure. This observation is due to the intrinsic overestimated electrostatic interaction in the FixQ model. While the ScaleQ model does predict less ordered structures than the FixQ model, one should note that the peaks of the ScaleQ model are still higher than the polarizable Drude results. This phenomenon illustrates that the ScaleQ model cannot fully address the many-body polarization effects. The closer to the interface, the more different the 2D RDF of the ScaleQ model is that from the Drude model.

Another interesting phenomenon seen in the 2D RDFs is that the first peak in the gcation–cation(r) splits into two peaks in the interfacial layer. The two dominant orientations for cations at the interface are (I) the imidazolium ring is normal to the surface with the alkyl chain perpendicular to the surface as well; (II) the ring is parallel to the surface with the alkyl chain perpendicular to the surface. When we look at the probability density distribution of the angle between the imidazolium ring normal and the surface normal (Figure 5), we can see that the Drude model predicts a much higher possibility for the imidazolium ring to be parallel to the surface, which also coincides with experiment.50 When the ring is parallel to the surface, the crossing area of the cation increases, and the peak of the 2D RDF shifts to a higher value. Therefore, the reason why the first peak split is from the two different ring orientations, with orientation I for the first subpeak and orientation II for the second subpeak.

Figure 5.

Figure 5

Open in a new tab

Probability density distribution of cos(θ) in the interfacial layer, where θ is the angle between the imidazolium ring normal and the surface normal.

Figure 4.

Figure 4

Open in a new tab

2D radial distribution functions (RDFs) of the center of mass (COM) between cations and anions. The top, center, and bottom rows are anion–anion, cation–anion, and cation–cation 2D RDFs, respectively. The left, center, and right columns are 2D RDFs using the Drude, ScaleQ, and FixQ models, respectively.

Surface Tension

Another important interfacial property is the surface tension, which is given by

graphic file with name jp2c07981_m002.jpg 2

where Πxx, Πyy, and Πzz are the principal components of the pressure tensor, Lz is the length of the simulation box along the interface normal, and 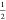Inline graphic comes from the fact that there are two equivalent vacuum-liquid interfaces in a simulation box. The surface tensions calculated by three models for different liquid phase thicknesses are shown in Figure 5. Considering the error bars, we can conclude that the thickness of the RTIL layer has no impact on the surface tension, at least for the studied length scales. The surface tension predicted by the FixQ, ScaleQ, and Drude models is 43.0, 37.8, and 25.4 mN/m (the averages of all three layer thicknesses’ data), respectively, while the experimental value is about 31.5 mN/m.54 Obviously, none of the three models can completely accurately predict the surface tension, as they all differ from the experimental value. While the FixQ model overestimates the surface tension by 36%, the ScaleQ model significantly improves it by 16.5% (overestimating it by 20%). By contrast, the Drude model underestimates the surface tension by 19.4%. In fact, it is often the case that a polarizable force field will predict a “softer” interface and “faster” dynamics than experiments, which will be discussed later. This result points to the possibility that a more accurate polarizable model may require a different and continuously adjusted effective many-body polarizability as the ions approach the interface, as one would expect from quantum electronic structure considerations.

Residence Time of Interfacial Ions

In addition to the structural properties of the interfacial layers, the way in which dynamical properties change within different layers is also vital. The first question one may ask about the dynamics of interfacial ions is how long can a cation or anion stay in the same layer? To answer such a question, we first find the survival probability L(t) of an ion in the interfacial and subinterfacial layer, which is the probability that an ion in a given layer at a time t0 remains in the layer at the time t0 + t. A representative survival probability as a function of time is shown in Figure 6. We find that L(t) is well-described by a biexponential function

graphic file with name jp2c07981_m004.jpg 3

where t is time, and τ1 and τ2 are the characteristic correlation times. Then we can evaluate the residence time by integrating the survival probability function L(t), given by

graphic file with name jp2c07981_m005.jpg 4

A summary of residence times in the interfacial and subinterfacial layers using the different models is listed in Table 3. Since the system’s thickness does not influence the interfacial properties, the values are averaged over the three systems (thicknesses). The individual value for each system can be found in the Supporting Information. For all three model results, the residence time of the ions in the interfacial layer is much longer than that in the subinterfacial layer. The ratio of residence times in the interfacial and subinterfacial layer for the cation, TCatInt/TCat, is 6.26, 4.48, and 5.55, for the FixQ, ScaleQ, and Drude models, respectively. The ratio for the anion, TAnInt/TAn, is 1.65, 2.19, and 1.96. The longer residence time can be partly explained by the available exit pathways: in the case of interfacial ions, they can only exit to the subinterfacial layer, while in the case of the subinterfacial layer, they can exit to either the interfacial layer or the central layer. Other influencing factors, like diffusion and reorientation dynamics, can contribute to such behavior as well.

Figure 6.

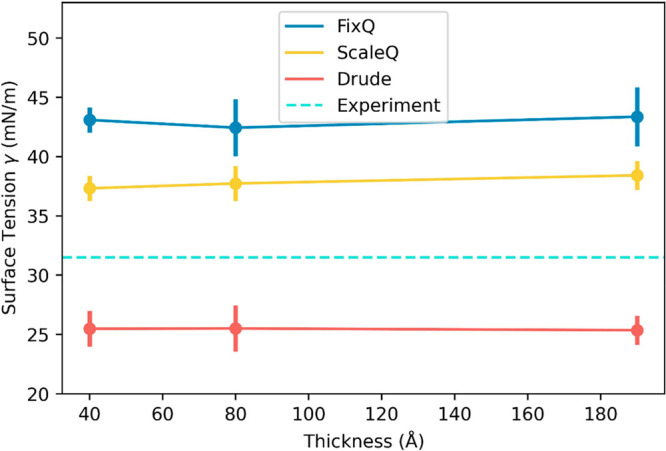
Figure 6

Open in a new tab

Surface tensions of different layer thicknesses using three models. The light blue dashed line shows the experimental data54 for reference.

Table 3. Residence Time of Cations and Anions in the Interfacial and Subinterfacial Layers Using the FixQ, ScaleQ, and Drude Models.

Residence Time (ns) Cation Interfacial Cation Subinterfacial Anion Interfacial Anion Subinterfacial
FixQ 37.1 ± 5.7 5.92 ± 0.86 22.6 ± 3.0 13.7 ± 1.9
ScaleQ 5.26 ± 0.36 1.17 ± 0.08 5.18 ± 0.37 2.37 ± 0.25
Drude 4.57 ± 0.28 0.824 ± 0.038 3.24 ± 0.22 1.65 ± 0.09
Open in a new tab

As is evident from Table 3, the FixQ model predicts considerably longer residence times for interfacial and subinterfacial cations and anions than the other two models. For example, the residence times of interfacial cations are about 37, 5.3, and 4.6 ns for the FixQ, ScaleQ, and Drude models, respectively. It is noteworthy that the ScaleQ model improves the dynamics compared to the FixQ model, as indicated by the decreasing residence time. However, the improvement for cations and anions is different, especially for interfacial ions. While the ratio of the residence time of interfacial cations and anions is 1.64 and 1.41 using the FixQ and Drude models, the ratio using the ScaleQ model is 1.01. The relative dynamics of interfacial cations and anions using the ScaleQ model differs from the other two models. The unique behavior predicted by the ScaleQ model can be that of either the increased kinetics of the cation being too high or the increased kinetics of the anion is too low. This difference is a direct result of the scaled-charge. The ScaleQ model assumes that one can inexplicitly account for the charge transfer and many-body polarization effects by scaling down the atomic charges. However, such effects do not identically impact the dynamical properties of cations and anions, especially when the ions are close to the interface. When an ion comes close to the interface, the total number of the surrounding ions becomes less, which leads to weakening electronic polarization effects. But the scaled-charge remains the same, which may cause an overestimation of the many-body polarization effects. The unphysical behavior of scaled-charges near the interface can lead to an incorrect prediction of the interfacial properties, such as the residence time.

Reorientation Correlation Time

The reorientation correlation functions of cations and anions were evaluated to characterize the reorientation dynamics in the interfacial, subinterfacial, and central layers. The correlation function is defined as

graphic file with name jp2c07981_m006.jpg 5

where ei stands for a unit vector in the direction of the RT vector on the ith cation or the NT vector on the ith anion, as depicted in Figure 3. The correlation function can be well-fit by a triexponential function

graphic file with name jp2c07981_m007.jpg 6

The correlation time T is obtained by integrating the correlation functions,

graphic file with name jp2c07981_m008.jpg 7

and these are shown in Tables 4 and 5 for cations and anions, respectively. Due to the strong orientational preference of the cations at the interface, it is not surprising that the correlation time for the cations in the interfacial layer is always longer than that of the central layers, no matter what model is used. The strong tendency of the alkyl tails protruding into the vacuum and keeping a highly ordered structure in the interfacial layer greatly slows down the rotational dynamics compared to that in the liquid phase. However, the situations are different for cations in the subinterfacial layer. In the case of the cation, while the Drude model predicts a slightly higher correlation time of the subinterfacial layer than the central layer, both FixQ and ScaleQ models predict a lower correlation time of the subinterfacial layer than the central layer, which is indicated by the values of T(sub)/T(central) being above or below 1. In most cases, reorientation dynamics in the subinterfacial layer depends primarily on the available free volume required to permit a vector rotation. Considering the density profiles of the three models, we find that the density of anions in the subinterfacial layer predicted by the Drude model is considerably higher than that predicted by the other two models, which indicates a lower free volume for the cation vector to reorientate in the case of the Drude model. Also, recalling the orientational preference of cations in the subinterfacial layer, we find that cations using the Drude model show a slightly higher orientational preference than the other two models. Such a preference also slightly prevents the cation vector from orientating. The low free volume for the reorientation of the cation’s vector, together with the orientational preference, ultimately results in a higher correlation time for cations in the subinterfacial layer. For anions, the situation is similar, but T(Sub)/T(Central) is always below 1. Considering the smaller volume needed for the anion vector to reorientate and the lower density of cations in the subinterfacial layer, which indicates a higher free volume for the anions, it is reasonable that T(Sub)/T(Central) is always less than 1, even for the Drude model.

Table 4. Reorientation Correlation Time of Cations in Interfacial, Subinterfacial, and Central Layers Using the FixQ, ScaleQ, and Drude Models.

Cation Reorientation Correlation Time (ns) Interfacial Layer Subinterfacial Layer Central Layer T(Sub)/T(Central)
FixQ 4.61 ± 0.10 2.53 ± 0.60 3.34 ± 0.23 0.756
ScaleQ 1.00 ± 0.07 0.326 ± 0.031 0.387 ± 0.021 0.843
Drude 1.52 ± 0.05 0.229 ± 0.007 0.204 ± 0.012 1.12
Open in a new tab

Table 5. Reorientation Correlation Time of Anions in Interfacial, Subinterfacial, and Central Layers Using the FixQ, ScaleQ, and the Drude Models.

Anion Reorientation Correlation Time (102 ps) Interfacial Layer Subinterfacial Layer Central Layer T(Sub)/T(Central)
FixQ 8.03 ± 1.08 5.74 ± 0.69 7.76 ± 0.32 0.740
ScaleQ 1.03 ± 0.05 0.576 ± 0.014 0.772 ± 0.013 0.746
Drude 1.28 ± 0.08 0.488 ± 0.014 0.518 ± 0.007 0.941
Open in a new tab

Interestingly, the ScaleQ model predicts a lower reorientation correlation time for cations and anions in the interfacial layer compared to the Drude model. In general, although the ScaleQ model can improve the dynamics of ionic liquids, its dynamics is still more sluggish than the Drude model, like self-diffusion coefficients and viscosities in the liquid phase. However, the model predicts a faster reorientation dynamics at the outermost interface. The electrostatic effect plays an important role in the reorientation of cations and anions at the interface, especially in this simulation where the cations and anion have both nonpolar and polar parts. The polar part prefers to be away from the liquid-vacuum interface, while the nonpolar part acts the opposite. Therefore, the greater the difference in polarity between the two parts, the harder it is for the ions to reorient. As we have discussed above, ions at the interface, which have a lower coordination number, undergo a less severe electron cloud distortion than those in the liquid phase and therefore have small induced dipoles. The scaled-down charge overaccounts for the polarization effect for the ions at the interface, which leads to a too-fast reorientation dynamics at the interface. The polarity difference for the ions in the Drude model may be larger than that in the ScaleQ model. This difference causes such lower reorientation correlation time in the ScaleQ model. This assumption can be verified from the side by Figure 3, where we can see that the Drude model predicts a stronger orientation preference than the ScaleQ model for both a cation and anion. Considering the different chemical environments at the vacuum-liquid interface from the bulk phase, the straightforward implementation of scaling down charges to mimic the many-body polarization effect is not likely to be a good substitute for the polarizable force field when studying interfaces.

Diffusion

To characterize the diffusion of the ions, we evaluated their self-diffusion coefficients by calculating the mean-square displacement (MSD) of the COM of the ions. The MSD in a direction α is defined by

graphic file with name jp2c07981_m009.jpg 8

where N is the number of cations or anions, rCOM,α(t) is the unwrapped position of the ith ion in the direction α, and ⟨•⟩ denotes the ensemble average. Considering the difference in the lateral and normal directions, we evaluated the MSDxy(t) and MSDz(t) in different layers, separately. Following the recommendations of a recent review,55 we estimated the self-diffusion coefficient using Einstein’s relation by

graphic file with name jp2c07981_m010.jpg 9

Figure 7 shows the MSDs for cations and anions in the central layer using the Drude model, together with the linear fits, as an example. The values of Dxy and Dz for cations and anions in the interfacial, subinterfacial, and central layers using the three models are listed in Table 6.

Figure 7.

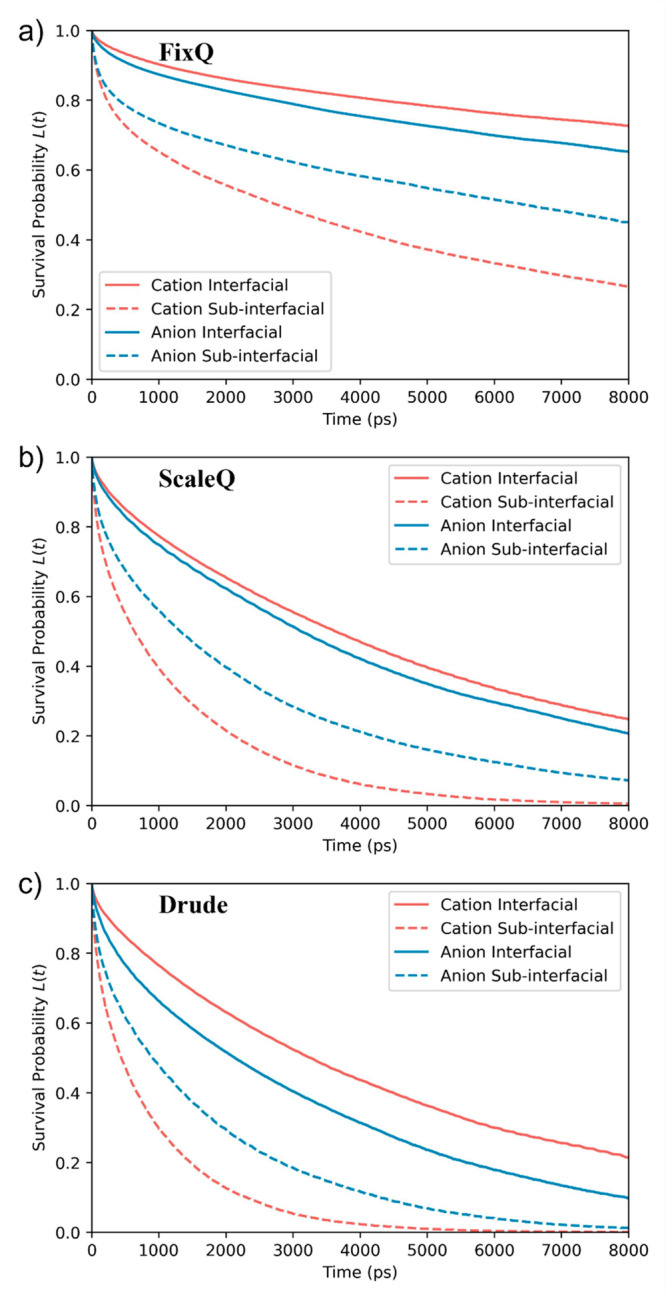
Figure 7

Open in a new tab

Survival probability of cations and anions in interfacial and subinterfacial layers using the (a) FixQ, (b) ScaleQ, and (c) Drude models.

Table 6. Self-Diffusion Coefficients of Cations and Anions in Different Layers.

Self-Diffusion Coefficient (10–11 m2 s–1)   Bulk Phase L1b Lateral L1 Normal L2b Lateral L2 Normal Central Lateral Central Normal
FixQ Ca 0.218 ± 0.006 0.276 ± 0.056 0.093 ± 0.011 0.345 ± 0.006 0.286 ± 0.044 0.244 ± 0.018 0.223 ± 0.019
Aa 0.173 ± 0.010 0.318 ± 0.055 0.081 ± 0.011 0.298 ± 0.022 0.235 ± 0.033 0.190 ± 0.021 0.186 ± 0.035
ScaleQ C 1.75 ± 0.07 3.63 ± 0.28 0.46 ± 0.10 2.89 ± 0.22 0.96 ± 0.13 2.35 ± 0.10 2.24 ± 0.05
A 1.32 ± 0.05 3.64 ± 0.10 0.54 ± 0.06 2.42 ± 0.21 0.88 ± 0.10 1.75 ± 0.11 1.73 ± 0.11
Drude C 4.92 ± 0.38 5.34 ± 0.21 0.451 ± 0.14 5.30 ± 0.44 1.88 ± 0.22 4.72 ± 0.17 4.34 ± 0.21
A 4.25 ± 0.18 5.44 ± 0.33 0.49 ± 0.19 4.15 ± 0.24 1.50 ± 0.18 4.17 ± 0.15 3.85 ± 0.33
Open in a new tab
a

C: cation, A: anion.

b

L1: interfacial layer, L2: subinterfacial layer.

For all models, we can see a remarkable difference between the normal and lateral self-diffusion coefficients in the interfacial and subinterfacial layers. In contrast, the difference in the central layer is much smaller as expected. The coefficients in the central layer are close to those of the bulk phase. The lateral diffusion Dxy in the interfacial layer is considerably faster than the normal diffusion Dz in the corresponding layers, by about 1 order of magnitude for the ScaleQ and Drude models. The difference between Dxy and Dz predicted by the FixQ model is only 4-fold, not as much as the difference in the other two models, partly due to the intrinsic slow dynamics of the FixQ model. Additionally, one should notice that the diffusion coefficients of a cation and anion in the interfacial layers are similar for the ScaleQ and Drude cases. Overall, the FixQ model suffers from low self-diffusion coefficients by 1 order of magnitude, as mentioned in a number of previous studies starting with the work of Yan et al.23 Fortunately, the ScaleQ model partly cures the sluggish dynamics and can give qualitatively correct results within the same order of magnitude as the Drude model and experimental data. Therefore, the following analysis of the diffusion is only based on the ScaleQ and Drude models.

The above unique diffusion phenomena, e.g., the fast lateral diffusion, slow normal diffusion, and similar self-diffusion coefficients of cations and anions, can be explained by the orientational preference of the ions in the interfacial layer. Due to the strong orientational preference of cations and anions in the interfacial layer, most cations and anions orient to be parallel to each other. Therefore, ions can easily have a collective movement in the lateral direction or exchange with their neighboring ions without reorientations, which can be faster than the random walk in the bulk phase. This movement partly explains the faster diffusion of ions in the lateral direction and the similar Dxy of cations and anions in the interfacial layer.

On the other hand, the normal diffusion is blocked and sluggish. First, the movement into the vacuum phase is prohibited, which partly reduces the diffusion. Second, considering the orientational preference of cations and anions in the interfacial layer and the size of ions, the anions are “jammed” between the head and tail of the cations, like a sandwich. The large cross-sectional area of the anions in the normal direction blocks both the cation and anions from the normal diffusion. The slow normal diffusion results in the “long” residence time of ions in the interfacial layer. For subinterfacial dynamics, the normal diffusion improves but is still lower than the bulk value. The interfacial layer’s high density and long residence time reduces the ions in the subinterfacial layer to move in the normal direction from one end, which contributes to the lower normal diffusion.

One should also note that the self-diffusion coefficient predicted by the Drude model is higher than the experimental data56 (D+exp = 2.58 × 10–11 m2 s–1, D– = 2.22 × 10–11 m2 s–1), which indicates faster dynamics in the Drude model. The induction interaction added in the polarizable force field should be attractive between atoms, which makes one expect slower dynamics. According to the original paper of the Drude model,38 they attribute the improved dynamics to the weaker long-range correlation, indicated by the less pronounced spatial distribution in the second solvation shell. The stronger attraction in the first solvation shell is observed in their spatial distributions, which coincides with the idea that the induction terms increase the attraction between atoms. On the other hand, the ScaleQ model predicts an overall less intensity in the spatial distribution, which is related to its low density.

One may notice that, in the central layer, the Dxy and Dz for the FixQ and ScaleQ models are higher than D in the bulk phase, while the Drude model predicts the opposite. This may be caused by the density differences. For the FixQ and ScaleQ models, their central layer density is lower than their bulk phase density, 1.424 vs 1.433 g/mL for the FixQ model and 1.389 vs 1.401 g/mL for the ScaleQ model. On the other hand, the central density for the Drude model is higher than the bulk phase, 1.422 vs 1.414 g/mL. The relative density difference between the central layer and bulk phase using different force fields may cause the above behavior.

Figure 8.

Figure 8

Open in a new tab

A representative figure for the center of mass mean-square displacements for the Drude model as a function of time for cations and anions in the central layer. The dash lines are linear fits to the MSDs.

Conclusions

Molecular dynamics simulations for the air–liquid interface of [C4mim][NTf2] at 300 K were carried out using three different kinds of force field: (a) FixQ: a nonpolarizable force field with each ion charge remaining unit; (b) ScaleQ: a nonpolarizable force field with the original atomic charged scaled down by 0.8; and (c) Drude: a polarizable force field with Drude oscillators. The three models were used to illustrate the effect of the scaled-charge and electric polarizability on simulating the interfacial properties of the common ionic liquid, [C4mim][NTf2]. To provide a comprehensive benchmark for the three models, we analyzed several structural and dynamical properties, including density profiles, orientation preference, 2D RDFs, surface tension, residence time, reorientation, and diffusion, in different layers. Based on the ITIM analysis, we could distinguish whether the ion is in the interfacial, subinterfacial, or central layer.

It is seen that the cation density at the interface for the Drude and ScaleQ models is reduced relative to that of the FixQ model. However, the Drude model predicts a higher anion density in the subinterfacial layer than in the interfacial layer, while the ScaleQ and FixQ models predict the opposite scenario. At the same time, the density oscillation beneath the subinterfacial layer of the ScaleQ and FixQ model is more pronounced than that of the Drude model. For different models, the other structural properties, like the orientational preference and 2D RDF, are similar in trend from the interfacial layer to the central layer, with several differences in the peak intensity and position. The surface tension predicted by the three models follows the trend: FixQ > ScaleQ > Drude, while all of them show at least a 20% deviation from the experimental value.

We further determined the residence time of ions in a certain layer. Overall, the residence time in the interfacial layer is higher than in the subinterfacial layer for all models. Cations always stay longer than anions in the interfacial layer, while the opposite is observed in the subinterfacial layer. The residence time predicted by the FixQ model is about 1 order of magnitude longer than the Drude model, while the residence time predicted by the ScaleQ model is much closer to the Drude model. Furthermore, the reorientation dynamics was evaluated for ions in different layers. While ions in the interfacial layer always have the slowest reorientation dynamics, the three models predict different results for ions in the subinterfacial layer. The FixQ and ScaleQ models predict that cations in the subinterfacial layer have a shorter reorientation correlation time than cations in the central layer, while the Drude model shows the opposite result.

Regarding the diffusive behavior of ions in different layers, we observed a significant difference in the lateral and normal direction, especially in the interfacial layer. With a strong orientation preference and local lateral clustering, ions at the interface have a faster lateral diffusion, due to the collective movement and easier neighboring ion exchange in the lateral direction. On the other hand, it is difficult for ions at the interface to diffuse in the normal direction because of the prolonged ion exchange between the interfacial and subinterfacial layers.

Overall, by comprehensively analyzing structural and dynamic properties related to the RTIL interface, we find that (a) the FixQ model cannot accurately predict structural nor dynamic properties, due to the lack of consideration of polarization effects and charge transfer; (b) the ScaleQ model largely improves some dynamical properties compared to the FixQ model, at least achieving the same order of magnitude with the polarizable Drude model (however, the ScaleQ model cannot fully account for the polarizable charge screening effect, especially at the interface); (c) the Drude model predicts a lower surface tension and higher self-diffusion coefficient than experiment. We note that none of the three methods are perfect for accurately predicting the interfacial properties, and so, further improvement of the force fields for ionic liquids seems essential for interface modeling via MD.

Acknowledgments

This research was supported by the Air Force Office of Scientific Research, under Award Number FA9550-21-1-0380. The computational resources for this research were provided by the University of Chicago Research Computing Center (RCC).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c07981.

  • Density profiles and residence times of different systems (PDF)

Author Contributions

S.C. and G.A.V. designed the research. S.C. performed the simulations. All authors analyzed the results and wrote the study.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry B virtual special issue “Honoring Michael R. Berman”.

Supplementary Material

jp2c07981_si_001.pdf (1.3MB, pdf)

References

  1. Hallett J. P.; Welton T. Room-Temperature Ionic Liquids: Solvents for Synthesis and Catalysis. 2. Chem. Rev. 2011, 111, 3508–3576. 10.1021/cr1003248. [DOI] [PubMed] [Google Scholar]
  2. Maton C.; De Vos N.; Stevens C. V. Ionic Liquid Thermal Stabilities: Decomposition Mechanisms and Analysis Tools. Chem. Soc. Rev. 2013, 42, 5963–5977. 10.1039/c3cs60071h. [DOI] [PubMed] [Google Scholar]
  3. Zhang Q.; Zhang S.; Deng Y. Recent Advances in Ionic Liquid Catalysis. Green Chem. 2011, 13, 2619–2637. 10.1039/c1gc15334j. [DOI] [Google Scholar]
  4. Osada I.; de Vries H.; Scrosati B.; Passerini S. Ionic-Liquid-Based Polymer Electrolytes for Battery Applications. Angew. Chem., Int. Ed. 2016, 55, 500–513. 10.1002/anie.201504971. [DOI] [PubMed] [Google Scholar]
  5. Vekariya R. L. A Review of Ionic Liquids: Applications towards Catalytic Organic Transformations. J. Mol. Liq. 2017, 227, 44–60. 10.1016/j.molliq.2016.11.123. [DOI] [Google Scholar]
  6. Berthod A.; Ruiz-Ángel M. J.; Carda-Broch S. Recent Advances on Ionic Liquid Uses in Separation Techniques. J. Chromatogr. A 2018, 1559, 2–16. 10.1016/j.chroma.2017.09.044. [DOI] [PubMed] [Google Scholar]
  7. Francis C. F. J.; Kyratzis I. L.; Best A. S. Lithium-Ion Battery Separators for Ionic-Liquid Electrolytes: A Review. Adv. Mater. 2020, 32, 1904205. 10.1002/adma.201904205. [DOI] [PubMed] [Google Scholar]
  8. Zeng S.; Zhang X.; Bai L.; Zhang X.; Wang H.; Wang J.; Bao D.; Li M.; Liu X.; Zhang S. Ionic-Liquid-Based CO2 Capture Systems: Structure, Interaction and Process. Chem. Rev. 2017, 117, 9625–9673. 10.1021/acs.chemrev.7b00072. [DOI] [PubMed] [Google Scholar]
  9. Mondal M. K.; Balsora H. K.; Varshney P. Progress and Trends in CO2 Capture/Separation Technologies: A Review. Energy 2012, 46, 431–441. 10.1016/j.energy.2012.08.006. [DOI] [Google Scholar]
  10. Hasib-ur-Rahman M.; Siaj M.; Larachi F. Ionic Liquids for CO2 Capture—Development and Progress. Chem. Eng. Process. 2010, 49, 313–322. 10.1016/j.cep.2010.03.008. [DOI] [Google Scholar]
  11. Iimori T.; Iwahashi T.; Kanai K.; Seki K.; Sung J.; Kim D.; Hamaguchi H.-o.; Ouchi Y. Local Structure at the Air/Liquid Interface of Room-Temperature Ionic Liquids Probed by Infrared–Visible Sum Frequency Generation Vibrational Spectroscopy: 1-Alkyl-3-methylimidazolium Tetrafluoroborates. J. Phys. Chem. B 2007, 111, 4860–4866. 10.1021/jp067162n. [DOI] [PubMed] [Google Scholar]
  12. Hantal G.; Cordeiro M. N. D. S.; Jorge M. What Does an Ionic Liquid Surface Really Look Like? Unprecedented Details from Molecular Simulations. Phys. Chem. Chem. Phys. 2011, 13, 21230–21232. 10.1039/c1cp22639h. [DOI] [PubMed] [Google Scholar]
  13. Paredes X.; Fernández J.; Pádua A. A. H.; Malfreyt P.; Malberg F.; Kirchner B.; Pensado A. S. Using Molecular Simulation to Understand the Structure of [C2C1im]+–Alkylsulfate Ionic Liquids: Bulk and Liquid–Vapor Interfaces. J. Phys. Chem. B 2012, 116, 14159–14170. 10.1021/jp309532t. [DOI] [PubMed] [Google Scholar]
  14. Tesa-Serrate M. A.; Marshall B. C.; Smoll E. J. Jr.; Purcell S. M.; Costen M. L.; Slattery J. M.; Minton T. K.; McKendrick K. G. Ionic Liquid–Vacuum Interfaces Probed by Reactive Atom Scattering: Influence of Alkyl Chain Length and Anion Volume. J. Phys. Chem. C 2015, 119, 5491–5505. 10.1021/jp5126238. [DOI] [Google Scholar]
  15. Paredes X.; Fernández J.; Pádua A. A. H.; Malfreyt P.; Malberg F.; Kirchner B.; Pensado A. S. Bulk and Liquid–Vapor Interface of Pyrrolidinium-Based Ionic Liquids: A Molecular Simulation Study. J. Phys. Chem. B 2014, 118, 731–742. 10.1021/jp406651f. [DOI] [PubMed] [Google Scholar]
  16. Konieczny J. K.; Szefczyk B. Structure of Alkylimidazolium-Based Ionic Liquids at the Interface with Vacuum and Water—A Molecular Dynamics Study. J. Phys. Chem. B 2015, 119, 3795–3807. 10.1021/jp510843m. [DOI] [PubMed] [Google Scholar]
  17. Yan T.; Li S.; Jiang W.; Gao X.; Xiang B.; Voth G. A. Structure of the Liquid–Vacuum Interface of Room-Temperature Ionic Liquids: A Molecular Dynamics Study. J. Phys. Chem. B 2006, 110, 1800–1806. 10.1021/jp055890p. [DOI] [PubMed] [Google Scholar]
  18. Choi E.; Yethiraj A. Entropic Mechanism for the Lower Critical Solution Temperature of Poly(ethylene oxide) in a Room Temperature Ionic Liquid. ACS Macro Lett. 2015, 4, 799–803. 10.1021/acsmacrolett.5b00355. [DOI] [PubMed] [Google Scholar]
  19. McDaniel J. G.; Yethiraj A. Influence of Electronic Polarization on the Structure of Ionic Liquids. J. Phys. Chem. Lett. 2018, 9, 4765–4770. 10.1021/acs.jpclett.8b02120. [DOI] [PubMed] [Google Scholar]
  20. Schröder C. Comparing Reduced Partial Charge Models with Polarizable Simulations of Ionic Liquids. Phys. Chem. Chem. Phys. 2012, 14, 3089–3102. 10.1039/c2cp23329k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Bedrov D.; Piquemal J.-P.; Borodin O.; MacKerell A. D. Jr.; Roux B.; Schröder C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. 10.1021/acs.chemrev.8b00763. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bedrov D.; Borodin O.; Li Z.; Smith G. D. Influence of Polarization on Structural, Thermodynamic, and Dynamic Properties of Ionic Liquids Obtained from Molecular Dynamics Simulations. J. Phys. Chem. B 2010, 114, 4984–4997. 10.1021/jp911670f. [DOI] [PubMed] [Google Scholar]
  23. Yan T.; Burnham C. J.; Del Pópolo M. G.; Voth G. A. Molecular Dynamics Simulation of Ionic Liquids: The Effect of Electronic Polarizability. J. Phys. Chem. B 2004, 108, 11877–11881. 10.1021/jp047619y. [DOI] [Google Scholar]
  24. Patel S.; Brooks C. L. Fluctuating Charge Force Fields: Recent Developments and Applications from Small Molecules to Macromolecular Biological Systems. Mol. Simul. 2006, 32, 231–249. 10.1080/08927020600726708. [DOI] [Google Scholar]
  25. Lamoureux G.; Roux B. t. Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys. 2003, 119, 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
  26. Ren P.; Ponder J. W. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J. Phys. Chem. B 2003, 107, 5933–5947. 10.1021/jp027815+. [DOI] [Google Scholar]
  27. Jiang W.; Hardy D. J.; Phillips J. C.; MacKerell A. D. Jr.; Schulten K.; Roux B. High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett. 2011, 2, 87–92. 10.1021/jz101461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Dequidt A.; Devémy J.; Pádua A. A. H. Thermalized Drude Oscillators with the LAMMPS Molecular Dynamics Simulator. J. Chem. Inf. Model. 2016, 56, 260–268. 10.1021/acs.jcim.5b00612. [DOI] [PubMed] [Google Scholar]
  29. Lemkul J. A.; Roux B.; van der Spoel D.; MacKerell A. D. Jr Implementation of Extended Lagrangian Dynamics in GROMACS for Polarizable Simulations Ssing the Classical Drude Oscillator Model. J. Comput. Chem. 2015, 36, 1473–1479. 10.1002/jcc.23937. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Huang J.; Lemkul J. A.; Eastman P. K.; MacKerell A. D. Jr Molecular Dynamics Simulations Using the Drude Polarizable Force Field on GPUs with OpenMM: Implementation, Validation, and Benchmarks. J. Comput. Chem. 2018, 39, 1682–1689. 10.1002/jcc.25339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Starovoytov O. N.; Torabifard H.; Cisneros G. A. Development of AMOEBA Force Field for 1,3-Dimethylimidazolium Based Ionic Liquids. J. Phys. Chem. B 2014, 118, 7156–7166. 10.1021/jp503347f. [DOI] [PubMed] [Google Scholar]
  32. Vázquez-Montelongo E. A.; Vázquez-Cervantes J. E.; Cisneros G. A. Current Status of AMOEBA–IL: A Multipolar/Polarizable Force Field for Ionic Liquids. Int. J. Mol. Sci. 2020, 21, 697. 10.3390/ijms21030697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. McDaniel J. G. Polarization Effects in Binary [BMIM+][BF4–]/1,2-Dichloroethane, Acetone, Acetonitrile, and Water Electrolytes. J. Phys. Chem. B 2018, 122, 4345–4355. 10.1021/acs.jpcb.8b01714. [DOI] [PubMed] [Google Scholar]
  34. Canongia Lopes J. N.; Pádua A. A. H. CL&P: A Generic and Systematic Force Field for Ionic Liquids Modeling. Theor. Chem. Acc. 2012, 131, 1129. 10.1007/s00214-012-1129-7. [DOI] [Google Scholar]
  35. Červinka C.; Pádua A. A. H.; Fulem M. Thermodynamic Properties of Selected Homologous Series of Ionic Liquids Calculated Using Molecular Dynamics. J. Phys. Chem. B 2016, 120, 2362–2371. 10.1021/acs.jpcb.5b11070. [DOI] [PubMed] [Google Scholar]
  36. Kowsari M. H.; Ebrahimi S. Capturing the Effect of [PF3(C2F5)3]−vs. [PF6]−, Flexible Anion vs. Rigid, and Scaled Charge vs. Unit on the Transport Properties of [Bmim]+-Based Ionic Liquids: A Comparative MD Study. Phys. Chem. Chem. Phys. 2018, 20, 13379–13393. 10.1039/C8CP01700J. [DOI] [PubMed] [Google Scholar]
  37. Young T.; Chen F.; Burba C. M. Quantitative Investigation of Ion Clusters in a Double Salt Ionic Liquid by Both Vibrational Spectroscopy and Molecular Dynamics Simulation. J. Phys. Chem. B 2020, 124, 3984–3991. 10.1021/acs.jpcb.0c01457. [DOI] [PubMed] [Google Scholar]
  38. Goloviznina K.; Canongia Lopes J. N.; Costa Gomes M.; Pádua A. A. H. Transferable, Polarizable Force Field for Ionic Liquids. J. Chem. Theory Comput. 2019, 15, 5858–5871. 10.1021/acs.jctc.9b00689. [DOI] [PubMed] [Google Scholar]
  39. Pártay L. B.; Hantal G.; Jedlovszky P.; Vincze Á.; Horvai G. A New Method for Determining the Interfacial Molecules and Characterizing the Surface Roughness in Computer Simulations. Application to the Liquid–Vapor Interface of Water. J. Comput. Chem. 2008, 29, 945–956. 10.1002/jcc.20852. [DOI] [PubMed] [Google Scholar]
  40. Lísal M.; Posel Z.; Izák P. Air–Liquid Interfaces of Imidazolium-Based [TF2N–] Ionic Liquids: Insight from Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2012, 14, 5164–5177. 10.1039/c2cp23572b. [DOI] [PubMed] [Google Scholar]
  41. Thompson A. P.; Aktulga H. M.; Berger R.; Bolintineanu D. S.; Brown W. M.; Crozier P. S.; in ’t Veld P. J.; Kohlmeyer A.; Moore S. G.; Nguyen T. D.; Shan R.; Stevens M. J.; Tranchida J.; Trott C.; Plimpton S. J. LAMMPS - a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. 10.1016/j.cpc.2021.108171. [DOI] [Google Scholar]
  42. Pádua A. A. H. FFTOOL. https://github.com/agiliopadua/fftool (accessed Oct 25, 2022).
  43. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  44. Pádua A. A. H. Clandpol. https://github.com/agiliopadua/clandpol (accessed Oct 25, 2022).
  45. Son C. Y.; McDaniel J. G.; Cui Q.; Yethiraj A. Proper Thermal Equilibration of Simulations with Drude Polarizable Models: Temperature-Grouped Dual-Nosé–Hoover Thermostat. J. Phys. Chem. Lett. 2019, 10, 7523–7530. 10.1021/acs.jpclett.9b02983. [DOI] [PubMed] [Google Scholar]
  46. Thole B. T. Molecular Polarizabilities Calculated with a Modified Dipole Interaction. Chem. Phys. 1981, 59, 341–350. 10.1016/0301-0104(81)85176-2. [DOI] [Google Scholar]
  47. Hantal G.; Darvas M.; Pártay L. B.; Horvai G.; Jedlovszky P. Molecular Level Properties of the Free Water Surface and Different Organic Liquid/Water Interfaces, as Seen from ITIM Analysis of Computer Simulation Results. J. Phys.: Condens. Matter 2010, 22, 284112. 10.1088/0953-8984/22/28/284112. [DOI] [PubMed] [Google Scholar]
  48. Nakajima K.; Nakanishi S.; Lísal M.; Kimura K. Surface Structure of Imidazolium-Based Ionic Liquids: Quantitative Comparison between Simulations and High-Resolution RBS Measurements. J. Chem. Phys. 2016, 144, 114702. 10.1063/1.4943887. [DOI] [PubMed] [Google Scholar]
  49. Baldelli S. Influence of Water on the Orientation of Cations at the Surface of a Room-Temperature Ionic Liquid: A Sum Frequency Generation Vibrational Spectroscopic Study. J. Phys. Chem. B 2003, 107, 6148–6152. 10.1021/jp027753n. [DOI] [Google Scholar]
  50. Rivera-Rubero S.; Baldelli S. Influence of Water on the Surface of Hydrophilic and Hydrophobic Room-Temperature Ionic Liquids. J. Am. Chem. Soc. 2004, 126, 11788–11789. 10.1021/ja0464894. [DOI] [PubMed] [Google Scholar]
  51. Fujii K.; Fujimori T.; Takamuku T.; Kanzaki R.; Umebayashi Y.; Ishiguro S.-i. Conformational Equilibrium of Bis(trifluoromethanesulfonyl) Imide Anion of a Room-Temperature Ionic Liquid: Raman Spectroscopic Study and DFT Calculations. J. Phys. Chem. B 2006, 110, 8179–8183. 10.1021/jp0612477. [DOI] [PubMed] [Google Scholar]
  52. Nakajima K.; Ohno A.; Hashimoto H.; Suzuki M.; Kimura K. Observation of Surface Structure of 1-Alkyl-3-methylimidazolium Bis(trifluoromethanesulfonyl)imide Using High-Resolution Rutherford Backscattering Spectroscopy. J. Chem. Phys. 2010, 133, 044702 10.1063/1.3465578. [DOI] [PubMed] [Google Scholar]
  53. Aguado A.; Wilson M.; Madden P. A. Molecular Dynamics Simulations of the Liquid–Vapor Interface of a Molten Salt. I. Influence of the Interaction Potential. J. Chem. Phys. 2001, 115, 8603–8611. 10.1063/1.1410393. [DOI] [Google Scholar]
  54. Rebelo L. P. N.; Canongia Lopes J. N.; Esperança J. M. S. S.; Filipe E. On the Critical Temperature, Normal Boiling Point, and Vapor Pressure of Ionic Liquids. J. Phys. Chem. B 2005, 109, 6040–6043. 10.1021/jp050430h. [DOI] [PubMed] [Google Scholar]
  55. Maginn E. J.; Messerly R. A.; Carlson D. J.; Roe D. R.; Elliot J. R. Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0]. Living J. Comput. Mol. Sci. 2018, 1, 6324. 10.33011/livecoms.1.1.6324. [DOI] [Google Scholar]
  56. Noda A.; Hayamizu K.; Watanabe M. Pulsed-Gradient Spin–Echo 1H and 19F NMR Ionic Diffusion Coefficient, Viscosity, and Ionic Conductivity of Non-Chloroaluminate Room-Temperature Ionic Liquids. J. Phys. Chem. B 2001, 105, 4603–4610. 10.1021/jp004132q. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp2c07981_si_001.pdf (1.3MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES