Implementing climate change projections in System Dynamics models

Abstract

Desertification is the degradation of drylands, which occupy an increasing proportion of the Earth's surface due to global warming. It is currently the most extensive biome on Earth, occupying 45% and one out of every three inhabitants of the planet live in them. One of the most effective ways to face desertification, as Land Degradation Neutrality points out, is prevention. For this purpose, simulation models are very useful tools. Specifically, System Dynamics models are particularly effective, since they allow bringing together the biophysical and socioeconomic variables involved in the formation of the problem. These integrative models, coupled with other tools such as sensitivity analyses, are used to generate desertification early warning indicators. The objective of this programming routine is to implement climate change scenarios in these simulation models. The script presented here was used to evaluate the sensitivity of dehesa rangelands productivity to the increase in the frequency and intensity of droughts due to climate change.

• •Integrated simulation models are useful tools to understand complex socioecosystems.
• •Land-use changes foster the alteration of key hydro-bio-geochemical processes.
• •By means of automated import processes and data analysis programming, it is possible to implement desertification early warning systems.

Graphical abstract

Specification table

Subject area:	Earth and Planetary Sciences
More specific subject area:	Climate change impact
Name of your method:	R-script for implementing climate change scenarios in Vensim models
Name and reference of original method:	N/A
Resource availability:	https://doi.org/10.6084/m9.figshare.21583023.v1
	https://doi.org/10.6084/m9.figshare.21616803.v1

Method details

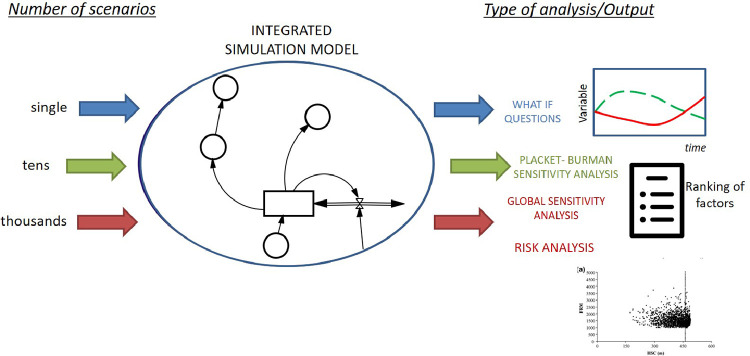
The objective of this R script is to implement climate change scenarios, generated by the Meteorological State Agency of Spain (AEMET) [1] in System Dynamics (SD) models programmed in Vensim [2]. SD models generate time trajectories of all their variables from a simulation scenario. However, it is possible to implement various types of analysis (Fig. 1; e.g., Sensitivity Analyses, ANOVA tests) simulating a large number of scenarios. For this it is necessary to automate the import, simulation and export of results. This can be done, for example, through Visual Basic programming, which allows to operate models from the Excel environment [3,4].

Fig. 1.

SD models can be used for different purposes. The most common use is to test different scenarios to ask what-if questions and compare the different time trajectories of the variables. However, it is possible to simulate tens or thousands of scenarios to implement various types of sensitivity analysis [5]. This allows to obtain a ranking of the influence of the various parameters of the model or to calculate the probability of collapse of the system [6].

This paper shows how to transform climate change scenarios provided by AEMET (https://www.aemet.es/es/serviciosclimaticos/cambio_climat) to Vensim scenarios. From each series of 95 years of daily data (i.e., about 34,675 values), five values are obtained for the five general climate parameters of a model that simulates rangeland productivity [7]. These five parameters are: (i) rfpm, Average probability of rainfall during one time step; (ii) rfdm, Average rainfall depth per rainy time step; (iii) rfdd, Standard deviation of rainfall depth across rainy time steps; (iv) retm, Average reference evapotranspiration depth per time step; and (v) recv, Standard deviation of reference evapotranspiration depth per time step.

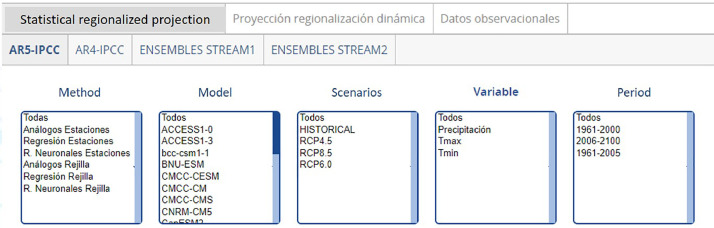
The original files downloaded from the AEMET web site include .dat files for each of the meteorological stations in Spain. The main considerations to take into account when programming the script are the following: (i) Precipitation and temperature data are originally provided by different global climate models. In order to use them at the local scale it is necessary to regionalize these data, for which there are several methods. In our case we are going to use data at the meteorological station level. In addition, it is possible to use historical data or data associated with different future scenarios of CO₂ emissions (RCP's). Not all the combinations allowed by AEMET (Fig. 2) have an associated data file. Thus, before running the script, it is necessary to perform several tests to choose the options that best suit our study; (ii) The daily data provided by AEMET must be adjusted to the integration step used by VENSIM. The minimum time step allowed by this program is 0.0078125 years, that is, about 2.8 days. It is necessary to convert the 365 typical values of a year into the 128 periods used by Vensim. To make these time series match the number of time steps per year in the model, i.e., 128 = 1/Time Step = 1/0.0078125, we summed consecutive daily data by groups of two or three days randomly positioned within each year in the series, i.e., we used a different random permutation of 109 3-day groups and 19 2-day groups for each year. For a small third group of datasets that included 360-day years we used random permutations of 104 3-day groups and 2 2-day groups; (iii) AEMET provides heterogeneous three type of files: (a) series with leap years, where all months of the series are of 31 days, that is, with years of 372 days; (b) series with all years of 365 days; (c) series with years of 360 days.

Fig. 2.

Options available for downloading AEMET climate projection data. Note that the AEMET website is in Spanish. We have translated some of the headings for a better understanding.

The following is a description of the script that allows to transform the AEMET climate change scenarios into data importable by Vensim. We have programmed several scripts according to the type of year considered (with or without leap years). Here we refer to the most complex script, i.e. the one used for data series including leap years. The reader can find the files used for this excercise in Figshare (doi: 10.6084/m9.figshare.21616803).

1. After downloading data we get files with extension .tar.gz. The first commands of the script set the working directory, and unzip .tar.gz file with “untar” function. After that, we obtain as many .dat files as weather stations are included in the initial file. Then we select the station we are interested in (see the complete list in the associated repository to this paper) and eliminate the first three rows and the first two columns of the original files (the headers). The code creates three .txt files (cleanfile_P; cleanfile_Tx; cleanfileTm) and converts them in three matrices. The number of rows of each matrix corresponds to multiplying the 12 months of the year by the 95 years of projection (2006–2100). Thus, we have 35,340 records or, in other words, 95 years of 372 days (all months are considered as 31 days). Note that the AEMET variable depends on the data selection. It is therefore necessary to change the name according to the selection made.

#Set up working directory

setwd(getwd())

#Load data

#AEMET file type:.tar.gz

Aemet_P <- "precip.MRI-CGCM3.RCP85.2006-2100.ANALOGOS.tar.gz"

Aemet_Tx<- "tmax.MRI-CGCM3.RCP85.2006-2100.ANALOGOS.tar.gz"

Aemet_Tm<- "tmin.MRI-CGCM3.RCP85.2006-2100.ANALOGOS.tar.gz"

#Unzip files

untar(Aemet_P)

untar(Aemet_Tx)

untar(Aemet_Tm)

#Select meteorological station

station<-3087

#Create by concatenation the .dat file for the selected station

file_P<-paste("precip.",station,".MRI-CGCM3.RCP85.2006

         -2100.ANALOGOS.dat",sep="")

file_Tx<-paste("tmax.",station,".MRI-CGCM3.RCP85.2006

         -2100.ANALOGOS.dat",sep="")

file_Tm<-paste("tmin.",station,".MRI-CGCM3.RCP85.2006

         -2100.ANALOGOS.dat",sep="")

#Read the file removing the first two rows and the first three columns

cleanfile_P<-read.table(file_P, header = F, skip=2)[-c(1:3)]

cleanfile_Tx<-read.table(file_Tx, header = F, skip=2)[-c(1:3)]

cleanfile_Tm<-read.table(file_Tm, header = F, skip=2)[-c(1:3)]

#Create txt files

write.table(cleanfile_P, file = "cleanfile_P.txt",sep = "\t",

         row.names = FALSE,col.names = FALSE)

write.table(cleanfile_Tx, file = "cleanfile_Tx.txt",sep = "\t",

         row.names = FALSE,col.names = FALSE)

write.table(cleanfile_Tm, file = "cleanfile_Tm.txt",sep = "\t",

         row.names = FALSE,col.names = FALSE)

#Create a matrix with the above data

#precipitation PPT, max temperature TMX, min temperature TMN

PPTMTd=matrix(scan("cleanfile_P.txt",0),ncol=31,byrow=TRUE)

TMXMTd=matrix(scan("cleanfile_Tx.txt",0),ncol=31,byrow=TRUE)

TMNMTd=matrix(scan("cleanfile_Tm.txt",0),ncol=31,byrow=TRUE)

2. Transpose the matrix for the subsequent calculation of the potential evapotranspiration (PET) (matrixes of 31 × 1140). Change units to mm and °C; AEMET data are in tenths of mm and tenths of degree. Convert the value −999, with which AEMET signals the absence of data, to N/A to exclude them from calculus.

#Days in rows (31), months in columns (12×95=1140)

PPTMd=t(PPTMTd)

TMXMd=t(TMXMTd)

TMNMd=t(TMNMTd)

# Recoding of -999 s values so as not to operate with them

PPTMd[PPTMd==-999]=NA

TMXMd[TMXMd==-999]=NA

TMNMd[TMNMd==-999]=NA

# Precipitation in mm, temperatures in Celsius degrees (Original scenarios in tenths)

PPTM=PPTMd/10 # In tenths of mm

TMXM=TMXMd/10 # In tenths of degree

TMNM=TMNMd/10 # In tenths of degree

3. Calculation of daily Potential Evapotranspiration (PET) according to Hargreaves' method [8]. Note that the script uses the Spanish acronym for potential evapotranspiration, ETP. The simplified formulation of the method has been implemented following the work of Sanchez (2022) [9]. In addition, the routine takes into account the bugs in the original file, in which there are some records where Tmax<Tmin.

# Average daily temperature

TMDM=(TMXM+TMNM)/2

# Daily thermal amplitude

# There is Tmin > Tmax in the original file!!! They have to be made zero

RTPM=TMXM-TMNM

which(RTPM<0)

RTPM[RTPM<0]=0

# Hargreaves ET0 factor without R0

FET0M=0.0023*(TMDM+17.78)*sqrt(RTPM)

# Extraterrestrial solar radiation for 40° latitude

# (Dehesas in Caceres is 39.4°)

R0=c(6.1,8.3,11.1,14.2,16.2,17.1,16.7,15.0,12.2,9.2,6.7,5.6)

# Simplified Hargreaves ET0

ETPM=c()

iR0=rep(c(1:12),95)

for(i in 1:1140) {

  ETPMi=FET0M[,i]*R0[iR0[i]]

  ETPM=cbind(ETPM,ETPMi)}

4. The daily values of Precipitation (PPTM) and potential evapotranspiration (ETPM) are converted into vectors of 35,340 elements.

PPTV0=as.vector(PPTM)

ETPV0=as.vector(ETPM)

5. Eliminate the records that do not contain information, as this routine works with years of 372 days (i.e., considers that all months are 31 days, 31 × 12= 372). It is necessary to eliminate the days 29, 30 and 31 of the February months of the years that are not leap years, as well as all the days 31 of the 30-day months. The length of these vectors is 34,698 elements.

PPTB=na.omit(PPTV0)

ETPB=na.omit(ETPV0)

6. The extra value provided by leap years is ignored, making all years of 365 days. For this purpose, the 29th of February of the series is detected. There are three important data for this: (i) The number of days between January 1, 2005 (first data of the scenario) and the first February 29 is 790; (ii) In the 95-year series there are 23 leap years; (iii) There are 1461 days between one leap year and another. The vectors now have 34,675 values.

for(i in 1:23) {

PPTB[790+(i-1)*1461]=-999

}

PPT=PPTB[PPTB!=-999]

for(i in 1:23) {

ETPB[790+(i-1)*1461]=-999

}

ETP=ETPB[ETPB!=-999]

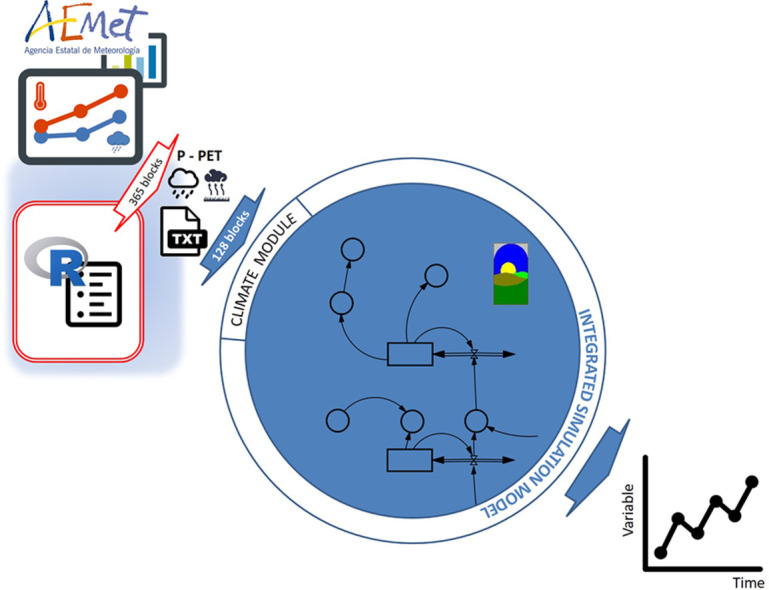
7. Fit the 365 annual PPT and ETP values into the 128 values (PPTag and ETPag) supported by Vensim. Blocks of 2 or 3 units are used to determine how the 365 starting values add up. The series of 128 blocks will consist of 109 three-element blocks and 38 2-element blocks. Their order is random, i.e., each of the 95 years in the series has a different sequence of blocks. Fig. 2 illustrates how to go from a sequence of 365 values to 128. Each of the final vectors has 12,160 elements (128 × 95). These are the values that will be used by the model in Vensim. Fig. 3

Fig. 3.

The 365 daily precipitation and temperature values must be converted into 128 values, which Vensim can use. For this purpose, the original values are aggregated in blocks of two or three elements.

set.seed(0)

vag1=c()

csg1=1:128 # Segment counter in one year

for (i in 1:95) {

di1=c(rep(2,19),rep(3109)) # Initial distribution of blocks

pdi1=sample(di1) # Permutation of the above distribution

vag1y=rep(csg1,pdi1)

vag1=c(vag1,vag1y)

csg1=csg1+128

}

length(vag1)

vag1f=factor(vag1)

PPTag=c(tapply(PPT,vag1f,sum))

ETPag=c(tapply(ETP,vag1f,sum))

8. In this last part of the script, simple arithmetic operations are performed to calculate the five simulation model parameters. To obtain the three related to rainfall we build the vector RFY. The mean probability of rainfall, rfpm, is calculated by dividing the number of rainy days (i.e., excluding those without rain), by the total number of days (i.e., 128 periods in a Vensim year times the 95 years of the series (2006–2100)). The other two (mean precipitation, rfdm; and standard deviation, rfdd) are obtained by simply calculating the mean and standard deviation of RFY. The two parameters related to evapotranspiration (retm and recv) are calculated by implementing the corresponding statistics to the ETPag vector. After calculation, they are accumulated in a vector that is exported in a format compatible with Vensim (in this case a .txt file).

RFY=PPTag[PPTag!=0]

rfpm=length(RFY)/(128×95)

rfpm

rfdm=mean(RFY) # Average precipitation per Vensim time step

rfdm

rfdd=sd(RFY)

rfdd

retm=mean(ETPag)

retm

recv=sd(ETPag)/retm

recv

plot(1:12,160,PPTag,type='l')

plot(1:12,160,ETPag,type='l')

RES=c(rfpm,rfdm,rfdd,retm,recv)

SD models can be considered virtual laboratories in which simple experiments can be performed. The results generated by the model can be analyzed in many ways. The most classical approach is the implementation of "what if" questions, in which different scenarios are run and the results interpreted in relative terms. In this case, the use of AEMET climate change data was intended to conduct a multi-way ANOVA test.

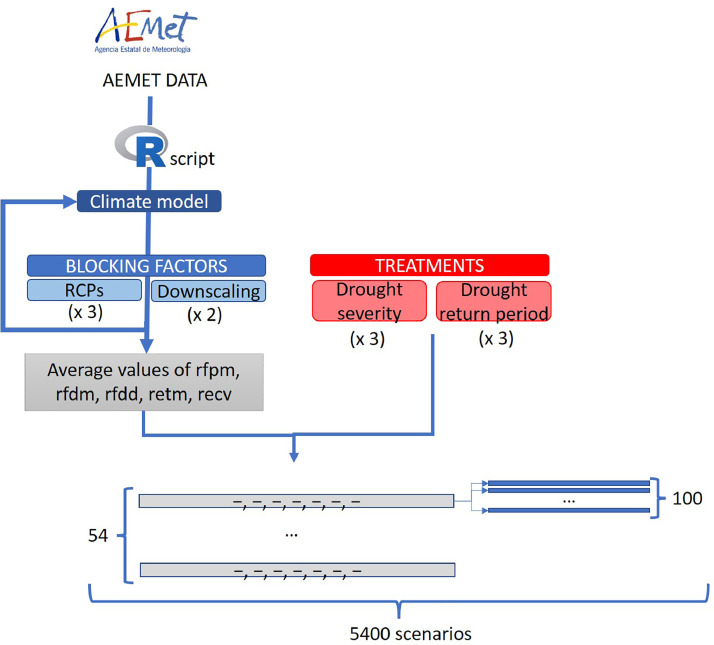
ANOVA studies the influence of one or more factors on one or more response variables. In our case, the factors represent different types of droughts (characterized by their frequency and intensity). The response is evaluated from an economic (Average annual earnings per active farmer), livestock (Average stocking rate), and environmental (Remaining soil depth) point of view. For this purpose, 5400 simulation scenarios have been generated (see Fig. 4) from two blocking factors, and two treatment factors. The former are three RCPs (4.5, 6, 8.5; Fig. 2, Scenarios Table), and two downscaling methods, i.e., process by which coarse-resolution Global Climate Models outputs are translated into local climate information (Analog and SDSM; Fig. 2, Method textbox). The latter refers to three levels for both the frequency and intensity of droughts (Drought severity, i.e., maximum fractional decrease in the probability of rainfall per time step during a drought -ranges from 0 to 1-: 0.17, 0.35, 0.5; and Drought return period: 8,12,16 years).

Fig. 4.

Configuration of the 5400 scenarios that are simulated in the model. After obtaining the mean values of the model parameters by running the script (Table 1), 54 combinations are formed (3 RCPs X 2 Downscaling methods X 3 Drought scarcities X 3 Droughts return periods). Each of these 54 scenarios characterizes the precipitation from the SD model. From each scenario, 100 random precipitation scenarios are generated. Thus, we have 54 × 100 simulation scenarios.

The script is used to generate 5 climate parameter values for each combination of the two factors considered (Table 1). The value of each parameter is the average obtained by running the script as many times as there are climate models (Fig. 2, Model textbox) available for the combinations of RCPs scenarios and downscaling methods.

Table 1.

Average values of the general climate parameters used in the multi-way ANOVA for each combination of levels of the blocking factors ‘RCP’ and ‘Downscaling method’.

	RCP
	4.5	6.0	8.5	4.5	6.0	8.5
	ANALOG			SSDM
rfpm	0.768	0.776	0.744	0.442	0.445	0.431
rfdm	4.966	5.126	4.451	4.323	4.504	4.538
rfdd	6.914	7.143	6.385	4.322	4.729	4.657
retm	8.953	8.898	9.381	9.730	9.720	10.088
recv	0.618	0.619	0.616	0.623	0.622	0.620

A hundred simulations (replicates) were run for each of the 3·2·3·3 = 54 cells in the analysis. These were obtained by varying the value of the random seed from 1 to 100. Note that this seed is involved in determining the outcomes of the Bernoulli trial and the sampling from the log-normal distribution. With them the climate module of the SD model calculates, respectively, the probability of rain in a time step, and the amount of rain in that time step. A 300-year simulation period was used for all of them with the aim of enabling long-term processes to clearly manifest their effects, especially those driven by soil erosion.

The multi-way ANOVA evaluated the main effects and all the possible interactions between factors. This has shown that most of the main effects and interactions turned out to be highly significant although sensitivity of response variables to increases in the frequency and severity of droughts under climate change would be low or very low. Our study suggests that the low sensitivity of Spanish dehesas to the worsening of droughts could be explained by a widespread conservative use of supplementary feeding.

Strictly speaking, the outputs of a SD model like the implemented should not be considered as predictions. The reason is that the background of the equations used is of a socio-ecological nature, i.e., they do not respond to laws of a physical and universal nature. Models that are founded on economic, social and even biological formulations try to explore the future, but cannot forecast what will happen [10]. This is an important limitation of SD modeling, which may go unnoticed since it is an eminently quantitative methodology. However, SD modelers and their users should always keep in mind that SD is a "back and forth path between the qualitative and the quantitative." [11]

The interested reader can find in Figshare the script (https://doi.org/10.6084/m9.figshare.21583023.v1) and data (https://doi.org/10.6084/m9.figshare.21616803.v1) including: (i) the AEMET weather stations code (.xls file); (ii) three .tz files that contain the daily data of precipitation and maximum and minimum temperatures for the period 2006–2100 of the statistical regionalization projection, according to the "Análogos Estaciones" method, the model "MRI-CGCM3″ and the RCP 8.5 scenario (i.e., the example used in the script); (iii) three .txt files that are an intermediate output of the script for the attached data files and the meteorological station 3087; (iv) the output of the script, Vensim_parameters.txt.

CRediT authorship contribution statement

Jaime Martínez-Valderrama: Conceptualization, Methodology, Software, Writing – original draft, Visualization. Javier Ibáñez: Conceptualization, Methodology, Software, Data curation, Formal analysis, Writing – review & editing.

Declaration of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

• The interested reader can find the script at doi: 10.1016/j.agsy.2020.103021. In addition, it is possible to access to data that are useful for this script (doi: 10.6084/m9.figshare.21616803)