Geometrical frustration versus Kitaev interactions in BaCo₂(AsO₄)₂

Significance

The exactly solvable Kitaev model of bond-dependent near-neighbor interactions has drawn attention to quantum spins on the honeycomb lattice. But exotic quantum magnetism may also arise from competing interactions beyond nearest neighbors. Combining state-of- the-art theory and neutron scattering, we show that ferromagnetic nearest-neighbor interactions between effective spin-1/2 Co²⁺ spins in BaCo₂(AsO₄)₂ are frustrated by antiferromagnetic third neighbor interactions. While an in-plane field suppresses the resulting incommensurate order, a $\widehat{\mathbf{c}}-$ oriented field enhances quantum fluctuations. The spin Hamiltonian that we obtain will inform the search for quantum spin liquid physics in BaCo₂(AsO₄)₂ subjected to tilted fields.

Abstract

Recently, Co-based honeycomb magnets have been proposed as promising candidate materials to host the Kitaev spin liquid (KSL) state. One of the front-runners is BaCo₂(AsO₄)₂ (BCAO), where it was suggested that the exchange processes between Co²⁺ ions via the surrounding edge-sharing oxygen octahedra could give rise to bond-dependent Kitaev interactions. In this work, we present and analyze a comprehensive inelastic neutron scattering (INS) study of BCAO with fields in the honeycomb plane. Combining the constraints from the magnon excitations in the high-field polarized state and the inelastic spin structure factor measured in zero magnetic field, we examine two leading theoretical models: the Kitaev-type $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model and the XXZ $\text{-}{J}_1\text{-}{J}_3$ model. We show that the existing experimental data can be consistently accounted for by the XXZ $\text{-}{J}_1\text{-}{J}_3$ model but not by the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model, and we discuss the implications of these results for the realization of a spin liquid phase in BCAO and more generally for the realization of the Kitaev model in cobaltates.

There have been tremendous efforts to realize the Kitaev spin liquid (KSL), which is the ground state of the exactly solvable spin-1/2 model with the bond-dependent Ising interactions on the honeycomb lattice. The KSL is characterized by exotic excitations such as ℤ₂ gauge fluxes and Majorana fermions (1 –10), and may serve as a platform for topological quantum computation (11, 12). In the majority of candidate Kitaev materials, the physical mechanism to induce the bond-dependent Kitaev interaction relies on exchange processes between spins formed by 4d and 5d ions with large spin–orbit coupling (SOC), such as Ru³⁺ and Ir⁴⁺ (13, 14). However, in such materials, relatively large non-Kitaev interactions induce magnetic order at low temperature in place of the KSL (15 –27). One is thus left with the hope of potentially driving a system in close proximity to a KSL ground state using external tuning parameters such as the magnetic field, external pressure, and chemical doping (20, 28 –36).

A new mechanism for a more ideal material realization of the Kitaev model has recently been put forward for high-spin 3d ⁷ cobaltates (37, 38). It was suggested that exchange processes involving the t _2g and e _g orbitals can lead to a dominant ferromagnetic Kitaev interaction between the J _eff = 1/2 pseudospins with relatively weak non-Kitaev couplings. The honeycomb cobaltates are exciting as Kitaev candidate materials from an experimental point of view because large single crystals with few detectable structural defects can be grown, which is not the case for van der Waals materials like α-RuCl₃ and H₃LiIr₂O₆. Additionally, Kitaev materials based on Ir⁴⁺ are hampered by significant neutron absorption from ¹⁹¹Ir and a steep reduction of intensity with increasing wave vector transfer Q due to the magnetic form factor, complicating neutron scattering studies. Co²⁺-based materials face none of these challenges.

One candidate 3d ⁷ Kitaev material is the layered honeycomb magnet BaCo₂(AsO₄)₂ (see Fig. 1A ), hereafter referred to as BCAO. Heat capacity, magnetization, and neutron scattering studies show that BCAO develops incommensurate antiferromagnetic (AFM) order at T _N = 5.5 K with an ordering wavevector of k _c  = (0.27, 0, −1.31). At low temperatures, BCAO undergoes two successive phase transitions with an applied in-plane field: first at μ ₀ H _c1 = 0.33 T into a commensurate ordered state with wavevector k _c  = (1/3, 0, −1.31) and a second into a uniform and almost fully magnetized state at a critical field μ ₀ H _c2 = 0.55 T (39 –42). The critical field and temperature are very small for a transition metal oxide, indicating the tenuous nature of the magnetic order. Yet the field-driven state is almost fully magnetized, which indicates that BCAO has dominant ferromagnetic interactions. Here, we report measurements of the spin-wave excitations in the field-driven ferromagnetic (FM) state and use these in conjunction with thermomagnetic data to establish the underlying spin Hamiltonian for BCAO.

Fig. 1.

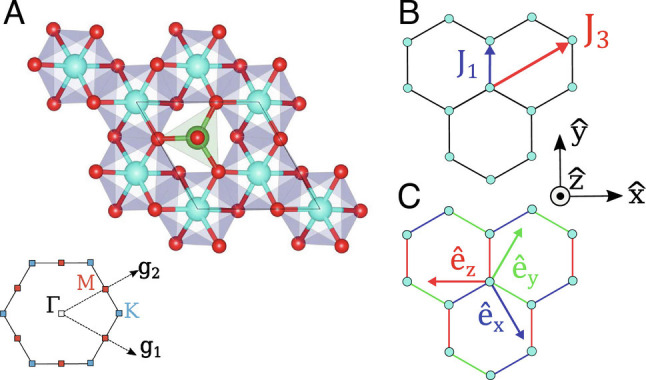
(A) Honeycomb lattice of BCAO viewed along the c-axis. Cobalt ions are in blue, oxygen in red, and arsenic in green. The first Brillouin zone of the hexagonal lattice is presented with the reciprocal lattice vectors g ₁ and g ₂. The high symmetry points M and K are depicted by the red and blue squares, respectively. (B) Representation of the couplings in the XXZ $\text{-}{J}_1\text{-}{J}_3$ model. The crystallographic frame is shown to the right in the black axes. (C) Local spin-frame for Kitaev interaction on the honeycomb lattice as seen from above. The x, y, and z bonds are shown in blue, green, and red coloring, respectively.

Notwithstanding the suggestions that Kitaev interactions might be realized in BCAO, an ab initio study suggested a different description (43). This investigation reported that trigonal distortions play an important role in the physics of BCAO and that it forms an easy-plane XXZ magnet with significant geometrical frustration associated with large third nearest-neighbor AFM interactions (XXZ $\text{-}{J}_1\text{-}{J}_3$ model). Previous studies on isostructural BaCo₂(PO₄)₂ were able to completely describe the ground state using a similar model (44).

In this work, we scrutinize the magnetic interactions in BCAO via a combination of inelastic neutron scattering studies (INS) and classical theoretical analyses. Little experimental work has been done to distinguish the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model with large Kitaev interactions from the XXZ $\text{-}{J}_1\text{-}{J}_3$ model in BCAO or, in fact, any cobaltates. Here, we report two detailed INS experiments: 1) a zero-field experiment with wavevector transfer Q in the (h k0) scattering plane and 2) an experiment with Q in the (h0l) plane and a magnetic field applied along the perpendicular [010] direction. This mapping of the magnetic excitation spectrum enables a critical examination of the two competing models. Our results are summarized as follows: We tightly constrain where BCAO may lie in parameter space for each model using linear spin-wave theory (LSWT) in the field-polarized regime. Within these constrained subspaces, we then examine the magnetic ground states that are realized classically. While both models accommodate incommensurate magnetic orders, the relevant spiral order with an ordering wavevector between the Γ and M points can be stabilized only in the XXZ $\text{-}{J}_1\text{-}{J}_3$ model. Additionally, molecular dynamics (MD) calculations indicate that the dynamical spin-structure factor at zero field is incompatible with large ferromagnetic Kitaev interaction, whereas all current data can be adequately accounted for using an XXZ $\text{-}{J}_1\text{-}{J}_3$ spin Hamiltonian with only weak bond-dependent interactions. Finally, for a suitably chosen parameter set of the XXZ $\text{-}{J}_1\text{-}{J}_3$ model, we are able to account for our measured in-plane magnetization curve, which features three successive plateaus separated by two field-induced phase transitions and only weak anisotropy for different in-plane directions. This is not the case for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model, for which the M(H) curves depend strongly on the applied in-plane field direction. Thus, in-plane anisotropy of M(H) curves can serve as a simple indicator for bond-dependent interactions on the honeycomb lattice. In summary, we show that BCAO does not realize the Kitaev model but rather is a geometrically frustrated easy-plane magnet with predominantly isotropic in-plane exchange interactions. We further provide a highly constrained set of exchange constants for this model.

Our work highlights the need for a thorough examination of the exchange interactions in the honeycomb cobaltates, a number of which have been proposed as KSL candidates. While a set of exchange parameters with a large Kitaev interaction may reproduce the observed INS excitation spectra in the high-field polarized state with a LSWT fit, it is important to examine whether this parameter set is consistent with the zero-field ordered state and thermodynamic measurements. Even though BCAO does not appear to have strong Kitaev interactions based on our work, it still may be close to a QSL driven by geometrical frustration and the quasi-2D nature of the spin system. The emergence of a continuum for an out-of-plane field upon the suppression of order revealed in THz spectroscopy (45) might be a signature of such a proximate QSL whose characteristics would most likely differ significantly from the nonabelian KSL. As a result, we speculate on a potential out-of-plane field-induced QSL in BCAO using the extracted exchange parameters and propose directions for future works.

Experimental Results

Static and Dynamic Spin Correlations.

Two INS experiments were performed on plates of single crystalline BCAO; see Methods for details. Constant energy slices in the (h0ℓ) scattering plane captured in the MACS experiment are shown in Fig. 2. Slices at T = 1.7(1) K are shown in Fig. 2A–D , and slices at T = 15.0(1) K are in Fig. 2E–H . Fig. 2A shows elastic scattering at 1.7 K where the 15-K data in Fig. 2E were subtracted as a background. Magnetic satellite peaks surrounding the $(0\overline{1}0)$ and $(1\overline{1}0)$ nuclear Bragg peak evidence the incommensurate magnetic order that forms below T _N . Magnetic satellite peaks are even apparent near the origin. The different intensities of the six satellite peaks surrounding a given nuclear Bragg peak reflect the structure factor of the magnetic order. The full width at half maximum (FWHM) vertical Q-resolution of MACS at $\mathbf{Q}=(100)$ is Δ Q = 0.09 Å⁻¹ = 0.2c^*. Thus, this (h k0) plane measurement does not access the nominal $\mathbf{k}=(0.27,0,-1.3)$ magnetic wave vector. The appearance of the magnetic Bragg peaks in Fig. 2A despite this is a first indication of the quasi-2D nature of the magnetic order: The magnetic peaks have tails extending along c^*, so they can be detected near l = 0. This is distinct from resolution effects and is made clearer in the second measurement in the (h0l) scattering plane (Fig. 3).

Fig. 2.

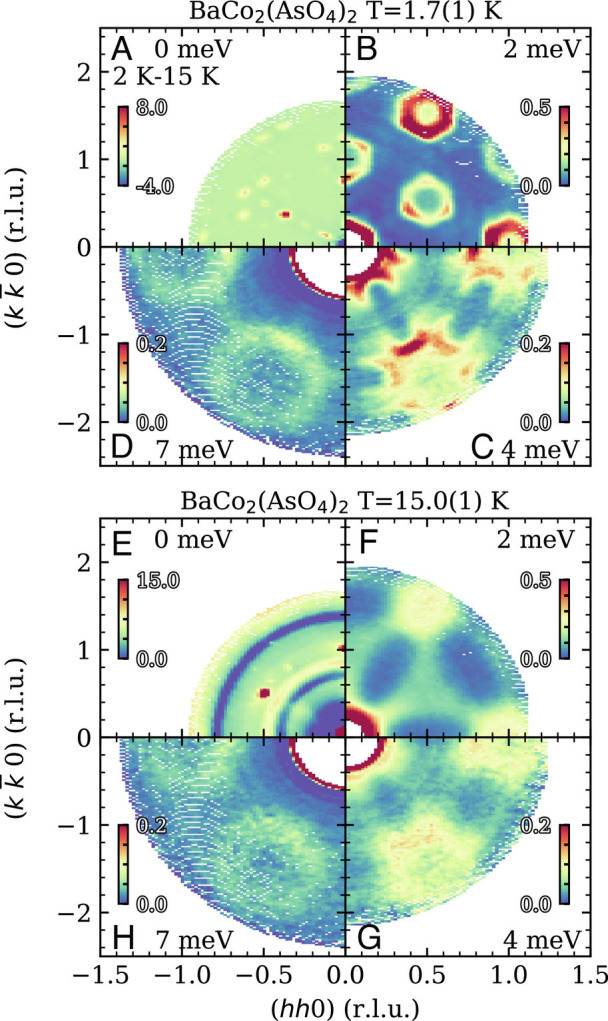
Zero-field neutron scattering intensity for BaCo₂(AsO₄)₂ as a function of energy transfer and temperature in the (h k0) scattering plane. Panels (A–D) show scattering at T = 1.7(1) K and (E–H) at T = 15.0(1) K. Energy transfers for each quadrant varied as labeled. Sample-out measurements were used as backgrounds for all measurements except (A), which shows the difference between elastic data acquired at T = 1.7(1) K and T = 15.0(1) K.

Fig. 3.

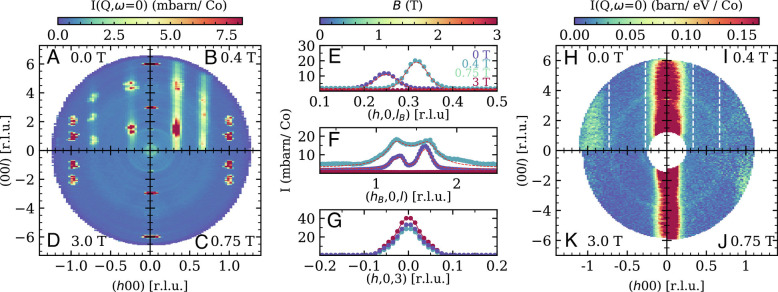
Elastic magnetic scattering from BaCo₂(AsO₄)₂ at T = 1.7 K as a function of field applied perpendicular to the scattering plane and along the $(\overline{1}20)$ direction. The scattering has been averaged in the energy transfer window of ±0.1 meV and k ∈ [ − 0.1, 0.1] along the (0k0) direction. The short-ranged nature of the correlations is evident at zero field (A) and in the commensurate ordered state at μ ₀ H = 0.4 T (B) through the broadness of the peaks in the (00l) direction. Panels (E and F) further highlight this, comparing cuts at the respective incommensurate wavevectors q(H)≡{q _h (H),0, q _l (H)}. For μ ₀ H = 0 T, q = (0.27, 0, −1.31) and for μ ₀ H = 0.4 T q = (1/3, 0, −1.31). Panel (G) compares cuts along the (h00) direction over the (003) structural Bragg peak. The increase in intensity in the field-polarized 3 T phase may be directly accounted for by the induced in-plane moment. The full width of the averaging windows for cuts in (E) and (G) are Δ k = 0.1 and Δ l = 0.6 and for (F) from Δ h = Δ k = 0.1. (H–K) Constant energy slices around the Γ point gap energy at four representative fields. The energy windows for panels (H–J) begin at ℏω = 0.4 meV and extend to ℏω = 1.58 meV, 1.80 meV, 1.90 meV, and 2.29 meV, respectively. Dashed white lines are shown at the incommensurate ordering wavevector for each respective field, with no lines for the magnetized phases without AFM order.

The spectrum of excitations extends well beyond k _B T _N  ≈ 0.5 meV, which is characteristic of a quasi-two-dimensional magnet with competing interactions where the ordering temperature is deeply suppressed relative to the exchange energy scale (46). With increasing energy transfer, a faceted ring of intensity centered at Γ points with increasing diameter is observed Fig. 2B–D . This indicates anisotropic dispersive excitations with the lowest energy mode at the Γ point as for a ferromagnet.

Even though BCAO is in the paramagnetic phase at T = 15 K, dynamic spin correlations give rise to a peak in low energy INS at the Γ point Fig. 2F . This indicates dynamic ferromagnetic correlations and is consistent with previous THz and inelastic neutron scattering studies (42, 45, 47). While some broadening indicating loss of spin-wave coherence is apparent, hexagonally faceted rings of inelastic magnetic scattering centered at the Γ point are clearly seen in Fig. 2 G and H . This indicates that dynamic correlations within honeycomb planes are established well above T _N .

Elastic scattering in the (h0ℓ) plane is shown in Fig. 3 for three different magnetic fields applied within the honeycomb plane. Complex peak structures are observed at the nuclear Bragg peaks (101) and (102). These reflect the mosaic distribution of the multicrystal sample that defines the transverse momentum resolution within the (h0ℓ) scattering plane. Fig. 3 B and D shows that elastic magnetic scattering beyond the nuclear allowed Bragg peaks is absent for in-plane fields of 0.75 T and beyond. In zero field (Fig. 3A ), magnetic Bragg peaks are seen at the incommensurate ordering wavevector $k_c=(0.27(1),0,-1.31(1))$ . The ordering wavevector becomes commensurate within the honeycomb plane $k_c=(1/3,0,-1.31)$ in a field of μ ₀ H  =  0.4 T applied along the $(1\overline{2}0)$ direction (Fig. 3C ). In both the 0-T and 0.4-T measurements, the magnetic scattering extends along the (00ℓ) direction, which indicates a reduced correlation length along the c-axis.

Fig. 3F shows cuts through these elastic scattering data along the (00ℓ) direction through the magnetic peaks for both μ₀ H = 0 T and μ₀ H = 0.4 T. The Lorentzian fits (dashed red lines) indicate correlation lengths of ξ = 70(2) Å and ξ = 22(1) Å along c in the incommensurate and the commensurate phases, respectively. These may be compared to the interlayer spacing of d = 7.64 Å, indicating a quasi-two-dimensional order and weak interactions between honeycomb layers. Correlations along (h00), in contrast, are limited by the instrumental resolution. After correcting for the resolution measured at the nuclear (003) Bragg peak, we infer a correlation length exceeding ∼300 Å or ∼20 × a as shown in Fig. 3E . Fig. 3G shows that in the fully field-polarized state at μ₀ H = 3 T, the (003) Bragg peak gains strength, which is consistent with magnetic diffraction from the magnetized cobalt. The 24(1)% increase of the (003) peak intensity in the 3-T applied field corresponds to an induced magnetization of 2.4(7) μ _B /Co, which may be compared to the magnetization of 2.9(1) μ _B /Co obtained from magnetization data.

It is interesting to contrast the $\mathbf{Q}$ -dependence of the elastic magnetic scattering as depicted in Fig. 3A–G with that of the low energy inelastic scattering in Fig. 3H–J . Integrating over energy transfer from ℏω = 0.4 meV through the Γ point excitation energy for each value of the applied field, we find a rod of scattering extending along $\mathbf{c}$ and passing through the Γ point. This contrasts with the $\mathbf{Q}$ -dependence of the elastic magnetic scattering, which at 0 T and 0.4 T has a finite in-plane component as apparent in Fig. 3A–C and also indicated by the dashed lines in Fig. 3 H and I . The dynamic spin correlations in BCAO thus resemble those of a 2D FM at all fields and contain no evidence of a soft mode with a wave vector matching that of the low-field AFM order.

Dispersive Magnetic Excitations.

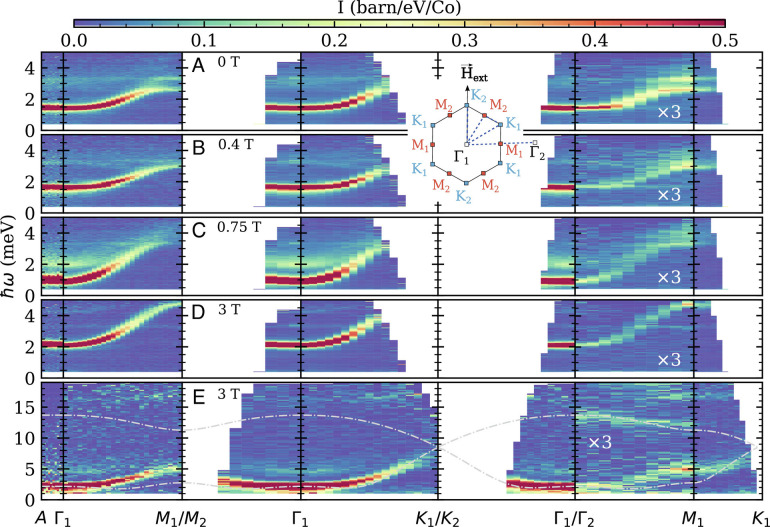
$\mathbf{Q}$ -ω slices through INS data for $\mathbf{Q}$ varying along high symmetry directions in the hexagonal Brillouin zone are shown for four values of magnetic field applied along the $(1\overline{2}0)$ direction in Fig. 4. The momentum space labels used on the horizontal axis are defined in the inset. In the almost fully magnetized state at 3 T (Fig. 4 D and E ), the scattering qualitatively follows expectations for a 2D easy plane honeycomb ferromagnet. There is a coherent gapped mode with lowest energy at the Γ point. In this partially polarized state, a sharp flat two-magnon mode is visible near 4.3(1) meV (Fig. 4 D and E ). At the lower fields (Fig. 4A–C ), there are strong diffuse contributions to the scattering near twice the field-dependent gap energy. At zero field in Fig. 4A , where the magnetic order has an incommensurate modulation within the basal plane, there are multiple modes at the M points indicative of a large unit cell. The first panels of these subplots show that there is no observable dispersion along (00ℓ), again pointing toward very weak magnetic interaction between honeycomb layers.

Fig. 4.

Magnetic excitation spectrum of BCAO as a function of field along high symmetry directions in the hexagonal Brillouin zone at T = 1.7 K. The path in r.l.u. notation is $(00\left[\ell ,+,\frac{1}{2}\right])-(00\ell )-(\frac{1}{2}0\ell )/(0\frac{1}{2}\ell )-(00\ell )-(\frac{1}{3}\frac{1}{3}\ell )/(\frac{\overline{1}}{3}\frac{2}{3}\ell )-(00\ell )/(10\ell )-(\frac{1}{2}0\ell )-(\frac{1}{3}\frac{1}{3}\ell )$ . This is represented by the dashed blue lines pictured in the diagram of the Brillouin zone, where H _ext denotes the direction of the applied field. In (A–D), ℓ ∈ [1, 3] for the in-plane slices in the high resolution E _i = 6 meV configuration. For the Γ-A direction, the path of L to $L+\frac{1}{2}$ is averaged over several Brillouin zones (L = 1, 2, 3, 4). For the Γ ₂ − M ₁ path, intensity has been scaled by a factor of three as indicated, and $R\overline{3}m$ symmetry operations have been applied to enhance statistics. The transverse-Q averaging window is 0.1 Å⁻¹ in all cases. Panel (E) shows the μ ₀ H = 3 T and E _i = 27 meV high energy configuration where ℓ ∈ [1, 9]. Data dominated by the tail of elastic scattering at energies below the FWHM elastic instrumental resolution of Δℏω = 0.15 meV for the low energy configuration and Δℏω= 1.5 meV for the high energy configuration have been masked. In frames (A–D), the enhanced count rate at 3.4(1) meV arises from a spurious accelerator-related process.

Once the AFM order is suppressed at μ ₀ H = 0.75 T, a magnon remains with a gap of ℏω = 1.0 meV and a continuum of two magnon excitations centered at ℏω  =  2.0 meV. This can be more clearly seen through cuts of the intensity at the Γ point as a function of field, as shown in Fig. 5. An unusual feature of the scattering is a difference in the dispersion relation between high symmetry paths that differ only in their orientation with respect to the applied magnetic field and thus the magnetization. The high symmetry zone boundary points nearest to the horizontal scattering plane are denoted M ₁ and K ₁, whereas the points closest to the vertical field direction are denoted M ₂ and K ₂ (see sketch in Fig. 4). Though the geometry of the instrument limits experimental access along the latter directions, a flattening of the mode may be observed at all nonzero fields in Fig. 4 for the K ₂-Γ ₁ and M ₂-Γ ₁ paths that lie along and at 30° to the field direction, respectively, when compared to the K ₁-Γ ₁ and M ₁-Γ ₁ paths that form larger angles with the field direction. This is direct evidence of SOC and anisotropic magnetic interactions.

Fig. 5.

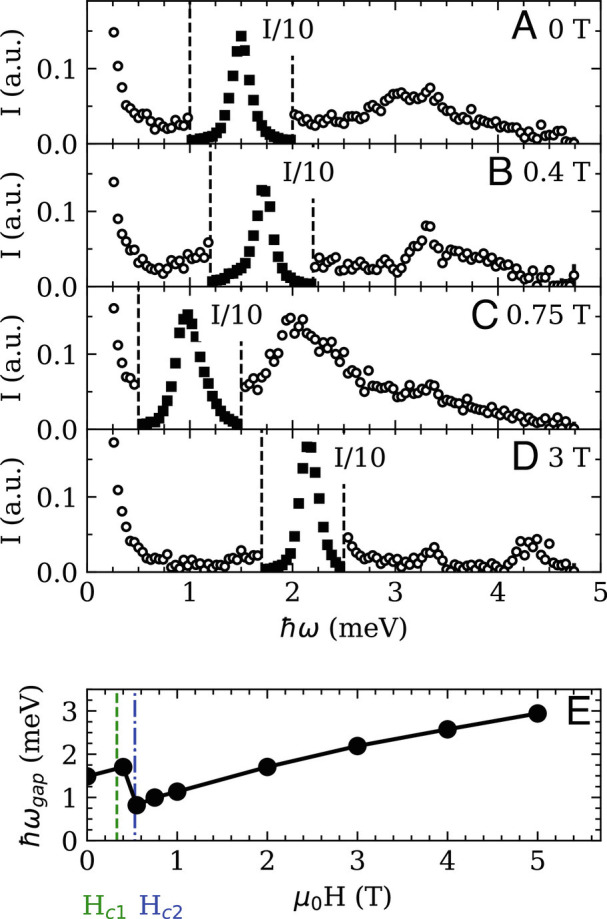
(A–D) Magnetic excitation spectrum for ${\mathrm{BaCo}}_2{({\mathrm{AsO}}_4)}_2$ at the Γ point for four different magnetic field strengths applied along the $(\overline{1}20)$ direction. Intensity data near the main peak in each spectrum have been scaled down by a factor of 10 and are shown as filled symbols. (E) The lowest Γ−point mode energy as a function of magnetic field applied along the ( $\overline{1}20)$ direction. In frames (A–D), the enhanced count rate at 3.X meV arises from a spurious accelerator-related process.

Fig. 4E shows a complementary higher-energy measurement in the 3 T field-polarized phase. A second magnon mode is observed near ℏω = 12 meV for wave vector transfer between Γ ₂ and M ₁. For a fully polarized magnet with two magnetic ions per unit cell, one indeed expects two magnon bands. This upper mode provides additional constraints on the model Hamiltonian. At the Γ point, the intensity of the upper magnon mode is zero due to the spin-structure factor, so that this excitation is not visible in Raman or THz optical spectroscopy. The broad excitation visible near ℏω = 15 meV in Fig. 4E is identified as a phonon through Raman scattering (45).

Fig. 5A–D shows the spectrum of inelastic magnetic scattering at the Γ point. For the lower fields where BCAO is not fully magnetized, a two-magnon continuum is visible as a broad peak centered at twice the gap mode energy. Fig. 4A shows an anomaly in the main magnon dispersion relation as it enters the two-magnon continuum (48). The broad two-magnon peak is particularly strong when the one-magnon gap is smallest at 0.75 T (Fig. 5C ), and magnons with energies beyond the two-magnon energy scale acquire significant physical width even though BCAO is uniformly magnetized at 0.75 T. Such interaction effects do not occur for the Heisenberg ferromagnet in a field where single magnons are exact eigenstates. At lower fields, the noncollinear and incommensurate nature of the ground state may play an important role in allowing spin waves to interact with the two-magnon continuum. These effects cannot be captured by the conventional 1/S expansion and the associated LSWT. When the system is fully magnetized at 3 T, the gap increases, the intensity of the two-magnon excitation decreases, and it approaches the resolution limit (Fig. 5D ). Though the magnon dispersion relation still intersects the two-magnon mode, there is no longer an anomaly. LSWT should provide a good account of the one magnon branch in this almost fully magnetized state. In this work, LSWT dispersions were calculated using both analytical methods and the SpinW package (49). The full field dependence of the gap at the Γ point is consistent with previous THz studies (45).

Analysis

Model Spin Hamiltonians.

There are currently two competing theoretical proposals for the microscopic description of BCAO. Following the theoretical prediction that a dominant Kitaev interaction can be obtained in high-spin 3d ⁷ cobaltates (37, 38), recent experiments were interpreted in terms of a $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model

$${\mathcal{H}}_{JK\Gamma \Gamma \text{'}}={\displaystyle \sum _{〈i,j〉\in \gamma }{S}_i^T{H}_{K,\gamma }^{\left(1\right)}{S}_j},$$ [1]

where

$$\begin{array}{cc}\hfill H_{K,x}^{(1)}& =\left(\begin{array}{ccc}J+K& {\mathrm{\Gamma }}^{\prime }& {\mathrm{\Gamma }}^{\prime }\\ {\mathrm{\Gamma }}^{\prime }& J& \mathrm{\Gamma }\\ {\mathrm{\Gamma }}^{\prime }& \mathrm{\Gamma }& J\end{array}\right),H_{K,y}^{(1)}=\left(\begin{array}{ccc}J& {\mathrm{\Gamma }}^{\prime }& \mathrm{\Gamma }\\ {\mathrm{\Gamma }}^{\prime }& J+K& {\mathrm{\Gamma }}^{\prime }\\ \mathrm{\Gamma }& {\mathrm{\Gamma }}^{\prime }& J\end{array}\right),\hfill \\ \hfill H_{K,z}^{(1)}& =\left(\begin{array}{ccc}J& \mathrm{\Gamma }& {\mathrm{\Gamma }}^{\prime }\\ \mathrm{\Gamma }& J& {\mathrm{\Gamma }}^{\prime }\\ {\mathrm{\Gamma }}^{\prime }& {\mathrm{\Gamma }}^{\prime }& J+K\end{array}\right),\hfill \end{array}$$ [2]

with a large ferromagnetic Kitaev coupling and small isotropic and off-diagonal terms (i.e., K <  0 and |K|≫|J|,|Γ|,|Γ′|). The spins in this model are represented in the Kitaev frame (KF) defined in Fig. 1C . The most general form of the nearest-neighbor coupling matrix consistent with the symmetry of BCAO contains six independent terms and is given in SI Appendix . The simpler form used here neglects the lifting of C _2v symmetry associated with the puckering of the honeycomb layer.

Alternatively, recent ab initio calculations (43) suggest that BCAO can be described by an XXZ $\text{-}{J}_1\text{-}{J}_3$ model where the spin Hamiltonian is approximately isotropic within the basal plane

$${\mathcal{H}}_{\text{XXZ-}{J}_1\text{-}{J}_3}={\displaystyle \sum _{i,j\in \gamma }{S}_i^T{H}_{\text{XXZ},\gamma }^{\left(1\right)}{S}_j+{\displaystyle \sum _{i,j}{S}_i^T{H}_{\text{XXZ}}^{\left(3\right)}}}{S}_j,$$ [3]

with

$$\begin{array}{cc}\hfill H_{\text{XXZ},z}^{(1)}& =\left(\begin{array}{ccc}{J}_{\mathit{xy}}^{(1)}+D& E& 0\\ E& J_{\mathit{xy}}^{(1)}-D& 0\\ 0& 0& J_z^{(1)}\end{array}\right),\hfill \\ \hfill H_{\text{XXZ},y}^{(1)}& =U_{2\pi /3}^T{H}_{\text{XXZ},z}^{(1)}{U}_{2\pi /3},\hfill \\ \hfill H_{\text{XXZ},x}^{(1)}& =U_{2\pi /3}{H}_{\text{XXZ},z}^{(1)}{U}_{2\pi /3}^T,\hfill \\ \hfill H_{\text{XXZ}}^{(3)}& =\left(\begin{array}{ccc}{J}_{\mathit{xy}}^{(3)}& 0& 0\\ 0& J_{\mathit{xy}}^{(3)}& 0\\ 0& 0& J_z^{(3)}\end{array}\right),\hfill \end{array}$$ [4]

where the second sum is taken over third nearest-neighbors, the spins are represented in the crystallographic frame (CF) (Fig. 1B ), and U _2π/3 denotes a 2π/3 rotation about the crystallographic c-axis perpendicular to the honeycomb plane. The most general form of $H_{\text{XXZ},\alpha }^{(1)}$ consistent with the symmetry of BCAO is given in the SI Appendix . The simpler four-parameter form used here is based on ref. (43). In this model, the global U(1) symmetry of the pure X X Z model is broken by the D and E terms. These are assumed to be small albeit finite to open a gap in the magnetic excitation spectrum as observed in this work (Figs. 4A and 3H–J ). The dipole interaction between NN Co site may be estimated by $U\approx \frac{{\left(g\mu B\right)}^2}{r_{nn}^3}<{10}^{-2}\text{meV}$ , which is insignificant compared to the scale of exchange interactions and the applied field in this AFM material.

It is important to note that both models can be described in either the crystallographic frame (CF) or the Kitaev frame (KF). The coordinate transformation is described in SI . While the most general bilinear nearest-neighbor spin Hamiltonian consistent with the space group symmetry involves six parameters, the J K Γ Γ′ and XXZ $\text{-}{J}_1\text{-}{J}_3$ models are different approximations with just four parameters each. As a result, the J K Γ Γ′ interaction is most conveniently represented in the Kitaev frame (( 2 )), while the XXZ $\text{-}{J}_1\text{-}{J}_3$ model is more conveniently expressed in the crystallographic frame Eq. 4 . Expressing the XXZ nearest-neighbor interaction in the Kitaev frame results in $K=D-\sqrt{2}F\approx 0$ ( SI Appendix ). Thus, the two models are distinct approximations relative to the most general form of the interactions. In the following, we critically examine both proposals. To discriminate between the two, we constrain the microscopic coupling constants and determine how accurately they can reproduce experimental observations such as the INS spectrum, the ground state magnetic order, and the field-dependent magnetization.

It is also assumed that the essential physics of BCAO can be captured by a purely two-dimensional model. This assumption can be tested using LSWT. Using the dispersion from A-Γ ₁ (Fig. 4, column 1), we place an upper limit on the interlayer coupling J ₁′. As can be seen in Fig. 4, there is no noticeable dispersion along this path. By tuning J ₁′ in LSWT, we find an upper limit of |J ₁′| ≈ 0.3 meV, at which point the dispersion predicted in LSWT exceeds the instrumental resolution of Δℏω = 0.06 meV (FWHM). We therefore may reasonably model BCAO as a purely two-dimensional spin system.

Field Dependence of the Magnon Dispersion in the Polarized Regime.

To fit a model with a large number of free parameters, it is useful to identify constraints that restrict the problem to a smaller region of phase space. In our case, a straightforward method to initially restrict the set of coupling constants to an experimentally relevant subspace is to fit the field dependence of the Γ point magnon gap in the polarized regime illustrated in Fig. 5E and the position of the second mode at the zone center (Fig. 4E ). Within LSWT, the energies of these modes in the field-polarized state at the Γ point are

$$E_{JK\Gamma {\Gamma }^{\prime }}^{(1)}(k=0)=\sqrt{|h{|}^2+3S(\Gamma +2{\Gamma }^{\prime })|h|},$$ [5a]

$$\begin{array}{l}{E}_{JK\Gamma {\Gamma }^{\prime }}^{(2)}(k=0)=\left[\left((6J+2K-2\Gamma -4{\Gamma }^{\prime })S-\left|h\right|\right)\right.\\ {\left.\left((6J+2K+\Gamma +2{\Gamma }^{\prime })S-\left|h\right|\right)\right]}^{1/2},\end{array}$$ [5b]

and

$$E_{\text{XXZ}}^{(1)}(k=0)=\sqrt{|h{|}^2+3S(J_z^{(1)}+J_z^{(3)}-J_{xy}^{(1)}-J_{xy}^{(3)})|h|},$$ [6a]

$$\begin{array}{l}{E}_{\text{XXZ}}^{(2)}(k=0)=\left[\left(6(J_{xy}^{(1)}+J_{xy}^{(3)})S-\left|h\right|\right)\right.\\ {\left.\left(3(J_{xy}+J_{xy}^{(3)}+Jz+J_z^{(3)})S-\left|h\right|\right)\right]}^{1/2},\end{array}$$ [6b]

for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ and XXZ $\text{-}{J}_1\text{-}{J}_3$ models, respectively. Here, h = g μ _B B, and we use the ab initio determined g−factors g _{a b}  = 5 and g _c  = 2.7 (43) for in-plane and out-of-plane fields, respectively. For both models, these mode energies depend on only two specific combinations of the exchange parameters: 3J + K and Γ + 2Γ′ for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model. For the XXZ $\text{-}{J}_1\text{-}{J}_3$ model, the Γ point magnon energies are controlled by $J_{\mathit{xy}}^{(1)}+J_{\mathit{xy}}^{(3)}$ and $J_z^{(1)}+J_z^{(3)}$ . They are independent of D and E, which must therefore be constrained by other data.

To find a specific combination of couplings that agrees with the field-dependent Γ-point mode energies, we introduce the goodness-of-fit measure

$$\begin{array}{c}{\chi }^2={\displaystyle \sum }_{i,n}\frac{{\left(E_i^{\text{exp}}(Hn)-E_i^{\text{fit}}(Hn)\right)}^2}{{(\text{Δ}{E}_i^{\text{exp}}(Hn))}^2},\end{array}$$ [7]

Here, the sum extends over the Γ-point modes (i = 1, 2) and the applied fields H _n  >  H _c2, where scattering data were acquired (Fig. 5E ). $\text{Δ}{E}_i^{\text{exp}}(H_n)$ is the experimental uncertainty in the mode energies obtained from Lorentzian fits to the INS peaks (Fig. 5 A–D ).

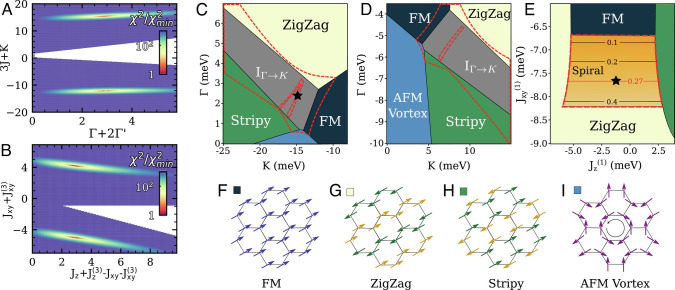
The resulting map of the normalized χ ² is presented in Fig. 6 A and B for the two models. For each, we obtain two localized regions in parameter space that reproduce the field dependence of the zone center magnon energies. These regions are given by

Fig. 6.

(A and B) Normalized goodness of fit χ ² for the field dependence of the Γ−point mode for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ and XXZ $\text{-}{J}_1\text{-}{J}_3$ models. (C and E) Classical phase diagram around the only regions where incommensurate order was observed for the restricted parameter space that reproduces the field-dependent Γ−point mode energies. (C and D) correspond to the constraints Γ + 2Γ′=3.0 meV and 3J + K = −12.1 meV, whereas (E) corresponds to $J_{\mathit{xy}}^{(1)}+J_{\mathit{xy}}^{(3)}=-5.0$ meV and $J_z^{(1)}+J_z^{(3)}=-2.0$ meV. The red dashed lines enclose the regions where the Luttinger–Tisza approximation fails, and the ground state is instead determined by a combination of simulated annealing and a variational single-Q Ansatz. The contour lines in the spiral phase of (E) represent the magnitude of the ordering wavevector. The black stars in panels (C) and (E) are the representative points used for both models (see Eqs. 14 and 13 ). (F–I) Representative spin configurations for the reported classical commensurate phases with the corresponding color in the phase diagrams.

$$\left\{\begin{array}{l}3J+K=-12.1(1)\text{meV},\hfill \\ \Gamma +2{\Gamma }^{\prime }=3.0(1) \text{meV},\hfill \end{array}\right.$$ [8a]

and

$$\left\{\begin{array}{l}3J+K=15.2(1)\text{meV},\hfill \\ \Gamma +2{\Gamma }^{\prime }=3.0(1) \text{meV},\hfill \end{array}\right.$$ [8b]

for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model, and

$$\left\{\begin{array}{l}{J}_{xy}^{(1)}+J_{xy}^{(3)}=-5.0(1)\text{meV},\\ J_z^{(1)}+J_z^{(3)}=-2.0(1)\text{meV},\end{array}\right.$$ [9a]

and

$$\left\{\begin{array}{l}{J}_{xy}^{(1)}+J_{xy}^{(3)}=4.0(1)\text{meV},\\ J_z^{(1)}+J_z^{(3)}=7.0(1)\text{meV},\end{array}\right.$$ [9b]

for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model. We restrict the rest of our analysis to these four sets of constraints.

Magnetic Ground State.

To further constrain the parameters, we investigate whether the two models can reproduce the experimentally observed incommensurate magnetic order within this restricted parameter set. We note that the magnetic ground state of BCAO is not an entirely experimentally settled issue. The zero-field ordered state was long-accepted to be a simple spiral structure with incommensurate ordering wavevector between the Γ and M points (40). However, a recent spherical neutron polarimetry study (42) indicates that the magnetic structure is better described by double-zigzag spin-chains forming a ↑ ↑ ↓↓ pattern with some small out-of-plane canting angle. These are both frustrated incommensurate structures that lie close in energy. Subtle effects like quantum fluctuations or distortions of the lattice might favor either the incommensurate spiral or double-zigzag order. Here, we do not address such issues and look to stabilize the single $\mathbf{k}$ incommensurate spiral order for simplicity.

To obtain a classical magnetic phase diagram, we employ the Luttinger–Tisza approximation (50, 51), in which a direct solution of the classical model can be obtained by relaxing the constraint of fixed spin length at every site. In regions where the Luttinger–Tisza approximation fails (i.e., the resulting solution does not respect the hard constraints on the spin length on all sites), we have employed a combination of simulated annealing on finite clusters with 2 ⋅ 26² sites and variational single-Q Ansatz of the form

$$\begin{array}{c}{S}_i=\sqrt{1-{\alpha }_i^2}\left[\cos (Q·r_i){\widehat{e}}_i^x+\sin (Q·r_i){\widehat{e}}_i^y\right]+{\alpha }_i{\widehat{e}}_i^z,\end{array}$$ [10]

where the canting out of the rotation plane α _i and the orthonormal frames ( ${\widehat{\mathbf{e}}}_i^x,{\widehat{\mathbf{e}}}_i^y,{\widehat{\mathbf{e}}}_i^z$ ) are sublattice-dependent variational parameters. An extensive classical phase diagram for all reasonable values of the coupling constants that respect the constraints Eqs. 8 and 9 was performed by varying the two largest remaining free parameters for both models (i.e., J and Γ for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model and $J_{\mathit{xy}}^{(1)}$ and $J_z^{(1)}$ for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model). We will present this extensive phase diagram in an upcoming publication. Here, we report the experimentally relevant regions where incommensurate magnetic order was observed for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model in Fig. 6 C and D and for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model in Fig. 6E .

For the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model, we find two regions that support a ground state where the ordering wavevector is between the Γ and K points. This phase is represented in gray in Fig. 6 C and D , and we label it as I _Γ → K . Such a magnetic order is not pertinent to the ground state of BCAO where the ordering wavevector is between the Γ and M points. To investigate whether this incommensurate spiral order could be stabilized by the introduction of a third nearest-neighbor isotropic interaction J ₃, we updated the constraints presented in Eq. 8 to account for this new coupling and obtained the corresponding phase diagram by varying K and Γ as presented in Fig. 6 C and D for J ₃ ranging from −5 meV to 5 meV. The details of this analysis will be presented in a future publication. For all values of J ₃, the right Γ to M ordering is not observed in the presence of a significant Kitaev term. Thus, we find no values of the coupling constants for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model with large Kitaev interactions that can reproduce the field dependence of the Γ point magnon energies and the correct classical ground state even with the addition of third nearest-neighbor Heisenberg interactions. This is already a cogent indication that the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model with large bond-dependent interactions may not provide an accurate description of BCAO.

In contrast, it has been reported that the XXZ $\text{-}{J}_1\text{-}{J}_3$ model on the honeycomb lattice supports spiral incommensurate order with an ordering wavevector that smoothly interpolates between the Γ and M points with a specific magnitude of |k _c | = 0.27 for $J_{\mathit{xy}}^{(3)}/|J_{\mathit{xy}}^{(1)}|\approx 0.34$ and $J_{\mathit{xy}}^{(1)}<0$ (52). This incommensurate spiral region is represented in Fig. 6E , where there exists a line that reproduces the experimentally determined incommensurate wavevector between zigzag and stripy phases that are stabilized for large values of $|J_z^{(1)}|$ . This spiral phase with |k _c | = 0.27 is also stable to the addition of anisotropic terms provided that they are sufficiently small (i.e., approximately if |D|,|E|< 0.2 meV). It is consequently natural to account for both the field dependence of the gap and the incommensurate magnetic structure of BCAO with the XXZ $\text{-}{J}_1\text{-}{J}_3$ model.

Molecular Dynamics.

Within this restricted parameter space, we can compute the dynamical spin structure factors (DSSF) of both models to directly compare against the INS results. The momentum and energy-dependent dynamic structure factor is given by

$$\begin{array}{c}{\mathcal{S}}^{\mu \nu }(q,\omega )=\frac{1}{2\pi N}{\displaystyle \sum }_{i,j}^N\int \text{dt}{e}^{-iq·(r_i-r_j)+i\omega t}〈S_i^{\mu }(t)S_j^{\nu }(0)〉,\end{array}$$ [11]

where N is the number of lattice sites. We investigated the spectrum with unpolarized neutrons, described by

$$\begin{array}{c}\mathcal{S}(q,\omega )=\frac{1}{2}{\displaystyle \sum }_{\mu ,\nu }\left[{\widehat{z}}_{\mu }·{\widehat{z}}_{\nu }-\frac{({\widehat{z}}_{\mu }·q)({\widehat{z}}_{\nu }·q)}{q^2}\right]{\mathcal{S}}^{\mu \nu }(q,\omega ).\end{array}$$ [12]

Here, ${\widehat{z}}_{\mu }$ are the basis vectors for the KF for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model or the CF for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model. We study the classical limits of both models using finite temperature Monte Carlo and obtain the DSSF using MD. The details of the numerical techniques can be found in supplementary information.

Based on the constraints described in the previous sections, we choose the parameters

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J_{\mathit{xy}}^{(1)}& =-7.6\mathrm{meV},\hfill \\ \hfill J_z^{(1)}& =-1.2\mathrm{meV},\hfill \\ \hfill J_{\mathit{xy}}^{(3)}& =2.5\mathrm{meV},\hfill \\ \hfill J_z^{(3)}& =-0.85\mathrm{meV},\hfill \\ \hfill D& =0.1\mathrm{meV},\hfill \\ \hfill E& =-0.1\mathrm{meV},\hfill \end{array}\end{array}$$ [13]

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J& =0.97\mathrm{meV},\hfill \\ \hfill K& =-15.0\mathrm{meV},\hfill \\ \hfill \mathrm{\Gamma }& =2.5\mathrm{meV},\hfill \\ \hfill {\mathrm{\Gamma }}^{\prime }& =0.25\mathrm{meV},\hfill \end{array}\end{array}$$ [14]

as the best fit for both models. We note that Eq. 13 may equivalently be written in the KF and that Eq. 14 may be written in the CF. The corresponding Hamiltonian parameters are given in the supporting material. The two models support the incommensurate spiral and I _Γ → K phases respectively, as depicted in Fig. 6. For XXZ $\text{-}{J}_1\text{-}{J}_3$ , the remaining free parameters $J_z^{(1)}$ , D, and E were chosen to be small enough in magnitude to yield the correct spiral order, approximately reproduce the gap observed at zero field in Fig. 4A , and provide the best reproduction of the neutron scattering in the polarized regime as presented in Fig. 4C–E . However, even with our tight constraints on the allowed parameter sets, we note that there may be other proximate parameter sets that yield similar results. The parameters for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model were also chosen to provide the best fit to the neutron scattering data in the polarized regime within the I _Γ → K phase.

Fig. 7 shows the constant energy slices of the DSSF for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ (Fig. 7A–H ) and the XXZ $\text{-}{J}_1\text{-}{J}_3$ (Fig. 7I–P ) models, which may be compared to the experimental results in Fig. 2. The $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model does not reproduce any qualitative features seen in the in-plane scattering experiments apart from a buildup of spectral weight at the Γ point due to the ferromagnetic nature of the dominant Kitaev term. In contrast, the XXZ $\text{-}{J}_1\text{-}{J}_3$ model is remarkably able to reproduce many features in the higher energy cuts. The resemblance is especially striking when comparing the DSSF around 2 meV and above with the 15 K experimental measurements where the observed six-fold rotationally symmetric high-intensity hexagonal structure joined by low-intensity oval pockets is clearly reproduced in the DSSF. We also present the DSSF along a path in the first Brillouin zone for both models in Fig. 8 A and B , which may be compared with the corresponding neutron scattering data in Fig. 6A . It should be emphasized that even though the underlying spiral magnetic order is consistent with BCAO, it is highly nontrivial that the XXZ $\text{-}{J}_1\text{-}{J}_3$ model also account for the full excitation spectrum. The better agreement between numerical results and high-temperature data is expected since we are dealing with purely classical two-dimensional simulations.

Fig. 7.

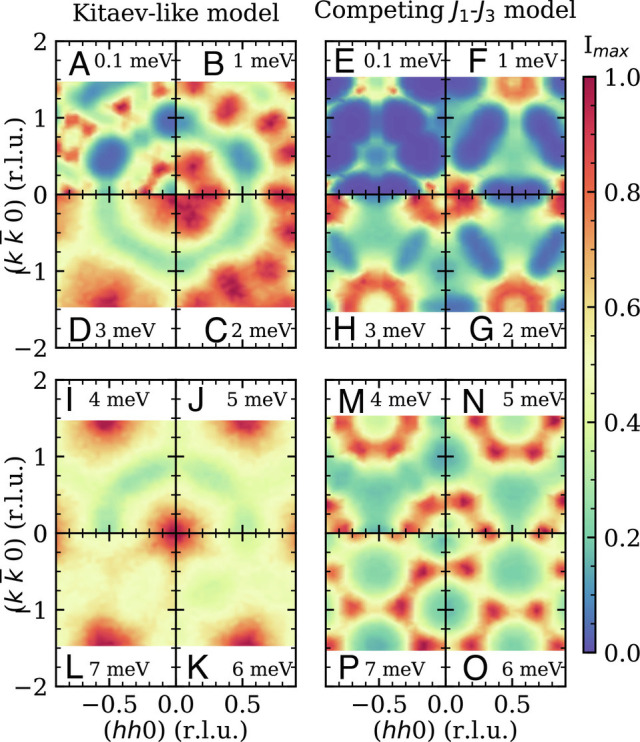
(A to P): Constant energy slices of the dynamical spin structure factor $\mathcal{S}(Q,\omega )$ calculated by molecular dynamics at T = 2 K. These may be compared to the experimental results in Fig. 2. Color scales are arbitrary but consistent within each model. Subplots in the left column (A–D and I–L) with blue spines show constant energy slices for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model and subplots in the right column (E–G and M–P) for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model with the parameter set presented in Eqs. 14 and 13 , respectively.

Fig. 8.

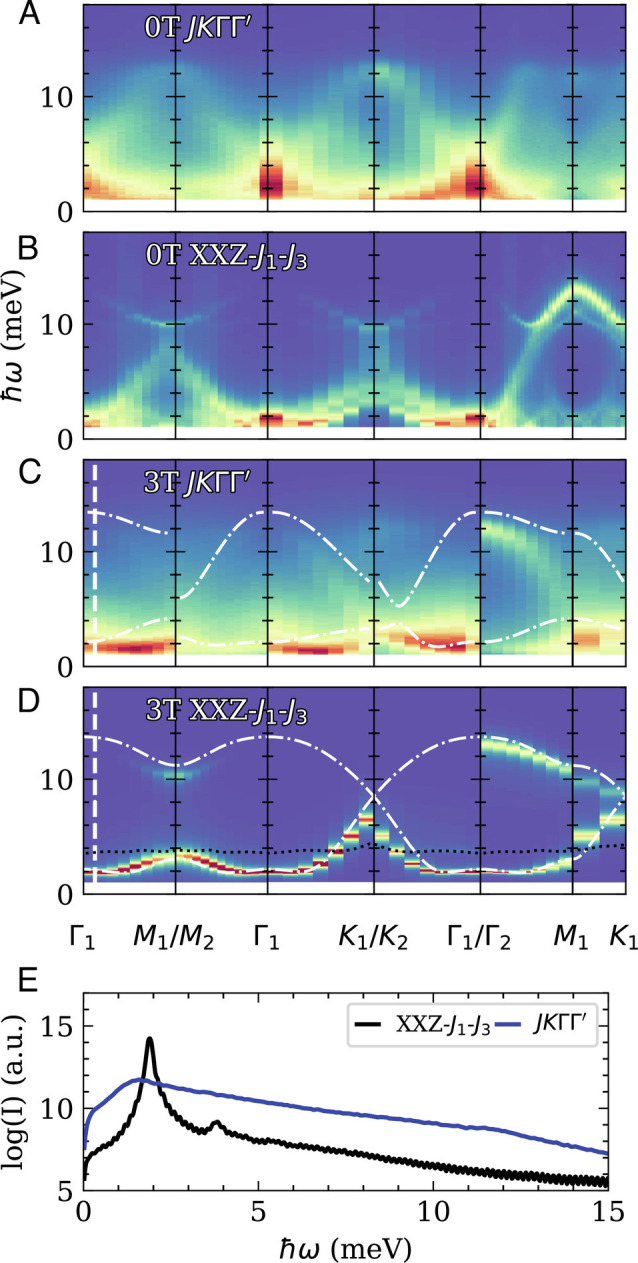
Dynamical spin-structure factor obtained by MD between high symmetry points for both the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model (A and C) and the XXZ $\text{-}{J}_1\text{-}{J}_3$ model (B and D) with an in-plane field of 0 T at T = 1 K and 3 T at T = 2 K, respectively. Parameters used for both models are given by Eqs. 14 and 13 . The LSWT dispersion for each model and set of parameters are overlaid in (C) and (D) using the dashed dotted line. For the XXZ $\text{-}{J}_1\text{-}{J}_3$ case, the dotted black line represents the lower edge of the two-magnon continuum calculated using the LSWT dispersion. (E) Intensity cut near the Γ point (along the vertical dashed line in C and D) for both models at 3 T.

Next, we present the DSSF as a function of energy between high symmetry points in the field-polarized regime at μ ₀ H = 3 T with the LSWT dispersion overlaid in Fig. 8 C and D . The MD results for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model with our parameters show good agreement with experimental measurements reported in Fig. 4 D and E . As can be seen from the intensity cut near the zone center in Fig. 8E , MD simulations even capture the two-magnon mode reported in Fig. 5D and THz spectroscopy (45, 47). In contrast, the experimental results are not well described by our parameter set for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model. LSWT for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model predicts a magnon dispersion that differs significantly when comparing the Γ − M ₁ with the Γ − M ₂ path. Such a large anisotropy is incompatible with our INS measurements presented in Fig. 4. MD further predicts a continuum with no clear resonances as highlighted by the intensity cut near the Γ point presented in Fig. 8E . The sharp magnon bands observed experimentally are compatible with the XXZ $\text{-}{J}_1\text{-}{J}_3$ model but clearly inconsistent with our MD simulation of the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model.

The magnon dispersions predicted from LSWT and MD for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model seem to be in close correspondence for the whole scattering path considered. The most significant discrepancy is around the Γ point where the LSWT magnon band is concave down with a minimum around the incommensurate ordering wavevector, whereas the MD bands are flatter and concave up as the experimental data for BCAO (Fig. 4). This disagreement between LSWT and MD indicates the presence of important nonlinearities, which are taken into account in MD but ignored in LSWT and which lead to a significant renormalization of the magnon dispersion. Indeed, we observe that for larger values of the magnetic field, the negative concavity of the LSWT is progressively suppressed until it is concave up as observed in MD ( SI Appendix ). For such large fields, the relative importance of nonlinearities is progressively suppressed, and thus, MD and LSWT are expected to be in excellent agreement. This comparison between predictions from MD and LSWT suggests that the lack of a minimum in the dispersion relation near the incommensurate wave vector is a nonlinear effect.

In-Plane Magnetization.

As a final comparison between the two models and experiments, we examine the in-plane magnetization for different magnetic field orientations. Increasing the field from zero, three successive magnetization plateaus can be observed in Fig. 9A , where the transitions from one plateau to the next correspond to the field-induced magnetic phase transitions at H _c1 and H _c2, respectively. Measuring the magnetization with magnetic fields along the x- and y-axes of the CF (Fig. 1B ), only a very small anisotropy is observed around the first and second transitions. Using our parameter set for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model, the qualitative resemblance between the measurements and the magnetization curves obtained from finite temperature Monte Carlo at T = 0.695 K is striking (Fig. 9B ). The three successive plateaus are clearly observed, and the small anisotropy between the curves for the two different field orientations near the transitions is reproduced. We have verified that the intermediate field-driven phase also has an ordering wavevector of magnitude |k _c |=1/3 as observed experimentally.

Fig. 9.

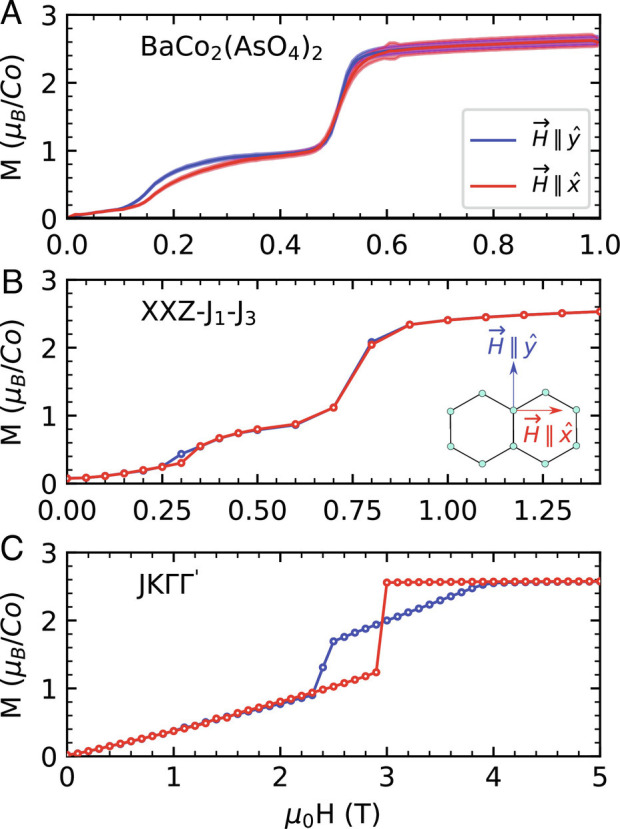
(A) In-plane angle-dependent magnetization for ${\mathrm{BaCo}}_2{({\mathrm{AsO}}_4)}_2$ measured on a small single crystal sample. The red (blue) curve corresponds to a field orientation along the $\widehat{\mathbf{x}}$ -axis ( $\widehat{\mathbf{y}}$ -axis) as depicted in the inset. For clarity, the magnetization curves are shown only for an increasing field from 0 T. (B) Magnetization curves calculated using Monte Carlo methods for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model with the set of exchange parameters given in ( 13 ) at a temperature of T = 0.695 K and (C) for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model with the parameter set in ( 14 ) (T = 0 K).

In stark contrast, as presented in Fig. 9C , the magnetization curves predicted from Monte Carlo at T = 0 K for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model with our parameter set yields magnetization curves that differ significantly for the two directions. For a field along the y-axis, Monte Carlo for the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model yields an intermediate field-induced phase transition before the transition to the field polarized phase, whereas for a field along the x-axis, there is a single low-field transition directly to a fully polarized state. It should additionally be noted that, especially for the magnetic field along the $\widehat{\mathbf{y}}$ -direction, the system transitions to the polarized regime at a much larger value of the magnetic field than in experiments. The temperatures in each case are chosen such that they most closely reproduce the experimentally observed M(H) curves, the details of which are in the SI Appendix .

Discussion and Conclusions

Though our initial interest in BCAO was as a candidate Kitaev material, our results strongly favor the XXZ $\text{-}{J}_1\text{-}{J}_3$ over the Kitaev model. We are able to differentiate between the two models by examining the zero-field ground state of BCAO using constraints from LSWT. We find that the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model cannot simultaneously reproduce the field dependence of the Γ point modes and the magnetic order found in BCAO. Even with the addition of a third nearest-neighbor Heisenberg interaction, the Γ − M point incommensurate order reported for BCAO is incompatible with dominant ferromagnetic Kitaev interactions. In contrast, the spiral magnetic order is reproduced in the XXZ $\text{-}{J}_1\text{-}{J}_3$ picture with parameters that also reproduce the Γ point mode versus field. Perhaps the most striking contrast between the two models is seen in our calculated DSSF results presented in Fig. 7. Qualitatively, it is immediately obvious that the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model fails to describe the zero-field INS, whereas the XXZ $\text{-}{J}_1\text{-}{J}_3$ model is able to capture some highly nontrivial features. Some of these features are the result of a strong renormalization of the excitation spectra from nonlinear magnon-magnon interactions as revealed through a comparison of MD results to LSWT.

The in-plane magnetization curves obtained for the XXZ $\text{-}{J}_1\text{-}{J}_3$ model at finite temperature are in remarkable qualitative agreement with our BCAO measurements and can even reproduce subtle features such as a weak in-plane anisotropy. In contrast, the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model yields a highly anisotropic magnetization that cannot be reconciled with experiments. Our work provides compelling evidence that BCAO should be described as an XXZ $\text{-}{J}_1\text{-}{J}_3$ model system with only small bond-dependent interactions. This description is able to reproduce many nontrivial measurements, where the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model fails. Furthermore, we provide strong constraints on the exchange parameters in this model to enable quantitative comparisons between theory and experiments on BCAO.

Our work stresses the need for a critical reexamination of the proposal for Kitaev physics in cobaltates. These materials may not in fact fall within the regime of interest that was considered in the theoretical proposals for Kitaev physics in 3d systems (37, 38). Specifically, to generate dominant Kitaev interactions in 3d transition metal compounds, direct hopping was assumed to be much weaker than ligand-assisted hopping. The easy-plane anisotropy we observe suggests that local distortions of the crystal field environment may play an important role in these compounds. Thorough experimental and ab initio theoretical examinations of the exchange interactions of the cobaltate KSL candidates are needed. For a firm conclusion, it is important to ensure that the proposed model is compatible with the observed ground state order and magnetization data. Compounds in need of such reassessment include Na₂Co₂TeO₆, Na₃Co₂SbO₆ (53 –56), and Li₃Co₂SbO₆ (57, 58), which all feature strong easy-plane anisotropy and field-driven transitions (53) analogous to BCAO.

In contrast to the XXZ $\text{-}{J}_1\text{-}{J}_3$ model, at high fields, the thermodynamic properties of the $\mathrm{JK}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\prime }$ model vary strongly with the in-plane field direction (Fig. 9C ) (26, 59 –61). Such strong in-plane anisotropy has in fact been observed for the leading Kitaev candidates α-RuCl₃ (62 –64) and β−Li₂IrO₃ (65), but it is not present for BCAO (Fig. 9). Magnetization measurements versus in-plane field direction can thus be an effective method to screen potential model systems. For cobaltates whose magnetization cannot be accounted for by the XXZ $\text{-}{J}_1\text{-}{J}_3$ model, single-crystal INS with an in-plane field can subsequently be employed to establish the spin Hamiltonian as we have done for BCAO in this work.

Although BCAO does not appear to realize large Kitaev-type interactions but rather an XXZ $\text{-}{J}_1\text{-}{J}_3$ model, its physical properties are still of great interest. BCAO now presents a rare case of an almost perfect two-dimensional honeycomb magnet with well-known values for its dominant exchange interactions ( Eq. 13 ). Previous theoretical investigations indicate that a QSL ground state may be possible for in-plane isotropic models with competing interactions on the honeycomb lattice (66 –68). Thus, the competition between first and third nearest-neighbor interactions that we have documented for BCAO may place this material in proximity to a QSL. Although the theoretical work indicates that a second nearest-neighbor interaction (which seems to be negligible for BCAO) is needed to stabilize a QSL, a QSL might be accessible for BCAO in the presence of a suitably oriented external magnetic field. This possibility has, to our knowledge, not been explored yet. The continuum scattering reported by THz spectroscopy with a large c-oriented field (45) may signal the onset of such a phase. Possibly related to this, the strong interaction between the one- and two-magnon modes reported here (Fig. 3) is also unusual and interesting. Thus, there are promising directions for future studies of BCAO and the extended family of honeycomb cobaltates.

Materials and Methods

Materials Synthesis.

Two sets of crystals were grown for these experiments. The MACS experiment used 0.88(1) g of sample, while the SEQUOIA and HYSPEC samples totaled 0.96(1) g. All these crystals were grown by a flux method and have a dark purple coloring (39). No stacking faults or secondary phases were detected through single-crystal X ray diffraction. The T = 293(2) K lattice constants observed are a = b = 5.007(1) Å, and c = 23.491(5) Å (69), and the system crystallizes in space group $R\overline{3}$ (No. 148).

Magnetic Neutron Scattering.

Three neutron scattering experiments were performed. The first was performed on the Multi Axis Crystal Spectrometer (MACS) instrument at National Institute of Standards and Technology (NIST) in an “orange” ⁴He flow cryostat with a 1.5-K base temperature. For this experiment, many plate-like crystals of BaCo₂(AsO₄)₂ were coaligned in the (h k0) scattering plane. The final neutron energy was fixed at E _f = 5 meV, and the monochromator was in the double-focusing high flux mode. Measurements were performed at T = 1.7(1) K and T = 15.0(1) K, with 16 h and 18 h of counting time, respectively. Measurements were taken at energy transfers of 0 meV, 2 meV, 4 meV, and 8 meV for both temperatures. No magnetic field was applied in this experiment.

The second experiment was conducted at the SEQUOIA instrument at Oak Ridge National Laboratory (ORNL) on a second set of crystals with a total mass of 0.96(1) g. These crystals were coaligned in the (h0l) scattering plane, and the experiment was performed in a vertical field magnet such that the field was applied along the $\mathbf{b}$ -axis, which is parallel to the $(\overline{1}20)$ direction. Measurements were taken using the E _i  = 21 meV high flux configuration with Fermi chopper frequency of 120 Hz. Measurements were conducted with the samples at T = 2 K, 15 K, and 50 K and total proton charge of 74 C, 80 C, and 40 C, respectively. The resulting data are displayed in supplementary information.

The third experiment was run on the Hybrid Spectrometer (HYSPEC) instrument at ORNL using the same set of crystals as on SEQUOIA aligned in the (h0l) plane. We used an Oxford Instruments 14-T vertical field magnet with HYSPEC in the unpolarized high flux 300-Hz configuration with incident energies E _i  = 6 meV and E _i  = 27 meV. The main configuration was the low energy E _i  = 6 meV mode at fields of 0 T, 0.4 T, 0.55 T, 0.75 T, 1 T, 2 T, 3 T, 4 T, and 5 T. The net proton charge on target for each field was 140 C, 72 C, 30 C, 101 C, 30 C, 30 C, 75 C, 30 C, and 30 C, respectively, with a Fermi chopper frequency of 360 Hz. The higher energy E _i  = 27 meV configuration was used for μ ₀ H = 3 T with a total proton charge of 44 C and a 420-Hz Fermi chopper frequency. Analysis of the scattering from ORNL experiments was performed using the MANTID Project software package (70).

In-plane Magnetization.

Low-T magnetization measurements were performed on a high-quality single crystal of BCAO as a function of the applied magnetic field strength and orientation within the honeycomb planes. The sample was a 0.88(2) mg plate that was aligned using a Laue diffractometer to an accuracy better than 1°. The sample was mounted on a quartz rod and oriented such that the applied field was along the $\widehat{\mathbf{y}}$ direction as indicated in Fig. 1B . The sample was then cooled from 300 K to 2 K in zero field. A full hysteresis loop was measured at T = 2 K in the applied field range μ ₀ H ∈ [ − 1, 1] T. The sample was then warmed to 20 K and cooled back to T = 2 K in zero field, and the hysteresis loop was remeasured to establish reproducibility. The sample was then carefully rotated in 15° steps until the field was along the $\widehat{x}$ direction, repeating the zero field cooled magnetization scans for each orientation. Here, we present only data acquired for the $\widehat{x}$ and $\widehat{y}$ field directions. These measurements were run in a Quantum Design MPMS3 SQUID magnetometer.

Note Added in Proof.

While writing this paper, we became aware of three ab initio theoretical investigations of BCAO. Two of them (71, 72) corroborate our conclusion regarding the nature of magnetic interaction in BCAO and propose a coherent microscopic theory for it. Another (73) observes the formation of spin–orbit-entangled J _eff = 1/2 moments that could potentially support the claim of Kitaev physics. Ref. (71) importantly finds that the double-zigzag state is energetically competitive with the incommensurate spiral state (classical ground state as shown in our work) and can be stabilized by quantum fluctuations or relaxation of local atomic positions.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Inelastic neutron scattering event data and magnetization measurements have been deposited in Oak Ridge National Laboratory Spallation Neutron Source, National Institute of Standards and Technology. Data may be accessed directly at https://www.ncnr.nist.gov/ncnrdata/ and the ORNL analysis cluster. Reduced forms of INS data can be uploaded to a persistent repository if needed. All study data are included in the article and/or SI Appendix . Raw inelastic neutron scattering data is prohibitively large in file size to share effectively. These are available on the ORNL analysis cluster. Reduced versions of the data presented in the text can be shared most efficiently and are available upon reasonable request.