Information-processing dynamics in neural networks of macaque cerebral cortex reflect cognitive state and behavior

Significance

What does it mean to say that the brain “processes information?” Scientists often discuss the brain in terms of information processing—animals take in information from their environment through their senses and use it to make decisions about how to act in the world. In this work, we use a mathematical framework called information theory to explore how signals from the environment influence brain activity and how brain activity in turn informs on behaviors. We found that different brain regions process information in dynamic and flexible ways, with signals flowing up and down the hierarchy of sensorimotor processing depending on the demands of the moment. This shows how “computation” in the brain can reflect complex behaviors and cognitive states.

Abstract

One of the essential functions of biological neural networks is the processing of information. This includes everything from processing sensory information to perceive the environment, up to processing motor information to interact with the environment. Due to methodological limitations, it has been historically unclear how information processing changes during different cognitive or behavioral states and to what extent information is processed within or between the network of neurons in different brain areas. In this study, we leverage recent advances in the calculation of information dynamics to explore neural-level processing within and between the frontoparietal areas AIP, F5, and M1 during a delayed grasping task performed by three macaque monkeys. While information processing was high within all areas during all cognitive and behavioral states of the task, interareal processing varied widely: During visuomotor transformation, AIP and F5 formed a reciprocally connected processing unit, while no processing was present between areas during the memory period. Movement execution was processed globally across all areas with predominance of processing in the feedback direction. Furthermore, the fine-scale network structure reconfigured at the neuron level in response to different grasping conditions, despite no differences in the overall amount of information present. These results suggest that areas dynamically form higher-order processing units according to the cognitive or behavioral demand and that the information-processing network is hierarchically organized at the neuron level, with the coarse network structure determining the behavioral state and finer changes reflecting different conditions.

Animal nervous systems are often described as “information-processing engines”: Organisms take in information about the world around them through sensory organs, learn statistical regularities in the incoming information, and use those to navigate and interact with their environment. As a distributed network of neurons, information processing takes place both within and between many different specialized brain areas. Between-area processing can be further categorized as feedforward processing (from primary sensory areas to motor areas) and feedback processing (from motor areas back to sensory areas; Fig. 1A). Despite a growing number of studies demonstrating the involvement of multiple areas in different behavioral-related processing (1–4), it remains unclear to what degree information processing in the brain’s network of neurons is restricted to within specific areas, as opposed to multiareal feedforward and feedback interactions. Furthermore, it is unclear whether the intraareal and interareal processing network structure at the neuron level is static or changes dynamically in response to the demands of particular cognitive or behavioral states. For example, does information processing within and between areas change for typical monkey behavioral states such as perception of a fruit, the internal preparation to grasp the fruit, and the actual movement execution for grabbing the fruit (Fig. 1B)?

Fig. 1.

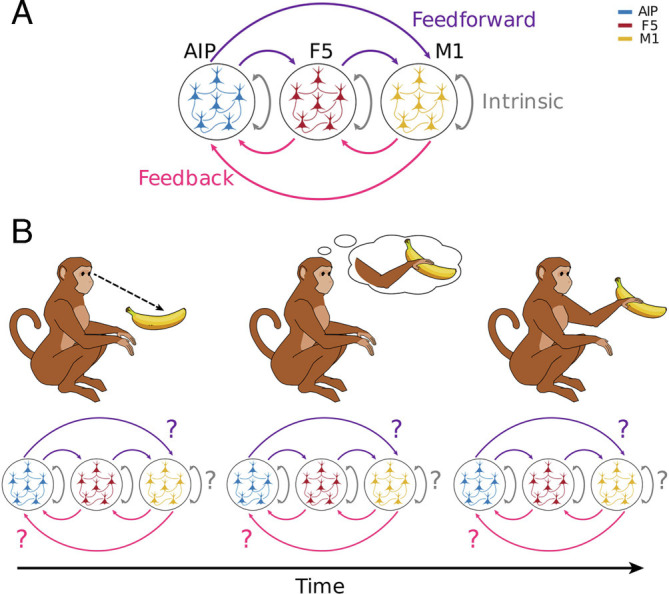
Possibilities of intraareal and interareal information processing with changes of behavioral states. Information processing associated with object recognition, movement planning, and execution takes place in multiple, distinct brain areas of the frontoparietal grasping network. It is unknown how information processing is distributed over those areas and how that distribution “updates” as the task progresses. (A) A schematic view of all possibilities of interareal and intraareal processing of information within and between consecutive cortical areas. Depicted is the frontoparietal grasping network (M1, AIP, and F5) investigated in this study and described in more detail below. Information processing is divided into feedforward, feedback, and intrinsic processing, as the three major directions indicated by color. (B) Schematic illustration showing that it is still unclear whether information processing between and within areas changes for different behavioral states, illustrated by the example of the perception of a fruit, the internal preparation to grasp the fruit and the actual movement execution for grabbing the fruit.

Given the technical limitations of whole-brain recording, it is useful to focus on subsets of areas that display a range of intrinsic, feedforward, and feedback modes of processing to fully understand how they relate. A natural system is the set of brain areas known to be involved with perception and movement execution. In macaque monkeys, the frontoparietal grasping network specifically has been shown to be strongly involved in visuomotor transformations and the execution of grasping movements and is composed of the anterior intraparietal area (AIP), the ventral premotor cortex (F5), and the primary motor cortex (M1) (5–8). Moreover, several studies demonstrated that AIP and F5 are strongly reciprocally connected, as are F5 and M1 (9–13) suggesting this network to be a compelling candidate to study intraareal and interareal processing.

When studying the activity of simultaneously recorded neurons, however, information processing is often vaguely defined. The mathematical fields of information theory and

the theory of information dynamics offer a general framework to study information flow and processing. Information dynamics breaks the concept of information processing into three parts (14): information storage how much the past activity of a neuron informs on its future, e.g., LTP or LTD (15), information transfer how much the past of a source neuron informs a target neuron’s future, e.g., synaptic communication (16, 17), and information modification the “nonlinear” computation that occurs when a neuron integrates distinct streams of information into something greater than the sum of its parts (18–21).

These three dynamics can be formalized using information theory (22) (Basic Theory of Information Dynamics). Previous work using information dynamics to study recorded neuronal networks found that the degree of information modification changes during development (21), and in the same developmental windows, particular patterns of information transfer are “locked-in” (23). Furthermore, the capacity for information modification is heterogeneously distributed across neurons of the network and concentrated in high-degree, rich-club neurons (24–27). Information transfer (28) has been applied to a variety of neural recordings (see ref. (16) for a comprehensive review) and allows researchers to estimate effective network models of interacting neurons. Finally, active information storage has provided insights into stimulus–response and preferences in visual processing systems (15).

Despite the wealth of analyses that have been done using information theory to investigate neural activity, it has not yet been widely applied to the problem of behavior-related information processing at the neural network level. Similarly, differences in neural information dynamics have not been thoroughly investigated within and between areas during complex behaviors. Much of the above-cited work has been done in neural cultures or anesthetized animals, as opposed to behaving organisms interacting with a complex environment. To address this gap, we examined the information dynamics and the associated effective network structures of neural populations from three cortical areas (AIP, F5, and M1) in the frontoparietal grasping network of three macaques. During recordings, monkeys performed a delayed sensorimotor transformation task involving the transformation of visual information into movement plans, the memorization of these movement plans, and finally the required processing to execute one of two grasping movements (for details, see ref. (29)).

With these data, we can estimate the neuron-level information dynamics in different cognitive and behavioral states, allowing us to directly assess the relationship between information dynamics and complex behaviors. Furthermore, by casting patterns of information transfer as effective connectivity networks, we can examine the degree of intrinsic, feedforward, and feedback information processing within and between the three areas and how changes in behavior alter the information dynamics within and between them. We found that different behavioral states were associated with significant reconfigurations of the global effective network structure, with movement, in particular, being associated with an increase in the overall information flowing through the system and an increase in the amount of synergistic information processing. Within and between the different areas, we found that 1) information processing was strong both within and between AIP and F5 during visuomotor transformation; 2) during memorization of movement plans, information processing remained high within areas but strongly decreased between AIP and F5; and 3) globally, information processing was strongest during movement execution in decreasing order from M1 to F5 to AIP both within and between areas, showing a more pronounced pattern in the feedback direction. Moreover, in all three behavioral states, the network-wide patterns of information storage and transmission were different for each of the two different grasping conditions. Together, these findings suggest that the information-processing structure at the neuron level changes depending on the behavioral state and task condition. While state changes are predominantly associated with changes in information processing between areas, condition changes are predominately associated with fine-scale reconfiguration of the network structure.

A. Basic Theory of Information Dynamics.

A natural mathematical framework for assessing these computational dynamics is information theory (14, 22), which describes how the activity of interacting elements of a complex system constrains the space of possible states of the whole system. In practice, for spike counts of sparse firing neurons, as in the case of the recorded neurons in this study, this requires counting the distribution of patterns of states between interacting elements. For example, when considering the dependency between the spiking activity of two neurons X_i and X_j, we must count the number of times X_i = 0 and X_j = 0, how many times X_i = 0 and X_j = 1, how many times X_i = 1 and X_j = 1, etc, for all 2^k combinations. When considering temporal sequences, the logic is the same: how frequently the pattern [0, 1, 1] is followed by a 0 instead of a 1 and so on. A significant advantage of information theory is that, being based only on marginal, joint, and conditional probabilities of patterns of events, it is both model-free and sensitive to nonlinear relationships between interacting elements (30). Information theoretic analysis is then “epistemically modest,” as it does not require presupposing particular generating functions or relationships. This makes it ideal for complex, nonlinear systems, such as networks of neurons of brains, where the underlying generative dynamic is unknown and nonlinearities can play a key role (31).

Information theory quantifies how knowledge of a variable, or set of interacting variables, reduces the uncertainty of an observer watching the system. The central object of study is the entropy of a random variable, which quantifies an observer’s uncertainty about the state of a variable under study. For a discrete random variable X, with support set χ, the entropy H(X) is canonically given as:

$$\begin{array}{c}\hfill H(X)=-\sum _{x\in \mathcal{X}}P(X=x)log(P(X=x)).\end{array}$$ [1]

When measured in bits (i.e., the base of the logarithm is two), the entropy of X quantifies the minimum number of yes/no questions required to completely specify the state of X with total certainty. Given two variables X and Y, we can calculate the mutual information between the two as the degree to which knowing the state of one variable reduces our uncertainty about the state of the other. Formally,

$$\begin{array}{c}\hfill I(X;Y)=H(X)-H(X|Y),\end{array}$$ [2]

where H(X|Y) is the conditional entropy of X given Y. The difference between our initial uncertainty about X and the remaining uncertainty after accounting for Y is the amount of uncertainty about X that Y resolves.

For temporally extended processes, we can break down the total information structure of the system in three information dynamics: active information storage, information transfer, and information modification. Information storage quantifies the degree to which knowing the past of a variable, or set of variables, decreases our uncertainty about its immediate future:

$$\begin{array}{c}\hfill AIS(X)=I(X_{0:t-1};X_t),\end{array}$$ [3]

where X_{0 : t − 1} is the joint state of all past states of variable X, and X_t is the immediate next state. In the context of neurons, a process that generates nontrivial AIS might be hyperpolarizing a neuron, which will reduce the probability that it will fire in the immediate future (15).

For sets of interacting variables, we can generalize the active information storage to quantify how much information is “transferred” from a source neuron to a target neuron by determining how much knowing the past of a prospective “source” variable X reduces our uncertainty about the future of a “target” variable Y (above and beyond the information stored in the target):

$$\begin{array}{c}\hfill TE(X\to Y)=I(X_{0:t-1};Y_t|Y_{0:t-1}).\end{array}$$ [4]

TE(X → Y) is referred to as the transfer entropy from X to Y. The canonical example here is that of synaptic communication: Knowing that an excitatory presynaptic neuron spiked increases our certainty that the postsynaptic neuron will spike in the near future. Importantly, the I/O functions of neurons themselves are highly complex (32), and so, the future behavior of the neuron may depend on the collective behavior of all the upstream sources, which can be quantified with the multivariate transfer entropy:

$$\begin{array}{c}\hfill mTE(\mathbf{Z}\to Y)=I({\mathbf{Z}}_{0:t-1};Y_t|Y_{0:t-1}),\end{array}$$ [5]

where Z is an ensemble of neurons. Fig. 2A, shows a schematic representation of how mTE was estimated in this study. To recover the effect of a single-source neuron on the target neuron in the context of all other informative sources, we use the conditional multivariate transfer entropy (33–35):

$$\begin{array}{c}\hfill mTE(X\to Y|\mathbf{Z})=I(X_{0:t-1};Y_t|Y_{0:t-1},{\mathbf{Z}}_{0:t-1}).\end{array}$$ [6]

Fig. 2.

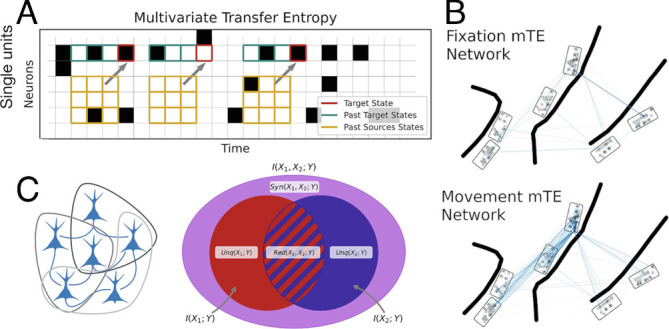
Information dynamics: inference of multivariate transfer entropy (mTE) transfer entropy networks and triadic synergy. (A) Schematic view explaining the intuition behind the multivariate transfer entropy. Spike events were first binned in nonoverlapping 5-ms windows, and three history bins of all neurons were used to predict each target neuron’s future. Red squares illustrate three examples of immediate future time points we intend to predict. Green squares illustrate three history spike bins of the target neuron, whereas the orange squares represent three history spike bins of all other neurons that may inform on the future of the target neuron. Note that the actual transfer entropy algorithm takes all time points into account, not only the three examples of immediate future time points illustrated in this schematic view. (B) Two example mTE transfer entropy networks for two different behavioral epochs, displayed as anatomical networks. The individual nodes reflect the anatomical positions of all simultaneously recorded neurons, the line shadings represent the relative amount of information transfer between neurons, the boxes reflect the implanted multielectrode arrays, and the thick black lines reflect the sulci of the cortex as shown with more detail in Fig. 3B. (C) Visualization of the triadic partial information decomposition. (Left) Schematic view of all possible sets of three neurons of the depicted neural network. Note that only all possible triads of the significant mTE networks were used to estimate triadic synergy (SI Appendix, Materials and Methods). (Right) Venn diagram illustrating how the total information of two source neurons informing a target neuron can be decomposed into a redundant part, two unique parts, and the synergistic part.

Fig. 2B shows two example mTE transfer entropy networks for two different behavioral epochs, displayed as anatomical networks. Finally, the third information dynamic, information modification, refers to information produced when multiple incoming “streams” intersect and are nontrivially changed. This is operationalized as the “synergy” (18, 36) (for mathematical details; SI Appendix, Materials and Methods and Fig. 2C). As can be seen from the diagram, the calculation of synergy also produces additional information dynamics: “redundant” and “unique” information terms. Synergy can be understood as the information provided by a set of source neurons about a target neuron that cannot be extracted from any simpler combination (i.e., the marginals) and can thus most intuitively be associated with information processing. Redundancy, in contrast, reflects the information that is duplicated over both parents and could be learned by observing one or the other. Unique information is the part of a target neuron’s activity that can only be expressed by the spiking of an individual source neuron. While the existence of synergy in biological neural networks is extremely well documented (27), evidence that behavioral-related neural processes can be captured with the computation of synergy is still lacking.

1. Results

A. Behavioral Task and Single Neuron Recordings.

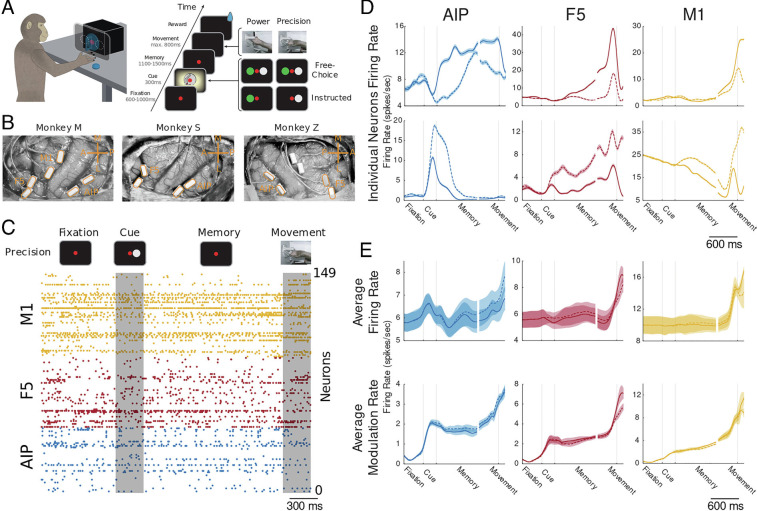
To study behavior-related neural information processing within and between areas, we utilize data recorded from three monkeys (S, Z, and M). Monkeys were trained to perform a delayed grasping task (Fig. 3A). The task was divided into four epochs: 1) an initial fixation epoch, which was the same for all conditions; 2) a cue epoch, in which the monkeys were either instructed or free to choose to grasp a target with one of two possible grip types (power or precision grip; monkey M was only trained to perform the instructed context); 3) a memory epoch, in which the monkeys had to prepare and remember the corresponding grip type, and 4) a movement epoch, in which the monkeys performed the corresponding grip type (for details, SI Appendix, Materials and Methods). All monkeys performed the task with high accuracy percentage trials correct (±SD) for monkey S: 95 ± 1%, monkey Z: 98 ± 3%, and monkey M: 94 ± 2%, indicating that all monkeys performed the task as well as both grasping conditions in a similar manner.

Fig. 3.

Behavioral task, electrode array implantation, and behavioral dependent firing rate modulations. (A) schematic view of the behavioral task is shown. Monkeys were placed in front of a grasping box with a masked monitor that was superimposed on the handle of the box. Monkeys were trained to execute one of two distinct grip types (precision grip or power grip) depending on the visual cue. Each trial of the task was initialized by the monkeys placing both hands on handrest buttons and fixating a red disc, followed by the cue epoch, in which one of the displayed cues was presented. After the cue offset, the monkeys had to continue fixing the red disc and prepare and memorize the appropriate movement. Finally, by turning off the red disc, monkeys were instructed to execute the appropriate grip type within a limited amount of time. (B) Surgical view of implanted floating microelectrode arrays in monkey M (Left), monkey Z (Middle), and monkey S (Right). Monkeys were implanted with two floating microprobe arrays per area (4 to 6 total, 32 electrodes each), in the cortical areas AIP, F5, and M1 of the frontoparietal grasping network. (C) Spike raster of all simultaneously recorded neurons of monkey M for one example precision condition trial. Spiking of all neurons is color-coded by area (M1 yellow, F5 red, and AIP blue). (D) Average firing rates of six representative neurons (two per area) over the time course of the task, separately for the two grasping conditions (solid line: precision condition; dashed line: power condition). Neurons in the Top row show stronger firing rates for the precision condition, whereas neurons in the Bottom row prefer the power condition. Shaded error bars represent SE across trials. (E) Top  row: Average firing rate across all neurons for all recording sessions and monkeys separated by area and grip condition (solid line: precision condition; dashed line: power condition). Shaded error bars represent SE across recording sessions of all three monkeys. Bottom  row: Same as in (D) but for average modulation rate. The modulation rate is the absolute difference in firing rate to baseline.

While monkeys performed the task, we simultaneously recorded large populations of well-isolated neurons from the ventral premotor cortex (area F5), the anterior intraparietal area (AIP), and for one monkey from the hand area of the primary motor cortex (M1). For this purpose, two 32-channel microelectrode arrays were chronically implanted per area resulting in 128 recorded channels for monkeys S and Z and 192 recording channels for monkey M (see surgical pictures for all three monkeys in Fig. 3B). For all following analyses, we used four recording sessions from monkey S with on average 82.8 ± 5.7 SD neurons, three sessions from monkey Z with on average 53 ± 5.6 SD neurons, and three sessions from monkey M with on average 134.3 ± 23.7 SD neurons. Depicted in Fig. 3C is the spiking activity of all simultaneously recorded neurons during a precision condition trial of a representative recording session of monkey M. Neurons of all three areas were active during the task, and even behavior-dependent modulations are evident for some neurons, especially during the movement period. For a more systematic evaluation of behavior-dependent modulations, we calculated the average firing rates per neuron over the time course of the task separately for the two grasping conditions (see Fig. 3D for two representative neurons per area with precision condition and power condition preference, respectively). The majority of neurons in all three areas show strong and reliable task- and condition-dependent modulations in the firing rate. Yet, average firing rates across all neurons per area showed only weak task- and no condition-dependent modulations (Fig. 3E, Top row). This apparent discrepancy can be explained by a similar number of neurons with increased firing rates for both grasping conditions. To test this assumption, we estimated the average modulation rate across all neurons per area. The modulation rate is estimated as the absolute difference in the firing rate from baseline, in this case, fixation epoch. As expected, the average modulation rate strongly increased during all three behaviorally relevant epochs (cue, memory, and movement) for both grasping conditions in all three areas (Fig. 3E, Bottom row). Note that the similar level of the modulation rate for both grasp conditions provides further evidence that monkeys performed both grasping conditions in a similar manner. Together, these results suggest that all areas are involved in task-dependent information processing. However, task-dependent changes in firing rates are only an indirect indicator of information processing. Furthermore, the mere presence of changes in the firing rate does not provide any evidence about whether and how information processing changes for different behavioral states between and within areas.

B. Information Dynamics.

Behavior-dependent changes in information dynamics were estimated by computing AIS, conditional mTE, and triadic synergy between the continuous spike counts (nonoverlapping 5-ms windows) of all simultaneously recorded neurons (SI Appendix, Materials and Methods). All three measures were computed over the time course of the task with a sliding window of 800 ms and separated by the grasping condition (incremental step size of 100 ms). The result is an array of windows: 23 time windows × 2 grasping conditions). Note that in order to reduce the influence of behavior-dependent firing rate changes, the AIS and the mTE measures were significance-tested with conservatively estimated surrogate data (shuffling spikes within 25-ms windows and recomputing the corresponding measure; for details, SI Appendix, Materials and Methods). In addition, all values (AIS, mTE, and synergy) were normalized by dividing by the Shannon entropy of the receiver neuron, following (27), which provides a control for variable firing rates.

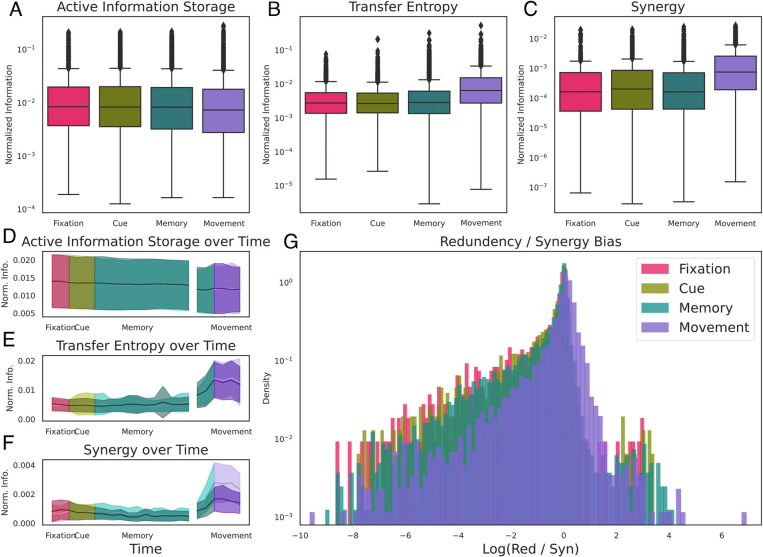
For a first assessment of differences in information dynamics during behavioral changes, we compared the average values of the three basic normalized information dynamics per behavioral epoch across both grasping conditions, all neurons and areas (Fig. 4A–C). Kruskal–Wallis ANOVA found a small, but significant difference between all four behavioral states for AIS (H = 67, P = 4.27 × 10⁻¹⁵). The effect size change in AIS values, however, was very small: The highest value was 0.014 ± 0.024 (in the fixation condition), while the smallest was 0.012 ± 0.021 (Cohen’s D = 0.1). This suggests that during the movement condition, the degree to which information is being “stored” in individual neurons is decreased, possibly in favor of information flowing from source neurons to target neurons. There was a stronger, significant difference in mTE between behavioral states (H = 1555.649, P <  10⁻²⁰). Here, the lowest average mTE was observed in the fixation period (0.005  ±  0.007), and the highest was observed in the movement period (0.013  ±  0.02, Cohen’s D = 0.46). The strongest significant difference was found with synergy (H = 1520.213, P <  10⁻²⁰), with the smallest synergy being seen in the memory condition (0.001 ± 0.002) and the highest, as expected, being seen in the movement state (0.002 ± 0.003, Cohen’s D = 0.54). Time-resolving information dynamics over all time windows and for both grasping conditions (Fig. 4D–F) show that the distributions of all three information dynamics were largely similar within behavioral states and between conditions. The only exception was the memory state, where the mTE and the synergy started to increase before the onset of movement. This is unsurprising since movement-related processing in cortical motor areas precedes movement onset by at least the amount of neuronal distance to the arm and hand (37, 38).

Fig. 4.

Behavioral state–dependent changes of information dynamics. All displayed information dynamics are averaged across all neurons of all three brain areas and the recording sessions of all three monkeys. (A–C) The differences in AIS (Left), mTE (Middle), and synergy (Right) between the four behavioral states of the task averaged across all sliding windows per task epoch and both conditions. There is no significant difference for AIS over time; however, mTE and synergy show increases during the movement epoch. (D–F) Time-resolved dynamics of AIS, mTE, and synergy over the time course of the task separately for the two grasping conditions (solid, power condition; shaded, precision condition). Shaded error bars represent SE across recording sessions of all three monkeys. Color-coded are the four behavioral epochs of the task (window contains 200 ms or more of the next epoch). (G) Distribution of synergy/redundancy bias across all significant effective neural connections for all four behavioral states, averaged across all sliding windows per task epoch. All states are, on average, synergy biased, even though the movement period is associated with a distinct increase in the proportion of redundant information.

B.1. Redundancy/synergy bias.

The measure of information modification (synergy) also reveals an additional set of information-processing “modes,” formalized by the partial information decomposition (PID) framework (39, 40), which reveals two different ways in which information can flow through a system: a redundancy-dominated mode, where information is duplicated and sent through many channels simultaneously or a synergy-dominated mode, where information is distributed over higher-order combinations of multiple channels. These distinct modes may be thought of as different “ways” that the nervous system can distribute, process, and represent information.

We can assess which of these modes dominates the overall joint mutual information I(S₁, S₂; T) by normalizing the value of each atom (i.e., the portion of the joint-MI that is redundant, unique, or synergistic) by the total mutual information. Note that this normalization is different from the one reported above (where the value of every information dynamic is normalized by the entropy of the receiver neuron). We found that the distribution of information flow across all significant effective triads was synergy dominated during all behavioral states (Fig. 4G). Furthermore, we found that the effective connection-wise values of synergy, redundancy and the ratio of the two remained relatively constant across the first three behavioral states (i.e., fixation, cue, memory). The transition from memory to movement, however, was associated with a marked increase in the relative redundancy of information flow across the network of neurons (Δ = −74.4 ± −27.3%, U = 10084455.0, P <  10⁻¹⁰). No other transition (fixation → cue or cue → memory) was significant, despite the very large number of samples in each distribution. This indicates that the transition from “cognitive” states to motor states is associated with a particular increase in the relative dominance of redundant information communicated within the network.

C. Interareal Analysis.

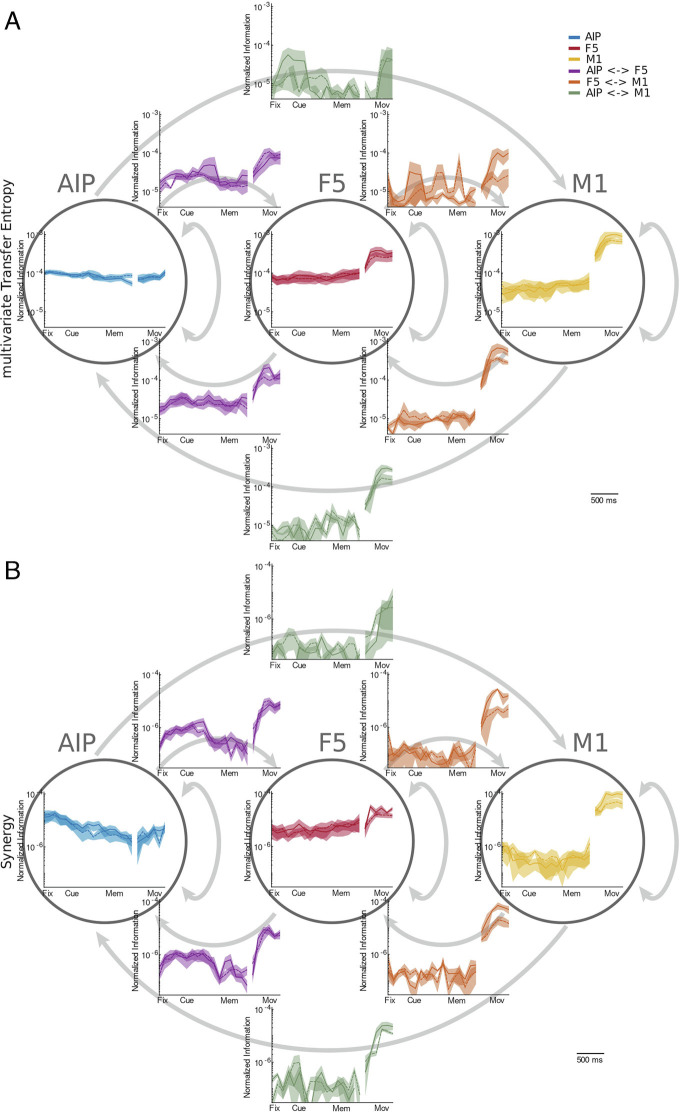
Given the behavior-dependent changes in information dynamics over the course of the task, we next examined the degree to which the different types of information processing change within and between areas. To compare information dynamics of the different types within and between areas, we computed the average mTE and synergies for all neuron pairs within each area and also between all pairs of areas separately in the forward and backward directions. Depicted in Fig. 5 are the time-resolved average mTE and synergy dynamics over all time windows and grasping conditions for all areas and area combinations across all neuron pairs, recording sessions, and monkeys. The dynamics of both synergy and mTE are highly similar; consequently, we will not describe them separately in this section and instead refer to the overall pattern of “information processing.” Overall information processing was highest within areas, followed by directly connected areas, and weakest between AIP and M1. Encouragingly, the overall information processing reflects the known anatomical connection strength, which we interpret as providing validation of our methods.

Fig. 5.

The information dynamics of mTE and synergy within and between the areas AIP, F5, and M1. All displayed information dynamics are averaged across all neural connections within each area or between each area pair and all recording sessions of all three monkeys. Since both mTE and synergy are directed measures, the information dynamics between areas can be separated into the feedforward and feedback directions. (A) Strength of normalized multivariate transfer entropy over time and separately for both conditions (solid, precision condition; dashed, power condition) within areas (within circles) and between areas (different source and target areas; arrows indicate the feedforward and feedback direction). Shaded error bars represent SE across recording sessions of all three monkeys. We can see that the degree of information processing varies greatly between areas for different behavioral states. The arrangement of areas and interactions corresponds to Figs. 1 and 7. (B) The same as (A), but for normalized triadic synergy.

In AIP, despite an overall high level of information processing, there was surprisingly little change over the course of the task. In F5, in contrast, information processing increased during movement execution after remaining largely constant during the more “cognitive” behaviors. The increase in information processing during movement was even higher in M1, while information processing was lower during all other epochs in comparison to the other two areas. Between areas, the amount of information processing was surprisingly similar in both the feedforward and feedback directions, suggesting processing in both directions to be of equal importance for the visuomotor transformations and the execution of grasping movements. There were, however, significant differences between the different interareal combinations. Areas AIP and F5 showed increased interareal information processing around the cue epoch, in contrast to processing within both areas (which remained largely constant), suggesting that the processing between these areas is of particular importance for the transformation of visual information into movement plans. Apart from the already-high level of information processing within areas, no interareal connection showed an increased level of information processing during the memory epoch, suggesting that the act of “holding information in memory” is an area specific, rather than a global process. In contrast, all interareal combinations showed a strong increase in information processing during movement execution, suggesting the control of movement execution to be a rather globalized process not limited to M1.

In addition to the condition-dependent changes in synergistic processing, the PID framework allows us to also explore the redundant and unique information atoms (SI Appendix, Materials and Methods). For a better comparison between the different types of information processing, we averaged information processing for the three most important behavioral epochs of interest—cue, memory, and movement—to assess how different types of information flowed through the system. SI Appendix, Fig. S1 shows the relative average amount of mTE, synergistic, redundant, and unique information for all areas and interareal pairs, displayed as adjacency matrices for better comparability. As we have already observed in the comparison of mTE and synergy, temporal dynamics of all information types are generally similar. On closer inspection, however, small differences between the information types become apparent. During the visuomotor transformation around the cue epoch, synergistic and redundant information processing between AIP and F5 was stronger relative to the two other types of information processing. During memory, low levels of mTE, synergistic, and redundant information processing were present between AIP and F5, in contrast to unique information. Presented as adjacency matrices, the aforementioned global information-processing patterns during movement execution become clearly apparent. Furthermore, it becomes clear that all types of information processing during movement execution are more intense in the feedback direction than in the feedforward direction.

Taken together, these results suggest that 1) processing between areas in the feedback direction is essential for this supposedly simple task and 2) that the extent to which information is processed between areas depends strongly on behavioral state, in contrast to information processing within areas.

C.1. Network dynamics.

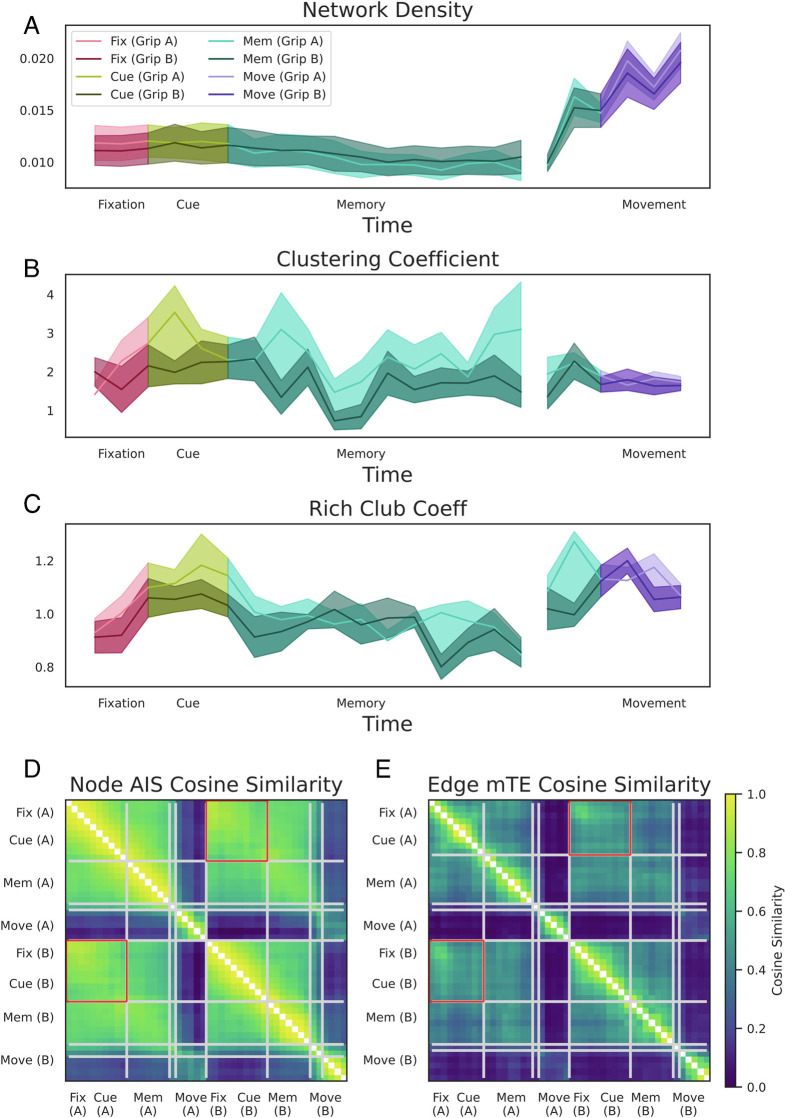
To assess how information processing changes over time and across conditions in fine detail, we next analyzed the information transfer network structure (41, 42). To capture the changes in the network structure, we calculated the network measures: 1) network density, the ratio of connections to neurons; 2) the clustering coefficient, an indicator of how densely directly connected neurons are interconnected; and 3) the rich-club coefficient, an indicator of connection density of strongly connected neurons (SI Appendix, Materials and Methods). By analyzing information transfer at the network level with neuron resolution, we observed that the onset of the cue is associated with a transient reconfiguration of the network structure (Fig. 6A–C). While the total amount of information transfer and connections across the networks did not significantly change in response to cue onset (Figs. 4E and 6A), the normalized clustering coefficient was significantly increased during the cue epoch for both grip types A (precision grip) and B (power grip cluster-based surrogate test, P <  10⁻²⁰ for all windows and all grip types, see Methods) (29, 43). Similarly, for both grip types, the normalized rich-club coefficient was significantly higher during the cue epoch for both grip types (Fig. 6C; cluster-based surrogate test, P = 0.002 for Grip A and P = 0.048 for Grip B). We can also see a significant increase in the normalized rich-club coefficient for both grip types during the movement epoch (P <  10⁻²⁰ for all windows and all grip types). Together, these results suggest that the transition from a passive cognitive state (fixation, memory) to an active cognitive state (perception of a visual cue or motor execution) is associated with marked changes to the information-processing network structure. Furthermore, these changes are lost when considering average information dynamics of individual neurons (Fig. 4D–F for comparison). For example, an increase in the rich-club coefficient is seen in both the cue epoch and during the movement epoch, suggesting that the presence of rich-club structure is particularly important for active states. Interestingly, the emergence of a rich-club structure as well as an increased cluster coefficient occurs during the cue epoch without a corresponding change in the total amount of information transfer of the network, suggesting that it might be a true reallocation of a fixed quantity of computational resources.

Fig. 6.

Differences in the effective network structure between behavioral states and grasping conditions. All displayed network measures are averaged across all recording sessions of all three monkeys. (A–C) Temporal dynamics (estimated based on the sliding windows) for the three measures of network topology separately for both grasping conditions (solid, precision condition; dashed, power condition): network density (A), normalized global clustering coefficient (B), and the normalized rich-club coefficient (C). Shaded error bars represent SE across recording sessions of all three monkeys. The network density increased dramatically in the movement epoch but remained constant during all “cognitive” states. In contrast, the networks showed a transient reconfiguration during the cue epoch: increasing the hierarchical rich-club structure and becoming more clustered. (D and E) Pairwise cosine similarity matrices of AIS neuron-level and mTE connection-level values over all time windows of both conditions. Gray lines indicate the boundaries of similar information network structure clusters as determined with a clustering algorithm. Note that the fixation and cue epoch clusters of both conditions belong to one cluster, indicated by the red box around the off-diagonal part of the cluster. Also note that the inferred clusters map onto boundaries between different behaviors.

C.2. AIS and mTE similarity clustering.

In addition to various behavioral states, monkeys also performed two different grasping conditions. Although all analyses above did not reveal any differences in processing between the two grasp conditions (Figs. 4D–F, 5, and 6A–C), the possibility remains that differences in the information dynamics exist at the of fine-grained network level with neuron resolution, which are lost at any larger scale. For this purpose, we examined condition-dependent differences in the AIS values across neurons and mTE values across network connections. For both measures, we estimated the cosine similarity between the neurons and connections, respectively, of all time windows of all behavioral states and for both grip types averaged across all recording sessions of all monkeys. The resulting cosine similarities are depicted as similarity matrices (Fig. 6 D and E). For both matrices, the values on the diagonal represent the similarity over time of first the precision grip (A) and then the power grip condition (B). The off-diagonal values thus represent the similarity between conditions over time. Over the time course of the task in both conditions, the AIS values across neurons and the mTE network structure were most dissimilar between the movement period and all other epochs. On closer examination, however, there are also differences between the fixation and cue epoch and the memory epoch. In direct comparison of both conditions, we can observe that the AIS values across neurons and the mTE-networks were most similar during the fixation epoch. Following fixation, the similarity of the networks decreased and condition-dependent difference became apparent during the cue, memory, and movement epoch. Note that despite the similarity of network reconfiguration of both conditions over time, the fine-grained information dynamics at the network level are highly dissimilar during the movement period. To verify behavioral state and condition differences, we used a multiresolution consensus clustering (MRCC) algorithm (44). MRCC is an unsupervised community detection algorithm that in this case identifies groups of AIS and mTE values over time and across conditions of increased similarity (see the squares along the diagonal in Fig. 6 D and E). MRCC revealed that all but the combined fixation and cue epoch of both conditions (see the red squares in Fig. 6 D and E) formed separate clusters. The across-condition fixation and cue cluster is to be expected because the fixation epoch is the only epoch that is independent of the behavioral condition. Thus, this result confirms that the AIS values across neurons and the mTE network structure are 1) not statistically different during fixation and 2) statistically different during all other epochs. Note that the across-condition cluster also comprises the cue epoch, which is probably due to the large sliding window size of 800 ms. Interestingly, the independent condition-specific clusters identified by the MRCC algorithm showed a similar temporal structure for both conditions resembling behavioral states such as memory and movement. Taken together, despite no significant condition-dependent differences on average, both AIS and mTE showed significant differences at the neuron and connection levels, respectively. Thus, these results suggest that the fine-grained structure of the information dynamic networks reconfigures for different conditions, forming distinct “information-processing architectures.”

D. Relating Structure & Functional Information Dynamics.

Previous studies performed on organotypic brain slices showed that synergistic information dynamics were highest between neurons with a high degree (24–26). Yet, the meaning of synergistic processes in neural networks remains unclear. Therefore, it is important to scrutinize this relationship in the intact brain during behaviorally relevant processing. To assess this, we correlated each of the information dynamics for every neuron against local network measures (SI Appendix, Fig. S2; local clustering coefficient and in-strength, as a proxy for local rich club). The in-strength, the sum of all directed in-coming transfer entropies, quantifies the total amount of information that flows into a target neuron. In-strength is high when a neuron receives a lot of information from the rest of the system and low when a neuron is more segregated from the rest of the network. The clustering coefficient quantifies whether a given neuron’s neighbors tend to also be connected, forming a dense, local environment. It can be thought of as reflecting how locally integrated part of a network is. We found no significant relationships between either in-strength or local clustering coefficient and neuron-level AIS (SI Appendix, Fig. S2 A and B). However, we found a strong, significant correlation between the in-strength of a neuron and the average mTE flowing into it (SI Appendix, Fig. S2C, r = 0.86, P <  10⁻¹⁰). While this is unsurprising, it is not entirely trivial: A low in-degree neuron and a high in-degree neuron might have the same in-strength, but different average incoming transfer entropies. Similarly, we found a strong, significant correlation between the average mTE of a neuron and its local clustering coefficient (SI Appendix, Fig. S2D, r = 0.44, P <  10⁻¹⁰), which indicates that the information processing occurring in a single neuron is informed by the local connectivity pattern of that neuron’s neighbors. Finally, we found strong, significant correlations between synergy and both in-strengths (SI Appendix, Fig. S2E, r = 0.657, P <  10⁻¹⁰) and local clustering coefficient (SI Appendix, Fig. S2F, r = 0.653, P <  10⁻¹⁰). As with the transfer entropy results, these results show that a neuron’s location in the effective connectivity network relative to other neurons informs the type of information processing it predominately performs.

2. Discussion

In this work, we have used information theory to study behavior-related changes in patterns of information processing in neural networks spanning multiple brain areas of the macaque frontoparietal grasping network. We investigated 1) how information processing changes during different cognitive and behavioral states over the course of a behavioral task, 2) to what degree information processing is restricted to within specific areas, or distributed between areas, 3) to what degree this interareal processing structure is fixed or changes dynamically for different behavioral states, and 4) whether behavioral condition-dependent differences are present at the fine-grained information-processing network structure. For this purpose, we estimated different types or components of “information processing” referred to as “information dynamics” (45): the active information storage (how the past activity of a single neuron informs on its future), transfer entropy (how the past of a set of source neurons informs on a single target neuron’s future), and the information modification/synergy (information from the joint-state of multiple sources about a target’s future that is irreducible to any simpler combination of sources).

We found that information processing of different types changes during different cognitive and behavioral states. Furthermore, the degree of information processing taking place within a single area, as opposed to between areas, strongly depended on the behavioral state. During visuomotor transformation, areas AIP and F5 formed a processing unit (Fig. 7A). During memory, this unit unexpectedly fell apart, despite the amount of information processed within each area remaining constant (Fig. 7B). Finally, the highest level of information processing occurred during the movement execution. In contrast to the two previous behavioral states, movement execution appeared to be a global process with the greatest amount of computation occurring between all areas, especially M1 (Fig. 7C). Movement execution-related processing between areas was more pronounced in the feedback direction suggesting that online feedback to earlier areas is an essential part of movement execution. While the average information-processing dynamics were the same for different conditions across the different cognitive and behavioral states, significant condition-dependent differences became apparent at the fine-scale network level with neuron resolution. Our results suggest that connected areas can dynamically form functional units that together enable the required cognitive or behavioral state, while fine-grained reconfigurations of the network structure reflect different behavioral conditions. These ensembles of areas are flexible: multiarea units can subsequently fall apart to reform into other multiarea processing units according to the cognitive and behavioral demands.

Fig. 7.

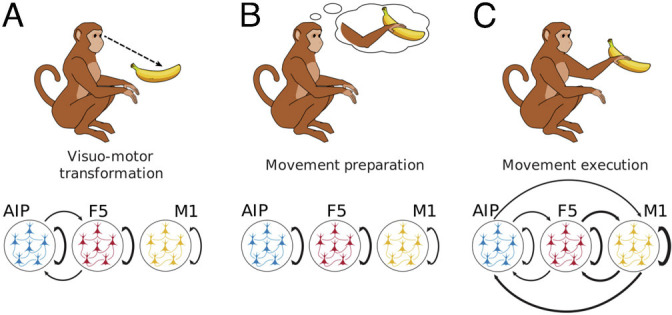
Variable feedforward and feedback dynamics during different behavioral states. Here, we can see how different cognitive and behavioral epochs are associated with different patterns of information processing within and between areas. During the cue and early memory epoch, when monkeys are transforming the information from their environment into a movement plan, strong interareal information processing is present between AIP and F5 in both the feedforward and feedback directions. In contrast, during the memory epoch where monkeys have to retain the instructed movement, information processing was primarily present within areas. Finally, during the execution of the movement, information was processed globally within and between areas, outgoing from M1, with dominance of processing in the feedback directions.

This work unifies previous findings about information dynamics, behavior-related neural population dynamics, and the structure of networks of neurons. Prior work on information dynamics has demonstrated the existence of synergistic processing in dissociated cultures (20, 25): Synergistic dynamics can be sensitive to local network structure (46) and vary over time (21). Similar analyses have been done for AIS (15) and TE (16, 17), although until now it has been a mystery how these different modes of processing relate to cognition and behavior.

Previous work on frontoparietal neural rate dynamics has demonstrated that neural populations respond to movement preparation as well as movement execution, but with independent dynamics for both processes (37, 47, 48). Therefore, preparation-related information must be “transformed” into movement execution-related information. However, analyses of population dynamics do not allow a direct estimate of computation. Historically, the amount of information processed was either estimated based on correlation analyses (49) or indirectly inferred via an artificial neural network model (50). Prior work on the inference of network connectivity at the neuron level has demonstrated the presence of strong interareal and intraareal connectivity and an area spanning rich club of neurons (29), but its behavioral relevance was elusive.

We found significant cognitive and behavioral state-related changes to information-processing architecture. Both mTE and synergy significantly increased in the movement epoch, while synergy additionally increased during the cue epoch (Fig. 4). The observed increase in information processing in both epochs is in agreement with the cognitive and behavioral requirements: During the cue epoch, monkeys must actively observe and integrate instructions, while during the movement epoch, monkeys must actively move arm and hand to grasp the target with the required grip type. In contrast to these active periods, monkeys must remain still during fixation and memory epochs, which suggests a lower degree of information processing during these steady periods. This assumed relationship between the estimated amount of information processing and the behavioral requirements is further supported by the finding that the mTE effective network dynamics vary between active and steady states (Fig. 6 B and C). In particular, the presence of an effective rich-club network structure distinguished active and steady states (no significant rich-club during steady states, significant rich-club during active states). Surprisingly, active and steady states were not accompanied by systematic differences in the average population rate and modulation rate (Fig. 3E), suggesting that the observed changes in processing are due to reconfiguration of the effective network structure.

Not only did information network dynamics resemble the cognitive and behavioral states, but the increase in information processing and network dynamics preceded the movement onset. The so-called internal movement onset in the brain, however, has been shown to precede the real movement onset (37, 38) simply because nerve signals take time to arrive at the appropriate arm muscles, and arm muscle potentials need time to build up to lift the arm and hand. Therefore, the observed mismatch of information processing with the movement epoch also further supports the assumed relationship between information dynamics and behavior. Although the lack of significant differences in average information processing between conditions seems disappointing at first glance, it further validates our findings. Both grasp conditions have equally salient cues, can be assumed to be equally difficult to prepare for, and presumably require a comparable amount of effort to perform. Given these facts, it is not surprising that the total amount of information required for both was similar. A similar level of information processing between the two conditions serves as cross-validation of our results. Thus, our findings suggest that the estimated information dynamics at the network level capture the true behaviorally relevant processing or at least parts of it.

Given the evidence that information theory allows us to capture the underlying processing in the frontoparietal network of neurons, three questions arise: 1) Why is information processed between areas and not exclusively within areas? 2) Why do the areas that form a processing unit change depending on the behavioral state? 3) How are different multiarea processing units formed?

Regarding the first question, there exist compelling evidence that large populations of neurons in multiple areas are modulated in a similar way during the same cognitive or behavioral task (1–4). This high degree of correlated activity or information is made possible by the strongly reciprocal connection of mammalian cortical areas (51, 52). Additionally, there is strong evidence coming from neuroimaging that the pattern of correlated activity is constantly changing despite static connectivity (53, 54). These results suggest that the cortex should be viewed more as a single interconnected network of neurons than as a structure divided into areas. Consequently, information is likely to be globally communicated and presumably also processed. Our results of strong processing in both the feedforward and feedback directions provide evidence for this proposal. A more global integration may also allow for greater flexibility and the integration of more factors simultaneously than a classical hierarchical processing structure.

Regarding the second question, it may be beneficial to flexibly recombine processing from multiple areas according to behavioral demand. For the given task, first visual information must be transformed into a movement plan. It has been demonstrated that areas AIP and F5 are involved in visuomotor transformation, but M1 is not (5, 6, 8). Therefore, it makes sense that AIP and F5 form a processing unit during visuomotor transformation not involving M1. Neurons of both areas also show elevated and prolonged activity during memory periods (5, 6). Surprisingly, we found that the processing units of AIP and F5 fell apart during memory, although memory may require less “processing” and something more akin to “storage” (not to be confused with the measure of AIS reported here). A large number of studies have shown that mainly M1, but also F5, is involved in movement execution (8, 37, 55, 56). In a recent study, a mechanism has been proposed for how a movement plan is translated into movement execution in the premotor and motor cortices (57). Our finding of high levels of information processing within and between M1 and F5 during movement execution is consistent with this hypothesis. In contrast, little is known about the involvement of area AIP in movement execution. Only a single study showed that the movement trajectories from the whole arm and hand can be decoded from AIP during movement execution (7). Thus, our results suggest that the number of cortical areas involved in the required processing for movement execution is larger than previously thought. We speculate that the strong feedback processing might be necessary to align precise details of the movement with different sensory areas, the evaluation of the movement, or learning.

Regarding the third question, a one study has explored how dynamic communication is established between cortical areas (58). However, most results about dynamic communication capture cofluctuations of different brain signals and reveal little about multiarea processing units. Nevertheless, oscillatory synchrony has been proposed as a coordinative mechanism for interareal communication (29), which might also be involved in the dynamic formation of multiarea processing units.

Another intriguing finding is that condition-dependent differences were present in the fine-scale network structure of information processing starting during the cue epoch until the end of the tasks, despite no significant differences in the average amount of information processing (Fig. 6D–F and SI Appendix, Fig. S2). As mentioned before, both grasp conditions have equally salient cues, can be assumed to be equally difficult to prepare, and require a comparable level of effort to perform. Therefore, a similar average level of information processing may be expected. On the other hand, it is also evident that information processing must be different for the two grasping conditions. Consequently, the observed differences in the processing network structure at the neuron level most likely reflect the distinct, fine-scale neuronal computations underlying different conditions. Thus, the methods described here provided a powerful tool to study neural computations in the network during different cognitive and behavioral processes. In this study examining the behavioral state and condition-dependent differences in the information-processing network structure, it becomes apparent that behavioral state differences are larger than condition-dependent differences. Moreover, the network state during fixation as well as during cue and memory of both conditions is more similar to each other than the network state during movement execution of both conditions. We suggest that the active execution of a movement leads to a much more drastic change in the information-processing structure than different cognitive states. In contrast, the finer but distinct differences between conditions remained relatively stable. Taken together, these results suggest a hierarchy in information processing in which the coarse network structure determines the behavioral state and finer changes in the network structure reflect different conditions.

In total, information dynamics represents an appealing framework with which to explore the brain as an integrated whole and can be easily adapted to assess computational processes at multiple scales. Given the extensive public data available to neuroscientists, we are optimistic that information dynamics can provide insights into the relationship between the brain, behavior, computation, and dynamics. In particular, information dynamics marries two well-established frameworks in modern neuroscience: computational approaches and dynamical systems approaches (38, 50, 57, 59–61). Sometimes called “computational mechanics” (62), information dynamics analysis can provide a bridge between approaches to provide insights that may not be obvious from either one.

Materials and Methods

Neural activity was recorded simultaneously from many channels in two female and one male rhesus macaque monkeys (animals S, Z, and M; body weight 9, 7, and 10 kg, respectively). Detailed experimental procedures have been described previously (29, 63). All procedures and animal care were in accordance with German and European law and were in agreement with the Guidelines for the Care and Use of Mammals in Neuroscience and Behavioral Research (National Research Council, 2003). The behavioral task is described in SI Appendix, section 2.A. The electrode implantation and data recording is described in SI Appendix, section 2.B. The data preprocessing of the neural signals is described in SI Appendix, section 2.C. The sliding window analysis for information dynamics is described in SI Appendix, section 2.D. The calculation of AIS and mTE network dynamics is described in SI Appendix, section 2.E and F. The similarity analysis of mTE and AIS is described in SI Appendix, section 2.G. The calculation of synergy as part of the partial information decomposition is described in SI Appendix, section 2.H.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (CSV)

Dataset S02 (CSV)

Dataset S03 (CSV)

Dataset S04 (CSV)

Dataset S05 (CSV)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix. Previously published data were used for this work; B. Dann, J. A. Michaels, S. Schaffelhofer, H. Scherberger, Uniting functional network topology and oscillations in the fronto-parietal single unit network of behaving primates. ELife, 5, e15719 (2016). https://doi.org/10.7554/eLife.15719.