Abstract
Red blood cell (RBC)-based systems are under extensive development as platforms for the delivery of various biomedical agents. While the importance of the membrane biochemical characteristics in relation to circulation kinetics of RBC delivery systems has been recognized, the membrane mechanical properties of such carriers have not been extensively studied. Using optical methods in conjunction with image analysis and mechanical modeling, we have quantified the morphological and membrane mechanical characteristics of RBC-derived microparticles containing the near-infrared cargo indocyanine green (ICG). We find that these particles have a significantly lower surface area, volume, and deformability as compared to normal RBCs. The residual hemoglobin has a spatially distorted distribution in the particles. The membrane bending modulus of the particles is about twofold higher as compared to normal RBCs and exhibits greater resistance to flow. The induced increase in the viscous characteristics of the membrane is dominant over the elastic and entropic effects of ICG. Our results suggest that changes to the membrane mechanical properties are a result of impaired membrane–cytoskeleton attachment in these particles. We provide a mechanistic explanation to suggest that the compromised membrane–cytoskeleton attachment and altered membrane compositional and structural asymmetry induce curvature changes to the membrane, resulting in mechanical remodeling of the membrane. These findings highlight the importance of membrane mechanical properties as an important criterion in the design and engineering of future generations of RBC-based delivery systems to achieve prolonged circulation.
Keywords: cell-based therapeutics, cell membrane viscoelasticity, drug delivery, erythrocyte engineering, microparticles
Graphical Abstract
INTRODUCTION
Cell-based systems present a new type of platform in contemporary medicine for the delivery of a wide range of therapeutic, imaging, and biosensing cargos.1-4 In particular, red blood cells (RBCs) are an attractive platform due to their potential biocompatibility, particularly if derived autologously, low immunogenicity, natural mechanisms for elimination, and innate ability for prolonged circulation.5-7 For example, RBC delivery systems containing asparaginase have been investigated for the treatment of specific types of acute lymphoblastic leukemia, and in combination with chemotherapy, for the treatment of advanced pancreatic cancer in clinical trials.8,9
A particularly important issue related to applications of RBC-based carrier systems is their longevity in the blood-stream. Normal human RBCs have a lifespan of ~90–120 days before they are removed from circulation by the spleen due to physiological senescence or pathological alterations. The membrane biochemical profile of RBCs is one of the key determinants of RBC longevity. Specific membrane glycoproteins, CD47, CD55, and CD59, prevent phagocytic uptake by macrophages, protect the RBCs from complement damage, and prevent the formation of membrane-attack complexes, respectively. Another important mechanism is related to the role of the membrane phospholipid, phosphatidylserine (PS), which is normally confined to the inner leaflet of the membrane. Flipping of PS to the outer leaflet, either as a result of RBCs’ senescence or induced during the fabrication of RBC-based carrier systems serves as a signal for phagocytosis by splenic macrophages.10,11
While the importance of membrane biochemical characteristics in relation to the longevity of RBC-based carriers has been recognized, the morphological characteristics and membrane mechanical properties of such carriers have not been extensively studied. The normal biconcave discoidal shape and the extensive membrane deformability allow for the repeated passage of RBCs through narrow capillaries and nanosized (~200–400 nm) splenic endothelial slits during their lifetime. Reduced deformability of RBCs is associated with the premature removal of RBCs from circulation.12 Therefore, it can be expected that deviations from the natural shape and membrane deformability would have consequences in relation to the circulation time of RBC-based platforms, and ultimately, the desired efficacy that they are expected to achieve.
Using quantitative phase imaging (QPI) and optical tweezers in conjunction with image analysis and mechanical modeling, herein, for the first time, we have quantified the morphological and membrane mechanical characteristics of RBC-derived microparticles containing the near-infrared cargo indocyanine green (ICG). We refer to these materials as RBC ghostsICG since in a similar fashion to the common methodologies used in the fabrication of RBC-based delivery systems containing other cargos,13-15 the construction process is based on the formation of hemoglobin-depleted RBC ghosts as an intermediate structure, which, in this case, becomes loaded with ICG. We have chosen ICG since it is an FDA-approved chromophore with a long-standing history in clinical applications and clinical research related to optical imaging and laser-based therapeutics.16,17 ICG has also been encapsulated into RBC-based delivery systems for optical imaging and light-based theranostics.18,19
We present results that demonstrate that the surface area, volume, and deformability of RBC ghostsICG are significantly reduced as compared to RBCs. The residual amount of hemoglobin in these particles has a distorted spatial distribution. The bending modulus of the membrane bilayer in RBC ghostsICG is ~2.3 times higher as compared to RBCs. The membrane of RBC ghostsICG also exhibits greater resistance to flow. The presence of ICG lowers the stiffness properties of the membrane, consistent with reductions in membrane elastic and entropic forces. Based on our findings and analysis, we propose that the membrane attachment to the cytoskeleton network is impaired and provide a mechanistic explanation for membrane remodeling in RBC-based systems based on induced changes to the membrane curvature. The altered physical and mechanical characteristics have implications relevant to the longevity of the RBC-based delivery system in circulation. Our findings further highlight the importance of membrane mechanical properties as a crucial criterion in the design and engineering of future generations of RBC-based delivery systems.
MATERIALS AND METHODS
Fabrication of RBC Ghosts and RBC GhostsICG.
Human RBCs were separated from whole blood (BioVIT, Inc., Hicksville, NY) by centrifuging 1 mL of whole blood for 10 min (1600g at 4 °C). The supernatant containing the plasma and buffy coat was removed, and the resulting packed erythrocytes were washed twice with isotonic (310 mOsm) phosphate-buffered solution (PBS) (Fisher Scientific, Hampton, NH), referred to as 1× PBS (pH ~ 8.0). The plasma was used for refractive index measurements of RBC ghosts and RBC ghostsICG.
To form RBC ghosts and RBC ghostsICG, RBCs were subjected to hypotonic treatment (80 mOsm PBS, pH ~ 8.0). The centrifugation process (20,000g, 15 min, 4 °C) was repeated until an opaque pellet was obtained. The pellet containing the resulting RBC ghosts was resuspended in 1 mL of 1× PBS. To load ICG (MP Biomedicals, Santa Ana, CA) into RBC ghosts, 350 μL of RBC ghosts suspended in 1× PBS was incubated with 155 μL of an ICG stock solution, 350 μL of Sørenson’s buffer (Na2HPO4/NaH2PO4, 140 mOsm, pH ~ 8.0), and 145 μL of nanopure water for 5 min at 4 °C in the dark. The concentration of ICG in this loading buffer was 100 μM. The suspension was then centrifuged and washed twice with 1× PBS at 20,000g for 20 min at 4 °C to form RBC ghostsICG. The resulting RBC ghostsICG were then resuspended in 1 mL of 1× cold PBS.
Optical Tweezers and Quantitative Phase Imaging.
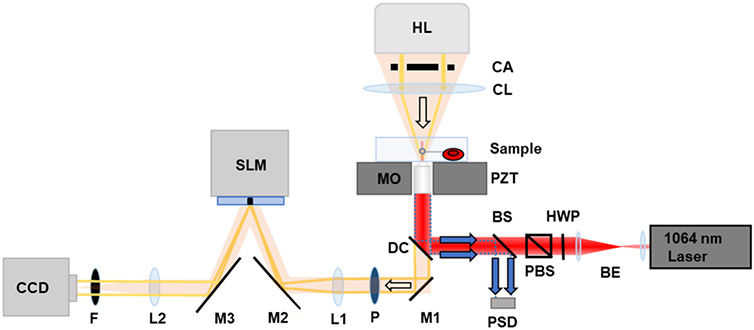
The instrumentation platform consisting of optical tweezers and quantitative phase imaging (QPI) is shown in Figure 1. The optical trap was formed using a 1064 nm laser (Coherent, Prisma -1064-8-V). The beam was expanded by a beam expander. A half-wave plate and a polarizing beam splitter were used to reduce the intensity of the laser light before entering into an inverted microscope (Nikon, Ti-Eclipse). The beam was reflected from a dichroic mirror (Chroma, Z900DCSP) and filled the back aperture of a 100× oil immersion objective (Nikon Plan Fluor, NA = 1.3) that focused the light to form an optical trap.
Figure 1.
Schematic of combined optical tweezers and the quantitative imaging system. BE: beam expander, HWP: half-wave plate, PBS: polarizing beam splitter, BS: beam splitter (90:10), PSD: position-sensitive detector, DC: dichroic mirror, MO: microscope objective, PZT: piezoelectric translation stage, CA: condenser annulus, HL: halogen lamp, P: polarizer, M1, M2, and M3: mirrors, SLM: spatial light modulator, F: filter, CCD: charge-coupled detector camera, and L1 and L2: 500 mm lens. The light orange path indicates the direction of QPI light. The red path indicates the direction of the laser light for optical trapping, and the blue arrows indicate the direction for bead position tracking.
We optically trapped 4.2 μm diameter sulfate-modified polystyrene beads (ThermoFisher Scientific, F8858) and used them as handles for membrane tether extraction as well as sensors for measuring the force profiles. To facilitate the adhesion of the beads to the membrane, prior to trapping experiments, they were coated by incubating them with lysine at a concentration of 20 mg·mL−1 in distilled water at 4 °C for ~24 h.
We tracked the displacement of the beads from the trapping center during tether pulling and force relaxation experiments using a position-sensitive detector (PSD) (On-Trak, PSM 2-2). A 90/10 beam splitter reflected the back-scattered light from the bead onto the PSD. The differential output voltage from the PSD was amplified (On-Trak, OT-301) and then digitized using an analog-to-digital converter (National Instruments, BNC2110) at sampling rate of 1000 Hz. We used LabVIEW software (National Instruments, LabVIEW 7) to record the data.
To calibrate the output voltage of the PSD in response to bead displacement, we applied known drag forces to an optically trapped bead while recording the resulting differential voltage signal from the PSD. The drag force was generated by driving a piezoelectric translation stage (PZT) (Physik Instrumente, model P-527.C3) at varying velocities using triangular waveforms of known amplitude (150 μm) and frequencies (6.7, 13.3, 20.0, 26.7, 33.3, and 40.0 Hz). The resolution of PZT was 10 nm in the x and y directions and 2 nm in the z direction (laser beam propagation direction). The viscous drag force on a spherical object is related to the velocity of the fluid by Stoke’s equation 20
| (1) |
where η is the viscosity of the medium (8.90 × 10−4 Pa·s for water at 298 K), r is the radius of the bead (2.1 μm), ν is the velocity of the fluid, and h is the height of the optically trapped bead from the bottom of the plate. Calibrations were performed at trapping height of 10 μm from the coverslip at room temperature (298 K). Concurrently, an electron-multiplying charge-coupled device (EM-CCD) (C9100-13, Hamamatsu) sampling at 100 fps was used to capture videos of bead displacement. An open-source particle tracking Matlab code, UmUTracker, made available by Zhang et al.21 for download was used to determine the bead displacement from the video. The voltage output from the PSD was plotted against bead displacement captured by the video and linearly fitted to obtain a voltage-displacement calibration (V·μm−1) (illustrative calibration provided in Supporting Figure S1). The applied drag force was plotted against the PSD voltage output and linearly fitted to obtain force–voltage calibration (pN·V−1) (illustrative calibration provided in Supporting Figure S2). The stiffness of the optical trap was then determined as the product of the slopes of these two calibration lines (~425 pN·μm−1).
QPI was realized through a custom-built interferometric system.22,23 Samples were illuminated using a 100W halogen lamp source through a condenser annulus and condenser lens. The same 100× oil immersion objective was used for both optical trapping and QPI. The light after sample illumination was filtered to a center wavelength of 595 ± 25 nm prior to exiting the microscope. A mirror (M1) directed the scattered and unscattered light to a linear polarizer. The unscattered light forms an image of the condenser annulus at the focal plane of lens L1 (f = 500 mm) on a reflective spatial light modulator (SLM) (Hamamatsu LCOS-SLM X-10468). The SLM was used to introduce four phase shifts in π/2 increments to the unscattered light. The unscattered components interfered with the scattered light to form an image of the sample, which was focused onto the EM-CCD by lens L2 (f = 500 mm). An IR filter (F) was placed in front of the EM-CCD to filter the extraneous 1064 nm light from the optical trap. To accommodate the full rearrangement of the nematic liquid crystals in the SLM, field delays of 100 ms were used between the phase modulations. We acquired 10 phase-shifted images every second.
We designate the image intensity at a given pixel location i, j resulting from the interference between the scattered light and unscattered light at four different phase modulations as I0, Iπ, Iπ/2, I3π/2, respectively. Values of the phase difference (Δφ) associated with each interference signal intensity are given as
| (2) |
We subsequently obtained the resulting phase maps as
| (3) |
where β is the ratio of the amplitude of scattered to the unscattered light intensity at a given pixel location.22,24
We had previously22 validated the accuracy of QPI in size measurements using polystyrene beads with known mean diameters of 400 nm and 630 nm and an index of refraction npolystyrene = 1.591 at 595 nm in air25 seeded on glass-bottom dishes and also by comparisons with AFM-based measurements of a pattern of depths (179 ± 15 nm) etched within a microchip. The EM-CCD pixels size was calibrated with a 10 μm spacing ruler and determined as 140 nm. The spatial noise of the QPI system was ~0.02 rad, as determined by measuring the standard deviation of the phase from the background.
Sample Preparation for Tether Pulling.
RBCs, RBC ghosts, or RBC ghostsICG were seeded onto poly-d-lysine-coated glass-bottom dishes (MaTtek, P35GC-1.0-14C). To firmly adhere the sample to the glass-bottom dishes for tether pulling experiments, we centrifuged the RBCs at 1000g for 30 min and the RBC ghosts/RBC ghostsICG at 1200g for 1 h in glass-bottom dishes. Since the deformability of RBCs can be impaired as they age,26 we only pulled tethers from discoidal RBCs with lateral diameters between 7 and 9 μm and circularly shaped RBC ghosts/RBC ghostsICG with lateral diameters between 4 and 5 μm, as determined by visual inspection through counting pixels of the obtained CCD images. Experiments on RBCs were performed within 2 weeks after receiving the blood and on the same day that they were isolated. Experiments with RBC ghosts and RBC ghostsICG were carried out within 2 weeks after fabrication.
Tether Pulling Protocol.
A bead was optically trapped and its position zeroed on the PSD. Adherent RBCs, RBC ghosts, or RBC ghostsICG were brought into contact with the trapped bead by the PZT stage. Bead-membrane contact was confirmed both visually and by detecting a nonzero output voltage of the PSD. After 10–30 s of bead-membrane contact, the sample was displaced away from the optical trap at a constant velocity of 1 μm·s−1 up to a length of 10 μm. Pulling was then stopped to allow for the tether force to relax to equilibrium. Example videos of the tether pulling process from an RBC, RBC ghost, and RBC ghostICG are provided in Supporting Videos S1, S2, and S3, respectively.
Elongation Index Analysis.
We used the elongation index (EI) to quantitatively characterize the overall shape of RBCs, RBC ghosts, and RBC ghostsICG in response to membrane pulling from phase-contrast images at Iπ/2 captured on the EM-CCD. The EI is defined as
| (4) |
where Xlength and Ylength are the respective lengths along and perpendicular to the axis of deformation at the time point immediately before the membrane was detached from the underlying cytoskeleton. The lengths were determined from the measurements of the number of pixels on the EM-CCD image in the indicated directions.
Determination of Refractive Indices.
To estimate the tether diameter from the quantitative phase images of tethers, the refractive index mismatch between the sample and the medium must be known. The refractive index of RBCs is largely dependent on the intracellular concentration of hemoglobin, where the relationship between the hemoglobin concentration and the refractive index of an RBC is given as 27
| (5) |
where n0 is the refractive index of the media (in our case, 1× PBS), α is the specific refractive index increase of hemoglobin, and C is the concentration of hemoglobin. Using the data reported by Gienger et al.,28 we estimate α as ~0.00023 L·g−1 and C ~ 337 g·L−1 at 595 nm for oxygenated hemoglobin. With n0 = nPBS = 1.335 at 595 nm,29 we estimate nRBC = 1.413. Since RBC membrane tethers have been shown to contain hemoglobin,30 we used nRBC for the tether diameter estimations in RBCs.
To determine the refractive index of RBC ghost membranes, we captured quantitative phase images of RBC ghosts in media with two different refractive indices consisting of 1× PBS and human blood plasma. We first determined the refractive index of human blood plasma as follows. Plasma was obtained from the supernatant of centrifuged whole blood. Using QPI, we obtained images of 630 nm diameter polystyrene beads in deionized water and plasma (Supporting Figure S3). We selected beads that were nonaggregated for analysis. As the bead is spherical, the diameter of the bead corresponds to the thickest optical path and will induce the largest phase shift; hence, the maximum phase value for a bead will correspond to the bead diameter. The relationships for the bead phase in water (φbeadH2O), plasma (φbeadplasma), and bead diameter (dbead) are given as
| (6) |
| (7) |
where λ is the center wavelength of excitation (595 nm), nbead = 1.591, and nH2O = 1.332. Assuming that the value of dbead is the same in water and plasma, we can rewrite eq 6 in terms of dbead, substitute into eq 7, and solve for nplasma as
| (8) |
We found φbeadH2O = 1.722 ± 0.017 rad (mean ± standard error (SE)) and φbeadplasma = 1.589 ± 0.015 rad (mean ± SE). Then, using eq 8, we determined nplasma = 1.352 ± 0.003 (mean ± SE). Our estimated mean value is ~0.4% higher than the reported value of ~1.347 at 595 nm for rabbit plasma.31
The expression for the average phase of RBC ghosts obtained in PBS (φRBC ghostPBS) and plasma (φRBC ghostplasma) is related to the thickness of the sample and refractive index mismatch by the following relationships
| (9) |
| (10) |
where nplasma =1.352, dRBC ghost is the average thickness of the RBC ghost and nRBC ghost is the refractive index of the RBC ghost. Assuming that the value of dRBC ghost is the same in 1× PBS and plasma, we can then rewrite eq 9 in terms of dRBC ghost, substitute into eq 10, and solve for nRBC ghost as
| (11) |
Using eq 11, we estimated nRBC ghost = 1.347 ± 0.004 and nRBC ghostICG = 1.351 ± 0.009 (mean ± SE) at 595 nm. We present phase maps of RBC ghosts and RBC ghostsICG in 1× PBS and plasma obtained by QPI in Supporting Figure S4. The RBC ghosts imaged in 1× PBS yielded φRBC ghostPBS = 0.126 ± 0.010 rad (mean ± SE), while imaging in plasma resulted in φRBC ghostplasma = −0.138 ± 0.070 rad (mean ± SE), confirming that the mean refractive index of RBC ghost membranes (1.343) is higher than that of 1× PBS (1.335) but lower than the mean value for plasma (1.352) at 595 nm. The mean ± SE phase values of RBC ghosts (0.126 ± 0.0164 rad) and RBC ghostsICG (0.177 ± 0.03 rad) in 1× PBS were not significantly different from each other (p > 0.05).
Tether Diameter Analysis.
To estimate the tether diameters at the end of force relaxation, we averaged 10 frames of a given tether image obtained by QPI. We first identified pixels associated with the membrane tether as those that had a sudden increase in the phase (~1 to 2 orders of magnitude), delineating the boundary between the background and the tether. Along the length of the tether, we examined pixels corresponding to the in-plane thickness of the tether (perpendicular to the length of the tether, ~3 to 4 pixels for each cross section of the tether). Assuming cylindrical tethers, we used the pixels with maximum phase values as those that corresponded to the tether diameter. We then obtained an average of the phases associated with the tether diameter along the length of the tether. The average tether diameter phase and the tether diameter (dtether) are related by the expression
| (12) |
where is the average diameter phase, λ is the center excitation wavelength (595 nm), nmembrane is the refractive index of the membrane.
Quantification of Morphological Characteristics and Hemoglobin Profiling.
From the phase maps obtained by QPI, we quantified the volume, surface area, hemoglobin content, and hemoglobin concentration using MATLAB. The quantitative phase images were first segmented by binarization and thresholding to remove the background. The segmented phase maps were then converted into height maps. The volume of each sample was determined by integrating the height map over the projected sample area, as given by32
| (13) |
where V is the volume, h(x, y) is the height determined from the phase map, and dx and dy are the width and length of the pixel sizes. The surface area (SA) of the sample was determined by32
| (14) |
where and are the directional gradients along the x and y directions, respectively, and A is the projected area of the sample.
Hemoglobin content (HBC) was obtained from the phase maps φ(x, y) using the expression33
| (15) |
with α = 2.3 × 10−4 L·g−1, and dA being the area differential of the sample. The hemoglobin concentration was then determined by dividing the hemoglobin content by the volume of the sample.
Mechanical Modeling.
We fitted the solution (Supporting eq S6) of the Maxwell–Weichert body (Supporting Figure S5)34 to the measured tether force relaxation data using the curve fitting toolbox in MATLAB. The initial guesses for each of k and μ values were based on the reported values of these parameters for other tissues.35 In our subsequent analyses, we used fits that provided an r2 value greater than 0.90.
Presentation of Data and Statistics.
Results for various physical properties are reported in box-and-whisker plots. The bottom line of the box represents the 25th quartile and the top line represents the 75th quartile of the data. Median values of each quantity are indicated by the horizontal lines within each box. Mean values are indicated by the square in the center of the box-and-whisker plot. The whiskers show the outliers of the measured values. Statistical analysis was performed using a two-tailed Student’s t-test with unequal variance. All values are reported as mean ± SE.
RESULTS AND DISCUSSION
Morphological and Hemoglobin Characterizations by QPI.
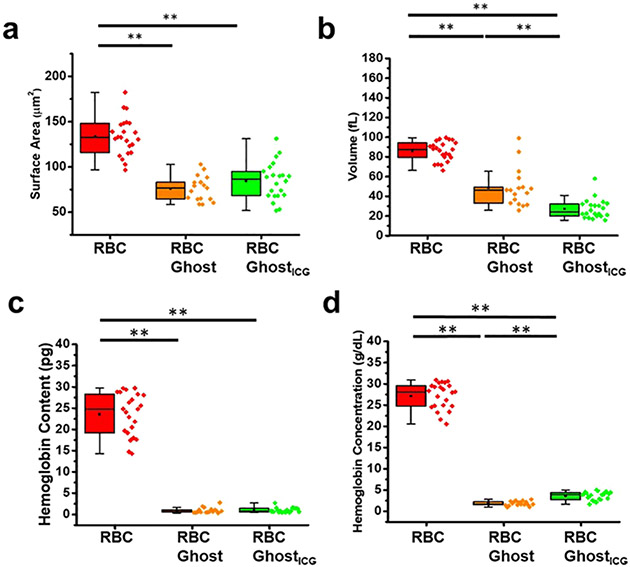
The mean ± SE values of normal human RBCs’ surface area were 133.73 ± 4.35 μm2 (Figure 2a), similar to mean ± SE values of 139.6 ± 7.4 and 135 ± 10 μm2 (mean ± standard deviation (SD)) by other investigators.36,37 Mean ± SE values of the surface area for hemoglobin-depleted RBC ghosts (76.04 ± 3.33 μm2) and RBC ghostsICG (84.5 ± 4.34 μm2) were significantly lower as compared to the mean value for RBCs (p < 0.01) (Figure 2b), indicating the loss (shedding) of surface materials during the fabrication process.
Figure 2.
Morphological and hemoglobin quantification. (a) Surface area, (b) volume, (c) hemoglobin content, and (d) hemoglobin concentration for RBCs (n = 23), RBC ghosts (n = 17), and RBC ghostsICG (n = 22). Individual values of the data are presented by the diamond symbols. ** indicates a statistically significant difference (p < 0.01) in mean values between the indicated pairs.
Our estimated mean ± SE volume of RBCs (85.82 ± 2.04 fL) (Figure 2b) is similar to mean ± SD values reported by Park et al.33 (89.7 ± 11.9 fL), Linderkamp et al.38 (88.2 ± 14.8 fL) for unfractionated adult human RBCs, and within the range of ~60–130 fL for RBCs obtained from healthy individuals.32 Mean volumes of RBC ghosts (48.27 ± 4.75 fL) and RBC ghostsICG (27.13 ± 2.07 fL) were significantly lower than RBCs (p < 0.01). There was also a statistically significant difference between the mean volumes of RBC ghosts and RBC ghostsICG (p < 0.01).
Our estimated mean ± SE hemoglobin content (23.54 ± 1.04 pg) (Figure 2c) and hemoglobin concentration (27.14 ± 0.63 g·dL−1) per cell (Figure 2d) are within the respective ranges of ~20–40 pg and 25–45 g·dL−1 for RBCs reported by others.39 Hemoglobin contents of RBC ghosts (0.94 ± 0.16 pg) and RBC ghostsICG (1.00 ± 0.12 pg) as well as the concentration of hemoglobin, 1.84 ± 0.13 g·dL−1 for RBC ghosts and 3.58 ± 0.21 g·dL−1 for RBC ghostsICG, were significantly lower as compared to RBCs (p < 0.01), indicating that most of the hemoglobin was depleted during the fabrication of the constructs. Illustrative absorption spectra for RBC ghosts and RBC ghostsICG (Supporting Figure S6) confirm the presence of residual hemoglobin, consistent with previous studies involving the formation of erythrocyte ghosts.40,41 The higher hemoglobin concentration in RBC ghostsICG as compared to RBC ghosts (p < 0.01) (Figure 2d) is attributed to the smaller volume of RBC ghostsICG (Figure 2b).
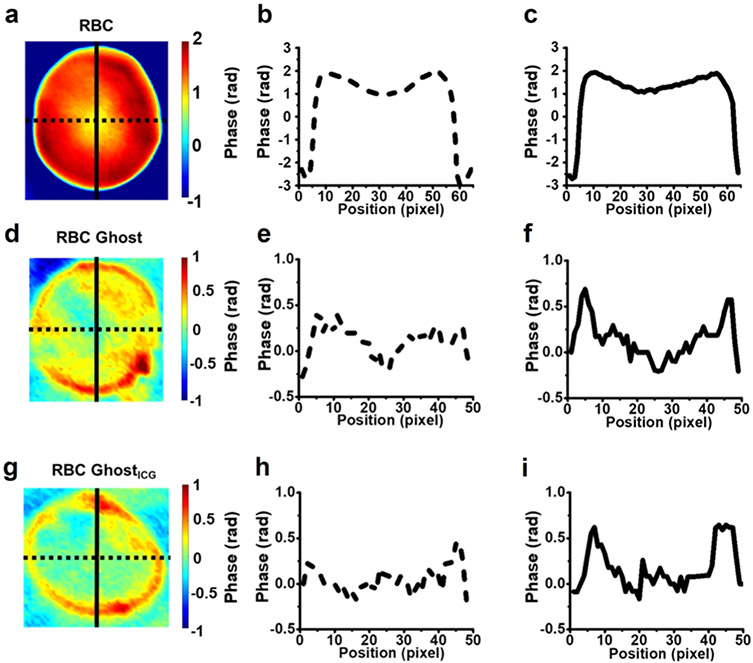
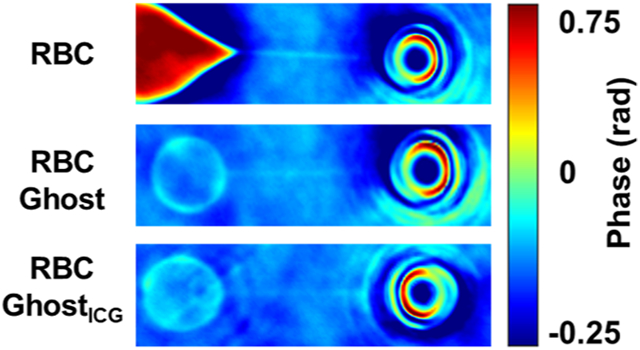
We present illustrative images of an RBC, RBC ghost, and RBC ghostICG obtained by QPI at a 595 ± 25 nm illumination wavelength and the corresponding horizontal and vertical line scans of the phase values through their centers (Figure 3). Although the spectral peaks for oxyhemoglobin (OxHb) are at 418, 547, and 578 nm, there is sufficient absorption at 590 nm (Supporting Figure S6) to generate phase maps. The RBC exhibits a central region of a low phase (Figure 3a), consistent with the presence of the signature “dimple” in the center of an RBC, surrounded by regions of higher phase values, indicative of the areas with higher OxHb localization. The horizontal and vertical line scans for the RBC demonstrate that the phases had nearly symmetrical spatial distributions and similar values along both scan lines (Figure 3b,c). These results are indicative of the symmetrical localization and quantity distribution of OxHb in the RBC. Based on the analysis of the line scans, the mean ± SE diameters for RBCs (n = 10) measured in isotonic PBS along the horizontal and vertical scan lines were 8.79 ± 0.31 and 8.67 ± 0.56 μm, respectively.
Figure 3.
Optical images and hemoglobin distributions. (a) Representative phase map of an RBC. (b) Left-to-right and (c) top-to-bottom line scans through the center of the RBC image. (d) Representative phase map of an RBC ghost. (e) Left-to-right and (f) top-to-bottom line scans through the center of the RBC ghost image. (g) Representative phase map of an RBC ghostICG. (h) Left-to-right and (i) top-to-bottom line scans through the center of the RBC ghostICG image. All images were obtained by QPI at an illumination wavelength of 595 ± 25 nm.
Illustrative phase maps of the RBC ghost and RBC ghostICG obtained by QPI and the associated horizontal and vertical line scans (Figure 3d-i) demonstrate that there were reductions in the phase values as compared to those for an RBC. These results indicate the presence of residual hemoglobin in RBC ghosts, and are consistent with the absorption spectra that showed the existence of the Soret and Q bands associated with OxHb (Supporting Figure S6). The phase maps also show a distortion in the spatial symmetry of the phase values (Figure 3d,g). The line scans further demonstrate that the spatial distribution of the phase values differs from each other along the horizontal and vertical directions (Figure 3e,f,h,i). These results are indicative of the heterogeneities in localization and quantity of the residual hemoglobin in the RBC ghost and RBC ghostICG. The respective mean ± SE diameters of RBC ghosts (n = 9) along the horizontal and vertical scan lines were 5.13 ± 0.92 and 5.10 ± 0.69 μm, and significantly smaller than the corresponding diameters for RBCs (p < 0.01). Similarly, the respective mean ± SE diameters of RBC ghostsICG (n = 9) along the horizontal (5.78 ± 0.63 μm) and vertical (5.81 ± 0.60 μm) scan lines were significantly smaller than the corresponding diameters for RBCs (p < 0.01).
Mechanical Deformations and Force Measurements.
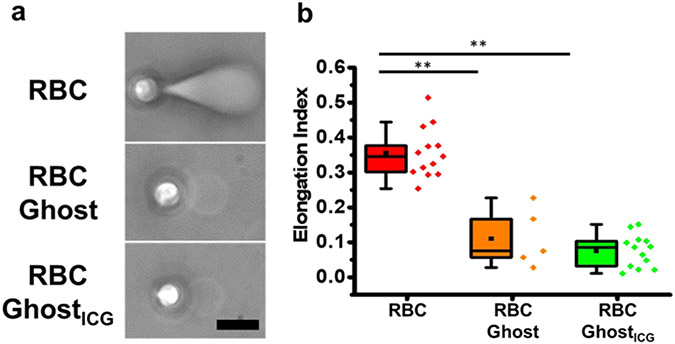
Phase-contrast images of an RBC, RBC ghost, and RBC ghostICG demonstrate that pulling the membrane of RBC before it became detached from the cytoskeleton was associated with visibly extensive deformation of the RBC into a “bullet” shape, consistent with previous observations.42 Such deformations were not observed when pulling the membranes of RBC ghost and RBC ghostsICG (Figure 4a). The mean ± SE values of the elongation index (EI) (eq 4) for RBCs, RBC ghosts, and RBC ghostsICG immediately prior to membrane detachment were 0.36 ± 0.02, 0.11 ± 0.04, and 0.08 ± 0.01, respectively (Figure 4b). The statistically significant lower mean value of EI for RBC ghosts and RBC ghostsICG is indicative of their reduced deformability as compared to RBCs.
Figure 4.
Pulling response. (a) Representative phase-contrast images of an RBC, RBC ghost, and RBC ghostsICG in response to membrane pulling by an optically trapped bead. Images are at the instant of time immediately prior to membrane detachment from the cytoskeleton. Scale bar = 5 μm and applies to all images. (b) Box-and-whisker plots of the elongation index for RBCs (n = 13), RBC ghosts (n = 5), and RBC ghostsICG (n = 13). Individual values of the data are presented by the diamond symbols. ** indicates a statistically significant difference (p < 0.01) in the mean value of EI between the indicated materials.
We present illustrative videos of membrane tethers pulled from an RBC, RBC ghost, and RBC ghostsICG (Supporting Videos S1-S3). Although the RBC underwent a dramatic morphological change from its biconcave discoidal shape during the pulling process (Supporting Video S1), both the RBC ghost (Supporting Video S2) and RBC ghostsICG (Supporting Video S3) retained their overall shapes.
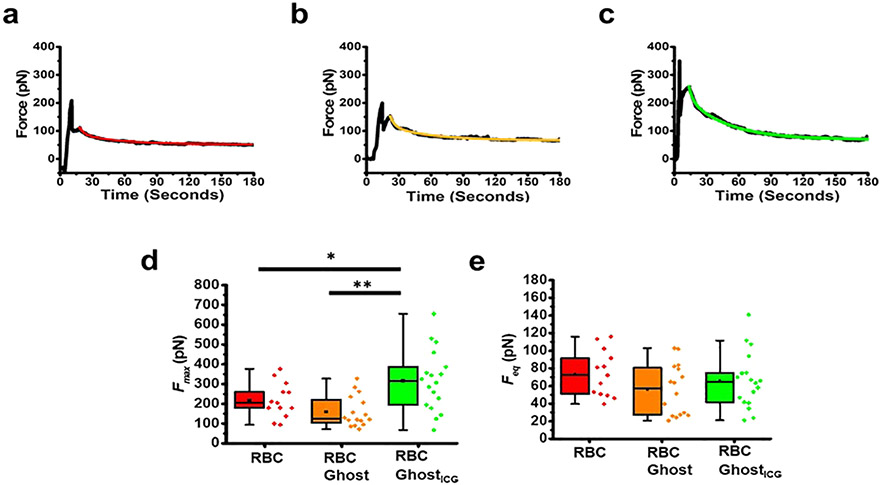
We provide representative force profiles associated with tethers pulled at a velocity of 1 μm·s−1 from RBCs, RBC ghost, and RBC ghostICG (Figure 5a-c) along with the corresponding mathematical fits to force relaxations (Supporting eq S6). The negative force values prior to membrane pulling are due to the object pushing the trapped bead in the direction opposite to the pulling direction. The start of the pulling process was associated with a rapid increase in force, reaching the maximum value Fmax, the force required to form a membrane tether. Subsequently, there was a sudden reduction in the force, indicative of the membrane detachment from the cytoskeleton and formation of a tether. The increase in force during tether elongation (i.e., the time interval between reaching Fmax and when pulling stops) is primarily due to the viscous drag between the membrane lipids and the cytoskeleton.43 Pulling was stopped when tether was elongated to 10 μm. From that time point on, force relaxation took place, ultimately reaching the equilibrium value, Feq. The resulting profiles are consistent with those associated with membrane tethers pulled from RBCs and other mammalian cells.44-47
Figure 5.
Force profiles associated with membrane tether pulling. Illustrative tether force profiles for (a) RBC, (b) RBC ghost, and (c) RBC ghostICG. Black traces and the corresponding mathematical fits (colored traces: red for RBC, orange for RBC ghosts, and green for RBC ghostsICG) to the tether force relaxation based on the solution to the five-parameter generalized Maxwell–Weichert model (Supporting eq S6) are shown. Corresponding r2 values associated with the fits are 0.98, 0.95, and 0.99 for the RBC, RBC ghost, and RBC ghostICG, respectively. Box-and-whisker plots of (d) Fmax and (e) Feq for tethers extracted from RBCs (n = 13), RBC ghosts (n = 16), and RBC ghostsICG (n = 18). Individual values of the data are presented by the diamond symbols. Statistical significances are indicated as *(p < 0.05) and **(p < 0.01) between the indicated pairs.
From the onset of membrane pulling until the instant that the membrane becomes locally detached from the cytoskeleton to form a tether, energy is utilized to (1) bend the membrane and increase its curvature as it moves from the cell body to a nearly cylindrically shaped tether at a higher curvature, (2) surmount the adhesion energy between the membrane and the cytoskeleton, and (3) overcome the viscous resistance during pulling.46,48,49 The value of Fmax represents the combined contributions of these energetics to the formation of a membrane tether. Although there was not a statistically significant difference between the mean values of Fmax for RBCs (217 ± 24.3 pN) and RBC ghosts (153 ± 19.6 pN), the mean value of Fmax for RBC ghostsICG (317 ± 36.3 pN) was significantly higher as compared to those for RBCs (p < 0.05) and RBC ghosts (p < 0.01) (Figure 5d).
As the tether is elongated, membrane lipids are drawn into the tether while they slip against the cytoskeleton and transmembrane proteins. Once tether elongation stops, the membrane lipids continue to flow from the cell body, where the membrane is held at low tension into the tether where the membrane is under high tension. At equilibrium, the net flow of the lipids becomes zero, and the tension in the tether (σtether) is balanced against the tension in the cell membrane (σcell) and the adhesion between the membrane and the cytoskeleton (W0)50
| (16) |
Based on the minimization of the free energy of the tether at equilibrium and assuming a cylindrically shaped tether, it can be shown that23
| (17) |
and
| (18) |
where κ is the membrane bilayer bending modulus and dtether is the tether diameter at equilibrium. The bending modulus defines the energy to deform the membrane bilayer from its spontaneous curvature to a mean curvature. The spontaneous curvature results from the asymmetric properties of the monolayers, namely, differences in the spontaneous curvature of each of the monolayers, as determined by the degree and distribution of nonhomogeneities (e.g., due to various types of lipids) in each monolayer structure, as well as the differences in the area of the outer and inner monolayers.51
The mean Feq values for RBCs (73 ± 7.3 pN), RBC ghosts (55 ± 7.0 pN), and RBC ghostsICG (66 ± 7.4 pN) were not significantly different from each other (Figure 5e). These results suggest that the differences in σtether for RBCs, RBC ghosts, and RBC ghostsICG were balanced by the differences in their respective values of κ to ultimately result in statistically insignificant differences among the mean values of Feq.
Estimates of the Membrane Bilayer Bending Modulus.
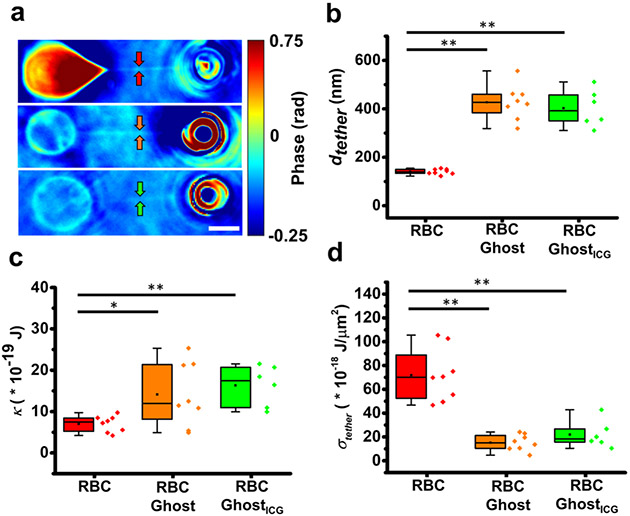
We used QPI to estimate the values of dtether pulled from RBCs, RBC ghosts, and RBC ghostsICG, and subsequently, used that information to quantify the values of κ and σtether. In contrast to the RBC ghosts and RBC ghostsICG, pulling a tether from the RBCs results in a dramatic change in its shape (Figure 6a). The mean ± SE value of dtether at equilibrium for tethers pulled from RBCs was 140 ± 3.9 nm (Figure 6b), somewhat larger than the mean value of 92 nm reported by Gómez et al. using scanning electron microscopy (SEM).44 The difference in the value of dtether as estimated by QPI and SEM may be due to fixation of the cells after tether pulling in preparation for SEM and subsequent use of geometrical approximations to estimate the tether diameter.52 The respective mean ± SE values of dtether for RBC ghosts (427 ± 25.3 nm) and RBC ghostsICG (402 ± 30.1 nm) were significantly larger than the mean value for RBCs (p < 0.01).
Figure 6.
Tether imaging and mechanical characterizations. (a) Representative images of membrane tethers pulled from an RBC (top panel), RBC ghost (middle panel), and RBC ghostICG (bottom panel) obtained by QPI at the time when the tether forces had relaxed to equilibrium. Arrows point to the respective tethers. The scale bar on the panel represents 5 μm. (b) Tether diameter (dtether), (c) membrane bending modulus (κ), and (d) tether tension (σtether) for RBCs (n = 8), RBC ghosts (n = 8), and RBC ghostsICG (n = 6). Individual values of the data are presented by the diamond symbols. Statistical significances are indicated as *(p < 0.05) and **(p < 0.01) between the indicated pairs.
Measurement of dtether provides a quantitative method to gain insight into the membrane–cytoskeleton attachment integrity. As these attachments become compromised, more membrane is liberated to flow into the tether, resulting in larger tethers. Therefore, the smaller value of dtether for RBCs is indicative of the proper attachment of the membrane to the cytoskeleton, whereas the larger values for RBC ghosts and RBC ghostsICG suggests that the attachment of the membrane to the cytoskeleton has become compromised, possibly allowing for more membrane and cytoskeletal proteins to flow into the tether.
Using eqs 17 and 18, we obtain the expressions for κ and σtether as
| (19) |
and
| (20) |
From the measurements of Feq and dtether and using eq 19, we estimated the mean ± SE values of κ as (7.0 ± 0.7) × 10−19 J (~170 kBT), (14.1 ± 2.7) × 10−19 J (~342 kBT), and (16.3 ± 0.8) × 10−19 J (~396 kBT) for RBCs, RBC ghosts, and RBC ghostsICG, respectively (Figure 6c), with kB as the Boltzmann constant (~1.38 × 10−23J·K−1) and T = 298 K. Incorporation of ICG into RBC ghosts to form RBC ghostsICG resulted in a slight, but not statistically significant, increase in the value of κ as compared to RBC ghosts. Nevertheless, this value of κ was still significantly higher as compared to κ for RBCs (p < 0.01) (Figure 6c).
Our estimated mean value of κ for RBCs is within the range of ~(2–9) × 10−19 J, as reported by other investigators.44,53-55 Variations in the membrane composition and age of RBCs could result in differences in the estimate of κ.55 Our finding of increased κ for RBC ghosts and RBC ghostsICG is consistent with those by Park et al. who reported a nearly fourfold increase in the membrane bending modulus as the normally shaped RBCs transitioned from discocytes to spherocytes.56 Using eq 20 in conjunction with measurements of Feq and dtether, we estimated the mean ± SE value of σtether as (71.9 ± 7.9) × 10−18 J·μm−2 for RBCs, similar to the mean value of 81 × 10−18 J·μm−2 reported by Gómez et al.44 We found that the values of σtether for RBC ghosts ((15.2 ± 2.4) × 10−18 J·μm−2) and RBC ghostsICG ((22.0 ± 1.9) × 10−18 J·μm−2) were significantly lower than the corresponding value for RBCs (Figure 6d).
The spontaneous curvature of the bilayer () is defined as51
| (21) |
where and are the respective spontaneous curvatures of the outer and inner leaflets. Using eq 21, our estimates of for RBCs, RBC ghosts, and RBC ghostsICG membrane tethers are 7.09, 2.38, and 2.26 μm−1, respectively. The positive values of indicate that the directions of the bilayer bending coincide with those for the outer monolayer, and the area of the outer monolayer exceeds the area of the inner monolayer.51 The lower value of for RBC ghosts and RBC ghostsICG is indicative of a smaller difference between the spontaneous curvatures of the outer and inner monolayer areas.
The higher value of the bending modulus for RBC ghosts and RBC ghostsICG is consistent with their lower as compared to the RBC membrane curvature and indicative of altered compositional and structural asymmetries in their monolayers. These altered asymmetries may be attributed to the spatial reorganization of the phospholipids, such as changes to their packing density in the leaflets and relocalization of the lipid raft domains containing cholesterol to change the bilayer curvature and act as modulators of membrane bending rigidity. Such redistributions may also cause differential stress in the bilayer where the two leaflets experience different lateral tensions. For example, altered partitioning of cholesterol in the monolayers can create differential stress to change the bending modulus.57
Previous fluorescence imaging of RBC ghostsICG show that ICG resides within the membrane of RBC ghostsICG in addition to the cytosolic core.58 Since the mean values of κ for RBC ghosts and RBC ghostsICG were not significantly different from each other, it is possible that at the ICC concentration utilized (100 μM), there was none or minimal bias in ICG distribution within the inner or outer leaflets to further contribute to changes in the spontaneous curvature and area of each monolayer, and to the differential stress already induced in the bilayer by other membrane constituents.
Similar to the membranes of other eukaryotic cells, the outer leaflet of the RBC membrane contains phosphatidylcholine and sphingomyelin, which have zwitterionic head groups with a mixture of cations and anions. The inner leaflet contains PS, which has a net negative charge. Amphipathic compounds preferentially intercalate their hydrophobic portions into the nonpolar parts of the lipids with their ionic portions exposed at the water–membrane interface. Based on the asymmetrical charge distributions in the membrane bilayer, anionic amphipathic molecules preferentially intercalate into the outer monolayer and crenate the membrane, whereas cationic molecules preferentially distribute into the inner monolayer and convert the membrane into cup shapes.59 Hypotonic treatment of RBCs, even without ICG loading, can result in translocation of PS to the outer leaflet,58,60 hence altering the mechanical and electrical asymmetry of the bilayer. Since ICG is a negatively charged amphipathic molecule, its natural tendency would be to intercalate into the outer leaflet due to repletion by the negatively charged PS, normally located in the inner leaflet. However, if some of the PS molecules are translocated to the outer leaflet in RBC ghosts and RBC ghostsICG, then it would become possible for ICG to intercalate into both leaflets and in domains distant from PS.
Previous studies based on pulling membrane tethers from mouse fibroblasts61 and blebbing human melanoma cells62 that lack cytoskeletal support report values of σcell in the range of (1–3) × 10−18 J·μm−2. For tethers pulled from HEK cells with disrupted membrane–cytoskeleton attachments,45 σcell has been estimated as ~5 × 10−18 J·μm−2. Since the value of σcell is nearly independent of cell type and σtether > σcell, the dominant determinant of tension in the tether is W0, the adhesion strength between the membrane and the cytoskeleton (see eq 16). Therefore, our estimates of σtether suggest that W0 is significantly lowered in RBC ghosts and RBC ghostsICG as compared to RBCs, an indication of impaired membrane–cytoskeleton adhesion in RBC ghosts and RBC ghostsICG. The surface area loss (Figure 2a) as a result of membrane vesiculation is attributed to compromised integrity of the membrane–cytoskeleton attachment63 and is associated with reduced RBC deformability.12 It is also reported that specific lipid domains are shed during vesiculation,64 further supporting that the reduced surface area in RBC ghostsICG can be associated with redistribution of the remaining lipid domains in the membrane.
The main determinants of membrane cohesion are a system of vertical linkages that connect the lipid bilayer to the RBC cytoskeleton. This cytoskeleton is primarily composed of spectrin tetramers formed by the head-to-head association of parallel α and β heterodimer chains, actin and its associated proteins (tropomyosin, tropomodulin, adducin, dematin), protein 4.1R, and ankyrin.65 Particularly relevant to the structural integrity of the membrane are the ankyrin- and protein 4.1R-based cytoskeletal protein complexes that connect to the membrane via the interaction with the cytoplasmic domains of various transmembrane linkage proteins. Band 3 and RhAG, linking the membrane to ankyrin, which, in turn, binds to β-spectrin, are thought to be the dominant determinants of membrane cohesion.63 Disruption of band 3 linkage in the ankyrin–spectrin complex further leads to dissociation of a large proportion of spectrin tetramers into dimers.66 Since band 3 is thought to serve as a binding site for hemoglobin,67 depletion of hemoglobin may contribute to conformational changes of band 3.
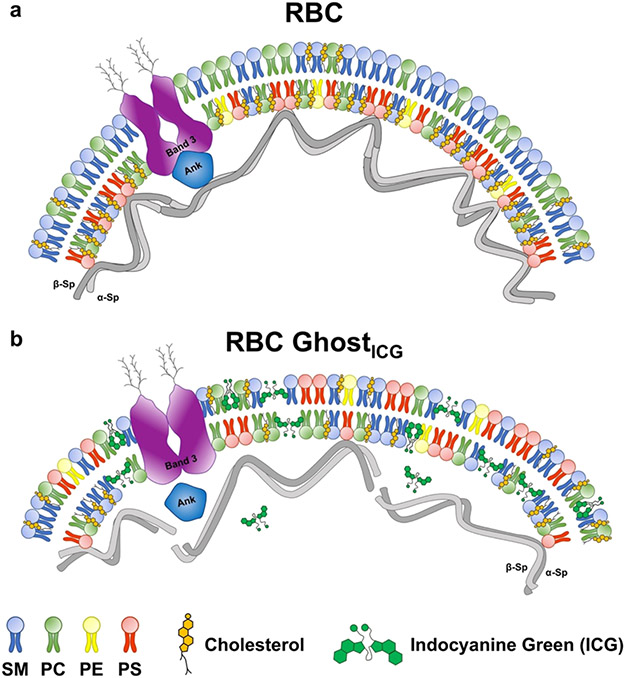
Another vertical linkage to maintain the mechanical stability of the membrane is mediated by the interaction of PS with specific residues on α and β-spectrin chains, protein 4.1R, and other cytoskeletal proteins.65,68 Therefore, lowered values of W0 for RBC ghosts and RBC ghostsICG suggest that the vertical linkages between the lipid bilayer and the cytoskeleton, such as those provided by band 3, RhAG, and PS, may be weakened or abolished. In the case of PS, the abolished linkages can result from the translocation of PS to the outer leaflet. Disrupted vertical linkages between the membrane and the cytoskeleton and alterations in the membrane asymmetry can also induce curvature changes to the bilayer and remodel the membrane. These remodelings are conceptually presented in Figure 7, and provide possible mechanisms for increased values of κ for RBC ghosts and RBC ghostsICG (Figure 6c).
Figure 7.
Conceptual illustration of the curvature change as a mechanism for membrane remodeling in RBC ghostsICG. (a) In RBCs, the membrane natural curvature is determined by the asymmetrical membrane structure resulting from asymmetrical distribution of phospholipids in the outer and inner leaflets, with phosphatidylserine (PS) primarily localized within the inner monolayer, and the presence of vertical transmembrane protein linkages such as band 3 as well as PS that connect to the cytoskeletal ankyrin (Ank)-based complex, which, in turn, binds to spectrin (sp). (b) In RBC ghostsICG as well as RBC ghosts (not shown), the membrane curvature is decreased due to changes in the membrane asymmetry that results from redistribution of the membrane phospholipids, particularly PS and cholesterol, disruption of the connections between PS and linkage proteins (band 3) with ankyrin, and conformational changes in membrane proteins (e.g., band 3). SM: sphingomyelin, PC: phosphatidylcholine, and PE: phosphatidylethanolamine.
Viscoelastic Properties.
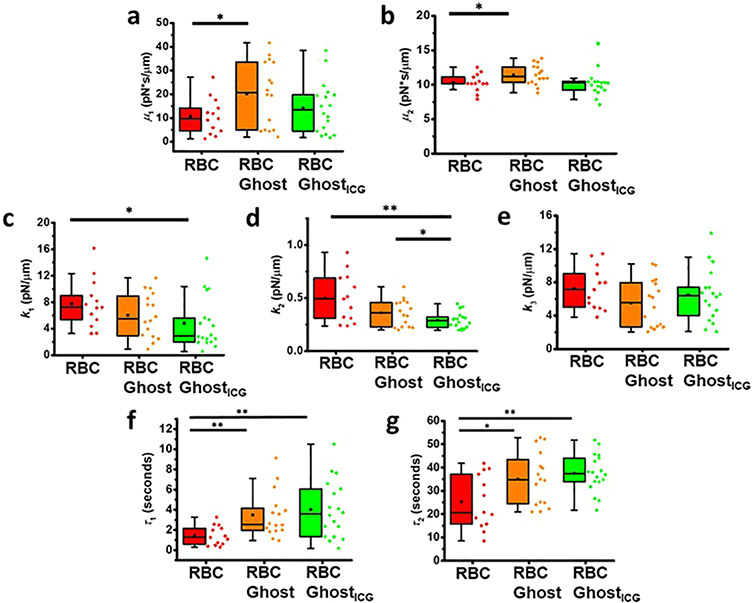
We estimated the values of the mechanical parameters associated with the Maxwell–Weichert model (Supporting Figure S5) by fitting an analytical solution34 (Supporting eq S6) to the measured force relaxation profiles. The mean values of friction coefficients μ1 (21.0 ± 3.3 pN·s·μm−1) and μ2 (11.7 ± 0.5 pN·s·μm−1) for RBC ghosts were significantly higher than those for RBCs (μ1 = 10.7 ± 2.1, and μ2 = 10.3 ± 0.4 pN·s·μm−1) (p < 0.05) (Figure 8a,b), indicating that the membrane of RBC ghosts was more viscous and resistant to flow, consistent with the images shown in Figures 4a and 6a and Supporting Videos S1 and S2.
Figure 8.
Estimates of viscoelastic parameters. (a) Friction coefficient μ1, (b) friction coefficient μ2, (c) high stiffness k1, (d) low stiffness k2, (e) equilibrium stiffness k3, (f) short force relaxation characteristic time τ1, and (g) long force relaxation characteristic time τ2 associated with RBCs (n = 13), RBC ghosts (n = 16), and RBC ghostsICG (n = 18). Individual values of the data are presented by the diamond symbols. Statistical significance is indicated as *(p < 0.05) and **(p < 0.01) between the indicated pairs.
The flow of the lipids within the bilayer is dampened by viscous dissipation during the in-plane shear deformation of the membrane. This viscous damping can arise from the structural barriers presented by transmembrane proteins and the cytoskeletal network against which the lipids slide. Since our results suggest that the attachment of the membrane to the cytoskeletal cortex is impaired in RBC ghosts, a source of resistance to lipids flow is likely the higher viscous drag against the transmembrane proteins whose conformations are altered. Increased values of μ1 and μ2 for RBC ghosts may also be a result of changes in the spatial redistribution of the lipids in the membrane to affect the frictional processes within the membrane and the subsequent flow characteristics.
For RBC ghosts, the mean value of μ1 was significantly larger than the mean value of μ2 (p < 0.05). These results are further indications of structural differences in the RBC ghost membrane, which resulted in lipid flow characterized by two different values of friction coefficients. When ICG was incorporated into RBC ghosts, the values of μ1 (14.3 ± 2.5 pN·s·μm−1) and μ2 (10.5 ± 0.5 pN·s·μm−1) became comparable to those for RBCs, suggesting that the presence of ICG within the bilayer may have led to reduced frictional effects, for example, by binding to some of the transmembrane proteins to reduce the viscous slippage of the lipids against the proteins.
Mean values of the stiffness values k1 (4.8 ± 0.9 pN·μm−1) and k2 (0.29 ± 0.02 pN·μm−1) for RBC ghostsICG were significantly lower than the corresponding values for RBCs (k1 = 7.8 ± 1.0, k2 = 0.5 ± 0.06 pN·μm−1) (Figure 8a,b). The mean value of k2 for RBC ghostsICG was also significantly lower than the value for RBC ghosts (0.38 ± 0.03 pN·μm−1) (p < 0.05). In comparison to the mean values of k1, the mean values of k2 were about an order of magnitude smaller for RBCs, as well as for RBC ghosts and RBC ghostsICG. The latter results suggest that two distinct phenomena are associated with the energy of membrane extension. The higher stiffness parameter k1 can be attributed to membrane area expansion arising from changes in the spacings between the molecules comprising the bilayer as well as those providing attachments to the cytoskeletal cortex and corresponds to the contribution of the energetic force associated with membrane elasticity. A lower value of k1 for RBC ghostsICG suggests that the intercalated ICG molecules in the monolayers could offer a mechanism to reduce the resistance of the bilayer to planar stretching. For example, a particular arrangement could be the presence of the lipophilic portions of the ICG molecules between the phospholipid tails in each monolayer to increase the spacing between the phospholipid molecules (see Figure 7b).
The lower stiffness parameter k2 is consistent with the contribution of the entropic repulsive forces between the monolayers. Such forces may be attributed to the presence of the out-of-plane undulations of the monolayers that result from various configurations that the monolayers can adopt. Intercalation of ICG in the monolayers could provide a mechanism to lower the entropic force by reducing the out-of-plane undulations.
The stiffness parameter k3 represents the spring-like property of the tether at equilibrium. Its mean value for RBCs (7.3 ± 0.71 pN·μm−1) was comparable to the mean value of 10.3 pN·μm−1 for membrane tethers pulled from human RBCs, as reported by other investigators.44 The mean values of k3 were not significantly different from each other for RBCs, RBC ghosts (5.4 ± 0.68 pN·μm−1), and RBC ghostsICG (6.4 ± 0.75 pN·μm−1) (Figure 8c), consistent with the absence of statistically significant differences among the mean values of Feq (Figure 5e).
The combined effects of the two friction coefficients (μ1 and μ2) and stiffness values (k1 and k2) can be evaluated using the characteristic times associated with force relaxation (Supporting eq S2). Values of relaxation characteristics time τ1 were about an order of magnitude shorter than the values for τ2 for RBCs as well as RBC ghosts and RBC ghostsICG (Figure 8f,g). At the instant when tether elongation stops, there is an area differential between the two leaflets where the inner monolayer is partially compressed and the outer monolayer is stretched. This area differential drives the transport of the lipids into the tether until force relaxation is completed. We attribute the short characteristic time (τ1) to the Marangoni convective flow of lipids from regions of low to high membrane tension during the first stage of relaxation69 and the long characteristic time (τ2) to the diffusive flow of lipids during the second phase of relaxation.45 Specifically, the mean ± SE values of τ1 for RBCs, RBC ghosts, and RBC ghostsICG were 1.4 ± 0.3, 3.5 ± 0.5, and 4.0 ± 0.7 s, respectively (Figure 8f). The respective mean ± SE values of τ2 were 25.3 ± 3.2, 34.5 ± 2.7, and 37.5 ± 1.9 s for RBCs, RBC ghosts, and RBC ghostsICG, respectively (Figure 8g). The mean values of τ1 and τ2 for RBCs were both significantly shorter than the corresponding values for RBC ghosts and RBC ghostsICG, further supporting the fact that membrane flow characteristics are altered in the RBC-derived constructs.
In summary, the formation of RBC ghosts and RBC ghostsICG is accompanied by a reduction in the bending modulus of the membrane bilayer as compared to RBCs (Figure 6c), impaired membrane flow characteristics (Figures 4b, 6a, and 8f,g), and increased frictional effects in the membrane in the case of RBC ghosts (Figure 8a,b). The presence of ICG, when used at a 100 μM concentration to fabricate the RBC ghostsICG, appears to affect the elastic and entropic characteristics of the membrane (Figure 8c,d); however, the induced increase in the viscous characteristics of the membrane during the formation of the ghosts is dominant over the elastic and entropic effects of ICG since both RBC ghosts and RBC ghostsICG have similar membrane flow dynamics (Figure 8f,g).
Implications for Biomedical Applications of RBC-Based Microparticle Delivery Systems.
Our results indicate that the membrane mechanical properties of RBC ghostsICG, as an example of erythrocyte-based delivery systems, are compromised, resulting in constructs that are not as deformable as normal RBCs. This reduced deformability can impair the ability of these particles to pass through the endothelial slits of the spleen, causing them to become trapped within the spleen and removed from circulation. Our recent in vivo study indicates that ~35% of the injected amount of RBC ghostsICG remained in the blood for 24 h following intravenous injection in healthy mice.11 Spleen, liver, and lungs, organs of the reticuloendothelial system rich in macrophages, contained ~40% of the injected RBC ghostsICG at 24 h.11
Changes in the mechanical characteristic may also affect the interaction of the particles with macrophages. In particular, rigidity and shape of the RBC are thought to override the signaling by CD47, with rigidified RBCs completely engulfed by macrophages in a shorter time than native RBCs.70 In light of such findings, it is possible the RBC-based particles that are less deformable (more rigid) than native RBCs, will be engulfed by macrophages more efficiently. Our findings suggest the need for the design and engineering of the next generation of RBC-based delivery systems with appropriate mechanical characteristics to achieve improved deformability and prolonged circulation.
CONCLUSIONS
Using optical methods in conjunction with image analysis and mechanical modeling, we have provided quantitative information related to morphological characteristics, hemoglobin content, and membrane mechanical properties of an RBC-based delivery system containing the FDA-approved near-infrared material, indocyanine green. We find that these material properties are significantly altered in these particles. As a result, the membrane of the particles is less deformable and more resistant to flow. We attribute these changes to impaired membrane–cytoskeleton attachment in the particles. These changes in material properties have implications related to the circulation time of RBC-based delivery systems and highlight the importance of membrane mechanical properties as an important criterion in the design and engineering of such delivery systems.
Supplementary Material
ACKNOWLEDGMENTS
This study was supported in parts by a grant from the National Institutes of Arthritis and Musculoskeletal and Skin Diseases (2R01-AR068067-05A1).
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.2c03472.
Additional experimental details; methods; and results including calibration profiles, QPI-based imaging of polystyrene beads and RBC-based particles, mechanical model formulation and solution, and absorption spectra (PDF)
Tether pulling from an RBC (Video S1) (AVI)
Tether pulling from an RBC ghost (Video S2) (AVI)
Tether pulling from an RBC ghostICG (Video S3) (AVI)
The authors declare the following competing financial interest(s): Author B.A. has a financial interest in Radoptics LLC, which is pursuing the commercial development of optical RBC-based particles. This interest did not interfere with the scientific work, judgment, and objectivity of the investigators in regard to the experimental procedures, analyses, and reporting and interpretation of results, or any other aspect of the study. All the remaining authors declare that they have no conflict of interests.
Contributor Information
Thompson Lu, Department of Bioengineering, University of California, Riverside, Riverside, California 92521, United States.
Chi-Hua Lee, Department of Biochemistry, University of California, Riverside, Riverside, California 92521, United States.
Bahman Anvari, Department of Bioengineering and Department of Biochemistry, University of California, Riverside, Riverside, California 92521, United States.
REFERENCES
- (1).Masterson C; McCarthy SD; O’Toole D; Laffey JG The Role of Cells and Their Products in Respiratory Drug Delivery: The Past, Present, and Future. Expert Opin. Drug Delivery 2020, 17, 1689–1702. [DOI] [PubMed] [Google Scholar]
- (2).Sier VQ; de Vries MR; van der Vorst JR; Vahrmeijer AL; van Kooten C; Cruz LJ; de Geus-Oei L-F; Ferreria V; Sier CFM; Alves F; Muthana M Cell-Based Tracers as Trojan Horses for Image-Guided Surgery. Int. J. Mol. Sci 2021, 22, No. 755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Di W; Tan X; Calderon IAC; Neal Reilly AA; Niedre M; Clark HA Real-Time Particle-by-Particle Detection of Erythrocyte-Camouflaged Microsensor with Extended Circulation Time in the Bloodstream. Proc. Natl. Acad. Sci. U.S.A 2020, 117, 3509–3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Hirschberg H; Madsen JL Cell Mediated Photothermal Therapy of Brain Tumors. J. Neuroimmune Pharmacol 2017, 12, 99–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Villa CH; Anselmo AC; Mitragotri S; Muzykantov V Red Blood Cells: Supercarriers for Drugs, Biologicals, and Nanoparticles and Inspiration for Advanced Delivery Systems. Adv. Drug Delivery Rev 2016, 106, 88–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Han X; Wang C; Liu Z Red Blood Cells as Smart Delivery Systems. Bioconjugate Chem. 2018, 29, 852–860. [DOI] [PubMed] [Google Scholar]
- (7).Vankayala R; Mac JT; Burns JM; Dunn E; Carroll S; Bahena EM; Patel DK; Griffey S; Anvari B Biodistribution and Toxicological Evaulation of Micron- and Nano-Sized Erythrocyte-Derived Optical Particles in Healthy Swiss Webster Mice. Biomater. Sci 2019, 7, 2123–2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Hammel P; Fabienne P; Mineur L; Metges J-P; Andre T; De La Fouchardiere C; Louvet C; El Hajbi F; Faroux R; Guimbaud R; Tourgeron D; Bouche O; Lecomte T; Rebischung C; Tournigand C; Cros J; Kay R; Hamm A; Gupta A; Bachet J-B; El Hariry I Erythrocyte-Encapsulated Asparaginase (Eryaspase) Combined with Chemotherapy in Second-Line Treatment of Advanced Pancreatic Cancer: An Open-Label, Randomized Phase Iib. Trial. Eur. J. Cancer 2020, 124, 91–101. [DOI] [PubMed] [Google Scholar]
- (9).Hunault-Berger M; Leguay T; Huguet F; Leprêtre S; Deconinck E; Ojeda-Uribe M; Bonmati C; Escoffre-Barbe M; Bories O; Chantal H; Chevallier P; Rousselot P; Reman O; Boulland M-L; Lissandre L; Turlure P; Bouscar D; Sanhes L; Legrand O; Lafage-Pochitaloff M; Béné MC; Liens D; Godfrin Y; Ifrah N; Dombret H Group for Research on Adult Acute Lymphoblastic Leukemia (GRAALL)A Phase 2 Study of L-Asparaginase Encapsulated in Erythrocytes in Elderly Patients with Philadelphia Chromosome Negative Acute Lymphoblastic Leukemia: The Graspall/Graall-Sa2-2008 Study Am. J. Hematol 2015. 90811818 DOI: 10.1002/ajh.24093. [DOI] [PubMed] [Google Scholar]
- (10).Zwaal RFA; Comfurius P; Bevers EM Surface Exposure of Phosphatidylserine in Pathological Cells. Cell Mol. Life. Sci 2005, 62, 971–988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Tang JC; Lee C-H; Lu T; Vankayala R; Hanley T; Azubuogu C; Li J; Nair MG; Jia W; Anvari B Membrane Cholesterol Enrichment of Red Blood Cell-Derived Microparticles Results in Prolonged Circulation. ACS Appl. Bio Mater 2022, 5, 650–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Huisjes R; A B; van Solinge WW; Schiffelers RM; Kaestner L; Wijik V Squeezing for Life - Properties of Red Blood Cell Deformability. Front. Physiol 2018, 9, No. 656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Muzykantov VR Drug Delivery by Red Blood Cells: Vascular Carriers Designed by Mother Nature. Expert. Opin. Drug Delivery 2010, 7, 403–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Hu CJ; Fang RH; Zhang L Erythrocyte-Inspired Delivery Systems. Adv. Healthcare Mater 2012, 1, 537–547. [DOI] [PubMed] [Google Scholar]
- (15).Millán CG; Marinero MLS; Castañeda AZ; Lanano J Drug, Enzyme and Peptide Delivery Using Erythrocytes as Carriers. J. Controlled Release 2004, 95, 27–49. [DOI] [PubMed] [Google Scholar]
- (16).Lee Y-J; van den Berg N; Orosco RK; Rosenthal E; Sorger JM A Narrative Review of Fluorescence Imaging in Robotic-Assisted Surgery. Laparoscopic Surg. 2021, 5, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Xu P-Y; Zheng X; Kankala RK; Wang S-B; Chen A-Z Advances in Indocyanine Green-Based Codelivery Nanoplatforms for Combinatorial Therapy. ACS Biomater. Sci. Eng 2021, 7, 939–962. [DOI] [PubMed] [Google Scholar]
- (18).Hanley T; Vankayala R; Lee C-H; Tang JC; Burns JM; Anvari B Phototheranostics Using Erythrocyte-Based Particles. Biomolecules 2021, 11, No. 729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Wang D; Haytham A; Mayo L; Tao Y; Saeedi O Automated Retinal Microvascular Velocimetry Based on Erythrocyte Mediated Angiography. Biomed. Opt. Express 2019, 10, 3681–3697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Sarshar M; Wong WT; Anvari B Comparative Study of Methods to Calibrate the Stiffness of a Single-Beam Gradient-Force Optical Tweezers over Various Laser Trapping Powers. J. Biomed. Opt 2014, 19, No. 115001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Zhang H; Stanger T; Wiklund K; Rodriguez A; Andersson M Umutracker: A Versatile Matlab Program for Automated Particle Tracking of 2d Light Microscopy or 3d Digital Holography Data. Comput. Phys. Commun 2017, 219, 390–399. [Google Scholar]
- (22).Sarshar M; Lu T; Anvari B Combined Optical Micro-manipulation and Interferometric Topography (Commit). Biomed. Opt. Express 2016, 7, 1365–1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Lu T; Anvari B Characterization of the Viscoelastic Properties of Ovarian Cancer Cells Membranes by Optical Tweezers and Quantiative Phase Imaging. Front. Phys 2020, 8, No. 582956. [Google Scholar]
- (24).Wang Z; Millet L; Mir M; Ding H; Unarunotai S; Rogers J; Gillette MU; Popescu G Spatial Light Interference Microscopy (Slim). Opt. Express 2011, 19, 1016–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).McGrory MR; King MD; Ward AD Using Mie Scattering to Determine the Wavelength-Dependent Refractive Index of Polystyrene Beads with Changing Temperature. J. Phys. Chem. A 2020, 124, 9617–9625. [DOI] [PubMed] [Google Scholar]
- (26).Kim J; Lee H; Shin S Advances in the Measurement of Red Blood Cell Deformability: A Brief Review. J. Cell Biotechnol 2015, 1, 63–79. [Google Scholar]
- (27).Zhernovaya O; Sydoruk O; Tuchin V; Douplik A The Refractive Index of Human Hemoglobin in the Visible Range. Phys. Med. Biol 2011, 56, 4013–4021. [DOI] [PubMed] [Google Scholar]
- (28).Gienger J; Smuda K; Müller R; Bär M; Neukammer J Refractive Index of Human Red Blood Cells between 290 Nm and 1100 Nm Determined by Optical Extinction Measurements. Sci. Rep 2019, 9, No. 4623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Hoang VT; Stepniewski G; Czarnecka K; Kasztelanic R; Long VC; Xuan KD; Shao L; M Ś; Buczyński R Optical Properties of Buffers and Cell Culture Media for Optofluidic and Sensing Applications. Appl. Sci 2019, 9, No. 1145. [Google Scholar]
- (30).Waugh RE; Bauserman RG Physical Measurements of Bilayer-Skeletal Separation Forces. Ann. Biomed. Eng 1995, 23, 308–321. [DOI] [PubMed] [Google Scholar]
- (31).Liu S; Deng Z; Li J; Wang J; Huang N; Cui R; Zhang Q; Mei J; Zhou W; Zhang C; Ye Q; Tian J Measurement of the Refractive Index of Whole Blood and Its Components for a Continuous Spectral Region. J. Biomed. Opt 2019, 24, 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Pham HV; Bhaduri B; Tangella K; Best-Popescu C; Popescu G Real Time Blood Testing Using Quantitative Phase Imaging. PLoS One 2013, 8, No. e55676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Park H; Lee SY; Ji M; Kim K; Son Y; Jang S; Park Y Measuring Cell Surface Area and Deformability of Individual Human Red Blood Cells over Blood Storage Using Quantitative Phase Imaging. Sci. Rep 2016, 6, No. 34257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Murdock DR; Ermilov SA; Spector AA; Popel AS; Brownell WE; Anvari B Effects of Chlorpromazine on Mechanical Properties of the Outer Hair Cell Plasma Membrane. Biophys. J 2005, 89, 4090–4095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Llaudet-Planas E; Vives-Corrons JL; Rizzuto V; Gómez-Ramírez P; Navarro JS; Coll Sibina MT; García-Bernal M; Ruiz Llobet A; Badell I; Velasco-Puyó P; Dapena JL; Mañú-Pereira MM Osmotic Gradient Ektacytometry: A Valuable Screening Test for Hereditary Spherocytosis and Other Red Blood Cell Membrane Disorders. Int. J. Lab Hematol 2018, 40, 94–102. [DOI] [PubMed] [Google Scholar]
- (36).Engström KG; Meiselman HJ Optical and Mathematical Corrections of Micropipette Measurements of Red Blood Cell Geometry During Anisotonic Perifusion. Cytometry 1994, 17, 279–286. [DOI] [PubMed] [Google Scholar]
- (37).Waugh RE; Narla M; Jackson CW; Mueller TJ; Suzuki T; Dale GL Rheologic Properties of Senescent Erythrocytes: Loss of Surface Area and Volume with Red Blood Cell Age. Blood 1992, 79, 1351–1358. [PubMed] [Google Scholar]
- (38).Linderkamp O; Wu PY; Meiselman HJ Deformability of Density Separated Red Blood Cells in Normal Newborn Infants and Adults. Pediatr. Res 1982, 16, 964–968. [DOI] [PubMed] [Google Scholar]
- (39).Lew VL; Raftos JE; Sorette M; Bookchain RM; Mohandas N Generation of Normal Human Red Cell Volume, Hemoglobin Content, and Membrane Area Distributions by “Birth” or Regulation? Blood 1995, 86, 334–341. [PubMed] [Google Scholar]
- (40).Kostić IT; Lj Ilić V; Đorđević V; Bukara K; Mojsilović SB; Nedović VA; Burgarski DS; Veljović Đ; Mišić D; Bugarski BM Erythrocyte Membranes from Slaughterhouse Blood as Potential Drug Vehicles: Isolation by Gradual Hypotonic Hemolysis and Biochemical and Morphological Characterization. Colloids Surf., B 2014, 122, 250–259. [DOI] [PubMed] [Google Scholar]
- (41).Bukara K; Jovanic S; Drvenica IT; Stancic A; Ilic V; Rabasovic MD; Pantelic D; Jelenkovic B; Bugarski B; Krmpot AJ Mapping of Hemoglobin in Erythrocytes and Erythrocyte Ghosts Using Two Photon Excitation Fluorescence Microscopy. J. Biomed. Opt 2017, 22, No. 026003. [DOI] [PubMed] [Google Scholar]
- (42).Dao M; Lim CT; Suresh S Mechanics of the Human Red Blood Cell Deformed by Optical Tweezers. J. Mech. Phys. Solids 2003, 51, 2259–2280. [Google Scholar]
- (43).Hochmuth RM; Evans EA Extensional Flow of Erythrocyte Membrane from Cell Body to Elastic Tether. I. Analysis. Biophys. J 1982, 39, 71–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Gómez F; Silva LS; de Sousa Araújo G; Frases S; Pinheiro AAS; Agero U; Pontes B; Viana NB Effect of Cell Geometry in the Evaluation of Erythrocyte Viscoelastic Properties. Phys. Rev. E 2020, 101, No. 072603. [DOI] [PubMed] [Google Scholar]
- (45).Khatibzadeh N; Gupta S; Farrell B; Brownell WE; Anvari B Effects of Cholesterol on Nano-Mechanical Properties of the Living Cell Plasma Membrane. Soft Matter 2012, 8, 8350–8360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Li Z; Anvari B; Takashima M; Brecht P; Torres JH; Brownell WE Membrane Tether Formation from Outer Hair Cells with Optical Tweezers. Biophys. J 2002, 82, 1386–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Pontes B; Ayala Y; Fonseca MCC; Romão LF; Amaral RF; Salgado LT; Lima FR; Farina M; Viana NB; Moura-Neto V; Nussenzveing HM Membrane Elastic Properties and Cell Function. PLoS One 2013, 8, No. e67708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Hochmuth F; Shao JY; Dai J; Sheetz MP Deformation and Flow of Membrane into Tethers Extracted from Neuronal Growth Cones. Biophys. J 1996, 70, 358–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Hochmuth RM; Marcus WD Membrane Tethers Formed from Blood Cells with Available Area and Determination of Their Adhesion Energy. Biophys. J 2002, 82, 2964–2969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Sheetz MP Cell Control by Membrane-Cytoskeleton Adhesion. Nat. Rev. Mol. Cell Biol 2001, 2, 392–396. [DOI] [PubMed] [Google Scholar]
- (51).Zimmerberg J; Kozlov MM How Proteins Produce Cellular Membrane Curvature. Nat. Rev. Mol. Cell Biol 2006, 7, 9–19. [DOI] [PubMed] [Google Scholar]
- (52).Pontes B; Viana NB; Salgado LT; Farina M; Moura Neto V; Nussenzveing HM Cell Cytoskeleton and Tether Extraction. Biophys. J 2011, 101, 43–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Hwang WC; Waugh RE Energy of Dissociation of Lipid Bilayer from the Membrane Skeleton of Red Blood Cells. Biophys. J 1997, 72, 2669–2678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Evans EA Bending Elastic Modulus of Red Blood Cell Membrane Derived from Buckling Instability in Micropipet Aspiration Tests. Biophys. J 1983, 43, 27–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Strey H; Peterson M; Sackmann E Measurement of Erythrocyte Membrane Elasticity by Flicker Eigenmode Decomposition. Biophys. J 1995, 69, 478–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Park Y; Best CA; Badizadegan K; Dasari RR; Feld MS; Kuriabova T; Henle ML; Levine AJ; Popescu G Measurement of Red Blood Cell Mechanics During Morphological Changes. Proc. Natl. Acad. Sci. U.S.A 2010, 107, 6731–6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Hossein A; Deserno M Spontaneous Curvature, Differential Stress, and Bending Modulus of Asymmetric Lipid Membranes. Biophys. J 2020, 118, 624–642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Jia W; Burns JM; Villantay B; Tang JC; Vankayala R; Lertsakdadet B; Choi B; Nelson JS; Anvari B Intravital Vascular Phototheranostics and Real-Time Circulation Dynamics of Micro- and Nanosized Erythrocyte-Derived Carriers. ACS Appl. Mater. Interfaces 2020, 12, 275–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Sheetz MP; Singer SJ Biological Membranes as Bilayer Couples. A Molecular Mechanism of Drug-Erythrocyte Interactions. Proc. Natl. Acad. Sci. U.S.A 1974, 71, 4457–4461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Schrier SL; A Z; Hervé P; Kader JC; Devaux PF Transmembrane Redistribution of Phospholipids of the Human Red Cell Membrane During Hypotonic Hemolysis. Biochim. Biophys. Acta 1992, 1105, 170–176. [DOI] [PubMed] [Google Scholar]
- (61).Raucher D; Stauffer T; Chen W; Shen K; Guo S; York JD; Sheetz MP; Meyer T Hosphatidylinositol 4,5-Bisphosphate Functions as a Second Messenger That Regulates Cytoskeleton-Plasma Membrane Adhesion. Cell 2000, 100, 221–228. [DOI] [PubMed] [Google Scholar]
- (62).Dai J; Sheetz MP Membrane Tether Formation from Blebbing Cells. Biophys. J 1999, 77, 3363–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Mohandas N; Gallagher PG Red Cell Membrane: Past, Present, and Future. Blood 2008, 112, 3939–3948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Leonard C; Conrard L; Guthmann M; Pollet H; Carquin M; Vermylen C; Gailly P; Van Der Smissen P; Mingeot-Leclercq MP; Tyteca D Contribution of Plasma Membrane Lipid Domains to Red Blood Cell (Re)Shaping. Sci. Rep 2017, 7, No. 4264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Lux SE Anatomy of the Red Cell Membrane Skeleton: Unanswered Questions. Blood 2016, 127, 187–199. [DOI] [PubMed] [Google Scholar]
- (66).Blanc L; Salomao M; Guo X; An X; Gratzer W; Mohandas N Control of Erythrocyte Membrane-Skeletal Cohesion by the Spectrin-Membrane Linkage. Biochemistry 2010, 49, 4516–4523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Shaklai N; Yguerabide J; Ranney HM Classification and Localization of Hemoglobin Binding Sites on the Red Blood Cell Membrane. Biochemistry 1977, 16, 5593–5597. [DOI] [PubMed] [Google Scholar]
- (68).Manno S; Takakuwa Y; Mohandas N Identification of a Functional Role for Lipid Asymmetry in Biological Membranes: Phosphatidylserine-Skeletal Protein Interactions Modulate Membrane Stability. Proc. Natl. Acad. Sci. U.S.A 2002, 99, 1943–1948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Dommersnes PG; Orwar O; Brochard-Wyart F; Joanny JF Marangoni Transport in Lipid Nanotubes. Europhys. Lett 2005, 70, 271–277. [Google Scholar]
- (70).Sosale NG; Rouhiparkouhi T; Bradshaw A; Dimova R; Lipowsky R; Discher DE Cell Rigidity and Shape Override Cd47’s “Self’-Signaling in Phagocytosis by Hyperactivating Myosin-Ii. Blood 2015, 125, 542–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.