一种用于可穿戴康复训练系统的微型磁流变液阻尼器的仿真与优化设计研究

Abstract

为解决传统步态康复训练设备体积大、动力响应慢、智能可控性差的问题，本文利用磁流变液剪切屈服强度随施加的磁场强度变化而变化的特性，运用科学计算软件，基于扩充的宾汉姆（Bingham）模型，对磁流变液阻尼器主要结构参数及其输出的作用力进行仿真优化研究，并对尺寸确定后的阻尼器进行三维建模，在此基础上根据阻尼器的设计使用要求，利用有限元分析软件对主要受力部件进行受力分析、强度校核以及拓扑优化，最终设计了一款适用于可穿戴康复训练系统的微型磁流变液阻尼器，对轻量化、便携化、智能化的康复训练设备的设计具有参考价值。

引言

生物医学工程领域，针对受损关节、脑卒中以及脑瘫康复所用的步态康复训练设备中传统动力调整机构往往存在体积庞大、动力响应慢、智能可控性差等问题^[1-2]，本文引入了磁流变液阻尼器（magnetorheological fluid damper，MRFD）作为系统的作用力输出装置，以期实现系统性能的提升。这种阻尼器的主要优势在于，在受控的磁场环境中，阻尼器产生的阻尼力具有输出响应速度快且精度高的特点，将其应用于汽车悬挂系统、飞机起落架等机械结构的减震装置时已展现出良好的应用前景^[3-5]；除此以外，还可应用于生物医学工程领域，如手功能康复训练系统、手术机器人的力反馈器^[6-7]，以及假肢膝关节的阻尼力输出装置^[8]等对输出响应速度有较高要求且需要对阻尼力实时动态调节的场景。

磁流变液阻尼器是一种以磁流变液（magnetorheological fluid，MRF）作为阻尼液的动态阻尼器。其可通过改变外加磁场强度继而改变磁流变液的剪切屈服强度，且该变化响应迅速可靠，进一步可实现对设备输出力的实时动态调节。另外，通过简化磁流变液阻尼器的结构，可缩小阻尼器的几何尺寸，从而实现设备整体的轻量化和结构的紧湊化，这对于穿戴式康复设备的便携化与智能化至关重要，同时在一定程度上突破了传统动力调整机构的局限性。

为了对应用于穿戴式康复设备的微型磁流变液阻尼器进行优化设计，有必要结合磁流变阻尼液的特性和实际需要，研究与之相适配的阻尼器机械结构及其相关参数。本文将基于扩充的宾汉姆（Bingham）模型对磁流变液所输出的作用力进行仿真，以此对活塞结构参数进行优化，并利用有限元分析软件对其主要零部件进行应力校核以及拓扑优化，最终给出一种用于穿戴式康复设备的微型磁流变液阻尼器的优化设计方法。

1. 基本方法

为了得到设计合理并优化的磁流变液阻尼器，首先要对磁流变液特性进行研究，然后结合其特性，研究相应阻尼器的机械结构与磁流变液的合理优化配置，最终实现磁流变液阻尼器的优化设计。

1.1. 结构设计

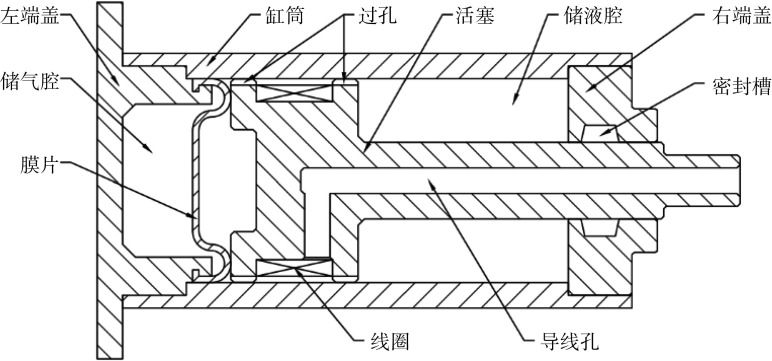
广泛应用的传统单杆式磁流变液阻尼器结构如图1所示，主要由两侧端盖、缸筒、内活塞、外活塞、活塞杆、线圈以及膜片等零部件组成。由于液体的不可压缩特性，单杆式阻尼器的活塞做往复运动时，有杆腔与无杆腔之间存在体积差，导致无法运动，故需要有密封条件良好的储气腔储存体积可压缩的气体，同时需要膜片或类似结构将储气腔与储液腔隔绝开，才能够满足使用要求。线圈，通过接通电流产生外加于磁变流体的电磁场；活塞杆处，为中空设计，方便布置控制电磁线圈的导电线。阻尼器工作时，过孔周围磁场强度受到缠绕于内活塞上的线圈电流控制，磁流变液的粘度与剪切屈服强度随之变化，液体受迫流经位于外活塞上的过孔，对外输出连续可调的阻尼力。外活塞与缸筒之间、活塞杆与端盖之间都需要相应的密封设计。

图 1.

Schematic diagram of the structure of traditional magnetorheological fluid damper

传统磁流变液阻尼器结构示意图

若按照传统磁流变液阻尼器结构等比例缩小，制成微型磁流变液减震器，其内部的微小复杂结构难以加工，制造成本将大幅提高。考虑到在正常工作时，阻尼器内的磁流变液将在有杆腔与无杆腔间往复流动，故取消外活塞设计，减少原活塞处的密封装置，并在内活塞外沿开槽，作为液体过孔。将活塞杆与活塞做一体化设计，以简化零件结构，降低制作成本。活塞与活塞杆仍做中空设计，以布置磁场线圈导线。膜片与活塞杆与端盖间的密封装置予以保留。经简化后的磁流变液阻尼器结构如图2所示。

图 2.

Schematic diagram of simplified design of magnetorheological fluid damper

简化设计的磁流变液阻尼器结构示意图

经简化设计的微型磁流变液阻尼器不仅能够实现传统磁流变液阻尼器的功能，且结构简单，便于加工，有利于实现各零部件主要尺寸的微型化。

1.2. 仿真与分析

磁流变液阻尼器结构实现了微型化，但其主要性能参数，如阻尼力输出特性等，是否能够满足应用的要求，可通过计算机仿真进行验证。

1.2.1. 磁流变体数学模型

磁流变液是磁流变液阻尼器中的关键材料，它的特性关系到阻尼器的动态响应行为，理论上，其特性可用不同类型的数学模型进行描述，如修正的布克-温（Bouc-wen）模型等参数化模型^[9-11]，或神经网络模型等非参数化模型^[12]。考虑到本文所述设备的应用场景，以及对控制精度与响应速度的要求，且在设计初期需要得知阻尼器的最大输出阻尼力，选择扩充的宾汉姆模型^[13]较为合适，其数学模型如式(1)所示：

1

式中，F_d是阻尼器所产生的阻尼力；L是活塞有效长度；A_p是活塞的有效面积；h是孔道直径；τ_y是磁流变液的屈服强度，与阻尼器线圈电流有关；sgn()为符号函数，指出括号内参数的正负号；是阻尼器活塞与缸体间的相对速度；η是磁流变液的动力粘度系数；D是缸体内径；f₀为蓄能器引起的阻尼器出力偏差（可忽略）。其中，磁流变液的屈服强度τ_y计算公式如式（2）所示：

2

式中，、，均为与磁流变液性能相关的系数^[14]；I为电流大小；e为自然常数。

考虑在本磁流变液阻尼器上存在回复力作用，故在扩充的宾汉姆模型中增加一线性项以模拟弹簧所起的作用，弹簧弹力与阻尼器所提供的阻尼力共同作用，形成作用力F，得到改进的模型结构如图3所示。

图 3.

Diagram of simulation model structure

仿真模型结构图

图3中，忽略蓄能器所引起的阻尼器出力偏差，在并联弹簧后，阻尼器所输出的作用力F如式（3）所示：

3

式中，k为弹簧的弹性系数，x为活塞与缸筒间的相对位移。

由式（3）可以看出，磁流变液阻尼器所输出的作用力F可以分解为三项：其中第一项是与磁流变体剪切应力和速度方向有关的流体内摩擦力，可以通过改变阻尼器内充填的磁流变液的剪切屈服强度控制其大小，为可控阻尼力，记作F1，与过孔孔道直径h成反比；第二项与速度呈线性关系，可以看作为粘滞力，为不可控阻尼力，记作F2，与孔道直径h的三次方成反比；第三项为弹簧所提供的弹力，与弹簧的弹性系数和弹簧的形变量有关，记作F3。由此可见，在磁流体物理特性确定的条件下，过孔的孔道直径h是影响输出阻尼力的关健参数，是仿真时要特别研究的参数。

1.2.2. 受力分析与拓扑优化

由于本文所研究的微型磁流变液阻尼器在实际工况中需要承受较大外力，在阻尼器各主要结构尺寸确定后，还需通过软件对各零部件进行三维建模，借助计算机辅助工程分析软件Workbench 2019 R2（ANSYS Inc., 美国）对阻尼器的主要受力部件进行受力分析，并对其强度、刚度进行校核。

若受力分析结果显示其结构应力满足使用要求，且材料安全裕度较大时，为了实现轻量化设计，应对所设计的零件进行结构拓扑优化，以减轻重量，同时节约材料，降低成本。

2. 结果分析

2.1. 孔道直径优化

考虑到微型化的要求，本文所研究的微型磁流变液阻尼器各主要尺寸相对传统磁流变液阻尼器均有大幅缩小，而缸径、行程等受结构及使用要求限制保持不变。基于并联弹簧改进后扩充的宾汉姆模型，如式（3）所示，阻尼器中流体过孔孔道直径h将是对所输出的阻尼力有显著影响的重要参数，通过建立适当的模型和仿真，找出最佳参数值。

依据前文所述改进后扩充的宾汉姆模型，借助科学计算工程软件MATLAB R2019b（MathWorks Inc., 美国）的可视化仿真工具Simulink，对模型进行模块化建模和仿真。阻尼器所输出阻尼力的模块框图如图4所示。

图 4.

Block diagram of the acting force of simulation module

作用力仿真模块框图

图4中，I为线圈电流值，单位：A；sin为阻尼器外加正弦位移激励，单位：mm；v代表对位移求导，得到阻尼器活塞相对缸筒的速度；F1、F2、F3分别代表前文所述摩擦力、粘滞力与弹簧弹力；add表示三项相加；F代表最终得到阻尼器作用力输出值，单位: N。

基于本文所述微型磁流变液阻尼器，模型中弹簧弹性系数k取7 N/mm，动力粘度系数η取1 Pa∙s，活塞的有效长度L为4 mm，缸体内径D为16 mm，活塞的有效面积A_p为200 mm²。

阻尼器主要结构尺寸设定依据如下：① 为了使设备结构尽可能紧凑的同时，方便采购阻尼器内部其他标准化配件，降低设备整体制作成本，缸体内径设为16 mm；② 考虑到实际加工难易程度，活塞有效长度设为4 mm；③ 由于本文所述阻尼器实际工况为下压状态，即活塞向膜片方向运动，故活塞有效面积为活塞无杆侧横截面积，大小为200 mm²；④ 受紧凑结构限制，所选弹簧弹性系数k为7 N/mm。

传统磁流变液阻尼器孔道直径h的最优取值为0.8~2.0 mm^[15]，相较于此，在本微型磁流变液阻尼器中，孔道直径的上限设为1.0 mm，下限为0.1 mm。

确定孔道直径h取值范围为0.1~1.0 mm，间隔为0.1 mm。阻尼器电磁线圈输入电流为1 A，以便穿戴设备电源供电。参照常人的单足步态频率^[16]，设置阻尼器外部施加的正弦位移激励频率为1 Hz，以模拟进行康复训练患者的单足步态频率；正弦位移激励幅值为18 mm^[6]，以模拟阻尼器的最大行程。阻尼器最大作用力与孔道直径的仿真结果如图5所示。

图 5.

Simulation results of maximum acting force and hole diameter

最大作用力与孔道直径仿真结果

由图5可知，当孔道直径h为0.1 mm时作用力过大，而孔道直径h大于0.6 mm时作用力过小且变化不明显，均不再考虑。取孔道直径h为0.2~0.6 mm，间隔0.1 mm，0~3 s内阻尼器作用力随时间变化曲线如图6所示。

图 6.

Curves of acting force versus time variation under different hole diameters

不同孔道直径下作用力与随时间变化曲线

由图6可知，阻尼器作用力F在时域上呈余弦函数变化规律，不同孔道直径下作用力最大值大致出现在同一时刻，图像在0值附近不连续，但不影响读取作用力最大值数据。

由于磁流变液的剪切屈服强度受周围环境磁场影响，而磁场直接受线圈电流控制，故进一步对孔道直径h为0.2、0.3、0.4 mm时阻尼器做输出的最大阻尼力与电流的对应关系进行仿真研究，以确定孔道直径尺寸以及最大工作电流大小，其结果如图7所示。

图 7.

Corresponding relationship between maximum acting force and current value under different hole diameters

不同孔道直径下最大作用力与电流值的对应关系

为了确定阻尼器行程，仍需进一步对所施加的外部正弦激励的幅值进行仿真优化。在该仿真过程中认为患者单足步态频率不变，即外部正弦激励频率恒定为1 Hz。考虑到患者进行康复训练时的稳定性与安全性，阻尼器行程不宜过长，而行程过短则影响训练效果，故外部正弦激励的幅值取值范围为10~20 mm，间隔为1 mm，线圈电流为1 A，仿真结果如图8所示。

图 8.

Corresponding relationship between maximum acting force and damper stroke

最大作用力与阻尼器行程的对应关系

2.2. 结构受力分析

为了方便患者穿戴进行康复训练，需对各主要尺寸进行微型化设计，其最大整体尺寸为50 mm，而内部最小构件的最大几何尺寸为10 mm。实际工况中，考虑成人的最大重量及其一般行走运动时所产生的动态载荷，单个阻尼器最大的负载外力F_max设为600 N，在此基础上考虑阻尼器不同内部结构所能承受的最大应力。因此在阻尼器各主要结构尺寸确定后，要结合主要受力部件的材料强度、刚度等参数，对受力部件进行受力分析。由于钢材的含碳量越高，材料抗拉强度越高，而导磁能力就越低，为了兼顾材料强度与磁场的要求，缸筒选用20钢，活塞选用电工纯铁（DT4）^[17]，其余零件材料选用铝合金。

选择设备在正常工况下所受最大外力为阻尼器的主要受力部件的载荷，借助有限元分析软件对其进行受力分析，进行材料的强度、刚度校核，从而设计最佳尺寸与结构。以下为阻尼器活塞的分析与校核的操作过程：

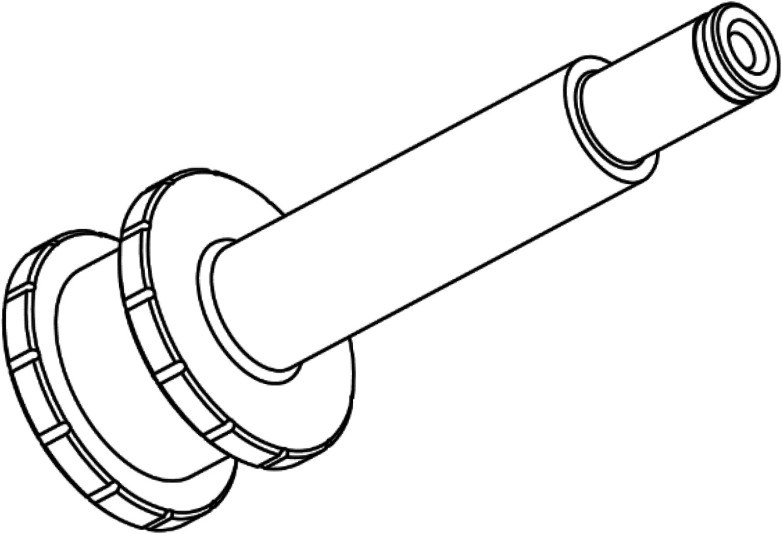
（1）在计算机辅助设计软件中对阻尼器活塞进行三维建模，如图9所示。

图 9.

3D modeling design drawing of damper piston

阻尼器活塞三维建模设计图

由前文所述，本装置中磁流变液阻尼器的内活塞、外活塞与活塞杆为一体化（简称为活塞）结构，活塞的孔道直径为0.3 mm，有效长度为4 mm，外径为16 mm；活塞杆阶梯处半径为3 mm，活塞杆半径为4 mm。

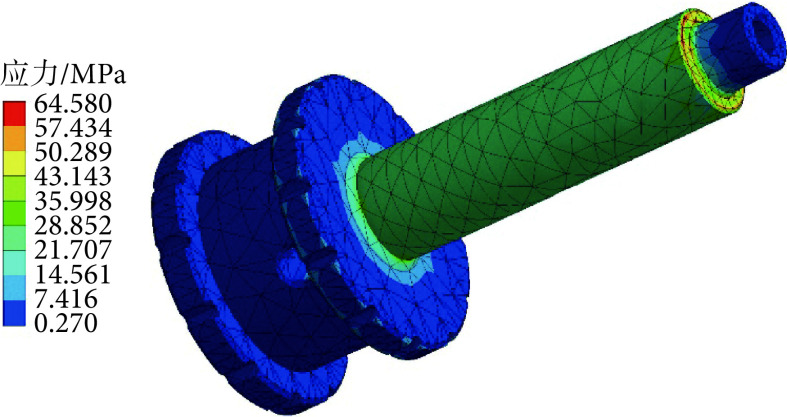
（2）选择计算该零件的应力分布情况，其具体结果如图10所示：

图 10.

Stress nephogram of the damper piston

阻尼器活塞的应力云图

如前文所述，活塞材料选用电工纯铁DT4，其密度为7.87 g/cm³，杨氏模量为80.65 GPa，泊松比为0.291，屈服强度为160 MPa。将活塞无杆侧端面以及外围柱面设为固定约束，在活塞杆阶梯处施加朝向活塞的力，值为600 N；设置固定约束面25个，施力面1个，网格对角线长度为43.775 mm，网格最小边长为0.241 93 mm，网格平均表面积为14.537 mm²。

2.3. 拓扑优化

由阻尼器主要受力部件的受力分析可知，其材料安全裕度较大，理论上可以进行进一步结构优化，以达到轻量化的目的，使可穿戴设备更加便携，减轻患者进行康复训练时由于所用装置过重造成的额外负重。

使用有限元分析软件，在静力分析的基础上，对阻尼器的主要受力部件进行了结构拓扑优化，在保证阻尼器工作稳定可靠的前提下实现器件的轻量化。在微型磁流变体阻尼器中活塞为阻尼器的核心机械部件，出于安装配合考虑，将活塞无杆侧端面、活塞外围柱面以及活塞杆阶梯处设为参考面，即受约束表面，不对其进行操作，其余部分设为优化面，可对其进行减重设计。设置不同的质量保留比例，进行拓扑优化。质量保留比例为85%时的拓扑优化结果如图11所示。

图 11.

Optimized calculation results of piston topology (85% weight retention)

活塞拓扑优化计算结果（85%质量保留）

由于当质量保留比例设置为85%及以下时，零件实体不连续，不具备工程可实现性，故列出质量保留比例为90%时的计算结果，如图12所示。

图 12.

Optimized calculation results of piston topology (90% weight retention)

活塞拓扑优化计算结果（90%质量保留）

3. 讨论

由对孔道直径h的仿真结果可知，在电流大小、磁场变化频率及磁场强度一定的情况下，磁流变液阻尼器经微型化设计后，使作用力变化较大的孔道直径区间为0.1~0.6 mm，当孔道直径大于0.6 mm时，其变化对作用力无明显影响；孔道直径为0.1 mm时作用力过大，且不易加工，不适用于本系统使用场景，故不予考虑。

由最大作用力与线圈电流仿真结果可知，当线圈电流小于1.5 A时，阻尼器所输出的最大作用力与电流大小近似成正比。结合本系统使用场景对作用力及所携带电源的要求，确定孔道直径为0.3 mm，最大工作电流为1 A。

由最大作用力与阻尼器行程的仿真结果可知，阻尼器所输出的最大作用力与阻尼器行程近似成正比。综合考虑患者进行康复训练时的稳定性与安全性，最终阻尼器行程设置为15 mm。

至此，阻尼器各项主要结构参数均已确定。当单足步态频率为1 Hz，线圈电流为1 A时，单个阻尼器可对外输出的最大作用力为300 N。

由活塞的受力分析结果可知，该零件的最大应力为64.6 MPa，出现在活塞杆阶梯处，而所选用电工纯铁材料的屈服强度为160 MPa，此时材料安全裕度为147%，能够满足使用要求。其余主要受力部件的受力分析与强度校核过程同上，其材料屈服强度与安全裕度均满足使用要求。

由活塞的拓扑优化结果可知，当活塞的质量保留比例为90%时，零件实体连续，可进行下一步工程设计，但由于活塞各尺寸较小，按优化结果加工会大大增加制造成本，而质量仅减少约1.5 g。综合考虑，认为拓扑优化结果对零件减重效果不明显，且会大幅增加加工成本，故保留原有设计。同上，对阻尼器其他主要受力部件进行相似操作后，减重效果不明显，原有设计均予以保留。

4. 结论

为了改善传统康复训练设备中动力机构的不足，本文提出了一种微型磁流变液阻尼器的设计。该设计利用磁流变液的材料特性，参考传统磁流变液阻尼器，对其结构进行简化，基于扩充的宾汉姆模型，借助可视化仿真工具对该阻尼器所输出的作用力进行了仿真，得出了微型化磁流变液阻尼器尺寸不可盲目参考经验值的结论，须针对其关键结构参数，如孔道直径等进行优化设计，最终形成了一套选取微型磁流变液阻尼器关键结构参数的方法。设计者可依此方法，通过仿真确定各主要结构参数，优化关键参数如孔道直径尺寸、工作电流大小以及阻尼器行程的取值，并对尺寸确定后的阻尼器进行三维建模，在此基础上根据阻尼器在应用场景中可能受到的最大外力，利用有限元分析软件对主要受力部件进行受力分析、强度校核以及拓扑优化设计，最终确定满足使用要求且工程可实现的微型磁流变液阻尼器设计方案。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：解世君主要负责前期调查研究、设备结构设计、实验方法设计、数据记录与分析以及论文初稿撰写；易卫东主要负责研究课题监管与指导以及论文审阅修订；杨墨欣主要负责实验方法设计、数据记录与分析以及论文审阅修订；陈永锐主要负责提供实验指导、数据分析指导以及论文审阅修订。

Funding Statement

国家重点研发计划（2020YFC2006702）

Ministry of Science and Technology of the People's Republic of China