基于焦点损失函数的嵌套长短时记忆网络心电信号分类研究

Abstract

心电图（ECG）可直观地反映人体心脏生理电活动，在心律失常检测与分类领域中具有重要意义。针对ECG数据中类别不平衡对心律失常分类带来的消极作用，本文提出一种用于不平衡ECG信号分类的嵌套长短时记忆网络（NLSTM）模型。搭建NLSTM学习并记忆复杂信号中的时序特征，利用焦点损失函数（focal loss）降低易识别样本的权重；然后采用残差注意力机制（residual attention mechanism），根据各类别特征重要性修改已分配权值，解决样本不平衡问题；再采用合成过采样技术算法（SMOTE）对麻省理工学院与贝斯以色列医院心律失常（MIT-BIH-AR）数据库进行简单的人工过采样处理，进一步增加模型的分类准确率，最终应用MIT-BIH-AR数据库对上述算法进行实验验证。实验结果表明，所提方法能有效地解决ECG信号中样本不平衡、特征不突出的问题，模型的总体准确率达到98.34%，较大地提升对少数类样本的识别和分类效果，为心律失常辅助诊断提供可行的新方法。

引言

据世界卫生组织提供的数据表明，每年心血管疾病（cardiovascular disease，CVD）导致的死亡人数约占全世界死亡人数的三分之一；其中老年人作为心血管疾病的高发群体，针对老年人群所患心血管疾病的诊断手段提出了更高要求。心律失常是心血管疾病中最常见的一种病况^[1]，许多心血管疾病病发初期通常伴有心律失常的出现；而心电图（electrocardiogram，ECG）可以直接反映心脏的电活动变化，是诊断心律失常的重要手段^[2]。医生通过分析ECG数据进行心律失常诊断，但这种基于人工经验的判断方法很容易造成漏诊、误诊，且需耗费大量时间，因此基于计算机辅助的心律失常分类的医疗手段应运而生^[3-5]，其中大多数分类算法集中在传统的机器学习领域。Dutta等^[6]提出一种基于最小二乘支持向量机的自动医疗诊断工具，对ECG信号进行三分类，准确率达到95.82%。Li 等^[7]使用小波包分解、小波包熵提取ECG信号特征，并结合随机森林对ECG信号进行分类，在麻省理工学院-贝斯以色列医院心律失常（the Massachusetts institute of technology and Beth Israel hospital arrhythmia， MIT-BIH-AR）数据库^[8]上进行验证，准确率达到94.61%。Mondéjar-Guerra等^[9]提取RR间期和波形形态学特征，采用组合支持向量机作为分类器，在ECG信号四分类上取得94.5%的准确率。

上述基于传统机器学习的ECG信号分类算法主要有预处理、特征提取、特征分类^[10-11]等步骤，虽然这些算法表现出良好的分类性能，但其存在着依赖手工提取特征的局限^[12]。相较于传统方法，基于深度学习的方法具有从输入的数据中自动提取有效特征并完成分类的能力^[13-14]。刘光达等^[15]提出一种结合前向反馈神经网络和卷积神经网络（convolutional neural networks，CNN）的心律失常诊断算法，总体准确率达到91.5%；Xiao等^[16]使用概率神经网络将ECG信号分为正常和心律不齐类别，在MIT-BIH-AR数据库上达到96.5％的分类准确率；Li等^[17]将小波包分解与遗传算法-反向传播神经网络相结合，完成特征提取并实现ECG信号六分类，准确率达到97.78%。

在ECG数据集中，正常节律与心律失常样本数量差异较大，带来样本不平衡问题；例如，MIT-BIH-AR数据库中正常节律有近十万个，然而室性期前收缩不到八千个。上述算法并未针对ECG数据中样本不平衡问题做出相应处理和验证，无法证明其在实际应用中的普适性和鲁棒性。本文提出基于嵌套长短时记忆网络（nested long short-term memory，NLSTM）^[18]的心律失常分类混合模型，并在NLSTM模型中加入残差注意力机制（residual attention mechanism），选择性遗忘局部特征，并于全局特征分配更强注意力；利用焦点损失函数（focal loss）^[19]聚焦学习小样本类别的相关特征，进而与大样本类别进行区分完成准确分类；为进一步提升分类性能，基于少数类样本合成过采样技术（synthetic minority over-sampling technique，SMOTE）^[20]适量扩充不平衡数据集中的小样本类别数目，增强特征，提高分类性能。本文针对ECG信号中的不平衡问题进行充分探讨，寻求一种鲁棒性与准确性更高的ECG信号分类方法，以促进精准辅助医疗与人工智能的有效结合。

1. 数据处理

1.1. 小波阈值去噪

由于硬件电路固有特性以及ECG数据采集环境的干扰，所采集的ECG信号中夹杂着各种噪声，例如：基线漂移、肌电扰动、工频干扰等。为提高分类精度，避免噪声干扰产生误判，对ECG信号的预处理是尤为必要的。本文运用小波变换对ECG信号进行尺度分解、阈值处理和重构信号来滤除噪声^[21]。

小波变换是一种在非平稳时间序列数据分析中常用的方法，能放大局部特征，保护有用的突变信号，有效地将信号与噪声区分开来，连续信号f(t)小波变换的函数如式（1）所示：

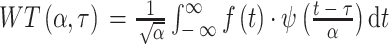1

式中，α为尺度因子，是一个总大于0的连续变量，τ为平移因子；为对基本小波函数Ψ(t)作伸缩，WT(α, τ)为信号f(t)的小波变换值。

ECG信号经小波分解后，信号的重要特征主要由幅值较大的小波系数进行表征，而噪声的小波系数幅值较小，可根据幅值差异选取一个合适的阈值，将幅值小于阈值的小波系数判定为噪声并置为零，幅值大于阈值的小波系数予以保留或者进行压缩，最后对小波系数进行小波逆变换，达到去噪目的。多贝西（Daubechies，Db）小波函数族的特征与ECG信号的QRS波相似，能谱集中在低频附近^[22]，能够有效地与ECG信号中的噪声进行区分；故本文选取6阶Daubechies小波函数^[23]作为式(1)中的小波函数，并设定小波分解的层数为8。去噪前后的ECG信号波形对比如图1所示。

图 1.

Comparison of ECG signal wavelet denoising

ECG信号小波去噪对比

1.2. R波峰值检测及心拍分割

一个完整的心拍波形由当前P波起始至下一个P波起始，如图2所示。当出现心律失常时，心拍波形会发生变化，例如：出现心脏左右束支的传导阻滞、心室扩大等情况时，QRS波群出现增宽和变形，因此通过波形变化能够有效地检测心律失常。与幅值较小的P波不同，R波幅值大、易辨识且不易受到噪声干扰，所以通常选取R波点作为基准点对波形进行定位，进而再定位到P波位置。本文使用潘-托普金斯（Pan-Tompkins）算法^[24]确定R波位置，对ECG信号进行分割，向前截取149个样本点，向后截取150个样本点，构成包含R波基准点在内的共300个样本点作为一个样本心拍。

图 2.

Heartbeat waveform of ECG signal

ECG信号心拍波形

2. 算法原理

2.1. 嵌套长短时记忆网络

传统的长短时记忆网络（long short-term memory，LSTM）面对长序列数据时，极易出现梯度弥散或爆炸问题，导致LSTM仅具备短时记忆，无法在长时间序列数据中获取足够特征。为了解决时序数据的长期依赖问题，Moniz 等^[18]提出了NLSTM神经网络，通过记忆历史数据中的附加信息来提高预测性能。NLSTM的单元结构如图3所示。

图 3.

Architecture of NLSTM unit

NLSTM单元结构

NLSTM具有多层内存，由内外两层LSTM相嵌套，内部存储单元为内层LSTM。外部存储单元可以自由地、选择性地读写内部单元的记忆信息，NLSTM从整体上提高了传统LSTM神经网络结构的鲁棒性，能够对长序列ECG信号进行强记忆和处理。

传统LSTM单元的存储单元状态c_t更新如式（2）所示：

2

其中， 和 分别为现在的输入信息与过去的输出信息。

NLSTM的更新方式与传统LSTM一致，但内部存储单元状态c_t的更新增加两部分，如式（3）所示：

3

式中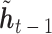，为t − 1时刻内部单元的输出，由存储单元状态c_{t − 1}和函数f_t决定；I_t为t时刻内外过渡输入，由外部单元t时刻输入x_t、外部输入到内部权重W_xi、外部单元t − 1时刻输出h_{t − 1}、外部输出到内部权重W_hi、过渡偏置b_i及激活函数 计算得到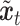；为t时刻内部单元的输入，由输入到存储权重W_xc、输出到存储权重W_hc、存储单元偏置b_c、内外过渡输入I_t及激活函数 计算得来。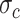 为外部存储单元激活函数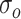， 为输出激活函数。

由于NLSTM内部存储单元的存在，外部存储单元状态c_t的更新如式（4）所示：

4

NLSTM网络通过外部记忆和内部记忆的结构形成层次记忆，可以记忆和处理更长期的信息。因此，NLSTM网络能够代替LSTM或其他扩展，具有高精度低误差的性能，可以完成对复杂ECG信号特征的处理与记忆。

2.2. 残差注意力机制

注意力机制是一种模拟人类注意力的模型，通过对不同信息分配不同权重^[25]，从而提取ECG信号中更具区分性的特征。将NLSTM网络的输出v_o作为注意力机制的输入，通过非线性变换得到隐藏信息，再使用输出激活函数对其进行归一化操作，从而得到NLSTM网络的超参数，并对其进行处理，具体计算方法如式(5)~(7)所示：

5

6

7

式中，b_i为i时刻的偏置，o_i为原始隐藏层状态，e_i表示隐藏层状态向量o_i被处理后的向量，S为新隐藏层的状态，α_i是每个原始隐藏层状态在新的隐藏层状态中所占的比重大小。

但传统注意力机制仅能分析当前信息的重要程度，缺乏对先前信息的捕捉能力。本文基于残差网络的思想对其进行改进，提出残差注意力机制，提高对ECG信号特征提取的能力。残差注意力机制的架构如图4所示，利用捷径（shortcut）将输入与输出连接^[26]，降低数据中信息的冗余度，进行信息的过滤，增加信息的可用性。残差注意力机制的输出如式（8）所示：

图 4.

Architecture of residual attention mechanism

残差注意力机制架构

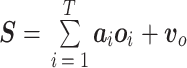8

2.3. 数据增强-SMOTE算法

相对于正常节律样本，心律失常样本属于极少数样本，样本不平衡会导致少数样本特征被多数样本特征所埋没，从而导致神经网络的分类准确率下降。解决这类问题通常是对多数类样本欠采样或对少数类样本过采样，而欠采样会导致样本特征丢失，因此本文使用SMOTE算法过采样少数类样本以进行适量扩充。

SMOTE算法^[20]是一种广泛使用的过采样方法，该算法在少数类别中为样本找到k个最近邻，并在原始样本和所选近邻之间进行线性插值，得到M个原始数据集中不存在的新样本。该方法能够在不复制样本的情况下生成新的样本，合成数据的公式如式（9）所示：

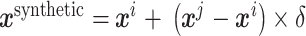9

式中，xⁱ代表所考虑的少数样本类；x^j是xⁱ的k近邻中随机插值的样本；δ取值区间为[0, 1]，用于控制合成样本与xⁱ间的距离；x^synthetic沿着xⁱ和x^j之间的直线以及向量xⁱ相交的直线的方向生成。

2.4. 焦点损失函数

样本数量较少的类别往往是分类问题中需要关注的重点。在模型训练过程中，不同类别之间的数据存在着较大的数量差距，模型所关注和学习的总是样本数量较多的类别，导致对少数类样本的拟合过差，进而无法得到正确的分类结果。Lin等^[19]提出focal loss，代替交叉熵损失函数（cross-entropy loss）来解决类别不平衡的问题，交叉熵与focal loss的定义如式（10）、式（11）所示：

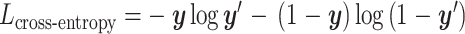10

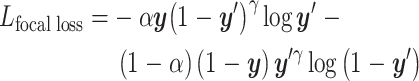11

式中，y为实际类别； 为类别预测值；参数α用于平衡正、负样本对损失值的影响；γ为一个正的可调参数，它能够自适应地调节样本被减权重的速率，使模型更多地关注不易区分的样本，减少容易区分的样本的影响。

focal loss能够自适应地改变难分类的样本和易分类样本在损失函数里的权重，可解决严重的样本不平衡问题，而且不需要计算复杂的权值映射，使模型能够更好地捕捉信号特征。

2.5. ECG信号分类算法流程

算法的实验流程如图5所示，整体实验可以分为以下三个步骤进行：

图 5.

Flowchart of ECG signal classification algorithm

ECG信号分类算法流程图

（1）数据预处理：首先对ECG信号进行小波阈值去噪，并采用Pan-Tompkins算法定位R波；根据R波位置划分心拍后，对所有数据进行归一化，使其落入[0, 1]区间，最后采用SMOTE算法进行数据增强；

（2）模型训练：将训练集的数据输入NLSTM模型进行训练，获取ECG数据的时序特征；

（3）分类结果输出：focal loss自适应改变难易样本的特征学习权重；残差注意力机制更改输出特征权重值，进而得到分类结果。

3. 实验结果与分析

3.1. 实验数据与模型参数

本文实验数据来源于MIT-BIH-AR数据库（网址为：https://www.physionet.org/content/mitdb/ 1.0.0/），经过权威专家的诊断和标注，是目前国际上进行相关研究通用的数据来源，被广泛使用于近年来心律失常研究中。MIT-BIH-AR数据库有48条记录，包含了十几种类型的心律失常数据，每条记录长达30 min，采样频率为 360 Hz。其中有4 条编号分别为102、104、107、217的记录包含起搏心跳，不具足够的实用性，并会对实验分析造成干扰，因此去除这四条记录；而后根据R波位置对余下的44条ECG记录进行切割。以数据集中最常见并且数量较多的四类心拍类型作为分类标签，除正常节律外，另三类属老年人发病率和致死率较高的心拍类型，分别为室性期前收缩、右束支传导阻滞和左束支传导阻滞。对其进行选择并随机划分获取96 738个心拍样本作为原始不平衡训练集，5 000个心拍样本作为原始不平衡测试集。心拍类型-单字符缩写对应关系如表1所示。

表 1. Heartbeat training set based on MIT-BIH arrhythmia database.

基于MIT-BIH-AR数据库的心拍训练集

心拍类型	标注符号	心拍数量/个	数据增强后 心拍数量/个
正常节律心拍	N	74 510	74 510
室性期前收缩	V	6 902	13 804
右束支传导阻滞	R	7 255	21 765
左束支传导阻滞	L	8 071	32 284

如表1所示，由于N类的样本数量足够，故仅对V、R、L三类过采样。SMOTE算法在随机过采样样本时存在一定的盲目性，若采样至与N类心拍数量相等，模型易出现过拟合问题，同时会破坏其他心拍数据的原始特征。根据二-三分类原则，将V、R、L三类按2、3、4倍进行扩充，扩充后见表1中“数据增强后心拍数量”，使得这三类样本数量的总和与N类大致相等，构成一个二元分类问题，二分类结束后再进行三分类，可在较大程度提高分类准确率。

模型共采用5层NLSTM，每一层由10个NLSTM单元构成。在模型训练阶段，设置学习率为0.01，并自适应跟随训练加深逐步降低，更好地拟合数据特征。经过实验验证，最终设置批次大小（batch_size）为1 024，训练轮次（epoch）为100。与此同时，为了避免训练、测试的心拍来自于同一条记录，将心拍随机打乱索引；对于实验数据，得益于神经网络中神经元的随机失活（dropout）思想^[27]，对数据进行离散随机训练，每个epoch只训练训练集中的一部分数据，可以有效地避免过拟合现象。

3.2. 实验环境

本文研究涉及的数据处理平台为：ECG数据预处理及心拍类型划分平台MATLAB（2016b，MathWorks，美国）；NLSTM网络模型框架、focal loss及残差注意力机制实现平台TensorFlow（1.4.0，Google，美国）；SMOTE及其他ECG信号分类模型实现平台Python（3.6.2，Google，美国）。

3.3. 评价指标

为准确评估算法在分类中的表现，选择总体准确率（accuracy，Acc）来评价分类性能，但由于心拍数量的不平衡，准确率可能会被主类别（N类）严重扭曲。因此，精准率（precision，Pre）、召回率（recall，Rec）和F1分数也一并作为衡量模型性能和有效性的指标，其计算公式如式（12）~式（15）所示：

12

13

14

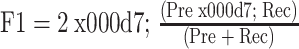15

式中，真阳性（true positive，TP）表示正类别中正确分类样本的数量；真阴性（true negative，TN）表示负类别中正确分类样本的数量；假阳性（false positive，FP）表示正类别中错误分类样本的数量；假阴性（false negative，FN）是负类别中错误分类样本的数量。

3.4. 平衡数据集下的NLSTM模型性能验证

为将实验全面化，首先利用平衡数据集对NLSTM模型性能进行验证，而后再针对不平衡数据进行更为全面的实验。从原始训练数据中两次随机选取N、V、R、L类各2 500个样本数据，前一次作为训练集，后一次作为测试集，对CNN、单向长短时记忆网络（unidirectional long short-term memory，ULSTM）、NLSTM三种模型的分类效果进行验证。三种模型的准确率如图6所示，对比可知，NLSTM的Acc相较于CNN与ULSTM分别提高了1.43%和1.94%，并从Pre和Rec的调和平均F1分数看出，NLSTM要优于CNN与ULSTM，NLSTM的记忆能力能够更好挖掘时序数据之间的潜在特征，提高模型的分类准确率。

图 6.

Acc comparison of each models

各模型Acc对比

经由NLSTM分类的四类心拍的详细参数如表2所示，NLSTM在Pre、Rec、F1分数这三种评价指标上的值均在95%以上，在 N、L两种类型的心拍检测上，Rec高达 99%。

表 2. Classification experiment results of each algorithm under the balanced training set.

平衡集下各算法分类实验结果

方法	心拍类型					Pre	Rec	F1	Acc
		N	V	R	L
NLSTM	N	2 493	23	0	5	98.89%	99.72%	99.30%	98.07%
	V	3	2 389	56	14	97.03%	95.56%	96.29%
	R	4	31	2 444	0	98.59%	97.76%	98.17%
	L	0	57	0	2 481	97.75%	99.24%	98.49%
CNN	N	2 490	23	1	7	98.77%	99.60%	99.18%	96.64%
	V	3	2 334	51	48	95.81%	93.36%	94.57%
	R	6	7	2 441	46	97.64%	97.64%	97.64%
	L	1	136	7	2 399	94.34%	95.96%	95.14%
ULSTM	N	2 489	28	2	3	98.69%	99.56%	99.12%	96.13%
	V	4	2 297	51	58	95.31%	91.88%	93.56%
	R	5	32	2 440	52	96.48%	97.60%	97.03%
	L	2	143	7	2 387	94.01%	95.48%	94.74%

3.5. 残差注意力-NLSTM模型

为提升NLSTM模型的分类能力，在NLSTM网络结构的末端加入残差注意力机制，将原模型的输出作为残差注意力机制层的输入，使注意力集中在对分类结果影响较大的全局特征上，模型的整体准确率在原始NLSTM模型的基础上增加了0.22%，四类心拍分类的详细参数如图7所示。V类的F1分数达到了96.86%，提高了0.57%，残差注意力-NLSTM模型在三种评价指标上的值均在95% 以上，因此分类的效果要优于单一的NLSTM。因为FP和FN的少量变化，部分类别的Pre和Rec存在一定波动，而两者调和平均数F1分数是稳定上升的，证明分类方法的有效性及准确性。

图 7.

Performance comparison of NLSTM before and after combining residual attention

NLSTM结合残差注意力前后性能对比

3.6. 残差注意力-NLSTM-focal loss 模型

本节及之后将采用原始不平衡数据集对模型进行验证。focal loss优越的权重分配原则会对网络超参数进行调整，令神经元同时学习小样本和大样本类别，并可能会分配更多权重于小样本以学习到更多全局特征。以交叉熵为基准，验证了focal loss对不平衡ECG数据进行分类的可行性。经过不断的实验对比，最终设置式（11）中参数为α = 0.75，γ = 2时，不平衡数据集分类效果达到最佳。相同环境及模型下，交叉熵与focal loss的分类评价指标如表3所示。

表 3. Cross-entropy and focal loss experimental results and comparison.

交叉熵与focal loss实验结果及对比

评价指标		Pre	Rec	F1	Acc
交叉熵	N	94.66%	98.97%	96.76%	92.47%
	V	72.69%	76.31%	74.46%
	R	92.97%	81.09%	86.62%
	L	87.40%	57.72%	69.52%
focal loss	N	98.31%	98.39%	98.35%	96.10%
	V	88.04%	77.12%	82.22%
	R	93.19%	94.40%	93.79%
	L	85.24%	92.54%	88.74%

实验结果表明，采用focal loss的网络模型性能更好，Acc达到96.10%，相比交叉熵提高3.63%；N类和V类的Pre分别提高了3.65%和15.35%；R类和L类的Rec分别提高了13.31%和34.82%。focal loss使得NLSTM网络更侧重于容易误分心拍的特征学习，提高心律失常分类的准确性。

3.7. SMOTE-残差注意力-NLSTM-focal loss模型

过量扩充样本数量将会导致特征冗余，故本文采用SMOTE算法仅对少样本类别进行处理，使三类心律失常类别数量总和与N类数量达到相对平衡状态，进而抑制样本不平衡对模型性能的消极影响，进一步提高focal loss下的模型性能，旨在达到平衡数据集的分类的精度。数据增强后的数据分布如表1所示。

在不平衡心律失常分类仿真实验中，对训练集采用SMOTE算法进行数据增强处理，测试集不做处理，以体现模型真实的泛化能力。数据增强后的混淆矩阵及评价指标如表4所示，实验结果表明，Acc从原来的96.10%提高到了98.34%，该分类方法对这四类心拍的识别有效，Pre达到了93%以上，模型性能甚至超越了平衡数据集的标准。

表 4. Experimental results of arrhythmia classification after SMOTE.

SMOTE后心律失常分类实验结果

心拍类型	心拍类型				Pre	Rec	F1	Acc
	N	V	R	L
N	3 812	19	8	12	99.22%	98.99%	99.10%	98.34%
V	18	340	0	8	93.15%	92.90%	93.02%
R	7	2	368	0	97.87%	97.61%	97.74%
L	5	4	0	397	95.20%	97.78%	96.48%

为进一步验证本文所提模型的有效性，选取近期其他算法进行对比；各文献的具体分类方法和分类准确率如表5所示，实验数据来源均基于MIT-BIH-AR数据库。其中，Acharya等^[28]采用CNN模型对处理后的不平衡数据集进行分类，Acc仅达94.23%；由此可见，本文提出的算法精度更高，具有更加明显的优势，同时本文实验验证时均使用完整心拍数据，更加贴近真实情况，由此得到的实验结果也更具说服力。

表 5. Classification effects comparison of methods from other literature.

其它文献方法分类效果比较

文献	特征提取	分类器	Acc
Li等[7]	小波熵+RR间期特征	随机森林	94.43%
Mondéjar-Guerra等[9]	小波变换 + 高阶统计量 + 一维二进制	多个支持向量机	94.62%
Li等[17]	小波包分解	概率神经网络 + 遗传算法	98.08%
刘光达等[15]	前向反馈神经网络 + CNN		92.6%
Acharya等[28]	CNN		94.23%
本文方法	残差注意力 + focal loss + NLSTM		98.34%

各模型在ECG信号分类上的Acc是值得关注的，但在实际应用中，各模型的算法能耗也是非常重要的指标；而耗时可以充分表征模型在实际运用中的算法能耗，故本文对各模型在单个心拍上的特征提取、训练及测试耗时进行统计分析，结果如表6所示。

表 6. Time consumption of each model.

各模型的时间损耗

文献	特征提取耗时/ ms	训练耗时/ ms	测试耗时/ ms	总耗时/ ms
Li等[7]	46.47	2.37	0.25	49.09
Mondéjar-Guerra等[9]	19.01	20.04	0.03	39.08
Li等[17]	135.24	26.91	1.28	163.43
刘光达等[15]	0	29.22	1.92	31.14
Acharya等[28]	0	21.13	2.45	23.58
本文方法	0	10.57	0.08	10.65

虽然单个心拍的检测耗时仅为毫秒级别，但在医学治疗或者便携穿戴式心电监测设备中，将会一次性采集大量的心拍作为参考，使得总耗时产生较大差异。就各模型在心拍分类的Acc及耗时而言，本文所提方法具有更快的运行速度及更高的分类准确率；文献[17]的准确率与本文相近，但其耗时最长，并不利于实际应用；而文献[15，28]虽同样省略特征提取步骤，但并未采取更具针对性的网络架构，准确率低且耗时略长。

基于以上分析，本文模型可以实现对ECG信号准确而快速的检测与分类，其时间损耗能够满足临床治疗分析的实时性需求，具有较好的普适性，可为便携穿戴式心电监测设备提供有效的分类依据。

3.8. 贡献度对比

根据各项指标前后变化，对各方法的贡献程度进行量化比较。依托于NLSTM网络，残差注意力机制辅助网络形成对心拍全局特征的长期记忆，贡献占比为23.11%；而focal loss使网络模型集中学习少数样本特征，较大程度提升算法在不平衡数据集下的分类能力，贡献占比为54.63%；SMOTE增强小样本占比，使特征突出，更易捕捉，贡献占比为22.26%。

4. 结论

针对ECG数据中类别失衡，以及现有模型在长时间序列训练中信息丢失的问题，本文提出一种基于残差注意力机制与focal loss的NLSTM心律失常分类模型，该模型能够集中提取ECG信号的全局特征并形成长期记忆，并增强对少数类样本特征的学习，进而有效解决数据不平衡问题；同时使用SMOTE算法少量增加小样本类别数目，能有效提升ECG数据的丰富程度，进一步提升模型对ECG信号分类的准确性与鲁棒性。本文模型相较于传统特征提取方法和其他深度学习模型效果更佳，Acc达到98.34%，F1分数高达99.10%。该方法将人工智能与ECG信号分类有效地结合，用作诊断心血管疾病的计算机辅助工具，推动了智慧医疗的进一步发展。

在未来的工作中，继续将网络轻量化，并将其训练后的完整模型进行迁移，应用于便携穿戴式心电监测设备中，实现实时监测预警的效果；并对更多不同类型的心律失常患者进行临床验证。此外，本文算法是一种通用算法，可推广至其他生理时间序列的不平衡数据集，譬如心音信号、脉搏信号等。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：许诗雨是本研究的实验设计者与执行人，完成数据分析，论文初稿撰写；莫思特参与论文框架设计、对论文修改提出建设性意见，并审核同意发表；闫惠君、黄华参与实验设计和实验结果分析；吴锦晖、张绍敏指导实验设计与实际运用；杨林参与论文想法的讨论和修改论文。全体作者阅读并同意最终的作者排序与论文内容。

Funding Statement

国家高技术研究发展计划（2018YFC2002100）

National High-tech R&D Program