Abstract
图像配准在肝脏疾病的计算机辅助诊断和手术规划方面具有重要的临床意义。基于深度学习的配准方法使得肝脏电子计算机断层扫描(CT)图像配准具有较高的实时性和准确度。然而,现有方法在配准具有大位移和大形变的图像时,存在配准后图像的纹理信息发生改变的问题,因而难以将其应用在后续的图像处理与临床诊断中。基于此,本文提出一种新颖的基于纹理滤波的无监督配准方法,实现了肝脏 CT 图像的配准。该方法首先基于 L0 梯度最小化的纹理滤波算法消除 CT 图像中肝脏表面的纹理信息,使得配准过程仅参考两幅图像的空间结构信息进行配准,从而解决纹理改变的问题。然后,基于级联网络配准具有大位移和大形变的图像,循序渐进地将待配准图像与参考图像在空间结构上对齐。此外本文还提出一种新的衡量指标——直方图相关系数,以衡量配准后纹理改变的程度。实验结果表明,本文所提出的方法具有较高的配准精度,有效地改善了级联网络中存在纹理改变的问题,并且提升了在空间结构对应和抗折叠性能两方面的配准效果。因此,本文所提方法或有助于提升医学图像配准的科学性,促进医学图像配准安全可靠地应用在肝脏疾病的计算机辅助诊断和手术规划方面。
Keywords: 肝脏电子计算机断层扫描影像, 无监督配准, 纹理滤波, 级联网络, 衡量指标
Abstract
Image registration is of great clinical importance in computer aided diagnosis and surgical planning of liver diseases. Deep learning-based registration methods endow liver computed tomography (CT) image registration with characteristics of real-time and high accuracy. However, existing methods in registering images with large displacement and deformation are faced with the challenge of the texture information variation of the registered image, resulting in subsequent erroneous image processing and clinical diagnosis. To this end, a novel unsupervised registration method based on the texture filtering is proposed in this paper to realize liver CT image registration. Firstly, the texture filtering algorithm based on L0 gradient minimization eliminates the texture information of liver surface in CT images, so that the registration process can only refer to the spatial structure information of two images for registration, thus solving the problem of texture variation. Then, we adopt the cascaded network to register images with large displacement and large deformation, and progressively align the fixed image with the moving one in the spatial structure. In addition, a new registration metric, the histogram correlation coefficient, is proposed to measure the degree of texture variation after registration. Experimental results show that our proposed method achieves high registration accuracy, effectively solves the problem of texture variation in the cascaded network, and improves the registration performance in terms of spatial structure correspondence and anti-folding capability. Therefore, our method helps to improve the performance of medical image registration, and make the registration safely and reliably applied in the computer-aided diagnosis and surgical planning of liver diseases.
Keywords: liver computed tomography images, unsupervised registration, texture filtering, cascaded network, texture similarity
引言
医学图像配准,指在任意两幅医学图像之间建立一种空间对应关系,通过这种对应关系可以使一幅图像变换到另一幅图像所在的空间结构中。临床诊断中,图像配准可以帮助医生从不同成像设备获取的医学图像或者不同时间获取的来自相同成像设备的医学图像获取信息并进行融合互补,提高疾病诊断精度[1-3]。对于计算机辅助诊断而言,医学图像配准可以辅助器官和肿瘤分割、多模态图像融合以及疾病分类等研究[4-6]。
近年来,传统配准方法例如弹性体(Elastix)、阿恩特(Ant)已经在各种任务上实现了较好的配准效果[7-8],但是这些方法所需的配准时间较长,不适用于实时的临床应用。最近,基于深度学习的医学图像配准方法呈现出巨大的优势,不仅在配准效果上可与众多传统方法媲美,而且消耗的时间远远小于传统配准方法。然而,基于深度学习的配准方法大多集中于脑部图像配准[9-11]。由于脑部图像产生的位移较小,因此这些方法迁移到位移和形变均较大的肝脏图像中并不能取得较好的效果。一些论文提出了通过多级级联网络配准具有大位移和大形变医学图像的方法[12-14],在肝脏电子计算机断层扫描(computed tomography,CT)图像中应用取得了良好的配准效果。但是通过多级级联网络产生的空间变换可能使得配准后的图像与参考图像极为相似,不仅空间结构一致,纹理方面也趋于相同。而在肝脏 CT 图像中,纹理特点直接反映了肿瘤或病变组织的类型,如图 1 所示,绿色箭头标注了肝脏病灶的位置,血管瘤和肝癌的病灶具有不同的纹理信息,这些纹理信息是临床诊断和计算机辅助诊断过程中的重要依据,因此纹理信息的改变将会严重影响疾病诊断的精确度。由此可见,迫切需要一种不改变纹理信息的肝脏 CT 图像配准方法。此外,现有的配准衡量指标一般采用戴斯(Dice)系数和特征点距离等,这些指标均针对于配准后解剖结构的对应程度而提出,未有衡量配准图像与原图像在纹理信息上的对应程度的指标。
图 1.
Texture features in liver CT images
肝脏 CT 图像中的纹理特征
针对上述问题,本文提出了一种新型的三维无监督深度学习配准框架用于肝脏 CT 图像中。首先对肝脏 CT 图像进行基于 L0 梯度最小化的纹理滤波处理,该方法可以消除三维医学图像中的大部分复杂的纹理信息和图像噪声,保留显著的空间结构信息;然后采用级联网络对输入图像进行循序渐进的配准,以解决大位移和大形变问题;最后提出一种直方图相关系数衡量配准后图像的纹理信息与原图像的对应程度,以关注配准前后肝脏 CT 图像纹理信息变化。实验证明,本文所提出的方法不仅可以实现高精度配准,而且有效地保留了肝脏影像中的纹理信息。因此,本文的方法对于提升医学图像配准的科学性,使得医学图像配准安全可靠地应用在肝脏疾病的计算机辅助诊断和手术规划方面具有重要意义。
1. 方法
本文提出的配准框架如图 2 所示。假设 If 为配准过程中的参考图像,Im 为待配准图像,配准后图像为 Ir。配准的过程即将待配准图像 Im 配准到参考图像 If 所在的空间结构之中,从而得到配准图像 Ir。参考图像 If 和待配准图像 Im 均为三维 CT 图像。首先,Im 与 If 经过纹理滤波后分别得到 Sm 与 Sf,然后将 Sm 与 Sf 输入至级联网络进行配准。由于滤波后的两幅图像 Sm 与 Sf 不包含纹理信息,因此级联网络仅按照两幅图像的空间结构对应进行配准,并预测出用于指导配准的变形场  。最后利用
。最后利用  对 Im 进行插值变换得到最终的配准图像 Ir,该过程可被记为 Ir = Im
对 Im 进行插值变换得到最终的配准图像 Ir,该过程可被记为 Ir = Im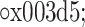 。
。
图 2.
Unsupervised cascaded network registration model based on texture filtering
基于纹理滤波的无监督级联式配准模型
1.1. 基于 L0 梯度最小化的纹理滤波
L0 梯度最小化算法最早由 Xu 等[15]提出,主要用于解决二维自然图像的平滑问题。本文将其应用在医学图像中,并且在此基础上实现了针对三维医学图像的纹理滤波。基于 L0 梯度最小化的纹理滤波以 L0 梯度数量为正则项,通过限制非零梯度的数量完成纹理滤波。
假设 I 和 S 分别表示输入图像和纹理滤波后的图像。纹理滤波的目标函数如式(1)所示:
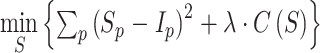 |
1 |
其中,∑p(Sp − Ip)2保证了图像 I 和 S 在每个像素点 p 的相似度,λ 为非负参数,作用是控制纹理滤波的程度,λ 越大,纹理滤波程度越高。C(S)代表图像 S 的 L0 梯度的统计,其定义如式(2)所示:
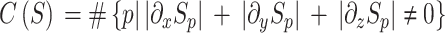 |
2 |
其中,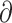 xSp、
xSp、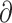 ySp 和
ySp 和  zSp 分别表示图像 S 的任意像素点 p 沿着 x、y 和 z 方向的偏导数。#{}的功能是计算|
zSp 分别表示图像 S 的任意像素点 p 沿着 x、y 和 z 方向的偏导数。#{}的功能是计算| xSp| + |
xSp| + |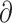 ySp| + |
ySp| + | zSp|的值不为 0 的像素点数量之和,|
zSp|的值不为 0 的像素点数量之和,| xSp| + |
xSp| + |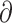 ySp| + |
ySp| + | zSp|代表了图像 S 在像素点 p 的梯度能量。由于 C(S)对全局不连续性进行了统计建模,故无法通过传统的梯度下降法或其他离散优化方法优化目标函数,因此,本文采用交替最小化算法优化上述目标函数。
zSp|代表了图像 S 在像素点 p 的梯度能量。由于 C(S)对全局不连续性进行了统计建模,故无法通过传统的梯度下降法或其他离散优化方法优化目标函数,因此,本文采用交替最小化算法优化上述目标函数。
为了使用交替最小化算法,式(2)改写为如式(3)所示:
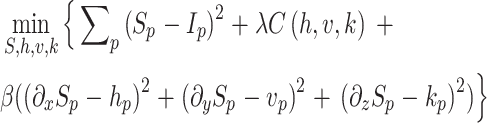 |
3 |
其中,h、v、k 为引入的辅助变量,hp、vp、kp 分别表示 h、v、k 在像素点 p 的元素,C(h,v,k)= #{p||hp| + |vp| + |kp| ≠ 0},β 是通过迭代方式更新的参数,用于控制变量(hp,vp,kp)及其对应的梯度( xSp,
xSp,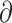 ySp,
ySp,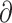 zSp)之间的相似度。当 β 足够大时,式(1)与式(3)接近。
zSp)之间的相似度。当 β 足够大时,式(1)与式(3)接近。
交替最小化算法将式(3)分解为两个子问题加以解决,分别为:
(1)已知 hp、vp 和 kp,计算 S 以最小化式(3)。式(3)可以另被写为如式(4)所示:
 |
4 |
为了采用快速傅里叶变换估计式(4)中的 S,式(4)改写为如式(5)所示:
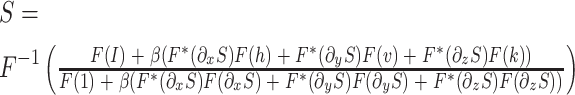 |
5 |
其中,F(·)代表快速傅里叶变换,F−1(·)代表快速傅里叶的反变换,F*(·)表示在快速傅里叶变换基础上取其共轭复数形式,F(1)表示阶跃函数 δ(1)的傅里叶变换。
(2)已知 S,计算 hp、vp 和 kp 以最小化式(3)。式(3)可以另被写为如式(6)所示:
 |
6 |
式(6)可以在空间上分解,分别对每个 hp、vp 和 kp 进行估算。分解后的式(6)如式(7)所示:
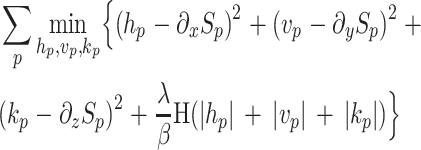 |
7 |
其中,关于 H(|hp| + |vp| + |kp|)的计算如式(8)所示:
 |
8 |
对于每一个像素点 p,式(7)可以被写为如式(9)所示:
 |
9 |
其中,Ep 代表像素点 p 的目标函数值,为了使 Ep 达到最小值,需要满足如式(10)所示的条件:
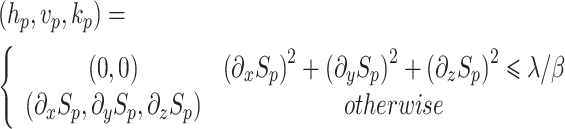 |
10 |
因此,结合式(8)和(9),可以求解出使 Ep 达到最小值的(hp,vp,kp)。
利用两个子问题进行交替最小化的算法框图参见算法 1——L0 梯度最小化算法。参数 β 从最小值 β0 开始自动进行迭代,每次都乘以速率 κ,直到 β ≥ βmax。
算法 1:
STN1:输入,图像 I,纹理滤波权重 λ,参数 β0,βmax,κ;
步骤 2:初始化,S←I,β←β0;
步骤 3:已知 S,根据式(10)求解 hp、vp 和 kp;
步骤 4:已知 hp、vp 和 kp,根据式(5)更新 S;
步骤 5:β←κβ;
步骤 6:重复步骤 3、4、5,直至 β ≥ βmax;
步骤 7:输出,处理后的图像 S。
1.2. 基于级联网络的无监督配准模型
参考图像和待配准图像经过纹理滤波后,输入到基于级联网络的无监督配准模型中进行配准。如图 3 所示,级联网络的基本框架由多个子网络构成,通过多个子网络,可以循序渐进地将待配准图像配准到参考图像所在的空间结构中。
图 3.

The framework of cascaded network
级联网络框架
1.2.1. 级联网络
由于肝脏 CT 图像的配准任务具有大位移和大形变的特点,这里采用级联网络进行配准。级联网络由多个子网络组成,如图 3 所示。不失一般性,第 k 个子网络以参考图像 Sf 和待配准图像  (k = 1,2,
(k = 1,2, )为输入,预测一个变形场
)为输入,预测一个变形场 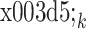 。对于第一个子网络,
。对于第一个子网络,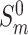 = Sm。然后,每个子网络预测的变形场
= Sm。然后,每个子网络预测的变形场 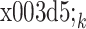 需要和前级子网络预测的变形场
需要和前级子网络预测的变形场  进行合成,形成在本级最终起作用的变形场
进行合成,形成在本级最终起作用的变形场 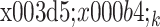 ,变形场合成的迭代操作记为
,变形场合成的迭代操作记为 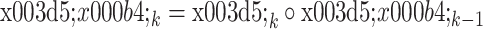 ,其中“
,其中“ ”表示由 Jaderberg 等[16]提出的空间变换器网络(spatial transformer network,STN)。最后,在每级子网络后,待配准图像
”表示由 Jaderberg 等[16]提出的空间变换器网络(spatial transformer network,STN)。最后,在每级子网络后,待配准图像 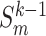 利用本级起作用的变形场
利用本级起作用的变形场  完成一次配准,得到下一级的待配准图像
完成一次配准,得到下一级的待配准图像 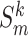 ,该操作记为
,该操作记为 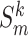 =
= 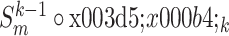 。
。 和 Sf 将输入至下一个级联的子网络中继续配准。通过多次配准使得 Sf 和
和 Sf 将输入至下一个级联的子网络中继续配准。通过多次配准使得 Sf 和 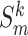 之间的相似度不断增大,从而循序渐进地将 Sm 配准到 Sf 所在的空间结构中。由于 STN 是一个可微分的模块,满足神经网络反向传播梯度的需要,因此可以实现对级联网络的端到端训练。
之间的相似度不断增大,从而循序渐进地将 Sm 配准到 Sf 所在的空间结构中。由于 STN 是一个可微分的模块,满足神经网络反向传播梯度的需要,因此可以实现对级联网络的端到端训练。
1.2.2. 子网络
级联网络中的子网络采用的是卷间网络(volume tween network,VTN)[12],如图 4 所示,VTN 网络遵循编码器—解码器的结构,以参考图像和待配准图像沿着通道所在维度拼接而成的多维向量作为输入,为了表示方便,四维的特征层在图 4 中以二维表示,面积较小的特征层意味着更低的空间分辨率,通道数量标注在每一层的上方,弯曲的箭头代表箭头始端的特征层与箭头末端的特征层沿着通道所在维度进行叠加。在编码器部分,VTN 网络采用带步长的三维卷积层将每层的空间分辨率减少一半以及将每层的通道数量增加一倍,但是从第四个卷积层开始,每降低一次分辨率都将在该三维卷积层后增加一个不改变空间分辨率和通道数量的三维卷积层;在解码器部分,VTN 网络使用三维反卷积层(或称为转置卷积层)逐步恢复至原来空间分辨率和通道数量。类似于 U-net 网络[17],在三维卷积层和三维反卷积层之间加入了跳跃连接,可以将在编码器学习到的特征直接传播到解码器的反卷积特征层,以帮助对变形场  的预测。
的预测。
图 4.

Structure of VTN
VTN 网络结构
1.2.3. 损失函数
无监督配准模型不需要任何数据标签,直接以参考图像与配准后的图像的差异指导模型的训练,为了以无监督的方式训练配准模型,本文对每级子网络产生的变形场 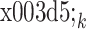 计算总变差损失值 LTV 以保证产生的变形场具有平滑性,以互相关损失函数计算参考图像和待配准图像之间的相似度损失值 Lsim。在训练过程中,直到所有损失值计算完成后,再将所有损失值相加进行梯度反向传播以更新网络的参数,从而实现对所有子网络的端到端训练。两个损失函数的详细定义如下所示:
计算总变差损失值 LTV 以保证产生的变形场具有平滑性,以互相关损失函数计算参考图像和待配准图像之间的相似度损失值 Lsim。在训练过程中,直到所有损失值计算完成后,再将所有损失值相加进行梯度反向传播以更新网络的参数,从而实现对所有子网络的端到端训练。两个损失函数的详细定义如下所示:
(1)互相关系数损失函数:
互相关系数损失函数 Lsim 的作用是衡量两幅图像之间线性相关的程度,其定义如式(11)和式(12)所示:
 |
11 |
 |
12 |
其中,CorrCoef(·)的作用是计算两幅图像之间的相关系数,Cov 表示两幅图像之间的方差,例如,Cov[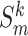 ,Sf]的定义如式(13)所示:
,Sf]的定义如式(13)所示:
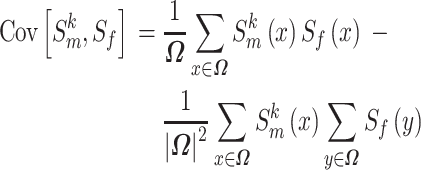 |
13 |
其中,Ω 表示图像所定义的空间。互相关系数损失函数值 Lsim 越小,表示两幅图像之间的线性相关程度越高,配准效果越好。
(2)总变差损失函数:
总变差损失函数的作用是使得产生的变形场  具有平滑特性,其定义如式 (14) 所示:
具有平滑特性,其定义如式 (14) 所示:
 |
14 |
综上所述,总的损失函数如式(15)所示:
 |
15 |
其中,k 代表级联的子网络个数,μ 代表总变差损失函数的权重。
2. 实验与结果
2.1. 实验数据
本文实验采用的数据集包括医学十项全能分割比赛的数据集(Medical Segmentation Decathlon,MSD)(网址为:https://decathlon-10.grand-challenge.org/)、北京友谊医院提供的公开数据集(public datasets provided by Beijing Friend Hospital,BFD)(网址为:https://drive.google.com/open?id=17IiuM74HPj1fsWwkAfq-5Rc6r5vpxUJF)以及肝脏分割挑战赛的公开数据集(Segmentation of Liver,Sliver)(网址为:http://www.sliver07.org/index.php),其中,MSD 包含 1 064 例 CT 图像,BFD 包含 92 例 CT 图像,Sliver 包含 22 例 CT 图像,MSD 和 BFD 数据集在实验中作为训练集,Sliver 数据集在实验中作为测试集。
2.2. 实验设计
原始三维肝脏 CT 图像首先经过裁剪和去除不相关的区域后,重采样为 128 × 128 × 128 的尺寸。纹理滤波算法中的 λ 设置为 0.08,κ 设置为 2,β0 和 βmax 分别设置为 2λ 和 105。式(15)中的 μ 取值为 1.0,级联网络采用亚当(Adam)优化器共训练 105 次[18],初始学习率为 10−4,每运行 6 × 104 次学习率减半,每运行 8 × 104 次学习率再次减半。本文共训练了三个模型,分别为 S_VTN_2、S_VTN_4、S_VTN_6,模型名字后面的数字代表级联的子网络的个数。
本文所需的实验配置如下:处理器(IntelCore i7-3770 CPU@4GHz,Intel,美国)、深度学习框架(TensorFlow, Google,美国)、独立显卡(Tesla v100,Nvidia,美国)。
2.2.1. 比较方法
(1)传统方法:Elastix 在传统方法中对肝脏的配准表现最好,因此本文与其进行了比较。
(2)基于单级网络的配准模型:Balakrishnan 等[11]提出的体素变形网络(VoxelMorph)是基于深度学习的配准方法中的基线方法,具有较强的比较意义。
(3)基于多级级联网络的配准模型:为了衡量本文提出的纹理滤波算法对多级级联网络带来的性能提升,本文与级联数量分别为 2、4、6 的多级级联网络配准模型进行比较,这些模型的名字分别记为 VTN_2、VTN_4、VTN_6。
2.2.2. 衡量指标
(1)直方图相关系数
肝脏 CT 图像的纹理信息主要由血管和肿瘤组织的亮度变化决定,发生较大位移或者较大形变的肝脏 CT 图像在配准前后的灰度值分布应该成线性相关,否则,即表示配准之后肝脏的纹理信息发生了变化。基于此,本文提出直方图相关系数以衡量在纹理信息对应上的配准效果。直方图相关系数表示为 HistCoeff,其定义如式(16)所示:
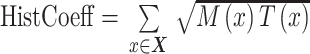 |
16 |
其中,X 代表肝脏区域所在空间,M(·)和 T(·)分别代表两幅图像在肝脏区域内的灰度值的直方图统计。直方图相关系数越高,代表纹理保持特性越好。
(2)Dice 系数
Dice 系数可以衡量两个区域之间的相似性,从而反映了在空间结构对应上的配准质量。Dice 系数定义如式(17)所示:
 |
17 |
其中,A 和 B 分别代表配准图像和参考图像的肝脏分割掩模。
(3)特征点距离
特征点距离可以衡量空间结构对应方面的配准质量,其定义是配准图像的解剖学特征点坐标与真实解剖学特征点坐标之间的平均欧式距离。Sliver 数据集包含由三位专家标注的解剖学特征点,可以据此计算各个特征点之间的平均距离。特征点距离越小,配准后的空间对应特性越好。
(4)折叠比例
图像折叠使得产生的变形场不可逆,违反了解剖学意义上的对应。de Vos 等[14]提出了一种可以衡量变形场引起图像折叠程度的方法,该方法确定了变形场中每个点 p(i,j,k)的雅可比行列式,如式(18)所示:
 |
18 |
如果式(18)的值为 1 则表示在 p 点没有发生体积变化,大于 1 则表示膨胀,在 0~1 之间则表示收缩,小于等于 0 则表示该点为奇点,奇点会引起图像折叠。通过计算引起图像折叠的点在整个变形场中所占的比例,就可以计算出图像折叠的比例,以此衡量变形场的拓扑保留特性。
2.3. 结果分析与讨论
2.3.1. 可视化分析
基于 L0 梯度最小化的纹理滤波方法对图像进行滤波后的效果如图 5 所示,肝脏表面具有一块非常明显的病变区域,当纹理滤波权重 λ 由 0.02 增大至 0.08 时,纹理滤除程度逐渐增高,当纹理滤波权重 λ 为 0.08 时,纹理滤波后的肝脏表面已经几乎没有任何病变区域的纹理特征,并且较好地保留了原图的空间结构,因此本文在后续实验中固定参数 λ = 0.08。该结果证明本文提出的纹理滤波方法可以有效实现对三维医学图像的纹理滤波,满足后续采用无监督方法进行配准的要求。
图 5.
The results of texture filtering algorithm
纹理滤波算法效果展示
不同方法的配准效果如图 6 所示,为了方便观察肝脏中的肿瘤,本文选取了三维 CT 图像中最具代表性的切片并以彩色形式展示,图中红色圈标注了具有肿瘤的肝脏表面,待配准图像的肝脏表面存在一个非常明显的肿瘤边缘。经过配准后,VoxelMorph、VTN_4 和 VTN_6 配准后的图像可以较好地对齐到参考图像,但是其肿瘤的边缘经过配准后变得模糊,而通过本文方法(S_VTN_4、S_VTN_6)配准后的图像的肿瘤边缘维持了待配准图像中肿瘤边缘的特点。
图 6.
Comparison of registration performance of different methods
不同方法的配准结果比较
2.3.2. 量化分析
本文在 Sliver 数据集上量化了基于纹理滤波的级联网络对配准性能产生的影响,并与传统方法 Elastix、单级网络 VoxelMorph 以及无纹理滤波的级联网络进行了对比,结果如表 1 所示。根据表 1 中的结果,传统方法 Elastix 的配准结果在 Dice 系数上仅能达到 0.83,在特征点距离上高达 16.81,VoxelMorph 的配准结果在 Dice 系数上可以达到 0.918,在特征点距离上达到 14.19,而级联网络(VTN_2、VTN_4、VTN_6、S_VTN_2、S_VTN_4、S_VTN_6)在 Dice 系数上均可以达到 0.92 以上,在特征点距离上小于 13.75。因此,从配准精度上看,级联网络 > VoxelMorph > Elastix。随着级联网络级数的增加,无纹理滤波的级联网络(VTN_2、VTN_4、VTN_6)的 Dice 系数虽然逐渐提升到 0.954,但是其直方图相关系数下降至 0.959,而本文提出的基于纹理滤波的级联网络(S_VTN_2、S_VTN_4、S_VTN_6)在 Dice 系数上和普通的级联网络表现相当,并且在直方图相关系数上其结果一直维持在 0.962 以上。值得注意的是,本文提出的基于纹理滤波的级联网络在反映空间对应程度的特征点距离指标上也优于无纹理滤波的级联网络,例如,VTN_6 的特征点距离为 11.52,而 S_VTN_6 的特征点距离为 11.47;并且本文方法也减少了配准过程中发生的折叠现象,例如,VTN_4 中的折叠比例为 7.96 × 10−3,而 S_VTN_4 中的折叠比例为 7.92 × 10−3。基于无监督学习的配准方法是直接比较参考图像和待配准图像之间的相似度训练神经网络,而神经网络强大的拟合能力容易使得配准过度的现象发生,而且参考图像和待配准图像中的噪声也会影响神经网络预测的变形场,由于配准是一个无金标准的任务,因此基于深度学习的配准方法难以消除这些噪声带来的影响;本文方法通过纹理滤波使得级联网络仅仅关注两幅图像之间的空间信息,使得级联网络在配准精度和配准科学性上均取得优异的效果。
表 1. Comparison of registration performance of different methods (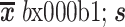 ).
).
不同方法的性能比较(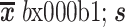 )
)
| 方法 | Dice 系数 | 特征点距离 | 直方图相关系数 | 折叠比例 |
| Elastix | 0.830 ± 0.026 | 16.81 ± 3.58 | 0.963 ± 1.50 × 10−3 | 0 |
| VoxelMorph | 0.918 ± 0.023 | 14.19 ± 2.81 | 0.961 ± 2.30 × 10−3 | 8.24 × 10−2 ± 8.63 × 10−3 |
| VTN_2 | 0.920 ± 0.022 | 13.75 ± 2.20 | 0.964 ± 4.20 × 10−3 | 2.93 × 10−2 ± 1.50 × 10−2 |
| VTN_4 | 0.948 ± 0.017 | 11.75 ± 2.18 | 0.961 ± 5.20 × 10−3 | 7.96 × 10−3 ± 5.00 × 10−3 |
| VTN_6 | 0.954 ± 0.015 | 11.52 ± 1.94 | 0.959 ± 4.10 × 10−3 | 2.51 × 10−3 ± 1.30 × 10−3 |
| S_VTN_2 | 0.920 ± 0.022 | 13.50 ± 1.70 | 0.966+2.80 × 10−3 | 2.65 × 10−2 ± 1.30 × 10−2 |
| S_VTN_4 | 0.948 ± 0.017 | 11.68 ± 2.14 | 0.963 ± 2.00 × 10−3 | 7.92 × 10−3 ± 5.40 × 10−3 |
| S_VTN_6 | 0.954 ± 0.014 | 11.47 ± 1.79 | 0.962 ± 2.10 × 10−3 | 2.50 × 10−3 ± 1.40 × 10−3 |
综上所述,实验结果证明了本文提出的基于纹理滤波的级联网络不仅解决了配准肝脏 CT 图像中存在的大位移、大形变的问题,同时也解决了纹理改变的问题,并在一定程度上增加了空间对应程度,减少了折叠现象的发生。
虽然上述实验结果可以证明本文所提出的方法在配准精度和配准科学性上均具有优势,但是本文也存在着两方面不足,需要在日后的研究中进一步完善。首先,本文在实验中固定了基于 L0 梯度最小化的纹理滤波算法的参数,在实际使用过程中,由于肝脏病变区域的纹理复杂多变,仍需要根据纹理滤波的效果适当调整参数,以获得更为可靠的结果。除此之外,本文方法的时间消耗在 8~12 s,相比于其他基于深度学习的配准算法,增加了一定的时间消耗,但是由于依然优于传统配准算法,因此该方法适用于肝脏疾病诊断及手术规划等实际临床应用。
3. 结论
本文提出了一种针对于肝脏 CT 图像的基于纹理滤波的无监督配准方法。该方法首先基于 L0 梯度最小化原理实现了一种针对于三维医学图像的纹理滤波方法,可以有效地滤除参考图像和待配准图像的纹理细节,避免后续的配准过程被纹理信息所影响。然后采用级联网络对纹理滤波后的参考图像和待配准图像进行循序渐进的配准,以解决大位移和大形变问题。实验结果表明,本文所提出的方法具有较高的配准精度,可以有效改善配准过程中发生的纹理改变的情况,并且提升了在空间结构上的对应程度以及抗图像折叠的配准性能,对医学配准应用在临床和计算机辅助诊断上具有较强的指导意义。
利益冲突声明:本文全体作者均声明不存在利益冲突。
Funding Statement
国家自然科学基金(61871135,81830058);上海市科委“科技创新行动计划”(20DZ1100104)
National Natural Science Foundation of China; Science and Technology Commission of Shanghai Municipality
Contributor Information
翌 郭 (Yi GUO), Email: guoyi@fudan.edu.cn.
源源 汪 (Yuanyuan WANG), Email: yywang@fudan.edu.cn.
References
- 1.Schregel K, Tsogkas I, Peter C, et al. Outcome prediction using perfusion parameters and collateral scores of multi-phase and single-phase CT angiography in acute stroke: need for one, two, three, or thirty scans?. J Stroke, 2018, 20(3): 362-372.
- 2.Grabherr S, Doenz F, Steger B, et al Multi-phase post-mortem CT angiography: development of a standardized protocol. Int J Legal Med. 2011;125(6):791–802. doi: 10.1007/s00414-010-0526-5. [DOI] [PubMed] [Google Scholar]
- 3.Brenner R, Metens T, Bali M, et al Pancreatic neuroendocrine tumor: added value of fusion of T2-weighted imaging and high b-value diffusion-weighted imaging for tumor detection. European Journal of Radiology. 2012;81(5):e746–e749. doi: 10.1016/j.ejrad.2012.01.032. [DOI] [PubMed] [Google Scholar]
- 4.Fu Y, Liu S, Li H, et al Automatic and hierarchical segmentation of the human skeleton in CT images. Phys Med Biol. 2017;62(7):2812–2833. doi: 10.1088/1361-6560/aa6055. [DOI] [PubMed] [Google Scholar]
- 5.El-Gamal F A Elmogy M, Atwan A. Current trends in medical image registration and fusion. Egyptian Informatics Journal. 2016;17(1):99–124. [Google Scholar]
- 6.Aljabar P, Wolz R, Rueckert D. Manifold learning for medical image registration, segmentation, and classification. Machine Learning in Computer-Aided Diagnosis: Medical Imaging Intelligence and Analysis, 2012: 351-372.
- 7.Klein S, Staring M, Murphy K, et al Elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging. 2010;29(1):196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
- 8.Avants B, Tustison N, Song G Advanced normalization tools(ANTS) Insight Journal. 2009;2(365):1–35. [Google Scholar]
- 9.Balakrishnan G, Zhao A, Sabuncu M R, et al. An unsupervised learning model for deformable medical image registration//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City: IEEE, 2018: 9252-9260.
- 10.Zhang J. Inverse-consistent deep networks for unsupervised deformable image registration. arXiv preprint, 2018, arXiv: 1809.03443.
- 11.Balakrishnan G, Zhao A, Sabuncu M R, et al VoxelMorph: a learning framework for deformable medical image registration. IEEE Trans Med Imaging. 2019;38(8):1788–1800. doi: 10.1109/TMI.2019.2897538. [DOI] [PubMed] [Google Scholar]
- 12.Lau T, Luo J, Zhao S, et al. Unsupervised 3D end-to-end medical image registration with volume tweening network. arXiv preprint, 2019, arXiv: 1902.05020.
- 13.Zhao Shengyu, Dong Yue, Chang E, et al. Recursive cascaded networks for unsupervised medical image registration//2019 IEEE/CVF International Conference on Computer Vision (ICCV), 2019: 10599-10609.
- 14.de Vos B D, Berendsen F F, Viergever M A, et al A deep learning framework for unsupervised affine and deformable image registration. Med Image Anal. 2019;52:128–143. doi: 10.1016/j.media.2018.11.010. [DOI] [PubMed] [Google Scholar]
- 15.Xu L, Lu C, Xu Y, et al Image smoothing via L0 gradient minimization. Association for Computing Machinery Transactions on Graphics. 2011;30(6):174–186. [Google Scholar]
- 16.Jaderberg M, Simonyan K, Zisserman A. Spatial transformer networks. Advances in Neural Information Processing Systems. 2015: 2017-2025.
- 17.Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation// International Conference on Medical Image Computing and Computer-assisted Intervention. Springer Cham, 2015: 234-241.
- 18.Kingma D P, Ba J. Adam: a method for stochastic optimization. arXiv preprint, 2017, arXiv: 1412.6980.






