运动想象脑电信号分类算法的研究进展

Abstract

运动想象指想象特定动作但实际上并不执行该动作的行为，已经在神经科学等领域得到广泛关注。运动想象脑电信号分类算法主要根据脑电信号所包含的生理信息，尤其是从生理信息中提取出的特征，对各类运动想象任务进行区分。近年来，运动想象脑电信号分类算法在分类器与机器学习策略两方面出现了一些新的研究进展。分类器方面，一些研究对传统机器学习分类器进行了改进，深度学习与黎曼几何分类器也已在该领域得到广泛应用。机器学习策略方面，出于提高分类准确率等目的，集成学习、自适应学习与迁移学习等机器学习策略被引入到运动想象脑电信号的分类中。本文综述讨论了运动想象脑电信号分类算法的研究进展，希望能够对各分类器与机器学习策略进行总结评价，为开发更高性能的分类算法提供思路。

引言

运动想象（motor imagery，MI）指想象特定动作但实际上并不执行该动作的行为，在神经科学等领域得到广泛关注^[1]。大脑进行 MI 活动时会产生各种形式的信号，可通过不同手段测量。其中，脑电（electroencephalogram，EEG）测量的是大脑产生的头皮电活动，具有无创、高时间分辨率、低成本等特点^[2]。而基于运动想象脑电（motor imagery EEG，MI-EEG）信号的脑-机接口（brain-computer interface，BCI）可以帮助用户在大脑与外部设备间建立直接通道，完成操纵双臂机器人、控制无人机、驾驶虚拟汽车等任务^[3-5]。

不同 MI 任务的 EEG 信号通常伴随着不同的感觉运动节律（sensory motor rhythm，SMR），即各脑区特定频段功率的升高或降低^[6-7]。可以通过共空间模式（common spatial pattern，CSP）等算法从 SMR 中提取特征向量，并送入线性判别分析（linear discriminant analysis，LDA）、支持向量机（support vector machines，SVM）、K 值最近邻（k-nearest neighbor，KNN）、朴素贝叶斯分类器（naive Bayesian classifier，NBC）等传统机器学习分类器，完成训练与预测过程^[8]。分类算法是区分不同肢体 MI 的关键，直接关系着分类结果准确与否，在 MI 的各类应用中有极为重要的意义。然而，MI-EEG 信号存在着一些不利于分类的固有特性（如非平稳性），为其分类算法带来一定的挑战^[9]。

近年来，机器学习领域不断发展，MI-EEG 信号的分类算法也出现了一些新的进展。一方面，在分类器上，部分研究对传统机器学习分类器进行了一定改进，而一些新型分类器也展现出巨大的潜力。另一方面，在机器学习策略上，一些通用的机器学习策略与各种分类器紧密结合，尝试从不同角度提升分类器的性能。

基于此，本文的后续部分将依次从分类器与机器学习策略两个方面对 MI-EEG 信号分类算法的研究进展进行综述。其中，分类器部分主要包含改进后的机器学习分类器、深度学习与黎曼几何分类器，机器学习策略部分主要包含集成学习、自适应学习与迁移学习。最后，本文也将给出 MI-EEG 信号分类算法的总结与展望。

1. 分类器研究进展

1.1. 改进后的机器学习分类器

传统机器学习分类器原理简单，技术成熟，在 MI-EEG 信号的分类中经久不衰。然而，其通用于不同的研究领域，未必与 MI-EEG 信号的特点相吻合。因此，部分研究对传统机器学习分类器进行了一些改进。

机器学习分类器可以分为线性与非线性分类器。其中，线性分类器易于建模与解释，其表达形式一般可以写作：

1

式（1）中的 w 与 b 被学得后，该线性分类器的模型就可以确定^[10]。LDA 与 SVM 均为较典型的线性分类器。其中，LDA 的目标为寻找超平面区分不同类别的数据，使不同类别的数据投影后类内协方差最小而类间协方差最大，而 SVM 的目标则为利用核函数寻找超平面，使不同类别的数据边界之间的距离最大^[8]。

部分研究对 LDA 与 SVM 进行了改进。收缩线性判别分析（shrinkage LDA，sLDA）使用收缩率对类间协方差矩阵进行正则化，具有更强的鲁棒性，适用于训练样本较少的情形，有助于实现少校准的在线 MI-EEG 信号分类^[11]。支持矩阵机（support matrix machines，SMM）利用矩阵的迹，将式（1）中的向量 w 替换为矩阵 W，保留原始矩阵的结构信息，以适应 MI-EEG 信号的高维度特性。而正则化支持矩阵机（regularized SMM，RSMM）则可以进一步提高 SMM 的分类准确率，其与 SVM、SMM 在 BCI 竞赛 III 数据集 IVa 的分类准确率如图 1^[12]所示。

图 1.

Classification accuracies of three classifiers on BCI Competition III dataset IVa^[12]

三种分类器在数据集 BCI 竞赛 III 数据集 IVa 的分类准确率^[12]

亦有研究对 KNN 与 NBC 等非线性分类器进行了改进。KNN 的目标为依据各特征向量间的度量距离将未知特征向量归为其 K 个最近邻向量中的优势类^[8]。与之相比，模糊 K 值最近邻（fuzzified KNN，FKNN）不仅计算特征向量之间的距离，也判断特征向量对类别的隶属程度，在指定数据集上将分类准确率提高了 7.9%～13.2%^[13]。NBC 的目标为利用最大后验概率规则，将未知特征向量归为所属概率最高的类别^[10]。加权朴素贝叶斯分类器（weighted NBC，WNBC）则在 NBC 的基础上为多个时频段提取到的特征进行加权，在 BCI 竞赛 III 数据集 IVa 上取得了 86.38% 的平均分类准确率，高于 LDA 等其他分类器^[14]。

综上所述，传统机器学习分类器本身性能良好，因此，部分研究仅围绕 MI-EEG 信号的高维度等固有特性，对传统机器学习分类器进行了针对性的修改。改进后的机器学习分类器一般体量轻捷，容易实现。但这些方法通常只能小幅度地提升分类准确率等指标，也难以进一步优化。

1.2. 深度学习

传统机器学习分类器与改进后的机器学习分类器均需在分类操作前进行特征提取。与之相比，深度学习方法不仅可以对提取到的特征进行分类，也可以从原始信号中自行学习特征并完成分类。目前为止，已有多种深度学习方法被用于 MI-EEG 信号的分类中，如卷积神经网络（convolutional neural network，CNN）与循环神经网络（recurrent neural network，RNN），再如深度信念网络（deep belief network，DBN）。这些深度学习方法的应用可以缓解 MI-EEG 信号高维与低信噪比特性带来的问题^[15]。

卷积操作在信号处理中应用广泛，以之为基础的 CNN 通常能够获得高于浅层算法的分类准确率^[16]。CNN 能够接受输入的特征并进行分类，如利用 MI-EEG 信号的时间包络相应地设计与优化 CNN，可在 BCI 竞赛 IV 数据集 IIa 中取得比竞赛最优方法高出 7% 的分类准确率^[17]。再如，以小波变换（wavelet transform，WT）为基础，将不同导联的时频信号结合后提取特征，设计低复杂度的 CNN，可在 BCI 竞赛 II 数据集 IIIa 上取得 90% 的分类准确率^[18]。

如前所述，CNN 亦可直接从数据中学习特征并进行分类。这一端到端的模型有助于简化 BCI 系统的设计，促进 BCI 系统的应用。在没有预处理或特征提取操作的情况下，使用 CNN 结构完成特征提取与分类等步骤，可以在 100 名被试上取得 94.6% 的分类准确率^[19]。

与 CNN 相比，RNN 具有记忆能力，可以总结前期输入的状态作为后期输入的辅助信息，更易于从时间序列中提取特征^[20]。典型的 RNN 结构有长短时记忆网络（long short term memory，LSTM）与门控循环单元（gated recurrent unit，GRU）。前者通过输入门、输出门、遗忘门等单元防止无关的输入和输出进入存储器，方便保存长序列数据的特征；后者具有更新门与重置门结构，支持每个循环单元获取不同时间范围内的依赖关系。在 BCI 竞赛 IV 数据集 IIa 上将两种 RNN 结构、CNN 结构、线性核 SVM 分别与对应特征结合后进行比较，其分类准确率如图 2^[21]所示。

图 2.

Classification accuracies of four algorithms on BCI Competition IV dataset IIa^[21]

四种算法在数据集 BCI 竞赛 IV 数据集 IIa 的分类准确率^[21]

DBN 是由受限玻尔兹曼机（restricted Boltzmann machine，RBM）堆叠而成的。RBM 包含一个可见层和一个隐藏层，可见层接收输入，而隐藏层则尽可能地重建输入^[22]。可以通过快速傅里叶变换（fast Fourier transform，FFT）和小波包分解（wavelet package decomposition，WPD）获得 EEG 信号的频域表示，训练少数 RBM，并构成高鲁棒的频率深度信任网络（frequential DBN，FDBN）^[23]。

亦有研究尝试将不同的深度学习模型进行结合。例如，LSTM 与 CNN 相结合后，在特定数据集上的分类准确率可以达到 86.7%，高于单独使用 LSTM 或 CNN^[24]。此外，一些新近出现的深度学习策略也被引入 MI-EEG 信号的分类中，如克服数据失真与扭曲的胶囊网络（capsule networks，CapsNet）^[25]。

深度学习在各个机器学习领域都掀起一股新的浪潮，MI-EEG 信号的分类领域也不例外。然而，深度学习在 MI-EEG 信号的分类中尚面临一些问题。首先是数据集问题。大型数据集较为稀少，不利于深度学习方法的训练，需要更多的研究机构提供高质量的 MI-EEG 信号数据集。再次是训练成本问题。MI-EEG 信号的分类往往要面向在线 BCI 系统，而深度学习方法训练普遍耗时，通常只能离线使用，需要浅层网络进一步发展。最后是可解释性问题。大多数深度学习方法中间过程的可解释性不佳，需要将功率等信息与网络的输出进行对照，以进一步优化网络结构。目前为止，深度学习在 MI-EEG 信号的分类领域尚未体现出显著优势^[26]。

1.3. 黎曼几何分类器

MI-EEG 信号的低平稳与低可靠性可能会为分类带来一系列问题。黎曼几何是数学的一个分支，研究局部表现为欧式的平滑弯曲空间，有希望成为解决这些问题的突破口^[27]。

黎曼几何中，由 MI-EEG 信号的样本协方差矩阵构成的空间被称为黎曼流形，而黎曼距离可以对黎曼流形中协方差矩阵间的关系进行度量：

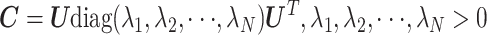2

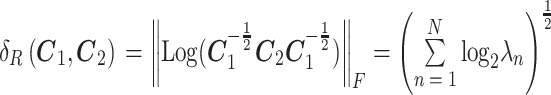3

式（2）中，diag（·）表示对角矩阵，λ₁，λ₂，λ_N 为矩阵的 N 个特征值。式（3）中的 δ_R（C₁,C₂）即为协方差矩阵 C₁ 与 C₂ 之间的黎曼距离。此外，对于 S 个试次的样本协方差矩阵而言，可以通过求取它们的黎曼均值进行切线空间映射：

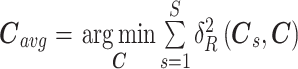4

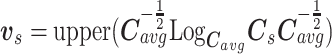5

式（4）中，C_avg 为黎曼流形上 S 个试次样本协方差矩阵的黎曼均值。式（5）中 upper（·）函数表示提取矩阵的上三角元素并将其加权平铺为一维向量，v_s 表示第 s 个试次样本协方差矩阵映射到切线空间后得到的特征向量。

黎曼流形及其切线空间示意如图 3^[28]所示。其中，C_avg 为样本协方差矩阵 C₁ 与 C₂ 的黎曼均值，v₁ 与 v₂ 为 C₁ 与 C₂ 以 C_avg 为切点映射后的向量。基于此，可以将黎曼几何分类器分为两类：黎曼流形上的分类器与切线空间上的分类器。前者以黎曼均值最小距离法（minimum distance to Riemannian mean，MDRM）为代表，后者以切线空间线性判别分析（tangent space LDA，TSLDA）为代表。MDRM 通过计算样本协方差矩阵与不同类别黎曼均值的距离进行归类，在 BCI 竞赛 IV 数据集 IIa 中的四分类平均准确率为 63.2%，与其他传统分类器结果相似。TSLDA 将各样本协方差矩阵映射到切线空间后再使用 LDA 进行训练与预测，在 BCI 竞赛 IV 数据集 IIa 中的平均分类准确率达到 70.2%，远高于其他分类算法^[29]。

图 3.

Representation of Riemannian manifold and its tangent space^[28]

黎曼流形及其切线空间示意图^[28]

黎曼几何分类器依然存在着一定的改进空间。针对 MDRM 算法中的维度诅咒，正则化黎曼均值最小距离法（regularized MDRM，RMDRM）基于正则化技术解决了协方差矩阵维度数大于试次数时性能不佳的问题，在 BCI 竞赛 III 数据集 IIIa 上获得比 MDRM 算法高出 9.27% 的平均分类准确率^[30]。广义学习黎曼空间量化（generalized learning Riemannian space quantization，GLRSQ）将应用于欧式空间的学习矢量量化（learning vector quantization，LVQ）推广到黎曼流形，以有监督的方式训练数据并更新模型，为每个类别学习多个代表。在指定数据集上的平均 Kappa 值高于 MDRM 与 TSLDA 算法^[31]。

除 LDA 外，切线空间上也存在其他分类器，如以极限学习机（extreme learning machine，ELM）为基础的正则化嵌入切线空间极限学习机（ELM on tangent space of regularized embedding，ELM-TS-RE）。ELM-TS-RE 包含基于黎曼图的降维、切线空间映射与极限学习机，在 BCI 竞赛 IV 数据集 IIa 上的平均 Kappa 值为 0.584，高于竞赛最优算法的 0.570^[32]。

黎曼几何分类器有许多独到之处，如等价于 EEG 源空间的操作，如对异常值的高鲁棒性，再如较强的泛化能力^[28]。然而，其依然存在着一些问题，如计算通常较复杂，再如特征维度在导联数量较多时会迅速膨胀，导致分类准确率的下降。这些问题尚待后续研究予以解决。

2. 机器学习策略研究进展

2.1. 集成学习

集成学习策略通过组合多个简单且性能良好的弱分类器对 MI-EEG 信号的类别进行区分。套袋法（bagging）与提升法（boosting）是两种常见的集成学习策略，前者将原始数据集进行划分，并行训练弱分类器，以投票等方式输出分类结果；后者关注被弱分类器错误分类的数据，对数据的权重进行调整，串行训练各弱分类器^[33]。

随机森林（random forest，RF）即为一种基于 bagging 的分类器。RF 包含多个决策树，并以投票的方式得到最终结果，具有分类精度高、计算速度快、易于发现鉴别性特征等优点^[34]。此外，集成学习也可以用于其他分类器，如集成支持向量学习（ensemble support vector learning，ESVL）以 SVM 为基础，将各 SVM 分类器的输出映射为概率进行合并，在 BCI 竞赛 IV 数据集 IIa 与 IIb 上的平均分类准确率达到 82.5%^[35]。再如，将集成学习应用于 ELM，可以在 BCI 竞赛 IV 数据集 IIa 上取得 86.14% 的平均分类准确率，高于相同特征下非集成 ELM 的 84.38%^[36]。

在分类器选择合理的前提下，集成学习可以有效地提升分类性能，减少 MI-EEG 信号分类中的方差与偏差。但引入集成学习的分类器训练成本也相对更高，且集成学习对弱分类器的准确性与多样性都有着一定的要求，常常不能达到预定效果。在 MI-EEG 信号的分类中，选择何种分类器进行集成，选择何种方式对分类器进行集成，依然存在着一定的探索空间。

2.2. 自适应学习

被试的认知状态会随着实验进行而改变，导致其 MI-EEG 信号产生波动^[37]。自适应学习是解决这一问题的有力工具。引入自适应学习后，分类器的参数将随着新数据出现被增量更新，有助于分类器跟踪变化的特征^[38]。

不少分类器均可与自适应学习结合。如可以利用 LDA 的分类结果等参数判断是否应该选择样本加入训练数据，适应长期 MI 实验中被试可能产生的疲劳现象^[39]。再如，可以基于概率加权 K 值最近邻（probabilistic weighted KNN，PWKNN）算法丰富训练数据集，并以无监督自适应的方式执行分类器的集成。该方法在 BCI 竞赛 IV 数据集 IIb 上取得 74.65% 的平均分类准确率，远高于其他非自适应的集成方法。

自适应学习策略还常常与模糊系统相关联。模糊系统的基础是模糊逻辑（fuzzy logic，FL），其使用一组 IF-THEN 规则表示从给定输入到输出的映射。在定义输入和输出空间后，通过隶属度函数定义相应的模糊集，可以将模糊规则应用到系统中^[40]。自适应神经模糊推理系统（adaptive neuro-fuzzy interface system，ANFIS）在利用模糊系统优势的同时，可以自行对模糊规则进行调整。一种典型的 ANFIS 结构如图 4^[41]所示。在输入 x₁ 与 x₂ 被模糊化后，分别计算其模糊规则的激励强度并进行归一化。此后，计算各条规则的结果，通过去模糊化得到输出结果 y。而基于 ANFIS 的递归结构使每个 ANFIS 针对一类 MI-EEG 信号进行训练，以区分多类 MI-EEG 信号，可在在线实验中取得 85.52% 的分类准确率^[41]。

图 4.

A typical ANFIS structure^[41]

一种典型的 ANFIS 结构^[41]

BCI 通常需要面向在线甚至实时应用，这也需要分类算法适应 EEG 信号在 MI 过程的变化。相较于光明的前景，自适应学习方法（尤其是无监督的自适应学习方法）研究内容反而略显不充分。这一方向值得更深入的探索与讨论，其在 MI-EEG 信号的分类中可能会发挥更重要的作用。

2.3. 迁移学习

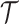被试的性别、年龄、情绪等因素，都会影响被试 MI 任务的表现，导致被试内与被试间数据分布的变异性。迁移学习被引入 MI-EEG 信号的分类，以缓解这些变异性带来的问题^[42]。在给出迁移学习的定义前，需要先给出域 及任务 的定义：

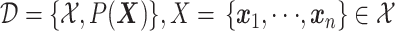6

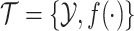7

式（6）中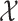， 表示特征空间，X 表示特定的学习样本，P（X）表示 X 的边际概率分布。式（7）中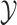， 表示标注空间，f（·）表示预测函数。对于源域 与目标域 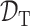及其对应的源任务 与目标任务 ，迁移学习的定义为：在 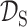≠ 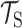或 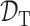≠ 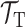的前提下，利用 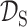与 的知识，改善目标预测函数 f_T（·）。即在源域与目标域不同或源任务与目标任务不同的情况下，通过源域及目标域中的知识，改善目标任务^[43]。

迁移学习在 MI-EEG 信号的分类领域有着广泛的应用。例如，基于有监督加权逻辑回归的迁移学习方法（supervised weighted logistic regression-based transfer learning，S-wLTL）将正则化参数添加到分类器的目标函数中，以使分类参数尽可能接近其他相似被试的分类参数，在 BCI 竞赛 IV 数据集 IIa 上取得 75.6% 的平均分类准确率，高于 CSP 与 SVM 结合的 70.4%^[44]。再如，使用其他被试的 MI-EEG 信号对 CNN 模型进行预训练，并通过微调策略进一步训练个体模型，在跨被试分类中可以取得 75.9% 的准确率^[45]。

迁移学习也存在着一些问题，如迁移不足和负迁移。迁移不足意味着迁移学习的效果不明显或达不到预期，通常是因为迁移的知识与目标域不匹配，需要调整训练方式，学习适合于目标域的表示方法。而负迁移指迁移学习对目标域中的任务产生负面影响，通常是因为目标域和源域之间差异过大，需要添加正则化等约束条件解决^[46]。尽管存在着上述不足，迁移学习在跨时间、跨被试，乃至跨数据集的 MI-EEG 信号分类中起着重要的作用，不失为迈向无校准 BCI 系统的关键步骤^[47]。

3. 结论

如前所述，MI-EEG 信号的分类领域在近年来出现了一些新的进展。在分类器方面，不少研究对传统分类器进行了适当的改进，而深度学习与黎曼几何分类器也被引入这一领域。在机器学习策略方面，为提升 MI-EEG 信号分类中的各项性能，集成学习、自适应学习与迁移学习等机器学习策略也与各类分类器紧密结合，从不同的角度提升了分类器的性能。

分类准确率与鲁棒性是 MI-EEG 信号分类算法的关键指标。为提高分类准确率，深度学习尝试自行学习具有鉴别性的特征，集成学习尝试结合各分类器的长处，迁移学习则尝试降低被试内与被试间的数据分布变异性。而为了增强 MI-EEG 信号分类算法的鲁棒性，黎曼几何分类器使用几何平均值对 EEG 信号进行处理，集成学习使用投票等方式降低方差，自适应学习则尝试适应 MI-EEG 信号的分类过程中信号的波动。

MI-EEG 信号分类算法的计算复杂度与校准时间也较为重要，直接关系到其能否应用于在线环境。为了减小算法的计算复杂度，一些浅层网络被提出，亦有降维方法被应用到黎曼几何分类器中。而自适应学习与迁移学习则为无校准 BCI 系统奠定了基石，在提高算法性能的同时，也改善了用户的使用体验。

MI-EEG 信号分类算法依然存在着一些待改进的内容。首先是在保持分类准确率的同时，如何快速得到分类结果的问题，这有助于实现高准确率的在线 MI-EEG 信号分类，促进 BCI 系统的真正落地。其次是如何改进 MI-EEG 信号的分类算法，以面向复合肢体或复杂运动的 MI 任务分类，而这需要类间模糊性更低的分类算法。最后是寻找更适宜同自适应学习与迁移学习相结合的分类器，实现彻底的无校准 MI-BCI 系统。总之，MI-EEG 信号分类算法的进一步发展，依然是挑战与机遇并存。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金资助项目（61976152，81601565，81630051，62006014）；第四届中国科协青年人才托举工程（2018QNRC001）；天津市科技重大专项与工程（17ZXRGGX00010）