Abstract
机器人骨折复位通常是固定骨折近端,机器人带动骨折远端按照规划的复位路径向近端运动。为提高复位手术的精准性和安全性,有必要了解复位中肌肉力和复位力的变化规律。本文基于骨骼肌组织的肌肉力分析骨折复位力,由 Haeufle 四元素骨骼肌模型,综合考虑下肢羽状肌的羽状角对肌肉力特性的影响,提出一种股骨骨骼肌肉模型 PA-MTM,对比分析不同肌肉模型的骨骼肌的肌肉力。对比仿真分析两种复位路径下的肌肉力及复位力变化情况。结果表明,羽状角越大对肌肉力的影响越大;股骨骨折复位,轴向牵引力最大且股二头肌短头起主要作用,轴向牵引力最大值为 472.18 N,复位合力最大值为 497.28 N,验证了新型骨骼肌肉模型的合理性。
Keywords: 损伤股骨, 骨骼肌肉模型, 肌肉力, 复位力
Abstract
Robot-assisted fracture reduction usually involves fixing the proximal end of the fracture and driving the distal end of the fracture to the proximal end in a planned reduction path. In order to improve the accuracy and safety of reduction surgery, it is necessary to know the changing rule of muscle force and reduction force during reduction. Fracture reduction force was analyzed based on the muscle force of femoral. In this paper, a femoral skeletal muscle model named as PA-MTM was presented based on the four elements of skeletal muscle model. With this, pinnate angle of the skeletal muscle was considered, which had an effect on muscle force properties. Here, the muscle force of skeletal muscles in different muscle models was compared and analyzed. The muscle force and the change of the reduction force under different reduction paths were compared and simulated. The results showed that the greater the pinnate angle was, the greater the influence of muscle strength was. The biceps femoris short head played a major role in the femoral fracture reduction; the force in the z direction contributed the majority to the resulting force with maximums of 472.18 N and 497.28 N for z and resultant, respectively, and the rationality of the new musculoskeletal model was verified.
Keywords: injured femoral, musculoskeletal model, musculoskeletal force, reduction force
引言
股骨骨折是创伤骨科的常见病,且随着全球老龄化和交通运输的发展呈逐年增加的趋势[1]。多由高能量直接损伤所致,如车祸伤、直接暴力打击、强力挤压等,也可见于高处坠落伤、机器绞伤等间接暴力导致的损伤;其骨折常伴有重叠、成角及旋转等,有些还伴有严重的软组织损伤,治疗起来比较棘手,而良好的复位手段是股骨干骨折治疗的关键[2]。传统人工骨折复位手术,复位过程中医生牵引和保持骨折的复位状态,体力消耗比较大,复位效果依赖医生经验,而且医患双方会多次受到射线辐射影响。随着医疗科学技术的发展,国内外开始研发机器人辅助骨折复位[3-5],这不仅大大节省了医生的体力,而且能有效提高骨折复位精度,并通过远程操作替代术者的人工复位,减少辐射。
目前,为提高复位精度和复位操作的安全性,术前需要进行精准的复位路径规划[6-8]。由于骨折周围复杂的生物力学环境和解剖力学特性,骨折复位过程中有可能对肌肉等软组织造成损伤,因而有必要清楚了解骨折骨肌组织的生物力学特性,分析骨折周围肌肉组织的肌肉力对复位的干扰和影响,分析骨折复位过程中的肌肉力及复位力。
关于骨骼肌肉模型有两大类:Huxley 模型和 Hill 模型[9]。Huxley 模型是 1957 年由 Huxley 提出的横桥和肌动蛋白结合的横桥动力学模型(cross-bridge model),横桥是指肌球蛋白分子马达。Huxley 模型是源于肌肉的基本结构,从微观角度给出了肌肉收缩的本构模型,由于该模型包含多个难以确定的参数,故国内外学者多采用 Hill 肌肉模型。Hill 肌肉模型是 Hill[10]于 1938 年在青蛙肌肉实验的基础上提出的宏观肌肉模型,在一定程度上能反映肌肉的力学特性。但由于该模型过于简化,与真实肌肉结构相差较大,不能真实反映肌肉力大小。
一些学者对 Hill 模型进行了改进。1989 年,Zajac[11]考虑肌腱对肌肉与骨骼之间力传递的影响,将肌腱简化为串联弹性元,并引入羽状角,修正了 Hill 模型。2007 年 Günther 等[12]对仔猪后腿进行实验研究获得肌肉参数,通过在串联单元处引入阻尼元,可抑制肌肉收缩时产生的高频振荡,提出了能较为真实反映肌肉力的四元素模型。2013 年 Millard 等[13]对比了弹性肌腱模型、弹性肌腱阻尼模型和刚性肌腱模型等三种骨骼肌模型的计算速度和生物学准确性,表明弹性肌腱阻尼模型的计算速度更快,生物学准确性更高。2014 年 Haeufle 等[14]结合了 Günther 等[12]的研究中在串联单元处引入阻尼元以及 Van Soest[15]、Mörl 等[16]的研究中对离心收缩力-速度关系的修正,建立骨骼肌的肌肉-肌腱复合体模型(muscle tendon complex,MTC),该模型包括串联弹性单元、并联弹性单元、串联阻尼单元和收缩元,采用该模型进行肘关节的屈曲仿真分析,仿真结果表明该模型较符合真实情况,且该模型同样适用于部分下肢肌肉。
解剖学中,通常将肌腱与肌纤维间的夹角称为羽状角(pinnate angle),反映肌纤维排列方向与肌腱的关系[17]。Folland 等[18]研究表明羽状角可影响肌肉向肌腱、骨传递的力。由于下肢骨骼肌在解剖结构上大多存在羽状角,Haeufle 四元素模型 MTC 未考虑羽状角对肌肉力的影响,利用该模型进行下肢含羽状角骨骼肌的肌肉力分析时可能不够准确。
机器人骨折复位手术时,由于机器人运行速度比较慢,同时忽略皮肤、血管、神经等组织对复位操作的影响,仅仅考虑肌肉组织对复位的影响,因此骨折复位力主要用于克服肌肉组织的牵拉阻力[19]。国内外学者通过理论分析或实验对骨折复位力开展研究。2008 年 Graham 等[19]建立搜索最佳复位路径的模型,可实时输出断骨移动时肌肉产生的力和力矩,通过仿真得到中轴骨折复位力最大为 428 N。2011 年 Joung 等[20]为提高机器人骨折复位的安全性,设计能够计算骨折复位力的骨骼肌肉模型,由导航系统测量髋部和远端股骨的坐标,由此确定肌肉的长度,基于 Hill 肌肉模型计算肌肉力,模拟髋部骨折复位,获得两种复位路径下的最大复位力分别为 273、382 N。2015 年 Li 等[21]研发长骨骨折复位机器人系统,基于 Hill 肌肉模型和 Kane 方法,建立机器人与肌肉骨骼系统模型,在 Matlab/Simulink 软件中进行仿真分析,根据规划的复位路径模拟骨折复位,模型输入为断骨远端相对于近端的典型位姿,输出 Stewart 机构支杆的作用力和肌肉力,得到支杆作用力和肌肉力的最大值分别为 600、230 N。研究表明复位过程中,股二头肌短头对复位力影响最大,且沿轴向拉伸时复位力的大小变化最为显著。2018 年朱庆[22]设计了柔性驱动股骨干骨折复位机器人系统,通过观察复位过程中复位力和力矩的变化确定最佳复位路径,四种复位路径下,复位力最大可达 521 N。上述研究表明复位力与复位路径密切相关,不同的复位路径,复位力也不同。而上述国内外关于骨折复位力理论研究,大多是基于 Hill 肌肉模型。
本文为提高机器人骨折复位力分析的准确性,基于 Haeufle 四元素模型 MTC,考虑羽状角对下肢骨骼肌肌肉力特性的影响,建立一种羽状角-肌肉肌腱骨骼肌模型(pinnate angle-muscle tendon model,PA-MTM),包括主动收缩元、并联弹性单元、串联弹性单元、阻尼单元和羽状角。与 Haeufle 四元素模型 MTC 相比,该模型增加羽状角,更符合下肢骨骼肌的真实解剖结构。基于新型骨骼肌模型,通过股骨干骨折周围肌肉群的肌肉力分析,由骨折远端的力平衡方程确定骨折复位力。根据骨折计算机断层扫描(computed tomography,CT)数据逆向建模生成三维模型,结合股骨的解剖学模型获得肌肉附着点坐标,进行骨折复位过程仿真,对比分析不同复位路径下各肌肉力和复位力,验证所提出的新型骨骼肌肉模型的合理性,以期为机器人股骨骨折复位的安全性及路径规划择优提供参考。
1. 骨骼肌模型及肌肉力
骨骼肌的结构如图 1 所示,骨骼肌由肌腹和肌腱两部分组成。肌腹主要由骨骼肌纤维(肌细胞)组成,骨骼肌由肌束并行排列而成,肌束由肌纤维并行排列组成,而肌纤维又由肌原纤维并行排列组成,肌原纤维则由轴向串联的肌小节组成;微观上,肌小节主要由粗肌丝和细肌丝构成,构成粗肌丝的肌球蛋白在细肌丝上集体做功,引起了粗细肌丝的相对滑移,即肌小节的收缩,无数肌小节的收缩带来了肌原纤维的收缩、肌纤维的收缩,从而导致骨骼肌的收缩[23]。肌腱位于肌腹的两端,连接骨骼和肌腹,在神经系统的支配下,骨骼肌可以实现自主收缩,产生肌肉力,肌肉力在肌腱的传递下作用到骨骼上,将肌腹部分产生的力作用于骨骼。
图 1.
Structure of skeletal muscle
骨骼肌宏观结构
骨骼肌的形态多变,本质上是由肌纤维排列模式的不同造成的。按照肌纤维的排列模式,骨骼肌可分为平行肌和羽状肌,羽状肌可分为单羽状肌、双羽状肌和多羽状肌[24],如图 2 所示。羽状肌的肌纤维较短,生理横截面积较大,肌力较强,多分布于力量型的下肢;而平行肌的肌纤维较长,生理横截面积较小,肌力较弱,多分布于发挥灵巧作用的上肢[25]。
图 2.
Variety of skeletal-muscle shapes
骨骼肌形态的多样性
本文基于 Haeufle 等提出的四元素模型 MTC,考虑羽状角对肌肉力特性的影响,建立适用于下肢骨骼肌的新型肌肉模型 PA-MTM,如图 3 所示。其中,CE 为收缩元,由肌球蛋白微丝与肌动蛋白微丝组成,在神经系统支配下,可产生主动肌力;PEE 为并联弹性单元,由肌束膜及肌纤维膜组成,其中结缔组织具有弹性,当肌肉处于拉伸状态时产生弹力,反映肌肉的被动特性;SEE 为串联弹性单元,表示肌腱、肌节间 Z 盘及肌微丝等组织,反映肌腱的被动特性;SDE 为串联阻尼单元,用于抑制高频振荡;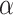 为羽状角,描述肌纤维的排列方向与肌腱之间的夹角。
为羽状角,描述肌纤维的排列方向与肌腱之间的夹角。
图 3.
Skeletal muscle model PA-MTM
骨骼肌模型 PA-MTM
则有肌纤维和肌腱单元构成的力平衡方程:
 |
1 |
其中,
 |
2 |
其中, 为肌肉力,
为肌肉力,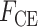 为收缩单元产生的力,
为收缩单元产生的力,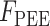 为与收缩元并联的弹性单元产生的力,
为与收缩元并联的弹性单元产生的力,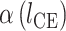 为肌纤维与肌腱的夹角,
为肌纤维与肌腱的夹角,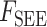 为串联弹性单元产生的力,
为串联弹性单元产生的力,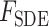 为串联阻尼单元产生的力。
为串联阻尼单元产生的力。
1.1. PA-MTM 的羽状角
肌肉收缩时羽状角并非定值,会随着肌纤维长度的变化而改变。研究表明[11],肌肉收缩过程中,肌纤维的长度改变,而宽度不变,如图 4 所示,则羽状角 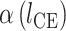 为:
为:
图 4.
Diagram of pinnate angle change
羽状角变化示意图
 |
3 |
 |
4 |
 |
5 |
其中, 为肌纤维的宽度,
为肌纤维的宽度,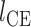 为肌纤维的当前长度,
为肌纤维的当前长度,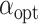 为最优肌纤维长度
为最优肌纤维长度  处的夹角,
处的夹角,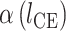 为当前羽状角。
为当前羽状角。
1.2. PA-MTM 的四元素
主动收缩元、串联弹性单元、并联弹性单元和串联阻尼单元的力分别计算如下[12, 14-15],式中与下肢肌肉骨骼模型相关的参数如表 1 所示[12]。
表 1. Parameters related to lower limb musculoskeletal model[12].
下肢骨骼肌肉模型相关参数[12]
| 元素 | 参数 | |||
| 力-长度关系 |
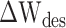
|
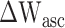
|
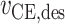
|
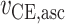
|
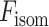
|
0.14 | 0.57 | 3 | 4 |
| 力-速度关系 |
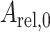
|
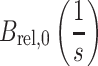
|
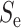
|
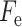
|
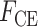
|
0. 1 | 1 | 2 | 1.8 |
| 并联弹性单元 |
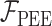
|
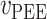
|
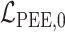
|
|
| PEE | 1 | 2.5 | 0.9 | |
| 串联弹性单元 |

|
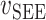
|
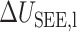
|
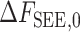
|
| SEE | 0.1825 | 2 | 0.073 |
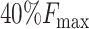
|
| 阻尼参数 |
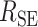
|
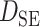
|
||
| SDE | 0.01 | 0.3 | ||
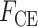 为收缩元所产生的主动力,与收缩单元的激活因子 q、长度
为收缩元所产生的主动力,与收缩单元的激活因子 q、长度 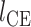 和收缩速度
和收缩速度 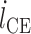 相关:
相关:
 |
6 |
其中,激活因子 q 代表肌肉的激活程度。肌肉激活程度反映的是肌肉在神经系统的刺激下受到激活的程度,激活度越高,表明肌肉的兴奋程度越高,肌肉产生的主动收缩力也越大;当 q = 0 时,肌肉不能主动收缩产生主动力,若肌肉处于拉伸状态,则会产生被动力。
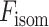 是关于收缩元长度
是关于收缩元长度 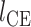 的函数,
的函数,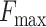 是当收缩元长度
是当收缩元长度 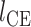 为最优肌纤维长度
为最优肌纤维长度 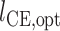 时的最大等长力:
时的最大等长力:
 |
7 |
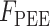 为并联弹性元在被动拉伸时所产生的力:
为并联弹性元在被动拉伸时所产生的力:
 |
8 |
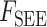 为串联弹性元所产生的力,肌腱组织当中也存在与肌腹部分相似的弹性特性:
为串联弹性元所产生的力,肌腱组织当中也存在与肌腹部分相似的弹性特性:
 |
9 |
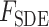 为串联阻尼单元所产生的力,它是一种粘性阻尼力:
为串联阻尼单元所产生的力,它是一种粘性阻尼力:
 |
10 |
1.3. PA-MTM 的收缩动力学
由肌纤维和肌腱单元构成的力平衡方程(1),可得肌纤维收缩速度 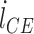 的二次方程:
的二次方程:
 |
11 |
其中,
 |
12 |
 |
13 |
 |
14 |
其中,
 |
15 |
解得:
 |
16 |
其中,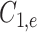 、
、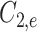 、
、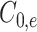 是将上面的
是将上面的  换成
换成 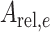 、
、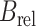 换成
换成 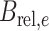 得到的。
得到的。
1.4. 肌肉力计算
首先,假设初始条件 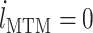 ,给定肌肉的初始长度
,给定肌肉的初始长度 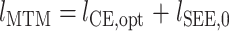 ,其中
,其中 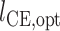 为肌肉的最优肌纤维长度,
为肌肉的最优肌纤维长度,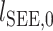 为肌腱的松弛长度,肌肉的相关参数见文献[26];分别假设激活因子
为肌腱的松弛长度,肌肉的相关参数见文献[26];分别假设激活因子 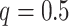 、
、 ,则由力平衡方程式(1)得肌肉初始肌纤维长度
,则由力平衡方程式(1)得肌肉初始肌纤维长度 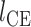 。然后计算其他未知量:
。然后计算其他未知量: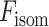 、
、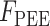 、
、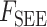 、
、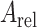 、
、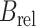 、
、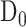 、
、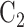 、
、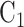 、
、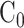 、
、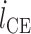 、
、 、
、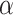 ;得到肌肉的初始肌肉力
;得到肌肉的初始肌肉力 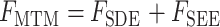 。
。
分别采用 Hill 模型、Haeufle 等建立的四元素模型 MTC、本文提出的 PA-MTM 模型,对比分析股二头肌短头、股二头肌长头、股直肌、缝匠肌、半膜肌、半腱肌的肌肉力,各肌肉的初始条件相同,肌肉力计算结果如图 5 所示。
图 5.
Comparison of muscle force by different models
采用不同肌肉模型的肌肉力对比
在给定的肌肉长度下,当激活因子 q = 0.5 时,此时肌肉既可产生主动力,也可产生被动力。如图 5 所示,股二头肌短头、缝匠肌和半腱肌在三种不同骨骼肌模型下肌肉力相差不大。而股二头肌长头、半膜肌和股直肌,采用 PA-MTM 模型比 Haeufle 的四元素模型的肌肉力大 10~25 N,Hill 模型的肌肉力则远小于另外两种模型的肌肉力。
在给定的肌肉长度下,当激活因子 q = 0 时,此时肌肉只能产生被动力。如图 5 所示,除缝匠肌外,股二头肌短头、股直肌等肌肉在 Haeufle 等建立的四元素模型 MTC、PA-MTM 模型两种骨骼肌模型下所计算的肌肉力差别较大,可以看出羽状角的引入对骨骼肌只存在被动力时所产生的影响较为明显。
采用 Haeufle 四元素模型、PA-MTM 骨骼肌模型,在激活因子 q = 0.5 时,不同肌肉的肌肉力差值与肌肉羽状角之间的关系如图 6 所示,横坐标为不同肌肉的羽状角,纵坐标为两种模型下肌肉力的差值。可以看出,下肢骨骼肌中,肌肉初始条件相同时,肌肉的羽状角越大,两模型的肌肉力计算结果差值越大,即羽状角越大对肌肉力的影响越大。
图 6.
The difference in muscle force with pinnate angle
肌肉力差值与羽状角
不同骨骼肌的羽状角是不同的,且羽状角大小随肌肉长度变化而变化。由图 5 和图 6 可看出,采用不同肌肉模型时,骨骼肌的肌肉力差值因羽状角的不同而不同。因此,建立肌肉模型时不能忽略羽状角,尤其是羽状角比较大的骨骼肌。
2. 骨折复位力分析
股骨被强有力的骨骼肌包裹着,大腿肌肉是人体最强大、厚实的肌肉群[27],如图 7 所示。当在外力作用下,肌肉受到刺激产生收缩力作用在骨折断骨远端从而产生移位偏差,骨折复位时,又会产生拉力作用阻碍骨折复位。
图 7.
Muscle distribution in lower limbs
下肢肌肉分布
肌肉力与羽状角 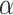 、肌纤维长度
、肌纤维长度 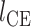 、肌肉长度
、肌肉长度 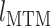 等可变参数有关,也与最优羽状角
等可变参数有关,也与最优羽状角 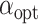 、最优肌纤维长度
、最优肌纤维长度  、肌腱的松弛长度
、肌腱的松弛长度 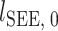 等不变参数有关[26]。
等不变参数有关[26]。
影响股骨骨折复位力的骨骼肌主要有股二头肌(股二头肌短头、股二头肌长头)、股四头肌(股直肌、股中间肌、股外侧肌、股内侧肌)、缝匠肌、半膜肌、半腱肌等。根据表 2 肌肉的附着点位置以及股骨骨折的逆向模型,确定肌肉起止点的坐标及肌肉的作用线[28],如图 8 所示。
表 2. The attachment point and coordinates of the muscle.
肌肉的附着点及坐标
| 肌肉名称 | 起点 | 止点 | 起点坐标/mm | 止点坐标/mm |
| 缝匠肌 | 髂前上棘 | 胫骨上端内侧面 | (2.20,–29.13,255.58) | (–11.51,–35.58,–245.98) |
| 股二头肌短头 | 股骨粗线 | 腓骨小头 | (–13.59,–5.70,5.78) | (–54.94,–0.49,–209.52) |
| 股二头肌长头 | 坐骨结节 | 腓骨小头 | (51.68,48.89,153.74) | (–54.94,–0.49,–209.52) |
| 半膜肌 | 坐骨结节 | 胫骨内侧髁后面 | (57.15,41.30,168.60) | (13.08,17.09,–200.69) |
| 半腱肌 | 坐骨结节 | 胫骨上端内侧面 | (51.89,49.98,148.91) | (6.86,–1.19,–222.38) |
| 股直肌 | 髂前下棘 | 胫骨粗隆 | (31.55,–16.09,232.67) | (–8.70,–52.76,–136.62) |
| 股外侧肌 | 股骨粗线 | 胫骨粗隆 | (–11.70,–0.44,–19.50 ) | (–8.70,–52.76,–136.62) |
| 股中间肌 | 股骨前面 | 胫骨粗隆 | (–1.48,–4.49,–22.45) | (–8.70,–52.76,–136.62) |
| 股内侧肌 | 股骨粗线 | 胫骨粗隆 | (7.90,–0.60,–19.76) | (–8.70,–52.76,–136.62) |
图 8.
The attachment points and action lines of the muscles
肌肉的附着点和作用线
如图 8 所示,断骨近端的坐标系 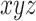 固定,远端坐标系
固定,远端坐标系 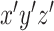 移动,远端坐标系坐标原点
移动,远端坐标系坐标原点 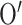 在近端坐系中的坐标为
在近端坐系中的坐标为 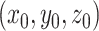 ,肌肉 i 的附着点 A、B 在近端坐标系的坐标为
,肌肉 i 的附着点 A、B 在近端坐标系的坐标为 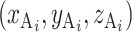 和
和 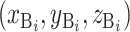 ,点 B 在远端坐标系的坐标为
,点 B 在远端坐标系的坐标为 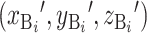 。肌肉 i 的长度为
。肌肉 i 的长度为
 |
17 |
骨折复位前,通常患者被注射了肌肉松弛剂。复位过程中肌肉处于非激活状态,收缩元无法主动收缩产生主动力,只有串联弹性元和并联弹性元由于肌肉被拉伸而产生被动力[18]。则骨折复位时的骨骼肌力为:
 |
18 |
肌肉力 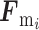 方向与 xoy 平面的夹角
方向与 xoy 平面的夹角 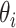 为
为
 |
19 |
令  ,即
,即 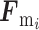 在
在 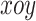 平面上的投影。
平面上的投影。
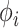 为
为 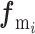 与
与 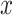 轴的夹角:
轴的夹角:
 |
20 |
 |
21 |
 |
22 |
则作用于股骨骨折远端的肌肉力合力为:
 |
23 |
其大小为:
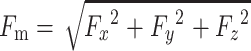 |
24 |
在骨折复位过程中,骨折远端受力平衡,根据力平衡原理:
 |
25 |
其中,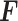 为复位机器人作用在股骨骨折远端的复位力,
为复位机器人作用在股骨骨折远端的复位力,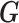 为股骨骨折远端的重力。
为股骨骨折远端的重力。
3. 复位力仿真分析
3.1. 复位路径
本研究采用医生提供的一名成年女性患者的下肢 CT 数据,患者为股骨中段骨折,螺旋 CT 获取原始的 DICOM 数据。患者取仰卧位,位于扫描视野中心位置,沿股骨干长轴方向进行扫描,扫描范围由髋骨至胫腓骨中段。CT 参数:层厚 0.625 mm、层间距 0.625 mm,数据收集直径 500 mm,分辨率 512 × 512,共 937 张 CT 图片,扫描图像以 DICOM 格式存储。患者已签署扫描医学影像知情同意书。
股骨骨折逆向重建的三维模型如图 9 所示。基于患者股骨骨折的 CT 扫描数据进行逆向建模,建立股骨骨折的三维模型。在 Mimics 20.0 软件中将 CT 扫描数据进行阈值分割、布尔操作、区域增长、蒙版编辑、空洞填充等操作,建立下肢骨骼蒙板并分割,进而生成 3D 模型,同时将健侧股骨的模型关于矢状面进行镜像,导出 stl 格式的下肢骨骼点云模型;将点云模型导入 Geomagic studio 软件中,进行“网格医生”处理,修复有问题的三角形面片;基于健侧股骨的镜像模型进行患侧股骨骨折远端与近端的拟合配准,根据断骨远端的转换矩阵得到股骨骨折的移位偏差和旋转偏差,股骨骨折模型绕 x、y、z 轴的旋转偏差分别为–8.47、3.69、2.18 rad,沿 x、y、z 轴的移位偏差分别为 –8.80、–41.69、–30.02 mm。
图 9.
Three-dimensional model of reverse reconstruction of femoral fracture
股骨骨折逆向重建的三维模型
对比分析不同复位路径下的复位力。采用课题组规划的双平面复位路径[29](路径 1),首先将断骨远端的姿态与近端姿态调整一致,再根据移位偏差在 xoy 和 yoz 两个平面内分别进行路径规划,得到如图 10a 所示的复位路径点,红圈代表在 xoy 平面内的复位路径点,蓝圈代表在 yoz 平面的复位路径点;采用课题组规划的 A*算法的空间复位路径(路径 2),得到的复位路径点如图 10b 所示;图中  为起点,
为起点,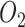 为终点。
为终点。
图 10.
The reduction path point of path planning
路径规划的复位路径点
a.双平面复位路径(路径 1);b.空间复位路径(路径 2)
a. bi-plane reduction path (path1); b. spatial reduction path (path2)
3.2. 复位力仿真
采用 Matlab 软件编写计算肌肉力和复位力的函数,在 Simulink 中进行复位力仿真分析[14],如图 11 所示为股骨骨折复位仿真流程图。根据骨骼肌肉的附着点以及该模型的骨折位置可知,影响上述股骨骨折类型复位的骨骼肌主要有股二头肌短头、股二头肌长头、股直肌、缝匠肌、半膜肌和半腱肌。
图 11.
Simulation flow chart
仿真流程图
在两种复位路径下,各肌肉在复位过程中的肌肉力变化曲线如图 12 所示。从图中可看出:在两种路径下股二头肌短头在复位过程中皆起主要作用,且在复位过程中产生的最大肌肉力为 265.47 N,此时断骨远端沿轴向拉伸 30.02 mm。文献[21]中,骨折的轴向移位偏差为 20 mm,垂直于轴向移位 40 mm,复位过程中,股二头肌短头对复位力的影响最大,且轴向拉伸至 20 mm 时,股二头肌短头所产生的肌肉力为 230 N。
图 12.

Muscle force with different reduction path
不同复位路径的肌肉力变化
在股骨骨折复位时,虽然影响骨折复位的主要肌肉——股二头肌短头和缝匠肌的羽状角较小,但其他股直肌、半腱肌等骨骼肌的羽状角较大,亦影响较大,因此,计算复位力时,也不能忽略羽状角的影响。
图 13 为复位过程中复位力及其沿 x、y、z 轴方向的分力的变化曲线,从图中可以看出,股骨骨折复位过程中,两种复位路径下沿股骨干轴向的复位力最大,最大值为 472.18 N,且最大骨折复位合力为 497.28 N。
图 13.

Reduction force
复位力
在复位操作时,肌肉不能产生主动力,只有被动力在起作用,且辅助骨折复位机器人在复位过程中移动缓慢,此时肌肉力的大小只与肌肉长度相关,由于两种复位路径的起点和终点相同,从图 12~13 可以看出,在两种复位路径下各力的最小值和最大值相等,而且采用课题组双平面路径规划的路径 1 进行骨折复位仿真,复位过程中,复位力及肌肉力的变化更加平缓。
采用路径 1 时,初始阶段断骨远端在 xoy 平面内仅仅沿 x 轴移动时,肌肉力的变化趋势较为平缓,当断骨远端开始在 yoz 平面内沿着 y 和 z 轴移动时,肌肉力的变化趋势变得陡峭,而在最后阶段又变得比较平缓,此时断骨远端沿着 y 轴移动;采用路径 2 时,初始阶段断骨远端在三维方向上进行移动,肌肉力的变化趋势较为陡峭,当断骨远端仅沿着 y 轴移动时,肌肉力及复位力的变化趋势变得平缓,说明轴向位移的变化对复位力的影响最大。
4. 结论
本文结合 Haeufle 四元素模型中引入的串联阻尼、离心收缩力-速度关系以及羽状角对肌肉力特性的影响,建立一种新型骨骼肌肉模型 PA-MTM,较符合下肢骨骼肌的真实结构。由于肌肉力与骨骼肌的长度 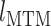 、肌肉的速度
、肌肉的速度 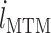 、激活程度
、激活程度 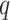 等参数有关,给定各骨骼肌长度、速度及激活程度,对比分析股二头肌短头、股二头肌长头、股直肌、半膜肌、半腱肌和缝匠肌等六种骨骼肌,在相同肌肉长度下,采用 Hill 模型、Haeufle 四元素模型、PA-MTM 肌肉模型三种不同模型计算的肌肉力。本文所提出 PA-MTM 骨骼肌模型的肌肉力计算结果大于不考虑羽状角的 Haeufle 四元素骨骼肌模型,且肌肉的羽状角越大,不同模型下的肌肉力计算结果差值越大。根据股骨骨折模型的骨折偏差,规划不同复位路径,进行骨折复位仿真分析,获得最大复位合力为 497.28 N,最大轴向复位力为 472.18 N,同时,通过与文献[19, 21, 30]的复位力分析结果对比,验证了新型骨骼肌模型 PA-MTM 的合理性。本研究可为机器人骨折复位力监控及复位路径择优提供参考。
等参数有关,给定各骨骼肌长度、速度及激活程度,对比分析股二头肌短头、股二头肌长头、股直肌、半膜肌、半腱肌和缝匠肌等六种骨骼肌,在相同肌肉长度下,采用 Hill 模型、Haeufle 四元素模型、PA-MTM 肌肉模型三种不同模型计算的肌肉力。本文所提出 PA-MTM 骨骼肌模型的肌肉力计算结果大于不考虑羽状角的 Haeufle 四元素骨骼肌模型,且肌肉的羽状角越大,不同模型下的肌肉力计算结果差值越大。根据股骨骨折模型的骨折偏差,规划不同复位路径,进行骨折复位仿真分析,获得最大复位合力为 497.28 N,最大轴向复位力为 472.18 N,同时,通过与文献[19, 21, 30]的复位力分析结果对比,验证了新型骨骼肌模型 PA-MTM 的合理性。本研究可为机器人骨折复位力监控及复位路径择优提供参考。
未来将开展下肢骨肌模型肌肉力及复位力实验测试,进一步验证该模型的准确性。
利益冲突声明:本文全体作者均声明不存在利益冲突。
Funding Statement
国家重点研发计划项目(2017YFB1304202)
National Key R& D Program of China
References
- 1.韩巍, 刘文勇, 王军强, 等 计算机辅助股骨干骨折复位技术研究进展. 北京生物医学工程. 2013;32(1):101–105. doi: 10.3969/j.issn.1002-3208.2013.01.20.. [DOI] [Google Scholar]
- 2.曹延祥, 赵燕鹏, 娄盛涵, 等 计算机辅助股骨干骨折治疗研究进展. 中国数字医学. 2017;12(2):24–27, 33. [Google Scholar]
- 3.孙小刚. 股骨干骨折复位辅助机器人系统研制. 南京: 东南大学, 2016.
- 4.Li Changsheng, Wang Tianmiao, Hu Lei, et al A visual servo-based teleoperation robot system for closed diaphyseal fracture reduction. Proc Inst Mech Eng H. 2015;229(9):629–637. doi: 10.1177/0954411915595827. [DOI] [PubMed] [Google Scholar]
- 5.Abedinnasab M H, Farahmand F, Gallardo-Alvarado J The wide-open three-legged parallel robot for long-bone fracture reduction. J Mech Robot. 2017;9(1):015001. doi: 10.1115/1.4035495. [DOI] [Google Scholar]
- 6.Kim W Y, Ko S Y Hands-on robot-assisted facture reduction system guided by a linear guidance constraints controller using a pre-operatively planned goal pose. Int J Med Robot Comput Assist Surg. 2019;15(2):e1967. doi: 10.1002/rcs.1967. [DOI] [PubMed] [Google Scholar]
- 7.Buschbaum J, Fremd R, Pohlemann T, et al Computer-assisted fracture reduction: A new approach for repositioning femoral fractures and planning reduction paths. Int J Comput Assist Radiol Surg. 2015;10(2):149–159. doi: 10.1007/s11548-014-1011-2. [DOI] [PubMed] [Google Scholar]
- 8.Buschbaum J, Fremd R, Pohlemann T, et al Introduction of a computer-based method for automated planning of reduction paths under consideration of simulated muscular forces. Int J Comput Assist Radiol Surg. 2017;12(8):1369–1381. doi: 10.1007/s11548-017-1562-0. [DOI] [PubMed] [Google Scholar]
- 9.耿慧玉. 人体骨骼肌生物力学建模与仿真. 哈尔滨: 哈尔滨理工大学, 2019.
- 10.Hill A V The heat of shortening and the dynamic constants of muscle. Proc Roy Soc B. 1938;126(843):136–195. [Google Scholar]
- 11.Zajac F E Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17(4):359–411. [PubMed] [Google Scholar]
- 12.Günther M, Schmitt S, Wank V High-frequency oscillations as a consequence of neglected serial damping in Hill-type muscle models. Biol Cyber. 2007;97(1):63–79. doi: 10.1007/s00422-007-0160-6. [DOI] [PubMed] [Google Scholar]
- 13.Millard M, Uchida T, Seth A, et al Flexing computational muscle: modeling and simulation of musculotendon dynamics. J Biomech Eng. 2013;135(2):021005. doi: 10.1115/1.4023390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haeufle D F B, Günther M, Bayer A, et al Hill-type muscle model with serial damping and eccentric force-velocity relation. J Biomech. 2014;47(6):1531–1536. doi: 10.1016/j.jbiomech.2014.02.009. [DOI] [PubMed] [Google Scholar]
- 15.Van Soest A J, Bobbert M F The contribution of muscle properties in the control of explosive movements. Biol Cyber. 1993;69(3):195–204. doi: 10.1007/BF00198959. [DOI] [PubMed] [Google Scholar]
- 16.Mörl F, Siebert T, Schmitt S, et al Electro-mechanical delay in Hill-type muscle models. J Mech Med Biol. 2012;12(5):1250085. doi: 10.1142/S0219519412500856. [DOI] [Google Scholar]
- 17.刘瑞东, 李庆 激活后增强效应的生理机制、影响因素与应用策略. 成都体育学院学报. 2017;43(6):58–64. [Google Scholar]
- 18.Folland J P, Williams A G Morphological and neurological contributions to increased strength. Sports Med. 2007;37(2):145–168. doi: 10.2165/00007256-200737020-00004. [DOI] [PubMed] [Google Scholar]
- 19.Graham A E, Xie S Q, Aw K C, et al Bone-muscle interaction of the fractured femur. Orthop Res. 2008;26(8):1159–1165. doi: 10.1002/jor.20611. [DOI] [PubMed] [Google Scholar]
- 20.Joung S, Shikh S S, Kobayashi E, et al. Musculoskeletal model of hip fracture for safety assurance of reduction path in robot-assisted fracture reduction// 5th Kuala Lumpur International Conference on Biomedical Engineering. Berlin: Heidelberg, 2011: 116-120.
- 21.Li Changsheng, Wang Tianmiao, Hu Lei, et al Robot-musculoskeletal dynamic biomechanical model in robot-assisted diaphyseal fracture reduction. Biomed Mater Eng. 2015;26(S1):365–374. doi: 10.3233/BME-151324. [DOI] [PubMed] [Google Scholar]
- 22.朱庆. 柔性驱动股骨干骨折复位机器人系统研究. 南京: 东南大学, 2018.
- 23.安贤俊. 人体肌肉组织的生物力学建模及其有限元仿真. 哈尔滨: 哈尔滨理工大学, 2015.
- 24.Warwic R, Willems P L. Gray's Anatomy. 35th Ed. Edinburgh: Longman Group Ltd, 1973.
- 25.李永胜, 陈维毅 单羽状骨骼肌平面模型的修正. 医用生物力学. 2007;22(3):277–281. [Google Scholar]
- 26.Arnold E M, Ward S R, Lieber R L, et al A model of the lower limb for analysis of human movement. Ann Biomed Eng. 2010;38(2):269–279. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.高士濂. 实用解剖学图谱下肢分册. 上海: 上海科学技术出版社, 2004: 63-67.
- 28.单大卯. 人体下肢肌肉功能模型及其应用的研究. 上海: 上海体育学院, 2003.
- 29.程利亚. 骨创伤复位机器人设计及复位路径规划. 上海: 上海大学, 2019.
- 30.Zhu Qing, Liang Bin, Wang Xingsong, et al Force–torque intraoperative measurements for femoral shaft fracture reduction. Comput Assist Surg. 2016;21(sup1):37–44. doi: 10.1080/24699322.2016.1240311. [DOI] [Google Scholar]













