Skip to main content
NCBI home page
Sheng Wu Yi Xue Gong Cheng Xue Za Zhi = Journal of Biomedical Engineering logoLink to Sheng Wu Yi Xue Gong Cheng Xue Za Zhi = Journal of Biomedical Engineering
. 2020 Feb;37(1):87–95. [Article in Chinese] doi: 10.7507/1001-5515.201903019

大鼠牙槽骨理想模型的流固耦合数值模拟研究

Fluid-solid coupling numerical simulation on ideal porous structure of rat alveolar bone

睿 罗 1, 振达 赵 2, 慧杰 冷 2, 波 霍 1,*
PMCID: PMC9927654  PMID: 32096381

Abstract

载荷作用下松质骨孔隙中的液体流动是刺激骨组织细胞产生生物学响应并调控骨重建的主要因素。因此，阐明牙槽骨内孔隙结构中的液体流动情况对于深入理解力学作用在牙槽骨内的传导过程以及牙齿发育、正畸牙移动等细胞水平的调控机制具有重要意义。此工作首先进行了大鼠牙齿正畸的动物实验，并基于微计算机断层扫描（micro-CT）图像构建了牙齿-牙周韧带-牙槽骨有限元模型，分析了咬合力或正畸力作用下牙槽骨中的应变状态；进而构建了理想模型，应用流固耦合数值模拟方法，分析了动态咬合力加载下无正畸加载、正畸拉伸加载、正畸压缩加载三种情况下骨内液体的流动情况。模拟结果表明，动态咬合力作用下，沿咬合方向排列的骨小梁表面流体剪应力水平高于非咬合方向排列的骨小梁，正畸力对骨内液体的流动没有影响。上述结果说明，临床上通过调整牙齿咬合面形状等方法改变咬合力的方向，会在牙槽骨表面引起不同水平的流体剪应力，进而刺激骨组织表面的细胞产生响应，最终调控牙槽骨的结构重建。

Keywords: 牙槽骨, 骨小梁, 流固耦合, 孔隙结构, 流体剪应力

引言

牙槽骨包括固有牙槽骨、密质骨及松质骨等几部分，其中松质骨位于密质骨和固有牙槽骨之间，由骨小梁和骨髓组成。牙槽骨的结构变化非常活跃，与牙齿发育、乳牙替换、恒牙移动等生理过程密切相关。这种结构的重建过程可由牙齿受到的载荷（如咬合力或正畸力）调控，主要表现为骨小梁的排列方向与咬合力相适应，以最有效的排列方式来抵抗外加载荷。实际上，骨的结构重建主要由成骨细胞主导的骨形成过程及破骨细胞主导的骨吸收过程组成。在咬合力或正畸力的作用下，骨基质的变形会引起附着于其上的细胞产生相应的应变；松质骨内孔隙体积的改变也会引起孔隙内液体的流动，从而在细胞表面产生流体剪应力[1]。许多研究已经证明，相对于基质的变形，流体刺激会在骨组织细胞中引起更为显著的生物学响应[2-4]。因此，阐明牙槽骨内孔隙结构中的液体流动情况对于深入理解力学作用在牙槽骨内的传导过程以及牙齿的发育形成、正畸牙移动等细胞水平的调控机制具有重要意义。

受限于在体测量实验技术的缺乏，数值模拟是研究骨内液体流动空间分布和动态变化的有效方法。2012 年有学者构建了包含骨小梁孔隙结构的理想松质骨模型，使用流固耦合数值模拟方法计算了其中的液体流动、压力和流体剪应力等参数的分布[5]。2015 年的另一项研究使用微计算机断层扫描技术（micro computed tomography，micro-CT）扫描猪的股骨，通过三维重建得到其真实的松质骨几何模型，也应用流固耦合数值模拟方法研究了骨小梁孔隙结构中的流体剪应力和压力分布[6]。但目前还没有关于牙槽骨内液体流动情况的数值模拟研究，因此咬合力或正畸力作用下牙槽骨内骨小梁表面流体剪应力的大小和分布尚不清楚，从而难于判断牙槽骨中细胞所处的力学微环境。

本文针对大鼠的正畸牙移动模型，利用有限元方法分析了牙槽骨中的应变分布，进而构建了理想模型，应用流固耦合数值模拟方法，得到了动态咬合力加载下，无正畸力、正畸压缩和正畸拉伸三种加载情况下骨内液体的流动情况，对比分析了咬合力方向、非咬合力方向骨小梁表面流体剪应力的差异，以及拉伸、压缩对骨小梁表面流体剪应力的影响。

1. 材料和方法

1.1. 动物实验

本实验从北京大学医学部实验动物科学部购置一只 6～8 周龄的 SPF 级雌性 SD 大鼠［许可证号：SCXK（京）2016-0010］。将大鼠麻醉后置于手术台上，以上颌 2 颗切牙作为支抗牙，使用镍钛拉簧对其上颌右侧第一磨牙施加 0.8 N 正畸力 20 天（见图 1a）。镍钛拉簧的一端通过直径为 0.2 mm 的结扎丝固定于第一磨牙与第二磨牙之间，另一端连接测力计并测定正畸力，之后将其固定在两颗切牙颈部 0.5～1.0 mm 的固位槽中。进而将光固化树脂均匀覆盖于切牙表面和固位沟处，并用 LED 光固化灯固化树脂 40 s。将大鼠下颌切牙磨短并用树脂覆盖断面处，以防止其磨断口腔内的结扎丝。在正畸治疗期间，每日检查弹簧是否正常。大鼠在接受正畸治疗前使用 Co60灭菌饲料，正畸治疗后，每天被喂食三次动物奶粉。实验过程中所有操作均得到北京大学实验动物伦理委员会的批准，并且符合《实验动物护理和使用指南》的要求。

图 1.

Finite element analysis on alveolar bone

牙齿-牙周韧带-牙槽骨有限元模型的建立

a. orthodontic experiment. b. micro-CT image of alveolar bone, the dash lines indicate the displacement transduced on alveolar bone. Finite element model of tooth-periodontal ligament-alveolar bone: c. buccal view; d. distal view. Strain distribution of alveolar bone: e. occlusal loading; f. orthodontic loading

a. 大鼠正畸实验。b. 牙槽骨 micro-CT 照片，虚线表示牙槽骨受到的位移载荷。牙齿-牙周韧带-牙槽骨有限元模型：c. 颊侧视角；d. 远中视角。牙槽骨的 von Mises 应变分布：e. 咬合力加载，f. 正畸力加载

图 1

Open in a new tab

1.2. 牙齿-牙周韧带-牙槽骨的有限元模型

将大鼠处死后取出其上颌骨，经 micro-CT 扫描后导入 Mimics 软件对其右侧第一磨牙处牙周组织进行三维重建（见图 1b）。如图 1c、d 所示，将重建后的牙齿-牙周韧带-牙槽骨结构导入 ANSYS 中进行有限元计算。牙齿、牙周韧带、牙槽骨均采用均匀各向同性线弹性材料，弹性模量分别为 20 000、0.7、2 000 MPa，泊松比分别为 0.3、0.45、0.3[7-8]。在牙槽骨的底部及远中面施加固定约束，不同组织间设定为绑定接触。模拟大鼠咬合时，对牙齿咬合面施加 4 N 咬合力[9]；模拟正畸实验时，对牙齿远中面施加大小为 0.8 N 的线载荷。图 1e、f 分别为该模型在 4 N 咬合力或 0.8 N 正畸力加载下牙槽骨的应变分布。咬合、正畸加载下牙槽骨前 1% 应变的平均值分别为 650、167 με。此数据将作为理想模型咬合、正畸位移加载的幅值。

1.3. 理想模型几何模型的建立

松质骨是由大量骨小梁连接而成的多孔网状结构，骨小梁的排列方向主要沿咬合方向。骨小梁的直径在 40～120 μm 之间[10-11]，骨小梁间隙在 150～700 μm 之间[10, 12-14]。本研究以大鼠上颌骨右侧第一磨牙近中牙根远中附近松质骨为基础，构建了由一定数目骨小梁组成的总体尺寸为 2 160 μm × 2 160 μm × 2 160 μm 的理想模型，见图 2a。该理想模型包含 7 × 7 根沿 Z 方向（咬合方向）的骨小梁，4 × 7 根沿X、Y方向（非咬合方向）的骨小梁。骨小梁直径为 80 μm，在X、Y方向上间隔为 280 μm、Z方向上间隔 560 μm。该理想模型位于充满骨髓液的大小为 2 660 μm × 2 660 μm × 2 660 μm 的液体域中。

图 2.

Establishment of ideal model of alveolar bone and boundary condition

牙槽骨理想模型

a. boundary condition; b. displacement loading along occlusal direction; c. displacement loading along orthodontic direction

a. 边界条件；b. 咬合位移加载曲线；c. 正畸位移加载曲线

图 2

Open in a new tab

1.4. 理想模型边界条件及材料参数

本文中松质骨与骨髓液的材料参数均参考前人的文献所得。松质骨骨小梁采用均匀各向同性线弹性材料模型，弹性模量为 3 GPa，泊松比为 0.3[7, 15]。骨髓液的粘度系数会随应变率的升高而降低，但有研究表明在低应变率下，使用 85 Pa∙s 的常值粘度系数或实验获取的随应变率变化的粘度系数进行计算，得到的流体剪应力分布无显著差异。因此本研究将骨髓液假设为密度 1 g/cm3、粘度系数 85 Pa∙s 的牛顿流体[6, 16]。本研究中骨髓液会在松质骨变形的驱动下产生流动，反之液体流动也会使骨发生相应变形，属于双向流固耦合问题，即在流场与固体结构中分别求解，并在每个时间步长内耦合迭代，直至流体与固体边界处的解收敛后再继续推进。理想模型的边界条件如图 2a 所示。咬合过程中，该处松质骨的上表面受到牙齿传来的咬合力，产生沿咬合方向的正弦时变位移，在其底部施加固定约束。考虑正畸加载时，临床上一般认为牙齿一侧的牙槽骨受压力，发生骨吸收，其对侧受拉力，发生骨形成。但是已经有研究表明正畸力作用下牙槽骨不会出现明显的拉力侧或压力侧，牙齿远中侧的牙槽骨既会受到拉力也会受到压力[17]，因此在固体域的一个侧面施加拉伸或压缩位移载荷。

牙槽骨在咬合力或正畸力作用下最大应变分别为 650 με 和 167 με，该应变值被假设为理想模型中骨小梁在咬合力或正畸力作用下的最大应变，将其乘以骨小梁长度即可求得最大变形量分别为 1.4 μm 和 0.36 μm，以此作为理想模型咬合、正畸位移加载的幅值。咬合位移加载曲线如图 2b 所示，频率为 2 Hz，频率参考大鼠咬合的频率[18-19]。正畸压缩位移加载曲线如图 2c 所示，选择在 0.24 s 内将正畸位移加至 0.36 μm，之后维持恒定位移加载至 1 s。为避免载荷加载速度突变，在 0.24 s 附近对位移加载速度进行了平滑处理。考虑到被分割区域的松质骨应与其他骨小梁相连的实际情况，在固体域的其余侧面施加弹性系数为 3 GPa 的弹性基础约束，以模拟其周围区域对中心区域的力学作用。流体域的六个面为允许流体自由进出的开边界。该模型在 COMSOL 软件中以四面体单元进行网格划分，总计 1 412 222 单元。为避免边界影响，分析数据时选取固体域内部的 2 × 5 × 5 根骨小梁作为研究对象。

1.5. 模拟数据的统计分析

本文模拟计算结果的数据显示为平均值 ± 标准差，并对不同组数据进行了单因素方差分析，P < 0.05 时认为差异有统计学意义。

2. 结果

2.1. 咬合加载对牙槽骨内不同方向骨小梁表面流体剪应力的影响

图 3a 显示了咬合位移加载下 1/4 周期时刻（t = 0.875 s）骨小梁表面流体剪应力分布，图 3b 为相应时刻液体流速及骨小梁 von Mises 应力分布图。从上述结果可以看出，沿咬合方向的骨小梁表面有较大的流体剪应力。在咬合加载下，牙槽骨内高水平应力集中在沿咬合方向的骨小梁及其与非咬合方向骨小梁的连接处；越靠近加载端液体流速越大。为了更加直观地观察松质骨内部的液体流动，图 3c、d 展示了沿咬合方向 1/3 位置处截面内的流体剪应力及流速分布。孔隙内的固液交界面上具有较高的流体剪应力与流速。外层液体相较于内层具有更高的流体剪应力。

图 3.

Fluid flow within alveolar bone under occlusal loading at t = 0.875 s

咬合加载下牙槽骨内液体流动（t = 0.875 s）

a. distribution of fluid shear stress on trabecular surface. b. von Mises stress and streamline. Fluid flow within the section at 1/3 position along occlusal direction（axis Z）: c. fluid shear stress; d. fluid velocity

a. 骨小梁表面流体剪应力分布。b. 松质骨应力与流线图。咬合方向（Z轴）1/3 位置处液体流动：c. 流体剪应力分布；d. 流速分布

图 3

Open in a new tab

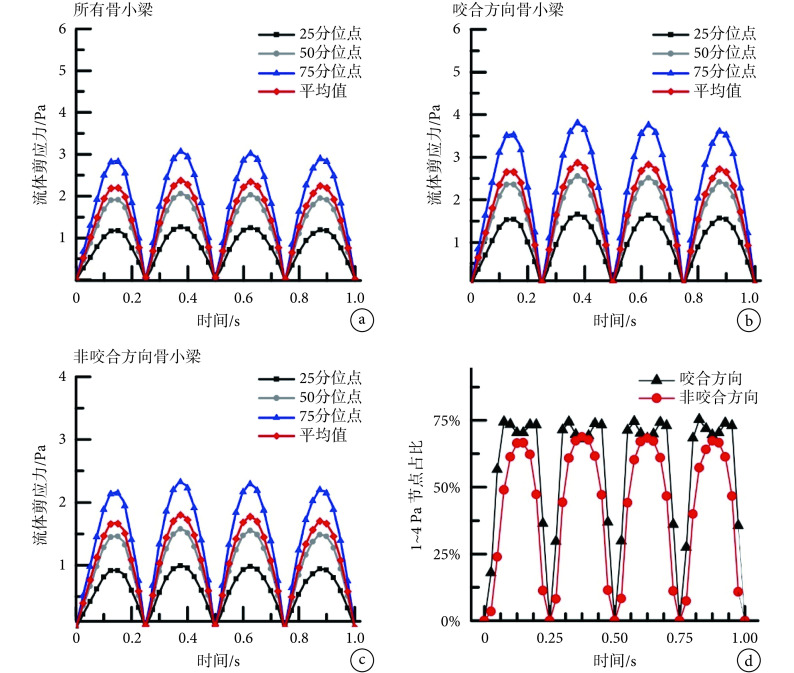
图 4a 为骨小梁表面流体剪应力按照大小顺序排列时四分位点及平均值随时间的变化。此结果表明，骨小梁表面流体剪应力在每个加载周期的 1/4 时刻附近达到最大值，其均值最高为 2.4 Pa，应该注意的是此时间点处咬合位移加载速度最大。图 4b、c 分别为咬合方向排列骨小梁（Z方向）及非咬合排列骨小梁（X、Y方向）表面流体剪应力不同分位点及平均值随时间的变化。咬合方向排列骨小梁表面流体剪应力的 25、50、75 分位点及均值都高于非咬合方向排列的骨小梁。体外骨组织细胞培养实验已经证实，当施加的流体剪应力在 1～4 Pa 时，成骨细胞将会产生力刺激响应[20]。因此，在图 4d 中对咬合排列及非咬合排列骨小梁表面流体剪应力 1～4 Pa 的节点数占比进行了统计比较，可以看出沿咬合方向排列骨小梁表面约有 70% 的区域在超过一半周期的时间内受到利于成骨细胞响应的剪应力，而非咬合方向排列骨小梁只有 40% 左右。以上结果表明，咬合过程中沿咬合方向排列的骨小梁表面受到的流体刺激要显著高于非咬合方向骨小梁，推测力学作用下此处成骨细胞会被激活，从而利于启动骨形成过程。

图 4.

Fluid shear stress on trabecular surface under occlusal loading

咬合加载下骨小梁表面流体剪应力

The quartile and average values of fluid shear stress on trabecular surface vs. time: a. total trabeculae; b. the trabeculae along occlusal direction; c. the trabeculae perpendicular to occlusal direction. d. the proportion of the nodes with fluid shear stress in 1−4 Pa over loading duration

骨小梁表面流体剪应力四分位点及平均值随时间的变化：a. 所有骨小梁；b. 咬合方向排列骨小梁；c. 非咬合方向排列骨小梁。d. 流体剪应力 1～4 Pa 节点占总结点百分比

图 4

Open in a new tab

2.2. 正畸加载对牙槽骨骨小梁表面流体剪应力的影响

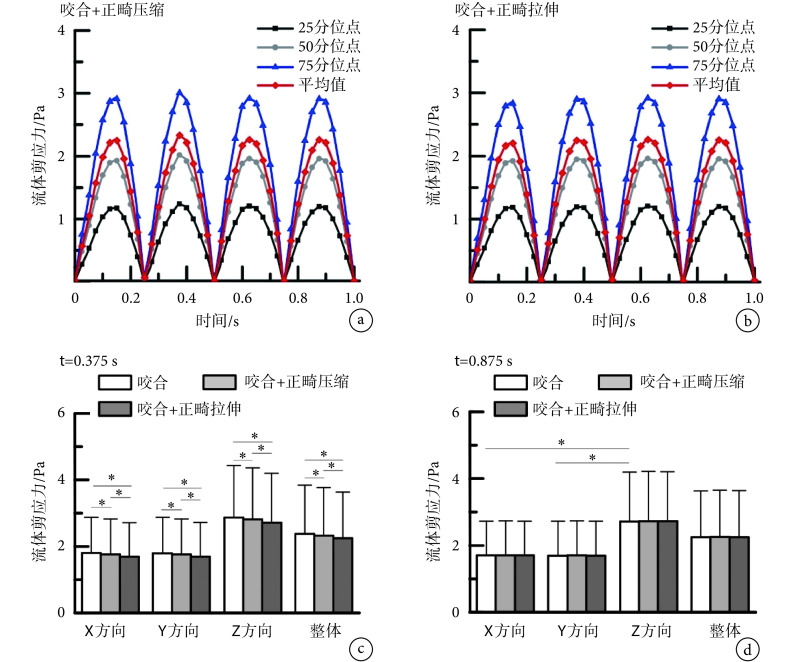
图 5a、c 分别为咬合与正畸压缩、咬合与正畸拉伸加载下 1/4 周期时刻（t = 0.875 s）骨小梁表面流体剪应力分布，图 5b、d 为相应时刻液体流速及骨小梁 von Mises 应力分布图。由上述图可以看出，正畸压缩加载和正畸拉伸加载下骨小梁表面流速分布、流体剪应力分布在t = 0.875 s 与咬合加载下基本一致，但是沿正畸方向排列的骨小梁固体应力更大。正畸压缩和正畸拉伸加载下，骨内液体的流动仅在压缩或者拉伸恒定前有区别。如图 5e、f 所示，加载过程中，液体主要沿动态加载的合力方向流动。图 6a、b 为正畸压缩、拉伸加载下骨小梁表面流体剪应力四分位点及平均值随时间的变化。在t = 0.375 s，即正畸位移加载恒定后的第一个周期的幅值处，正畸压缩加载下骨小梁表面流体剪应力的 25、50 分位点及平均值稍大于正畸拉伸加载下骨小梁，略小于咬合加载下骨小梁。但是在两个周期后，拉伸或是压缩状态下的骨小梁表面流体剪应力都与咬合加载下骨小梁表面流体剪应力没有差异。在图 6c、d 中，对t = 0.375 s、t = 0.875 s 两个时刻咬合、咬合与正畸压缩、咬合与正畸拉伸加载条件下骨小梁表面的最大流体剪应力均值进行了比较。t = 0.375 s 时，咬合加载下骨小梁表面流体剪应力均值略大于正畸压缩加载下骨小梁，而正畸拉伸加载下骨小梁表面流体剪应力最低。然而在t = 0.875 s 时，咬合与正畸共同作用下沿X、Y、Z方向排列的骨小梁表面流体剪应力都与无正畸作用时没有显著差异。该结果表明，正畸力施加在骨小梁上的瞬间会影响骨小梁表面的流体剪应力，但是在一段时间后，无论是拉伸还是压缩，对骨小梁表面的流体剪应力都几乎没有影响。

图 5.

Fluid flow within alveolar bone under orthodontic loading

正畸加载下牙槽骨内液体流动

Dstribution of fluid shear stress on trabecular surface at t = 0.875 s: a. orthodontic compression loading; c. orthodontic tension loading. Distribution of von Mises stress and streamline at t = 0.875 s: b. orthodontic compression loading; d. orthodontic tension loading. Distribution of von Mises stress and streamline at t = 0.125 s: e. orthodontic compression loading; f. orthodontic tension loading

t = 0.875 s 时骨小梁表面流体剪应力分布：a. 正畸压缩加载；c. 正畸拉伸加载。t = 0.875 s 时松质骨应力与流线图：b. 正畸压缩加载；d. 正畸拉伸加载。t = 0.125 s 时松质骨应力与流线图：e. 正畸压缩加载；f. 正畸拉伸加载

图 5

Open in a new tab

图 6.

Fluid flow within alveolar bone under different loading conditions

不同加载条件下牙槽骨内液体流动

Quartile and average values of fluid shear stress on trabecular surface vs time: a. orthodontic compression loading; b. orthodontic tension loading. Comparison of maximum fluid shear stress on trabecular surface: c. t = 0.375 s; d. t = 0.875 s. *, P < 0.05

骨小梁表面流体剪应力四分位点及平均值随时间的变化：a. 正畸压缩加载；b. 正畸拉伸加载。骨小梁表面的最大流体剪应力均值比较：c. t = 0.375 s；d. t = 0.875 s。*，P < 0.05

图 6

Open in a new tab

3. 讨论

松质骨是骨重建最为活跃的区域，目前越来越受到骨生物力学领域研究人员的关注，但较少有研究关注牙槽骨中的液体流动问题。牙槽骨的孔隙结构较为复杂，受限于计算量的限制，很难对整体牙槽骨真实模型进行计算。因此本研究使用多尺度分析的方法，首先建立牙齿-牙周韧带-牙槽骨的有限元模型，得到咬合或正畸加载下牙槽骨的应变，将其作为理想模型的边界条件。其次以牙槽骨孔隙结构的几何参数为基础，构建了由不同排列方向骨小梁组成的理想模型。该理想模型相较于真实模型更利于分析不同加载条件和骨小梁排列方向对其表面流体剪应力的影响。相较于使用流体动力学模型对骨内液体流动进行计算，本研究使用的流固耦合数值模拟方法能更为准确地反映外力作用下骨组织变形导致的液体流动。

大量研究已经表明，骨组织会优化其结构以适应所处的力学载荷环境。在缺乏力学刺激的情况下会发生骨矿丢失，而运动和力学刺激会促进骨内矿物含量增加。松质骨中骨小梁主要沿主应力方向生长，从而以最有效的结构形式承受外部载荷。流体剪应力作用下，骨组织细胞会发生钙响应[21- 22]，从而参与调控骨形成[23-24]。除此之外，骨细胞受到液体刺激还会抑制破骨细胞的形成[25-26]。本研究结果显示，咬合过程中沿咬合方向排列的骨小梁表面有更多的区域在超过一半的时间内受到 1～4 Pa 的流体剪应力，推测其表面的成骨细胞更容易发生生物学响应，从而促进咬合方向骨小梁的形成，这也在一定程度上解释了牙槽骨内骨小梁主要沿咬合方向排列的原因。

本研究结果表明，正畸力施加在骨小梁上的瞬间会影响骨小梁表面的流体剪应力，这可能是由于压缩和拉伸完全加载前，骨内液体流动的不同导致的。但是在正畸加载保持恒定一段时间后，无论是拉伸还是压缩加载，对骨小梁表面的流体剪应力都没有影响。骨小梁表面的流体剪应力只会受到动态加载的影响，而恒定载荷对其没有影响。这说明正畸过程中牙槽骨发生的骨重建与其内部孔隙的液体流动无关。牙周韧带中混杂着不同种类的细胞，如成纤维细胞、成骨细胞以及具有多种分化潜能的间充质干细胞等，而力学刺激会对间充质干细胞的分化产生影响[27-28]。除此之外成纤维细胞也可以感受和响应力学刺激，通过分泌骨保护素和破骨细胞分化因子等参与调控牙槽骨吸收，以影响破骨前体细胞的破骨向分化[29]。因此，正畸力作用下牙周韧带的调控作用才是牙槽骨结构重建行为的主要原因。

本文以大鼠真实松质骨孔隙结构为基础，构建了理想模型，应用流固耦合数值模拟方法，得到了动态咬合力加载下，无正畸加载、正畸压缩加载和正畸拉伸加载三种情况下骨内液体的流动情况。模拟结果表明，沿咬合方向排列的骨小梁表面流体剪应力水平高于非咬合方向排列的骨小梁，正畸力对骨内液体的流动几乎没有影响。考虑到临床上有时会通过调整牙齿咬合面形状等方法改变咬合力的方向，本文结果表明这会在牙槽骨表面引起不同水平的流体剪应力，进而刺激骨组织表面的细胞产生响应，最终调控牙槽骨的结构重建。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

科技部重点研发计划（2018YFF0300800）；国家自然科学基金（11572043）

References

  • 1.Fritton S P, Weinbaum S Fluid and solute transport in bone: Flow-Induced mechanotransduction. Annu Rev Fluid Mech. 2009;41:347–374. doi: 10.1146/annurev.fluid.010908.165136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Smalt R, Mitchell F T, Howard R L, et al Induction of NO and prostaglandin E2 in osteoblasts by wall-shear stress but not mechanical strain. Am J Physiol. 1997;273(4 Pt 1):E751–E758. doi: 10.1152/ajpendo.1997.273.4.E751. [DOI] [PubMed] [Google Scholar]
  • 3.Owan I, Burr D B, Turner C H, et al Mechanotransduction in bone: osteoblasts are more responsive to fluid forces than mechanical strain. Am J Physiol. 1997;273(3 Pt 1):C810–C815. doi: 10.1152/ajpcell.1997.273.3.C810. [DOI] [PubMed] [Google Scholar]
  • 4.You J, Yellowley C E, Donahue H J, et al Substrate deformation levels associated with routine physical activity are less stimulatory to bone cells relative to loading-induced oscillatory fluid flow. J Biomech Eng. 2000;122(4):387–393. doi: 10.1115/1.1287161. [DOI] [PubMed] [Google Scholar]
  • 5.Birmingham E, Grogan J A, Niebur G L, et al Computational modelling of the mechanics of trabecular bone and marrow using fluid structure interaction techniques. Ann Biomed Eng. 2013;41(4):814–826. doi: 10.1007/s10439-012-0714-1. [DOI] [PubMed] [Google Scholar]
  • 6.Metzger T A, Kreipke T C, Vaughan T J, et al The in situ mechanics of trabecular bone marrow: the potential for mechanobiological response. J Biomech Eng. 2015;137(1):011006. doi: 10.1115/1.4028985. [DOI] [PubMed] [Google Scholar]
  • 7.Kawarizadeh A, Bourauel C, Jager A Experimental and numerical determination of initial tooth mobility and material properties of the periodontal ligament in rat molar specimens. Eur J Orthod. 2003;25(6):569–578. doi: 10.1093/ejo/25.6.569. [DOI] [PubMed] [Google Scholar]
  • 8.Gonzales C, Hotokezaka H, Arai Y A, et al An in vivo 3D Micro-CT evaluation of tooth movement after the application of different force magnitudes in rat molar. Angle Orthodontist. 2009;79(4):703–714. doi: 10.2319/071308-366.1. [DOI] [PubMed] [Google Scholar]
  • 9.Ro J Y Bite force measurement in awake rats: a behavioral model for persistent orofacial muscle pain and hyperalgesia. J Orofac Pain. 2005;19(2):159–167. [PubMed] [Google Scholar]
  • 10.Hassumi J S, Mulinari-Santos G, da Silva Fabris A L, et al Alveolar bone healing in rats: micro-CT, immunohistochemical and molecular analysis. J Appl Oral Sci. 2018;26:e20170326. doi: 10.1590/1678-7757-2017-0326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.茹楠, 庄丽, 白玉兴 牙齿移动过程中牙槽骨显微结构动态变化的微型CT研究. 中华口腔医学杂志. 2011;46(4):237–240. doi: 10.3760/cma.j.issn.1002-0098.2011.04.012. [DOI] [PubMed] [Google Scholar]
  • 12.Alikhani M, Alikhani M, Alansari S, et al Therapeutic effect of localized vibration on alveolar bone of osteoporotic rats. PLoS One. 2019;14(1):e0211004. doi: 10.1371/journal.pone.0211004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.庄丽, 屈克勤, 周玉玲, 等 大鼠颌骨骨皮质切开术后骨小梁三维结构的改变. 中华口腔正畸学杂志. 2016;23(2):77–81. doi: 10.3760/cma.j.issn.1674-5760.2016.02.004. [DOI] [Google Scholar]
  • 14.董晨, 于玲敏, 金光春 显微CT下下颌骨松质骨结构的解剖学评价. 广东医学. 2017;38(z2):20–22. doi: 10.3969/j.issn.1001-9448.2017.z2.008. [DOI] [Google Scholar]
  • 15.Abe H, Hayashi K, Sato M. Data book on mechanical properties of living cells, tissues, and organs. Tokyo: Springer, 1996.
  • 16.Metzger T A, Shudick J M, Seekell R, et al Rheological behavior of fresh bone marrow and the effects of storage. J Mech Behav Biomed Mater. 2014;40:307–313. doi: 10.1016/j.jmbbm.2014.09.008. [DOI] [PubMed] [Google Scholar]
  • 17.Cattaneo P M, Dalstra M, Melsen B Strains in periodontal ligament and alveolar bone associated with orthodontic tooth movement analyzed by finite element. Orthod Craniofac Res. 2009;12(2):120–128. doi: 10.1111/j.1601-6343.2009.01445.x. [DOI] [PubMed] [Google Scholar]
  • 18.Khan J, Benoliel R, Herzberg U, et al Bite force and pattern measurements for dental pain assessment in the rat. Neurosci Lett. 2008;447(2/3):175–178. doi: 10.1016/j.neulet.2008.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Kim S H, Son C N, Lee H J, et al Infliximab partially alleviates the bite force reduction in a mouse model of temporomandibular joint pain. J Korean Med Sci. 2015;30(5):552–558. doi: 10.3346/jkms.2015.30.5.552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Lu X L, Huo B, Chiang V, et al Osteocytic network is more responsive in calcium signaling than osteoblastic network under fluid flow. J Bone Mineral Res. 2012;27(3):563–574. doi: 10.1002/jbmr.1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Donahue S W, Jacobs C R, Donahue H J Flow-induced calcium oscillations in rat osteoblasts are age, loading frequency, and shear stress dependent. Am J Physiol Cell Physiol. 2001;281(5):C1635–C1641. doi: 10.1152/ajpcell.2001.281.5.C1635. [DOI] [PubMed] [Google Scholar]
  • 22.Roy B, Das T, Mishra D, et al Oscillatory shear stress induced calcium flickers in osteoblast cells. Integr Biol (Camb) 2014;6(3):289–299. doi: 10.1039/c3ib40174j. [DOI] [PubMed] [Google Scholar]
  • 23.Chen N X, Ryder K D, Pavalko F M, et al Ca2+ regulates fluid shear-induced cytoskeletal reorganization and gene expression in osteoblasts . Am J Physiol Cell Physiol. 2000;278(5):C989–C997. doi: 10.1152/ajpcell.2000.278.5.C989. [DOI] [PubMed] [Google Scholar]
  • 24.Zayzafoon M Calcium/calmodulin signaling controls osteoblast growth and differentiation. J Cell Biochem. 2006;97(1):56–70. doi: 10.1002/jcb.20675. [DOI] [PubMed] [Google Scholar]
  • 25.Kim C H, You L, Yellowley C E, et al Oscillatory fluid flow-induced shear stress decreases osteoclastogenesis through RANKL and OPG signaling. Bone. 2006;39(5):1043–1047. doi: 10.1016/j.bone.2006.05.017. [DOI] [PubMed] [Google Scholar]
  • 26.Tan S D, De Vries T J, Kuijpers-Jagtman A M, et al Osteocytes subjected to fluid flow inhibit osteoclast formation and bone resorption. Bone. 2007;41(5):745–751. doi: 10.1016/j.bone.2007.07.019. [DOI] [PubMed] [Google Scholar]
  • 27.Zhang Chunxiang, Lu Yanqin, Zhang Linkun, et al Influence of different intensities of vibration on proliferation and differentiation of human periodontal ligament stem cells. Arch Med Sci. 2015;11(3):638–646. doi: 10.5114/aoms.2015.52370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Bright R, Hynes K, Gronthos S, et al Periodontal ligament-derived cells for periodontal regeneration in animal models: a systematic review. J Periodontal Res. 2015;50(2):160–172. doi: 10.1111/jre.12205. [DOI] [PubMed] [Google Scholar]
  • 29.Kook S H, Jang Y S, Lee J C Human periodontal ligament fibroblasts stimulate osteoclastogenesis in response to compression force through TNF-alpha-mediated activation of CD4+T cells. J Cell Biochem. 2011;112(10):2891–2901. doi: 10.1002/jcb.23205. [DOI] [PubMed] [Google Scholar]

Articles from Sheng Wu Yi Xue Gong Cheng Xue Za Zhi = Journal of Biomedical Engineering are provided here courtesy of West China Hospital of Sichuan University

RESOURCES