认知负载状态下的精神分裂症患者脑电图特异性研究

Abstract

认知功能损害是精神分裂症的三大原发症状之一，在疾病早期发现和高危人群风险预警等方面具有重要价值。为了研究精神分裂症患者在认知负载状态下的脑电图特异性，本试验收集 17 例精神分裂症患者和 19 例健康受试者的脑电信号作为对照，基于小波变换提取各频段信号，计算非线性动力学及脑功能网络属性等特征，并利用机器学习算法将两类人群进行自动分类分析。试验结果表明，两组受试者在认知负载状态下，Fp1 和 Fp2 导联在 α、β、θ、γ 这 4 个频带的关联维数和样本熵的差异均具有统计学意义，提示大脑额叶功能损伤是精神分裂症认知功能损害的重要原因。进一步基于机器学习的自动分类分析结果表明，将非线性动力学与脑功能网络属性相结合作为分类器的输入特征，所得分类效果最优，其结果显示准确率为 76.77%、敏感度为 72.09%、特异性为 80.36%。本研究结果表明，脑电信号的非线性动力学和脑功能网络属性等特征，或可作为精神分裂症早期筛查和辅助诊断的潜在生物标记物。

引言

精神分裂症是一种常见于临床且病因复杂的重症精神疾病，具有发病早、病程长的特点。临床症状主要分为阴性症状、阳性症状和认知功能损害症状。其中阴性症状（功能减少和缺失）和认知功能损害症状（注意力障碍、工作记忆受损）极易使患者致残^[1]，阳性症状（猜疑、妄想、幻觉等）则增加了疾病复发的可能性。至今，关于精神分裂症疾病的诊断标准、病因和病理生理机制尚未达成一致结论，精神分裂症仍具有很强的疾病异质性，而精神分裂症患者的认知功能损害症状是精神失调的显著表征之一，这种缺陷在疾病的早期进程中便已显现^[2-4]。现已有研究表明，认知功能损害的严重程度可以预测患者社会能力强弱^[5]，也可作为判断精神分裂症治疗效果的指标^[6]，因此对精神分裂症的认知功能损害进行研究具有现实意义。

脑电图（electroencephalogram，EEG）监测具有非损伤性、时间分辨率高、操作简便以及价格便宜等优势，现已广泛应用于精神分裂症认知功能的研究中。随着近年相关信号处理理论的发展以及复杂网络分析技术的兴起，基于自发脑电信号的分析研究逐渐增加，目前已经得出一些结论，如：精神分裂症患者在执行认知任务中，其脑电信号波形中慢波减弱、快波增强^[7]；Leicht 等^[8]的研究表明，认知负载过程会在正常人中诱发高能量 γ 波，但精神分裂症患者的脑电信号中则难以观察到同类信号等。尽管前人研究说明了脑电信号分析在认知功能评估的可行性，但整体研究数量较少，针对目前类似研究尚不全面、结论并未统一的情况，本文将用关联维数、样本熵（sample entropy，SampEn）及脑网络属性特征指标对精神分裂症患者的脑电信号进行分析，前二者分析的是单个独立导联的局部脑电信号，后者分析的是全脑的功能连接情况，故而能获得尽可能多的可量化的脑电信号特征值，既给脑电信号特异性多角度分析提供了条件，又利于后续的自动分类研究。

本文旨在通过计算脑电信号的特征指标，结合机器学习的支持向量机（support vector machine，SVM）分类理论，完成认知负载状态下精神分裂症患者的自动分类研究，从而寻找认知负载状态下精神分裂症患者脑电信号的特异性指标，探索用于临床评估精神分裂症患者认知功能的量化指标，同时也为精神分裂症疾病的早期筛查和辅助诊断提供新的方向。

1. 脑电数据采集与预处理

1.1. 数据入组

本文患者数据来自 2016 年 12 月—2017 年 7 月于广州医科大学附属脑科医院住院的精神分裂症患者。

入组标准：① 符合美国《精神疾病诊断与统计手册》（diagnostic and statistical manual of mental disorders，DSM-IV-TR）中精神分裂症的诊断标准，且病程 ≥ 2 年；② 阳性与阴性症状量表（positive and negative syndrome scale，PANSS）评分近 4 周波动在 20% 以内，临床疗效总评量表（clinical global impression，CGI）评分 ≤ 4 分；③ 患者最多接受两种抗精神病药治疗，且所有精神科类药物种类稳定达 4 周，近 4 周没有增加药物剂量；④ 同意参与本研究且签署书面知情同意书。

排除标准：① 肝、肾、心、脑等器质性病变；② 听力障碍；③ 视力障碍；④ 符合除精神分裂症外其它 DSM-IV-TR 轴 I 诊断，如重度抑郁、双向情感障碍等。

同时期，通过网络招募健康志愿者人群，需满足无精神疾病史，且不符合 DSM-IV-TR 任何精神疾病的诊断，此外还需满足无精神疾病家族史的要求，所有受试者均同意参与本研究并签署书面知情同意书。

最终，精神分裂症患者组纳入 17 人，其中男性 10 人，女性 7 人，年龄平均（34.53 ± 7.52）岁，受教育程度（11.00 ± 2.46）年，均为右利手；作为对照的健康组纳入 19 人，其中男性 5 人，女性 14 人，年龄平均（27.95 ± 7.13）岁，受教育程度（12.58 ± 2.32）年，均为右利手。两组在性别、教育年限方面的差异不具有统计学意义（P > 0.05），但患者组的年龄明显高于健康组（ P < 0.001）。

1.2. 认知负载试验设计

传统基于怪球（Oddball）范式的认知负载试验中，通常是将不同频率的纯音作为偏差刺激和标准刺激，但精神分裂症患者对纯音频率的敏感度较低，且这一类音频很难持续地吸引受试者的注意力，一定程度上降低了试验结果的信效度和准确性。

为了确保能够采集到配合度最高的数据，在认知负载试验中，采用录音播报数字的方式代替传统的纯音，偶数为标准刺激，奇数为偏差刺激（即靶刺激）。试验开始前向受试者详细介绍本试验全部流程，让受试者于坐位姿势保持放松状态，并调整电极位置使噪声和伪迹最小。认知试验中，播放录音，共将播报 40 个 0～99 中的数字，其中奇偶数比例为 1：4，每 3 s 播报一个数字，要求受试者在听到数字后首先判断这个数字是否为奇数，并记住全部奇数的个数，在全部 40 个数字播报完毕后，测试人员向受试者询问记住的全部奇数个数并完成记录。

1.3. 数据采集和预处理

本研究利用数字脑电图机（UEA-B，中科新拓，中国）采集了受试者认知状态下的 16 导脑电信号，采样率为 1 000 次/s，以耳极为参考电极，采用 10/20 国际电极放置标准安放电极，利用脑电图机内置的 50 Hz 陷波器去除工频干扰。整个试验流程分为 3 个部分：第一部分是受试者在安静闭眼状态下采集 2 min 的脑电信号；第二部分是受试者按照 1.2 小节所述认知负载流程，采集 3 min 的脑电信号；第三部分是受试者继续在安静闭眼状态下采集 3 min 的脑电信号。采集完成后，专业人员将采集到的数据中含有伪迹的信号剔除，并通过独立成分分析（independent component analysis，ICA）算法去除肌电信号和眨眼信号，使用小波阈值去噪法去除其他噪声，最后利用小波包分解的方式提取脑电信号中 α、β、θ、δ 和 γ 频带并进行后续分析。

1.4. 统计学方法

数据分析采用统计产品与服务解决方案软件 SPSS 22.0（IBM Inc.，美国）统计软件，计量资料以均数 ± 标准差表示，使用双样本 t 检验分析，不存在对照时使用 χ² 检验分析，P < 0.05 视为差异具有统计学意义。

2. 非线性动力学分析

2.1. 特征选择

本研究选取关联维数和样本熵作为非线性动力学特征指标，计算选定合适的时间延迟 τ 和嵌入维数 m，构建充分反映系统特性的相空间。其中，时间延迟 τ 利用自相关系数法求得，嵌入维数 m 利用几何不变量法求得。

时间序列的自相关函数表示的是在距离 τ 的 2 个向量间的互相关联程度，不同的 τ 值则对应不同的函数曲线，当自相关函数值不断下降时则对应得到不同的时间延迟 τ，而当自相关函数值下降为初始值的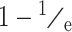（ ）时所对应的时间延迟 τ 为相空间重构的最佳时间延迟，依据上述方法在本研究中最终选定时间延迟 τ = 5。依据此时间延迟 τ 进而确定最佳的嵌入维数 m，最佳嵌入维数 m 的选择过程实际上为观察关联维数饱和程度变化的过程，随着嵌入维数 m 的不断增大，当关联维数数值随嵌入维数 m 的增大不再增大或这种增加程度不明显时，为最佳嵌入维数 m，由此确定嵌入维数 m = 16。

2.2. 特征分析

2.2.1. 关联维数

关联维数描述了混沌运动中自由度信息，在本研究中反映的是脑电信号自身的关联程度，即更复杂的信号具有更高的关联维数，也更接近混沌状态，关联维数 D₂ 的计算公式如式（1）所示，其中相关积分 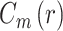的计算公式如式（2）所示。

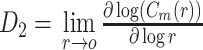1

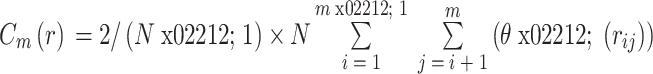2

其中，N 表示脑电信号数据长度，θ 表示单位阶跃函数，r_ij 表示重构相空间中 ij 两点间距离。

2.2.2. 样本熵

样本熵（以符号 SampEn 表示）同样也是一种反应脑电信号复杂度变化的指标，它是基于近似熵理论提出的一种不计数自身匹配的非线性特征，更复杂的信号对应更高的样本熵，也更接近混沌状态。样本熵的计算公式如式（3）所示，其中 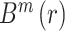的计算公式如式（4）所示。

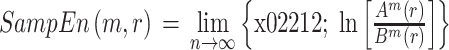3

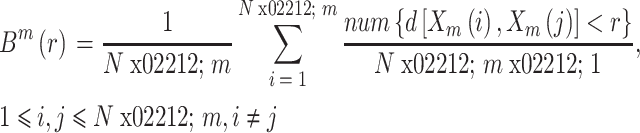4

基于维度为 m 的矢量进行计算可得 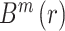，同理，对于维度为 m + 1 的矢量计算，可求出 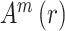。其中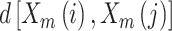， 表示第 i 个矢量与第 j 个矢量间的距离，N 表示脑电信号长度，r 表示相似容限，取值一般为 0.1～0.25，本研究中取 0.2，m 表示矢量维度，一般取值为 2。

3. 脑功能网络的构建

3.1. 脑功能网络的构建及阈值的选取

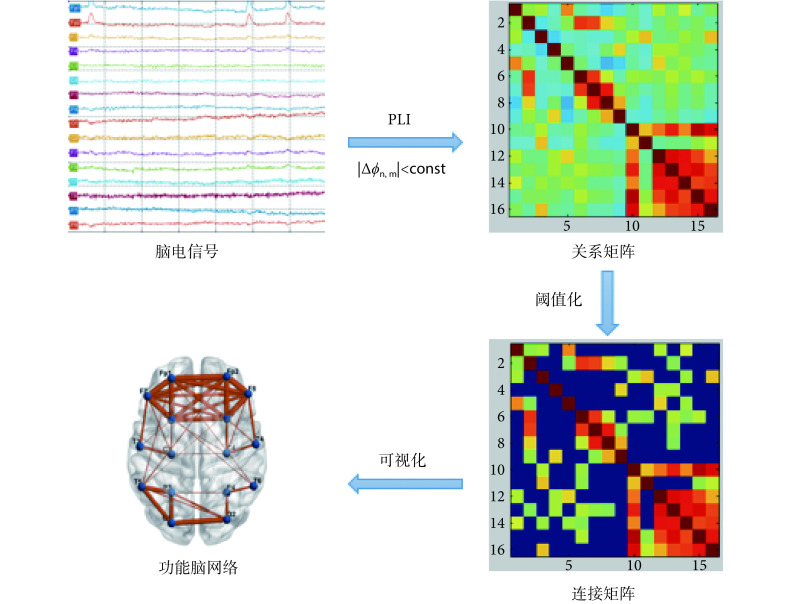
依据脑功能网络构建的一般方法，如图 1 所示，选取 16 导联作为网络的节点，其中每个节点分别表示不同的脑区，并在导联名称上加以区分，如 Fp 表示前额叶，P 表示顶叶，O 表示枕叶等；选取相位滞后指数（phase-lag index，PLI）分别量化脑电信号各通道两两之间的相互作用关系，得到 16 × 16 的关系矩阵，并根据其数值衡量对应脑区之间功能连接强弱；选择合适的阈值并进行阈值化得到该阈值下的连接矩阵，最后根据该连接矩阵构建脑功能网络。

图 1.

Flow chart of functional brain network construction

脑功能网络构建流程图

利用脑网络稀疏度选择最合适的阈值，稀疏度即脑网络中真实存在的连接数量和可能存在的连接数量的比值，它可以使得脑网络不同连接定义的差别最小化，稀疏度和阈值一一对应，故而确定稀疏度即可确定阈值。在较大阈值范围内研究脑网络拓扑属性能够在一定程度上解决单一阈值的局限性。根据厄多斯-瑞利（Erdos-Renyi）随机图模型^[9]，若要保证具有 N 个节点的网络是全连接，其连接稀疏度应该大于 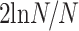，在本研究中 N = 16，则连接稀疏度最小为 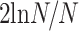= 34%。同时结合小世界属性确定稀疏度上限，随着连接稀疏度的连续增加，对应的小世界属性值持续减小，典型小世界网络中，其小世界属性值 σ 远大于 1，而 σ = 1 时，对应的连接稀疏度为 73%。综上，本研究在 34%～73% 的取值区间以及步长为 1% 的脑网络稀疏度范围内构建不同的脑功能网络。强度通过阈值的连接被保留下来，超过阈值的连接被略去，最后得到的连接边在图 1 中用红线表示出来，至此脑网络便构建完成。

3.2. 各导联间相互作用关系分析

两个系统之间的严格锁相要求它们的相位差保持恒定，但有时仅要求相位差有界即可（界限小于 2π）。PLI 能够反映相位同步性，若 ϕ₁ 和 ϕ₂ 分别是两个时间序列的相位，∆ϕ 是相位差或者相对相位，则 n 相对 m 的相位同步表达如式（5）所示，且 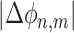小于某个常量，其中 n 和 m 均为整数，表示序列中某一时刻。

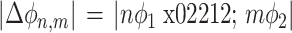5

依据上述表达方式，相位同步可以被用于嘈杂、非稳定和混沌的信号中。在本研究中，限定 m = 1，n = 1。通过基于希尔伯特变换的解析信号得到 2 个信号的瞬时相位。解析信号 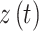由真实的时间序列 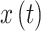计算得到，如式（6）所示，其中 PV 代表柯西主值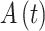， 代表瞬时振幅，ϕ（t）代表瞬时相位。

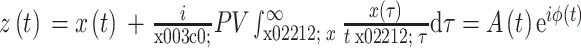6

已有研究表明，PLI 在检测同步性相关的真实变化时，可以得到与同步似然性一致的良好检测性能，但相较于同步似然性，PLI 仅关注信号间耦合关系，受到来自同一来源信号的影响更小^[10]，即不受容积传导效应影响。在计算全局 PLI 基础上，也可以进一步计算平均 PLI 以获得较佳的局部属性。Stam^[11]在研究中，将每个脑半球脑磁图信号分为额叶、颞叶、中央、顶叶和枕叶 5 个区域，随后计算各个区域内部或者任两个区域之间所有信号的平均，并将这种平均后的 PLI 作为一种新方法得到了良好的特异性结果。

3.3. 脑网络特征指标

3.3.1. 最短路径长度

最短路径即节点 i 与节点 j 之间边数最少的一条路径，这条最短路径上所经过边的数量为最短路径长度 l_ij。脑网络的最短路径长度 L 体现的是整体统计特性，以实现信息传递的快捷和系统资源的节省，计算方法如式（7）所示，其中 n 表示所有节点数量。

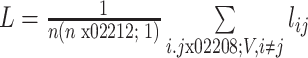7

3.3.2. 聚类系数

节点 i 的聚类系数 C_i 定义为与节点 i 有 k 条边相连的节点之间实际存在的连接边数 E_i 与可能存在的最大边数 k_i（k_i - 1）的比值，该系数描述了网络节点的聚集程度，计算方法如式（8）所示，而脑网络的聚类系数是通过计算网络中所有节点的聚类系数再取平均后得到的。

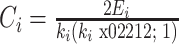8

3.3.3. 全局效率

全局效率 E_glob 的定义为脑网络中所有节点间距离的调和平均数的倒数，它能够反映信息在网络中传递速度的快慢，衡量脑网络的信息传输能力。较高的全局效率意味着信息在脑网络中传递或者交换时需要的代价消耗较低，数学表达式如式（9）所示，其中变量的含义与上述公式相同。

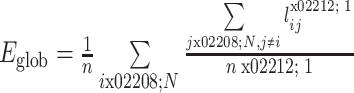9

3.3.4. 局部效率

脑网络子图 A_i 代表的是由与节点 i 直接相连（节点 i 除外）的所有节点构成的子图，其局部效率反映的是脑网络系统的容错性和脑网络防御随机攻击的能力，脑网络子图 A_i 的局部效率 E_i-local 数学表达式如式（10）所示，其中 a_ij 表示 i 与 j 两个节点间是否有边相连，若有则为 1，反之为 0。

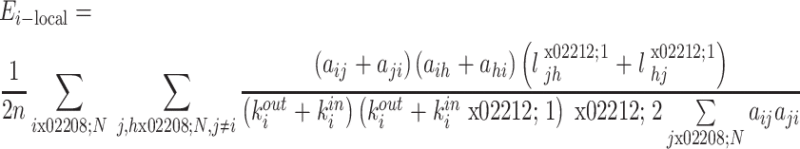10

3.3.5. 度

度是与该节点有边相连的节点个数，描述了节点间的连接统计特性，能够反映节点 i 在脑网络中的重要程度，度越大代表这个节点在脑网络中越重要。节点度 k_i 的计算公式如式（11）所示。

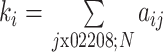11

4. 分类模型的构建

4.1. 分类算法的选择

机器学习研究的主要内容是一种在计算机上从数据中产生“模型”的算法，即“学习算法”。在这个学习算法基础上，本文将经验数据输入系统，系统基于这些数据构建对应的模型，从而在面对新情况时，系统基于这个模型可以返回一个相应的判断。机器学习中的学习算法主要分为三类，分别是监督学习、非监督学习和强化学习，而主流的分类器有人工神经网络、SVM、最近邻居法、高斯混合模型、朴素贝叶斯方法、决策树和径向基函数分类等^[12]。

SVM 是主要用于数据的分类和回归的监督学习方法，相对于其他分类方法可以更充分地反映出结构风险最小化原则，对于样本集外的数据也表现出良好的适应性，还可利用核函数有效解决非线性问题，并且在解决高维空间中的多维问题表现出独特优势，再结合多种算法可以建立模式类似的模型，从而简化复杂问题^[13]。基于以上优点并考虑脑电信号的非线性和特征选取的多元化，最终选择 SVM 分类算法。

4.2. 分类模型的构建

由于精神分裂症患者病程存在很大的不稳定性，因此在符合入组标准基础上，愿意配合且有能力完成本研究中认知负载试验的患者数量相对较少，故而无法获取大量的患者及年龄、性别匹配的健康对照志愿者脑电信号作为本研究中数据。而 SVM 为确保分类识别的准确性，对训练集有一定的要求，同时需明确测试集和预测集应存在差异。为了解决数据集的有限性和需要 SVM 分类结果具有较高准确性这二者之间的矛盾，本研究中引入交叉验证方法。交叉验证核心思想是将测试数据集作为预测数据集的一部分，将剩余数据作为训练集以完成学习分类，并不断重复上述过程，直到所有的数据集均被预测完为止。引入交叉验证后，其准确率则为全部测试数据集的预测准确率均值^[13]。

在本研究中，选用“留一验证法”，即每次只选用原样本中的一项数据作为预测数据，剩余数据均作为训练集，并不断重复这个过程，直到所有的数据集均被预测一次后结束这个过程。理论上，在“留一验证法”过程中每一次得到的 SVM 是不同的，但考虑到在这个训练过程中，每一次使用的数据集大体相同，差异微小可以忽略不计，因此 SVM 对数据预测的效果近似相同，即将基于“留一验证法”所得 SVM 的预测准确率当作其对整体数据预测的准确率^[14]。上述 SVM 算法是在 Chang 等^[15]开发的 Libsvm 平台上实现的。

5. 结果与分析

5.1. 非线性动力学分析结果

本文将经过预处理后的脑电信号，经过计算得到相应关联维数和样本熵，并运用多元回归方法，减少变量对结果的影响，将结果进行双样本 t 检验时，依据伪发现率（false discovery rate，FDR）方法实现多重比较校正^[16]，得到患者组和健康组在相关指标上的组间差异，并以直方图的形式表现出来，如图 2 所示。

图 2.

Correlation dimension and sample entropy differences among groups in each rhythm

各频带下关联维数及样本熵结果组间差异

*P < 0.05，** P < 0.01

*P < 0.05，** P < 0.01

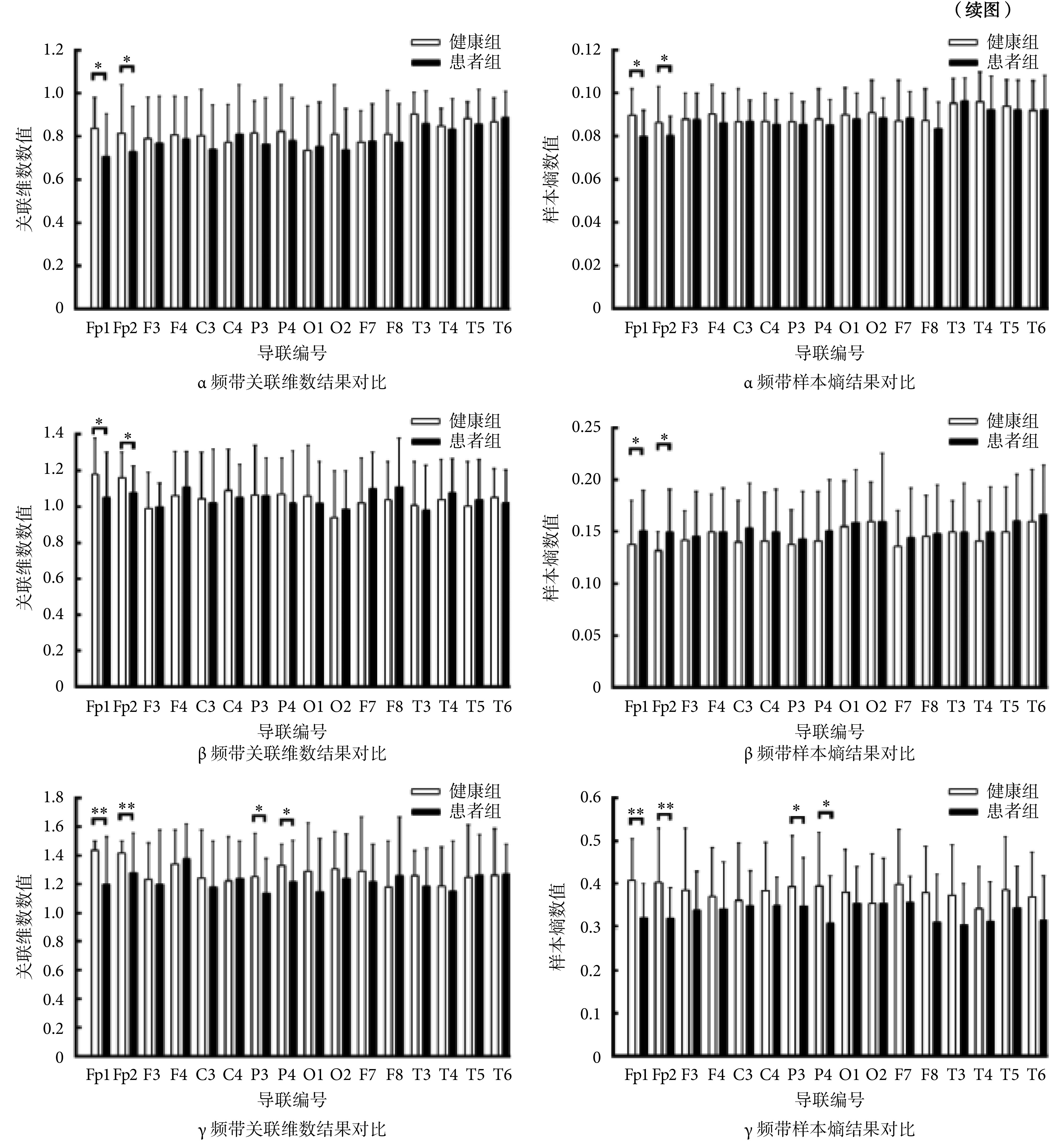
由图可看出，认知负载状态下，两组人群的关联维数和样本熵特征差异均存在统计学意义（P < 0.01），具体表现相似，均为除 δ 频带外其余频带下的 Fp1、Fp2 导联，θ 频带下的 O1 和 O2 导联以及 γ 频带下的 P3 和 P4 导联。Fp 导联代表的是大脑的前额皮质区域，这表明患者组在前额皮质激活中可能出现明显的功能紊乱并影响其认知功能。

此外还注意到，患者组在 α、β、θ、γ 这 4 个频带下的关联维数和样本熵在 Fp1 和 Fp2 导联数值极为相近，而健康组在各个频带内的相关指标均有 Fp1 显著高于 Fp2，表明大脑前额皮质左侧区域本应表现出更复杂的信号状态，但由于患者认知功能受损，无法完成这一任务。因此，患者组的异常表现可能的作用机制为认知过程中大脑左半侧参与度受到抑制，相应右半侧受抑制不足。

5.2. 脑功能网络特征分析结果

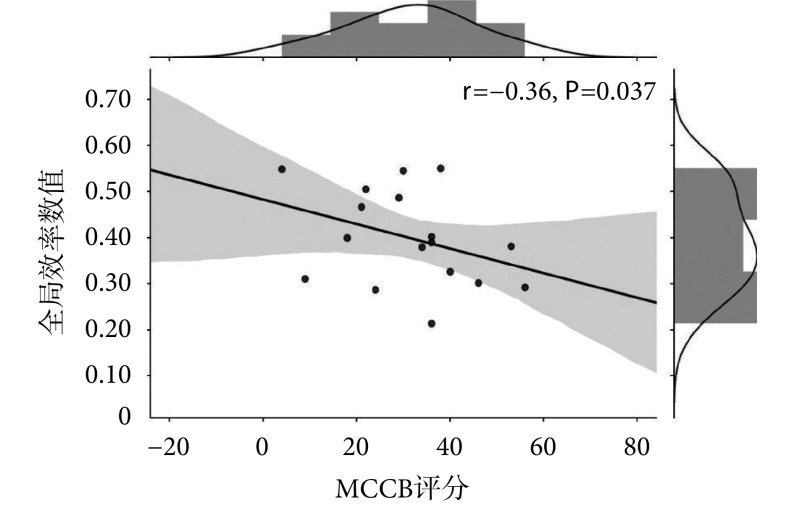
在构建好的脑功能网络中分析计算两组受试者全局属性特征值的组间差异，结果表明在认知负载状态下，两组受试者在聚类系数、最短路径长度、全局效率以及局部效率这 4 个脑网络测度中差异均具有统计学意义。为了寻找可以量化评估精神分裂症患者认知功能的客观指标，将上述组间差异具有统计学意义的全局属性与节点属性特征指标与患者的 MATRICS 共识认知成套测验（MATRICS consensus cognitive battery，MCCB）评分做皮尔森相关分析。结果表明，在上述组间差异具有统计学意义的所有网络属性特征指标中，只有全局效率结果与患者的临床 MCCB 评分相关，具体结果如图 3 所示。

图 3.

Correlation between global efficiency and MCCB score

全局效率与 MCCB 评分相关性

5.3. 分类结果与分析

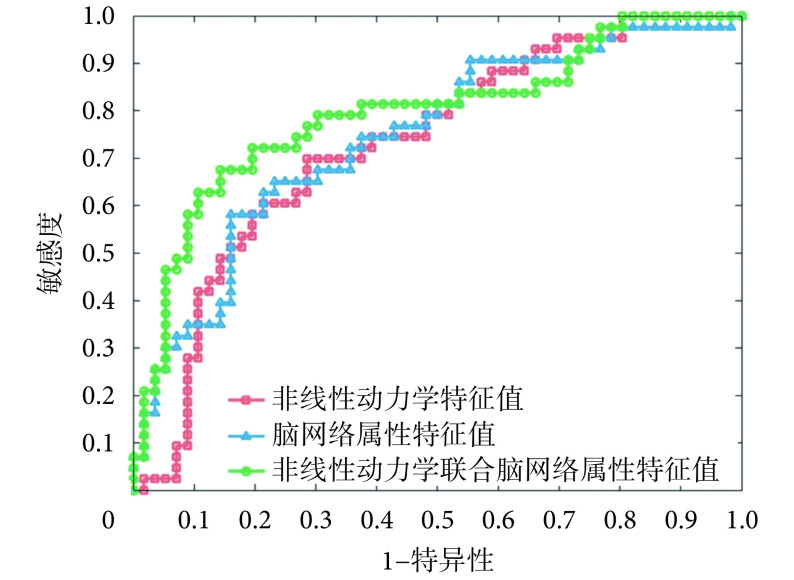
根据上述方法构建分类模型，使用的数据集为计算得到的脑电信号非线性动力学特征值和脑网络属性特征值。并采用敏感度、特异性和准确率这三个指标评价自动分类结果。依据自动分类结果，绘制了受试者工作特征（receiver operating characteristic，ROC）曲线，用以综合反映敏感度和特异性连续变量。通过使用不同的数据集进行分类得到不同的结果，其 ROC 曲线如图 4 所示。通过将两种类型的指标纳入数据集进行分类得到的结果为最优解，结果为准确率 76.77%、敏感度 72.09% 和特异性 80.36%，总体看来可以取得较好的分类效果。

图 4.

The ROC curves corresponding to automatic classifica tion results

各自动分类结果对应的 ROC 曲线

在用 SVM 两组人群进行分类时，分类权重最大的 10 个特征值依次为：γ 频带 Fp2 导联样本熵、γ 频带 Fp1 导联样本熵、F4 导联节点度值、T3 导联节点度值、全局效率、γ 频带 Fp2 导联关联维数、γ 频带 Fp1 导联关联维数、θ 频带 Fp2 导联样本熵、α 频带 Fp1 导联样本熵和聚类系数。这一结果也验证了前额皮质区域和 γ 频带在认知功能上的重要作用。

6. 结论

本文通过采集认知负载状态下的精神分裂症患者和正常人的脑电信号，计算了两组受试者的非线性动力学特征并构建了脑功能网络计算特征参数，最后利用机器学习方法对认知负载状态下精神分裂症患者脑电信号特异性进行研究。结果表明，基于本研究中所得脑网络属性特征和非线性动力学特征作为数据集实现的自动分类，总体上可以得到较好的分类效果，这不仅证明了本研究的可行性与实用性，同时为后续临床客观评估精神分裂症患者认知功能提供了参考，也为精神分裂症的早期筛查和辅助诊断提供了新方向。

受限于本研究的实验条件、参与对象，另外对精神分裂症病理生理学知识的了解还不够，本研究也存在一些值得改进的地方。在实验设计方面，可以增加后续研究入组人数，并对入组人群进行细化分类，如按照病程的长短、药物的使用情况不同等；在信号处理方面，可以对脑电信号进行更深入的处理分析，在增加导联数量的同时跟进最新的分析方法，如进行源定位等处理，以便更好地理解疾病的发生机制；在应用方面，努力将本研究中的采集及处理分析方法模块化，不断优化改进成一个能够方便临床使用的早期筛查和辅助诊断的系统，造福广大民众。最后从长远来看，还应考虑将脑电信号与其他技术联合，进行多模态的大脑量化研究分析，为探寻精神分裂症生理病理演变情况和可能机制上做出一定贡献。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金（31771074，81802230）；广东省科技计划前沿与关键技术创新专项资金（2016B010108003）；广东省科技计划公益研究与能力建设专项资金（2016A020216004）；广东省协同创新与平台环境建设专项资金（2017A040405059）；广东省科技重点领域研发计划项目（2018B030335001）；广州市产学研协同创新重大专项（201604020170，201704020168，201704020113，201807010064，201803010100，201903010032）