一种基于频谱约束的多频动态电阻抗断层成像算法

Abstract

本文旨在提出一种基于频谱约束的多频动态电阻抗断层成像（EIT）算法。在已知成像域内各组分电导率频谱的情况下，通过重构独立于频率的参数——体积分数变化，同时利用多个激励频率下的测量电压差重构一帧时差图像，从而大大增加测量数据量以改善逆问题的病态性。数值仿真实验显示，该算法较传统阻尼最小二乘算法具有更小的图像伪影，且在低信噪比情形下具有更小的位置误差和形变误差。本研究有望为动态 EIT 提供一种有效利用多频信息的方法，并为在已知各组分电导率频谱情况下的动态 EIT 发展提供一个新思路。

引言

电阻抗断层成像（electrical impedance tomography，EIT）是在人体表面放置一定数量的电极，并通过这些电极向人体施加微小的电流激励，同时测量响应电压，使用逆问题求解算法重建出体内阻抗分布及变化信息。它具有无创、无辐射、动态监测、功能成像等优势，具有良好的应用前景^[1]。

EIT 从应用的角度可以分为解剖结构成像和功能成像^[2]。解剖结构成像主要有静态成像和频差成像。静态成像是指给定某一时刻边界电压值重构体内阻抗分布的绝对值，其不依赖初始阻抗分布但是对模型误差和测量噪声敏感；频差成像则利用两个频率下的电压差值重构体内阻抗随频率的变化量，正处于发展初期，具有很强的应用前景。功能成像主要是时差成像，即利用不同时刻边界电压差重构体内阻抗随时间的变化量，时间分辨率高，可以实现连续动态 EIT 监测，而且由于采取边界电压差值，很大程度上削弱了模型误差，是目前在临床应用最广泛的方法。但该法存在着依赖初始阻抗分布、对测量噪声敏感和不适用于阻抗变化大的成像目标等问题^[3]。

目前各种 EIT 成像方法面临的主要问题是病态性，它的实质是物体内部阻抗分布和表面测量电压之间存在非线性关系，且这种关系难以获得，导致内部重构阻抗随着测量电压中很小的噪声剧烈变化，非常不利于连续动态的 EIT 监测。实际应用中还需对这种关系进行离散化处理，这使得观测数据量大大减小，进一步加剧病态性。目前常规解决方法是利用阻抗分布的先验知识，结合正则化代价函数的方式来得到稳定解^[3]。

本文提出一种基于频谱约束的多频动态电阻抗断层成像算法，它同时利用多个频率下的时差数据重构一帧体积分数变化，成倍增加观测数据量从而减小逆问题的病态性，且合并正则化方法将提高 EIT 图像的质量和抗噪能力。该法不同于以往的频差成像，本质上是一种利用多频数据的时差成像方式，因此可以实现功能成像。

1. 体积分数成像

1.1. 体积分数模型

体积分数模型是体内各种组织分布的一种表现形式，通常和有限元法（finite element method，FEM）结合起来，估计体内电导率分布^[4]。该模型基于以下三个假设：（1）成像区域是由 T 种具有不同电导率特性的组织构成的，分别是 t₁ t_j t_T。（2）每种组织在不同频率激励下的电导率是已知的，j 组织在第 i 个激励频率下的电导率是 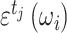。（3）第 n 个剖分面元的电导率等于各组织电导率的线性加权和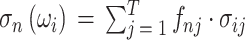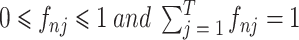： （ ）。这其中的加权系数 f_nj 即 j 组织在面元 n 中的体积分数。显然，如果第 n 个面元中仅包含一种组织 j，那它的电导率就是该组织的电导率：σ_n（ω_i）= σ_ij。

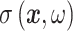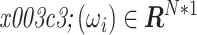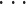以二维区域 Ω 为例，该区域内的电导率分布随频率变化定义为 ，其中 x 是空间位置，ω 是激励电流频率。然后对 Ω 做有限元剖分，每个面元内的电导率是连续一致的，于是得到了电导率向量 ，其中 N 是剖分面元数。又因为每个面元可能包含 T 种或部分组织，因此在每个面元内对每种组织设一体积分数值，例如 f_nj 即面元 n 内第 j 种组织的体积分数，便得到了体积分数矩阵 F_matrix∈R^T*N，其中第 n 列是面元 n 的各组织占比，第 j 行是组织 j 在各个面元的占比，之后将其按列向量化得到 。最后任意时刻采用 M 个激励频率（ω₁ ω_i ω_M）施加激励电流，每个激励频率下可以得到一个边界电压向量 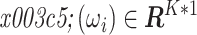，其中 K 是一个激励频率下的所有边界电压值个数。将这 M 个边界电压向量纵向拼接可得该时刻的边界电压向量 υ（t），将该边界电压向量和背景帧 υ（t₀）作差可以得到该时刻的边界电压变化向量∆υ（t）。其中 F 形如式（1）：

1

基于以上假设推导体积分数变化和边界电压变化之间的关系即体积分数变化重构的正问题模型。

首先根据上面的假设（3）可以得出体积分数和电导率之间的线性关系：

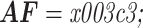2

其中 是由电导率频谱构成的系数矩阵，其形式如下：

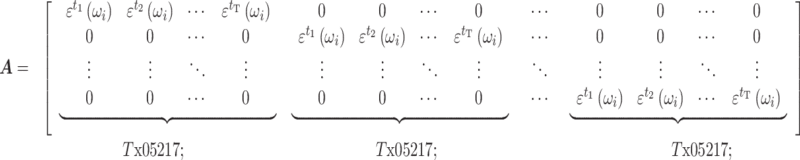3

已知在传统电导率重构时，不含噪声理想状态下的离散正问题：

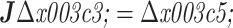4

其中雅克比矩阵 J∈R^K*N，它的计算方式有直接求导法和伴随场法^[2]：

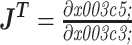5

结合式（2）和式（4）可以得到理想状态下体积分数重构的离散正问题方程：

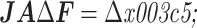6

其中的矩阵 J、矩阵 A 和边界电压向量 υ 都是随频率变化的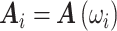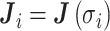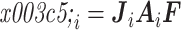， ， ， 。只有体积分数向量 F 不随频率变化。

1.2. 体积分数重构

为了实现同时利用多个频率下的时差数据重构一帧体积分数变化，构造以下目标函数 Φ，使得所有频率下的数据差二范数最小。

7

其中∆υ 是任意时刻边界电压和背景帧之间的边界电压差向量，S 是一个组装矩阵，内含 M 个元素矩阵，每个元素矩阵是由一个频率下的雅克比矩阵和系数矩阵相乘得到的，它形如：

8

该目标函数也可以写成如式（9）各个频率下数据差二范数之和的形式，二者是等效的^[5]。

9

之后选择 Tikhonov 正则化方式^[6]，目标函数变成了：

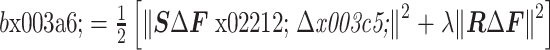10

目标函数是可微的，其一阶和二阶导数由链式法则可得。其中 λ 是正则化参数，它代表着正则化程度，维持着数据匹配和噪声抑制之间的平衡。λ 过大则图像过正则化，空间分辨率低；λ 过小则图像正则化不足，主要被噪声控制，无法分辨重构目标^[7]。本文采用 L 曲线法确定正则化参数，该法操作简单且有效，是目前应用最广泛的正则化参数选取方法^[8]。R 是正则化矩阵，R = I 的形式被称为 Levenberg-Marquardt 法，简称 LM 法；R = diag（S^TS）的形式称为标准 Tikhonov 法，也称 NOSER 法；R 还可以是一些微分算子的离散形式，以起到滤波的作用^[9]。本文采用标准 Tikhonov 法。

为了满足任何一个面元内所有体积分数和为 1，即 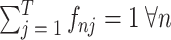，在目标函数中替换 ，对应的 t₁ 组织通常是背景组织，这样将重构 T−1 种组织（f₂ 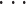f_j 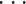f_T）的体积分数变化量∆F_T−1，而 S 矩阵也将对应地变化成 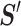。其次为了满足任何一个体积分数值在 0、1 之间，即 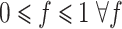，对重构结果施加边界条件以保证 F_T−1 中的每个元素被限制在区间［0，1］之间。最终得到目标函数 ：

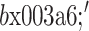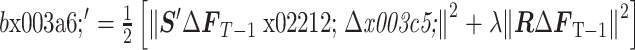11

对∆F_T−1 的求解将采取逆问题算法，当得到求解式之后，将∆υ 代入求解式即可得到∆F_T−1。

具体流程如下：

步骤 1：设定背景帧 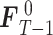值。

步骤 2：令一阶导数为零得到目标函数的步进方向 。

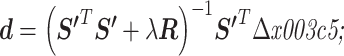步骤 3：利用前一步得到的步进方向求得前景帧的 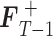值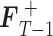， = + d，并对其施加限制条件得到 F_T−1，具体的限制条件是 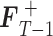每个元素要 ≥ 0 且 ≤ 1。

步骤 4：利用 F_T−1 减去背景帧 值即可得到区域内部体积分数变化量∆F_T−1。

最后，为了与传统时差图像作对比，利用体积分数和电导率的线性关系将成像区域内体积分数变化转化得电导率变化，将电导率变化利用色阶表示在成像区域内，得到电导率变化图像。

2. 图像评价指标

参考 Adler 等^[10]提出的 EIT 图像评价体系后，本文采用位置误差（position error，PE）、形变误差（shape deformation，SD）、图像噪声（image noise，IN）三项指标来评价算法性能。首先定义重建目标区域（region of perturbation，RP），其满足如下两个条件^[4]：① t₂ 组织体积分数变化大于最大 t₂ 组织体积分数变化的 0.5 倍的面元集合；② 按照条件① 提取的所有区域中，覆盖面积最大的连通区域集合。

2.1. 位置误差

位置误差衡量重建图像准确表达真实目标位置的程度：

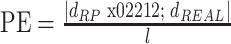12

其中，d_RP 和 d_REAL 分别表示重建目标重心和预设目标重心至模型中心的距离，l 为重建模型长轴长度。PE 应尽可能的小，并在全局范围内具有较高一致性，该指标对准确判断目标的位置起着至关重要的作用。

2.2. 形变误差

形变误差衡量重建图像准确表达真实目标形状的程度：

13

其中，A_C 和 A_RP 分别表示区域 C 和区域 RP 所包含的面元个数。SD 应该是小且一致的，较大的 SD 可能会导致对图像的不正确解释。

2.3. 图像噪声

图像噪声是衡量算法抗噪声性能的一项指标：

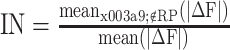14

分子是位于重建目标区域外的体积分数变化的平均值；分母是所有面元体积分数变化的平均值。IN 越小，代表图像伪影越少。

3. 仿真实验

为了测试基于频谱约束的多频动态 EIT 算法的性能，采取圆型 FEM 模型进行仿真实验。

3.1. 实验步骤

实验采用 16 电极，对侧激励、邻近测量模式。如图 1 所示，生成模板采用 10 层剖分的圆域模型，内含 441 个结点、800 个单元；重构模板采用 8 层剖分的圆域模型，内含 289 个结点、512 个单元。生成和重构采用稀疏不同模板的目的是避免逆问题陷阱^[2]。如图 2 所示，将背景帧设置成均匀分布的 t₁ 组织，前景帧设置成均匀分布的 t₁ 组织内含一个由 t₂ 组织构成的重建目标，前景帧一共设置 5 个，分别具有不同径向位置的目标 0～4。其中 t₁ 组织仿真正常脑组织，t₂ 组织仿真脑缺血组织，电导率频谱如图 3 所示，其值通过查阅文献后截取三个频点来获得，截取的方法在讨论中详细阐述^[11]。然后用生成模板生成边界电压差数据并对其添加两种水平的高斯噪声，信噪比分别是 60 dB 和 80 dB。最后分别采用阻尼最小二乘算法和基于频谱约束的多频动态 EIT 算法对这 5 个目标进行图像重建。阻尼最小二乘算法是目前临床应用最广泛且最稳定的时差成像算法^[12]，它的重构公式是 ，其中的 J 是雅克比矩阵^[13]，λ 是正则化参数且同样采用 L 曲线法确定，R 是正则化矩阵取 R = diag（J^TJ），最后由一个激励频率下的边界电压差值∆υ 可以算出此频率下的电导率变化∆σ。阻尼最小二乘算法采用频率标签 2 下的边界电压差数据重构，原因是该频率下的缺血组织与正常脑组织具有最大的电导率差异。

图 1.

Finite element meshes

有限元剖分示意图

图 2.

Background frame and foreground frames

背景帧和前景帧设置

图 3.

Spectrums of two tissues

两种组织的电导率频谱

本研究还进行了初步的多组织仿真实验，将组织数 T 扩展到 3 以进一步验证算法的有效性。其中 t1 组织是背景组织，t2 组织仍是缺血组织，新增一种 t3 组织血液，在此基础上进行体积分数变化的重构。

3.2. 实验结果

阻尼最小二乘算法和基于频谱约束的多频动态算法在信噪比 80 dB 和 60 dB 下的重建结果分别如图 4 和图 5 所示。

图 4.

Reconstructed images under signal-to-noise ratio of 80 dB

信噪比 80 dB 下仿真实验结果

图 5.

Reconstructed images under signal-to-noise ratio of 60 dB

信噪比 60 dB 下仿真实验结果

由图 4 可知，两种算法在高信噪比的时候，重构目标类似且形状清晰位置准确，但是传统的阻尼最小二乘算法仍然在背景部分具有明显的伪影，尤其是在重构目标靠近中心时。说明当测量情况理想时，两算法都可以重构出满意的图像，但基于频谱约束的多频动态算法具有更强的伪影抑制能力。

由图 5 可知，两种算法在低信噪比的时候，重构图像存在明显不同。传统阻尼最小二乘算法图像受噪声的影响大，图像伪影严重而且目标形变严重，尤其是在目标靠近中心时图像伪影会影响对目标的判断；而基于阻抗频谱约束的多频算法图像伪影明显少于前者，且具有更小的图像形变，即使是在目标靠近中心时仍然可以清晰地判断目标。说明当测量情况不理想时，阻尼最小二乘算法存在失效风险，而基于阻抗频谱约束的多频算法仍然具有良好的成像结果。

综合图 4 和图 5 可知，基于阻抗频谱约束的多频算法在不同信噪比下都具有更强的伪影抑制能力，在低信噪比下还具有更小的形变误差，较阻尼最小二乘算法更适合临床应用。

算法性能评价结果如表 1～表 3 所示，包括两种算法在不同位置和不同信噪比下的位置误差、形变误差和图像噪声。在高信噪比下，基于频谱约束的多频动态算法具有同阻尼最小二乘算法相近的位置误差和形变误差，且二者的位置误差都很小，新算法主要优势是具有更小的图像噪声，这点也与重建图像相对应。在低信噪比下这种优势更加明显，基于频谱约束的多频动态算法具有更强的噪声抑制能力，同时具有更小的位置误差和形变误差。

表 1. Position error evaluation results of two algorithms.

位置误差评价结果

目标	信噪比 60 dB			信噪比 80 dB
	基于频谱约 束的多频动 态算法	阻尼最小 二乘算法		基于频谱约 束的多频动 态算法	阻尼最小 二乘算法
0	0.025 1	0.057 7		0.000 1	0.003 0
1	0.026 9	0.039 7		0.004 0	0.004 1
2	0.023 2	0.025 0		0.003 2	0.003 3
3	0.022 8	0.023 8		0.003 8	0.004 2
4	0.005 8	0.017 4		0.002 1	0.002 9

表 3. Image noise evaluation results of two algorithms.

图像噪声评价结果

目标	信噪比 60 dB			信噪比 80 dB
	基于频谱约 束的多频动 态算法	阻尼最小 二乘算法		基于频谱约 束的多频动 态算法	阻尼最小 二乘算法
0	0.250 3	0.285 0		0.199 3	0.204 0
1	0.189 9	0.262 0		0.104 6	0.122 9
2	0.140 4	0.240 5		0.089 6	0.111 3
3	0.127 5	0.143 8		0.076 4	0.093 5
4	0.073 2	0.096 8		0.061 2	0.085 6

表 2. Shape deformation evaluation results of two algorithms.

形变误差评价结果

目标	信噪比 60 dB			信噪比 80 dB
	基于频谱约 束的多频动 态算法	阻尼最小 二乘算法		基于频谱约 束的多频动 态算法	阻尼最小 二乘算法
0	0.203 3	0.235 8		0.260 0	0.266 7
1	0.181 7	0.198 3		0.107 5	0.107 5
2	0.151 7	0.190 0		0.055 8	0.083 3
3	0.150 8	0.190 0		0.077 5	0.077 5
4	0.048 3	0.085 0		0.047 5	0.048 3

多组织的仿真实验结果如图 6 所示，该法在成像前就对组织进行了划分，成像后可以方便地筛选出各个组织的目标图像，这是传统阻尼最小二乘算法所没有的优势。但缺血目标成像效果不如出血目标，原因是本研究采用的频点下缺血目标电导率较背景变化远小于出血目标，因此还需要进一步探讨组织个数 T 对成像结果的影响，以实现最优的多组织多目标成像。

图 6.

Multi-tissue case setup and reconstruction results

多组织成像目标和重构结果

4. 讨论

本文在正则化基础上从算法模型入手建立了一种利用多频信息进行时差成像的算法。算法基于组织的阻抗谱信息，将体积分数模型引入阻抗成像领域，找到了一个独立于频率的成像参数——体积分数变化，同时使用多个频率下的测量值进行一帧时差成像，能有效增加独立方程数，改善逆问题病态性，从而提高重构图像质量。仿真结果表明该算法较阻尼最小二乘算法具有更强的伪影抑制能力，在低信噪比下还具有更小的位置误差和形变误差，更适合临床应用场景。

但需要注意的是：（1）频率数取决于重构模板和激励测量模式的选择。频率数不是越多越好，只要满足在逆问题方程中，所有频率下的测量数大于等于未知的体积分数个数即可。过多的频率数会增加计算时间，而过少的频率数将不能体现该算法的优越性，文中选择频率数为 3 即可。（2）不同频点下正常与病变组织电导率差异大小会对谱成像算法的性能造成影响，选择不同组织的电导率差异较大的频点，将获得更好的成像效果。本文首先仿真生成所有频点下的边界电压差数据，然后计算各个频点下边界电压差数据的相关系数，选取正交性最大的三组数据来成像。鉴于本文 EIT 硬件系统在 50 kHz 时具有较高的信噪比，频点选择在 50 kHz 及其左右展开，截取的频谱中心频率设置在 50 kHz，当其他频点和 50 kHz 下的边界电压差数据具有较高的相关性时，将舍弃这个频点。（3）本法需要事先获取完整的组织电导率谱信息，可以通过查阅文献获得，也可以通过测量获得。但以上两种方式获得的组织频谱都存在一定的误差，会影响成像结果。

综上所述，本文利用体积分数模型，将多频信息整合进时差成像中，通过增加重构一帧图像的信息量，来改善图像质量。但重构结果很大程度上依赖于引入信息的准确度，因此电导率频谱信息的获取和筛选至关重要，最优的频点选择方法和频谱误差如何影响重构结果以及如何减小这种影响值得进一步探讨。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金面上项目（61771475）；陕西省自然科学基金（2014JM2-6092）；国家自然科学基金重点项目（51837011）