Abstract
口腔正畸研究中,牙颌组织模型对有限元分析结果有着重要影响。目前,常用的牙槽骨有限元模型主要有均质和非均质两种类型。均质型模型对牙槽骨进行整体材料赋值,每个网格单元的力学特性均相同;而非均质型模型则依据牙槽骨每个网格单元所处的计算机断层扫描(CT)图像灰度值对网格单元进行差别赋值。为了探究不同牙槽骨模型对牙周膜生物力学响应的影响,我们选择一例临床患者作为研究对象,构建了其下颌尖牙、牙周膜和两种牙槽骨模型,分别对尖牙施加 1 N 的根向压入力和 2 Nmm 根向扭矩,分析牙周膜在不同载荷形式下的静水压应力和最大对数主应变。研究结果表明无论尖牙平动或转动,牙周膜的力学响应均会受到牙槽骨模型的影响。相比于均质型模型,当牙槽骨模型为非均质模型时,尖牙沿根向平动时牙周膜的最大应力和应变分别降低了 13.13% 和 35.57%;尖牙沿根向转动时牙周膜最大应力和应变分别降低了 19.55% 和 35.64%。均质型牙槽骨模型会诱导正畸医生选择一个较小的矫治力,非均质牙槽骨模型更能体现真实牙槽骨骨质特性的差异性,更有利于获得准确的分析结果。
Keywords: 口腔正畸, 有限元模型, 牙槽骨, 牙周膜, 生物力学
Abstract
In the study of oral orthodontics, the dental tissue models play an important role in finite element analysis results. Currently, the commonly used alveolar bone models mainly have two kinds: the uniform and the non-uniform models. The material of the uniform model was defined with the whole alveolar bone, and each mesh element has a uniform mechanical property. While the material of the elements in non-uniform model was differently determined by the Hounsfield unit (HU) value of computed tomography (CT) images where the element was located. To investigate the effects of different alveolar bone models on the biomechanical responses of periodontal ligament (PDL), a clinical patient was chosen as the research object, his mandibular canine, PDL and two kinds of alveolar bone models were constructed, and intrusive force of 1 N and moment of 2 Nmm were exerted on the canine along its root direction, respectively, which were used to analyze the hydrostatic stress and the maximal logarithmic principal strain of PDL under different loads. Research results indicated that the mechanical responses of PDL had been affected by alveolar bone models, no matter the canine translation or rotation. Compared to the uniform model, if the alveolar bone was defined as the non-uniform model, the maximal stress and strain of PDL were decreased by 13.13% and 35.57%, respectively, when the canine translation along its root direction; while the maximal stress and strain of PDL were decreased by 19.55% and 35.64%, respectively, when the canine rotation along its root direction. The uniform alveolar bone model will induce orthodontists to choose a smaller orthodontic force. The non-uniform alveolar bone model can better reflect the differences of bone characteristics in the real alveolar bone, and more conducive to obtain accurate analysis results.
Keywords: oral orthodontics, finite element model, alveolar bone, periodontal ligament, biomechanics
引言
临床正畸治疗中,错位牙齿的矫正主要依靠患者口腔佩戴的正畸矫治器。矫治器形变产生矫治力,矫治力首先作用在错位牙齿的牙冠上,并通过牙体传递给牙周膜,进一步经过牙周膜的缓冲、吸收作用于牙槽骨,进而激发牙槽骨改建,最终在矫治力的作用下,牙齿逐渐移动到理想位置[1-4]。在牙齿移动过程中,牙周膜作为介于牙齿和牙槽骨之间的一层结缔纤维组织,在激发骨改建、诱导牙齿移动中起着重要作用[5-6]。有研究表明牙齿矫治过程中的移动速度与牙周膜的应变密切相关[7-8],牙根的吸收情况则与牙周膜的应力有关[9-10]。因此,研究牙周膜受载之后的生物力学响应对于明确正畸矫治机制、优化正畸治疗方案具有非常重要的意义。
对于牙周膜生物特性的研究方法主要包括实验测试和有限元模拟。牙周膜作为人体生物组织,一方面实验材料来源非常有限;另一方面,牙周膜一般厚度仅有 0.2~0.3 mm[11],极易遭到破坏而失去生物活性,存放条件非常苛刻[12]。另外,对于牙周膜的临床测试也因患者意愿、装置结构复杂、跟踪记录周期长、数据处理繁琐等因素难以获得直接有效的试验结果[13]。因此,在实验条件有限的情况下,更多的人采用有限元法对其进行研究。目前有限元法已广泛用于口腔正畸医疗领域,具有准确度高、重复性好和可操作性强等优点,受到越来越多的研究人员青睐[9, 14]。
在采用有限元法对正畸矫治机制进行研究时,构建牙颌组织有限元模型至关重要。正畸过程中涉及到的牙颌组织主要包括牙齿、牙周膜和牙槽骨。牙齿相比于其他牙颌组织具有很高的硬度,弹性模量可达 20 GPa[15-16],因此在有限元分析中多把牙齿设定为刚体[10, 17]。牙周膜因其厚度较薄、尺寸较小,则一般假定为厚度均匀、均质、各向同性的超-黏弹性体[12, 18]。对于牙槽骨模型的构建方法则主要有两种:第一种是采用非均匀有理 B 样条(non-uniform rational b-splines,NURBS)曲面拟合的方式将牙槽骨三角面片网格模型转化为实体模型,然后将其导入有限元软件进行整体网格划分、材料赋值得到牙槽骨有限元模型[3, 19]。这种建模方法获得牙槽骨模型每个网格单元的材料特性都相同,属于均质型模型。虽然有些学者按照牙槽骨骨质特性将其人为地分为皮质骨和松质骨[7, 19],但对于整个皮质骨或者松质骨而言,模型的每个单元材料特性也都一样。另一种方法则直接利用牙槽骨三角面片网格模型生成体网格模型,并依据模型中每个网格单元所处的计算机断层扫描(computed tomography,CT)图像灰度值对单元进行差别材料赋值[18, 20],不再利用有限元软件进行网格划分和材料赋值,这种建模方法获得牙槽骨模型每个网格单元的材料特性均不相同,属于非均质模型。
目前,上述两种建模方法均有使用,如 Liao 等[9]为了研究牙周膜在正畸力优化中的作用构建了精细的均质型牙槽骨模型,Ashrafi 等[15]、Cozzani 等[16]和 Benaissa 等[19]也都在自己最新的研究中采用了第一种建模方法;而 Wu 等[18]、Liu 等[20]和 Bujtar 等[21]则采用第二种方法构建了非均质牙槽骨模型用于有限元分析计算。Liu 等[20]进一步对比分析了两种建模方法在构建下颌骨有限元模型中的优劣势,结果表明非均质模型更有利于构建具有复杂几何构造的颌骨模型。而针对不同类型的牙槽骨模型,牙周膜受载之后的生物力学响应是否存在差异却鲜有报道。多数学者习惯采用第一种建模方法构建均质型的牙槽骨模型,对于模型的材料赋值也通常机械式地借鉴他人的材料参数,然而有限元模型的精确度对其分析结果却有着不可忽视的影响。
为此,我们将基于一例临床患者的螺旋 CT 图像数据,选择其下颌尖牙作为研究对象,构建其牙颌组织有限元模型,分别将其牙槽骨设置为均质型模型和非均质型模型,对尖牙施加牙根向的压入力和扭矩,研究不同牙槽骨模型作用下的牙周膜应力和应变,进而明确不同牙槽骨仿真模型对牙周膜生物力学响应的影响,协助相关研究人员选择合适的牙槽骨建模方法,从而提高有限元分析的准确性。
1. 材料和方法
1.1. 牙颌组织有限元模型构建
参照医学伦理审查办法,在受试者知情同意的前提下选择浙江大学医学院第二附属医院一例临床病例作为研究对象,依据患者的螺旋 CT 图像数据构建其下颌尖牙牙颌组织有限元模型。首先,将患者 CT 数据导入医学影像处理软件 Mimics 15.0(Materialise 公司,勒芬,比利时),通过阈值设定、掩膜编辑、区域增长和三维建模等手段建立尖牙及其牙槽骨的三角面片网格模型。接着将尖牙和牙槽骨的三角面片网格模型导入网格模型处理软件 3-Matic 7.0(Materialise 公司,勒芬,比利时),将尖牙模型向外偏置 0.25 mm 之后与牙槽骨模型求交,然后减去原来的尖牙模型,获得具有均匀厚度 0.25 mm 的牙周膜三角面片网格模型[18, 22]。进一步利用 3-Matic 7.0 软件的网格编辑功能,对初步生成的三角面片网格模型进行网格细化、均匀等优化处理,然后基于模型表面的三角网格直接生成体网格模型,该体网格模型可直接被有限元分析软件 Abaqus 6.13(达索 SIMULIA 公司,波士顿,美国)调用,且不需要再进行网格划分。导入有限元 Abaqus 6.13 之后牙颌组织模型如图 1 所示,主要包括尖牙、牙周膜和牙槽骨,其中牙周膜和牙槽骨的网格单元数量分别为 3 416 和 1 915。为了保证模型精度和网格质量,我们进行了相应的模型收敛性分析。当牙周膜和牙槽骨模型进一步精细化,网格数量均增加 1 倍时,牙周膜的最大静水压应力变化量小于 5%(模型收敛性测试时的标准误差)。因此,在这项研究中模型的精度和网格质量是可接受的。模型中网格单元类型均为四节点线性杂交四面体单元(C3D4H)。
图 1.
Finite element models of dental tissues
牙颌组织有限元模型
1.2. 模型材料参数定义
尖牙相比于其他牙颌组织具有更高的硬度和弹性模量,因此在有限元分析中将其设定为刚体[10, 17]。牙周膜具有较薄的厚度和较小的尺寸,不仅具有类似固态橡胶的超弹性,还具有类似液态高分子材料的黏性[23-24],这里将其假定为一种均质的超-黏弹性体,使用二阶 Ogden 超弹性模型和均一化的应力松弛函数模型共同描述其生物力学特性,如式(1)和(2)所示[25-26]。其中, 是应变能密度函数,
是应变能密度函数, 、
、 和
和  是应变能的三个主伸长率,
是应变能的三个主伸长率, 且
且  ,
, 是容积率,
是容积率, 是剪切模量,
是剪切模量, 是超弹性材料系数,
是超弹性材料系数, 是体积模量的倒数,
是体积模量的倒数, 是多项式的阶数。
是多项式的阶数。 是均一化的应力松弛函数,
是均一化的应力松弛函数, 是能量函数的系数,
是能量函数的系数, 是松弛时间常量,
是松弛时间常量, 是时间。公式(1)和(2)中使用的材料参数列于表 1[18, 25-26],G(I)、K(I)和 TAU(I)是牙周膜黏弹性模型参数的 Prony 形式,I 是阶数。
是时间。公式(1)和(2)中使用的材料参数列于表 1[18, 25-26],G(I)、K(I)和 TAU(I)是牙周膜黏弹性模型参数的 Prony 形式,I 是阶数。
表 1. Parameters of the second-order Ogden model and normalised relaxation function.
二阶 Ogden 模型和归一化的松弛函数模型参数
| 二阶 Ogden 模型参数 | 均一化的松弛函数模型参数 | |||||||||
 /MPa /MPa |
 /MPa /MPa |

|

|
 /MPa /MPa |
 /MPa /MPa |
I | G(I) | K(I) | TAU(I) | |
| 0.005 54 | 0.11 | 0.25 | 0.115 3 | 0.121 6 | 0.97 | 1 | 0.027 697 | 0 | 0.139 27 | |
| 2 | 0.097 697 | 0 | 10.419 | |||||||
 |
1 |
 |
2 |
对于牙槽骨模型材料参数的定义将采用两种方式,一种依据牙槽骨网格单元所处的 CT 图像灰度值  将其定义为非均质模型,另一种则对整体模型进行统一赋值定义为均质模型。将 1.1 中构建的牙槽骨体网格模型重新导入 Mimics 15.0,利用软件自带的材料赋值功能参照经验公式(3)~(5)对牙槽骨的骨质密度
将其定义为非均质模型,另一种则对整体模型进行统一赋值定义为均质模型。将 1.1 中构建的牙槽骨体网格模型重新导入 Mimics 15.0,利用软件自带的材料赋值功能参照经验公式(3)~(5)对牙槽骨的骨质密度  、弹性模量 E 和泊松比
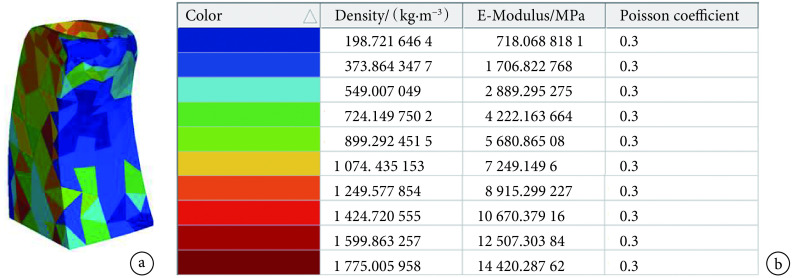
、弹性模量 E 和泊松比  进行定义[20, 27]。赋值完成之后的牙槽骨体网格模型如图 2a 所示,模型中的网格单元被赋予不同的颜色表示其拥有不同的材料参数,每种颜色代表的材料参数如图 2b 所示。该材料赋值方法的基本依据是不同骨密度的牙槽骨经扫描会获得不同灰度值的 CT 图像,如式(3)所示,骨质越致密其 CT 图像灰度值就越高。另外,牙槽骨的弹性模量与其骨密度也存在密切联系,如式(4)所示,牙槽骨骨密度越大其弹性模量越大,因此可以建立牙槽骨 CT 图像灰度值与弹性模量之间的内在关系,并以此为基础实现非均质牙槽骨模型的材料赋值,该方法被许多国内外学者所认可[20-21]。对于均质型牙槽骨模型材料参数的定义则直接将非均质模型中的网格单元进行统一赋值,取弹性模量 490 MPa,泊松比 0.3[9],从而保证均质模型和非均质模型具有完全相同的网格单元和节点。在这项对比研究中,除牙槽骨模型的力学特性不同以外,其他设置均完全相同,所以分析结果的差异性可能主要体现在牙槽骨弹性模量上。为此,我们进一步假设将均质型牙槽骨模型的弹性模量提高 10 倍至 4 900 MPa,其大小接近非均质牙槽骨模型中不同区域牙槽骨弹性模量的中间值,研究牙槽骨弹性模量可能对牙周膜力学响应产生的影响。为方便后续的分析讨论,将均质型(E = 490 MPa)牙槽骨模型编号为①,非均质型牙槽骨模型编号为②,均质型(E = 4 900 MPa)牙槽骨模型编号为③。在有限元分析过程中,所有模型均假设为各向同性体。
进行定义[20, 27]。赋值完成之后的牙槽骨体网格模型如图 2a 所示,模型中的网格单元被赋予不同的颜色表示其拥有不同的材料参数,每种颜色代表的材料参数如图 2b 所示。该材料赋值方法的基本依据是不同骨密度的牙槽骨经扫描会获得不同灰度值的 CT 图像,如式(3)所示,骨质越致密其 CT 图像灰度值就越高。另外,牙槽骨的弹性模量与其骨密度也存在密切联系,如式(4)所示,牙槽骨骨密度越大其弹性模量越大,因此可以建立牙槽骨 CT 图像灰度值与弹性模量之间的内在关系,并以此为基础实现非均质牙槽骨模型的材料赋值,该方法被许多国内外学者所认可[20-21]。对于均质型牙槽骨模型材料参数的定义则直接将非均质模型中的网格单元进行统一赋值,取弹性模量 490 MPa,泊松比 0.3[9],从而保证均质模型和非均质模型具有完全相同的网格单元和节点。在这项对比研究中,除牙槽骨模型的力学特性不同以外,其他设置均完全相同,所以分析结果的差异性可能主要体现在牙槽骨弹性模量上。为此,我们进一步假设将均质型牙槽骨模型的弹性模量提高 10 倍至 4 900 MPa,其大小接近非均质牙槽骨模型中不同区域牙槽骨弹性模量的中间值,研究牙槽骨弹性模量可能对牙周膜力学响应产生的影响。为方便后续的分析讨论,将均质型(E = 490 MPa)牙槽骨模型编号为①,非均质型牙槽骨模型编号为②,均质型(E = 4 900 MPa)牙槽骨模型编号为③。在有限元分析过程中,所有模型均假设为各向同性体。
图 2.
Non-uniform model of alveolar bone
非均质牙槽骨模型
a. 牙槽骨体网格模型;b. 不同颜色代表的材料参数
a. volume mesh model of alveolar bone; b. material parameters represented by colour coding
 |
3 |
 |
4 |
 |
5 |
1.3. 有限元模型约束条件及载荷
有限元分析中,牙槽骨的底部完全固定,矫治力施加在尖牙牙冠的中心位置,如图 1 所示,牙周膜与牙槽骨、牙周膜与尖牙之间的接触关系均为绑定。临床正畸治疗中,牙齿整体移动所需要的最佳矫治力范围为 1.0~1.5 N[4],牙齿绕根向转动所需要的最佳矫治力矩范围为 2.0~3.0 Nmm[28]。因此,选择分别对尖牙施加 1 N 的根向压入力和 2 Nmm 的根向扭矩,研究不同载荷形式下牙周膜对均质型和非均质型牙槽骨模型力学响应的差异,主要参考牙周膜静水压应力和最大对数主应变。
2. 结果
当对尖牙施加 1 N 大小的根向压入力时,牙周膜对① 均质型(E = 490 MPa)和② 非均质型牙槽骨模型的应力和应变响应如图 3 所示。牙周膜应力为正值表示牙周膜处于受压的状态,反之,牙周膜应力为负值表示牙周膜处于受拉的状态。牙周膜应变为正值表示牙周膜处于受拉的状态,而牙周膜应变为负值则表示牙周膜处于受压的状态。从图 3 中可以看出,尖牙受 1 N 根向压入力时,对于不同类型的牙槽骨模型,牙周膜最大和最小应力应变出现的位置基本相同,但是具体数值却不一样。如表 2 所列,与① 均质型牙槽骨模型(E = 490 MPa)相比,当牙槽骨模型为② 非均质模型时,牙周膜的最大应力降低了 13.13%,同时最小应力提高了 49.29%;牙周膜的最大应变降低了 35.57%,最小应变则提高了 18.83%。可见,对于不同类型的牙槽骨模型,在牙齿平动时牙周膜的应力和应变响应均存在一定差异。
图 3.
Loading 1 N force to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
对尖牙施加 1 N 根向压入力,不同牙槽骨模型作用下的牙周膜应力和应变云图
表 2. The effect of alveolar bone models on PDL stress and strain under different loads.
不同载荷形式下,牙槽骨模型对牙周膜应力应变的影响
| 载荷形式 | 牙槽骨模型 | 牙周膜最大应力/MPa | 牙周膜最小应力/MPa | 牙周膜最大应变 | 牙周膜最小应变 |
| 1 N 根向压入力 | ① 均质型,E = 490 MPa | 8.074E-2 | −1.962E-2 | 4.967E-3 | 6.447E-5 |
| ② 非均质型 | 7.014E-2 | −2.929E-2 | 3.200E-3 | 7.661E-5 | |
| ② 与① 比较 | ↓13.13% | ↑49.29% | ↓35.57% | ↑18.83% | |
| 2 Nmm 根向扭矩 | ① 均质型,E = 490 MPa | 2.159E-2 | −2.794E-2 | 3.471E-3 | 3.108E-4 |
| ② 非均质型 | 1.737E-2 | −1.675E-2 | 2.234E-3 | 1.208E-4 | |
| ③ 均质型,E = 4 900 MPa | 1.729E-2 | −1.712E-2 | 2.249E-3 | 1.256E-4 | |
| ② 与① 比较 | ↓19.55% | ↓40.05% | ↓35.64% | ↓61.13% | |
| ③ 与① 比较 | ↓19.92% | ↓38.73% | ↓35.21% | ↓59.59% |
当对尖牙施加 2 Nmm 的根向扭矩时,牙周膜对① 均质型(E = 490 MPa)和② 非均质型牙槽骨模型的应力和应变响应如图 4 所示。从图 4 中可以看出对于不同类型牙槽骨模型①和②,牙周膜最小应力、最大和最小应变出现的位置基本相同,但牙周膜最大应力出现的位置却不相同。此外,牙周膜最大和最小应力应变值也因牙槽骨模型的不同而存在一定差异。如表 2 所列,与① 均质型牙槽骨模型相比,当牙槽骨模型为② 非均质模型时,牙周膜的最大和最小应力分别降低了 19.55% 和 40.05%,牙周膜最大和最小应变分别降低了 35.64% 和 61.13%。可见,对于不同类型的牙槽骨模型,在牙齿转动时牙周膜的应力和应变响应也存在一定差异。
图 4.
Loading 2 Nmm moment to the canine along its root direction, the stress and strain nephograms of PDL with different alveolar bone models
对尖牙施加 2 Nmm 根向扭矩,不同牙槽骨模型作用下的牙周膜应力和应变云图
如图 4 所示,当对尖牙施加 2 Nmm 的根向扭矩时,不同弹性模量的均质型牙槽骨模型①和③ 对牙周膜应力应变响应的影响也存在一定差异。当牙槽骨弹性模量提高至 4 900 MPa 之后,所引起的牙周膜最小应力、最大和最小应变出现的位置基本相同,但具体数值因牙槽骨弹性模量的不同而有所差异。如表 2 所列,当牙槽骨的弹性模量提高 10 倍之后,牙周膜的最大和最小应力值分别降低了 19.92% 和 38.73%,牙周膜最大和最小应变值也分别降低了 35.21% 和 59.59%。可见,矫治力作用下牙周膜的生物力学响应很大程度上受牙槽骨弹性模量的影响。
3. 讨论
通过上述的有限元分析可知,无论在牙齿平动或是转动时,牙槽骨模型均会对牙周膜的生物力学响应产生影响。当牙槽骨由① 均质模型转为② 非均质模型时,牙周膜的最大应力值在一定程度上降低了。有研究表明牙周膜的应力与牙齿移动过程中的牙根吸收有关[9-10],当牙周膜应力过大时会造成牙周膜局部血流闭塞,诱发牙根吸收[1-2]。可见采用均质型牙槽骨模型研究矫治力作用下牙周膜的应力时更偏向于获得较高的应力值,进而选择一个更保守的矫治力。另一方面,牙周膜的应变与矫治过程中牙齿的移动速度相关,在一定范围内牙周膜的应变越大则牙齿的移动速度就越快[7-8],当采用均质型牙槽骨模型研究牙周膜的应变分布时会获得一个较大的应变值,进而认为牙齿已具有较高的移动速度,同样会引导正畸医生选择一个较小的矫治力。矫治力过小会延长正畸治疗周期,降低患者配合治疗的意愿,难以实现理想的正畸治疗[4]。
另外,我们假设将① 均质型牙槽骨模型弹性模量增大 10 倍,重点分析了在尖牙受到 2 Nmm 的根向扭矩时,牙周膜对不同弹性模量的牙槽骨力学响应的差异性。从有限元分析结果(表 2)可以看出在模型网格和节点完全相同的情况下,当牙槽骨弹性模量提高之后,牙周膜的最大应力和最大应变均有所降低。所以,采用高弹性模量的牙槽骨模型进行有限元分析时,分析结果会引导正畸医生选择较高的矫治力,相反,低弹性模量的牙槽骨模型则会诱导医生选择一个更低的矫治力。然而,更高或者更低的矫治力均不利于正畸治疗[4, 8-9]。为了获得更加安全高效的正畸治疗,明确载荷作用下牙周膜的生物力学响应至关重要。因此,根据患者牙槽骨的实际情况,设定合适的牙槽骨力学参数,对于采用有限元法研究正畸治疗非常重要。
牙槽骨作为结构复杂的人体生物组织,内部含有神经管、骨小梁、骨髓小腔等组织结构,不同区域的力学特性差异很大[7, 17]。位于牙槽骨表层的骨组织骨质致密、强度高,称为皮质骨;位于牙槽骨内部的骨组织则骨质疏松,呈海绵状,称为松质骨[20, 27]。在认识到牙周膜生物力学响应受牙槽骨力学特性影响的前提下,构建符合人体牙槽骨生物力学特性的有限元模型对于提高有限元分析结果的精确度有着积极促进作用。相比于均质型牙槽骨模型,非均质型牙槽骨模型模糊了皮质骨和松质骨的界限,依据每个网格单元所处的 CT 图像灰度值对网格单元进行材料赋值,突显出牙槽骨不同区域骨质特性的差异性,更加贴近牙槽骨实际状况,有利于获得更加准确的分析结果。值得注意的是,非均质牙槽骨模型的整体材料属性在一定程度上受其网格单元尺寸的影响。模型中网格尺寸越小,每个单元越能依据其所在的微小局部 CT 图像进行个性化材料赋值,越容易获得更加细致的、差异性的牙槽骨模型。当网格尺寸变大时,其所覆盖的 CT 图像区域也更大,即便覆盖区域的 CT 图像有一定差异,也无法对该网格单元实现多种材料赋值。如图 2a 所示,从牙槽骨的横断面来看,皮质骨和松质骨的分界面并不明显,其中一部分原因就是该断面上牙槽骨网格单元的尺寸过大。不过,从模型收敛性测试结果来看,边缘区域过大的牙槽骨网格单元并没有对牙周膜的力学响应产生不可忽视的影响。
在非均质牙槽骨模型中,采用 CT 图像灰度值进行材料赋值的网格单元中最大的弹性模量是 14 420.28 MPa,其量级与其他研究中报道的皮质骨弹性模量 13 700 MPa 非常接近[7, 17],间接证明了材料赋值公式的准确性。另外,如图 2a 所示,牙槽骨模型表面的部分区域被表示低弹性模量的蓝色所覆盖,这与处于真实牙槽骨表面的皮质骨力学特性不符。这主要是因为人体牙槽骨外还附着有骨膜和牙龈等组织结构,在牙槽骨模型构建过程中,有一部分口腔软组织被当作牙槽骨进行了重建,但这并不会对有限元分析结果产生影响,从中我们也可以发现非均质模型的另外一个优点。一般来说,对于牙槽骨模型边界的划定主要依靠人工进行手动分割,操作者的熟练程度和工作经验直接影响着牙槽骨模型的结构和大小,如果采用均质模型进行建模,那么模型构造上可能就与真实的牙槽骨存在结构差异,在一定程度上影响了分析结果。而当采用非均质建模方法时,因模型中的所有网格单元均依据其所在的 CT 图像灰度值进行材料赋值,即便有一部分外层软组织或者牙槽骨内部的骨髓小腔、神经管空腔等力学特性远异于骨组织的组织结构,被误以为牙槽骨进行有限元建模,也会因其 CT 图像灰度值偏低被赋予相应的材料参数,不会因模型精度影响有限元分析结果。
4. 结论
以一例临床病例作为研究对象,基于患者的 CT 图像构建了其尖牙、牙周膜和牙槽骨的有限元模型。其中,牙槽骨模型分别设定为均质模型和非均质模型,其他牙颌组织模型设定均相同。通过对尖牙施加根向矫治力和扭矩探究牙周膜在不同牙槽骨模型下的应力应变响应。结果表明:(1)无论牙齿平动或是转动,当牙槽骨为均质模型时,牙周膜在同等条件下会产生更大的应力和应变,会误导正畸医生选择一个较小的矫治力;(2)牙周膜的生物力学响应受牙槽骨力学参数影响较为显著,当牙槽骨弹性模量由 490 MPa 增大 10 倍至 4 900 MPa 时,牙周膜的最大应力和应变值分别降低了 19.92% 和 35.21%;(3)相比于均质牙槽骨模型,非均质牙槽骨模型依据每个网格单元所处的 CT 图像灰度值对模型进行材料赋值,更能体现真实牙槽骨组织骨质特性的差异性,有助于提高有限元分析的精确性。研究结果为构建更加精确的牙颌组织有限元模型提供了技术支持。
利益冲突声明:本文全体作者均声明不存在利益冲突。
Funding Statement
浙江省教育厅一般科研项目(Y201941138);浙江省自然科学基金(LQ20E050013);宁波市自然科学基金(2019A610243);国家自然科学基金(51775506);浙江省公益技术应用研究项目(LGG19E050022,LGF18H140002)
The General Research Project Foundation of Zhejiang Provincial Education Department; The Zhejiang Provincial Natural Science Foundation of China; The Ningbo Municipal Natural Science Foundation of China; The National Natural Science Foundation of China; The Public Welfare Technology Application Research Project of Zhejiang Province, China
References
- 1.Kim T, Suh J, Kim N, et al Optimum conditions for parallel translation of maxillary anterior teeth under retraction force determined with the finite element method. Am J Orthod Dentofac. 2010;137:639–647. doi: 10.1016/j.ajodo.2008.05.016. [DOI] [PubMed] [Google Scholar]
- 2.Lombardo L, Stefanoni F, Mollica F, et al Three dimensional finite-element analysis of a central lower incisor under labial and lingual loads. Prog Orthod. 2012;13:154–163. doi: 10.1016/j.pio.2011.10.005. [DOI] [PubMed] [Google Scholar]
- 3.赵志河, 李宇 正畸牙移动细胞生物力学研究进展. 医用生物力学. 2010;25(6):393–398. doi: 10.3871/j.1004-7220.2010.06.398.. [DOI] [Google Scholar]
- 4.Wu J L, Liu Y F, Peng W, et al A biomechanical case study on the optimal orthodontic force on the maxillary canine tooth based on finite element analysis. J Zhejiang Univ-Sci B. 2018;19:535–546. doi: 10.1631/jzus.B1700195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kawarizadeh A, Bourauel C, Jager A Experimental and numerical determination of initial tooth mobility and material properties of the periodontal ligament in rat molar specimens. Eur J Orthodont. 2003;25(6):569–578. doi: 10.1093/ejo/25.6.569. [DOI] [PubMed] [Google Scholar]
- 6.Natali A N, Pavan P G, Carniel E L, et al Viscoelastic response of the periodontal ligament: an experimental-numerical analysis. Connect Tissue Res. 2004;45(4-5):222–230. doi: 10.1080/03008200490885742. [DOI] [PubMed] [Google Scholar]
- 7.Qian Y L, Fan Y B, Liu Z, et al Numerical simulation of tooth movement in a therapy period. Clin Biomech. 2008;23(S1):S48–S52. doi: 10.1016/j.clinbiomech.2007.08.023. [DOI] [PubMed] [Google Scholar]
- 8.李再金. 口腔正畸力模拟及牙齿移动调制研究. 哈尔滨: 哈尔滨工业大学, 2014.
- 9.Liao Z P, Chen J N, Li W, et al Biomechanical investigation into the role of the periodontal ligament in optimising orthodontic force: a finite element case study. Arch Oral Biol. 2016;66:98–107. doi: 10.1016/j.archoralbio.2016.02.012. [DOI] [PubMed] [Google Scholar]
- 10.Field C, Ichim I, Swain M V, et al Mechanical responses to orthodontic loading: a 3-dimensional finite element multi-tooth model. Am J Orthod Dentofac. 2009;135(2):174–181. doi: 10.1016/j.ajodo.2007.03.032. [DOI] [PubMed] [Google Scholar]
- 11.王洪宁, 秦行林, 刘东旭, 等 基于micro-CT成像的仿真牙周膜有限元建模探讨. 口腔疾病防治. 2016;24(5):283–287. doi: 10.12016/j.issn.2096-1456.2016.05.005. [DOI] [Google Scholar]
- 12.仵健磊, 彭伟, 董辉跃, 等 基于超-黏弹性的牙周膜本构模型构建及模拟. 中国生物医学工程学报. 2018;37(2):194–201. doi: 10.3969/j.issn.0258-8021.2018.02.009. [DOI] [Google Scholar]
- 13.Konermann A, Malat R A, Skupin J, et al In vivo determination of tooth mobility after fixed orthodontic appliance therapy with a novel intraoral measurement device. Clin Oral Invest. 2017;21:1283–1289. doi: 10.1007/s00784-016-1881-5. [DOI] [PubMed] [Google Scholar]
- 14.Masakazu H, Taiji A, Teruko T Y Computer simulation of orthodontic tooth movement using CT image-based voxel finite element models with the level set method. Comput Method Biomec. 2016;19(5):474–483. doi: 10.1080/10255842.2015.1042463. [DOI] [PubMed] [Google Scholar]
- 15.Ashrafi M, Ghalichi F, Mirzakouchaki B, et al Numerical simulation of hydro-mechanical coupling of periodontal ligament. P I Mech Eng H. 2020;234(2):171–178. doi: 10.1177/0954411919887071. [DOI] [PubMed] [Google Scholar]
- 16.Cozzani M, Sadri D, Nucci L, et al The effect of Alexander, Gianelly, Roth, and MBT bracket systems on anterior retraction: a 3-dimensional finite element study. Clin Oral Invest. 2020;24(3):1351–1357. doi: 10.1007/s00784-019-03016-6. [DOI] [PubMed] [Google Scholar]
- 17.Marangalou J H, Ghalichi F, Mirzakouchaki B Numerical simulation of orthodontic bone remodeling. Orthod Waves. 2009;68(2):64–71. doi: 10.1016/j.odw.2008.12.002. [DOI] [Google Scholar]
- 18.Wu J L, Liu Y F, Wang D C, et al Investigation of effective intrusion and extrusion force for maxillary canine using finite element analysis. Comput Method Biomec. 2019;3:1–9. doi: 10.1080/10255842.2019.1661390. [DOI] [PubMed] [Google Scholar]
- 19.Benaissa A, Merdjib A, Bendjaballah M Z, et al Stress influence on orthodontic system components under simulated treatment loadings. Comput Meth Prog Bio. 2020;195:105569. doi: 10.1016/j.cmpb.2020.105569. [DOI] [PubMed] [Google Scholar]
- 20.Liu Y F, Fan Y Y, Dong H Y, et al An investigation of two finite element modeling solutions for biomechanical simulation using a case study of a mandibular bone. J Biomech Eng-T Asme. 2017;139(12):121006. doi: 10.1115/1.4037633. [DOI] [PubMed] [Google Scholar]
- 21.Bujtar P, Sandor G K B, Bojtos A, et al Finite element analysis of the human mandible at 3 different stages of life. Or Surg Or Med Or Pa. 2010;110(3):301–309. doi: 10.1016/j.tripleo.2010.01.025. [DOI] [PubMed] [Google Scholar]
- 22.Toms S R, Eberhardt A W A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. Am J Orthod Dentofac. 2003;123(6):657–665. doi: 10.1016/S0889-5406(03)00164-1. [DOI] [PubMed] [Google Scholar]
- 23.魏志刚, 汤文成, 严斌, 等 基于黏弹性模型的牙周膜生物力学研究. 东南大学学报: 自然科学版. 2009;39(3):484–489. [Google Scholar]
- 24.Oskui I Z, Hashemi A Dynamic tensile properties of bovine periodontal ligament: a nonlinear viscoelastic model. J Biomech. 2016;49(5):756–764. doi: 10.1016/j.jbiomech.2016.02.020. [DOI] [PubMed] [Google Scholar]
- 25.Toms S R, Dakin G J, Lemons J E, et al Quasi-linear viscoelastic behavior of the human periodontal ligament. J Biomech. 2002;35(10):1411–1415. doi: 10.1016/S0021-9290(02)00166-5. [DOI] [PubMed] [Google Scholar]
- 26.Wei Z G, Yu X L, Xu X G, et al Experiment and hydro-mechanical coupling simulation study on the human periodontal ligament. Comput Methods Programs Biomed. 2014;113(3):749–756. doi: 10.1016/j.cmpb.2013.12.011. [DOI] [PubMed] [Google Scholar]
- 27.Liu Y F, Wang R, Baur D A, et al A finite element analysis of the stress distribution to the mandible from impact forces with various orientations of third molars. J Zhejiang Univ-Sci B. 2018;19:38–48. doi: 10.1631/jzus.B1600552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wu Jianlei, Liu Yunfeng, Li Boxiu, et al Numerical simulation of optimal range of rotational moment for the mandibular lateral incisor, canine and first premolar based on biomechanical responses of periodontal ligaments: a case study. Clin Oral Investig. 2021;25(3):1569–1577. doi: 10.1007/s00784-020-03467-2. [DOI] [PubMed] [Google Scholar]