Abstract
传统基于脑电(EEG)的抑郁症研究将电极视为孤立节点,忽略了它们之间的关联性,难以发掘抑郁症患者异常大脑拓扑改变。为此,本文提出一种基于脑功能网络(BFN)的抑郁症识别框架,为避免容积导体效应,相位延迟指数用于构建BFN;以加权与二值化BFN信息互补为基础,选取“小世界”特性密切相关及最小生成树特定脑区BFN指标,采用递进式指标分析策略寻找抑郁症识别潜在标识物。本文以48名受试者静息态EEG数据用于验证方案,结果表明组间同步性在左颞、右顶枕、右额脑区明显改变;加权BFN最短路径长度和聚类系数,二值化BFN左颞和右额的叶子分数及右顶枕的直径与患者健康问卷9项(PHQ-9)之间具有相关性,且获得最高94.11%的识别率。此外,研究发现相对于健康对照者,抑郁症患者的信息处理能力明显下降。通过上述结论,期望本研究结果可为BFN构建与分析提供新的思路,为抑郁症识别潜在标识物的发掘提供新的方法。
Keywords: 抑郁症, 脑功能网络, 静息态脑电, 相位延迟指数
Abstract
Traditional depression research based on electroencephalogram (EEG) regards electrodes as isolated nodes and ignores the correlation between them. So it is difficult to discover abnormal brain topology alters in patients with depression. To resolve this problem, this paper proposes a framework for depression recognition based on brain function network (BFN). To avoid the volume conductor effect, the phase lag index is used to construct BFN. BFN indexes closely related to the characteristics of “small world” and specific brain regions of minimum spanning tree were selected based on the information complementarity of weighted and binary BFN and then potential biomarkers of depression recognition are found based on the progressive index analysis strategy. The resting state EEG data of 48 subjects was used to verify this scheme. The results showed that the synchronization between groups was significantly changed in the left temporal, right parietal occipital and right frontal, the shortest path length and clustering coefficient of weighted BFN, the leaf scores of left temporal and right frontal and the diameter of right parietal occipital of binary BFN were correlated with patient health questionnaire 9-items (PHQ-9), and the highest recognition rate was 94.11%. In addition, the study found that compared with healthy controls, the information processing ability of patients with depression reduced significantly. The results of this study provide a new idea for the construction and analysis of BFN and a new method for exploring the potential markers of depression recognition.
Keywords: Depression, Brain function network, Resting state electroencephalogram, Phase lag index
引言
抑郁症是一种常见精神疾病,持续情绪低落、兴趣减退是其典型临床症状[1]。据世界卫生组织披露,全球约有2.64亿人不同程度受其影响[2],每年约有85万人直接或间接因其导致自杀身亡。重度抑郁症复发率约为78%左右,完全治愈概率小[3]。相对于多数身体疾病,抑郁症潜在神经机制和病理学机制尚不清楚。针对抑郁症高发病率、高死亡率、高复发率等特点,为了避免随时间推移造成大脑不可逆转的损伤,本文基于脑功能网络(brain functional network,BFN)展开了抑郁症识别研究。
近年来,随着生物医学工程、神经科学、计算机科学等多学科交叉融合,研究人员发现大脑生理信号的异常改变与抑郁症密切相关,他们以磁共振成像(magnetic resonance imaging,MRI)、脑磁图(magnetoencephalography,MEG)和脑电图(electroencephalograms,EEG)为基础数据分别从大脑结构和功能视角展开了大量相关研究。Yao等[4]通过对抑郁症患者MRI形态学特征研究发现,随着抑郁症程度不断加深患者海马区和杏仁核区的萎缩不断向其他区域扩展。基于MEG特征Alageel等[5]研究发现抑郁症患者右顶叶和额叶皮质活动明显弱化。更多研究以EEG信号特征为切入点,先后利用多模态EEG信号特征融合、EEG信号特征与语音信号特征融合、EEG信号特征不同生成策略实现了自动抑郁症识别[3, 6-7]。
基于特征的抑郁症识别方法有其固有优势,且人脑又是一种极为复杂的系统,若仅以形态学特征或生理学特征为基础开展研究,难以揭示抑郁症患者异常的大脑拓扑改变规律。随着以图论为基础的复杂网络发展,使用MRI、MEG和EEG等生理数据构建BFN成为可能,随着对BFN核心拓扑研究的不断深入,越来越多证据表明BFN拓扑异常改变与抑郁症存在密切关联[8]。Yu等[9]指出连通性是研究精神疾病患者脑功能异常的有效方法,BFN为神经系统疾病识别研究提供了新的途径。
从BFN层面对抑郁症识别进行研究,需解决两个关键问题:① 何种类型数据更适合于BFN构建?② 如何分析BFN以发掘抑郁症识别的潜在标志物。针对第一个关键问题,众所周知,MRI数据具有较高的空间分辨率,MEG数据和EEG数据具有较高的时间分辨率[10]。BFN连通性被定义为空间上分离的不同神经元之间协调的时间依赖性活动[11]。因此,相对于MRI数据,EEG和MEG数据更适合于BFN构建。且EEG数据获取具有非侵入、安全、易采集、低成本等优势,经综合考虑,本文使用EEG数据作为BFN构建的基础数据。而第二个关键问题,本文则以加权与二值化BFN信息互补为基础展开研究与探索。因此,本研究的开展将为BFN构建与分析提供新思路,为抑郁症识别潜在标识物的发掘提供新方法。
1. 实验及数据预处理
1.1. 实验数据
本研究所用EEG数据来自精神障碍分析的多模式开放数据集(a multi-modal open dataset for mental-disorder analysis,MODMA Dataset)(http://modma.lzu.edu.cn/data/index/)[12],本课题组已签署实验数据使用协议,并获得授权可以使用该数据集中的全部数据。MODMA Dataset包含四种类型的抑郁症患者及对应健康对照受试者数据,包括:① 128通道的事件相关电位(event-related potentials,ERP)数据;② 128通道的静息态EEG数据;③ 3通道的静息态EEG数据;④ 音频数据。
本研究使用MODMA Dataset中第二类数据,该数据包括24名抑郁症患者和29名健康对照受试者,基本信息如下:① 抑郁症患者,患者健康问卷9项(patient health questionnaire 9-items,PHQ-9)得分≥5分,简明国际神经精神障碍访谈检查(mini international neuropsychiatric interview,MINI)得分≥17分;② 健康对照受试者,PHQ-9得分<5分,MINI得分<17分;③ 受试者年龄18~52岁之间,小学以上文化程度,智力正常。④ EEG数据采样率为250 Hz,采集时长约5 min。
为保证组间性别及年龄尽可能匹配,本研究仅使用了24名抑郁症患者(男性∶女性 = 13∶11)和24名健康对照受试者(男性∶女性 = 13∶11)的EEG数据。两组PHQ-9得分的均值±标准差分别为:18.33 ± 3.50和2.58 ± 1.79,组间P < 0.001,差异具有统计学意义。在保证研究有效性和减少计算量的基础上,本文选取均匀分布64通道EEG数据用于BFN的构建。
1.2. 数据预处理
EEG数据采集过程不可避免地会引入噪声,研究表明抑郁症相关的EEG信号主要分布在0.5~50 Hz之间[13],将有限冲激响应带通滤波器用于消除低频漂移和高频噪声。EEG信号噪声主要来源于眼电(electrooculogram,EOG)干扰,即使静息状态下,眨眼所产生EOG信号振幅也是EEG信号振幅十倍以上,在0~16 Hz之间EOG信号噪声与EEG信号严重重叠。为此,本文采用Peng等[14]提出的离散小波变换和自适应噪声消除模型剔除EEG信号中的EOG信号噪声,以获得更加纯净的EEG数据。
2. 本文方法
2.1. BFN构建
网络G = (V, E)是由节点和节点之间的边构成,V是节点集,E是边集。本文中EEG信号对应电极被定义为节点,节点之间的依赖关系被定义为边,同步性被作为依赖关系的载体。为了避免容积导体效应,相位延迟指数(phase lag index, PLI)用于计算节点之间的同步性[15]。任意EEG信号 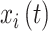 和
和 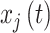 ,t时刻相位差
,t时刻相位差 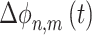 计算过程如式(1)所示:
计算过程如式(1)所示:
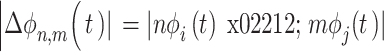 |
1 |
其中,n和m为整数,神经科学中取值为1; 和
和 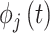 是信号
是信号 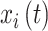 和
和 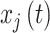 的瞬时相位,如式(2)所示:
的瞬时相位,如式(2)所示:
 |
2 |
其中,arctan是反正切函数,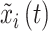 是
是 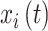 的希尔伯特变换,如式(3)所示:
的希尔伯特变换,如式(3)所示:
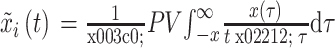 |
3 |
其中,PV是柯西主值。长度L的两个时间序列之间PLI被定义为相位差  的不对称测量,如式(4)所示:
的不对称测量,如式(4)所示:
 |
4 |
其中,sign是符号函数。
研究表明抑郁症患者与健康对照受试者的EEG信号在theta(4~8 Hz)频段存在明显差异[16],EEG信号周期为12 s时,基于PLI构建的BFN趋于最佳状态[17]。因此,本文使用theta频段作为兴趣频段,每12 s计算一次EEG信号通道之间的PLI以生成邻接矩阵。通过计算邻接矩阵对应位置平均值得到64 × 64邻接矩阵Cij,其定义如式(5)所示,进而绘制两组的BFN。
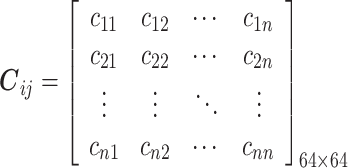 |
5 |
2.2. 加权BFN指标
复杂网络理论阐明了健康人群BFN具有稳定的“小世界”特性,即较小的最短路径长度和较大的聚类系数,而此结论对于精神疾病患者并不成立[18]。因此,本文选择最短路径长度和聚类系数作为加权BFN的初始指标。
最短路径长度能够刻画网络全局连接特性和功能集成特性。若任意两节点i和j之间存在最短路径Lij,则加权BFN中任意两个节点之间的最短路径长度为Lij = 1/wij,其中wij是邻接矩阵Cij中相应位置的元素,N是加权BFN的总节点数量。加权BFN的最短路径长度L是节点最短路径长度的平均值,定义如式(6)所示:
 |
6 |
聚类系数能够刻画网络局部连接特性和功能隔离特性,节点聚类系数Ci是邻接节点互为邻居的概率,定义如式(7)所示:
 |
7 |
其中,i, k, j是加权BFN中任意三节点,wij, wik, wjk是式(5)邻接矩阵中相应位置的元素。加权BFN的聚类系数C是节点聚类系数的平均值,定义如式(8)所示:
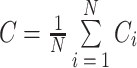 |
8 |
2.3. 二值化BFN指标
为研究组间差异性、提高组间可比性、避免加权BFN稀疏敏感度问题,本文以信息互补为理论基础,采用最小生成树(minimum spanning tree,MST)对加权BFN进行二值化。MST保证了组间差异性主要由拓扑差异产生,本文采用克鲁斯卡尔算法构造MST,其过程如图1所示,其中使用G = (V, E)表示原始BFN,V是节点集,E是边集;MST(V, TE)是原始BFN对应的初始MST,TE是MST的边集,初始值为空,即TE={};ei是BFN中的任意边。
图 1.
MST construction of weighted BFN
加权BFN的MST构造
MST提供了原始网络的核心拓扑信息[19],本文选择神经科学领域所公认的能够有效分析精神疾病的典型MST属性:度、叶子分数、直径、介子中心、树层次、离心率等作为二值化BFN的初始指标[20]。度k描述了与节点直接相连接的边数,计算过程如式(9)所示:
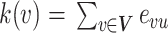 |
9 |
其中,v和u是节点集V中的任意两个节点,evu表示由节点v和u所连接构成的边。
叶子分数Lf描述了叶子节点数量与MST总节点数量之比,计算过程如式(10)所示:
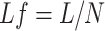 |
10 |
其中,L表示叶子节点数量,N表示MST总节点数量。
直径d描述了给定节点的最短路径长度,计算过程如式(11)所示:
 |
11 |
其中,TE(v)表示MST边集TE中经过节点v边的子集,max{}表示求集合中最大值。
介子中心BC描述了通过给定节点最短路径的比例,计算过程如式(12)所示:
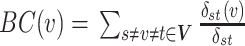 |
12 |
其中,s, v, t是节点集V中的任意三个不相同节点,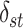 是s和t之间最短路径的数目,
是s和t之间最短路径的数目, 是节点s和t之间最短路径通过节点v的数目。
是节点s和t之间最短路径通过节点v的数目。
树层次Th是MST的整合能力和中心节点过载之间平衡关系的量化度量,计算过程如式(13)所示:
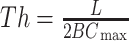 |
13 |
其中,BCmax是最大的BC。
离心率E描述了给定节点到其余节点距离的最大值,计算过程如式(14)所示:
 |
14 |
其中,d(v, u)表示v节点到节点集V中任意其它节点u的距离。
2.4. 递进式潜在标识物挖掘
为了发掘抑郁症识别的潜在标识物,提出递进式初始指标分析策略。第一步:采用非参数置换检验评估BFN组间差异具有统计学意义的初始指标[21],首先计算BFN组间初始指标均值差异(t值)作为检验统计量的观察值,接着全部受试者被随机分配至抑郁症组和健康对照组,保持组间受试者数量不变,重复计算1 000次重排列后组间t值,得到组间差异检验零分布,使用t值大于检验统计量观察值的样本排列比例作为组间差异P值,P < 0.05,则差异具有统计学意义。
基于PHQ-9的面对面访谈是抑郁症诊断的基础,生物指标或者BFN指标与量表得分之间相关性被广泛用于评估相应指标是否能够作为诊断有关疾病的潜在标识物[22-23]。基于此,递进式分析策略第二步为:基于皮尔逊相关系数分析差异具有统计学意义的指标与PHQ-9得分之间的相关性,P < 0.05,则具有相关性。
2.5. 识别性能评估
评估抑郁症识别潜在标识物是否有效,本文采用K近邻 (K-nearest neighbor,KNN)分类器,已有研究表明KNN分类器在抑郁症识别领域优于其他分类器[6, 24-26]。为获得具有统计学意义的结果,KNN分类器执行10折交叉验证。本研究中准确率(accuracy),敏感性(sensitivity)和特异性(specificity)用于识别性能的评估。数学软件MATLAB R2018a版(MathWorks Inc.,美国)用于实现KNN分类和10折交叉验证。
3. 结果
3.1. 二值化BFN差异
克鲁斯卡尔算法所生成两组的邻接矩阵及对应MST电极分布如图2所示,此图并不能完全清晰展示组间二值化BFN差异。为此,计算两组邻接矩阵的差异矩阵,进而绘制差异矩阵对应BFN的三维图,如图3所示,上排为左半球和右半球的外侧视图,下排为左半球和右半球的内侧视图,中间为全脑背侧图。从图3左、右图对应位置的三维图可以看出,相比于健康对照组,抑郁症组左颞(left temporal,LT)和右顶枕(right parietal-occipital,RPO)脑区的连接密度增加,即同步性增加;右额(right frontal,RF)脑区连接密度减少,即同步性减少。此结果其意味着抑郁症组和健康对照组之间的二值化BFN差异主要分布在LT、RPO、RF三个脑区,即抑郁症患者BFN在这三个脑区出现了拓扑异常。
图 2.

Adjacency matrix and corresponding MST electrode distribution
邻接矩阵及对应MST电极分布
图 3.

Three-dimensional diagram of difference matrix corresponding BFN
差异矩阵对应BFN的三维图
3.2. 抑郁症识别潜在标识物
本文以非参数置换检验对全脑加权BFN功能集成属性最短路径长度、功能隔离属性聚类系数、以及二值化BFN的LT、RPO、RF等脑区初始指标进行评估。全脑加权BFN的最短路径长度和聚类系数的组间差异结果如图4所示,箱形图中心线代表均值,星号(*)代表差异具有统计学意义(P < 0.05)。从图4可看出,无论最短路径长度还是聚类系数两组间差异均具有统计学意义。相比于健康对照组,抑郁症组最短路径长度增加、聚类系数降低,意味着抑郁症患者这两项指标出现了异常,因此全脑加权BFN的最短路径长度和聚类系数可作为抑郁症识别的潜在标志物候选对象。二值化BFN在LT、RPO、RF三个脑区初始指标的组间差异结果如图5所示,可以看出两组间在LT脑区的叶子分数、树层次、离心率,RPO脑区的直径,以及RF脑区的叶子分数和直径的差异均具有统计学意义,此意味这六项指标可作为抑郁症识别潜在标志物的候选对象。
图 4.
Difference analysis of whole brain weighted BFN (*P < 0.05)
全脑加权BFN差异性分析(*P < 0.05)
图 5.

Difference analysis of binarized BFN (*P < 0.05)
二值化BFN差异性分析(*P < 0.05)
基于递进式初始指标分析策略,使用皮尔逊相关系数评估具有统计学意义的BFN指标与PHQ-9得分之间相关性,结果如图6所示,r表示相关系数,P值为概率,斜线表示拟合曲线。从图6可知,全脑加权BFN最短路径长度和聚类系数与PHQ-9得分两者具有相关性,二值化BFN中LT和RF的叶子分数以及RPO的直径与PHQ-9得分之间也具有相关性。因此,这五项BFN指标被作为抑郁症识别的潜在标志物。考虑篇幅限制,图中未列出与PHQ-9得分不相关的指标。
图 6.

BFN index correlated with PHQ-9 score
PHQ-9评分相关的BFN指标
3.3. 潜在标志物识别性能
评估上述五项BFN指标识别抑郁症的性能,将其输入至KNN分类器(k=3, 搜索算法=“kd-tree”)进行10折交叉验证,当五项指标共同作为输入时,最低分类准确率是86.42%,敏感性、特异性分别是81.56%和91.58%(如图7所示:迭代-5);最高分类准确率是94.35%,敏感性、特异性分别是91.84%和97.36%(如图7所示:迭代-9);10折交叉验证的平均准确率是89.91%。因此,这五项指标共同作为潜在标识物可以有效识别抑郁症。
图 7.

Recognition result of 10-fold cross validation
10折交叉验证的识别结果
每项指标单独作为潜在标志物的抑郁症识别性能结果如表1所示,五项指标作为潜在标志物识别能力由强到弱依次为:全脑聚类系数、最短路径长度、LT-叶子分数、RF-叶子分数、RPO-直径。
表 1. Recognition ability of BFN index alone as potential bio marker.
BFN指标单独作为潜在标识物的识别能力
| 潜在标志物 | 准确率 | 敏感性 | 特异性 |
| 最短路径长度 | 90.25% | 87.32% | 92.83% |
| 聚类系数 | 94.11% | 92.98% | 95.37% |
| LT-叶子分数 | 89.34% | 92.87% | 86.44% |
| RPO-直径 | 84.12% | 90.72% | 80.19% |
| RF-叶子分数 | 87.66% | 89.37% | 83.44% |
3.4. 泛化性能
为了验证本文提出方法的泛化能力,采用来自亚利桑那大学公开抑郁症EEG数据集(https://unmm-my.sharepoint.com/personal/jcavanagh_unm_edu/_layouts/15/onedrive.aspx)[27]进行验证。该数据集共包括46名(男性∶女性 = 12∶34)抑郁症患者和75名(男性∶女性 = 35∶40)健康对照受试者的64通道EEG数据。两组的贝克抑郁自评量表(Beck depression inventory,BDI)均值 ± 标准差分别为22.22 ± 4.90和1.73 ± 1.65,组间P<0.01,差异具有统计学意义。
根据本文所提出方法,计算上述公开数据集中全脑加权BFN最短路径长度和聚类系数、LT-叶子分数、RPO-直径、RF-叶子分数,然后将这些指标共同输入至KNN分类器(参数设置与上文相同)进行10折交叉验证,获得了87.53%的平均准确率,此结果略低于MODMA Dataset 上的89.91%平均准确率。此外,将五项指标分别作为抑郁症识别的潜在标识物,识别结果如表2所示。可以看出无论五项潜在标识物共同或者独立作为KNN分类器的输入,准确率均有略微下降,但整体而言没有明显下降,说明了本文所提出方法在一定程度上具有健壮的泛化能力。
表 2. Generalization performance verification result of five index.
五项指标泛化性能验证结果
| 潜在标志物 | 准确率 | 敏感性 | 特异性 |
| 最短路径长度 | 90.05% | 86.96% | 93.14% |
| 聚类系数 | 93.83% | 96.17% | 91.49% |
| LT-叶子分数 | 85.21% | 82.25% | 88.17% |
| RPO-直径 | 81.08% | 89.72% | 80.19% |
| RF-叶子分数 | 86.43% | 87.21% | 85.65% |
4. 讨论
由于研究方法的不同,有关抑郁症的研究也存在相悖结论。Zhou等[28]发现抑郁症患者大脑功能连接数量增加,而Connolly等[29]发现抑郁症患者大脑功能连接数量减少。本文基于MST差异矩阵分析发现相对于健康对照受试者,抑郁症患者BFN的同步性发生改变,LT和RPO脑区同步性明显增加,RF脑区同步性明显降低。作者推测此结果是抑郁症患者大脑信息处理功能异常在BFN层面的表现形式,此结论也得到了相关研究的间接验证,Joormann等[30]指出抑郁症患者情绪调节能力存在明显下降的趋势,Leistedt等[31]发现抑郁症患者BFN信息处理能力下降。本研究揭示抑郁症患者部分脑区的BFN同步性存在失衡,但是抑郁症患者大脑信息处理功能异常的原因还需进一步探索以获得更为可靠的结论。
小世界网络是一种最优的网络组织结构,健康人群EEG数据或MEG数据构建的BFN具有稳定的“小世界”特征,而通常精神疾病患者的BFN“小世界”特征往往出现了弱化趋势[18]。本研究发现抑郁症组与健康对照组的最短路径长度和聚类系数差异具有统计学意义,全脑加权BFN最短路径长度增加,聚类系数减小。其意味着抑郁症患者“小世界”特性存在随机化趋势,为进一步验证该结论,本文分析了两组的 “小世界”特征指数,其定义如式(15)所示:
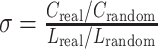 |
15 |
Creal和Lreal是原始网络的聚类系数与最短路径长度,Crandom和Lrandom是原始网络对应随机网络的聚类系数与最短路径长度。 > 1代表网络具有“小世界”特性,且
> 1代表网络具有“小世界”特性,且  值越大网络的“小世界”特性越强[32]。抑郁症组和健康对照组的“小世界”特性指数差异性结果如图8所示,可以看出两组的
值越大网络的“小世界”特性越强[32]。抑郁症组和健康对照组的“小世界”特性指数差异性结果如图8所示,可以看出两组的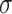 值均大于1,其说明了两组的BFN均具有“小世界”特性。相比于健康对照组,抑郁症组“小世界”特性指数明显下降,该结果意味着抑郁症患者BFN出现了随机化趋势。
值均大于1,其说明了两组的BFN均具有“小世界”特性。相比于健康对照组,抑郁症组“小世界”特性指数明显下降,该结果意味着抑郁症患者BFN出现了随机化趋势。
图 8.
Comparison of “small world” characteristic indexes between groups
组间“小世界”特征指数对比
5. 结论
本文旨在通过探索抑郁症患者BFN异常变化,进而不断向抑郁症发病神经机制真相逼近。基于静息态EEG数据的加权和二值化BFN组间对比发现,相对于健康对照组,抑郁症组BFN同步性发生了改变,如LT和RPO脑区同步性增加,RF脑区同步性减少,这些改变可能是抑郁症患者大脑信息处理功能异常在BFN层面的外在表现形式。通过对比组间“小世界”特征指数发现抑郁症患者的BFN出现了随机化趋势。全脑加权BFN的聚类系数作为KNN分类器输入可获得最高94.11%的抑郁症识别率。
重要声明
利益冲突声明:本文全体作者均声明不存在利益冲突。
作者贡献声明:张冰涛负责研究方案设计,文章构思,论文撰写;周文颖负责实验数据处理与论文修改;李延林负责数据分析;常文文负责论文指导,审阅;徐斌斌负责图表绘制。
伦理声明:本研究通过了兰州大学第二附属医院伦理委员会的审批(批文编号:2015-017)。
Funding Statement
国家自然科学基金资助项目(61962034);甘肃省自然科学基金资助项目(20JR10RA211);兰州交通大学‘天佑青年托举人才计划’基金资助项目;甘肃省高等学校青年博士基金资助项目(2021QB-053)
National Natural Science Foundation of China; Science and Technology Department of Gansu Province; Lanzhou Jiaotong University; Education Department of Gansu Province
References
- 1.Zhang Bingtao, Yan Guanghui, Yang Zhifei, et al Brain functional networks based on resting-state EEG data for major depressive disorder analysis and classification. IEEE Trans Neural Syst Rehabil Eng. 2021;29(1):215–229. doi: 10.1109/TNSRE.2020.3043426. [DOI] [PubMed] [Google Scholar]
- 2.World Health Organization (WHO). Depression. (2018-09-21)[2021-12-10]. https: //www.who.int/health-topics/depressiontab=tab_1.
- 3.Zhang Xiaowei, Shen Jian, Din Z U, et al Multimodal depression detection: fusion of electroencephalography and paralinguistic behaviors using a novel strategy for classifier ensemble. IEEE J Biomed Health Inform. 2019;23(6):2265–2275. doi: 10.1109/JBHI.2019.2938247. [DOI] [PubMed] [Google Scholar]
- 4.Yao Z J, Fu Y, Wu J F, et al Morphological changes in subregions of hippocampus and amygdala in major depressive disorder patients. Brain Imaging Behav. 2020;14(3):653–667. doi: 10.1007/s11682-018-0003-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alageel A, Albalawi F F, Aldosary F. Magnetoencephalography (MEG)-based biomarkers for depression//The 21st Annual ISBD Conference: Global Advances in Bipolar Disorder and Depression, Sydney: Wiley, 2019, 2019(21): 20-23.
- 6.Cai H S, Qu Z D, Hu B, et al Feature-level fusion approaches based on multimodal EEG data for depression recognition. Information Fusion. 2020;59(2020):127–138. [Google Scholar]
- 7.Li X W, Zhang X, Hu B, et al Depression recognition using machine learning methods with different feature generation strategies. Artif Intell Med. 2019;99:101696. doi: 10.1016/j.artmed.2019.07.004. [DOI] [PubMed] [Google Scholar]
- 8.Zeng Lingli, Shen Hui, Liu Li, et al Identifying major depression using whole-brain functional connectivity: a multivariate pattern analysis. Brain. 2012;135(5):1498–1507. doi: 10.1093/brain/aws059. [DOI] [PubMed] [Google Scholar]
- 9.Yu Haitao, Lei Xinyu, Song Zhenxi, et al Supervised network-based fuzzy learning of EEG signals for Alzheimer's disease identification. IEEE Transactions on Fuzzy Systems. 2020;28(1):60–71. doi: 10.1109/TFUZZ.2019.2903753. [DOI] [Google Scholar]
- 10.Zhang B T, Lei T, Liu H, et al. EEG-based automatic sleep staging using ontology and weighting feature analysis, Comput Math Method M, 2018, 2018: 6534041.
- 11.Fingelkurts A A, Kähkönen S. Functional connectivity in the brain-is it an elusive concept?. Neurosci Biobehav Rev, 2005, 28(8): 827-836.
- 12.Cai H S, Gao Y W, Sun S T, et al. MODMA dataset: a multi-modal open dataset for mental-disorder analysis. (2019-11-01) [2021-12-10]. http: //modma.lzu.edu.cn/data/index/.
- 13.Zhang Bingtao, Zhou Wenying, Cai Hanshu, et al Ubiquitous depression detection of sleep physiological data by using combination learning and functional networks. IEEE Access. 2020;8:94220–94235. doi: 10.1109/ACCESS.2020.2994985. [DOI] [Google Scholar]
- 14.Peng H, Hu B, Shi Q X, et al Removal of ocular artifacts in EEG-an improved approach combining DWT and ANC for portable applications. IEEE J Biomed Health Inform. 2013;17(3):600–607. doi: 10.1109/JBHI.2013.2253614. [DOI] [PubMed] [Google Scholar]
- 15.司慧芳, 谢天, 高军峰, 等 基于相位延迟指数的脑功能网络及测谎研究. 电子学报. 2018;46(7):1742–1747. doi: 10.3969/j.issn.0372-2112.2018.07.029. [DOI] [Google Scholar]
- 16.Li X W, Zhu J, Hu B, et al. A resting-state brain functional network study in MDD based on minimum spanning tree analysis and the hierarchical clustering. Complexity, 2017, 2017: 9514369.
- 17.Fraschini M, Demuru M, Crobe A, et al The effect of epoch length on estimated EEG functional connectivity and brain network organisation. J Neural Eng. 2016;13(3):036015. doi: 10.1088/1741-2560/13/3/036015. [DOI] [PubMed] [Google Scholar]
- 18.梁夏, 王金辉, 贺永 人脑连接组研究:脑结构网络和脑功能网络. 科学通报. 2010;55(16):1565–1583. [Google Scholar]
- 19.Li N, Hou J C, Sha L Design and analysis of an MST-based topology control algorithm. IEEE T Wirel Commun. 2005;4(3):1195–1206. doi: 10.1109/TWC.2005.846971. [DOI] [Google Scholar]
- 20.Bullmore E, Sporns O Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10(3):186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- 21.Zhang Junran, Wang Jinhui, Wu Qizhu, et al Disrupted brain connectivity networks in drug-naive, first-episode major depressive disorder. Biol Psychiatry. 2011;70(4):334–342. doi: 10.1016/j.biopsych.2011.05.018. [DOI] [PubMed] [Google Scholar]
- 22.Sun S T, Li X W, Zhu J, et al Graph theory analysis of functional connectivity in major depression disorder with high-density resting state EEG data. IEEE Trans Neural Syst Rehabil Eng. 2019;27(3):429–439. doi: 10.1109/TNSRE.2019.2894423. [DOI] [PubMed] [Google Scholar]
- 23.Bian Zhijie, Li Qiuli, Wang Lei, et al Relative power and coherence of EEG series are related to amnestic mild cognitive impairment in diabetes. Front Aging Neurosci. 2014;6:11. doi: 10.3389/fnagi.2014.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cai Hanshu, Zhang Xiangzi, Zhang Yanhao, et al A case-based reasoning model for depression based on three-electrode EEG data. IEEE Trans Affect Comput. 2020;11(3):383–392. doi: 10.1109/TAFFC.2018.2801289. [DOI] [Google Scholar]
- 25.Cai H S, Han J S, Chen Y F, et al. A pervasive approach to EEG-based depression detection. Complexity, 2018, 2018: 5238028.
- 26.Li X W, Hu B, Sun S T, et al EEG-based mild depressive detection using feature selection methods and classifiers. Comput Methods Programs Biomed. 2016;136:151–161. doi: 10.1016/j.cmpb.2016.08.010. [DOI] [PubMed] [Google Scholar]
- 27.Cavanagh J F, Bismark A W, Frank M J, et al Multiple dissociations between comorbid depression and anxiety on reward and punishment processing: evidence from computationally informed EEG. Comput Psychiatr. 2019;3:1–17. doi: 10.1162/CPSY_a_00024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhou Yuan, Yu Chunshui, Zheng Hua, et al Increased neural resources recruitment in the intrinsic organization in major depression. J Affect Disord. 2010;121(3):220–230. doi: 10.1016/j.jad.2009.05.029. [DOI] [PubMed] [Google Scholar]
- 29.Connolly C G Wu J, Ho T C, et al. Resting-state functional connectivity of subgenual anterior cingulate cortex in depressed adolescents. Biological Psychiatry. 2013;74(12):898–907. doi: 10.1016/j.biopsych.2013.05.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Joormann J, Gotlib I H Emotion regulation in depression: relation to cognitive inhibition. Cogn Emot. 2010;24(2):281–298. doi: 10.1080/02699930903407948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Leistedt S J, Nathalie C, Martine D, et al Altered sleep brain functional connectivity in acutely depressed patients. Hum Brain Mapp. 2009;30(7):2207–2219. doi: 10.1002/hbm.20662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu Yong, Liang Meng, Zhou Yuan, et al Disrupted small-world networks in schizophrenia. Brain. 2008;131(4):945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]





