脑-机接口中错误相关电位的解码算法研究

Abstract

基于错误相关电位（ErrP）的错误自检测有助于改善脑-机接口系统的实用性。但单试次 ErrP 信号的准确识别仍是阻碍这一技术发展的难题。为了衡量不同算法解码 ErrP 信号的能力，本文使用两个不同的公开数据集，对研究与相关应用中常见的 4 种线性判别分析算法、2种支持向量机、逻辑回归以及判别典型模式匹配（DCPM）共 8 个算法展开对比。文中主要分析了算法的分类正确率和算法性能随训练集样本数量的变化情况。实验结果表明 DCPM 具有最佳的综合性能。本研究揭示了各算法性能与训练样本数目和 ErrP 试验范式间的相互影响，为研究与实际应用中 ErrP 解码算法的选择提供参考。

引言

脑-机接口（brain-computer interface，BCI）是一种不依赖于外周神经或肌肉的通信通道，允许人脑与外部设备实时交互通信^[1]。在各类 BCI 技术中，基于脑电图（electroencephalogram，EEG）的 BCI 解码从头皮电极记录下来的大脑信号，以区分人的各种意图；因其具备低成本、快响应、易携带等优点，被广泛用于汽车、轮椅等设备导航以及鼠标和浏览器等计算机部件的控制。

在 BCI 的各种应用中，解码器经常会曲解受试者的意图并提供完全错误的结果，这主要是脑电图信号幅值低、噪声强、非平稳、非高斯的性质造成的^[2]。目前，即使是训练有素的受试者也难以避免错误；当受试者意识到自己犯错或正在观察的行为中出现错误时，大脑即产生同错误关联的事件相关电位，称为错误相关电位（error-related potentials，ErrP）^[3]。ErrP 信号已被证明是人类固有的反馈机制，这意味着在人犯错误的情况下，ErrP 可以不经训练地、自然地在大脑中产生。同时，ErrP 是一种稳定的电位，受生理结构变化影响小，基于 ErrP 训练的分类器即使在几个月之后仍具有相近的性能^[4]。因此，如果能准确识别 ErrP 信号，使 ErrP 同其他 BCI 范式结合构成的混合 BCI 就能监测系统运行情况、预防错误发生或对发生的错误进行改正，从而提高系统性能。

早在 2000 年，Schalk 等^[5]就提出 ErrP 作为诱发信号使得它更容易与其他 BCI 相结合以提高系统性能。广泛的研究表明，ErrP 信号可以在单个试次中被可靠地检测到，并且可以构成实时 BCI 系统的一部分。2015 年 Zhang 等^[6]对 30 名受试者开展了模拟汽车驾驶和真实汽车驾驶任务，通过 ErrP 信号监测导航指示方向中的错误，使用线性判别分析（linear discriminant analysis，LDA）获得了 69.8% 的离线正确率（accuracy，Acc）和 68.2% 的在线正确率。同年，Spüler 等^[7]设计了一款游戏，要求 10 名受试者在游戏中通过手柄操纵光标避开移动的物体，并使用支持向量机（support vector machine，SVM）算法对碰撞诱发的 ErrP 进行分类，达到平均 75% 的正确率。2017 年 Kim 等^[8]使用 xDAWN 空间滤波器与 SVM 算法对机械臂模拟人手部运动过程诱发的 ErrP 进行分类，在 7 名受试者中达到平均 91% 的平衡正确率（balanced accuracy）。2018 年 Zhang 等^[9]要求 22 名受试者通过运动想象（motor imagery，MI）操控外骨骼运动，在指令执行前通过视觉反馈将运动结果呈现给受试者，利用 ErrP 监测 MI 解码的错误，该研究对比了逻辑回归（logistic regression，LR）、K 最邻近（K-nearest neighbor，KNN）和 SVM 算法对受试者 ErrP 信号的分类性能，其中 SVM 具有最好的表现，识别正确率的平均值超过 90%。2019 年 Wirth 等^[10]使用逐步线性判别分析（stepwise linear discriminant analysis，SWLDA）对两个不同任务诱发的两种不同类型 ErrP 信号进行分类，分别达到平均 65.2% 和 65.6% 的正确率。

综上，不同类型现实应用中 ErrP 的识别正确率在较大范围内变化，相较广泛应用的稳态视觉诱发电位（steady-state visual evoked potentials，SSVEP）、P300 成分等视觉型 BCI，其可用性处于较低水平。ErrP 幅值约 10 μV，信噪比低，受试者间波形差异大，ErrP 的稳定波形需要通过多个试次叠加平均获得^[11]，但在线系统中用于监测受试者实时错误的 ErrP 信号要求在单试次内准确检测，这些因素是目前 ErrP 解码困难的主要原因。

当前 ErrP 分类算法繁多，各算法在不同范式与应用场景中的表现不尽相同，且少有文献对 ErrP 实用系统中常用算法的性能进行系统对比，研究者难以对实际应用中算法解码 ErrP 的能力做出准确判断。本文使用两个不同的公开数据集，对 ErrP 现实应用中常出现的解码算法——包括 LDA、SWLDA、收缩线性判别分析（shrinkage linear discriminant analysis，SKLDA）、贝叶斯线性判别分析（bayesian linear discriminant analysis，BLDA）、线性支持向量机（linear support vector machine，LSVM）、多项式核函数支持向量机（polynomial kernel support vector machine，PSVM）、LR、判别典型模式匹配（discriminative canonical pattern matching，DCPM）算法识别两个不同数据集 ErrP 信号的性能进行分析。在预处理方法固定的情况下，本研究从算法基准性能与算法解码能力随训练样本数目变化两方面，对各算法的性能表现展开系统分析，分析过程中还关注了算法解码能力在不同范式中的变异性，综合多种因素探究 ErrP 解码规律。本研究将有助于 ErrP 混合 BCI 系统中解码算法的选用，为进一步开发新型 ErrP 解码算法提供新思路。

1. 数据描述

1.1. 数据集 1

本研究使用的公开数据集 1 来自 2015 年卡格尔（Kaggle）主办的 BCI 挑战赛@神经工程会议（BCI Challenge @ IEEE neural engineering conference 2015，BCI Challenge @ NER2015）（网址：https://www.kaggle.com/c/inria-bci-challenge），其中包含 26 名受试者的数据，年龄在 20～37 岁之间，所有受试者均没有任何 BCI 应用经验。数据采集使用脑电采集系统（Synamps2，Neuroscan Inc，美国），56 导联电极遵循 10-20 国际标准放置，参考电极置于鼻尖，接地电极置于肩膀处。信号原始采样率为 600 Hz，贡献者提供的信号被降采样到 200 Hz。

受试者在试验中执行 P300 字符拼写任务，范式流程如图 1 所示，Margaux 等^[12]对此进行了深入的解释，此处仅简要描述任务。在每次试验开始时，目标字母被绿色圆圈标记 1 s，间隔 1 s，单次刺激由屏幕中先点亮后熄灭的 6 个字符组成，刺激间间隔为 0.11 s，其中点亮 0.06 s，熄灭 0.05 s，36 个字符闪烁 1 遍为 1 个刺激序列，序列刺激重复呈现 2 轮或 4 轮；2 轮重复保证 ErrP 诱发数量足够用于分析，4 轮刺激保证 ErrP 诱发质量。序列刺激结束 2.5～4 s 后，屏幕中央出现结果反馈，呈现 1.3 s，受试者休息 0.5 s 后继续下一目标字符拼写。如果拼写的字母是单词的最后一个字母，间隔 1 s 后开始下一单词的拼写。

图 1.

Flow chart of experimental paradigm in dataset 1

数据集 1 试验范式流程图

每名受试者都经过 5 组试验，要求使用 P300 拼写器执行 5 个字母单词的拼写任务。前 4 组试验有 12 个单词，第 5 组试验有 20 个单词。因此，26 名受试者共有 26 ×（5 × 12 × 4 + 5 × 20）= 8 840 试次，其中有 6 261 个非靶的试次（无 ErrP 信号）和 2 579 个靶试次（有 ErrP 信号）。

1.2. 数据集 2

本研究使用的数据集 2 来自公开数据库——欧盟脑机交互的未来：地平线 2020 计划（the future of brain/neural computer interaction：horizon 2020，BNCI horizon 2020）（网址：http://bnci-horizon-2020.eu/database/data-sets），其中包含 6 名受试者的数据，采集过程中 64 导联按照 10-20 国际标准放置，以 512 Hz 采样率记录受试者脑电信号。每名受试者共进行两次试验（间隔数天进行），本文仅使用每名受试者第一次试验的数据。

数据集 2 试验示意图如图 2 所示，Chavarriaga 等^[4]对试验细节进行了详细描述，此处仅简要叙述试验过程。任务中，受试者坐在计算机前注视屏幕中心，画面中显示光标（绿色正方形）和目标（蓝色正方形）位置。在每个试次中，光标朝向目标所在位置沿水平方向移动，持续约 2 s；到达目标后，光标将保持在原地，并在距离当前光标位置不超过 3 个位置处绘制新的目标。在试验期间，受试者无法控制光标的移动，仅被要求监视光标的行为。为了诱发 ErrP 信号，在每个试次中，光标沿错误方向（目标位置相反的方向）移动的概率约为 20%。每次试验由 10 个部分组成，每个部分包含约 50 个试次，持续约 3 min。

图 2.

Experimental paradigm in dataset 2

数据集 2 试验示意图

2. 解码算法

2.1. 线性判别分析相关算法

LDA 是确定两类间最优分类超平面的经典算法，它将高维样本数据投影到低维空间，使得样本数据在新的空间中类间距离与类内距离之比取得最大值^[13]。该算法计算简单，在两个类别服从高斯分布且协方差相等时，LDA 能提供最优的高鲁棒分类。在二值分类问题中，LDA 同最小二乘回归等价，其目标函数如式（1）所示：

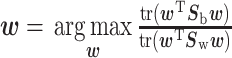1

其中，tr（·）代表矩阵的迹，S_b 为类间散度矩阵，S_w 为类内散度矩阵。通过求解 S_w^-1S_b 的最大特征值和对应特征向量，得到投影向量 w；设 b 为偏置项，x_i∈R^{（Nt × Nc）× 1} 是第 i 个样本向量，其中 N_c 为导联数目，N_t 为采样点数目，则决策函数如式（2）所示：

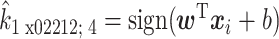2

传统 LDA 算法在样本数目等于或远小于特征维度时，类内散度矩阵往往不可逆（奇异）或病态，导致结果无法计算或算法不稳定。为此研究者提出了 SWLDA、SKLDA、BLDA 等算法。SWLDA 通过逐步回归选取差异具有统计学意义的特征以降低特征维度^[14]，SKLDA 通过收缩协方差估计缓解小样本下原协方差矩阵的奇异或病态问题^[15]，BLDA 使用正则化来防止小样本数据集的过拟合，同时通过贝叶斯分析，自动快速地从训练数据中估计出正则化程度以避免费时的交叉验证^[16]。

2.2. 支持向量机相关算法

SVM 的核心思想是通过核函数将向量映射到更高维的空间中，构造一个最优分类超平面，使得分类间隔最大，分类间隔越大，分类器误差上界越小^[7]。对于二分类问题，给定一个训练样本集{（x_i，y_i）|i = 1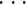，，N}，其中 x_i 是第 i 个样本向量，N 为训练集样本数目，y_i∈{± 1}是训练样本 x_i 的类别标记。SVM 算法通过某一映射 φ（x）= z，z∈F 将特征映射到高维空间 F，并在此空间中构造最优分类超平面，该超平面可由最优化问题求解，如式（3）所示：

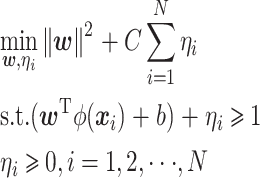3

式中，w 为费舍尔（Fisher）特征向量，b 为偏置项，C 为自定义的惩罚系数，η_i 为训练样本相对超平面的偏差，用于控制样本偏差与 SVM 泛化能力间的平衡。通过拉格朗日乘子法将上式转化为对偶形式，如式（4）所示：

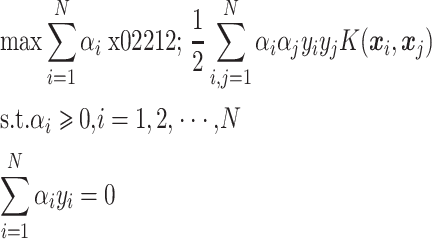4

式中，α_i 为拉格朗日乘子，核函数 K（x_i，x_j）= φ（x_i）∙φ（x_j）将高维空间的内积运算转化为低维空间上的函数运算，使得原本在低维空间中线性不可分的样本在高维空间中线性可分。求解上述问题的 α_i，再根据拉格朗日乘子式求出最优特征向量 w 和最优偏置 b，其最终决策函数如式（5）所示：

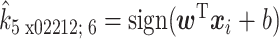5

本文使用的核函数为线性核函数和多项式核函数。算法参数由数据集 1 中随机选择的一名受试者通过十折交叉验证确定。以 PSVM 为例，对多项式阶次与惩罚系数 C 进行网格化搜索，选取使十折交叉验证错误率最小的参数值，并将该参数用于数据集 2 中。其他需要参数选择的算法同样在该名受试者身上通过类似方法确定具体参数。线性核函数取惩罚系数 C = 20，多项式核函数阶数设为 2，惩罚系数 C = 4。

2.3. 逻辑回归

LR 是描述数据样本 x_i 属于类别 l 的广义线性模型。算法假设预测变量 y_i 服从伯努利分布，并由此确定链接函数的形式为逻辑函数 f（·），f 将线性回归的结果映射为 0～1 之间的概率，从而完成二分类^[17]。该算法对过拟合与数据中出现的异常值具有良好的鲁棒性^[18]。逻辑函数如式（6）所示：

6

回归系数向量 w 可通过最大似然估计获得，如式（7）所示：

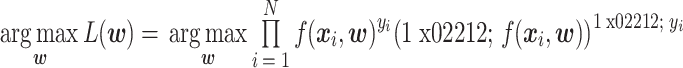7

其中，L（·）为样本的似然函数，x_i 为第 i 试次的数据，y_i∈{0，1}是训练样本类别标记。其最终决策函数如式（8）所示：

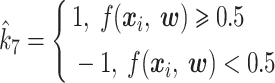8

2.4. 判别典型模式匹配

DCPM 算法由天津大学神经工程团队提出，用于解码 1 μV 以下的极微弱事件相关电位^[19]。该算法首先使用判别空间模式（discriminative spatial patterns，DSP）抑制脑电图中的共模噪声，通过典型相关分析（canonical correlation analysis，CCA）增强脑电信号特征，最后构建类别模板进行模板匹配实现分类。

设训练集样本 X_i∈R^{Nt × Nc}（i = 1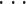，，n）分属两个类别，n_l 为第 l 类的样本数目，满足 n₀ + n₁ = n，此处 n 表示训练集样本个数。y_i∈{± 1}表示样本 X_i 对应的标签。DSP 空间滤波器的类间散度矩阵 R_b 与类内散度矩阵 R_w 如式（9）和（10）所示：

9

10

其中 ∈R^{Nt × Nc} 为第 l 类的叠加平均后的模板信号，X∈R^{Nt × Nc} 为所有类别叠加平均后的模板。投影矩阵 W 由对应的最优化问题求解，如式（11）所示：

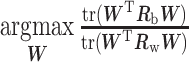11

该最优化问题可转化为广义特征值问题，投影矩阵 W 即特征值对应的特征向量，实验中取对应特征值占比 99% 的特征向量组成投影矩阵。

通过 DSP 空间滤波器可以滤除两类信号之间的共模噪声，而后基于 CCA 算法构建空间投影矩阵 U_l，V_l 如式（12）所示：

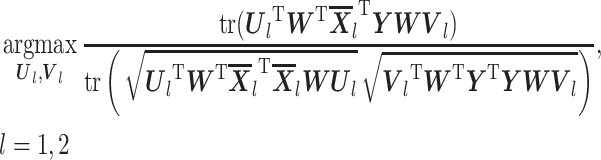12

其中， 是对应于第 l 类的所有试次的平均模板，Y 是测试样本信号。利用 CCA 寻找一组最优解，使得两个整体之间有最大关联的权重，即令上式计算得到的数值最大。

而后在模板匹配过程中，由训练集数据构建模板，根据刺激方式的不同，模板构建也可进行相应调整，特征向量 ρ_l 表示平均模板和测试样本信号之间的相似性，如式（13）所示：

13

其中，corr（·）代表皮尔森相关系数，dist（·）表示欧氏距离。训练样本和测试信号的相似性越大，系数 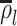则越大，如式（14）所示：

14

本文中，仅选取欧氏距离即特征向量 ρ_l 的第 2 个元素用于决策，预测 Y 的模式如式（15）所示：

15

3. 对比方法

3.1. 数据预处理

预处理前，将数据集 2 中脑电信号降采样至 200 Hz 与数据集 1 保持一致。两个数据集中的脑电信号转参考至左右乳突的平均值，使用巴特沃兹滤波器对数据进行 1～10 Hz 带通滤波，通过阶次为 3、窗口宽度为 31 的多项式平滑滤波器平滑滤波后数据。以反馈开始时刻为 0 时刻，截取 − 0.2～0.8 s 的数据，使用 − 0.2～0 s 的数据去除基线，以 0～0.8 s 数据作为时域特征。分类时选取 FP1、FP2、F7、F3、Fz、F4、F8、FC5、FC1、FC2、FC6、T7、C3、Cz、C4、T8、TP7、CP5、CP1、CP2、CP6、TP8、P7、P3、Pz、P4、P8、PO7、POz、PO8、O1、O2 共 32 个导联的数据。测试 4 种 LDA 算法、2 种 SVM 算法以及 LR 算法时，用于训练和测试的样本在完成预处理后进一步降采样至 40 Hz。

3.2. 算法性能指标选择

本研究使用平衡正确率、曲线下面积（area under the curve，AUC）、真阳性率（true positive rate，TPR）3 个参数衡量算法性能。平衡正确率为真阳性率与真阴性率的算术平均值，能够较好克服正确率在数据集类别分布不平衡的情况下难以准确衡量分类器性能的问题。曲线下面积为受试者操作特征曲线下的面积，使用真阳性率与假阳性率的秩进行计算，能避免不平衡类别与分类器阈值选择带来的影响，是度量分类器性能的常用指标。真阳性率为正确预测的靶试次数目占靶试次总数的比例。在集成了 ErrP 错误更正机制的 BCI 系统中，由于正确试次相较错误试次更易获得，正确试次数目通常远多于错误试次，使得系统容易达到较高的真阴性率（true negative rate，TNR）而真阳性率处于较低水平，当分类器真阳性率过低时系统将难以更正错误，致使基于 ErrP 的错误更正功能失效。因此将真阳性率单独列出作为分类器性能指标，以适应不同系统选择算法的需要。

3.3. 算法性能对比方式

算法在实际应用中应该根据在线使用需要达到的指标进行评估，除了 3.2 节中提到的性能指标外，这一过程还涉及参数的选择、模型训练所需要的样本数量、算法的收敛性、算法的收敛速度等因素，这些难以进行综合系统的量化评估，因此本文仅在以下设置中进行对比分析。

首先，本研究对各算法重复 10 次 10 折交叉验证取结果的平均值，以确定每个算法的基准性能，然后在不同训练样本数目（40、60、80、100、120、140、160、180、200、220 和 240 个试次）100 个测试样本的条件下，测试了各算法性能随训练样本数目的变化情况。由于数据集中每名受试者包含的 ErrP 试次数目各不相同，因此在随机选择训练样本和测试样本进行计算时，根据靶试次和非靶试次的比例划分，每种训练样本数目抽取 10 次并对结果取平均值。

3.4. 统计学检验方法

本研究使用统计产品与服务解决方案（statistical product and service solutions，SPSS）软件（IBM SPSS Statistics，IBM Corporation，美国）进行统计分析。使用单因素重复测量方差分析交叉对比不同算法之间性能差异，使用双因素重复测量方差分析探究算法因素和训练集样本数目因素对曲线下面积的共同作用。如果数据不符合球度检验（Mauchly’s test of sphericity），则进行格林豪斯-盖舍校正（Greenhouse-Geisser correction），相关的事后检验使用图基法（Turkey’s test）进行，α 级别设置为 0.05。

4. 结果与讨论

4.1. 数据集 1 中算法基准性能分析

使用 8 种算法解码数据集 1 中 ErrP 信号，交叉验证后取 25 名受试者的平均值以确定各算法的基准性能，结果如表 1 所示。使用单因素重复测量方差分析交叉对比不同算法的曲线下面积、平衡正确率与真阳性率如图 3 所示。结果表明，不同算法之间的性能指标差异均具有统计学意义（曲线下面积：F（3.76，90.43）= 58.80，P < 0.01，平衡正确率：F（4.05，97.11）= 29.72，P < 0.01；真阳性率：F（1.40，56.51）= 35.64，P < 0.01）。

表 1. 8 The performance of 8 algorithms decoding the ErrP signal in dataset 1 and dataset 2.

8 种算法解码数据集 1 与数据集 2 中 ErrP 信号的表现

算法	曲线下面积（%）			平衡正确（%）			真阳性率（%）
	数据集 1	数据集 2		数据集 1	数据集 2		数据集 1	数据集 2
LDA	65.64 ± 7.39	64.81 ± 5.54		65.64 ± 7.39	64.81 ± 5.54		56.75 ± 12.00	56.97 ± 7.54
BLDA	74.48 ± 12.34	85.27 ± 6.80		67.31 ± 9.07	73.65 ± 5.28		71.61 ± 14.38	87.13 ± 7.17
SWLDA	77.19 ± 10.48	84.53 ± 7.32		69.73 ± 9.39	70.09 ± 7.83		73.88 ± 15.39	43.14 ± 15.17
SKLDA	76.41 ± 10.72	82.96 ± 7.40		70.06 ± 9.15	73.28 ± 5.06		65.97 ± 16.15	83.85 ± 10.67
LSVM	75.97 ± 8.77	83.11 ± 6.38		68.63 ± 8.15	73.69 ± 6.21		56.32 ± 14.49	58.93 ± 9.72
PSVM	77.17 ± 8.47	83.33 ± 6.32		69.24 ± 8.05	73.89 ± 6.19		55.50 ± 15.36	58.96 ± 9.70
LR	68.70 ± 8.28	73.51 ± 6.43		67.74 ± 7.78	71.56 ± 5.96		57.12 ± 12.43	64.51 ± 9.58
DCPM	82.60 ± 9.47	83.69 ± 10.02		76.02 ± 8.47	76.59 ± 8.88		77.10 ± 10.26	77.54 ± 8.75

图 3.

The performance of 8 algorithms in dataset 1 and the statistical significance

8 种算法在数据集 1 中的表现及差异统计学意义

*P < 0.05；**P < 0.01

*P < 0.05; **P < 0.01

DCPM 算法的曲线下面积为 82.60% ± 9.47%，平衡正确率为 76.02% ± 8.47%，两参数优于其他所有算法（P < 0.05）；DCPM 的真阳性率为 77.10% ± 10.26%，较 SKLDA 与 SWLDA 大致相同，优于其他算法（P < 0.05），表现出对 ErrP 波形特征的准确检测能力，总体看解码性能最佳。LR 算法表现同 LDA 算法相近，解码 ErrP 信号的能力低于其它算法，两者之间差异不具有统计学意义。BLDA、SWLDA、SKLDA、LSVM、PSVM 的解码能力表现大致相近，PSVM 的曲线下面积为 77.17% ± 8.47%，略高于 LSVM 的 75.97% ± 8.77%（P < 0.05）；SVM 相关算法性能表现同 LDA 相关算法中表现较好的 SKLDA 与 SWLDA 相近，在真阳性率方面略低于 SKLDA 和 SWLDA（P < 0.05）。

4.2. 数据集 1 与数据集 2 中算法基准性能对比分析

由于数据集 2 中仅含 6 名受试者数据，较小的样本量造成统计学检验的效力不足，因此仅展示各算法解码数据集 2 中 ErrP 信号的结果，而不进行统计学检验。使用 8 种算法解码数据集 1 与数据集 2 中的 ErrP 信号，结果如表 1 和图 3 所示。同数据集 1 相比，数据集 2 中算法性能相关指标高于数据集 1。根据表 1，将算法对应的曲线下面积、平衡正确率和真阳性率，按从大到小编号，序号越小说明算法性能越好；平均两个数据集中的各算法排名结果，按各算法平均排名的由小到大编号，序号越小则算法在两个数据集中的解码性能越出色，如表 2 所示。由总排名可知，DCPM 算法在两个数据集中综合表现最佳，LDA 算法与 LR 算法在两个数据集中表现最差，它们的解码能力在两个不同的数据集中有良好的一致性。但部分算法在两个不同的数据集中表现并不相同，BLDA 算法在数据集 1 中各排名的平均值为 5.3，而在数据集 2 中这一数值为 2.0，仅次于 DCPM 算法，说明 BLDA 对数据集 2 中的 ErrP 信号具有更强的解码能力；SWLDA 算法与 BLDA 算法的情况相反，其解码数据集 1 中 ErrP 信号的表现更佳。尽管 BLDA、SWLDA 较其他算法，更容易受到数据集的影响而表现出不一致的 ErrP 解码性能，但大部分算法的表现基本一致，尤其是 DCPM 算法，在两个不同的数据集中均展现出对 ErrP 信号的良好识别能力。

表 2. The ranking of 8 algorithm’s metrics in dataset 1 and dataset 2 and total ranking of algorithm performance.

8 种算法的评价指标在数据集 1 与数据集 2 中的排名与算法表现总排名

算法	曲线下面积排名			平衡正确率排名			真阳性率排名			排名的平均值		总排名
	数据集 1	数据集 2		数据集 1	数据集 2		数据集 1	数据集 2		数据集 1	数据集 2
LDA	8	8		8	8		6	7		7.3	7.7	8
BLDA	6	1		7	4		3	1		5.3	2.0	2
SWLDA	2	2		3	7		2	8		2.3	5.7	4
SKLDA	4	6		2	5		4	2		3.3	4.3	3
LSVM	5	5		5	3		7	6		5.7	4.7	6
PSVM	3	4		4	2		8	5		5.0	3.7	5
LR	7	7		6	6		5	4		6.0	5.7	7
DCPM	1	3		1	1		1	3		1.0	2.3	1

4.3. 算法因素与训练集样本数目对算法解码性能的影响分析

数据集 1 与数据集 2 中算法性能随训练集样本数目变化如图 4 所示。总体上看各算法的分类性能随训练样本数目的增多而增强，其中 DCPM 算法解码数据集 1 中 ErrP 信号的表现突出，在所有训练样本数目下均明显优于其他算法；BLDA 算法在数据集 2 中的表现仅次于 DCPM，大幅度优于其在数据集 1 中的表现。

图 4.

The performance of 8 algorithms changes with the number of training samples in dataset 1 and dataset 2

数据集 1 与数据集 2 中算法性能随训练集样本数目变化情况

在数据集 1 中，对算法（LDA、BLDA、SWLDA、SKLDA、LSVM、PSVM、LR、DCPM）和训练集样本数量（40、140、240）两个因素进行双因素重复测量方差分析，以确定它们对曲线下面积的影响。结果显示，算法因素、训练集样本数量因素均会影响算法性能指标（算法：F（2.80，67.10）= 73.81，P < 0.01；训练集样本数量：F（1.047，35.17）= 130.30，P < 0.01），且部分算法的性能指标会因训练集样本数目的不同而发生变化，算法与训练集样本数目之间存在交互作用（F（5.38，129.11）= 14.27，P < 0.01）。

4.4. 不同训练样本数目下算法解码性能分析

分别使用较小样本数目（40 个样本）、中等样本数目（140 个样本）和较大样本数目（240 个样本）训练各算法，单因素重复测量方差分析显示，算法之间的差异具有统计学意义（40 个样本：F（3.07，76.75）= 58.85，P < 0.01；140 个样本：F（2.979，74.47）= 61.99，P < 0.01；240 个样本：F（3.321，83.03）= 56.97，P < 0.01），事后检验的结果如图 5 所示。SWLDA 的曲线下面积受训练集样本数目的影响最为明显。在训练集样本数目较少时，除 LDA 外其他算法的曲线下面积均大于 SWLDA（P < 0.05）；随着训练算法使用样本数量的增加，SWLDA 的曲线下面积迅速增加，PSVM 与 DCPM 算法大于 SWLDA（P < 0.05）;当训练算法使用的样本数目较大时，仅 DCPM 算法的曲线下面积大于 SWLDA（P < 0.05）。SVM 对训练集样本数目同样表现出一定敏感性，当训练集样本数目由 140 个增加至 240 个时，PSVM 与 LSVM 算法之间曲线下面积的差异具有统计学意义。

图 5.

The performance of 8 algorithms in dataset 1 and the statistical significance under different number of training samples

不同训练集样本数目下 8 种解码算法在数据集 1 中的表现及差异统计学意义

*P < 0.05；**P < 0.01

*P < 0.05; **P < 0.01

4.5. 不同训练样本数目下算法训练所需时间分析

在数据集 1 中，使用不同数量样本训练 8 种算法，各算法训练时间随训练样本数目变化情况如图 6 所示。由于算法训练时间不仅受算法本身数学形式影响，同一算法编程方式的不同也会影响算法训练时间，因此以上结果仅供参考。从图 6 可得，需要迭代求解的 SWLDA、BLDA、LR 算法其训练时间远高于 LDA、DCPM、SKLDA 等存在解析解的算法。同样需要迭代求解的 LSVM、PSVM 算法，与 LDA 等具有解析解的算法训练时间相近，这一现象可能是算法优化较好，同时在 ErrP 的应用场景下算法收敛较快造成的。

图 6.

The training time of the algorithm varies with the number of training samples in dataset 1

数据集 1 中算法训练时间随训练集样本数目变化

5. 讨论与结论

实际应用中解码算法选择需考虑可获得的样本数目、训练时间、试验范式等多种因素影响。本研究使用两不同范式的公开数据集，从算法基准性能、算法性能与训练样本数目间的相互影响、使用不同数目样本训练算法所消耗时间三个角度，探究实际应用中 8 个常用算法解码 ErrP 信号的性能表现。其中，DCPM 对 ErrP 信号的解码效果最佳，在不同试验范式和不同训练集样本数目下均能保持优秀的解码能力。算法中 DSP 空间滤波器直接使用二维脑电数据，降低了训练集样本数目较少而数据维度过高时矩阵病态或奇异的概率，对脑电信号中共模噪声有明显的抑制效果，同时简单直接的运算过程节省了算法训练及分类的时间成本^[18-20]。SVM 的优秀设计使其具有理想的理论性质，能够最大化类别之间的间隔以提供良好的泛化能力，从而可以使用少的训练样本达到较好的解码水平；但 SVM 参数选择过程较为缓慢，且最终表现同 SWLDA、SKLDA 相比没有显著优势，使得选用该类算法的性价比降低。LDA 相关算法中，SWLDA 与 SKLDA 在解决 ErrP 分类问题时，具有同 SVM 算法相近的表现，相比于 SVM 算法所需的参数选择和 LDA 面对高维数据的奇异性问题，SWLDA 和 SKLDA 的使用更为便捷迅速且 SKLDA 在训练样本较少时表现优秀。需要注意的是，如果信号中的鉴别性信息不足或参数设置有误，SWLDA 将无法提供一个收敛的模型。LDA 同 LR 算法性能表现并不突出，实际应用场景必须使用 LDA 算法的情况下，建议使用 SKLDA 替代 LDA 算法。

综上所述，在引入 ErrP 自动更正机制的实用 BCI 系统中，可采用单试次 ErrP 检测实现对受试者或机器错误的实时监测，其中的关键是 ErrP 的单试次检测算法。在 8 个常用算法中，DCPM 算法在各种情况下均具有最佳性能表现。相较于 LDA 相关算法，DCPM 在训练样本数量较少或特征数目过多时更好地解决了小样本造成的奇异性问题，使得适用情况更广；相较于 SVM 相关算法，DCPM 避免了使用时进行的长时间参数选择过程，使得应用过程更简便。综上所述，本文的研究结果有助于 ErrP 错误检测算法的选择与改进，从而帮助 ErrP 实时监测技术在 BCI 在线系统中的应用。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金（61976152，81601565，81630051）；第四届中国科协青年人才托举工程（2018QNRC001）；天津市科技重大专项与工程（17ZXRGGX00020）

National Natural Science Foundation of China; China Association for Science and Technology; Tianjin Science and Technology Commission