Abstract
Mammography guidelines have weakened in response to evidence that mammograms diagnose breast cancers that would never eventually cause symptoms, a phenomenon called “overdiagnosis.” Given concerns about overdiagnosis, instead of recommending mammograms, US guidelines encourage women aged 40–49 to get them as they see fit. To assess whether these guidelines target women effectively, I propose an approach that examines mammography behavior within an influential clinical trial that followed participants long enough to find overdiagnosis. I find that women who are more likely to receive mammograms are healthier and have higher socioeconomic status. More importantly, I find that the 20-year level of overdiagnosis is at least 3.5 times higher among women who are most likely to receive mammograms. At least 36% of their cancers are overdiagnosed. These findings imply that US guidelines encourage mammograms among healthier women who are more likely to be overdiagnosed by them. Guidelines in other countries do not.
1. Introduction
The U.S. Preventive Services Task Force (USPSTF) weakened their mammography guidelines in 2009 (USPSTF, 2009) in response to evolving evidence from clinical trials. Although their previous guidelines recommended regular mammography for asymptomatic women aged 40 and older (USPSTF, 2002), their updated guidelines left the mammography decision for women in their 40s to individual women and their doctors. The precise USPSTF guidelines, as confirmed in 2016, state: “The decision to start screening mammography in women prior to age 50 years should be an individual one. Women who place a higher value on the potential benefit than the potential harms may choose to begin biennial screening between the ages of 40 and 49 years” (Siu, 2016). The USPSTF recommends regular mammography for women aged 50 to 74 and does not provide guidelines for women older than 74 given insufficient evidence.
These guidelines raise a question that motivates my analysis: do the current USPSTF guidelines for women in their 40s induce mammograms among the women most likely to benefit from them? To address this question, I propose an approach to inform targeting within clinical guidelines that examines behavior within a clinical trial. I apply this approach to data from a clinical trial that has been important to the evolution of mammography guidelines. I proceed in two steps. First, I investigate selection heterogeneity: are women who are more likely to receive mammograms different from other women? Second and more importantly, I investigate treatment effect heterogeneity: are women who are more likely to receive mammograms more likely to experience better or worse health outcomes because of them?
Mammograms, X-ray images of the breast, can lead to better health outcomes through the early detection and treatment of breast cancer that would eventually cause symptoms. The promise of screening is to detect cancers when they are small and presumably easiest to treat (American Cancer Society, 2019). Many women believe that all breast cancers begin in a small curable form before they invariably grow, spread, and kill (Silverman et al., 2001). However, the natural history of breast cancer is more complicated. Some tumors grow quickly, but others grow slowly, do not grow at all, or even shrink (Kaplan and Porzsolt, 2008).
Mammograms can lead to worse health outcomes through the early detection and treatment of breast cancer that would not eventually cause symptoms. The article that conveys the 2016 USPSTF guidelines notes, “The most important harm is the diagnosis and treatment of noninvasive breast cancer that would otherwise not have become a threat to a woman’s health, or even apparent, during her lifetime (that is, overdiagnosis and overtreatment)” (Siu, 2016). Overdiagnosis is distinct from false-positive diagnosis. A woman with a false-positive diagnosis learns from further tests that she does not have cancer, but a woman with an overdiagnosis learns from the same tests that she does have cancer. Almost all women with breast cancer pursue subsequent therapy, so they never know if their cancer would not have caused symptoms and was thus overdiagnosed. Bleyer and Welch (2012) find that as mammography increased dramatically, diagnosis of early-stage breast cancer more than doubled while diagnosis of late-stage breast cancer fell only slightly, suggesting that 31% of breast cancers detected in the United States in 2008 were overdiagnoses.
Overdiagnosis of breast cancer is an important health outcome because breast cancer can impose significant physical, financial, and psychological costs. Chemotherapy and radiotherapy can increase mortality by inducing secondary leukemia, lung cancer, and heart disease (Taylor et al., 2017). Surgery has other risks, including severe pain years later (Gärtner et al., 2009). Breast cancer diagnosis and associated therapies can impose substantial financial costs, even for women with comprehensive health insurance (Arozullah et al., 2004). In a study of low-income women, 27% had not returned to work five years after a breast cancer diagnosis (Blinder et al., 2013). Diagnosis of breast cancer can impose serious costs even among women who choose to watch and wait. In the New England Journal of Medicine, Welch and Fisher (2017) note that “psychological effects of overutilization and overdiagnosis are also worrisome: turning people into patients may undermine their sense of resilience, which is fundamental to health.”
The main concern that has spurred changes in guidelines is that overdiagnosis can be so harmful that the harms of mammograms can outweigh the benefits. To inform the 2016 USPSTF guidelines, the task force conducted a meta-analysis (Nelson et al., 2016) of clinical trials conducted worldwide (Habbema et al., 1986; Tabar et al., 1995; Nyström et al., 2002; Bjurstam et al., 2003; Miller et al., 2014; Moss et al., 2015). I provide background on the trials and analyze how their mortality results have evolved in Kowalski (2021b). Combining the latest results across trials, the meta-analysis does not find a statistically significant reduction in all-cause mortality across all age groups or within any age group. Furthermore, some trials show imprecise increases in all-cause mortality within some age groups, suggesting that the harms can outweigh the benefits (Nyström et al., 2002; Miller et al., 2014). In addition, no trials show statistically significant reductions in breast cancer mortality for women in their 40s. Some trials do show statistically significant reductions in breast cancer mortality for women in older age groups, but breast cancer mortality need not capture all harms of mammography, especially because overdiagnosis may lead to deaths not clearly caused by breast cancer. Given limited evidence showing benefits, there is a stronger rationale to engage with evidence showing harms through overdiagnosis.
Growing concern about overdiagnosis has prompted the weakening of mammography recommendations around the world to the point that the current USPSTF recommendations are stronger than those in many other countries. Mammography guidelines made by different authorities rely on the same trials considered by the USPSTF but place more weight on some than others. Within the United States, the American College of Radiology is the only major authority that recommends annual mammograms for all women in their 40s (CDC, 2020). Guidelines from the American College of Physicians and American Academy of Family Physicians are similar to those from the USPSTF for women in their 40s, as are guidelines from the American Cancer Society for women aged 40–44. All of these guidelines leave mammography decisions up to individual women and their doctors under the implicit assumption that doing so effectively recommends mammograms to women most likely to benefit from them. Outside the United States, European Breast Guidelines do not recommend mammography for any asymptomatic women aged 40–44 (Schünemann et al., 2019) and are therefore weaker. Guidelines in most large individual European countries, including the United Kingdom, Switzerland, France, and Spain, are even weaker in the sense that they do not recommend mammography for any asymptomatic women through age 49 (Ebell et al., 2018).1 Canadian guidelines are even weaker in that they recommend against mammography for asymptomatic women through age 49 (Klarenbach et al., 2018).
One explanation for why the Canadian guidelines are the weakest is that the Canadian National Breast Screening Study (CNBSS), a large trial that has been influential to the USPSTF guidelines, provides some of the most compelling evidence on overdiagnosis. If mammograms only lead to early detection of breast cancer that would eventually cause symptoms, incidence in the control arm should completely “catch up” as breast cancers that cause symptoms are diagnosed. Incidence was still higher in the intervention arm 15 years after a Swedish trial ended, indicating overdiagnosis (Zackrisson et al., 2006). In the CNBSS, incidence remained meaningfully higher in the intervention arm 25 years after the first participants enrolled (Baines et al., 2016), and the difference from the control arm is statistically significant. This difference is striking because mammography in the control and intervention arms likely converged after the active study period of the trial as mammography became widely available (Baines et al., 2016). Therefore, results from the CNBSS likely reflect the impact of starting mammography sooner, rather than starting mammography ever. These results are particularly relevant for the USPSTF guidelines because the previous weakening affected whether women should begin mammography in their 40s.
I use data shared with me by the investigators of the CNBSS (CNBSS, 2015) to examine whether overdiagnosis varies with mammography behavior to inform the current USPSTF guidelines. Crucially for the approach that I propose, the CNBSS data contain information on mammography behavior: whether women in the study actually received mammograms, conditional on their random assignment during the active study period. To the best of my knowledge, the CNBSS is the only trial considered by the meta-analysis that informs the USPSTF guidelines (Nelson et al., 2016) that tracked takeup of mammograms for all participants, including those in the control arm. These data show that during the active study period after the initial enrollment year, a substantial fraction of women in the control arm received mammograms, and some women in the intervention arm did not.
To allow overdiagnosis to vary with mammography behavior, I specify a heterogeneous treatment effect model in which the “treatment” is mammography. I begin with a model that relies only on the well-known local average treatment effect (LATE) assumptions of Imbens and Angrist (1994). Vytlacil (2002) shows that the LATE assumptions are equivalent to the Heckman and Vytlacil (2005) generalized Roy (1951) model of the marginal treatment effect (MTE) (Björklund and Moffitt, 1987). I therefore draw on the MTE literature (Heckman and Vytlacil, 1999, 2001, 2005; Carneiro et al., 2011; Brinch et al., 2017; Cornelissen et al., 2018; Mogstad et al., 2018; Kowalski, 2021a) to define heterogeneous selection and to make an ancillary assumption to identify heterogeneous treatment effects. I identify heterogeneous selection under the LATE assumptions alone by comparing outcomes and covariates across three groups formed by the interaction of mammography behavior and random assignment. Drawing on terminology from Angrist et al. (1996), “never takers” are the least likely to receive mammograms because they do not receive them regardless of random assignment, “compliers” are more likely to receive mammograms because they receive them if and only if assigned to the intervention arm, and “always takers” are the most likely to receive mammograms because they receive them regardless of random assignment. Comparisons across these three groups yield richer insights than the comparison across the two trial arms because they reflect mammography behavior. I use them to identify selection heterogeneity, to provide empirical motivation for the ancillary assumption, and to identify treatment effect heterogeneity under the ancillary assumption. I identify treatment effect heterogeneity by obtaining a lower bound on the average treatment effect for always takers that I compare to the average treatment effect for compliers, also known as the LATE.
First, I find heterogeneous selection: women more likely to receive mammograms are healthier in terms of long-term breast cancer incidence and all-cause mortality. They also have higher socioeconomic status and are more likely to practice several other health behaviors seen as beneficial. They are more likely to be nonsmokers, and they have lower body mass index.
Second and more importantly, I find treatment effect heterogeneity that aligns with the selection heterogeneity I find: women more likely to receive mammograms are more likely to be overdiagnosed by them. Furthermore, the magnitude of heterogeneity in overdiagnosis is meaningful. Among women most likely to receive mammograms, the always takers, at least 206 out of 10,000 are overdiagnosed. This level of overdiagnosis is at least 3.5 times higher than the level of overdiagnosis among compliers, 58 out of 10,000, as estimated by the LATE. Measured as a share of breast cancers in the intervention arm, the overdiagnosis rate is at least 36% among always takers and 14% among compliers. I also find suggestive evidence that women more likely to receive mammograms are more likely to be harmed by them in terms of long-term all-cause mortality. The treatment effects on all-cause mortality 20 years after enrollment are not statistically different from zero or from each other, which is unsurprising given that none of the trials included in the meta-analysis that informs the USPSTF guidelines (Nelson et al., 2016) show statistically significant effects on all-cause mortality. However, the implied lower bound on the average treatment effect for always takers is economically significant in the sense that at least 4.9% of their deaths would not have occurred otherwise.
There are several plausible explanations for my findings. My first finding is intuitive if we expect that women who are healthier and of higher socioeconomic status will be more likely to practice health behaviors seen as beneficial, including mammography. This finding is consistent with empirical evidence on socioeconomic status and health behaviors (Goldman and Smith, 2002; Cutler and Lleras-Muney, 2010; Oster, 2020). My second finding is perhaps counterintuitive if we expect that women who are more likely to benefit from mammograms in terms of long-term health outcomes will be more likely to receive them. However, given my first finding that women more likely to receive mammograms have higher socioeconomic status, Welch and Fisher (2017) provide a rationale for my second finding. Analyzing breast cancer incidence and mortality in US counties over time, they find greater rates of overdiagnosis in counties with higher socioeconomic status. They explain that “wealthier people are exposed to increased observational intensity: they are likely to be screened more often and by means of such tests...that can detect smaller abnormalities, undergo more follow-up testing, undergo more biopsies, and they may be served by health systems that have a lower threshold for labeling results as abnormal.” The differential overdiagnosis that I find is consistent with their finding and explanation. Furthermore, it is plausible that women more likely to receive mammograms also pursue more aggressive therapies (Myerson et al., 2018), providing a potential mechanism for differential mortality. Consistent with this mechanism, I find suggestive evidence that among women diagnosed with breast cancer during the active study period who had at least part of a breast removed, women more likely to receive mammograms were more likely to have an entire breast removed.
An alternative and potentially problematic explanation for my findings is that although women more likely to receive mammograms are healthier on other dimensions, they are more likely to receive mammograms because they have higher underlying breast cancer risk. As one response to this concern, I take a conservative approach to sample selection in my main analysis sample. The CNBSS conducted extensive baseline surveys and clinical exams. I use variables collected through these means to exclude women with a family history of breast cancer and women with potential knowledge of increased breast cancer risk. As another response, I examine characteristics of the breast cancers detected during the active study period. I find suggestive evidence that breast cancers detected in women more likely to receive mammograms are smaller and less invasive, which could indicate that women more likely to receive mammograms are healthier in terms of their tumor characteristics, corroborating the selection heterogeneity that I find, or that women more likely to receive mammograms are more likely to be diagnosed with breast cancer given the same tumor characteristics, corroborating the treatment effect heterogeneity that I find.
My findings imply that the current USPSTF guidelines for women in their 40s conflate the women most likely to receive mammograms with the women most likely to benefit from them. I arrive at this implication by relating always takers within the CNBSS to women who receive mammograms under the current guidelines. Under the same analogy, compliers would receive mammograms under the previous stronger guidelines but not under the current guidelines, and never takers would not receive mammograms under either set of guidelines. The magnitude of the overdiagnosis rate found by Bleyer and Welch (2012) under the previous stronger guidelines supports the analogy. Under it, the 31% overdiagnosis rate that they find represents an average among always takers and compliers. In the CNBSS, I find overdiagnosis rates of at least 36% for always takers and 14% for compliers, which could average to the rate from the US findings despite differences in empirical settings. The overdiagnosis that I find among compliers implies that the previous weakening of the USPSTF guidelines had merit, which is to be expected because the weakening was partially based on results from the CNBSS, which reflect overdiagnosis for compliers. However, the overdiagnosis that I find among always takers is a new result. It implies that there could be merit in a further weakening of the USPSTF guidelines such that they do not recommend or recommend against mammography for all asymptomatic women in their 40s, in line with recommendations from other countries. The magnitudes of overdiagnosis I find imply that a further weakening of the USPSTF guidelines could be even more effective at reducing overdiagnosis than the previous weakening.
My findings advance the literature on mammography and overdiagnosis. Whereas the meta-analysis that informs the USPSTF mammography guidelines (Nelson et al., 2016) examines average health impacts within clinical trials, I examine how the effects of mammography vary with mammography behavior, which is important because guidelines can only have an impact through behavior. Outside of the clinical trial literature, a large literature examines mammography behavior in response to policy interventions that yield natural experiments, but it provides no evidence on how selection into mammography or treatment effects of mammography vary with such behavior (Kelaher and Stellman, 2000; Habermann et al., 2007; Kadiyala and Strumpf, 2011, 2016; Finkelstein et al., 2012; Kolstad and Kowalski, 2012; Bitler and Carpenter, 2016, 2019; Fedewa et al., 2015; Mehta et al., 2015; Ong and Mandl, 2015; Lu and Slusky, 2016; Zanella and Banerjee, 2016; Cooper et al., 2017; Jacobson and Kadiyala, 2017; Buchmueller and Goldzahl, 2018; Myerson et al., 2020). This literature has been limited because the methods that it employs do not allow it to recover selection heterogeneity and corresponding treatment effect heterogeneity. Furthermore, it rarely engages with the possibility of overdiagnosis as a health impact, perhaps because individual-level data on mammography behavior that follow individuals in a randomized or natural experiment for long enough to identify overdiagnosis are not widely available.
Two papers corroborate the selection heterogeneity that I find within natural experiments, but consistent with the literature, they do not examine corresponding treatment effect heterogeneity. Kim and Lee (2017) analyze a national cancer screening program in Korea that generated discontinuities in eligibility and find selection heterogeneity such that women more likely to receive mammograms are healthier in terms of cancer incidence six years afterward, body mass index, blood glucose, and cholesterol. Einav et al. (2020) analyze mammography takeup before and after age 40 in the United States. Their findings demonstrate that the selection heterogeneity that I find on health behaviors and cancer incidence is relevant to current USPSTF guidelines.
I advance the methodological literature on clinical trials by proposing an approach that relates treatment effect heterogeneity to behavior within a trial to improve targeting within guidelines. In the process, although doing so is not my focus, I also contribute to the literature on treatment effect heterogeneity. The brunt of my contributions to that literature appear in my work on the Oregon Health Insurance Experiment (Kowalski, 2021a), which I introduced in an earlier working paper (Kowalski, 2016) and apply here. However, I have divided that working paper such that some content only appears here. Specifically, in this paper, I identify treatment effect heterogeneity using an ancillary assumption that is weaker than the linearity assumption that I impose elsewhere. Brinch et al. (2017) propose this weaker assumption in conjunction with a related assumption to test treatment effect homogeneity, but I demonstrate here that I can test treatment effect homogeneity with only one assumption. I also demonstrate how to motivate the assumption theoretically and empirically, and I show that it implies a bound on the average treatment effect for always takers that is central to my findings. I also perform inference without a power-limiting Bonferroni correction. In my only other directly related work (Kowalski, 2020a), I do not break new ground, but I use stylized examples to illustrate recent advances to the literature on treatment effect heterogeneity. I also provide a Stata command (Kowalski et al., 2018) that can be used to apply these advances to examine selection and treatment effect heterogeneity in other clinical trials.
In the next section, I provide more information on the CNBSS data and published results. In Section 3, I present the model. In Section 4, I present my two main findings. I show that my findings are robust to a wide variety of alternative specifications in Section 5. I conclude by discussing implications for guidelines in Section 6.
2. CNBSS Background and Replication of Results
Viewing the CNBSS as an influential trial, my focus is not to evaluate the CNBSS itself or previous work on it. Rather, my focus is to extend analysis of the CNBSS to examine how the results vary with mammography behavior. I begin by providing background and replicating published results.
The CNBSS enrolled almost 90,000 women aged 40–59 between 1980 and 1985. All women were given a clinical breast examination at enrollment before random assignment to an intervention or control arm.2 To evaluate the randomization, Miller et al. (2002) report balance tests among women in their 40s at enrollment, and they do not find many meaningful differences between the intervention and control arms. I conduct similar balance tests with the variables available to me, and I find results consistent with theirs. The independent Cochrane review considers the CNBSS as one of only three mammography trials with adequate randomization (Gøtzsche and Jørgensen, 2013).
Intervention arm women received access to annual mammograms and clinical breast examinations during the active study period, which consisted of enrollment and 3 to 4 years after enrollment. The data show that some women in the intervention arm did not receive mammograms after the enrollment year during the active study period. Some did not return to study centers and others returned but refused mammography (Miller et al., 1992a). These women cited “excessive distance to center, painful mammography, fear of radiation, lack of time, and preference for own physician,” and they reported less support from family, friends, and physicians (Baines et al., 1990). Following the clinical breast examination at enrollment, control arm women in their 40s at enrollment received usual care in the community, and control arm women in their 50s at enrollment received access to annual clinical breast examinations in each subsequent year of the active study period. The data show that a substantial fraction of control arm women received mammograms during the active study period, which is not surprising given that a CNBSS investigator noted in the early 1980s that “many believe that if they demand a mammogram, their doctor will accede to their request” (Baines, 1984). Although the CNBSS collected data on mammography for all participants during the active study period, it did not continue doing so afterward.
However, the CNBSS data include two important long-term health outcomes—breast cancer incidence and all-cause mortality—through linkage to cancer registries that are complete across Canada (Baines et al., 2016) and the Canadian mortality database. The CNBSS is the only trial considered by the meta-analysis that informs the USPSTF guidelines (Nelson et al., 2016) that allows for examination of breast cancer incidence and all-cause mortality at least 20 years after enrollment for all participants. The Cochrane review deems the CNBSS as at low risk of attrition bias (Gøtzsche and Jørgensen, 2013). The breast cancer incidence data include invasive breast cancer as well as non-invasive ductal carcinoma in situ (DCIS). DCIS tumors are considered to be of ultralow risk, but the word “carcinoma” causes alarm, which has prompted proposals to rename DCIS tumors “indolent lesions of epithelial origin (IDLE)” (Esserman and Varma, 2019). Since many DCIS tumors can only be diagnosed by mammograms, it is important that they are included in analyses of overdiagnosis.
I can closely or exactly replicate the latest results published by the CNBSS investigators. Importantly, I can closely replicate the Baines et al. (2016) result on breast cancer incidence that shows overdiagnosis, and it is statistically significant.3 I can also exactly replicate the latest results on all-cause and breast cancer mortality. These results show higher all-cause mortality in the intervention arm than the control arm (Miller et al., 2014), but the difference is not statistically significant. Breast cancer mortality is slightly lower in the intervention arm (Miller et al., 2014), but this difference is not statistically significant either. In terms of statistical significance, the long-term results are consistent with results published at earlier follow-up lengths (Miller et al., 1992a,b, 1997, 2000, 2002, 2014).
In the replication results that serve as the foundation for my analysis, I depart from the latest published results in four ways to increase the relevance of my findings to the USPSTF guidelines for women in their 40s. First, I only include women aged 40–49 at enrollment in my main analysis sample, and I examine robustness among women aged 50–59 at enrollment. Second, because the USPSTF guidelines are intended for asymptomatic women without a genetic predisposition for breast cancer, and because I aim to exclude women with potential knowledge of increased breast cancer risk, I exclude women if they report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms. I also exclude women if a nurse found abnormalities or referred them for review. My main analysis sample includes 19,505 women. I examine robustness in the full sample of 50,430 women aged 40–49 at enrollment and in the subsample of excluded women. Third, to make the timing of my findings easier to interpret, I report results at a fixed follow-up length of 20 years after enrollment, as opposed to a fixed calendar date that reflects various follow-up lengths. I also examine robustness at earlier follow-up lengths. Fourth, when analyzing mortality, I only examine all-cause mortality because it is less subjective than breast cancer mortality and because it can capture a wider range of collateral harms.
3. Model of Behavior within the CNBSS
As the foundation for the model, I rely on the LATE independence and monotonicity assumptions of Imbens and Angrist (1994). I present implications of these assumptions using simple figures. The figures motivate the identification of selection heterogeneity under the LATE assumptions and the identification of treatment effect heterogeneity under a single ancillary assumption beyond the LATE assumptions.
3.1. First Stage: Mammography
In the model, the treatment is mammography, which I represent with the binary variable D. In the main specification, I set D = 1 if a participant receives a mammogram in at least one year during the active study period after the enrollment year, and I set D = 0 otherwise. The instrument Z is a binary variable such that Z = 1 represents random assignment to the intervention arm and Z = 0 represents random assignment to the control arm.
I illustrate implications of the first stage of the model in Figure 1. In my main analysis sample, 19% of control women and 95% of intervention women receive mammograms, so the probability of treatment in control pC is 0.19 and the probability of treatment in intervention pI is 0.95. The top line depicts the fraction treated in control, and the middle line depicts the fraction treated in intervention. By the LATE independence assumption, which requires that assignment to intervention or control is random, the bottom line depicts the fraction treated in intervention and control on the same line. This line characterizes the fraction treated p if the entire sample were assigned to intervention or control. The observed probabilities of treatment in intervention and control partition the line into three ranges. I label the ranges using terminology from Imbens and Angrist (1994) in which “always takers” receive treatment regardless of random assignment, “compliers” receive treatment if and only if assigned to the intervention arm, and “never takers” do not receive treatment regardless of random assignment. The LATE monotonicity assumption precludes “defiers” who receive treatment if and only if assigned to the control arm because it requires that assignment to the intervention arm weakly increases mammography for every participant in the trial.
Figure 1:

Ranges of the Fraction Treated p for Always Takers, Compliers, and Never Takers: Always Takers are More Likely to Receive Mammograms Than Compliers, Who are More Likely to Receive Mammograms Than Never Takers
Note. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. pC is the fraction treated in control P(D = 1 | Z = 0) and pI is the fraction treated in intervention P(D = 1 | Z = 1). The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review.
The main implication of the first stage of the model that I emphasize with Figure 1 is that there is an ordering from always takers to compliers to never takers, which has been shown by Imbens and Rubin (1997) and Vytlacil (2002). In the CNBSS, I interpret this ordering in terms of mammography behavior within the trial. Always takers are the most likely to receive mammograms (they receive them with probability 1), followed by compliers (they receive them with the probability of assignment to intervention), followed by never takers (they receive them with probability 0). This interpretation is useful for the analogy of always takers to the women who receive mammograms under the current USPSTF guidelines, compliers to the women who would receive mammograms under the previous but not the current USPSTF guidelines, and never takers to the women who would not receive mammograms under either guidelines.
3.2. Second Stage: Health Outcomes
I relate a health outcome Y, breast cancer incidence or all-cause mortality, to mammography D as follows:
where YT represents the potential outcome when treated (D = 1), and YU represents the potential outcome when untreated (D = 0). The LATE independence assumption implies that both potential outcomes are independent of assignment to intervention.
The main implication of the second stage of the model that I emphasize with Figure 2 is that it is possible to derive average treated outcomes of always takers and compliers and average untreated outcomes of compliers and never takers (Imbens and Rubin, 1997; Katz et al., 2001; Abadie, 2002, 2003). I provide a graphical depiction of this derivation in the CNBSS in Figure 2. Consider treated women in control. These women must be always takers, so their average outcome yields an estimate of the average treated outcome of always takers.4 I plot this value, 571 breast cancers per 10,000 women, over the support of the fraction treated p for always takers using a dotted line to indicate that it represents a treated outcome. Next consider untreated women in intervention. These women must be never takers, so their average outcome yields an estimate of the average untreated outcome of never takers.5 I plot this value, 667 breast cancers per 10,000 women, using a dashed line to indicate that it represents an untreated outcome. Estimation of the average treated and untreated outcomes of compliers requires a little more work. To estimate the average treated outcome of compliers, consider treated women in intervention. The average outcome of these women, 453 breast cancers per 10,000 women, represents a weighted average treated outcome of always takers and compliers, so I plot it over the full support for always takers and compliers. Because we know the fraction of this support attributable to always takers, and we have estimated their average outcome, we can back out an estimate of the average treated outcome of compliers.6 I plot this value, 424 breast cancers per 10,000 women, over the support for compliers. The derivation of the average untreated outcome of compliers, 366 breast cancers per 10,000, is similar.7
Figure 2:

Derivation of Average Breast Cancer Incidence for Always Takers, Compliers, and Never Takers: Averages for Treated and Untreated Compliers Depicted with Lighter Shading
Note. The outcome Y is breast cancer incidence, measured 20 years after enrollment for all participants, based on initial diagnosis and the exact calendar date of enrollment. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. pC is the fraction treated in control P(D = 1 | Z = 0) and pI is the fraction treated in intervention P(D = 1 | Z = 1). The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review.
In Figure 3, I remove content from Figure 2 to depict comparisons across always takers, treated and untreated compliers, and never takers more cleanly. As I show with an arrow, the LATE, the average treatment effect for compliers, is equal to the difference between the average treated and untreated outcomes of compliers (Imbens and Rubin, 1997). This treatment effect on breast cancer incidence 20 years after enrollment indicates that the level of overdiagnosis among compliers is 58 cancers per 10,000 women and that the rate of overdiagnosis among treated compliers is 14% (=58/424). I emphasize with the figure that the LATE says nothing about the average treatment effect for always or never takers, which represent sizeable and distinct fractions of women. The average treatment effect for any group is equal to the average treated outcome minus the average untreated outcome. Always takers are treated by definition, so it is not possible to estimate their average untreated outcome or their average treatment effect without ancillary assumptions. Similarly, never takers are untreated by definition, so it is not possible to estimate their average treated outcome or their average treatment effect without ancillary assumptions. However, the average outcomes that can be derived for always and never takers appear very different from the average outcomes of compliers. By 20 years after enrollment, 5.71% of always takers and 6.67% never takers have been diagnosed with breast cancer, as compared to 4.24% of treated compliers and 3.66% of untreated compliers. These comparisons provide the variation that I use as a starting point to identify how selection and the treatment effect vary with mammography behavior.
Figure 3:
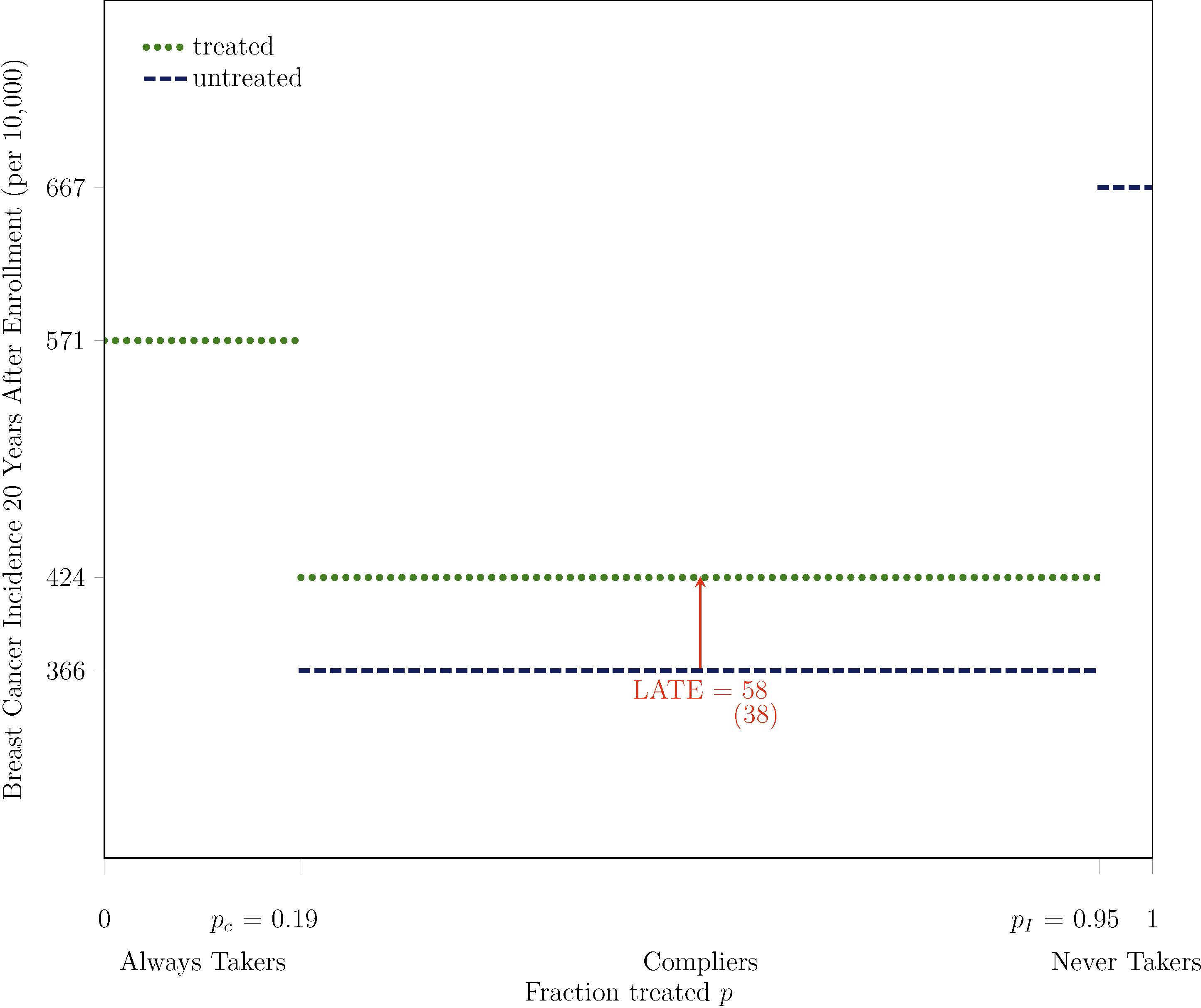
Average Breast Cancer Incidence for Always Takers, Compliers, and Never Takers
Note. Bootstrapped standard errors are under point estimates in parentheses. The outcome Y is breast cancer incidence, measured 20 years after enrollment for all participants, based on initial diagnosis and the exact calendar date of enrollment. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. pC is the fraction treated in control P(D = 1 | Z = 0) and pI is the fraction treated in intervention P(D = 1 | Z = 1). The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review.
3.3. Definitions of Selection and Treatment Effect Heterogeneity in the Model
Following Kowalski (2021a), I define selection and treatment effect heterogeneity on Y along the fraction treated p using functions from the MTE literature (see Carneiro and Lee, 2009; Brinch et al., 2017):
The first function, which I refer to as the “marginal untreated outcome (MUO)” function, defines what I refer to as “selection heterogeneity” along the fraction treated p. Selection heterogeneity generalizes the concept of “selection bias,” as defined by Angrist (1998) and Heckman et al. (1998) among others, which is equal to the difference in average untreated outcomes between treated and untreated participants:
Selection bias depends on the fraction of the sample assigned to intervention, a parameter chosen as part of the trial design, because assignment to intervention determines treatment D for compliers. Furthermore, selection bias is not identified without ancillary assumptions. In contrast, a different special case of selection heterogeneity does not depend on the fraction of the sample assigned to intervention, and it is identified without ancillary assumptions. Randomization makes identification possible by generating exogenous variation in the fraction treated p, thereby making the average untreated outcome of compliers distinguishable from the average untreated outcome of never takers.
The second function is the “marginal treatment effect (MTE)” function of Heckman and Vytlacil (1999, 2001, 2005). It defines treatment effect heterogeneity along the fraction treated p. In the CNBSS, the MTE function characterizes how the impact of mammography on a health outcome changes as women become less likely to receive mammograms.
The third function, which I refer to as the “marginal treated outcome (MTO)” function, characterizes the sum of selection and treatment effect heterogeneity along the fraction treated p. It is tempting to assert that there should be no material distinction between treated and untreated outcomes. However, the treatment effect is defined as the treated outcome minus the untreated outcome, not the untreated outcome minus the treated outcome. The treatment effect has magnitude and direction, which is why I represent the LATE with an arrow in Figure 3. Renaming the untreated outcome as the treated outcome and vice versa would change the direction of the treatment effect, illustrating why there is a material distinction between treated and untreated outcomes in the definitions of selection and treatment effect heterogeneity. Under the reversed definition of the treatment, there would still be a material distinction: heterogeneity in treated outcomes would capture selection heterogeneity, and heterogeneity in untreated outcomes would capture the sum of selection and treatment effect heterogeneity.
4. Findings
Applying the model to the CNBSS, I identify and estimate how selection and treatment effect vary with mammography behavior. First, under the model that assumes no more than the LATE assumptions, I find selection heterogeneity: women who are more likely to receive mammograms are healthier in terms of long-term breast cancer incidence and all-cause mortality. Baseline covariates that measure socioeconomic status and health behaviors, as well as results from the literature, corroborate this finding. This finding informs an ancillary assumption that I impose to identify treatment effect heterogeneity. Second and more importantly, under the ancillary assumption, I find treatment effect heterogeneity: the 20-year level of overdiagnosis is at least 3.5 times higher among women most likely to receive mammograms, such that at least 36% of their cancers are overdiagnosed. I also find suggestive evidence that corroborates this finding: cancers detected among the women more likely to receive mammograms are smaller and less invasive.
4.1. Selection Heterogeneity: Women More Likely to Receive Mammograms are Healthier
I identify selection heterogeneity by testing the null hypothesis that the following test statistic is equal to zero:
| (1) |
I refer to this test as the “untreated outcome test” because it compares the average untreated outcomes of compliers and never takers. This test is equivalent or similar to tests proposed by Bertanha and Imbens (2020), Guo et al. (2014), and Black et al. (2020), generalized by Mogstad et al. (2018).8 Unlike previous literature, I demonstrate in Kowalski (2021a) that the untreated outcome test identifies a special case of selection heterogeneity by expressing the untreated outcome test statistic in (1) as a weighted integral of the MUO function.9 Identification stems from randomization, which generates compliers and never takers.
Applying the untreated outcome test in the CNBSS, I find selection heterogeneity on breast cancer incidence and all-cause mortality. As shown in Figure 4, the test statistic indicates that average breast cancer incidence among untreated compliers was 3.01 percentage points lower, almost 50% lower, than it was among never takers. The test statistic is statistically different from zero, and the untreated outcome test rejects selection homogeneity on breast cancer incidence at the 0.3% level.10 The test also rejects selection homogeneity on all-cause mortality. The 20-year all-cause mortality rate is 4.28% for untreated compliers and 9.90% for never takers. The 5.62 percentage point difference in all-cause mortality between these two groups is meaningfully large, and it is statistically different from zero at the 0.1% level. All-cause mortality and breast cancer incidence are both measures of health, and compliers are more likely to receive mammograms than never takers. Therefore, the selection heterogeneity that I find indicates that women more likely to receive mammograms are healthier.
Figure 4:
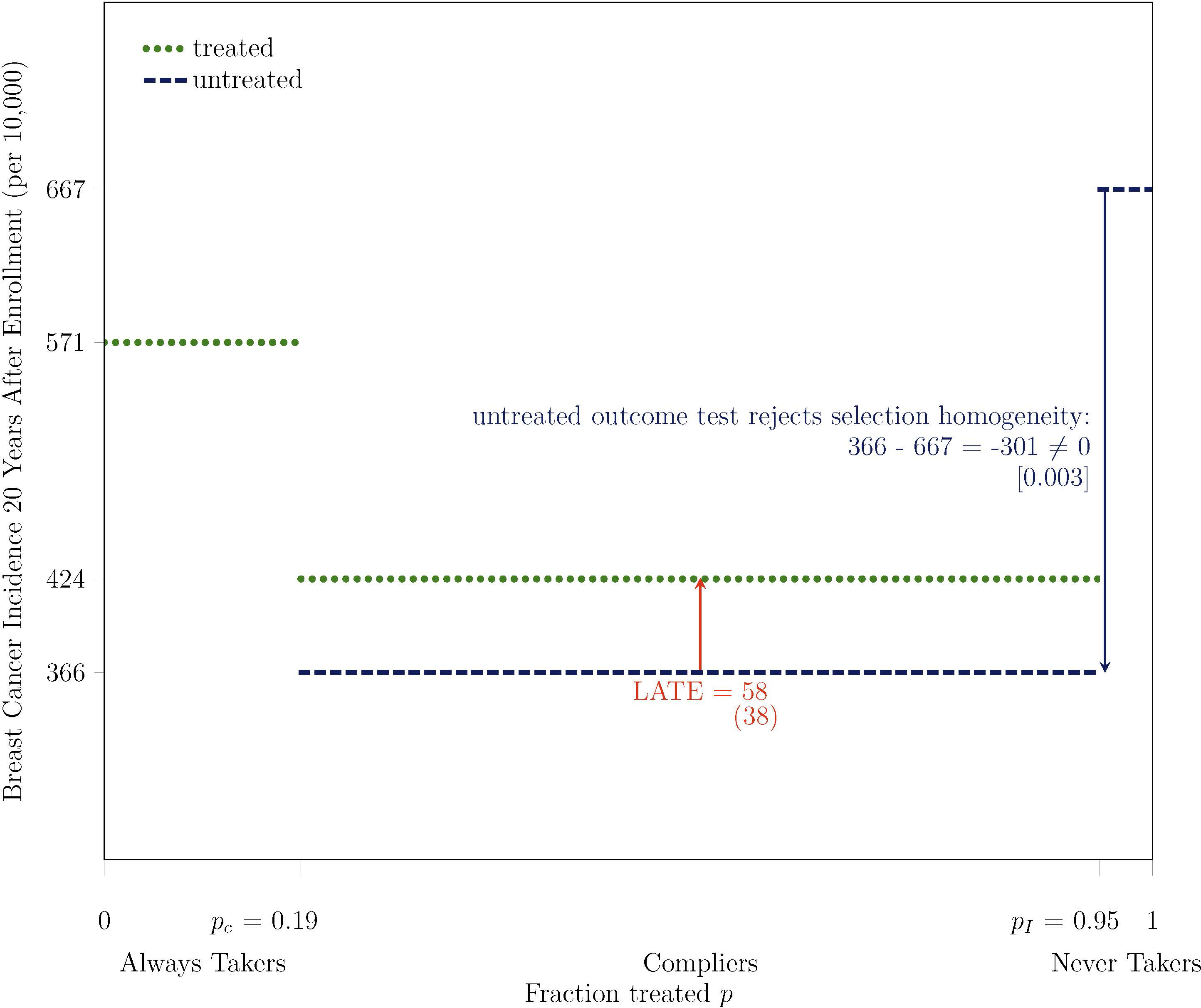
Untreated Outcome Test Rejects Selection Homogeneity on Breast Cancer Incidence at 0.3% Level: Women More Likely to Receive Mammograms are Healthier
Note. Bootstrapped standard errors are under point estimates in parentheses, and two-tailed bootstrapped p-values are under test statistics in brackets. The outcome Y is breast cancer incidence, measured 20 years after enrollment for all participants, based on initial diagnosis and the exact calendar date of enrollment. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. pC is the fraction treated in control P(D = 1 | Z = 0) and pI is the fraction treated in intervention P(D = 1 | Z = 1). The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review.
Recast in terms of the untreated outcome test, evidence from Kim and Lee (2017) and Einav et al. (2020) also indicates selection heterogeneity such that women more likely to receive mammograms are healthier. Kim and Lee (2017) compare average cancer incidence of compliers and never takers, finding that compliers are less likely to have cancer. They restrict analysis to untreated compliers in some specifications, but they also consider an average of treated and untreated compliers in others, which could taint the selection heterogeneity that they find in those specifications with an implicit treatment effect for treated compliers. Einav et al. (2020) compare treated compliers to never takers. They obtain cancer incidence for never takers through a clinical model.
4.1.1. Baseline Covariates Corroborate Selection Heterogeneity
The untreated outcome test shows selection heterogeneity based on the comparison of average untreated health outcomes of compliers and never takers. I do not observe untreated health outcomes of always takers by definition. However, I do observe baseline covariates for always takers, as well as compliers and never takers. I use these baseline covariates as proxies for untreated health outcomes, allowing me to investigate whether the selection heterogeneity that I find also applies over the range of the fraction treated p from always takers to compliers.
To derive average baseline covariates for always takers, compliers, and never takers, I begin with the same approach that I demonstrate in Figure 2 with a covariate X in lieu of an outcome Y. That approach yields a different average outcome for treated and untreated compliers, but average baseline covariates should be the same for treated and untreated compliers by the LATE independence assumption. I therefore obtain an average baseline covariate for all compliers by weighting the average baseline covariates for treated and untreated compliers by the probabilities of treated and untreated compliers in the sample, which are equal to the probabilities of assignment to intervention and control.11
As shown in Table 1, baseline measures of socioeconomic status tend to vary monotonically from always takers to compliers to never takers, with always takers having the highest socioeconomic status. These patterns are consistent with an extensive literature that shows a positive correlation between socioeconomic status and health (see National Center for Health Statistics (2012) for a review). Measures of baseline health behavior suggest a potential mechanism: women more likely to receive mammograms are more likely to practice other health behaviors seen as beneficial. As shown, smoking status, body mass index, and breast self-examination vary monotonically from always takers to compliers to never takers, and many of the differences are statistically significant. Overall, analysis of baseline covariates corroborates the selection heterogeneity that I find from compliers to never takers. It also supports extension of the finding of selection heterogeneity such that in the absence of mammograms, always takers would have the best health outcomes, followed by compliers, followed by never takers.
Table 1:
Baseline Covariates Corroborate Selection Heterogeneity: Women More Likely to Receive Mammograms Have Higher Socioeconomic Status and Are More Likely to Practice Other Health Behaviors Seen as Beneficial
| Means |
Difference in Means |
||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | |||
| Always Takers | Compliers | Never Takers | (1)–(2) | (2)–(3) | |
|
| |||||
| Baseline Socioeconomic Status | |||||
| In work force | 0.65 (0.01) | 0.64 (0.00) | 0.65 (0.02) | 0.02 (0.01) | −0.02 (0.02) |
| Age at first birth | 24.28 (0.11) | 23.98 (0.04) | 23.57 (0.21) | 0.30 (0.13) | 0.41 (0.22) |
| No live birth | 0.16 (0.01) | 0.15 (0.00) | 0.13 (0.02) | 0.01 (0.01) | 0.01 (0.02) |
| Married | 0.80 (0.01) | 0.81 (0.00) | 0.75 (0.02) | −0.01 (0.01) | 0.06 (0.02) |
| Husband in work force if alive | 0.81 (0.01) | 0.81 (0.00) | 0.76 (0.02) | −0.00 (0.01) | 0.05 (0.02) |
| Baseline Health Behavior | |||||
| Non-Smoker | 0.78 (0.01) | 0.75 (0.00) | 0.63 (0.02) | 0.03 (0.01) | 0.12 (0.02) |
| Body Mass Index | 23.87 (0.10) | 24.42 (0.04) | 24.48 (0.22) | −0.56 (0.11) | −0.06 (0.23) |
| Used oral contraception | 0.74 (0.01) | 0.71 (0.00) | 0.67 (0.02) | 0.03 (0.01) | 0.04 (0.02) |
| Used estrogen | 0.13 (0.01) | 0.13 (0.00) | 0.15 (0.02) | −0.00 (0.01) | −0.02 (0.02) |
| Any mammograms prior to enrollment | 0.23 (0.01) | 0.13 (0.00) | 0.13 (0.02) | 0.10 (0.01) | −0.00 (0.02) |
| Practiced breast self-examination | 0.47 (0.01) | 0.44 (0.00) | 0.38 (0.02) | 0.03 (0.01) | 0.06 (0.02) |
Note. Bootstrapped standard errors are under point estimates in parentheses. Each line of the table reports statistics on a different baseline covariate X. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review. Some differences between statistics might not appear internally consistent because of rounding.
4.2. Treatment Effect Heterogeneity: Women More Likely to Receive Mammograms Experience Higher Levels of Overdiagnosis
The evidence that average baseline health outcomes decrease from always takers to compliers to never takers provides justification for an ancillary assumption that I use to identify treatment effect heterogeneity on a health outcome Y. The assumption requires weak monotonicity of untreated outcomes from always takers to compliers to never takers:
where the empirical direction of selection heterogeneity determines the direction of the weak monotonicity. While the model imposes the LATE monotonicity assumption in the first stage, M.1 imposes a related weak monotonicity in the second stage.
Brinch et al. (2017) impose M.1 in conjunction with an analogous weak monotonicity assumption on the MTO function. I advance the literature here by recognizing that either of the Brinch et al. (2017) assumptions is sufficient to test for treatment effect heterogeneity. I only impose M.1 because the selection heterogeneity that I find in terms of untreated outcomes and covariates provides empirical support for it. In contrast, alternative assumptions on the MTO or MTE functions entail assumptions about treatment effect heterogeneity. I prefer not to identify treatment effect heterogeneity with assumptions about treatment effect heterogeneity.
In Figure 5, I demonstrate that M.1 yields an upper bound on the average untreated outcome of always takers in the CNBSS, which implies a lower bound on the average treatment effect for always takers. It is well-known that it is possible to estimate bounds on the average treatment effect for always takers using bounds that arise from the natural range of outcomes (Robins, 1989; Manski, 1990; Balke and Pearl, 1997) or from ancillary assumptions (Imbens and Rubin, 1997). The ancillary assumptions made by Olsen (1980), Heckman (1979), and Brinch et al. (2017), discussed by Kline and Walters (2019), also imply bounds on the average treatment effect for always takers, but those assumptions are stronger than M.1 and more difficult to motivate in the CNBSS.
Figure 5:
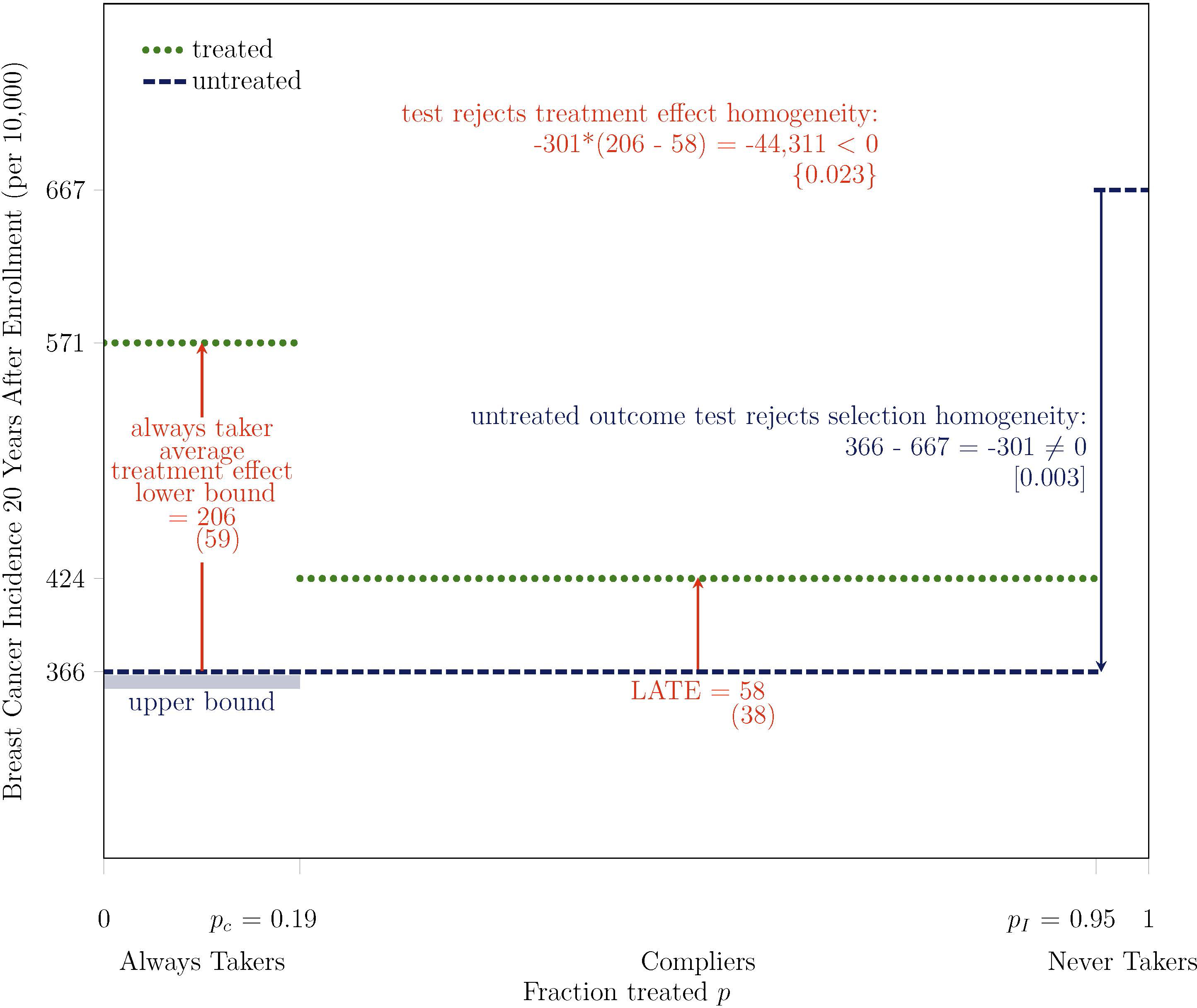
Test Rejects Treatment Effect Homogeneity on Breast Cancer Incidence at 2.3% Level: Overdiagnosis is at Least 3.5 Times Higher Among Women Most Likely to Receive Mammograms, At Least 36% (= 206/571) of Their Cancers are Overdiagnosed
Note. Bootstrapped standard errors are under point estimates in parentheses, two-tailed bootstrapped p-values are under test statistics in brackets, and one-tailed bootstrapped p-values are under test statistics in curly braces. The outcome Y is breast cancer incidence, measured 20 years after enrollment for all participants, based on initial diagnosis and the exact calendar date of enrollment. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. pC is the fraction treated in control P(D = 1 | Z = 0) and pI is the fraction treated in intervention P(D = 1 | Z = 1). The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review. Some differences between statistics might not appear internally consistent because of rounding.
As shown in Figure 5, the lower bound on the average treatment effect for always takers is larger than the LATE, the average treatment effect for compliers, which provides evidence of treatment effect heterogeneity. I conduct a formal test of the null hypothesis of treatment effect homogeneity which rejects the null hypothesis if the following test statistic is negative:
| (2) |
The term in the first line of (2) is the untreated outcome test statistic, which determines whether the bound on the average treatment effect for always takers is an upper bound or a lower bound. The term in the second line is the difference between the bound on the always taker average treatment effect and the LATE. For internal consistency with inference that I perform on other quantities, I perform inference using a nonparametric bootstrap with 1,000 replications. That is, I report a one-tailed p-value equal to the fraction of bootstrap replications in which the test statistic in (2) is positive. Because this inference approach relies on a single test statistic, it is more powerful than the approach proposed by Brinch et al. (2017). That approach effectively conducts separate tests on the signs of the first and second terms of (2) and then tests whether both signs are equal using a Bonferroni correction to account for multiple hypothesis testing, which is power-reducing. Accordingly, the test rejects the null hypothesis of treatment effect homogeneity at the 4.3% level under the Brinch et al. (2017) approach and at the 2.3% level under my proposed approach.
The statistical significance of the treatment effect heterogeneity is important, but its magnitude is also meaningful, as are the magnitudes of the treatment effects themselves. As depicted in Figure 5, the average treatment effect for compliers, the LATE, indicates that by 20 years after enrollment, breast cancer incidence among compliers who received mammograms during the active study period was 0.58 percentage points higher than it would have been otherwise. To put this magnitude in context, 20-year breast cancer incidence was 424 per 10,000 among treated compliers, so the LATE indicates that 14% (=0.58/4.24) of breast cancers, almost 1 in 7, were overdiagnosed. Turning to always takers, the lower bound on the average treatment effect indicates that breast cancer incidence among always takers who received mammograms during the active study period was at least 2.06 percentage points higher than it would have been otherwise. Thus, the average treatment effect for always takers was at least 3.5 (=2.06/0.58) times higher than it was for compliers. Therefore, the 20-year level of overdiagnosis is at least 3.5 times higher among the women most likely to receive mammograms, the always takers, than it is among compliers. Furthermore, given that the 20-year breast cancer incidence rate among always takers is 5.71%, at least 36% (=2.06/5.71) of their breast cancers are overdiagnosed.
The rates of overdiagnosis that I estimate within my main analysis sample, at least 36% among always takers and 14% among compliers, fall squarely within the range of overdiagnosis estimates from literature. Estimates vary in their data sources, their identification strategies, the types of breast cancers that they consider, and the denominators that they use to calculate overdiagnosis rates. In a review that includes estimates from clinical trials as well as natural experiments created by population screening programs, estimates have been reported as high as 52% (Gøtzsche and Jørgensen, 2013). Within the CNBSS, Miller et al. (2014) reports an overdiagnosis rate of 22%, and Baines et al. (2016) report several different overdiagnosis rates that vary from 5% to 48%. Baines et al. (2016) obtain the overdiagnosis rate of 5% by comparing incidence in intervention and control. This approach provides an average measure of overdiagnosis among all women under the implicit assumption that overdiagnosis is zero among always and never takers.
I do not provide an estimate of overdiagnosis for never takers. The term “never taker” gets its meaning within the active study period. After the active study period, some never takers received mammograms in response to symptoms or new screening initiatives. Those mammograms make it possible to observe the long-term breast cancer incidence of never takers even though they did not receive mammograms during the active study period. Had they received mammograms during the active study period, they could have been overdiagnosed. To bound that overdiagnosis, I could make additional assumptions. However, an assumption analogous to M.1 on the MTO function is difficult to defend, and an assumption analogous to M.1 on the MTE function yields results that are uninformative about overdiagnosis or underdiagnosis.12 Furthermore, in the analogy to the USPSTF guidelines, never takers do not receive mammograms under previous, current, or weaker guidelines, so the treatment effect for them is less policy-relevant than the treatment effects for always takers and compliers.
4.2.1. Breast Cancer Characteristics Corroborate Treatment Effect Heterogeneity
One potential concern with my finding of treatment effect heterogeneity, which shows that women more likely to receive mammograms are more likely to be overdiagnosed by them, is that M.1 does not actually hold, such that always takers would actually have higher breast cancer incidence than compliers in the absence of mammograms. This could be the case if always takers receive mammograms because they know that they have a higher risk of breast cancer than compliers, despite appearing healthier on other dimensions. To address this concern, in addition to selecting the sample to exclude women with a family history of breast cancer and women with potential knowledge of increased breast cancer risk, I compare average characteristics of the breast cancers detected among always takers and treated compliers during the active study period.
As shown in Table 2, I find suggestive evidence that breast cancers detected among always takers are smaller and less invasive than breast cancers detected among treated compliers. One potential explanation for this evidence is selection heterogeneity such that always takers with breast cancer are healthier than compliers with breast cancer, which corroborates my finding of selection heterogeneity such that women more likely to receive mammograms are healthier. A second potential explanation is that mammography has a larger average treatment effect on breast cancer diagnosis for always takers relative to compliers such that given the same or better underlying health, always takers are more likely to be diagnosed with breast cancer. The second explanation corroborates my finding of treatment effect heterogeneity such that women more likely to receive mammograms are more likely to be overdiagnosed by them.
Table 2:
Suggestive Evidence that Women More Likely to Receive Mammograms Have Breast Cancers That Are Smaller and Less Invasive and Undergo More Aggressive Procedures
| Means |
Difference in Means |
||
|---|---|---|---|
| (1) | (2) | (1) – (2) | |
| Always Takers | Treated Compliers | ||
| Tumor Size Among Breast Cancers (in mm) | 13 (2) | 18 (3) | −5 (4) |
| Share of Invasive Breast Cancer Among Breast Cancers (%) | 73 (9) | 75 (7) | −2 (13) |
| Share of Mastectomy Among Breast Cancers with Mastectomy or Lumpectomy (%) | 45 (9) | 23 (7) | 22 (14) |
Note. Bootstrapped standard errors are under point estimates in parentheses. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. Each outcome Y is restricted to the years for which treatment is defined during the active study period. Lumpectomy is a procedure that involves partial removal of a breast, and mastectomy is a more aggressive procedure that involves complete removal of a breast. The instrument Z is equal to one if a participant is assigned to intervention. The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review.
5. Robustness
I examine the robustness of my two main findings by estimating my main specification with an alternative outcome, alternative sample restrictions, alternative definitions of mammography, and alternative follow-up lengths. To facilitate comparisons with my main specification depicted in Figure 5, I summarize important statistics in Table 3. A specification shows selection heterogeneity if the untreated outcome test rejects in column (1), and a negative sign on the untreated outcome test statistic indicates that women more likely to receive mammograms are healthier. Similarly, a specification shows treatment effect heterogeneity if the test rejects in column (4), and a negative sign on the test statistic indicates that women more likely to receive mammograms experience a larger average treatment effect from them.
Table 3:
Summary of Findings Depicted in Figure 5 and Robustness to Alternative Outcomes, Sample Restrictions, and Definitions of Mammography
| (1) | (2) | (3) | (4) | ||
|---|---|---|---|---|---|
| N | Untreated Outcome Test Rejects Selection Homogeneity | Always Taker Average Treatment Effect Lower Bound | Local Average Treatment Effect LATE | Test Rejects Treatment Effect Homogeneity (1)*((2)–(3))<0 | |
|
| |||||
| Main Specification | |||||
| Outcome is breast cancer incidence, sample is main analysis sample, treatment is defined as mammogram in at least one active study period after enrollment | |||||
| Breast cancer incidence | 19,505 | −301 [0.003] | 206 (59) | 58 (38) | −44,311 {0.023} |
|
| |||||
| Alternative Outcomes | |||||
| All-cause mortality | 19,505 | −562 [0.000] | 22 (55) | −13 (39) | −19,923 {0.290} |
|
| |||||
| Alternative Sample Restrictions | |||||
| All excluded participants aged 40–49 at enrollment | 30,925 | −1,237 [0.000] | 309 (45) | 79 (44) | −284,634 {0.000} |
| All participants aged 40–49 at enrollment | 50,430 | −826 [0.000] | 298 (36) | 69 (30) | −189,397 {0.000} |
| All participants aged 50–59 at enrollment | 39,405 | −1,555 [0.000] | 419 (53) | 39 (34) | −591,037 {0.000} |
| All participants | 89,835 | −1,156 [0.000] | 332 (30) | 55 (22) | −319,660 {0.000} |
|
| |||||
| Alternative Definitions of Mammography | |||||
| At least two active study period years after enrollment | 19,505 | −341 [0.000] | 239 (90) | 54 (35) | −63,347 {0.019} |
| At least three active study period years after enrollment | 19,505 | −330 [0.000] | 167 (142) | 55 (36) | −36,927 {0.206} |
| All active study period years after enrollment | 19,505 | −178 [0.005] | 158 (181) | 64 (42) | −16,656 {0.312} |
Note. Bootstrapped standard errors are under point estimates in parentheses, two-tailed bootstrapped p-values are under test statistics in brackets, and one-tailed bootstrapped p-values are under test statistics in curly braces. Some p-values are zero if the test rejects the null hypothesis in all 1,000 bootstrap replications. Each outcome Y is measured 20 years after enrollment per 10,000 participants for all participants, based on initial occurrence and the exact calendar date of enrollment. In the main specification, the treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review. Some differences between statistics might not appear internally consistent because of rounding.
5.1. Alternative Outcome
In the main specification, the outcome is breast cancer incidence. In Figure 6 and Table 3, I also examine all-cause mortality. As I previously discussed, I find selection heterogeneity in terms of all-cause mortality that is consistent with the selection heterogeneity that I find in terms of breast cancer incidence: women more likely to receive mammograms are healthier on both dimensions. The results that I present here also provide suggestive but not statistically significant evidence of treatment effect heterogeneity on all-cause mortality that is consistent with the treatment effect heterogeneity that I find in terms of breast cancer incidence: women more likely to receive mammograms are more likely to be harmed by them on both dimensions.
Figure 6:
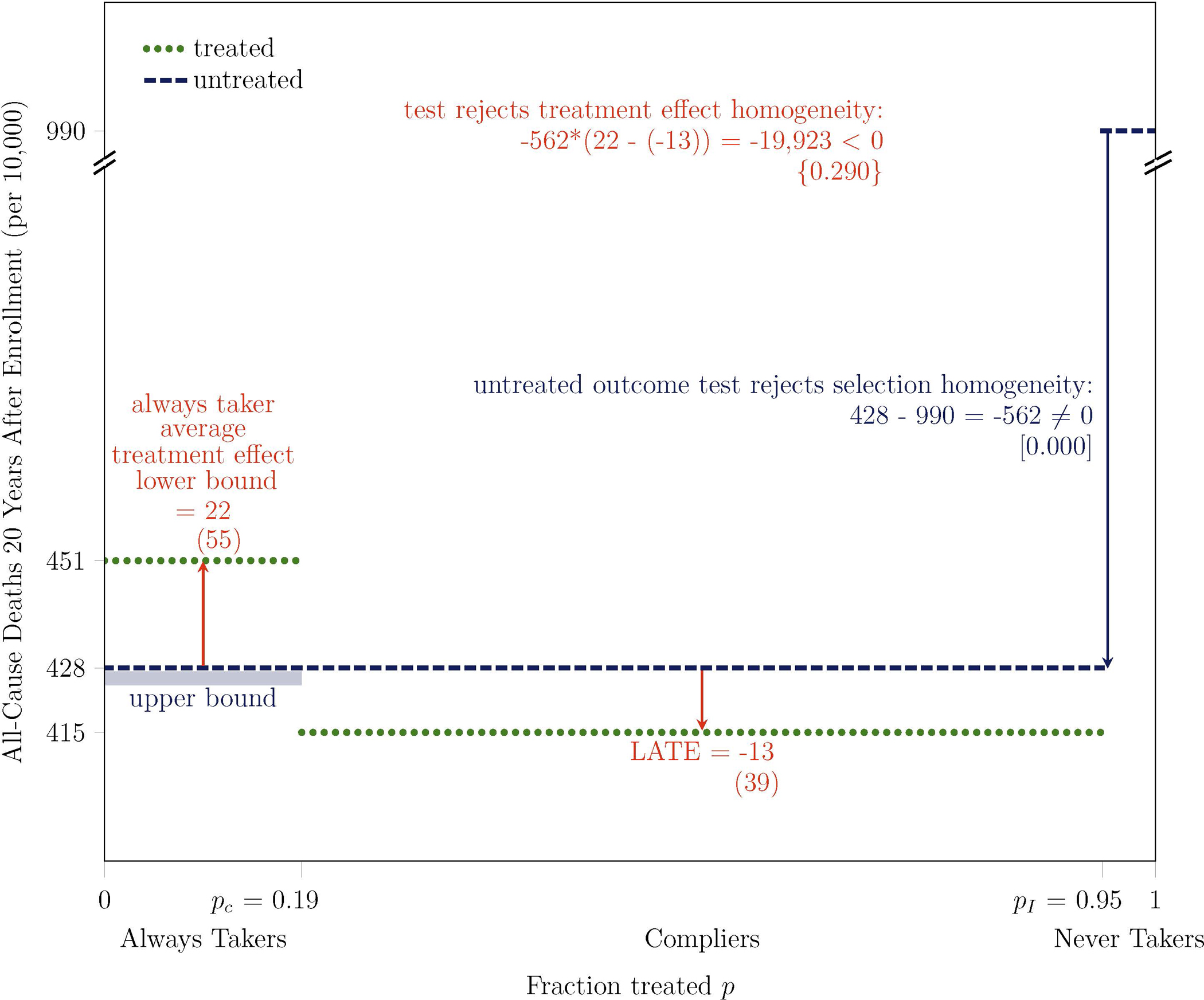
Untreated Outcome Test Rejects Selection Homogeneity on All-Cause Mortality at 0.0% Level: Women More Likely to Receive Mammograms are Healthier
Note. Bootstrapped standard errors are under point estimates in parentheses, two-tailed bootstrapped p-values are under test statistics in brackets, and one-tailed bootstrapped p-values are under test statistics in curly braces. Some p-values are zero if the test rejects the null hypothesis in all 1,000 bootstrap replications. The outcome Y is all-cause mortality, measured 20 years after enrollment for all participants, based on the exact calendar date of enrollment. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. pC is the fraction treated in control P(D = 1 | Z = 0) and pI is the fraction treated in intervention P(D = 1 | Z = 1). The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review. Some differences between statistics might not appear internally consistent because of rounding.
The magnitude of the lower bound on the average treatment effect on all-cause mortality for always takers suggests that they experience at least an additional 22 deaths per 10,000 participants when they receive mammograms, suggesting that at least 4.9% (= 22/451) of their deaths would not have occurred otherwise. For comparison, the World Health Organization estimates the number of road traffic deaths in the entire U.S. population each year at 1.1 per 10,000 people (World Health Organization, 2015). Therefore, the lower bound on the average treatment effect for always takers, which is measured over a 20-year period, is comparable to the rate of road traffic deaths over a period of the same length.
Why might women more likely to receive mammograms be more likely to experience harm from them, as measured in terms of all-cause mortality? As shown in the first two rows of Table 2, I find suggestive evidence that women more likely to receive mammograms have breast cancers that are smaller and less invasive. Virtually all women diagnosed with breast cancer during the active study period underwent lumpectomy or mastectomy. Whereas lumpectomy involves only partial removal of the breast, mastectomy is a more aggressive procedure that involves complete removal of the breast. The third row of Table 2 shows that, among women with breast cancer who underwent either of these procedures during the active study period, 45% of always takers underwent the more aggressive procedure of mastectomy, compared to only 23% of compliers. Furthermore, in an observational study of over 34,000 Canadian breast cancer patients, Kumachev et al. (2016) find that women from neighborhoods with higher socioeconomic status are more likely to receive adjuvant chemotherapy or radiotherapy, despite being diagnosed at an earlier stage. I have shown that women more likely to receive mammograms have higher socioeconomic status. These results suggest that women more likely to receive mammograms may receive more aggressive therapies for smaller, less invasive breast cancers. More aggressive therapies could lead to increased collateral harms in the form of all-cause mortality.
The suggestive evidence that I find of an impact on all-cause mortality for always takers does not necessarily extend to compliers and never takers. The LATE on all-cause mortality provides suggestive evidence that compliers experience 13 fewer deaths from all causes per 10,000 women when they receive mammograms. I cannot obtain a treatment effect for never takers without further assumptions.13 The lack of statistically significant results on all-cause mortality within the CNBSS and in other trials motivates my focus on statistically significant results on breast cancer incidence.
5.2. Alternative Sample Restrictions
Previous analyses have shown that the CNBSS had “if anything, more risk factors for breast cancer” than the Canadian population (Miller et al., 1992a). In the main specification, I consider a sample of women aged 40–49 who do not report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms. I also exclude women if a nurse found abnormalities or referred them for review. Relative to excluded women, women in the main analysis sample have lower breast cancer incidence: 442 versus 651 per 10,000. They also have lower all-cause mortality: 456 versus 511 per 10,000. They are less likely to have had any mammograms prior to enrollment: 15% versus 35%; and they are less likely to have practiced breast self-examination: 45% versus 54%.
In Table 3, I examine the robustness of my findings in the samples of all excluded participants aged 40–49 at enrollment, all participants aged 40–49 at enrollment, all participants aged 50–59 at enrollment, and all participants. My findings of selection and treatment effect heterogeneity hold in all reported samples. The results for treatment effect heterogeneity demonstrate robustness under M.1, which requires that women more likely to receive mammograms have better health in the absence of mammograms in terms of breast cancer incidence, but they do not inform whether M.1 holds.
5.3. Alternative Definitions of Mammography
In the main specification, I define mammography D such that D = 1 if a participant receives a mammogram in at least one year during the active study period after the enrollment year, and I set D = 0 otherwise. I assess robustness to narrower definitions of mammography that require mammograms in more years of the active study period in Table 3. Given the available data, I cannot examine robustness to definitions that include mammography after the active study period.
I find selection heterogeneity under all definitions of mammography, and I find treatment effect heterogeneity under the first alternative definition of mammography. The test for treatment effect homogeneity is not statistically significant under the two narrowest definitions of mammography, but it indicates treatment effect heterogeneity in the same direction. The two narrowest definitions are arguably too extreme because they require that “treated” participants must receive mammograms in three or more active study period years after enrollment, so it is notable that the results yield the same qualitative conclusions.
5.4. Alternative Follow-up Lengths
In the main specification, breast cancer incidence is measured 20 years after enrollment. Table 4 summarizes results for breast cancer incidence at all earlier annual follow-up lengths. The untreated outcome test statistic is negative at all follow-up lengths, consistent with selection heterogeneity such that women more likely to receive mammograms are healthier. Furthermore, the test rejects treatment effect homogeneity at the 3% level or less at all follow-up lengths after the first year, consistent with treatment effect heterogeneity such that women more likely to receive mammograms experience higher levels of overdiagnosis.
Table 4:
Summary of Findings Depicted in Figure 5 and Robustness to Alternative Follow-up Lengths
| (1) | (2) | (3) | (4) | ||
|---|---|---|---|---|---|
| Years Since Enrollment | N | Untreated Outcome Test Rejects Selection Homogeneity | Always Taker Average Treatment Effect Lower Bound | Local Average Treatment Effect LATE | Test Rejects Treatment Effect Homogeneity (1)*((2)–(3))<0 |
|
| |||||
| Main specification: 20 | 19,505 | −301 [0.003] | 206 (59) | 58 (38) | −44,311 {0.023} |
| 19 | 19,505 | −269 [0.013] | 196 (58) | 52 (37) | −38,565 {0.023} |
| 18 | 19,505 | −311 [0.000] | 210 (56) | 54 (35) | −48,503 {0.010} |
| 17 | 19,505 | −322 [0.000] | 214 (55) | 49 (34) | −52,975 {0.005} |
| 16 | 19,505 | −342 [0.000] | 232 (54) | 56 (32) | −60,245 {0.003} |
| 15 | 19,505 | −381 [0.000] | 211 (50) | 84 (31) | −48,650 {0.015} |
| 14 | 19,505 | −404 [0.000] | 201 (49) | 80 (29) | −49,046 {0.020} |
| 13 | 19,505 | −431 [0.000] | 223 (48) | 75 (28) | −63,808 {0.007} |
| 12 | 19,505 | −443 [0.000] | 191 (44) | 64 (27) | −56,156 {0.010} |
| 11 | 19,505 | −423 [0.000] | 195 (43) | 55 (25) | −59,084 {0.004} |
| 10 | 19,505 | −419 [0.000] | 200 (42) | 47 (23) | −64,017 {0.000} |
| 9 | 19,505 | −413 [0.000] | 192 (40) | 34 (22) | −64,955 {0.000} |
| 8 | 19,505 | −409 [0.000] | 175 (37) | 35 (21) | −57,386 {0.000} |
| 7 | 19,505 | −393 [0.000] | 177 (35) | 46 (18) | −51,740 {0.000} |
| 6 | 19,505 | −412 [0.000] | 185 (33) | 50 (17) | −55,761 {0.000} |
| 5 | 19,505 | −382 [0.000] | 180 (32) | 45 (15) | −51,581 {0.000} |
| 4 | 19,505 | −393 [0.000] | 152 (29) | 46 (13) | −41,568 {0.003} |
| 3 | 19,505 | −354 [0.000] | 104 (23) | 37 (11) | −23,679 {0.012} |
| 2 | 19,505 | −337 [0.000] | 63 (18) | 25 (9) | −12,632 {0.030} |
| 1 | 19,505 | −342 [0.000] | 35 (11) | 20 (6) | −5,194 {0.097} |
Note. Bootstrapped standard errors are under point estimates in parentheses, two-tailed bootstrapped p-values are under test statistics in brackets, and one-tailed bootstrapped p-values are under test statistics in curly braces. Some p-values are zero if the test rejects the null hypothesis in all 1,000 bootstrap replications. The outcome Y is breast cancer incidence, measured at various years since enrollment for all participants, based on initial diagnosis and the exact calendar date of enrollment. The treatment D is mammography, which is equal to one if a participant receives a mammogram in at least one year during the active study period after the enrollment year. The instrument Z is equal to one if a participant is assigned to intervention. The main analysis sample includes women aged 40–49 at enrollment and excludes those who report any breast cancer in their family, any previous breast cancer diagnosis, any other breast disease, or any symptoms, as well as those for whom a nurse found abnormalities or referred them for review. Some differences between statistics might not appear internally consistent because of rounding.
Whether overdiagnosis can be estimated in the short term is controversial due to the concept of lead time, “the time from detection of preclinical cancer by screening to detection of clinical (symptomatic) cancer in the absence of screening” (Baker et al., 2014). Short follow-up lengths might not allow for enough lead time, such that excess breast cancer detection in the intervention arm could just reflect lead time instead of overdiagnosis. However, once there is evidence of overdiagnosis in the long term, estimates from the short term can also be interpreted as estimates of overdiagnosis (Zahl et al., 2013; Baines et al., 2016). Consequently, my findings at earlier follow-up lengths could also reflect overdiagnosis. As shown in Table 4, the LATE is positive and statistically significant in the first year, and it is still statistically significant at longer follow-up lengths. The general increase in the LATE on breast cancer diagnosis across follow-up lengths complements my finding in Kowalski (2020b) that an additional 7 deaths per 100,000 women occur in the intervention arm relative to the control arm in each additional year since enrollment in the CNBSS.
6. Implications for Mammography Guidelines
Even though the CNBSS began decades ago, my findings are relevant today. Current USPSTF guidelines for women in their 40s are based in part on findings of overdiagnosis from the CNBSS. In light of these findings, the USPSTF made an implicit analogy between compliers in the CNBSS and compliers with its guidelines. Under the analogy, the USPSTF weakened its guidelines such that only always takers would receive mammograms. Using data from the CNBSS and a model that considers always takers as well as compliers, I provide new evidence that always takers experience higher rates of overdiagnosis than compliers, which provides a rationale to further weaken the current guidelines.
However, many important factors have changed since the CNBSS began. One way to account for them is to run new trials, such as the WISDOM (Esserman, 2017) and Age X (Patnick et al., 2018) trials currently in progress. However, overdiagnosis can take decades to identify. It therefore seems prudent for the USPSTF to make the most of available evidence.
The same model that I have used to obtain my findings also allows me to consider their external validity given changes in important factors. I first consider changes in the group who would be affected if the current guidelines were weakened, women who receive mammograms in the absence of a recommendation. I then consider changes in the magnitude of overdiagnosis and changes in the harms from overdiagnosis.
The fraction of women who receive mammograms in the absence of a recommendation is much larger in the United States today than it was in Canada in the 1980s. Previous guidelines, public outreach efforts, insurance coverage, risk aversion, and financial incentives all encourage mammography. Always takers comprise 19% of my main analysis sample from the CNBSS. A follow-up survey found that annual mammography was acceptable to 59% of the control arm (Baines et al., 1990). In the most recent data, 58% of US women in their 40s reported receiving a mammogram in the past two years, which is only three percentage points lower than it was in 2008 before the USPSTF updated its guidelines (National Center for Health Statistics, 2019). Some of the women who still receive mammograms could be comparable to CNBSS compliers, which would support the case for weaker guidelines on the basis of previous evidence of overdiagnosis. Comparability to always takers would further support the case for weaker guidelines on the basis of my findings. I find that always takers have higher socioeconomic status, and socioeconomic status is higher in the United States today than it was in Canada in the 1980s. Furthermore, recent evidence from the United States under current guidelines for women in their 40s corroborates my finding that women more likely to receive mammograms are healthier (Einav et al., 2020). This evidence does not address my finding that women more likely to get mammograms are also more likely to be overdiagnosed.
Overdiagnosis could be larger in the United States today than it was in the CNBSS due to an increase in breast cancer diagnoses and a decrease in the underlying rate of breast cancer. New screening technologies find ever-smaller tumors that might never cause symptoms. Magnetic resonance imaging provides a high-resolution image and tomosynthesis provides a three-dimensional image. Both technologies diagnose more tumors than x-ray mammography alone and yield more false positives (Leach et al., 2005; Bernardi et al., 2016). Furthermore, the underlying rate of breast cancer has decreased with the decrease in menopausal hormone therapy (Ravdin et al., 2007). Therefore, a larger fraction of new diagnoses may be overdiagnoses, especially among high socioeconomic status women screened with the latest technology.
The harms from overdiagnosis are likely lower in the United States today than they were in the CNBSS. Evidence emerged in the 1980s that radical mastectomy is no more effective at treating early-stage breast cancer than less aggressive surgeries (Veronesi et al., 1981), and its use has declined. New evidence shows that aggressive use of chemotherapy (Sparano et al., 2018) and radiotherapy (Whelan et al., 2019) is unnecessary, perhaps because many tumors are overdiagnosed. Genetic tests have improved prediction of which tumors will metastasize with the goal of reducing harmful therapy (Brufsky, 2014). Given these changes, the suggestive evidence I find that women more likely to receive mammograms are more likely to be harmed by them in terms of long-term all-cause mortality seems less relevant. These changes seem to suggest that more women should be screened because physical harms from breast cancer therapies are smaller. However, breast cancer therapies are not just getting less harmful. They are also getting more effective at treating advanced breast cancers. As the advantage of treating breast cancer early declines, so does the advantage of detecting breast cancer early. Over time, there may be no need for any women to receive mammograms before developing symptoms, especially not women who are more likely to be overdiagnosed by them.
Changes in attitudes toward mammography since the CNBSS began blunt the impact of USPSTF recommendations. Women who have undergone mammography are accustomed to “peace of mind” from being told they do not have breast cancer (Silverman et al., 2001). It is difficult to take away a service that has become customary, especially since there is a tendency to prefer doing something over doing nothing. Even though the Affordable Care Act ties coverage of other services to USPSTF guidelines, mammograms must be covered regardless.14 In part because so many factors encourage mammography, the cost of screening and subsequent evaluation now stands at an average of $353 annually among women in their 40s with private health insurance, amounting to $2.13 billion nationally (Kunst et al., 2020). Reducing mammograms provides a rare opportunity to improve health while decreasing costs, but very few forces currently push for fewer mammograms. If the USPSTF weakens their guidelines, other entities might eventually follow as they have historically. Drastic changes in mammogram policy can be difficult (Kolata, 2009), but a natural place to start is among younger women. Under a recommendation against mammography for women in their 40s, younger women who have never had a mammogram will not have to change their behavior.
Beyond informing changes to the current USPSTF mammography guidelines, my findings demonstrate an approach through which behavior within clinical trials can inform other guidelines. Whenever the USPSTF determines that “there is at least moderate certainty that the net benefit is small,” it “recommends selectively offering this service to individual patients based on professional judgment and patient preferences” (USPSTF, 2017) as it has done for mammograms. These recommendations presuppose selection and treatment effect heterogeneity such that the individuals most likely to benefit from a treatment will be the most likely to receive it. However, they are not based on evidence of selection and treatment effect heterogeneity. By demonstrating that it is possible to examine selection and treatment effect heterogeneity using the same clinical trial data currently used to develop guidelines, I enhance the ability of future guidelines to target treatments toward individuals most likely to benefit from them and away from individuals most likely to be harmed by them.
Acknowledgments
Saumya Chatrath, Neil Christy, Tory Do, Simon Essig Aberg, Bailey Flanigan, Ryan Fraser, Katie Laursen, Pauline Mourot, Srajal Nayak, Dominik Piehlmaier, Ljubica Ristovska, Sukanya Sravasti, and Matthew Tauzer provided excellent research assistance. I thank Anthony Miller, Teresa To, Cornelia Baines, and Claus Wall for sharing data from the Canadian National Breast Screening Study and for answering questions and providing helpful background information. They have reviewed this manuscript per our data use agreement. All errors are my own. I thank the editor, anonymous reviewers, Zach Brown, Zoey Chopra, Emily Horton, Pat Kline, Lee Lockwood, Magne Mogstad, Michael Ricks, Brock Rowberry, Atheendar Venkataramani, graduate public finance students at the University of Michigan, and seminar participants at the American Economic Association Annual Meeting, ASHEcon, the Canadian Health Economics Study Group, Columbia University, the London-Paris Public Economics Workshop, NBER Aging, NBER Health Care, the North American Summer Meetings of the Econometric Society, Indiana University, Princeton, and the University of Michigan for helpful comments. I also thank Heidi Nelson for useful advice. NSF CAREER Award 1350132 and NIA Grant P30-AG12810 provided support. I dedicate my research on breast cancer to Elisa Long.
Footnotes
Guidelines in Sweden are a notable exception, as they recommend mammography for women in the same age range (Ebell et al., 2018).
Randomization was conducted at the individual level and stratified by 5-year age at enrollment and study center (Miller et al., 1992a). The randomization process did not intentionally vary the probability of assignment to intervention across strata, so strata controls are not required.
In the Baines et al. (2016) calculation of overdiagnosis 25 years after the first CNBSS participants enrolled, the difference in breast cancer incidence between the intervention and control arms is 0.41% (=7.43% - 7.02%). In my replication, the difference is 0.44% (=7.51% - 7.07%). Both differences are statistically significant.
E[YT | always takers] = E[Y | D = 1;Z = 0].
E[YU | never takers] = E[Y | D = 0;Z = 1].
The test proposed by Bertanha and Imbens (2020) is similar because they develop their test for a regression discontinuity context, but it is effectively an equivalent test. Bertanha and Imbens (2020) propose this test as one component of a test for external validity, but they do not propose it as a test of selection heterogeneity. Similarly, Guo et al. (2014) propose this test as one component of a test for unmeasured confounding, but they do not discuss it as a test for selection heterogeneity. Black et al. (2020) propose this test as one of two tests for selection.
I express the untreated outcome test statistic as , where ω(p, pL, pH) = 1{pL ≤ p < pH}/(pH − pL). The first term represents the average untreated outcome of compliers, and the second term represents the average untreated outcome of never takers.
For inference, I conduct a nonparametric bootstrap with 1,000 replications and report a two-tailed p-value constructed from the largest confidence interval that excludes zero.
Weak monotonicity of the MTO function would be difficult to defend in the CNBSS. It would imply that the sum of selection and treatment effect heterogeneity is weakly monotonic from always takers to never takers to compliers. However, my two main findings show that 1) selection heterogeneity is increasing in the fraction treated p and 2) treatment effect heterogeneity is decreasing in the fraction treated p. Therefore, it is unclear if their sum should be decreasing or increasing in the fraction treated p. Baseline covariates only inform selection heterogeneity; they do not inform the sum of selection and treatment effect heterogeneity. It could be more palatable to impose weak monotonicity of the MTE function. As discussed in the introduction, the literature posits mechanisms though which women with high socioeconomic status are diagnosed with more breast cancer even if their cancers are smaller. Because I find that women more likely to receive mammograms have higher socioeconomic status, there is reason to believe that the treatment effect of mammography is larger for women more likely to receive mammograms. However, alone, weak monotonicity of the MTE function does not identify an average treatment effect for never takers. In conjunction with M.1, it would imply that the average treatment effect for never takers is smaller than the LATE.
The resulting bound is uninformative in the sense that it does not yield compelling evidence that never takers are either overdiagnosed or underdiagnosed. It implies that mammography during the active study period would have overdiagnosed at most 58 breast cancers per 10,000 women. It allows for a treatment effect of zero, which would imply that no breast cancers would have been overdiagnosed. It also allows for a negative treatment effect, which would not make much sense. It would imply that fewer long-term breast cancers would have been diagnosed among never takers if they had received mammograms during the active study period, which is unrealistic since mammograms detect breast cancer. I emphasize that a negative treatment effect on breast cancer incidence would not imply underdiagnosis. A negative treatment effect on all-cause mortality would imply underdiagnosis, but I do not find compelling evidence of underdiagnosis, as I discuss when I consider robustness.
Per footnote 12, weak monotonicity of the MTO function on all-cause mortality would be difficult to defend. Weak monotonicity of the MTE function, imposed in conjunction with M.1, would imply that the average treatment effect for never takers is at most the LATE.
Section 2713 of the Affordable Care Act (2010) states that “recommendations of the United States Preventive Services Task Force regarding breast cancer screening, mammography, and prevention issued in or around November 2009 are not considered to be current.”
Data Availability Statement
This paper uses confidential, deidentified data from the Canadian National Breast Screening Study (CNBSS) obtained through an individual data sharing agreement supported by the National Bureau of Economic Research and the University of Toronto, the host institution for the CNBSS data. Per the terms of this agreement, I am not permitted to share these data. Interested researchers may submit their own data request application to Dr. Anthony Miller (ab.miller@utoronto.ca), the CNBSS PI, at the University of Toronto. My analysis code is available in the Zenodo digital repository: https://doi.org/10.5281/zenodo.6210284.
References
- Abadie A (2002). Bootstrap tests for distributional treatment effects in instrumental variable models. Journal of the American Statistical Association 97(457), 284–292. [Google Scholar]
- Abadie A (2003). Semiparametric instrumental variable estimation of treatment response models. Journal of Econometrics 113(2), 231–263. [Google Scholar]
- Affordable Care Act (2010). The Patient Protection and Affordable Care Act, Sec. 2713, Coverage of Preventive Services. [Google Scholar]
- American Cancer Society (2019). Breast Cancer Facts & Figures 2019–2020. Atlanta: American Cancer Society, Inc. https://www.cancer.org/content/dam/cancer-org/research/cancer-facts-and-statistics/breast-cancer-facts-and-figures/breast-cancer-facts-and-figures-2019-2020.pdf. Online. Accessed July 21, 2021. [Google Scholar]
- Angrist J (1998). Estimating the labor market impact of voluntary military service using social security data on military applicants. Econometrica 66(2), 249–288. [Google Scholar]
- Angrist JD, Imbens GW, and Rubin DB (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association 91(434), 444–455. [Google Scholar]
- Arozullah AM, Calhoun EA, Wolf M, Finley DK, Fitzner KA, Heckinger EA, Gorby NS, Schumock GT, and Bennett CL (2004). The financial burden of cancer: estimates from a study of insured women with breast cancer. J Support Oncol 2(3), 271–278. [PubMed] [Google Scholar]
- Baines CJ (1984). Impediments to recruitment in the Canadian national breast screening study: response and resolution. Controlled Clinical Trials 5(2), 129–140. [DOI] [PubMed] [Google Scholar]
- Baines CJ, To T, and Miller AB (2016). Revised estimates of overdiagnosis from the Canadian national breast screening study. Preventive Medicine 90, 66–71. [DOI] [PubMed] [Google Scholar]
- Baines CJ, To T, and Wall C (1990). Women’s attitudes to screening after participation in the national breast screening study. a questionnaire survey. Cancer 65(7), 1663–1669. [DOI] [PubMed] [Google Scholar]
- Baker SG, Prorok PC, and Kramer BS (2014). Lead time and overdiagnosis. Journal of the National Cancer Institute 106. [DOI] [PubMed] [Google Scholar]
- Balke A and Pearl J (1997). Bounds on treatment effects from studies with imperfect compliance. Journal of the American Statistical Association 92(439), 1171–1176. [Google Scholar]
- Bernardi D, Macaskill P, Pellegrini M, Valentini M, Fantò C, Ostillio L, Tuttobene P, Luparia A, and Houssami N (2016). Breast cancer screening with tomosynthesis (3d mammography) with acquired or synthetic 2d mammography compared with 2d mammography alone (storm-2): a population-based prospective study. The Lancet Oncology 17(8), 1105–1113. [DOI] [PubMed] [Google Scholar]
- Bertanha M and Imbens GW (2020). External validity in fuzzy regression discontinuity designs. Journal of Business & Economic Statistics 38(3), 593–612. [Google Scholar]
- Bitler M and Carpenter C (2019, August). Effects of direct care provision to the uninsured: Evidence from federal breast and cervical cancer programs. Working Paper 26140, National Bureau of Economic Research. https://www.nber.org/papers/w26140. [Google Scholar]
- Bitler MP and Carpenter CS (2016). Health insurance mandates, mammography, and breast cancer diagnoses. American Economic Journal: Economic Policy 8(3), 39–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Björklund A and Moffitt R (1987). The estimation of wage gains and welfare gains in self-selection models. The Review of Economics and Statistics, 42–49. [Google Scholar]
- Bjurstam N, Björneld L, Warwick J, Sala E, Duffy SW, Nyström L, Walker N, Cahlin E, Eriksson O, Hafström L-O, et al. (2003). The Gothenburg breast screening trial. Cancer 97(10), 2387–2396. [DOI] [PubMed] [Google Scholar]
- Black DA, Joo J, LaLonde R, Smith JA, and Taylor EJ (2020, June). Simple tests for selection: Learning more from instrumental variables. Working Paper 2020–048, Human Capital and Economic Opportunity Global Working Group. http://humcap.uchicago.edu/RePEc/hka/wpaper/Black_Joo_LaLonde_etal_2020_simple-tests-selection-learning-iv.pdf. [Google Scholar]
- Bleyer A and Welch HG (2012). Effect of three decades of screening mammography on breast-cancer incidence. New England Journal of Medicine 367(21), 1998–2005. [DOI] [PubMed] [Google Scholar]
- Blinder V, Patil S, Eberle C, Griggs J, and Maly RC (2013). Early predictors of not returning to work in low-income breast cancer survivors: a 5-year longitudinal study. Breast Cancer Research and Treatment 140(2), 407–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinch CN, Mogstad M, and Wiswall M (2017). Beyond LATE with a discrete instrument. Journal of Political Economy 125(4), 985–1039. [Google Scholar]
- Brufsky AM (2014). Predictive and prognostic value of the 21-gene recurrence score in hormone receptor–positive, node-positive breast cancer. American Journal of Clinical Oncology 37(4), 404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchmueller TC and Goldzahl L (2018). The effect of organized breast cancer screening on mammography use: Evidence from France. Health Economics 27(12), 1963–1980. [DOI] [PubMed] [Google Scholar]
- Carneiro P, Heckman JJ, and Vytlacil EJ (2011). Estimating marginal returns to education. The American Economic Review 101(6), 2754–2781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro P and Lee S (2009). Estimating distributions of potential outcomes using local instrumental variables with an application to changes in college enrollment and wage inequality. Journal of Econometrics 149(2), 191–208. [Google Scholar]
- CDC (2020). Breast cancer screening guidelines for women. https://www.cdc.gov/cancer/breast/pdf/breast-cancer-screening-guidelines-508.pdf. Online. Accessed July 21, 2021.
- CNBSS (2015). Canadian National Breast Screening Study: Cumulative Data 1980–2005. University of Toronto. [Google Scholar]
- Cooper GS, Kou TD, Dor A, Koroukian SM, and Schluchter MD (2017). Cancer preventive services, socioeconomic status, and the affordable care act. Cancer 123(9), 1585–1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornelissen T, Dustmann C, Raute A, and Schönberg U (2018). Who benefits from universal child care? estimating marginal returns to early child care attendance. Journal of Political Economy 126(6), 2356–2409. [Google Scholar]
- Cutler DM and Lleras-Muney A (2010). Understanding differences in health behaviors by education. Journal of Health Economics 29(1), 1–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebell MH, Thai TN, and Royalty KJ (2018). Cancer screening recommendations: an international comparison of high income countries. Public Health Reviews 39(7). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einav L, Finkelstein A, Oostrom T, Ostriker A, and Williams H (2020). Screening and selection: The case of mammograms. American Economic Review 110(12), 3836–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esserman LJ (2017). The WISDOM Study: breaking the deadlock in the breast cancer screening debate. NPJ Breast Cancer 3(1), 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esserman LJ and Varma M (2019). Should we rename low risk cancers? BMJ 364, k4699. [DOI] [PubMed] [Google Scholar]
- Fedewa SA, Goodman M, Flanders WD, Han X, Smith RA, Ward EM, Doubeni CA, Sauer AG, and Jemal A (2015). Elimination of cost-sharing and receipt of screening for colorectal and breast cancer. Cancer 121(18), 3272–3280. [DOI] [PubMed] [Google Scholar]
- Finkelstein AF, Taubman S, Wright BJ, Bernstein M, Gruber J, Newhouse JP, Allen HL, Baicker K, and the Oregon Health Study Group (2012). The Oregon health insurance experiment: Evidence from the first year. The Quarterly Journal of Economics 127(3), 1057–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gärtner R, Jensen M-B, Nielsen J, Ewertz M, Kroman N, and Kehlet H (2009). Prevalence of and factors associated with persistent pain following breast cancer surgery. JAMA 302(18), 1985–1992. [DOI] [PubMed] [Google Scholar]
- Goldman DP and Smith JP (2002). Can patient self-management help explain the SES health gradient? Proceedings of the National Academy of Sciences 99(16), 10929–10934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gøtzsche PC and Jørgensen KJ (2013). Screening for breast cancer with mammography. Cochrane Database of Systematic Reviews (6). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Z, Cheng J, Lorch SA, and Small DS (2014). Using an instrumental variable to test for unmeasured confounding. Statistics in Medicine 33(20), 3528–3546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habbema J, Oortmarssen G. J. v., van Putten DJ, Lubbe JT, and Maas P. J. v. d. (1986). Age-specific reduction in breast cancer mortality by screening: an analysis of the results of the health insurance plan of greater New York study. Journal of the National Cancer Institute 77(2), 317–320. [PubMed] [Google Scholar]
- Habermann EB, Virnig BA, Riley GF, and Baxter NN (2007). The impact of a change in Medicare reimbursement policy and HEDIS measures on stage at diagnosis among Medicare HMO and fee-for-service female breast cancer patients. Medical care 45(8), 761–766. [DOI] [PubMed] [Google Scholar]
- Heckman J (1979). Sample selection bias as a specification error. Econometrica 47(1), 153–162. [Google Scholar]
- Heckman JJ, Ichimura H, Smith J, and Todd P (1998). Characterizing selection bias using experimental data. Econometrica 66(5), 1017–1098. [Google Scholar]
- Heckman JJ and Vytlacil E (2005). Structural equations, treatment effects, and econometric policy evaluation. Econometrica 73(3), 669–738. [Google Scholar]
- Heckman JJ and Vytlacil EJ (1999). Local instrumental variables and latent variable models for identifying and bounding treatment effects. Proceedings of the National Academy of Sciences 96(8), 4730–4734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ and Vytlacil EJ (2001). Local instrumental variables. In Hsiao C, Morimune K, and Powell JL (Eds.), Nonlinear Statistical Modeling: Proceedings of the Thirteenth International Symposium in Economic Theory and Econometrics: Essays in Honor of Takeshi Amemiya, pp. 1–46. Cambridge University Press. [Google Scholar]
- Imbens GW and Angrist JD (1994). Identification and estimation of local average treatment effects. Econometrica 62(2), 467–475. [Google Scholar]
- Imbens GW and Rubin DB (1997). Estimating outcome distributions for compliers in instrumental variables models. The Review of Economic Studies 64(4), 555–574. [Google Scholar]
- Jacobson M and Kadiyala S (2017). When guidelines conflict: A case study of mammography screening initiation in the 1990s. Women’s Health Issues 27(6), 692–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadiyala S and Strumpf E (2016). How effective is population-based cancer screening? regression discontinuity estimates from the US guideline screening initiation ages. In Forum for Health Economics and Policy, Volume 19, pp. 87–139. De Gruyter. [DOI] [PubMed] [Google Scholar]
- Kadiyala S and Strumpf EC (2011). Are United States and Canadian cancer screening rates consistent with guideline information regarding the age of screening initiation? International Journal for Quality in Health Care 23(6), 611–620. [DOI] [PubMed] [Google Scholar]
- Kaplan RM and Porzsolt F (2008, 11). The Natural History of Breast Cancer. Archives of Internal Medicine 168(21), 2302–2303. [DOI] [PubMed] [Google Scholar]
- Katz LF, Kling JR, Liebman JB, et al. (2001). Moving to opportunity in Boston: Early results of a randomized mobility experiment. The Quarterly Journal of Economics 116(2), 607–654. [Google Scholar]
- Kelaher M and Stellman JM (2000). The impact of medicare funding on the use of mammography among older women: implications for improving access to screening. Preventive Medicine 31(6), 658–664. [DOI] [PubMed] [Google Scholar]
- Kim HB and Lee S (2017). When public health intervention is not successful: Cost sharing, crowd-out, and selection in Korea’s national cancer screening program. Journal of Health Economics 53, 100–116. [DOI] [PubMed] [Google Scholar]
- Klarenbach S, Sims-Jones N, Lewin G, Singh H, Thériault G, Tonelli M, Doull M, Courage S, Garcia AJ, and Thombs BD (2018). Recommendations on screening for breast cancer in women aged 40–74 years who are not at increased risk for breast cancer. CMAJ: Canadian Medical Association Journal 190(49), E1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kline P and Walters CR (2019). On Heckits, LATE, and numerical equivalence. Econometrica 87(2), 677–696. [Google Scholar]
- Kolata G (2009, November). Get a mammogram. No don’t. Repeat. New York Times. [Google Scholar]
- Kolstad JT and Kowalski AE (2012). The impact of health care reform on hospital and preventive care: evidence from Massachusetts. Journal of Public Economics 96(11–12), 909–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowalski A (2016, June). Doing more when you’re running LATE: Applying marginal treatment effect methods to examine treatment effect heterogeneity in experiments. Working Paper 22363, National Bureau of Economic Research. http://www.nber.org/papers/w22363. [Google Scholar]
- Kowalski A (2020a, October). How to examine external validity within an experiment. Working Paper 24834, National Bureau of Economic Research. http://www.nber.org/papers/w24834. [Google Scholar]
- Kowalski A (2020b, November). Reconciling seemingly contradictory results from the Oregon health insurance experiment and the Massachusetts health reform. Working Paper 24647, National Bureau of Economic Research. http://www.nber.org/papers/w24647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowalski A (2021a, July). Reconciling Seemingly Contradictory Results from the Oregon Health Insurance Experiment and the Massachusetts Health Reform. The Review of Economics and Statistics, 1–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowalski A, Tran Y, and Ristovska L (2018). MTEBINARY: Stata module to compute Marginal Treatment Effects (MTE) With a Binary Instrument. Statistical Software Components, Boston College Department of Economics. [Google Scholar]
- Kowalski AE (2021b, May). Mammograms and mortality: How has the evidence evolved? Journal of Economic Perspectives 35(2), 119–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumachev A, Trudeau ME, and Chan KK (2016). Associations among socioeconomic status, patterns of care, and outcomes in breast cancer patients in a universal health care system: Ontario’s experience. Cancer 122(6), 893–898. [DOI] [PubMed] [Google Scholar]
- Kunst N, Long JB, Xu X, Busch SH, Kyanko KA, Richman IB, and Gross CP (2020, 05). Use and Costs of Breast Cancer Screening for Women in Their 40s in a US Population With Private Insurance. JAMA Internal Medicine 180(5), 799–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leach MO, Boggis C, Dixon A, Easton D, Eeles R, Evans D, Gilbert FJ, Griebsch I, Hoff R, Kessar P, et al. (2005). Screening with magnetic resonance imaging and mammography of a UK population at high familial risk of breast cancer: a prospective multicentre cohort study (MARIBS). Lancet 365(9473), 1769–1778. [DOI] [PubMed] [Google Scholar]
- Lu Y and Slusky DJ (2016). The impact of women’s health clinic closures on preventive care. American Economic Journal: Applied Economics 8(3), 100–124. [Google Scholar]
- Manski CF (1990). Nonparametric bounds on treatment effects. The American Economic Review 80(2), 319–323. [Google Scholar]
- Mehta SJ, Polsky D, Zhu J, Lewis JD, Kolstad JT, Loewenstein G, and Volpp KG (2015). ACA-mandated elimination of cost sharing for preventive screening has had limited early impact. The American Journal of Managed Care 21(7), 511. [PMC free article] [PubMed] [Google Scholar]
- Miller AB, Baines CJ, To T, and Wall C (1992a). Canadian national breast screening study: 1. breast cancer detection and death rates among women aged 40 to 49 years. CMAJ: Canadian Medical Association Journal 147(10), 1459–1476. [PMC free article] [PubMed] [Google Scholar]
- Miller AB, Baines CJ, To T, and Wall C (1992b). Canadian national breast screening study: 2. breast cancer detection and death rates among women aged 50 to 59 years. CMAJ: Canadian Medical Association Journal 147(10), 1477–1488. [PMC free article] [PubMed] [Google Scholar]
- Miller AB, To T, Baines CJ, and Wall C (1997). The Canadian national breast screening study: update on breast cancer mortality. JNCI Monographs 1997(22), 37–41. [DOI] [PubMed] [Google Scholar]
- Miller AB, To T, Baines CJ, and Wall C (2000). Canadian national breast screening study-2: 13-year results of a randomized trial in women aged 50–59 years. Journal of the National Cancer Institute 92(18), 1490–1499. [DOI] [PubMed] [Google Scholar]
- Miller AB, To T, Baines CJ, and Wall C (2002). The Canadian national breast screening study-1: breast cancer mortality after 11 to 16 years of follow-up: a randomized screening trial of mammography in women age 40 to 49 years. Annals of Internal Medicine 137(5_Part_1), 305–312. [DOI] [PubMed] [Google Scholar]
- Miller AB, Wall C, Baines CJ, Sun P, To T, and Narod SA (2014). Twenty five year follow-up for breast cancer incidence and mortality of the Canadian national breast screening study: randomised screening trial. BMJ 348, g366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogstad M, Santos A, and Torgovitsky A (2018). Using instrumental variables for inference about policy relevant treatment effects. Econometrica 86(5), 1589–1619. [Google Scholar]
- Moss SM, Wale C, Smith R, Evans A, Cuckle H, and Duffy SW (2015). Effect of mammographic screening from age 40 years on breast cancer mortality in the uk age trial at 17 years’ follow-up: a randomised controlled trial. The Lancet Oncology 16(9), 1123–1132. [DOI] [PubMed] [Google Scholar]
- Myerson RM, Lakdawalla D, Colantonio LD, Safford M, and Meltzer D (2018, February). Effects of expanding health screening on treatment - what should we expect? what can we learn? Working Paper 24347, National Bureau of Economic Research. http://www.nber.org/papers/w24347. [Google Scholar]
- Myerson RM, Tucker-Seeley RD, Goldman DP, and Lakdawalla DN (2020). Does medicare coverage improve cancer detection and mortality outcomes? Journal of Policy Analysis and Management 39(3), 577–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Center for Health Statistics (2012). Health, United States, 2011: With special feature on socioeconomic status and health. [PubMed]
- National Center for Health Statistics (2019). Use of mammography among women aged 40 and over, by selected characteristics : United states, selected years 1987 – 2015. https://www.cdc.gov/nchs/data/hus/2018/033.pdf. Online. Accessed July 21, 2021.
- Nelson HD, Fu R, Cantor A, Pappas M, Daeges M, and Humphrey L (2016). Effectiveness of breast cancer screening: Systematic review and meta-analysis to update the 2009 us preventive services task force recommendation effectiveness of breast cancer screening. Annals of Internal Medicine 164(4), 244–255. [DOI] [PubMed] [Google Scholar]
- Nyström L, Andersson I, Bjurstam N, Frisell J, Nordenskjöld B, and Rutqvist LE (2002). Long-term effects of mammography screening: updated overview of the Swedish randomised trials. The Lancet 359(9310), 909–919. [DOI] [PubMed] [Google Scholar]
- Olsen RJ (1980). A least squares correction for selectivity bias. Econometrica: Journal of the Econometric Society, 1815–1820. [Google Scholar]
- Ong M-S and Mandl KD (2015). National expenditure for false-positive mammograms and breast cancer overdiagnoses estimated at $4 billion a year. Health Affairs 34(4), 576–583. [DOI] [PubMed] [Google Scholar]
- Oster E (2020, June). Health recommendations and selection in health behaviors. American Economic Review: Insights 2(2), 143–60. [Google Scholar]
- Patnick J, Baker K, Barnes I, Beral V, Pan H, Peto R, Reeves G, Richards M, and Shaw K (2018). Nationwide cluster-randomised trial of extending the NHS breast screening age range in England: AgeX trial protocol. http://www.agex.uk/. Online. Accessed November 10, 2020.
- Ravdin PM, Cronin KA, Howlader N, Berg CD, Chlebowski RT, Feuer EJ, Edwards BK, and Berry DA (2007). The decrease in breast-cancer incidence in 2003 in the United States. New England Journal of Medicine 356(16), 1670–1674. [DOI] [PubMed] [Google Scholar]
- Robins JM (1989). The analysis of randomized and non-randomized aids treatment trials using a new approach to causal inference in longitudinal studies. Health Service Research Methodology: A Focus on AIDS, 113–159. [Google Scholar]
- Roy AD (1951). Some thoughts on the distribution of earnings. Oxford Economic Papers 3(2), 135–146. [Google Scholar]
- Schünemann HJ, Lerda D, Quinn C, Follmann M, Alonso-Coello P, Rossi PG, Lebeau A, Nyström L, Broeders M, Ioannidou-Mouzaka L, et al. (2019). Breast cancer screening and diagnosis: A synopsis of the European breast guidelines. Annals of Internal Medicine. [DOI] [PubMed] [Google Scholar]
- Silverman E, Woloshin S, Schwartz L, Byram S, Welch HG, and Fischhoff B (2001). Women’s views on breast cancer risk and screening mammography: a qualitative interview study. Medical Decision Making 21(3), 231–240. [DOI] [PubMed] [Google Scholar]
- Siu AL (2016). Screening for breast cancer: US preventive services task force recommendation statement. Annals of Internal Medicine 164(4), 279–296. [DOI] [PubMed] [Google Scholar]
- Sparano JA, Gray RJ, Makower DF, Pritchard KI, Albain KS, Hayes DF, Geyer CE Jr, Dees EC, Goetz MP, Olson JA Jr, et al. (2018). Adjuvant chemotherapy guided by a 21-gene expression assay in breast cancer. New England Journal of Medicine. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabar L, Fagerberg G, Chen H-H, Duffy SW, Smart CR, Gad A, and Smith RA (1995). Efficacy of breast cancer screening by age. new results Swedish two-county trial. Cancer 75(10), 2507–2517. [DOI] [PubMed] [Google Scholar]
- Taylor C, Correa C, Duane FK, Aznar MC, Anderson SJ, Bergh J, Dodwell D, Ewertz M, Gray R, Jagsi R, et al. (2017). Estimating the risks of breast cancer radiotherapy: evidence from modern radiation doses to the lungs and heart and from previous randomized trials. Journal of Clinical Oncology 35(15), 1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- USPSTF (2002). Screening for breast cancer: Recommendations and rationale. Annals of Internal Medicine 137(5), 344–346. [DOI] [PubMed] [Google Scholar]
- USPSTF (2009). Screening for breast cancer: U.S. preventive services task force recommendation statement. Annals of Internal Medicine 151(10), 716–726. [DOI] [PubMed] [Google Scholar]
- USPSTF (2017). Grade definitions. U.S. preventive services task force. November 2017. https://www.uspreventiveservicestaskforce.org/Page/Name/grade-definitions. Online. Accessed June 8, 2018. [Google Scholar]
- Veronesi U, Saccozzi R, Del Vecchio M, Banfi A, Clemente C, De Lena M, Gallus G, Greco M, Luini A, Marubini E, et al. (1981). Comparing radical mastectomy with quadrantectomy, axillary dissection, and radiotherapy in patients with small cancers of the breast. New England Journal of Medicine 305(1), 6–11. [DOI] [PubMed] [Google Scholar]
- Vytlacil E (2002). Independence, monotonicity, and latent index models: An equivalence result. Econometrica 70(1), 331–341. [Google Scholar]
- Welch HG and Fisher ES (2017). Income and cancer overdiagnosis — when too much care is harmful. New England Journal of Medicine 376(23), 2208–2209. [DOI] [PubMed] [Google Scholar]
- Whelan TJ, Julian JA, Berrang TS, Kim D-H, Germain I, Nichol AM, Akra M, Lavertu S, Germain F, Fyles A, et al. (2019). External beam accelerated partial breast irradiation versus whole breast irradiation after breast conserving surgery in women with ductal carcinoma in situ and node-negative breast cancer (RAPID): a randomised controlled trial. The Lancet 394(10215), 2165–2172. [DOI] [PubMed] [Google Scholar]
- World Health Organization (2015). Global status report on road safety 2015. http://www.who.int/violence_injury_prevention/road_safety_status/2015/en/. Online.
- Zackrisson S, Andersson I, Janzon L, Manjer J, and Garne JP (2006). Rate of over-diagnosis of breast cancer 15 years after end of Malmö mammographic screening trial: follow-up study.BMJ 332(7543), 689–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahl P, Jørgensen KJ, and Gøtzsche P (2013). Overestimated lead times in cancer screening has led to substantial underestimation of overdiagnosis. British Journal of Cancer 109(7), 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanella G and Banerjee R (2016). Experiencing breast cancer at the workplace. Journal of Public Economics 134, 53–66. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This paper uses confidential, deidentified data from the Canadian National Breast Screening Study (CNBSS) obtained through an individual data sharing agreement supported by the National Bureau of Economic Research and the University of Toronto, the host institution for the CNBSS data. Per the terms of this agreement, I am not permitted to share these data. Interested researchers may submit their own data request application to Dr. Anthony Miller (ab.miller@utoronto.ca), the CNBSS PI, at the University of Toronto. My analysis code is available in the Zenodo digital repository: https://doi.org/10.5281/zenodo.6210284.


