The automatic evaluation of steno-occlusive changes in time-of-flight magnetic resonance angiography of moyamoya patients using a 3D coordinate attention residual network

Abstract

Background

Moyamoya disease (MMD) is a rare cerebrovascular occlusive disease with progressive stenosis of the terminal portion of internal cerebral artery (ICA) and its main branches, which can cause complications, such as high risks of disability and increased mortality. Accurate and timely diagnosis may be difficult for physicians who are unfamiliar to MMD. Therefore, this study aims to achieve a preoperative deep-learning-based evaluation of MMD by detecting steno-occlusive changes in the middle cerebral artery or distal ICA areas.

Methods

A fine-tuned deep learning model was developed using a three-dimensional (3D) coordinate attention residual network (3D CA-ResNet). This study enrolled 50 preoperative patients with MMD and 50 controls, and the corresponding time of flight magnetic resonance angiography (TOF-MRA) imaging data were acquired. The 3D CA-ResNet was trained based on sub-volumes and tested using patch-based and subject-based methods. The performance of the 3D CA-ResNet, as evaluated by the area under the curve (AUC) of receiving-operator characteristic, was compared with that of three other conventional 3D networks.

Results

With the resulting network, the patch-based test achieved an AUC value of 0.94 for the 3D CA-ResNet in 480 patches from 10 test patients and 10 test controls, which is significantly higher than the results of the others. The 3D CA-ResNet correctly classified the MMD patients and normal healthy controls, and the vascular lesion distribution in subjects with the disease was investigated by generating a stenosis probability map and 3D vascular structure segmentation.

Conclusions

The results demonstrated the reliability of the proposed 3D CA-ResNet in detecting stenotic areas on TOF-MRA imaging, and it outperformed three other models in identifying vascular steno-occlusive changes in patients with MMD.

Introduction

Moyamoya disease (MMD) is a chronic cerebrovascular disorder characterized by progressive stenosis and occlusion of large intracranial arteries, such as the distal internal cerebral artery (ICA), proximal middle cerebral artery (MCA), and anterior cerebral artery (ACA). Patients with MMD experience an elevated risk of complications such as ischemic and hemorrhagic strokes, which result in disability and high mortality (1,2). Surgical vascular reconstruction can alleviate the symptoms and prevent complications from MMD, with preoperative brain vascular imaging evaluation being crucial in evaluating clinical threshold for the surgery. Time of flight magnetic resonance angiography (TOF-MRA) is a noninvasive and nonradiative imaging technique that has been used for MMD diagnosis by assessing the degree of cerebral artery stenosis and has become a reliable alternative to conventional methods such as digital subtraction angiography (DSA). However, screening large numbers of images can be time-consuming and can increase inter- and intra-reader variability, which can be alleviated by implementing an automatic MRA data analysis method to aid doctors in clinical diagnosis.

In medical image analysis, deep learning (DL) techniques, including multimodality image registration (3), tumor image segmentation (4), disease diagnosis (5), and magnetic resonance (MR) image synthesis (6), have been used because of their advantageous features, such as the capacity to learn informative representation and extract features in a self-taught manner (7). A few studies have attempted to apply DL techniques for the diagnosis of MMD. The 2D convolutional neural network (CNN) was developed to distinguish MMD from plain skull radiograph images (8) and brain T2-weighted imaging (T2WI) slices (9). These studies demonstrate the feasibility of using DL for the detection of MMD. The limitation of learning MMD pathological information from 2D imaging and capturing 3D vessel characteristics using 2D CNNs is that it cannot consider the contextual connectivity and learn the information among imaging slices. A recent study detected MMD in 2D DSA imaging using a DL-based system combined with 2D CNN, bidirectional convolutional gated recurrent unit (BiConvGRU), and 3D CNN, which extracts spatial information using 2D CNN and preprocesses temporal features with BiConvGRU and 3D CNN, and then fuse extracted features to classify ischemic MMD (10). However, invasiveness and radiation exposure of DSA may lead to some potential risks. To our knowledge, no studies are using DL techniques to diagnose MMD from TOF-MRA.

A few attempts have been made to use DL to detect stenosis or occlusion of cerebral arteries on 3D TOF-MRA, while most of them have focused on intracranial aneurysm detection (11-16) or intracranial artery segmentation (17-19). Compared with tumor or intracranial aneurysms, the scope of vascular stenosis is less clear, and more complex to label and learn using a network. Therefore, detecting stenosis or occlusion lesions using DL from TOF-MRA remains challenging. For example, a DL-based method was proposed to train an ICA stenosis detection model by first extracting the artery centerline through an artery tracing technique and then generating multiplanar reformatted images based on the centerline (20). However, the two-step processing of artery tracing and multiplanar reformation may introduce cumulative errors before input into the detection network, although it takes time for human corrections. The 3D squeeze-and-excitation residual network (SE-ResNet) detected moderate ICA stenosis, however, it did not consider the severe stenotic or occlusive lesions in the MCA segments (21).

This study proposes a deep voxel-based network 3D coordinate attention residual network (3D CA-ResNet) for MMD stenosis detection, evaluates its capacity to detect 3D vessel characteristics, and further observes the lesion characteristics of MMD by locating and showing the stenosis or occlusion lesion on 3D vascular structure segmentations and raw images. The proposed network was trained with sub-volumes extracted from TOF-MRA images of patients with MMD and healthy controls, and its performance was verified by comparing it with the well-known 3D visual geometry group (VGG) (22), 3D ResNet (23), and 3D SE-ResNet networks through standard quantitative methods. We present the following article in accordance with the TRIPOD reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-22-799/rc).

Methods

Subjects

The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Ethics Committee of the Seventh Medical Center of the PLA General Hospital, and the participants all signed the informed consent form. This study included 50 previously untreated patients consecutively diagnosed with MMD at the Seventh Medical Center of the PLA General Hospital between September 2001 and November 2017. Data from these patients, which included 31 women and 19 men, were retrospectively analyzed. Table 1 presents the baseline characteristics of the 50 patients. The median age of the patients was 39.5 years (interquartile range, 31.25–49.5 years), and all of them had been diagnosed with MMD via magnetic resonance imaging (MRI), MRA, and DSA, according to the diagnostic guidelines in Japan (24). A control group of 50 age- and sex-matched healthy individuals were also selected to assess the diagnostic accuracy. The control group included 23 women and 27 men with a median age of 39.0 years (interquartile range, 34.0–44.0 years).

Table 1. The baseline characteristics of the subjects.

Characteristic	Total	Learning group (training + validating)	Testing group
Moyamoya disease group	50	40 [80]	10 [20]
Age (years), median (IQR)	39.5 (31.25–49.5)	41.0 (31.75–50.0)	33.0 (28.25–42.25)
Sex (female), n [%]	31 [62]	24 [60]	7 [70]
MRA grade, n
1	1	1	0
2	26	23	5
3	18	12	3
4	5	4	2
Control group, n [%]	50	40 [80]	10 [20]
Age (years), median (IQR)	39.0 (34.0–44.0)	38.5 (33.75–43.25)	41.0 (34.5–45.75)
Sex (female), n [%]	23 [46]	17 [43]	6 [60]

IQR, interquartile range; MRA, magnetic resonance angiography.

The TOF-MRA was performed for each patient, and the resulting data were divided into two groups: learning data for DL, and testing data to test the diagnostic accuracy, the latter of which corresponded to 20% of the total data, including ten patients with MMD (20%) and ten healthy controls (20%). Twenty percent of the learning data were selected as validation data to optimize the DL network. To make the distribution of the training data and testing data consistent with the real distribution of the sample, the age, gender, and stenosis degree of the training data and testing data were matched when dividing the data, as shown in Table 1.

MRI examination

TOF-MRA head images were obtained using two 3.0 T MR scanners (HDx, Signa MR 750 System, GE Healthcare, Milwaukee, WI, USA). The TOF-MRA imaging parameters were as follows: slice thickness of 1.4/1.2 mm, number of slices 164/172, pixel spacing of 0.4,297/0.4,688 mm, matrix size of 512×512, repetition time 21 ms, echo time 2.4/2.3 ms and multi-channel receivers. To diagnose arterial stenosis on TOF-MRA images, two expert radiologists used the Warfarin-Aspirin Symptomatic Intracranial Disease method (25) to evaluate the degree of stenosis and labeled the stenosis of arteries using ITK-SNAP toolbox (26). Two radiologists identified severe stenosis or occlusion as red and mild stenosis as yellow. A senior radiologist further checked the evaluation and labeling procedures.

Data preprocessing

As the training data were obtained from multiple scanners with different imaging conditions, image alignment was first performed to obtain images with comparable settings. First, the nearest neighbor interpolation method was used to resample the images to a 0.5-mm isotropic space, and a z-score normalization was applied to the resampled images to standardize the signal intensities to the distribution with a mean of 0 and variance of 1. We extracted regions of interest (ROIs) from the resampled images to minimize the effects of different imaging conditions and remove the skull or eye regions with high signals. ROIs with a size of 120×160×192 were extracted based on the reference points on the M1 part of the bilateral MCAs, which include most of the stenosis cases in the data in this region.

Using an entire image or a large input size in a 3D model architecture poses several challenges, such as large graphics processing unit (GPU) memory consumption and long training times. To fit the input images into the computer memory and increase training data, patch extraction was performed by dividing the ROI of each subject into small patches of size 60×64×96 pixels with a stride of 30×32×96 that overlapped among patches, which were classified as stenotic or normal patches depending on whether they contained stenotic arteries. Determining the patch size also depends on the size of the stenotic area, which is the minimum size required to cover the stenotic area. Therefore, we obtained training patches from the training group, similar to the validation and testing groups. Data cleaning was applied to the training and validation patches to focus the model on artery stenosis, in which, the patches with the stenosis accounting for less than 0.05% of the total region were removed. As the number of stenotic patches was below the number of normal patches in Table 2, data augmentation of stenotic patches was performed to balance the amount of data in both classes, with the ratio of the normal to stenotic patches as 2:1. Augmentation varied with the shifting of width and height, flipping about the x-, y- and z-axes, and scaling. The voxel was shifted within ±8 pixels, flipped about a random axis, and scaled. This method was also used for random augmentation during the training. Moreover, to avoid detection bias and improve the convergence of the models, all the training patches were shuffled and standardized before being input into the network.

Table 2. The quantity statistics of the patches.

Grouping categories	Number of normal patches	Number of stenosis patches
Training group (64%)	1,305	189
Validating group (16%)	311	67
Testing group (20%)	417	63

Detection method

Proposed deep network

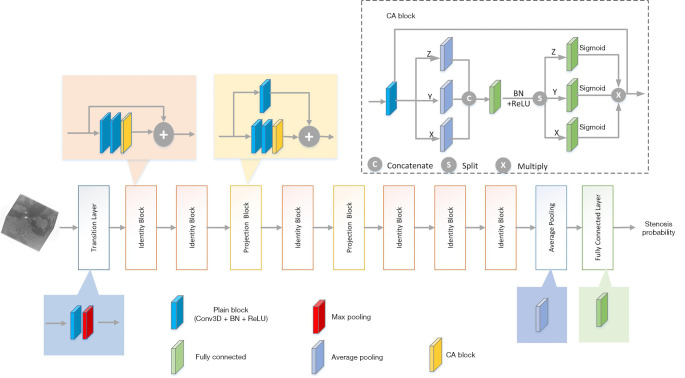
To address the problem of training accuracy degradation with increasing network depth, this study used a modified 3D ResNet (23) as the base architecture to enable the deepening of the network, and firstly integrated a 3D coordinate attention (CA) structure adapted from the original CA block (27) into the non-identity branch of the residual blocks in the 3D ResNet to improve its performance. The 3D CA block and 3D CA-ResNet architectures are illustrated in Figure 1. The 3D CA-ResNet includes transition, residual (identity and projection), and CA type blocks, and the explanation of those blocks are as follow.

Figure 1.

Architecture of the 3D ResNets. The 3D CA-ResNet adds a coordinate attention block to the residual blocks of the 3D ResNet. The CA block first performs average pooling along the x, y and z coordinates and then encodes spatial information through concatenation and convolution, obtaining attention weights from three 1×1×1 convolution operations. BN, batch normalization; CA, coordinate attention; Conv3D, three dimensional convolution layer; ReLU, Rectified Linear Unit.

Transition block

The transition block is composed of a plain block and a max pooling layer. The plain block represents a convolutional operation, followed by batch normalization and a Rectified Linear Unit (ReLU) activation function, with the convolutional operation using 3×3×3 filters, except in the first transition block, in which a 7×7×7 filter kernel is employed. As a computational unit, the plain block uses a filter kernel set $K=\left[k_1,k_2,k_3,\dots ,k_C\right]$ to transform an input $X\in R^{X^{\text{'}}\times Y^{\text{'}}\times Z^{\text{'}}\times C^{\text{'}}}$ into a feature map $U\in R^{X\times Y\times Z\times C}$, which is defined as:

$$u_c=BN\left(\delta \left(k_c*X\right)\right)=BN\left(\delta \left({\displaystyle \sum _{\text{s}=1}^{{\text{C}}^{\text{'}}}{k}_c^s\ast x^s}\right)\right)$$ [1]

where $k_C=\left[k_C^1,k_C^2,k_C^3,\dots ,k_C^{C^{\text{'}}}\right]$, $X=[x^1,x^2,x^3,\dots ,x^{C^{\text{'}}}]$, $U=\left[u_1,u_2,u_3,\dots ,u_C\right]$, $u_C\in R^{X\times Y\times Z}$, ∗ denotes convolution, δ denotes the ReLU operator, BN denotes batch normalization, k_c is the parameter of the c-th filter, $k_c^s$ denotes a single channel of the k_c filter, and x^s refers to s-th channel of input X. To simplify the notation, the bias terms are omitted.

Residual blocks

Depending on the difference between the dimensions of the input data and output data, there are two types of shortcut connection implementations: identity and projection blocks, as shown in Figure 2.

Figure 2.

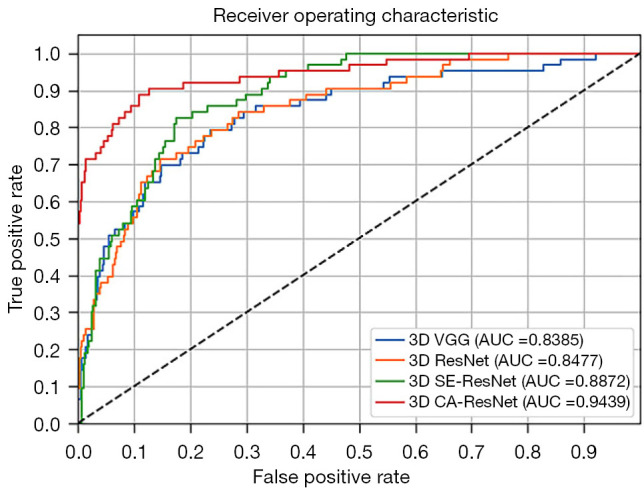
ROC curves and the AUCs of the four models evaluated. The 3D CA-ResNet further outperformed the conventional networks, 3D VGG, 3D ResNet, and 3D SE-ResNet, with significant differences among different ROCs (P<0.05). AUC, area under the curve; CA, coordinate attention; 3D, three-dimensional; ResNet, residual network; ROC, receiver operating characteristic; SE-ResNet, squeeze-and-excitation residual network; VGG, visual geometry group.

Identity block, where the dimensions of the input data and output data are equal, can be defined as:

$$U=F\left(X,\left\{K_i\right\}\right)+X$$ [2]

where X represents the input data, U denotes the output data, and F is function that represents the residual mapping. In this study, the residual mapping was applied to the two plain blocks. Therefore, F(X,{K_i}) = BN(δ(K₂BN(δ(K₁X)))) where K₁ and K₂ denote the filter kernel sets to be learned.

On the other hand, projection blocks perform a linear projection to match the dimensions of the input data and output data, with the shortcut connection was implemented by a plain block with a stride of 2. Formally, projection blocks can be defined as:

$$U=\text{F}\left(X,\left\{K_i\right\}\right)+K_{s}X$$ [3]

Here, K_s represents a linear projection that is only used to match the dimensions.

CA block

Two operations, coordinate information encoding and CA generation, are performed to encode channel-wise dependencies and long-range spatial information.

In coordinate information encoding, one dimensional (1D) average pooling with three pooling kernels (1, X, Y), (Z, 1, Y) and (Z, X, 1), on the input $U=\left[u_1,u_2,u_3,\dots ,u_C\right]$ are utilized to obtain long-range interactions along the z-, x- and y-directions. Thus, the c-th channel of the collection of the channel descriptors $S=\left[s_1,s_2,s_3,\dots ,s_C\right]$ at the z-th position in dimension Z can be formulated as:

$$S_C^Z=\frac{1}{X\times Y}{\displaystyle \sum _{i=1}^X{u}_C\left(i,j,z\right)}$$ [4]

Analog definitions of S apply for dimension X and dimension Y.

In CA generation, a transformation is performed to fully utilize the spatial information resulting from coordinate information encoding. The transformation should meet three criteria: be simple, take advantage of captured spatial information, and can be able to capture channel-wise relationships. The transformation consists of a concatenation layer, a split layer, and four 1×1 convolutional layers, which can be written as:

$$f=\delta \left(F_s\left[s^x,s^y,s^z\right]\right)$$ [5]

where [,] represents the concatenation operation, F_s indicates a 1×1 convolutional transformation, and δ denotes the ReLU function. $F\in R^{\frac{C}{r}\times \left(X+Y+Z\right)}$ is the intermediate feature map with the reduction ratio r. Splitting f into three separate tensors and applying another three 1×1 convolutional transformations to them, with the same channel number of the input U, yields the channel weights $\tilde{S}=\left[{\tilde{s}}_1,{\tilde{s}}_2,{\tilde{s}}_3,\dots ,{\tilde{s}}_C\right]$ along dimension X:

$${\tilde{S}}^x=\sigma \left(F_x\left[f^x\right]\right)$$ [6]

where σ is the sigmoid function, $f^x\in R^{\frac{C}{r}\times X}$ is the tensor along the dimension X and F_x indicates a 1×1 convolutional transformation along dimension X. Definitions similar to ${\tilde{S}}^x$ apply for ${\tilde{S}}^{{}_y}$ and ${\tilde{S}}^z$. Finally, the c-th channel of the final output $\tilde{U}=\left[{\tilde{u}}_1,{\tilde{u}}_2,{\tilde{u}}_3,\dots ,{\tilde{u}}_C\right]$ is represented by:

$${\tilde{u}}_c={\tilde{s}}_c^x\cdot {\tilde{s}}_c^y\cdot {\tilde{s}}_c^z\cdot u_c$$ [7]

CA-ResNet

The CA-ResNet is obtained by inserting the CA block into the non-identity branch of the residual block. Thus, the representations of the identity and projection blocks can be written as:

$$R=\tilde{U}\left\{F\left(X,\left\{K_i\right\}\right)\right\}+X$$ [8]

And

$$R=\tilde{U}\left\{F\left(X,\left\{K_i\right\}\right)\right\}+K_{s}X$$ [9]

where R is the output of the non-identity branch, and the definitions of the remaining symbols are the same as in the preceding sections.

Experiment

The images in the dataset used for training were originally in NIFTI format (.nii) and were converted into Numpy arrays using the SimpleITK library (28). The four models evaluated in this study, namely 3D VGG, 3D ResNet, 3D SE-ResNet, and 3D CA-ResNet, were implemented in Python (version 3.6) using the Keras framework (version 2.3.1) and trained and tested using patches, as explained in Section 2.3 on an NVIDIA GeForce RTX 2070 GPU with CUDA10.1 and CUDNN 7.6.5.

The 3D VGG in our study was designed by expanding and adapting a VGG16 from 2D to 3D using a convolutional layer with stride two instead of a pooling layer, and the network from the previous study (21) was used as 3D SE-ResNet. The 3D ResNet and 3D CA-ResNet were designed to match the feature map dimensions and network depth, as shown in Figure 1. Table 3 lists the components of the four models. The initial learning rate was 0.001, and it was reduced by a factor of 10 for every 20 epochs. All models were optimized using the Adam optimizer with β1 =0.9 and β2 =0.999 and trained based on patched 3D data with a binary cross-entropy loss function. Considering GPU memory limitations, the batch size was set to 32, with each batch containing samples from each class. To avoid overfitting, an “early stopping callback” was used as a training strategy to monitor the model performance during the validation and training stages. The early stopping patience epoch was set to 17, and the upper bound epoch was assigned a maximum of 200 early stopping epochs. Thus, if the validation loss has started to increase during the training process, the “early stopping callback” mechanism was first triggered. If the validation loss continued to grow during the next 17 epochs, the training process was stopped, automatically determining the number of training epochs. The weights of the four networks were randomly initialized with a uniform distribution and subsequently fine-tuned using stochastic gradient descent during the backpropagation phase.

Table 3. The architectures of networks.

Network	Structure
3D VGG	14 convolutional layers, 1 max-pooling layer, 1 average pooling layer, and 1 fully connected layer
3D ResNet	1 transition layer (consists of a 7×7 convolutional layer and a 2×2 max pooling), 8 residual blocks, 1 average pooling layer, and 1 fully connected layer
3D SE-ResNet	17 convolutional layers, 1 max-pooling layer, 1 average pooling layer, and 15 fully connected layers
3D CA-ResNet	The structure is similar to that of 3D ResNet except that the residual blocks contain 8 coordinate attention blocks

3D, three-dimensional; VGG, visual geometry group; ResNet, residual network; SE-ResNet, squeeze-and-excitation residual network; CA-ResNet, coordinate attention residual network.

Performance evaluation

All models were evaluated at the patch level and analyzed at the subject level. As the sensitivity and specificity were considered equally important in the study, the Youden Index (29) was used to select the threshold that defined whether a patch/subject had stenosis. Additionally, performance metrics, including sensitivity, specificity, accuracy, positive predictive value (PPV), negative predictive value (NPV), and the area under the receiver operator characteristic curve (AUC), were calculated using statistical t-test analysis. The proposed model was also processed using 5-fold cross-validation to increase the reliability and effectiveness of the proposed model and reduce the bias error.

Visual assessment

During the patch-based tests, the models predicted the probability of stenosis in an individual patch from the test data and compared the predicted result with the ground truth as diagnosed by radiologists. In the subject-based analyses, the stenosis probabilities were predicted for all the patches from one subject, and the top three probability values were averaged to determine whether the subject was an MMD patient. Then, if the subject was classified as having the disease, a stenosis probability map was generated to locate the stenotic lesion to patch and compared with the TOF-MRA corresponding to the subject to judge the accuracy of prediction and stenosis distribution. The maximum intensity projection was used to display the probability maps in three directions and the ground truth with labeled stenosis region, as shown in Figure S1.

Post-processing was performed using a voxel voting algorithm to finely locate the stenosis regions at the voxel level, where the stenosis regions were shown based on 3D vascular structure segmentation obtained using a Hessian multiscale filter (30). The stenosis probability of each voxel in the entire image was obtained from the predicted stenosis probability of the patch, and the voxel probability value of the overlapping patch area was the superposition value of the adjacent patches with overlapping regions. The stenosis probability of a region higher than the threshold value was taken as the positive region and automatically contoured using an ellipse.

To interpret the features learned by the models from the patches, a gradient-weighted class activation map (Grad-CAM) visualization tool was utilized to generate a heat map that represented the contribution of each pixel on the image to the class stenosis/normal. To assess the generalization of the proposed 3D CA-ResNet model for stenosis detection, subject-level analyses were performed on patients with varying degrees of stenosis by visualizing and locating the identified stenosis region.

Results

Stenosis detection rates of CNNs

The performance of the four models in discriminating between stenosis and normal patches/subjects were evaluated using testing data. Under the condition that the sensitivity and specificity were equally important, the probability thresholds were chosen to distinguish stenotic from normal patches with 3D VGG, 3D ResNet, 3D SE-ResNet, and 3D CA-ResNet, were 0.0938, 0.1789, 0.0436 and 0.0338, respectively.

Table 4 shows the detection rates, and the bar graph with extract numbers of true positive (TP), true negative (TN), false positive (FP), and false negative (FN) is shown in Figure S2. The overall sensitivity, specificity, and accuracy of the 3D CA-ResNet were 87.30%, 89.21%, and 88.96%, respectively, which were significantly higher than those of 3D SE-ResNet, 3D ResNet, and 3D VGG. The sensitivity of 3D SE-ResNet was higher than those of 3D VGG and 3D ResNet, but its specificity and accuracy were below those of 3D ResNet. The NPVs of all four models were between 40% and 60% higher than their PPVs, suggesting that all four models were more effective in excluding stenosis detection.

Table 4. Evaluation results of four models.

Indicators	Sensitivity/TPR	Specificity	Accuracy	Precision/PPV	NPV
Formula	TP/(TP + FN)	TN/(TN + FP)	(TP + TN)/(TP + FN + TN + FP)	TP/(TP + FP)	TN/(TN + FN)
3D VGG	77.78%	76.50%	76.67%	33.33%	95.80%
3D ResNet	69.84%	85.37%	83.33%	41.90%	94.93%
3D SE-ResNet	80.95%	82.49%	82.29%	41.13%	96.63%
3D CA-ResNet	87.30%	89.21%	88.96%	55.00%	97.89%

3D, three-dimensional; VGG, visual geometry group; ResNet, residual network; SE-ResNet, squeeze-and-excitation residual network; CA-ResNet, coordinate attention residual network; TPR, true positive rate; TP, true positive; FP, false positive; TN, true negative; FN, false negative; PPV, positive predictive value; NPV, negative predictive value.

To further evaluate the generalization performance of 3D CA-ResNet on a given dataset, the 5-fold cross-validation was utilized to 3D CA-ResNet model as shown in Table 5. The results show the robustness of 3D CA-ResNet in detecting the stenosis with an overall average accuracy of 84.48% and sensitivity of 83.17%, whereas the normal patches were accurately detected with an average specificity of 84.68%. It is clearly seen that this increases the reliability of the proposed model and proves the generalization performance of 3D CA-ResNet on different datasets.

Table 5. Evaluation results of 3D CA-ResNet throughout 5-fold cross validation.

Fold test	Sensitivity/TPR	Specificity	Accuracy	Precision/PPV	NPV
1st fold	80.76%	88.30%	87.08%	57.27%	95.94%
2nd fold	80.00%	80.25%	80.21%	42.86%	95.59%
3rd fold	95.52%	75.06%	77.92%	38.32%	99.04%
4th fold	81.11%	88.97%	87.50%	62.93%	95.33%
5th fold	78.46%	90.84%	89.71%	57.30%	96.42%
Total	83.17%	84.68%	84.48%	51.74%	96.46%

3D CA-ResNet, three-dimensional coordinate attention residual network; TPR, true positive rate; PPV, positive predictive value; NPV, negative predictive value.

Figure 2 shows the four models’ receiver operating characteristic (ROC) curves and the areas under the curve (AUCs). Consistent with the above results, 3D CA-ResNet outperformed the other three conventional models (3D SE-ResNet, 3D ResNet, and 3D VGG), with AUC 0.06, 0.10, and 0.11 higher than those of the other models. The 3D SE-ResNet outperformed the conventional models (3D VGG and 3D ResNet). Although the accuracy of 3D SE-ResNet was lower than that of 3D ResNet, its high AUC value and ROC curve indicated that it generalizes better than 3D ResNet. The comparison of the AUCs was statistically significant (P<0.05).

All four models successfully classified the twenty subjects in the testing data, including ten patients with MMD and ten healthy controls, although the averaged probability values differed.

Visualization analysis

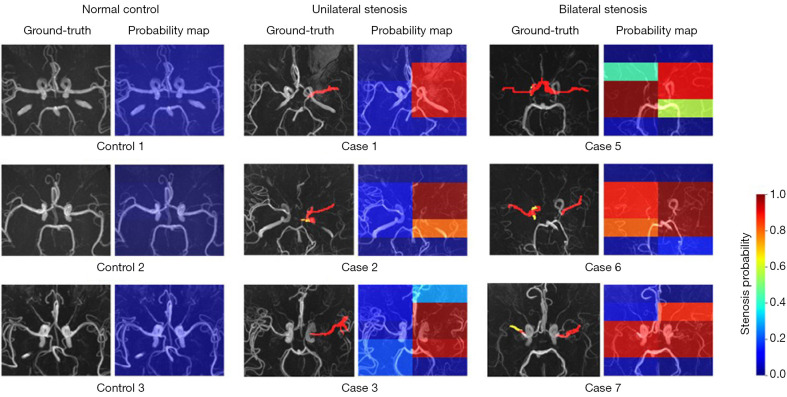
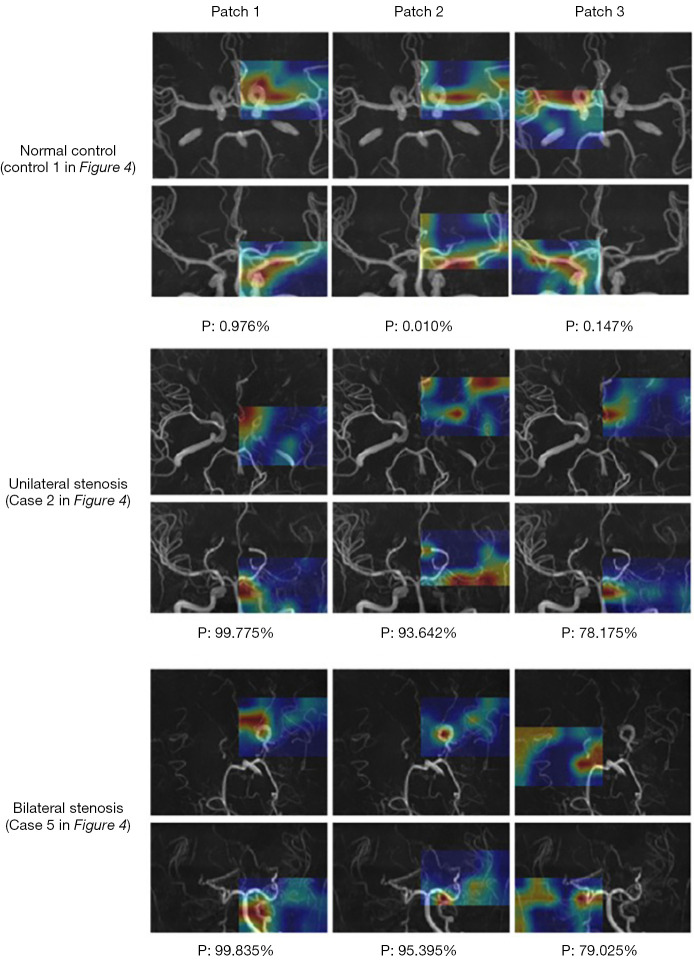
To investigate the performance of the models in identifying the location of lesions in MMD patients, stenosis probability maps corresponding to subjects with bilateral and unilateral stenosis and healthy controls were visually analyzed. The higher “temperature” color, such as red and yellow, corresponded to higher stenosis probabilities. Figure 3 shows the 3D CA-ResNet accurately predicted the stenosis region with high probability values mainly distributed around the MCA segment or distal ICA labeled as the ground truth. Moreover, the probability values in the normal regions of the healthy controls were close to zero, as indicated by the blue color in Figure 3.

Figure 3.

Probability maps of three healthy controls, three patients with unilateral stenosis, and three patients with bilateral stenosis. The red and yellow masks in the ground truth respectively represent severe and mild stenosis/occlusion. The color in the probability maps corresponds to the stenosis probability value as shown by the color bar on the right.

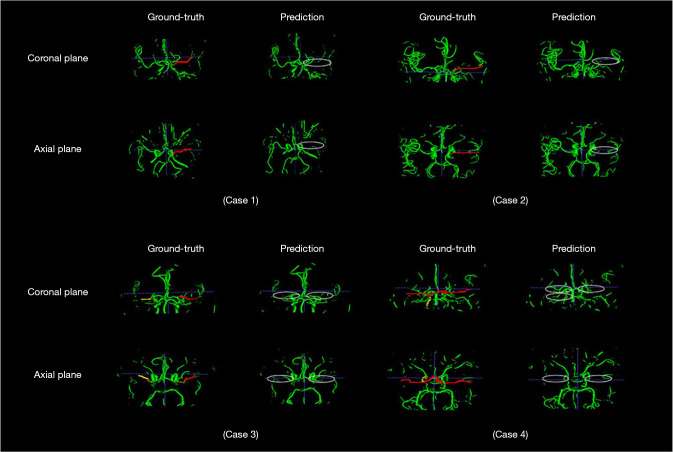
To finely locate and display the stenosis region, the overlapping regions of positive blocks were visually shown as stenotic or occlusion lesions on 3D vascular structure segmentation, as shown in Figure 4. It is obviously investigated that the stenosis region was mainly distributed around the MCA segment or distal ICA depicted in stenosis probability maps.

Figure 4.

Vessel segmentations of two patients with unilateral stenosis and two with bilateral stenosis. The red and yellow in ground truth, represent severe and mild stenosis/occlusion labeled or supplemented by experts, and the green is the normal vessels. The ellipses in prediction contain the stenosis or occlusion lesions predicted and voted by the proposed model and post-processing method.

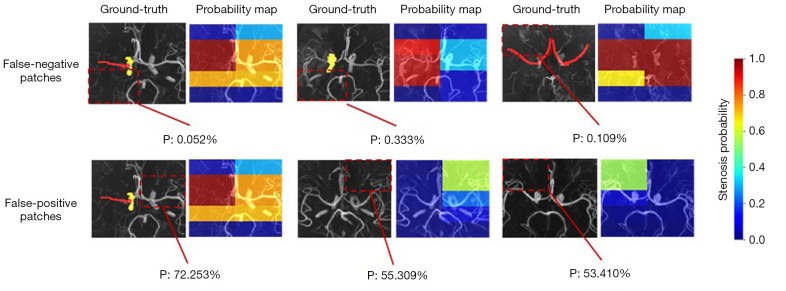
However, even when the test data were correctly classified at the subject level, there were eight false-positives and 45 false-negatives at the patch level, as shown in Figure 5. The positive region was too small to be found in the false-negative patches, as shown for the three cases in Figure 5, and the false-positive results may have been caused by small vessels or artifacts in the patches.

Figure 5.

False-negative and false-positive cases. The patches predicting a stenosis/occlusion are marked with a red dotted line, and the corresponding probabilities are shown at the bottom. The red and yellow masks in the ground-truth, respectively represent severe and mild stenosis/occlusion. Top: there were three cases with false-negative patches where the positive area was too small to be found. Bottom: there were three normal arteries with false-positive patches where small vessels or artifacts might have caused the false-positive results. P, probability.

Heat maps showed the features learned by the model, as shown in Figure 6. The high “temperature” on the heat maps represented the features that contributed the most to discriminating stenotic from normal vessels. It was shown that the feature regions specific to stenosis, were discontinuous and concentrated on residual vessel areas for patients with MMD, while the areas highlighted were continuously distributed throughout the vessels and more dispersed in healthy controls.

Figure 6.

Heat maps for healthy controls and moyamoya patients with bilateral stenosis and unilateral stenosis obtained with 3D CA-ResNet. The three patches with the top three stenosis probabilities were chosen in bilateral and unilateral stenosis cases, and chose patches around the middle cerebral artery for healthy controls. These patches were highlighted in the transverse and coronal planes, where the red and yellow colors represent the feature captured by the model in each patch as the main factors determining the patch prediction results. The corresponding stenosis probabilities were shown at the bottom. 3D CA-ResNet. Three-dimensional coordinate attention residual network.

Discussion

This study developed a practical DL-based method on TOF-MRA imaging for the stenotic lesion diagnosis of patients with MMD. Four networks, namely 3D CA-ResNet, 3D SE-ResNet, 3D ResNet, and 3D VGG, were used to distinguish stenotic patches from normal patches. The results indicated that all the four networks could be trained to detect stenosis with high sensitivity and specificity automatically and that the 3D CA-ResNet outperformed the other three networks. Thus, the proposed method allows the automatic generation of visualized post-processed TOF-MRA images, which may facilitate the clinical diagnosis of MMD.

The proposed framework demonstrated combining a CA mechanism with a ResNet to learn complex vascular structures. Specifically, the 3D CA-ResNet outperformed the other tested models (3D VGG, 3D ResNet, and 3D SE-ResNet), especially in sensitivity, specificity, and accuracy. The performance improvement of 3D CA-ResNet does not result in a significant computational cost because the implementation of CA only consists of several average pooling layers and 1×1 convolutional layers. The results of 3D CA-ResNet being more robust than 3D ResNet and 3D SE-ResNet also proved the importance of long-term dependence on precise positional information in capturing object structures during visual tasks. The 3D ResNet is superior to the 3D VGG, confirming the benefits of residual block deepening networks in improving performance. The inconsistency in accuracy and AUC between the 3D SE-ResNet and 3D ResNet maybe because of the non-uniformity of the test data. However, because the accuracy depends on selecting classification thresholds, we believe that 3D SE-ResNet is relatively superior to 3D ResNet in detecting vascular changes in MMD.

Processing and analyzing whole 3D medical volumes using 3D CNNs lead to a low execution speed and high memory requirements. To address this problem, the inputs in 3D model architectures are cropped images or sub-volumes, and then the patched images are used as input in this study. The selection of patch size depends on the types and characteristics of the lesions. To determine the patch size in this study, the 3D CA-ResNet was trained and tested with patches of different sizes, and the performance of the model trained on patches of size 60×64×96 was better than those trained on size 30×32×48 and size 45×48×72, as shown in Table S1. This may be attributed to the fact that the larger patches covered a sufficiently large stenotic or occlusive segment, which helps capture the lesion features, whereas the small patches could not learn the characteristics of the stenotic lesion well as they were unable to cover the stenotic segments fully.

Our study had some limitations. First, although the proposed 3D CA-ResNet method performed better than the other DL methods evaluated, there were still false-negative and false-positive cases at the patch level, as shown in Figure 5. Distinguishing between stenotic and normal arteries remains challenging because of their irregularity, especially for the small vessels. Moreover, additional data are required to improve the effectiveness of artificial intelligence. Second, although conventional X-ray DSA is the gold standard for MMD diagnosis, doctors accept TOF-MRA and can be routinely used due to its convenience and low cost. Even though the MRA score has been well established for evaluating patients with MMD in clinical practice, it might be affected by artifacts produced by signal saturation and off-resonance near the skull. More preprocessing methods are required to reduce the influence of artifacts and improve the performance and generality of automated detection methods. Third, although our method can assess stenosis based on patches and automatically diagnose MMD, it requires artificial points to select the ROI regions. Therefore, the workflow for diagnosing MMD is not been entirely automated. Finally, the detection of the patients is just the first step for diagnosis. And the patch is not small enough to locate the stenotic part precisely on the ICA, MCA, ACA, or posterior cerebral artery (PCA) segments. Even though this study could successfully find the positive patch and show the lesion at the voxel level, the vessel and stenosis region should be more accurately located at the voxel level from a clinical perspective, because it is important for MMD staging by Houkin score system (31) which needs to locate the steno-occlusion at the MCA, ACA, or PCA segments precisely. To show the degree of stenosis and make it easier for doctors to diagnose stenosis, future studies should focus on the positive patches detected using this method, develop techniques to evaluate the stenosis grade of the lesion, show the stenosis or occlusion at the voxel level, and finely locate them on whole-brain images and 3D vascular structure segmentations. Moreover, the ability of the network to detect small stenoses in the ACA and/or PCA warrants further study.

Conclusions

We proposed a DL method for evaluating TOF-MRA datasets to identify steno-occlusive changes and detect MMD using a 3D CA-ResNet. Also confirmed that this network outperformed conventional 3D networks including 3D VGG, 3D ResNet, and the recently proposed network 3D SE-ResNet. The automatic DL-based generation of post-processed TOF-MRA images allows the proposed method to aid radiologists in the clinical diagnosis of MMD.

Supplementary

The article’s supplementary files as

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Ethics Committee of the Seventh Medical Center of the PLA General Hospital, and the participants all signed the informed consent form.