脑肌电信号同步耦合分析方法研究进展

Abstract

运动神经系统通过神经振荡活动传递运动控制信息，从而引起相应肌肉的同步性振荡活动并反映运动响应信息，然后反馈至大脑皮层，使其能够感知肢体的状态。这种同步振荡活动可反映皮层肌肉功能耦合的连接信息。其中，耦合的强弱由多种因素决定，包括肌肉收缩的力量、注意力、运动意图等，因此分析不同因素影响下的脑肌电信号同步耦合的强弱对运动功能评价及控制方法等研究有重要意义。针对脑肌电信号同步耦合的分析方法，本文主要介绍与比较了线性方法中的相干性分析和格兰杰因果分析，以及非线性方法中的互信息以及传递熵，总结了各方法在脑肌电信号同步耦合的应用研究，以便于相关领域的科研工作者更系统地了解目前脑肌电信号同步耦合分析方法的研究进展。

引言

肌电（electromyography，EMG）信号是神经肌肉活动产生的信号。通过表面电极测量所得的肌电信号称为表面肌电（surface electromyography，sEMG）信号^[1]，表面肌电信号记录的是人体骨骼肌表面在神经、肌肉活动时所产生的生物电信号。肌电信号的变化与诸多因素相关，并可实时准确地反应神经肌肉的功能状态，可作为神经肌肉功能评价的有效方法^[2-3]。脑电（electroencephalography，EEG）信号是通过放置在头皮表面电极记录的人体神经元电活动的宏观综合表现，可反映大脑不同状态的信息^[4]。

脑电信号和肌电信号能直接反映运动神经系统的功能状态，所以皮层肌肉间的耦合连接可通过脑肌电信号的同步耦合分析来测量。脑肌电信号同步耦合分析即获取大脑运动意识驱动与肌肉运动响应之间的功能联系特征。脑肌电同步耦合分析研究可应用于康复治疗、康复评估和假肢控制等多个研究领域^[5]。目前在脑卒中、帕金森、脑外伤和肌萎缩侧索硬化症等患者康复过程中^[6-7]，运动功能评价的主要依据是康复医师的主观经验或依靠监测患者的肌力状态，难以客观、准确地评定康复效果。而脑肌电交互作用能够反映患者运动功能缺失的神经机制，采用脑肌电信号同步耦合分析评估会更加客观和准确，以便于进一步指导开展更好的康复治疗。

脑肌电信号同步耦合中含有线性耦合特征和非线性耦合特征，分析方法可分为线性方法和非线性方法两大类。近年来，研究人员广泛使用线性方法中的相干性分析和格兰杰因果（Granger causality，GC）分析以及非线性方法中的互信息（mutual information，MI）和传递熵（transfer entropy，TE）方法分析脑肌电耦合的效果，本文将对这些脑肌电同步耦合分析方法以及其应用情况进行探讨和综述，以期给相关领域的科研工作者选择不同的脑肌电信号同步耦合分析方法提供理论指导和方法借鉴。

1. 线性方法

1.1. 相干性分析

相干性分析是从频域上量化两个时间序列的线性相关程度，其测量方法定义为两信号的互谱密度函数对各自自谱密度函数的归一化，设 x 和 y 为两组时间序列，则计算公式如式（1）所示：

1

其中，C_xy 为 x、y 的相干系数，S_xx、S_yy 分别代表 x、y 的自谱密度函数，S_xy 代表 x、y 的互谱密度函数。相干性分析针对脑肌电信号计算其在频域上的线性相关性，可以定量地评价不同神经区域间的相关性程度。采用相干函数表征大脑皮层与肌肉之间的同步耦合也称为皮层肌肉相干性（cortico-muscular coherence，CMC）分析。

相干性分析因具有计算简便的优势，目前已有很多国内外学者采用此方法初步探究脑肌电信号同步耦合的影响因素。陈迎亚^[8]的研究表明，随着恒定握力的增加，beta 频段（13～30 Hz）的皮层肌肉相干性随之降低。Ushijima 等^[9]研究表明，胫骨前肌在弱自主收缩期间，皮层肌肉相干性的峰值随肌肉运动时间的增加而显著增大。因此，皮层肌肉相干性对评估患者的运动功能具有重要意义。Zheng 等^[10]研究表明，在上肢肌肉维持恒定力输出时，注意力可影响皮层肌肉相干性，且注意力越集中，相干性越强，此研究对神经损伤患者的康复训练过程中是否加入注意力因素具有指导性意义。

脑肌电信号同步耦合存在时间延迟，如果不加以考虑，可能会降低相干水平。由此，Xu 等^[11]提出了一种具有时滞的皮层肌肉相干性（cortico-muscular coherence with time lag，CMCTL）的分析方法，其分析效果与生理学事实更接近。高云园等^[12]分别选取大脑运动区和躯体感觉区的脑电信号和肌电信号做多频段双向耦合相干性分析。这一研究虽弥补了相干性不能确定耦合方向的不足，但其仅分析了健康人的脑肌电信号的数据，是否适用于运动功能障碍患者有待进一步分析研究。

此外，虽然传统相干性分析具有计算简便、易于实现、结果可靠、效率高等优势，但仍然存在一些缺陷，包括：难以区分脑肌电信号之间的耦合是源自皮层振荡施加于肌肉，还是肌肉活动的本体感受，也不能体现皮层肌肉间的因果关系等，因此尚需进一步探寻更有效的分析方法。

1.2. 格兰杰因果分析

大脑皮层与肌肉之间的相关振荡不仅可以从发出命令的大脑皮层传导至肌肉（下行），而且同时也由肌肉反馈回大脑皮层（上行）。这样的振荡回路使大脑皮层能够感知肢体的功能状态，并整合从输入到响应的信息流动。1988 年，Grange^[13]提出了格兰杰因果关系分析方法在神经网络领域得到了广泛的应用，其定义为：在 y 的回归中加入 x 变量值可以提高预测的性能，则称 x 引起 y。其中 x 和 y 的因果传递关系可表示为如式（2）、（3）所示：

2

3

其中，S_xx 和 S_yy 分别为 x 和 y 的自谱密度函数，Γ 和 Σ 为 H_yx 和 H_xy 的方差，符号*代表转置共轭。

由于格兰杰因果分析可描述信息间的双向因果性传递规律，诸多研究采用此方法分析不同运动模式对上行和下行方向脑肌电信号耦合的影响。Witham 等^[14]将格兰杰因果分析与相干性分析比较，研究表明脑肌电信号耦合复杂的本质源于脑肌电信号的双向传递。牛晓辰^[15]采用此方法探究正走和倒走运动中脑肌电信号的功能性关联，研究发现与正走相比，倒走时股直肌与胫骨前肌在 alpha 频段（8～13 Hz）和 beta 频段（13～30 Hz）处下行和上行方向脑肌电耦合的强度均有所下降，为倒走中的运动康复评价提供了理论依据。

虽然格兰杰因果分析方法有着可以定向研究的优势，但也存在一些不容忽视的问题，如：难以确定模型阶数、频率分辨率受限等。此外，基于小波变换的方法具有高频率、高分辨率的特点，由此，谢平等^[16]提出了小波—格兰杰因果方法（wavelet transform-Granger causality，WT—GC），并采用此方法对不同手部力量下脑肌电同步耦合特征进行分析，其优势在于能够更全面地揭示脑肌电同步耦合的频谱特征和方向性信息，还可以体现动态力学信号在时域和频域上的特征。

2. 非线性方法

2.1. 互信息

1950 年，Shannon^[17]建立了信息理论，用于研究在收到一个讯号之前，如何科学地度量该讯号的不确定性。互信息是信息论里一种有用的信息度量^[4]，可以看成一个随机变量中包含的关于另一个随机变量的信息量，即两个随机变量之间的相关程度。互信息值越大，说明两个信号越相关，反之则相关性越小。两个随机变量 x 与 y 互信息的计算公式如式（4）所示：

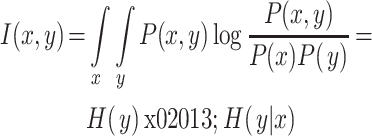4

其中，H（y）表示 y 的熵，可衡量 y 的不确定度，H（y|x）表示已知 x 的情况下，y 的不确定度。

互信息方法广泛应用于非线性系统，因此许多研究人员考虑采用此方法研究脑肌电信号的非线性耦合特征。Kim 等^[18]研究表明，受试者在具有运动意图的主动运动时，脑肌电信号的互信息量显著高于没有运动意图的被动运动，为开发用户意图康复系统的研究提供了理论基础。传统的互信息方法无法体现序列之间信息流动方向且不能排除共同信号源的影响。Jin 等^[19]改进了互信息方法，提出了将时延互信息（time delay mutual information，TDMI）应用于脑肌电信号同步耦合的研究，研究发现线性和非线性信息流均来自于对侧感觉运动皮层并传导至肌肉，此研究首次在脑肌电信号的相互作用中分离线性和非线性信息流。

2.2. 传递熵

Schreiber^[20]于 2000 年定义了传递熵，传递熵的概念源于互信息，它与传递信息相关。传递熵是基于转移概率定义的非对称性测量方法，包含着方向性和动态信息，可用于研究复杂系统的非线性时间序列间的信息传递关系^[21]。传递熵的特点是非线性、不依赖于既定模型、可定量分析等。它考虑的是变量间的信息量传递，而不需要假定变量间具有特定形式的关系。对于两列信号 X = x_t 和 Y = y_t，传递熵的计算方法如式（5）所示：

5

其中 = （x_t， ，x_t-m+1）， = （y_t， ，y_t-n+1），m 和 n 为 x_t 和 y_t 的延迟嵌入向量维数。

近几年，大部分国内外专家学者采用传递熵与其他方法结合的方式分析脑肌电信号非线性同步耦合以及因果性传递的特征。So 等^[22]采用小波—传递熵评估抓取过程中皮层传导至肌肉的信息流，研究结果显示，在运动的过渡阶段（从放松到抓取）传递的信息减少，在抓球期间传递的信息增加。张园园等^[23]采用小波—传递熵的方法研究表明，恒定握力下，beta 频段传递熵值在下行方向上明显强于上行方向，随着握力水平的增加，gamma 频段（30～100 Hz）传递熵值在上行方向上出现峰值，并高于下行方向且同步振荡幅值增加，此研究对患者上肢康复评价具有一定指导作用。与采用相干性分析研究不同恒定握力下耦合强度相比，该算法能有效刻画不同频段、不同传递方向上的脑肌电信号间非线性耦合特征。

谢平等^[24]为研究不同时间尺度上脑肌电耦合特征，提出基于多尺度传递熵分析方法，该研究揭示了脑肌电耦合强度在不同时间尺度上有所差异。在此基础上，谢平等^[25]又提出了将变分模态分解与传递熵方法结合，构建变分模态分解—传递熵（the variational mode decomposition-transfer entropy，VMD-TE）模型。将经验模态分解应用到多尺度划分之中，优势在于将便于提取脑电信号和肌电信号的时频特征以及分析不同方向和频段间的耦合特征。

3. 脑肌电信号同步耦合分析方法比较

本文所介绍的线性方法可有效地定量描述脑肌电信号间的线性耦合关系。其中，相干性分析是目前研究脑肌电信号同步耦合最为广泛使用的方法。它具有易实现、效率高和可靠性高的优势，但其不能体现皮层肌肉间的因果关系，而格兰杰因果分析可体现因果性传递，所以在研究上行和下行方向的脑肌电信号同步耦合方面得到了广泛的使用。非线性方法可充分表达大脑皮层与肌肉之间的高度复杂的非线性特征，这对于分析脑肌电信号同步耦合的综合特征具有重要意义。与互信息相比，传递熵最大的优势在于它可以体现脑肌电信号同步耦合信息传递关系。但是传递熵方法的研究起步较晚，目前还有很多相关内容尚在探索中。脑肌电信号同步耦合分析方法的比较如表 1 所示。

表 1. Comparison of analysis methods for electroencephalography-electromyography synchronous coupling.

脑肌电信号同步耦合分析方法比较

分析方法	方法类别	传递性	优势	劣势
相干性分析	线性	单向	易实现、可靠、效率高	只能体现单向传递性
格兰杰因果分析	线性	双向	可描述双向因果传递、计算相对简单	模型阶数难确定、频率分辨率受限
互信息	非线性	单向	可分离线性和非线性信息流	不能排除共同信号源的影响
传递熵	非线性	双向	非线性、不依赖于既定模型、定量分析、可描述双向因果传递	起步较晚、未广泛使用

4. 总结与展望

本文对常用的脑肌电信号同步耦合的线性和非线性分析方法的研究发展现状进行了概述和总结，包括相干性分析、格兰杰因果分析、互信息以及传递熵。相干性分析从频域角度量化脑肌电信号间线性相关程度，因易于实现而广泛使用，但其只能体现单向传递性。格兰杰因果分析可衡量脑肌电信号耦合双向因果性传递的线性相关程度。互信息是通过信息量反应脑肌电信号间的相关程度，但无法体现信息流动方向。传递熵是基于互信息的非线性方法，它不依赖于既定模型和因果性传递的特征，使其在分析脑肌电信号同步耦合中具有一定的优势。线性方法的理论较为成熟且易于实现，因此，国内外关于脑肌电信号同步耦合的研究大多基于线性算法。近年来，随着非线性分析方法的不断完善，其应用于脑肌电信号同步耦合的方面也逐渐受到重视。随着分析方法的不断升级，对脑肌电信号同步耦合的研究将会更加深入和成熟，更有利于应用到假肢控制、康复治疗和评价等领域。

Funding Statement

国家自然科学基金面上项目（61473193）；上海市科委“科技创新行动计划”资助项目（16441905202）；上海理工大学国家自然科学基金培育项目（ZR18PY10）