Abstract
现有的心律失常分类方法通常采用人为选取心电图（ECG）信号特征的方式，其特征选取具有主观性，且特征提取复杂，导致分类准确性容易受到影响等。基于以上问题，本文提出了一种基于判别式深度置信网络（DDBNs）的心律失常自动分类新方法。该方法所构建的生成受限玻尔兹曼机（GRBM）自动提取心拍信号形态特征，然后引入具有特征学习和分类能力的判别式受限玻尔兹曼机（DRBM），依据提取的形态特征和 RR 间期特征进行心律失常分类。为了进一步提高 DDBNs 的分类性能，本文将 DDBNs 转换为使用柔性最大值（Softmax）回归层进行监督分类的深度神经网络（DNN），通过反向传播对网络进行微调。最后，采用麻省理工学院与贝斯以色列医院心律失常数据库（MIT-BIH AR）进行实验验证，对于数据来源一致的训练集和测试集，该方法整体分类精度可达 99.84% ± 0.04%；对于数据来源非一致的训练集和测试集，通过主动学习（AL）方法扩充少量训练集，该方法整体分类精度可达 99.31% ± 0.23%。实验结果表明了该方法在心律失常自动特征提取和分类上的有效性，为深度学习自动提取 ECG 信号特征及分类提供了一种新的解决方法。
Keywords: 心律失常, 判别式深度置信网络, 受限玻尔兹曼机, 特征提取, 柔性最大值回归层
Abstract
Existing arrhythmia classification methods usually use manual selection of electrocardiogram (ECG) signal features, so that the feature selection is subjective, and the feature extraction is complex, leaving the classification accuracy usually affected. Based on this situation, a new method of arrhythmia automatic classification based on discriminative deep belief networks (DDBNs) is proposed. The morphological features of heart beat signals are automatically extracted from the constructed generative restricted Boltzmann machine (GRBM), then the discriminative restricted Boltzmann machine (DRBM) with feature learning and classification ability is introduced, and arrhythmia classification is performed according to the extracted morphological features and RR interval features. In order to further improve the classification performance of DDBNs, DDBNs are converted to deep neural network (DNN) using the Softmax regression layer for supervised classification in this paper, and the network is fine-tuned by backpropagation. Finally, the Massachusetts Institute of Technology and Beth Israel Hospital Arrhythmia Database (MIT-BIH AR) is used for experimental verification. For training sets and test sets with consistent data sources, the overall classification accuracy of the method is up to 99.84% ± 0.04%. For training sets and test sets with inconsistent data sources, a small number of training sets are extended by the active learning (AL) method, and the overall classification accuracy of the method is up to 99.31% ± 0.23%. The experimental results show the effectiveness of the method in arrhythmia automatic feature extraction and classification. It provides a new solution for the automatic extraction of ECG signal features and classification for deep learning.
Keywords: arrhythmia, discriminative deep belief networks, restricted Boltzmann machine, feature extraction, softmax regression
引言
心电图（electrocardiogram, ECG）已广泛作为心脏疾病预防和诊断的重要非侵入性临床工具。通常，医生可对短期 ECG 信号进行视觉检测来诊断心律失常，而对动态心电图仪长期记录的 ECG 信号，无法仅依靠视觉检测。随着计算机科学的发展，ECG 信号的自动分类分析技术应运而生，现已在心律失常的诊断和分析中起着重要作用，成为辅助临床诊断心脏疾病的重要手段。
近十几年，针对心律失常的检测和分类发展出了几种模式识别方法[1-3]，主要涉及三个步骤：预处理、波形检测和分段、特征提取和分类。首先，对信号进行预处理，包括：基线漂移、工频干扰、肌电干扰等噪声去除[4]；然后，波形的检测和分段，包括：P 波，QRS 波群和 T 波等特征点检测，并根据以上特征点将 ECG 信号按心拍进行分段[5]；最后，特征提取和分类，包括：使用形态、时域和变换域等信息表示心拍特征[6-8]，使用主成分分析，独立成分分析和线性判别分析等进行特征降维[9]，以及使用神经网络和支持向量机（support vector machine, SVM）等实现 ECG 信号分类[10-11]。
上述特征提取的方法很大程度上依赖于对 ECG 信号特征的人为设计和选择，其有效性受诸多因素影响。最近，深度学习提供了一种特征提取和分类同时进行的方法可避免对人为设计特征的依赖。Acharya 等[12]开发了一个 11 层的卷积神经网络（convolutional neural network, CNN），实现了自动检测正常和心肌梗塞心律失常的算法，该模型含噪准确率为 93.53%，无噪准确率为 95.22%。Rahhal 等[13]对于自动分类 ECG 信号，采用深度学习与主动学习（active learning, AL）结合的方法，在特征学习阶段，通过由堆叠的去噪自动编码器（stacked denoising autoencoders, SDAEs）和其输出层添加柔性最大值（Softmax）回归层构建的深度神经网络（deep neural network, DNN）进行分类。Luo 等[14]使用改进的频率切片小波变换提取 ECG 信号时频特征，送入由 SDAEs 的编码器层和 Softmax 回归层构成的 DNN，同时通过对心拍样本进行微调来实现 ECG 信号分类，其所提模型实现了 97.5%的总体准确度。Tan 等[15]将 CNN 与长短期记忆网络结合，提取 ECG 信号特征，实现对冠状动脉疾病的自动诊断。Yang 等[16]通过堆叠稀疏自动编码器（stacked sparse autoencoders, SSAEs）深度学习网络提取 ECG 信号特征，送入 Softmax 分类器实现 ECG 信号的分类。Meng 等[17]采用原始 ECG 信号与 RR 间期作为输入，通过 4 层深度置信网络（deep belief networks, DBNs）进行无监督特征学习，提取的特征被送到 SVM 用于训练，自动识别 6 类心拍类型，总体精度 98.49%。Wu 等[18]将 DBNs 与 Softmax 分类器结合，完成特征提取，并实现 5 类 ECG 信号分类。熊博等[19]通过 SDAEs 与 Softmax 分类器，设计了 DNN 算法，实现了心律失常患者类型的自动分类。Yildirim[20]开发了 7 层基于深度双向小波的长短期记忆网络（deep bidirectional long-short term memory network-based wavelet sequences, DBLSTM-WS），实现了 5 类心拍分类，总体精度为 99.39%。
为了自动学习心拍信号的形态特征，并同时融入反映其心律变异的 RR 间期特征，提高心律失常的自动分类性能，本文采用由生成受限玻尔兹曼机（generative restricted Boltzmann machine, GRBM）与判别式受限玻尔兹曼机（discriminative restricted Boltzmann machine, DRBM）堆叠而成的判别式深度置信网络（discriminative deep belief networks, DDBNs）作为特征提取与分类的初始深度学习模型。由于输入网络的 ECG 信号为连续值，因此采用高斯—伯努利受限玻尔兹曼机（gaussian-bernoulli restricted Boltzmann machine, GB-RBM）作为 DDBNs 模型的首层，采用伯努利—伯努利受限玻尔兹曼机（bernoulli-bernoulli restricted Boltzmann machine, BB-RBM）作为 DDBNs 模型隐含层。为了进一步增强 DDBNs 的性能，完成初始化后，本文将 DDBNs 转换为使用 Softmax 回归层进行监督分类的 DNN，采用反向传播对网络进行微调，进而实现正常节律、左束支传导阻滞、右束支传导阻滞、室性早搏、房性早搏、起搏心拍共 6 类心律失常类型的自动分类。为深度学习自动提取 ECG 信号特征及分类提供了一种新的解决方法。
1. 实验数据
本文使用由美国麻省理工学院与贝斯以色列医院心律失常数据库（massachusetts institute of technology and beth israel hospital arrhythmia database, MIT-BIH AR）（网址为：https://physionet.org/cgi-bin/atm/ATM）提供的可公开使用的数据进行训练与测试。该数据库由 48 个双导联记录组成，涉及改良肢体导联 II（modified limb lead II, MLII）和胸部导联 V1、V2、V4、V5，每条记录约 30 min，以 360 Hz 采样，包含 R 波位置和心拍数据类型注释。
本文选取 MLII 数据中 6 类心拍数据用于实验，它们包括正常节律、左束支传导阻滞、右束支传导阻滞、室性早搏、房性早搏和起搏心拍，心拍数据波形如图 1 所示。参照文献[4, 19] 心电评估数据构成模式，选择 23 条具有代表性 ECG 信号记录按心拍构成数据集。在保证训练集和测试集数据来源一致的条件下，利用留出法将数据集按 2∶1 比例分为训练集和测试集。数据集各类心拍样本分布如表 1 所示。
图 1.
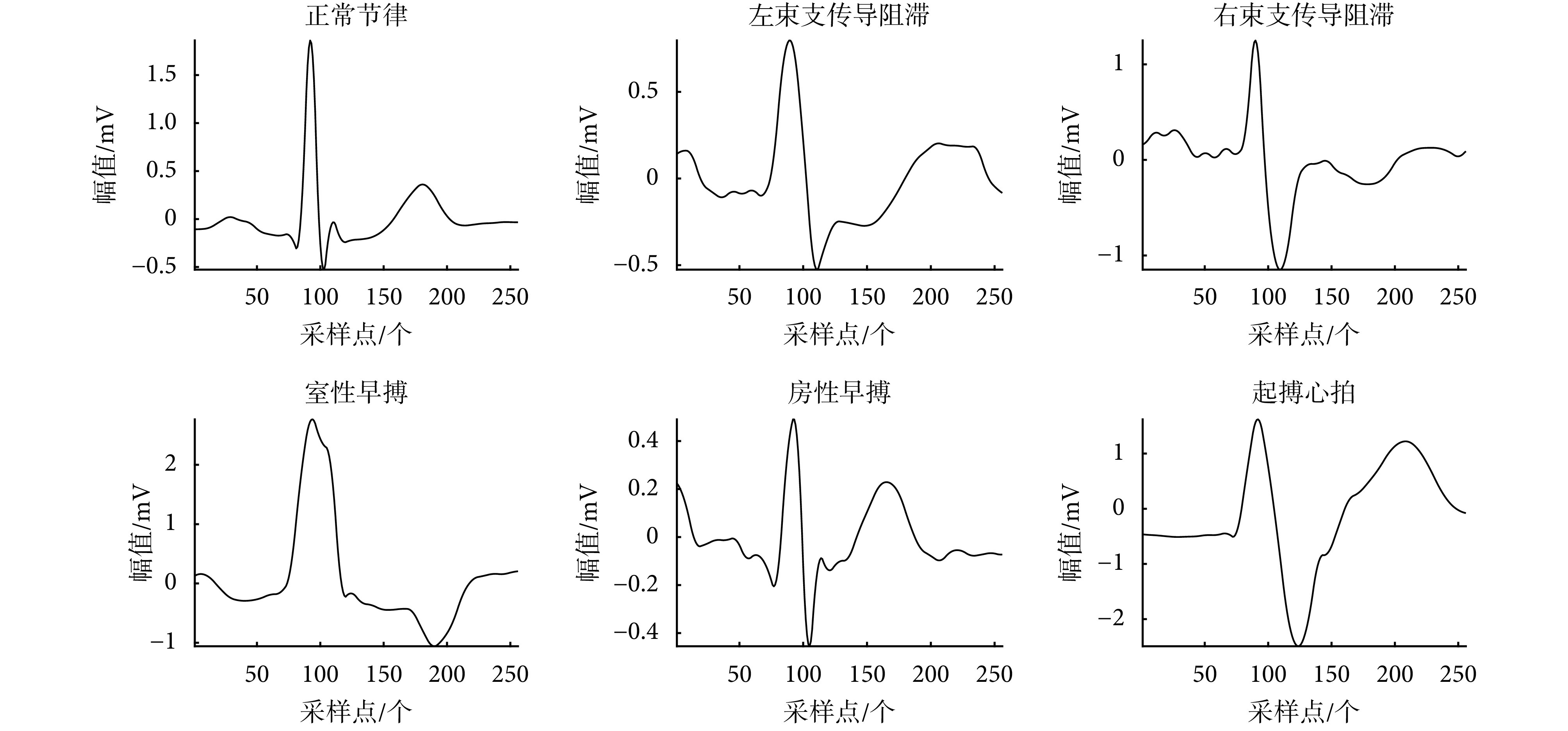
Six types of heart beat waveforms
6 类心拍波形图
表 1. Heart beat category distribution.
心拍类别分布
| 心拍类型名称 | 符号 | 记录号 | 训练集 | 测试集 | 合计 |
| 正常节律 | N | 103，113，115，123，220，234 | 7 987 | 3 994 | 11 981 |
| 左束支传导阻滞 | L | 109，111，207，214 | 5 379 | 2 690 | 8 069 |
| 右束支传导阻滞 | R | 118，124，212，231 | 4 512 | 2 257 | 6 769 |
| 室性早搏 | V | 119，200，221，233 | 1 663 | 832 | 2 495 |
| 房性早搏 | A | 209，222，232 | 1 314 | 658 | 1 972 |
| 起搏心拍 | P | 107，217 | 2 410 | 1 206 | 3 616 |
| 合计 | 23 265 | 11 637 | 34 902 |
2. 特征提取与分类
2.1. DDBNs 模型构建
本文构建了一个含 3 个隐含层的 DDBNs 模型，用于心拍信号的特征提取与分类。首先，将零均值单位方差归一化的单心拍 ECG 信号波形送入 DDBNs 的前两层 GRBM，其首层采用 GB-RBM，第二层采用 BB-RBM，并通过无监督学习获得该网络参数，由此获得第
个心拍样本的形态特征Fi，
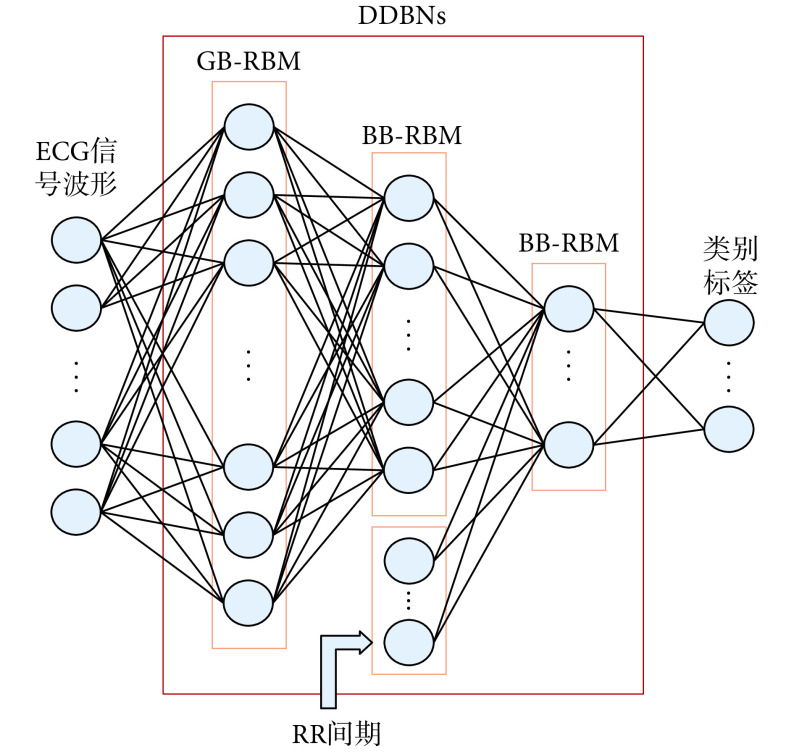
。此后，融入包括当前心拍 RR 间期、下一心拍 RR 间期、相邻 RR 间期差异度（即当前 RR 间期减去下一个 RR 间期除以这两个 RR 间期的均值）构成的三维间期特征：Ri = {r1, r2, r3}，并将其送入 DDBNs 的顶层 DRBM[17]，即一层 BB-RBM。然后通过有监督学习，获得该网络参数，完成心律失常的分类。本文构建的 DDBNs 模型结构如图 2 所示。
图 2.
DDBNs model structure
DDBNs 模型结构
2.1.1. GRBM
DBNs 是学习提取训练数据深层次表示的图形模型，由堆叠的受限玻尔兹曼机（restricted Boltzmann machine, RBM）组成。RBM 是具有可见层和隐含层互连的典型神经网络，在同一层中的任何两个神经元之间没有连接[21]。在可见层上具有二元输入的 RBM 为 BB-RBM；而在可见层上具有实值输入的 RBM 为 GB-RBM。BB-RBM 与 GB-RBM 的能量函数定义分别如式（1）、式（2）所示：
 |
1 |
 |
2 |
其中，θ1 = {wij, bi, cj}，θ2 = {wij, bi, cj, σi} 表示 RBM 待训练参数，nv 和 nh 分别为可见层与隐含层单元个数，vi 是可见层神经元，hj 是隐含层神经元，wij 是连接可见层和隐含层单元的权值，bi 和 cj 分别为可见层和隐含层神经元偏置，σi 是可见层神经元 vi 的高斯分布的标准差。对于 BB-RBM，可见层和隐含层的条件概率如式（3）、式（4）所示；对于 GB-RBM，可见层和隐含层的条件概率如式（5）、（6）所示：
 |
3 |
 |
4 |
 |
5 |
 |
6 |
其中，δ = 1/1 + e−x为逻辑斯谛（logistic）函数，η（·|μ, σ2）表示高斯分布的均值μ和方差σ2的概率密度函数。由于输入数据是实值，因此上述 GB-RBM 用于 DDBNs 的首层，随后的隐含层由 BB-RBM 组成。
2.1.2. DRBM
与以往在 DBNs 顶层添加分类器的研究方法不同，本文将具有分类能力的 DRBM 置于网络顶层，利于连贯地完成 ECG 信号特征的学习和分类。相比于文献[4, 13-14, 16-19]等的方法，该模型具有对参数和信号预处理不敏感等优势，降低了网络模型的学习和分类耗时，并提高了网络分类精度。GRBM 只能对输入数据进行特征学习，而除此之外 DRBM 可以对输入和关联目标类的联合分布进行建模[22]，如图 3 所示。
图 3.
Joint distribution model of DRBM
DRBM 的联合分布模型
DRBM 是采用具有两组可见层的单个 RBM 来训练联合密度模型。除了表示输入数据的单元 A 外，还有一个相当于“Softmax”的分类标签单元 B。通过计算样本在每个类别标签下的概率，从而预测最可能的类别y[23]，其中
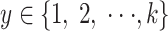，k为样本类别数。
2.2. DDBNs 模型训练
堆叠构建 DDBNs 的 RBM 训练能通过最大化训练样本的似然度进行，如式（7）所示：
 |
7 |
对θ1,2 对数概率求导，需求
的条件概率分布和
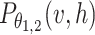的联合概率分布，其中容易计算出
，但是
则需采用对比散度（contrastive divergence, CD）等算法计算。本文采用持续自由能对比散度（free energy in persistent contrastive divergence, FEPCD）与 CD 的综合算法，即首层采用 FEPCD 算法，其余层采用 CD 算法，对 RBM 模型进行训练[24]。
整体 DDBNs 模型采用贪婪的分层方式进行训练，无标签数据送入 GRBM 网络中，经过逐层无监督训练，每层 RBM 的输入为前一层的输出，以从样本中学习到高层次的特征结构。顶层 DRBM 通过有监督学习，得到测试样本在各类别下的后验概率，由此输出对样本分类的判别结果。
2.3. DDBNs 模型有监督微调
DDBNs 的逐层预训练完成后，将其转换为使用 Softmax 回归层作为输出的 DNN，通过最小化式（8）损失函数，反向传播来调整网络参数，执行监督分类，结构如图 4 所示。
图 4.
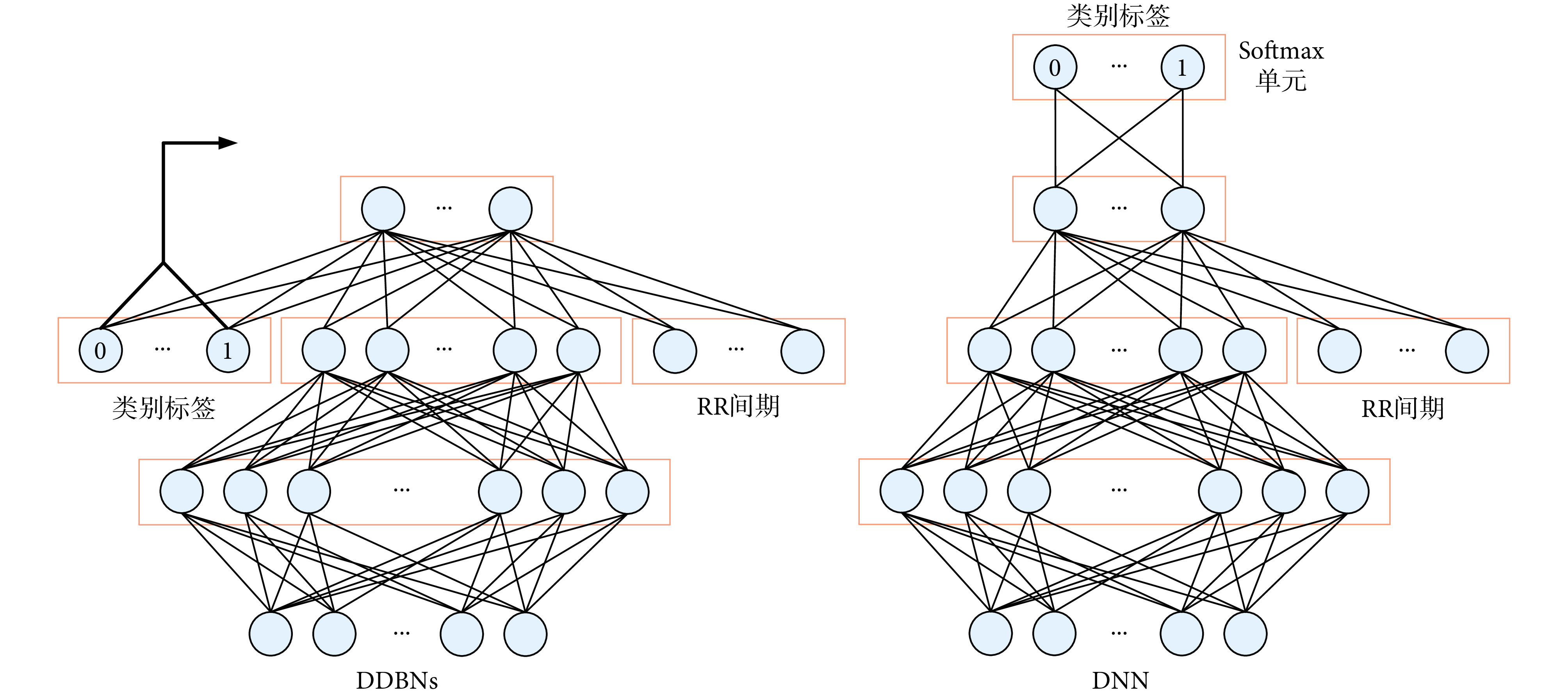
Conversion of DDBNs to DNN using Softmax classification
DDBNs 转换为 Softmax 分类的 DNN
 |
8 |
其中，
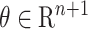是 Softmax 的模型参数，m为训练样本数，k 为样本类别数，1（·） 为指示函数，代表如果该项为真，取 1，否则取 0，y 为样本类别标签，xi 为顶层的输入心拍特征，n 为顶层输入神经元个数。第一项是指 Softmax 层的交叉熵损失函数，k 维向量元素采用
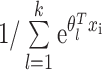函数项实现概率分布的归一化，使得所有类别的概率总和为 1；第二项是衰减惩罚项，实现过大参数的惩罚。
3. 实验与结果分析
3.1. ECG 信号预处理
ECG 信号送入 DDBNs 网络前，需经过滤波、R 峰定位和归一化。首先，对信号进行 9 尺度小波分解，将第 1 层细节系数（90～180 Hz）和第 9 层近似系数（0～0.35 Hz）置零，其他小波系数进行自适应小波阈值滤波处理后重构，去除基线漂移及高频干扰等。MIT-BIH AR 中 103 组记录的某 10 s ECG 信号滤波前后对比如图 5 所示。然后通过 R 峰定位来确定心拍位置；最后，参考 Wu 等[25]的心拍分割方法，即选取 340 个采样点心拍数据长度，包含 R 峰前 139、后 200 个采样点。经对 MIT-BIH AR 心律失常数据统计分析，发现文献[25]选取的心拍数据长度包含了 P 波前及 T 波后的数据，因此确定本实验包括 P 波和 T 波的心拍长度为 256 个采样点，即取 R 峰前 90、后 165 个采样点。
图 5.
ECG signal filtering effect comparison
ECG 信号滤波效果对比
对送入 DDBNs 的 256 维采样点 x 与三维 RR 间期特征 r 进行归一化处理。对 x 归一化，得到一个心拍归一化样本
，送入网络首层，如式（9）所示：
 |
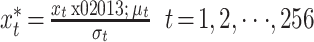9 |
其中，μt 为训练集心拍样本的第 t 个均值，σt 为训练集心拍样本的第 t 个标准差。而对当前心拍 RR 间期、下一心拍 RR 间期、相邻 RR 间期差异度三维间期特征 R 中的特征 r 归一化，得到一个心拍的间期特征
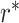，结合 GRBM 提取的形态特征，送入 DRBM 实现分类，如式（10）所示：
 |
10 |
其中，rtmax 为训练集 RR 间期特征的第t个最大值，rtmin 为训练集 RR 间期特征的第 t 个最小值。
3.2. DDBNs 模型训练与性能评估
首先，构建 DDBNs 初始化模型，用 MIT-BIH AR 的训练集对 DDBNs 预训练，并使用其权值初始化，然后使用反向传播微调整个模型。预训练阶段，使用 FEPCD 与 CD 结合的训练方法。参数设置：首层 GB-RBM 学习率：0.01；其余层 BB-RBM 学习率：0.1；动量：[0.5, 0.4, 0.3, 0.2, 0.1, 0]；批次尺寸：100；训练次数：50。微调阶段，使用小批量梯度优化方法，参数设置：学习率：1；动量：0.5；批次尺寸：100；训练次数：200；λ：1 × 10−7。本实验的计算机环境为：中央处理器（central processing unit, CPU）（Core i7-6700 @ 3.4 GHz, Intel, 美国）；随机存取存储器（random access memory, RAM）（DDR4 16 GB, Samsung, 韩国）；图形处理器（graphics processing unit, GPU）（GeForce GTX 1070, NVIDIA, 美国）。
为便于对心拍信号分类结果的性能评估，本文使用以下 6 个标准测量指标[1]：灵敏度（sensitivity, Se），正检测率（positive predictivity, Pp），特异性（specificity, Sp），假阳性率（false positive rate, FPR），假阴性率（false negative rate, FNR）和整体精度（overall accuracy, OA）。
3.3. 实验结果分析
深度学习网络的初始化和训练等具有一定随机性，导致不同次的分类结果有偏差。因此本文通过对数据集进行 10 次实验，利用平均值 ± 标准差的统计方法计算 OA，对基于 DDBNs 的心拍信号分类的准确度和稳定性进行评估。
为了获得较优的模型结构，本文设计比较了 4 种不同结构的 DDBNs 对 ECG 信号进行特征提取与分类的结果，其测试后 OA 如表 2 所示。其中 DDBNs-1 结构不含 GRBM 层，DDBNs-2 至 DDBNs-4 分别含有 1、2、3 层 GRBM。
表 2. Overall accuracy of four DDBNs.
4 种 DDBNs 下的 OA
| 结构名称 | 网络结构 | OA（%） | |
| 微调前 | 微调后 | ||
| DDBNs-1 | 256(259)-100-6 | 88.42 ± 2.35 | 99.74 ± 0.12 |
| DDBNs-2 | 256-100(103)-50-6 | 97.59 ± 1.08 | 99.76 ± 0.10 |
| DDBNs-3 | 256-500-250(253)-100-6 | 99.23 ± 0.19 | 99.84 ± 0.04 |
| DDBNs-4 | 256-500-250-100(103)-50-6 | 98.97 ± 0.41 | 99.80 ± 0.06 |
通过对比，利用 DDBNs-3 结构的 OA 效果最好，其具有最高的平均值和最低的标准差，因此本文后续继续采用 DDBNs-3 结构：256-500-250（253）-100-6 作为进一步性能测试的模型。该模型中的 253，代表该层输入为上一层输出的 250 维心拍信号形态特征结合 3 维 RR 间期特征。训练 DDBNs-3，至分类前学习到的各类 ECG 信号的 100 维心拍特征如图 6 所示，可以观察到它们是稀疏而有区别的。如表 3 所示，给出了 DDBNs-3 在测试集上进行 ECG 信号心律失常分类的混淆矩阵。如表 4 所示，给出了心拍分类前 5 个测量指标的测试结果。
图 6.
Six types of heart beat features learned by DDBNs
DDBNs 学习到的 6 类心拍特征
表 3. Confusion matrix of heart beat classification result.
心拍分类结果混淆矩阵
| 真实心拍
类别 |
算法心拍识别结果 | ||||||
| N | L | R | V | A | P | 合计 | |
| N | 3 990 | 0 | 0 | 1 | 3 | 0 | 3 994 |
| L | 0 | 2 687 | 0 | 3 | 0 | 1 | 2 691 |
| R | 0 | 0 | 2 257 | 0 | 0 | 0 | 2 257 |
| V | 0 | 2 | 0 | 824 | 3 | 2 | 831 |
| A | 1 | 0 | 0 | 1 | 656 | 0 | 658 |
| P | 0 | 0 | 0 | 1 | 1 | 1 204 | 1 206 |
| 合计 | 3 991 | 2 689 | 2 257 | 830 | 663 | 1 207 | 11 637 |
表 4. Test results of heart beat classification.
心拍分类测试结果
| 心拍类型 | Se（%） | Pp（%） | Sp（%） | FPR（%） | FNR（%） |
| N | 99.90 | 99.97 | 99.99 | 0.01 | 0.10 |
| L | 99.85 | 99.93 | 99.98 | 0.02 | 0.15 |
| R | 100 | 100 | 100 | 0 | 0 |
| V | 99.16 | 99.28 | 99.94 | 0.06 | 0.84 |
| A | 99.70 | 99.94 | 99.94 | 0.06 | 0.30 |
| P | 99.83 | 99.75 | 99.98 | 0.03 | 0.17 |
DDBNs-3 与文献[18]所提 DBNs 与 Softmax 结合方法（简写为：DBNs + Softmax）的性能对比如表 5 所示，其中ttrain 为训练集上的训练时间，ttest 为测试集上单个样本的测试时间。
表 5. Performance comparison between DDBNs and DBNs + Softmax.
DDBNs 与 DBNs + Softmax 性能对比
| 结构名称 | 网络结构 | ttrain/s | ttest/μs | OA（%） |
| DDBNs-3 | 256-500-250(253)-100-6 | 588.46 | 62.80 | 99.84 ± 0.04 |
| DBNs + Softmax | 256-500-250(253)-100-6 | 625.39 | 77.32 | 99.80 ± 0.06 |
与文献[18]的 DBNs + Softmax 分类器的方法对比可知，采用 DDBNs 特征提取与分类的方法具有更好的性能。本文方法分别与双树复小波变换（dual tree complex wavelet transform, DTCWT）结合人工神经网络（artificial neural networks, ANN）（简写为：DTCWT+ANN）[8]、近邻保持嵌入（neighborhood preserving embedding, NPE）算法结合 SVM（简写为：NPE+SVM）[11]、DBNs 结合 SVM（简写为：DBNs + SVM）[17]、DBNs + Softmax[18]、SDAEs 与 Softmax（简写为：SDAEs + Softmax）[19]、DBLSTM-WS[20] 6 种方法也进行性能对比，如表 6 所示。最终，与上述方法比较的结果显示了本文方法的有效性。
表 6. Heart beat classification method comparison.
心拍分类方法对比
| 实验方法 | NSe（%） | LSe（%） | RSe（%） | VSe（%） | ASe（%） | PSe（%） | OA（%） |
| DTCWT + ANN[8] | 98.07 | 80.65 | 82.26 | 84.25 | − | 97.79 | 94.64 |
| NPE + SVM[11] | 99.64 | 99.11 | 99.09 | 96.80 | 84.33 | 99.83 | 99.00 |
| DBNs + SVM[17] | 99.04 | 99.50 | 99.31 | 97.89 | 89.72 | 99.72 | 98.49 |
| DBNs + Softmax[18] | 99.20 | 100 | 100 | 99.10 | 98.30 | − | 99.50 |
| SDAEs + Softmax[19] | 99.92 | 99.25 | 99.79 | 98.87 | 97.41 | 100 | 99.43 |
| DBLSTM-WS[20] | 99.54 | 98.93 | 100 | 98.03 | − | 99.66 | 99.39 |
| 本文 | 99.90 | 99.85 | 100 | 99.16 | 99.70 | 99.83 | 99.84 |
3.4. 实用性深入测试
为了评估 DDBNs 模型在心律失常自动分类实际应用场景中的性能，本文采用 MIT-BIH AR 中不同的患者记录分别构成训练集和测试集，其分布如表 7 所示。
表 7. Heart beat category distribution.
心拍类别分布
| 数据集 | 记录号 | N | L | R | V | A | P | 合计 |
| 训练数据集 | 100，105，107，108，111，114，116，118，201，203，207，208，
209，215，219，222，228，233 |
30 218 | 3 578 | 2 249 | 3 447 | 891 | 2 076 | 42 459 |
| 测试数据集 | 103，106，109，119，124，205，214，217，221，223，231，232 | 12 309 | 4 491 | 3 177 | 2 409 | 1 461 | 1 540 | 25 387 |
由于训练集和测试集来源不同，其数据分布差异使得心律失常的自动分类具有挑战性。若单纯采用 DDBNs 与其微调算法模型，对表 7 数据集进行 ECG 信号心律失常分类结果一般，分类 OA 为 61.32% ± 3.17%，尤其在训练集和测试集分布明显差异的 L 和 A 两类别分类准确度更低。为了克服这一不足，有效扩大标记训练集是一解决途径。参照文献[13]运用的 AL 方法，本文在完成所提 DDBNs 微调算法基础上，通过 AL 方法从测试数据中挑选少量数据进行标记，并参与 DDBNs 模型的有监督微调，在保证算法实时性的同时，提高分类算法的适应性和准确性。
在加入主动学习的实验中，本文保持 DDBNs 初始化模型与微调参数设置不变，在 AL 阶段的参数设置如下：迭代数 iter（·） = 5，每次选取标记样本数NAL = 10。即，每条测试记录通过 5 次 AL 算法迭代过程，共选择 50 个样本送入 DDBNs 微调模型中，更新模型参数。采用 DDBNs-3 结构作为本次性能测试模型，在测试集上进行 ECG 信号心律失常分类的混淆矩阵如表 8 所示，其 6 类心拍分类测试结果如表 9 所示。
表 8. Confusion matrix of heart beat classification result.
心拍分类结果混淆矩阵
| 真实心拍类别 | 算法心拍识别结果 | ||||||
| N | L | R | V | A | P | 合计 | |
| N | 12 302 | 0 | 0 | 3 | 3 | 1 | 12 309 |
| L | 16 | 4 435 | 0 | 40 | 0 | 0 | 4 491 |
| R | 1 | 0 | 3 173 | 0 | 3 | 0 | 3 177 |
| V | 12 | 5 | 0 | 2 372 | 1 | 19 | 2 409 |
| A | 48 | 0 | 9 | 9 | 1 395 | 0 | 1 461 |
| P | 1 | 0 | 0 | 5 | 0 | 1 534 | 1 540 |
| 合计 | 12 380 | 4 440 | 3 182 | 2 429 | 1 402 | 1 554 | 25 387 |
表 9. Test results heart beat classification.
心拍分类测试结果
| 心拍类型 | Se（%） | Pp（%） | Sp（%） | FPR（%） | FNR（%） | OA（%） |
| N | 99.94 | 99.37 | 99.40 | 0.60 | 0.06 | 99.31 ± 0.23 |
| L | 98.75 | 99.89 | 99.98 | 0.02 | 1.25 | |
| R | 99.87 | 99.72 | 99.96 | 0.04 | 0.13 | |
| V | 98.46 | 97.65 | 99.75 | 0.25 | 1.54 | |
| A | 95.48 | 99.50 | 99.97 | 0.03 | 4.52 | |
| P | 99.61 | 98.71 | 99.92 | 0.08 | 0.39 |
4. 结论
本文提出了一种基于 DDBNs 的 ECG 信号自动分类方法，将 GRBM 提取的心拍信号形态特征与其 RR 间期特征有机融合送入 DRBM 进行心律失常分类，使 DRBM 的特征学习和分类能力有效发挥，同时克服了人为特征设计及选取的影响。经 MIT-BIH AR 测试实验，在训练和测试集数据来源一致时，本文方法识别正常节律、左束支传导阻滞、右束支传导阻滞、室性早搏、房性早搏和起搏心拍 6 类形态，分类准确率达到 99.84% ± 0.04%，取得了优于基于传统特征选择与其他深度学习方法的结果；在训练和测试集数据来源非一致时，对通过 AL 方法扩充少量训练集的措施进行了初步尝试，6 类心拍信号的分类准确率可达 99.31% ± 0.23%，也取得了满意的效果。实验结果表明，本文所构建的提取 ECG 信号波形形态特征与 RR 间期特征融合后，结合 DRBM 特征进行心律失常自动特征提取和分类的有效性，为深度学习自动提取 ECG 信号特征及分类提供了一种新方法。
DDBNs 在 ECG 信号分类上拥有一定前景。由于训练数据类别数量的不均衡，导致小样本数据识别误差高于大样本；而引入 AL 方法后，DDBNs 模型的优化和扩大训练集标记数据该如何有效选择，未来这些问题都是值得深入探究的研究课题。
Funding Statement
国家自然科学基金资助项目（51805120）；黑龙江省自然科学基金资助项目（F200912）；国家大学生创新创业训练计划项目（201710214010）
References
- 1.de Chazal P. O'Dwyer M, Reilly R B Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans Biomed Eng. 2004;51(7):1196–1206. doi: 10.1109/TBME.2004.827359. [DOI] [PubMed] [Google Scholar]
- 2.Alvarado A S, Lakshminarayan C, Principe J C Time-Based compression and classification of heartbeats. IEEE Trans Biomed Eng. 2012;59(6):1641–1648. doi: 10.1109/TBME.2012.2191407. [DOI] [PubMed] [Google Scholar]
- 3.Homaeinezhad M R, Atyabi S A, Tavakkoli E,et al ECG arrhythmia recognition via a neuro-SVM–KNN hybrid classifier with virtual QRS image-based geometrical features. Expert Syst Appl. 2012;39(2):2047–2058. doi: 10.1016/j.eswa.2011.08.025. [DOI] [Google Scholar]
- 4.白洋. 基于深度置信网络的心律失常分类算法研究. 保定: 河北大学, 2016.
- 5.Bono V, Mazomenos E B, Chen T A, et al Development of an automated updated selvester QRS scoring system using SWT-Based QRS fractionation detection and classification. IEEE J Biomed Health Inform. 2014;18(1):193–204. doi: 10.1109/JBHI.2013.2263311. [DOI] [PubMed] [Google Scholar]
- 6.Dima S M, Panagiotou C, Mazomenos E B, et al On the detection of myocadial scar based on ECG/VCG analysis. IEEE Trans Biomed Eng. 2013;60(12):3399–3409. doi: 10.1109/TBME.2013.2279998. [DOI] [PubMed] [Google Scholar]
- 7.Kutlu Y, Kuntalp D Feature extraction for ECG heartbeats using higher order statistics of WPD coefficients. Comput Methods Programs Biomed. 2012;105(3):257–267. doi: 10.1016/j.cmpb.2011.10.002. [DOI] [PubMed] [Google Scholar]
- 8.Thomas M, Das M K, Ari S Automatic ECG arrhythmia classification using dual tree complex wavelet based features. AEU-International Journal of Electronics and Communications. 2015;69(4):715–721. doi: 10.1016/j.aeue.2014.12.013. [DOI] [Google Scholar]
- 9.Martis R J, Acharya U R, Min L C ECG beat classification using PCA, LDA, ICA and discrete wavelet transform. Biomed Signal Process Control. 2013;8(5):437–448. doi: 10.1016/j.bspc.2013.01.005. [DOI] [Google Scholar]
- 10.Yu S N, Chou K T Integration of independent component analysis and neural networks for ECG beat classification. Expert Syst Appl. 2008;34(4):2841–2846. doi: 10.1016/j.eswa.2007.05.006. [DOI] [Google Scholar]
- 11.高兴姣, 李智, 陈珊珊, 等 基于近邻保持嵌入算法的心律失常心拍分类. 生物医学工程学杂志. 2017;34(1):1–6. [Google Scholar]
- 12.Acharya U R, Fujita H, Oh S L, et al Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals. Inf Sci. 2017;415-416:190–198. doi: 10.1016/j.ins.2017.06.027. [DOI] [Google Scholar]
- 13.Rahhal M M A, Bazi Y, Alhichri H, et al Deep learning approach for active classification of electrocardiogram signals. Inf Sci. 2016;345:340–354. doi: 10.1016/j.ins.2016.01.082. [DOI] [Google Scholar]
- 14.Luo Kan, Li Jianqing, Wang Zhigang, et al Patient-specific deep architectural model for ECG classification. J Healthc Eng. 2017:1–13. doi: 10.1155/2017/4108720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tan J H, Hagiwara Y, Pang W, et al Application of stacked convolutional and long short-term memory network for accurate identification of CAD ECG signals. Comput Biol Med. 2018;94:19–26. doi: 10.1016/j.compbiomed.2017.12.023. [DOI] [PubMed] [Google Scholar]
- 16.Yang Jianli, Bai Yang, Lin Feng, et al A novel electrocardiogram arrhythmia classification method based on stacked sparse auto-encoders and softmax regression. International Journal of Machine Learning and Cybernetics. 2018;9(10):1733–1740. doi: 10.1007/s13042-017-0677-5. [DOI] [Google Scholar]
- 17.Meng H, Zhang Y. Classification of electrocardiogram signals with deep belief networks//IEEE 17th Int Conference Comput Sci Eng, Chengdu: IEEE, 2014: 7-12.
- 18.Wu Z, Ding X, Zhang G, et al. A novel features learning method for ECG arrhythmias using deep belief networks//IEEE 6th Int Conference Digital Home (ICDH), Guangzhou: IEEE, 2016: 192-196.
- 19.熊博, 李鑫, 时亚松 基于稀疏降噪自动编码机的心律失常自动分类. 激光杂志. 2018;39(4):152–156. [Google Scholar]
- 20.Yildirim O A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Comput Biol Med. 2018;96:189–202. doi: 10.1016/j.compbiomed.2018.03.016. [DOI] [PubMed] [Google Scholar]
- 21.Hinton G E, Salakhutdinov R R Reducing the dimensionality of data with neural networks. Science. 2006;313(5786):504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- 22.Bengio Y, Chapados N, Delalleau O A, et al Detonation classification from acoustic signature with the restricted Boltzmann machine. Computational Intelligence. 2012;28(2):261–288. doi: 10.1111/coin.2012.28.issue-2. [DOI] [Google Scholar]
- 23.Hinton G E A practical guide to training restricted Boltzmann machines. Lecture Notes in Computer Science. 2012;7700:559–619. doi: 10.1007/978-3-642-35289-8. [DOI] [Google Scholar]
- 24.Keyvanrad M A, Homayounpour M M Deep belief network training improvement using elite samples minimizing free energy. International Journal of Pattern Recognition and Artificial Intelligence. 2015;29(5):1–18. [Google Scholar]
- 25.Wu Z, Ding X, Zhang G A novel method for classification of ECG arrhythmias using deep belief networks. Int J Comput Intell Appl. 2016;15(4):1–14. [Google Scholar]