Abstract
心血管疾病(CAD)已经严重威胁着人类健康。对血管壁力学性质的实验测量和建模分析可以为疾病的诊断、支架的植入,以及人工血管的设计等提供理论依据。动脉血管壁有主动和被动的力学性能,被动力学性能主要由弹性纤维和胶原蛋白纤维的含量和结构决定;主动力学性能则由平滑肌细胞(VSMC)的收缩实现。大量研究表明,动脉血管壁的双层膜结构模型可以很好地反映血管的力学性能,血管壁的周向、轴向、径向应力都有重要作用。本文综述了近年来血管壁力学性质测量和力学性能建模方面的研究进展,以及该研究方向面临的挑战和机遇,以期为临床心血管疾病的治疗提供支持。
Keywords: 心血管力学, 应力和应变, 血管壁本构模型, 血管壁主动力学性质, 血管壁被动力学性质
Abstract
Coronary artery diseases (CAD) have always been serious threats to human health. The measurement, constitutive modeling, and analysis of mechanical properties of the blood vessel wall can provide a tool for disease diagnosis, stent implantation, and artificial artery design. The vessel wall has both active and passive mechanical properties. The passive mechanical properties are mainly determined by elastic and collagen fibers, and the active mechanical properties are determined by the contraction of vascular smooth muscle cells (VSMC). Substantial studies have shown that, the two-layer model of the vessel wall can feature the mechanical properties well, and the circumferential, axial and radial strain and stress are of great significance in arterial wall mechanics. This study reviewed recent investigations of mechanical properties of the vessel wall. Challenges and opportunities in this area are discussed relevant to the clinical treatment of coronary artery diseases.
Keywords: cardiovascular mechanics, stress and strain, vessel wall constitutive model, vessel wall active mechanical properties, vessel wall passive mechanical properties
引言
血液循环系统是人类赖以生存的基础,为生命体的活动提供了能量传送的纽带。调查显示,心血管疾病在中国已成为重大的公共卫生问题,防治心血管病刻不容缓[1]。心血管系统是一个以心脏为中心的力学驱动系统,在血液循环过程中,血液流动、血细胞和血管的变形以及血液和血管的相互作用等均具有力学规律。心血管治疗设备的使用也受体内外因素的影响,其中力学因素具有直接而明显的作用[2-4],例如小口径人工血管和可降解支架的研究为患者带来了希望,但由于一系列相关的血流动力学和软组织力学问题,现阶段的治疗还是与短期或长期不良心血管事件直接相关[5-6]。
血管中的血液流动情况复杂多变,会影响血管壁的形态和功能。一些心血管系统疾病,如高血压、糖尿病、动脉粥样硬化、动脉瘤、主动脉夹层等,会导致血管壁微结构的变化从而改变血管壁的力学性能[7-13]。随着定量生理学和生物医学工程学的发展,血管壁的力学性质成为研究生长和疾病领域的主要关注对象[14],进而发展成为一个新的学科——生物力学。动脉血管的力学性能可分为主动力学性能和被动力学性能。主动力学性能是指血管在外力的作用下所展现出来的主动收缩的能力,反映了平滑肌细胞的主动舒缩现象[15];被动力学性能是指当血管受到外力作用时主要由弹性蛋白和胶原纤维等细胞外基质所调控的对外界应力刺激的反应[16]。现阶段,许多学者研究了血管的被动力学性能,但是对主动力学性能的研究还相当有限[17]。本文首先综述了近年来血管壁力学性质不同维度的测量方法,并在此基础上介绍了利用实验数据进行数学建模的研究进展和代表性研究成果。此外,文中还介绍了该研究方向面临的挑战和机遇,以期为临床心血管疾病的治疗提供支持。
1. 血管壁力学性质测量
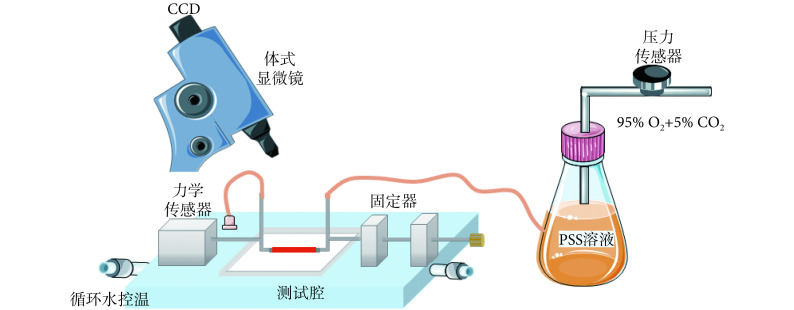
血管壁的应力-应变与各向同性弹性体不同,是非线性关系。根据血管壁的三层结构和多种成分的复杂性,可将血管壁看作是一种复合材料,具有特殊的力学性质,因此在对血管壁进行力学测试时,会出现蠕变现象和松弛现象[2]。如图 1 所示,肌动描记器(myograph)主要用于 60 μm 或更大直径的管状组织被动和主动应变的测量,包括静脉、动脉、支气管、输尿管等[18-20],为平滑肌的组织学、形态学、生理学、病理学特别是药理学研究提供一种解决方案。除设备外,在血管的力学性能测试实验中需要考虑的因素还包括:测试环境、测试方法(单轴拉伸、双轴拉伸、冲压拉伸等)、预处理方法、测试时间、环境温度、组织完整性等[21]。
图 1.
Myograph
肌动描记器
it can perform tension and expansion experiments on blood vessels and measure the mechanical properties in circumferential, axial and radial directions
可对血管执行冲压拉伸实验,测量血管周向、轴向、径向力学性质
1.1. 血管单轴力学性质测量
血管的单轴力学性质测量较为常见,在单轴拉伸实验中,对目标血管或管壁上获取的条状组织进行长度方向的拉伸,记录力-伸长率之间的关系并建模,来研究血管单轴方向的力学性质[22]。很多研究中提出的血管壁本构模型表明,由于血管内平滑肌细胞近似周向排列,血管壁的舒缩主要表现为周向应力[23-26]。单轴拉伸实验数据多用于验证模型的有效性,以确定生物材料参数[27]。尽管大多数研究提出本构模型是对血管的周向应力-应变关系进行探讨,但是一些研究也对血管的不同方向分别进行单轴测试实验,以求全面研究血管壁的力学性能。例如,Niestrawska 等[28]对人类腹主动脉的周向和轴向分别进行单轴拉伸测试实验,得到的柯西应力与拉伸比的曲线证明了动脉血管壁的各向异性和非线性。
1.2. 血管双轴力学性质测量
与单轴拉伸实验测量比较,针对周向、轴向两个方向进行测量的双轴载荷研究的开展相对较少[29-30]。Lu 等[20, 31]利用肌动描记器分别对大鼠弹性动脉和肌性动脉进行了双轴载荷试验,通过压力传感器测量得到在血管舒张和收缩时轴向力发生的变化。另外一些研究也通过双轴冲压拉伸实验证明了血管轴向力对血管壁内应力分布的影响,并提出轴向力在维持血管稳定性方面具有重要作用[19]。Hayman 等[32]的研究显示与被动状态相比,血管中平滑肌细胞的收缩减少了颈动脉屈曲,这表明平滑肌细胞收缩会使动脉沿轴向缩短。通过将影响大鼠平滑肌细胞功能的基因敲除,并对基因敲除的大鼠主动脉进行双轴测试实验,Murtada 等[33]提出血管壁平滑肌细胞可引起多轴反应,在周向和轴向都扮演了重要角色。基于双轴力学性能测试实验和数值优化分析,本文团队[19]率先提出了双轴主动应变能函数,又进一步将单层的主动和被动应变能函数扩展为双层模式,并提出了双层血管壁力学模型来计算血管壁内应力与应变的分布[18]。通过研究兔颈总动脉的双轴特性,Takamizawa 等[34]也提出了双轴主动应变能函数,并用来描述狭窄血管的力学特性,模型与实验数据拟合良好,佐证了上述观点。在研究小鼠血管壁力学性能时,Caulk 等[35]分别执行单轴等距实验、双轴等距实验和单轴等距冲压实验,结果表明血管平滑肌的收缩能力按照单轴等距冲压、双轴等距到单轴等距实验的次序依次降低。这提示了在对血管进行测试时,为了更全面地研究血管真实情况,需要考虑血管在体受力情况下血管壁的构型。
1.3. 血管三维力学性质测量
在双轴实验的基础上对血管施加扭转载荷,记录血管扭矩和切应力的情况可实现血管三维方向的力学性能测试,即冲压-拉伸-扭转实验[36]。Luo 等[37]通过三维重建猪冠状动脉平滑肌细胞形态,证明血管壁内径向应力、应变分布可能会影响平滑肌细胞的取向和迁移,对血管功能有着较为直接的影响,然而在实际研究中径向应力经常被忽略。Sommer 等[38]通过扭转实验测试得到血管壁剪切模量随着轴向预拉伸的增加和周向压力的增加而增加。
三维测量实验[30, 37, 39-40]得到的实验数据可以更好地验证三维血管本构模型,有助于推导新的本构模型。相比于一维和二维测量,三维实验测量得到的实验数据通过有限元模拟后还可得到更逼真的应力-应变关系,从而更好地用于研究血管壁的力学性质[41]。
2. 血管壁力学性能建模
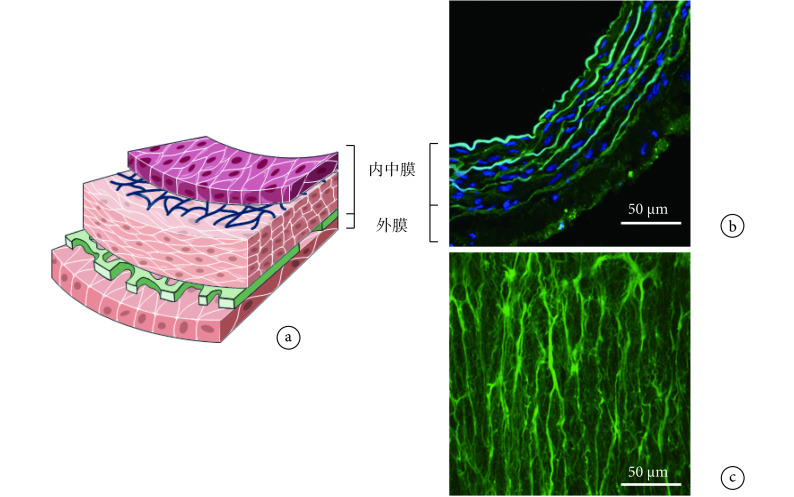
动脉血管壁的力学性能是由血管主要组成成分——血管平滑肌细胞、弹性蛋白和胶原蛋白纤维共同决定的,可通过主动和被动力学模型来进行描述[7, 15, 42]。图 2 为动脉血管壁双层膜结构示意图以及血管中主要成分的显微结构染色示意图。对血管微结构成像有利于建立符合血管性质的微观结构模型,从而研究血管壁的力学性质。此外,对动脉血管壁主动和被动力学性能的研究可极大地提高我们对血管壁微观结构、管壁力学和血流动力学的理解,有利于探究血管生长和重塑的病理生理机制,提高对心血管疾病的认知水平和临床诊疗水平。
图 2.
Macrostructure and microstructure of artery wall
动脉血管壁宏观结构及显微结构
a. schematic diagram of the layered structure of rat abdominal artery (intima-media and adventitia); b. the cross-sectional view of rat abdominal artery (blue indicates the smooth muscle cell nucleus marked by DAPI); c. longitudinal-sectional view of rat abdominal artery (adventitia)
a. 腹主动脉壁分层结构示意图(内中膜和外膜);b. 腹主动脉壁横截面视图(蓝色表示 DAPI 标记的平滑肌细胞核);c. 腹主动脉纵切面视图(外膜)
2.1. 血管壁粘弹性特征
血管属于生物软组织,具有滞后、松弛、蠕变、各向异性和非线性应力应变关系,其机械行为不仅受短时间内弹性或粘弹性的控制,而且还受数小时至数月时间范围内血管生长和重塑的控制。动脉血管随着血流量的持续增加而增大,随着血压升高而增厚,随着年龄的增长而变硬,它们在动脉瘤扩张中改变大小和形状,并且在动脉粥样硬化中具有明显不同的组成和性质。很多病例表明,血管在健康和疾病方面经历了显著的增长和重塑,得益于动脉血管的软组织特性[43]。Valdez-Jasso 等[44]使用一个四参数(线性)开尔文粘弹性模型和两个五参数非线性粘弹性模型来预测绵羊和人胸主动脉和颈动脉的粘弹性特性,实验数据结果表明最佳模型选择取决于动脉类型。在离体实验条件下,颈动脉比胸主动脉更硬,血管类型或实验条件之间的粘弹性增益和松弛参数没有显著差异。Amabili 等[45]使用叠加在初始拉伸值上的不同频率的单轴谐波激励,通过轴向和周向血管条的单轴拉伸测试以及 Gasser-Ogden-Holzapfel 材料模型[46](HGO 模型)来表征三个主动脉层的粘弹性行为,实验数据结果证明了所采用的粘弹性模型的合理性。Zhang 等[47]采用准线性粘弹性模型研究了生理负荷条件下兔胸主动脉的搏动应力,归一化应力松弛函数为各向同性,而应力-应变关系为各向异性和非线性。结果表明,与纯弹性响应相比,动脉的粘弹性特性降低了周向应力和应变的大小和变化速率,由于粘弹性,径向壁运动也相应减少。这些发现表明,血管的寿命每年承受数百万次的周期性机械载荷,粘弹性有益于延长血管的疲劳寿命。
2.2. 血管壁的双层模型
根据微观成分、形态和功能不同,血管壁主要分为内膜、中膜和外膜三层。内膜主要由内皮细胞组成,在血管生理调控、物质运输中起重要作用[15, 48],但因为在大多数正常动脉中厚度极薄,在总的力学性能上贡献较少,因此多采用内中膜(intimal-media)和外膜(adventitia)的双层结构来研究血管壁的力学性质,构建本构模型[18, 31, 36, 49]。近来,由于多光子显微镜技术的发展,已经可视化并测量了许多组织的微观结构以辅助模型的确定和拓展[50-51]。Wang 等[36]进一步将血管壁的分层特性应用于血管壁三维现象学本构模型中。本文团队[18]通过内中膜和外膜的冲压拉伸实验,发现两层结构之间存在残余应力,内中膜承受了大部分的周向张力。
2.3. 血管壁被动力学性能建模和分析
2.3.1. 血管壁被动力学性能的本构模型分类
为了分析病变血管的力学机制以及血管在支架、人工血管等外力作用下的变化趋势,需构建符合血管壁性质的本构模型。血管壁的本构模型总体可分为现象学模型和微结构模型两大类。现象学模型认为血管壁在受力变形时的特性变化源于能量的变化,可假设血管壁具有某种形式的应变能函数,通过应变能函数导出其应力-应变的本构关系,研究血管壁的被动力学性质。现象学模型多采用指数形式或者幂函数形式表述应变能函数,能够很好地拟合应力-应变曲线,但式中参数通常没有实际的物理意义。以 Fung 模型为代表的现象学模型被引入用作血管壁的本构模型,可有效地拟合实验数据以研究血管壁的拟弹性被动力学性能[52]。Fung 模型可以写为如下形式:
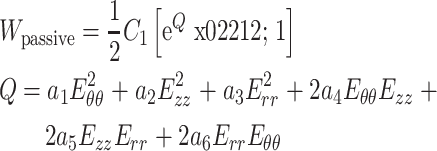 |
1 |
其中,
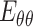 、
、
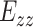 、
、
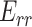 为周向、轴向、径向的格林应变,
为周向、轴向、径向的格林应变,
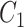 、
、
 为物质常数。以 Fung 模型为基础,其他一系列模型也用于研究血管壁被动力学性质[47, 53-56]。
为物质常数。以 Fung 模型为基础,其他一系列模型也用于研究血管壁被动力学性质[47, 53-56]。
在 1971 年,Azuma 等分析了血管壁主要成分的流变学特性,并揭示了血管壁的力学性质主要取决于血管壁微观组成成分、形态等因素。此后,多种基于血管壁微结构的本构模型相继被提出。血管壁微结构本构模型中比较有代表性的研究是 Lanir[57-58]首次提出的纤维组织流体基底型本构模型。流体基底型微结构模型认为受被动应力时,纤维组织是弹性蛋白和胶原纤维的复合物,而平滑肌细胞和其他物质则被认为是一种流体状基质。弹性蛋白和胶原蛋白均嵌入流体状基质,仅承受非流体静载荷,例如张应力和剪切力,而基质的作用是承受静载荷。这种简化意味着纤维与组织的变形相同。流体基底型微结构模型在建模时考虑了每个纤维组织的微观参数,可以很好地描述弹性纤维和胶原蛋白纤维的变形特征[59]。整体应变能函数是单个纤维应变能函数的总和,其形式写作:
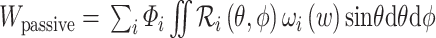 |
2 |
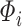 、
、
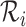 、
、
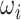 、
、
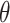 和
和
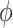 分别表示体积比、纤维方向密度函数、纤维应变能函数、分析角和极坐标角度,但其应变能函数是积分形式,限制了本构模型向有限元分析的进一步发展[39]。
分别表示体积比、纤维方向密度函数、纤维应变能函数、分析角和极坐标角度,但其应变能函数是积分形式,限制了本构模型向有限元分析的进一步发展[39]。
Holzapfel 等[46, 60]提出了固体基底型微结构本构模型。对于固体基底型模型,它将血管壁材料性能分为各向同性和各向异性两部分,认为压缩的胶原纤维是各向异性的主要来源,以增强项的形式分布于弹性纤维、平滑肌细胞、细胞基质等组成的各向同性基底项中,以此来解释超弹性力学行为[61-62],其形式如下:
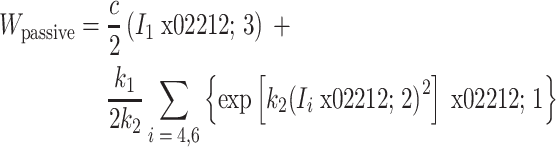 |
3 |
其中
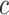 、
、
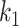 、
、
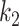 代表不同成分的材料参数,
代表不同成分的材料参数,
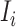 是 Cauchy-Green 张量
是 Cauchy-Green 张量
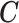 的第
的第
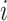 阶不变量。虽然这些参数没有实际物理意义,但是该模型考虑了血管壁成分的各向异性、非均质性以及各组分的几何特征[63]。固体基底型微结构本构模型还利用对角度分散的纤维组织进行角度积分(angular integration,AI)和广义结构张量(generalized structure tensor,GST)[64]来构建血管模型,这使得固体基底型模型在有限元方法应用方面具有很大潜力[65]。该模型也可应用于除动脉壁外的软骨、角膜和心脏瓣膜等多种组织中[23, 66-68]。现阶段,使用较多的固体基底型模型为 HGO 模型[46]。基于 HGO 模型,其他一系列模型也被用于研究血管壁被动力学性质。
阶不变量。虽然这些参数没有实际物理意义,但是该模型考虑了血管壁成分的各向异性、非均质性以及各组分的几何特征[63]。固体基底型微结构本构模型还利用对角度分散的纤维组织进行角度积分(angular integration,AI)和广义结构张量(generalized structure tensor,GST)[64]来构建血管模型,这使得固体基底型模型在有限元方法应用方面具有很大潜力[65]。该模型也可应用于除动脉壁外的软骨、角膜和心脏瓣膜等多种组织中[23, 66-68]。现阶段,使用较多的固体基底型模型为 HGO 模型[46]。基于 HGO 模型,其他一系列模型也被用于研究血管壁被动力学性质。
2.3.2. 血管壁被动力学性能分析
在诸如主动脉的弹性动脉中,弹性纤维是一层层卷曲柔性网状结构,层间有连接纤维,在高压下扩张,低压下回缩,这保证了动脉的可扩张性,弹性蛋白通常被认为是各向同性材料[7]。胶原蛋白纤维在自然组织中离散分布[69],使材料具有各向异性;其状态呈现出连续可变的波浪状结构,受力后卷曲的胶原纤维逐渐变直,有效承重的胶原蛋白质量分数随着组织拉伸的增加而增加[70],使血管壁在较高的应变条件下对抗进一步扩张,保证了血管结构完整性[71-73]。胶原蛋白具有较高的硬度,并且随年龄的增长硬度增加,血管壁的拟弹性模量增大[74]。弹性纤维、胶原蛋白纤维和细胞骨架的共同作用主导了血管壁的被动力学性能。实验观察也证实了以上的观点,认为单个弹性蛋白的本构模型是线性的,而胶原纤维的本构模型则是非线性的[75-76]。
为了更好地理解动脉血管壁的被动力学性能,Rachev 等[70]对弹性蛋白和胶原蛋白之间的相互作用进行了数学建模,提出了两种成分在自然状态下具有预拉伸比的概念。类似于血管内微观结构引起的残余应力会影响材料的力学行为[77],血管成分的预拉伸比可影响血管对外界应力应变的响应机制,即在较高的应变状态下,预拉伸比越高,动脉的变形能力越差,周向应力越低。
动脉血管壁力学环境的变化,例如压力、流速和轴向拉伸比的变化等,会引起动脉适应性反应,例如生长、萎缩和重塑。由于疾病的影响,血管壁的微观结构可能会发生明显改变,如高血压会导致动脉壁增厚;动脉粥样硬化的血管中弹性蛋白出现破碎和降解,动脉变得僵硬;衰老还会影响残余应力/应变,使得动脉节段径向切开形成的扇形的张开角增大,并且张开角在可见动脉粥样硬化的血管中更大[7]。以上变化均会引起血管壁力学性质的改变,人们为此进行了很多相关的研究。
Sáez 等[63]基于血管微结构建立了人体颈动脉的本构模型,用有限元方法重建并模拟了颈动脉硬化患者特定的颈动脉几何形状,提供了动脉变形的微观结构描述。基于 HGO 模型[46],Leng 等[78]模拟了主动脉粥样硬化斑块衰竭和撕裂的过程,利用有限元分析的方法获得了斑块撕裂路径上的界面强度和临界能量释放率,为研究动脉粥样硬化Ⅰ型撕裂的病理生理机制提供了有效工具。Ahuja 等[79]对患有主动脉夹层的猪主动脉进行双轴实验,测量了血管壁的被动力学性能,实验数据验证了 HGO 超弹性应变能函数及其本构模型的优效性,该模型可协助计算治疗主动脉夹层病变的支架所需的各项应力。为了研究动脉瘤破裂前的血管壁力学性能,Ayyalasomayajula 等[80]开发了动脉外膜胶原网络的有限元模型,基于单轴拉伸数据及多光子显微镜拍摄的胶原纤维形态学参数重建胶原网络并进行数值分析,得到在接近血管破裂的载荷下,胶原纤维的破裂可能性为 2%。
2.4. 血管壁主动力学性能建模和分析
血管被动力学模型已经被广泛地研究[17, 25, 31, 81],但与其相对的主动力学特性研究较少,血管壁主动性能的本构模型还相当匮乏。基于血管单轴力学性质测量,一些科研工作者提出了周向的主动应变能函数[24-26, 82-86]。本文团队[19]对猪冠状动脉血管进行了双轴冲压拉伸实验,利用无钙离子溶液(可以使平滑肌细胞充分舒张,血管没有主动应力)和钾离子溶液(平滑肌细胞充分收缩,主动应力最大)刺激血管,在周向和轴向上获得血管的应力-应变关系。基于实验设计和数值优化分析,确定了血管壁三轴主动应变能函数。三轴主动应变能函数可以写为:
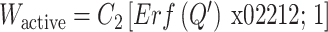 |
4 |
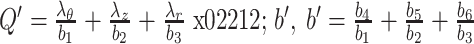 |
5 |
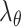 、
、
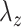 、
、
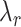 为周向、轴向、径向的应变,
为周向、轴向、径向的应变,
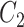 和
和
 为物质常数。本文团队[18]又进一步扩展了单层的主动和被动应变能函数为双层模式,并提出了双层血管壁力学模型来计算血管壁内的应力与应变的分布。研究发现,相对于外层,血管壁内层承受了大部分周向张应力,平滑肌细胞的主动收缩可降低所有层内的应力和应变。我们验证了三轴主动应变能函数,并且计算了双层血管壁内的应力与应变分布。研究发现,在正常生理态下相对于周向和轴向应力,血管壁径向应力可以忽略不计,但是在高血压和其他心血管疾病时,局部血管壁径向应力可以达到周向应力的一半,则必须加以考虑[87]。最近,基于小鼠肺动脉双轴拉伸实验,Ramachandra 等[88]测量了主动和被动条件下血管壁的拉伸性能,利用非线性本构关系对被动条件下的数据进行了分析,对主动力学性能也做了较为简单的分析。此外,Chen 等[50-51, 76]基于弹性纤维、胶原蛋白纤维和平滑肌细胞的微结构,提出了三维微观结构的三轴非对称本构模型,以预测血管壁宏观应力分布和估计微观下单个纤维和细胞的材料参数,是首个具有平滑肌细胞收缩功能的三维冠状动脉微结构模型,具有很高的预测性和描述性,并得到了实验数据的验证。
为物质常数。本文团队[18]又进一步扩展了单层的主动和被动应变能函数为双层模式,并提出了双层血管壁力学模型来计算血管壁内的应力与应变的分布。研究发现,相对于外层,血管壁内层承受了大部分周向张应力,平滑肌细胞的主动收缩可降低所有层内的应力和应变。我们验证了三轴主动应变能函数,并且计算了双层血管壁内的应力与应变分布。研究发现,在正常生理态下相对于周向和轴向应力,血管壁径向应力可以忽略不计,但是在高血压和其他心血管疾病时,局部血管壁径向应力可以达到周向应力的一半,则必须加以考虑[87]。最近,基于小鼠肺动脉双轴拉伸实验,Ramachandra 等[88]测量了主动和被动条件下血管壁的拉伸性能,利用非线性本构关系对被动条件下的数据进行了分析,对主动力学性能也做了较为简单的分析。此外,Chen 等[50-51, 76]基于弹性纤维、胶原蛋白纤维和平滑肌细胞的微结构,提出了三维微观结构的三轴非对称本构模型,以预测血管壁宏观应力分布和估计微观下单个纤维和细胞的材料参数,是首个具有平滑肌细胞收缩功能的三维冠状动脉微结构模型,具有很高的预测性和描述性,并得到了实验数据的验证。
平滑肌细胞内存在肌球蛋白和肌动蛋白,随着肌球蛋白网络结构的运动,肌球蛋白和肌动蛋白丝之间相对滑动。平滑肌细胞内肌丝结构和肌丝重叠现象会在血管发育、生长和重塑的过程中影响平滑肌细胞的排列方式[89],因此,肌动蛋白和肌球蛋白的细丝组织和细丝晶格间距会在平滑肌细胞变形时发生变化,从而影响其主动张力的形成[90],对维持血管张力和阻力、调节血管的主动力学性能有着决定性作用[38]。越来越多医学遗传学证据表明,平滑肌细胞对于应力的响应异常会导致动脉瘤或动脉夹层等疾病[91-94]。血管壁主动应变能函数反映了平滑肌细胞主动舒缩现象,由于平滑肌细胞的复杂微观环境、耦合力学以及化学动力学的限制,针对血管主动力学性质的研究一直被限制在现象学模型中[95-96]。
最近,Murtada 等[97]考虑了整体肌肉变形与细丝组织和晶格间距之间的关系,提出了一种新的多尺度动脉主动收缩的数学模型。该模型在研究分子、细胞和组织层面结构和功能的基础上对血管进行建模,假设动脉主动收缩时是由各向异性细胞外基质构成不可压缩的厚壁圆柱体,并将肌动蛋白丝和肌球蛋白丝之间的丝晶格间距以及肌丝重叠现象考虑在内。该模型能够很好地拟合单轴和双轴测试中得到的血管主动收缩数据,并对参数进行敏感性研究,识别平滑肌细胞的功能变化。Coccarelli 等[98]开发了一种多组分数学建模框架,包含了血管对机械刺激的主动力学反应,并对每个平滑肌细胞使用一组非线性微分方程组建模,这些方程组解释了细胞内的离子信号,特别是钙离子动力学。在一定的生理参数值范围内,解释细胞收缩的综合模型所产生的模拟结果在定性和定量上都与实验观测结果相吻合。该模型还说明了细胞间耦合的增加如何导致平滑肌协调和血管张力的形成。但直接研究疾病状态下血管壁主动力学性能变化的报道还比较少见。
3. 结论和展望
心血管疾病是需要人们长期攻坚的课题,心血管疾病如高血压、动脉粥样硬化、血管痉挛、动脉瘤等,会影响血管壁的主动和被动力学性能。深入了解动脉血管壁的力学性能可极大地提高我们对血管壁力学和血管中血流动力学的理解,为我们深入地探索血管生长和重建的病理生理机制提供生物力学新思路,并为精确地预测粥样斑块的稳定和破裂趋势提供诊断与防治依据。
然而生物体中,血管壁的结构、组成和形态随着血管环境的变化而变化,血管壁力生物学的响应机制更是十分复杂,管壁力学性能测量实验或建模计算可能无法全面表征管壁的病理生理特点,需要更深化的研究。进一步的研究需要聚焦于:第一,基于血管壁微结构模型研究动脉血管三维、双层膜结构的主动和被动力学性能。血管壁力学特性的研究不仅要考虑各组分含量,更需要去探究各成分的存在结构甚至超微结构,以及各组织结构从健康状态到患病状态的变化。截至目前,人们对于血管结构的研究仅停留在定性描述的阶段,定量分析仍相当困难,这就需要更清晰的成像技术以及三维图像处理算法。同时,可以结合临床血管内外的观测手段(如计算机断层扫描、磁共振成像、血管内超声、光学相干断层扫描等),基于微结构模型的有限元分析与患者血管特定的几何形状和结构相结合,推动计算机辅助临床诊断和干预治疗。第二,人工智能(artificial intelligence,AI)技术越来越引起社会关注,业已广泛应用于医疗图像理解、遗传编程、药物筛选等临床领域。当人工智能技术和血管壁的主动和被动力学模型相结合,可以辅助诊断各种心血管疾病,以及服务于医疗器械设计,如心血管微创介入手术机器人的优化设计。第三,现阶段血管壁软组织力学多聚焦于正常血管壁的实验测量和理论建模,针对病变血管壁的力学分析相对较少。基于现有的各种动物模型,应用多种实验技术和理论方法,结合各种人工智能手段,我们需要系统研究不同心血管疾病、不同部位血管壁的主动和被动力学特性,建立一个完善的数据库,进而服务于血管壁力学生物学机制探索和临床医疗器械的优化设计。
利益冲突声明:本文全体作者均声明不存在利益冲突。
Funding Statement
深圳市科创委孔雀团队计划(KQTD20180411143400981)
References
- 1.Hu S, Gao R, Liu L, et al Summary of the 2018 report on cardiovascular diseases in China. Chin Circul J. 2019;34(3):209–220. [Google Scholar]
- 2.Fung Y C, Cowin S C Biomechanics. Mechanical properties of living tissues. Bioviscoelastic Solids. 1994;61(4):464–465. [Google Scholar]
- 3.姜宗来 心血管生物力学研究的新进展. 医用生物力学. 2010;25(5):313–315, 351. doi: 10.3871/j.1004-7220.2010.5.315.. [DOI] [Google Scholar]
- 4.Han Y, Huang K, Yao Q P, et al Mechanobiology in vascular remodeling. Natl Sci Rev. 2018;5(6):933–946. doi: 10.1093/nsr/nwx153. [DOI] [Google Scholar]
- 5.Akintewe O O, Roberts E G, Rim N G, et al Design approaches to myocardial and vascular tissue engineering. Annu Rev Biomed Eng. 2017;19:389–414. doi: 10.1146/annurev-bioeng-071516-044641. [DOI] [PubMed] [Google Scholar]
- 6.Sotomi Y, Onuma Y, Collet C, et al Bioresorbable scaffold: The emerging reality and future directions. Circ Res. 2017;120(8):1341–1352. doi: 10.1161/CIRCRESAHA.117.310275. [DOI] [PubMed] [Google Scholar]
- 7.Holzapfel G A, Ogden R W Biomechanical relevance of the microstructure in artery walls with a focus on passive and active components. Am J Physiol Heart Circ Physiol. 2018;315(3):H540–H549. doi: 10.1152/ajpheart.00117.2018. [DOI] [PubMed] [Google Scholar]
- 8.Konidala S, Gutterman D D Coronary vasospasm and the regulation of coronary blood flow. Prog Cardiovasc Dis. 2004;46(4):349–373. doi: 10.1016/j.pcad.2003.10.001. [DOI] [PubMed] [Google Scholar]
- 9.Mulvany M J, Halpern W Contractile properties of small arterial resistance vessels in spontaneously hypertensive and normotensive rats. Circ Res. 1977;41(1):19–26. doi: 10.1161/01.RES.41.1.19. [DOI] [PubMed] [Google Scholar]
- 10.Young M A, Vatner S F Regulation of large coronary arteries. Circ Res. 1986;59(6):579–596. doi: 10.1161/01.RES.59.6.579. [DOI] [PubMed] [Google Scholar]
- 11.Landmesser U, Hornig B, Drexler H. Endothelial function: A critical determinant in atherosclerosis?. Circulation, 2004, 109(21 Suppl 1): II27-1133.
- 12.Pahlavan P S, Niroomand F Coronary artery aneurysm: A review. Clin Cardiol. 2006;29(10):439–443. doi: 10.1002/clc.4960291005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lu X, Bean J S, Kassab G S, et al Protein kinase c inhibition ameliorates functional endothelial insulin resistance and vascular smooth muscle cell hypersensitivity to insulin in diabetic hypertensive rats. Cardiovasc Diabetol. 2011;10:48. doi: 10.1186/1475-2840-10-48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim J, Wagenseil J E Bio-chemo-mechanical models of vascular mechanics. Ann Biomed Eng. 2015;43(7):1477–1487. doi: 10.1007/s10439-014-1201-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen H, Kassab G S Microstructure-based biomechanics of coronary arteries in health and disease. J Biomech. 2016;49(12):2548–2559. doi: 10.1016/j.jbiomech.2016.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gasser T C. Vascular tissue biomechanics: Constitutive modeling of the arterial wall. 2019.
- 17.Humphrey J D. Cardiovascular solid mechanics. New York: Springer-Verlag, 2002.
- 18.Huo Y, Zhao X, Cheng Y, et al Two-layer model of coronary artery vasoactivity. J Appl Physiol. 2013;114(10):1451–1459. doi: 10.1152/japplphysiol.01237.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huo Y, Cheng Y, Zhao X, et al Biaxial vasoactivity of porcine coronary artery. Am J Physiol Heart Circ Physiol. 2012;302(10):H2058–2063. doi: 10.1152/ajpheart.00758.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lu X, Kassab G S Vasoactivity of blood vessels using a novel isovolumic myograph. Ann Biomed Eng. 2007;35(3):356–366. doi: 10.1007/s10439-006-9243-0. [DOI] [PubMed] [Google Scholar]
- 21.Carpenter H J, Gholipour A, Ghayesh M H, et al A review on the biomechanics of coronary arteries. Int J Eng Sci. 2020;147:103201. doi: 10.1016/j.ijengsci.2019.103201. [DOI] [Google Scholar]
- 22.Holzapfel G A, Niestrawska J A, Ogden R W, et al Modelling non-symmetric collagen fibre dispersion in arterial walls. J R Soc Interface. 2015;12(106):20150188. doi: 10.1098/rsif.2015.0188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Holzapfel G A, Ogden R W Modelling the layer-specific three-dimensional residual stresses in arteries, with an application to the human aorta. J R Soc Interface. 2010;7(46):787–799. doi: 10.1098/rsif.2009.0357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rachev A, Hayashi K Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions in arteries. Ann Biomed Eng. 1999;27(4):459–468. doi: 10.1114/1.191. [DOI] [PubMed] [Google Scholar]
- 25.Carlson B E, Secomb T W A theoretical model for the myogenic response based on the length-tension characteristics of vascular smooth muscle. Microcirculation. 2005;12(4):327–338. doi: 10.1080/10739680590934745. [DOI] [PubMed] [Google Scholar]
- 26.Yang J, Clark J W Jr., Bryan R M, et al The myogenic response in isolated rat cerebrovascular arteries: Vessel model. Med Eng Phys. 2003;25(8):711–717. doi: 10.1016/S1350-4533(03)00101-2. [DOI] [PubMed] [Google Scholar]
- 27.Holzapfel G A, Ogden R W An arterial constitutive model accounting for collagen content and cross-linking. J Mech Phys Solids. 2019;136:103682. [Google Scholar]
- 28.Niestrawska J A, Viertler C, Regitnig P, et al Microstructure and mechanics of healthy and aneurysmatic abdominal aortas: Experimental analysis and modelling. J R Soc Interface. 2016;13(124):20160620. doi: 10.1098/rsif.2016.0620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wagner H P, Humphrey J D Differential passive and active biaxial mechanical behaviors of muscular and elastic arteries: Basilar versus common carotid. J Biomech Eng. 2011;133(5):051009. doi: 10.1115/1.4003873. [DOI] [PubMed] [Google Scholar]
- 30.Stalhand J A, Klarbring G A, Holzapfel A A mechanochemical 3D continuum model for smooth muscle contraction under finite strains. J Theor Biol. 2011;268(1):120–130. doi: 10.1016/j.jtbi.2010.10.008. [DOI] [PubMed] [Google Scholar]
- 31.Lu X, Pandit A, Kassab G S Biaxial incremental homeostatic elastic moduli of coronary artery: Two-layer model. Am J Physiol Heart Circ Physiol. 2004;287(4):H1663–H1669. doi: 10.1152/ajpheart.00226.2004. [DOI] [PubMed] [Google Scholar]
- 32.Hayman D M, Zhang J, Liu Q, et al Smooth muscle cell contraction increases the critical buckling pressure of arteries. J Biomech. 2013;46(4):841–844. doi: 10.1016/j.jbiomech.2012.11.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Murtada S I, Ferruzzi J, Yanagisawa H, et al Reduced biaxial contractility in the descending thoracic aorta of fibulin-5 deficient mice. J Biomech Eng. 2016;138(5):051008. doi: 10.1115/1.4032938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Takamizawa K. Biaxial contractile mechanics of common carotid arteries of rabbit. J Biomech Eng, 2015, 137(3). DOI: 10.1115/1.4028988.
- 35.Caulk A W, Humphrey J D, Murtada S I Fundamental roles of axial stretch in isometric and isobaric evaluations of vascular contractility. J Biomech Eng. 2019;141(3):0310081–03100810. doi: 10.1115/1.4042171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang C, Garcia M, Lu X, et al Three-dimensional mechanical properties of porcine coronary arteries: A validated two-layer model. Am J Physiol Heart Circ Physiol. 2006;291(3):H1200–H1209. doi: 10.1152/ajpheart.01323.2005. [DOI] [PubMed] [Google Scholar]
- 37.Luo T, Chen H, Kassab G S 3D reconstruction of coronary artery vascular smooth muscle cells. PLoS One. 2016;11(2):e0147272. doi: 10.1371/journal.pone.0147272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sommer G, Regitnig P, Költringer L, et al Biaxial mechanical properties of intact and layer-dissected human carotid arteries at physiological and supraphysiological loadings. Am J Physiol-Heart C. 2010;298(3):H898–H912. doi: 10.1152/ajpheart.00378.2009. [DOI] [PubMed] [Google Scholar]
- 39.Hollander Y, Durban D, Lu X, et al Experimentally validated microstructural 3D constitutive model of coronary arterial media. J Biomech Eng. 2011;133(3):031007. doi: 10.1115/1.4003324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chen H, Guo X, Luo T, et al A validated 3D microstructure-based constitutive model of coronary artery adventitia. J Appl Physiol. 2016;121(1):333–342. doi: 10.1152/japplphysiol.00937.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sommer G, Benedikt C, Niestrawska J A, et al Mechanical response of human subclavian and iliac arteries to extension, inflation and torsion. Acta Biomater. 2018;75:235–252. doi: 10.1016/j.actbio.2018.05.043. [DOI] [PubMed] [Google Scholar]
- 42.Chen H, Kassab G S Microstructure-based constitutive model of coronary artery with active smooth muscle contraction. Sci Rep. 2017;7(1):9339. doi: 10.1038/s41598-017-08748-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ambrosi D, Ben Amar M, Cyron C J, et al Growth and remodelling of living tissues: Perspectives, challenges and opportunities. J R Soc Interface. 2019;16(157):20190233. doi: 10.1098/rsif.2019.0233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Valdez-Jasso D, Bia D, Zocalo Y, et al Linear and nonlinear viscoelastic modeling of aorta and carotid pressure-area dynamics under in vivo and ex vivo conditions . Ann Biomed Eng. 2011;39(5):1438–1456. doi: 10.1007/s10439-010-0236-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Amabili M, Balasubramanian P, Bozzo I, et al Layer-specific hyperelastic and viscoelastic characterization of human descending thoracic aortas. J Mech Behav Biomed Mater. 2019;99:27–46. doi: 10.1016/j.jmbbm.2019.07.008. [DOI] [PubMed] [Google Scholar]
- 46.Holzapfel G A, Ogden R W On the tension-compression switch in soft fibrous solids. Eur J Mech A/Solid. 2015;49:561–569. doi: 10.1016/j.euromechsol.2014.09.005. [DOI] [Google Scholar]
- 47.Zhang W, Liu Y, Kassab G S Viscoelasticity reduces the dynamic stresses and strains in the vessel wall: Implications for vessel fatigue. Am J Physiol Heart Circ Physiol. 2007;293(4):H2355–H2360. doi: 10.1152/ajpheart.00423.2007. [DOI] [PubMed] [Google Scholar]
- 48.Bauer M, Morales-Orcajo E, Klemm L, et al Biomechanical and microstructural characterisation of the porcine stomach wall: Location- and layer-dependent investigations. Acta Biomater. 2019;102:83–99. doi: 10.1016/j.actbio.2019.11.038. [DOI] [PubMed] [Google Scholar]
- 49.Pandit A, Lu X, Wang C, et al Biaxial elastic material properties of porcine coronary media and adventitia. Am J Physiol Heart Circ Physiol. 2005;288(6):H2581–H2587. doi: 10.1152/ajpheart.00648.2004. [DOI] [PubMed] [Google Scholar]
- 50.Chen H, Slipchenko M N, Liu Y, et al Biaxial deformation of collagen and elastin fibers in coronary adventitia. J Appl Physiol. 2013;115(11):1683–1693. doi: 10.1152/japplphysiol.00601.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chen H, Luo T, Zhao X, et al Microstructural constitutive model of active coronary media. Biomaterials. 2013;34(31):7575–7583. doi: 10.1016/j.biomaterials.2013.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Fung Y C, Fronek K, Patitucci P Pseudoelasticity of arteries and the choice of its mathematical expression. Am J Physiol. 1979;237(5):H620–H631. doi: 10.1152/ajpheart.1979.237.5.H620. [DOI] [PubMed] [Google Scholar]
- 53.Zhang W, Lu X, Kassab G S Shear modulus of porcine coronary artery in reference to a new strain measure. Biomaterials. 2007;28(31):4733–4738. doi: 10.1016/j.biomaterials.2007.07.025. [DOI] [PubMed] [Google Scholar]
- 54.Zhang W, Chen H Y, Kassab G S A rate-insensitive linear viscoelastic model for soft tissues. Biomaterials. 2007;28(24):3579–3586. doi: 10.1016/j.biomaterials.2007.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang W, Kassab G S A bilinear stress-strain relationship for arteries. Biomaterials. 2007;28(6):1307–1315. doi: 10.1016/j.biomaterials.2006.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhang W, Wang C, Kassab G S The mathematical formulation of a generalized Hooke’s law for blood vessels. Biomaterials. 2007;28(24):3569–3578. doi: 10.1016/j.biomaterials.2007.04.030. [DOI] [PubMed] [Google Scholar]
- 57.Lanir Y Constitutive equations for fibrous connective tissues. J Biomech. 1983;16(1):1–12. doi: 10.1016/0021-9290(83)90041-6. [DOI] [PubMed] [Google Scholar]
- 58.Lanir Y A structural theory for the homogeneous biaxial stress-strain relationships in flat collagenous tissues. J Biomech. 1979;12(6):423–436. doi: 10.1016/0021-9290(79)90027-7. [DOI] [PubMed] [Google Scholar]
- 59.Humphrey J D, Yin F C A new constitutive formulation for characterizing the mechanical behavior of soft tissues. Biophys J. 1987;52(4):563–570. doi: 10.1016/S0006-3495(87)83245-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Holzapfel G A, Gasser T C, Ogden R W A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast. 2000;61(1-3):1–48. [Google Scholar]
- 61.Holzapfel G A, Gasser T C, Stadler M A structural model for the viscoelastic behavior of arterial walls: Continuum formulation and finite element analysis. Eur J Mech A/Solid. 2002;21(3):441–463. doi: 10.1016/S0997-7538(01)01206-2. [DOI] [Google Scholar]
- 62.Gasser T C, Ogden R W, Holzapfel G A Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sáez P, Peña E, Martínez M A A structural approach including the behavior of collagen cross-links to model patient-specific human carotid arteries. Ann Biomed Eng. 2014;42(6):1158–1169. doi: 10.1007/s10439-014-0995-7. [DOI] [PubMed] [Google Scholar]
- 64.Holzapfel G A, Ogden R W Comparison of two model frameworks for fiber dispersion in the elasticity of soft biological tissues. Eur J Mech A/Solids. 2017;66:193–200. doi: 10.1016/j.euromechsol.2017.07.005. [DOI] [Google Scholar]
- 65.Li K, Ogden R W, Holzapfel G A Computational method for excluding fibers under compression in modeling soft fibrous solids. Eur J Mech. 2016;57:178–193. doi: 10.1016/j.euromechsol.2015.11.003. [DOI] [Google Scholar]
- 66.Bevan J A, Hwa J J Myogenic tone and cerebral vascular autoregulation: The role of a stretch-dependent mechanism. Ann Biomed Eng. 1985;13(3-4):281–286. doi: 10.1007/BF02584245. [DOI] [PubMed] [Google Scholar]
- 67.Holzapfel G A, Ogden R W, Sherifova S On fibre dispersion modelling of soft biological tissues: A review. Proc Math Phys Eng Sci. 2019;475:2224. doi: 10.1098/rspa.2018.0736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Holzapfel G A, Gasser T C Computational stress-deformation analysis of arterial walls including high-pressure response. Int J Cardiol. 2007;116(1):78–85. doi: 10.1016/j.ijcard.2006.03.033. [DOI] [PubMed] [Google Scholar]
- 69.Li K, Ogden R W, Holzapfel G A A discrete fibre dispersion method for excluding fibres under compression in the modelling of fibrous tissues. J R Soc Interface. 2018;15(138):20170766. doi: 10.1098/rsif.2017.0766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rachev A, Shazly T A structure-based constitutive model of arterial tissue considering individual natural configurations of elastin and collagen. J Mech Behav Biomed Mater. 2019;90:61–72. doi: 10.1016/j.jmbbm.2018.09.047. [DOI] [PubMed] [Google Scholar]
- 71.Wang Y, Zeinali-Davarani S, Zhang Y Arterial mechanics considering the structural and mechanical contributions of ECM constituents. J Biomech. 2016;49(12):2358–2365. doi: 10.1016/j.jbiomech.2016.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Carboni M, Desch G W, Weizsacker H W Passive mechanical properties of porcine left circumflex artery and its mathematical description. Med Eng Phys. 2007;29(1):8–16. doi: 10.1016/j.medengphy.2006.01.004. [DOI] [PubMed] [Google Scholar]
- 73.Humphrey J D. Cardiovascular solid mechanics: Cells, tissues, and organs. Springer Science & Business Media, 2013.
- 74.Hayashi K, Hirayama E Age-related changes of wall composition and collagen cross-linking in the rat carotid artery – in relation with arterial mechanics. J Mech Behav Biomed Mater. 2017;65:881–889. doi: 10.1016/j.jmbbm.2016.10.007. [DOI] [PubMed] [Google Scholar]
- 75.Annovazzi L, Genna F An engineering, multiscale constitutive model for fiber-forming collagen in tension. J Biomed Mater Res A. 2010;92A(1):254–266. doi: 10.1002/jbm.a.32352. [DOI] [PubMed] [Google Scholar]
- 76.Chen H, Liu Y, Zhao X, et al A micromechanics finite-strain constitutive model of fibrous tissue. J Mech Phys Solids. 2011;59(9):1823–1837. doi: 10.1016/j.jmps.2011.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Sigaeva T, Sommer G, Holzapfel G, et al Anisotropic residual stresses in arteries. J R Soc Interface. 2019;16(151):20190029. doi: 10.1098/rsif.2019.0029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Leng X, Davis L, Deng X, et al. An inverse analysis of cohesive zone model parameter values for human fibrous cap mode I tearing. arXiv, 2018: 1806.05013.
- 79.Ahuja A, Noblet J N, Trudnowski T, et al Biomechanical material characterization of stanford type-B dissected porcine aortas. Front Physiol. 2018;9:1317. doi: 10.3389/fphys.2018.01317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Ayyalasomayajula V, Pierrat B, Badel P A computational model for understanding the micro-mechanics of collagen fiber network in the tunica adventitia. Biomech Model Mechanobiol. 2019;18(5):1507–1528. doi: 10.1007/s10237-019-01161-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Lee Y U, Naito Y, Kurobe H, et al Biaxial mechanical properties of the inferior vena cava in C57BL/6 and CB-17 SCID/bg mice. J Biomech. 2013;46(13):2277–2282. doi: 10.1016/j.jbiomech.2013.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Cornelissen A J, Dankelman J, Vanbavel E, et al Balance between myogenic, flow-dependent, and metabolic flow control in coronary arterial tree: A model study. Am J Physiol Heart Circ Physiol. 2002;282(6):H2224–H2237. doi: 10.1152/ajpheart.00491.2001. [DOI] [PubMed] [Google Scholar]
- 83.Yang J, Clark J W Jr, Bryan R M, et al The myogenic response in isolated rat cerebrovascular arteries: Smooth muscle cell model. Med Eng Phys. 1002;14(7):691–709. doi: 10.1016/s1350-4533(03)00100-0. [DOI] [PubMed] [Google Scholar]
- 84.Algranati D, Kassab G S, Lanir Y Flow restoration post revascularization predicted by stenosis indexes: Sensitivity to hemodynamic variability. Am J Physiol Heart Circ Physiol. 2013;305(2):H145–H154. doi: 10.1152/ajpheart.00061.2012. [DOI] [PubMed] [Google Scholar]
- 85.Algranati D, Kassab G S, Lanir Y Why is the subendocardium more vulnerable to ischemia? A new paradigm. Am J Physiol Heart Circ Physiol. 2011;300(3):H1090–H1100. doi: 10.1152/ajpheart.00473.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Algranati D, Kassab G S, Lanir Y Mechanisms of myocardium-coronary vessel interaction. Am J Physiol Heart Circ Physiol. 2010;298(3):H861–H873. doi: 10.1152/ajpheart.00925.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lu Y, Wu H, Li J, et al Passive and active triaxial wall mechanics in a two-layer model of porcine coronary artery. Sci Rep. 2017;7(1):13911. doi: 10.1038/s41598-017-14276-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Ramachandra A B, Humphrey J D Biomechanical characterization of murine pulmonary arteries. J Biomech. 2019;84:18–26. doi: 10.1016/j.jbiomech.2018.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Haspinger D C, Murtada S L, Niestrawska J A, et al Numerical analyses of the interrelation between extracellular smooth muscle orientation and intracellular filament overlap in the human abdominal aorta. ZAMM. 2018;98(12):2198–2221. doi: 10.1002/zamm.201800113. [DOI] [Google Scholar]
- 90.Millman B M The filament lattice of striated muscle. Physiol Rev. 1998;78(2):359–391. doi: 10.1152/physrev.1998.78.2.359. [DOI] [PubMed] [Google Scholar]
- 91.Milewicz D M, Trybus K M, Guo D C, et al Altered smooth muscle cell force generation as a driver of thoracic aortic aneurysms and dissections. Arterioscler Thromb Vasc Biol. 2017;37(1):26–34. doi: 10.1161/ATVBAHA.116.303229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Chen P Y, Qin L, Li G, et al Smooth muscle cell reprogramming in aortic aneurysms. Cell Stem Cell. 2020;26(4):542–557. doi: 10.1016/j.stem.2020.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Fan T, Zhou Z, Fang W, et al Morphometry and hemodynamics of coronary artery aneurysms caused by atherosclerosis. Atherosclerosis. 2019;284:187–193. doi: 10.1016/j.atherosclerosis.2019.03.001. [DOI] [PubMed] [Google Scholar]
- 94.Huang X, Liu D, Yin X, et al Morphometry and hemodynamics of posterior communicating artery aneurysms: Ruptured versus unruptured. J Biomech. 2018;76:35–44. doi: 10.1016/j.jbiomech.2018.05.019. [DOI] [PubMed] [Google Scholar]
- 95.Lu D, Kassab G S Role of shear stress and stretch in vascular mechanobiology. J R Soc Interface. 2011;8(63):1379–1385. doi: 10.1098/rsif.2011.0177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Kassab G S, Navia J A Biomechanical considerations in the design of graft: The homeostasis hypothesis. Annu Rev Biomed Eng. 2006;8:499–535. doi: 10.1146/annurev.bioeng.8.010506.105023. [DOI] [PubMed] [Google Scholar]
- 97.Murtada S I, Humphrey J D, Holzapfel G A Multiscale and multiaxial mechanics of vascular smooth muscle. Biophys J. 2017;113(3):714–727. doi: 10.1016/j.bpj.2017.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Coccarelli A, Edwards D H, Aggarwal A, et al A multiscale active structural model of the arterial wall accounting for smooth muscle dynamics. J R Soc Interface. 2018;15(139):20170732. doi: 10.1098/rsif.2017.0732. [DOI] [PMC free article] [PubMed] [Google Scholar]