基于脑网络参数优化的青少年抑郁症患者与健康人群分类识别研究

Abstract

To enhance the accuracy of computer-aided diagnosis of adolescent depression based on electroencephalogram signals, this study collected signals of 32 female adolescents (16 depressed and 16 healthy, age: 16.3 ± 1.3) with eyes colsed for 4 min in a resting state. First, based on the phase synchronization between the signals, the phase-locked value (PLV) method was used to calculate brain functional connectivity in the θ and α frequency bands, respectively. Then based on the graph theory method, the network parameters, such as strength of the weighted network, average characteristic path length, and average clustering coefficient, were calculated separately (P < 0.05). Next, using the relationship between multiple thresholds and network parameters, the area under the curve (AUC) of each network parameter was extracted as new features ( P < 0.05). Finally, support vector machine (SVM) was used to classify the two groups with the network parameters and their AUC as features. The study results show that with strength, average characteristic path length, and average clustering coefficient as features, the classification accuracy in the θ band is increased from 69% to 71%, 66% to 77%, and 50% to 68%, respectively. In the α band, the accuracy is increased from 72% to 79%, 69% to 82%, and 65% to 75%, respectively. And from overall view, when AUC of network parameters was used as a feature in the α band, the classification accuracy is improved compared to the network parameter feature. In the θ band, only the AUC of average clustering coefficient was applied to classification, and the accuracy is improved by 17.6%. The study proved that based on graph theory, the method of feature optimization of brain function network could provide some theoretical support for the computer-aided diagnosis of adolescent depression.

引言

根据世界卫生组织 2017 年的调查报告，全球已有 3.2 亿抑郁症患者，其中青少年抑郁症患者占比 7%^[1]，并且呈现逐年增多的趋势，因此针对青少年抑郁症患者及时诊断的相关研究也受到了越来越多的重视。脑电图（electroencephalogram，EEG）作为一种辅助诊断的工具，可以反映大脑的功能性变化^[2]。通过对 EEG 信号构建脑网络并进行图论量化分析，能在临床上辅助诊断抑郁症^[3]，但是计算机辅助诊断青少年抑郁症，目前仍存在理论测试的精度较高而实际测试时精度不稳的问题^[4]。

如今，随着社交网络思维方法的引入，通过信号间关系构建脑网络进行数据分析已经成为研究热点。目前，已有多个研究发现了抑郁症患者其脑功能连接受损的情况^[5-6]，如 Li 等^[7]利用同步性指标研究抑郁症患者的脑功能连接变化，发现额叶/前额相位延迟滞后指数的增加与大脑的认知补偿机制有关。Lee 等^[8]研究了吸毒且重度抑郁症青少年在静息态下的脑功能连接，研究结果发现，前肢环路异常可能是青春期抑郁症的特征之一。随着脑网络构建和数据分析方法的兴起，基于图论的方法研究计算网络参数已应用于各个研究领域。Guo 等^[9]研究了核磁环境下抑郁症患者的静息态脑功能网络，结果发现抑郁组和对照组均表现出典型的小世界特征。美国密苏里大学的 Shim 等^[10]研究了抑郁症患者在静息态下功能连接的改变，发现大脑功能网络指数的紊乱可能反映了抑郁症患者情绪处理的改变，而网络参数则可作为有效的生物学指标。因此基于以上研究，本研究拟将网络参数作为特征，通过对其进行对比分析，从而实现对青少年抑郁症患者和健康者进行分类。

此前，机器学习已广泛应用于与抑郁症相关的分类研究中。如 Mumtaz 等^[11]以 EEG 频带功率为特征，使用决策树方法进行分类，准确率可达 80%。Alkaysi 等^[12]利用极限学习机直接对抑郁症患者与健康人的脑电信号进行分类，精度达到 92%。Mumtaz 等^[13]采集了抑郁症患者在静息态下的脑电数据，分别使用小波变换、短时傅里叶变换和经验模式分解提取特征，然后采用逻辑回归模型进行分类并对比分析，结果发现，利用小波变换所提取的特征分类精度最高，达到 87.5%。因此基于以上相关研究，本研究拟采用机器学习对所提取的特征进行分类。

为了尽可能地提高分类精度，本研究提出了基于脑功能网络参数的特征优化方法。首先，分别采集了 16 名女性青少年抑郁患者和 16 名女性青少年健康受试者在静息态下 4 min 的 EEG 信号，经过预处理后，将信号分为 80 个试次。然后，通过相位锁定指数（phase locking value，PLV）计算邻接矩阵，进一步构建脑功能网络，同时，利用比例阈值对全局网络参数进行优化，即提取脑网络参数的曲线下面积（area under curve，AUC）作为特征。最后，分别利用优化前后的网络参数作为特征进行分类，并对比分析。结果表明，采用优化后的网络参数作为特征，分类精度均有所提升，且利用 α 频段下的平均特征路径长度的 AUC 进行分类，精度最高，可达 82%。本研究通过优化网络参数，不仅能够有效地从全局角度分析脑功能网络，而且对提升未来临床诊断的准确率也具有重要意义。

1. 相位锁定指数和图论分析

1.1. 相位锁定指数

PLV 是测量两个信号段之间同步性的方法^[7]。该方法适用于对重复刺激的响应，并在不同的试次中，寻找两个信号之间相位差变化较小的延迟。假设给定两个信号序列 x，y 和感兴趣频率 f，计算信号 x 和 y 的每个延迟在频率 f 处的 PLV，其步骤如下：

（1）对信号进行带通滤波。

（2）对滤波后的信号以频率 f 为中心进行伽柏小波卷积，卷积算子如式（1）所示：

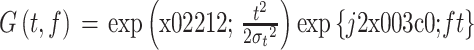1

其中， 为 7/f，t 为信号序列对应的时间。

（3）在 t 时刻，计算信号间的 PLV 值（以符号 PLV 表示），如式（2）所示：

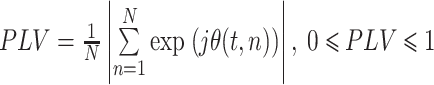2

其中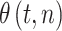， 代表了两个信号的相位差值 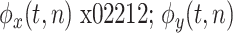，而 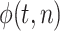是从所有时间 t 中所提取出的卷积相位，n 代表了试次数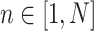， ，本研究中将信号分为 80 个试次，因此 N 取值为 80。如果在某一试次中两个信号的相位差值变化很小，那么 PLV 的值就越接近于 1，反之，其值越接近于 0。

1.2. 网络参数计算

本研究使用图论量化脑网络，其中，脑网络由边和节点组成。由于本研究使用 64 导脑电帽采集信号，将每个导联看作 1 个节点，故共有 64 个节点，节点之间相连的支路即为边。在加权网络中，PLV 的值则代表网络节点间的连接强度。在图论中，通常采用强度、平均特征路径长度、平均聚类系数等参数作为量化指标，因此本文使用如下三种网络参数进行研究与分析。

1.2.1. 强度

强度表示网络节点间的相关程度。强度值越高，意味着整个大脑的连接越紧密。通常，连接强度值是根据网络中所有节点间的连接权重之和来估计的，网络强度 S 的计算方式如式（3）所示：

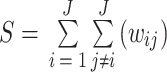3

其中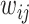， 为邻接矩阵中第 i 行和第 j 列的元素。

1.2.2. 平均特征路径长度

平均特征路径长度是所有网络节点间最短路径长度的平均值，常用其对宏观网络的特性进行研究与分析。平均特征路径长度 L_w 的计算如式（4）所示：

4

在加权网络中，最短路径长度通常为两个节点间边的权重的倒数。式中，J 为加权网络中的节点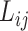， 为任意两个节点 i 和 j 最短路径的边数。

1.2.3. 平均聚类系数

平均聚类系数可用于表征网络的集团化程度。在加权网络中，如果节点 i 的度为 3，聚类系数则定义为这 3 个节点之间实际存在的边数与可能存在的所有边数之比，因此，节点 i 的聚类系数 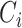的计算如式（5）所示：

5

其中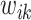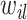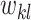， 、 、 为邻接矩阵中的元素，代表连接权重。最终，根据节点总数对所得 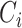求均值，可得到平均聚类系数 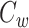，如式（6）所示。

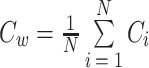6

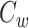的值越接近 1，则代表网络的连接程度越紧密；其值越接近于 0，则表明连接程度越松散，甚至可能存在多个节点互不相连。

2. 脑电数据采集和分析

2.1. 受试者数据来源

所有受试者均在常州市第一人民医院经过临床诊断，被分为抑郁青少年和健康青少年。通过对数据进行筛选，参与本研究的数据选取受试者均为女性，有抑郁青少年 16 例，设为抑郁组；健康青少年 16 例，设为对照组；年均（16.3 ± 1.3）岁，抑郁组和对照组之间的年龄差异无统计学意义（P > 0.05）。在试验前，受试者均使用汉密顿抑郁量表（Hamilton depression rating scales，HDRS）进行检测 ^[14]，结果显示抑郁组得分高于对照组。两组青少年的试验研究均已通过常州市第一人民医院伦理委员会批准，所有受试者或其监护人都签署了知情同意书，自愿参加本试验。

2.2. 数据采集及试验过程

本次试验采用 64 导联 EEG 采集系统（GES300，Electrical Geodesics Inc，美国），脑电帽的电极位置分布如图 1 所示。试验中，采样频率设置为 500 Hz，电极阻抗设定在 50 kΩ 以下，利用采集软件 Net Station 4.5（Electrical Geodesics Inc，美国）记录数据，带通滤波为 0.5～40 Hz，参考电极为 Cz。试验采集了受试者们在静息闭眼状态下的 EEG 数据，时长约 4 min，整个采集过程保持安静。

图 1.

64 channel electrode position

64 导联电极位置

2.3. 数据处理

2.3.1. 数据预处理

本研究使用数据处理分析软件 Matlab 2016a（Math Work Inc，美国）对所采集的数据进行预处理，具体步骤包括：带通滤波（0.5～40 Hz）、伪迹检测、坏导联替换、参考点转换，并使用独立成分分析（independent component analysis，ICA）去除眼动伪迹以及其他噪声。对预处理后的数据，每 3 s 进行一次分段，并将每段作为 1 个试次，因此构建了共计 80 个试次的三维矩阵（维度：64 × 500 × 80）。

2.3.2. 频段的选择

通常，对 EEG 数据的研究集中在 0～70 Hz 之间，其中涵盖了 δ、θ、α、β、γ 频段。在先前的研究中，通过不同的同步性测量方法，发现脑功能连接在 θ 和 α 频段处出现了断裂^[10]。该结果表明，在这两个频段中，很可能存在关于脑网络的有效特征。因此，本次研究主要定位于 θ、α 频段。

2.4. 脑功能网络

2.4.1. 脑功能网络构建

本研究利用 PLV 构建了大脑功能网络，功能网络的构建与社交网络类似，是根据两个信号之间的相位，计算其同步性，通过同步性直观地反映网络强度，为后续的分类研究打下理论基础。

2.4.2. 图论分析

构建脑功能网络后，需要对其进行量化。本研究通过图论参数来表征网络特性，分别在单一阈值下以及多重阈值下，计算了强度、平均聚类系数和平均特征路径长度。

2.4.3. 网络参数优化

本研究使用了 PLV 计算邻接矩阵并构建脑功能网络，分别计算了 64 导联 EEG 信号的 PLV 值。然而，对网络的分析涉及阈值的选择，目前较为常见的选择方法有两种：一种是根据所有受试者的整体情况逐渐增大阈值，从而进行选择；另一种是将网络中确定存在的边数与理论存在的边数之比作为阈值。本研究基于加权邻接矩阵，对网络中的所有连接强度值进行降序排列，按照一定比例选出较大的强度值。为了在增益和损耗条件下保证最佳的网络连接性，本研究对每个受试者的脑功能网络进行阈值分析并比较，以 0.01 为步长，在 0.01～0.80 范围内确定最佳阈值。

比例阈值选取的核心是先对邻接矩阵右上角的权值进行升序排列，并记录下对应的矩阵位置，计算出此时需要的最高项系数。根据最高项系数调节比例阈值，确定所需要保留的 PLV 值^[15]。

当比例阈值取 0.04 时，本研究计算发现 θ 和 α 频段的网络参数差异具有统计学意义（P < 0.05）。但是，单个比例阈值无法反映宏观的网络参数变化，当阈值不同时，网络参数的值也存在差异。为了更好地优化网络参数，本研究采用计算网络参数的 AUC 作为优化方案。由于一个阈值就对应一个网络参数值，因此共计算了 79 组网络参数值，构建了多重阈值和网络参数值之间的关系图，并算出每个网络参数的 AUC。

3. 结果

3.1. 功能连接性结果

为了构建脑功能网络，先计算了抑郁组和对照组在 θ 和 α 频段处的脑功能连接，其邻接矩阵分别如图 2、图 3 所示。PLV 的取值介于 0～1，其值越接近 1，则说明信号之间的同步性就越强。由图 2、图 3 可知，α 频段的连接强度明显高于 θ 频段，同时，抑郁组比对照组呈现更大的连接强度。

图 2.

Average adjacency matrix of two groups of subjects in θ band

θ 频段两组受试者的平均邻接矩阵图

图 3.

Average adjacency matrix of two groups of subjects in α band

α 频段两组受试者的平均邻接矩阵图

为了更好地反映大脑之间连接的紧密程度，根据邻接矩阵进一步构建脑网络。如图 4 和图 5 所示，在脑网络拓扑图中，每个节点能量的大小（标准化为 ［0，1］）代表该节点与其他节点连接的密集程度，而节点间的连接强度则使用线条的粗细和颜色的深浅来表示，线条越粗，颜色越深，代表着连接强度越大。图 4 表明在 θ 频段，抑郁组的大脑连接紧密度较为均衡，而对照组大脑右半球的连接紧密程度比左半球要高。而图 5 的结果显示，在 α 频段，对照组在大脑右侧的连接强度高于抑郁组，而抑郁组在左颞区的连接紧密度高于对照组。

图 4.

The brain network topology of the two groups of subjects in θ band

θ 频段两组受试者的脑网络拓扑图

图 5.

The brain network topology of the two groups of subjects in α band

α 频段两组受试者的脑网络拓扑图

3.2. 特征提取

3.2.1. 网络参数结果

本研究分别计算了最佳比例阈值为 0.04 时，在 θ 频段和 α 频段处的强度、平均特征路径长度和平均聚类系数，个体网络参数共计 32 个（抑郁组 16 个，对照组 16 个），分别如图 6、图 7、图 8 所示。

图 6.

Strength values of each subject in θ and α frequency band

θ 和 α 频段两组各受试者强度值

图 7.

Average characteristic path length value of each subject in θ and α frequency band

θ 和 α 频段各受试者平均特征路径长度值

图 8.

Average clustering coefficient of each subject in θ and α frequency band

θ 和 α 频段各受试者平均聚类系数

为了能够更直观地展现网络的特征，本研究除了使用图论进行量化，将强度、平均特征路径长度和平均聚类系数作为评估网络的指标，还分别计算了 32 个受试者的网络参数的均值 ± 标准差，如表 1 所示。

表 1. Network parameter calculation results of depression group and control group（ ） .

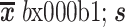抑郁组和对照组的网络参数计算结果（ ）

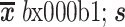分组	θ 频段				α 频段
	强度	平均特征路径长度	平均聚类系数		强度	平均特征路径长度	平均聚类系数
抑郁组	35.91 ± 4.34	6.57 ± 1.60	0.22 ± 0.05		37.61 ± 4.24	6.67 ± 1.54	0.22 ± 0.05
对照组	35.39 ± 5.51	5.49 ± 0.88	0.17 ± 0.02		35.38 ± 5.55	5.43 ± 0.94	0.17 ± 0.02
P	0.020	0.018	0.002		0.013	0.012	0.001

从表 1 中可以看出，抑郁组 α 频段的参数值均比 θ 频段的高，而且抑郁组的参数值比对照组的高。经过 t 检验分析，发现两组受试者在强度、平均特征路径长度、平均聚类系数上的差异都具有统计学意义（P < 0.05）。

3.2.2. 网络参数优化结果

本研究以平均聚类系数为例，构建了多重阈值和网络参数值之间的关系。如图 9 所示，一个比例阈值对应了一个网络参数，通过求得网络参数的 AUC 作为优化后的分类特征。

图 9.

Relation graph of proportional threshold and network parameters

比例阈值和网络参数关系图

最终，两组受试者在不同频段下网络参数的 AUC 如表 2 所示。

表 2. AUC of the depression group and the normal group with different network parameters.

抑郁组和正常组在不同网络参数下的 AUC

分组	AUC
	θ 频段				α 频段
	强度	平均特征路径长度	平均聚类系数		强度	平均特征路径长度	平均聚类系数
抑郁组	134.47 ± 17.50	0.63 ± 0.15	0.04 ± 0.01		135.26 ± 14.17	0.53 ± 0.08	0.04 ± 0.01
对照组	121.97 ± 16.83	0.64 ± 0.15	0.03 ± 0.01		123.23 ± 18.15	0.52 ± 0.09	0.03 ± 0.01
P	0.002	0.024	0.012		0.003	0.015	0.012

通过多重阈值和网络参数值之间的关系可以看出，提取网络参数的 AUC 作为特征不仅能反映整体特征稳定的变化趋势，还能减少个体差异性带来的影响。但是这也可能忽略了特征最为明显的部分，不利于从生物机制的角度进行分析。

3.3. 分类结果和性能

为了对两组受试者进行分类，分别提取整体的网络参数和优化后的网络参数作为特征，并构建了 6 个特征矩阵，利用支持向量机（support vector machine，SVM）算法进行分类，并采用留一交叉验证法（高斯核函数）作比较。如表 3 所示，从整体来看，将优化后的参数作为分类特征，精度都有所提升，其中 α 频段下的分类精度都高于 θ 频段。从参数优化前后的分类效果来看，在 θ 频段下，使用强度的 AUC 进行分类，精度只提升了 2%，使用平均特征路径长度的 AUC 进行分类，精度提升了 11%，使用平均聚类系数的 AUC 进行分类，精度则提升了 18%；在 α 频段下，使用强度的 AUC 作为特征，精度比优化前提升了 7%，使用平均特征路径长度的 AUC 作为特征，精度提升了 13%，使用平均聚类系数的 AUC 作为特征，精度提升了 10%。

表 3. Classification results of SVM in θ、α frequency band.

SVM 在 θ、α 频段下的分类结果

特征	θ 频段				α 频段
	灵敏性	特异性	精度		灵敏性	特异性	精度
强度	50%	38%	69%		56%	88%	72%
平均特征路径长度	94%	38%	66%		63%	75%	69%
平均聚类系数	81%	19%	50%		59%	71%	65%
强度 AUC	71%	71%	71%		76%	82%	79%
平均特征路径长度 AUC	77%	55%	77%		91%	73%	82%
平均聚类系数 AUC	94%	41%	68%		81%	69%	75%

4. 讨论

本研究将功能连接网络和网络参数的优化应用于抑郁症患者的分类研究中。通过使用 PLV 方法计算 64 导联 EEG 信号的邻接矩阵，并构建脑网络，可以将非线性的 EEG 信号转换为更加直观的网络参数，不仅有利于对信号的进一步研究，对临床诊断抑郁症也具有辅助作用。为了验证网络参数作为特征的有效性，对于选取的 32 个独立样本（抑郁组 16 个，对照组 16 个），分别在 θ、α 频段下计算了脑功能网络的强度、平均特征路径长度和平均聚类系数，然后使用 SVM 分类器，同时采用留一交叉验证法进行分类，但实际分类精度并不是很高。因此，为了改善分类效果，本研究使用比例阈值对网络参数进行全局优化，将在多重阈值下网络参数的 AUC 作为新特征并进行分类。结果显示，对 θ、α 频段处的三种网络参数进行特征优化，分类精度均有明显提高，这表明该方法不仅减少了单个阈值对网络参数的扰动性，还增加了全局特征的稳定性。

本研究需要指出的是，计算网络参数的 AUC 作为优化方法，虽然能够有效地提升分类精度，但是无法用于研究极端条件下的特异性质。从另一个角度说，这是一种特征的处理和选择过程，因此该方法更适用于提升人机交互下诊断疾病的准确率与测试的稳定性。另外，该方法作为计算机辅助诊断技术来说也是可行的，可若在实际使用时遇到无法解决的极端情况，需要进一步细化数据，即从全局到局部对脑网络进行分析。

在研究中已发现抑郁组和对照组的连接密度和强度在额区、颞区、枕区有较大差异，为了进一步的深入分析，后续将会着重于对不同脑区的研究，并计算其网络参数，从而细化不同脑区的参数特征，并研究比例阈值的变化对局部网络参数值的影响，进而提升分类效果，提高临床辅助诊断的质量。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

江苏省科技厅社会发展项目（BE2018638）；常州市社会发展项目（CE20195025）；首批中外合作办学平台联合科研项目“人机智能与交互国际联合实验室”；江苏省研究生培养创新计划项目（KYCX20_2559）